Abstract
Abnormally high shear stresses encountered in vivo induce spontaneous activation of blood platelets and formation of aggregates, even in the absence of vascular injury. A three-dimensional multiscale computational model—platelet adhesive dynamics—is developed and applied in Part I and Part II articles to elucidate key biophysical aspects of GPIbα-von-Willebrand-factor-mediated interplatelet binding that characterizes the onset of shear-induced platelet aggregation. In this article, the hydrodynamic effects of the oblate spheroidal shape of platelets and proximity of a plane wall on the nature of cell-cell collisions are systematically investigated. Physical quantities characterizing the adhesion probabilities between colliding platelet surfaces for the entire range of near-wall encounters between two platelets are obtained for application in platelet adhesive dynamics simulations of platelet aggregation explored in a companion article. The technique for matching simulation predictions of interplatelet binding efficiency to experimentally determined efficiencies is also described. Platelet collision behavior is found to be strikingly different from that of spheres, both close to and far from a bounding wall. Our results convey the significant effects that particle shape and presence of a bounding wall have on the particle trajectories and collision mechanisms, collision characteristics such as collision time and contact area, and collision frequency.
INTRODUCTION
Platelets flow close to the endothelial lining of the blood vessel wall and periodically contact the lumenal surface, thereby providing a means for surveillance of the endothelial surface for lesions and irregularities. These microscopic disk-shaped blood cells remain dormant until induced by either physiological or pathological phenomena to activate and initiate thrombosis. In the event of a vascular injury, platelets are recruited from the bloodstream to the injured site, where they assemble to form the bulk of the hemostatic plug that seals off the lesioned area and curtails blood loss.
Initial platelet binding to the exposed subendothelial surface at the injured vascular region involves the association of GPIbα with subendothelial collagen-bound von Willebrand factor (vWF). von Willebrand factor exists in plasma in a range of sizes, each molecule containing varying numbers of repeating identical subunits ranging from 2 (500 KDa; vWF dimer) to 80 (20,000 KDa; ultralarge vWF (ULVWF)) (1–3). Under normal conditions, in the absence of a vascular injury, platelets interact with circulating plasma vWF minimally in blood. However, under conditions of pathological shear stress (>80 dyn/cm2) typical of stenosed regions of the vasculature, plasma vWF spontaneously (i.e., in the absence of exogenous chemical agonists or exposed subendothelium) binds to platelet GPIbα receptors, causing platelet activation, and subsequent platelet aggregation via platelet integrin receptor αIIbβ3-vWF binding resulting in formation of shear-induced platelet thrombi (4–6). Such thrombi can occlude the narrowed lumen of atherosclerosed coronary or cerebral arteries, obstructing blood flow and causing ischemic heart disease or stroke. Notably, shear-induced platelet-vWF aggregate formation has been found to occur at significantly lower shear stresses (>15 dyn/cm2) in vitro with ULVWF; at this stress level binding of platelets with normal vWF is not observed (1). The kinetics of vWF binding to circulating platelets is thus expected to be a function of shear rate and vWF multimer size.
Few attempts have been made to develop computational models to elucidate the individual and combined influence of hydrodynamic shear flow, platelet shape, presence of bounding walls, and receptor-ligand molecular binding kinetics, on physiological and pathological thrombus formation. Theoretical fluid mechanical studies of three-dimensional multiparticle nonspherical particulate (ellipsoidal) flows (7–9), especially for bounded flows, are much less commonly available than those for spheres, since it is much more challenging to determine hydrodynamic interactions between two or more nonspherical shapes in an unbounded or bounded region than between spherical particles. This accounts for the relative abundance of fluid mechanical solutions in the literature for flow of spheres in a variety of boundaries and shear flow conditions, which have been adapted by biomedical researchers for studying blood-cell adhesive phenomena (10–14). Sphere-sphere collisions have been well characterized in an unbounded medium and well-defined collision frequency parameters have been computed taking into consideration the influence of hydrodynamic interactions between particles (10). Activated platelets are somewhat spherical in shape, although they have a rough surface with many filopodia extending in different directions. However, unactivated platelets are far from spherical in shape, instead appearing as flattened ellipsoids. Such a vast difference in shape is expected to influence the manner in which the cells collide, their frequency of collision, collision contact time, collision contact area, and the magnitude of shear and normal forces acting on the platelet(s) and on interplatelet bonds formed between two cells (15).
We have developed a new numerical simulation model called platelet adhesive dynamics (PAD) to study platelet-platelet collisions and formation of platelet aggregates in linear shear flow near a bounding wall. Since platelet (oblate-spheroid) collisions have not been adequately characterized to date, the PAD model is used to perform a comprehensive characterization of the collision behavior of two flowing platelets subjected to linear shear flow in the presence of a bounding wall. In small arteries and arterioles, red blood cells (RBCs) concentrate within the core of the vessel and push platelets toward the wall periphery. Our studies of platelet-platelet interactions are confined to the region of flow adjacent to the vessel wall within the cell-depleted plasma layer where RBCs are primarily absent, and accordingly the presence of RBCs was not incorporated into our simulations. The hydrodynamic effects of the proximity of a planar wall and the specific effects of particle shape (oblate spheroid versus sphere) on collision phenomena in linear shear flow are quantified by determining various collision metrics such as collision frequency, collision contact time, and platelet surface area that enters the contact region during a collision.
The adhesive dynamics model, as developed by Hammer and Apte (14) and modified by King and Hammer (16), is adapted here for a different cell-surface geometry and a uniquely different binding algorithm to study the transient binding interactions mediated by GPIbα-vWF-A1 associations between two platelets flowing in solution at pathologically high shear rates. Knowledge of the hydrodynamic interactions between platelets during brief encounters in flow and quantified metrics of the same describing the physics of platelet-platelet collisions facilitates the development of a method to validate the predicted aggregation behavior of two platelets that involves comparing simulated binding efficiencies with experimentally observed efficiencies tabulated in the literature (17,18). The effects of different vWF multimer sizes and experimentally determined normal and platelet-type VWD GPIbα-vWF-A1dissociation binding kinetics on platelet transient aggregation behavior is studied using PAD. Our simulation predictions of adhesive phenomena provide insight into the biophysical mechanisms of pathological platelet-vWF association in solution as opposed to at the subendothelial surface, typical of disease conditions such as TTP and 2B/platelet-type VWD.
The development and application of PAD to study the transient aggregation of two platelets is described in our Part I and Part II articles. Part I details the hydrodynamic flow model and relevant flow geometry, the qualitative and quantitative characteristics of hydrodynamic collision encounters between two platelets, and the derivation of collision metrics necessary for application of the PAD model to simulate platelet-platelet binding. We studied the influence of a bounding wall on the physics of platelet-platelet collisions, and quantified with respect to proximity of the wall, collision rate, collision contact time, surface contact areas on both platelets, and other metrics to 1), provide a clear picture of the physical mechanisms taking place during particle encounters, and 2), facilitate comparison among collisions between two particles in different geometries. The method employed for matching the predicted platelet aggregation behavior with that quantified by experimental means (17,18) is also described in Part I. Part II (in this issue) discusses the development of the adhesion model of the transient formation of GPIbα-vWF-GPIbα bond bridges between two platelets flowing in linear shear flow near a planar surface at high shear rates. The application of PAD to discern the influence of vWF size and binding kinetic parameters on interplatelet binding phenomena at high shear rates >4000 s−1 is covered in the second article.
METHODS
Our multiscale numerical simulation of multiplatelet adhesive dynamics and three-dimensional (3-D) particle motion in shear flow includes hydrodynamic interactions between moving and stationary surfaces, and is comprised of two distinct yet interconnected algorithms: 1), adhesive dynamics calculations, and 2), hydrodynamic mobility calculations. The general methodology used for conducting multiplatelet adhesive dynamics simulations near a bounding surface closely follows the multiparticle adhesive dynamics model developed by King and Hammer (16) to study the influence of hydrodynamic interactions between flowing and bound leukocytes on the selectin-mediated rolling properties of these cells on a surface. Briefly, the solution technique first involves calculation of all forces and torques acting on each particle in the fluid system, such as forces due to gravity, bond forces resulting from stretching or compression of bond springs, and repulsion between two surfaces in close proximity. This is followed by numerical solution of a set of relevant fluid mechanical equations that solve the mobility problem, in which the forces and torques acting on the particles are specified, along with the external far-field flow, and the rigid body motions, i.e., the translational and rotational velocities of these particles, are determined. Although a comprehensive exposition of the general algorithm has been documented by King and Hammer (16), a succinct description of the same is provided here. A detailed description of the adhesive dynamics model for platelet-von Willebrand factor and platelet-platelet binding that includes all assumptions made and their respective justifications is presented in Part II.
Hydrodynamic calculations
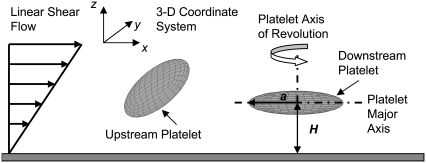
The hydrodynamic problem involves the creeping motion of two rigid oblate spheroid particles in a semi-infinite three-dimensional domain, D, bounded by an infinite plane at z = 0 (Fig. 1). Individual particle size was fixed at 2 × 2 × 0.5 μm3, with a platelet major radius of a = 1 μm. The Reynolds number of this system was calculated as NRE = 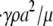 = O(10−2) < 1, where
= O(10−2) < 1, where 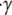 = 10,000 s−1 is the shear rate, a = 1 μm is the particle radius, ρ = 1.0239 g/cm3 is the density of blood plasma, and μ = 1.2 cP is the viscosity of plasma. The flow is well within the Stokes regime. The Stokes equation is
= 10,000 s−1 is the shear rate, a = 1 μm is the particle radius, ρ = 1.0239 g/cm3 is the density of blood plasma, and μ = 1.2 cP is the viscosity of plasma. The flow is well within the Stokes regime. The Stokes equation is
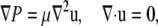 |
(1) |
where u is the velocity, P is the pressure, and μ is the viscosity of the fluid. The ambient flow is linear shear,
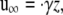 |
(2) |
where 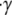 is the shear rate and z is the distance from the infinite flat wall (Fig. 1). The no-slip condition on all surfaces is assumed. At the surface of the wall (z = 0), the velocity is zero,
is the shear rate and z is the distance from the infinite flat wall (Fig. 1). The no-slip condition on all surfaces is assumed. At the surface of the wall (z = 0), the velocity is zero,
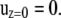 |
(3) |
At the spheroid surface, the velocity consists only of the rigid body motion of the particle,
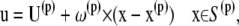 |
(4) |
where U(p) is the translational velocity, ω(p) is the rotational velocity, and x(p) is the centroid of platelet particle p.
FIGURE 1.
Schematic diagram showing two platelets translating and rotating in shear flow near an infinite plane wall. The major radius, a, and centroid height, H, are defined as is the coordinate system and flow direction.
The completed double layer-boundary integral equation method (CDL-BIEM) (19), a boundary elements solution technique to solve the integral representation of the Stokes equation, was used to solve Eqs. 1–4. The platelet surface was discretized into 384 QUAD9 elements (depicted in Fig. 1), giving rise to 1538 nodal points on each platelet. The integral representation of the Stokes equation is shown below.
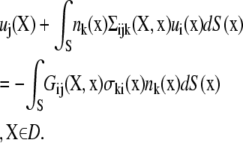 |
(5) |
Here, Gij is the singularity solution due to a point force on the bounding surface, S, at x acting in the j direction in the fluid. n is the normal at x and points out of the particle and into the fluid. σ is the stress tensor and is given by
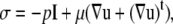 |
(6) |
where superscript t denotes the transpose operator and I is the identity matrix. Σijk is the ikth component of the stress tensor corresponding to flow produced by a point force at x in the j direction. The solution method as described by Phan-Thien et al. (20) for particulate flow near a plane wall is followed here. The integration is carried out over the bounding surface, S = 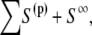 where S∞ is the infinite plane, S(p) is the bounding surface of particle p = 1,…,N, where N is the number of particles in domain D. The integrals on the RHS and LHS of Eq. 5 are known as the single-layer and double-layer potentials, respectively, based on analogy with electrostatic potential theory. Equation 5 is termed a boundary integral equation (BIE) when X is evaluated at the particle surface (i.e., X ∈ S(p)). It has been shown that a BIE containing only the single-layer potential is sufficient to represent the Stokes disturbance flow problem for particles undergoing rigid body motion. However, this integral equation takes the form of a Fredholm integral equation of the first kind, which for a mobility problem is generally ill-posed and becomes increasingly numerically unstable for more refined boundary element meshes (19). An alternative formulation of the integral Stokes equation involves only the double-layer term. This double layer representation, by itself, is incapable of exerting any force or torque on the fluid and possesses null solutions; this results in an indeterminate system. Power and Miranda (21) addressed the shortcomings of the double layer and developed a solution technique to complete the double-layer representation. To complete the range, they incorporated into the integral representation a velocity field arising from a known distribution of point forces and torques placed at the center of each particle. The null space of the double-layer kernel has a dimension of 6N, each null solution corresponding to the rigid body motion of each particle. Power and Miranda coupled the forces and torques acting at the center of each particle with the null solutions on the particle surfaces to produce 6N additional linearly independent equations needed to make the double-layer density fully determinate, i.e., to obtain a unique solution. Successive convergence of the iterative equation is possible only after appropriate (mathematical) deflation of the endpoint +1 eigenvalue (19). The final form of the boundary integral equations is
where S∞ is the infinite plane, S(p) is the bounding surface of particle p = 1,…,N, where N is the number of particles in domain D. The integrals on the RHS and LHS of Eq. 5 are known as the single-layer and double-layer potentials, respectively, based on analogy with electrostatic potential theory. Equation 5 is termed a boundary integral equation (BIE) when X is evaluated at the particle surface (i.e., X ∈ S(p)). It has been shown that a BIE containing only the single-layer potential is sufficient to represent the Stokes disturbance flow problem for particles undergoing rigid body motion. However, this integral equation takes the form of a Fredholm integral equation of the first kind, which for a mobility problem is generally ill-posed and becomes increasingly numerically unstable for more refined boundary element meshes (19). An alternative formulation of the integral Stokes equation involves only the double-layer term. This double layer representation, by itself, is incapable of exerting any force or torque on the fluid and possesses null solutions; this results in an indeterminate system. Power and Miranda (21) addressed the shortcomings of the double layer and developed a solution technique to complete the double-layer representation. To complete the range, they incorporated into the integral representation a velocity field arising from a known distribution of point forces and torques placed at the center of each particle. The null space of the double-layer kernel has a dimension of 6N, each null solution corresponding to the rigid body motion of each particle. Power and Miranda coupled the forces and torques acting at the center of each particle with the null solutions on the particle surfaces to produce 6N additional linearly independent equations needed to make the double-layer density fully determinate, i.e., to obtain a unique solution. Successive convergence of the iterative equation is possible only after appropriate (mathematical) deflation of the endpoint +1 eigenvalue (19). The final form of the boundary integral equations is
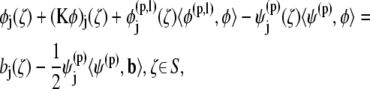 |
(7) |
where φj is the unknown surface density of the double-layer distribution, 𝒦 stands for the double-layer surface integral operator, 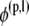 are the orthonormalized null solutions corresponding to the translational (l = 1, 2, 3) and rotational (l = 4, 5, 6) motions of particle p, and the angled brackets represent the inner product
are the orthonormalized null solutions corresponding to the translational (l = 1, 2, 3) and rotational (l = 4, 5, 6) motions of particle p, and the angled brackets represent the inner product 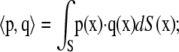 p takes on values from 1 to N, l takes on values from 1 to 6,
p takes on values from 1 to N, l takes on values from 1 to 6, 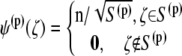 are the orthonormalized eigenvectors of the adjoint operator K†,
are the orthonormalized eigenvectors of the adjoint operator K†,
 |
where F(α) and T(α) are the force and torque acting on cell α at the center of mass 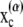 of the particle, and
of the particle, and 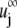 is any ambient fluid velocity that is a valid solution of the Stokes equation.
is any ambient fluid velocity that is a valid solution of the Stokes equation.
These equations are solved by successive iteration for φ. Once the double-layer density, φ, is determined, the surface velocity field can be obtained as follows:
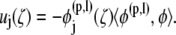 |
(8) |
By taking the inner product of Eq. 8 and φ(n,m) (n = 1,…,N; m = 1,2,3,4,5,6), the rigid body motion of particle n can be extracted. Once the translational and rotational velocities of the particles are obtained, positions of nodal points on each particle surface, centroid of each particle, and bond endpoints are updated and the simulation proceeds to the next time step.
Maul et al. (22) carried out an experimental and computational study of the sedimentation of “platelets” (hexagonal flakes) near a wall at low Reynolds numbers to verify the reliability of CDL-BIEM for predicting particle-wall hydrodynamic interactions for the case of a platelet shape, which has two disparate length scales. They showed that this computational method remains efficient and stable and gives good agreement with the experimental results. Further, we extensively validated the flow behavior of a platelet near a wall as predicted by this numerical technique (23). We found excellent agreement between 1), the numerical results of Maul et al. (22), 2), the analytical results of Kim et al. (24), and 3), the analytical solution of Jeffery (25), and our theoretical predictions of platelet 3-D motion near a wall in both quiescent fluid and linear shear flow (23).
Short-range repulsive force calculations
Both particle and wall surfaces were coated with a steric layer to model the glycocalyx layer and surface roughness of biological cells (16), and also to account for the presence of finite-sized vWF molecules bound to the platelet surface. This surface roughness layer comprises bumpy regions with a maximum thickness of 50 nm. It was assumed that fluid could easily pass through this layer, causing no or minimal modification to the existing flow field. In other words, the glycocalyx layer is assumed to be a layer on the cell surface that has negligible hydrodynamic effects, such that the platelets' bounding surfaces that hydrodynamically influence the flow of nearby cells can exclude the thickness of the glycocalyx. A very short-range repulsive force that acts between the outer edges of the surface roughness layers or glycocalices was included in the model to account for nonspecific short-range interactions, such as electrostatic repulsion, that strongly dominate when cell membranes, glycocalices, or glycoproteins contact each other (26). This contact force is an empirical relationship of the form
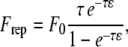 |
(9) |
where F0 = 500 pN·m, τ = 2000 μm−1, and ɛ is the surface-to-surface separation based on the distance between the tips of the opposing surface roughness layers (16). This repulsive force is directed along a line segment connecting the two nodes on either of the two opposing surfaces that are in closest proximity to each other. At distances <20 nm between the interacting surfaces, the magnitude of repulsive force exerted becomes significant. At 15 nm separation, the repulsive force is 0.0374 pN, which is approximately two times the Stokes drag force on a 1-μm-diameter sphere sedimenting at 1 μm/s in a fluid of viscosity 1 cP. Bell et al. also used an exponential relation, albeit of a different form, to empirically model the distance-dependent nonspecific interaction energy that results in a net repulsion between the cell-cell surfaces (27). For purely hydrodynamic simulations, a thinner steric layer of 40 nm was provided on each surface to model the glycocalyx and surface roughness of the cells, and also to prevent any surface overlap during a collision encounter between two surfaces. Note that except for the calculation of repulsive force acting between two opposing surfaces, the separation distance between the two surfaces was always measured from the edges of the “real” surfaces and not from the outer edge of the steric layers on these surfaces.
Numerical implementation
The CDL-BIEM code was written in Fortran 95 and double-precision was used for all calculations. Simulations were executed on dual-core AMD-Opteron SUNFire X2100 (2.4 GHz) processors. Runtime was a function of the time step, shear rate, and number of iterations required for results to converge at each time step. Integration of the double layer during simulations showed rapid convergence, with usually two iterations necessary to obtain a relative error <0.0005, when the particles were not within reactive contact distance. We used an initial time step of 10−6 s for nonadhesive platelet mobility calculations and 10−7 s for platelet aggregation simulations, since the stiffness of the bond springs increases the sensitivity of numerical calculations to changes in cell position. For simulations of platelets undergoing reactive collisions (aggregation), the time step was allowed to dynamically change depending on the level of difficulty encountered during convergence of the double layer calculations. Specifically, the time step was reduced by an order of magnitude whenever the number of fixed-point iterations required for attaining convergence increased by 100. Hydrodynamic collisions without reaction could be resolved even at the smallest particle-particle separation distances without requiring reduction in the time step. Explicitly added lubrication forces to compensate for numerically underpredicted lubrication effects were disregarded in our model, since the distances over which the lubrication approximation becomes important are less than the surface roughness layer of thickness 50 nm.
The most stable orientation for unactivated platelets in linear shear flow is with their major axis parallel to the surface (horizontal orientation). Platelet rotational velocity in linear shear flow is highly nonlinear with respect to its orientation; the rotational velocity is large when the axis of revolution of the platelet becomes nearly parallel to the flow direction. Thus, platelets remain in nonhorizontal orientations for rather short periods of time as compared to the time in which they maintain stable horizontal orientations (23). Hence, all simulations were started with initial platelet orientations such that the axes of revolution of both platelets were perpendicular to the surface. Effects of gravity on platelet motion near the vessel wall were neglected because of the disparate timescales of the settling time of cells under gravity versus travel time in the direction of shear flow. An order-of-magnitude estimate of the relative difference in timescales can be obtained by comparing the Stokes settling velocity of a sphere of equivalent platelet volume in plasma with the velocity of a freely flowing object in linear shear flow at a distance of 1.5 μm from the vessel surface. The Stokes settling velocity is given by 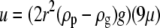 = 0.0293 μm/s, where μ = 1.2 cP is the viscosity of plasma, r = 0.63 μm is the volume-equivalent spherical radius of a platelet, ρg = 1.0239 g/cm3 is the density of plasma, and ρp = 1.0645 g/cm3 is the density of human platelets (28). The flow velocity at 1.5 μm from the wall at a linear shear rate of 4000 s−1 is 6000 μm/s, which is O(105) larger than the Stokes settling velocity. This justifies the neglect of gravity at high shear rates. Note that the presence of the wall will further reduce the Stokes velocity in any direction of settling.
= 0.0293 μm/s, where μ = 1.2 cP is the viscosity of plasma, r = 0.63 μm is the volume-equivalent spherical radius of a platelet, ρg = 1.0239 g/cm3 is the density of plasma, and ρp = 1.0645 g/cm3 is the density of human platelets (28). The flow velocity at 1.5 μm from the wall at a linear shear rate of 4000 s−1 is 6000 μm/s, which is O(105) larger than the Stokes settling velocity. This justifies the neglect of gravity at high shear rates. Note that the presence of the wall will further reduce the Stokes velocity in any direction of settling.
Matching simulation predictions to experimental results
Huang and Hellums (17) determined the overall collision efficiency, ηc, of platelets aggregating at high shear rates by fitting parameters of the mathematical expression derived for aggregation rate as determined from the population balance equation (PBE) to the experimental observations of shear-induced platelet aggregation. Platelets were modeled as rigid spheres, and the Smoluchowski equation for predicting the collision frequency of spherical particles in linear shear flow assuming linear particle trajectories was multiplied by the collision efficiency parameter, ηc, to generate a coalescence kernel. To distinguish the cell-cell “binding efficiency” from the hydrodynamic effects between particles in flow, one must account for a corrective factor called the “hydrodynamic efficiency”, ηh, that provides a measure of the effect of hydrodynamic interactions between spheres on the collision outcome of particles encountering one another in unbounded shear flow. The collision frequency for two spherical particles flowing in linear shear flow far from any bounding surfaces was compared for the cases of linear spherical (Smoluchowski) trajectories, with no interparticle hydrodynamic effects, versus particle trajectories influenced by hydrodynamic interactions between spheres (reactive collision gap defined as 128 nm). The collision frequency (Eq. 12) for spherical particle trajectories influenced by hydrodynamic interactions was found to be 0.53 times that for flowing spheres that possessed linear trajectories, yielding the “hydrodynamic efficiency” for this system, ηh = 0.53. By dividing the overall collision efficiency by this factor, we obtain the binding efficiency of all particles that undergo collisions. Konstantopoulos et al. (29) experimentally measured the fraction of suspended platelets that bound large vWF multimers when subjected to high shear rates. For n colliding platelets, the total number of all possible collisions = 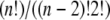 or nC2. The number of all possible collisions between vWF-positive platelets is n+C2, and the number of collisions between vWF-negative platelets is n−C2, where subscripts n+ and n− denote the total numbers of vWF-positive and vWF-negative platelets, respectively. The total number of all possible collisions that can occur between a vWF-positive platelet and a vWF-negative platelet = (n+)(n−). Collisions that occur between two vWF-negative platelets will not result in any kind of binding between the two cells, whereas in all other cases, there is a finite probability for platelet-platelet binding. Table 1 reproduces the results of Huang and Hellums (17) and illustrates the stepwise method employed to estimate the binding efficiency between a vWF-positive platelet and a vWF-negative platelet.
or nC2. The number of all possible collisions between vWF-positive platelets is n+C2, and the number of collisions between vWF-negative platelets is n−C2, where subscripts n+ and n− denote the total numbers of vWF-positive and vWF-negative platelets, respectively. The total number of all possible collisions that can occur between a vWF-positive platelet and a vWF-negative platelet = (n+)(n−). Collisions that occur between two vWF-negative platelets will not result in any kind of binding between the two cells, whereas in all other cases, there is a finite probability for platelet-platelet binding. Table 1 reproduces the results of Huang and Hellums (17) and illustrates the stepwise method employed to estimate the binding efficiency between a vWF-positive platelet and a vWF-negative platelet.
TABLE 1.
Calculation of binding efficiency for two colliding platelets
| 1 Shear rate, γ (s−1) | 2 Collision efficiency, ηc (17) | 3 Binding efficiency, ηb = ηc/ηh, where ηh = 0.53 | 4 Fraction of platelets that are L-vWF+ (29) f | 5 Fraction of all possible collisions that are between L-vWF+ platelets only = 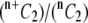 ∼ f2 when n is large ∼ f2 when n is large |
6 Fraction of all possible collisions that are between L-vWF+ and L-vWF− platelets = 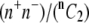 ∼ 2f(1 − f) when n is large ∼ 2f(1 − f) when n is large |
7 ηb specific for collisions between L-vWF+ and L-vWF− platelets = column 3/column 6 |
|---|---|---|---|---|---|---|
| 4500 | 0.0015 | 0.0028 | 0.035 | 0.0012 | 0.068 | 0.041 |
| 5400 | 0.0018 | 0.0034 | 0.038 | 0.0014 | 0.073 | 0.047 |
| 6300 | 0.0037 | 0.0070 | 0.040 | 0.0016 | 0.077 | 0.091 |
| 7200 | 0.0044 | 0.0083 | 0.041 | 0.0016 | 0.079 | 0.105 |
| 7700 | 0.008 | 0.0151 | 0.041 | 0.0016 | 0.079 | 0.191 |
| 8000 | 0.01 | 0.0189 | 0.042 | 0.0017 | 0.080 | 0.236 |
Important assumptions that were made in the development of Table 1 are listed below:
A 1:1 correlation is assumed between transient platelet-platelet binding and platelet aggregation, i.e., the fraction of collisions that result in interplatelet contact via GPIbα-vWF bonds during a collision is assumed to result in the formation of permanent aggregates via αIIbβ3-vWF binding or any other receptor-ligand binding that mediates permanent platelet-platelet aggregation.
For the calculation of binding efficiency between two colliding platelets, it is assumed that all possible combinations of collisions took place over the duration of the shear-induced platelet aggregation experiments carried out by Huang and Hellums, which ranged from 20 to 100 s.
RESULTS
We first examined the effects of particle shape and the influence of the proximity of a plane surface (vessel wall) on platelet collisions in shear flow before studying the biophysical aspects of platelet-platelet bridging via formation of GPIbα-vWF-GPIbα bonds. Metrics that define important characteristics of platelet collisions relevant to this study are collision frequency, contact duration during a collision, and extent of surface area on each colliding platelet that enters the particle-particle reactive zone. The latter two characteristics of a two-particle collision can be combined to produce a metric called the time-integral of contact area that is an indicator for the probability of an adhesion event between the two blood cells that briefly encounter each other during flow. Adequate knowledge of the physics of cell collisions and contacting lends insight into the biophysical aspects of cell-cell binding in a flow environment and enables quantitative comparisons to be drawn regarding effects of particle shape, presence of bounding walls, and initial particle flow trajectories on the outcome of adhesive interactions between flowing cells.
Hydrodynamic collisions between platelets: effects of particle shape and proximity of a plane wall when flow is symmetric about the flow plane
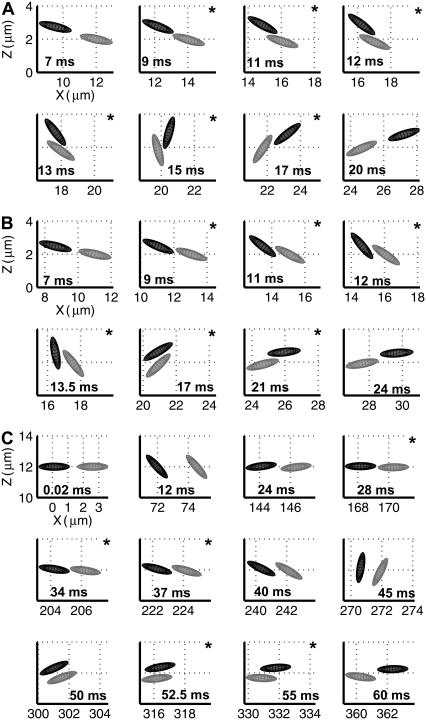
We first studied the characteristics of hydrodynamic encounters between two platelets in linear shear flow for those cases in which flow is symmetric about the xz plane (plane of flow; Fig. 1), i.e., the distance in the y-direction (normal to the flow plane) between the centroids of both platelets is zero throughout the duration of flow. A hydrodynamic encounter of one platelet with another platelet is defined as a “collision” if, during flow, the two platelets come within reactive binding distance to each other. During a collision, the platelet surfaces need not necessarily have physically come into contact. The reactive distance between the two platelets was set at 260 nm for this set of platelet flow simulations (adhesion absent). The reactive gap of 260 nm was calculated based on the total bond length of two GPIbα receptor molecules bound to a single vWF multimer of average size that bridges the two receptors on different platelets by forming a bond at either endpoint of the multimer. For the case of symmetric flow about the xz plane, platelet-platelet collisions were observed to occur through several distinct mechanisms. Sphere-sphere collisions, on the other hand, are characterized by a single mechanism in which the faster-flowing sphere collides with and rolls over the slower-flowing sphere. The naming convention for the two platelet particles is explained in Fig. 1. One mechanism of collision between two platelet particles is here termed a “glide-over” mechanism (Fig. 2 A), which is characterized by the upstream, or faster-flowing, platelet flowing over the downstream, or slower, platelet and thereby reactively contacting it, followed by simultaneous rotation and separation of the two platelets. In the “glide-under” mechanism of collision, the upstream platelet flows to a limited extent beneath the downstream platelet as a result of simultaneous rotation, and then rotates with the first and separates (Fig. 2 B). A third mechanism is characterized by intermittent contacting and occurs when the platelets begin flow at approximately the same height. Here, one observes a succession of contacting followed by a brief period of no contact that lasts for several rotations (Fig. 2 C). The mechanisms of platelet collisions are not limited to the three examples described here. These particular three were described because they are representative of many platelet collisions and demonstrate the considerable differences between sphere-sphere collisions and platelet-platelet collisions. The mechanism by which a platelet collision takes place depends on the initial distance between the platelets in the velocity, the velocity gradient, and the vorticity direction, i.e., in the x, y, and z directions.
FIGURE 2.
Three series of sequential frames depicting the different mechanisms observed for collisions between two platelets when flow is symmetric about the flow plane. (A) Glide-over mechanism. (B) Glide-under mechanism. (C) Intermittent-contact mechanism. Frames containing a star in the right-hand upper corner indicate that the two platelets depicted are within reactive contact distance of each other. The times during flow corresponding to the particle orientations are indicated in the respective frames. The imposed fluid shear rate is 500 s−1.
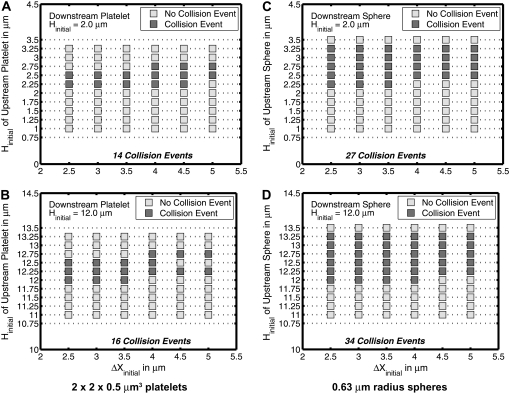
We tested an entire range of starting positions of two platelets that allowed for symmetric flow about the flow plane, to determine the starting configurations that resulted in a platelet-platelet collision. Fig. 3, A and B, conveys the relative starting positions of two platelets that bring about a collision, as well as starting configurations that do not lead to close encounters that could result in interplatelet binding, and includes both situations in which 1), the wall has a dominating effect on platelet flow trajectories, and 2), wall effects are negligible. The same sets of initial conditions were repeated for two spherical particles, in which the particle volume was set equal to that of a platelet (sphere of radius 0.63 μm) (Fig. 3, C and D). Fig. 3, A–D, shows that sphere-sphere collisions appear to be approximately twice as numerous as platelet-platelet collisions when the flow is symmetric about the flow plane, i.e., the Δy gap between the two hydrodynamically interacting particle centroids is 0. Also, the occurrence of a particle-particle collision is observed to be less frequent closer to the surface than farther from the surface. The wall clearly has strong hydrodynamic effects on collision outcomes, because particles that would collide when their initial relative positions are far from the surface, do not necessarily do so when the cells are brought in close proximity to the wall.
FIGURE 3.
Plots of the initial configurations of two particles in linear shear flow that either do or do not result in a collision. For all configurations shown in these plots, the initial difference between the particle centroids in the y-direction is zero. The downstream platelet was given a starting height, as indicated in the individual plots, that was not varied over the range of initial configurations. The upstream platelet position was varied in both the x- and the z-direction. The abscissa in all plots is the initial difference in the x-direction between both platelet centroids. (A) Plot for initial platelet-platelet configurations near the wall. (B) Plot for initial platelet-platelet configurations far from the wall. (C) Plot for initial sphere-sphere configurations near the wall. (D) Plot for initial sphere-sphere configurations far from the wall.
Characteristics of platelet-platelet collisions: effect of proximity of the wall
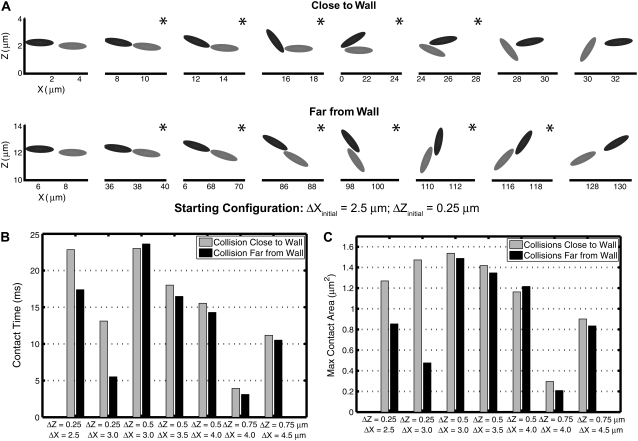
We quantified certain important aspects of platelet-platelet collision events whose starting configurations are marked by dark gray boxes in Fig. 3, A and B. We examined individual platelet trajectories, time duration of cell-cell contact during a collision, average surface area of contact, maximum instantaneous area of contact with respect to each platelet, and the time integral of the contact area for each platelet. The latter quantity provides, from a flow perspective, a measure of the adhesion probability between the two cell surfaces. It was apparent from the visualization of colliding platelet trajectories and comparison of the quantified metrics that the influence of the wall on the collision outcome was significant for certain initial configurations, but minimal for other configurations. The influence of wall proximity was found to be more important for initial configurations in which the relative distance between the two platelet centroids in the z-direction was smaller, i.e., 0.25 μm. Fig. 4 A shows the time evolution of motion of two colliding platelets close to and far from the wall for an initial configuration in which the platelets were placed 2.5 μm apart in the x-direction and 0.25 μm apart in the z-direction at the start of the simulation. These two representative collision trajectories are qualitatively different. The difference between the mechanisms of collision close to and far from the wall is clearly visible in Fig. 4 A. During the collision occurring close to the surface, the upstream platelet pivots about one end of the downstream platelet, and after rotating, slides over the platelet and then flows away. When far from the surface, the colliding platelets are observed to rotate together with a slight overlap of the contact regions and then separate. The contact time, tc, during collision close to the wall was found to be 22.84 ms (shear rate 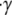 = 500 s−1), 31% greater than the contact time during collision far from the wall, which was 17.39 ms. The maximum instantaneous contact area,
= 500 s−1), 31% greater than the contact time during collision far from the wall, which was 17.39 ms. The maximum instantaneous contact area, 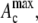 on one of the two colliding platelets during collisions close to and far from the wall were 1.27 μm2 and 0.85 μm2, respectively. We also calculated the time integral of contact area as
on one of the two colliding platelets during collisions close to and far from the wall were 1.27 μm2 and 0.85 μm2, respectively. We also calculated the time integral of contact area as 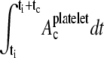 for each platelet, where ti is the time at which the two platelets first come within colliding distance. The time integral of contact area for the close-to-wall collision was found to be 10.0 μm2-ms and 9.7 μm2-ms for the upstream and downstream platelets, respectively, which can be compared with the time integral of contact area obtained for the far-from-wall collision, found to be 6.1 μm2-ms and 6.0 μm2-ms for the upstream and downstream platelets, respectively.
for each platelet, where ti is the time at which the two platelets first come within colliding distance. The time integral of contact area for the close-to-wall collision was found to be 10.0 μm2-ms and 9.7 μm2-ms for the upstream and downstream platelets, respectively, which can be compared with the time integral of contact area obtained for the far-from-wall collision, found to be 6.1 μm2-ms and 6.0 μm2-ms for the upstream and downstream platelets, respectively.
FIGURE 4.
Plots comparing the collision behavior of two platelets close to and far from the surface for seven different starting configurations that result in a collision. (A) A series of sequential frames showing the platelet trajectories during collision close to and far from the surface for an initial configuration of two platelets in which the distance between the platelet centroids was 2.5 μm in the x-direction and 0.25 μm in the z-direction. Frames containing a star in the righthand upper corner indicate that the two platelets depicted are within reactive contact distance of each other. (B) Comparison between contact durations for seven different starting configurations when the two platelets were placed close to or far from the wall. (C) Comparison of maximum instantaneous contact areas on one of the two platelets for seven different starting configurations when the two platelets were placed close to or far from the wall.
Fig. 4, B and C, compares the contact time and maximum instantaneous contact area on one of the two colliding platelets for collisions taking place close to and far from the surface. For initial configurations in which the distance in the z-direction between the platelet centroids is larger, i.e., 0.5 or 0.75 μm, the collision behavior was usually found to be similar. An incremental change in the Δx distance between the two platelets is found to have dramatic consequences on the contact properties. Slight modification in the initial x-distance between two platelet cells results in a slight deviation in the relative z-positions at the time of contact, and/or can profoundly affect the relative orientations of the individual platelets due to shear-induced rotation when they reach near-contact distances. A slight change in the initial x-separation can possibly convert a glide-under collision into a glide-over collision or convert a cell-cell encounter from a no-contact event into a collision event. Maximum contact areas, average contact areas, and therefore the time integral of contact area were always found to be slightly different for each of the two platelets interacting in the collision, for the collisions that were analyzed. This is expected because of the asymmetric interactions between nonspherical particles during close encounters.
Collision frequency: effect of particle shape and proximity of a plane wall
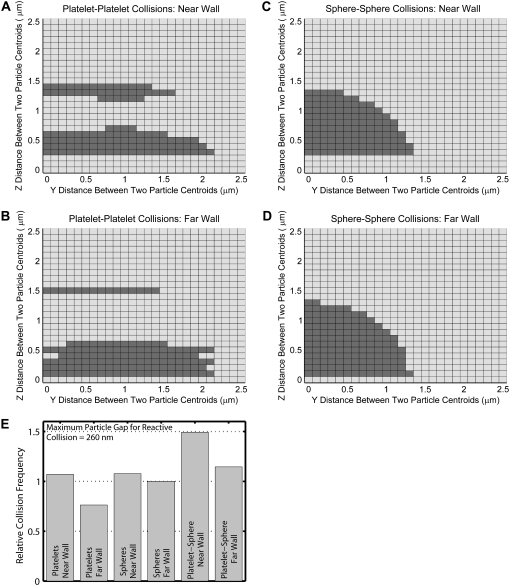
The effect of particle shape and proximity of a bounding wall on the particle trajectories can be concisely quantified and compared by determining the collision frequencies of platelet and spherical particles suspended in fluid undergoing shear. We performed a rigorous series of simulations in which two particles were given an initial separation distance of 10 μm (10 times the platelet radius) in the flow direction (x-direction), so that particle-particle hydrodynamic interactions at the start of flow would be small initially and thus the aggregate effects of hydrodynamic interactions between the two particles and the wall could be systematically compared. The full range of relative positions between two particles was tested by varying the relative distances between the particle centroids in the y- and z-directions (Fig. 5). For one set of simulations, the downstream particle was given an initial height of 1.5 μm, thus allowing the study of the influence of the wall on the fate of particle-particle encounters (Fig. 5, A and C). For another set of simulations, the downstream particle was initially placed 12 μm from the surface, to determine the effects of particle shape on particle collisions independent of wall effects (Fig. 5, B and D). These simulations were performed for two platelet cells (Fig. 5, A and B), and two spherical particles of equivalent platelet volume (sphere of radius 0.63 μm) (Fig. 5, C and D). Fig. 5, A–D, shows the full range of initial particle-particle configurations that were tested. A darkened square in the figure indicates that the corresponding initial relative particle position results in a collision. The maximum reactive distance was set to 260 nm for these collisions.
FIGURE 5.
Grid maps depicting the initial relative particle positions that result in a homogeneous particle-particle collision based on a reactive particle gap of 260 nm for different particle shapes and distances from the wall. (A–D) Two-dimensional grids depicting incremental relative separations in the y- and z-directions between two particles that begin flow at 10.0 μm apart in the flow direction (x-direction). A shaded square indicates the occurrence of a collision for the corresponding initial particle configuration. Each 2-D grid depicts 676 different initial particle configurations. (A) Collision pattern for two platelets flowing near the surface, in which the downstream platelet begins flow at a height of 1.5 μm. (B) Collision pattern for two platelets flowing far from the surface, in which the downstream platelet begins flow at a height of 12.0 μm. (C and D) Collision patterns for two spheres, each of radius 0.63 μm, with the same starting initial configurations as in A and B, respectively. (E) Comparison of collision rates for all four different conditions depicted in A–D, as well as collision rates for heterogeneous platelet-sphere collisions, as depicted in Fig. 7, A and B, after normalizing with the collision rate for far-wall sphere flow (Eq. 13).
The frequency of collision between two particles in a flow environment is a function of the relative velocity between them. If particles of a single size and shape are suspended in a shearing fluid, with a concentration of 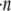 particles/volume, and the relative velocity between any two flowing particles is vrel, then the collision rate between particles suspended in a fluid and a single flowing particle, p, can be calculated as
particles/volume, and the relative velocity between any two flowing particles is vrel, then the collision rate between particles suspended in a fluid and a single flowing particle, p, can be calculated as
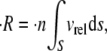 |
(10) |
where S is the far upstream cross-sectional area through which all particles that pass eventually collide with a particle, p, located downstream of S, and this area lies in the plane containing the velocity gradient direction (z plane) and the vorticity direction (y plane). dS is the incremental surface area through which particles of volumetric concentration 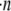 are flowing with a velocity of vrel relative to particle p. The rate at which collisions occur per unit volume between any two particles in the shearing fluid is given by
are flowing with a velocity of vrel relative to particle p. The rate at which collisions occur per unit volume between any two particles in the shearing fluid is given by
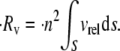 |
(11) |
In linear shear flow, the relative velocity between two particles sufficiently separated from each other such that the hydrodynamic interaction is minimal, is 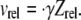 In these surface integrals, to calculate
In these surface integrals, to calculate  (Eq. 11), S has been discretized, such that ΔS = 0.01 μm2. Note that each individual trajectory simulation is performed with much greater spatial accuracy. Equation 11 is rewritten, after discretizing the surface integral, as
(Eq. 11), S has been discretized, such that ΔS = 0.01 μm2. Note that each individual trajectory simulation is performed with much greater spatial accuracy. Equation 11 is rewritten, after discretizing the surface integral, as
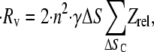 |
(12) |
where ΔSc = all ΔS that result in a collision. A factor of 2 is incorporated, since the collision behavior as mapped in Figs. 5–7 is symmetric about the y axis (vorticity direction). Therefore, in our simulations, ΔS is varied incrementally only in the positive y-direction. A comparison of collision rates for two different geometries or particle shapes can be easily performed as shown below, when the shear rate is unchanged:
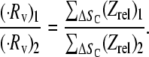 |
(13) |
Fig. 5 E compares the rate or frequency of successful collisions that occur between two particles, observed in Fig. 5, A–D, after normalization by the collision rate for 0.63-μm spheres (Fig. 5 D), in which the collision mechanism involved is essentially independent of wall boundary effects.
FIGURE 6.
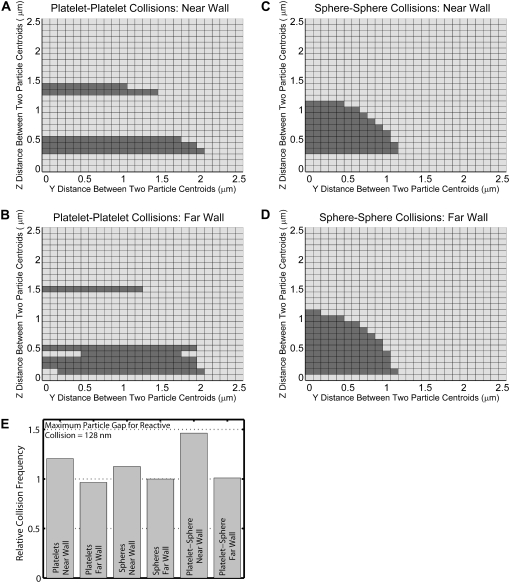
Grid maps depicting the initial relative particle positions that result in a homogeneous particle-particle collision based on a reactive particle gap of 128 nm for different particle shapes and distances from the wall. (A–D) Two-dimensional grids depicting incremental relative separations in the y- and z-directions between two particles that begin flow 10.0 μm apart in the flow direction (x-direction). A shaded square indicates the occurrence of a collision for the corresponding initial particle configuration. Each 2-D grid depicts 676 different initial particle configurations. (A) Collision pattern for two platelets flowing near the surface, in which the downstream platelet begins flow at a height of 1.5 μm. (B) Collision pattern for two platelets flowing far from the surface, in which the downstream platelet begins flow at a height of 12.0 μm. (C and D) Collision patterns for two spheres, each of radius 0.63 μm, with starting initial configurations as in A and B, respectively. (E) Comparison of collision rates for all four different conditions depicted in A–D, as well as collision rates for heterogeneous platelet-sphere collisions depicted in Fig. 7, C and D, after normalizing with the collision rate for far-wall sphere flow (Eq. 13).
FIGURE 7.
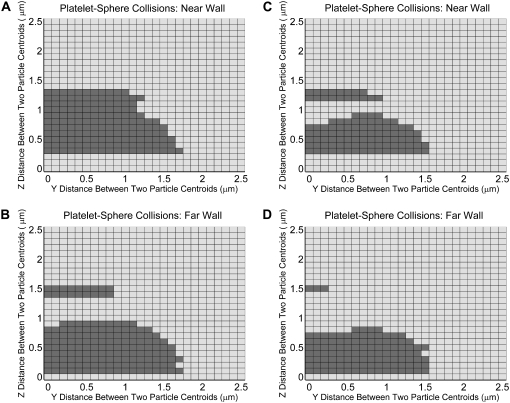
Grid maps depicting the initial relative particle positions that result in a heterogeneous particle-particle collision for different particle shapes and distances from the wall. (A–D) Two-dimensional grids depicting incremental relative separations in the y- and z-directions between two particles that begin flow 10.0 μm apart in the flow direction. A shaded square indicates the occurrence of a collision for the represented initial particle configuration. Each 2-D grid depicts 676 different initial particle configurations. (A) Collision pattern for a sphere and a platelet flowing near the surface, in which the platelet is positioned downstream of the sphere and begins flow at a height of 1.5 μm. (B) Collision pattern for a sphere and a platelet flowing far from the surface, in which the platelet is positioned downstream of the sphere and begins flow at a height of 12.0 μm. Collisions depicted in A and B are based on a reactive particle gap of 260 nm. (C and D) Same conditions as in A and B, respectively, except that the reactive particle gap is 128 nm.
The collision behavior of two particles both of the same size and shape as mapped in Fig. 5, A–D, is strikingly different for spheres and oblate spheroids, although the only difference between both shapes is simply a reduction of the spheroid radius in one direction. The wall effect manifests as a slight rearrangement in the collision pattern when the colliding spheres are brought closer to the wall, and in a somewhat more pronounced change in the collision pattern for flowing platelets. Fig. 5 E provides more insight into the effects of the wall on the overall particle collision frequency. The presence of the wall acts to boost the collision rate for particles of either shape. Because the platelet has a disc shape, it is intuitively expected that at larger z-separations between the two platelets, collisions will be rare and therefore the platelet collision frequency should be less than that for spheres when wall effects are unimportant. This is evident from Fig. 5 E, where the platelet far-wall collision frequency is 0.76 times that for spheres. The wall-induced increase in the collision rate for platelets (40% increase) is much more than that for spheres (7.7% increase). It is interesting to note that the disproportionate increase in collision rates for both particle shapes due to wall presence results in similar collision frequencies for platelets and spheres close to the wall (<1% difference). Note that although there are fewer incidences of particle collision closer to the wall compared to far from the wall, more of the near-wall collisions take place when the particles have higher relative velocity differences, and this accounts for the increased rates of collision.
We repeated the collision frequency analysis for a reactive collision gap between two particles equal to approximately half the value used in the previous simulations (lb = 260 nm), i.e., lb =128 nm (Fig. 6). This is also the equilibrium bond length used in the adhesive dynamics simulations of vWF bridging two GPIbα receptors located on different platelets. Fig. 6 E shows a comparison, similar to that depicted in Fig. 5 E, of the collision frequencies for platelet and spherical-shaped particles in both the presence and absence of bounding wall effects, normalized by the collision rate for 0.63-μm spheres, in which wall effects are unimportant (Fig. 6 D), for a reactive gap lb of 128 nm. The relative frequencies of collision shown in Fig. 6 E are qualitatively similar to that in Fig. 5 E. Although the platelet far-wall collision rate is less than the sphere far-wall collision rate, the difference is less pronounced. The wall again acts to enhance the collision rates of the particles, and this enhancement is ∼25% for the case of platelet collisions (as opposed to 13% for sphere collisions). Close to the wall, platelet-shaped particles have a collision frequency higher than that for spheres when the reactive particle gap is decreased to 128 nm. From both Figs. 5 E and 6 E, it appears that the wall has a greater hydrodynamic influence on platelet-platelet collisions than it does on sphere-sphere collisions.
Collision patterns are partially a function of the particle-particle reactive gap since a larger reactive gap effectively increases the size of the particle, which in turn increases the multitude of initial relative particle positions that result in a collision. As lb is decreased, the distinct influence of platelet shape on collision frequency increases, since the “effective” particle aspect ratio inclusive of the particle reactive gap tends to approach the actual physical aspect value (i.e., for lb = 260 nm, the “effective” aspect ratio of a platelet is 0.40, whereas for lb = 128 nm, the “effective” aspect ratio of a platelet is 0.335). Therefore, the collision frequency is dependent on the size of the reactive particle gap. For spheres, the ratio of “total collision encounters” close to and far from the wall remains the same upon reduction of lb (Table 2 A). Although there is a decrease in effective particle size, there is no change in the aspect ratio of the particle. Since the spherical particle shape does not change with a reduction in the reactive collision gap, the relative effect of the wall remains unchanged, although the total number of collisions decreases. The ratio of the number of collision encounters close to the wall to the number far from the wall measures the effect of the wall but does not embody the characteristic distribution of initial particle configurations that result in a collision. This distribution is a function of the particle size, particle shape, reactive gap between the two particles, and distance from the wall. Table 2 shows that the ratio of the total numbers of collision encounters close to and far from the wall for sphere-sphere collisions is essentially the same for both reactive collision gaps considered here, which signifies that the wall has an equal effect on the nature of sphere-sphere collisions whether the reactive collision gap is 260 nm or 128 nm. Table 2 further calculates the ratio of total collision encounters for platelet-platelet collisions and demonstrates the wall effect as a function of the effective aspect ratio. Note that the effective aspect ratio of a particle has no effect on the hydrodynamic flow behavior of the particle or on hydrodynamic interactions between particle surfaces or wall effects, but only influences the collision attributes of particle-particle encounters such as collision time, collision contact area, and collision frequency.
TABLE 2.
Number of two-particle encounters out of a total of 676 encounters that result in a hydrodynamic collision for two-sphere and two-platelet flows
| Total collision encounters | ||
|---|---|---|
| Sphere-sphere collisions | lb = 260 nm | lb = 128 nm |
| A: near-wall | 120 | 85 |
| B: far-wall | 136 | 96 |
| Ratio, A/B | 0.882 | 0.885 |
| Platelet-platelet collisions | lb = 260 nm | lb = 128 nm |
| A: near-wall | 120 | 85 |
| B: far-wall | 133 | 105 |
| Ratio, A/B | 0.902 | 0.809 |
We also investigated the wall effect on spatial collision patterns and collision frequency for a platelet-sphere system, in which both the platelet and spherical-shaped particle have equivalent volumes. Fig. 7 comprises four collision grid maps for hydrodynamic encounters between a sphere and a platelet initially positioned downstream of the sphere. Fig. 7, A and B, is for a reactive collision gap of 260 nm, and Fig. 7, C and D, depicts collision patterns based on a reactive collision gap of 128 nm between the two particle surfaces. If particle concentration 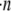 is the same for spherical and platelet particles in this system and also for the platelet-platelet and sphere-sphere systems described in Figs. 5 and 6, then their respective collision frequencies can be compared as shown in Figs. 5 E and 6 E. The wall has a sizeable effect in boosting the platelet-sphere collision rate in both Figs. 5 E (30% increase in near-wall collision rate compared to platelet-sphere far-wall collision rate) and 6 E (44% increase in near-wall collision rate compared to platelet-sphere far-wall collision rate). Note that the collision maps depicted in Figs. 5–7 do not provide information on the effect of varying the initial relative platelet angular orientations on collision outcomes.
is the same for spherical and platelet particles in this system and also for the platelet-platelet and sphere-sphere systems described in Figs. 5 and 6, then their respective collision frequencies can be compared as shown in Figs. 5 E and 6 E. The wall has a sizeable effect in boosting the platelet-sphere collision rate in both Figs. 5 E (30% increase in near-wall collision rate compared to platelet-sphere far-wall collision rate) and 6 E (44% increase in near-wall collision rate compared to platelet-sphere far-wall collision rate). Note that the collision maps depicted in Figs. 5–7 do not provide information on the effect of varying the initial relative platelet angular orientations on collision outcomes.
Detailed collision characteristics of near-wall platelet-platelet collisions
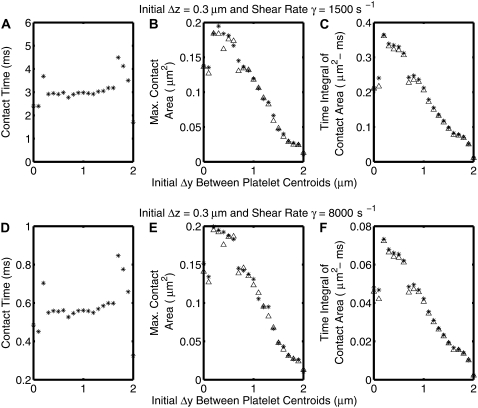
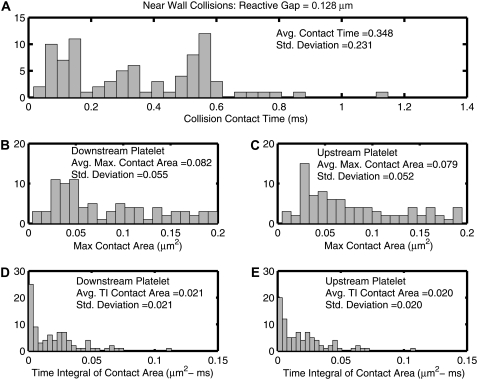
The collision characteristics for two platelets flowing close to the wall that exhibit a collision grid map as shown in Fig. 6 A (lb = 128 nm) were fully determined for a fluid shear rate of 1500 s−1. The collision contact time, maximum instantaneous contact surface area on both colliding platelets, and time integral of contact area for both platelets were quantified for each initial relative platelet configuration in Fig. 6 A that resulted in a platelet collision, and are plotted as histograms in Fig. 8. To ensure that the quantified collision metrics were independent of the time step chosen for each successive iteration (Δt = 10−6 s), near-wall collision encounters for starting platelet centroid separations of Δz = 0.5 μm and Δy = 0.0–1.7 μm (18 distinct collisions in total) were repeated using a time step of Δt = 0.5 × 10−6 s and in some cases a lower time step of Δt = 10−7 s. The average relative error in the prediction of collision contact time at a time step of Δt = 10−6 s was found to be 0.26%, with a maximum relative error of 2.2% and a minimum of 0.0%. The chosen time step of 10−6 s is thus found to be a reasonable choice with respect to both accuracy and speed of computation (relative to computational time required at lower time steps).
FIGURE 8.
Histograms of quantified collision characteristics for platelet-platelet collisions occurring close to a bounding wall at a shear rate of 1500 s−1. The reactive collision gap is set at a maximum of 128 nm. All 85 collision encounters depicted by Fig. 6 A are included. The platelets begin flow 10 μm apart in the flow direction. (A) Histogram of the contact time between two platelets during collision. (B and C) Histograms of the maximum instantaneous surface contact area of the downstream and upstream platelets, respectively, during a collision. (D and E) Histograms of the time integral of contact area for the downstream and upstream platelets, respectively. The average value of the collision metric, as well as the standard deviation from the average value, is noted within each histogram.
Interestingly, the histograms of the time integral of the contact area do not show trends similar to that shown by the histograms of maximum contact areas and collision times. The histograms of the collision times and maximum contact areas both show few instances near zero and attain maxima away from the origin. On the other hand, the histogram trends for the time integral of contact area are different, and maxima occur at the origin itself. Although Fig. 4, B and C, depicts a strong correlation between the collision times and maximum contact areas, it is important to note that although this may be valid for flows symmetric about the flow plane, a strong correlation does not exist for asymmetric flows. The instantaneous contact area depends on the relative platelet positions during collision. More favorable contact positions that involve significant overlap of the platelet faces require that the distance between the platelet centroids in the y direction be nonzero. Collisions that involve larger contact areas that result from favorable relative positions or orientations of adjacent platelet faces are not necessarily synonymous with large contact times.
The average of all plotted values of the time integral of contact area gives a measure of the average adhesion probability between two colliding platelets, and is characteristic of the nature of platelet-platelet collisions close to a wall. Since the standard deviations of the quantified metrics (Fig. 8) are of the same order of magnitude as the averages, the range over which the collision duration, maximum collision contact area, and time integral of contact area vary is substantial when all initial configurations that produce a collision event are taken into consideration. To ensure adequate representation of the characteristics of platelet-platelet collisions close to a bounding surface without requiring exhaustive adhesive dynamics simulations for each unique collision event, three representative initial platelet configurations were chosen from the multitude of initial configurations that result in a cell-cell collision, such that the following three time integrals of contact area are realized:
Average time integral of contact area – 0.5 × SD
Average time integral of contact area
Average time integral of contact area + 0.5 × SD.
These are referred to as representative collision types I–III, respectively. Table 3 lists the values of the time integral of contact area (ATI) of representative collisions that were used for simulating adhesive dynamics of platelet-platelet binding close to the wall, and also lists the two-platelet initial configurations that provide the ATI values desired within a reasonable difference (<4%).
TABLE 3.
Initial platelet-platelet configurations chosen for three representative near-wall platelet collisions that characterize platelet collisions near a planar boundary
| Initial platelet-platelet configurations that provide the desired ATI values
|
ATI of initial platelet-platelet configurations that produce representative collisions
|
|||
|---|---|---|---|---|
| Representative collision number | Δz (μm) | Δy (μm) | Downstream platelet | Upstream platelet |
| I | 0.5 | 1.5 | 0.0492 | 0.0456 |
| II | 0.5 | 1.0 | 0.1048 | 0.0959 |
| III | 0.3 | 1.2 | 0.1588 | 0.1525 |
Low Reynolds number flows, i.e., Stokes flows, scale linearly with the shear rate. Therefore, the flow behavior is ideally independent of the flow shear rate. However, in our two-platelet adhesive dynamics model there exists a very short-range repulsive force between the two particles that becomes significant when the glycocalyx layers of the colliding particles come within a distance of 15 nm from each other, and this repulsive force does not scale with the fluid shear level. At a different shear rate, the same magnitude of repulsive force may cause the platelets to orient slightly differently with respect to the wall and each other. In the two-platelet adhesive dynamics simulations that were carried out at high shear rates of flow, the highest shear rate considered was 8000 s−1. The entire set of collisions characteristics shown in Fig. 8 were requantified for a shear rate of 8000 s−1.
The nature of collisions was found in all cases to be qualitatively, and in most cases quantitatively, the same for shear rates of both 8000 s−1 and 1500 s−1 for all initial platelet configurations that result in a collision near the wall. The trends in collision contact time, maximum instantaneous contact area on both colliding platelets, and ATI for both platelets with incremental increase in the initial Δy between the platelet centroids (Δz = 0.3 μm) for shear rates of both 1500 s−1 and 8000 s−1 are depicted in Fig. 9. The trends are the same for both shear rates. Fig. 10 is similar to Fig. 8, except that the fluid shear rate for all simulations is 8000 s−1 and the time step for each iteration is smaller (Δt = 10−7 s).
FIGURE 9.
Plots demonstrating the trends of three different collision characteristics as a function of the initial Δy separation between the two platelet centroids for an initial Δz = 0.3 μm. (A–C) Shear rate, γ = 1500 s−1. (D–F) Shear rate, γ = 8000 s−1. Crosses indicate the downstream platelet and ▵ the upstream platelet.
FIGURE 10.
Histograms of quantified collision characteristics for platelet-platelet collisions occurring close to a bounding wall at a shear rate of 8000 s−1. The reactive collision gap is set at a maximum of 128 nm. All 85 collision encounters depicted in Fig. 6 A are included. The platelets begin flow 10 μm apart from each other in the flow direction. (A) Contact time between two platelets during collision. Maximum instantaneous surface contact area of the downstream (B) and upstream (C) platelets during a collision is shown. Time integral of contact area for the downstream (D) and upstream (E) platelets is shown. The average value of the collision metric, as well as the standard deviation from the average value, is noted within each histogram.
In pure Stokes flows, the collision contact time for two particles at a shear rate of 8000 s−1 is 0.1875 times that observed at a fluid shear rate of 1500 s−1, since the contact duration non-dimensionalized by shear rate should be the same regardless of the imposed shear rate. This has been shown previously for platelet flipping motion on a planar surface coated with vWF (30). On scaling the collision contact time, as well as the platelet ATI with shear rate, the collision metrics at different shear rates can be compared and their differences quantified. The average difference in the collision contact time, maximum instantaneous contact areas on both platelets, and ATI values for both platelets at the two different shear rates range from ∼1–5%. Thus, certain initial platelet separations do result in slightly different collision characteristics at the two different shear rates. These differences can be attributed to the presence of the short-range repulsive force, which acts between two surfaces in near contact with each other as discussed in the previous paragraph. The effect of the nonlinear interparticle repulsive force on the collision characteristics with increase in fluid shear rate can be gauged by determining the ratio of the average ATI values at both shear rates and comparing this “average ratio” with the inverse ratio of the corresponding shear rates. In reversible shear flows,
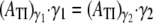 |
or
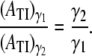 |
In our simulations, 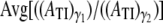 = 0.1989 for both platelets while
= 0.1989 for both platelets while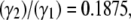 where γ1 = 8000 s−1 and γ2 = 1500 s−1. The cell-cell repulsive force, which is independent of the fluid shear rate, is observed to be slightly less effective in keeping cells apart at higher shear rates (when cells are subjected to higher shear forces) than at lower shear rates, as intuitively expected. Thus, there is, on average, a slight increase in the intimacy of the collision between two platelet particles at higher shear rates.
where γ1 = 8000 s−1 and γ2 = 1500 s−1. The cell-cell repulsive force, which is independent of the fluid shear rate, is observed to be slightly less effective in keeping cells apart at higher shear rates (when cells are subjected to higher shear forces) than at lower shear rates, as intuitively expected. Thus, there is, on average, a slight increase in the intimacy of the collision between two platelet particles at higher shear rates.
DISCUSSION
This article presents a detailed characterization of the full gamut of collisions observable in a two-platelet linear shear flow system in close proximity to a planar wall. A two-particle hydrodynamic encounter in shear flow was recognized as a collision event if the particle surfaces came within a distance of each other that was less than or equal to a predefined reactive gap that supports interplatelet reactions that result in the formation of bridging bonds. Two main features of our scheme for characterizing platelet-platelet collisions are 1), qualitative and quantitative comparison of platelet collision behavior with that observed for sphere-sphere systems, and 2), quantification of the hydrodynamic effects of a plane wall on the physics of platelet-platelet and sphere-sphere collisions. Comparisons of platelet collisions with sphere collisions were made for two fundamental reasons: 1), the platelet shape (oblate spheroid) is similar to the spherical shape except that in the case of an oblate spheroid, the axis of one of three mutually orthogonal dimensions is smaller, to produce a flattened or squashed sphere, and 2), extensive fluid mechanical theoretical and experimental studies of sphere flows in unbounded and bounded media have been conducted over the past century. Flow phenomena regarding spherical particulate motion in shearing fluid in Stokes flows are relatively well established, and theoretical tools for studying and modeling sphere flows are relatively abundant. Thus, a comparison of platelet flow with sphere flow affords more useful and instructive insight into the significant features of platelet-platelet hydrodynamic flow encounters.
We have shown that platelet-platelet collisions are qualitatively and quantitatively different from sphere-sphere collisions in terms of the mechanism of collision (particle trajectories), spatial collision patterns, and collision frequencies. Presence of a planar wall has profound effects on the spatial collision patterns, nature of particle collisions (mechanism of collision, collision time, and collision contact area), and collision frequency. The wall effect on collision frequency is observed to be greater for platelet collisions than for sphere collisions. For platelet collisions near a bounding wall in linear shear flow, we quantitatively characterized all 85 unique collision events between two platelets as depicted in Fig. 6 A. The time integral of contact area is an important metric that effectively combines two useful collision metrics, time duration of a collision and instantaneous contact area on either particle surface, to provide a comparative measure of the ability of two particles to undergo a reactive event, and was determined for all 85 unique near-wall collisions between two platelets. This metric was used to select three representative collisions from all possible platelet collisions in close proximity to a wall. These three representative collisions were used to carry out more extensive simulations of platelet-platelet encounters that include adhesive interactions, which are described in a companion article.
In the absence of any external force, such as gravity or interparticle attraction/repulsion, particle interactions are perfectly reversible in Stokes flows due to the linearity of the Stokes equations (31). When additional interparticle interactions are superimposed upon the hydrodynamic interactions that arise due to flow, the resulting particle collisions are no longer reversible (32). We have shown previously that the short-range surface-surface repulsive force acts to prevent two surfaces from collapsing into each other and does not cause particle drift (from the wall in the case of platelet-wall interactions) (23). The presence of interparticle forces introduces irreversibility (and nonlinear scalability if the equations governing the body forces are nonlinear with respect to the scaling variable) in the flow solution, i.e., if the flow is reversed, the flow trajectories of the particles cannot be retraced. Since the short-range repulsive force is independent of the shear rate imposed, a change in shear rate in our simulations therefore does not guarantee that the colliding flow paths of the simulated particles will perfectly superimpose with flow trajectories at other shear rates. Metrics defining near-wall platelet collision behavior were obtained at two different shear rates, 1500 s−1 and 8000 s−1, to discern the effects of the very short-range repulsive force that acts between the two particle-surface roughness layers on the scalability of hydrodynamic platelet collisions with shear rate as predicted by PAD simulations. It was found that the imposed particle-particle repulsive force has, on average, a minor effect on the scalability of the hydrodynamic solution with respect to shear rate for the range of shear rates studied. In real flow experiments conducted at different shear rates, the flow paths when nondimensionalized with respect to shear rate are not expected to superimpose perfectly due to many other nonlinear factors in the surrounding fluid, such as inertia and interparticle forces that affect the platelet flow trajectories (30). The presence of an interparticle repulsive force was tantamount to an average increase in the time integral of contact area of a reactive contact event by ∼6% over a 5.3-fold range of shear rates. The range of shear rates considered in our adhesion studies is less than twofold and ranges from 4500 to 8000 s−1.
Huang and Hellums (17,18,33) developed a mathematical model of the dynamics of shear-induced platelet aggregation and aggregate break-up using the single-component population balance equation. Their equation parameters were estimated by fitting the model equations to experimental data obtained from uniform shear-induced platelet aggregate formation observed in a cone-and-plate viscometer at all shear rates >3000 s−1. The holistic effects of 1), kinetics of participating adhesive phenomena, such as rate equations, for GPIbα or αIIBβ3 binding to vWF; 2), influence of shear on binding dynamics; and 3), hydrodynamic effects that govern the physics of particle-particle contact, such as hydrodynamic interactions between the particles, duration of contact, and influence of particle shape, were all combined into a single parameter termed “collision efficiency ηc”. Platelets were modeled as hard spheres, and an additional parameter was included to account for void fraction present in platelet aggregates of various sizes. The overall collision efficiency was quantified for platelet aggregation at a range of high shear rates and in the presence and absence of chemical agonists. Such quantifications provide insightful understanding of the relative roles of magnitude of shear and other factors, like the effect of an agonist; however, the individual roles of various biophysical factors such as shear force, particle shape, and binding kinetics that contribute to the process of platelet aggregation, and their individual extents of contribution cannot be ascertained from their model.
The aim of this article was to present the fluid mechanical method used to predict hydrodynamic collisions between two platelet-shaped cells in shear flow in a semi-infinite 3-D region, and to investigate the collision behavior of platelets by quantifying the relevant collision metrics and comparing flow phenomena for platelet collisions with those for sphere collisions. Our Part II article discusses the development and application of an adhesive dynamics model for platelet GPIbα receptor binding to vWF multimers in solution and GPIbα-vWF-GPIbα bridging of two platelets. Platelet transient aggregation behavior and relevant trends in bond characteristics as a function of vWF multimer size, different binding kinetics, and imposed shear rate in the fluid, as predicted by PAD, are covered in Part II.
Acknowledgments
This work was supported by a National Science Foundation Career Award (BES–0448788) and a National Institutes of Health grant (HL087317) to M.R.K. and a National Institutes of Health and Biomedical Imaging and Bioengineering fellowship (EB005104) to N.A.M.
Michael R. King's present address is Dept. of Biomedical Engineering, Cornell University, Ithaca, New York.
Editor: Gaudenz Danuser.
References
- 1.Li, F., C. Q. Li, J. L. Moake, J. A. Lopez, and L. V. McIntire. 2004. Shear stress-induced binding of large and unusually large von Willebrand factor to human platelet glycoprotein Ibα. Ann. Biomed. Eng. 32:961–969. [DOI] [PubMed] [Google Scholar]
- 2.Arya, M., B. Anvari, G. M. Romo, M. A. Cruz, J. F. Dong, L. V. McIntire, J. L. Moake, and J. A. Lopez. 2002. Ultralarge multimers of von Willebrand factor form spontaneous high-strength bonds with the platelet glycoprotein Ib-IX complex: studies using optical tweezers. Blood. 99:3971–3977. [DOI] [PubMed] [Google Scholar]
- 3.Fischer, B. E., G. Kramer, A. Mitterer, L. Grillberger, M. Reiter, W. Mundt, F. Dorner, and J. Eibl. 1996. Effect of multimerization of human and recombinant von Willebrand factor on platelet aggregation, binding to collagen and binding of coagulation factor VIII. Thromb. Res. 84:55–66. [DOI] [PubMed] [Google Scholar]
- 4.Alevriadou, B. R., J. L. Moake, N. A. Turner, Z. M. Ruggeri, B. J. Folie, M. D. Phillips, A. B. Schreiber, M. E. Hrinda, and L. V. McIntire. 1993. Real-time analysis of shear-dependent thrombus formation and its blockade by inhibitors of von Willebrand factor binding to platelets. Blood. 81:1263–1276. [PubMed] [Google Scholar]
- 5.Ikeda, Y., M. Handa, K. Kawano, T. Kamata, M. Murata, Y. Araki, H. Anbo, Y. Kawai, K. Watanabe, I. Itagaki, K. Sakai, and Z. M. Ruggeri. 1991. The role of von Willebrand factor and fibrinogen in platelet aggregation under varying shear stress. J. Clin. Invest. 87:1234–1240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Peterson, D. M., N. A. Stathopoulos, T. D. Giorgio, J. D. Hellums, and J. L. Moake. 1987. Shear-induced platelet aggregation requires von Willebrand factor and platelet membrane glycoproteins Ib and IIb-IIIa. Blood. 69:625–628. [PubMed] [Google Scholar]
- 7.Yoon, B. J., and S. Kim. 1990. A boundary collocation method for the motion of two spheroids in Stokes flow: hydrodynamic and colloidal interactions. Int. J. Multiphase Flow. 16:639–649. [Google Scholar]
- 8.Pozrikidis, C. 2006. Interception of two spheroidal particles in shear flow. J. Non-Newt. Fluid Mech. 136:50–63. [Google Scholar]
- 9.Claeys, I. L., and J. F. Brady. 1993. Suspensions of prolate spheroids in Stokes flow. Part 1. Dynamics of a finite number of particles in an unbounded fluid. J. Fluid Mech. 251:411–442. [Google Scholar]
- 10.Tandon, P., and S. L. Diamond. 1997. Hydrodynamic effects and receptor interactions of platelets and their aggregates in linear shear flow. Biophys. J. 73:2819–2835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tandon, P., and S. L. Diamond. 1998. Kinetics of β2-integrin and L-selectin bonding during neutrophil aggregation in shear flow. Biophys. J. 75:3163–3178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Long, M., H. L. Goldsmith, D. F. Tees, and C. Zhu. 1999. Probabilistic modeling of shear-induced formation and breakage of doublets cross-linked by receptor-ligand bonds. Biophys. J. 76:1112–1128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Helmke, B. P., M. Sugihara-Seki, R. Skalak, and G. W. Schmid-Schonbein. 1998. A mechanism for erythrocyte-mediated elevation of apparent viscosity by leukocytes in vivo without adhesion to the endothelium. Biorheology. 35:437–448. [DOI] [PubMed] [Google Scholar]
- 14.Hammer, D. A., and S. M. Apte. 1992. Simulation of cell rolling and adhesion on surfaces in shear flow: general results and analysis of selectin-mediated neutrophil adhesion. Biophys. J. 63:35–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mody, N. A., and M. R. King. 2005. Dynamics of platelet aggregation and adhesion to reactive surfaces under flow. In Principles of Cellular Engineering: Understanding the Biomolecular Interface. M. R. King, editor. Elsevier Academic, New York. 267–295.
- 16.King, M. R., and D. A. Hammer. 2001. Multiparticle adhesive dynamics. Interactions between stably rolling cells. Biophys. J. 81:799–813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Huang, P. Y., and J. D. Hellums. 1993. Aggregation and disaggregation kinetics of human blood platelets: Part II. Shear-induced platelet aggregation. Biophys. J. 65:344–353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Huang, P. Y., and J. D. Hellums. 1993. Aggregation and disaggregation kinetics of human blood platelets: Part I. Development and validation of a population balance method. Biophys. J. 65:334–343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kim, S., and S. J. Karilla. 1991. Microhydrodynamics: Principles and Selected Applications. Butterworth-Heinemann, Stoneham, MA.
- 20.Phan-Thien, N., D. Tullock, and S. Kim. 1992. Completed double-layer in half-space: a boundary element method. Comput. Mech. 9:121–135. [Google Scholar]
- 21.Power, H., and G. Miranda. 1987. 2nd Kind integral-equation formulation of Stokes flows past a particle of arbitrary shape. SIAM J. Appl. Math. 47:689–698. [Google Scholar]
- 22.Maul, C., S. T. Kim, V. Ilic, D. Tullock, and P. T. Nhan. 1994. Sedimentation of hexagonal flakes in a half-space: numerical predictions and experiments in Stokes flow. J. Imaging Sci. Technol. 38:241–248. [Google Scholar]
- 23.Mody, N. A., and M. R. King. 2005. Three-dimensional simulations of a platelet-shaped spheroid near a wall in shear flow. Phys. Fluids. 17:1432–1443. [Google Scholar]
- 24.Kim, M.-U., K. W. Kim, Y.-H. Cho, and B. M. Kwak. 2001. Hydrodynamic force on a plate near the plane wall. I. Plate in sliding motion. Fluid Dyn. Res. 29:137–170. [Google Scholar]
- 25.Jeffery, G. B. 1922. The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A. 102:161–179. [Google Scholar]
- 26.Lauffenburger, D. A., and J. J. Linderman. 1993. Receptors: Models for Binding, Trafficking and Signaling. Oxford University Press, New York.
- 27.Bell, G. I., M. Dembo, and P. Bongrand. 1984. Cell adhesion. Competition between nonspecific repulsion and specific bonding. Biophys. J. 45:1051–1064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Martin, J. F., T. Shaw, J. Heggie, and D. G. Penington. 1983. Measurement of the density of human platelets and its relationship to volume. Br. J. Haematol. 54:337–352. [DOI] [PubMed] [Google Scholar]
- 29.Konstantopoulos, K., T. W. Chow, N. A. Turner, J. D. Hellums, and J. L. Moake. 1997. Shear stress-induced binding of von Willebrand factor to platelets. Biorheology. 34:57–71. [DOI] [PubMed] [Google Scholar]
- 30.Mody, N. A., O. Lomakin, T. A. Doggett, T. G. Diacovo, and M. R. King. 2005. Mechanics of transient platelet adhesion to von Willebrand factor under flow. Biophys. J. 88:1432–1443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Batchelor, G. K., and J. T. Green. 1972. The hydrodynamic interaction of two small freely-moving spheres in a linear flow field. J. Fluid Mech. 56:375–400. [Google Scholar]
- 32.daCunha, F. R., and E. J. Hinch. 1996. Shear-induced dispersion in a dilute suspension of rough spheres. J. Fluid Mech. 309:211–223. [Google Scholar]
- 33.Huang, P. Y., and J. D. Hellums. 1993. Aggregation and disaggregation kinetics of human blood platelets: Part III. The disaggregation under shear stress of platelet aggregates. Biophys. J. 65:354–361. [DOI] [PMC free article] [PubMed] [Google Scholar]