Intrinsic Bending and Structural Rearrangement of Tubulin Dimer: Molecular Dynamics Simulations and Coarse-Grained Analysis

Abstract

Microtubules are long polymers of αβ-tubulin heterodimers. They undergo a process known as dynamic instability, in which the ends of a microtubule switch stochastically between phases of slow growth and rapid shrinkage. The molecular mechanisms inducing the depolymerization of microtubules were attributed to the hydrolysis of the guanosine triphosphate (GTP) nucleotide bound to the β-tubulin. The hydrolysis of GTP is thought to cause microtubule instability by promoting outward curving of the protofilaments constituting the microtubule lattice. The bending of protofilaments is associated with the structural transformation of a tubulin dimer from straight to curved conformations. However, the nature of intrinsic bending of the dimer remains elusive. This study uses molecular dynamics (MD) simulations and coarse-grained analysis to reveal the intrinsic bending, as well as the local structural rearrangements, of the unassembled tubulin dimer as the dimer relaxes from its lattice-constrained, straight conformation of a zinc-induced tubulin sheet. The effect of the nucleotide state on dimer-bending is investigated by the introduction of γ-phosphate into the β-tubulin to form GTP-bound tubulin. In agreement with recent experimental studies that proposed nucleotide-independent curved conformations, both guanosine diphosphate (GDP)-bound and GTP-bound tubulin dimers were found to have curved conformations, but with a tendency toward smaller bending in the GTP-tubulin than in the GDP-tubulin. The perturbation induced through the introduction of γ-phosphate is posited to play a role in straightening the intradimer bending. The local structural rearrangements of GDP-tubulin because of the bending mode of motion of the dimer reveal that one of the three functional domains, the intermediate domain, exhibits significantly lower bending deformation compared with the others, signifying a dynamic connection to the functionally defined domains.

INTRODUCTION

Microtubules (MTs) are cytoskeletal filaments found in all eukaryotic cells, with functions ranging from mechanical support to cell motility, intracellular transport, and mitosis (1). They are assembled by the self-associations of αβ-tubulin dimers. Tubulin is a stable dimer of two largely homologous globular proteins α-tubulin and β-tubulin that share 40% sequence homology (2). The head-to-tail binding of these heterodimers results in protofilaments that run along the length of MTs. The lateral interactions between (typically) 13 parallel protofilaments complete the assembly of the MT wall. The polymerization of MTs is a polar process in which the plus end (terminated by β-tubulins) polymerizes more quickly than the minus end (terminated by α-tubulins). The polymerization of the plus ends switches alternately between phases of slow growth and rapid disassembly in an abrupt, stochastic manner (3). This behavior of MTs is called dynamic instability, and occurs under physiological conditions (3). It is an important subject that is not fully understood.

A key observation to dynamic instability is the occurrence of guanosine triphosphate (GTP) hydrolysis at the β-tubulin. In solution, each tubulin dimer is bound to two GTP molecules, one on each monomer. The nucleotide bound to α-tubulin is buried at the interface between the two monomers, and is nonexchangeable, whereas that of β-tubulin is exposed to the surface and is exchangeable (4,5). Upon polymerization, the nucleotide bound to β-tubulin undergoes GTP hydrolysis, forming a guanosine diphosphate (GDP) nucleotide. The MT lattice, consisting of GTP-tubulin (i.e., a tubulin dimer with GTP bound to both α- and β-subunits), is more stable in terms of depolymerization than a lattice of GDP-tubulin (GTP bound to α-tubulin, and GDP bound to β-tubulin). Previously, the origin of dynamic instability was explained on the basis of a kinetic viewpoint for MT assembly (3). According to the kinetic viewpoint, if polymerization occurs at a rate slower than GTP hydrolysis, then the GDP-tubulins dissociate easily, leading to fast depolymerization. This depolymerization is perceived to be curbed by the formation of layers of GTP-tubulins known as a GTP-cap that stabilizes the depolymerization (3). As a result, dynamic instability may be described in terms of the kinetic lag between polymerization and hydrolysis that leads to the presence or lack thereof of a GTP-cap. However, the size and nature of the GTP-cap, or conclusive evidence on the availability of such a cap, is still lacking (6,7).

By contrast, recent structural observations, based on a mechanical/structural viewpoint (8,9), provided new insights into dynamic instability. During polymerization, the ends of MTs grow into sheets of protofilaments that wrap into tubes (9,10). Upon depolymerization, the protofilaments splay apart, to curve outward in a manner similar to a “ram's horn” (10), followed by dissociations into individual dimers or curved oligomers (9). In the presence of MT-associated proteins (MAPs) or certain divalent cations such as Ca²⁺, the protofilaments bend backward on themselves, to form stable rings (11,12). These morphological changes were linked to GTP hydrolysis, on the grounds that the resulting GDP-tubulin has a curved conformation (13). In general, tubulin dimers are thought to exist in two conformations: straight and curved (13). They are conceived to have straight conformations when bound to GTP or buried within the MT lattice, whereas they are curved when bound to GDP (12). Consequently, when found in the MT lattice, GDP-tubulins are constrained in a straight GTP-like conformation, whereas their relaxed ground-state conformation is curved. The tension caused by restraining GDP-tubulin in an unstable GTP-like conformation results in a stored mechanical energy within the lattice that serves as a driving force for rapid MT depolymerization (14), and hence dynamic instability.

Several experiments were conducted to demonstrate directly the curved conformation of GDP-tubulin that is believed to be at the core of dynamic instability. For example, Muller-Reichert et al. (12) conducted a cryo-electron microscopy study of cold-induced and calcium-induced MT depolymerization, to reveal the curved conformation of GDP-tubulin. Ravelli et al. (15) investigated an unpolymerized GDP-tubulin oligomer in complex with colchicine and the stathmin-like domain of MT-destabilizing protein RB3 (tubulin-colchicine:RB3-SLD). They also found a curved conformation of GDP-tubulin, albeit in the presence of the depolymerizing agent. In the absence of depolymerizing agents, on the other hand, Wang and Nogales (16) found a curved conformation using a cryo-electron microscopy reconstruction of double-layered tubes of GDP-tubulin. It seems evident from these experiments that GDP-tubulin has a curved conformation. However, each of these experiments involved external influences that may have affected the intrinsic bending of the dimer. For instance, the cold temperature and high calcium concentration in the cold-induced and calcium-induced depolymerization experiment (12) were likely to affect the conformations of the dimer. This is because temperature is known to affect the dissociation of proteins, whereas ends of MT protofilaments are known to form stable rings at high concentrations of divalent cations. Moreover, the curved conformation of the GDP-tubulin oligomer studied in the presence of depolymerizing agent RB3 could be affected by the long, helical stathimin-like domain (SLD) of RB3 bound to it. Even the double-layered tube experiment conducted in the absence of depolymerizing agents, as performed by Wang and Nogales (16), could have affected the curved conformations of GDP-tubulin, possibly by the constraint needed to conform the dimer into a double-layer tubular structure.

The situation becomes even more complicated under in vivo conditions, where conformational changes are induced by the presence of cellular factors and antimitotic agents (17,18). For example, proteins such as mitotic centrosome-associated kinesin (MCAKs) that bind to the ends of MT induce destabilizing conformational changes, causing protofilament peels independent of the nucleotide state of the tubulin (19). Therefore, it is clearly of interest to know the structural changes of tubulin dimers under conditions that are free from interfering proteins or drugs that apparently complicate a clear understanding of dynamic instability. Furthermore, the process that promotes dynamic instability cannot be fully captured by static experiments, including the experiment that resolved the crystal structure of tubulin-colchicine:RB3-SLD (15). Therefore, despite current advancements in revealing dimer structure, a complete understanding of the underlying structural mechanism leading to dynamic instability is yet to be achieved. In particular, the molecular origin triggering dynamic instability remains a matter of debate. For example, the widely accepted concept of nucleotide-dependent transition from straight GTP-like conformation to curved GDP-like conformation as a cause for MT depolymerization was disputed by Buey et al. (20), on the grounds that both GTP-tubulin and GDP-tubulin have curved confirmations. They argued that “contrary to what was thought, unassembled tubulin-GTP is in the inactive, curved conformation as in tubulin-GDP rings, and it is driven into the straight microtubule conformation by the assembly contact.” This argument is in contrast with the notion that associates straight conformation to GTP-tubulin. The notion of nucleotide-independent curved conformation arose in the last few years, and a recent experimental study supports this idea (21).

In light of the above discussion, our study investigated the molecular origin of dynamic instability by examining conformational changes of unassembled tubulin dimers. Computer simulations can provide insights into such matters. Because it is a crucial question for understanding dynamic instability, this study asked, “What is the intrinsic bending of GDP-tubulin dimer in the absence of external factors or any presumptions that may affect its true nature?” Then, to assess the effect of nucleotide state on the intrinsic bending of the dimer, this study examined the global conformational changes of GTP-bound tubulin. In particular, this study sought to resolve the issue of curved versus straight conformation of GTP-bound tubulin. Unfortunately, no crystal structures are available for GTP-bound αβ-tubulin. Nevertheless, it is possible to construct GTP-tubulin from the structure of GDP-tubulin by introducing a γ-phosphate into the molecule. The perturbation induced because of the change in nucleotide state can be examined for any global conformational changes. Similar approaches were used in studying nucleotide-induced structural changes of the protein filamentous temperature-sensitive (FtsZ) (22). Other studies that used such a procedure include those that successfully predicted the hinges of the conformational transition between active and inactive states of Ha-ras-p21 (23,24).

This study also examined the local structural rearrangements of the dimer that may contribute to MT polymerization or depolymerization. In particular, the conformational changes at the monomer and the dimer levels, arising from the occurrence of GTP hydrolysis, were investigated. This was done by examining the local and global conformational changes of GDP-tubulin as it relaxes from a lattice-constrained straight conformation, in analogy to events during GTP-hydrolysis that release GDP-tubulin from the MT lattice. In general, the overarching goal of our study was to investigate the dynamic processes that cause local and global conformational changes leading to dynamic instability. To this end, molecular dynamics (MD) simulation and coarse-grained (CG) analysis were used to assess the dynamic nature of bending in unassembled GDP- and GTP-bound tubulin dimers.

This article is organized as follows: a brief description of the model and simulations are given in Methods. A detailed description of the system can be found elsewhere (4,5). The results of MD simulations and the CG analysis are presented in Results and Discussion. Concluding remarks are given in Conclusions.

METHODS

The three-dimensional crystal structure of the tubulin heterodimer was first resolved by Nogales et al. (4) (Protein Data Bank [PDB] identification code 1TUB), and later refined by Löwe et al. (5) (PDB identification code 1JFF). The atomic structure was resolved using electron crystallography of taxol-stabilized, zinc-induced tubulin sheets, which are formed by the antiparallel association of protofilaments (4). The protofilaments in the tubulin sheet are considered to be analogous to those in the microtubule lattice (5). Thus, the crystal structure of a GDP-tubulin dimer from a zinc-induced sheet serves as a prototype for studying the structural rearrangement of the dimer in the event of GTP hydrolysis, providing insights into the nature of tubulin-bending during MT depolymerization. The model of the tubulin dimer and details of the simulation methods are presented below.

Model: GDP-tubulin

A tubulin dimer consists of 451 residues of α-tubulin and 445 residues of β-tubulin. The MD simulations of a GDP-tubulin dimer were performed using an initial structure taken from Löwe et al. (5) (PDB identification code 1JFF). Several amino-acid residues, including those in the C termini, are not resolved in the experimental structure. For example, the coordinates of residues α:35–60 in the α-tubulin are missing from 1JFF. in addition, the coordinates of the C termini in both monomers are not fully resolved. This model does not include the missing residues of the C termini. However, the coordinates found in 1TUB were used for the missing residues α:35–60 of the α-tubulin. The coordinates of the remaining missing residues were generated using the internal coordinate facilities of the program CHARMM (25). Moreover, the residue numbering of β-tubulin in the PDB file consists of discontinuities in which pairs of residues β:44 and β:47, and β:360 and β:369, are covalently bonded. Sequential numbering is used here, and references will be made in accordance with the numbering of the PDB file when necessary.

The composition of the protein model consists of one GTP molecule bound to the α-tubulin, and one GDP molecule bound to the β-tubulin. The model also contains a magnesium ion from the PDB file 1JFF. The dimer was solvated by the TIP3P model of explicit water (26), using a cubic cell of 125 preequilibrated water molecules. The cubic cell of water was replicated and truncated to form a simulation box of truncated octahedral symmetry. The dimer complex was then inserted into the water box by removing water molecules whose oxygen molecules were within 2.4 Å of the ions and the heavy atoms of the proteins and the nucleotides. The final system contained 150,510 water molecules and 13,432 atoms of GDP-tubulin dimer complex (including GTP, GDP, and Mg), such that the total number of atoms of the whole system was 164,110. The surrounding water solvated the protein by at least 13 Å on each side of the periodic box. The dimer consisted of 23 residues of histidines, and they were protonated in accordance with their distances from nearby donors or acceptors. The net charge of the dimer, nucleotides, and magnesium ion complex system was −36 at pH 7. Potassium chloride (KCl) was used as counterions to neutralize the system, according to the physiological concentration of 140 mM. The SOLVATE 1.0 program (27) was used to place the counterions, based on the Debye-Huckle distribution. The numbers of potassium and chlorine ions that were adjusted to yield the ionic strength of the system close to 140 mM were 102 and 66, respectively.

Model: GTP-tubulin

This modeling protocol was repeated for the GTP-tubulin dimer, except that a γ-phosphate was introduced into the GDP molecule belonging to the β-tubulin, so that the GDP-bound tubulin dimer was converted into a GTP-bound tubulin dimer. The total number of particles and counterions used to neutralize the system was modified by the addition of γ-phosphate. The solvated system contained a total number of 164,377 atoms. The numbers of potassium and chlorine ions that yielded the ionic strength of 140 mM were 78 and 41, respectively. The perturbation induced in the protein structure, attributable to the addition of γ-phosphate, was studied by using this model.

MD simulations

All atom MD simulations of tubulin dimer were performed using the NAMD 2.5 simulation package (28), along with the CHARMM22 force field (29). The system was first constructed by using the CHARMM program. Then the NAMD program was used for the equilibration and production runs. The trajectories obtained from the NAMD simulations were finally analyzed by the CHARMM analysis facility (25). The simulations were performed under periodic boundary conditions, based on the truncated octahedral symmetry, with a major axis of ∼123 Å in length. Nonbonded interactions were cut off at 12 Å, and had a switching function from 8 Å to 12 Å. The long-range electrostatic interactions were computed using the particle-mesh Ewald method (30), with a tolerance of 1.0 × 10⁻⁶. All hydrogen bonds were constrained to the heavy atoms by the SHAKE algorithm (31) with a tolerance of 1.0 × 10⁻⁸, allowing simulation time steps of 2 fs. The system was equilibrated in multiple steps for ∼50 ps, using an equilibration protocol similar to that used for the simulation of an actin system (32). A detailed description of the equilibration protocol can be found elsewhere (32). The simulation was then continued for a production run in the constant NPT ensemble for a duration of ∼17 ns for GDP-tubulin, and ∼15 ns for GTP-bound tubulin. Because this study examines major conformational changes in addition to local rearrangements, a total of six independent simulations of GDP- and GTP-bound tubulins were conducted for inspection, to address the concern that the structures may have become trapped in local energy minima. These simulations were examined for major variations in the nature of bending, such as straight versus curved bending, or radially outward versus tangential bending directions. No significant variations were found, except for slight variations in the extent of bending or directions (see Supplementary Material, Data S1 for comparisons of independent simulations).

Coarse-graining

To examine the local structural rearrangements of the dimer at the level of secondary structures, and later to study the vibrational modes of motion of these structures, CG sites were formed, based on the center-of-mass positions of the α-helices and β-sheets. The helices and β-sheets in this analysis were designated in accordance with previous representations (4,5), where the 12 helices and the 10 β-sheets of each monomer were denoted by the symbols H1–H12 and B1–B10, respectively (see Nogales et al. (4) and Löwe et al. (5) for nomenclatures.) The CG analysis, based on secondary structures, reduced the complexity of the system while providing relevant information on the conformational changes of the dimer. In the vibrational mode analysis, a different level of coarse-graining that is based on the C_α carbon atoms of the amino-acid residues was used in addition to the center-of-mass-based CG sites.

Quasiharmonic analysis

One useful tool for studying the collective modes of motion in proteins is quasiharmonic analysis (QHA). This method is based on the fluctuations of atomic coordinates obtained from the trajectories sampled during MD simulations. Consequently, the anharmonicity of the potential surface governing the protein dynamics is implicitly incorporated. From the MD trajectories, both the average coordinates and the covariance matrix of the fluctuations about the average coordinates are calculated. Then the quasiharmonic vibrational modes and the corresponding quasiharmonic frequencies are determined by the diagonalization of the mass-weighted fluctuation matrix.

RESULTS AND DISCUSSION

Here we present the results of MD simulations and the QHA of unassembled tubulin dimers. First, the intrinsic intradimer bending of GDP-tubulin is examined. Then the effect of nucleotide state on the bending of the dimer is examined by comparing GDP- and GTP-bound tubulin. Finally, the local structural transformations of GDP-bound tubulin that may arise from GTP hydrolysis are investigated by examining the dynamics of GDP-tubulin through MD simulations and QHA.

Intrinsic intradimer bending of GDP-tubulin

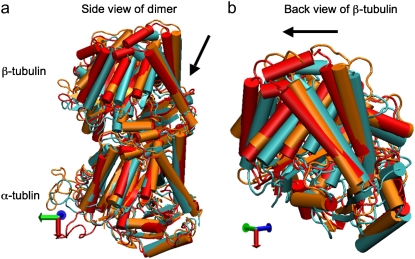
The primary question to be addressed involves the intradimer bending of GDP-tubulin when the dimer is released from its lattice-constrained straight conformation. The MD simulations, performed using the straight structure as a starting configuration, provide this information when the equilibrium structure of the dimer from simulations is compared with the original straight structure of the dimer from tubulin sheets. This comparison is performed by orienting one structure with respect to the other. In this case, the C_α atoms of α-tubulin in the straight αβ-tubulin dimer are used as reference for the orientation. In Fig. 1, the superposition of the straight GDP-tubulin from the experimental structure, and the GDP-tubulin from the MD simulation, are shown together with the structure of GTP-bound tubulin (discussed below). The dimer from the MD simulation undergoes oscillatory motion around an average curved conformation. Therefore, the superposition with the straight structure is based on the average structure of GDP-tubulin, where the averaging was performed using the last 5 ns of data of the equilibrated MD simulation.

FIGURE 1.

Illustration of average coordinates of GTP-tubulin from MD simulations, superimposed with the average coordinates of curved GDP-tubulin from a simulation and straight GDP-tubulin from a zinc-induced tubulin sheet. The average curved tubulin dimers from the simulation are calculated by orienting each frame with respect to the straight tubulin dimer, based on the C_α atoms of α-tubulin. For better clarity, the superimposed dimer structures are shown in different views: (a) side view consisting of the whole dimer, and (b) back view consisting of only the β-tubulin monomer. Arrows indicate the directions of bend, as viewed from different angles. Red and orange represent the average GDP-tubulin and GTP-tubulin, respectively, from MD simulations; cyan represents the straight GDP-tubulin from the tubulin sheet.

It is evident from Fig. 1 that the free GDP-tubulin exhibits a curved conformation, revealing that GDP-tubulin has an intrinsically curved conformation, as witnessed in the RB3-tubulin complex experiment (15). However, slight variations were observed in the direction of bending from that seen in the RB3-tubulin complex (see Data S1 for a discussion of the structure of free GDP-tubulin from the MD simulation, compared with that of GDP tubulin from the RB3-tubulin complex experiment). Despite subtle variations, this study is in agreement with the overall notion that the intradimer bending of GDP-tubulin is incompatible with the formation of canonical lateral contacts in MTs (16). In other words, this study confirms the intrinsically curved nature of GDP-bound tubulin dimer.

Nucleotide dependence of intradimer bending

A fundamental issue in the study of dynamic instability involves straight versus curved conformations of GTP-tubulin dimer. As mentioned in the Introduction, the general belief is that GTP-bound tubulin dimer exists in the active state, corresponding to the straight conformation amenable to MT wall formation. This prediction is based on the observation that GDP-containing protofilaments from the peeling ends of depolymerizing MTs have a greater tendency to form ring polymers than GTP-tubulin dimers do (33). On the other hand, a recent study (20) argued that unassembled GTP-tubulins are in inactive, curved conformations. In the past, predictions concerning the curved GTP-tubulin dimer were based on other tubulin family proteins whose structures were resolved by crystallography. Among these is the FtsZ dimer, known to be a prokaryotic homologue of the tubulin dimer (34). The FtsZ dimer and the tubulin dimer polymerize into similar protofilaments. The FtsZ dimer was found to exhibit a curved conformation as the RB3-bound tubulin dimer (34), except for a bend direction toward the inside of the MT, as opposed to the outward bending of the RB3-tubulin complex. Based on these studies, it was reported that proteins in the tubulin family exhibited curved conformations, irrespective of their nucleotide state (see Table 1 of Buey et al. (20)). However, recent experimental study supported the notion of a nucleotide-independent curved conformation based on the αβ-tubulin dimer (21). Rice et al. (21) probed the conformation of unpolymerized αβ-tubulin by examining allocolchicine binding affinities. They argued that colchicine-like drugs bind in an open cleft between α- and β-tubulin that becomes substantially occluded in the straight conformation. If GTP were to alter the balance between straight and curved conformations, measurable nucleotide-dependent differences in the allocolchicine binding affinity would result. However, they found that the measured affinity of αβ-tubulin for allocolchicine is independent of the nucleotide state. Hence they concluded that any nucleotide-dependent conformational changes that might occur in αβ-tubulin could not involve domain rearrangements that would significantly alter the curvature of the heterodimer. To support this observation, they also examined the small-angle x-ray scattering profile for αβ-tubulin:GTP and αβ-tubulin:GDP, and found results that were essentially identical and indicative of a curved conformation. Based on these and other studies on the crystal structure of γ-tubulin bound to both GDP and GTP nucleotides and kinetic simulations, Rice et al. (21) concluded that major conformational changes do not occur in response to GTP binding, and that the unpolymerized αβ-tubulin differs significantly from the polymerized αβ-tubulin.

Our study used MD simulations of GTP-tubulin dimer to assess the effect of nucleotide state on the bending behavior of tubulin dimer, serving as a means to analyze the above observations. This was achieved through the introduction of γ-phosphate into the structure of GDP nucleotide located at the exchangeable site of the dimer. The effect of this perturbation was examined by comparing the structure of GTP-tubulin from MD simulations with the structure of GDP-tubulin from simulations and GDP-tubulin (straight) from zinc-induced tubulin sheets, as shown in Fig. 1. Because the GTP-tubulin dimer from the simulation was also under constant motion, the average coordinates of the dimer were used for comparison, similar to the comparison performed for GDP-tubulin. It is evident from Fig. 1 that the free tubulin dimers are curved, irrespective of nucleotide state. This observation is in agreement with the prediction of Rice et al. (21) described above. It is also in agreement with the prediction of Buey et al. (20), based on tubulin family proteins. In this regard, a new, comprehensive experimental analysis of FtsZ protein has emerged that predicts the nature of conformational changes on nucleotide state (35). By examining the structures of FtsZ protein from different organisms under different nucleotide states (GTP, GDP, and empty), Oliva et al. (35) revealed the absence of a nucleotide-dependent conformational change. They predicted that the immediate effect of GDP to GTP exchange in FtsZ protofilaments is to promote a longitudinal association of monomers into protofilaments, but not a conformational change in monomers (35). Therefore, the absence of a curved to straight transition upon changing the nucleotide state of the tubulin dimer in our analysis supports, and is supported by, the absence of significant nucleotide-dependent conformational changes in the FtsZ protofilament.

In terms of bending directions, Fig. 1 reveals that both GDP- and GTP-bound tubulins exhibit similar tangential bends, as opposed to the radially outward bending of the RB3-tubulin complex (see Fig. S1 in Data S1). In this respect, both dimers exhibit a bending behavior that resembles the intradimer bending of GDP-tubulin seen previously (16). On the other hand, even though no significant conformational transformation that can be defined as a curved-to-straight transition has occurred, an interesting feature in Fig. 1 is the slight difference in the extent of bending of GDP- and GTP-tubulin. (For the statistical relevance of this observation, the relative bending of GDP- and GTP-tubulin was examined by comparing different independent simulations, and the result is shown in Fig. S2, a and b in Data S1.) As shown in Fig. 1, the average bending of GTP-tubulin is smaller than that of GDP-tubulin. This result leads to an interesting observation, because it implies that the perturbation induced by the change in nucleotide state facilitates the straightening of the dimer. This observation is in agreement with the findings in a study of guanylyl (α,β)methylenediphosphonate (GMPCPP)-bound tubulin (16). By performing a cryo-electron microscopy experiment involving the tubulin dimer bound to the nonhydrolysable GTP analogue GMPCPP, Wang and Nogales illustrated the curved nature of GTP-tubulins (16). However, the curved conformation observed in the GMPCPP-tubulin dimer was markedly smaller than that of GDP-tubulin (16). Thus the authors posited a structural pathway, associating the binding of GTP nucleotide at the exchangeable site with the straightening of the dimer, as a possibility for GTP-driven MT assembly.

The difference between GDP- and GTP-tubulin in the extent of curving seen in our analysis is not dramatic. However, this result supports the notion of straightening upon GTP binding. A significant straightening that may lead to a curved-to-straight conformational change may occur upon the assembly of the dimer into MTs, through the binding of lateral or longitudinal MT contacts. This idea was suggested by Buey et al. (20), and was supported by the experimental work of Oliva et al. (35) on FtsZ that involved a new model, in which lateral interaction helped determine the curvature of FtsZ protofilaments. Another explanation for the small difference seen in this analysis, as opposed to the marked difference seen in GMPCPP-tubulin, could be related to the long-range allosteric effects of the GTP nucleotide upon polymerization into protofilaments. The allosteric effect of the GTP nucleotide may induce changes at the immediate interdimer interface along the protofilament, rather than at the intradimer interface that is 4 nm away. As a result, significant conformational changes from the nucleotide state might arise at the interdimer interface, rather than at the intradimer interface. Any of these factors, or a combination of them, may account for the difference between the small amount of straightening observed in our analysis and in the GMPCPP-tubulin experiments. These suggestions may be explored through large-scale MD simulations of dimer-dimer interactions, and work in this direction is in progress.

In general, our study predicts a curved conformation of GTP-tubulin, similar to that of GDP-tubulin, but to a lesser extent. Next, the local structural changes of the dimer in the event of GTP hydrolysis to GDP will be examined based on the dynamic behavior of GDP-tubulin revealed by MD simulations and QHA.

Structural rearrangements

Local conformational changes

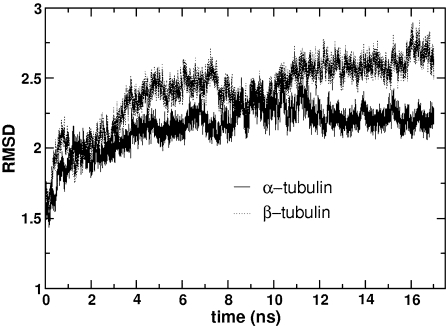
It is known from free-energy analysis that the energy released during GTP hydrolysis is stored within the microtubule lattice (36). This means that GDP-tubulins in the microtubule lattice or zinc-induced sheet are under mechanical strain that will undergo structural transformations upon release. This transformation is considered to affect mainly the β-tubulin. For example, Nogales et al. (33) stated that major conformational changes are likely to occur in β-tubulin, because GTP-hydrolysis occurs within this monomer. Amos and Lowe (37) hypothesized that hydrolysis could change the relative orientation of the N-terminal and intermediate domains of β-tubulin. In each of these examples, the dominant conformational changes were thought to occur within β-tubulin. This hypothesis can be tested by measuring monomer-level conformational changes that can be determined by evaluating the root mean-square atomic deviations (RMSDs) of each monomer separately, where each monomer is first oriented with respect to its own original crystal structure, to remove rigid-body translations and rotations. If the conformational changes are confined to β-tubulin, a more significant deviation from the crystal structure should be observed in β-tubulin than in α-tubulin. Fig. 2 shows the C_α RMSD of each of the two monomers as a function of time. As expected, the overall RMS deviation of the β-tubulin in GDP-tubulin (mean RMSD, 2.401 ± 0.233) is higher than that of the α-tubulin (mean RMSD, 2.153 ± 0.169). Although the difference in the overall RMSD values of the two monomers is not so dramatic, the relative difference is noted, with the larger deviations from the crystal structure being in the β-tubulin, as proposed.

FIGURE 2.

The C_α RMSD of α-tubulin and β-tubulin in the GDP-tubulin dimer from their crystal structures. The analysis was performed by orienting each monomer with respect to its own original structure, to remove the rigid-body translations and rotations of one monomer with respect to the other.

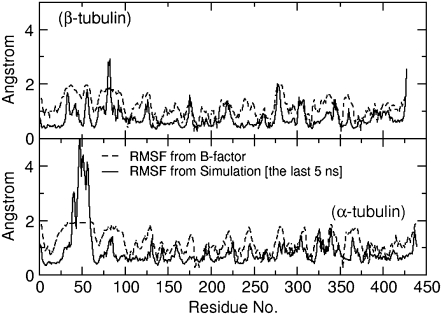
To examine in more detail the local structural transformations of GDP-tubulin upon relaxation from its lattice-constrained structure, the root mean-square atomic fluctuations (RMSFs) of each monomer in the dimer were investigated. Fig. 3 shows the isotropic RMSFs of each monomer, based on the last 5-ns trajectories of the C_α atoms. Fig. 3 also shows the RMSFs evaluated from the x-ray temperature factors or the isotropic B-factors, where the data for the B-factors are extracted from the 1JFF PDB file (5). It can be seen in Fig. 3 that, excluding the region corresponding to residues α:35–60 that were not resolved by crystallography, the RMSFs of residues in β-tubulin were relatively higher than those in α-tubulin. Consider, for instance, the values of the RMSF in each monomer corresponding to four residues of the monomer with the largest C_α fluctuations (Fig. 3). In β-tubulin, these residues and their RMSFs in decreasing order are 2.92 Å (β:82), 2.55 Å (β:427), 2.01 Å (β:277), and 1.81 Å (β:56). A similar set of residues in α-tubulin include 1.71 Å (α:339), 1.69 Å (α:326), 1.63 Å (α:437), and 1.40 Å (α:85) (the residues in β-tubulin β:56, β:82, β:277, and β:427 correspond to β:58, β:84, β:279, and β:437, respectively, in Nogales et al. (4) and Löwe et al. (5)). Therefore, these observations support the proposition that relatively higher conformational changes occur in β-tubulin than in α-tubulin.

FIGURE 3.

The RMSF of C_α atoms in α-tubulin and β-tubulin in the GDP-tubulin dimer, using MD data from the last 5 ns of the simulation run. For comparison, the RMSF calculated from the isotropic experimental B-factors is included, where RMSF =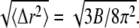 Data for the B-factor were extracted from the 1JFF PDB file (5).

Deformations in secondary structures

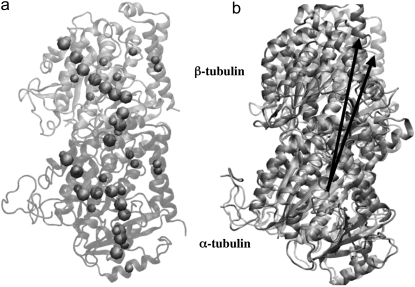
To gain further insight into the local structural rearrangements of the dimer in the event of GTP hydrolysis, the bending deformation of the dimer was examined at a CG level representing the rigid secondary structure. To quantify the bending deformations of rigid secondary structures, the angle Θ subtended by the center of mass of each secondary structure, i.e., the angle traced by helices and β-sheets, was measured. (The angles are identified by first removing trivial motions of rigid body translations and rotations by orienting the trajectories of the dimer from the simulations with respect to the original straight structure by aligning the C_α atoms of the tubulin dimer. Next, a reference point defining a fixed laboratory frame is selected based on which vectors joining the reference point to the center of mass of the secondary structure are drawn. In this analysis, the center of mass of the straight tubulin dimer is used to mark the fixed reference point. At each instant of time, sets of vectors joining the fixed reference point to the center of mass of each secondary structure of the tubulin dimer are drawn for both the straight and the curved conformations.) This description is rendered in Fig. 4. Fig. 4 a shows the position of the center of mass of each rigid structure that serves as a coarse-graining site, and Fig. 4 b, shows the angle traced by the center of mass of a particular helix. The vectors shown in Fig. 4 b, represent the vectors joining the center of mass of α-tubulin to that of a particular helix at two instants of time. The angle subtended by these vectors corresponds to the angle traced by the secondary structures.

FIGURE 4.

(a) Straight (crystal) structure of the GDP-tubulin dimer, together with center-of-mass positions of the 12 major helices and 10 β-sheets, as defined by Nogales et al. (4). Positions of the center of mass in each monomer are shown by CG spheres. The bigger spheres represent the center-of-mass positions of the β-sheets, whereas smaller spheres represent those of helices. (b) Straight and curved conformations of the GDP-tubulin dimer with a pair of vectors demonstrate the angle traced by a particular secondary structure as an example.

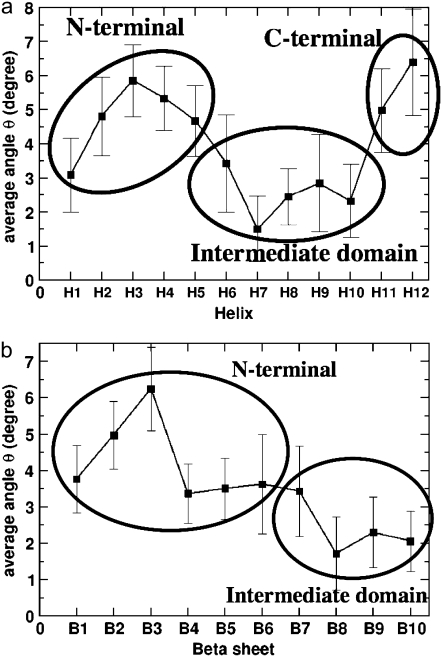
On the basis of this measurement, the nature of the deformation of secondary structures (helices and β-sheets) of the GDP-tubulin dimer was examined in connection with the three functional domains of tubulin, i.e., the N-terminal domain, the intermediate domain, and the C-terminal domain. Each of these domains is categorized on the basis of their functions (4).The N-terminal domain serves as a nucleotide-binding domain. (The N-terminal domain is composed of six parallel β-strands alternating with α-helices, forming a Rossmann fold that is a folding typical of nucleotide binding proteins. This terminal includes residues 1–205 with α-helices H1 and H2 lying on one side of the sheet of β-strands with helices H3, H4, and H5 on the other side.) The intermediate domain serves as a taxol-binding domain. (The intermediate domain consists of residues 206–381 that forms a mixture of β-sheets and the surrounding five α-helices. This domain consists of a helix H8 that is parallel to the longitudinal interface of the two monomers and a core helix H7 that connects the nucleotide binding domain with the intermediate domain). The C-terminal domain serves as a binding surface for motor proteins. (The C-terminal consists of two antiparallel helices H11 and H12 that form the crust of the protofilaments on the outside surface of microtubule on which the motor proteins bind and move.) Our study examines the fluctuations in the three domains to see if there is any correspondence between the functionally defined domains and their dynamics. Figure 5, a and b presents the average behavior of the fluctuations in these domains, where averaging is performed by evaluating the time average of the instantaneous Θ values that quantifies the bending fluctuation (arising from dimer oscillation) of the helices and β-sheets of β-tubulin. (The time evolution of the instantaneous bending fluctuations of the structural motifs, i.e., the data from which the average bending angle was extracted are shown in Figs. S3 and S4 in Data S1.) It can be seen in the plots of Fig. 5 that the magnitudes of bending deformations within different functional domains of GDP-tubulin, and especially in the intermediate domain, are distinctively different. Overall, helices in the intermediate domain exhibit relatively low local rearrangement compared with helices in the N-terminal or C-terminal domains. Similarly, β-sheets within the intermediate domain exhibit relatively low bending deformations relative to those in the N-terminal. These observations signify the correspondence between the functionally defined domains and their dynamics.

FIGURE 5.

Time averages of bending angles traced by (a) the α-helices and (b) the β-sheets of β-tubulin in the GDP-tubulin dimer. The instantaneous bending angles of each structural motif were measured by orienting each snapshot of the dynamic trajectory with respect to the straight structure of the dimer from the tubulin sheet, where the α-tubulin of the sheet was used as a reference for the orientation. Error bars were determined by calculating the standard deviation of the data.

The variations of flexibility in the three domains, and in particular the low flexibility of the intermediate domain, may be explained by a number of reasons. One explanation may be related to helix H8 that lies parallel to the interface between the two monomers. This helix experiences a wide range of longitudinal interactions across the interface. As a result, it endures a strong hindrance against the bending mode of motion. Another helix, H7, is the core helix connecting the N-terminal and the intermediate domain, and it may also experience strong steric repulsion because of its diagonal layout that bridges different domains. In contrast, the helices in the N-terminal and C-terminal domains are exposed to surfaces and are relatively free to move, compared with structures in the intermediate domain. The relatively low deformation of the intermediate domain thus signifies the role played by the domain in resisting the bending mode of motion occurring during GTP hydrolysis. In general, the functionally defined domains exhibit distinct bending deformations in GDP-tubulin, with the lowest deformation corresponding to the intermediate domain.

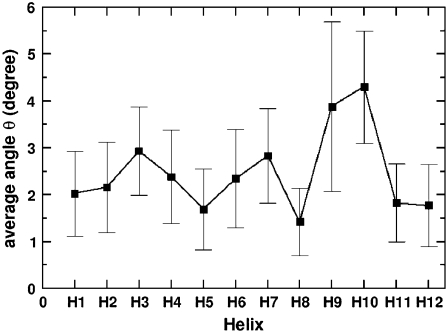
To explore these behaviors within GTP-tubulin, a similar analysis was performed in which the average bending of helices in β-tubulin was measured for GTP-tubulin. Fig. 6 shows the results of this analysis. Overall, the average bending of local structures in GTP-tubulin is smaller than of those in GDP-tubulin, except for some of the structures within the intermediate domain. However, the relative dynamics of structural motifs in the intermediate domain of GTP-tubulin are not as distinctively small as what was found in GDP-tubulin, although the relative bending of H8 is the smallest. The difference in local deformations between GDP- and the GTP-tubulin may be a consequence of the difference in the local environment of GTP-tubulin that possesses an additional γ-phosphate in β-tubulin.

FIGURE 6.

Time averages of bending angles traced by the α-helices of β-tubulin in the GTP-tubulin dimer. The calculations were performed in a manner similar to those for GDP-tubulin. Error bars were determined by calculating the standard deviation of the data.

Quasiharmonic analysis

The cooperative motion of secondary structures, in which sets of helices and β-sheets move collectively, can be well-characterized by a QHA that describes the collective mode of motion. Here we present the results of QHA, where the dominant motions of the low-frequency modes and their relevance to MT polymerization are examined. The QHA of this study was performed at two levels of coarse-graining. The first level considers the positions of C_α carbon atoms as CG sites. This selection is similar to that of the CG sites in the elastic network model, which treats C_α atoms as CG sites representing amino-acid residues (38). The second level of coarse-graining is based on the centers of masses of the secondary structures, similar to the last section. For both levels of coarse-graining, the trajectories of CG sites were obtained from the all-atom MD runs. In particular, the CG site trajectories, determined from the last 5 ns of the equilibrated all-atom MD simulations, were used for construction of the covariance matrix. (See the discussion in Data S1 that examines the choice of a 5-ns time scale in ensuring the convergence of low-frequency modes for sampling functionally relevant motions.)

Low-frequency modes

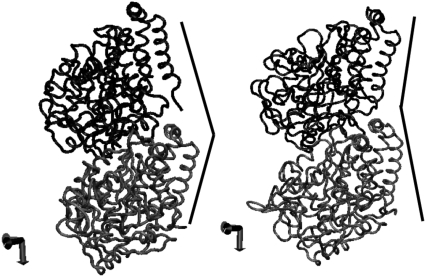
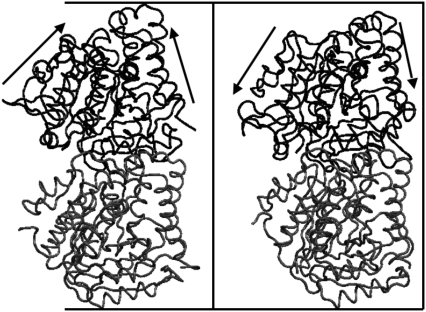
Based on the quasiharmonic frequency and eigenvector of each mode, the collective displacement of the system along a particular mode can be determined by constructing the CG quasiharmonic trajectories. Overall, the quasiharmonic trajectories reveal different types of concerted movements that may be categorized under twisting, bending, compression, or a combination of these. For example, a graphical representation of one of the important low-frequency modes of the C_α-based CG sites is given in Fig. 7. Fig. 7 represents the bending mode of motion corresponding to the fourth lowest frequency mode of GDP-bound tubulin, where the images represent snapshots of two extrema conformations. This mode is similar to the bending mode of motion found in the elastic network calculation (39). However, the bending fluctuation in this analysis is centered about a curved conformation, as opposed to the wobbling motion of the elastic network model that is centered about a straight conformation. This subtle difference can be attributed to the fact that the elastic network Hamiltonian treats the straight conformation as a reference structure, which by construction becomes the lower-energy conformation, thereby biasing the oscillation about this conformation. Another interesting observation corresponds to the fifth lowest frequency mode that can be identified as a compression/stretching-like movement. The compression type of motion in this mode may be regarded as longitudinal compression, but longitudinal compression is also coupled with a lateral expansion that may occur because of the need to relieve steric repulsions arising from the compression process. A similar observation was made in the elastic network model, where coupled longitudinal and lateral compression/stretching was shown (39). Fig. 8 shows snapshots of the compression motion arising from the fifth lowest frequency mode of GDP-tubulin dimer.

FIGURE 7.

Snapshots of the bending mode of motion of C_α-based CG sites of the GDP-tubulin dimer corresponding to mode 4. The images represent the two extreme fluctuations of the quasiharmonic trajectories constructed based on the quasiharmonic mode and frequency of mode 4. The lines indicate the bending directions.

FIGURE 8.

Snapshots of the stretching/compression mode of motion of C_α-based CG sites corresponding to mode 5 of GDP-bound tubulin. The images represent two extreme fluctuations of the quasiharmonic trajectories constructed, based on the quasiharmonic mode and frequency of mode 5. Arrows indicate the directions of motion revealed by the movie.

Other low-frequency modes that may be relevant for MT polymerization correspond to the lowest three quasiharmonic modes. Among these, the collective motion of the third lowest frequency mode (mode 3) of GDP-tubulin exhibits a twist-like motion, with an opposite-sense rigid-body rotation of the two monomers. In particular, the mode demonstrates the rolling tendency of the two monomers toward each other, giving rise to a slight shift in the positions of interfacial contacts. Consequently, the mode may affect the longitudinal interaction of the dimer within the MT protofilament. The twist-like motion of mode 3 of GDP-bound tubulin is shown in Movie S3. The remaining two lowest modes of GDP-tubulin, i.e., modes 1 and 2, exhibit a complex motion that consists of mixed types of collective motions. The motion of these modes is also shown as movies in Movie S1 and Movie S2, allowing for easier visualization. The movies are based on the trajectories of the modes. As seen in the movies, the lowest frequency mode (mode 1) undergoes a compression-like motion that also includes twist-like behavior. The second lowest mode also involves a twist-like motion of β-tubulin, coupled with the stretching of α-tubulin along the protofilament. These modes may contribute to MT polymerization by affecting the lateral and longitudinal contacts through the twisting and stretching or compression motions within the modes.

Finally, with regard to GTP-bound tubulin, similar behavior was observed in the overall motion of the low-frequency quasiharmonic modes. Generally speaking, the different collective modes of motion that are recognized as bending or compression, for instance, of a particular low-frequency mode in GDP-tubulin are also found in GTP-tubulin. However, there are local variations in the motions of structural motifs within each mode. Movie S4 and Movie S5 show the collective motion of low-frequency modes in GTP-bound tubulin (Movies S4 and S5 show low-frequency modes 2 and 3, respectively).

Fluctuations of functionally relevant structures

The different types of collective movements observed within low-frequency modes can be presumed to have specific contributions to MT assembly or disassembly. To gain a better understanding of the local structural reorganization in a specific mode and to propose the likely contributions of the mode to lateral or longitudinal interactions, the fluctuations of CG sites, based on the displacements along the individual modes, can be examined. To simplify the discussion and focus on major deformations, descriptions are restricted to fluctuations within β-tubulin, which is known to undergo larger conformational changes. Here we discuss the fluctuation behavior of functionally relevant structures.

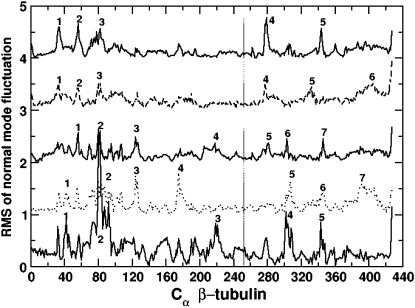
The fluctuation of a CG site along a particular mode of motion can be computed by using the eigenvalue and eigenvector of the mode. Fig. 9 shows the RMS fluctuation of the C_α atoms of β-tubulin in GDP-tubulin for quasiharmonic modes 1–5, where fluctuations are measured from the average CG coordinates of the last 5-ns MD runs. As shown in Fig. 9, regions of high flexibility are detected by the magnitudes of the RMS fluctuation data. For clarity, these regions are marked by numbers 1–7. Inspection of these structural regions reveals that the majority of structures with high fluctuations are loops, as expected. However, not all loops have high flexibility within all low-frequency modes. One functionally relevant loop with such behavior is loop B5–H5 (the region marked by the number 4 in mode 2.) This loop, defined as the T–5 loop by Nogales et al. (4), is known to have residues that are involved in both nucleotide-ribose binding and longitudinal contacts along the protofilaments (5). The loop is found to have high RMS fluctuation only within mode 2. It has low flexibility within all the remaining four low-frequency modes. The lack of significant flexibility in the four low-frequency modes except for mode 2 may indicate the dominant mode of motion governing the overall fluctuation of the loop that is demonstrated by the isotropic RMSF (Fig. 3).

FIGURE 9.

Fluctuations of C_α-based CG sites in the β-tubulin of GDP-tubulin dimer. Abscissa represents residue numbers of C_α atoms in β-tubulin. The RMS fluctuations of the lowest five quasiharmonic modes are shown. For clarity, the magnitudes are shifted vertically from mode 1 to mode 5. In each mode, numbers from 1 to 7 mark regions with high flexibility. The structure of residues near these regions can be determined by referring to the secondary structure elements given by Nogales et al. (4). The numbering here is referred to in the text, in conjunction with the secondary structures given by Nogales et al. (4), in regard to different structures.

Another important structure in β-tubulin which is pertinent to MT polymerization is the loop connecting helices H7 and H8. This loop consists of residues β:241–β:250 (i.e., residues β:243–β:252, according to the numbering of Nogales et al. (4)), and is referred to as the T–7 loop by Nogales et al. (4). In the MT lattice, this loop is found across the nucleotide site of contiguous subunits along the protofilament, and is known to interact with the nucleotide of the neighboring subunit along the protofilament (40). Fig. 9 indicates that loop T–7 has low RMS fluctuation in all five low-frequency modes. The low flexibility of the loop is likely attributable to its interaction with the nucleotide across the longitudinal interface. Interestingly, loop T–7 comprises highly conserved residues that extend to their bacterial homologue FtsZ (40,41). The low RMS fluctuation observed in this region signifies the low flexibility of the conserved residues. Another adjacent structure within β-tubulin that is engaged in the interaction across the longitudinal interface includes helix H8. As seen in Fig. 9, the C_α atoms within this structure and, in particular, those of β:Lys252 (they are marked by vertical lines for each mode in Fig. 9) display low RMS fluctuations in all modes considered. This is especially interesting because it is known that interaction with the nucleotide across the longitudinal interface is completed by Lys252 of helix H8 in β-tubulin (i.e., β:Lys254, according to the numbering of Nogales et al. (4)), which interacts with the γ-phosphate of the N-site nucleotide (5). The relative rigidity of helix H8 and the surrounding residues, as manifested by low RMS fluctuation, reflects the longitudinal interaction at the interface of the two monomers.

In contrast to the low flexible regions discussed above, regions in β-tubulin corresponding to the loop H1–B2, and the overall region between H2 and B3, are found to exhibit high fluctuations within all five low-frequency modes. (In Fig. 9, these regions are marked by 1 and 2 for modes 1, 2, and 3, and by 1, 2, and 3 for modes 4 and 5.) The loop H1–B2 is known to have functional relevance for MT assembly, where the major lateral contacts in MT polymerization occur between the M-loops (loop B7–H9) of one dimer and the H1–B2 loops of the neighboring dimer in adjacent protofilaments (5). The relatively high flexibility of the H1–B2 loop facilitates the accessibility of the loop for lateral interactions, signifying the contribution of these modes to lateral interactions. A larger contribution to the lateral interaction may be expected from those modes exhibiting high fluctuation within both the M-loop and H1–B2 loop (5). In this regard, modes 3, 4, and 5, corresponding to twisting, bending, and compression-like movements, respectively, show high flexibility within the M-loop (in Fig. 9, these are regions marked by 5 for mode 3, and by 4 for both modes 4 and 5) in addition to the H1–B2 loop. These modes of motion may thus be considered to make a more significant contribution to the lateral interactions than do the lowest two modes. In general, the different levels of fluctuations of the regions described above reveal how the structures that have significant functional relevance for MT polymerization/depolymerization are affected by the lowest-frequency modes.

CONCLUSIONS

Dynamic instability is a ubiquitous process that is essential for the proper functioning of cells. It involves the slow growth of MTs, followed by fast depolymerization in an abrupt, stochastic manner. The origin of dynamic instability was attributed to the bending of GDP-tubulin that arises from the occurrence of GTP hydrolysis. This notion inspired research focused on revealing the conformation of GDP-bound tubulin that was critical for understanding dynamic instability. As a result, a number of experimental studies revealed the curved confirmation of the GDP-tubulin dimer (12,15,16). However, these experiments involved external factors that may have influenced the intrinsic bending of the dimer. Moreover, the experiments provided only static conformations of the dimer, and lacked sufficient information on the dynamic processes triggered by GTP hydrolysis that led to fast depolymerization. Therefore, this study sought to reveal the intrinsic bending of the GDP-tubulin dimer.

Another aspect of our study involved the examination of a straight versus curved conformation of the GTP-bound tubulin dimer. In the past, GTP-tubulins were considered to have a straight conformation, compatible with MT polymerization. However, recent studies argued against the straight conformation of GTP-tubulin (20,35). These studies suggest that unassembled αβ-tubulins adopt a curved conformation irrespective of nucleotide state, and the conformational changes that lead to the straightening are consequences of lattice assembly. These conclusions were largely based on indirect observations, e.g., of the structures of FtsZ that are tubulin homologues of prokaryotes. However, Rice et al. (21) illustrated the curved conformation of αβ-tubulin through different measures, and employed kinetic simulations in addition to two-solution probes of the conformation of αβ-tubulin. The two-solution probes involved allocolchicine binding affinities and the small-angle x-ray scattering profile of unpolymerized αβ-tubulin. Based on these and the structural studies of γ-tubulin bound to both GTP and GDP nucleotides, the authors supported the notion of GTP-tubulin straightening upon lattice assembly. They posited that lateral self-assembly drives αβ-tubulin conformational changes, whereas GTP plays a secondary role in tuning the strength of longitudinal contacts within the MT lattice.

To address these issues and examine different aspects of dynamic instability, our study investigated unpolymerized tubulin dimer by focusing on three topics: 1), the intrinsic bending of GDP-tubulin dimer; 2), the nucleotide dependence of tubulin dimer bending; and 3), the dynamic behavior of GDP-tubulin dimer and its local structural rearrangements.

The GDP-tubulins were found to have an intrinsically curved structure, supporting the notion that the ground state of GDP-tubulin is a curved conformation. The dimer was found to swing into a curved conformation soon after its release from the lattice-constrained straight structure, and then to oscillate around the curved conformation, with varying local deformations. The nucleotide dependence of tubulin-dimer bending was examined by converting GDP-bound tubulin into GTP-bound tubulin through the introduction of γ-phosphate into β-tubulin. Based on this modification, the intrinsic conformation of GTP-bound tubulin was found to exhibit a curved conformation, similar to GDP-tubulin. In that regard, this study agrees with the observations made by Rice et al. (21), and supports the notion proposed by Buey et al. (20) that tubulin dimers are curved, irrespective of nucleotide state. In terms of the extent of bending, GTP-tubulin was found to exhibit a tendency toward smaller bending, similar to that seen in GMPCPP (16), but to a lesser extent. This slight difference in the extent of bending between GDP- and GTP-bound tubulin dimers may be related to the local perturbation induced by the γ-phosphate of the GTP-nucleotide. The small bending difference observed in our study may be considered to be the effect of fine-tuning attributable to the GTP-nucleotide, as suggested by Rice et al. (21). By contrast, major straightening of the dimer may arise from the longitudinal or lateral dimer-dimer interactions occurring upon lattice assembly.

In terms of local deformations of the dimer, β-tubulin exhibited higher deformations than α-tubulin when examined at the monomer level. On the other hand, within the β-tubulin of the GDP-tubulin, the three functional domains showed distinct levels of deformation. In particular, the intermediate domain exhibited low bending deformation, suggesting a dynamical correspondence for the functionally defined domains. Within the intermediate domain of β-tubulin, regions corresponding to helices H7 and H8 and the loop connecting the helices showed relatively low deformations, revealing the most rigid-like structure of the dimer. Such distinctive deformations of the intermediate domain were not observed within the GTP-tubulin dimer, which exhibited an overall lower local deformation relative to GDP-tubulin. This may be related to the additional γ-phosphate that may affect the local environment of the dimer.

Local structures with functional relevance for MT polymerization were also examined by conducting quasiharmonic CG analysis within the realm of the low-frequency modes of GDP-tubulin. The region corresponding to the T–7 loop, containing conserved residues, was found to exhibit low fluctuation within all low-frequency modes. By contrast, regions corresponding to the H1–B2 loop and the M-loop, which are known to be involved in lateral interactions during MT assembly, exhibited high fluctuations within the low-frequency modes, suggesting the contribution of these modes to MT polymerization. For comparison, the overall bending modes of GTP-tubulin were also examined and found to have similarities with those of GDP-tubulin.

More generally, this work sets the stage for the development of a multiscale CG model for MT polymerization and dynamical instability. The key modes of motion identified in our analysis can serve as the basis for a low-resolution CG model of αβ-tubulin heterodimers, while retaining the essential dynamical features from the molecular level that influence greater-length and time-scale MT phenomena. Work in this direction is in progress.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.