Tryptophan-Tryptophan Energy Migration as a Tool to Follow Apoflavodoxin Folding

Abstract

Submolecular details of Azotobacter vinelandii apoflavodoxin (apoFD) (un)folding are revealed by time-resolved fluorescence anisotropy using wild-type protein and variants lacking one or two of apoFD's three tryptophans. ApoFD equilibrium (un)folding by guanidine hydrochloride follows a three-state model: native ↔ unfolded ↔ intermediate. In native protein, W128 is a sink for Förster resonance energy transfer (FRET). Consequently, unidirectional FRET with a 50-ps transfer correlation time occurs from W167 to W128. FRET from W74 to W167 is much slower (6.9 ns). In the intermediate, W128 and W167 have native-like geometry because the 50-ps transfer time is observed. However, non-native structure exists between W74 and W167 because instead of 6.9 ns the transfer correlation time is 2.0 ns. In unfolded apoFD this 2.0-ns transfer correlation time is also detected. This decrease in transfer correlation time is a result of W74 and W167 becoming solvent accessible and randomly oriented toward one another. Apparently W74 and W167 are near-natively separated in the folding intermediate and in unfolded apoFD. Both tryptophans may actually be slightly closer in space than in the native state, even though apoFD's radius increases substantially upon unfolding. In unfolded apoFD the 50-ps transfer time observed for native and intermediate folding states becomes 200 ps as W128 and W167 are marginally further separated than in the native state. Apparently, apoFD's unfolded state is not a featureless statistical coil but contains well-defined substructures. The approach presented is a powerful tool to study protein folding.

INTRODUCTION

Although much has been learned about protein folding during the last decade, many mechanistic and dynamical aspects of this process are still unknown. An important breakthrough has been the realization that a free energy landscape or folding funnel better describes protein folding instead of a single protein folding pathway (1). In this model an unfolded protein descends along a funnel that describes its free energy until it reaches the native state of minimal free energy. The multidimensional landscape often contains local minima hosting metastable folding intermediates (2). In principle there are many routes to the native state, and which pathways are taken depends on details of the system under investigation such as amino acid sequence, topology, and experimental conditions (3).

Various aspects of both the denaturant-induced equilibrium (un)folding and the kinetic folding of both flavodoxin (FD) and apoflavodoxin (apoFD) (i.e., FD lacking the flavin mononucleotide (FMN) cofactor) from Azotobacter vinelandii have been characterized in detail (4–6). This characterization shows that the folding energy landscape of apoFD is rugged and contains local minima in which different folding intermediates reside (7). The protein populates a molten globule-like intermediate during its thermal- and denaturant-induced equilibrium (un)folding (8–11). Here, time-resolved polarized fluorescence spectroscopy is used as a new approach to study apoFD folding. The methodology is used to reveal submolecular details of denaturant-induced equilibrium (un)folding of apoFD.

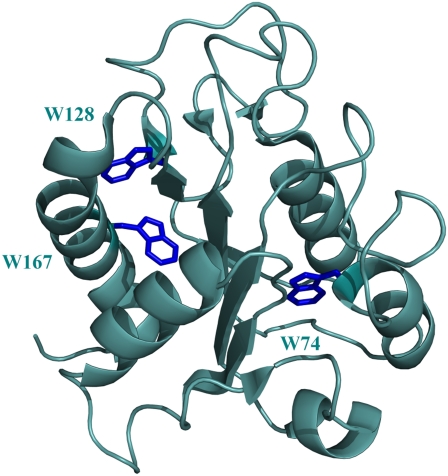
The three-dimensional structure of the 179-residue FD is characterized by a five-stranded parallel β-sheet surrounded by α-helices at either side of the sheet (Fig. 1) (12). This FD-like topology is one of the five most commonly observed protein folds (13). It is shared by nine superfamilies, which exhibit little or no sequence similarity and comprise a broad range of unrelated proteins with different functions (14).

FIGURE 1.

Cartoon representation of the x-ray structure of A. vinelandii flavodoxin in which the tryptophan residues are colored dark blue (Protein Data Bank code 1Y0B). The FMN cofactor is not incorporated.

ApoFD is structurally identical to FD except for some dynamic disorder in the flavin-binding region (15). The guanidine hydrochloride (GuHCl) induced equilibrium (un)folding of apoFD has been studied extensively by circular dichroism and steady-state (polarized) fluorescence (4), and it was found that a three-state folding model (native ↔ unfolded ↔ intermediate) excellently describes all data. The thermodynamic parameters associated with each involved, folding transition could be determined including the relative population of each folding species as a function of GuHCl concentration. The molten globule-like intermediate maximally populates at 1.8 M GuHCl (4). Remarkably, at this denaturant concentration steady-state fluorescence anisotropy is maximal and has a value of 0.09. In the case of native apoFD the anisotropy value is only 0.04, and unfolded apoFD has an anisotropy value of 0.06 (4).

The fluorescence of apoFD arises mainly from its three tryptophans (Fig. 1). W74 is located in α-helix 3, W128 is close to β-strand 5a and W167 is in helix 5 of the protein. NMR spectroscopy has shown that the tertiary structures surrounding both W128 and W167 are indistinguishable for apoFD and FD (15). The precise orientation of the indole of W74 is not known for apoFD, although regarding the conformational features of apoFD it must have a position roughly like the one in FD. As suggested by Bollen et al. (4) the low fluorescence anisotropy of native apoFD might be caused by Förster resonance energy transfer (FRET) between the tryptophan residues closest in space.

The strikingly low fluorescence anisotropy of native apoFD prompted us to perform polarized time-resolved fluorescence measurements to study FRET between tryptophans as a function of GuHCl concentration. Time-resolved fluorescence anisotropy has emerged as a powerful tool to establish FRET between pairs of fluorophores and to estimate relative distances and orientations between them. This tool has been used to study homotransfer in many systems (16–21). Although these experiments cannot provide precise positions of tryptophans, they enable us to determine local geometric changes that accompany overall structural changes during (un)folding and to differentiate between dynamical and structural properties of native, intermediate, and unfolded forms of apoFD.

MATERIALS AND METHODS

Materials

All chemicals used were of the highest purity available. The concentration (C, in M) GuHCl was determined by measuring the refractive index of samples with (S) and without (B) GuHCl using the empirical relationship (22): C = 57.147 × (S − B) + 38.68 × (S − B)² − 91.6 × (S − B)³.

Protein expression and purification

The C69A variant of A. vinelandii FD is used to avoid covalent protein dimerization and is similar to WT FD regarding both redox potential and stability of apoprotein (8,23) and is referred to as WT protein.

Three variants of FD, which contain either a single tryptophan residue (W74), the W74/W128 pair, or the W74/W167 pair, were generated through the replacement of tryptophans by phenylalanines using oligo-directed mutagenesis.

Recombinant FD and WFF, WFW and WWF variants were obtained and purified as described (8). ApoFD was subsequently prepared by trichloroacetic acid precipitation, washing of the FMN-free precipitate and redissolving the apoprotein in buffer. Finally, oligomeric molecules were removed via gel filtration. In all experiments the protein concentration was 4 μM in 100 mM potassium pyrophosphate buffer, pH = 6.0, at 25°C.

Steady-state optical spectra and polarized time-resolved fluorescence data

Absorption spectra were measured on a Cary-5E spectrophotometer (Varian, Houten, The Netherlands). Steady-state fluorescence spectra were obtained with a Fluorolog 3.2.2 (Horiba Jobin Yvon, Optilas, Alphen aan den Rijn, The Netherlands) spectrofluorometer. All collected fluorescence spectra were corrected for wavelength-dependent instrumental response characteristics.

Time-resolved fluorescence measurements were performed using the time-correlated single photon counting technique as described elsewhere (24). The excitation wavelength was 300 nm, the pulse duration was less than 0.2 ps, pulse energies were at the pJ level and the repetition rate of excitation pulses was 3.8 × 10⁶ pulses s⁻¹. The samples (1 mL in 10 mm light-path fused silica cuvettes) were at 25°C. The emission filter was a Schott UV-DIL (Schott, Mainz, Germany) 348.8 nm (Δλ = 5.4 nm) interference filter. Decay curves were collected in 4096 channels of a multi-channel analyzer using a channel time spacing of 5.0 ps. Measurements consisted of ten repeated sequences of 10 s duration of parallel (I_‖(t)) and perpendicularly (I_⊥(t)) polarized fluorescence emission. Background fluorescence emission was measured under the same conditions. For the deconvolution procedure, the dynamic instrumental response function was determined using a freshly made solution of p-terphenyl in a mixture of 50/50 (v/v) cyclohexane and CCl₄ (25).

The total fluorescence decay (I(t) = I_‖(t) + 2 I_⊥(t)) was analyzed using a sum of discrete exponentials with lifetimes τ_i and amplitudes α_i. The time-dependent fluorescence anisotropy r(t) (r(t) = (I_‖(t) – I_⊥(t))/ I(t)) was calculated in a global manner from parallel and perpendicular intensity components using an appropriate model (26). An example of the analysis of fluorescence and anisotropy decay of WFF apoFD is shown in SI-1 in Supplementary Material, Data S1.

Fluorescence depolarization due to energy transfer

For two tryptophan residues that are able to exchange excited-state energy by the Förster mechanism, the fluorescence anisotropy decay has the following form (27–29):

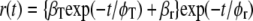(1a)

or

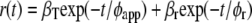(1b)

with φ_T being the correlation time of resonance energy transfer, φ_r the rotational correlation time of the protein molecule, and φ_app the apparent correlation time with 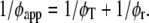β_T and β_r are functions of intramolecular and intermolecular angles between emission and absorption transition moments. The correlation time for reversible transfer φ_T between a pair of identical, isoenergetic chromophores (i.e., tryptophans) is given by:

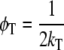(2)

with k_T being the rate constant for energy transfer, which is given by the Förster equation (30):

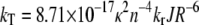(3)

with κ² being the orientation factor for the relevant transition dipole moments, n the refractive index of the donor-acceptor intervening medium (31) (for native apoFD n = 1.6 (32)), k_r the radiative rate constant (ns⁻¹) (33), J the integrated spectral overlap of the (acceptor) tryptophan absorbance and (donor) fluorescence spectra (cm³ M⁻¹), and R the distance (nm) between donor and acceptor. In the case of unidirectional energy transfer, when the excited-state energy of one tryptophan is lower than that of the other, the correlation time is given by

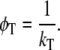(4)

RESULTS AND DISCUSSION

Time-resolved fluorescence anisotropy of native apoFD and its tryptophan variants

Flavodoxins are remarkably rigid according to NMR relaxation studies. The backbone of the protein shows an almost complete absence of internal mobility and all three tryptophans of flavodoxin are immobilized in the protein matrix (34,35). Structural comparisons of the solution structure of flavodoxin and corresponding crystal structures show that these structures are virtually identical (36). NMR data show that the overall folds of both FD and apoFD are similar (15,36) and both molecules are spherical.

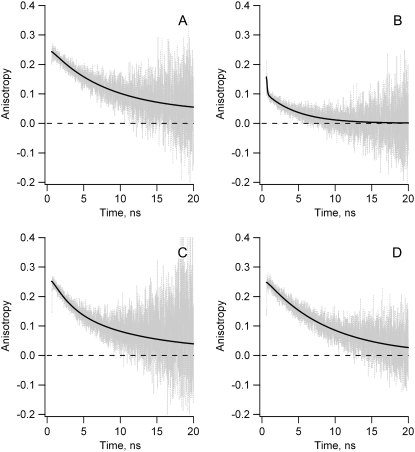
In Fig. 2 A the fluorescence anisotropy decay is shown of the single tryptophan variant W74-F128-F-167 (WFF) of apoFD in absence of denaturant. The data analysis procedure is available as supporting information (SI-1 in Data S1. WFF is the only available variant in this study in which FRET between tryptophans cannot take place. Therefore, the depolarization observed must be a result of overall protein rotation, which has a rotational correlation time φ_r that equals 10.4 ns. This value is also used to describe overall rotation of the other apoFD variants and is fixed during the corresponding fitting procedures. The initial anisotropy of WFF apoFD is ∼0.25, which is commonly observed for tryptophan (37,38).

FIGURE 2.

Experimental fluorescence anisotropy decay curves r(t) (gray lines) and associated fits (black lines) obtained for fully folded native WT apoFD and tryptophan variants of apoFD. (A) W74-F128-F167: decay fitted to β_rexp(−t/φ_r) with φ_r = 10.4 ns (β_r = 0.24), χ² = 1.04. (B) WT apoFD: decay fitted to β_T1exp(−t/φ_T1) + β_T2exp(−t/φ_T2) + β_r}exp(−t/φ_r) with φ_T1 = 0.05 ns (β_T1 = 0.05), φ_T2 = 6.9 ns (β_T2 = 0.07), and φ_r = 10.4 ns (fixed, see text) (β_r = 0.04), χ² = 1.01. (C) W74-F128-W167: decay fitted to β_T1exp(−t/φ_T1) + β_r}exp(−t/φ_r) with φ_T1 = 3.3 ns (β_T1 = 0.10), and φ_r = 10.4 ns (fixed, see text) (β_r = 0.15), χ² = 1.10. (D) W74-W128-F167: fitted to β_rexp(−t/φ_r) with φ_r = 8.5 ns (β_r = 0.25), χ² = 1.05.

In Fig. 2 B anisotropy decay is shown for native wild-type (WT) apoFD, which contains three tryptophans at positions 74, 128, and 167 (Fig. 1). A major part of the anisotropy signal rapidly decays on the ps time scale followed by a much slower decay process on the nanosecond timescale. When the anisotropy decay of native WT apoFD is fitted to r(t) = {β_T1exp(−t/φ_T1) + β_T2exp(−t/φ_T2) + β_r}exp(−t/φ_r) with φ_r fixed to 10.4 ns, φ_T1 equals 0.05 ns and φ_T2 equals 6.9 ns (Fig. 2 B). We show below that the 50-ps transfer correlation time is due to FRET from W167 to W128 (see also SI-3 in Data S1). This transfer is fast because both tryptophans are only 7 Å apart. The depolarization observed on the nanosecond timescale (6.9-ns transfer correlation time) is ascribed to FRET from W74 to W167 (vide infra). The corresponding transfer time is significantly slower than 50 ps because of the larger separation of the tryptophans involved (i.e., 15 Å) and the R⁻⁶ dependence of the transfer rate.

Fig. 2 C–D show anisotropy decay curves that were obtained for variants W74-F128-W167 (WFW) and W74-W128-F167 (WWF) in absence of denaturant. These variants lack the fast 50-ps transfer correlation time that is characteristic for FRET from W167 to W128 in WT apoFD. Anisotropy of both variants of apoFD have an initial value of 0.25, whereas this anisotropy value is apparently ∼0.16 for WT protein. This relatively low latter value is due to the deconvolution procedure because a large part of the depolarization occurs within the instrument response time (39).

WFW apoFD shows bi-exponential anisotropy decay because protein rotation and FRET between W74 and W167 contribute to anisotropy decay (Fig. 2 C). Fitting r(t) = {β_T1exp(−t/φ_T1) + β_r}exp(−t/φ_r) to the time-dependent anisotropy data and fixing φ_r to 10.4 ns, φ_T1 is found to equal 3.3 ns. It will be discussed below why this transfer correlation time of 3.3 ns differs from the 6.9 ns transfer correlation time component detected for WT apoFD. This transfer correlation time due to FRET between W74 and W167 is 66 times slower than the 50-ps transfer process mentioned above as both tryptophans are separated by 15 Å whereas W128 and W167 are separated by only 7 Å. Based on the R⁶-dependency of the Förster transfer correlation time, a ratio of ∼100:1 between both transfer correlation times would be expected and indeed this ratio is in qualitative agreement with the observation made. The transfer time also depends on other parameters than interchromophore distance, albeit in a less dramatic way.

FRET between W74 and W128 in WT apoFD is substantially slower than between W74 and W167 in WFW apoFD. No clear bi-exponential anisotropy decay is observed for WWF apoFD in absence of denaturant (Fig. 2 D). Fitting of a single exponentially decaying function to the latter anisotropy decay results in a correlation time of 8.5 ns. Using r(t) = {β_T1exp(−t/φ_T1) + β_r}exp(−t/φ_r) and fixing φ_r to 10.4 ns, φ_T1 is found to equal 32 ns, but the 67% confidence interval ranges from 15 to 122 ns. Nevertheless, the transfer time that corresponds to transfer between W74 and W128 is about one order of magnitude larger than the one corresponding to transfer between W74 and W167. This difference is largely because of the separation between W74 and W128 that is larger than the one between W74 and W167 (i.e., 20 Å versus 15 Å, respectively).

The fluorescent-state energy of W128 is lower than those of both W74 and W167. The latter can already be inferred from W128 being located at the protein surface where it faces a more polar environment than W74 and W167 do, which both are positioned in the protein interior, thus leading to a lowering of W128's excited-state energy (38,40) The exposure of W128 to solvent is further substantiated by D₂O exchange measurements (15), as the indole proton of W128 exchanges faster than those of W74 and W167. In addition, the fluorescence emission maximum of WT protein is clearly red-shifted (i.e., lower energy) with respect to those of the WFF and WFW variants, which both lack W128, due to the presence of the solvent accessible W128 (SI-2 in Data S1). As a result, W128 acts as a sink, and nearly unidirectional irreversible transfer of excitation energy occurs from W167 to W128 and from W74 to W128.

Because energy transfer toward W128 is unidirectional and transfer from W167 to W128 is two orders of magnitude faster than transfer from W167 to W74, W167 transfers nearly all its excitations to W128, and transfer from W167 to W74 will be virtually absent. As a consequence, in the presence of W128, FRET from W74 to W167 is also an irreversible process, characterized by rate constant k_T (Eq. 4). When W128 is not present, like in WFW native apoFD, FRET between W74 and W167 is instead a reversible process and is characterized by rate constant 2k_T (Eq. 2). In the case of WFW native apoFD, the transfer correlation time associated with FRET between W74 and W167 equals 3.3 ns. One would thus expect a transfer time of 6.6 ns for FRET between W74 and W167 in native WT apoFD. Indeed, the observed transfer correlation time of 6.9 ns is in good agreement with the latter value.

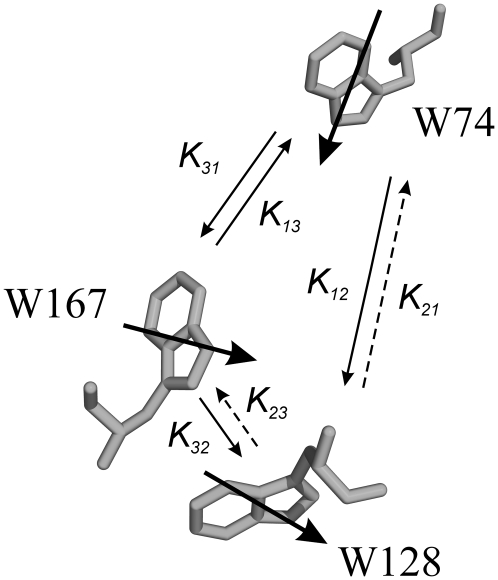
Fig. 3 shows the main energy transfer processes that occur in WT native apoFD as derived from the anisotropy measurements described above. The rate constants k_T for transfer between each tryptophan pair can also be estimated using the Förster equation (Eq. 3) and the crystal structure of FD. The rate constants thus obtained are qualitatively consistent with those derived from experimental results (SI-3 in). An exact match would be fortuitous given the uncertainty in parameters like refractive index, transition dipole moment orientations, and spectral overlap function of individual tryptophan pairs.

FIGURE 3.

Orientation of tryptophans in native flavodoxin. Bold arrows represent transition dipole moments of tryptophan residues. Thin arrows correspond to rates of energy transfer (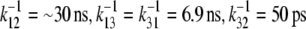). In the native state of WT apoFD, k₂₁ and k₂₃ are negligibly small and k₃₁ only plays a role in the absence of W128.

Dependence of transfer times of apoFD on denaturant concentration

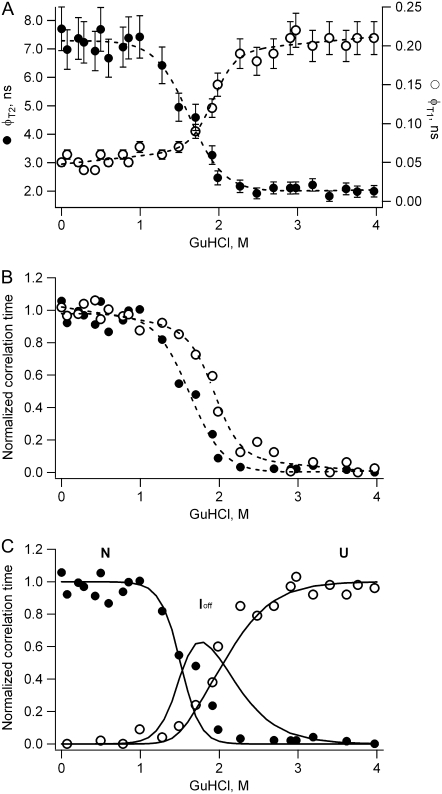
The GuHCl-induced unfolding of apoFD can be followed by measuring steady-state fluorescence anisotropy (4). This approach reveals the presence of a folding intermediate, the anisotropy of which is higher than that of both the folded and unfolded state of apoFD. Here, GuHCl-induced unfolding of apoFD is followed by time-resolved fluorescence anisotropy measurements. Thus the obtained data are used to recover denaturant-dependent steady-state anisotropy values. These recovered anisotropy data agree rather well with directly measured steady-state anisotropy data (4) (SI-4 in Data S1). However, time-resolved data provide additional information. The anisotropy kinetics of WT apoFD are analyzed using the following equation: r(t) = {β_T1exp(−t/φ_T1) + β_T2exp(−t/φ_T2) + β_r}exp(−t/φ_r), where φ_T1 reflects transfer from W167 to W128 and φ_T2 transfer from W74 to W167, at least in native apoFD, and φ_r describes overall protein rotation. The overall rotational correlation time of the protein is extracted from denaturant-induced unfolding experiments in which the WFF single tryptophan containing variant of apoFD is used. This rotational correlation time is corrected for increase in viscosity of the solution and increase in hydrodynamic radius of apoFD upon increasing the concentration of GuHCl (R. Engel, personal communication). The obtained denaturant-dependent φ_T1 and φ_T2 values are presented in Fig. 4 A.

FIGURE 4.

(A) Dependence of the slow transfer time (φ_T2, solid circles) and the fast transfer time (φ_T1, open circles) of WT apoFD on GuHCl concentration. Error bars represent estimated standard errors. (B) Data as shown in A, but now data points are scaled between 0 and 1, and the φ_T1 values are flipped across a horizontal line of value 0.5 to allow easy comparison of transition midpoints. In A and B dashed lines are fits of a sigmoid equation to the data to serve as a guide to the eye. (C) Data as shown in A, but now data points are scaled between 0 and 1 and are shown together with the fractional populations of native (N), off-pathway intermediate (Ioff), and unfolded (U) apoFD (solid lines) (4).

Both φ_T1 and φ_T2 change markedly upon protein unfolding but when transfer correlation time φ_T1 becomes larger, opposite behavior is observed for φ_T2. Fig. 4 B shows that the decrease of φ_T2 occurs at a concentration of GuHCl that is lower than the concentration at which increase of φ_T1 commences. The denaturant concentration range in which φ_T2 starts to decrease substantially coincides with the range in which the native state disappears and in which the folding intermediate of apoFD becomes populated. The unfolded state of apoFD appears at higher concentrations of denaturant at which the value of φ_T1 also increases. In Fig. 4 C rescaled values of φ_T1 and φ_T2 are plotted together with previously obtained fractional populations of native, intermediate, and unfolded apoFD (4), all as a function of concentration denaturant. Although the population profiles do not perfectly match the transfer correlation-time profiles, it is clear that both native and intermediate states are characterized by similar φ_T1 transfer times. In contrast, φ_T2 changes upon formation of the intermediate state and shows no observable additional change upon full population of unfolded apoFD.

Interpretation of observed changes in transfer correlation times

Upon unfolding apoFD, transfer correlation time φ_T1 rises from 50 ps to ∼200 ps (Fig. 4). In addition, differences that exist in excited-state energies of tryptophans diminish and most likely disappear. W128 no longer acts as an energy sink, and as a result the correlation time that describes transfer between W167 and W128 reduces by a factor of 2 (φ_T1 = 50 ps would become 25 ps). Instead, a rise of φ_T1 is observed, which is (partly) due to increased separation between W128 and W167. Upon unfolding apoFD no large change of the corresponding orientation factor κ² is expected. κ² is calculated to be 0.87 for native protein (SI-3 in Data S1) and is expected to approach a value of 0.67 for randomly oriented tryptophans in unfolded apoFD. Upon unfolding native apoFD, a progressive red shift is observed in the corresponding fluorescence spectra, which causes the overlap integral to decrease (SI-5 in Data S1). In SI-5 in Data S1 the relative changes in theoretical transfer rate constants between tryptophan pairs in WT apoFD are presented as a function of changes in overlap integral, refractive index, and radiative rate constant, respectively. Only a small increase in distance between W167 and W128 suffices to explain the observed increase in transfer time φ_T1.

In contrast, upon apoFD unfolding, φ_T2 decreases from 6.9 ns (native state) to ∼2 ns (intermediate and unfolded state). The 6.9-ns component is associated with transfer from W74 to W167. The observed decrease of φ_T2 upon disappearance of native apoFD might be because of a change in the rate(s) of transfer between W74 and W167, but alternatively, might also reflect a concomitant change in flexibility/local dynamics of the tryptophans involved. To investigate the role of a potential change in tryptophan flexibility, we studied the time-resolved anisotropy behavior of WFF, WWF, and WFW apoFD as a function of GuHCl concentration.

The native state of the WFF variant has a correlation time of 10.4 ns due to overall protein rotation. At 1 M GuHCl an additional correlation time of ∼0.4 ns appears due to local dynamics of W74. The corresponding amplitude increases to ∼60% of the total amplitude at 2 M GuHCl. This short correlation time falls in the range 0.4–0.9 ns for up to 3.6 M GuHCl. Thus, at all denaturant concentrations the correlation time associated with flexibility of tryptophan is significantly shorter than the above-mentioned 2-ns transfer correlation time detected for both WT folding intermediate and unfolded WT protein. Tryptophan flexibility is thus characterized by a correlation time that is faster than the transfer correlation time φ_T2 of WT apoFD at each denaturant concentration used. Moreover, the onset of increased flexibility is manifested by the appearance of a short component and not by the gradual decrease of a relatively slow component.

The WWF variant, in which hardly any energy transfer between W74 and W128 is detected, shows flexibility of tryptophans at 1.2 M GuHCl as a correlation time of 0.5–1.0 ns appears. The corresponding amplitude rises to 60% at 2 M GuHCl. In case this 0.5–1.0 ns correlation time would be due to FRET one would expect that this correlation time would become longer upon increasing the concentration denaturant. The latter is not observed.

Energy transfer from W74 to W128 might also accelerate upon apoFD unfolding. However, as mentioned, the fluorescence anisotropy decay of the WWF variant does not show any increased FRET rates upon unfolding; merely increased flexibility of the corresponding tryptophans is observed. Therefore, the observed decrease in transfer correlation time from 6.9 ns to 2 ns upon unfolding WT apoFD is assigned entirely to changes in FRET efficiency between W74 and W167.

In apoFD variant WFW, FRET can only occur between W74 and W167. As discussed, native WFW apoFD has a transfer correlation time of 3.3 ns. This transfer correlation time is twice as short as the correlation time that characterizes energy transfer between W74 and W167 in WT apoFD because in WFW apoFD energy transfer between both tryptophans is not unidirectional (Eq. 4) but reversible (Eq. 2). Upon unfolding, this 3.3-ns transfer correlation time decreases to ∼1.5 ns. Tryptophan flexibility is observed only above 1.7 M GuHCl, which is characterized by a correlation time of 0.2–0.3 ns (associated amplitude 20%) at 2.3 M GuHCl. Full details of the analysis are given in SI-6 in Data S1. Even at the highest concentration of denaturant, WFW apoFD still shows a correlation time due to energy transfer that has relatively high amplitude of ∼50%.

Whereas the correlation times that correspond to energy transfer between W74 and W167 in the native state of WT and WFW apoFD differ by a factor of two, these correlation times are nearly equal (i.e., 1.5–2 ns) in both unfolded proteins. This equality is explained by the following. Upon unfolding apoFD the fluorescence spectra show a progressive red shift (SI-5 in Data S1). The difference in excited-state energy of the tryptophans decreases and most likely disappears. W128 no longer acts as an energy sink, and as a result the correlation time that describes energy transfer between W74 and W167 reduces by a factor of 2 (φ_T2 = 6.9 ns would become 3.45 ns). A further reduction of φ_T2 is due to a change in orientation factor κ². In native WT apoFD FRET from W74 to W167 is associated with a value of κ² of 0.44 (SI-3 in Data S1). In unfolded apoFD both tryptophans will be more randomly oriented toward one another and hence κ² increases toward a value of 0.67. Actually, the increase in κ² upon unfolding apoFD does not completely account for the decrease in observed φ_T2 and a slight decrease in distance between both tryptophans upon apoFD unfolding could be possible. The decrease in inter-tryptophan distance upon apoFD unfolding is required to account for the transfer correlation time associated with unfolded apoFD (i.e., φ_T2 = 2 ns). This reduction in distance is unexpected because upon unfolding at 4 M GuHCl the hydrodynamic radius of the protein increases by nearly 36% (R. Engel, personal communication).

Molecular details of apoFD folding

As opposed to steady-state fluorescence anisotropy measurements, time-resolved polarized measurements enable the quantitative description of the various processes that lead to fluorescence depolarization. As demonstrated here, the methodology can be successfully applied to analyze the denaturant-induced equilibrium unfolding of a multiple tryptophan containing protein. Submolecular details of geometric changes that accompany overall structural changes during (un)folding are revealed. Average properties of native, intermediate, and unfolded forms can be determined. As a result, hitherto unknown insights into molecular details of protein folding are obtained.

The molten globule-like intermediate that populates to significant extents during denaturant-induced equilibrium unfolding of apoFD acts as a trap during kinetic apoFD folding (4). The intermediate is a relatively stable off-pathway species that populates heavily during refolding and needs to unfold to produce native protein. A comparison of fluorescence and far-UV circular dichroism data in the transition zone of denaturant-induced equilibrium unfolding shows that the intermediate has conserved secondary structure (∼65% of native α-helicity) but that it lacks the characteristic structure of native apoFD (4,5).

Time-resolved anisotropy data (Fig. 4) now show that the relative positions and orientations of the W128/W167 pair in the off-pathway intermediate and in native apoFD are comparable, as both states are characterized by similar φ_T1 values. Both tryptophans thus have a native-like geometry in the helix containing intermediate. In contrast, the geometric features of the W74/W167 pair differ from those in native protein as φ_T2 becomes smaller upon populating the intermediate. No observable additional change in φ_T2 occurs upon unfolding this latter state (Fig. 4). Non-native structure thus exists between W74 and W167 in the off-pathway intermediate of apoFD.

The rate of transfer between W167 and W128 is fast in both native apoFD and the intermediate (transfer rate (50 ps⁻¹)). It thus seems peculiar that the intermediate has a steady-state fluorescence anisotropy value of ∼0.09 whereas in the case of native apoFD this value is only 0.04. However, the fluorescence of the intermediate is strongly quenched compared to that of native protein as all its tryptophans are solvent accessible (4). As Perrin's equation shows, the concomitant shortening of the average fluorescence lifetime leads to an increase in fluorescence anisotropy (see SI-4 in Data S1) that is responsible for the relatively high value of the steady-state anisotropy of the intermediate.

Upon population of the unfolded state by unfolding both native apoFD and off-pathway intermediate, transfer correlation time φ_T1 increases (i.e., φ_T1 increases from 50 ps to ∼200 ps). As discussed, only a small increase in distance between W128 and W167 is required to explain this increase. In unfolded apoFD, W128 and W167 are solvent accessible and randomly oriented with respect to one another but apparently have a native-like separation of ∼7 Å. In contrast, transfer correlation time φ_T2 becomes shorter upon unfolding native apoFD to either off-pathway folding intermediate or unfolded state (i.e., φ_T2 decreases from 6.9 ns to 2 ns). This decrease is a result of W74 and W167 becoming solvent accessible and randomly oriented toward one another and apparently W74 and W167 are near-natively separated by ∼15 Å in the folding intermediate and in unfolded apoFD. Both tryptophans may actually be slightly closer in space than in the native state.

At 4 M GuHCl, apoFD is fully denatured and its hydrodynamic radius is 38 ± 4 Å as shown by fluorescence correlation spectroscopy (R. Engel, personal communication). Compared with the hydrodynamic radii of other chemically denatured proteins, this radius falls well within the range of what is expected for a random coil of 179 residues (41). However, the study presented here shows that unfolded apoFD is characterized by near-native separations of tryptophans in the W128/W167 and W74/W167 pairs, respectively. Apparently, apoFD's unfolded state is not a featureless statistical coil at 4 M GuHCl. Recently however, it has become clear that a protein chain can behave as a random coil even if it is comprised of a significant amount of non-random segments (42).

Tryptophan plays an important role in extensive long-range tertiary interactions in the denatured state of lysozyme and these interactions affect protein folding (43). It needs to be revealed whether the near-native separations of tryptophans in the W128/W167 and W74/W167 pairs of unfolded apoFD have implications for apoFD folding. It is not apparent whether productive folding to native apoFD or nonproductive folding to the off-pathway intermediate are differently affected as both folding routes involve maintenance of the intertryptophan separations within the W128/W167 and W74/W167 pairs, respectively.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.