Frequency-Dependent Shear Impedance of the Tectorial Membrane

Abstract

Microscale mechanical probes were designed and bulk-fabricated for applying shearing forces to biological tissues. These probes were used to measure shear impedance of the tectorial membrane (TM) in two dimensions. Forces were applied in the radial and longitudinal directions at frequencies ranging from 0.01–9 kHz and amplitudes from 0.02–4 μN. The force applied was determined by measuring the deflection of the probes' cantilever arms. TM impedance in the radial direction had a magnitude of 63 ± 28 mN · s/m at 10 Hz and fell with frequency by 16 ± 0.4 dB/decade, with a constant phase of −72 ± 6°. In the longitudinal direction, impedance was 36 ± 9 mN · s/m at 10 Hz and fell by 19 ± 0.4 dB/decade, with a constant phase of −78 ± 4°. Impedance was nearly constant as a function of force except at the highest forces, for which it fell slightly. These results show that the viscoelastic properties of the TM extend over a significant range of audio frequencies, consistent with a poroelastic interpretation of TM mechanics. The shear modulus G′ determined from these measurements was 17–50 kPa, which is larger than in species with a lower auditory frequency range. This value suggests that hair bundles cannot globally shear the TM, but most likely cause bulk TM motion.

INTRODUCTION

The mammalian sense of hearing relies on a series of mechanical processes that deflect the sensory bundles of hair cells in the cochlea. Overlying these bundles is an acellular gel called the tectorial membrane (TM), which is believed to play a critical mechanical role in cochlear function. While the inner ears of all vertebrates have gelatinous structures overlying the hair cell bundles, the mammalian TM has a number of unique specializations that are believed to affect its mechanical properties. The TM is anisotropic, with an increased stiffness in the radial direction that has been attributed to the presence of collagen fibers (1–3). The TM also contains a number of other proteins that contribute to its mechanical properties. Genetic changes to these proteins, such as α-tectorin (4,5), β-tectorin (6), and collagen type XI (7), lead to significant hearing loss. These studies show a correlation between TM molecular structure and cochlear function. However, the mechanical properties of the TM that determine its interaction with cochlear structures such as hair bundles are not well established, particularly at audio frequencies.

The TM is located in close proximity to the mechanosensitive bundles of hair cells. Since these bundles are sensitive to shearing deflection, the response of the TM to shearing forces is of significant interest to cochlear mechanics. We have recently shown that radial forces applied to one location on a freely suspended TM launch traveling waves that propagate longitudinally along the TM (8). These waves may contribute significantly to cochlear tuning and sensitivity, if they can be excited in vivo; that is, if outer hair cell (OHC) hair bundles and cochlear fluids displace the bulk of the TM rather than causing internal shear.

The shear impedance of the TM is a critical factor in determining whether waves can be excited, as well as the velocity and extent of wave propagation. Shear moduli predicted from the velocity of TM wave propagation were significantly larger than most other estimates of that property. However, the results of these previous studies (reviewed in (9)) are not easily applied to the wave measurements. Many of these studies were performed on species that have a much lower range of best frequencies than the mice used for the wave measurements. Moreover, the other studies largely applied transverse forces at frequencies ≤10 Hz, while the wave measurements applied radial forces in the 1–20 kHz frequency range.

In this study, we present a novel technique for measuring the mechanical response of the TM to shearing forces over a wide range of frequencies and levels. A set of probes was designed and microfabricated specifically for applying shearing forces to the TM. These probes were used to apply shearing forces in both the radial and longitudinal directions at frequencies ranging from 10 Hz to 9 kHz. The use of video methods to measure motion enabled nanometer-scale measurement of TM motion not only at the point of force application but also as a function of distance from the probe. Our findings provide an independent characterization of TM shear properties that can be compared to both wave measurements and low-frequency material properties studies. These measurements can also help determine whether the TM undergoes internal shearing or bulk displacement in vivo.

METHODS

Tectorial membrane isolation

TM specimens were prepared using methods similar to those described previously (2). Adult, male mice (strain B6129F1, 25–35 g, Taconic) were asphyxiated with CO₂ and decapitated. The cochlea was isolated from the surrounding tissue while immersed in artificial endolymph (AE: 174 mM KCl, 2 mM NaCl, 0.02 mM CaCl₂, and 5 mM HEPES adjusted to pH 7.3), a fluid similar to the one bathing the TM in vivo. The bony casing of the cochlea was gently chipped away using the tip of a scalpel blade, and portions of TM were teased off of the organ of Corti with an eyelash glued to a glass pipette. TM segments were ∼0.5–1 mm in length, 150–250 μm wide, and 35–50 μm thick in the region where impedance was measured. A TM sample was transferred to a glass slide containing AE in a circular area delineated with a liquid blocker pen (Electron Microscopy Sciences, Ft. Washington, PA). The TM specimen was gently floated to the surface of the glass slide, which was coated with 0.3 μL Cell-Tak (BD Biosciences, Bedford, MA), a bioadhesive that immobilized the surface of the TM facing the glass slide. The endolymphatic surface was attached to the glass slide, so that mechanical impedance was measured on the surface that faces OHCs. Material properties were measured from portions of TM isolated from the apical half of the cochlea from six mice. One of these TMs did not adhere properly to the glass slide, and yielded impedance measurements that were an order-of-magnitude smaller than the others. This TM could be distinguished by the fact that the amplitude of motion did not decrease significantly with distance from the probe. This TM was excluded from the results presented in this article, leaving measurements from five TMs. Because of the small variability in the measurements, this sample size was deemed sufficiently large.

Microfabricated shearing probes

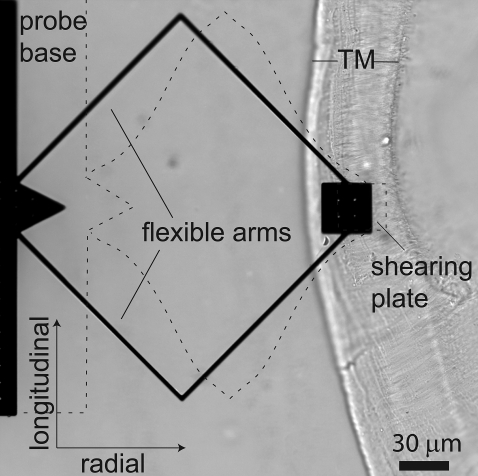
A microfabricated probe used to apply shearing forces to the TM is pictured on a TM preparation in Fig. 1. The probe design consisted of a large base coupled to a shearing plate by a pair of bent cantilever arms. Forces applied to the base were coupled to the plate through these arms. When the plate was brought into contact with the TM, some of this force was transmitted to the TM while some bent the cantilever arms. The symmetric geometry caused the shearing plate to deflect when the arms were bent. The amount of deflection—that is, the relative motion of the shearing plate and the base—depended on the relative impedance of the TM and the cantilever arms. The cantilever arms bent in response to forces in both the radial and longitudinal directions, so the probe was used to measure impedance in two dimensions.

FIGURE 1.

Microfabricated probe on a TM specimen. The probe consisted of a base and shearing plate connected by two flexible arms. The probe was capable of applying force in the radial and longitudinal directions, indicated by the arrows in the lower left-hand corner. Displacements applied to the probe base caused bending of the cantilever arms, as illustrated with dashed lines (bending is exaggerated for clarity). The radial fibrillar structure of the TM is readily visible in the image and was used to align the radial and longitudinal axes, the radial axis being parallel to the radial fibrils.

The shearing plate has a 3 × 3 array of protrusions spaced 10 μm apart on the surface facing the TM. The 2 × 2 array of holes visible in Fig. 1 are spaced equidistant from these protrusions. These holes allowed the chemical etchant to penetrate the plate during the fabrication process to free the protrusions. The protrusions, which are <2 μm high, served two purposes. First, they facilitated the release of the plate from the underlying substrate, allowing the probe to be isolated in one piece. Second, the protrusions approximate the positions of the stereocilia of OHCs, ensuring that the probe made a firm contact with the TM. Thus, the mechanical impedance of the TM measured by this probe approximated the impedance that would be seen by a 3 × 3 array of OHCs.

A large number of probes with cantilever arms of various lengths were microfabricated in polysilicon using the MUMPs process (MEMSCAP, North Carolina). The probe design works best when the probe impedance is comparable to that of the TM. If the probe impedance is significantly smaller, very little force will be coupled to the TM. If the probe impedance is significantly larger, the cantilever arms will not be deflected by a detectable amount. The variety of probes manufactured on a single chip spanned this range. The probes chosen to apply forces to the TM had arms that were 3 μm wide, 2 μm thick, and 100 μm long for each straight segment. The shearing plate had dimensions of 30 × 30 μm². Using a nominal Young's modulus of 160 GPa for polysilicon (10), these dimensions predict a stiffness of 2.8 N/m in the radial direction and 0.7 N/m in the longitudinal direction.

Displacements of the probe base were applied by a macroscopic mount. This mount consisted of a T-shaped head attached to piezoactuators at each endpoint of the T. The piezoactuators in the mount were driven by a three-channel piezocontroller (Thorlabs, Newton, NJ) that received sinusoidal signals from the computer. The direction of motion was adjusted by altering the input signals to the piezocontroller. All piezoactuators were driven with various AC signals added to a common DC offset. Driving all three piezoactuators with a common AC signal moved the probe base away from the macroscopic mount (the radial direction). Driving the left and right piezoactuators with opposing AC signals moved the probe base parallel to the mount in the horizontal plane (the longitudinal direction). The third piezoactuator allowed application of out-of-plane oscillatory forces. This mode was not used in the experiments presented in this article.

Motion measurements

TM displacements were quantified using computer microvision (11,12). A light microscope (Zeiss Axioplan, Thornwood, NY) using transmitted illumination with a long-working distance condenser with 0.9 numerical aperture (NA) and a 40× water immersion objective (0.8 NA) was used to view the specimen. Images were acquired with a grayscale charge-coupled device camera (model No. CA-D4-1024A, Dalsa, Waterloo, Ontario), which has 1024 × 1024 pixels and digitizes image brightnesses with 12-bit resolution. The video microscope was supported by a pneumatic vibration-isolation table that damped vibrations of the floor. The maximum frame rate of the video imager was lower than the frequency of probe motion (10–9000 Hz), so stroboscopic illumination with a high intensity green LED was used to slow the apparent motion. To quantify sinusoidal motions, eight images of the target were acquired at evenly spaced phases of the stimulus period. Displacements between images obtained at successive phases were estimated directly from the video images (11,13). These displacement estimates were used to reconstruct time waveforms of motion. This technique allowed measurements of motion both of the microfabricated force probe and of portions of the TM distant from the probe. The noise floor of this system under these operating conditions was assessed by measuring the apparent motions that resulted when the piezoactuators were driven by signals of zero amplitude. These measurements indicated that the noise floor was close to 3 nm.

Applying force to the tectorial membrane

The shearing plate was moved into position above the TM using a micromanipulator. The probe was lowered until small deformations of the fibrillar structure of the TM were visible, indicating that the plate was in contact with the TM. The radial fibrils of the TM were also used to help orient the radial and longitudinal axes (Fig. 1). The shearing plate was placed in the thickest part of the TM near the marginal zone to minimize the area of TM that contacted the arms of the probe. TM displacements in response to radial and longitudinal forces were recorded. Force was varied by changing the voltage applied to the piezoactuators driving the probe. The magnitude of the voltage was varied from 1.5 to 45 V, and the order of voltage application was randomized. The magnitude of the force was calculated by multiplying the difference between base and plate displacement by the probe spring constant (Eq. 3). Stimulus frequencies were applied in a random order in the radial and longitudinal directions. The voltage was adjusted at each frequency so that the magnitude of displacement of the probe base was held roughly constant versus frequency (∼0.5 μm for radial motion and ∼1.0 μm for longitudinal motion).

Impedance calculation

Mechanical impedance, defined as the ratio of applied force to resulting velocity, is important for characterizing the mechanical interactions of structures in the cochlea in response to sound stimulation. This impedance is often described as the sum of an inertial term (force proportional to acceleration), a damping term (force proportional to velocity), and an elastic term (force proportional to displacement). When the mechanical properties of the material are linear and the force can be represented as an integral of sinusoidal components at different frequencies, acceleration (and displacement) can be represented as velocity multiplied (divided) by the angular frequency ω and shifted by 90° in the positive (negative) direction. In the frequency domain, the impedance of the TM is thus described by

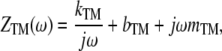(1)

where k_TM is the elastic stiffness, b_TM is the damping, m_TM is the inertial mass, and 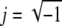represents a phase shift of +90°; i.e., the real and imaginary components of impedance form a vector whose length is the impedance magnitude and whose angle is the impedance phase. Thus, for a purely elastic TM impedance, the slope of magnitude versus frequency would be 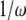(−20 dB/decade when both axes are plotted on a logarithmic scale) with a phase of −90°, a purely viscous TM impedance would have a constant magnitude with a phase of zero, and a purely inertial TM impedance would have a slope of +20 dB/decade with a phase of +90°.

Because the mechanical force probe acts as a stiffness, the force F_mp it applies to the TM is proportional to the deflection of its cantilever arms; that is, F_mp = k_mp(X_b(ω) – X_p(ω)), where k_mp is the net stiffness of the arms, and X_b(ω) and X_p(ω) are the displacement of the probe base and shearing plate, respectively. The resulting velocity of the TM equals the velocity jωX_p(ω) of the shearing plate, so the equation relating the motion of the mechanical force probe to the impedance of the TM is given by

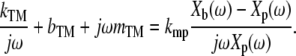(2)

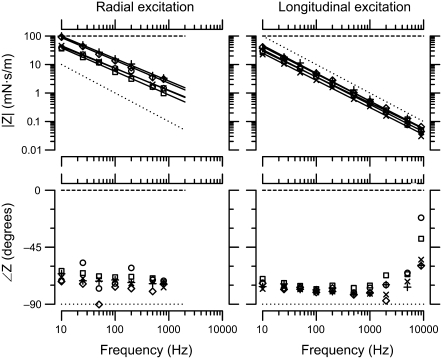
As is shown in Fig. 7 below, the measured TM impedance was between that of a purely elastic and a purely viscous material, with no significant contribution from TM mass. Consequently, the imaginary part of Z_TM in the current measurements was attributed entirely to stiffness.

FIGURE 7.

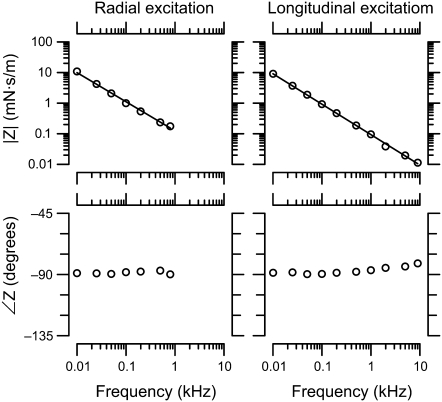
TM impedance versus frequency. The magnitude (top) and phase (bottom) of TM shear impedance are plotted versus frequency for both radial (left) and longitudinal (right) forces. Different symbol types represent individual TMs. The lines represent least-squares power-law fits to measurements from individual TMs. The slopes of these power-law relations were −16 ± 0.4 dB/decade and −19 ± 0.4 dB/decade for radial and longitudinal forces, respectively. The dotted and dashed lines represent the frequency response of a pure elastic spring (slope −20 dB/decade and phase −90°) and a pure viscous damper (slope 0 and phase 0°), respectively.

MICROFABRICATED PROBE CALIBRATION

Determining probe stiffness

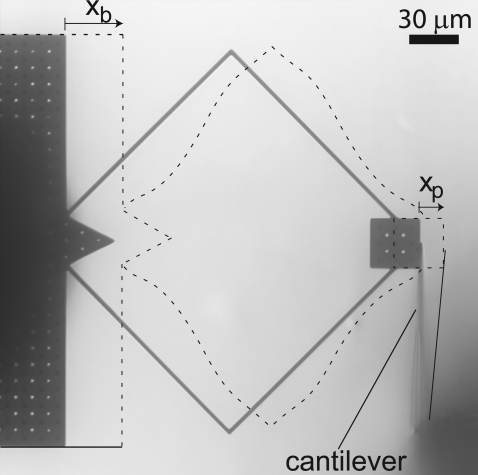
The forces generated by the microfabricated probe were calibrated by pushing against an atomic force cantilever (NP-S series, Veeco Metrology Group, Chadds Ford, PA) with spring constant k_c = 0.58 N/m nominally (Fig. 2). The relative displacement X_b(ω) – X_p(ω) between the base and plate of the probe was compared to the deflection X_p(ω) of the cantilever. Since the probe and cantilever behaved as linear springs (see below), the force F generated by the probe was

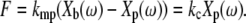(3)

Because atomic force cantilevers are manufactured with a wide tolerance for their spring constants, a thermal fluctuation technique was employed to determine k_c (14). The stiffness of the cantilever found using this technique was 0.57 N/m, close to the nominal value.

FIGURE 2.

Calibration of microfabricated probe with atomic force cantilever. The schematic (dashed lines) depicts deflection of the shearing plate and atomic force cantilever when a radial force was applied to the base of the probe. The schematic is superimposed on an image of the probe and cantilever when no force was applied. The load imposed by the cantilever deflected the flexible arms, so that X_p < X_b. The displacements in this figure are greatly exaggerated for clarity. For calibration in the longitudinal direction, the atomic force cantilever was rotated 90° and placed against a shearing plate edge parallel to the radial axis.

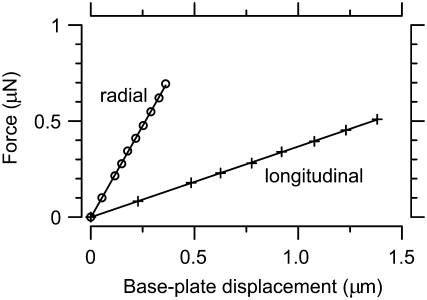
A 50× dry objective was used to image calibration motions (stimulus frequencies 0.01, 0.1, 0.5, 1, and 9 kHz). Force was varied by changing the voltage applied to the piezoactuators (1.5–30 V). The order of force application was randomized. Fig. 3 shows the force applied by a probe as a function of base-plate displacement in the radial and longitudinal directions. The stiffness k_mp varied across probes from 1.7 to 2.4 N/m in the radial direction and 0.36 to 0.41 N/m in the longitudinal direction. These values are somewhat smaller than those predicted from probe geometry, but the difference is within the fabrication tolerance for the probes. The probe was ∼4–6 times stiffer in the radial direction than in the longitudinal direction. The phase difference between base and plate motions was on average 0.6°. Since the atomic force cantilever behaves like a spring in this range of frequencies (the cantilevers are designed to have resonances near 100–150 kHz, and to be elastic at lower frequencies), the small phase difference indicates that the microfabricated probe is also springlike.

FIGURE 3.

Force versus probe deflection. Forces were applied in the radial (○) and longitudinal (+) directions at 100 Hz. Spring constants for the probes were determined by averaging the slopes of the least-squares linear fit curves (solid lines) over three frequencies in the radial direction and four frequencies in the longitudinal direction (other frequencies not shown): 1.7 ± 0.4 N/m and 0.36 ± 0.01 N/m, respectively, for this probe. Note that all ranges reported in this study are mean ± SD unless otherwise specified.

Measuring frequency dependence of probe

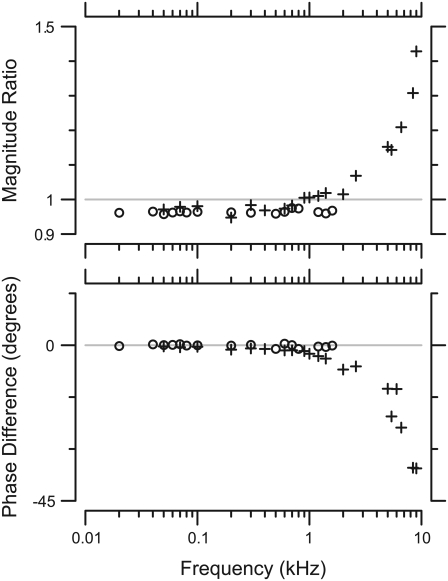
The frequency dependence of probe impedance was measured by applying force at various frequencies to the same AFM cantilever used above. Since the AFM cantilever is known to be springlike at these frequencies, any deviation from a pure stiffness in the measurements was attributed to the microfabricated probe. A 50× dry objective was used to image motions. Stimulus frequencies, applied in a random order, ranged from 10 to 9000 Hz. The range of stimulus frequencies was limited by the stability of the macroscopic mount. The large mass of the mount caused unstable motion at >1600 Hz in the radial direction and at >9000 Hz in the longitudinal direction. Fig. 4 shows measured AFM cantilever impedance versus frequency when driven by radial and longitudinal probe motions. Over the frequency range tested, the measured impedance did not deviate significantly from that of a pure stiffness. This finding indicates that the microfabricated probe responded as a pure stiffness over the frequency range measured.

FIGURE 4.

Measured cantilever impedance versus frequency. The left plot shows the impedance of the atomic force cantilever as measured by the force probe for radial excitation, and the right is for longitudinal excitation. The least-squares power-law fit lines (solid lines) to the magnitudes had slopes of ∼−1, and the phase stayed near −90°.

The effect of water on the probe

Since the probe must be immersed in fluid to apply forces to the TM, we measured the effect of fluid on probe motion. Because the impedance of fluid was small over most of the frequency range studied, the relative motion of the probe base and shearing plate described in Eq. 2 was typically below the noise floor of the measurement system. Since the impedance formulation in Eq. 2 depends on this relative motion, measurements of the impedance of water were in the noise floor over most of the frequency range investigated. To circumvent this problem, we report the ratio 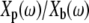of displacements of the shearing plate and probe base. Rearranging Eq. 2 and substituting Z_fluid = b_fluid + jωm_fluid for Z_TM yields

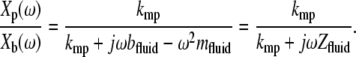(4)

This equation highlights two important differences between measurements of impedance and measurements of the ratio of plate to base displacement. First, when Z_fluid is small, 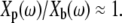Second, because Z_fluid is in the denominator of Eq. 4, a phase lead measured in 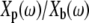corresponds to a phase lag in the fluid impedance Z_fluid and vice versa.

Motions of the probe were imaged using a 40× water immersion objective. The frequency responses of the probe in the radial and longitudinal directions were examined. Stimulus frequencies were presented in a random order. The measured motions as a function of frequency are shown in Fig. 5. Over most of the frequency range measured, the plate and base moved in phase. The magnitude of plate motion <1 kHz was 0.97 ± 0.01 times that of the base. When the images were shifted to stop the apparent motion of the base, the plate could still be seen to move, so the difference between base and plate motion cannot be attributed to measurement error. This difference could be due to the viscous load imposed on the probe at low frequencies (assuming that the inertial load is negligible in this frequency range). Alternately, it could be due to transverse motion of the shearing plate resulting from its lack of attachment to any substrate. Either way, the fluid load imposed on the shearing probe at low frequencies is negligible.

FIGURE 5.

Motion of probe in water. The graphs show the magnitude (top) and phase (bottom) of the ratio of plate displacement to base displacement for radial (○) and longitudinal (+) motions. The magnitude and phase of the ratio for radial motions remained relatively constant through the frequency range measured. For longitudinal motions, the magnitude and phase remained constant until ∼2 kHz. Above that frequency the magnitude increased and the phase decreased.

At >2 kHz for longitudinal displacements, the magnitude of plate motion increased and the phase lagged relative to base displacement. The magnitude increase requires a reduction in the denominator of the right side of Eq. 4. Such a reduction requires a negative real term in jωZ_fluid, and is therefore due to fluid mass. Similarly, the phase lag seen at high frequencies requires an imaginary term, which can only come from fluid viscosity. In other words, both the viscous and inertial effects of fluid contribute to probe motion at high frequencies, as would be expected if the probe were mechanically loaded by a fluidic boundary layer (15). The stiffness of the probe forms a mechanical resonance with the inertia of the fluid, and this resonance is damped by fluid viscosity.

RESULTS

Time waveforms of tectorial membrane motion

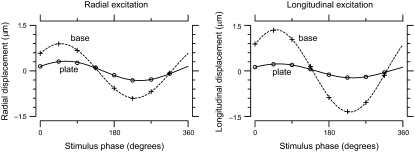
Fig. 6 shows typical motions of the base and plate of the probe over one stimulus cycle. The motions of the base and plate were fit by sinusoidal functions (higher harmonics were typically at least 20 dB smaller than the fundamental), and the magnitude of motion was larger at the probe base than at the plate which was in contact with the TM. Although the plate displacements for radial and longitudinal forces were similar in amplitude, the base displacements required to generate those plate displacements were approximately twice as large for longitudinal forces as for radial forces. Since the ratio of plate to base displacement depends on the relative impedance of the probe and TM, and the probe is approximately five times less stiff in the longitudinal direction, this finding implies that the TM was approximately twice as stiff in the radial than the longitudinal direction at this frequency. The probe base and shearing plate moved in nearly parallel trajectories; orthogonal motions were on average 15 dB smaller. Forces applied to the TM caused displacements not only at the probe location, but over a significant distance in both the radial and longitudinal directions (Supplementary Material, Data S1).

FIGURE 6.

Typical motions of probe on TM over one stimulus cycle. The left plot shows radial displacement over one stimulus cycle for radial excitation, and the right one shows longitudinal displacement for longitudinal excitation. The motions of the base (plusses) and plate (circles) were approximated by sinusoidal functions (dashed and solid curves). The amplitude of motion of the plate, which contacted the TM, was smaller than that of the base. These measurements were for TM preparation 3 at stimulus frequency 100 Hz.

Tectorial membrane impedance versus frequency

Fig. 7 shows TM impedance versus frequency for five TM specimens. For reference, the figure also shows the frequency response of a pure elastic spring (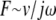) and a pure viscous damper (F ∼ v). The slope of the least-squares fit power-law relation between frequency and impedance was −16 ± 0.4 dB/decade for radial forces and −19 ± 0.4 dB/decade for longitudinal forces. These slopes did not show significant variations with frequency for forces in either direction. Both values were less than the slope of −20 dB/decade expected for purely elastic materials, but greater than the slope of 0 expected for purely viscous materials. The magnitude and phase values were tightly clustered in a narrow range. At 10 Hz, the magnitudes of the least-squares power law fits to impedance were 63 ± 28 mN · s/m in the radial direction and 36 ± 9 mN · s/m in the longitudinal direction. No obvious correlation between impedance magnitude and TM width was seen, although the range of TM widths in this study was small. For individual TMs, the impedance at 10 Hz was 1.7 ± 0.4 times larger in the radial than the longitudinal direction. For a single TM, impedance measurements were highly repeatable (Data S1).

The phase of impedance was nearly constant at −72 ± 6° for radial forces and −78 ± 4° for longitudinal forces at frequencies <5 kHz. At the highest frequencies for longitudinal forces, the phase increased somewhat. This phase lead is consistent with an increase in fluid impedance, as shown in Fig. 5 and described in Eq. 4. Because the fluid environment around the probe in the measurements of Fig. 7 differs from that of Fig. 5, the data of Fig. 7 have not been corrected for the effect of the fluid. However, the fluid in isolation increased probe motion by <3 dB, so the effect of the fluid on measured impedance magnitude is expected to be small compared to the variability across TMs. Such a small difference is not easily resolved due to the logarithmic scale used in Fig. 7.

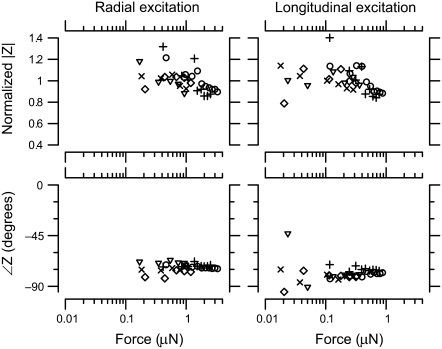
Normalized TM impedance versus applied force is shown in Fig. 8 for a 100 Hz stimulus. The magnitude of impedance was nearly constant with increasing force for low force values. At larger forces (>1 μN for radial forces and >0.3 μN for longitudinal forces), the impedance magnitude decreased only slightly with increasing force. The phase of impedance was nearly constant at all levels for both radial and longitudinal forces. Phase measurements at the lowest longitudinal forces showed significant scatter, presumably because of the small amplitudes involved.

FIGURE 8.

TM impedance versus force. The left panel shows normalized magnitude and phase of TM impedance as a function of applied force in response to radial forces at 100 Hz, and the right panel shows the same measurement for longitudinal forces. The different symbol types represent different TMs. The magnitudes were normalized to their average value across forces for each TM.

DISCUSSION

A novel technique for measuring shear impedance

Although many techniques exist for measuring shear impedance, most face significant difficulties when applied to the TM. Commercial parallel-plate rheometers require large sample sizes compared to the volume of the TM, and cannot be operated at audio frequencies. The magnetic bead method we have used previously (2) was limited to the low end of the audio range of frequencies and forces, and required significant sample preparation. Indentation methods confound compressive and shearing forces, and often require isotropic models for their interpretation ((9,16,17); but see (3)). The shearing probe technique we have presented here overcomes many of these limitations, enabling direct measurement of TM shear impedance at audio frequencies.

The advantages of the shearing probe technique stem largely from the microscale bulk fabrication method. Because the probes are bulk-fabricated, they can be made in large numbers with mechanical properties that are fairly consistent across probes. Moreover, the probe design enables testing material properties over a wide range of impedances by varying the geometry. The microscale design allows the probe to be operated at audio frequencies, and the probe impedance is dominated by stiffness at frequencies up to at least 9 kHz. In comparison to the magnetic bead method, the process of calibrating the stiffness of the probes is relatively straightforward. Moreover, the probe allows forces to be applied in two dimensions without adjusting the preparation, placement of the probe is much simpler, and contact between the probe and the TM is more reliable. Finally, the microfabricated probe applies shearing forces directly, simplifying interpretation of results.

There are a few issues that must be taken into account when using shearing probes. First, the method of determining contact with the TM is subjective, so it is possible that contact between the probe and TM could vary across specimens. In addition, the arms that support the shearing plate sometimes contact the TM, increasing both the effective surface area of contact and stiffness of the probe. Because of the small width and thickness of the TM, boundary effects can play a significant role in interpreting measured impedance in terms of material properties, as discussed below. Finally, at high frequencies the probes can exhibit complex modes of motion, particularly when submerged in fluid. With proper care, the effect of these disadvantages can be minimized.

Frequency dependence of TM shear impedance

The TM shear impedance measurements indicate that the TM is mostly elastic, with the viscous component of impedance at least three times smaller at all frequencies in both the radial and longitudinal directions. The magnitudes of both the elastic and viscous components of TM shear impedance decreased with frequency (Fig. 7). In the longitudinal direction, this decrease was nearly linear, but in the radial direction the magnitude decreased significantly slower than linearly with frequency. In other words, the effective stiffness of the TM increased with frequency (since stiffness for these measurements is the imaginary part of impedance multiplied by frequency) while the effective viscosity decreased. The radial stiffness increased by roughly a factor of two with each decade in frequency, while the radial damping decreased by approximately a factor of five. Since our measurements were made at (nearly) constant displacement, the frequency-dependent stiffness might seem consistent with a strain-rate-dependent impedance, e.g., strain hardening of collagen fibrils. However, shear impedance was nearly constant or decreased slightly with increasing force at a given frequency (Fig. 8). Since increasing either frequency or amplitude increases the strain rate, the observed frequency dependence does not reflect a dependence of impedance on strain rate. This distinction is significant because it shows that the TM responds at low force levels as a Newtonian material (i.e., level-independent impedance) with a frequency-dependent impedance.

The decrease in the real (lossy) part of shear impedance with frequency is primarily due to the TM, since the effect of external fluid is negligible at least for frequencies up to 2 kHz (Fig. 5). There are at least two potential explanations for this frequency-dependent damping. The first is the presence of glycosaminoglycan (GAG) molecules in the TM. GAGs are highly-charged molecules that have been found in abundance in the TM (18–22). Solutions of hyaluronic acid, a GAG molecule, have a viscosity that decreases with increasing strain rate due to GAG-GAG interactions (23). Although such a nonlinearity might account for the measured decrease in TM damping with frequency, this explanation implies that viscosity should also decrease by a factor of five for every factor-of-10 increase in intensity at a given frequency. Our measurements of the level dependence of shear impedance do not show such a decrease. This final point suggests that GAG-GAG interactions alone may not fully account for the frequency-dependent damping.

A second explanation for the frequency-dependent damping is the presence of microscopic pores within the TM through which fluid can flow. This poroelastic interpretation accurately predicts the mechanical properties of cartilage, which is biochemically similar to the TM (24,25). In such a model, the TM consists of an elastic matrix with pores. Deformations of the TM both stretch the elastic matrix and drive fluid flow through the pore network. The viscous contribution to shear impedance at a given frequency is determined by the distribution of pore sizes relative to the size of the viscous boundary layer of the fluid at that frequency. As the frequency increases, the boundary layer thickness decreases relative to the size of the pores, so the net viscous damping decreases. Since the boundary layer thickness is not level-dependent, such models support the observation that the viscous contribution to shear impedance should vary with frequency but not with stimulus level.

Effect of TM attachment on measured stiffness

In the measurements reported here, one surface of the TM was rigidly attached to a glass slide. Such geometric constraints may have a significant effect on the relationship between material properties (such as shear modulus G′) and shear impedance. When a viscoelastic tissue is sheared between two parallel plates, the motion of tissue as a function of depth falls between the gap-loading and surface-loading extremes (26). In the gap-loading extreme, the distance between plates is small compared to the shear wavelength λ_s, so that inertial effects are unimportant and the tissue moves in phase as a function of depth. In the surface-loading extreme, the distance between plates is large compared to λ_s so that a damped wave propagates through the thickness of the tissue, and the tissue sample becomes effectively infinite in thickness. The critical dimension λ_s is given by

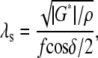(5)

where G* = G′ + jωη is the complex shear modulus, G′ is the elastic shear modulus, η is the shear viscosity, ρ is the density, f is the driving frequency, and δ is the phase shift between stress and strain (27).

The relation between G* and Z depends on the thickness of the sample and the stimulus frequency. For a sample with semi-infinite thickness, this relation is given by

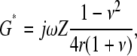(6)

while if the TM is considered thin then the relation can be approximated by

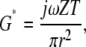(7)

where ν is Poisson's ratio (assumed to be 0.5 at audio frequencies), r is the effective radius of the force probe including any surrounding tissue that moves (roughly 50 ± 10 μm), and T is TM thickness, ∼50 μm near the cochlear apex (28). At 10 Hz for radial forces, these two equations give |G*| values that range from 7–20 and 17–50 kPa, respectively. The large range in values indicates the uncertainty in estimating the effective contact radius r. From these values of |G*| we can determine that λ_s ≫ 50 μm for the range of frequencies measured in this study, so the tissue is in the gap-loading limit. In other words, the attachment of the TM to the glass slide has a significant effect on the measured shear impedance.

The derivation above also means that Eq. 7 is appropriate for determining G*. Given the phase angle of the impedance measurements, |G′| ≈ 0.94|G*| is at the high end of values reported in other studies. Shoelson et al. (16) reported G′ values of 1–9 kPa, while Richter et al. (9) reported 0.1–1 kPa. Gueta et al. (17) reported Young's modulus, and found that the limbal region in the apex was significantly stiffer than the rest of the TM. From their measurements we can estimate G′ to be ∼40 kPa in the limbal region and 10 kPa for the rest of the TM in the cochlear apex. We have recently reported values of 16 kPa in the mouse cochlear apex estimated from measurements of shear wave propagation (8), comparable to the smallest estimates in the current study. The wide range of G′ estimates is not surprising, in light of the many differences between the studies. One clear difference is the species: the studies which reported lower values were done using guinea pig (16) and gerbil (9) TMs, while the larger values were reported from studies of mouse TMs (8,17). The range of best frequencies is significantly higher in mouse than in gerbil or guinea pig. Since Richter et al. (9) showed that TM G′ values correlate to best frequency in a single species, mechanical considerations suggest that G′ should be larger in species that hear in a higher frequency range. Second, our measurements were made at higher frequencies than the other studies, which were limited to stimulus frequencies of 10 Hz and below. Since G′ increases with frequency in our measurements, these frequency differences would make our measurements larger. Finally, the direction of force application varies across studies. The radial fibrillar structure of the TM is expected to increase TM stiffness primarily in the radial direction. Our estimate of G′ for longitudinal forces is roughly half as large as for radial forces, consistent with previous measurements (2,9). If the increased G′ radially is due to the fibrillar structure of the TM (3), then G′ estimates made from applying transverse forces would be expected to be smaller than our radial estimates.

Comparison to previous shear impedance measurements

An earlier dynamic measurement of shear impedance by our group reported point stiffnesses of 0.1–0.3 N/m at 10 Hz, roughly 1–2 orders of magnitude smaller than the point stiffnesses reported here (2). Several factors are likely to contribute to this difference. First, the shearing probes used here had a larger area than the beads in the earlier study. This increased area exerts force on more of the TM, accounting for approximately a difference of a factor of 2–3 in shear impedance. Second, the space constants measured in the previous study (20 μm) were smaller than those measured here (Data S1), suggesting that a smaller volume of TM resisted the forces applied by the beads, accounting for roughly another factor of two. A third factor is that the bath in the earlier study was quite small, and tended to evaporate quickly. Such evaporation increases the charge concentration of the fluid, and this increase can have a significant effect on TM mechanical properties (29,30). Finally, and perhaps most important, in the earlier study, the beads had a tendency to roll as well as translate in the applied magnetic field. Such rolling would not be resisted by the TM shear impedance, so the measured impedance would be artificially reduced. Unfortunately it was not possible to quantify the amount of rolling in the previous study, so the extent to which this effect contributes to the difference between studies is unknown.

TM interactions with hair bundles

The TM has been shown to move in response to sound stimulation in the cochlea (31). This motion is presumably driven by the hair bundles of OHCs, which are inserted into the TM and may couple active as well as passive mechanical forces to the TM (32,33). For this reason it is important to compare the relative stiffness of the TM and hair bundles. Such comparisons have led to a variety of conclusions in different studies. We have previously reported that the TM is significantly stiffer than hair bundles (2,34). Other studies have suggested that the TM is somewhat stiffer (9), comparably stiff (16), or significantly less stiff (35) than hair bundles.

To compare the impedance of the TM and hair bundles, we assumed that the force applied by the probe was distributed over a longitudinal extent of TM that encompassed the probe plus two space constants in either direction (130 μm total). The stiffness of one OHC hair bundle, 5 mN/m (36) was multiplied by 50, the approximate number of OHCs in this region, to yield a net bundle stiffness of 0.25 N/m. At 10 Hz, the shear stiffness of the TM was 3–6 N/m for the probe we used, and this value increased with frequency. Thus the hair bundles would not be able to induce relative shear within the TM by any significant amount.

However, hair bundles could potentially move the bulk of the TM. At low frequencies, the mass of the TM is relatively easy to move. If the limbal attachment of the TM is sufficiently compliant, the hair bundles of OHCs could drive bulk deflection of the TM. In this context it is relevant to note that OHC bundles have recently been shown to exert mechanical force in response to deflections (32,33). Such forces could contribute to the bulk motion of the TM in the form of longitudinally propagating waves of radial motion (8). These forces would be optimally coupled to the TM when the impedance of the hair bundles and the mass of the TM are comparable, which happens in the 1–10 kHz range for the apical TM segments measured here. This frequency range overlaps with the range of best frequencies for the apex of the mouse cochlea, suggesting that the interaction of TM waves with hair bundles may contribute significantly to frequency selectivity in the cochlear apex.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.