Approximate Model of Cooperative Activation and Crossbridge Cycling in Cardiac Muscle Using Ordinary Differential Equations

Abstract

We develop a point model of the cardiac myofilament (MF) to simulate a wide variety of experimental muscle characterizations including Force-Ca relations and twitches under isometric, isosarcometric, isotonic, and auxotonic conditions. Complex MF behaviors are difficult to model because spatial interactions cannot be directly implemented as ordinary differential equations. We therefore allow phenomenological approximations with careful consideration to the relationships with the underlying biophysical mechanisms. We describe new formulations that avoid mean-field approximations found in most existing MF models. To increase the scope and applicability of the model, we include length- and temperature-dependent effects that play important roles in MF responses. We have also included a representation of passive restoring forces to simulate isolated cell shortening protocols. Possessing both computational efficiency and the ability to simulate a wide variety of muscle responses, the MF representation is well suited for coupling to existing cardiac cell models of electrophysiology and Ca-handling mechanisms. To illustrate this suitability, the MF model is coupled to the Chicago rabbit cardiomyocyte model. The combined model generates realistic appearing action potentials, intracellular Ca transients, and cell shortening signals. The combined model also demonstrates that the feedback effects of force on Ca binding to troponin can modify the cytosolic Ca transient.

INTRODUCTION

This article describes an approximate model of activation and force generation in cardiac myofilament that recapitulates many experimental characterizations. Specifically, the experimental characterizations that weighed most heavily in model development are described below:

1. Steady-state force-sarcomere length relations (F-SL relations).

2. Steady-state force-calcium relations (F-Ca relations) including SL effects.

3. Steady-state sarcomere length-calcium relations (SL-Ca relations) for unloaded cells.

4. Steady-state force-velocity relations (F-V relations).

5. Isometric twitches including Ca activation and SL effects.

6. K_tr including Ca activation and temperature effects.

7. Cell shortening twitches as function of activator Ca.

8. Effects of SL control on the intracellular Ca transients.

The last quarter century has seen the development of models to understand many aspects of myofilament responses. As described in a previous review (1), there are still difficulties in developing predictive models given that the underlying muscle biophysics has yet to be fully resolved. Another difficulty lies in trying to compress the spatial aspects of myofilaments at the molecular level into a tractable system of equations. Moreover, if computational speed is desired, then the system must be fairly simple and implemented with ordinary differential equations (ODEs) instead of partial differential equations or Monte Carlo approaches typically required for explicit consideration of the spatial aspects. Much of the following work involves making approximations to maintain a system of ODEs, so emphasis is placed on the simplifying assumptions and their inherent limitations. Much of the model derives squarely from work performed over the last half-century; however, new approximations are developed in the Ca-activation and mean crossbridge strains that differ from previous work. These approximations help bridge the spatial scales where local interactions are critical to emergent behavior but cannot be directly implemented in mass-action or mean-field approaches.

We develop this model in the middle ground where phenomenological approximations are allowed with careful consideration to the relationships of the underlying mechanisms that cannot be explicitly modeled. We have also attempted to strike a reasonable balance between mechanistic detail and model parsimony while including sufficient cellular machinery to recapitulate a wide range of experimental protocols. For example, length- and temperature-dependent effects are included, and the passive restoring force is represented so that experimental protocols in isolated cell shortening can be simulated. Ultimately, we hope that this model will provide the community with an approximate and predictive representation that retains enough mechanistic underpinnings to provide the flexibility and extensibility that existing models do not.

METHODS

Description of sarcomere geometry

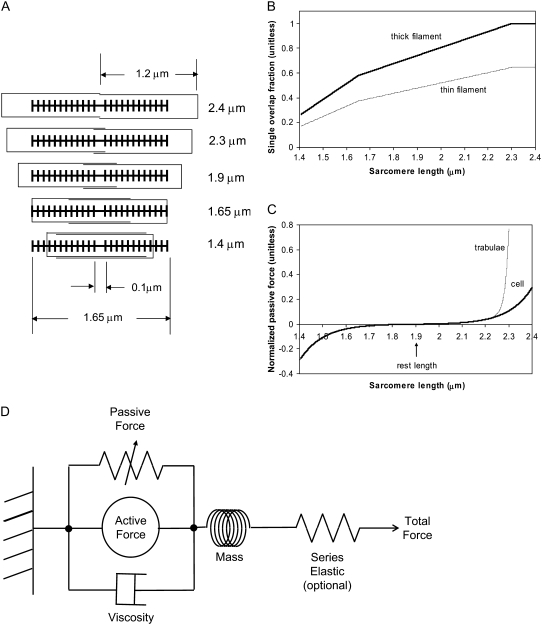
The lengths assumed for the thick and thin filaments are shown in Fig. 1 A. The fraction of crossbridges (XBs) that can strongly bind and generate force depends on the overlap of the thick filament (myosin) and the thin filament (actin and regulatory proteins). To implement length dependence, we define the single-overlap fraction of the thick filament (referred to as SOV_thick) that reports the fraction of thick filament that is apposed to single-overlap thin filament. The assumption is that the only effective strongly-bound XBs occur in the single overlap region. Hence, the thick-filament, single-overlap fraction is used in calculations for maximally activated force. This assumption comes directly from classic sliding filament theory (2).

FIGURE 1.

Modeling sarcomere length effects. (A) The assumed sarcomere geometry is defined using the filament lengths as shown. Specific examples are chosen to show the maximal length (2.4 μm), start of the plateau region (2.3 μm), rest length (1.9 μm), the point where thick filaments contact the z-line (1.65 μm), and the minimal length (1.4 μm). (B) The thick-filament overlap fraction gives the fraction of myosin heads in the single-overlap regions that can form effective force-generating actin-myosin interactions. Hence this value gives the maximum normalized force given full activation. The thin-filament overlap fraction is defined in a similar manner but does not reach unity as the whole thin filament never exists in the single overlap zone. (C) Passive force attributed to titin and other cytoskeletal elements is shown as a function of sarcomere length. The passive force for cells is assumed to reflect across the abscissa at the rest length. For trabeculae, the passive force has an additional component attributed to collagen so that force increases steeply above 2.2 μm and effectively limits sarcomere length to 2.3 μm. (D) In addition to active crossbridge forces and the passive forces just described, the model contains additional components including a viscosity element and a mass element. The series elastic element is optional and is used to simulate experimental protocols with fixed muscle lengths in which the internal sarcomeres shorten as compliant end connections are stretched.

The single-overlap function for the thick filament is shown in Fig. 1 B (see Eqs. 42–46 for mathematical formulation; please refer to Tables 1–3 for the parameters and default conditions used in this work). The maximal possible force corresponds to sarcomere lengths (SLs) in the range 2.3–2.4 μm for which the whole thick filament is in the single-overlap region so that SOV_thick = 1. Between 1.65 and 2.3 μm, the SOV_thick decreases at a constant rate as the thin filaments cross over in the center region of the sarcomere. In the range 1.4–1.65 μm, the SOV_thick decreases at an even faster rate as the thick filament is assumed to cross the z-line, and crossbridges are assumed not to form in the region past the z-line. This aspect to the model is speculative as the actual interactions between the thick filament and z-line are not currently understood. However, some experimental characterizations in trabeculae contract down to sarcomere lengths of ∼1.5 μm (3), which supports this assumption. The maximal Ca-activated force linearly decreases with sarcomere length from 2.15 to ∼1.7 μm where a faster rate of decrease is seen, similar to the model prediction. Moreover, experimental protocols in isolated cells show sarcomere lengths in the range 1.4–1.5 μm under maximal shortening (4). Afterwards the cells recover normal function after relaxation, suggesting a nondestructive interaction between the thick filaments and the z-disk for sarcomere lengths below the thick-filament length.

TABLE 1.

Parameters for model

Parameter	Value	Units
Sarcomere geometry
SLmax	2.4	μm
SLmin	1.4	μm
lengththick	1.65	μm
lengthhbare	0.1	μm
lengththin	1.2	μm
Temperature dependence
TmpC	Range = 15–37	°C
Qkon	1.5	Unitless
Qkoff	1.3	Unitless
Qkn_p	1.6	Unitless
Qkp_n	1.6	Unitless
Qfapp	6.25	Unitless
Qgapp	2.5	Unitless
Qhf	6.25	Unitless
Qhb	6.25	Unitless
Qgxb	6.25	Unitless
Ca binding to troponin to thin filament regulation
kon	50	μM−1 s−1
koffL	250	s−1
koffH	25	s−1
perm50	0.5	Unitless
nperm	15	Unitless
kn_p	50	s−1
Kp_n	500	s−1
Thin filament regulation and crossbridge cycling
fapp	500	s−1
gapp	70	s−1
gslmod	6	Unitless
hf	2000	s−1
hfmdc	5	Unitless
hb	400	s−1
gxb	70	s−1
σp	8	Unitless
σn	1	Unitless
Mean strain of strongly-bound states
x0	0.007	μm
φ	2	Unitless
Normalized active and passive force
SLrest	1.9	μm
PContitin	0.002	(Unit normalized force)
PExptitin	10	Unitless
SLcollagen	2.25	μm
PConcollagen	0.02	(Unit normalized force)
PExpcollagen	70	Unitless
Calculation of complete muscle response
Mass	0.00005 (rat)	(Unit normalized force) s2μm−1
	0.00025 (rabbit)
Viscosity	0.003	(Unit normalized force) s μm−1
	Range = 0.0–1.0	(Unit normalized force)
KSE	Range = 1.0–200.0	(Unit normalized force) μm−1

TABLE 2.

Default initial conditions

Variable	Value	Units
SL	1.9	μm
NNoXB	0.99	Probability
PNoXB	0.01	Probability
NXB	0.97	Probability
PXB	0.01	Probability
XBPreR	0.01	Probability
XBPostR	0.01	Probability
xXBPreR	0	μm
xXBPostR	x0	μm
IntegralForce	0	(Unit normalized force) s

TABLE 3.

Default initial conditions—parameters for default calcium transient (rat, 22.5°C)

Parameter	Value	Units
τ1	0.02	s
τ2	0.11	s
Caamplitude	1.45	μM
Cadiastolic	0.09	μM

A second overlap fraction is defined for interactions along the length of the thin filament (referred to as SOV_thin). The single-overlap function for the thin filament is shown in Fig. 1 B. Note that the single-overlap function for the thin filament varies between 0.17 at 1.4 μm and 0.64 at 2.4 μm. Hence, roughly one-third of the thin filament does not participate in actin-myosin interactions, even at sarcomere lengths that produce maximal force (2.3–2.4 μm) where 100% of the thick filament can participate (SOV_thick = 1). The difference in the single-overlap function for the thin filament and the thick filament is attributed solely to the geometry of the sarcomere (see Eqs. 45 and 46). The single-overlap fraction for the thin filament is used to calculate the Ca binding to troponin that depends on crossbridge interaction. Specifically, higher affinity binding can occur in the vicinity of crossbridges, and as such, the thin filament single-overlap function is used to calculate the Ca binding and activation of the thin filament.

While active force of muscles is attributed to the action of cycling crossbridges, the complete muscle response involves contributions of other entities including passive force and other visco-elastic elements as shown in Fig. 1 D. We assume a rest length of 1.9 μm that corresponds to the point of no passive force as shown in Fig. 1 C. Above the rest length, the passive force is positive and increases total muscle force. Below the rest length, the passive force is negative and hence acts as a restoring force to decrease total force. As shown in Fig. 1 C, the passive force for cells is assumed to be reflected around the resting length. The justification for this is that titin is thought to contribute to passive force, and passive force will be roughly symmetric around the rest-length of titin (as assumed elsewhere, see Fig. 6 in (5)). For this reason, this component is named for titin, although other sources such as cytoskeletal components could also contribute. For trabeculae, the passive force has an additional component so that force increases steeply above 2.2 μm and effectively limits the maximal length of cells to 2.3 μm. This feature is assumed to correspond to the effects of collagen with convolutions that can initially unfurl easily, but once taut, become very stiff. With both components, the passive force curve matches the curvature and steepness of experimental characterizations (3,6), although there is variability in the zero crossing that corresponds to the rest-length (e.g., 1.9–2.0 μm in (6) versus in 2.0–2.1 μm in (3)).

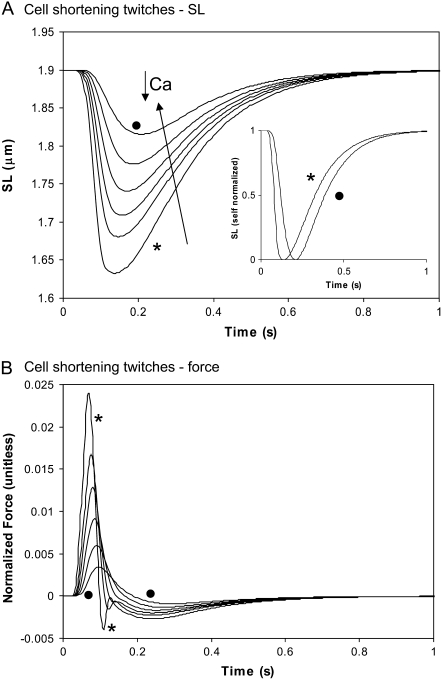
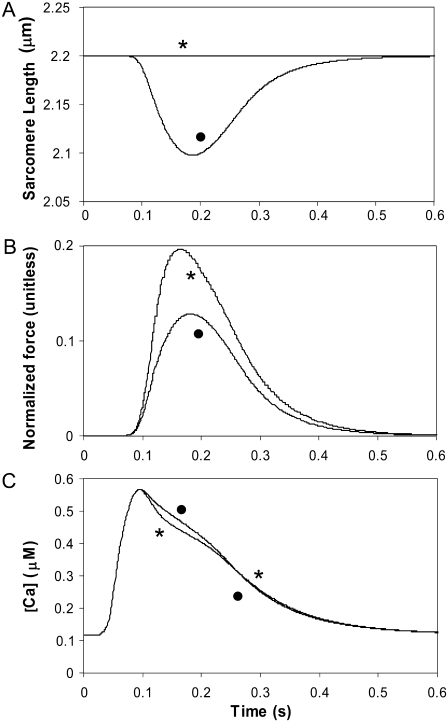
FIGURE 6.

Cell shortening twitches as a function of Ca activation. (A) The cell is allowed to shorten from rest length against the passive restoring force. The sarcomere length is shown for the same Ca transients as in Fig. 5 B with peak values of 1.45 (), 1.25, 1.15, 1.05, 0.95, and 0.85 (•) μM. Note that increased Ca activation decreases the time to peak shortening while the relengthening phase shows less dependence on Ca activation. The inset shows self-normalized sarcomere length (1 = rest length, 0 = minimum length) for peak values of 1.45 () and 0.85 (•) μM. The times from 50% shortening to 50% relaxation are 0.247 s () and 0.229 (•). (B) The total muscle force (active plus passive) is plotted for the corresponding traces in panel A. Data correspond to rat at 22.5°C.

Other visco-elastic elements are also included. The muscle is assumed to have a Newtonian viscosity element set to the mean value found experimentally (0.3% F_max μm⁻¹ s⁻¹ from (6)). A small mass term is also included. The effect of the mass is to prevent instantaneous changes in muscle shortening velocity for quick release protocols, a feature that improves the stability of the integration of the model equations. Tuning this parameter can also improve response times. Specifically, large values can generate underdamped responses that overshoot and ring. On the other extreme, small mass values can produce overdamped responses. We choose a midrange value between these extremes. Finally, a linear series elastic element can be included to simulate the effects of compliant end connections that occur in real muscle preparations. Hence the muscle can shorten internally at the active force element even through the total muscle length is fixed. No fixed value is assumed for the elastic element, but instead parametric studies are used to illustrate the effect on muscle responses.

Regulatory Ca-binding to troponin

The presence of strongly-bound crossbridges is assumed to increase the binding affinity of the nearby regulatory units (RUs). This is embodied by assuming Ca binding to two populations of troponin regulatory sites that correspond to the higher affinity with strongly-bound crossbridges and to lower affinity sites without strongly-bound crossbridges. Here, “high” and “low” refer to the single regulatory binding site and should not be confused with the two high-affinity, nonregulatory sites on cardiac Troponin C. The high and low affinity sites are calculated as the fractional population with Ca bound (CaTrop_H and CaTrop_L, respectively),

(1)

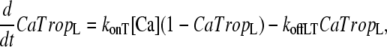(2)

where k_onT is the complete rate constant for binding, [Ca] is the concentration of Ca, k_offHT is the complete rate constant for unbinding from high-affinity sites, and k_offLT is the complete rate constant for unbinding the low affinity sites.

While the rates in the model represent a diverse set of state transitions, a standard definition format is maintained. The format is explained using the following example for generic total rate constant k_xT,

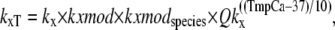(3)

where k_x is the base rate constant under default conditions; kxmod is a modifier based on other parameters or states (e.g., crossbridge strain); kxmod_species is modifier based on species (e.g., rat or rabbit); and Qk_x is the Q10 value for 10° changes in the temperature as specified by TmpC. All transition rates can be represented in the above form, although not all rates have explicit kxmod and kxmod_species terms. The net effect of the Q10 terms is to decrease the rates below the default values as defined at 37°C. The T in the subscript differentiates the total transition rate k_xT from the base-rate value under default conditions denoted by k_x.

For these specific examples, the total Ca binding is assumed to be diffusion-limited and is the same for high- and low-affinity cases. We assume a relatively low temperature dependence so that

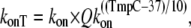(4)

where k_on is 50 μM⁻¹ s⁻¹ and Qk_on is 1.5.

The corresponding total rate for unbinding rate for the high- and low-affinity cases are defined as

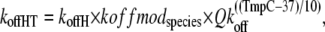(5)

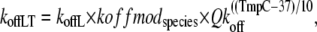(6)

where k_offH is 25 s⁻¹; k_offL is 250 s⁻¹; kxmod_species is 1.0 for rat and 0.9 for rabbit; and Qk_off is 1.2. The off-rate k_offH is smaller than k_offL by a factor of 10 to account for the higher affinity of troponin associated with strongly-bound crossbridges. The 10-fold increase is similar to experimental estimates of ∼8.6-fold (7) and ≥10 fold (8). Note that Qk_on > Qk_off so that Ca sensitivity decreases with lower temperature as suggested by experimental results (9–11).

Ca-based activation

We assume that steep Ca sensitivity in activation results from nearest-neighbor interactions of troponin and tropomyosin along the thin filament. Indeed, explicit modeling of this process underscores the plausibility of this assumption (1,12). For the modeling here, we seek to avoid explicit spatial representation of nearest-neighbor interactions as these cannot be represented as ODEs. Instead, we assume that thin-filament activation is a steeply nonlinear function of [Ca] as a phenomenological representation of the effects of nearest-neighbor interactions. Similar nonlinear functions have been employed in previous modeling efforts to capture the assumed effects end-to-end interactions of RUs (13–16).

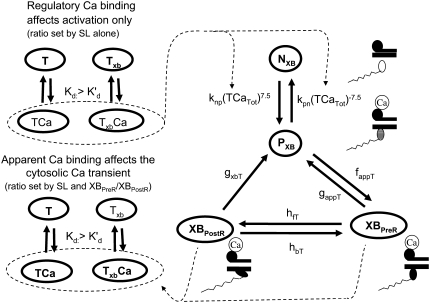
To implement Ca-based activation, we assume that troponin and tropomyosin act as RUs that exist in one of two states, N or P (Fig. 2). State N represents a nonpermissive state that prevents the formation of strongly-bound crossbridges. State P represents a permissive conformation of the regulatory proteins that can permit transitions to strongly-bound crossbridge states. First, we can consider the case in which no crossbridges can form (outside of the single-overlap region between the thick and thin filaments) and use the notation N_NoXB and P_NoXB to indicate the absence of nearby crossbridges. In this region, the following equations hold:

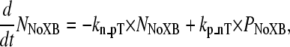(7)

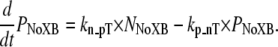(8)

The transition rates k_{n_pT} and k_{p_nT} are set so that the fraction of permissive RUs is a nonlinear function of the fraction of RUs with Ca bound and not directly to intracellular [Ca] itself. Mathematically, the nonlinearity is incorporated using

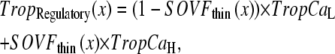(9)

where Trop_Regulatory(x) is the fraction of thin filament RUs that have Ca bound; x is the sarcomere length; and SOVF_thin(x) is the single-overlap function for the thin filament. We assume nearest-neighbor cooperativity so that the shift of an RU to a permissive state is represented by a nonlinear function called permtot defined as

(10)

where the half-activation constant perm₅₀ = 0.5 and the Hill coefficient n_perm = 15.

FIGURE 2.

Model construction. States N_XB and P_XB represent nonpermissive and permissive conformations of the regulatory proteins, respectively. The next transition is to the XB_PreR state, short for prerotated, that is strongly bound with the head extended. The transition to the post-rotated force-generating XB_PostR state, short for post-rotated, represents the isomerization to induce strain in the extensible neck region. For the activation process, the fraction of troponin with bound Ca (TCa) is used to set the transition rate between N_XB and P_XB using a strong nonlinearity function to represent cooperativity. The model assumes that troponin for regulation has affinity set by the thin-filament overlap (and hence ultimately sarcomere length) which tracks the fraction of regulatory proteins with nearby crossbridges that can attach (see Fig. 1). Higher affinity is assumed to represent the cooperative effects of attached crossbridges on Ca binding. Calculation of apparent Ca binding is similar but uses thin-filament overlap fraction and also assumes that affinity increases only after crossbridges strongly bind to populate the XB_PreR and XB_PostR states. The regulatory and apparent Ca binding terms are calculated separately to avoid a global feedback from strongly-bound crossbridges to Ca binding. Such feedback can produce a nonphysiological Ca sensitivity (see text for details).

Then permtot modifies the forward rate for nonpermissive to permissive transitions as

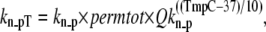(11)

where k_{n_p} = 50 s⁻¹ and Qk_{n_p} = 1.6. Working in the opposite direction, the permissive to nonpermissive transition rate is modified by the inverse of permtot in the formulations

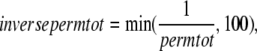(12)

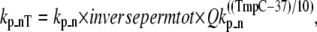(13)

where k_{p_n} = 500 s⁻¹ and Qk_{p_n} = 1.6. Note that a maximum value is placed on inversepermtot to insure that k_{p_nT} is not greater than k_{p_n} × 100 = 50,000 s⁻¹. This limit is set to prevent the numerical integrator from requiring very small time steps that result when transition rates are very large. Note that the limit has very minor effects on model behavior as k_{n_pT} ≪ k_{p_nT}, and all RUs are effectively nonpermissive when the limit is reached.

Crossbridge cycling—computing state occupancy

For the case of RU activation with subsequent crossbridge formation, the situation is somewhat more complicated. Ca-induced changes in the regulatory proteins are generally assumed to permit actin-myosin interactions. However, strongly-bound crossbridges are also found to produce thin-filament activation, even in the absence of activator Ca (17,18). To best capture such interactions, activation and crossbridge cycling are combined in a coupled system (Fig. 2) that is adapted from the work of Razumova et al. (19). This set of states represents an ensemble of myosin heads and the associated actin and regulatory proteins.

State N_XB represents a nonpermissive state that prevents the formation of strongly-bound crossbridges. State P_XB represents a permissive conformation of the regulatory proteins, and the nearest myosin is assumed to be in a detached or weakly-bound state. In this model, the detached and weakly bound crossbridge states are lumped together. These states are analogous to states N_NoXB and P_NoXB described above for the case of no nearby myosin. The XB_PreR state is strongly bound, but the myosin head has not isomerized to rotate and induce strain in the neck region. Hence, this state contributes to stiffness but does not generate force in the absence of net motion. The XB_PostR state is a strongly-bound, post-isomerization state in which the crossbridge head has rotated to put distortion equal to x₀ in the extensible link. Returning to the weakly bound state is unidirectional and is assumed to consume one ATP. In contrast, the other transitions are bidirectional and do not involve ATP hydrolysis. The complete set of equations is

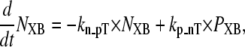(14)

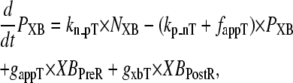(15)

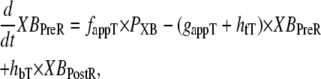(16)

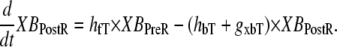(17)

As in the work of Razumova et al. (19), the force is proportional to the fractional occupancy of the strongly-bound states multiplied by the respective mean distortion of these states. The mean distortion states XB_PreR and XB_PostR are tracked by variables xXB_PreR and xXB_PostR, respectively. While the full mathematical formulation is presented below, a brief description suffices for now. Crossbridges become strongly bound with a transition from P_XB to XB_PreR with an assumed distortion of 0. The rotation of the myosin from XB_PreR to XB_PostR is assumed to induce an increase in distortion equal to x₀. Hence, in the absence of net motion between the thick and thin filaments, xXB_PreR is 0 and xXB_PostR is x₀.

While the basic framework derives from Razumova et al. (19), the transition rates have been modified in both general and specific ways. In general, the base rates are larger in the current formulation that corresponds to 37°C. The current model also includes a term xbmod_species (1.0 for rat or 0.2 for rabbit) that scales all crossbridge cycling rates to account for species-based differences. For specific changes, the crossbridge attachment rate to the first strongly-bound state XB_PreR is now given by

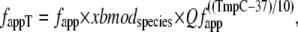(18)

where f_app = 500 s⁻¹ and Qf_app is defined at the end of this section. Note that except for the species and temperature dependence, the rate is fixed. The original formulation in Razumova et al. (19) has a cooperative attachment term that is not retained.

The reverse rate is similar except for a modifier g_appslmod that increases the detachment rate at shorter sarcomere lengths. The exact definition is

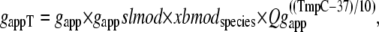(19)

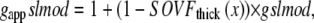(20)

where g_app = 70 s⁻¹; Qg_app is defined at the end of this section; x is the sarcomere length; and the constant gslmod = 6 is used to scale the effects of the thick-filament, single-overlap fraction on the strongly- to weakly-bound transition rate.

The construction of g_appslmod that increases the detachment rate at shorter sarcomere lengths is speculative and ad hoc but has some justification. One or two strongly-bound crossbridges anywhere along the thin filament may suffice to hold the whole thin filament permissive even in the absence of activator Ca. We represent this effect by decreasing detachment rates for conditions for which more crossbridges can be recruited (i.e., as SOVF_thick (x) increases at longer sarcomere length). In terms of model responses, the construction produces isometric twitches for which the final relaxation has faster time rates of force decline as sarcomere length decreases, as seen experimentally (20,21). Note however, that sarcomere length has been shown not to affect the tension cost (ATPase rate/force) in experimental studies (22), so a similar SL-dependence is not applied to 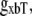the ATP-consuming detachment transition rate.

The forward transition rate h_fT between the strongly-bound states XB_PreR to XB_PostR is defined as

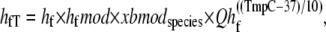(21)

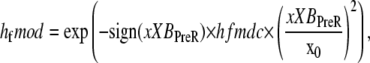(22)

where h_f = 2000 s⁻¹; Qh_f is defined at the end of this section; and the constant hfmdc = 5 sets the extent to which mean strain of the prerotated state affects the isomerization rate. The net effect is to increase the forward rate as xXB_PreR becomes more negative as occurs during muscle shortening. Conversely, a lengthening muscle will produce a positive xXB_PreR to decrease the isomerization rate. The backward transition rate h_bT from XB_PostR to XB_PreR. is defined by

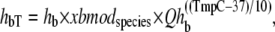(23)

where h_b = 400 s⁻¹ and Qh_b is defined at the end of this section.

In the original work of Razumova et al. (19), the isomerization transition rates (corresponding to h_fT and h_BT) had no strain dependence. We found that strain dependence on forward transition rate h_fT was needed to produce shortening velocities comparable to experimental measures. In principle, similar effects could be produced by a strain-dependent decrease in reverse rate h_bT. However, in this model, strain dependence on backward transition rate h_bT produces instabilities. Hence, no strain dependence is included in h_bT. As discussed later, the full system of equations can show instability and oscillations under some parameter choices.

In the original work of Razumova et al. (19), the isomerization transition rates play a much smaller role in shaping responses as compared to the ATP-consuming detachment transition rate, at least for the protocols simulated in that study. Hence, only the ATP-consuming detachment transition rate is assumed to have strain-dependent terms in the Razumova et al. study. For this study, we carry over the strain-dependence from that study in the rate modifier gxbmd, defined as

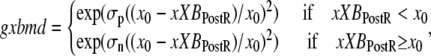(24)

where constants σ_p = 8 and σ_n = 1 set the effects of strain for positive and negative shortening velocities, respectively. The effect of σ_p > σ_n is to increase the ATPase rate more for shortening than for lengthening protocols. Note that the values chosen differ from those in the original study which would have corresponded to σ_p = 1 and σ_n = 8. The total rate is

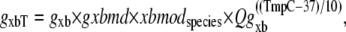(25)

where g_xb = 70 s⁻¹ and Qg_xb is defined below.

The temperature dependence of the crossbridge cycling transition rates are uniformly (except for one case) set to a default Q10 value of 6.25. Specifically, Qf_app = 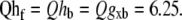By setting the Q10 values to be equal, the relative population of states should be roughly constant as temperature changes. While this is an obvious simplification, the values produce reasonable temperature-induced changes in maximal shortening velocity, twitch duration, and K_tr. While 6.25 appears large, values as large as 6.7 have been reported for reactions in the crossbridge cycle (23). Note that there is one exception in our model in that Qg_app = 2.5. There are two justifications. One is that Qf_app and Qg_app best correspond to k₄ and k₋₄ in (23) with Q10 values equal to 6.7 and 2.5, respectively. In addition, the differential in Q10 values in the model produces a maximal Ca-activated force that increases with temperature, as seen in experimental studies (9–11).

Crossbridge cycling—computing force and mean strain

As in the work of Razumova et al. (19), the force is proportional to the fraction of occupancy of the strongly-bound states (XB_PreR and XB_PostR) multiplied by the average distortion of these states (xXB_PreR. and xXB_PostR). Mathematically, one can write

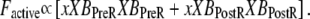(26)

The fractional occupancies of the strongly-bound states are computed as described previously. Note that Eq. 26 constitutes a mean-field approximation, while spatially explicit approaches calculate force as the expected value of developed force for all strongly-bound crossbridges. Specifically, in a spatially explicit model, we could write for the population of crossbridges

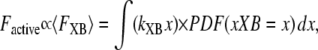(27)

where the first term in the integral is the force of an attached crossbridge as a linear spring constant k_XB multiplied by the distortion x. The second term in the integral is the probability density function of an attached strongly-bound crossbridge with distortion x. This representation is derived from the classic modeling work of Huxley (24) and is used in more current models with explicit spatial representations that require partial differential equations (e.g., (25,26)).

However, for our spatially compressed model, we assume that

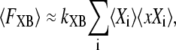(28)

where 〈X_i〉 is the occupancy of state X_i, 〈xX_i〉 is the mean distortion of state X_i, and the summation is over all strongly-bound states. A similar mean-field approximation is made in previous modeling to decrease the computation complexity and produces reasonable results under many conditions (for a more in-depth discussion, see (19)). Understanding the mean-field approximation is key for understanding the model construction that follows.

The mean strain of crossbridge states are computed by assuming full activation of the thin filament. Hence, all RUs are assumed to be permissive, and Ca-based activation events plays no role in the strain calculation. Note that assuming full thin-filament activation leads to a different formulation for mean distortion of states than that of earlier work from which the model is based. In the earlier study (19), mean distortion is assumed to depend on both the fractional occupancy of states as well as the transitions between states. To carry this approach over to the model here, then mean distortion would include the state-occupancy terms (P_XB, XB_PreR, and XB_PostR). However, the occupancy of these states is strongly influenced by Ca-based activation, and as a result, the kinetics of computing crossbridge strain become strongly Ca-dependent. We avoided this construction to ensure that the mean distortion of the states would depend only on the relative sliding of the filaments and the intrinsic cycling rates of crossbridges. The rationale for the construction depends on the assumption that strong nearest-neighbor coupling between RUs will produce large stretches of thin filament that are permissive. These effects are assumed to be local and not affected by bulk fraction of cycling crossbridges that are represented by the state-occupancy terms. The arguments are somewhat involved, and are deferred to the Discussion.

With the assumption of full thin-filament activation, the mean distortion xXB_PreR and xXB_PostR are calculated as

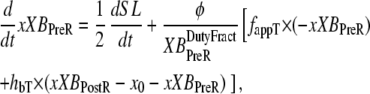(29)

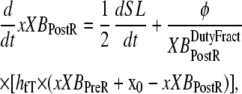(30)

where is the velocity of sarcomere length (note that SL in this instance is a model variable, although “SL” is the general abbreviation for sarcomere length); φ is an empirically derived scaling term; an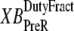d and 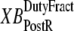are the fraction of units in states XB_PreR and XB_PostR assuming full thin-filament activation.

The motivation for the mean distortion follows from considering the interplay of two effects: net motion between the thin and thick filaments and the gain or loss of distortion as crossbridges change states. The first effect is embodied in the first terms on the right hand sides of Eqs. 29 and 30. Namely, the 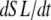terms generate a proportional change in mean crossbridge distortions that track the net sliding of the thick and thin filaments. The ½-scaling term accounts for the effects of sarcomere geometry in which the thick filaments are symmetric, and the full sarcomere shortening velocity is double the net rate of change between half-thick filaments and the associated thin filaments.

The gain or loss of distortion as crossbridges change state during cycling is embodied in the second quantities on the right-hand sides of Eqs. 29 and 30. Consider first Eq. 30, which is the simpler of the two. Here xXB_PostR assumes a value similar to xXB_PreR + x₀ when the forward transition rate is large. Hence, a high forward rate of isomerization will tend to produce xXB_PostR that tracks xXB_PreR with added strain x₀. Turning to Eq. 29, the backward transition for isomerization is represented by the term h_bT × (xXB_PostR − x₀ − xXB_PreR). In computing xXB_PreR, another factor is the effect of the transition from a weakly-bound to a strongly-bound state (from state P_XB to state XB_PreR). These new strongly-bound crossbridges are assumed to attach with 0 mean distortion, so that a high rate of attachment should decrease xXB_PreR. This effect is incorporated by the f_appT × (−xXB_PreR) term, which will force xXB_PreR toward 0 with a rate proportional to f_appT.

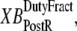So far we have used only attachment rates to compute mean strains. Intuitively, any change in mean distortion as a result of crossbridge cycling should also depend on detachment rates. In the current formulation, we consider detachment rate indirectly by calculating and which are the fractions (or alternatively, duty cycles) of units in states XB_PostR and XB_PreR assuming full thin-filament activation. These values are calculated by assuming that k_{n_pT} ≫ k_{p_nT} so that only states P_XB, XB_PreR, and XB_PostR are populated. Using the King-Altman rule (27), the steady-state population of states can be determined from the transition rates as

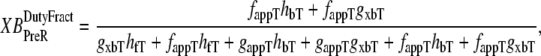(31)

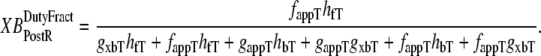(32)

In Eqs. 29 and 30, the inverses of 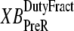and 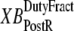are used as scaling factors for second terms on the right-hand sides to represent the dependence on the length of time a crossbridge remains in a given state. If crossbridges are cycling quickly through the crossbridge cycle, then one can assume that the rates into the strongly-bound states will be high while the total occupancy can be low as result of fast turnover. The inclusion of the inverses of 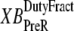and 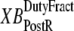in the calculation of mean strain captures the effect of turnover rate, on how quickly crossbridge can refresh strain.

With the above definitions in place, Eqs. 29 and 30 can be interpreted as phenomenological formulations to compute mean distortion as the interplay of the net motion of thick and thin filament and the effect of crossbridge cycling. Consider two simple cases. If crossbridges are slowly cycling, upon assuming small values for f_appT, h_fT, and h_bT, the 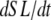term will dominate. Then the mean distortion is determined primarily by the net motion of thick and thin filament. In contrast, when there is no motion between the thick and thin filaments (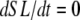), crossbridge cycling dominates. One can easily see that xXB_PreR will tend to 0 as the weak-to-strong transition will generate new crossbridges with net distortions of 0. In contrast, xXB_PostR will tend to xXB_PreR + x₀ and hence x₀. Such results are consistent with current theories for crossbridge dynamics. In our phenomenological approach, φ is an empirically derived scaling term that weighs the relative contribution of the 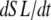term with the contribution of the crossbridge turnover terms. With φ = 2, the model generates reasonable, albeit phenomenological, values for mean distortions over a wide range of velocities and crossbridge cycling rates.

Calculation of normalized active force

One complication in developing myofilament models is the method to report output force. Similar to previous work in this area (15), we report a normalized force with a maximum value of 1 with no assumptions on the exact choice of transition rates. With such an approach, competing models can be developed and compared without having to constantly renormalize results. The approach can be implemented by choosing scaling factors such that state occupancies are normalized to the maximum values possible under optimal conditions. In the model generated here, this situation occurs for high Ca activation, isosarcometric, physiological temperature, and maximal single overlap of thick and thin filaments. These conditions can be simulated by assuming k_{n_pT} ≫ k_{p_nT} so that the system is fully activated. Isosarcometric conditions (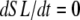) and physiological temperature (37°C) produce the largest values for the transition rates and the maximal steady-state occupancies for force-generating states. Assuming SL = 2.3 μm generates that SOV_thick = 1 and SOV_thin = 0.64.

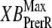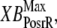The two scaling factors for state occupancy computed under optimal conditions are and which are the fraction of strongly-bound crossbridges under the optimal conditions above. In this case, Eqs. 31 and 32 simplify to

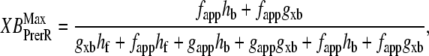(33)

(34)

Note that Eqs. 33 and 34 are very similar to Eqs. 31 and 32 with the important change that the default rate values are used in the latter versus the total rate values in the former (e.g., f_app versus f_appT).

The full definition of normalized active force is

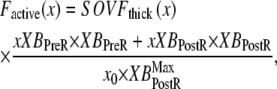(35)

where x is the sarcomere length. The SOVF_thick (x) term is a scaling factor for the contribution of sarcomere geometry to the number of recruitable crossbridges. Note that no 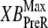term exists in the denominator on the right-hand side of Eq. 35. Under isosarcometric conditions, xXB_PreR will be 0 so there is no contribution by the XB_PreR state under the optimal conditions defined above.

Apparent Ca-binding to troponin

For the regulatory Ca binding as described in Eq. 9, the ratio of low- and high-affinity troponin units is set by thick- and thin-filament overlap as determined by sarcomere length. Hence, the regulatory Ca binding assumes a higher affinity if thin filament is in the single-overlap region and does not depend on whether the crossbridges are strongly bound. In contrast, the apparent Ca binding that is assumed to be sensed by a cell is calculated by assuming that the affinity of troponin increases only if nearby crossbridges are in strongly-bound states. In other words, the force-dependent Ca binding to troponin that affects the intracellular [Ca] transient is computed differently from the assumed regulatory binding of Ca to troponin that switches on and off the attachment of crossbridges (see Eqs. 1, 2, and 9). The apparent Ca binding is formulated below.

The fraction of strongly-bound crossbridges is

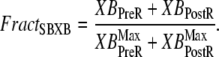(36)

Then the apparent Ca binding is calculated by assuming that troponin in the single-overlap region exhibits high affinity in proportion to 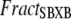as

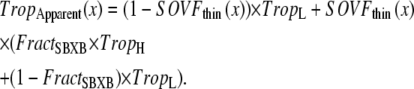(37)

The motivation of separately calculating regulatory and apparent binding is described in detail in the Discussion.

Running the complete muscle model

If the simulation is assumed to be isosarcometric, then 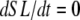and SL is fixed at its initial value SL₀. If the sarcomere is assumed to contract or expand, then the following ODE is solved to compute SL,

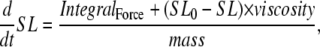(38)

where viscosity and mass are defined as shown in Fig. 1 D. Integral_Force is defined so that normalized forces are summed and integrated over time in the formulation

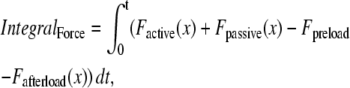(39)

where F_active (x) is defined in Eq. 35; and F_passive (x) is shown in Fig. 1 C (and defined in the Appendix). The term F_preload is a constant force that corresponds to an applied force that would induce an initial sarcomere length that is larger than the resting length. Hence, this term balances the passive force so that F_preload = F_passive(SL₀). The afterload term is used in one of two ways. For an isotonic contraction, the afterload term is fixed after the release. For a fixed muscle length (isometric) contraction, the afterload is computed as a series elastic element (see Fig. 1 D) used to simulate compliant ends of the muscle. The exact formulation is

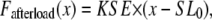(40)

where x is the sarcomere length, and KSE is the stiffness in units of normalized force per μm.

While the model is essentially defined by the equations alone, a few notes on the implementation are in order. The model source code, parameters to recreate figures, and sample output files are provided in Supplementary Material, Data S1. An implementation is also available in CellML, an XML markup language to store and exchange computer-based mathematical models (see http://www.cellml.org/models/rice_wang_bers_detombe_2008_version01). The model comprises a stiff set of nonlinear ODEs that can be problematic for some numerical integrators. The model is implemented in C code using the CVODE integrator (28). In addition, the model has been implemented in XPP for which multiple integrators can be selected (http://www.math.pitt.edu/∼bard/xpp/xpp.html). In XPP, the CVODE integration method runs for the widest range of protocols, while other methods often failed for some protocols or parameter choices. When multiple integration methods execute successfully, the results are consistent. However, there are cases where the model can produce ringing and low amplitude oscillations that are a property of the equations and not of the integrator choice. This observation should not be too troubling given that the nonlinear equations are highly interconnected with feedback terms. Moreover, the mean-field approaches for Ca activation and crossbridge cycling are obvious departures from reality, so inherent stability should not be automatically assumed. Indeed, even real muscle can show oscillations that are more prevalent in conditions producing submaximal crossbridge cycling (29,30). In the modeling work here, instabilities are exacerbated by manipulations that lower the crossbridge cycling rates (e.g., by lower temperatures) as well as certain parameter choices that produce large strain dependences on transition rates.

Modification to model rabbit myofilaments

The model is adjusted by decreasing transition rates in the crossbridge cycle by a factor of 5 to simulate the changes in myosin isoforms (rat is predominately V1 while rabbit is V3). In the absence of direct experimental data, the factor of 5 is set empirically in the model to generate twitch response in rabbit that look similar to experimental measures. The assumed species difference is reasonable compared to crossbridge cycling rate differences between rat and guinea pig that has been estimated to be a factor-of-6 faster in rat (31). The only other changes are a slight increase in Ca sensitivity and a factor-of-5 increase in the mass term in rabbit which help to improve the rate of relaxation. These modifications are relatively simplistic, and we expect that more specific changes in other aspects of the model will be needed to better recapitulate all the species differences. However, a minimal set of changes is made as there is much less experimental data to characterize the myofilament responses in rabbit as compared to rat.

Coupling to cardiac electrophysiology and Ca-handling mechanisms

One goal of this work is to develop a model of the myofilaments that is suitable for coupling to existing models of cardiac models of cardiac electrophysiology and Ca-handling mechanisms that exist in the literature. To illustrate this purpose, we coupled our rabbit-modified myofilament model to the Chicago rabbit ventricular myocyte model (32). These models are coupled by using the cytosolic Ca concentration ([Ca]_c) from the Chicago model as the input to the myofilament model. A feedback pathway exists in that the buffering of the low-affinity, regulatory Ca-binding site on troponin is assumed to be controlled by the apparent Ca binding of the myofilament model as shown in Eq. 37. One complication exists in that Eq. 37 provides the total Ca bound to the regulatory site on troponin, whereas the Chicago model requires calculation of fluxes on to and off of buffers. To match this construction, we differentiate Eq. 37 with respect to time (see Eqs. 58–64). Note that Ca binding to troponin (Trop_H and Trop_L), the thin-filament overlap (SOVF_thin (x)), and the fraction of strongly-bound crossbridges (Fract_SBXB) can also change with time, so the chain rule is applied to terms with these variables (see Appendix for details).

RESULTS

F-Ca and SL-Ca responses

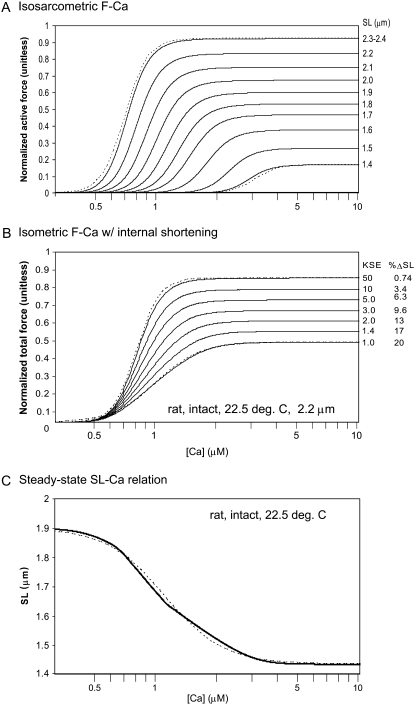
Fig. 3 A shows steady-state F-pCa relationships with the response of the model over a range of sarcomere lengths as labeled. Longer sarcomere length increases both Ca sensitivity (leftward shift) and maximal plateau force. The steepness as quantified by the Hill coefficient changes little with sarcomere length. The SL-dependence of F-Ca relations in Fig. 3 A can be compared with experimental data under sarcomere length control (33) with the exception that Ca₅₀ values are larger in skinned preparations than what is expected for intact fibers (3). Similar trends are observed in both model and experiment: sarcomere length increases maximal plateau force while the Ca sensitivity shows little change in the Hill coefficient (the dashed traces show true Hill functions with Hill coefficient = 7.6 for comparison). Note, however, that the shorter sarcomere lengths cannot be experimentally measured, and hence these responses are untestable model predictions. The model results at these shorter lengths continue the trends at the longer sarcomere length as a result of the mechanisms described below.

FIGURE 3.

Steady-state responses as a function of Ca. The plots show isometric force as a function of steady-state activator [Ca]. (A) Active force is shown for the sarcomere lengths as labeled that simulate isosarcometric conditions. The relations are similar to Hill functions as determined by the Ca-based activation assumed in the model. For comparison, two true Hill functions with Hill coefficient = 7.6 are shown by the dashed traces. (B) Total muscle force (active plus passive) are shown for fixed muscle length for which internal shortening can occur. The degree of shortening is controlled by the stiffness of the series elastic element as labeled for the different traces (units of KSE are normalized force per μm extension). The degree of shortening from the initial length of 2.2 μm is also shown for each trace. Two true Hill functions are shown by the dashed traces for comparison. For KSE = 50, the Hill coefficient = 7.6, and pCa50 = 6.1. For KSE = 1, the Hill coefficient = 4.0, and pCa50 = 6.0. (C) The steady-state sarcomere length is shown as a function of activator Ca. Here the muscle is shortening from the rest length of 1.9 μm against the passive restoring force. A Hill-like function can be fit to the sarcomere length as shown by the dashed line. Here the Hill coefficient = 3.0, and pCa50 = 5.9.

The observed SL-based changes come from changes in the thick- and thin-filament overlap fractions as sarcomere length changes. The maximal plateau force occurs when the thin filaments are fully activated and hence reflect the fractional recruitment of strongly-bound crossbridges as a function of sarcomere length. This fraction is set by the thick-filament overlap fraction (specifically by the SOVF_thick (x) term in Eq. 35). While the mechanism of increased Ca sensitivity in real muscle is under debate, the behavior of the model can be mechanistically explained. The increased Ca sensitivity results from a different ratio of high- and low-affinity sites as a function of thin-filament overlap fraction (see Fig. 1 B, and see the Appendix for the exact formulation). Activation is derived from the weighted sum of binding to high- and low-affinity binding sites as determined by the thin-filament overlap fraction (see Eq. 9).

The data in Fig. 3 A are isosarcometric and hence can be directly compared to experimental data with feedback sarcomere length control via laser diffraction techniques. However, much of the data in the literature is not SL-controlled and can have considerable internal shortening as a result of compliant end connections. Fig. 3 B shows F-pCa relationships that simulate increasing amounts of internal shortening. Each trace corresponds to an increasingly compliant end connection, specified by smaller KSE, which permits greater degrees of internal shortening (see Eq. 40). As compliance increases, internal shortening causes decreases in maximal plateau level and Ca sensitivity. Note that the apparent cooperativity, quantified by the Hill coefficient, also decreases as compliance increases. Here the dashed traces show true Hill functions with Hill coefficient = 7.6 for KSE = 50 and a Hill coefficient = 4.0 for KSE = 1. A similar change with an increasing end compliance is found in a earlier modeling study (see Fig. 2 in (34)). Such an observation is consistent with experimental characterizations that show greater apparent cooperativity with sarcomere length control compared to fixed total muscle length conditions (3,33).

A third characterization related to steady-state F-pCa is the SL-pCa relation in unloaded isolated cells. In this characterization, the cardiac cell sarcomere length indicates the point at which restoring force just balances the actively generated force for the given level of activator [Ca]. Fig. 3 C shows the steady-state SL-pCa response of the model that can compared to experimental data from isolated cells (35). The response is similar in both the maximal degree of shortening and in the range of activator [Ca] over which the cell shortens from rest length to maximal shortening. Note that the apparent cooperativity is less in the SL-pCa relations as compared to F-pCa relations under similar conditions (e.g., compare Fig. 3 C with 3, A and B). In the model, the decrease in apparent cooperativity results from the transition to shorter sarcomere lengths that decrease Ca sensitivity and maximal force so that greater activator [Ca] is required to continue cell shortening. As shown in Fig. 3 A, a shorter sarcomere length requires greater activator [Ca] for any given level of active force.

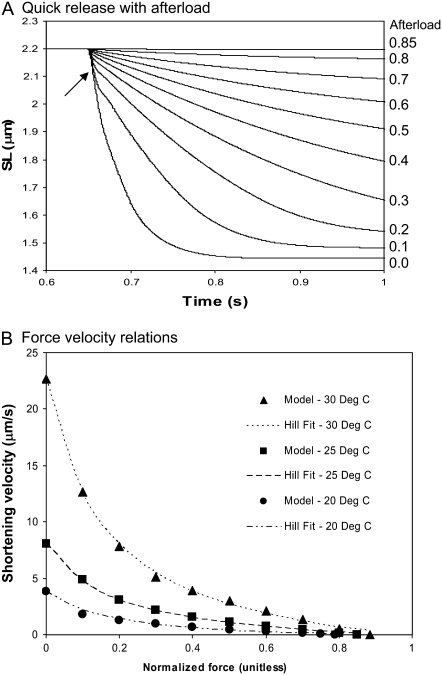
Force-velocity relations

Fig. 4 A shows the model responses for isotonic contractions against different fixed loads. The muscle is activated to a maximal level ([Ca] = 0.01 M), and length is held fixed until a release at 0.65 s. Directly after release, there is an initial fast transient (an example is shown by the small arrow in Fig. 4 A), after which the muscle contracts at a roughly constant velocity for some period. The velocity is determined by averaging over the roughly constant region. When velocity is plotted as a function of afterload in Fig. 4 B, the typical hyperbolic shape emerges that can be fit by a modified Hill equation (36),

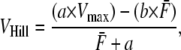(41)

where V_Hill is the Hill fit velocity, is normalized force, and a and b are empirically derived constants. The corresponding Hill fit parameters are a = 0.19, 0.19, and 0.16 normalized force units and b = 0.89, 1.6, and 3.7 μm/s for 20°, 25°, and 30°C, respectively. The parameters are chosen to minimize mean-square error for the data summed over the data points shown at each temperature.

FIGURE 4.

Force-velocity relationships. (A) The figure shows a simulation of an experiment with a quick release to a fixed afterload. The length is fixed and then released against a fixed afterload at 0.65 s. The traces correspond to different afterloads from 0 to 0.8, in 0.1 increments in normalized force. One additional trace at 0.85 represents isosarcometric conditions corresponding to maximal force. Note that the shortening velocity is relatively constant after a fast transient response directly after the release (shown by the arrow). Data are shown for rat at 25°C. (B) Force-velocity relations are generated from the protocol shown in panel A. The force is the afterload value and velocity is computed from the relatively constant value obtained after a transient directly after the release. When plotted in this fashion, the datapoints can be well fit by hyperbolic Hill relations as shown by the labeled traces. See text for details of the fitting procedure.

The results in Fig. 4 B compare well with real muscle in several respects. Unloaded shortening values are comparable to those measured experimentally. For example, in the model V_max values are 3.82, 8.03, and 22.7 μm/s for 20°, 25°, and 30°C, respectively. Similar mean values of 6.13, 12.7, and 23.4 μm/s are found experimentally for the same range of temperatures, although some variability is seen across different preparations (n = 26–97) (36). The degree of curvature of the hyperbolic Hill fit can be quantified by k = b/V_max. The k-values are 0.23, 0.20, and 0.16 for 20°, 25°, and 30°C, respectively. Experimental values are generally in the range of 0.15–0.25 for a wide variety of muscle preparations (37), and similar values are generally reported for cardiac muscle although high variability can be seen depending on experimental conditions and fitting procedures (see (13)).

Twitch responses

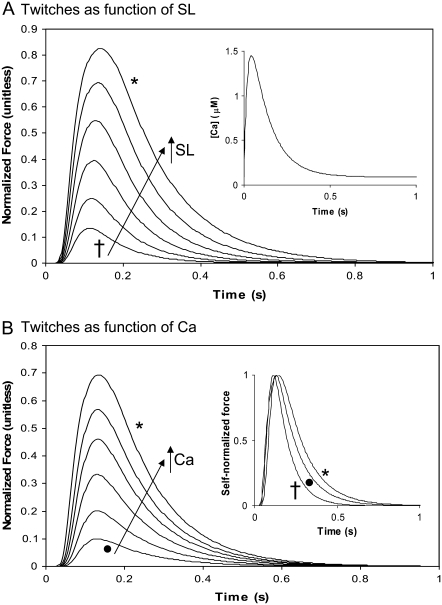
Another common experiment characterization uses dynamically changing activator [Ca] to produce twitches. The simplest situation to simulate is an isosarcometric contraction in which the sarcomere length remains fixed throughout the twitch. This situation is simulated in Fig. 5 for which either sarcomere length (Fig. 5 A) or activator Ca (Fig. 5 B) is varied. In Fig. 5 A, the sarcomere length is varied from 1.8 to 2.3 μm to show SL-dependent effects. The Ca transient is the same for each run (see Fig. 5, inset; and see the exact mathematical formulation in the Appendix) and corresponds to parameters fit to data at 22.5°C in Janssen et al. (38). Longer sarcomere length increases both peak force and twitch duration. The increase in peak force reflects the increased Ca sensitivity and maximal developed force as shown in Fig. 3 A. The time-to-peak force is relatively constant while increased sarcomere length leads to longer twitches. These features correspond well to experimental characterizations for rat at similar temperature (20,38,39).

FIGURE 5.

Isometric twitch force as a functions of sarcomere length and Ca activation. These plots show the active isosarcometric force. (A) sarcomere length is varied from 1.8 (†) to 2.3 () μm in increments of 0.1 μm. In each case, the activating Ca transient is the same as shown in the inset. (B) The sarcomere length is held constant at 2.3 μm while the peak activating Ca is scaled down. The traces show the responses for peak values of 1.45 (), 1.25, 1.15, 1.05, 0.95, and 0.85 (•) μM. The inset shows the force transients renormalized to have peak values of 1 in each case. The times from 50% activation to 50% relaxation are 0.140 s (†), 0.187 s (•), and 0.223 (). These traces show that decreasing sarcomere length or Ca activation decreases the twitch duration. The SL-dependent effect is larger because the crossbridge detachment rate g_appT is increased at shorter sarcomere lengths (see text for details). Data correspond to rat at 22.5°C.

Fig. 5 B shows isosarcometric twitches for which the activator Ca level is varied while holding sarcomere length fixed at 2.2 μm. The Ca transient is a scaled version of that shown in Fig. 5 A. The decreasing levels of activator Ca produce decreases in twitch force that are similar to those seen for decreases in sarcomere length in Fig. 5 A. Specifically, the peak force decreases, while the time to peak is relatively constant. The decrease in force is accompanied by a decrease in twitch duration, although the relative changes are smaller than those for decreases in sarcomere length. This difference can be seen in the inset of Fig. 5 B where the force traces are self-normalized to have maximum values equal to 1. The lowest peak Ca trace (solid circle) has shorter duration than the largest Ca trace (asterisk). In comparison, the shortest sarcomere length trace (cross) has the shortest duration. The additional effect at the shorter sarcomere length is that crossbridge detachment rates are increased as sarcomere length decreases (see Eqs. 19 and 20).

A second type of twitch can be simulated in which the cell contracts against its internal restoring force (similar to the case for Fig. 3 C). Here the sarcomere length is initially at the rest length of 1.9 μm, shortens to smaller length, and then returns to the rest length as shown in Fig. 6 A. The different traces show increasing levels of activator Ca with the same waveform as in the inset of Fig. 5 A, and the range of peak activator Ca are the same as in Fig. 5 B. The corresponding force traces are shown in Fig. 6 B. Here the total force is plotted as the sum of active and passive forces. The total instantaneous force is roughly proportional to the shortening velocity, so shortening stops near the point where total force is 0. However, the effect of the mass also contributes (see Fig. 1 D), so total instantaneous force is not exactly proportional to the shortening velocity. The effect of the mass will be greatest when contraction is fast. For example, the ringing near the bottom of the trace (asterisk) in Fig. 6 B illustrates that force may differ from 0 when dSL/dt = 0 at the minimum of the asterisked trace in Fig. 6 A. The net effect of the mass term is small (<0.005 units) even for the case of the fastest shortening rate.

Comparing the isosarcometric traces in Fig. 5 B with the cell shortening twitches in Fig. 6, similarities and differences can be observed with respect to changing activator Ca levels. Raising the Ca level increases peak force and produces a larger degree of shortening. Note that while the time-to-peak force is relatively constant in the isosarcometric case, the cell shortening case shows a decreased time-to-peak shortening with increasing Ca. In the shortening case, the decreasing time-to-peak is accompanied by a faster relaxation for higher Ca activation levels. Hence the total duration of the cell shortening is roughly the same. In the inset of Fig. 6 A, the smallest (solid circle) and the largest traces are self-normalized and show similar durations (e.g., compare time duration at 0.5 normalization). In contrast, the isosarcometric twitches prolong with slower relaxation for higher Ca activation levels as shown the inset of Fig. 5 B.

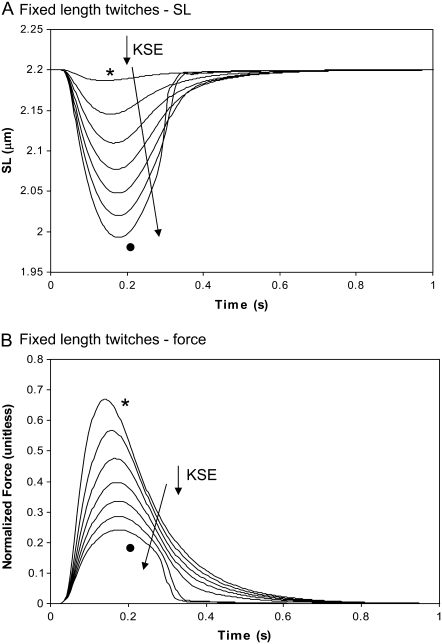
The differences between the isosarcometric and cell shortening twitches can be further illustrated by simulating fixed muscle-length twitches in which the degree of internal shortening is changed. In Fig. 7, the different traces correspond to increasing end compliances and larger degrees of internal shortening. For the case with the least end compliance (KSE = 50), there is a very small amount of internal shortening (asterisked trace in Fig. 7 A). The corresponding force transient in Fig. 7 B is very similar to the isosarcometric twitch in Fig. 5 for SL = 2.2 μm. As the end compliance increases (KSE decreases), the amount of internal shortening increases as shown in Fig. 7 A. With greater internal shortening, the total force as measured at the muscle end changes to show a later peak and increased rate of relaxation. The increased time-to-peak results because maximal recorded force coincides with the greatest lengthening of the series elastic element. As the compliance increases, this point occurs at a greater delay from the initiation of the twitch. The twitch duration decreases because relengthening hastens relaxation as seen experimentally (21). In the model, the relengthening increases the mean distortion of the strongly-bound crossbridge states, and in turn, decreases the forward rotation rate of the crossbridges (see Eq. 22) to hasten force decline.

FIGURE 7.

Fixed muscle twitches with internal shortening. The cell is held at a fixed total length, but a series elastic element allows for internal shortening. The traces correspond to different stiffness values of the series elastic element with values of 50 (), 10, 5, 3, 2, 1.4, and 1 (•) where units of KSE are normalized force-per-micrometer extension. (A) Sarcomere length is shown to illustrate the degree of internal shortening. (B) The total muscle force is shown for the same range of KSE values as in panel A. Greater degrees of internal shortening produce later times-to-peak force and also faster relaxation rates as myocyte relengthening increases crossbridge strain and has an effect on crossbridge cycling (see text for details). Data correspond to rat at 22.5°C.

K_tr

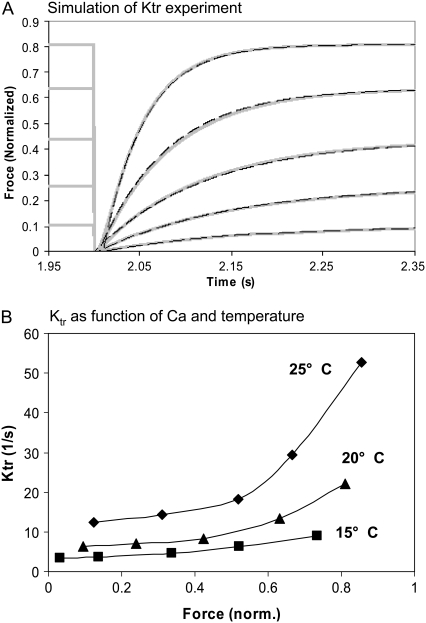
Another common characterization of muscle is K_tr, the rate of force development after a sudden length change that is thought to detach most crossbridges and drop the force to near zero. Simulation of K_tr experiments are carried out in the model by first applying a constant level of activator [Ca] until a steady response is obtained (as shown by the fixed force level before the 2 s window shown in Fig. 8 A). The crossbridge forward transition rates are decreased (f_appT and h_fT are 200-fold slower) and reverse rates are increased (g_appT and h_bT are 200-fold faster) for 2 ms to simulate the rapid removal of strongly-bound crossbridges by the quick release and restretch that is typical in experimental protocols. Intuitively, one could attempt a more direct mapping in the simulation to the mechanical perturbations in the experimental protocol. However, we want to simulate crossbridge attachment and force redevelopment that underlies the main phenomenon of K_tr. Attempting to simulate the fast crossbridge detachment events from the mechanical length changes would increase the complexity of the simulation. Moreover, one can question the value of simulating the fast force drop for which the theoretical underpinnings are less well understood than the force redevelopment steps.

FIGURE 8.

K_tr as function of Ca-level and temperature. (A) The model is activated by a constant level of activator [Ca] for 2 s until a steady response is obtained. To simulate quick release and restretch in real muscle K_tr protocols, the crossbridge transitions rates are modified for 2 ms to induce rapid removal of strongly-bound crossbridges in the model (see text from details). The recovery is well fit by a single exponential with rate K_tr that increases with the activation level. The shaded traces show the model responses, while the dashed overlays show the exponential fits. (B) K_tr is shown as function of Ca level for three temperatures as labeled. The 20°C trace corresponds to the data in panel A. Similar to experimental results (10,11), the rates increase with temperature with the divergence increasing at the highest activations levels. Data correspond to rat at the temperature labeled.

As shown in Fig. 8 A, the recovery is well fit by a single exponential (dashed traces) with K_tr rates that increase with the activation level. Likewise, experimental results show a recovery that is well fit by a single exponential with K_tr rate that increases with Ca-based activation level in cardiac muscle (40). While initial theories proposed that K_tr should reflect crossbridge turnover rates only, later interpretations suggest an interplay of Ca-based activation and turnover rates that causes K_tr rate to increase with Ca-activation level (41,42). The results from Fig. 8 A are plotted as a function of Ca level as the 20°C trace in Fig. 8 B. Also shown are corresponding results for 15° and 25°C. Similar to experimental results, the rates increase with temperature with the divergence increasing at the highest activation levels (10,11).

Unloaded cell shortening

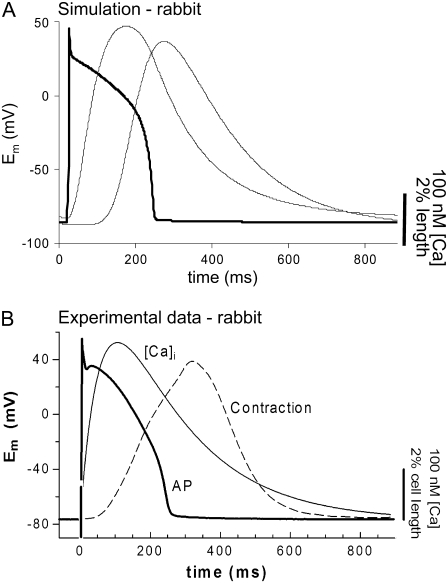
We coupled the myofilament model to the Chicago model of the rabbit ventricular myocyte (32). Note that all of the myofilament model data shown up to this point has been for rat at lower temperature. Now the myofilament model is adjusted to replicate rabbit (see Methods) at physiological temperature (37°C). Results are shown in Fig. 9 for the combined model and the similar experimental data (43). The responses show the action potentials, Ca transients, and cell shortening signals for both model (Fig. 9 A) and experimental characterizations (Fig. 9 B). Note that the particular experimental data set here shows a small and prolonged Ca transient that could be better replicated by decreasing L-type Ca influx and the forward rate of SERCA pump to 90% and 40% of the default values, respectively. Otherwise default values are used for the Chicago model.

FIGURE 9.

Simulation of cardiac cell with electrophysiology and Ca-handling mechanisms. (A) The myofilament model developed here is coupled to the Chicago model of the rabbit ventricular myocyte (32). Results are shown for the combined model (A) and the similar experimental data (B). The labeled responses show the action potentials, bulk myoplasmic Ca transients, and cell shortening signals. This figure illustrates suitability of the myofilament model for coupling with existing models of electrophysiology and Ca-handling mechanisms, and the ensemble model recapitulates common experimental characterization such as cell shortening. Data correspond to rabbit at 37°C.

Length effects on the Ca transient

The bulk cytosolic Ca transient from the Chicago model is used to compute the binding of Ca to the low affinity regulatory sites on troponin in the myofilament model. This step is straightforward, except that the Ca affinity of this site is a function of both sarcomere length and the fraction of strongly-bound crossbridges (Eq. 37). Because of this functional dependence, the amount of Ca bound to troponin will change as the fraction of strongly-bound crossbridges changes and as the sarcomere length increases or decreases.

Fig. 10 shows simulation of effects of internal shortening on the Ca transient. The protocol generates a steady output by stimulating the cell for nine beats at 1 Hz with fixed muscle length with internal shortening. Default values of the Chicago model are used. The protocol and extent of internal shortening is similar to that in an experimental study (44). For beat 10, either the cell is allowed to internally shorten as before (solid circle) or held at a fixed sarcomere length (asterisk) to simulate length control. Note that up to beat 10, the runs are equivalent so that all state variables such as sarcoplasmic reticulum loading and intracellular ion concentrations will be the same. The panels show the resulting sarcomere length (Fig. 10 A), force (Fig. 10 B), and bulk myoplasmic Ca transient (Fig. 10 C). As seen in experimental studies, the isosarcometric case shows increased force and a decrease in the Ca transient as compared to the uncontrolled case with internal shortening. In the model, the increased force produces augmented Ca-binding to troponin that initially decreases the Ca transient. Later the increased Ca bound to troponin is released so that the later Ca transient is slightly above the internal shortening case (compare solid circle and asterisked traces). In the experimental study, uncontrolled shortening also increases the Ca transient; however, a similar crossover feature cannot be detected as the noise level is too large and presumably would obscure such an effect if present. However, the crossover effect is seen in other studies (45,46) using long and short sarcomere length twitches, which produces larger changes in developed force and more distinct changes in the Ca transient.

FIGURE 10.

Simulation of internal shortening effects on the Ca transient. The combined myofilament model and Chicago model of the rabbit ventricular myocyte is used to simulate the effects of cell shortening on the Ca transient. The protocol generates a steady output by stimulating the cell for nine beats with fixed muscle length with internal shortening (KSE = 1 normalized force units per micrometer extension). Then for beat 10, either the cell is allowed to internally shorten as before (•) or held at a fixed sarcomere length () to simulate length control. The panels show the resulting sarcomere length (A), force (B), and bulk myoplasmic Ca transient (C) for each case. As seen in experimental studies, the isosarcometric case shows increased force and a decrease in the Ca transient. In the model, the increased force produces augmented Ca-binding to troponin that initially decreases the Ca transient. Later, the bound Ca is released, and the later Ca transient is slightly above the internal shortening case (compare the • and traces).

DISCUSSION

An ODE-based model is developed here based on traditional approaches; however, new formulations of some aspects are developed to overcome limitations associated with traditional mean-field approximations. The approximate and spatially compressed model presented here can recapitulate many of the commonly measured steady-state and dynamic responses seen in cardiac muscle. As in all modeling studies, the ability to generate realistic responses does not prove that the underlying biophysical mechanisms are correctly represented. The veracity of this statement is obvious for this study as we have clearly described a number of approximations that do not match the real biophysics. Specifically, we cannot directly represent nearest-neighbor interactions of RUs. Also, force is computed by a mean-field approach using the state-occupancy multiplied by the mean strain of the strongly-bound states. We accept these approximations as necessary to maintain the system as computationally efficient ODEs that are suitable for large-scale tissue simulations (1,47). In the following discussion, we focus on several of the limitations of our approach. Then our modeling approach is compared with existing published models.

Limitations

Assumption of spatially homogeneity

The model implicitly assumes several types of homogeneity. First the model assumes that myofilaments are activated by a uniform Ca concentration. This assumption conflicts with considerable evidence showing that Ca-induced Ca release is inherently spatial with specialized mechanisms to produce sarcoplasmic reticulum Ca release in response to local influx via L-type channels. However, at the level of the myofilaments, we expect that Ca is more uniformly distributed over the much longer time frame of the force generation. Computational modeling suggests spatial [Ca] gradients in the half-sarcomere are largest during the upstroke of the Ca transient, and the spatial gradients are small by 15 ms after the peak of the transient (48). Hence, except for the rapid upstroke, the gradients are generally small, and [Ca] is nearly uniform in space although changing with time.

A second homogeneity assumption is that all crossbridges are equally likely to bind and contribute equally to force generation in the single-overlap region. These assumptions are contradicted by evidence that suggest the intrinsic spacing of myosin and actin sites are different so that binding probabilities can be a function of the location along the thick and thin filaments (49). Moreover, this work also suggests that compliance in the filaments can produce a realignment of the binding site and can introduce cases where crossbridges can contribute different amounts of developed force depending on the number and location along the z-disk to m-line direction. Our model cannot capture these types of compliant realignment effects.

Mean-field approximations for crossbridge cycling

As described in Methods, the crossbridge state representation proposed here considers both the probability of strongly-bound states and the mean distortion of the states. Moreover, the mean strain affects the transition rates between crossbridge states. This representation conflicts with most common notions of crossbridge cycling in which strain affects the transitions rates on an individual crossbridge basis only. However, tracking such interactions requires partial differential equations (e.g., (24–26)) or Monte Carlo approaches (e.g., (49–51)). In fact, common notions suggest individual strain strongly affects the transition rates, so that mean-field approaches may prove difficult to apply. Specifically, the mean-field approach is best suited for conditions in which the population of states and the corresponding strains of the states are weakly correlated. Despite these observations, the representation proposed here produces reasonable results for the experimental protocols studied. Hence, the approximation appears useful for the purposes of this research effort.

Simplifications of known complexity

The modeling work contains important simplifications that are in conflict with known features of cardiac muscle. As a reasonable first approximation, the passive force is represented as a simple, time-invariant elastic element that is in series with a Newtonian viscous element. This formulation cannot reproduce experimental data showing more complexity and time variation in passive force (6). Likewise, the representations of a mass element and springlike series elastic elements are other linear simplifications that can only approximate reality (37). Our three-state crossbridge cycle is a simplification as many more states can be identified in biochemical studies (e.g., (26)). Likewise, we consider only two states for RUs (permissive and nonpermissive). In contrast, other research has suggested three states for thin-filament activation (52).

Comparison to previous modeling work

Sarcomere geometry

The length dependence of maximal activated force is assumed to reflect the overlap of thick and thin filaments resulting from sarcomere geometry. This basic premise can be traced back to the work of Gordon et al. (2) in skeletal muscle. However, such an approach to modeling maximal activated force in cardiac muscle requires assumptions about filament lengths that differ from skeletal muscle (1). The traditional assumption has been that skeletal and cardiac muscle have equivalent sarcomere geometries and filament lengths, and some modeling efforts reflect this premise (14,15). Other modeling efforts (13,53) have used fitting parameters to physiological data on maximal activated force rather than attempting to model the sarcomere geometry explicitly. An alternative explanation of the peak of force at lengths >2.0–2.2 μm range found for skeletal muscle is SL-dependent changes in lattice spacing. Some recent modeling efforts (14,54) have included the putative effects of lattice spacing to explain length-dependent effects. Similar lattice spacing effects are not included in the model here because appropriate length-dependent effects could be simulated based on sarcomere overlap changes alone. Moreover, controversy exists as to whether lattice spacing changes are large enough to produce length-dependent changes in Ca sensitivity and maximal force (1,55,56).

The first modeling work to assume different cardiac sarcomere geometry was that of Landesberg and Sideman (57); however, their experimental justification was mostly lacking. More recent characterizations (58) have shown that maximal activated force in cardiac muscle does peak at sarcomere length at 2.3–2.4 μm which is larger than the 2.0–2.2 μm range for skeletal muscle. In addition, maximal activated force is seen to linearly increase up to 2.15 μm in trabeculae (3), which contradicts the plateau in force expected for skeletal muscle geometry in the 2.0–2.2 μm range. Similarly, maximal force and ATPase rates are found to rise linearly through the 2.0–2.2 μm range (22). Such findings are most easily explained by an increase in recruitable crossbridges as a result of an increased single-overlap region.

The sarcomere geometry in Fig. 1 A is based on physiological data described above, although we have not found the exact anatomical data to confirm these assumptions. However, recent evidence suggests complexity in setting thin-filament lengths in skeletal and cardiac muscles. For example, a siRNA nebulin knockdown study performed in cultured cardiomyocytes resulted in the absence of localized tropomodulin and a 30% increase in thin filament lengths (59). However, nebulin is thought to be expressed in only a small fraction of cardiomyocytes in mouse (60) so the exact mechanism for producing longer lengths is unclear. In skeletal muscle that expresses a nebulin in a stoichiometric ratio with thin filaments, the role of setting length is also controversial (60,61). For example, wild-type mouse shows average thin filament lengths above 1.25 μm in three of four skeletal muscle types examined (60). This value is larger than 1.05–1.10 μm, which has been the traditional assumption for skeletal and cardiac muscle in most modeling work. The knockout of nebulin produced shorter but fairly uniform thin filament lengths of ∼1 μm in all skeletal muscle types examined, a finding that suggests a nebulin-independent mechanism for setting thin filament lengths (60). The nebulin-independent mechanism may correspond to that in cardiac muscle that is generally assumed to lack nebulin, but the story may not be that simple. The knockout of nebulin produced additional features such as ultrastructural abnormalities, an inability to maintain myofibrillar integrity during muscle contraction, and reduced contraction force. Hence, the removal of nebulin in skeletal muscle should not be considered to correspond directly to typical cardiac muscle sarcomere structure. Clearly, more study is required to understand the mechanisms of setting thin filament lengths in different muscle types.

Ca-based activation

In the spatially explicit modeling, activation of RUs (troponin/tropomyosin) from a nonpermissive to permissive state will increase the Ca affinity by approximately a factor of 10 for that unit. In the ODE approach, individual units are not tracked, so such an effect on a unit-by-unit basis cannot be directly implemented. A traditional mean-field approximation assumes a uniform increase in the Ca affinity for all units. As described previously (1), traditional mean-field approximations with global feedback of developed force on Ca-binding generate unphysiological responses such as F-Ca relations that are not cooperative enough at high and low Ca regions and are too cooperative in the middle region. This effect on F-Ca relations is generic and appears in a wide variety of models with different constructions and parameter sets (e.g., (13–15)). For a specific example, compare F-Ca results for models with global feedback on Ca binding (M1 and M2) with the model without (M5) in Fig. 5 of Schneider et al. (14). Another important issue arises in that strong global feedback of developed force on Ca-binding can generate hysteresis that is not seen in real muscle responses (47). Small amounts of global feedback of developed force on Ca-binding can be used with few deleterious effects (e.g., (15,62)), However, the resulting F-Ca relations may not be steep enough, and the small change in affinity will not produce the force-dependent changes in the intracellular Ca transient.

Besides the problems with steady-state responses, global feedback of developed force on Ca-binding can produce problems in dynamic responses. Specifically, Ca activation kinetics are generally assumed to be faster, whereas the crossbridge cycling kinetics are slower (e.g., (31,38)). Including global feedback terms of attached crossbridges on Ca binding cause the Ca-based activation steps to have slow kinetics that mirror the slower crossbridge attachment (42). The feedback results in unphysiological responses such as isosarcometric twitches that show a peak force that occurs later and later as peak force increases (15). In contrast, the time-to-peak force shows little change with peak force levels under length-control conditions (20,39). Moreover, the positive feedback of developed force on Ca-binding can produce a system that can show very long times to reach steady state as well as extreme sensitivity to parameters (47). Specifically, extreme sensitivity to parameters arise as multiple steady-state solutions can be reached from slightly different initial conditions.

The Ca-based activation in the model developed here requires a steep nonlinear relation between the binding of Ca to troponin and the shift from nonpermissive to permissive RUs. This construction follows directly from earlier work (15) that sought a phenomenological approach to capture the putative effects of end-to-end RU interactions. While the approach in the current model is essentially the same and could still be considered phenomenological, more recent spatially explicit models have shown that end-to-end interaction of RUs can produce a strong nonlinear effect. Specifically, a model using the Ising approach (12) shows strongly cooperative activation of the thin-filament simulated F-Ca relations that are very similar to Hill functions. Moreover, the model F-Ca relations show slight deviations from true Hill functions such that the low Ca region is somewhat more cooperative than the high Ca region as seen in many experimental studies (64–66). The spatially explicit approach is carried over to a second study using Monte Carlo approaches that include more detail such as crossbridges and the thick- and thin-filament structure of the sarcomere (51). This study also shows that end-to-end interaction of RUs produces steep F-Ca relations that resemble those measured experimentally.

While the steep nonlinearity in the model can produce realistic Ca sensitivity as seen in the spatially explicit models, it is not obvious how to incorporate force-dependent Ca-affinity in an ODE-based model without generating a traditional mean-field approximation. Our modeling efforts here propose a novel construction that artificially separates the Ca binding to troponin that is assumed to control thin-filament activation (termed “regulatory Ca binding”) and Ca binding that is sensed by the cell (termed “apparent Ca binding”). This approximation produces realistic Ca sensitivity with F-Ca relations that are similar to true Hill functions (Fig. 3 A). Also, the attachment of strongly-bound crossbridges can increase the apparent Ca binding to troponin that is thought to alter the intracellular Ca transient, as simulated in Fig. 10. However, our approach is an approximation because in reality, there is only one pool of troponin that plays both regulatory and buffering roles, although the effective roles may depend on the spatial and temporal scales that one considers.

To better illustrate the spatial scales, we propose different schematic examples of the thin filament as shown in Fig. 11. Assuming no nearest-neighbor coupling between the RUs, a random arrangement of permissive RUs is produced, as depicted in Fig. 11 A. Many existing models of the myofilaments have an implicit assumption that the strong binding of crossbridges is tightly controlled by the adjacent RUs. If one assumes little or no nearest-neighbor coupling between the RUs, then recruitment of crossbridges is assumed to be along the length to the thin filament in locations corresponding to permissive RUs. In contrast, Fig. 11 B shows an example with strong nearest-neighbor coupling between RUs so that uniformity is promoted between adjacent RUs. Now the 50% activation point corresponds to continuous run of RUs in the on-conformation followed by a run of RUs in the off-conformation. While this amount of coupling may be stronger than common intuition, our spatially explicit results predict correlation of RUs states at distances of roughly half the thin filament at 50% activation (12). Fig. 11 C shows an example of extreme coupling between RUs in which the whole thin filament switches from nonpermissive to permissive in unison as suggested by Brandt et al. (67). In this case, 50% activation can be represented in a cross-sectional view where whole thin filaments would be either in the on- or the off-conformation.

FIGURE 11.

Schematic representation of 50% thin-filament activation for different levels of nearest-neighbor cooperativity between RUs. (A) With no nearest-neighbor coupling between RUs, one predicts a random arrangement of activated RUs (raised) and attached, force-generating crossbridges (hatched). (B) With strong nearest-neighbor coupling between RUs, the 50% activation point can be represented by a continuous run of half the RUs in the on-conformation followed by a run of half the RUs in the off-conformation. (C) For the extreme amount of nearest-neighbor coupling between RUs, the whole thin-filament switches from nonpermissive to permissive in unison. In this case, 50% activation can be represented in a cross-sectional view of the sarcomere lattice where whole thin filaments would be either in the on- (•) or the off- (○) conformation. Hence, recruitment of RUs is at the level of whole thin filaments as opposed to along the length of the thin filament.

We propose that the picture in Fig. 11 C may be closer to reality than that of Fig. 11 A. With such a view, the concepts of spatial averages can change. A spatially compressed model computes a single scalar to represent the fraction of permissive RUs, and hence, the model cannot directly distinguish recruitment in the direction along the filament from recruitment in the cross-sectional plane. However, we have chosen the model construction to favor different views of recruitment for different purposes. For example, early in the activation process, the thin filament shifts to permissive conformation before crossbridges attach. Once the first crossbridge binds, its associated RU and the neighboring up- and downstream RUs will be permissive, assuming high nearest-neighbor cooperativity. From the point of view of the myosin heads located up- and downstream, the thin filament is permissive and attachment is facilitated (similar to the depictions in Fig. 11, B and C). Hence we assume thin-filament regulation is local to a given filament and not dependent on the bulk number of attached crossbridges elsewhere in the sarcomere. One additional feature is also important. The sarcomere single-overlap fraction sets the number of adjacent myosin heads and the potential number of crossbridges that can form on each thin filament. For this reason, we have formulated regulatory Ca binding that depends on sarcomere length but is not dependent on the bulk fraction of attached crossbridges (see Eq. 9).

Now consider the Ca binding sensed by the cell on the macroscopic scale. Again consider the extreme case for which the whole thin filament switches from nonpermissive to permissive in unison. Clearly a single activated thin filament would not be sensed by the cell in terms of Ca buffering. Hence, the first activated thin filament will have a negligible effect on the Ca transient. However, after a substantial fraction of thin filaments are activated, one would predict an effect. For example, if half of thin filaments are activated, then we expect roughly one-half of troponin to have high affinity in the extreme case. In our model, we attempt to capture this effect by using the fraction of strongly-bound crossbridges as a proxy for the recruitment of thin filaments in the cross-sectional plane. There is an additional effect in that not all RUs are in close proximity to a crossbridge because of the sarcomere geometry. Because of this effect, sarcomere length also plays a role in determining the number of permissive RUs. Hence, our formulation of apparent Ca binding that is sensed by the cell has contributions from both sarcomere length and the fraction of strongly-bound crossbridges (see Eq. 37).

Besides the spatial aspects just described, the difference in timescale can effect how the model variables are interpreted. For example, a typical twitch occurs over a longer timescale that reflects crossbridge kinetics more than Ca activation events (31,38). At this longer timescale, force and thin filament activation may track together closely as strongly-bound crossbridges tend to keep the thin filaments in a permissive conformation even after Ca has begun to dissociate from troponin (68). Hence, on the macroscopic scale over a long timeframe, the thin-filament activation and affinity for Ca may mirror the bulk population of strongly-bound crossbridges, whereas on the microscopic scale or short timeframe, the bulk attachment of crossbridges should not be an important variable for local activation events.

Three-state crossbridge scheme

The model is constructed around a three-state model that is adapted from the general approach of Campbell and co-workers (19,69,70). While many more crossbridge states have been identified biochemically, the three-state model retains enough machinery to recapitulate many measured phenomena including force-velocity relations, small step responses, and harmonic responses (19). The main differences in the work here is that we have added a more cooperative Ca-activation scheme; included more strain dependence in the crossbridge transition rates; and reworked the calculation of mean strain of the strongly-bound states. The Ca-activation approach is described above. In the model developed here, both the crossbridge forward isomerization rate h_fT and the ATP-consuming transition rate g_xbT are very strain-dependent. In contrast, the work of Razumova et al. (19) included strain dependence on the ATP consuming transition only (analogous to g_xbT in this study). For the protocols investigated in that study, strain-dependence on the ATP-consuming transition has the dominant effect, and including strain dependence on other transition rates produces relatively minor effects. Another change in the model here is faster transition rates for crossbridge cycling that correspond to higher temperatures. The higher cycling rates are also important to recapitulate a rapid unloaded shortening velocity that can be quite large even at subphysiological temperatures (e.g., 23.4 μm/s at 30°C (36)).

The modeling work here includes a new formulation of mean strain of the strongly-bound states. In the original model of Campbell and co-workers, calculation of mean strain has a dependence on the mean occupancy of the crossbridge states. Such an approach makes intuitive sense given that the model couples Ca-based activation to crossbridge cycling steps. For example, if one envisions the scenario shown in Fig. 11 A, then the binding of crossbridges and subsequent cycling will closely mirror the Ca-based activation steps. In contrast, if one considers the picture in Fig. 11, B and C, then crossbridge attachment is only affected by the local environment and not by the amount of the activation in the cross-sectional plane. Indeed, on the microscopic scale, consider the first strongly-bound crossbridge in a sarcomere. As the first crossbridge binds, its associated RU and the neighboring RUs up- and downstream will be permissive, assuming strong nearest-neighbor coupling. Neighboring myosins will also sense a permissive environment and crossbridges will bind and cycle with rates that are independent of Ca level. Hence on the local scale, the world is permissive and independent of Ca level, and the strain of crossbridges should depend only on their own intrinsic cycling rates and on the net motion of its thick and thin filaments. For these reasons, our computation of mean strain does not contain a contribution of mean population of the strongly-bound states.

In all modeling efforts, some level of abstraction is chosen as a compromise between parsimony and complexity. We chose a three-state crossbridge cycle and propose that it has several advantages over a more parsimonious two-state model for the crossbridge cycle as first proposed by Huxley (24). In this formulation, crossbridges are assumed to be either detached (i.e., equivalently weakly bound) or attached (i.e., equivalently strongly bound). We can outline the advantages of moving to the more complex three-state crossbridge cycle in the following three areas:

1. ATP utilization. A two-state approach requires that crossbridge detachment proceed via an ATP-utilizing path. However, this step is often characterized as slow, so relaxation is inhibited unless an unrealistically high ATP utilization is assumed or multiple power strokes are assumed per ATP hydrolyzed, a feature at odds with most current theories (1). The inability to reconcile faster relaxation with slow ATPase rates have led to speculation that a fast reverse power stroke can predominate under some conditions (31,72). With the three-state model, the system can relax back from the force-generating state to the relaxed state via fast reversible reactions that do not require energy usage (ATP hydrolysis) under many conditions. For example, during isometric twitches, this pathway will predominate and decrease ATP consumption under conditions where no net work is done, as first described by Fenn (73).

2. Crossbridge strain. Another difficulty associated with a two-state crossbridge representation is how to represent crossbridge strain. The Landesberg-Sideman models (74) and derivatives use an approach where the strain is an instantaneous function of velocity implemented with a viscosity-like term for unitary crossbridge force. The viscosity-like effect is also predicted by the Huxley model for which the mean-strain of a crossbridge population decreases for a constant shortening velocity (6). However, computing strain as an instantaneous function of velocity precludes the interplay of both shortening velocity and crossbridge turnover in determining strain. In comparison, Negroni and Lascano (53) employ a construction of a single spring with a movable attachment that represents the ensemble of the attached crossbridges. Here the moving attachment point can allow a resetting of strain with time, similar to the contribution of both shortening velocity and crossbridge turnover rates proposed here (Eqs. 29 and 30). In the three-state crossbridge cycle used here, we hope to provide a more direct mapping to the biophysics of crossbridge attachment and strain induction, although admittedly a mean-field approximation is still required that is ultimately at odds with a true spatially explicit calculation of strain.

3. Prolongation of relaxation. A side effect of the three-state model is that we found a prolongation of twitches at higher force levels (see inset of Fig. 5 B). The prolongation occurs as more time is required to transition back from the PostR state to the PreR state during the relaxation process. The prolongation is important to replicate isometric twitches for which twitch duration increases with twitch force (20). In contrast to previous work with a two-state crossbridge model, two and three crossbridges were assumed to attach cooperatively to produce similar prolongation effects (71). These model results do not confirm one mechanism over others, and indeed, multiple mechanisms could contribute to force-dependent prolongation of twitches.

CONCLUSIONS

An ODE-based model is developed here based on traditional approaches; however, new formulations of some aspects were developed to overcome limitations associated with mean-field approximations. Specifically, we propose that cooperative activation of the thin filament and the strain-dependent transitions of the crossbridge cycle are inherently local phenomena that can only be approximately described by nonspatial, state-variable models. We have attempted to strike a reasonable balance between mechanistic detail and model parsimony while including sufficient cellular machinery to recapitulate a wide range of the commonly measured steady-state and dynamic responses in cardiac muscle. Specifically, the steady-state responses are F-SL, F-Ca, SL-Ca, and F-V relations. Dynamic responses are isometric and cell-shortening twitches and K_tr including Ca-activation effects. The model responses are comparable to a wide range of experimental data available in the literature for rat at or near room temperature. With a small number of parameter changes, the model can be converted to represent rabbit at physiological temperature. This modified version of the myofilament model is coupled to the Chicago model of the rabbit ventricular myocyte, and the integrated model recapitulates the cellular electrophysiology, Ca handling, and myofilament responses. In the integrated model, changing sarcomere length and developed force can alter the intracellular Ca transient as seen in experimental measures. In conclusion, while containing many approximations, the model can replicate a wide range of experimental data. We hope that this model will provide the community with a relatively simple representation of cardiac myofilaments that retains enough mechanistic underpinnings to provide flexibility and extensibility for future model development.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

APPENDIX: Additional EQUATIONS

Sarcomere geometry

This is the end of the single-overlap region nearest the z-line:

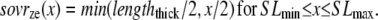(42)

This is the end of the single-overlap region nearest the center line:

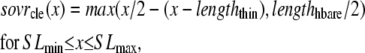(43)

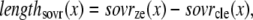(44)

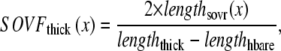(45)

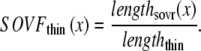(46)

Normalized passive force

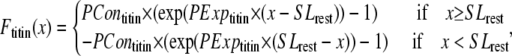(47)

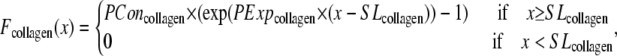(48)

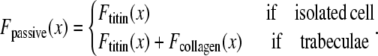(49)

Calculation of complete muscle response

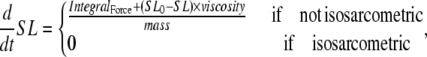(50)

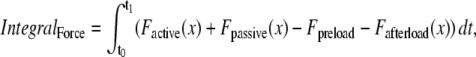(51)

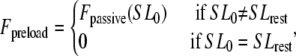(52)

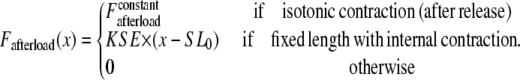(53)

Equation for simulated calcium transient

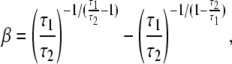(54)

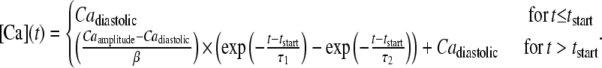(55)

Calculation of fluxes of Ca for apparent Ca binding

Apparent Ca binding is multiplied by total buffer concentration [Troponin] = 70 μM in the Chicago model:

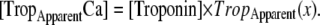(56)

Flux of Ca onto the buffer is calculated using time rate of change of Eq. 37 calculated with the chain rule:

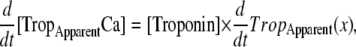(57)

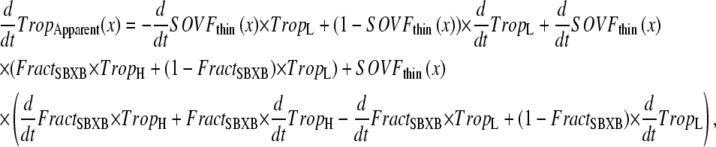(58)

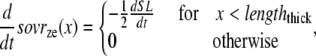(59)

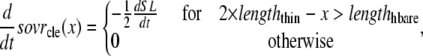(60)

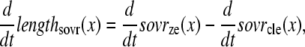(61)

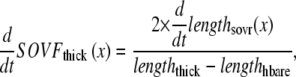(62)

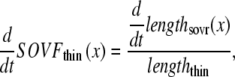(63)

(64)