Abstract
A three-dimensional multiscale computational model, platelet adhesive dynamics (PAD), is developed and applied in Part I and Part II articles to characterize and quantify key biophysical aspects of GPIbα-von-Willebrand-factor (vWF)-mediated interplatelet binding at high shear rates, a necessary and enabling step that initiates shear-induced platelet aggregation. In this article, an adhesive dynamics model of the transient aggregation of two unactivated platelets via GPIbα-vWF-GPIbα bridging is developed and integrated with the three-dimensional hydrodynamic flow model discussed in Part I. Platelet binding efficiencies predicted by PAD are in good agreement with platelet aggregation behavior observed experimentally, as documented in the literature. Deviations from average vWF ligand size or healthy GPIbα-vWF-A1 binding kinetics are observed in simulations to have significant effects on the dynamics of transient platelet aggregation, i.e., the efficiency of platelet aggregation and characteristics of bond failure, in ways that typify diseased conditions. The GPIbα-vWF-A1 bond formation rate is predicted to have piecewise linear dependence on the prevailing fluid shear rate, with a sharp transition in fluid shear dependency at 7200 s−1. Interplatelet bond force-loading is found to be complex and highly nonlinear. These results demonstrate PAD as a powerful predictive modeling tool for elucidating platelet adhesive phenomena under flow.
INTRODUCTION
Initial platelet tethering to the exposed arterial subendothelium is mediated by the interactions between GPIbα platelet surface receptors and the A1 domain of subendothelial collagen-bound multimeric plasma glycoprotein called von Willebrand factor (vWF) (1). At moderate to high shear rates (>500 s−1) typical of arteriolar blood flow, GPIbα-vWF-A1-mediated platelet tethering to the subendothelial surface is a critical requirement for enabling platelet-surface adhesion. The formation of platelet-surface tethers prolongs the duration of contact between the platelet and the surface to facilitate binding of other, slower-forming, irreversible bonds such as α2β1 with subendothelial collagen (2,3), and activated αIIbβ3 with collagen-bound vWF (4,5). The GPIbα platelet surface receptor on association with vWF can signal the binding event to the cell to activate the platelet, thereby activating other platelet surface receptors such as α2β1 and αIIbβ3 (6–9). GPIbα-vWF-A1 bonds exhibit selectinlike binding kinetics that include fast association and dissociation rates, dependence of dissociation rate on the magnitude of tensile or compressive force acting on the bond, and requirement of a critical level of shear flow for adhesion to occur (10–12). The physiological significance of GPIbα-vWF-A1 binding kinetics is illustrated by the genetic bleeding disorder von Willebrand disease (VWD). This disease is the result of a gain-of-function mutation in either the A1 domain of vWF (known as 2B-type VWD) or the GPIbα receptor (known as platelet-type VWD) that alters the binding kinetics to permit longer bond lifetimes and/or enhanced bond formation rates (10–15). These increased stabilizing interactions between the mutant GPIbα receptor and vWF permit sponta neous binding of flowing platelets to circulating vWF, which deplete the availability of vWF, especially large vWF multimers, for binding to subendothelial components during injury. Here, enhanced GPIbα-vWF binding activity manifests as platelet-vWF association in the blood rather than at the injured surface, the consequence of which is mild to moderate hemorrhage (16).
von Willebrand factor multimers are comprised of repeating identical subunits and exhibit a wide spectrum of molecular masses (500 KDa, for a vWF dimer, to 20,000 KDa, for ultralarge vWF (ULVWF)) (17–19). Higher-molecular-mass multimers are found to have an enhanced binding affinity to platelet surface receptors GPIbα and αIIbβ3, and greater potency in inducing platelet activation, as well as formation of platelet aggregates (17,19–24). In the absence of a vascular injury, flowing platelets interact minimally with circulating plasma vWF. However, on exposure to abnormally high shear stresses (>80 dyn/cm2), typical of atherosclerosed regions of the vasculature, platelet GPIbα receptors spontaneously associate with circulating plasma vWF, causing platelet activation and αIIbβ3-vWF-mediated platelet aggregation and thereby producing platelet thrombi that may have severe pathological consequences (25–27). Participation of both GPIbα and αIIbβ3 is necessary for the formation of stable shear-induced platelet aggregates (28,29), and vWF is the only ligand found to be capable of supporting in vitro platelet aggregation at high shear levels (26).
Platelets and endothelial cells secrete vWF at the time of injury. Both cell types secrete the entire gamut of vWF sizes found in the plasma, and also larger forms than those found in blood (24). ADAMTS-13, a plasma metalloprotease that cleaves vWF at the Tyr842-Met843 bond located in the A2 domain, regulates vWF multimer size in plasma (30). Compromised activity of this protease or excessive release of ultralarge forms of vWF from endothelial cells results in persistence of ULVWF multimers in the blood, causing a fatal disorder called thrombotic thrombocytopenic purpura (TTP) (24,31), characterized by thrombocytopenia, hemolytic anemia, shear-induced platelet aggregate formation, thrombotic occlusions in arterioles and capillaries, and ischemic organ damage. At the other end of the spectrum of vWF-related disorders, mutations causing conformational changes either in the A2 domain of vWF or in ADAMTS-13 that enhance the rate of proteolytic cleavage of vWF result in a deficiency of high-molecular-weight multimers in the blood. Association of platelets and vWF is effectively reduced in this hemostatic disorder (type-2A VWD) due to decreased affinity of the shorter vWF multimers for GPIbα, resulting in prolonged bleeding in patients.
This article is Part II of a computational study of the unique characteristics of hydrodynamic collisions between two flowing platelet-shaped cells, and the biophysical aspects of transient aggregation mediated by GPIbα-vWF-GPIbα bond bridges. Part I (in this issue) details a comparison of the collision characteristics of platelet-shaped cells with that of sphere-shaped cells and also examines the hydrodynamic effects of the proximity of a planar wall on the collision trajectories. Detailed quantifications are obtained that describe platelet near-wall collision phenomena for use in platelet adhesive dynamics (PAD) simulations of platelet-platelet adhesive interactions. The method employed for deriving platelet binding efficiencies for a range of high shear rates, based on the experimental observations of Huang and Hellums (32) and Konstantopoulos et al. (29), which are used for matching PAD simulation predictions of platelet aggregation with experiment, is presented in the first article.
In this article, we discuss the development of an adhesive dynamics model that is employed in a multiscale numerical simulation method called platelet adhesive dynamics, and we analyze the transient formation of GPIbα-vWF-GPIbα bond bridges between two platelets flowing in linear shear flow near a flat surface at high shear rates of >4000 s−1. The binding of circulating vWF multimers to platelet GPIbα receptors is modeled as a dynamic process dependent on GPIbα-vWF-A1 binding kinetics, and is characterized by a gradual time-dependent redecoration of the platelet surface with vWF molecules. Platelet aggregation characteristics, as predicted by the PAD model for six different high shear rates, are matched to quantified platelet aggregation behavior observed experimentally (29,32,33). Platelet aggregation behavior is studied as a function of the binding kinetics of healthy GPIbα-vWF-A1 bond formation (11) and that typical of platelet-type VWD (10,14), and also as a function of vWF multimer size. Useful metrics are quantified, such as the binding efficiency, number of bonds formed between two platelets in an aggregate, bond rupture forces, bond lifetimes, and bond force-loading histories, for a range of high shear rates (4500–8000 s−1). Implications of vWF multimer size and governing binding kinetics on the initial phase of high-shear-induced platelet aggregate formation are explored in this article.
METHODS
The PAD model is a multiscale three-dimensional (3-D) numerical simulation that integrates the adhesive dynamics of receptor-ligand binding with the 3-D hydrodynamic motion of multiple spheroids in shear flow near a stationary planar surface. The numerical technique employed for calculating the hydrodynamic mobilities of flowing particles in low Reynolds number flow near a surface is described in Part I. The general procedure for carrying out multiplatelet adhesive dynamics simulations is adopted from the multiparticle adhesive dynamics method developed by King and Hammer (34) to study the influence of spherical cell-cell hydrodynamic interactions on the selectin-mediated rolling of leukocytes on a surface, and is described in Part I.
Adhesive dynamics calculations
The general methodology of the adhesive dynamics (AD) algorithm formulated here is derived from the original AD development of Hammer and Apte (35) and the modified form of King and Hammer (34). vWF multimers are treated as virtual molecules, i.e., they are not modeled as separate hydrodynamic entities and therefore do not impose or experience a hydrodynamic force and torque. Binding equilibrium (thermodynamics) governs the number and extent of ligation of vWF multimers bound to a platelet cell at the start of the simulation. The adhesive dynamics model simulates the binding of two unactivated platelets at high shear rates via GPIbα-vWF-GPIbα bond bridges and is detailed in the sections below.
Surface distribution of receptors
Each platelet has 10,688 GPIbα receptors distributed uniformly about the surface, to achieve a surface density of ∼1500 receptors/μm2 (36) (see Table 1). A prespecified number of GPIbα receptors ranging from 12 to 54 receptors is allotted to each surface element of the 384 QUAD9 mesh in accordance with the area of the element. The GPIbα receptor exists as a subunit of the GPIb-IX-V complex, in which GPIbα disulphide linked to GPIbβ is noncovalently associated with GPIX and GPV. Half as many GPV receptors are present on the platelet surface as GPIb-IX complexes, implying that every GPV receptor is shared by two GPIb-IX complexes (37). In our model, 5344 random receptor point locations on the platelet surface are determined at the start of the simulation, with each point location representing two GPIb-IX-V complexes, or two GPIbα receptors.
TABLE 1.
Values of physical parameters used in simulations
vWF size and shape
A von Willebrand factor molecule of average size 149 × 77 × 4 nm3 has ∼18 A1 binding sites (nine dimers) (38). In the study of Siedlecki et al. (38), the vWF molecules had already undergone diffusion to a hydrophobic surface followed by adhesion and some spreading. We require the dimensions of the solution structure of a human vWF molecule of average size. Singh et al. (39) measured vWF size in solution using light scattering and the small-angle neutron scattering method, and characterized the vWF multimer as a prolate ellipsoid of average size 175 × 28 nm. We adopted these dimensions of the average size of vWF for use in our simulations and assumed that every multimer contains an average number of 18 A1 binding sites. The surface area of a prolate spheroid of these dimensions is SA = 0.049 μm2. The average distance between two A1 binding sites on the surface of this multimeric molecule is calculated as dvWF-A1 = 52 nm. The other vWF molecule of interest to us in our interplatelet binding modeling studies is ULVWF, which is not normally present in blood plasma at detectable levels, except at the time of secretion from endothelial cells and platelets (4). The physical dimensions of ULVWF have not been adequately documented in the literature. Slayter et al. analyzed the size and shape of individual vWF molecules and observed that vWF multimers are generally found to be present in blood in a range of sizes up to 460 nm (major axis diameter) and have a loosely coiled ellipsoidal shape (40). We chose to model a large vWF molecule (L-vWF) of dimensions 400 × 28 nm (SA = 0.11 μm2). Since L-vWF and ULVWF have been described as stringy threadlike molecules (40,41), we assumed that the thickness of the molecule remains approximately the same with an increase in molecular mass such that most of the A1 binding sites are available for association at the surface rather than being hidden within the interior of the protein. L-vWF is assumed to possess 34 A1 sites available on the surface for binding, so that dL-vWF-A1 is within 10% of dvWF-A1. The average distance between two A1 binding sites on this molecule is dL-vWF-A1 = 57 nm.
vWF concentration in plasma
Differing concentrations of vWF in plasma have been reported in the literature (21,38,42–45). If plasma vWF molecules contain, on average, 18 A1 binding sites (i.e., 9 vWF dimers), then the average molecular mass of a vWF multimer is 260 kD per subunit × 18 subunits = 4680 kD = 4680 × 103 g/mol. The vWF plasma concentration for an average vWF size of 18-mers is determined to be 2 nM based on molar and/or mass concentrations of vWF in plasma, as reported by Miura et al. (43), Kumar et al. (21), and Borchiellini et al. (45). A sample calculation is shown here. Kumar et al. reported the concentration of vWF in normal pooled plasma as 10 μg/ml. The molar concentration of vWF is calculated as 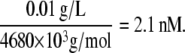
vWF binding properties
The two following vWF sizes are considered in our simulations.
n-vWF (vWF multimers of average size (diameter along major axis = 175 nm)).
In our model, vWF molecules can attach lengthwise to the platelet surface and bind multiple receptors. It is assumed that up to one-half of the total A1 binding domains present on the surface of a vWF multimeric molecule can bind a single platelet. The average platelet surface area per receptor point location, also termed “receptor node” (distinct from the nodes generated by the 384 QUAD9 mesh used to discretize the platelet surface), is calculated as 1332 nm2. The average distance between two receptor nodes is 36.5 nm. The maximum number of receptor nodes that an n-vWF molecule can bind is based on the length of the multimer and is calculated as 175/36.5 ≈ 4. An n-vWF molecule that docks onto a platelet surface is allotted a unique invariant group of four receptor nodes chosen in random fashion such that within each group, the receptor nodes are within a distance of 175 nm/1.5 from the first randomly chosen node in the group and also within the same distance from all other nodes in the same group. Binding of A1 sites on a vWF molecule can occur with receptors located at the allotted point locations only. The total GPIbα-vWF-GPIbα bond length is calculated to be 50 nm + 28 nm + 50 nm = 128 nm, where 50 nm is the length of the GPIbα stalk (46).
L-vWF (vWF multimers of large size (diameter along major axis = 400 nm).
The maximum number of receptor nodes on a platelet that a single L-vWF molecule can bind is 400/36.5 ≈ 10. A unique group of 10 randomly chosen receptor nodes is assigned to every L-vWF molecule that binds the platelet surface.
Platelet-vWF equilibrium binding
Each simulation is initiated with one of the two platelets bound by vWF molecules; the number and extent of ligation of the vWF multimers are dictated by the binding equilibrium of this receptor-ligand pair. We used the equivalent site hypothesis (ESH) equilibrium model (47) for multivalent ligand binding to monovalent receptors to determine the vWF distribution on the platelet surface at equilibrium. In this model, the two-dimensional cross-linking rate constants for both the forward and reverse reaction are assumed to be the same for all ligand binding sites, once the ligand has docked onto the surface via a single initial GPIbα-vWF-A1 bond. The equilibrium concentration of ligand (number of ligands/cell) bound by i receptor-ligand bonds is given by Eq. 1,
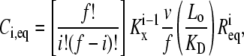 |
(1) |
where v is the total number of A1 binding sites present on the vWF surface; f is the total number of A1 binding sites available for binding to a single platelet; Kx is the two-dimensional cross-linking equilibrium constant (cells/number); Lo is the ligand concentration in solution (M), and is assumed to change negligibly during ligand-cell binding; KD is the three-dimensional dissociation constant for solution vWF bound to platelets via a single GPIbα-vWF-A1 bond (M); and Req is the equilibrium concentration of unbound receptors present on the cell surface (number of receptors/cell), which can be determined from the following implicit equation:
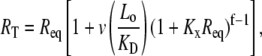 |
(2) |
where RT is the total number of GPIbα receptors present on the platelet surface.
The procedure followed to obtain a suitable KD value representative of shear-induced platelet GPIbα-vWF binding in solution for use in the ESH equilibrium binding model is discussed in Appendix A. The derived value of KD based on the experimental studies of Goto et al. (28) is 7.73 × 10−5 M. This value of KD yields Req = 10,472 and Ceq,1 = 5; Ceq,2 = 12; Ceq,3 = 17; Ceq,4 = 15; Ceq,5 = 9; Ceq,6 = 4; Ceq,7 = 1; Ceq,8 = 0; Ceq,9 = 0, for equilibrium binding of n-vWF to platelets, which results in a 2% platelet surface coverage of vWF based on this equilibrium dissociation constant. Miura et al. (43) predict a platelet surface coverage by vWF of 1.2% based on their measured KD values. If L changes negligibly after binding, i.e., if L ≫ nC/NAV, where C is the total number/cell of bound vWF molecules given by Eq. 1, n is the volume concentration of platelet cells in blood (2.75 × 1011 platelet cells/L) and NAV is Avogadro's number, then Eq. 1 applies. The binding of vWF to platelets as predicted by the ESH model results in a depletion of vWF molecules by only 1.4%, verifying the validity of Eq. 1. Accordingly, the calculated KD value of 7.73 × 10−5 M is used for further model development. The equilibrium binding conditions for two pathological cases of vWF-platelet binding (L-vWF-mediated binding (TTP) and platelet-type VWD) as predicted by the ESH model are discussed in Appendix B.
Model rules and assumptions governing binding
Two vWF molecules cannot bind to the same receptor nodes for reasons of steric blocking (Rule 1). In case a vWF molecule attempts to bind very close to another docked vWF molecule on the platelet surface (i.e., tries to bind receptors at one or more common receptor nodal positions) the molecule will be prevented from docking onto the cell.
Receptors at nodes where a vWF molecule is positioned are the only receptors on that platelet that can bind that molecule (Rule 2), i.e., a vWF multimer that has docked onto the surface of a platelet is immobile and does not reorient itself with respect to the surface.
Receptors from a maximum of 4 (or 10) receptor nodes depending on the vWF molecule size present on a platelet surface can bind a vWF molecule (Rule 3).
If a vWF molecule is positioned at a receptor node, the receptors located at that receptor node cannot participate in receptor-ligand binding to any other vWF molecule (steric blocking) whether located on the same platelet or on a second platelet (Rule 4).
A vWF molecule bound to a single platelet is always assumed to have its A1 binding sites positioned optimally close to the receptors at neighboring receptor nodes (with negligible deviation from equilibrium bond length) such that the cross-linking forward rate constant is the only parameter required to describe the forward binding rate (Rule 5).
Dynamics of platelet binding to soluble vWF
Formation of GPIbα-vWF bonds.
The procedure followed to calculate the on-rate, kon, for single bond association between platelet GPIbα and circulating vWF is discussed in Appendix C. Bond formation and dissociation is tested using probability formulations Pf (probability of forward reaction) and Pr (probability of reverse reaction), described in Hammer and Apte (35),
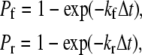 |
(3) |
where kf and kr are given in s−1 units and Δt is the simulation time step. Monte Carlo simulations are performed to test for the formation of new bonds between 1), platelet surface receptors and bound vWF molecules positioned at the corresponding receptor nodes (here, kf is given by the two-dimensional (2-D) cross-linking forward rate constant,  which has not been measured experimentally and is assumed to be the same as that for cross-linking of a vWF molecule by two different platelets (48)); and 2), receptors on a platelet and vWF molecules in solution at receptor nodes not occupied by a vWF molecule or whose receptors are not bound to vWF molecules on other platelets (Rules 1 and 4) (here,
which has not been measured experimentally and is assumed to be the same as that for cross-linking of a vWF molecule by two different platelets (48)); and 2), receptors on a platelet and vWF molecules in solution at receptor nodes not occupied by a vWF molecule or whose receptors are not bound to vWF molecules on other platelets (Rules 1 and 4) (here, 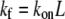 ) (see Table 2). A maximum of
) (see Table 2). A maximum of 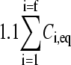 vWF molecules are allowed to bind a platelet cell at one time.
vWF molecules are allowed to bind a platelet cell at one time.
TABLE 2.
Values of binding kinetic parameters used in simulations
| Parameter | Definition | L-vWF | n-vWF | platelet-type VWD | References |
|---|---|---|---|---|---|
| lb (nm) | Equilibrium GPIbα-vWF-GPIbα bond length | 128 | 128 | 128 | (39,46) |
| KD (M) | 3-D dissociation constant | 7.73 × 10−5 | 7.73 × 10−5 | 1.55 × 10−5 | (28) |
| konL (s−1) | 3-D intrinsic on-rate | 1.38 × 10−4 | 1.22 × 10−4 | 1.39 × 10−4 | — |
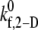 (s−1) (s−1) |
2-D cross-linking intrinsic on-rate | Determined by matching simulation results with experiment | Same as for L-vWF | Same as for L-vWF | — |
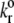 (s−1) (s−1) |
Intrinsic off-rate | 5.47 | 5.47 | 5.47/5 | (11,14,43) |
| γ (nm) | reactive compliance | 0.71 | 0.71 | 0.71 | (18) |
Dissociation of GPIbα-vWF bonds.
Shankaran et al. (49) estimated the shear force acting on a GPIbα-vWF complex in linear shear flow at 9600 s−1 to be of magnitude 1.5 pN (μ = 1.1 cP). In their study, vWF was modeled as a sphere of diameter 70 nm and the GPIbα receptor as a thread of 55 nm length extending from a spherical platelet of 2.04 μm diameter. Our model considers cell geometry or shape that is physiologically relevant, and is therefore different from that used in the study of Shankaran et al. (49). To accurately calculate the stresses acting on the bond, the vWF particle must be modeled as a finite-sized prolate spheroid. Shear force and torque are complex functions of the three-dimensional orientation of the particle. The actual force and torque acting on the vWF particles is not determinable from our simulation model since the vWF particles are modeled as virtual finite-sized particles. We used the estimate by Shankaran et al. of 1.5 pN as an approximation of the shear forces acting on a vWF particle bound to the platelet surface. The reverse rate constant is calculated using the Bell model for force-dependent dissociation rate of weak noncovalent bonds:
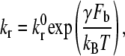 |
(4) |
where kr(Fb) is the bond dissociation rate, 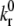 is the unstressed off-rate, γ is the reactive compliance, Fb is the applied force on the bond, and kBT is the product of Boltzmann constant and temperature (50). The Bell model parameters (
is the unstressed off-rate, γ is the reactive compliance, Fb is the applied force on the bond, and kBT is the product of Boltzmann constant and temperature (50). The Bell model parameters (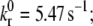 γ = 0.71 nm) used in this study for GPIbα-vWF dissociation kinetics were obtained from optical tweezer studies conducted by Arya et al. (11). The hydrodynamic shear force exerted on a bound vWF ligand is assumed to be shared equally by all bonds formed between a single platelet and the vWF multimer. Thus, the bond force Fb in Eq. 4 is given by
γ = 0.71 nm) used in this study for GPIbα-vWF dissociation kinetics were obtained from optical tweezer studies conducted by Arya et al. (11). The hydrodynamic shear force exerted on a bound vWF ligand is assumed to be shared equally by all bonds formed between a single platelet and the vWF multimer. Thus, the bond force Fb in Eq. 4 is given by 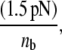 where nb is the total number of bonds formed between a vWF multimer and a platelet, and varies during the course of the simulation for each bound ligand. Bonds may break at any receptor node at which a vWF is bound. If all bonds between a vWF molecule and a platelet break, the molecule goes back into solution.
where nb is the total number of bonds formed between a vWF multimer and a platelet, and varies during the course of the simulation for each bound ligand. Bonds may break at any receptor node at which a vWF is bound. If all bonds between a vWF molecule and a platelet break, the molecule goes back into solution.
Platelet-platelet binding
Receptors located at one or more receptor nodes on a platelet can bind the A1 domain binding sites present on vWF multimers attached to another platelet in close vicinity. When two platelets come within binding distance (as dictated by the equilibrium bond length of GPIbα-vWF-GPIbα) to each other, binding of free GPIbα receptors on one platelet in close proximity to a vWF molecule bound to the opposing platelet's surface is tested using Eq. 3. All GPIbα-vWF-A1 bonds involved in the bridging of two platelet cells are treated as individual linear springs (Fig. 1). The mathematical relation for the rate of bond formation was obtained using Bell et al.'s (51) derived expression for the equilibrium constant for cell-cell bond bridging (34). The dependence of bond formation rate constant kf on the deviation bond length |xb − lb| is described by Eq. 5,
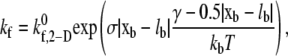 |
(5) |
where 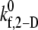 is the intrinsic cross-linking formation rate constant, σ is the spring constant, lb is the equilibrium bond length, xb is the distance spanning the endpoints of the GPIbα receptor on the platelet surface and the vWF-A1 binding site, and γ is the reactive compliance of the bond. The two-dimensional cross-linking forward rate constant
is the intrinsic cross-linking formation rate constant, σ is the spring constant, lb is the equilibrium bond length, xb is the distance spanning the endpoints of the GPIbα receptor on the platelet surface and the vWF-A1 binding site, and γ is the reactive compliance of the bond. The two-dimensional cross-linking forward rate constant 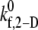 has not been well determined experimentally and is the single adjustable parameter in this model. The rate of formation, as well as the dissociation rate of interplatelet bonds, is calculated based on the following assumptions:
has not been well determined experimentally and is the single adjustable parameter in this model. The rate of formation, as well as the dissociation rate of interplatelet bonds, is calculated based on the following assumptions:
When a platelet-bound vWF multimer is within binding distance of another platelet, or if the vWF multimer is double-bound by two opposing receptor nodes on the bridged platelets, the vWF molecule is assumed to be equidistant from the two receptor nodes on either platelet surface that are either in close vicinity or, if additional bonds are being tested, already linked by the bridging vWF molecule.
The two GPIbα-vWF-A1 bonds that form a trimolecular GPIbα-vWF-GPIbα bond linking two platelets are always stressed equally.
The two GPIbα-vWF-A1 bonds that form a trimolecular GPIbα-vWF-GPIbα bond are oriented in the direction of the vector joining the two receptor nodal points located on either platelet surface that define the endpoints of the trimolecular bond.
FIGURE 1.
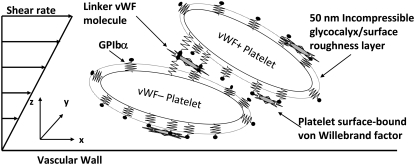
Schematic diagram of the platelet-platelet bridging model that depicts two platelets transiently aggregating in linear shear flow via GPIbα-vWF-GPIbα bond formation. A single vWF molecule can bind several receptors on a single platelet. Each platelet is coated with a 50-nm incompressible surface roughness layer equal to the height of the GPIbα surface receptors. Components of the diagram are not drawn to scale.
If a bond spring deviates from its equilibrium length, the bond imposes an instantaneous force and torque on the bridged cells that is a function of the deviation bond length and orientation of the stretched or compressed bond with respect to the participating bound surfaces (spring constant σ = 10 pN/nm (52)). Bonds can break between bound A1 sites on a vWF molecule and either platelet's receptors. The bond length used for determining the bond force, and therefore the bond dissociation rate constant (Eq. 4, where Fb = σ |xb – lb| and 2lb = 0.128 μm) for each platelet's receptor-ligand bond, is half the total distance between the linked receptor nodes on either platelet. When two platelets bind a vWF molecule and all bonds break between a vWF molecule and one of the two platelets, then the vWF molecule transfers to the other platelet. A critical assumption made is that the stressing of bonds between receptors and a vWF multimer only occurs at the receptor nodes participating in interplatelet binding. These stresses are not transmitted to adjacent receptor nodes where the vWF molecule may be bound. We assume that vWF is a flexible and linear molecule that absorbs the stresses at the point of action and does not transmit them along its length (a common assumption made with the cell surface) (Rule 6).
Receptor and ligand populations
It is assumed that all GPIbα receptors form a single population of active receptors and all A1 domains of vWF molecules are in an active “bindable” state. We did not consider a subpopulation of molecules that exist in or switch to a dormant or nonbinding state. Insufficient quantifications of such phenomena in the literature preclude the development of a more sophisticated model at this time.
RESULTS
Estimation of 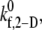 matching simulation predictions to published experimental results (L-vWF-mediated platelet-platelet binding)
matching simulation predictions to published experimental results (L-vWF-mediated platelet-platelet binding)
The single unknown parameter in the PAD model for platelet-platelet transient aggregation in high shear flow is the 2-D cross-linking intrinsic bond formation rate constant 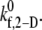 A randomized search was performed to obtain
A randomized search was performed to obtain 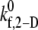 values that permit simulation predictions of the binding efficiency ηb for collisions between an L-vWF+ platelet and an L-vWF− platelet at a particular shear rate to match, to within 5%, experimentally derived values (29,32,33) tabulated in Table 1 of Part 1. Huang and Hellums obtained the experimentally derived overall collision efficiencies, ηc (32,33) (see Part I, Table 1) of platelets aggregating at high shear rates by determining parameters that matched a theoretical population balance rate equation (33) (see Part I) to the experimental observations of particle size distributions of platelet aggregates produced by shear-induced platelet aggregation. A cone-and-plate viscometer apparatus was used to subject unactivated platelets (concentration ∼300,000 platelets/μL) to a uniform high-shear environment (∼3200–10,000 s−1) over durations of 20–100 s at either 24°C or 37°C. The width of the gap between the cone and plate ranged from 30 μm at the inner edge to 120 μm at the outer edge. Their experimental study of platelet aggregation involved a majority of far-wall platelet collisions; however, our simulation model was developed to consider physiologically relevant situations such as platelet adhesion events close to the vascular wall. Hence, we studied wall effects on platelet adhesion events, since proximity to the wall significantly influences the collision mechanics (time integral of contact area and collision frequency) and collision and adhesion parameters were determined accordingly.
values that permit simulation predictions of the binding efficiency ηb for collisions between an L-vWF+ platelet and an L-vWF− platelet at a particular shear rate to match, to within 5%, experimentally derived values (29,32,33) tabulated in Table 1 of Part 1. Huang and Hellums obtained the experimentally derived overall collision efficiencies, ηc (32,33) (see Part I, Table 1) of platelets aggregating at high shear rates by determining parameters that matched a theoretical population balance rate equation (33) (see Part I) to the experimental observations of particle size distributions of platelet aggregates produced by shear-induced platelet aggregation. A cone-and-plate viscometer apparatus was used to subject unactivated platelets (concentration ∼300,000 platelets/μL) to a uniform high-shear environment (∼3200–10,000 s−1) over durations of 20–100 s at either 24°C or 37°C. The width of the gap between the cone and plate ranged from 30 μm at the inner edge to 120 μm at the outer edge. Their experimental study of platelet aggregation involved a majority of far-wall platelet collisions; however, our simulation model was developed to consider physiologically relevant situations such as platelet adhesion events close to the vascular wall. Hence, we studied wall effects on platelet adhesion events, since proximity to the wall significantly influences the collision mechanics (time integral of contact area and collision frequency) and collision and adhesion parameters were determined accordingly.
The binding efficiency is a quantitative measure of the probability of formation of at least one cell-cell bond bridge between two colliding cell surfaces. Three representative initial collision configurations (collision types I–III, determined in Part I) were selected to characterize the entire range of homogeneous hydrodynamic platelet collisions observed near a planar surface. To obtain the model-predicted overall binding efficiency for two colliding platelets for an assumed 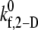 value at a particular shear rate, the binding efficiency, characteristic of each collision type, was first determined. For each of the six shear rates, and for every
value at a particular shear rate, the binding efficiency, characteristic of each collision type, was first determined. For each of the six shear rates, and for every 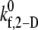 tested, at least 100 simulations of two-platelet collisions were conducted for each of the three representative initial collision configurations. The total number of collisions that resulted in a binding event (formation of a GPIbα-vWF-GPIbα bond bridge) established the efficiency of binding for that collision type. A weighted average of the binding efficiencies obtained for each of the three collision types provided the overall binding efficiency observed for two platelets (one L-vWF+ platelet and one L-vWF− platelet) for the assumed
tested, at least 100 simulations of two-platelet collisions were conducted for each of the three representative initial collision configurations. The total number of collisions that resulted in a binding event (formation of a GPIbα-vWF-GPIbα bond bridge) established the efficiency of binding for that collision type. A weighted average of the binding efficiencies obtained for each of the three collision types provided the overall binding efficiency observed for two platelets (one L-vWF+ platelet and one L-vWF− platelet) for the assumed 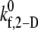 at the imposed fluid shear rate. The weights used for the averaging were linearly proportional to the number of near-wall collisions out of a total of 85 distinct observed collisions that each collision type represented. The weights were determined to be 0.488, 0.182, and 0.330 for collision types I–III, respectively.
at the imposed fluid shear rate. The weights used for the averaging were linearly proportional to the number of near-wall collisions out of a total of 85 distinct observed collisions that each collision type represented. The weights were determined to be 0.488, 0.182, and 0.330 for collision types I–III, respectively.
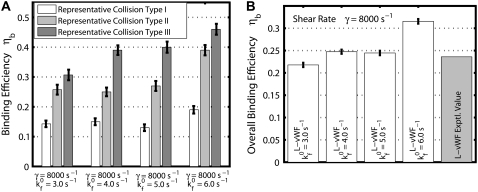
Fig. 2 A is a plot, based on simulation results, of the theoretically predicted binding efficiency between two colliding platelets for each of the three collision types, at an imposed fluid shear rate of 8000 s−1 for four different 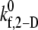 values. The error bars depicted in Fig. 2 A denote the standard error of the mean, which was determined using the bootstrap method (53). The overall binding efficiency, which is calculated based on the individual efficiencies for each representative collision type, is shown in Fig. 2 B. The model-predicted binding efficiency of 0.247 at
values. The error bars depicted in Fig. 2 A denote the standard error of the mean, which was determined using the bootstrap method (53). The overall binding efficiency, which is calculated based on the individual efficiencies for each representative collision type, is shown in Fig. 2 B. The model-predicted binding efficiency of 0.247 at 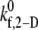 = 4.0 is within 5% of the experimentally derived value of 0.236 (29,32,33), also shown in Fig. 2 B. The
= 4.0 is within 5% of the experimentally derived value of 0.236 (29,32,33), also shown in Fig. 2 B. The 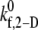 values that produce a good match between the theoretically predicted overall two-platelet binding efficiencies and the experimentally determined platelet binding efficiency (29,32,33) for all six different shear rates are listed in Table 3.
values that produce a good match between the theoretically predicted overall two-platelet binding efficiencies and the experimentally determined platelet binding efficiency (29,32,33) for all six different shear rates are listed in Table 3. 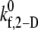 values listed in Table 3 for shear rates 4500, 5400, 6300, 7200, and 8000 s−1 have been estimated using linear interpolation (between
values listed in Table 3 for shear rates 4500, 5400, 6300, 7200, and 8000 s−1 have been estimated using linear interpolation (between 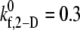 and 0.4 for γ = 4500 s−1; between
and 0.4 for γ = 4500 s−1; between 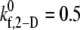 and 0.6 for γ = 5400 s−1; between
and 0.6 for γ = 5400 s−1; between 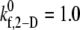 and 1.2 for γ = 6300 s−1; between
and 1.2 for γ = 6300 s−1; between 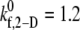 and 1.5 for γ = 7200 s−1; and between
and 1.5 for γ = 7200 s−1; and between 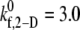 and 4.0 for γ = 8000 s−1; see Table 4 for binding efficiency values over which interpolations were performed), to obtain a better estimate of
and 4.0 for γ = 8000 s−1; see Table 4 for binding efficiency values over which interpolations were performed), to obtain a better estimate of 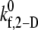 that provides a closer match to the desired binding efficiency. Overall platelet binding efficiencies, ηb, as observed from our simulations at fluid shear rates of 4500, 5400, 6300, and 7200 for a select range of assumed
that provides a closer match to the desired binding efficiency. Overall platelet binding efficiencies, ηb, as observed from our simulations at fluid shear rates of 4500, 5400, 6300, and 7200 for a select range of assumed 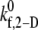 values are tabulated in Table 4. As expected, efficiency in platelet-platelet binding is observed to improve consistently with increase in the magnitude of
values are tabulated in Table 4. As expected, efficiency in platelet-platelet binding is observed to improve consistently with increase in the magnitude of 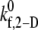 at any given shear rate.
at any given shear rate.
FIGURE 2.
Predicted binding efficiency for collisions between an L-vWF+ platelet and an L-vWF–platelet at an imposed fluid shear rate of 8000 s−1. (A) Binding efficiencies characteristic of the three representative collision types plotted for four different 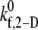 values. One hundred two-platelet collisions were simulated for each of the three representative collision types. (B) Overall binding efficiency calculated as a weighted average of the binding efficiencies determined for the three representative collision types for four different
values. One hundred two-platelet collisions were simulated for each of the three representative collision types. (B) Overall binding efficiency calculated as a weighted average of the binding efficiencies determined for the three representative collision types for four different 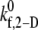 values. Error bars indicate mean ± SE.
values. Error bars indicate mean ± SE.
TABLE 3.
2-D cross-linking forward rate constant 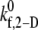 for six different shear rates that permit a good match between theoretically predicted and experimentally derived platelet binding efficiencies
for six different shear rates that permit a good match between theoretically predicted and experimentally derived platelet binding efficiencies
| Shear rate γ (s−1) | Binding efficiency ηb (L-vWF) Derived from experiment | Binding efficiency ηb (L-vWF) Predicted by simulations |
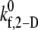 (s−1) (s−1) |
|---|---|---|---|
| 4500 | 0.041 | 0.041 | 0.33 |
| 5400 | 0.047 | 0.047 | 0.53 |
| 6300 | 0.091 | 0.090 | 1.06 |
| 7200 | 0.105 | 0.106 | 1.40 |
| 7700 | 0.191 | 0.184 | 2.50 |
| 8000 | 0.236 | 0.236 | 3.60 |
TABLE 4.
Observed platelet binding efficiencies based on PAD simulations for four different shear rates and a select range of assumed 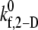 values
values
|
γ = 4500 s−1
|
γ = 5400 s−1
|
γ = 6300 s−1
|
γ = 7200 s−1
|
||||
|---|---|---|---|---|---|---|---|
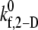 s−1 s−1
|
ηb |
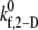 s−1 s−1
|
ηb |
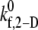 s−1 s−1
|
ηb |
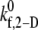 s−1 s−1
|
ηb |
| 0.3 | 0.0357 | 0.5 | 0.0427 | 1.0 | 0.0745 | 1.2 | 0.0891 |
| 0.4 | 0.0526 | 0.6 | 0.0573 | 1.1 | 0.1007 | 1.5 | 0.1138 |
| 0.6 | 0.0684 | 0.7 | 0.0663 | 1.2 | 0.1105 | 1.8 | 0.1395 |
The binding properties of the GPIbα-vWF-A1 bond that mediates platelet attachment to the surface and platelet-platelet aggregation, is modulated by the local fluid shear stress. In these simulations, 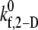 is the only kinetic parameter that incorporates the effects of the shear level in the fluid on the association properties of the GPIbα-vWF-A1 bond. The effective dissociation rate constant is a function of the bond force; the compressive or tensile force that acts on the GPIbα-vWF-A1 bond formed between two flowing platelets results from the relative translation and rotation of one platelet with respect to the other platelet and is primarily a function of the shear flow field as well as the shear rate. The estimated
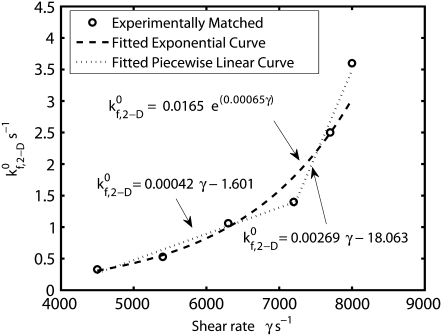
is the only kinetic parameter that incorporates the effects of the shear level in the fluid on the association properties of the GPIbα-vWF-A1 bond. The effective dissociation rate constant is a function of the bond force; the compressive or tensile force that acts on the GPIbα-vWF-A1 bond formed between two flowing platelets results from the relative translation and rotation of one platelet with respect to the other platelet and is primarily a function of the shear flow field as well as the shear rate. The estimated 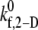 values that provide a good match between simulated and experimentally obtained values (29,32,33) of the two-platelet binding efficiency for six different fluid shear rates are plotted in Fig. 3 as a function of shear rate. An exponential function,
values that provide a good match between simulated and experimentally obtained values (29,32,33) of the two-platelet binding efficiency for six different fluid shear rates are plotted in Fig. 3 as a function of shear rate. An exponential function, 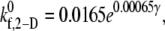 was fitted using the linear least-squares regression technique to the six
was fitted using the linear least-squares regression technique to the six  data points, with an average absolute error of 0.1807. A piecewise linear curve,
data points, with an average absolute error of 0.1807. A piecewise linear curve, 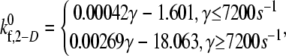 was also fitted using the linear least-squares regression technique to the six
was also fitted using the linear least-squares regression technique to the six  data points with an average absolute error of 0.0836. The predicted
data points with an average absolute error of 0.0836. The predicted 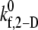 values appear to be consistent with a piecewise linear model of the dependence on the imposed fluid shear rate.
values appear to be consistent with a piecewise linear model of the dependence on the imposed fluid shear rate.
FIGURE 3.
Plot of the estimated 2-D cross-linking forward rate constant 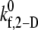 as a function of fluid shear rate obtained from matching simulation predictions to experimentally quantified binding efficiencies (29,32,33). An increasing exponential function and a piecewise linear function are fitted to six data points.
as a function of fluid shear rate obtained from matching simulation predictions to experimentally quantified binding efficiencies (29,32,33). An increasing exponential function and a piecewise linear function are fitted to six data points.
Predicted platelet binding efficiencies for n-vWF-mediated platelet aggregation and platelet-type VWD
The estimated 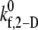 values tabulated in Table 3 provide a measure of the ability of a free GPIbα receptor present on a freely flowing platelet to bind a vWF multimer already bound to the surface of the same or another freely-flowing platelet. The sharp increase in
values tabulated in Table 3 provide a measure of the ability of a free GPIbα receptor present on a freely flowing platelet to bind a vWF multimer already bound to the surface of the same or another freely-flowing platelet. The sharp increase in 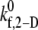 values at high shear rates of ∼8000 s−1 indicates a sharp transition of the receptor-ligand binding properties from a poorly binding, or unresponsive, state to an aggressive-binding, or responsive, state. The fluid shear stress appears to be instrumental in turning on a biomechanical switch to promote receptor-ligand association. The
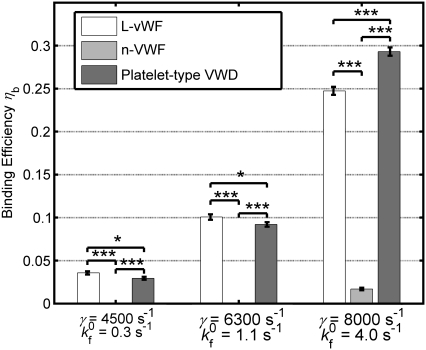
values at high shear rates of ∼8000 s−1 indicates a sharp transition of the receptor-ligand binding properties from a poorly binding, or unresponsive, state to an aggressive-binding, or responsive, state. The fluid shear stress appears to be instrumental in turning on a biomechanical switch to promote receptor-ligand association. The 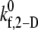 estimates were applied to two other cases of platelet-platelet binding in high shear flows. 1), n-vWF-mediated platelet-platelet binding in solution; and 2), n-vWF-mediated platelet-platelet binding in solution, in which GPIbα receptors possess a gain-of-function mutation that produces the phenotype commonly known as platelet-type von Willebrand disease (VWD). The two-platelet binding efficiency for these two additional cases was determined at three different shear rates: 4500 s−1, 6300 s−1, and 8000 s−1. A comparison of the binding efficiencies obtained from simulations for the three cases—L-vWF, n-vWF, and n-vWF + platelet-type VWD—is presented in Fig. 4.
estimates were applied to two other cases of platelet-platelet binding in high shear flows. 1), n-vWF-mediated platelet-platelet binding in solution; and 2), n-vWF-mediated platelet-platelet binding in solution, in which GPIbα receptors possess a gain-of-function mutation that produces the phenotype commonly known as platelet-type von Willebrand disease (VWD). The two-platelet binding efficiency for these two additional cases was determined at three different shear rates: 4500 s−1, 6300 s−1, and 8000 s−1. A comparison of the binding efficiencies obtained from simulations for the three cases—L-vWF, n-vWF, and n-vWF + platelet-type VWD—is presented in Fig. 4.
FIGURE 4.
Bar graph showing a comparison of the simulated two-platelet binding efficiencies for three different aggregation scenarios at three different high shear rates. Error bars indicate mean ± SE.
As predicted by our simulations, platelets that undergo collisions under normal conditions, in which n-vWF is present in solution, do not form any interplatelet bonds at shear rates 4500 s−1 and 6300 s−1. This is in good agreement with the experimental observations of the occurrence of detectable vWF-mediated shear-induced platelet aggregation only at fluid shear stresses of 80 dyn/cm2 and higher (26,49). Binding efficiencies determined for n-vWF-mediated binding of two platelets are significantly different from the binding efficiencies observed for L-vWF-mediated platelet binding and binding under conditions of platelet-type VWD (unpaired Student's t-test, p < 0.001). Binding efficiencies for n-vWF-mediated binding of two platelets inclusive of platelet-type VWD binding kinetics for the three different shear rates are found to be different from that for L-vWF-mediated binding. Note that the receptor occupancy at equilibrium is twofold greater in the case of platelet-type VWD than in the case of L-vWF-mediated aggregation. Binding efficiency is a function of receptor distribution on the platelet surface, ligand distribution on the platelet surface, the cross-linking forward rate constant, and the hydrodynamic characteristics of platelet collisions, i.e., the time integral of contact area and separation distance of surfaces during collision. The predicted binding efficiencies at a particular shear rate vary, as shown in Fig. 4 for the three different binding scenarios, as a result of the dissimilar extents of vWF distribution on one of the two colliding platelet surfaces, which in turn is dependent on vWF multimer size and the binding kinetics of the GPIbα-vWF-A1 bond.
Effects of Interplatelet bond formation on platelet-platelet collision properties
The formation of GPIbα-vWF-GPIbα bond bridges between two colliding platelets in shear flow is expected to alter the contact time during the collisions and therefore the duration over which the platelet surfaces remain in reactive contact. The formation of transient interplatelet bonds facilitates the formation of slower-forming permanent bonds such as activated integrins with their respective ligands that mediate the formation of stable platelet aggregates. The time integral of the contact area ATI (defined in Part I) was determined for all platelet collisions that resulted in interplatelet binding at the imposed fluid shear rate of 8000 s−1, and was compared to the ATI characteristic of nonreactive collisions. Table 5 tabulates the average percentage enhancement in ATI as a result of interplatelet bond formation for two platelet-platelet binding scenarios: 1), L-vWF, and 2), platelet-type VWD.
TABLE 5.
Change in collision properties due to interplatelet binding for the case of L-vWF-mediated platelet aggregation and (n-vWF + platelet-type VWD)-mediated platelet aggregation
| L-vWF
|
Platelet-type VWD
|
||||||
|---|---|---|---|---|---|---|---|
| Shear rate,γ (s−1) | Collision type | Avg. % change in ATI | Max. % increase in ATI | Max. % decrease in ATI | Avg. % change in ATI | Max. % increase in ATI | Max. % decrease in ATI |
| 8000 | I | 0.99 | 9.75 | 6.05 | 5.00 | 24.11 | 15.05 |
| 8000 | II | 2.25 | 11.48 | 1.64 | 5.86 | 40.70 | 3.38 |
| 8000 | III | 1.32 | 20.44 | 3.21 | −1.52 | 8.43 | 31.18 |
For L-vWF collision types I–III, n = 30, 35, and 35, respectively; for VWD collision types I–III, n = 38, 35, and 29, respectively, where n is the number of successful collisions.
On average, at a high shear rate of 8000 s−1, the formation of interplatelet bonds is observed to only marginally increase the intimacy of the cell-cell contact during a collision. As seen in Table 5, there is considerable variability in the effects of interplatelet bridging on the contacting properties of the bridged platelets. Interplatelet binding can result in a decrease in the time-integral of contact area, i.e., platelet bridging can reduce the extent of contact that normally occurs between two platelets in the absence of any reaction. The formation and rupture of bonds alter the original collision trajectories (usually slightly, but occasionally dramatically), although not necessarily the mechanism of collision. The extent of modification of the original paths depends on the location of the bonds formed with respect to each surface, the number of bonds formed, and the strength and lifetime of each bond formed. The new collision paths can occasionally result in decreased contact between the cells. If two or more bonds are formed, the alteration in collision trajectories that may lead to a lower time integral of contact area is often outweighed by the increase in contact time due to the restraint created by the bonds. Out of the 202 total successful collisions included in Table 5, 160, 37, and 5 involved the formation of one, two, and three bond bridges, respectively, between the two platelets. Of the 160 single-bond aggregation events, 69% had greater ATI than the nonreactive case. Of the 37 double-bond aggregation events, 81% involved an increase in ATI. All triple-bond aggregation events experienced greater cell-cell contact during a collision compared to the nonreactive collision event.
Characteristics of GPIbα-vWF-A1 bonds that mediate platelet-platelet binding
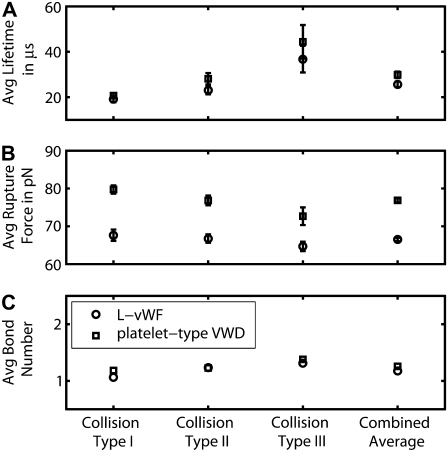
Characteristic binding properties such as bond lifetimes, bond rupture forces, and number of bond bridges that formed between two colliding platelet surfaces were quantified at an imposed fluid shear rate of 8000 s−1 for two binding scenarios: 1), L-vWF-mediated aggregation, and 2), n-vWF-mediated aggregation with platelet-type VWD. The average lifetime of a bond that bridges two colliding platelets at a fluid shear rate of 8000 s−1 and the average bond force at the time of rupture are plotted in Fig. 5, A and B, for the three representative collisions (types I–III) and for both L-vWF and VWD binding scenarios. A weighted average of the bond lifetime and the bond rupture force for the three representative collisions provides overall average values of the bond characteristics for each of the two binding scenarios, which are also plotted in Fig. 5, A and B. The average number of interplatelet bonds that formed during a single successful collision (a successful collision is one that results in at least one binding event) is plotted for each of the three representative collisions and also for the overall case in Fig. 5 C.
FIGURE 5.
Binding characteristics of the GPIbα-vWF-A1 bond that bridges two colliding platelets at a fluid shear rate of 8000 s−1 for two binding scenarios 1), L-vWF, and 2), platelet-type VWD. (A–C) The average bond lifetimes, average bond rupture forces, and average number of interplatelet bonds, respectively, formed during a successful collision, are plotted for the three representative collision types and the overall weighted case for both binding scenarios. Numbers of binding events, n, are 33, 42, and 46 for collision types I–III, respectively, in the case of L-vWF-mediated binding; and 45, 43, and 40 for collision types I–III, respectively, in the case of binding typical of platelet-type VWD. Error bars indicate mean ± SE.
The difference between the binding kinetics of L-vWF-mediated platelet aggregation and n-vWF-mediated platelet aggregation governed by platelet-type VWD binding kinetics is the fivefold-smaller dissociation rate constant for the latter case (see Table 2). As a result, larger average GPIbα-vWF-A1 bond rupture forces and bond lifetimes are observed for the case of platelet-type VWD (includes gain-of-function mutation in the receptor binding domain) as compared to that for L-vWF-mediated binding (lacking the gain-of-function mutation). Average bond rupture forces for L-vWF-mediated binding and platelet-type VWD are significantly different for all three representative collision types (p < 0.005 for all three cases, unpaired one-tailed Student's t-test). The overall average bond lifetimes for L-vWF-mediated binding and platelet-type VWD are also found to be significantly different (p < 0.05). In Fig. 5, the overall average bond lifetimes for the two cases differ by 4.2 μs. The difference in the overall average bond rupture forces for the two cases is 10.4 pN. Clearer insight into these quantitative results can be gained by studying the force-loading diagrams that are plotted in Figs. 6 and 7, and which are discussed below. Note that the binding characteristics—average bond lifetime and average bond rupture force—are expected to be the same for both L-vWF-mediated platelet aggregation and n-vWF-mediated platelet aggregation, since the dissociation kinetic parameters are the same in both cases.
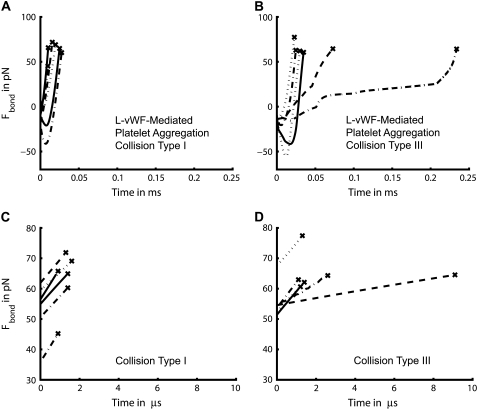
FIGURE 6.
Bond force-loading histories of 12 representative bonds for the case of L-vWF-mediated interplatelet binding. (A and B) Complete force-loading histories are plotted for interplatelet bonds that were created during type I (A) and type III (B) collisions (C and D) Partial force-loading histories are plotted for the last 10 pN of force, before rupture, experienced by bonds formed during type I (C) and type III (D) collisions.
FIGURE 7.
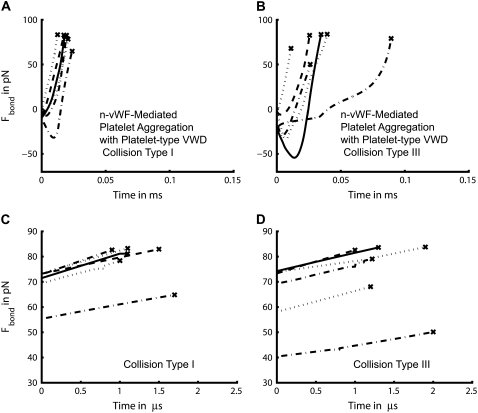
Bond force-loading histories of 12 representative bonds for the case of n-vWF-mediated interplatelet binding governed by platelet-type VWD binding kinetics. (A and B) Complete force-loading histories are plotted for interplatelet bonds that were created during type I (A) and type III (B) collisions Partial force-loading histories are plotted for the last 10 pN of force, before rupture, experienced by bonds formed during type I (C) and type III (D) collisions.
The average number of bonds that form between two colliding platelets is slightly different for platelet binding governed by platelet-type VWD binding kinetics and L-vWF-mediated platelet binding. The number of A1 domains of the platelet-surface bound vWF multimers available for binding to another platelet in the platelet-type VWD case (10,881 A1 domains (1209 × 9)) at equilibrium conditions is greater than that for the L-vWF case (7548 domains (444 × 17)) by 44%. The greater availability of ligand binding domains on the platelet surface in the former case appears to have a minor influence on enhancement of platelet aggregation in comparison to L-vWF-mediated binding, and this is also suggested by the binding efficiencies depicted in Fig. 4. Out of the 43 collisions that resulted in two or more binding events, 14% of such collisions involved two or more bonds coexisting for a finite period of time. Thus, the majority of binding events occurred independently of each other during platelet collisions, i.e., the next bond bridge formed only after the previous bond bridge broke.
As is evident from Fig. 5 A, larger average bond lifetimes coincided with greater duration of contact between the two colliding platelet surfaces during a collision. Platelet collisions are generally characterized by a relative sliding motion between the two colliding platelet surfaces, as demonstrated in Part I. Although short collisions involve quick sliding of one platelet surface over the second surface, collisions that are longer-lived involve collision trajectories that permit the local contacting platelet surfaces to be relatively stationary with respect to each other for part of the duration of the collision. This allows some of the interplatelet bonds formed during a collision of longer duration to experience relatively mild stresses for a longer time in comparison to the case of shorter-lived collisions. The average number of interplatelet bonds that form during a collision is also observed to increase modestly with increase in the collision duration. The maximum number of interplatelet bonds that formed during any collision was three. The GPIbα-vWF-A1 bond characteristics—i.e., bond lifetimes, bond rupture forces, and bond number—for the two binding scenarios (L-vWF-mediated binding and platelet-type VWD) at a fluid shear rate of 6300 s−1 are qualitatively similar in all respects to the binding characteristics depicted in Fig. 5 for a shear rate of 8000 s−1 (data not shown). Characterization of binding properties at lower shear rates was not feasible due to the scarcity of bond formation events, which made it difficult to determine average properties.
Bond force-loading histories
Platelet-platelet bond bridges were found to primarily break under tension, and barring only three rupture events, the remaining 246 bond breakage events that occurred at a shear rate of 8000 s−1 resulted from tensile failure. Fig. 6 plots the bond force-loading histories for six representative platelet-platelet bond bridges that formed during type I collisions and type III collisions for the case of L-vWF-mediated platelet aggregation. Note that type III collisions have a time integral of contact area that is threefold larger than that of type I collisions. The bond force histories for type II collisions were found to have a nature intermediate to that of types I and III (data not shown). Figs. 5 A, 6, A and B, and 7, A and B, show that bonds are more long-lived when formed during a type III collision than when formed during a type I collision. The force-loading on the bond is highly nonlinear and the bond forces are found to switch from compressive stress to tensile stress, with failure almost always occurring under tension. The bonds break under a high rate of increasing tensile force. Fig. 6, C and D, depicts the tensile force ramp that is exerted on each bridging bond over the last 10 pN of the life of the bonds before rupture. In Fig. 6, C and D, the time has been set to 0 s for those data points in the bond force history curves shown in Fig. 6, A and B, that correspond to 10 pN less than the bond rupture force. The bridging bonds at the time of rupture are found to experience a linear force ramp of 8.1 pN/μs on average (SD = 1.82) for the six binding events shown in Fig. 6 C, and 5.9 pN/μs on average (SD = 2.89) for the six binding events shown in Fig. 6 D. The conditions of bond breakage for collision type I appear more uniform compared to the conditions prevailing at the time of bond rupture for collision type III. In Fig. 6 C, the slope of each plotted force history curve and the slope of the first half of each curve has <2% difference, demonstrating the linearity of the force ramp that exists at the time of rupture. In Fig. 6 D, the slope of each plotted force history curve and the slope of the first half of each curve has <5% difference in all cases except one (14% difference).
In a similar way, plots of the bond force-loading histories for the case of n-vWF-mediated platelet binding governed by platelet-type VWD binding kinetics are presented in Fig. 7. As depicted in Fig. 7 A, the six representative GPIbα-vWF-A1 bonds that form during a type I collision experience an approximately linear force ramp of 8.3 pN/μs on average (SD = 1.9). The slope of each plotted force history curve and the slope of the first half of each curve has an average difference of 3.4% for the six cases. For the case of type III collisions, the six representative bridging bonds at the time of rupture experience an average approximately linear force ramp of 7.1 pN/μm (SD = 1.75) (Fig. 7 D). The slope of each plotted force history curve and the slope of the first half of each curve has an average of 7.0% difference for the six cases.
In Fig. 6 C (type I collision), the average duration over which a bond bridge experiences a 10-pN linear increase in bond force is 1.25 μs, whereas in the case of a type III collision (Fig. 6 D), the average lifetime of the bond over the last 10 pN of application of bond force is 2.78 μs. Thus, a linear ramp of bond force in the range of 6–8 pN/μs on average results in an increase in bond force of 10 pN over a duration of 1–3 μs. The observation of a 10-pN difference in the overall average bond rupture forces observed in Fig. 5 B corresponds to a 4.2-μs increase in bond lifetime, as shown in Fig. 5 A. This is of the same order of magnitude as the time duration over which a linear force ramp is experienced by the rupturing bonds for the last 10 pN of force application before failure.
DISCUSSION
Abnormally high hemodynamic shear stresses induce the binding of freely flowing platelets to circulating plasma vWF. This pathological occurrence is accompanied by platelet activation and formation of platelet thrombi that can critically hinder blood flow in the narrow regions of the vascular lumen. Ultralarge vWF multimers persist in blood in certain diseased conditions and are found to support shear-induced platelet aggregation at much lower shear levels in the fluid than that observed for vWF multimers of average size found in blood. Shear stress facilitates the interaction between the GPIbα platelet surface receptor and the vWF-A1 domain, and a critical level of shear stress is required to promote their association either at the subendothelial surface or in the fluid with no involvement of a surface.
The multiscale PAD computational model described here was developed to study the transient aggregation of platelets via formation of GPIbα-vWF-GPIbα bond bridges at high fluid shear rates during the onset of shear-induced pathological thrombosis. Chemical kinetic equations that describe binding of vWF multimers from solution to GPIbα platelet-surface receptors, as well as reversible vWF-mediated intraplatelet and interplatelet cross-linking reactions, were incorporated into the adhesive dynamics model. The simulation predictions of the efficiency of binding between two colliding platelets (one L-vWF+ and one L-vWF–) were matched to experimentally derived platelet binding efficiencies (29,32,33) by establishing the value of the 2-D cross-linking bond formation rate constant, the single unknown parameter of the PAD model, as a function of shear rate. The PAD model was used to quantify important binding characteristics such as binding efficiency, number of interplatelet bonds formed, bond lifetimes, bond force-loading history, and bond rupture forces for different types of hydrodynamic collisions, vWF multimer sizes, and binding kinetics. Such quantifications were useful in assessing the individual roles played by vWF size and kinetic rate constants in the outcome of interactions between flowing platelets. To our knowledge, this study is the first to consider nonspherical particle binding reactions, and include the effects of the presence of a plane wall.
SUMMARY OF RESULTS
Our simulations demonstrate that the extent of binding of vWF multimers to the platelet surface, as dictated by multimer size and the kinetics of receptor-ligand binding, strongly governs the ability of two platelets to aggregate, albeit transiently, in high shear flows. The ligand size plays an important role in determining the platelet receptor occupancy and therefore the efficiency with which a two-platelet collision results in binding. The forward rate constant was assumed to be the same for all binding scenarios considered at a particular shear rate. Predicted binding efficiencies plotted in Fig. 4 show that the multimer size itself contributes significantly to the success or failure of platelet aggregation. This is evident from the zero efficiency of binding predicted for n-vWF-mediated platelet aggregation for shear rates <8000 s−1. This result coincides with the experimental observation of negligible vWF-mediated platelet aggregation for fluid shear stresses <80 dyn/cm2 (26,49). The receptor-ligand binding affinity, the measure of which is the dissociation constant KD, also strongly influences the extent of platelet aggregation, as observed in the case of platelet-type VWD binding kinetics. Shear-induced platelet aggregation for the platelet-type VWD case is observed to occur in vitro at much lower shear rates (1500 s−1 and above) compared to that for the nondiseased condition (54,55). The cross-linking on-rate may be different for normal and mutant binding kinetics, and a larger on-rate can result in more powerful aggregation.
The estimated GPIbα-vWF-A1 cross-linking on-rate was found to increase rapidly with shear rate for values of γ > 7200 s−1, and more slowly at lower shear rates, in a piecewise, linearly dependent fashion, within the range of 4500 ≤ γ ≤ 8000 s−1. The duration of a cell-cell collision is inversely proportional to the fluid shear rate, and therefore the same magnitude of the cross-linking on-rate at a lower shear rate produces fewer binding events at a higher shear rate. Thus, either an exponential dependency or piecewise linear dependency of the on-rate on the fluid shear rate coupled with a sudden increase in slope (6.5-fold in this case) is likely to explain the pathological in vivo and in vitro observations of the sudden rise in platelet aggregation at high fluid shear rates. The properties of transient aggregation of platelets discussed in this article were found to be highly dependent on the initial relative positions of the platelets, since this determines the contact duration and extent of contact between the surfaces. Hence, for initial configurations that allow even more intimate contact between the platelets than those considered here, we can expect to observe more aggressive vWF-mediated bridging of the two platelets.
The formation of interplatelet bonds appears to only modestly increase the intimacy of platelet-platelet contact during a collision. In our simulations, a majority (79%) of the successful collisions at 8000 s−1 resulted in the formation of a single bond bridge between two platelets. By positioning the platelet receptors in clusters on the surface, and providing the vWF strings with greater mobility in our simulations, formation of a larger number of bond bridges may be expected. In our simulations, the formation of bond bridges was found to occur primarily independently, with the formation of a bond bridge having only a small effect on the probability of another bond forming. The bond force-loading histories were found to be highly nonlinear, whereas the bonds were predicted to rupture under a large linear ramp in tensile force of magnitude ranging between 6 and 8 pN/μs. The differences in binding characteristics between the cases of healthy binding kinetics and diseased binding kinetics specific to platelet-type von Willebrand disease were reconciled in a straightforward manner by studying the bond force histories. The predicted complex and nonlinear force-loading histories experienced by interplatelet bonds may be contrasted with the constant force-loading curves that are typical of bonds formed between a spherical cell and a surface (10,56).
Assumptions, limitations, and strengths of the PAD simulation model
Several limitations of this model should be noted. A vWF multimer bound to a platelet cannot physically reorient itself with respect to the platelet surface despite 1), formation and breakage of bonds, i.e., change in ligation with platelet GPIbα receptors during the course of the simulation, and 2), the effect of fluid forces on the ligand molecules in high shear flow. Another limitation is the inability of the simulated vWF molecules to protrude from the platelet surface as loose strings. Such protrusions effectively increase the surface capture area of a flowing platelet. Incorporation of finite-volume vWF particles can resolve these deficiencies of the model. In our simulations, vWF multimers distributed about the platelet surface and present in solution were monodisperse. There exists in blood a large polydispersity of vWF multimers. The size distribution of plasma vWF multimers is approximately Gaussian, with a slight skew toward the larger-sized multimers (40). We selected the average size of vWF as representative of the normal distribution of vWF in plasma. Abnormal presence of ULVWF and L-vWF in blood increases the apparent average size of circulating vWF. One of the largest vWF sizes normally present in plasma was selected to represent this pathological condition. For these reasons, and also for the sake of simplicity, we conducted platelet aggregation simulations by assuming monodispersity of ligand.
Although the simulation predictions of transient binding were matched to the experimental observations of stable aggregation, a 1:1 correspondence may not exist between platelet aggregation and platelet-platelet binding via GPIbα-vWF-A1 binding interactions. Bond lifetimes, number of bonds formed, and spatial distribution of bonds may affect the probability of the platelet and its αIIbβ3 receptors being activated and forming αIIbβ3-vWF bonds, or the manner in which this occurs. Platelet activation leads to ADP secretion, which can also influence the aggregation rate in experimental studies. Although numerous experimental studies have quantified the extent of aggregation of platelets at high shear rates, these data cannot be applied here, as the fraction of platelets that enter aggregate formation is dependent on 1), the collision behavior of the cells, and therefore the flow geometry of the experimental apparatus, and 2), the duration of the experiment.
GPIbα-vWF binding is incapable of mediating the formation of stable platelet aggregates (28). Our simulations show that interplatelet GPIbα-vWF-GPIbα bond bridges are short-lived and cannot overcome the dominating shearing forces that quickly separate the transient platelet aggregate. Although the fraction of high-shear-induced vWF-positive platelets is small compared to the total platelet population that is sheared in the presence of vWF multimers (28,29), Goto et al. (28) demonstrated that all vWF-positive platelets generated in a high-shear environment participate in aggregate formation. This supports our assumption that interplatelet bridge formation via GPIbα-vWF association will immediately or eventually result in creation of stable platelet aggregates mediated by αIIbβ3 platelet receptors. Despite the inability of the GPIbα-vWF bond to support stable interplatelet connections, this is the sole interaction that possesses the mechanical strength to sustain initial interplatelet contact under high shear flow (42). Such transient interplatelet associations are not only responsible for inducing αIIbβ3 receptor activation, but also promote αIIbβ3-receptor-mediated platelet bridging via vWF or fibrinogen. Platelets activated by exogenous agonists are also unable to “see” one another when subjected to high shear rates unless platelet-platelet bridging by GPIbα-vWF-GPIbα bonds first occurs (42).
GPIbα exists as a subunit of the GPIb-IX-V complex. This association of multiple molecules is expected to slow down its diffusion rate (57). In addition, a fraction of these molecules may be immobile on the surface due to various constraining factors. About 15% of these complexes present on the surface are found to be located in rafts on the resting platelet surface (58). The cytoplasmic domain of GPIbα is known to interact extensively with the cytoskeleton. Dong et al. (59) showed that this interaction plays an important role in regulating the receptor mobility. It was found that wild-type GPIb-IX complexes demonstrated negligible mobility in Chinese hamster ovary cells. In contrast, there was a marked increase in receptor mobility of mutant GPIb-IX complexes containing varying degrees of truncation of the receptor cytoplasmic domain. Accordingly, we did not incorporate “receptor diffusivity” into our transient platelet aggregation model, and the GPIbα receptors were assumed unable to freely diffuse about the platelet surface. Bell (48) showed that cross-linking reactions between cells are indeed possible even when receptors are immobile if the participating ligand is long and flexible, as is the case here.
Our model disregards the Brownian motion of vWF molecules. Diffusion of these submicron particles has the potential to influence the dynamics of binding and unbinding by 1), increasing the probability of close encounters between ligand molecules and surface receptors, which can lead to correct positioning of the molecules for binding with the surface receptors, thereby promoting bond formation (60), and 2), disrupting bonds due to bond stressing (61). These particles are nonspherical and reasonable Brownian motion estimates can be made by either simulating vWF as real particles, performing Brownian dynamics simulations (62), or including expressions that account for bidisperse particle encounters due to diffusive mechanisms (60).
A platelet aggregation model that included the hydrodynamic effects of sphere-sphere collisions and deterministic rate equations governing αIIbβ3 binding to fibrinogen (the linker molecule between two platelets) was proposed by Tandon and Diamond (63). They demonstrated that hydrodynamic interaction itself accounts for a significant reduction in the collision efficiency and therefore plays a key role in governing the success of a collision. A successful collision was defined as one in which the total number of bonds that formed between the two cells was greater than a predefined critical number based on the estimate for the fluid drag force acting to break the bonds, which was considered invariant with time. A number of simplifications were made in determining the receptor efficiency. A critical number of receptor-fibrinogen-receptor bonds were derived by assuming that all bonds are simultaneously stressed in equal measure. The effects of single or multiple bond formation and breakage on the modifications of cell trajectories were not included, and bond rupture due to external forces acting on the bonds was not addressed. This is a simplified picture of the binding requirements for aggregation, and a more relevant visualization can be obtained by considering the physical location of the bonds on the cell surface and the number of bonds present at any time. Our simulation model addresses these simplifications by tracking the physical location and properties of every platelet-platelet bond present in the fluid system, and one can therefore view a snapshot of the entire physical state of the system at every time step. However, the PAD model proposed here only accounts for interactions between two single platelets and does not model encounters between a platelet and an aggregate of two or more platelets, a fundamental and important feature of Tandon and Diamond's hydrodynamic model.
Mechanisms by which shear stress enhances GPIbα-vWF association and platelet activation
Platelet activation as a result of platelet-vWF binding is vWF-size-dependent and occurs only when vWF is in multimeric form (64). High-shear-induced binding of multivalent vWF to unbound platelets has been shown to cause a transmembrane calcium influx that activates the cell and thereby switches the αIIbβ3 receptor binding state from inactive to active (64). It is important to note that shear stress by itself, or the exposure of platelets to high shear and monomeric vWF molecules in suspension, is incapable of inducing intracellular calcium increase and therefore cannot promote platelet activation or αIIbβ3-receptor-mediated aggregation (49,64). The binding reaction between GPIbα and vWF-A1 alone is thus insufficient to promote platelet activation and the additional application of some critical force at the site of attachment to the GPIbα receptors on the platelet surface appears to be a requirement for successful outside-in signaling to activate the cell. Although the exact mechanism of platelet-vWF binding that triggers the signaling event is currently unresolved, it has been speculated that one or more of the following three shear-induced platelet-vWF binding mechanisms may be responsible for the onset of platelet activation: 1), a vWF multimer larger than a critical size when bound via a single receptor-ligand bond to a platelet may experience sufficient shearing force and thereby apply a mechanically activating force on the transmembrane domain of the bound receptor; 2), cross-linking reactions of a vWF multimer with two or more platelet receptors may trigger the signaling event either through application of greater mechanical force on the receptors or via receptor clustering; and 3), cross-linking reactions that mediate interplatelet contacts, which generate considerably larger forces at the sites of attachment on both platelets compared to the first two cases listed above (28). Shankaran et al. (49) have shown that shear stress level rather than interplatelet contact frequency appears to be the dominant factor responsible for the platelet activation process. Detailed simulations of finite-volume vWF-platelet binding incorporated in single-platelet and multiplatelet adhesive dynamics simulations can help estimate the forces experienced by platelet-vWF bonds that result from particle translation and rotation in shear flow.
The effects of increasing shear stress on the rate of GPIbα-vWF bond formation have not been quantified to date. Crystal structure studies of the wild-type and mutant GPIbα N-terminal domain and A1 domain of vWF have revealed some key insights into the physical mechanisms of shear-dependent activation (13,15,65), demonstrating that possibly a critical level of shear force imparted by blood flow can sufficiently perturb the conformational structure of the platelet receptor and/or vWF molecules to expose the appropriate binding site(s), and when this happens, bond formation is greatly favored. Contradictory observations (38,49,62,66,67) have made it hard to clarify whether unfolding of vWF protein from a globular conformation to an extended-chain state actually occurs, either in solution or when bound to the subendothelial surface, under the action of shear stress. Fluid shear stress is thus expected to be an important parameter that influences the on-rate/off-rate kinetics of this receptor-ligand pair. Note that the shear-stress-dependent mechanism of GPIbα-vWF binding is believed to be the same for either platelet-wall adhesion or platelet binding to circulating vWF (2). When subjected to the same fluid shear rate, the shear forces that act on the cells and protein surfaces in force-free and torque-free flow are comparatively much smaller compared to the fluid forces experienced by stationary platelets or vWF that are in contact with or bound to the surface (3,4).
The equilibrium binding state, as defined by KD, is possibly a function of the fluid shear rate. However, since little is known about the forward rate constant and binding affinity as a function of the shear level in the fluid, the parameter KD, which governs the initial vWF distribution on a platelet when the simulation initializes, was kept constant with respect to shear rate. It is possible that within the time taken for equilibrium binding to occur the platelet may activate and aggregate and this may involve associated phenomena such as shape change and degranulation. We chose, however, to initiate our simulations with equilibrium binding criteria since quantification of binding equilibria has been carried out by various research groups to a limited extent. Knowledge of the equilibrium binding state alone (as opposed to a kinetic model) is found to be sufficient in numerous models of receptor occupancy and cell signaling (47). On the other hand, there is a paucity of studies that measure or estimate the GPIbα-vWF association rate constant. Importantly, binding equilibrium conditions characterize the nature of binding as a function of vWF size and the binding kinetics. The focus of the present study was on simulating binding of vWF-positive platelets to other platelets to determine the effects of platelet shape, vWF size and binding kinetics on the biophysical aspects of platelet-platelet binding. The interaction of initially unligated platelets and vWF at high shear that leads to binding of vWF to the platelet surface is a separate kinetic study in its own right in which the model's binding parameters must be matched to an additional set of kinetic data plotted as a function of time. Although konL is calculated in our model, it is a simple approximation and not of critical importance to the kinetics of interplatelet binding for simulations of suitably short durations since initial equilibrium binding is already achieved.
L-selectin- and P-selectin-mediated rolling of leukocytes exhibit the shear threshold phenomenon, which is characterized by leukocyte tethering to vascular endothelium only above a certain critical fluid shear stress and by absence of tethering at local fluid shear stresses below the critical threshold. This shear threshold behavior has been recently resolved by a proposed two-state catch-slip model that describes the single-bond dissociation kinetics for selectins with its corresponding ligand (68). This model is characterized by two distinct bond dissociation pathways: 1), fast dissociation (weak binding) when the bond is negligibly stressed, and 2), slow dissociation (strong binding) when the bond is adequately stressed. To date, only the Bell model has been used to describe the GPIbα-vWF dissociation kinetics, and it does not account for the shear threshold effect exhibited by unactivated platelet interactions with surface-bound vWF. There is a critical need for the development of GPIbα-vWF binding kinetic models that are of greater physiological relevance, since the shear threshold effect is a central theme in platelet-vWF binding both in solution (pathological thrombosis) and at the subendothelial surface (hemostasis). Introduction of such improved kinetic equations in computer simulations of platelet binding to surface-bound vWF, as well as vWF in suspension, will perhaps enable recreation of platelet adhesive behavior with greater reliability and accuracy, providing better insight into the effects of fluid shear forces on platelet adhesive dynamics.
CONCLUSIONS
The development and application of the PAD model enabled us to obtain the following insights into platelet-platelet hydrodynamic and adhesive interactions in physiologically and pathologically relevant environments:
The physics of cell-cell collisions are a strong function of particle shape and proximity of physical flow boundaries, which strongly influence the fate of platelet-platelet encounters in the fluid. In particular, 1), homogeneous platelet (oblate spheroid) collision frequency increases by 25% when platelets far from any bounding surface are brought in close proximity to a wall (reactive gap = 128 nm); and 2), heterogeneous platelet-sphere (equal volume) collision frequency is 21% greater than homogeneous platelet collision frequency and 30% greater than homogeneous sphere collision frequency near a bounding wall (reactive gap = 128 nm).
A shift in average vWF ligand size in plasma to higher values, or reduction in the dissociation constant KD that describes GPIbα-vWF-A1 binding kinetics strongly influences the equilibrium binding kinetics and correspondingly increases platelet-platelet binding efficiency. Pathological consequences such as shear-induced platelet aggregation at shear rates (<5000 s−1) normally encountered in vivo can result.
The GPIbα-vWF-A1 bond formation rate is predicted to have piecewise linear dependence on the prevailing shear rate in the fluid such that the rate of association is a strong function of shear rate at
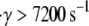 and a weak function of shear rate at
and a weak function of shear rate at 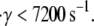
GPIbα-vWF-A1 bond lifetimes and bond rupture forces at
 were found to be of very short duration, 20–40 μs and ∼70 pN, respectively, for normal binding kinetics. Bond lifetimes appear to be an increasing function, and rupture forces appear to be a decreasing function, of the collision property, time integral of contact area.
were found to be of very short duration, 20–40 μs and ∼70 pN, respectively, for normal binding kinetics. Bond lifetimes appear to be an increasing function, and rupture forces appear to be a decreasing function, of the collision property, time integral of contact area.The force-loading curves for bond linkages that bind two platelet cells together in flow are highly complex and nonlinear. All GPIbα-vWF-A1 bonds ruptured at
 under a very high linear force ramp of 6–8 pN/μs.
under a very high linear force ramp of 6–8 pN/μs.
Models such as PAD that integrate particle-particle and particle-wall hydrodynamic effects and molecular level adhesive dynamics that govern stochastic cell-cell and cell-vascular wall adhesive interactions can be linked with predictive cell signaling models to simulate cell activation, probability of formation of integrin-ligand bonds, and release of granule contents from the platelet, leading to the development of a fully prothrombotic environment. Knowledge of the critical number of GPIbα receptors on a platelet surface required for binding one or more vWF multimers to bring about platelet activation, or the time lapse between binding of GPIbα to vWF and subsequent activation are needed to further our understanding of initial platelet activation. The scope of our study of platelet-platelet binding in solution via GPIbα-vWF-GPIbα bond bridging is somewhat limited by the dearth of experimental results available. As we increase our quantitative knowledge of platelet function and behavior through experimentation, the spectrum of physiological and pathological phenomena that can be computationally modeled will continue to expand.
Acknowledgments
This work was supported by a National Science Foundation Career Award (BES-0448788) and a National Institutes of Health (NIH) grant (HL087317) to M.R.K., and an NIH and Biomedical Imaging and Bioengineering fellowship (EB005104) to N.A.M.
APPENDIX A: PLATELET-VWF BINDING EQUILIBRIUM: USE OF THE EQUIVALENT SITE HYPOTHESIS (ESH) MODEL
GPIbα-vWF KD values reported in the literature
KD values for GPIbα-vWF binding have been experimentally determined by a number of research groups using static binding assays. Monomeric vWF-A1 binding to GPIbα has been measured (13,43,69). KD was found to be approximately 3.3 × 10−6 M and 3.0 × 10−6 M in two independent experimental studies (43,69) and 3.0 × 10−8 M in a third study (13). Miura et al. (43) also determined that the KD for plasma vWF binding to immobilized GPIbα was 3.4 μM. Several research groups determined the KD value for vWF multimer binding to platelets in the presence of ristocetin, a nonphysiological modulator; KD was found to be ≤20 nM in all cases (20,28,70). Larger multimers were consistently observed to have higher platelet affinities that resulted in increased platelet aggregation (17,19,20,22,71). This correlation between multimer size and binding activity is also seen in the case of vWF binding to other biomolecules such as heparin and fibrin (72,73). The mechanism of vWF binding to suspended platelets in the presence of ristocetin is different from that involved in shear-induced platelet-vWF binding (42). Also, KD for platelet GPIbα-vWF binding is possibly a function of the shear rate prevalent in the local fluid environment.
Testing ESH equilibrium model using KD values from the literature
The KD value of multimeric vWF is assumed here to be equal to the single-site dissociation constant KD of monomeric vWF-A1. Goldstein and Wofsy (74) derived a method for relating the two-dimensional cross-linking equilibrium constant KX to the three-dimensional equilibrium constant: KX = KA/d, where d is the average distance between two binding sites on the ligand. We follow the method of English and Hammer (75) for the estimation of d for a multivalent ligand. We assume that all binding sites are accessible for ligation with platelet surface receptors. Although this may be an oversimplification, little is known about the vWF equilibrium cross-linking constant, and the space sampled by free A1 binding sites of vWF molecules bound to receptors on a cell surface, and hence this straightforward estimation is made to preserve clarity and simplicity of the model. For a vWF molecule modeled as a prolate spheroid of dimensions 175 × 28 nm,
 |
Using the above values to solve Eqs. 1 and 2, we obtain the number of free receptors/cell, Req = 898, and the total number of vWF molecules bound/cell = 1899. Only 8.4% of the receptors are available for binding vWF multimers present on the surface of another platelet. The ESH model predicts strong and intense binding of vWF in solution to platelets at equilibrium. Such intense platelet-vWF binding is not intuitively expected given that at physiological shear rates, free vWF does not bind platelets, and at pathologically high shear rates the fraction of “vWF-positive” platelets is <0.05 at a shear rate of 12,000 s−1 (29).
English and Hammer (75) developed a model for viral docking to a cell surface in which the Brownian motion of a multivalent spherical ligand (virus) was simulated near a flat surface (cell) along with the dynamics of receptor-ligand adhesion. Viral docking was quantified and compared with the prediction of the ESH model. It was shown that the ESH model is an unsuitable model for predicting viral binding to cells due to its gross overprediction of the binding of virus particles to cells, especially of the number of bonds formed between each ligand and the cell surface. Although the virus was modeled as a rigid sphere in English and Hammer's adhesive dynamics simulations, vWF is a linear flexible loosely coiled molecule, and stronger binding may be observed for flexible and stringy molecules than for rigid spheres, since rigidity of particle shape and relative receptor location on the particle surface increases the difficulty of additional bond formation despite particle Brownian motion. Here, the overprediction of the bound state is attributed to use of an inappropriate KD that does not correctly represent shear-induced binding in solution.
Determination of a suitable KD value for shear-induced binding of GPIbα to vWF
Goto et al. (28) studied the binding of vWF to platelets in the presence of ristocetin and observed that an initial vWF solution concentration of 10 μg/ml led to the binding of 30,000 vWF subunit molecules/platelet. KD was found to be 5.3 μg/ml, which for an 18-mer (260 kD per monomer) vWF solution yields KD = 1.13 nM. The ESH model predicts Req = 0; Ceq = 2067 for a vWF solution concentration of 10 μg/ml. The maximum number of vWF multimers bound experimentally was found to be 42,125 vWF subunit molecules/platelet at an initial vWF solution concentration of 60 μg/ml. If on average each vWF molecule possesses 18 subunits, then the number of bound vWF molecules = 2340 per platelet. This maximum number of bound vWF molecules per platelet depends on the number of receptors/platelet and the average number of receptors bound/vWF molecule. The ESH model predicts Req = 0; Ceq = 2425 vWF molecules (RT = 10688 GPIbα receptors/platelet) bound to each platelet for a vWF solution concentration of 60 μg/ml, which is 3.6% greater than the experimental observation. We conclude that the ESH model may be suitable for predicting vWF equilibrium binding conditions.
Under shear-induced binding of vWF to platelets (28), ∼907 vWF subunit molecules/platelet (907/18 = 50 vWF molecules) were found to bind at an initial vWF concentration of 10 μg/ml at 10,800 s−1. The experiments of Goto and co-workers show that shear-induced vWF binding at a vWF solution concentration of 10 μg/ml is 33 times less than ristocetin-induced binding. The ESH model, which predicted 2067 bound vWF molecules/platelet for risotcetin-induced binding should then predict the binding of 2067/33 = 63 vWF molecules/platelet at equilibrium. This equilibrium state is predicted by the ESH model if a KD value of 7.73 × 10−5 M, obtained by trial and error, is used.
APPENDIX B: EQUILIBRIUM BINDING CONDITIONS FOR OTHER (PATHOLOGICAL) CASES OF VWF-PLATELET BINDING AS PREDICTED BY THE ESH MODEL
L-vWF-mediated binding
Using the value of KD determined above and L0 = 2.0 nM, the binding of a large vWF molecule (L-vWF) is calculated. We obtained Req = 8272 and Ceq,1 = 7; Ceq,2 = 25; Ceq,3 = 56; Ceq,4 = 85; Ceq,5 = 97; Ceq,6 = 85; Ceq,7 = 59; Ceq,8 = 32; Ceq,9 = 14; Ceq,10 = 5; Ceq,11 = 1; Ceq,12–17 = 0, and Ceq = 466 vWF molecules. For this case, L in solution changes by 10.6%. Since the change in ligand concentration in solution is substantial, the analytical solution for equilibrium binding, which is based on constant ligand concentration in solution, may not be valid.
n-vWF-mediated binding with platelet-type VWD binding kinetics
Binding kinetics for type 2B-VWD or platelet-type vWD is characterized by smaller bond dissociation rates and/or enhanced bond formation rates. Binding studies have shown that gain-of-function point mutations in the A1 binding domain of vWF or in the GPIbα binding domain cause a 3- to 20-fold decrease in the dissociation constant, KD, for platelet-surface binding via GPIbα-vWF-A1 interaction (10,43). We assume a fivefold decrease in KD for the platelet-type VWD binding model that results from a fivefold decrease in the off-rate (14,43). For KD = 1.55 × 10−5 M and L0 = 2.0 nM, the binding of n-vWF molecules is calculated. We obtain Req = 4287 and Ceq,1 = 10; Ceq,2 = 50; Ceq,3 = 144; Ceq,4 = 269; Ceq,5 = 334; Ceq,6 = 277; Ceq,7 = 147; Ceq,8 = 46; Ceq,9 = 6; and Ceq = 1283 vWF molecules. For this case, L in solution changes by 29%.
Explicit solution of the kinetic equations governing multivalent ligand binding to platelet receptors for those cases in which the analytical equilibrium solution is not valid
The kinetic equation set of the ESH model for multivalent ligand binding to cell surface receptors is as follows (57):
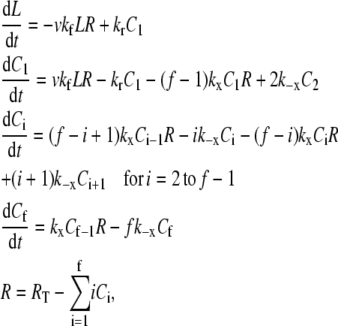 |
(B1) |
where L is the time-varying ligand concentration in solution, kx is the two-dimensional cross-linking forward rate constant, and k−x is the two-dimensional cross-linking reverse rate constant. For time-varying L, these f + 2 equations containing f + 2 unknowns can only be solved numerically. We tested the numerical algorithm employed (Runge-Kutta fourth-order method) for solving Eq. B1 by comparing the solution for equilibrium binding behavior for an n-vWF-platelet system obtained from the numerical solution of the kinetic equations (Eq. B1) with that calculated using the analytical solutions given by Eqs. 1 and 2. Both the analytical and numeric solutions were found to be the same. Solution of the kinetic equations to determine equilibrium binding also reveals the time duration over which equilibrium is established, which is 25 s for this system (C1, C2, ….Cf = 0 specify the initial conditions). Solving Eq. B1 numerically for an L-vWF-platelet system, we find that the analytical solution for constant solution ligand concentration overpredicts L-vWF multimer binding to platelets by 4.95%. The numerical solution for equilibrium binding is Req = 8373 and Ceq,1 = 7; Ceq,2 = 23; Ceq,3 = 52; Ceq,4 = 80; Ceq,5 = 92; Ceq,6 = 82; Ceq,7 = 57; Ceq,8 = 31; Ceq,9 = 14; Ceq,10 = 5; Ceq,11 = 1; Ceq,12–17 = 0; and Ceq = 444 vWF molecules. For this case, L in solution changes by 10.15%. Again solving Eq. B1 for the platelet-type VWD system, the solution at equilibrium is Req = 4519 and Ceq,1 = 8; Ceq,2 = 40; Ceq,3 = 122; Ceq,4 = 240; Ceq,5 = 314; Ceq,6 = 274; Ceq,7 = 154; Ceq,8 = 50; Ceq,9 = 7 and Ceq = 1209 vWF molecules. L in solution changes over the course of binding by 27.6%. The analytical solution given by Eqs. 1 and 2, which assumes L = Lo, overpredicts the binding of vWF multimers to diseased platelets by 6.12%.
APPENDIX C: CALCULATION OF FORWARD RATE CONSTANT FOR VWF ASSOCIATION WITH PLATELET SURFACE RECEPTOR GPIBα
The intrinsic forward rate constant for GPIbα binding to vWF in solution can be calculated as
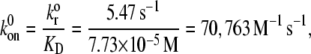 |
(C1) |
where 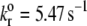 is the unstressed off-rate (11). Next, we determined the importance of diffusion in controlling the reaction (binding) rate. The forward transport rate constant for ligand molecules diffusing to a spherical cell surface is
is the unstressed off-rate (11). Next, we determined the importance of diffusion in controlling the reaction (binding) rate. The forward transport rate constant for ligand molecules diffusing to a spherical cell surface is  and the forward reaction rate constant is
and the forward reaction rate constant is  where DL = 4.5 × 10−8 cm2/s (40) is the average diffusion coefficient of vWF, a = 0.63 μm is the radius of a sphere with volume equal to that of a platelet of size 2 × 2 × 0.5 μm3, and R is the number of free receptors on the cell surface. The overall forward rate constant for ligand association per cell surface receptor is (for R = Req(n-vWF)) (57)
where DL = 4.5 × 10−8 cm2/s (40) is the average diffusion coefficient of vWF, a = 0.63 μm is the radius of a sphere with volume equal to that of a platelet of size 2 × 2 × 0.5 μm3, and R is the number of free receptors on the cell surface. The overall forward rate constant for ligand association per cell surface receptor is (for R = Req(n-vWF)) (57)
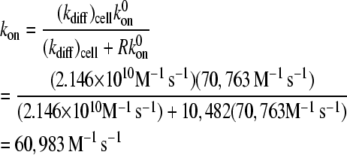 |
(C2) |
and, konL = 1.22 × 10−4 s−1.
Although these calculations were made considering a spherical geometry, it is assumed that this method of calculation for kon is approximately valid even for a cell shape in which the particle diameter is smaller in one of three mutually orthogonal directions with respect to the Cartesian coordinate system.
Michael R. King's present address is Dept. of Biomedical Engineering, Cornell University, Ithaca, New York.
Editor: Gaudenz Danuser.
References
- 1.Sakariassen, K. S., P. A. Bolhuis, and J. J. Sixma. 1979. Human blood platelet adhesion to artery subendothelium is mediated by factor VIII–Von Willebrand factor bound to the subendothelium. Nature. 279:636–638. [DOI] [PubMed] [Google Scholar]
- 2.Nieuwenhuis, H. K., J. W. Akkerman, W. P. Houdijk, and J. J. Sixma. 1985. Human blood platelets showing no response to collagen fail to express surface glycoprotein Ia. Nature. 318:470–472. [DOI] [PubMed] [Google Scholar]
- 3.Savage, B., F. Almus-Jacobs, and Z. M. Ruggeri. 1998. Specific synergy of multiple substrate-receptor interactions in platelet thrombus formation under flow. Cell. 94:657–666. [DOI] [PubMed] [Google Scholar]
- 4.Mendolicchio, G. L., and Z. M. Ruggeri. 2005. New perspectives on von Willebrand factor functions in hemostasis and thrombosis. Semin. Hematol. 42:5–14. [DOI] [PubMed] [Google Scholar]
- 5.Ruggeri, Z. M., L. De Marco, L. Gatti, R. Bader, and R. R. Montgomery. 1983. Platelets have more than one binding site for von Willebrand factor. J. Clin. Invest. 72:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Savage, B., E. Saldivar, and Z. M. Ruggeri. 1996. Initiation of platelet adhesion by arrest onto fibrinogen or translocation on von Willebrand factor. Cell. 84:289–297. [DOI] [PubMed] [Google Scholar]
- 7.Kasirer-Friede, A., M. R. Cozzi, M. Mazzucato, L. De Marco, Z. M. Ruggeri, and S. J. Shattil. 2004. Signaling through GP Ib-IX-V activates αIIbβ3 independently of other receptors. Blood. 103:3403–3411. [DOI] [PubMed] [Google Scholar]
- 8.Cruz, M. A., J. Chen, J. L. Whitelock, L. D. Morales, and J. A. Lopez. 2005. The platelet glycoprotein Ib-von Willebrand factor interaction activates the collagen receptor α2β1 to bind collagen: activation-dependent conformational change of the α2-I domain. Blood. 105:1986–1991. [DOI] [PubMed] [Google Scholar]
- 9.Yuan, Y., S. Kulkarni, P. Ulsemer, S. L. Cranmer, C. L. Yap, W. S. Nesbitt, I. Harper, N. Mistry, S. M. Dopheide, S. C. Hughan, D. Williamson, C. de la Salle, H. H. Salem, F. Lanza, and S. P. Jackson. 1999. The von Willebrand factor-glycoprotein Ib/V/IX interaction induces actin polymerization and cytoskeletal reorganization in rolling platelets and glycoprotein Ib/V/IX-transfected cells. J. Biol. Chem. 274:36241–36251. [DOI] [PubMed] [Google Scholar]
- 10.Doggett, T. A., G. Girdhar, A. Lawshe, D. W. Schmidtke, I. J. Laurenzi, S. L. Diamond, and T. G. Diacovo. 2002. Selectin-like kinetics and biomechanics promote rapid platelet adhesion in flow: the GPIbα-vWF tether bond. Biophys. J. 83:194–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Arya, M., A. B. Kolomeisky, G. M. Romo, M. A. Cruz, J. A. Lopez, and B. Anvari. 2005. Dynamic force spectroscopy of glycoprotein Ib-IX and von Willebrand factor. Biophys. J. 88:4391–4401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kumar, R. A., J. F. Dong, J. A. Thaggard, M. A. Cruz, J. A. Lopez, and L. V. McIntire. 2003. Kinetics of GPIbα-vWF-A1 tether bond under flow: effect of GPIbα mutations on the association and dissociation rates. Biophys. J. 85:4099–4109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Huizinga, E. G., S. Tsuji, R. A. Romijn, M. E. Schiphorst, P. G. de Groot, J. J. Sixma, and P. Gros. 2002. Structures of glycoprotein Ibα and its complex with von Willebrand factor A1 domain. Science. 297:1176–1179. [DOI] [PubMed] [Google Scholar]
- 14.Doggett, T. A., G. Girdhar, A. Lawshe, J. L. Miller, I. J. Laurenzi, S. L. Diamond, and T. G. Diacovo. 2003. Alterations in the intrinsic properties of the GPIbα-VWF tether bond define the kinetics of the platelet-type von Willebrand disease mutation, Gly233Val. Blood. 102:152–160. [DOI] [PubMed] [Google Scholar]
- 15.Dumas, J. J., R. Kumar, T. McDonagh, F. Sullivan, M. L. Stahl, W. S. Somers, and L. Mosyak. 2004. Crystal structure of the wild-type von Willebrand factor A1-glycoprotein Ibα complex reveals conformation differences with a complex bearing von Willebrand disease mutations. J. Biol. Chem. 279:23327–23334. [DOI] [PubMed] [Google Scholar]
- 16.Ruggeri, Z. M. 2004. Type IIB von Willebrand disease: a paradox explains how von Willebrand factor works. J. Thromb. Haemost. 2:2–6. [DOI] [PubMed] [Google Scholar]
- 17.Li, F., C. Q. Li, J. L. Moake, J. A. Lopez, and L. V. McIntire. 2004. Shear stress-induced binding of large and unusually large von Willebrand factor to human platelet glycoprotein Ibα. Ann. Biomed. Eng. 32:961–969. [DOI] [PubMed] [Google Scholar]
- 18.Arya, M., B. Anvari, G. M. Romo, M. A. Cruz, J. F. Dong, L. V. McIntire, J. L. Moake, and J. A. Lopez. 2002. Ultralarge multimers of von Willebrand factor form spontaneous high-strength bonds with the platelet glycoprotein Ib-IX complex: studies using optical tweezers. Blood. 99:3971–3977. [DOI] [PubMed] [Google Scholar]
- 19.Fischer, B. E., G. Kramer, A. Mitterer, L. Grillberger, M. Reiter, W. Mundt, F. Dorner, and J. Eibl. 1996. Effect of multimerization of human and recombinant von Willebrand factor on platelet aggregation, binding to collagen and binding of coagulation factor VIII. Thromb. Res. 84:55–66. [DOI] [PubMed] [Google Scholar]
- 20.Federici, A. B., R. Bader, S. Pagani, M. L. Colibretti, L. De Marco, and P. M. Mannucci. 1989. Binding of von Willebrand factor to glycoproteins Ib and IIb/IIIa complex: affinity is related to multimeric size. Br. J. Haematol. 73:93–99. [DOI] [PubMed] [Google Scholar]
- 21.Kumar, R. A., J. L. Moake, L. Nolasco, A. L. Bergeron, C. Sun, J. F. Dong, and L. V. McIntire. 2006. Enhanced platelet adhesion and aggregation by endothelial cell-derived unusually large multimers of von Willebrand factor. Biorheology. 43:681–691. [PubMed] [Google Scholar]
- 22.Moake, J. L., N. A. Turner, N. A. Stathopoulos, L. Nolasco, and J. D. Hellums. 1988. Shear-induced platelet aggregation can be mediated by vWF released from platelets, as well as by exogenous large or unusually large vWF multimers, requires adenosine diphosphate, and is resistant to aspirin. Blood. 71:1366–1374. [PubMed] [Google Scholar]
- 23.Furlan, M. 1996. Von Willebrand factor: molecular size and functional activity. Ann. Hematol. 72:341–348. [DOI] [PubMed] [Google Scholar]
- 24.Moake, J. L. 1995. Thrombotic thrombocytopenic purpura. Thromb. Haemost. 74:240–245. [PubMed] [Google Scholar]
- 25.Alevriadou, B. R., J. L. Moake, N. A. Turner, Z. M. Ruggeri, B. J. Folie, M. D. Phillips, A. B. Schreiber, M. E. Hrinda, and L. V. McIntire. 1993. Real-time analysis of shear-dependent thrombus formation and its blockade by inhibitors of von Willebrand factor binding to platelets. Blood. 81:1263–1276. [PubMed] [Google Scholar]
- 26.Ikeda, Y., M. Handa, K. Kawano, T. Kamata, M. Murata, Y. Araki, H. Anbo, Y. Kawai, K. Watanabe, I. Itagaki, K. Sakai, and Z. M. Ruggeri. 1991. The role of von Willebrand factor and fibrinogen in platelet aggregation under varying shear stress. J. Clin. Invest. 87:1234–1240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Peterson, D. M., N. A. Stathopoulos, T. D. Giorgio, J. D. Hellums, and J. L. Moake. 1987. Shear-induced platelet aggregation requires von Willebrand factor and platelet membrane glycoproteins Ib and IIb-IIIa. Blood. 69:625–628. [PubMed] [Google Scholar]
- 28.Goto, S., D. R. Salomon, Y. Ikeda, and Z. M. Ruggeri. 1995. Characterization of the unique mechanism mediating the shear-dependent binding of soluble von Willebrand factor to platelets. J. Biol. Chem. 270:23352–23361. [DOI] [PubMed] [Google Scholar]
- 29.Konstantopoulos, K., T. W. Chow, N. A. Turner, J. D. Hellums, and J. L. Moake. 1997. Shear stress-induced binding of von Willebrand factor to platelets. Biorheology. 34:57–71. [DOI] [PubMed] [Google Scholar]
- 30.Fujikawa, K., H. Suzuki, B. McMullen, and D. Chung. 2001. Purification of human von Willebrand factor-cleaving protease and its identification as a new member of the metalloproteinase family. Blood. 98:1662–1666. [DOI] [PubMed] [Google Scholar]
- 31.George, J. N., J. E. Sadler, and B. Lammle. 2002. Platelets: thrombotic thrombocytopenic purpura. Hematology Am. Soc. Hematol. Educ. Program. 2002:315–334. [DOI] [PubMed] [Google Scholar]
- 32.Huang, P. Y., and J. D. Hellums. 1993. Aggregation and disaggregation kinetics of human blood platelets: Part II. Shear-induced platelet aggregation. Biophys. J. 65:344–353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Huang, P. Y., and J. D. Hellums. 1993. Aggregation and disaggregation kinetics of human blood platelets: Part I. Development and validation of a population balance method. Biophys. J. 65:334–343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.King, M. R., and D. A. Hammer. 2001. Multiparticle adhesive dynamics. Interactions between stably rolling cells. Biophys. J. 81:799–813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hammer, D. A., and S. M. Apte. 1992. Simulation of cell rolling and adhesion on surfaces in shear flow: general results and analysis of selectin-mediated neutrophil adhesion. Biophys. J. 63:35–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Reininger, A. J., H. F. Heijnen, H. Schumann, H. M. Specht, W. Schramm, and Z. M. Ruggeri. 2006. Mechanism of platelet adhesion to von Willebrand factor and microparticle formation under high shear stress. Blood. 107:3537–3545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Berndt, M. C., Y. Shen, S. M. Dopheide, E. E. Gardiner, and R. K. Andrews. 2001. The vascular biology of the glycoprotein Ib-IX-V complex. Thromb. Haemost. 86:178–188. [PubMed] [Google Scholar]
- 38.Siedlecki, C. A., B. J. Lestini, K. K. Kottke-Marchant, S. J. Eppell, D. L. Wilson, and R. E. Marchant. 1996. Shear-dependent changes in the three-dimensional structure of human von Willebrand factor. Blood. 88:2939–2950. [PubMed] [Google Scholar]
- 39.Singh, I., H. Shankaran, M. E. Beauharnois, Z. Xiao, P. Alexandridis, and S. Neelamegham. 2006. Solution structure of human von Willebrand factor studied using small angle neutron scattering. J. Biol. Chem. 281:38266–38275. [DOI] [PubMed] [Google Scholar]
- 40.Slayter, H., J. Loscalzo, P. Bockenstedt, and R. I. Handin. 1985. Native conformation of human von Willebrand protein. Analysis by electron microscopy and quasi-elastic light scattering. J. Biol. Chem. 260:8559–8563. [PubMed] [Google Scholar]
- 41.Dong, J. F., J. L. Moake, L. Nolasco, A. Bernardo, W. Arceneaux, C. N. Shrimpton, A. J. Schade, L. V. McIntire, K. Fujikawa, and J. A. Lopez. 2002. ADAMTS-13 rapidly cleaves newly secreted ultralarge von Willebrand factor multimers on the endothelial surface under flowing conditions. Blood. 100:4033–4039. [DOI] [PubMed] [Google Scholar]
- 42.Goto, S., Y. Ikeda, E. Saldivar, and Z. M. Ruggeri. 1998. Distinct mechanisms of platelet aggregation as a consequence of different shearing flow conditions. J. Clin. Invest. 101:479–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Miura, S., C. Q. Li, Z. Cao, H. Wang, M. R. Wardell, and J. E. Sadler. 2000. Interaction of von Willebrand factor domain A1 with platelet glycoprotein Ibα-(1–289). Slow intrinsic binding kinetics mediate rapid platelet adhesion. J. Biol. Chem. 275:7539–7546. [DOI] [PubMed] [Google Scholar]
- 44.Ruggeri, Z. M., and J. Ware. 1992. The structure and function of von Willebrand factor. Thromb. Haemost. 67:594–599. [PubMed] [Google Scholar]
- 45.Borchiellini, A., K. Fijnvandraat, J. W. ten Cate, D. Pajkrt, S. J. van Deventer, G. Pasterkamp, F. Meijer-Huizinga, L. Zwart-Huinink, J. Voorberg, and J. A. van Mourik. 1996. Quantitative analysis of von Willebrand factor propeptide release in vivo: effect of experimental endotoxemia and administration of 1-deamino-8-D-arginine vasopressin in humans. Blood. 88:2951–2958. [PubMed] [Google Scholar]
- 46.Fox, J. E., L. P. Aggerbeck, and M. C. Berndt. 1988. Structure of the glycoprotein Ib.IX complex from platelet membranes. J. Biol. Chem. 263:4882–4890. [PubMed] [Google Scholar]
- 47.Perelson, A. S. 1981. Receptor clustering on a cell-surface. 3. Theory of receptor cross-linking by multivalent ligands: description by ligand states. Math. Biosci. 53:1–39. [Google Scholar]
- 48.Bell, G. I. 1979. A theoretical model for adhesion between cells mediated by multivalent ligands. Cell Biophys. 1:133–147. [DOI] [PubMed] [Google Scholar]
- 49.Shankaran, H., P. Alexandridis, and S. Neelamegham. 2003. Aspects of hydrodynamic shear regulating shear-induced platelet activation and self-association of von Willebrand factor in suspension. Blood. 101:2637–2645. [DOI] [PubMed] [Google Scholar]
- 50.Bell, G. I. 1978. Models for the specific adhesion of cells to cells. Science. 200:618–627. [DOI] [PubMed] [Google Scholar]
- 51.Bell, G. I., M. Dembo, and P. Bongrand. 1984. Cell adhesion. Competition between nonspecific repulsion and specific bonding. Biophys. J. 45:1051–1064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Chtcheglova, L. A., G. T. Shubeita, S. K. Sekatskii, and G. Dietler. 2004. Force spectroscopy with a small dithering of AFM tip: a method of direct and continuous measurement of the spring constant of single molecules and molecular complexes. Biophys. J. 86:1177–1184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Press, W. H., S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. 1992. Numerical Recipes in Fortran 77. The Art of Scientific Computing. Cambridge University Press, Cambridge, United Kingdom.
- 54.Murata, M., M. Fukuyama, K. Satoh, Y. Fujimura, A. Yoshioka, H. Takahashi, M. Handa, Y. Kawai, K. Watanabe, and Y. Ikeda. 1993. Low shear stress can initiate von Willebrand factor-dependent platelet aggregation in patients with type IIB and platelet-type von Willebrand disease. J. Clin. Invest. 92:1555–1558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ajzenberg, N., A. S. Ribba, G. Rastegar-Lari, D. Meyer, and D. Baruch. 2000. Effect of recombinant von Willebrand factor reproducing type 2B or type 2M mutations on shear-induced platelet aggregation. Blood. 95:3796–3803. [PubMed] [Google Scholar]
- 56.Alon, R., D. A. Hammer, and T. A. Springer. 1995. Lifetime of the P-selectin-carbohydrate bond and its response to tensile force in hydrodynamic flow. Nature. 374:539–542. [DOI] [PubMed] [Google Scholar]
- 57.Lauffenburger, D. A., and J. J. Linderman. 1993. Receptors: Models for Binding, Trafficking and Signaling. Oxford University Press, New York.
- 58.Lopez, J. A., I. del Conde, and C. N. Shrimpton. 2005. Receptors, rafts, and microvesicles in thrombosis and inflammation. J. Thromb. Haemost. 3:1737–1744. [DOI] [PubMed] [Google Scholar]
- 59.Dong, J. F., C. Q. Li, G. Sae-Tung, W. Hyun, V. Afshar-Kharghan, and J. A. Lopez. 1997. The cytoplasmic domain of glycoprotein (GP) Ibα constrains the lateral diffusion of the GP Ib-IX complex and modulates von Willebrand factor binding. Biochemistry (Mosc.). 36:12421–12427. [DOI] [PubMed] [Google Scholar]
- 60.Laurenzi, I. J., and S. L. Diamond. 2002. Bidisperse aggregation and gel formation via simultaneous convection and diffusion. Ind. Eng. Chem. Res. 41:413–420. [Google Scholar]
- 61.Mody, N. A., and M. R. King. 2007. Influence of Brownian motion on blood platelet flow behavior and adhesive dynamics near a plane wall. Langmuir. 23:6321–6328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Alexander-Katz, A., M. F. Schneider, S. W. Schneider, A. Wixforth, and R. R. Netz. 2006. Shear-flow-induced unfolding of polymeric globules. Phys. Rev. Lett. 97:138101. [DOI] [PubMed] [Google Scholar]
- 63.Tandon, P., and S. L. Diamond. 1997. Hydrodynamic effects and receptor interactions of platelets and their aggregates in linear shear flow. Biophys. J. 73:2819–2835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Ikeda, Y., M. Handa, T. Kamata, K. Kawano, Y. Kawai, K. Watanabe, K. Kawakami, K. Sakai, M. Fukuyama, I. Itagaki, A. Yoshioka and Z. M. Ruggeri. 1993. Transmembrane calcium influx associated with von Willebrand factor binding to GP Ib in the initiation of shear-induced platelet aggregation. Thromb. Haemost. 69:496–502. [PubMed] [Google Scholar]
- 65.Uff, S., J. M. Clemetson, T. Harrison, K. J. Clemetson, and J. Emsley. 2002. Crystal structure of the platelet glycoprotein Ibα N-terminal domain reveals an unmasking mechanism for receptor activation. J. Biol. Chem. 277:35657–35663. [DOI] [PubMed] [Google Scholar]
- 66.Novak, L., H. Deckmyn, S. Damjanovich, and J. Harsfalvi. 2002. Shear-dependent morphology of von Willebrand factor bound to immobilized collagen. Blood. 99:2070–2076. [DOI] [PubMed] [Google Scholar]
- 67.Schneider, S. W., S. Nuschele, A. Wixforth, C. Gorzelanny, A. Alexander-Katz, R. R. Netz, and M. F. Schneider. 2007. Shear-induced unfolding triggers adhesion of von Willebrand factor fibers. Proc. Natl. Acad. Sci. USA. 104:7899–7903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Evans, E., A. Leung, V. Heinrich, and C. Zhu. 2004. Mechanical switching and coupling between two dissociation pathways in a P-selectin adhesion bond. Proc. Natl. Acad. Sci. USA. 101:11281–11286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Cruz, M. A., R. I. Handin, and R. J. Wise. 1993. The interaction of the von Willebrand factor-A1 domain with platelet glycoprotein Ib/IX. The role of glycosylation and disulfide bonding in a monomeric recombinant A1 domain protein. J. Biol. Chem. 268:21238–21245. [PubMed] [Google Scholar]
- 70.Morisato, D. K., and H. R. Gralnick. 1980. Selective binding of the factor VIII/von Willebrand factor protein to human platelets. Blood. 55:9–15. [PubMed] [Google Scholar]
- 71.Chopek, M. W., J. P. Girma, K. Fujikawa, E. W. Davie, and K. Titani. 1986. Human von Willebrand factor: a multivalent protein composed of identical subunits. Biochemistry (Mosc.). 25:3146–3155. [DOI] [PubMed]
- 72.Suda, Y., A. Arano, Y. Fukui, S. Koshida, M. Wakao, T. Nishimura, S. Kusumoto, and M. Sobel. 2006. Immobilization and clustering of structurally defined oligosaccharides for sugar chips: an improved method for surface plasmon resonance analysis of protein-carbohydrate interactions. Bioconjug. Chem. 17:1125–1135. [DOI] [PubMed] [Google Scholar]
- 73.Ribes, J. A., and C. W. Francis. 1990. Multimer size dependence of von Willebrand factor binding to crosslinked or noncrosslinked fibrin. Blood. 75:1460–1465. [PubMed] [Google Scholar]
- 74.Goldstein, B., and C. Wofsy. 1994. Aggregation of cell surface receptors. Lect. Math Life Sci. 24:109–135. [Google Scholar]
- 75.English, T. J., and D. A. Hammer. 2004. Brownian adhesive dynamics (BRAD) for simulating the receptor-mediated binding of viruses. Biophys. J. 86:3359–3372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Cotran, R. S., S. L. Robbins, and V. Kumar. 1994. Robbins Pathologic Basis of Disease, 5th ed. W. B. Saunders Company, Philadelphia.
- 77.Popel, A. S., and P. C. Johnson. 2005. Microcirculation and hemorheology. Annu. Rev. Fluid Mech. 37:43–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Frojmovic, M., K. Longmire, and T. G. van de Ven. 1990. Long-range interactions in mammalian platelet aggregation. II. The role of platelet pseudopod number and length. Biophys. J. 58:309–318. [DOI] [PMC free article] [PubMed] [Google Scholar]