Abstract
The phosphorylation-dephosphorylation cycle is a common motif in cellular signaling networks. Previous work has revealed that, when driven by a noisy input signal, these cycles may exhibit bistable behavior. Here, a recently introduced theorem on network bistability is applied to prove that the existence of bistability is dependent on the stochastic nature of the system. Furthermore, the thermodynamics of simple cycles and cascades is investigated in the stochastic setting. Because these cycles are driven by the ATP hydrolysis potential, they may operate far from equilibrium. It is shown that sufficient high ATP hydrolysis potential is necessary for the existence of a bistable steady state. For the single-cycle system, the ensemble average behavior follows the ultrasensitive response expected from analysis of the corresponding deterministic system, but with significant fluctuations. For the two-cycle cascade, the average behavior begins to deviate from the expected response of the deterministic system. Examination of a two-cycle cascade reveals that the bistable steady state may be either propagated or abolished along a cascade, depending on the parameters chosen. Likewise, the variance in the response can be maximized or minimized by tuning the number of enzymes in the second cycle.
INTRODUCTION
The stochastic operation of biochemical systems, particularly important when the numbers of molecules involved are relatively low, has received increasing attention in recent years. For example, a number of studies have revealed the stochastic nature and importance of fluctuations in gene expression (1–4). Swain et al. (1) proposed a theoretical description of the extrinsic and intrinsic noise in gene expression, examined the contributions using stochastic kinetics, and proposed a method for characterizing the noise in experiments. Süel et al. (2) used experiments to show how a genetic circuit is dependent on noise. They developed a stochastic model of the circuit and proposed that the noise affects signal duration and allows excitability over a wide parameter range.
ATP-dependent phosphorylation events are ubiquitous in cellular signaling systems. Recent theoretical studies have focused on questions of how and why phosphorylation-dephosphorylation cycles (PdPC) exhibit steady-state oscillations or bistability (5,6). In those studies, bistable or oscillatory behavior is explained based on feedback mechanisms or coupled reaction systems.
The role of noise and stochasticity has also been examined in enzymatic cycles and signal cascades (7–11). Levine et al. (10) examined an enzymatic cycle using stochastic kinetics and looked at the effects of intrinsic fluctuations and extrinsic parameters on the ultrasensitive response. They found that in the ultrasensitive regime, the kinase/phosphatase ratio needs to be tuned to transmit a signal. They also found that large Michaelis-Menten constants lead to a fast switching time with a low number of molecules in response to changes in the signal. Thattai and van Oudenaarden (9) looked at a signal cascade using a Langevin technique and saw that after a few cascade steps, the signal noise can be attenuated. Shibata and Fujimoto (8) developed a relationship between signal gain and the noise in an enzymatic cycle and an ultrasensitive cascade. They also found that the extrinsic noise can be attenuated if the cascade works at saturation. Morishita et al. (7) looked at the transient dynamics of a signal cascade using stochastic kinetics. They determined the optimal number of molecules for maximal signal amplification for a given number of cascade steps. Specifically, they see that for 1–9 cascade steps, the optimal number of signaling molecules is between ∼10 and 50.
These studies have shown how extrinsic and intrinsic noise is important in stochastically modeled enzymatic cycles and signal cascades. However, they did not observe oscillations or bimodal/bistable steady states. Yet in a series of studies by Samoilov et al. (12) and Samoilov and Arkin (13), external noise was shown to affect bistability in the classic Goldbeter-Koshland model (14) of the phosphorylation-dephosphorylation switch. For these apparently simple systems, several questions remain regarding the bistable behavior. It remains to be understood how reversibility and energetic state may affect the noise-driven bistability. Given the relationship to the Goldbeter and Koshland model, it would be interesting to know whether stochasticity alters the expected ultrasensitive response of the enzymatic cycle. Tests for the possibility of bistability in any reaction network, which follow from a recently introduced theorem (15), can be applied to the reaction kinetics considered here to examine the origin of the bistability. There is also a question of how the noise-induced bistability is translated through an enzymatic cascade. This is particularly interesting since the mitogen-activated protein kinase cascade was shown to exhibit bistable behavior in a recent study (6). Another recent study (16) of T-cell binding models exhibited bimodal responses under stochastic conditions. They found that the response depends on the number of particles.
The original model of Goldbeter and Koshland treated the following system of two chemical reactions (14):
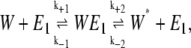 |
(1) |
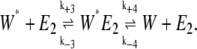 |
(2) |
Here E1 and E2 are enzymes catalyzing the transformation of W to W*. If E1 and E2 are kinase and phosphatase enzymes, respectively, and W and W* are unphosphorylated and phosphorylated substrates, then this system of reactions represents a phosphorylation-dephosphorylation cycle. Note that in the original work of Goldbeter and Koshland, these reactions were modeled as irreversible with k−2 and k−4 equal to zero. This assumption was made by Samoilov et al. (12) as well.
Qian examined this reaction system for the more general reversible case (17). He showed that the sensitivity of the phosphorylation-dephosphorylation cycle and the signal amplification in cascades of such cycles are dependent on the free energy of ATP hydrolysis driving the cycles. The system studied by Qian reduces to that of Goldbeter and Koshland (14) and Samoilov et al. (12) in the limit that the magnitude of the ATP hydrolysis potential becomes infinite. Here, we recast the stochastic simulations of Samoilov et al. using the thermodynamically feasible reaction system of Qian.
Samoilov et al. (12) examined the stochastic operation of the Eqs. 1 and 2 (with k−2, k−4 = 0) using both a Langevin equation and stochastic kinetic simulation and found evidence for noise-induced bistability in both approaches. Critical to their conclusions is the assumption that the activity of the enzyme, E1, varies stochastically. This external noise is not related to the fluctuations intrinsic to the cycle itself. Possible sources of fluctuations in E1 include, but are not limited to, production or degradation of enzymes, pH, or temperature fluctuations or any other modification of the enzyme activity.
The Langevin equation used by Samoilov et al. (12) for the evolution of W* is
 |
(3) |
where W0 = W + W*, k+2/+4 are the catalytic constants of the enzymes, K1/2 are the Michaelis-Menten constants for the substrate reaction, and Bt is a standard Brownian process. In this model the strength of the noise, σ, is related to the (constant) basal kinase concentration E1 by
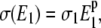 |
(4) |
where σ1 and p are constant parameters. For the values of rate constants used by Samoilov et al. (12), the noise gives rise to a bistable solution if σ1 = 0.2, p > 0.75, and 20 < E1 < 30. Using stochastic kinetic simulations, Samoilov et al. (12) also showed the existence of a bistable state by representing the external fluctuations in the number of molecules of E1 with two reactions:
 |
(5) |
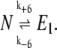 |
(6) |
Conceivably, equivalent results would be obtained for any other simulation scheme as long as the resulting fluctuations follow the requirements of Eq. 4.
This work seeks to understand noise-induced bistability by determining the role of thermodynamic reversibility and the effects on zero-order sensitivity for a noisy, fully reversible single enzymatic cycle. We further determine the parameters that lead to bistability in a noisy irreversible two-cycle cascade. Here we study PdPC systems using Gillespie's algorithm for stochastic kinetic simulation to determine the role of thermodynamics as a driving force in these systems. The following section describes the methods and theory behind our analysis. Next, the stochastic kinetic simulation for the PdPC and the two-cycle cascade is presented. Finally, the results of our analysis and stochastic simulations and the conclusions that are drawn are discussed.
THEORY AND METHODS
Possibility of network bistability
To eliminate the possibility of a bistable steady-state arising from the network itself we analyze the elementary reactions using two different techniques. First, a recent theorem by Craciun et al. (15) analyzes a reaction network by decomposing the elementary reactions and species into a system of nodes and edges in a graph. Using the species-reaction graph, one can classify the network properties and eliminate the possibility of multiple-steady states when deterministic kinetics is used to model the reaction network. Second, the Chemical Reaction Network Toolbox (18) is used, especially when Craciun's theorem cannot be applied. The Chemical Reaction Network Toolbox applies chemical reaction network theory (19–21) to examine a reaction network for the (possible) existence of multiple steady states when modeled deterministically. These tools allow us to understand whether the reaction networks considered allow multiple steady states because of the network structure of the stochastic description of the system.
Analysis of the PdPC
Our analysis of the PdPC cycle (Eqs. 1 and 2) is based on that of Qian (17), which is an extension of the Goldbeter-Koshland analysis (14) with the added assumption of fully reversible steps. Both of these analyses assume that in the limits of steady-state and deterministic kinetics, the fluxes through these reactions can be described by the familiar Michaelis-Menten equation. In the extended model of Qian (the reversible case), the sensitivity of the response can be described by three parameters: the ATP hydrolysis potential (γ); the basal level of phosphorylation in the absence of the kinase enzyme (μ); and the relative activity of the kinase (E1) versus the phosphatase (E2) (θ1). The relationship between these parameters and the kinetic parameters are described below. A detailed discussion of the effects of γ, μ, and θ can be found in Beard and Qian (22).
The ATP hydrolysis potential, γ, becomes important only in the extended model of Qian (17), where the reactions are fully reversible. To understand this, we rewrite Eqs. 1 and 2 with the ATP hydrolysis explicitly expressed:
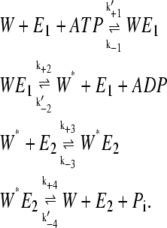 |
(7) |
Here the first-order rate constants k′+1, k′−2, and k′−4 are related to the pseudo first-order rate constants in Eqs. 1 and 2 as follows: k+1 = k′+1[ATP], k−2 = k′−2[ADP], and k−4 = k′−4[Pi]. These equations sum up to the overall reaction,
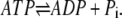 |
(8) |
The parameter γ is defined by
 |
(9) |
where [x] is the concentration of biochemical reactant x. Rewriting Eq. 9 as
 |
(10) |
where 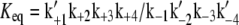 is the equilibrium constant of the reaction, we have
is the equilibrium constant of the reaction, we have
 |
(11) |
Thus the free energy of ATP hydrolysis is expressed in terms of γ as ΔGATP = −RT ln γ. As γ → ∞, the free energy becomes infinite and the cycle becomes irreversible.
The basal level of phosphorylation in the absence of the kinase enzyme, μ, is defined as
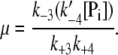 |
(12) |
It represents the level of W* when there is no kinase (E1) present and is usually very small. When the PdPC is modeled irreversibly (with k−4 = 0), then μ = 0. The control parameter, θ1 is defined as
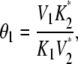 |
(13) |
with 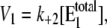 V2*
V2*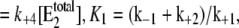 and
and 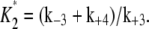 Here
Here 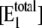 is the total concentration of kinase and
is the total concentration of kinase and  is the total concentration of phosphatase.
is the total concentration of phosphatase.
All three sensitivity parameters are related to the fraction of phosphorylated enzyme, f* = [W*]/[Wtotal], by the relation
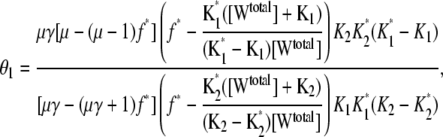 |
(14) |
where 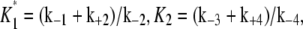 and
and 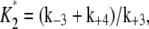 and [Wtotal] is the total concentration of the substrate, [W] + [W*]. This relationship arises from the deterministic kinetics of Eqs. 1 and 2 under the assumption of quasi-steady state, which remains valid when the enzyme concentrations are small compared to substrate concentrations. The relationship of f* to θ1 indicates how sensitive the cycle is to the control parameter, θ1.
and [Wtotal] is the total concentration of the substrate, [W] + [W*]. This relationship arises from the deterministic kinetics of Eqs. 1 and 2 under the assumption of quasi-steady state, which remains valid when the enzyme concentrations are small compared to substrate concentrations. The relationship of f* to θ1 indicates how sensitive the cycle is to the control parameter, θ1.
Stochastic rate constants used in simulation allow us to compute the probability of a given reaction occurring in a given volume in a given time interval. Therefore, the kinetic rate constants k±i must be transformed to stochastic (microscopic) rate constants c±i that account for the volume of the container that is simulated (23). In terms of the stochastic rate constants, γ is expressed
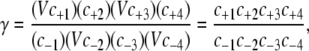 |
(15) |
where V is the reaction volume and c±i are the forward and reverse stochastic rate constants of reaction i. The volumes cancel out and the equations become independent of volume. In this work, we examine the effects of the thermodynamic driving force by varying γ from 100 to 1011 by changing the value of c−2 in the simulations below. The basal level of phosphorylation is then expressed as
 |
(16) |
The control parameter becomes
 |
(17) |
When the external noise reactions are included, the total amount of phosphatase (E2) is constant while the amount of kinase (E1) varies. Therefore, we examined the relationship between phosphorylation state and the mean value of the control parameter 〈θ1〉. It is important to note that for γ, μ, and θ1, the stochastic descriptions are independent of volume.
The manner in which the PdPC responds to changes in the above parameters is determined by stochastic kinetics simulation using Gillespie's algorithm (23). The individual elementary steps of the Samoilov et al. model of the noisy PdPC (Eqs. 1, 2, 5, and 6) were simulated. To perform the stochastic simulations, we used the freely available STOCKS software (Ver. 1.02) (24). The stochastic rate constants and initial conditions are given in Results for each of the systems studied. Throughout the simulations, the number of each molecule present was stored to a file every 0.01 time units. For all parameters studied here, the simulations quickly reached a bistable steady state (<0.1 time units) and were run for 20 time units. Probability distributions were determined from 100 independent simulations from the data collected after 0.1 time units.
Two-cycle cascade
To address the effects of the bistability on an enzymatic cascade, a two-cycle reaction scheme was built in which the molecule W* was involved in modifying another molecule, X. In this case the following reactions were added to the system of reactions of Eqs. 1, 2, 5, and 6:
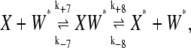 |
(18) |
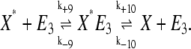 |
(19) |
For simplicity, the rate constants for this kinase reaction (Eq. 18) were assumed the same as the kinase of Eq. 1; rate constants for this phosphatase reaction (Eq. 19) were assumed the same as for Eq. 2. This two-cycle cascade was studied using stochastic kinetic simulation as described for the single cycle. The stochastic rate constants and initial conditions used to study the two-cycle cascade are described in Results.
RESULTS
Bistability does not arise from the network itself
The bistability analysis theorem of Craciun et al. (15) may be applied to the PdPC system described above both with and without the noise-supplying reactions of Eqs. 5 and 6 based on Fig. 1. For the simplest system of Eqs. 1 and 2, analysis of species-reaction graph reveals bistability that may not arise from the mass-action (deterministic) differential equations, because each cycle is a one-cycle, fulfilling the first requirement of the theorem, and no complex-pair is split by two even cycles, fulfilling the second requirement. Since both conditions are met, bistability cannot arise from mass-action differential equations. The application of Craciun's theorem is similar to a recent analysis by Angeli and Sontag (25) of enzymatic futile cycles. Using a deterministic approach and relevant conservation equations, they found that an enzymatic futile cycle converges to a unique steady state. Analysis of the deterministic PdPC from a variety of contexts as demonstrated by Samoilov et al. (12), Craciun's theorem (15), and Angeli (25) leads one to conclude that the deterministically modeled enzymatic cycle cannot exhibit multiple steady states.
FIGURE 1.
Species-reaction graph for Eqs. 1 and 2 following Craciun et al. (15). The boxes are reaction nodes and the circles are species nodes. Arcs connect the nodes and are labeled by the associated complex. When Eqs. 5 and 6 are also considered, the shaded nodes are added to the graph. Analysis of the species-reaction graphs is explained in the text and indicates that differential equations cannot give rise to bistable behavior from either system.
To simulate the noisy input of E1, Samoilov et al. (12) added reactions described by Eqs. 5 and 6. To address the question of whether multiple steady-states are possible in a deterministic system, we constructed the species-reaction graph of Fig. 1. In this case, the added reactions introduce three new cycles. Two of those are not one-cycles and are even-cycles. Thus, the first condition of the theorem is violated and the theorem falls silent. Further analysis with the Chemical Reaction Network Toolbox (18) reveals that this system has a deficiency of two. However, application of advanced deficiency theory (21) shows that it cannot admit multiple steady states. Thus, the bistability observed in the simulations of Samoilov et al. (12) are related to the stochastic nature of the system. Having verified that the bistability is induced by the stochastic external noise itself, we proceed to the response of the stochastically modeled cycle to changes in sensitivity parameters of Qian (17).
Reversibility removes the bistability
To investigate the effects of thermodynamic driving force on the PdPC system, the reaction network (Eqs. 1, 2, 5, and 6) was simulated using Gillespie's algorithm (23) at different values of γ. Parameter values and initial conditions for these simulations are given in Tables 1 and 2. The parameter c−2 was varied to control γ. Values are given in Table 3. These parameters corresponded to μ = 10−7 and 〈θ1〉 ≈ 0.0612. Steady-state probability distributions of the number of molecules were obtained from 100 repeated simulations.
TABLE 1.
The stochastic parameters used to model the enzymatic cycle (unless otherwise stated)
| Reaction | Forward | Reverse |
|---|---|---|
| 1 | 40 mol−1 s−1 | 10,000 s−1 |
| 2 | 10,000 s−1 | 0.004 mol−1 s−1 |
| 3 | 200 mol−1 s−1 | 100 s−1 |
| 4 | 5000 s−1 | 0.001 mol−1 s−1 |
| 5 | 10 mol−1 s−1 | 5 mol−1 s−1 |
| 6 | 10 s−1 | 0.2 s−1 |
TABLE 2.
The initial conditions for the enzymatic cycle (unless otherwise stated)
| Species | Value |
|---|---|
| E1 | 20 |
| E2 | 50 |
| W | 0 |
| W* | 2000 |
| WE1 | 0 |
| WE2 | 0 |
| N | 10 |
TABLE 3.
| Simulation | c−2 mol−1 s−1 | γ |
|---|---|---|
| A | 4 × 10−3 | 1011 |
| B | 4 × 10−1 | 109 |
| C | 4 × 101 | 107 |
| D | 4 × 103 | 105 |
| E | 4 × 105 | 103 |
| F | 4 × 107 | 101 |
| G | 4 × 108 | 100 |
The predicted distributions for W* and 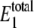 at different values of γ are shown in Fig. 2. For values of γ of ∼107 (set C) and below, the observed bistability disappears. For values of γ of ∼109 and above (sets A and B), the predictions converge. The distribution of
at different values of γ are shown in Fig. 2. For values of γ of ∼107 (set C) and below, the observed bistability disappears. For values of γ of ∼109 and above (sets A and B), the predictions converge. The distribution of 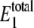 shows that the level stays at ∼20–30 molecules, regardless of the value of γ. Samoilov et al. (12) predicted the bistability for these rate constants when
shows that the level stays at ∼20–30 molecules, regardless of the value of γ. Samoilov et al. (12) predicted the bistability for these rate constants when 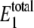 is in this range, which is the case for all values of γ in Fig. 2. These results suggest that the noise-induced bistability is dependent on a relatively high thermodynamic driving force. Interestingly, a phosphorylation potential of −60 kJoule · mol−1 corresponds to γ ≈ 1010. If the thermodynamic driving force drops significantly below this level, it no longer supports bistability. Hypothetical general relationships between thermodynamic driving force and bistability have been discussed previously (26).
is in this range, which is the case for all values of γ in Fig. 2. These results suggest that the noise-induced bistability is dependent on a relatively high thermodynamic driving force. Interestingly, a phosphorylation potential of −60 kJoule · mol−1 corresponds to γ ≈ 1010. If the thermodynamic driving force drops significantly below this level, it no longer supports bistability. Hypothetical general relationships between thermodynamic driving force and bistability have been discussed previously (26).
FIGURE 2.
Steady-state probability distribution of W* and 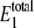 for varying values of γ using the single enzymatic cycle. The noise induces a bistability in W* at large values of γ, but this disappears with a fully reversible case as γ decreases. Selected distributions labeled with letters correspond to system parameters in Table 3. The average value of
for varying values of γ using the single enzymatic cycle. The noise induces a bistability in W* at large values of γ, but this disappears with a fully reversible case as γ decreases. Selected distributions labeled with letters correspond to system parameters in Table 3. The average value of 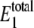 always stays between 20 and 30 molecules.
always stays between 20 and 30 molecules.
Sensitivity analysis near irreversibility
The role of the control parameter, θ1, on the cycle sensitivity was examined at constant γ = 1011 and μ = 10−7, by varying  Predicted probability distributions of
Predicted probability distributions of 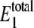 and W* for several different values of
and W* for several different values of  are shown in Fig. 3. Each curve in the figure corresponds to different values of
are shown in Fig. 3. Each curve in the figure corresponds to different values of  as indicated in Table 4. The predicted values of
as indicated in Table 4. The predicted values of 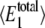 and 〈θ1〉 from each of the simulations are listed in Table 4 as well. Here we see that the distribution of
and 〈θ1〉 from each of the simulations are listed in Table 4 as well. Here we see that the distribution of  is more sensitive to 〈θ1〉 than to γ. The probability distribution of W* is found to exhibit bistable behavior for intermediate values of 〈θ1〉 (ranging from 0.0569 to 0.0912), but the extremes (sets A, J, K, and L) show only a single peak in the probability distribution.
is more sensitive to 〈θ1〉 than to γ. The probability distribution of W* is found to exhibit bistable behavior for intermediate values of 〈θ1〉 (ranging from 0.0569 to 0.0912), but the extremes (sets A, J, K, and L) show only a single peak in the probability distribution.
FIGURE 3.
Steady-state probability distribution of W* and 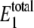 for varying values of 〈θ1〉 for the single enzymatic cycle. The noise induces a bistability only for intermediate values of 〈θ1〉. The inset shows the intermediate values of θ1, some of which exhibit bimodal distributions. Selected distributions labeled with letters correspond to system parameters in Table 4. The average value of
for varying values of 〈θ1〉 for the single enzymatic cycle. The noise induces a bistability only for intermediate values of 〈θ1〉. The inset shows the intermediate values of θ1, some of which exhibit bimodal distributions. Selected distributions labeled with letters correspond to system parameters in Table 4. The average value of 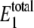 lies outside the range of 20–30 molecules when 〈θ1〉 increases.
lies outside the range of 20–30 molecules when 〈θ1〉 increases.
TABLE 4.
The number of enzyme molecules (E2) used to change  and 〈θ1〉; all other parameters are the same as in Tables 1 and 2
and 〈θ1〉; all other parameters are the same as in Tables 1 and 2
| Simulation | 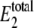 |
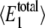 |
〈θ1〉 |
|---|---|---|---|
| A | 68 | 28.55 | 0.0428 |
| B | 51 | 28.46 | 0.0569 |
| C | 40 | 26.82 | 0.0684 |
| D | 34 | 24.94 | 0.0748 |
| E | 32 | 24.37 | 0.0777 |
| F | 31 | 24.02 | 0.0790 |
| G | 29 | 23.42 | 0.0824 |
| H | 27 | 22.86 | 0.0864 |
| I | 25 | 22.35 | 0.0912 |
| J | 22 | 21.55 | 0.0999 |
| K | 12 | 19.04 | 0.1618 |
| L | 2 | 16.55 | 0.8441 |
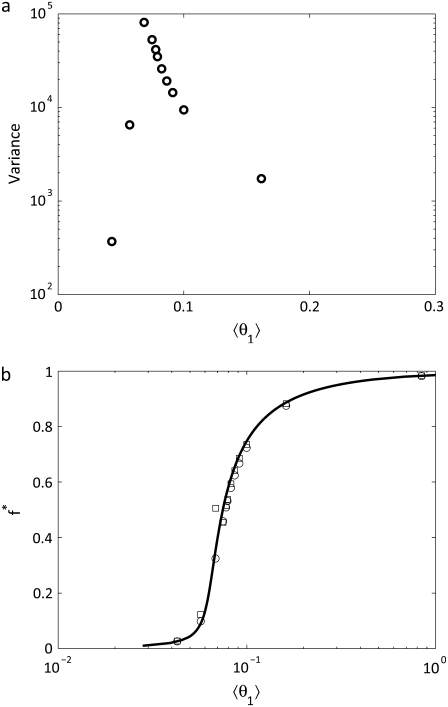
The variance of W* is plotted as a function of 〈θ1〉 in Fig. 4 A. Here there is a peak at 〈θ1〉 = 0.0684, which corresponds to f* ≈ 0.3. Fig. 4 B plots the response function f* as a function of 〈θ1〉. Here we see that the average value follows the response of Eq. 14, even if the mode (maximum of the probability distribution) does not. In some cases the mode and the average are quite different. This result highlights the likelihood of a cycle achieving states significantly different from the mean state and highlights the necessity of knowing the full probability distribution in understanding the response to changes in signal when the numbers of molecules are small. Gómez-Uribe and Verghese (27) and Goutsias (28) have introduced methods to capture stochastic chemical kinetics without direct Monte Carlo simulation employed here. While these methods can be powerful in describing the mean and variance of chemical species, they cannot reproduce the full probability distribution. The stochastic simulations employed in this work provide insight not available from deterministic methods, since only the direct stochastic simulation provides estimates of the fluctuations and associated probability distributions.
FIGURE 4.
(a) The variance of W* for the single enzymatic cycle as a function of 〈θ1〉. A maximum in the enzymatic cycle is found at 〈θ1〉 = 0.0684 which corresponds to f* ≈ 0.3. (b) The response of f* to as a function of 〈θ1〉 for the single enzymatic cycle at γ = 1011 and μ = 10−7. The solid line is the solution to Eq. 14, the circles are the average value, and the squares are the location of the maximum in the probability distribution.
Two-cycle cascade with and without noise
The two-cycle cascade was modeled both with and without the noise equations using irreversible cycles as described above. The resulting probability distributions are shown in Fig. 5. The parameter values for the stochastic simulations with noise are given in Tables 5 and 6. Stochastic simulations with noise predicted the average number of enzyme molecules to be  given the parameter values used. To directly compare the two probability distributions,
given the parameter values used. To directly compare the two probability distributions, 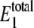 was set to 28 for the stochastic simulations without noise. It is determined that W* shows bistability but X* does not for the given set of parameter values, indicating that the effect is not necessarily transmitted through a cascade. Interestingly, the mean values for W* with and without the noise input were close (1700 with noise and 1735 without noise reactions) while the mean values of X* were closer (1850 with noise and 1853 without). However, both W* and X* are significantly influenced by the noise, since the probability distributions of the two cases are not the same. Samoilov and Arkin (13) speculate that the noise-induced bistability could be utilized downstream for further signal transduction. Next, we determine if parameter values exist for which this can occur.
was set to 28 for the stochastic simulations without noise. It is determined that W* shows bistability but X* does not for the given set of parameter values, indicating that the effect is not necessarily transmitted through a cascade. Interestingly, the mean values for W* with and without the noise input were close (1700 with noise and 1735 without noise reactions) while the mean values of X* were closer (1850 with noise and 1853 without). However, both W* and X* are significantly influenced by the noise, since the probability distributions of the two cases are not the same. Samoilov and Arkin (13) speculate that the noise-induced bistability could be utilized downstream for further signal transduction. Next, we determine if parameter values exist for which this can occur.
FIGURE 5.
The probability distribution of W* and X* from a simulation of a two-cycle cascade. Shown are distributions with (dotted line) and without (solid line) the noise reactions and with rate constants such that γ = ∞.
TABLE 5.
The stochastic parameters used to model the enzymatic cascade
| Reaction | Forward | Reverse |
|---|---|---|
| 1 | 40 mol−1 s−1 | 10,000 s−1 |
| 2 | 10,000 s−1 | 0 mol−1 s−1 |
| 3 | 200 mol−1 s−1 | 100 s−1 |
| 4 | 5000 s−1 | 0 mol−1 s−1 |
| 5 | 10 mol−1 s−1 | 5 mol−1 s−1 |
| 6 | 10 s−1 | 0.2 s−1 |
| 7 | 40 mol−1 s−1 | 10,000 s−1 |
| 8 | 10,000 s−1 | 0 mol−1 s−1 |
| 9 | 200 mol−1 s−1 | 100 s−1 |
| 10 | 5000 s−1 | 0 mol−1 s−1 |
TABLE 6.
The initial conditions for the enzymatic cascade
| Species | Value |
|---|---|
| E1 | 20 |
| E2 | 50 |
| W | 0 |
| W* | 2000 |
| WE1 | 0 |
| WE2 | 0 |
| N | 10 |
| E3 | 50 |
| X | 0 |
| X* | 2000 |
| XW* | 0 |
| X*E3 | 0 |
Tuning of the two-cycle cascade
To investigate the cascade more systematically, the level of E3, the phosphatase of the second PdPC in the cascade, was varied using the irreversible (γ = ∞) and external noise reactions, thereby changing the control parameter of the second cycle, 〈θ2〉, without having much impact on the control parameter of the first cycle. (For the parameter values used, 〈θ1〉 ≈ 0.06 with a standard deviation of <10%.)
The initial values of E3 used to vary 〈θ2〉 are listed in Table 7. The corresponding predicted probability distributions of W* and X* are shown in Fig. 6. There is little effect of varying E3 on the distribution of W*, but there is a large change in the distribution of X* as E3 increases. At lower values of E3, the distribution of X* has a long shoulder and a single peak. At larger values of E3, the distribution of X* has two peaks. To quantify this effect θ2 is computed, analogous to Eq. 17,
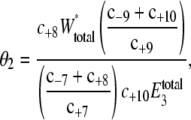 |
(20) |
where W*total = W* + XW* and 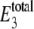 = E3 + X*E3. The ultrasensitivity relationship between θ1 and f* of Eq. 14 assumes that enzyme concentrations are small compared to the substrate. As noted in the original Goldbeter-Koshland analysis (14), when the ratio of enzyme to substrate becomes large (> 0.1), a revised relationship leads to a third-order polynomial equation
= E3 + X*E3. The ultrasensitivity relationship between θ1 and f* of Eq. 14 assumes that enzyme concentrations are small compared to the substrate. As noted in the original Goldbeter-Koshland analysis (14), when the ratio of enzyme to substrate becomes large (> 0.1), a revised relationship leads to a third-order polynomial equation
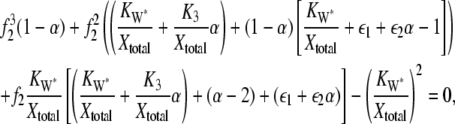 |
(21) |
where f2=X/Xtotal, Xtotal=X+X*+X*E3+XW*, ε1= W*total/Xtotal, ε2 = E3total/Xtotal,  and
and 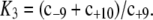 The relationship between f2 and f2* is given by
The relationship between f2 and f2* is given by
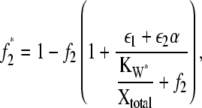 |
(22) |
where f2* = X*/Xtotal. Similar expressions exist for X*E3 and XW*. It was valid to compare the behavior of θ1 and f* to that predicted by Eq. 14 in Fig. 4 because for that case the ratio of enzyme to substrate was ≤0.01. Since for the second cycle of the cascade considered here the ratio ranges from 0.05 to 0.4, Eqs. 21 and 22 provide the appropriate deterministic model predictions for comparison to the stochastic behavior.
TABLE 7.
The number of enzyme molecules (E3) used to vary 〈θ2〉; all other parameters are the same as in Tables 5 and 6
| Simulation | 〈E3〉 | 〈W*total〉 | 〈θ2〉 |
|---|---|---|---|
| A | 100 | 257 | 0.2621 |
| B | 150 | 272 | 0.1854 |
| C | 200 | 292 | 0.1489 |
| D | 250 | 312 | 0.1272 |
| E | 300 | 326 | 0.1108 |
| F | 350 | 346 | 0.1007 |
| G | 400 | 360 | 0.0916 |
| H | 450 | 378 | 0.0857 |
| I | 500 | 388 | 0.0792 |
| J | 550 | 398 | 0.0737 |
| K | 600 | 403 | 0.0686 |
| L | 800 | 426 | 0.0543 |
FIGURE 6.
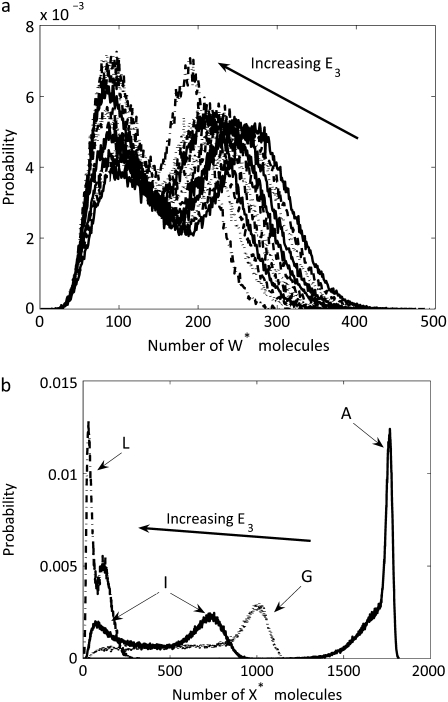
Steady-state probability distribution of W* and X* for the two-cycle cascade (with noise reactions) at various values of E3. As E3 increases, the bistability is maintained for W*. For X*, the distribution is bimodal only after E3 increases beyond a certain level. Selected distributions labeled with letters correspond to system parameters in Table 7.
There are some similarities between the behavior of the two-cycle cascade in Fig. 6 and that of the single-cycle results of Fig. 3. For the single-cycle system, as 〈θ1〉 increases, the two-peaked distribution disappears. This also occurs for the two-cycle system: as 〈θ2〉 is increased (by decreasing E3), the two-peaked distribution disappears. Relatively broad distributions of X* are obtained for the intermediate values of E3 (and correspondingly 〈θ2〉) used here. As the phosphatase level increases, the number of X* molecules decreases. Bistability in X* is apparent for values of E3 of ∼450 (set H) and higher.
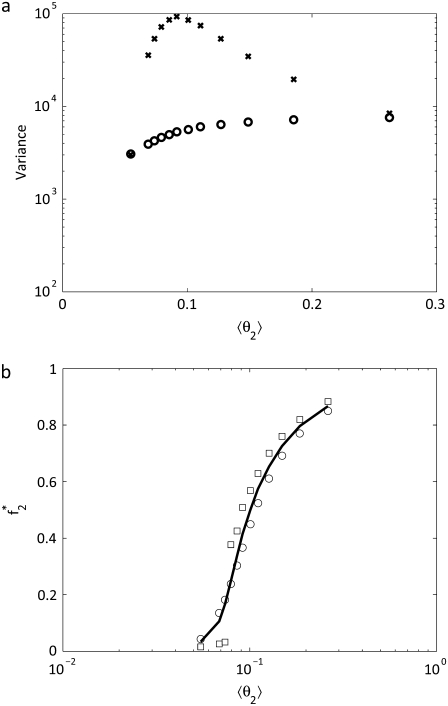
The relationship between f2* and 〈θ2〉 is plotted in Fig. 7 B. Comparing the fraction of X phosphorylated as a function of 〈θ2〉 to deterministic results predicted by Eqs. 21 and 22, we find that the stochastic result deviates slightly from the analytical expression obtained from steady-state analysis of the deterministic kinetic equations.
FIGURE 7.
(a) The variance of W* (circles) and X* (x-symbols) in a two-cycle cascade for different values of 〈θ2〉. The variance of W* is fairly constant while X* has a peak for intermediate values of 〈θ2〉. (b) The sensitivity of the second cycle in the cascade is shown by plotting f2* to different values of 〈θ2〉. The solid line is the solution to Eqs. 21 and 22, the circles are the average value, and the squares are the location of the maximum in the probability distribution.
The predicted variances of W* and X* for the two-cycle cascade are plotted in Fig. 7 A. Here the variance of W* is fairly constant over the values of 〈θ2〉 since the control parameter 〈θ1〉 remains fairly constant in these simulations. However the variance in X* has a maximum 〈θ2〉 ≈ 0.09 (which corresponds to f2* ≈ 0.35). The maximum in the variance of X* corresponds to the bistability and associated broad probability distribution observed for the value of E3 (= 400) at which the 〈θ2〉 ≈ 0.09.
Thus, in a certain range of parameter values, the two-cycle cascade can transfer bistability along the cascade. It is also possible to minimize the signal variance and even abolish the bistability. It is unknown whether either or both of these situations occurs in cells. It is also unclear whether the bistability in the two-cycle cascade occurs because of the external or internal noise. A broader exploration of the system parameters would be needed to evaluate this possibility. Our results suggest that the external noise is necessary for bistability in the cascade for the parameters examined here, but having not examined the full range of possibilities, we cannot eliminate the idea that other parameter sets could give rise to bistability even without the external noise reactions.
DISCUSSION
We have examined noise-induced bistability and sensitivity in phosphorylation-dephosphorylation cycles (PdPCs) and cascades, and the impact of reversibility and thermodynamic driving force on their operation. Using the bistability analysis theorem of Craciun et al. (15), it was shown that the reaction systems studied here cannot admit multiple steady states based on deterministic kinetics. Furthermore, it was shown that the bistability exists only when the system is driven by external noise and the enzymatic cycle operates far from metabolic equilibrium. In living cells, PdPCs are driven by ATP hydrolysis and thus may operate far from equilibrium. At relatively low levels of the ATP hydrolysis potential, the PdPC does not exhibit bistability. It was also shown that the average behavior of the single cycle obeys the sensitivity relationship between phosphorylation level and the control parameter predicted by steady-state analysis of the deterministic kinetic equations. However, the deterministic kinetic equations cannot reveal detailed information about the probability distribution of phosphorylation level and associated fluctuations. Under appropriate conditions (with external noise and at intermediate values of the control parameter), the probability distribution is bimodal. In this case, near the inflection of the system response to the control parameter, there exists large variability in the number of phosphorylated molecules.
Examining the role of noise in a two-cycle cascade, we find that the second substrate may or may not exhibit a noise-induced bistable steady state, although here it does alter the shape of the molecule distribution in either case. While we have shown that tuning of the cycles (by varying the phosphatase enzyme level) can maximize or minimize the variance in output of the cascade, a more complete analysis of the two-cycle cascade is needed to fully explore the parameters and conditions that control the responses of cascades. We find that the expected value of the single-cycle system obeys the ultrasensitive response predicted from steady-state analysis of the deterministic system while the two-cycle system begins to deviate. In the two-cycle case, the first cycle provides a noisy input to the second cycle.
A great deal remains to be learned about the role of multiple steps in signaling cascades. While full stochastic simulation using the Gillespie algorithm (23) is a critical tool for analyzing such systems, its expense become prohibitive for large networks. Therefore, powerful approximate methods (27,28) are expected to become increasingly useful for these applications.
Acknowledgments
This work was supported in part by National Institutes of Health grant No. GM068610.
Editor: Herbert Levine.
References
- 1.Swain, P. S., M. B. Elowitz, and E. D. Siggia. 2002. Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc. Natl. Acad. Sci. USA. 99:12795–12800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Süel, G. M., R. P. Kulkarni, J. Dworkin, J. Garcia-Ojalvo, and M. B. Elowitz. 2007. Tunability and noise dependence in differentiation dynamics. Science. 315:1716–1719. [DOI] [PubMed] [Google Scholar]
- 3.Lestas, I., J. Paulsson, N. E. Ross, and G. Vinnicombe. 2008. Noise in gene regulatory networks. IEEE Trans. Automat. Contr. 53:189–200. [Google Scholar]
- 4.Paulsson, J. 2004. Summing up the noise in gene networks. Nature. 427:415–418. [DOI] [PubMed] [Google Scholar]
- 5.Chickarmane, V., B. N. Kholodenko, and H. M. Sauro. 2007. Oscillatory dynamics arising from competitive inhibition and multisite phosphorylation. J. Theor. Biol. 244:68–76. [DOI] [PubMed] [Google Scholar]
- 6.Wang, X., N. Hao, H. G. Dohlman, and T. C. Elstonz. 2006. Bistability, stochasticity, and oscillations in the mitogen-activated protein kinase cascade. Biophys. J. 90:1961–1978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Morishita, Y., T. J. Kobayashi, and K. Aihara. 2006. An optimal number of molecules for signal amplification and discrimination in a chemical cascade. Biophys. J. 91:2072–2081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shibata, T., and K. Fujimoto. 2005. Noisy signal amplification in ultrasensitive signal transduction. Proc. Natl. Acad. Sci. USA. 102:331–336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Thattai, M., and A. van Oudenaarden. 2002. Attenuation of noise in ultrasensitive signaling cascades. Biophys. J. 82:2943–2950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Levine, J., H. Y. Kueh, and L. Mirny. 2007. Intrinsic fluctuations, robustness, and tunability in signaling cycles. Biophys. J. 92:4473–4481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Berg, O. G., J. Paulsson, and M. Ehrenberg. 2000. Fluctuations and quality of control in biological cells: zero-order ultrasensitivity reinvestigated. Biophys. J. 79:1228–1236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Samoilov, M., S. Plyasunov, and A. P. Arkin. 2005. Stochastic amplification and signaling in enzymatic futile cycles through noise-induced bistability with oscillations. Proc. Natl. Acad. Sci. USA. 102:2310–2315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Samoilov, M. S., and A. P. Arkin. 2006. Deviant effects in molecular reaction pathways. Nat. Biotechnol. 24:1235–1240. [DOI] [PubMed] [Google Scholar]
- 14.Goldbeter, A., and D. E. Koshland, Jr. 1981. An amplified sensitivity arising from covalent modification in biological systems. Proc. Natl. Acad. Sci. USA. 78:6840–6844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Craciun, G., Y. Tang, and M. Feinberg. 2006. Understanding bistability in complex enzyme-driven reaction networks. Proc. Natl. Acad. Sci. USA. 103:8697–8702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Artyomov, M. N., J. Das, M. Kardar, and A. K. Chakraborty. 2007. Purely stochastic binary decisions in cell signaling models without underlying deterministic bistabilities. Proc. Natl. Acad. Sci. USA. 104:18958–18963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Qian, H. 2003. Thermodynamic and kinetic analysis of sensitivity amplification in biological signal transduction. Biophys. Chem. 105:585–593. [DOI] [PubMed] [Google Scholar]
- 18.Feinberg, M., and P. Ellison. 1998. The Chemical Reaction Network Toolbox Ver. 1.1. Ohio State University, Columbus, OH. http://www.chbmeng.ohio-state.edu/feinberg/crnt.
- 19.Feinberg, M. 1987. Chemical reaction network structure and the stability of complex isothermal reactors. I. The deficiency zero and deficiency one theorems. Chem. Eng. Sci. 42:2229–2268. [Google Scholar]
- 20.Feinberg, M. 1988. Chemical reaction network structure and the stability of complex isothermal reactors. II: Multiple steady states for networks of deficiency one. Chem. Eng. Sci. 43:1–25. [Google Scholar]
- 21.Ellison, P., and M. Feinberg. 2000. How catalytic mechanisms reveal themselves in multiple steady-state data: I. Basic principles. J. Mol. Catal. Chem. 154:155–167. [Google Scholar]
- 22.Beard, D. A., and H. Qian. 2008. Biochemical signaling modules. In Chemical Biophysics: Quantitative Analysis of Cellular Systems. Cambridge University Press, Cambridge, UK.
- 23.Gillespie, D. T. 1977. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81:2340–2361. [Google Scholar]
- 24.Kierzek, A. M. 2002. STOCKS: STOChastic Kinetic Simulations of biochemical systems with Gillespie algorithm. Bioinformatics. 18:470–481. [DOI] [PubMed] [Google Scholar]
- 25.Angeli, D., and E. D. Sontag. 2008. Translation-invariant monotone systems, and a global convergence result for enzymatic futile cycles. Nonlinear Anal. Real World Appl. 9:128–140. [Google Scholar]
- 26.Qian, H. 2007. Phosphorylation energy hypothesis: open chemical systems and their biological functions. Annu. Rev. Phys. Chem. 58:113–142. [DOI] [PubMed] [Google Scholar]
- 27.Gómez-Uribe, C. A., and G. C. Verghese. 2007. Mass fluctuation kinetics: capturing stochastic effects in systems of chemical reactions through coupled mean-variance computations. J. Chem. Phys. 126:024109. [DOI] [PubMed] [Google Scholar]
- 28.Goutsias, J. 2007. Classical versus stochastic kinetics modeling of biochemical reaction systems. Biophys. J. 92:2350–2365. [DOI] [PMC free article] [PubMed] [Google Scholar]