Lipid Bilayer Structure Determined by the Simultaneous Analysis of Neutron and X-Ray Scattering Data

Abstract

Quantitative structures were obtained for the fully hydrated fluid phases of dioleoylphosphatidylcholine (DOPC) and dipalmitoylphosphatidylcholine (DPPC) bilayers by simultaneously analyzing x-ray and neutron scattering data. The neutron data for DOPC included two solvent contrasts, 50% and 100% D₂O. For DPPC, additional contrast data were obtained with deuterated analogs DPPC_d62, DPPC_d13, and DPPC_d9. For the analysis, we developed a model that is based on volume probability distributions and their spatial conservation. The model's design was guided and tested by a DOPC molecular dynamics simulation. The model consistently captures the salient features found in both electron and neutron scattering density profiles. A key result of the analysis is the molecular surface area, A. For DPPC at 50°C A = 63.0 Ų, whereas for DOPC at 30°C A = 67.4 Ų, with estimated uncertainties of 1 Ų. Although A for DPPC agrees with a recently reported value obtained solely from the analysis of x-ray scattering data, A for DOPC is almost 10% smaller. This improved method for determining lipid areas helps to reconcile long-standing differences in the values of lipid areas obtained from stand-alone x-ray and neutron scattering experiments and poses new challenges for molecular dynamics simulations.

INTRODUCTION

Biological function is intrinsically linked to membrane structure. The structural basis of biomembranes arises from fluid phase lipid bilayers with almost liquid-like conformational degrees of freedom, so that the structure is best described by broad statistical distributions rather than the sharp δ-functions typical of crystals (1). Due to the intrinsic disorder, which is most likely important for proper biological function, average structural information, which is valuable for understanding lipid-protein interactions and their functions (2), is not easily obtainable, especially in the biologically relevant fully hydrated state.

Neutron and x-ray scattering techniques have over the years been widely used in areas of structural biology, biophysics, and materials science (3,4). Although partially dehydrated samples lend themselves to traditional diffraction methods (5,6), the same cannot be said of fully hydrated, intrinsically disordered samples (1). However, in recent years a new diffraction method has taken advantage of the continuous diffuse scattering produced by undulating bilayers in the disordered liquid crystalline state (7,8). Instead of evaluating discrete Bragg diffraction peaks, commonly observed when studying highly positionally correlated material, this method utilizes the continuous scattering taking place over a range of mid to high scattering vectors (i.e., 0.2 Å⁻¹ < q < 0.8 Å⁻¹). Complementing these data, diffuse scattering from spherically isotropic, fully hydrated, unilamellar vesicles (ULVs) has been obtained to extend the low q range to 0.05 Å⁻¹, and a global combined analysis has been applied to x-ray data sets from both oriented multilayers and ULVs (9).

By increasing the amount and quality of data, these advances in experimental techniques have stimulated the development of more realistic models of membranes. A variety of structural models for scattering density profiles (SDPs) have been applied to membranes ranging from the simplest slab/box models to models dividing an individual lipid molecule into several component groups (10–13). With additional information made available from other experiments and/or results from simulations, model-based analysis then obtains values of parameters corresponding to various structural features. One of the most important parameters needed to accurately describe bilayer structure and lipid-lipid and lipid-protein interactions in biomembranes is the lipid's lateral area, A. In addition to playing a key role in describing membrane structure and its associated functions, knowledge of lateral lipid area is central to simulations (13). Molecular dynamics (MD) force fields are considered to be “well tuned” if they are able to reproduce experimental data; but recent studies suggest that the force fields, however carefully determined, may result in poor agreement with experiment when simulations are performed at the ideal zero surface tension condition (14). An alternative approach is to carry out simulations at constant, but nonzero tension or, equivalently, at a fixed surface area (13). However, the question then becomes, what value should the area/lipid be fixed to?

Despite their central role in membrane biophysics, values of lateral areas for lipid molecules had been very uncertain—although the largest discrepancies have been removed (1). Significant differences still remain when comparing lipid areas determined from x-ray and neutron scattering experiments (15). In both cases lipid area is calculated from bilayer thickness and volumetric information, but the two techniques focus on different thicknesses. The thickness best resolved by x-rays is the distance between the peaks in the electron density (ED) profile, which corresponds to the distance between lipid headgroups (phosphates), D_HH. The strategy to obtain the hydrocarbon chain thickness, which is necessary to determine lipid area, has been based on the distance from the phosphate to the interface of the hydrocarbon region, D_H1 (9). It was assumed that D_H1 is the same as for gel phase bilayers (16), which would follow if the headgroups are in the same orientation as those in the fluid phase. The uncertainties associated with D_H1 have previously been shown (13) to be the largest cause of error in the determination of A. On the other hand, in neutron scattering, the high contrast between protonated lipid and deuterated water defines the overall Luzzati thickness of the bilayer, D_B, from which A can be obtained directly from the accurately measured lipid volume, V_L (1).

Even though they are the two most robust experimentally determined parameters, D_HH and D_B cannot be compared directly and neither provides all the desired information about bilayer structure. Instead, models are used to determine the remaining structural parameters, where better parameter determination should ensue when more data are included. Simultaneous analysis of x-ray and neutron scattering data then allows either the inclusion of more features or better determination of those features. Additionally, it helps to minimize the number of plausible solutions, as has been noted for proteins structures in solution (17). An approach employing the joint refinement of x-ray and neutron data was previously applied to partially hydrated bilayers (12). The composition-space model proposed by the authors (18) was composed of 10 quasimolecular fragments requiring a total of 30 parameters. Although the number of parameters was eventually reduced to 16 by utilizing structural information made available from other experiments, these studies illustrated the challenges faced by the diffraction method.

Here we take a different approach for fully hydrated lipid bilayers. We begin with MD simulations that we then convert into ED and neutron scattering length density (NSLD) profiles. These profiles help with the nontrivial aspect of parsing a lipid molecule into components whose probability distributions apply to both ED and NSLD profiles. However, the underlying description is based on volume probability distributions, to which we apply the principle of spatial conservation. The robustness of the model and its associated parameters are then tested using F(q) data obtained from the MD simulation to see how well it recovers the known values of the structural parameters that are hidden in the simulated data in the same way as they are hidden in real data. After successfully testing the model using the simulated data, we use it to analyze two much studied lipid bilayers, namely liquid crystalline dipalmitoylphosphatidylcholine (DPPC) and dioleoylphosphatidylcholine (DOPC) bilayers. We emphasize that, although the design of our model is based on a simulation, in the analysis of real data the critical parameters, such as area, thickness, and width of the probability distributions, are free to fit the experimental data. In other words, the model only assumes the functional forms of the probability distributions, which are obtained from simulations and do not vary much with the detailed simulation. Our analysis does not assume numerical values of those parameters that can and should be different for different lipid bilayers.

MATERIALS AND METHODS

Synthetic 1,2-dioleoyl-sn-glycero-3-phosphatidylcholine (DOPC), 1,2-dipalmitoyl-sn-glycero-3-phosphatidylcholine (DPPC), 1,2-dipalmitoyl-D62-sn-glycero-3-phosphatidylcholine (DPPC_d62), 1,2-dipalmitoyl-sn-glycero-3-phosphocholine-N,N,N-trimethyl-D9 (DPPC_d9), and 1,2-dipalmitoyl-sn-glycero-3-phosphocholine-1,1,2,2-D4-N,N,N-trimethyl-D9 (DPPC_d13) were purchased from Avanti Polar Lipids (Alabaster, AL) and used without further purification. Oriented stacks of ∼1500 bilayers were prepared following the rock-and-roll method (16), and 600-Å-diameter ULVs were prepared according to Kučerka et al. (19). Samples used in neutron contrast variation (CV) experiments were first dispersed in D₂O and then, after extrusion, diluted with 18 MΩ-cm water (Millipore, Bedford, MA) or D₂O to produce the two external contrast conditions (i.e., 100% and 50% D₂O). The total lipid concentration for all ULV samples was ∼20 mg/ml.

Small-angle x-ray scattering

X-ray data were taken at the Cornell High Energy Synchrotron Source (CHESS) D-1 station. We selected 1.18 Å wavelength (λ) x-rays using multilayer monochromators (Osmic, Detroit, MI; Advanced Photon Source, Chicago, IL) having an energy dispersion of 1.5% (full width at half-maximum; FWHM). Scattered x-rays were collected using a 1024 × 1024 pixel array Medoptics charge-coupled device, with 47.19 μm linear dimension pixels. Images were corrected using calibration files supplied by CHESS. Every data set was normalized using the incident beam intensity measured through a semitransparent beam stop made of a 225-μm-thick molybdenum foil. In the case of ULV samples, background resulting from water was subtracted according to the procedure described in Kučerka et al. (19). Full q range scattering curves were obtained by combining the scattering form factors from ULV and oriented samples, as was previously done in Kučerka et al. (9). The excellent agreement between ULV and oriented bilayer data in the overlapping regions confirms the same bilayer structure for both sample preparations.

Small-angle neutron scattering

Neutron scattering data were taken at the NG-7 station (20) located at the National Institute of Standards and Technology (NIST) Center for Neutron Research. We selected 6 Å wavelength neutrons using a mechanical velocity selector, with an energy dispersion of 11% (FWHM). Three sample-to-detector distances (i.e., 1.3, 4, and 13.2 m) were used, resulting in a total scattering vector (q = 4π/λ sin(θ/2), where λ is the wavelength and θ is the scattering angle) of 0.003 < q < 0.3 Å⁻¹. Data were collected using a 640 mm × 640 mm two-dimensional ³He position-sensitive detector with a 5 mm × 5 mm resolution. Samples were taken up in standard, 1 mm path length quartz cylindrical, or so-called banjo, cells. Collected images were corrected using software supplied by NIST (21).

Experimental form factors F(q) were obtained from the measured scattering intensities I(q) for both neutrons and x-rays using

(1)

where P_LC(q) is the Lorentz correction and is equal to q for oriented bilayers and q² for ULVs, whereas P_TS(q) represents the difference between oriented and ULV bilayers. In the case of oriented bilayers, P_TS(q) is a constant, but in the case of ULVs it describes their “sphericity” and “polydispersity” (22). Despite its complicated form, P_TS in this study is constant over the entire experimental range (i.e., q > 0.03 Å⁻¹, and ULVs with a mean radius of 300 Å and a polydispersity of 75 Å). What this means is that when the Lorentz correction is applied, there should be no difference between the calculated form factors for oriented and spherical bilayers (Supplementary Material, Data S1). Experimentally, we have addressed the differences in structure between oriented and spherical bilayers using both neutron and x-ray scattering in Kučerka et al. (19). No difference between the two was concluded for q > 0.03 Å⁻¹. Consistent with these findings, our data here for ULVs do not show the features characteristic for curvature-induced structural changes, e.g., bilayer asymmetry.

Molecular dynamics simulations

MD simulations were performed using the CHARMM lipid force field version 32 (23). Periodic boundary conditions were applied using a constant number of atoms (N), temperature (T), lateral area (A), and normal pressure (Pn) to form NAPnT ensembles. The simulation temperature was set to 298 K. The system was constructed of 288 lipids, 144 per leaflet, and was hydrated to 32.5 water molecules per lipid. Simulations were run for 20 ns using NAMD, and analysis was performed from 10–20 ns of the simulation trajectory. A cutoff of 10 Å was used for van der Waals interactions (24), and particle mesh Ewald summation was used for electrostatic interactions. The time step was 2 fs, and all bonds involving hydrogens were fixed using the SHAKE algorithm, with a tolerance (relative deviation) of 10⁻⁶ Å. The frequency of regenerating the nonbonded list was set with a heuristic testing algorithm that updates based on the distance each atom moved since the last list update.

Probability distributions as a function of distance z along the bilayer normal were obtained for each atom in a lipid molecule. The NSLDs were obtained by first multiplying each nuclear distribution by the neutron scattering length and then summing over all nuclei. The ED profile was obtained similarly; atomic form factors were not used because atomic widths are negligible compared to the widths of distributions due to thermal disorder (13). The bilayer form factors F(q) as a function of q were obtained by Fourier transforming the ED and the various NSLDs with different isotopic composition.

Structural model of bilayer

For the model to fit the scattering data, it must faithfully represent the total SDP of the bilayer. Although a model that represents each individual atom can certainly be faithful, it would require too many parameters for the available data. As such, parameter parsimony requires the grouping of atoms into component groups. The grouping choice is ruled by the SDP's most distinct features. In the case of x-rays, the features with the most contrast are the electron-dense headgroups, providing the head-head spacing D_HH, as well as the terminal methyl groups in the bilayer center (11,13,25). In the case of neutrons, the greatest contrast is between the fully protonated lipids and deuterated water, resulting in the water distribution function and the overall bilayer thickness D_B. Neutrons are also made sensitive to the various bilayer features by selective deuteration of the lipid and by varying the ratio of D₂O and H₂O in the solvent (6). The challenge to successful modeling is to address all these features simultaneously.

Fig. 1 shows NSLD and ED distributions for a DOPC bilayer obtained from MD simulations. The left side of the figure shows the spatial distributions of the various moieties making up the lipid molecule (e.g., choline, phosphate). In the case of the NSLD profile, there are two additional distributions reflecting a specific choline analog (i.e., d9 and d13 choline). Each distribution shown was calculated by summing the scattering distributions of particular atoms, rather than summing atomic number densities and then multiplying them by the overall scattering density of each component. This way of calculating distributions becomes especially important when there is an anisotropic distribution of atoms with different scattering lengths (e.g., choline), which in the case of neutrons is further amplified by the negative NSLD contribution from hydrogen. For example, the ED distributions in Fig. 1 are nearly symmetric Gaussian functions for localized component groups, consistent with an almost symmetric distribution of electrons. However, NSLD profiles of the fully protonated choline reveal an asymmetric function resulting from the (CH₃)₃ groups in the choline. This distribution then consists of two Gaussian functions, neither of which has the same position as that of the choline's ED. On the other hand, the two deuterated (i.e., DPPC_d9 and DPPC_d13) choline analogs exhibit almost symmetric distributions—the result of eliminating the negative NSLD contributions from hydrogens.

FIGURE 1.

NSLD and ED profiles of a simulated DOPC bilayer versus the distance z along the bilayer normal. The left-hand side of the figure shows the individual lipid moieties (e.g., phosphate, choline, glycerol); the right-hand panel shows the partially combined components, thus reducing the total number of parameters needed for the SDP model. The combined component groups are as follows: carbonyl + glycerol (CG), phosphate+CH₂CH₂N (PCN), and the three CH₃ choline groups (CholCH3). Broken curves represent the partially (d9) and fully (d13) deuterated headgroup components (i.e., CD₂CD₂N and CholCD3). The choice of this combination is driven by the fact that each of the component groups has nearly the same functional form for all the different contrast conditions (e.g., ED of CholCH3 and NSLD of CholCH3 and CholCD3). Broken vertical lines mark the positions of the different groups.

Previous models have divided the lipid bilayer into four or five structural components consisting of the terminal methyl groups, methylene groups (with an occasional separation of a double bond), and the combined carbonyl/glycerol and phosphate/choline groups (10,11,13). However, as described, such models are valid only for fitting x-ray data or neutron data from lipid bilayers with deuterated cholines. For our SDP model, we propose a different combination of the lipidic atoms that should apply equally well to all the experimental data. We find that the most parsimonious, but still adequate, model has three structural components describing the lipid headgroup region, specifically carbonyl and glycerol (CG), phosphate and CH₂CH₂N (PCN), and the three CH₃ groups in the choline (CholCH3). Three additional groups are included in our SDP model to describe the hydrocarbon chain region, i.e., CH₂, CH, and CH₃ groups. Although it was not necessary to have separate distributions for the CH and CH₂ groups for x-ray models (11,13) because the ED of the double-bonded component group is similar to the ED of methylene groups, this is not the case for NSLDs. On the other hand, the terminal methyl “trough” is well resolved in ED profiles, whereas it is negligible in NSLD profiles. Therefore, all these features must be included in a model that aims to simultaneously describe both NSLD and ED profiles.

Although the SDP model is designed to obtain structure from x-ray and neutron scattering data, the primary description is neither in terms of ED nor NSLD. Instead, it is described by volume probability distributions, which should satisfy a spatial conservation principle whereby volume is conserved. For bilayers, the volume of a slab located between coordinate z (normal to the bilayer) and z + Δz must be constant as a function of z. Our implementation of such a principle first assigns the entire volume of the bilayer to the lipid's components and to water. This assignment does not provide for “free volume” and furthermore assumes that the volume of a component group is the same, on average, for different positions z of the component group. It is the same definition as that used for obtaining the volumes of component groups from simulations (26,27). Fig. 2 shows the volume probabilities obtained in this way from the current MD simulations of DOPC. To satisfy spatial conservation rigorously, the probabilities would sum precisely to unity for each value of z. As previously noted (26), the small size of the local deviations from unity that are seen in Fig. 2 supports these assumptions in the assignment of volumes to component groups. Compared to previous models, which had global spatial conservation (28), the new feature in the SDP model is to impose spatial conservation locally. Therefore, the volume probabilities of the component groups in the SDP model sum precisely to unity at each point z along the bilayer normal. In contrast, for models where spatial conservation was not rigorously incorporated, deviations up to ∼15% were required for the fits in Wiener et al. (12) and average deviations of ∼3% were required in Klauda et al. (13).

FIGURE 2.

The solid lines show the volume probability (volume fraction) distributions for the various SDP model components and combination components defined in Fig. 1. The probabilities were calculated from the symmetrized MD number histograms according to the procedure in Petrache et al. (26). The dashed lines show the best fits of SDP model functional forms to the corresponding component group distribution. The vertical dash-dot lines show the Gibbs dividing surface at position D_C for the hydrocarbon region with total thickness 2D_C and at position D_B/2 for water, where D_B is the Luzzati thickness of the entire bilayer. The top panel shows the sum of all probabilities.

Functional forms

In total, the SDP model consists of seven structural subgroups (Fig. 2), the distribution of water molecules (W) being one of them. The volume probability distributions of components CG, PCN, CholCH3, methine (CH), and terminal methyl groups (CH3) are described by Gaussians as follows:

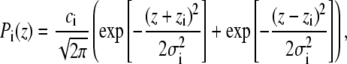(2)

where c_i is an integrated area underneath the curve and the two parts of the expression describe the two bilayer leaflets. The calculation of c_i is explained below.

As was previously shown (13), the hydrocarbon chain region (HC) is well represented using classical error functions

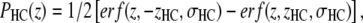(3)

where the error function

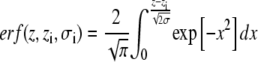(4)

has a step centered at z_i and a width of σ_i. The volume probability distribution for the methylene groups (CH2) can then be expressed as

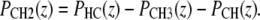(5)

This definition satisfies spatial conservation in the central hydrocarbon region where the total probability P_HC equals one.

Fig. 2 shows the functional forms in the SDP model in comparison to the simulated volume probability distributions. Although most of the components are reasonably well described by simple functional forms in the SDP model, water has clearly a more complex distribution that would require a proliferation of parameters (13). However, when we choose water to be the last group and apply the spatial conservation requirement

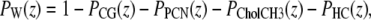(6)

no functional form is required for water. Fig. 2 shows that its ensuing SDP distribution represents the simulation data very well.

The water subtracted total SDP (Δρ) is then calculated as

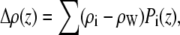(7)

where i = CG, PCN, CholCH3, CH, CH2, CH3. The model scattering form factors, which are compared to real and simulated form factors, are obtained from the Fourier transform

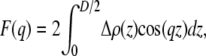(8)

where the integration extends from the bilayer center (z = 0) to a point (D/2) beyond which Δρ(z) = 0. The solid lines in Fig. 3 show x-ray and neutron scattering form factors, respectively, obtained from the SDP model.

FIGURE 3.

The lines show fits using the SDP model to (A) x-ray and (B) neutron scattering form factors F(q) obtained from an MD simulation. In the main panels, the simulated form factors, depicted by dots, were constrained to the typical experimental range and noise was added at the typical experimental level (NRS). In the insets, the data are noise free and cover an extended q range (SES).

Constraints

There are six different terms (i.e., five Gaussians and one error function) making up the SDP model. Although each function is defined by three parameters, the height of the hydrocarbon chain error function is fixed to one by imposing spatial conservation, whereas the mean position of the methyls is constrained by symmetry arguments to z_CH3 = 0. Another constraint is the total lipid volume V_L, which is accurately known from experiment (1) and from simulations (26). We also constrain the headgroup volume V_HL (including the glycerol and carbonyl groups) that has been reported to be between 319 and 331 ų for gel phase phosphatidylcholine bilayers (16) and whose range we assume also applies to fluid phase bilayers as the headgroup in both phases is solvated. Furthermore, the gel phase headgroup volumes are consistent with the value of 319 ų that we obtained from the fluid phase MD simulations here following the method of Petrache et al. (26) and using the component groups of our SDP model. The results of this volumetric analysis provided the basis for the following additional constraints.

We define four additional volumetric parameters that control volume allocation. Two of these are found in the headgroup region

(9)

and the other two in the hydrocarbon region

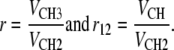(10)

In the fitting program, we constrained the volumetric parameters in Eqs. 9 and 10 and subsequent constraints using “soft” Bayesian constraints, which allow the values to deviate by ∼5% from a target value through the addition of quadratic penalty terms to the goodness of fit criterion (minimal sum of the weighted squares of the differences between the fit and data). These constraints increase the stability and robustness of our nonlinear least squares fitting program, especially when applied to incomplete and noisy experimental data.

All partial volumes can be merged into one relation for total lipid volume:

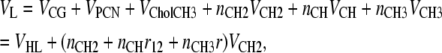(11)

where n_i are the number of type i components. Equations 9–11 then determine all the component volumes from the four constrained R_CG, R_PCN, r, and r₁₂ values and the volumes V_L and V_HL. The component volumes automatically constrain the height of the Gaussians in Eq. 2 as follows

(12)

where A is area/lipid.

Determination of lipid area A

Area/lipid A follows from the volume probability, which gives the Gibbs dividing surfaces for the water region and for the hydrocarbon region shown in Fig. 2. The Gibbs dividing surface for the hydrocarbon region is defined to be at D_C, which in the SDP model is given by z_HC in Eq. 3. The Gibbs dividing surface for the water region is defined to be at D_B/2. Thus, the parameter D_B, also known as the Luzzati thickness (1), affects the model structure through the water distribution. It is defined by the equality of the integrated water probabilities to the left of this surface and the integrated deficit of water probabilities to the right. This is written as follows

(13)

where D/2 is a point beyond which P_W(z) = 1. From this, D_B can be expressed in the form

(14)

Finally, the latter integral is equivalent to the integrated deficit of lipid probability and is equal to (D/2 − V_L/A). Equation 14 then yields the first of the following equalities:

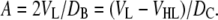(15)

The second equality in Eq. 15 follows from the equivalent derivation applied to the dividing surface between the hydrocarbon and headgroup regions. Even though the experimentally obtained F(q_z) contains information about the bilayer's structure in the z direction (along the bilayer normal), Eq. 15 allows us to evaluate the structure in the lateral direction, namely A. It should be emphasized that although the latter part of this equation was widely employed in previous ED models, the first equality has important implications in the case of neutron scattering. For protonated lipid bilayers dispersed in D₂O, neutrons are particularly sensitive to the overall bilayer thickness D_B. Equation 15 thus directly yields lipid area from highly precise measurements of V_L. Importantly, A appears in Eq. 12 for the lipid component distributions and becomes the central parameter in the SDP model.

RESULTS AND DISCUSSION

Test of SDP structural model

For these tests, our DOPC simulation provided the F(q) “data” within which structural parameters, such as the area/lipid A and the distributions of the individual components, are hidden in the same way as in experimental data. A nonlinear least squares program searched for those values of the SDP structural parameters that best fit the simulated F(q). Each test then has three criteria to evaluate success: 1), how well the SDP F(q) fit the simulated F(q); 2), how closely the SDP structural parameters compare to the known parameters from the simulation; and 3), how many constraints are required to obtain a robust fit and how well these constraints must be known.

First, we report our tests using F(q) data that are obtained directly from the simulations. These F(q) are quite smooth in q and may be computed to much larger q values than real data. As such, we call these smooth extended simulated (SES) data. The insets to Fig. 3 show that SDP provides excellent simultaneous fits to the SES x-ray and neutron F(q) data, thereby satisfying criterion 1. These fits are also very favorable for criterion 3 because only the values of total lipid volume (V_L) and lipid headgroup volume (V_HL) were constrained to values obtained from the simulations by the volumetric analysis (26). The V_L constraint is justified because it is known precisely from experiment and can be used for real data without concern, and the values of V_HL are known to ∼3%. Although criterion 2 was well satisfied for many of the important parameters, such as A, the positions of the component groups, and the thicknesses of the regions, the SDP model did not do a good job at distributing the volumes between the different components (not shown).

In our subsequent SES fitting, we constrained the volumetric parameters in Eqs. 9 and 10 using soft Bayesian constraints. We also soft constrained the width of the hydrocarbon Gibbs dividing surface (σ_HC) to ∼2.4 Å ± 5%, as Klauda et al. (13) did. We call these the “common” constraints because we use them for all data analyses. The SDP fit to the SES F(q) data with the common constraints showed small, but discernable differences for q > 0.2 Å⁻¹ neutron data, where experimental data are scarce. Balancing this negative effect on criterion 1, criterion 2 was better satisfied, as can be seen by comparing the structural parameters in the SES column of Table 1 to their actual simulated values. The fitting procedure was also more robust, better satisfying criterion 3.

TABLE 1.

Structural parameters as defined in the text and obtained from the MD simulation directly and through the SDP model analysis, where SES or NRS data were fitted

Data type	MD	SES	NRS	NRS	NRS	NRS	NRS
Data sets	Reference	All	All	X-ray + neutron external CV	Neutron all	Neutron external CV	X-ray only
VL	1295	1295**	1295**	1295**	1295**	1295**	1295**
VHL	319	319**	319**	319**	319**	319**	319**
RCG	0.48	0.46*	0.45*	0.45*	0.47*	0.47*	0.46*
RPCN	0.27	0.27*	0.26*	0.26*	0.27*	0.27*	0.28*
r	1.93	1.92*	1.92*	1.92*	1.94*	1.94*	1.97*
r12	0.81	0.81*	0.84*	0.83*	0.81*	0.80*	0.76*
DB	35.8	35.8	35.9	35.9	35.9	36.1	35.9
DHH	36.4	36.3	35.9	36.0	35.1	33.9	36.1
2DC	27.0	27.0	27.0	27.1	27.1	27.2	27.0
DH1	4.7	4.7	4.4	4.4	4.0	3.3	4.5
A	72.4	72.4	72.2	72.1	72.1	71.8	72.2
Additional constraints	–	–	σCH	σCH, σCholCH3	σCH, zCH, σCH3	σCH, zCH, σCholCH3, σCH3	σCH, zCH, σCholCH3, zCholCH3, DH1

The analysis was applied to the different combinations of x-ray and neutron CV data, where external CV includes nondeuterated lipids in 50% and 100% D₂O and “All” also includes perdeuterated lipids. The double asterisks (**) denote hard constrained parameters, and single asterisks (*) denote parameters restricted with a soft constraint (∼5%). Additional soft constrained parameters discussed in the text are listed in the final row of the table. The units for all numbers carry the appropriate power of Å.

There are still some discrepancies when the individual component distributions are compared in real space, as indicated in the SES column of Table 1. The largest difference is in the hydrocarbon chain region, more specifically, the distribution corresponding to the terminal methyl groups. It can already be seen from the volume probability profiles in Fig. 2 that the slowly decaying tails in the simulated distribution cannot be accurately represented by a simple Gaussian function. As was shown in Klauda et al. (13), assigning a second Gaussian to the methyl distribution does not significantly improve the overall quality of the fit to the ED F(q), so a second Gaussian that increases the number of adjustable parameters is to be avoided. However, this discrepancy in the methyl distribution then goes on to affect the other component distributions. As the integrated probabilities under the simulated and fitting curves must be the same, the missing tails in the methyl Gaussian result in its slightly increased height, which then gets balanced by the methylene and methine distributions at the bilayer center. Nevertheless, the total impact of this shortcoming on the evaluated area/lipid A is a difference of <0.1 Ų, as is shown in the SES column in Table 1.

The next question is whether the SDP model can obtain good values of A and the other structural parameters in Table 1 by fitting data that are comparable to those obtained from experiment. Tests have been performed using F(q) simulated data that have comparable q ranges to our experiments and that also have noise added of a comparable level. We call these noisy restricted simulated (NRS) data. The NRS x-ray data shown in the main panel of Fig. 3 A were divided into four intervals (q < 0.3 Å⁻¹, 0.3 Å⁻¹ < q < 0.5 Å⁻¹, 0.5 Å⁻¹ < q < 0.6 Å⁻¹, and 0.6 Å⁻¹ < q < 0.8 Å⁻¹), and the added random noise was increased with increasing q. The neutron data in Fig. 3 B were divided into two intervals (q < 0.17 Å⁻¹ and 0.17 Å⁻¹ < q < 0.3 Å⁻¹). The uncertainties assigned to x-ray and neutron F(q) were adjusted such that the total weight of all the neutron data versus the x-ray data corresponded to the ratio of their maximum q values (i.e., 0.3:0.8).

It is even easier to satisfy test criterion 1 for NRS data because the noise obscures the small misfits that are barely observable in the fit to the SES data. Therefore, all our SDP tests on NRS data focus on criteria 2 and 3. The NRS/all column in Table 1 shows results when x-ray and neutron data with all four scattering contrasts were fit to NRS data. The fitted SDP values still compare rather well with the MD simulation, although it was necessary to constrain another parameter in addition to the common set defined above. Surprisingly, the distribution of the methine (CH) Gaussian was not well determined until we soft constrained its width σ_CH. As is evident from Fig. 1, the CH groups can be distinguished only from the NSLD of nondeuterated hydrocarbon chain samples. Restricting the q range and introducing experimental noise to the neutron NRS data apparently loses this fine structure. In contrast, the NRS data are still sensitive to the bilayer thickness (D_B) so the area A = 2V_L/D_B is only 0.2 Ų different from its MD value.

The volume probabilities obtained in the preceding SDP fit (NRS/all column of Table 1) to NRS data are compared in Fig. 4, along with the simulated distributions. Almost all the component group distributions are faithful to the original simulations, exceptions being the methine (CH) and methylene (CH2) distributions. However, when added together their combination (CH2+CH) is in very good agreement with the simulated distribution. We note that this discrepancy was not present when the SDP model was used to fit SES data. As mentioned, the resulting low-resolution neutron scattering data better describe the overall bilayer structure (water distribution and the D_B thickness), whereas more detailed information (headgroup distribution and the D_HH thickness) is obtained from fits to high-resolution x-ray data. The fitted result in Fig. 4 is in very good agreement with these; so the SDP model is capable of capturing the most important structural features of a lipid bilayer when it is used to simultaneously fit x-ray and neutron scattering data with several contrasts.

FIGURE 4.

The solid lines show the volume probabilities obtained from the MD simulation (same as in Fig. 2). The dashed lines show the best fit to the full NRS data in column NRS/all in Table 1. An additional combination of methylene and methine groups is described by the gray lines (CH2+CH).

Table 1 also shows results of fits to fewer NRS data sets. It emphasizes the expected result that having fewer data sets generally requires more constraints. Removal of the neutron data sets with the internal CV for lipids (column NRS/x-ray + neutron external CV) requires an additional constraint on the CholCH3 group because it has little contrast in the remaining data as seen in Fig. 1. Removal of the x-ray data (NRS/neutron all) makes it difficult for the neutron data to distinguish the chain terminal methyls. More surprising is that the position of the methine CH groups is not well determined by neutron data, so a constraint on z_CH appears in these columns (NRS/neutron all and NRS/neutron external CV). Finally, column NRS/x-ray in Table 1 shows that fitting x-ray data alone requires the largest number of additional constraints. This is partly because there is little x-ray contrast for either the methine CH groups or the choline methyls. Inclusion of the methine groups is required primarily to accommodate neutron sensitivity and was not employed in older models for DOPC x-ray data (1,29). Also, the particular parsing of the choline group into methyls alone with the remainder of the choline added to the phosphate is required primarily to accommodate the neutron scattering length asymmetry of the headgroup. Although these considerations suggest that the SDP model is biased in favor of neutron data, this should not obscure the result, emphasized previously (13), that the D_H1 constraint is necessary when only x-ray NRS data are fit, either by the earlier H2 and HB models or now by the SDP model. The fact that this constraint is not required when neutron data are included in the SDP model is a major justification for the simultaneous analysis of neutron and x-ray scattering data.

A concern with applying constraints is the uncertainty in their target values for real data. Table 2 shows the effect that uncertainties in the values for parameters in the common constraint set have on the SDP value of area/lipid A. Each of these parameters was modified by ∼5% and fixed, one at a time, whereas the other parameters were determined by fitting. Even if we suppose that the individual uncertainties are additive, the propagated uncertainty in A is <2%, which is comparable to previously estimated uncertainties (29). We also note here that different combinations of constraints can produce nearly equivalent values for the structural parameters. Although the z positions of component groups are clearly poor choices that prejudge bilayer thickness and area, differences in component positions (such as D_H1) might be subject to sterochemical constraints. Our choice of the common set is based on our view that volumes are likely to be more reliably estimated by simulations, especially since they must sum to their experimentally measured value, as does the simulation in this work.

TABLE 2.

The deviation ΔA of area/lipid obtained by SDP fitting to the full set of NRS data when the value of each parameter was independently fixed at 5% above and below the simulated value

Parameter	ΔA [Å2]
r	0.2
r12	0.1
RCG	0.6
RPCN	0.1
σHC	0.3
sum	1.3

Application of the SDP model to experimental data

First, the SDP model with only one set of parameters was fit simultaneously to the nine sets of DPPC data obtained under different contrast conditions. Besides x-ray and neutron data from protonated bilayers, these include partially (DPPC_d9) and fully (DPPC_d13) deuterated choline headgroups and chain perdeuterated lipid molecules (DPPC_d62). In addition to using specifically deuterated DPPC molecules, neutron scattering experiments were also performed with bilayers dispersed in 50% and 100% D₂O solutions.

The fit to the DPPC x-ray form factors shown in Fig. 5 A is very good over the entire experimental q range. Such high quality data typically result in high-resolution profiles revealing many detailed structural features (Fig. 5 A, inset). In contrast, Fig. 5 B shows neutron scattering data with poorer counting statistics in the high q region, which is typically the case for SANS data from fluid bilayers in solution. Nevertheless, the low q region (q < 0.2 Å⁻¹) provides high quality information, reflecting the large scattering contrast between the lipid bilayer and solvent. Not surprisingly, the most intense scattering occurs from fully protonated bilayers in 100% D₂O, whereas the least intense scattering is observed from chain perdeuterated lipids dispersed in 100% D₂O. The total bilayer ED and NSLD profiles are shown in the insets to the figures, and the probability distributions of all components are displayed in Fig. 5 C. It should be noted that an SDP model also produced a result that fit the data better. However, it was discarded because it violated stereochemistry by placing the CholCH3 component too far (∼5 Å) from the PCN component to which it is covalently bonded. Similar unphysical solutions can often be found by nonlinear least square fitting programs.

FIGURE 5.

The solid lines show the result of simultaneous SDP fit to (A) x-ray and (B) neutron scattering data from DPPC at 50°C. X-ray experimental data are from Kučerka et al. (30) with the estimated uncertainties (±1 standard deviation) corresponding to the size of the data symbols for q < 0.6 Å⁻¹. The insets display the total ED and NSLD profiles for half the bilayer. (C) The SDP volume probability distributions.

Table 3 lists the values of parameters that were determined by the fits to all the DPPC data in column 2 and by the fit that used only the external contrast data in column 3. Both fits gave similar values for D_B and D_C and, therefore, for A (calculated using Eq. 15). Both fits also gave similar values for D_HH, in good agreement with the earlier reported D_HH = 37.8 Å (30) obtained using x-ray data only. Finally, although the areas for the benchmark DPPC lipid at 50°C have varied quite widely (1), the value here near 63 Ų is not very different from some reported previously: A = 62.9 Ų (31), A = 64.0 Ų (1), A = 64.2 Ų (30), and A = 62.0 Ų (32).

TABLE 3.

Structural results obtained from fitting the SDP model to DPPC experimental data measured at 50°C and DOPC at 30°C

	DPPC at 50°C internal/externalCV	DPPC at 50°C external CV	DOPC at 30°C external CV
VL	1229**	1229**	1303**
VHL	331**	331**	331**
RCG (0.48)	0.41*	0.41*	0.42*
RPCN (0.27)	0.29*	0.28*	0.26*
r (1.93)	1.94*	1.93*	1.96*
r12 (0.81)	–	–	0.79*
DB	39.1	39.0	38.7
DHH	38.0	38.0	36.7
2DC	28.6	28.4	28.8
DH1	4.7	4.7	3.9
A	62.8	63.1	67.4
zCG	14.8	14.7	14.8
σCG	2.07	2.11	2.05
zPCN	19.6	19.7	19.1
σPCN	2.58	2.62	2.41
zCholCH3	21.5	21.6	20.6
σCholCH3	2.98**	2.98**	2.98**
zCH	–	–	9.60
σCH	–	–	3.05**
σHC (2.44)	2.53*	2.47*	2.48*
σCH3	2.75	2.73	3.09

The second column shows results obtained using internal and external CV data; the other two columns used only external CV neutron scattering data. Hard constrained parameters are designated by ** and soft constrained parameters by *, with target values given in column 1. The units for all numbers carry the appropriate power of Å.

We next applied the SDP model to scattering data from DOPC at 30°C (Fig. 6). Due to the unavailablility of deuterated analogs of this lipid, the neutron data include only two external contrast conditions at 100% and 50% D₂O, as shown in Fig. 6 B. An additional soft constraint, not applicable for DPPC, was required for the width σ_CH of the double-bond distribution in DOPC.

FIGURE 6.

The solid gray lines show the best results of the simultaneous SDP fit to (A) x-ray and (B) neutron scattering data from DOPC at 30°C; the dashed line in A and solid black lines in B show poorer fits when A was constrained to 72.4 Ų. X-ray experimental data were adapted from Kučerka et al. (19) and Kučerka et al. (29) with the estimated uncertainties (±1 standard deviation) being the size of the data symbols for q < 0.6 Å⁻¹. The insets display the total ED and NSLD profiles for half the bilayer. (C) The results of the best fit in terms of SDP volume probability distributions.

Table 3 shows that many quantities have similar values for DPPC at 50°C and DOPC at 30°C. The first set of parameters corresponds to volumetric information. V_L was obtained from experimentally determined values (33–35), with V_HL fixed to 331 ų (16). Additional partial volumes were estimated from the MD simulation, and the ratios in Eqs. 9 and 10 were restricted to the estimated values with a soft constraint. Methylene volumes calculated from the results are slightly smaller for DOPC (27.7 ų) than for DPPC (28.1 ų), which can be attributed to the lower temperature of DOPC bilayers. The thicknesses, D_B and 2D_C, have similar values, but that is accidental. Because DOPC has a larger volume, a similar thickness means that the area/molecule A is larger. Therefore, the hydrocarbon region is more disordered, and that is consistent with the larger width σ_CH3 of the terminal methyls. On the other hand, the σ-widths of the other distributions have similar values, as might be expected. The most striking difference between the SDP results for DPPC and DOPC is the smaller value of D_H1 for DOPC; this requires different molecular packing in the interfacial headgroup region for these two lipids.

It was previously emphasized (13) that D_H1 is a key parameter that cannot be obtained robustly from x-ray data alone, and this is confirmed by our tests on the simulated data (Table 1). Previously, the gel phase value of D_H1 = 4.95 Å for DMPC (16) was assumed to be the same for all PCs in both the fluid and gel phases (1). However, the result that D_H1 = 3.9 Å for DOPC, together with D_H1 = 4.7 Å obtained for DPPC bilayers, questions the assumption that the value of D_H1 is independent of the particular lipid bilayer.

The smaller value of D_H1 for DOPC induces a larger D_C and, by Eq. 15, a smaller area A = 67.4 Ų than the A = 72.4 Ų previously reported from fitting the H2 model to the same x-ray data (29). When A was fixed to the value of 72.4 Ų in the SDP analysis, D_H1 = 5.02 Å became close to the value assumed in Kučerka et al. (29). Since x-ray scattering is most sensitive to the electron-dense headgroup peaks and therefore to D_HH, the adjustment of the D_H1 parameter allows comparably good fits for the two different areas, as shown in Fig. 6 A. In contrast, when A was fixed to the value of 72.4 Ų, the fit to the DOPC neutron data were considerably poorer between 0.10 and 0.14 Å⁻¹ as shown by the solid black lines in Fig. 6 B. Neutron scattering, especially from fully protonated lipid in D₂O, is most sensitive to the thickness D_B which, by Eq. 15, directly obtains A using only the highly accurate volume V_L. Therefore, when neutron scattering data are included, prior knowledge of D_H1 is not necessary.

It is of interest to compare the ED here with those obtained using the H2 model in Kučerka et al. (29). As the H2 model does not distinguish between the methylene and methine groups, we combined these distributions for the SDP model. Moreover, the H2 model uses a Gaussian function to represent the phosphate component and it places the choline together with the water distribution (13), whereas the SDP model separates these various groups into PCN (phosphate and CH₂CH₂N), CholCH3 (three choline CH₃ groups), and water distributions. Thus, to compare the headgroup results from the two models, we present these groups as a combined distribution of water and phosphatidylcholine (water + PC). The two types of modeling are consistent in that the total H2 ED profile shown in Fig. 7 and its corresponding F(q) (not shown) are practically indistinguishable from our results here. However, differences become apparent when comparing the various components. A minor difference is in the integrated size of terminal methyl and CG Gaussians. The two models differ by the ratio of their areas (7%) because these integrals multiplied by the area correspond to the same number of electrons. More importantly, the positions D_C of the methylene-like groups (combination of the methylene and methine groups) differ considerably, which is directly related to the differences in areas via Eq. 15. Finally, the water + PC distributions agree well in the vicinity of the electron-dense phosphate peak, whereas they differ for smaller z values.

FIGURE 7.

The results of component ED distributions obtained from the SDP simultaneous analysis of x-ray and neutron CV scattering data of DOPC at 30°C (solid lines) and those reported in Kučerka et al. (29) (broken lines). The methylene and methine groups are combined into one group (CH2CH), and the water + PC group accounts for the entire phosphatidylcholine and water distributions.

Fig. 7 shows that the individual distributions in the interfacial region can be altered with little impact on the total ED profile. Since the EDs of hydrocarbon chains and water are not so different (low scattering contrast), there is ambiguity in determining which contributes to the ED at a given position and therefore difficulty in determining D_C using only x-rays without assumptions (1,29). Neutron scattering, on the other hand, offers enormous contrast between the lipid molecule and D₂O and this provides vital additional information that is required to assign the distributions of the lipid components and the subsequent determination of lipid area.

The DOPC simulation in this work has a value D_H1 = 4.7 Å (Table 1), considerably larger than our SDP experimentally derived value of 3.9 Å. A simulation of DMPC also using the CHARMM potentials reported D_H1 = 5.28 Å with A = 60.6 Ų (13). If one supposes that D_H1 systematically decreases as area increases in simulations, then the predicted D_H1 for DOPC at A = 67.4 Ų would be larger than 4.7 Å, which would thereby increase the difference with the experimental SDP result. On the other hand, our result for A is similar to the values obtained from constant pressure MD simulations using GROMACS potentials (36,37), although the value of D_H1 from a recent DOPC simulation (S. A. Pandit, Dept. of Physics, University of South Florida, Tampa, FL, personal communication) is 4.8 Å. However, it is not straightforward to compare results of different simulations, as they were obtained using different simulation strategies and sampled over different statistics regimes. There have been extensive debates in the simulators community about the effects of the statistical treatment of simulations, their convergence on the typically achieved timescales, finite size effects, and inaccuracies in empirical force fields. Obviously, any of these aspects of the simulation procedure can contribute to the final uncertainty, though some are thought to be superior to others. Consistent with our finding of the discrepancies in the D_H1 parameter, Castro-Román et al. (38) recently suggested that lipid headgroup, water, and their interaction parameters in simulations need refinement. Clearly, there is additional work to be done to reconcile simulations and experiment, which can only benefit from approaches such as the one presented here.

CONCLUSIONS

We have developed a model (i.e., SDP) to simultaneously analyze x-ray and neutron scattering data from fully hydrated lipid bilayers. The model is based on volumetric distribution functions that are required to obey spatial conservation, and experimental volume data are incorporated into the analysis. Decisions regarding the specific separation of the submolecular components in the model were guided by an MD simulation. The model was thoroughly tested against the simulation by using only parameter values, data ranges, and uncertainties obtainable from experiment. This testing established that soft volumetric constraints suffice to provide robust fits, thereby allowing the model to determine the values of many parameters, such as thicknesses and area, as shown in Tables 1 and 3. A major advantage of adding neutron data is that the value of a key parameter, namely D_H1, that previously had to be constrained when fitting only x-ray data, can now be predicted.

We have applied the SDP model to extensive x-ray and neutron data from fully hydrated DPPC and DOPC bilayers. Although the area results for DPPC are consistent with previous x-ray data only results, DOPC results for A are almost 10% smaller. This is due to significantly larger D_B and D_C (Table 3) obtained in our results here compared with those values previously obtained from x-ray data only analysis, where D_C was calculated from D_HH (i.e., D_C = D_HH/2 − D_H1) assuming a single D_H1 for all PCs. However, the differences in D_H1 (Table 3) strongly suggest that D_H1 values are not independent of the particular lipid, and thus future studies should strive to combine neutron and x-ray scattering data to obtain more reliable bilayer structures. The smaller A and D_H1 values for DOPC bilayers also pose a challenge to MD simulations, including the one presented here.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.