Intermediates in dioxygen activation by methane monooxygenase: A QM/MM study

Abstract

Protein effects in the activation of dioxygen by methane monooxygenase (MMO) were investigated by using combined QM/MM and broken-symmetry Density Functional Theory (DFT) methods. The effects of a novel empirical scheme recently developed by our group on the relative DFT energies of the various intermediates in the catalytic cycle are investigated. Inclusion of the protein leads to much better agreement between the experimental and computed geometric structures for the reduced form (MMOH_red). Analysis of the electronic structure of MMOH_red reveals that the two iron atoms have distinct environments. Different coordination geometries tested for the MMOH_peroxo intermediate reveal that, in the protein environment, the μ-η²,η² structure is more stable than the others. Our analysis also shows that the protein helps to drive reactants towards products along the reaction path. Furthermore, these results demonstrate the importance of including the protein environment in our models and the usefulness of the QM/MM approach for accurate modeling of enzymatic reactions. A discrepancy remains in our calculation of the Fe-Fe distance in our model of H_Q as compared to EXAFS data obtained several years ago, for which we currently do not have an explanation.

Introduction

Soluble methane monooxygenase (sMMO) is a multicomponent enzyme complex that catalyzes the oxidation of methane to methanol in methanotrophic bacteria such as Methylococcus capsulatus (Bath) and Methylosinus trichosporium OB3b (Scheme 1):^1–8

Scheme 1.

The complex is at present believed to involve a minimum of three components. The hydroxylase (MMOH) catalyzes the oxidation reaction at a non-heme, carboxylate bridged dinuclear iron center held within a four-helix bundle. The reductase component (MMOR) is a flavin- and ferredoxin-containing protein that transfers electrons from NADH to reduce the diiron center of MMOH to its Fe(II)-Fe(II) state. Component B is a cofactorless protein required for efficient catalysis that also serves several regulatory roles. A fourth component, MMOD, has recently been characterized. Its function is still unclear, but it binds to MMOH and is a potent inhibitor of sMMO. It has been proposed to play a role in the assembly of the MMOH diiron center.⁹

An important reason for the attention devoted to sMMO is its ability to oxidize the C-H bond of methane selectively to methanol under ambient temperature and pressure conditions. The understanding of the mechanism by which the enzyme catalyzes this chemically challenging reaction would not only be of great academic interest but also of possible practical value for the biomimetic design of new catalysts for the industrial conversion of methane to methanol.^10–12 Substantial advances in the understanding of this mechanism at an atomic level have been accomplished these last years through structural and spectroscopic studies^{1, 3, 6–8} as well as computational investigations.^13–18

The catalytic cycle of sMMO can formally be divided into two steps: dioxygen activation and substrate oxidation (Figure 1). O₂ activation can occur once the diiron center in the resting, oxidized form MMOH_ox is reduced by MMOR to form MMOH_red. Then, diffusion of O₂ to the hydroxylase active site leads to the formation of MMOH_superoxo, which has an Fe(II)-Fe(III)(O₂⁻) iron core.¹⁹ Subsequently, MMOH_superoxo converts to the diamagnetic peroxo compound (MMOH_peroxo), the first intermediate spectroscopically characterized in the cycle after O₂ reacts with MMOH_red.^{8, 20–25} Based on comparisons with synthetic model compounds, cis-μ-1,2 peroxo, μ-η¹-η¹ or end-on structures were suggested^26–29 for MMOH_peroxo, whereas a μ-η²-η² butterfly structure has been proposed based on results from DFT studies.^{16, 19} The last step in dioxygen activation yields intermediate Q (MMOH_Q). This compound harbors two high-valent, antiferromagnetically-coupled, Fe(IV)-Fe(IV) atoms in nearly equivalent environments.^{20, 21, 30, 31} A Fe(IV)₂-(μ-O)₂ diamond core with a short Fe-Fe distance has been proposed for this intermediate based on an EXAFS study.³¹ This intermediate reacts to convert methane into methanol yielding MMOH_ox.^{21, 23, 25, 32} The final steps of the mechanism, in which a hydrogen is abstracted from substrate, followed by recombination of the substrate with the resulting OH moiety in the core to produce hydroxylated product (methanol, in the case of a methane substrate) have been discussed extensively in previous work.^{5, 8, 14, 33–40} In ref. [42], this reaction is modeled using quantum dynamical methods, and both concerted and “radical rebound” mechanisms (the latter involving a very short lived bound radical species) are shown to contribute to the reaction pathway. We shall not discuss substrate oxidation further in the present paper, which is focused on dioxygen activation.

Figure 1.

The catalytic cycle of MMOH. The part of the cycle corresponding to activation of dioxygen is shown in black while the oxidation of the substrate (hydroxylation of methane into methanol in vivo) is in light gray.

Extensive theoretical studies of dioxygen activation have been carried out in our group^{13, 14, 19, 41, 42} and others.^43–48 Those studies were based on model clusters of different sizes, using mainly Density Functional Theory (DFT). Calculations using large (~100 atom) models suggest that the protein plays a significant role in dioxygen activation, and that a more rigorous analysis of the protein contributions to the activation process would be useful. To date, the only quantum mechanics/molecular mechanics (QM/MM) calculations have focused on the study of MMOH_ox and MMOH_red using the ONIOM method^{49, 50} and on the hydroxylation of several substrates by MMOH_Q using the frozen orbital methodology.³⁹

The aim of the present paper is to analyze the structural and energetic effects of the protein on the different intermediates of the dioxygen activation pathway in the sMMO catalytic cycle. After describing the model and the methodology used for this study, the results obtained will be presented. They will be subsequently discussed in light of experimental data to gain insight into dioxygen activation mechanism and the role the protein matrix could play. To conclude, our results will be summarized.

Methods

Computational Methods

QM/MM methods

Over the past decade, we have developed the QM/MM program QSite⁵¹ based on a frozen orbital approach.^52–54 This program results from a tight coupling between Jaguar⁵⁵ and the protein modeling program IMPACT^{56, 57} developed by Levy and coworkers. The OPLS-AA^{58, 59} molecular mechanics force field is used for the treatment of the MM part while the pure QM part was treated at the DFT-B3LYP level of theory, with details as discussed in the next section.

The methodology has been extensively tested and shown to give reliable results for the relative conformational energies of dipeptides^52–54 and protonation energies of protein side-chains.^{52, 53} Moreover, it has successfully been applied to a number of biological systems¹³ such as the studies of the MMO hydroxylation step,³⁹ P450,^{60, 61} hemerythrin,⁶² triosephosphate isomerase (TIM),⁶³ class C β-lactamase and Penicillin binding protein (PBP).³⁹ The errors resulting from the QM/MM interface are quite small in an absolute sense (~0.5 kcal/mol) and are expected to be unimportant as compared to intrinsic errors in the DFT methodology.^{52, 53}

The antiferromagnetic coupling of the two iron atoms of intermediates in the catalytic cycle requires the use of unrestricted DFT (UDFT) methods to obtain reliable models. Until now this feature was not implemented into QSite and we therefore had to resort to a thermodynamic cycle, presented in Supporting Information, to get proper energetics. In the present study, the QM/MM//UDFT scheme recently implemented into QSite⁶⁴ has been used; the results obtained are compared to those generated using the previous scheme. The good agreement generally obtained between the two approaches validates the thermodynamic cycle used in our previous QM/MM studies.^{62, 65}

QM methods

The core computational method chosen for this study is density functional theory (DFT)⁶⁶ with the hybrid functional B3LYP.^67–69 An unrestricted DFT (UDFT) methodology was employed to model spin polarization efficiently for open shell orbitals of both irons. This method enables modeling of antiferromagnetic (AF) coupling between the two Fe atoms by the use of a broken symmetry (BS) wave function. The Jaguar⁵⁵ suite of ab initio quantum chemical programs was used for all standalone QM calculations. This program using pseudospectral methods is particularly efficient for treating large size systems such as those found in biology^{70, 71} and its high-quality initial-guess wavefunctions for metals are very useful for studying bioinorganic systems.^{72, 73}

The choice of the basis set is also an important issue in computational studies. Our previous studies have shown that geometry optimizations using a mixed basis set, such as LACVP**^74–76 for metals, 6-31G* on core atoms and 6-31G on the remaining atoms, gives reasonable results. For this study we used LACVP** for metals and 6-31G* on other atoms for consistency with QM/MM calculation, since frozen orbitals are only available with the 6-31G* basis set. Accurate energy determinations require single point calculations with larger basis sets of triple-ζ quality in the diiron core, such as the scheme we have previously used with LACV3P** on metals, cc-pVTZ(-f)⁷⁷ on core atoms and 6-31G** otherwise. We also add diffuse functions (cc-pVTZ(-f)++) onto both atoms of dioxygen because these atoms are strongly negatively charged in MMOH_Q. The results shown below indicate that the enhancement of the basis set on the core oxygen atoms yields improved results for the relative energetics of the various intermediates in the catalytic cycle.

Vibrational frequency calculations are highly computationally demanding tasks for big models. It is therefore necessary to use smaller models with lower quality basis sets for this purpose. In the present work, the LACVP**/6-31G** basis set was used for the core atoms and 6-31G was used otherwise.

Finally, we have recently developed a novel scheme for correcting errors in DFT energetics based on localized orbital corrections (LOC).⁷⁸ When applied to a data set of 222 molecules containing first and second row atoms for which accurate enthalpies of formation, ionization potentials, electron affinities or proton affinities are experimentally well known (G3 dataset⁷⁹), the mean absolute deviation (MAD) versus experiment for the B3LYP version of the methodology (B3LYP-LOC) is 0.8 kcal/mol, as compared to the MAD of 4.8 kcal/mol obtained for B3LYP alone. The methodology at present has only been robustly optimized and tested for first and second row atoms, but we can make a simple extension to apply it to the relative energetics of the various species involved in the MMOH catalytic cycle. We investigate the effects of these corrections for intermediates in MMO dioxygen activation. Although more work is required to achieve quantitatively accurate parametrization for transition metals, the localized corrections in their current form appear to provide significantly improved results for the relative energetics of the MMOH_Q and MMOH_peroxo states, as revealed by comparisons to experimental data.

Physical Model

Our QM/MM models are based on the QM/MM structure of MMOH_Q built in our previous study;⁶⁵ this structure in turn was initially derived starting from the crystal structure of the oxidized form.^{80, 81} Due to the fact that the QM/MM code QSite⁶⁴ was only able to handle at most 8000 atoms, and in order to restrict computational effort, only residues and water molecules within 35 Å of the active site of an α subunit of the α₂β₂γ₂ MMOH were included in our calculations (Figure 2). To mimic solvent screening, all surface residues not engaged in salt bridges were neutralized. The QM region includes Glu 114, Glu144, His 147, Glu 209, Glu 243, His 246, a water molecule, and the diiron core, including dioxygen- or solvent-derived ligands when present. Backbone cuts were performed for both His 147 and His 246, whereas side chain cuts were used for the other residues. It should be noted that in our previous calculations, side chain cuts were also used for both histidines. However, our QM/MM//RDFT calculations revealed that important forces are exerted on the frozen bonds of the histidines. Such important forces on the QM/MM boundaries might generate artifacts in the energy. Although these errors should cancel by the use of the thermodynamic cycle in QM/MM//RDFT calculations, they may be more important in the QM/MM//UDFT scheme.

Figure 2.

Structure of the oxidized MMOH_ox protein (PDB code 1MTY) represented in ribbon. The α subunits are depicted in green, the β subunits in purple and the γ subunits in pink. The QM/MM model used is shown in cartoon representation and is made of a sphere of 35 Å of the α subunit of protomer α (chain D in PDB code 1MTY). The QM part is represented in licorice in the panel (Graphic prepared with VMD⁸²). Solvent-derived ligands are omitted.

For the final system, the QM part and the whole QM/MM model were both neutral. The initial guess geometries of each intermediate were setup by modifying the diiron core and, when needed, Glu 243 in our model of MMOH_Q to match better the geometries of the pure QM models obtained in our previous study.¹⁹ This task was performed by using the program Maestro,⁸³ superimposing the QM cluster onto the MMOH_Q, changing distances and angles for the diiron core, and only modifying dihedral angles for Glu 243.

Pure QM calculations were carried out by taking the QM regions obtained in the QM/MM calculations, cutting the models between the C_α and the C_β, and then capping the dangling bonds with hydrogen atoms. Frequency calculations were performed on medium-sized models (~50 atoms) derived from the QM/MM//RDFT structures, modeling glutamates by acetates and histidines by imidazoles. All zero point energies (ZPE) and thermochemical corrections were derived from these calculations performed after optimization of the capping hydrogen atoms and without frequency scaling.

Results

Geometries and electronic structures of reaction cycle compounds

In this section, we analyze, for each compound of the catalytic reaction cycle, the geometry and electronic structure obtained to characterize the effect of the protein matrix and to determine the state of the species we are proposing.

Reduced form

The reduced form was modeled with two ferromagnetically coupled, high spin (S=2) iron(II) atoms in agreement with experimental evidence^{21, 84–86} and previous theoretical results.¹⁹ After QM/MM optimization, the structure obtained gives RMSDs for heavy atoms of the diiron cluster and the liganded side chains of 0.35 Å and 0.33 Å, respectively, with the crystal structures⁸⁷ of the two protomers (the RMSD between the protomers’ crystal structures is 0.15 Å). The QM/MM model for the reduced structure of the enzyme is in very good agreement with experiment (Figure 3). This result contrasts with the pure QM calculation using a large cluster model, for which a RMSD of 0.99 Å was found for almost the same heavy atoms as in the QM/MM for RMSD calculation.

Figure 3.

Optimized QM/MM structure of Hred (color) superimposed onto the corresponding crystal structure (gray). The first shell atom names are also displayed.

The distance between Fe(II) ions reflects dramatically improved agreement between the QM/MM and the experimental structures. In our calculation, a distance of 3.29 Å was found between iron atoms, comparable to the experimental distance of 3.27–3.31 Å (Table 1). In contrast, in the pure QM calculation, the distance was 3.64 Å, clearly beyond the range of experimental and theoretical errors, as noted in our previous papers.^{19, 41} The distances between the iron and coordinated atom of the various protein and solvent-derived ligands are qualitatively similar in both the QM/MM and the pure QM models when compared to experiment. However, a more quantitative examination of the results reveals the deviation of selected distances between the QM/MM models and the crystallographic structure to be close to the deviation observed between the two crystallographic protomers, whereas the deviation obtained with the QM model was almost twice as large (Table 1). A closer analysis shows that the poorer RMSD obtained with the QM model is mainly due to contributions from the bridging water molecule O14 (Figure 3) and to the oxygen O11 from Glu 243. It is also interesting to note that the structural agreement of the QM/MM model is better with protomer β than with protomer α (data not shown), and that this discrepancy is also due to O11 (Glu 243), O13 (axial water) and O14 (bridging water). Moreover, in protomer α, the water molecule O14 (Figure 3) is hydrogen bonded to both Glu 209 and to another water molecule located 2.96 Å away, whereas in protomer β the second water is farther away in the pocket (4.90 Å), precluding formation of a hydrogen bond with O14. In our QM/MM models the second water is not included. Thus, the choice of our model, structurally closer to protomer β, could explain its deviation from protomer α. These results also show that the geometry of the reduced state, and particularly the distances between iron ions and water molecules, are strongly dependent on the solvent hydrogen-bonding network, supporting the proposal that this network could play an important role during the reduction of MMOH_ox.^{44, 45} To test this hypothesis, we have built a new model including, in the MM region, the two water molecules present in the crystal structure of protomer α. The results obtained (data not shown) improved the agreement with the first-shell distances of protomer α (MAD of 0.142 Å) as well as the distance between Fe1 and O14. Interestingly, in presence of the new water molecules, Glu 209 and Fe2 are displaced whereas the other ligands are minimally perturbed (Figure 4). This effect is consistent with the proposed reduction mechanism,⁴⁵ and is also in good agreement with the fact that Fe2 is more labile than Fe1 in the reduced state.⁸⁷

Table 1.

Selected distances between irons and atoms in their first coordination sphere for our QM/MM model of the reduced form: MMOH_red and the experimental structure.^a

Distance (Å)	Model QM/MM	Model QM	Crystal protomer β	Deviation QMMM/Protomer β	Deviation QM/Protomer β	Deviation QMMM/QM	Deviation Protomer β/Protomer α
Fe2-Fe1	3.289	3.636	3.267	0.022	0.369	−0.347	−0.046
O3-Fe1	2.047	2.120	2.064	−0.017	0.056	−0.073	−0.069
O5-Fe1	2.039	2.066	2.283	−0.244	−0.217	−0.027	0.051
N7-Fe1	2.158	2.219	2.196	−0.038	0.023	−0.061	−0.083
O11-Fe1	2.475	2.246	2.315	0.160	−0.069	0.229	−0.126
O13-Fe1	2.109	2.140	2.184	−0.075	−0.044	−0.031	−0.301
O14-Fe1	2.312	2.346	2.528	−0.216	−0.182	−0.034	0.148
O6-Fe2	2.097	2.098	2.295	−0.198	−0.197	−0.001	0.015
O8-Fe2	1.950	1.964	2.070	−0.120	−0.106	−0.014	0.073
O10-Fe2	2.220	2.292	2.366	−0.146	−0.074	−0.072	−0.071
O11-Fe2	2.265	2.163	2.262	0.003	−0.099	0.102	−0.188
N12-Fe2	2.110	2.148	2.162	−0.052	−0.014	−0.038	−0.008
O14-Fe2	2.910	3.201	2.654	0.256	0.547	−0.291	−0.022
RMSD (A)				0.147	0.213	0.148	0.121

Figure 4.

QM/MM structure of Hred including two additional water molecules (color) superimposed onto the standard QM/MM model (gray). The two water molecules have an important effect on the position of Glu 209 and Fe2.

The QM/MM model shows that the protein matrix is responsible for the short Fe-Fe distance in the reduced state. Indeed, all previous QM models have consistently computed a substantially larger iron-iron distance than those found experimentally, and including second sphere ligands or electrostatic effects of the protein and solvent in a continuum model, did not entirely solve this problem.^{19, 41, 44, 50} To understand the origin of the short Fe-Fe distance found in the current study, we analyze our data and determine the forces acting on the various atoms of our QM/MM//RDFT model. The calculations of forces were carried out in vacuum and with point charges in place of MM atoms to distinguish electrostatic from strain effects of the protein. Forces acting on residues were obtained by summing up forces acting on all atoms of each residue.

The results are presented in Table 2/Figure 5 and show that strain forces (arrows in black on the right) and, to a lesser extent total forces (yellow arrows on the left), tend to keep residues of the active site grouped around the iron ions and to compress the active site. This property is particularly true for residues Glu 114, His 147, Glu 209 and His 246. The case of Glu 243 is different, because the protein tends to move it away from the diiron core. This result is consistent with the fact that, in the oxidized form, this ligand is rotated and no longer bonded to both Fe1 and Fe2. The origin of protein forces tending to keep the active site of the reduced form compact and thus driving the large decrease in the iron-iron distance is probably the four-helix bundle fold. Analysis shows that interactions leading to the contraction of the active site occur between helices B-C on one hand and E-F on the other hand (Figure 5 and Table 2). But it must be noted that, even if these interactions can at least partly explain the decreased Fe-Fe distance, interactions in the orthogonal direction (i.e. B–E and C–F) would be more efficient since they would be collinear with the iron-iron vector.

Table 2.

Norms of the resultant of forces exerted by the protein on each residue of the active site in our QM/MM//RDFT model of the reduced form.^b

Residues	Total force in mHartree/Bohr	“Tension” force in mHartree/Bohr
Glu 114	16.24	18.59
Glu 144	6.76	15.14
His 147	11.66	22.56
Glu 209	6.74	12.71
Glu 243	9.11	7.76
His 246	9.84	23.79
Fe1	13.16	10.39
Fe2	6.29	11.61
O13	2.74	3.17
14	3.27	2.48

Figure 5.

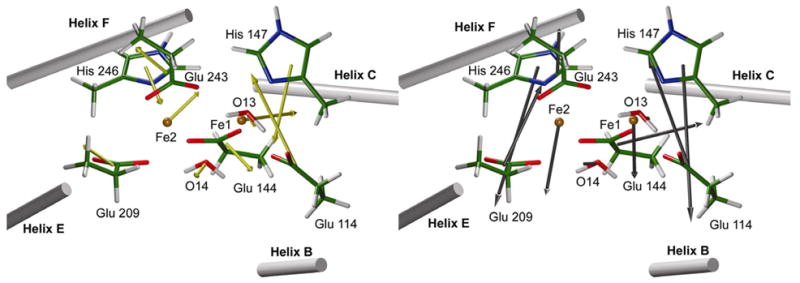
Forces of the protein acting on the QM residues of the active site. On the left, forces correspond to the entire forces (QM forces calculation carried out in vacuum). On the right, forces correspond to what we call “tension forces”, i.e. total forces minus the electrostatic forces of the protein (QM forces calculation with MM charge distribution of the protein included).

Forces exerted by the protein on each atom (data not shown) show very important forces of opposite directions on Nε₂ and Hε₂ of both histidines. This result is probably due to the well-conserved aspartates (Asp 143, Asp 242), hydrogen bonded to histidines, that attract Hε2 while the protein backbone tends to keep Nε2 atoms in place. This observation emphasizes the role of Asp 143 and Asp 242 as noted in our previous paper, and which were included in our cluster models therein.⁴¹

To determine the energy the protein has to expend to keep the iron atoms at a shorter distance than in the QM models, we carried out a QM optimization of the capped QM region of our QM/MM model, first constraining the positions of the iron ions and then allowing a full optimization. The results show that constraining the iron-iron distance at the value of our QM/MM model has a cost of 9.7 kcal/mol. The difference between the QM and QM/MM models is therefore not due to a flat potential energy surface along the iron-iron coordinate. Rather, the protein matrix effect is important energetically and the protein has to expand significant energy to keep the iron-iron distance at the experimentally observed value.

The electronic structure analysis of our model shows that there are 8 unoccupied low-energy beta-spin orbitals that are mainly centered on the iron ions. The beta-spin HOMO and HOMO-1 are also centered on Fe1 and Fe2 respectively (see detailed analysis in Supporting Information). Thus, the electronic structure of H_red is consistent with two high-spin ferrous iron atoms. But, despite their common oxidation state, the electronic structure reveals that the two iron atoms are not equivalent. Indeed, the two iron atoms are in different environments (Figure 6), with Fe1 having an octahedral geometry and Fe2 being in a square pyramidal environment.

Figure 6.

Coordination geometries of the two iron atoms in the reduced state. Fe1 is in an octahedral environment, the axial direction of which is defined by the vector Glu 144-O13 (Z₁ vector). Fe2 is in a square pyramidal environment, the axial direction of which is defined by the Fe2-Glu 209 direction (Z₂ vector). Directions X1, Y1 and Z2 are oriented toward the front of the page.

Reduced form without coordinated water (H_red-no-wat)

Geometry optimization of the reduced form of the enzyme, after departure of the loosely coordinated water molecule trans to the histidines (O14), yields a QM/MM structure similar to that of the original reduced enzyme model; the RMSD between them (without O14) is only 0.12 Å (Figure S-3). Differences are mainly due to a slight increase in the Fe-Fe distance from 3.29 Å to 3.38 Å, to a slight shift of Glu 243 so that the single-atom bridge between the two iron atoms is more effective, and to an important shift of the axial water on Fe1 (O13) due to an increase of the angle with His 147 (O13-Fe1-N_His147) from 92° to 102°. This similarity is also reflected at the electronic level; the same electronic configuration as in the reduced state is found for the iron cations. Since the electronic structure of the iron atoms is not affected by the water departure, the water is only bound to iron cations through electrostatic interactions. Given the fact that these iron atoms are in a relatively low oxidation state, and are surrounded by negatively charged ligands, the weak coordination of the water molecule can be rationalized. The departure of the water is also correlated with an increased Fe-Fe distance, probably because the water molecule helps to reduce electrostatic repulsion between the iron atoms, allowing them to stay closer in the pure reduced form.

Attack of dioxygen: formation of the superoxo intermediate

The first step in dioxygen activation is formation of H_superoxo. This electron transfer process, which involves different spin coupling schemes and different geometries, has been extensively studied in our previous paper.¹⁹ We basically follow the lowest energy path that was found therein: binding of dioxygen to form the undecet H_superoxo (S=5), then intersystem crossings (ISC) to yield H_superoxo in its triplet state (S=1) and then in its singlet state (S=0).

The structure of H_superoxo (S=5) obtained at the QM/MM level is slightly different from the one obtained via pure QM calculations;¹⁹ an RMSD between the two structures of 0.83 Å is obtained for the active site atoms. This RMSD is primarily due to differences located on the ligands of Fe2, because Glu 243 and dioxygen are less tilted toward Fe2, in a way similar to what was found in our earlier study⁴¹ (with which it has a RMSD of 0.72 Å), and His 246 does not rotate as in the pure QM calculation. The Fe-Fe distance of 3.44 Å is shorter than in our pure QM models (3.79 Å in [19] and 3.71 Å in [41]) therefore showing that the protein matrix tends also to decrease the Fe-Fe distance in the H_superoxo (S=5) state. Analysis (see Supporting Information) shows that this state has an electronic structure intermediate between those of H_red complexed with O₂ and a true H_superoxo form, since no π* orbital of O₂ is fully filled. Similar electronic structures with intermediate characters have already been pointed out in metal-dioxygen complexes.⁸⁸

The QM/MM structure of the triplet (S=1) H_superoxo is very similar to the one obtained for the undecet (S=5) state (RMSD of 0.10 Å). Electronic structure analysis (see Supporting Information) shows that the electron transfer occurs in this triplet state because the charge-transfer from Fe2 to dioxygen is much more important than in the undecet state. Thus, the electronic structure is consistent with a state mixing in approximately equal amounts those of a pure reduced enzyme state (no electron transfer to dioxygen) and a pure superoxo state (one electron transferred to dioxygen).

The structure of the singlet is closer to the structure of the undecet (RMSD of 0.04 Å) than the one of the triplet (0.08 Å). The electronic structure of this state of H_superoxo is compatible with a true superoxide species with the electron transferred to the dioxygen molecule coming from Fe2. This is consistent with the fact that dioxygen preferentially binds Fe2, and thus electron transfer from Fe2 is facilitated. It can therefore be noticed that, for this species, Fe2 appears to be less electrophilic than Fe1 while in a previous study⁸⁹ on MMO_Q (vide infra) the reverse was observed. This is actually not inconsistent, because the iron atoms in these species are in different oxidation states and moreover, we have shown (vide supra) that in the reduced state the iron atoms experience different ligand fields. It is therefore difficult to predict the electrophilicity of Fe1 and Fe2 without taking into account the particular state of the catalytic cycle in question.

The peroxide intermediate

The next step involves a second electron transfer from Fe1 to the dioxygen molecule to yield a peroxide intermediate. We have previously proposed two possible structures for this intermediate based on pure QM calculations.^{19, 41} We investigated both models with QM/MM, but also reconsidered two additional structures. All these possibilities are presented in Figure 7. It was previously shown,¹⁹ after extensive QM investigations, that for an ~100 atom model, the lowest energy structure was the μ-η²,η² butterfly arrangement in its singlet state. However, we investigated again all four alternatives at the QM/MM level to see whether the protein could change their relative energies. Moreover, we also investigated the possibility of a cis-μ-1,2 coordination of peroxide to the iron atoms since it has been recently shown that this coordination geometry was favored in a ribonucleotide reductase variant.⁹⁰

Figure 7.

Four tested geometries for H_peroxo. In the upper left, the structure is similar to H_superoxo with a shifted Glu 243 and the peroxide coordinated to iron in a μ-η², η¹ fashion. In the upper right, the peroxide adopts a μ-η²,η² butterfly arrangement. Both structures have been previously studied at the QM level. In the lower part, structures with peroxide coordinated to iron in a cis-μ-1,2 fashion are presented. On the left, the structure is similar to H_superoxo with a shifted Glu 243 (Aμ12H_peroxo), while on the right (Sμ12H_peroxo) it is similar to the μ-η²,η² butterfly peroxo arrangement with Glu 243 having the same conformation as in the crystal structure of the oxidized form.

The QM/MM μ-η²,η² butterfly structure displays a noticeable similarity to its pure QM counterpart (in both the undecet and singlet states); the RMSD between them is only 0.59 Å for both states. The Fe1-Fe2 distance in the QM/MM model (3.48 Å) is smaller than that in the undecet and singlet QM models (3.64 Å and 3.61 Å respectively, Table 3 and Table S-3), and the value of the dihedral angle Fe1-O1-O2-Fe2 (defined in Figure 8) is 144.8°.

Table 3.

Iron-Iron distances (in Å) for intermediates as calculated with QM/MM models and with big models at the pure QM level.^19c

Species	Sz(Sz+1)	QMM/MM	QM	Difference
Hred	9	3.29	3.64	0.35
Hred-no-wat	9	3.38	3.76	0.38
Hsuperoxo	11	3.44	3.79	0.35
Hsuperoxo	3	3.41	3.65	0.24
Hsuperoxo	1	3.46	3.51	0.05
Hperoxo (μ-η 2,η 2)	1	3.48	3.61	0.13
Hperoxo (μ-η 2,η 1)	1	3.27	3.36	0.09
Hperoxo (Aμ12)*	1	3.47	3.57	0.10
Hperoxo (Sμ12)*	1	3.64	4.02	0.38
HQ*	1	2.84	2.70	−0.14

Figure 8.

Geometry of the μ-η²,η² butterfly structure of H_peroxo and different conformers for the Aμ-1,2 H_peroxo structure. The dihedral angle between iron atoms and the peroxide moiety (φ) is also defined (Fe1-O1-O2-Fe2). The first gauche conformation (top left) has a negative angle close to −30 and the second conformer has a positive one close to 40. These two conformers have similar energies and have similar structures as those found in cis-μ-1,2-peroxo model compounds.²⁶ The last conformer (top right) is closer to the structures found in other cis-μ-1,2-peroxo model compounds.⁹¹, ⁹²

The μ-η²,η¹ (also called asymmetric APER¹⁹) structure proposed for H_peroxo is very similar structurally to the analogous geometry proposed for H_superoxo. The main differences observed are:

• - a more pronounced shift of Glu 243 in the peroxo species so that the oxygen bridges both irons more symmetrically.

• - a slight shift of dioxygen closer to both iron atoms and mainly toward Fe1.

The QM/MM structure obtained here is slightly different from the pure QM model previously obtained (RMSD of 0.77 Å). The protein modestly decreases the iron-iron distance from 3.36 Å to 3.27 Å. The dihedral angle involving the peroxide moiety and the iron centers is 102.6°.

Two structures were tested for the cis-μ-1,2 H_peroxo species. One (Aμ-1,2 H_peroxo) was based on the μ-η²,η¹ H_peroxo (asymmetric structure: Aperoxo) and the other (Sμ-1,2 H_peroxo) on the μ-η²,η² butterfly structure (Speroxo) (Figure 7). The QM/MM structure of Sμ-1,2 H_peroxo is very similar to that of the μ-η²,η² butterfly H_peroxo species with distances of 1.87 Å between the closer oxygen atom of the peroxo moiety and both Fe1 and Fe2. The Fe-Fe distance increases from 3.48 Å in the μ-η²,η² structure to 3.64 Å in the Sμ-1,2H_peroxo structure. This increase is relatively large compared to those for the other species and is probably due to the lack of a single-atom bridge between the iron atoms and the subsequent increased electrostatic repulsion between the two cations. This effect is more marked in the full QM calculation for which the Fe-Fe distance reaches 4.02 Å in the Sμ-1,2 structure compared to 3.61 Å for μ-η²,η² H_peroxo (Table 3). These results again emphasize the role of the protein, which tends to reduce the Fe-Fe distance, and suggest that this structure should be relatively high in energy in the protein matrix given the significant difference between QM and QM/MM iron-iron distances.

For the Aμ-1,2H_peroxo structure, based on the results from model compounds,^{26, 91, 92} three kinds of conformers might be considered depending on the value of the dihedral angle defined by the irons and oxygen atoms (Figure 8). Our QM/MM calculations evaluated these three different conformers in the protein environment. The cis conformer (Figure 8) was discarded since it is higher in energy by 10–15 kcal/mol than its counterparts. The two gauche structures have similar energies, and their Fe-O-O-Fe units resemble the structure of a model compound studied by Kim and Lippard²⁶ in which the corresponding dihedral angles is 53°. In the discussion below, we only describe the lowest energy structure (top middle in Figure 8).

The correspondence between the structure of Aμ-1,2 H_peroxo and those of the μ-η²,η² H_peroxo and μ-η²,η¹ H_peroxo is quite good. Their respective RMSDs are 0.24 Å and 0.19 Å ignoring the peroxide moiety and Glu 243 in the case of μ-η²,η² H_peroxo. This good agreement is also reflected by the Fe-Fe distance (Table 3), since the value in Aμ-1,2H_peroxo is essentially the same as found in μ-η²,η² H_peroxo. Therefore, the Aμ-1,2 H_peroxo structure seems to be a reasonable candidate for the H_peroxo intermediate in the protein environment. But the geometries of the peroxide moieties in the three structures are very different. The Aμ-1,2 and μ-η²,η¹ structures display short oxygen-oxygen distances (1.33 Å and 1.38 Å respectively), whereas in the μ-η²,η² structure this distance is substantially greater (1.49 Å). Based on compounds present in the Cambridge Structural Database,⁹³ these distances clearly indicate that the Aμ-1,2 and μ-η²,η¹ structures are more consistent with a superoxo species (1.33 Å), whereas the peroxo μ-η²,η² structure actually resembles a peroxide (1.45 Å). This assignment is further supported by the electronic structure analysis below.

The singlet μ-η²,η² butterfly structure affords two pseudo-octahedral environments at the iron atoms. Five virtual orbitals are centered on each iron atom and one empty σ* orbital is centered on the dioxygen moiety. This electronic structure is consistent with two anti-ferromagnetically coupled high-spin Fe(III) atoms, as found experimentally,^{20, 21} in octahedral environments.

On the other hand, the electronic structure of Aμ-1,2 H_peroxo can best be described as intermediate between a superoxo and a peroxo species because the second electron transfer does not appear to have been completed. Analysis of the orbitals shows that a π* orbital of dioxygen is not totally filled and that Fe1 is still partly in its reduced state (see Supporting Information). Thus, Aμ-1,2 H_peroxo is more consistent with a superoxo structure with strong charge transfer from Fe1(II) to the dioxygen moiety. The electronic structures of the μ-η²,η¹ H_peroxo and Sμ-1,2H_peroxo species are also better described as a superoxo species (see Supporting Information).

To characterize further the differences between the μ-η²,η² butterfly and the cis-μ-1,2 H_peroxo structures, we have also analyzed the frequencies corresponding to the O-O and Fe-O stretching modes for both ¹⁶O₂ and ¹⁸O₂ to determine the isotopic shift (a B3LYP/6-31G* scaling factor of 0.9614⁹⁴ was used for all frequencies). In case of the cis-μ-1,2 H_peroxo, a ν(¹⁶O-¹⁶O) frequency of 1004 cm⁻¹ was computed, compared to a value of 888 cm⁻¹ for a model compound²⁶ (Table 4). A shift of 48 cm⁻¹ was found in the case of the doubly isotopically substituted ¹⁸O₂, in good agreement with the shift of 46 cm⁻¹ observed experimentally.²⁶ The ν(Fe-¹⁶O) frequency was computed to be 441 cm⁻¹ with an isotopic shift of 20 cm⁻¹, compared to 415 cm⁻¹ [Δ¹⁸O=11cm⁻¹]²⁶ for the experimental results. In case of the μ-η²,η² H_peroxo structure, we obtained a ν(¹⁶O-¹⁶O) frequency of 815 cm⁻¹ and a ν(Fe-¹⁶O) value of 544 cm⁻¹ with isotopic shifts of 44 cm⁻¹ and 15 cm⁻¹ respectively. There is currently no model complex with this structure.

Table 4.

Summary of the frequencies for the ν(O-O) and ν(Fe-O) modes obtained from our theoretical models of A- μ1,2 H_peroxo and μ, η², η² H_peroxo.^d

	ν (16O-16O) (cm−1)	Δ [18 O2] (cm−1)	ν (Fe-16O) (cm−1)	Δ [18O2] (cm−1)
A-μ1,2 Hperoxo	1004 (975)	48	441 (429)	20
Fe2 (μ-O2)[(μ-O2CPh)]2 [HB(pz′)3]226	888	46	415	11
μ, η2, η2, Hperoxo	815 (823)	43.8	544 (473)	15.4

The higher ν(¹⁶O-¹⁶O) frequency found for the cis-μ-1,2 H_peroxo compared to the μ-η²,η² H_peroxo structure reveals its greater O-O bond order, and thus supports the superoxide character revealed by the electronic structure analysis. Compared to experiment, our calculations reveal enhanced superoxide character for this structure in the protein. In order to investigate whether a basis set effect was responsible for this behavior, the QM/MM models for the cis-μ-1,2 and the μ-η²,η² H_peroxo models were optimized again by using the lacv3p** basis set on iron atoms and the cc-pVTZ(-f)++ on both oxygen atoms of the peroxide. The frequency calculations were then performed with the same modifications to the usual basis set. The results obtained show that, from a structural point of view, the basis set has an effect since the peroxo oxygen-oxygen distance increases from 1.33 Å to 1.37 Å in case of the cis-μ-1,2 H_peroxo and from 1.49 Å to 1.51 Å in the case of the μ-η²,η² structure. These results indicate that the superoxo character of the cis-μ-1,2 H_peroxo is overestimated without the use of large basis sets (including diffuse functions) on the diiron core. Furthermore, the theoretical frequencies obtained with the large basis sets are in better agreement with experimental results on model compounds even without scaling (Table 4). For instance, the ν(¹⁶O-¹⁶O) frequency of the cis-μ-1,2 H_peroxo structure decreases to 975 cm⁻¹ due to the decreased superoxo character, but it is still not enough to reach a good agreement with the model compound (888 cm⁻¹).

The frequency obtained for the cis-μ-1,2 H_peroxo structure indicates that it has a strong superoxo character, even when large basis sets are used. This frequency is intermediate between the ranges of experimental frequencies usually assigned to peroxo and to superoxo as defined by Suzuki et al.⁹⁵ based on different molecular oxygen complexes.

Intermediate Q

The last step of dioxygen activation involves reduction of H_peroxo by the transfer of two electrons from iron atoms leading to the cleavage of the O-O bond. The resulting di(μ-oxo)diiron(IV) structure (H_Q) can formally be described as two O²⁻ ions coordinated to two Fe(IV) cations.

The main difference observed between structures obtained at the QM/MM level and at the QM level (RMSD of 0.73 Å between them) are rotations of Glu 209 and Glu 114 leading to slight differences in the structure of the Fe₂(μ-O)₂ quadrilateral. Interestingly, in the QM/MM model, the Fe-O distances appear to be somewhat asymmetric with the oxygen atoms both being closer to Fe1 than to Fe2, with average distances of 1.75 Å and 1.90 Å respectively (Figure 9). Asymmetry has also been reported from an analysis of the results of EXAFS experiments on H_Q.³¹ Our calculations reveal that the two iron centers are not equivalent, indicating a slightly diminished (between Fe^IV and Fe^III) oxidation state for Fe2 as compared to Fe1 (Fe^IV). This results from the fact that Fe2 appears to be slightly more electrophilic than Fe1 and thus attracts more the electrons from the oxygen atoms. This is consistent with our previous study⁸⁹ showing that Fe2 is actually the first iron atom reduced during the reaction between H_Q and methane. The iron-iron distance is larger in the QM/MM models (2.84 Å) than in the QM one (2.70 Å) and significantly larger than found by the analysis of the EXAFS data (2.46 Å).³¹ Our QM models have also shown that the singlet state has nearly symmetric Fe-O distances (1.76 Å and 1.82 Å), whereas in the nonet state these bonds were very asymmetric (1.69 Å and 2.13 Å). The analysis indicates this result is derived from a higher oxidation level of Fe1 compared to Fe2 (formally a Fe^V-Fe^III core) (see Supporting Information).

Figure 9.

Asymmetric structure for H_Q derived from QM/MM calculations.

The electronic structure obtained for the singlet state of H_Q is in good agreement with that expected for a di(μ-oxo)diiron(IV) species and has been presented in a previous paper.⁸⁹ Nonetheless, compared to the μ-η²,η² butterfly H_peroxo, strong delocalization of oxo electrons onto the iron atoms can be noticed, supporting an increased covalency between iron and oxygen atoms as has recently been proposed based on oxoiron(IV) model compounds.^{96, 97}

Energetic analysis

In this section we analyze the energies of our computed reaction cycle components comparing relative energies for QM/MM with the purely QM models discussed in ref. [19]. We consider all states discussed above with the exception of that in which the water is displaced from the cavity prior to binding of dioxygen. This state is not experimentally accessible, and there are considerable complexities in dealing with the free energies of binding of small molecules to the protein. Furthermore, examination of the reduced MMO crystal structure reveals a different number of waters in the cavities of the two α-subunit protomers, and the presence or absence of a second water molecule would have a significant effect on the calculated free energies of the state in question.

Along the same lines, we note that energy differences between the reduced enzyme and oxygenated intermediates also involve an estimation of the binding affinity of dioxygen to the protein. As indicated above, these quantities are subject to some uncertainty, so our expectation is that the calculation of the relative energy of the reduced enzyme compared to the other species will have increased error bars due to these issues.

The large basis set QM/MM//UDFT single point energies, supplemented by frequency calculations on models as discussed above, provide the starting point for our energetic analysis. We have additionally investigated the effects of two types of correction terms. Firstly, we constructed a Heisenberg spin model in order to improve the relative energetics of AF spin states as modeled via broken symmetry and unrestricted wave functions; details of the methodology are given in Supporting Information. Secondly, we introduce a new set of corrections based on the localized orbital correction (LOC) approach discussed earlier. LOC assigns correction parameters for atomic hybridization states and for each electron pair in a bonding orbital, depending upon the type of bond and its local environment. Our assessment of the relative energetics of structures in the MMO catalytic cycle utilizes the following key parameters of the methodology, derived from fitting to the G3 data set as discussed in detail in ref. [78]:

1. An O atom is assigned a correction factor of 1.8 kcal/mol when sp³ hybridized, and 1.0 kcal/mol when sp² hybridized.

2. An ordinary O-O single bond is assigned a correction factor of −2.0 kcal/mol and a double bond, −1.0 kcal/mol.

3. An ionic bond (NaCl is the prototypical example) is assigned a correction factor of −4.5 kcal/mol. This parameter works remarkably well for a wide range of “ionic” pairs, not only NaCl but formal charge separations assigned on the basis of classical valence bond theory as, for example, in CO or ozone. The success in describing ozone is particularly relevant to the present task; the corrected B3LYP-LOC atomization energy error is only −1.87 kcal/mol whereas the B3LYP error is 8.6 kcal/mol.

The physical rational for these corrections is based on the localized nature of the residual errors in DFT methods, which arise from erroneous treatment of nondynamical correlations of both unpaired and paired electrons. For electron pairs, B3LYP underestimates nondynamical correlation when the “size” of the localized orbital containing the pair is “small” compared to the bond length. The discrepancy is particularly large for ionic bonds with long distances, as is the case here for a subset of the Fe-O interactions. The number of ionic (non-covalent) electron pairs on the core oxygen atoms increases as one goes from H_superoxo (one) to H_peroxo (two) to H_Q (four) and hence, according to the theory, the total energy of these species is increasingly overestimated. We argue below that the correction terms restore the proper relative energetics of our intermediates.

Results obtained from our QM/MM B3LYP calculations using the high level basis set with diffuse functions on dioxygen atoms are presented in Table 5 for all species found to be relevant at a lower computational level. The Heisenberg exchange coupling constants (Table 6) were calculated for H_red, H_peroxo and H_Q. Moreover, in the case of H_superoxo, the formula for spin-projection cannot be applied because the metals are not equivalent, but the error induced by neglecting spin projection should be small since the differences between high-spin and broken symmetry energies are rather insignificant (less than 1 kcal/mol).

Table 5.

Detailed breakdown of the QM/MM//UDFT free energies (at 298 K) relative to the reduced state of putative intermediates for the activation of dioxygen reaction proposed based on QM/MM//RDFT results.^e

Model	HRed	HSuperoxo (11)	HSuperoxo (3)	HSuperoxo (1)	HPeroxo Aμ-1,2 (1)	HPeroxo μ,η2,η1 (1)	HPeroxo μ,η2,η2 (1)	HQ (1)
ΔEQM/MM-UDFT	0	4.64	1.72	5.65	−3.40	−6.28	−9.27	−8.86
ΔZPE	0	−3.5	−3.66	−2.71	−3.38	2.95	−2.75	−2.37
ΔΔHCorrections	0	0.21	0.81	−0.09	1.17	0.23	−0.22	−0.22
ΔS	0	−4.68	0.54	−12.21	2.26	−8.98	−13.25	−16.02
−TΔS	0	1.39	−0.16	3.64	−0.67	2.68	3.95	4.78
Spin-projection Corrections	-	-	-	-	−0.08	−0.04	−0.90	−1.76
ΔH	0	1.35	−1.13	2.85	−5.69	−3.14	−13.14	−13.21
ΔG	0	2.74	−1.29	6.49	−6.36	−0.46	−9.19	−8.43

Table 6.

Heisenberg exchange coupling constants (J) and corrections to the BS energies induced by spin projection for the QM/MM model.

Species	Sz(Sz+1)	J (cm−1)	ΔE (kcal/mol)
HRed	9	−25	−0.29
HRed-no-wat	9	23	0.26
HPeroxo A (μ-1,2)	11	−6	−0.08
Hperoxo (μ-η2,η1)	11	−2	−0.04
Hperoxo (μ-η2,η2)	11	−63	−0.90
HQ	9	−154	−1.76

The relative energies of intermediates found in our QM/MM calculations, presented in Figure 10, are qualitatively comparable with those along the best path previously identified.¹⁹ Some quantitative differences emerged, however, between the present QM/MM study and our previous purely QM models.

Figure 10.

Schematic reaction energy profile of the QM/MM intermediates as found with B3LYP (gray) and B3LYP-LOC (black).

First, we re-evaluated μ-1,2 models for the controversial structure of the H_peroxo intermediate. Our results show that the Aμ-1,2 H_peroxo structure appears to be slightly higher in energy compared to the μ-η²,η² species (Table 5). Nonetheless, given the relatively small energy difference, this structure might be a putative intermediate between H_superoxo and the μ-η²,η² form of H_peroxo. On the other hand, the Sμ-1,2 H_peroxo species which lacks a bridging atom between the iron atoms, was computed to be much higher in energy than the μ-η²,η² structure at the QM/MM//RDFT level. This species was therefore discarded as a possible intermediate in the reaction mechanism and further calculations were not performed on it.

The second main difference between the QM and QM/MM calculations is related to the relative energy between μ-η²,η² H_peroxo and H_Q. Actually, in our QM/MM calculations (Table 5), H_Q is higher in energy than H_peroxo by 0.7 kcal/mol. This result is surprising because experimentally H_Q can be kinetically trapped^{3, 8} and the reaction should thus be exothermic, presumably by a significant margin compared to kT, or one would see residual population of H_peroxo experimentally. Previous authors using different computational models have encountered the same problem.^{98, 99} Moreover, our new results are in contradiction to our previous findings reported in ref. [19], in which H_Q was 11.7 kcal/mol¹⁹ lower in energy than H_peroxo. The reason for this discrepancy has been identified as a structural difference between our QM/MM models of H_Q and the large QM model previously employed.¹⁹ In our QM models, Asp 242-Glu 243 peptide displays a different conformation than that in the crystallographic structures^{80, 81, 87} or other QM or QM/MM models (See Supporting Information Figure S-17). As pointed out by Siegbahn,¹⁰⁰ this previous conformation allows the formation of a new hydrogen bond between the dangling oxygen atom of Glu 243 and a backbone N-H unit. To check whether this new hydrogen bond was responsible for the significant stabilization of H_Q over H_peroxo in our large QM models in ref. [19], we constructed a big QM model of H_peroxo with the same backbone conformation. Our results reveal that this hydrogen bond also strongly lowers the energy of H_peroxo. However, the present QM/MM calculations indicate that such a hydrogen bond does not form inside the protein for either H_Q or H_peroxo due to the constraints and hydrogen bond network generated by the protein fold which are not present in the purely QM models. Thus the overstabilization of H_Q due to this hydrogen bond is no longer possible in the QM/MM models, and H_Q becomes slightly less stable than H_peroxo when calculated with the B3LYP density functional, as indicated above.

Because the above QM/MM results for the relative energies of H_peroxo and H_Q were in disagreement with experiment, we investigated whether this discrepancy could be explained by the intrinsic errors of B3LYP. We applied the B3LYP-LOC scheme outlined above, with simple approximations as discussed in Supporting Information, to the results obtained for all the structures previously found to be relevant for the dioxygen activation reaction. These findings are presented in Table 7. As can be seen, the corrections of the B3LYP-LOC scheme favor the dioxygen activation by MMO as a whole, because the series of intermediates contains an increasing component of charge transfer from the iron to the dioxygen atoms in the core (Figure 10). The correction is particularly important for the relative energies of H_peroxo and H_Q. We can see that, with B3LYP-LOC, H_Q is much more stabilized than H_peroxo. Based on this preliminary analysis, B3LYP errors may be the reason for the lower energy of H_peroxo compared to H_Q reported above. We hypothesize that these errors mainly arise due to underestimation of the contribution of ionic character bonds in using standard B3LYP results and the fact that these bonds are strongly involved in the dioxygen activation reaction.

Table 7.

Detailed breakdown of the B3LYP-LOC calculation based on the B3LYP free energies obtained using a big basis set with diffuse functions on atoms of dioxygen.^f

Model	HRed	HSuperoxo (11)	HSuperoxo (3) (red)	HSuperoxo (3) (1/2,1/2)	HSuperoxo (3) (superoxo)	HSuperoxo (1)	HPeroxo Aμ-1,2 (1)	HPeroxo μη2,η2(1)	HQ (1)
ΔG(B3LYP)	0	2.74	−1.29	−1.29	−1.29	6.49	−6.36	−9.19	−8.43
AT	2×1.0	2×1.0	2×1.0	1.0+1.4	1.0+1.8	1.0+1.8	2×1.8	2×1.8	2×1.0
BOND	−1.0	−1.0	−1.0	−0.5+-0.75	−0.5+-1.0	−0.5+-1.0	−2.0	−2.0	0.0
EBSC	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
RAD	2×1.7	2×1.7	2×1.7	1.7+0.85	1.7	1.7	0.0	0.0	0.0
CT	0.0	0.0	0.0	−2.25	−4.5	−4.5	2×−4.5	2×−4.5	4×−4.5
TOT Corrections	4.4	4.4	4.4	1.45	−1.5	−1.5	−7.4	−7.4	−16
ΔG(B3LYP-LOC)	0	2.74	−1.29	−4.24	−7.19	0.59	−18.16	−20.99	−28.83

Discussion

Nature of the H_peroxo intermediate

Several structures for H_peroxo have been investigated in this study. The results obtained allow us to discard the Sμ-1,2(1) H_peroxo based on its high energy compared to the other structures. It lacks a bridging ligand between the iron atoms that stabilizes the other structures. The QM/MM//RDFT results show that the μ-η²,η² H_peroxo and the Aμ-1,2 H_peroxo species are very similar in energy, whereas the μ-η²,η¹ H_peroxo is slightly higher. Finally, our QM/MM//UDFT results indicate that the μ-η²,η² H_peroxo is actually lower in energy than the Aμ-1,2 H_peroxo by 2.8 kcal/mol in the protein environment.

In the case of a ribonucleotide reductase variant,⁹⁰ the peroxo intermediate has a cis-μ-1,2 peroxo diiron(III) core structure. Although our pure QM calculations are compatible with such a hypothesis for H_peroxo, QM/MM models reveal that this structure is destabilized in the protein. Analysis shows that the main differences involve the two histidines which rotate in the QM model, and Glu 243, which forms a much better bridge in the QM structure. An important difference between the QM and QM/MM models is the 0.10 Å shorter iron-iron distance in the latter. This distance is consistent with the effect of the protein observed for all the species involved in the O₂ activation, from which, the energy discrepancy between the QM and QM/MM models can be rationalized. The energy of the Aμ-1,2 H_peroxo structure should be more sensitive to this distance because the overlap between the peroxo and iron orbitals will depend strongly on it. This point is supported by the fact that the Aμ-1,2 H_peroxo with a cis conformation (ϕ ~ 0 in Figure 8) is strongly destabilized by including the protein in our models. Therefore, the fact that the μ-η²,η² core structure is preferred over the Aμ-1,2 H_peroxo structure in MMOH appears to be a consequence of the fact that strain induced by the protein environment decreases the iron-iron distance.

As noted by Solomon et al.,⁹⁰ it is difficult to understand the similarity between the optical absorption spectra of the peroxo species in MMOH and RNR-R2 given that they have different binding modes. One possibility is that two peroxide species may be formed along the O₂ activation pathway. The energetics obtained in the current study and the sequence of structural and electronic changes that occur along the cycle are not inconsistent with such a hypothesis. Indeed, all our analyses of the Aμ-1,2 H_peroxo and the μ-η²,η² structures support the fact that the latter has a true peroxo nature whereas the former is intermediate between a superoxo and a peroxo species. The fact that Aμ-1,2 H_peroxo prevents a complete electron transfer to give a true peroxo species makes it a poor candidate for generating H_Q, which requires such a new electron transfer. In this context the μ-η²,η² structure appears to be a much better candidate for the intermediate preceding the formation of H_Q. Notably, a Q-type intermediate does not appear to form in ribonucleotide reductase. Possibly MMOB is involved in stabilizing the H_peroxo form that converts to H_Q. The possibility that two peroxo intermediates occur has been previously proposed by Lippard et al.²³ to explain the discrepancy between the rates of formation of H_peroxo as determined by stopped-flow optical spectroscopy and by Mössbauer or optical spectroscopy.

To summarize, our QM/MM calculations are in better agreement with a μ-η²,η² structure for H_peroxo prior the formation of H_Q, and do not exclude the possible existence of another intermediate between H_superoxo and H_peroxo having the structure of Aμ-1,2 H_peroxo.

QM/MM structure of H_Q

The structure obtained for H_Q in the current study features asymmetric coordination of the oxygen atoms that bridge the iron atoms, as was observed experimentally.³¹ This result is particularly interesting because our previous calculations at the QM level yielded a symmetric structure for the singlet state. The nonet state, very close in energy, was strongly asymmetric. This asymmetric structure was shown to be better described in terms of an Fe(III)-Fe(V) diiron core, whereas the symmetric case was better represented as an Fe(IV)-Fe(IV) diiron core. The protein environment, and most likely its electrostatic field, is probably responsible of some kind of mixing between these two oxidation state extrema. The calculations also demonstrate that the electronic structure of H_Q is particularly sensitive to the chemical environment since the geometry of the diiron core changes depending on the coupling chosen for the diiron core, and whether or not the protein is included in the model.

Role of the protein in dioxygen activation

The most interesting finding of the present QM/MM calculations is that the protein seems to play an active role in the catalysis, principally by differentially compressing the Fe-Fe distance for the various species in the catalytic cycle. This effect is consistently observed along the path from H_red to H_peroxo (Table 3). It has also been observed for H_red using ONIOM methods⁵⁰ but, whereas with our QM/MM methodology the agreement with the experimental Fe-Fe distance is very good (~ 0.02 Å), the results with ONIOM method were significantly less accurate (0.15–0.25 Å), probably due to quantitative errors in the QM/MM interface model employed in ref. [50].

From an energetic point of view, the effect of the protein is to decrease (make more negative relative to H_red) the energy of species between H_red and H_peroxo (Table 5 and discussion on the QM/MM//RDFT calculations in Supporting Information). It is therefore tempting to correlate stabilization with compression of the iron-iron distance. In this sense, the most reasonable explanation for the effect of the protein would be that it preferentially destabilizes H_red because the largest compression of the iron-iron distance is observed for this species. This strain energy is then released along the reaction pathway until arriving at H_peroxo. This hypothesis, previously suggested by several authors,^{41, 49} is strongly supported by our current results.

It is interesting that the protein appears to increase, rather than decrease, the Fe-Fe distance for our model of H_Q (by 0.14 Å). From a physical point of view, this result is not necessarily inconsistent with the behavior of the remaining species; the gas phase Fe-Fe separation for H_Q is substantially shorter than for any other structure, so if the protein forces are generated by an effective harmonic model with an implicit equilibrium distance intermediate between this value (2.70 Å) and the typical gas phase separation in the remaining species (~3.5 Å), the observed results can easily be rationalized. It is beyond the scope of the present paper to analyze the protein forces in sufficient detail to establish whether this picture is correct, but such an investigation is possible in principle, and will be considered in future publications.

There is finally, as noted above, an apparently large discrepancy between the calculated Fe-Fe distance for H_Q (2.84 Å) and the value extracted from analysis of EXAFS data in ref. [31] (2.46 Å). The excellent agreement that we now obtain for the structure of H_red with the crystallographic data of ref. [86] provides some confidence that the B3LYP/QM/MM methodology employed herein is capable of generating accurate structural predictions, given a reasonable initial starting geometry and electronic wavefunction. At the moment, we have to regard this discrepancy as an unresolved problem, with a number of possible solutions: (1) the structure of Q might be qualitatively different from what we assume here (although we are not aware of other plausible candidate structures with competitive energies that have been proposed); (2) the binding of MMOB might significantly alter the active site geometry, resulting in the reduction of the Fe-Fe distance; (3) There may be some difficulties in the interpretation of the EXAFS data. All of these avenues will need to be pursued in order to achieve convergence of theory and experiment.

Conclusion

The present theoretical QM/MM models reveal how the protein matrix can influence the diiron active site of MMOH by compressing the iron-iron distance. The energetic consequences are that the intermediates closer to the reduced form in the proposed reaction pathway (Figure 11) are more destabilized by the protein than those closer to H_Q.

Figure 11.

Destabilization energies (in kcal/mol) due to the protein matrix computed from our QM/MM//RDFT models (Δ[E_QM/MM - E_QM-RODFT] with H_Q taken as a reference in Table S-4 and discussion on the QM/MM//UDFT and QM/MM//RDFT in Supporting Information). The protein matrix effects destabilize more intermediates closer to the reduced form in the reaction pathway.

Different structures were investigated for H_peroxo. The results obtained with QM/MM models reveal that the cis-μ-1,2 H_peroxo is 2.8 kcal/mol higher in energy than the μ-η²,η² H_peroxo structure. Electronic structure and frequency calculations revealed that the cis-μ-1,2 H_peroxo species is intermediate between a superoxo and a peroxo species. These results suggest that a cis-μ-1,2 H_peroxo intermediate could precede the formation of the μ-η²,η² butterfly structure.

Very close energies were found for the μ-η²,η² H_peroxo and H_Q intermediates. By applying the B3LYP-LOC scheme recently developed in our laboratory, we suggested that this result is a consequence of systematic errors in the B3LYP functional. Although preliminary results obtained by applying a highly approximate version of our B3LYP-LOC methodology to the problem are encouraging, further investigation will required to ascertain the quantitative value of these corrections.

Supplementary Material

1. Supporting Information Available.

Thermodynamical cycle used in the QM/MM//RDFT studies, detailed electronic structure analysis of the species along the cycle, broken symmetry corrections methodology, structure of H_red-no-wat (Figure S-3), comparison of the QM/MM//RDFT versus QM/MM//UDFT scheme, spin populations, results for the QM/MM//RDFT models (Tables S-3, S-4), comparison of our previous pure QM structure for Q with our current QM/MM model (Figure S-17) and Complete ref 57.