A new method for estimating the usual intake of episodically-consumed foods with application to their distribution

Abstract

Objective

We propose a new statistical method that uses information from two 24-hour recalls (24HRs) to estimate usual intake of episodically-consumed foods.

Statistical Analyses Performed

The method developed at the National Cancer Institute (NCI) accommodates the large number of non-consumption days that arise with foods by separating the probability of consumption from the consumption-day amount, using a two-part model. Covariates, such as sex, age, race, or information from a food frequency questionnaire (FFQ), may supplement the information from two or more 24HRs using correlated mixed model regression. The model allows for correlation between the probability of consuming a food on a single day and the consumption-day amount. Percentiles of the distribution of usual intake are computed from the estimated model parameters.

Results

The Eating at America's Table Study (EATS) data are used to illustrate the method to estimate the distribution of usual intake for whole grains and dark green vegetables for men and women and the distribution of usual intakes of whole grains by educational level among men. A simulation study indicates that the NCI method leads to substantial improvement over existing methods for estimating the distribution of usual intake of foods.

Applications/Conclusions

The NCI method provides distinct advantages over previously proposed methods by accounting for the correlation between probability of consumption and amount consumed and by incorporating covariate information. Researchers interested in estimating the distribution of usual intakes of foods for a population or subpopulation are advised to work with a statistician and incorporate the NCI method in analyses.

When using dietary assessment among populations or individuals, investigators are often interested in capturing usual intakes – that is, long-term averages. The 24-hour dietary recall (24HR) provides rich details about dietary intake for a given day, but collecting more than two 24HRs per individual is impractical in large surveys such as the National Health and Nutrition Examination Survey (NHANES). Therefore, it is necessary to employ statistical methods to estimate usual dietary intake.

Researchers are interested in estimating the usual intake of foods to assess compliance with food-based dietary recommendations and to relate food intake to health parameters. Unlike most nutrients, which are consumed daily, estimating usual intake of episodically-consumed foods presents the following unique challenges for statistical modeling (see the Glossary for a definition of “statistical modeling” and related terms):

Glossary.

Definitions of common statistical terms and their use in the usual food intake model

Statistical Term	Definition	Use in usual food intake model
Statistical Model	A model is a mathematical formula used to quantify the relationship between two or more variables. The model is “statistical” when it also incorporates uncertainty in the relationship between the variables.	A statistical model is used to estimate usual food intake and to relate it to other variables of interest.
Two-part model	Sometimes there is a need for a more complex statistical model that includes two component parts.	In this paper, the model for food consumption models the probability of consuming a food as well as the usual amount consumed
Outcome Variable	The variable of interest in the analysis. Sometimes referred to as the dependent variable.	Usual food intake is the outcome variable for the two-part model. It is derived as the probability of consuming the food multiplied by the amount consumed on a consumption day.
Covariates	Variables that are related to the outcome variable. The term “covariate” is used to describe a general class of variables that may be of most interest, define a subpopulation, need to be adjusted for in the statistical analysis. Sometimes referred to as independent variables.	Responses to line items from a food frequency questionnaire may be used as a covariate to improve estimation from the 24HR alone; variables such as age and race may be used to define subpopulations for which usual intake is estimated.
Person-specific random effect	A term that is specific to an individual that refers to how an individual's value deviates from the average. It is considered “random” because the individuals in the study are considered as a random sample from a larger population.	Both parts of the statistical model include a person-specific random effect that describes the individual's frequency of consuming a particular food and the amount consumed.
Normality	Refers to a statistical distribution of a variable, specifically a bell-shaped curve. The tails of the normal distribution refer to the extreme values. If the data do not follow a normal distribution, then many commonly used statistical methods can not appropriately be used. By applying a function, such as the logarithm, data can be transformed to a more normal distribution	The amount part of the model is transformed to normality (using a Box Cox (power) transformation). In the model, the normality assumption must hold for the random effects after including the covariates of interest in the model. Including the covariates may help to make the distribution of these random effects more normally distributed.
Correlation	If two variables are associated with each other, they are said to be correlated. The opposite of correlation is independence, in which a change in one variable does not impact the value of another variable.	In this model, there are two types of correlation. First, the two person-specific effects are correlated. This means that we allow the individual's tendency to consume a food to be related to the amount that he or she consumes. Second, the covariates in the model are correlated with the outcome (food intake). For example, persons who report a higher frequency of intake on the FFQ generally have a higher probability of consuming a food on the 24HR.
Simulation Study	A simulation study is a method that statisticians use to validate their models. Many hypothetical random samples are generated (i.e., simulated), and statistical estimates are computed for each sample. The results are then averaged and compared to the “truth” that was used to generate the model.	In this paper, simulations were used to generate 365 days of pseudo-data for a series of individuals. Then different statistical methods to obtain estimates of the distribution of usual intake were run using the same generated data sets. Finally, these estimated distributions were compared to truth.

FFQ: Food Frequency Questionnaire

24HR: Twenty-four hour recall

1. accounting for days without consumption of a particular food or food group;

2. allowing for consumption-day amount data that are generally positively skewed and have extreme values in the upper tail of the intake distribution;

3. distinguishing within-person variability, which consists of day-to-day variation in intake and random reporting errors, from between-person variation;

4. allowing for the correlation between the probability of consuming a food and the consumption-day amount; and,

5. relating covariate information (for example, sex, age, race, ethnicity, or education level) to usual intake (1).

As discussed in Dodd et al. (1), two other methods have been used to estimate the distribution of usual intake of episodically-consumed foods with a few days of 24HRs: (i) the distribution of within-person means (WPM), and (ii) the method developed at Iowa State University for estimating the distribution of foods (ISUF) (2). The WPM method usually leads to biased estimates of the prevalence of either inadequate or excess food intake because it does not meet any of the challenges listed above. In particular, because the WPM method does not meet challenge (C), and thereby includes within-person variability, the variance of usual intake is inflated. The ISUF method meets the first three challenges, but it does not allow for correlation between probability and amount and cannot incorporate covariate information regarding usual intake.

This paper describes a new statistical method that was developed at the National Cancer Institute (NCI) to meet all five of the challenges noted above, using two 24HRs, and evaluates the new statistical method's application to estimating the distribution of usual intake of episodically-consumed foods.

Methods

Assumptions of the NCI Method

In the NCI method, we assume that the 24HR is an unbiased instrument for usual intake of episodically consumed foods. This assumption has two components. First, we assume that the 24HR does not misclassify the respondent's food consumption, i.e., if a food actually is consumed on a surveyed day, the food will be reported on the 24HR; and if a food is not consumed, it will not be reported on the 24HR. Second, we assume that the 24HR is an unbiased measure for the amount of food consumed on the consumption day. This does not mean that the 24HR captures the amount of food consumed by an individual exactly on each recall – at a given time an individual may report more or less than was actually consumed – but over many days it produces the correct average intake. This assumption will be discussed in detail later in the paper. In addition to the assumptions made about the 24HR, we make the usual assumptions for parametric regression analysis in our models. In particular, we assume that, after an appropriate transformation, the amount of food consumed on a consumption day is approximately normally distributed.

Overview of the NCI Method

The NCI method for estimating the usual intake of foods has two steps. The first step consists of fitting a two-part statistical model that describes the relationship between usual intake and covariates and estimates the variability of intake both within and between individuals. We adapted a two-part model with correlated person-specific random effects, developed by Tooze et al. (3), for this purpose. Similar to the ISUF method, the statistical model represents usual intake as the product of the probability to consume a food on a given day and the usual consumption-day amount. The amount data are transformed to approximate normality, using the Box-Cox transformation (4), as part of the model-fitting process. To account for the correlation between the probability and amount that exists for most foods, as described below, the two parts of the model are linked.

The second step of the method involves additional statistical procedures that, depending on the application of interest, are used to obtain the final “product” of the analysis. Examples of those products include estimates of the distribution of usual intake in a population or subpopulation of interest, or estimates of individual intakes. The latter may be used to assess diet-health relationships. Because these are clearly varying endpoints, different statistical procedures are required. However, because the data share a common structure in each case, the same statistical model is used to obtain parameter estimates, which are the inputs for the final step. This paper focuses on the statistical model and its application for estimating the distribution of usual intake for populations and subpopulations. Predicting individual usual intake and relating it to health outcomes are beyond the scope of this paper.

Details of the NCI Method

Statistical Model

The first part of the model estimates the probability of consuming a food (positive intake reported on the 24HR) using logistic regression with a person-specific random effect (mixed model). The logistic regression model incorporates covariates to represent the effect of personal characteristics, such as age, sex, or body mass index, on the probability of food consumption. The person-specific effect is a factor that allows an individual's consumption probability to differ from the population level. It may be thought of as the individual's personal tendency to consume a food. The probability of consumption is estimated from two or more 24HRs, accounting for covariates. Symbolically, Part I may be represented as:

$${\text{Logit}(\text{24HR Probability})=\text{Intercept}}_I+{\text{Slope}}_I\times {\text{Covariate}+\text{Person-Specific Effect}}_{\text{I}}$$ [1]

where, for probability p, $\text{logit}(\text{p})=\text{log}\left(\stackrel{\text{p}}{}/\underset{1-\text{p}}{}\right)$. The intercept, slope, and variance of the person-specific effect are the model parameters, and subscript I indicates their association with Part I. Although one covariate is shown in equation [1], the model allows for multiple covariates or no covariates.

The second part of the model specifies the consumption-day amount of a food using the 24HR data on a transformed scale. Similar to Part I, Part II may incorporate covariate information to estimate amount. As before, the covariates, which need not be the same covariates as in Part I, represent the effect of personal characteristics on the consumption-day amount. This part of the model also includes a person-specific effect as well as within-person variability due to day-to-day variation in an individual's intake and other sources of random error. The model for Part II is:

$${\text{Transformed 24HR Amount}=\text{Intercept}}_{\mathrm{II}}+{\text{Slope}}_{\mathrm{II}}\times {\text{Covariate}+\text{Person-specific Effect}}_{\mathrm{II}}+{\text{Within-person Variability}}_{\mathrm{II}}$$ [2]

where subscript II indicates that these parameters are associated with Part II, and differ from those in Part I. Two or more 24HRs on a number of individuals with reports of the food of interest are required to distinguish between- and within-person variation. The model is specified on the transformed scale where the person-specific effect and within-person random variability are normally distributed.

Links Between Parts I and II

Unlike the ISUF method, in which the two parts of the model are assumed to be independent and are estimated separately, the NCI method fits both parts simultaneously, which associates probability to amount in two different ways. First, the two person-specific effects are modeled as correlated random variables. Second, some covariates may be the same in both parts of the model, inducing correlation between them. By linking the two parts of the statistical model, the relationship between probability and amount is accounted for, meeting challenge (D) stated previously.

Fitting the Model

The model is fit by the maximum likelihood method, using a SAS software (version 8.2, SAS Institute, Cary, NC) macro. To account for the correlation, all of the model parameters are estimated at the same time using a non-linear mixed effects model. In addition, the Box-Cox transformation parameter is also estimated as part of the likelihood maximization procedure. The advantage of using the normality transformation within the modeling step, not before modeling as in other methods, is that the 24HR-reported amount is transformed to normality conditionally on the covariates in the model. Estimates are obtained for the model parameters presented in equations [1] and [2], and for the correlation between the person-specific effects.

Adding Information from Food Frequency Questionnaires (FFQ) as Covariates

As described by Subar et al. (5), frequencies from an FFQ, NCI's Diet History Questionnaire (DHQ), are generally positively related to the proportion of 24HRs with reported consumption of those foods. This demonstrates that food frequency information could be a useful covariate in estimating the probability of consumption. Additionally, because of the correlation between the probability of consumption and the amount consumed, frequency responses can contribute to estimating not only probability to consume, but amount as well (5). The sum of the frequencies of several individual FFQ items may be used to represent the frequency of consumption of a food group containing them. The relationship between the FFQ and the 24HR is often non-linear. Consequently, a polynomial model may be used to model the relationship between the FFQ and 24HR.

Estimating the Distribution of Usual Intake for the Population

To estimate the distribution of usual intake, the estimated model parameters are used to simulate a population that has the same characteristics (as described by the values of the covariates) and between-person variability as the sample on which the model was fit. The within-person variation in model [2] is not included since, by definition, it does not contribute to long-term intake.

First, the estimated intercept and slope(s) for the covariate(s) are used to obtain for each individual in the sample an estimate based on the covariate values used to fit the model. To these, it is necessary to add an estimate of the person-specific random effects. Because these effects are unobservable, we generate an estimate from their statistical distribution (bivariate normal with mean zero and variance parameters estimated from fitting the statistical model). To improve the precision of the estimated usual intake distribution, we generate 100 pseudo-persons for each individual in the sample, each with the same covariate values but different simulated person-specific effects.

Because we transform the consumption-day amount data using the Box-Cox transformation during the model fitting process, it is necessary to back-transform the amount data to the original scale before we can obtain estimates of the distribution of usual intake. The back-transformation is similar to the approach used in the method developed at Iowa State University for estimating usual nutrient intake distributions (6). It adds an adjustment term to make the mean of the back-transformed variable match the mean on the original scale as described by Dodd et al (1). Lastly, the mean, standard deviation, and percentiles are estimated empirically from this simulated population.

Estimating the Distribution of Usual Intake for a Subpopulation

Estimates of the distribution of usual intake for a subpopulation are made in the same way as those for the total population, except that covariates that define the subgroup are included in the NCI model. When making the estimates for a subpopulation, only the covariate values differ; all other variance components remain the same. This specification leads to smaller standard errors of estimated parameters than stratifying by subpopulation.

Correlation of Probability of Consumption and Amount Consumed on 24HRs in the Eating at America's Table Study

One of the challenges in developing this statistical model was to account for the phenomenon that occurs for some food groups: that those individuals who eat a food most frequently tend to eat more of it (Challenge D). To determine how often this happens, we used the Eating at America's Table Study (EATS) data to assess the proportion of food groups that exhibit a positive correlation between the probability of consumption and consumption-day amount on 24HRs. Details of the EATS, conducted in 1997-1998, are published elsewhere (7). We used data from 965 men and women, 20 to 70 years of age, from a national sample, who completed four 24HRs three months apart, followed by NCI's DHQ. The study was approved by the NCI Special Studies Institutional Review Board.

To determine what proportion of 27 Pyramid food groups (described in (5)) exhibited a significant correlation between probability of consumption and consumption-day amount, we calculated the proportion of respondents who reported consumption on none, one, two, three or four of the four 24HRs and the median portion size consumed for each category by sex. Spearman correlation coefficients between the number of recalls with consumption and the consumption-day amount were then computed.

Applying the Method: Example of Estimating the Distribution of Usual Intake

We also used the EATS data to (i) illustrate the application of the NCI method, in comparison with the WPM and ISUF methods, for estimating the distribution of usual intake for two food groups, whole grains and dark green vegetables, for men and women and (ii) estimate the distribution of usual intake by education level for whole grain consumption by men. In these analyses, only DHQ reported frequencies were used; the average portion size information (small, medium, large) was not used. This variable of reported frequencies is very similar to the Food Propensity Questionnaire (FPQ) used in the 2003-2006 NHANES (5). Daily frequencies were determined for each respondent for each food group by summing the line items belonging to each group. The covariate for whole grains included the frequency data for the following DHQ items: breads, crackers, hot cereals, popcorn, ready-to-eat cereal, rice or other cooked grains, and potato/tortilla/corn chips. The covariate for dark green vegetables included frequencies of broccoli, raw greens, cooked greens, and lettuce. The proportions of the line items in each category (e.g., the proportion of bread that was whole grain) were considered when deriving the frequency variables. (See (5) for further details.) To accommodate the non-linear relationship between the 24HR and the food-frequency variables, a polynomial model was used, that is, square root, linear, and quadratic functions of the food frequency variable were included as covariates in the statistical model.

We also estimated the distribution of usual intake of whole grain consumption for three subpopulations of men: those with a high school education or less, those with some college, and college graduates. This was achieved by including the indicator variables for education level as covariates in both parts of the statistical model.

Applying the Method: Simulation Study for Estimating the Distribution of Usual Intake

Simulation studies provide a means of comparing statistical methods to each other, as well as to a measure of true usual intake. We conducted a simulation study to evaluate the NCI method and to compare it to other currently available methods for estimating usual food intake distributions. Because we were interested in the performance of the methods for the minimum number of 24HR days, two days were chosen to compare six different methods of estimating usual intake: (i) the two-day WPM, (ii) the ISUF method, (iii) the standard NCI method with correlated person-specific effects and the FPQ as a covariate (as described above), (iv) the NCI method with correlated person-specific effects but without the FPQ (i.e., the covariate(s) generated by the FFQ were removed from the model fittings of equations [1] and [2]), (v) the NCI method with uncorrelated person-specific effects (i.e., the person-specific effects in equations [1] and [2] were assumed to be uncorrelated in the model fittings) with the FPQ, and (vi) the NCI method with uncorrelated person-specific effects without the FPQ. By comparing the NCI method both with and without the correlated person-specific effects and with and without the FPQ, we were able to isolate the effects of these components of the model in this simulation study.

We simulated 200 data sets, each with 2000 pseudo-persons, based on whole grain consumption by women in EATS. For each pseudo-person in a simulated data set, an FFQ frequency value was selected from the actual values in EATS. Next, a probability was generated for that individual, using the average probability from the EATS data stratified by FFQ frequency group (Figure 1a). For example, a pseudo-person who fell into FFQ group 5 (corresponding to a value between the 20^th to 25^th percentile, or approximately four times a week), would have about a 52% chance of consuming whole grains, based on the recall data for everyone in that group. Using this probability, 365 pseudo-days were generated for this person, with each one having the underlying chance of 52% of consuming a whole grain on that day. Next, for the days that were simulated to be consumption days, an average amount was generated for each consumption day using the mean consumption-day amounts from EATS represented in Figure 1b. For example, for a woman in group 5 (Figure 1b), the mean value of about 0.8 servings, plus or minus a randomly-generated value reflecting the variability about the mean, was used. Finally, two correlated person-specific effects (from a bivariate normal distribution), corresponding to probability and amount, were generated for each pseudo-person with a correlation equivalent to that found in the EATS data.

Figure 1.

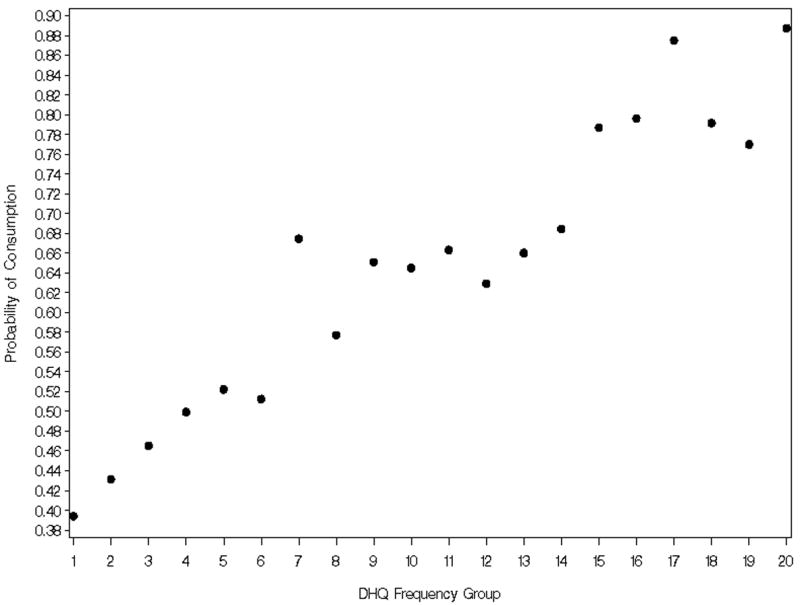
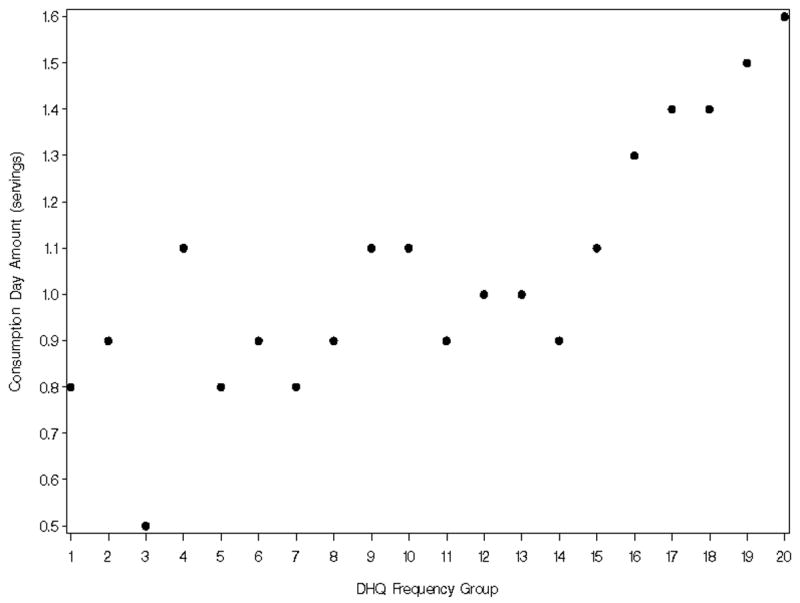
Figure 1a. Average probability of whole grains consumption by Diet History Questionnaire (DHQ) whole grains frequency group for women in the Eating at America's Table Study.

Figure 1b. Average whole grains consumption-day amount (servings) by Diet History Questionnaire (DHQ) whole grains frequency group for women in the Eating at America's Table Study.

After combining the simulated probability, consumption-day amount, and person-specific effects, each person in the data set has 365 days of pseudo-data, the mean of which is used to estimate true intake. The average percentiles estimated from all six methods above were compared to the percentiles of this true intake.

Results

Correlation of Probability of Consumption and Amount Consumed on 24HRs in EATS

Table 1 presents the proportion of respondents in EATS who consumed a food group on none, one, two, three, or four of the recall days, and the corresponding median amount, expressed as the number of Pyramid servings (8), consumed per day. Forty-five of the 54 (83%) food group by sex combinations (27 food groups for each sex) exhibited a positive correlation between the probability of consuming the food and the average consumption-day amount.

Table 1.

Percentage of persons consuming and median amount^a,b of food groups consumed per day on 24-hour recall by number of days food group was reported.

	Men (n=446) Number of 24HRsc with Reported Intake of Food Group					Women (n=519) Number of 24HRsc with Reported Intake of Food Group
	0	1	2	3	4	0	1	2	3	4
Alcohold
Percent consuming	46.4	18.4	13.5	9.2	12.6	58.4	21.0	10.0	5.8	4.8
Amount (drinks)	0.0	1.0	2.1	2.3	3.0	0.0	1.0	1.4	1.9	2.6
Cheesed
Percent consuming	6.3	14.1	22.6	33.6	23.3	6.9	18.7	26.6	29.7	18.1
Amount (servings)	0.0	0.6	0.7	0.9	1.0	0.0	0.4	0.6	0.7	0.7
Milkd
Percent consuming	1.1	7.0	12.6	27.1	52.2	2.5	7.7	16.4	25.4	48.0
Amount (servings)	0.0	0.3	0.6	0.7	1.3	0.0	0.2	0.4	0.6	1.0
Total_Dairyd
Percent consuming	0.2	2.0	4.7	14.8	78.3	0.2	1.7	6.2	18.1	73.8
Amount (servings)	0.0	0.9	0.9	1.2	1.7	0.0	0.2	0.5	0.8	1.3
Citrus,Melon,Berriesd
Percent consuming	5.2	12.3	22.6	30.0	29.8	6.2	14.5	25.2	27.4	26.8
Amount (servings)	0.0	0.1	0.8	0.9	1.6	0.0	0.1	0.5	0.9	1.3
Other Fruitd
Percent consuming	12.3	21.7	21.1	22.2	22.6	11.6	20.0	24.7	22.5	21.2
Amount (servings)	0.0	1.0	1.1	1.4	1.8	0.0	0.7	0.9	1.1	1.4
Total Fruitd
Percent consuming	1.1	6.3	14.6	22.0	56.1	2.5	5.4	15.2	25.0	51.8
Amount (servings)	0.0	0.3	1.1	1.2	2.2	0.0	0.2	0.6	1.3	1.9
Non-Whole Grainsd
Percent consuming	0.0	0.2	0.4	2.0	97.3	0.0	0.0	0.0	6.0	94.0
Amount (servings)	0.0	0.6	5.5	4.5	6.7	0.0	0.0	0.0	3.2	4.8
Whole Grainsd
Percent consuming	8.3	13.2	23.3	26.5	28.7	7.5	16.0	22.5	27.0	27.0
Amount (servings)	0.0	1.1	1.5	2.1	2.4	0.0	0.8	1.1	1.3	1.5
Total Grainsd
Percent consuming	0.0	0.2	0.2	1.6	98.0	0.0	0.0	0.0	2.7	97.3
Amount (servings)	0.0	0.6	6.4	5.0	8.1	0.0	0.0	0.0	4.2	5.8
Eggsd
Percent consuming	5.2	18.8	29.6	24.2	22.2	8.3	24.7	30.4	24.3	12.3
Amounte	0.0	0.1	0.4	0.5	0.7	0.0	0.1	0.3	0.5	0.4
Fishd
Percent consuming	45.7	33.2	16.1	3.6	1.3	51.8	32.9	11.6	2.9	0.8
Amounte	0.0	2.0	3.0	4.0	4.5	0.0	1.6	1.8	2.3	4.9
Franks and Sausages
Percent consuming	20.4	32.1	29.6	13.5	4.5	34.5	32.8	22.4	9.2	1.2
Amounte	0.0	2.0	2.1	2.1	2.3	0.0	1.5	1.3	1.4	1.7
Meatf
Percent consuming	6.5	14.1	22.0	30.5	26.9	7.1	17.0	28.1	31.0	16.8
Amounte	0.0	3.4	3.3	3.6	3.7	0.0	1.8	2.1	2.4	2.4
Nuts and Seedsd
Percent consuming	28.0	30.0	22.9	14.1	4.9	30.6	33.1	19.8	11.0	5.4
Amounte	0.0	0.3	0.4	0.5	0.4	0.0	0.2	0.3	0.4	0.5
Organ Meats
Percent consuming	97.3	2.5	0.2	0.0	0.0	96.3	3.5	0.2	0.0	0.0
Amounte	0.0	1.8	1.2	0.0	0.0	0.0	2.4	0.9	0.0	0.0
Poultryf
Percent consuming	19.1	32.3	28.7	15.5	4.5	18.9	32.8	28.7	15.8	3.9
Amounte	0.0	3.2	3.7	3.3	4.0	0.0	2.4	2.4	2.9	3.0
Soyd
Percent consuming	82.7	13.2	3.6	0.4	0.0	82.1	13.3	2.7	1.2	0.8
Amounte	0.0	0.1	0.2	6.0	0.0	0.0	0.0	0.9	0.6	1.4
Meat,Fish,Poultryd
Percent consuming	1.6	0.9	3.4	11.4	82.7	0.8	1.2	4.6	22.0	71.5
Amounte	0.0	1.8	5.0	5.3	6.1	0.0	1.7	2.8	3.2	3.7
Deep Yellow Vegetablesd
Percent consuming	24.0	33.6	24.4	13.2	4.7	19.3	35.8	26.6	13.7	4.6
Amount (servings)	0.0	0.3	0.5	0.6	0.8	0.0	0.3	0.4	0.4	0.7
Dark Green Vegetablesf
Percent consuming	52.0	28.5	14.6	4.3	0.7	43.4	29.5	19.3	6.4	1.5
Amount (servings)	0.0	0.8	1.1	1.1	1.1	0.0	0.7	0.8	1.1	1.2
Legumesf
Percent consuming	56.7	31.2	9.0	2.7	0.4	61.3	28.1	8.3	2.3	0.0
Amount (servings)	0.0	1.1	1.1	1.6	1.1	0.0	0.7	0.8	0.7	0.0
Other Vegetablesd
Percent consuming	0.0	0.9	6.3	23.5	69.3	0.0	1.3	6.9	26.2	65.5
Amount (servings)	0.0	0.3	0.9	1.0	1.5	0.0	0.5	0.5	0.8	1.1
Potatoesd
Percent consuming	12.1	24.2	29.6	22.4	11.7	14.5	26.2	28.3	21.6	9.4
Amount (servings)	0.0	2.0	2.3	2.7	2.7	0.0	1.5	1.6	1.9	1.8
Starchy Vegetablesg
Percent consuming	45.1	37.9	12.6	4.5	0.0	45.5	35.6	15.0	3.5	0.4
Amount (servings)	0.0	1.0	0.9	1.4	0.0	0.0	0.6	0.7	0.8	1.3
Tomatoesd
Percent consuming	1.8	7.8	22.2	37.4	30.7	1.9	11.8	26.2	34.5	25.6
Amount (servings)	0.0	0.7	0.6	0.8	0.9	0.0	0.5	0.5	0.6	0.6
Total Vegetablesd
Percent consuming	0.0	0.2	1.1	11.9	86.8	0.0	0.0	1.2	12.7	86.1
Amount (servings)	0.0	0.7	3.3	3.4	4.3	0.0	0.0	1.6	2.7	3.2

Source: Eating at America's Table Study (reference 7)

^aMedian amount consumed by category

^bServings in this table refer to pyramid servings (see http://www.ba.ars.usda.gov/cnrg/services/foodlink.html)

^c24 hour recall

^dCorrelation between number of consumption days and amount consumed (Spearman correlation): p<0.05 for men and women

^eOunces of cooked lean meat equivalents

^fCorrelation between number of consumption days and amount consumed (Spearman correlation): p<0.05 for women; p>0.05 for men

^gCorrelation between number of consumption days and amount consumed (Spearman correlation): p<0.05 for men; p>0.05 for women

Example of Estimating the Distribution of Usual Intake in EATS

Estimating the Distribution of Usual Intake

The smoothed distribution curve for whole grain consumption by women from the EATS data is represented in Figure 2. This figure illustrates the differences between the WPM, ISUF, and NCI methods using four days of 24HRs. First, even with four days of recall, it is still difficult to estimate empirically the lower tail of the distribution using WPMs, resulting in a large spike at zero. Second, because the WPM method does not distinguish within-person from between-person variability, its distribution has a longer tail. Although the ISUF software produced a warning that it should not be used for whole grains because significant correlation existed between the probability of consuming and the amount consumed, its results are presented here for illustration purposes. The curve for the NCI method is to the left of the ISUF curve below about 1.7 servings, at which point it shifts to the right of the ISUF curve for larger amounts. The difference between these curves is due to the positive correlation between probability and amount. Because those women who are less likely to eat whole grains eat smaller amounts when they do eat them, the area under the NCI method curve is larger in the lower part of the distribution than the area below the curve produced using the ISUF method, which assumes no relationship between probability and amount. For the same reason, this relationship reverses in the upper part of the area under the NCI method curve, reflecting that women who are more likely to eat whole grains eat larger amounts when they do eat them.

Figure 2.

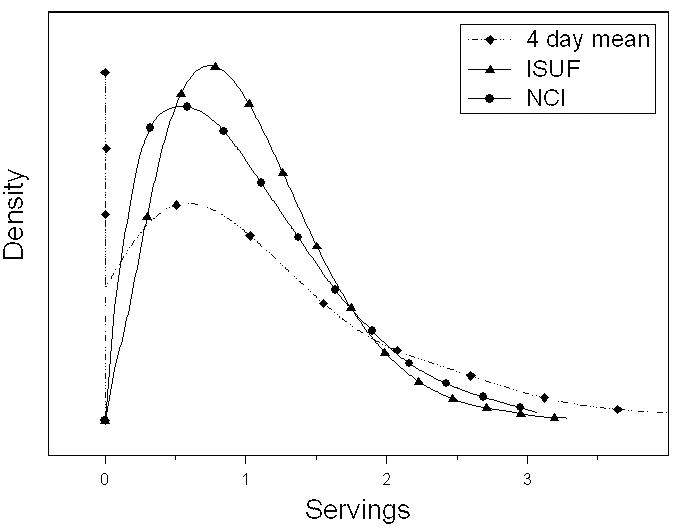
Estimated distributions of usual intake of whole grains for women in Eating at America's Table Study using different methods. The spike at zero for the 4-day mean (within-person mean of 4 24-hour recalls) represents 7.5% of the distribution. (ISUF: Iowa State University Foods method; NCI: National Cancer Institute method with correlated random effects and a food frequency questionnaire as a covariate.)

Estimating the Percent of Population Above or Below a Cutoff

Table 2 illustrates the differences among the three methods. For both dark green vegetables and whole grains, the four-day WPM method produces estimates that are higher than the ISUF and NCI methods in both of the tails, due to the large spike at zero and the longer tail in the upper end of the distribution.

Table 2.

Percentage of persons who consume below or above a cutoff number of servings using different methods.

	Women (n=519)			Men (n=446)
	4-day WPMa	NCIb	ISUFc	4-day WPMa	NCIb	ISUFc
Dark Green Vegetables
<0.10 servings	54.3	30.4	26.4	62.3	31.7	30.9
<0.25 servings	67.6	63.7	51.9	70.6	65.5	59.3
<0.5 servings	82.0	86.6	89.0	82.3	91.6	92.8
>1 serving	6.7	2.0	0.5	5.2	0.1	0.0
Whole Grains
<0.5 servings	37.2	26.0	17.9	27.6	17.2	9.4
<1 serving	60.5	57.4	55.5	43.3	37.9	29.7
>2 servings	14.8	8.6	5.4	30.0	29.0	26.4
>3 servings	3.9	1.1	0.3	13.5	11.1	7.9

Source: Eating at America's Table Study (reference 7)

^aWithin-person Mean Method (mean of 4 days)

^bNational Cancer Institute Method with correlated person-specific effects and food frequency information as a covariate

^cIowa State University Foods Method

Other differences between the NCI method and the ISUF method are determined by the strength of the correlation between probability of consumption and the amount consumed. This correlation coefficient is not significantly different from zero for dark green vegetable consumption by men in EATS, and, as can be seen in Table 2, the estimates from the NCI and ISUF methods are similar for men. In contrast, due to substantially correlated probability and amount for whole grains (r=0.29 for women and r=0.34 for men), the estimates of the number of people consuming less than 0.5 serving and greater than three servings of this food group are considerably lower in the ISUF method than the NCI method for both women and men.

Estimating the Distribution of Usual Intake for a Subpopulation

The percentages of men falling above or below specified cutoff values for servings of whole grains by education levels are given in Table 3. It is clear from this table that the proportion of men in EATS who consume whole grains differs by level of educational attainment.

Table 3.

Percentages of men who consume below or above a cutoff number of servings of whole grains by education levels.

	High School Education or Less (n = 83)	Some College (n = 157)	College Graduate (n = 206)
<0.5 servings	32.3	20.6	9.3
<1 servings	57.9	44.2	26.4
>2 servings	14.5	23.3	38.7
>3 servings	4.2	8.1	16.3

Source: Eating at America's Table Study (reference 7)

Simulation Study for Estimating the Distribution of Usual Intake

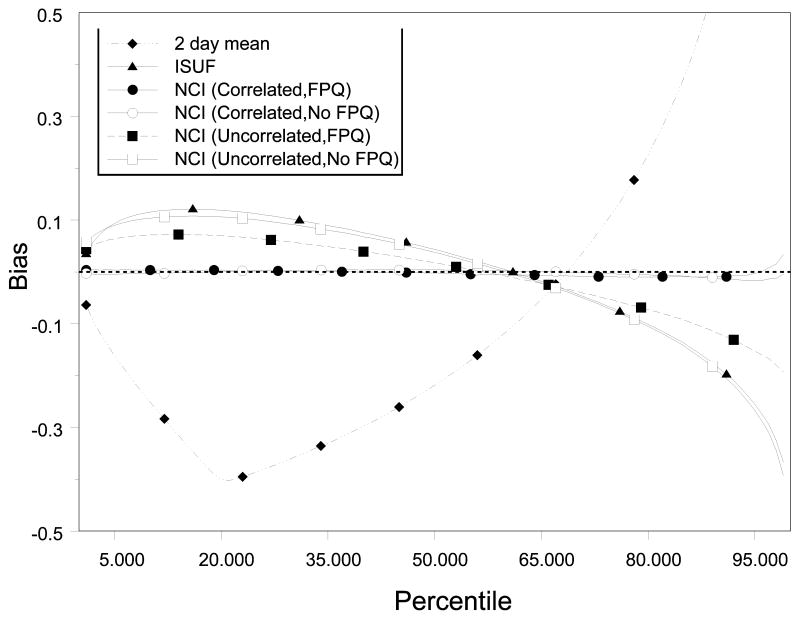
Figure 3 illustrates the average bias, defined as the difference between the estimate and simulated truth (the 365-day mean), of each of the methods. Except at the mean of the distribution, the two-day WPM estimate has a much greater bias than any of the other methods. The NCI method with correlated person-specific effects either with or without the FPQ produced estimates that are very close to the estimate from the 365-day mean, with essentially no bias for all percentiles.

Figure 3.

Bias of percentile estimates from simulations based on whole grains for women (from the Eating at America's Table Study). The dashed line at zero represents no bias. (2 day mean: within-person mean (WPM) of 2 days of simulated 24-hour recalls; ISUF: Iowa State University Foods method; NCI: National Cancer Institute method, specifying whether the person-specific effects are correlated or uncorrelated and whether the simulated Food Propensity Questionnaire (FPQ) is used as a covariate in the model.)

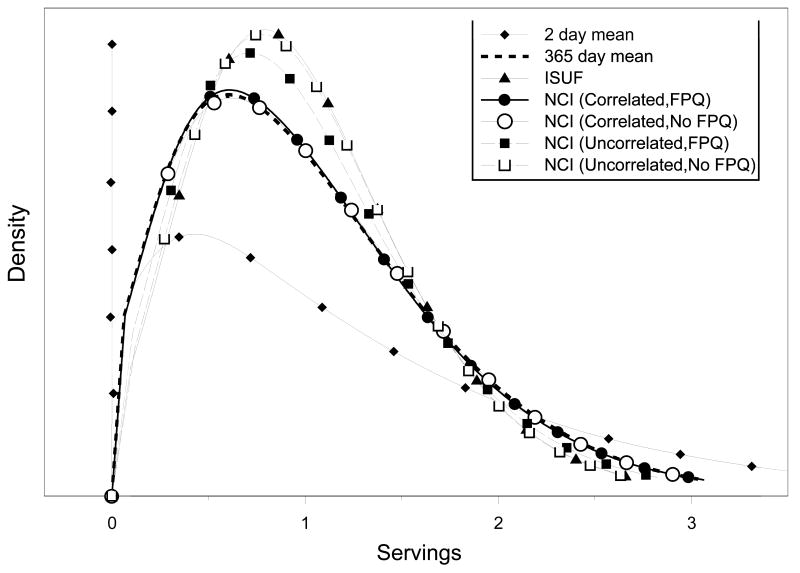
Figure 4 illustrates that the ISUF method and the NCI method with uncorrelated person-specific effects and without the FPQ produced very similar curves that are shifted from the 365-day mean curve. By ignoring correlation between probability and amount, these two methods tend to overestimate the amounts consumed by those with a low probability of consumption, and underestimate the amounts consumed by those with a high probability of consumption, leading to biased estimates. The NCI method with uncorrelated person-specific effects but with the FPQ led to the best results when compared to the same method without the FPQ. Including the shared covariate (the FPQ information) in both parts of the model captured some of the correlation between probability and consumption-day amount, although not as much as incorporating the correlated person-specific effects. Figures 3 and 4 illustrate that modeling the correlation between probability of consumption and consumption-day amount leads to the largest gains over the other methods.

Figure 4.

Smoothed distribution curves from simulations based on whole grains for women (from the Eating at America's Table Study). The spike at zero for the two-day mean represents 18% of the distribution. The 365-day mean represents true usual intake. (2 day mean: within-person mean (WPM) of 2 days of simulated 24-hour recalls; ISUF: Iowa State University Foods method; NCI: National Cancer Institute method, specifying whether the person-specific effects are correlated or uncorrelated and whether the simulated Food Propensity Questionnaire (FPQ) is used as a covariate in the model.)

Discussion

A statistical model used for estimating the usual intake of episodically consumed foods using two or more 24HRs per subject needs to appropriately account for the characteristics of such data. First, it must account for the spike at zero due to non-consumption of a food on the recalled days. This is achieved in the NCI method by representing usual intake as the product of the probability of consuming a food and the amount consumed on a consumption day. Additionally, the model must transform skewed distributions of the consumption-day amounts to approximate normality. It also must have the ability to distinguish within-person variability that results from day-to-day differences in intake and random reporting error from the variability among individuals. Like the ISUF method, the NCI method addresses all of these challenges. The NCI method overcomes the limitations of the ISUF method, however, by incorporating covariate information and by accounting for the correlation between the probability of consuming a food and the consumption-day amount. Because probability and amount are substantially correlated in a majority of food groups, as our findings from EATS illustrate, the ISUF method should not be used on most foods according to its own criterion.

The importance of using covariates in the model is highly dependent upon the application of interest. When interest is on estimating the distribution of usual intake in a subpopulation or population, it is not important how the between-person variation is partitioned between the part that is explained by covariates and the unexplained component captured by the person-specific effect, but how well person-specific effect and within-person random error can be transformed to normality. Including covariates in the model may make normality more realistic, with consequent improvement in estimating the distribution, especially its tails. This was not the case with our example. After allowing for correlated person-specific effects, our simulation study results indicated little difference between the NCI method with and without the FPQ. This may be because the 24HR reported amounts for whole grains (the basis for the simulated data) can be transformed to normality almost equally well unconditionally or conditionally on the FPQ. For foods without this characteristic, including the FPQ in the model may lead to some improvement in estimating the tails of the distribution. Because the FPQ may not be necessary to estimate the usual intake distribution of foods, it should be possible to estimate the usual intake distribution of foods from previous survey data with at least 2 24HRs per participant.

When the distribution of usual intake is estimated in subpopulations, incorporating covariates that characterize the subpopulation, such as age, sex, race, income, or education, may provide a substantial improvement by leading to more efficient estimation than does stratification. This advantage in efficiency is expected to increase as size of the subpopulation decreases. In addition, covariates may be used to adjust for temporal effects, such as seasonality and day-of-week effects, and the reduction in mean levels of intake that can occur with repeat 24HRs, the time-in-sample effect. This is done simply by including an indicator variable into the statistical model as a covariate to indicate that the second recall is being modeled, allowing its mean to be adjusted for repeat application of the recall, if necessary.

For predicting individual usual intake and relating it to health outcomes, the goal is to reduce unexplained between-person variation of intake, which may be achieved by including appropriate covariates in the model. Different types of covariates may be incorporated in the estimation of usual intake for this purpose, including personal characteristics associated with intake, as well as FPQ information. Because the FPQ frequencies are associated both with the probability of consuming a food and the amount consumed on the consumption day (5), incorporating food frequency information as a covariate in both parts of the model can explain at least part of between-person variation in the 24HR, therefore providing a better estimate of diet-health relations. Although the NCI statistical model is the first step in estimating individual usual intake, the development of additional statistical methodology for the second step is necessary; this work is currently underway.

Another benefit of including covariates in the statistical model is the improved ability to make inferences regarding the effects of these covariates on food consumption, similar to the purpose of the statistical models described by Haines et al (9) and Guenther et al. (10). Like these approaches, the NCI model allows the analyst to separate the effect of covariates on the decision to consume a food from the effect of covariates on the amount that is consumed when the food is eaten. The NCI model may be used to approximate the effects of individual covariates to determine which variables are associated with the probability of consumption and the consumption-day amount by making inferences about the strength of the relationships of the covariates with individual intake.

The NCI method was developed to meet the special challenges for estimating intake of episodically-consumed foods. Although some of those challenges (e.g., (A) and (D) listed in the introduction) are unique to episodically-consumed foods, others apply as well to nutrients or foods that are consumed on a daily basis. Part II of the NCI model (equation [2]) alone could be used to estimate usual intake for foods or nutrients that are consumed on a daily basis by nearly everyone. The ability to easily incorporate covariates in the estimation of usual intake makes the NCI method an attractive alternative to the ISU nutrient method.

Although the NCI method appears to present a substantial improvement over existing methods for estimating the distribution of usual intake for foods, it does have some limitations. First, the model never produces a true zero intake because the logistic regression that is used to model the probability of consumption does not predict a zero value. Furthermore, the model requires that a sufficient number of people consume a given food on at least two recalled days. For foods that are consumed very episodically in the population, such as organ meats, this condition may not be satisfied.

Most importantly, the model is based on the assumption that the 24HR is an unbiased instrument for measuring usual food intake. Many recent studies with doubly labeled water have found misreporting of energy intake on both the 24HR and FFQ, almost always in the direction of underreporting (11-14). This suggests that at least some foods are underreported as well. A few studies have investigated the extent and type of underreporting by food, and it appears that underreporting may be differential by food (15); although, unfortunately, it is impossible to know which foods, and by how much, are misreported on the 24HR. Due to this uncertainty, we follow the only available practical convention and assume that the 24HR is unbiased. For those foods that are reported with bias on the 24HR, the estimated intake will be biased as well. When the FFQ is used as a covariate in the model, it is allowed to involve systematic bias as well as random measurement error. It is important to note that, in the NCI method, the FFQ does not replace information from the 24HR but is being calibrated using the 24HR as a reference instrument. The method, therefore, includes useful information from the FFQ without subjecting the final estimates to its measurement error.

The NCI method has been developed and illustrated here using data from what we implicitly assumed to be a random sample of independent individuals, not a complex survey sample. We are presently working on its extension for complex surveys, such as NHANES, so that estimates of the distribution of usual intake in the US population may be made using the NCI method.

Conclusions and Applications

The NCI method to estimate usual intake of even episodically consumed foods using two 24-hour recalls represents an advance in dietary assessment. It provides distinct advantages over previously proposed methods by accounting for the correlation between probability of consumption and amount consumed and by incorporating covariate information. The software for implementing the method and the guidance for using it will be publicly available in the future. Researchers interested in estimating the distribution of usual intakes of food groups for a population or subpopulation or the percent of persons above or below a given standard, are advised to work with a statistician to incorporate this method in their analyses. A further application of the NCI method for estimating individual usual intake and relating it to health outcomes is forthcoming.