Temperature Dependence of Nucleotide Association and Kinetic Characterization of Myo1b

Abstract

Myo1b is a widely expressed myosin-I isoform that concentrates on endosomal and ruffling membranes and is thought to play roles in membrane trafficking and dynamics. It is one of the best characterized myosin-I isoforms and appears to have unique biochemical properties tuned for tension sensing or tension maintenance. We determined the key biochemical rate constants that define the actomyo1b ATPase cycle at 37 °C and measured the temperature dependence of ATP binding, ADP release, and the transition from a nucleotide inaccessible state to a nucleotide accessible state (k-alpha). The rate of ATP binding is highly temperature sensitive, with an Arrhenius activation energy 2-3 fold greater than other characterized myosins (e.g, myosin-II and myosin-V). ATP hydrolysis is fast, and phosphate release is slow and rate limiting with an actin dependence that is nearly identical to the steady-state ATPase parameters (V_max and K_ATPase). ADP release is not as temperature dependent as ATP binding. The rates and temperature dependence of ADP release are similar to k-alpha suggesting a similar structural change is responsible for both transitions. We calculate a duty ratio of 0.08 based on the biochemical kinetics. However, this duty ratio is likely to be highly sensitive to strain.

Myosin-Is are the single-headed, low-molecular-weight members of the myosin superfamily that are proposed to link cellular membranes with the actin cytoskeleton. Myosin-I isoforms bind phosphoinositides directly (1) and function in several important cellular processes, including membrane retraction, macropinocytosis, phagocytosis, membrane trafficking, cell-cell adhesion, and mechanical signal transduction (2-8).

The biochemical mechanisms of long-tail and short-tail myosin-I isoforms have been studied (9-12), with myo1b being the best characterized short-tail isoform (13-15). The myo1b ATPase mechanism (Scheme 1) is notable in that (a) the maximum rate of ATP binding and population of the myo1b^IQ weakly-bound states is > 30-fold slower than myosin-II, (b) nucleotide-free myo1b is in equilibrium between a state that binds nucleotide (AM′) and a state that does not bind nucleotide (AM), (c) the rate of transition between AM and AM′ (k_+α) states is similar to the rate of ADP release (k₊₅′), and (d) ADP release is slow and is accompanied by a rotation of the lever arm.

Scheme 1.

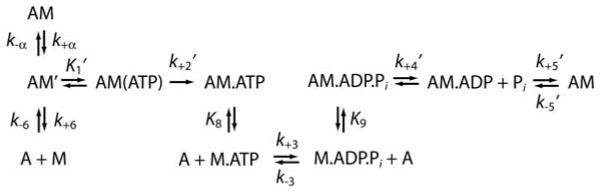
We proposed that the strikingly slow actomyo1b ATPase rate constants are a property of all short-tail myosin-I isoforms (11, 16). However, it has been shown recently that short-tailed Dictyostelium myosin-IE (not to be confused with vertebrate long-tail myo1e (11)) has kinetic rate constants that are substantially faster than vertebrate short-tail isoforms (12). Because of experimental convenience, nearly all kinetic characterizations of myosin ATPase cycles have been performed at temperatures between 18 – 25 °C, which is the range in which Dictyostelium cells live. There is no complete kinetic characterization of any vertebrate unconventional myosin at physiological temperature (37 °C), and it is possible that myosin-I rate constants are highly temperature sensitive. Therefore, it is important to determine the kinetic lifetimes of the myo1b intermediates at physiological temperature.

In this study, we determined the rate constants that define the rat myo1b ATPase cycle at 37 °C, and we provide the first measurement of the rates of ATP hydrolysis and phosphate release for myo1b. Our characterization has allowed us to calculate the myo1b duty ratio at physiological temperature and determine thermodynamic parameters of ATP binding and ADP release.

Materials and Methods

Reagents, Proteins, and Buffers

2′-Deoxy-methyanthraniloyl-labeled ATP (mantATP) was synthesized as described (17). ADP and ATP concentrations were determined spectrophotometrically before each experiment by absorbance at 259 nm, ε₂₅₉ = 15,400 M^-1cm^-1. MantATP concentrations were determined by absorbance at 255 nm, ε₂₅₅ = 23,300 M^-1cm^-1 (17).

Rabbit skeletal muscle actin was prepared and gel filtered (18). Actin concentrations were determined by absorbance at 290 nm, ε₂₅₉ = 26,600 M^-1cm^-1. Actin was labeled with pyrenyl iodoacetamide (pyrene-actin) and gel filtered (19). All actin was stabilized with a molar equivalent of phalloidin (Sigma). Calmodulin (CaM) was expressed in bacteria and purified as described (20).

Steady-state and transient experiments were performed in KMg25 buffer (10 mM Mops, 25 mM KCl, 1 mM MgCl₂, 1 mM EGTA, 1 mM DTT). The pH of the buffer was adjusted to pH 7.0 at 25 °C, and changed by less than 0.1 °C when the temperature was increased to 37 °C. Free CaM (1 μM) was included in all solutions that contain myo1b^IQ (21).

Myosin-I Expression and Purification

A construct consisting of the motor domain and first IQ motif of rat myo1b (myo1b^IQ) was expressed in Sf9 cells and purified as described (21). The concentration of myo1b^IQ was determined using the Coomassie Plus reagent (Pierce) using bovine serum albumin (BSA) as a standard. Based on previous work that validates myosin active-site concentrations (9, 10, 22, 23), BSA is an appropriate protein standard. Final stock concentrations were typically 5 – 10 mg/ml, and were stored at -20 °C in 50% glycerol. Preparations of four liter cultures yielded 4 – 15 mg of protein.

Kinetic Measurements

Transient kinetic measurements were made with an Applied Photophysics (Surrey, U.K.) SX.18MV stopped-flow. A 400 nm long-pass filter (Oriel) was used to monitor pyrene (λ_ex = 365 nm) and mantATP (λ_ex = 295 nm) fluorescence. The time courses in the figures show the average of 1 - 4 individual traces. Transients were fitted to exponential functions using the software supplied with the stopped-flow. Unless stated otherwise, all concentrations are given as final after mixing.

Solutions of actomyo1b contained apyrase (0.01 U/mL) when loaded into the stopped flow to ensure the mixtures were free of contaminating ADP and ATP. This apyrase concentration was high enough to remove contaminating nucleotide, but not high enough to interfere with the kinetic measurements. Solutions used for determining the rate of association of myo1b^IQ with pyrene-actin included 0.3 U/mL apyrase.

Transient phosphate (P_i) release was measured by stopped-flow using the coupled assay system containing the fluorescently labeled mutant of the phosphate binding protein (P_iBP) using an excitation wavelength of 425 nm and a 440 nm long-pass filter (24, 25). To remove contaminating phosphate, the instrument lines were incubated with 1 mM 7-methylguanosine and 0.2 U/mL nucleoside phosphorylase overnight. Stopped-flow solutions contained 100 μM 7-methylguanosine and 0.004 U/mL nucleoside phosphorylase. Measurements were made in sequential mixing mode at 37 °C. Myo1b^IQ (10 μM) was mixed with 5 μM ATP in the first mix and aged for 7 s, resulting in concentrations of 5 μM myo1b^IQ and 2.5 μM ATP. Myo1b^IQ and ATP was then mixed with actin, resulting in final concentrations of 2.5 μM myo1b^IQ, 1.25 μM ATP, and 0 – 80 μM actin. P_iBP was included in all solutions, and was present at a final concentration of 5 μM after mixing. Errors reported are standard errors in the fits.

Kinetic modeling was performed using the reaction outlined in scheme 1, where A is actin and M is myosin. The temperature dependence of the rates of ATP binding and ADP release were analyzed according to the Arrhenius relation:

$$\text{ln}\left(k\right)=\text{ln}\left(A\right)-\frac{E_{\text{a}}}{\text{RT}}$$ (eq.1)

where R is the gas constant (8.31451 J·mol^-1K^-1), T is the temperature in Kelvin, E_a is the activation energy, and A is the pre-exponential factor. The standard enthalpy change of the isomerization of the AM to AM′ states (K_α) was determined from a van't Hoff plot:

$$\text{ln}\left(K_{\alpha }\right)=\frac{-\Delta H°}{\text{RT}}+\frac{\Delta S°}{R}$$ (eq.2)

ΔH° is the enthalpy and ΔS° is the entropy.

Results

Myo1b^IQ Binding to Actin Filaments

A ∼75% fluorescence quenching upon strong binding of myo1b^IQ to pyrene-actin allowed us to monitor the association of myo1b^IQ with actin (k_-6; Scheme 1). Time courses of myo1b^IQ binding to actin at 37 °C follow single exponentials, and the observed rates depend linearly on the actin concentration (Figure 1). Data were modeled as:

Figure 1. Kinetics of myo1b^IQ association with actin filaments.

(Top) Actin concentration dependence of the observed rate (k_obs) of pyrene-actin binding to myo1b^IQ in KMg25 at 37 °C. A 5:1 actin to myo1b^IQ ratio was maintained for each actin concentration. The solid line is a linear fit to the data. (Bottom) Time course of pyrene-actin fluorescence increase after mixing 2.0 μM pyrene-actomyo1b^IQ with 100 μM unlabeled actin (final concentrations). The smooth line is the best fit of the data to a single exponential rate (k_obs= A(1-e^-k·t)).

where A* represents the unquenched fluorescent state of pyrene-actin. A linear fit to the data yields an apparent second-order rate constant of k_-6 = 8.2 ± 0.32 μM^-1s^-1 (Table I).

Table 1.

Rate and Equilibrium Constants for the Myo1b ATPase Cycle at 37 °C.^a

Actin Binding		Phosphate Release
k+6 (s-1)	0.0044 ± 0.00010b	k+4′ (s-1)	0.58 ± 0.056g
k-6 (μM-1s-1)	8.2 ± 0.32b	K9 (μM)	53 ± 9.8g
K6 (nM)	0.54 ± 0.024c
		ADP Release
ATP Binding		K5′ (μM)	0.84 ± 0.068b
1/K1′ (μM)	330 ± 25b	k+5′ (s-1)	6.7 ± 0.064b
k+2′ (s-1)	500 ± 15b	k-5′ (μM-1 s-1)	8.0 ± 0.65c
K1′k+2′ (μM-1 s-1)	1.5 ± 0.12c
K1′k+2′ (μM-1 s-1)	1.2 ± 0.041b,d	Nucleotide-Free Isomerization Step
K1′k+2′ (μM-1 s-1)	0.64 ± 0.020e	Kα	3.7 ± 0.65b
		k+α (s-1)	13 ± 1.0b
ATP Hydrolysis		k-α (s-1)	3.5 ± 0.67c
k3app (s-1)	41 ± 4.9f

^aKMg25 (10 mM MOPS (pH 7.0), 25 mM KCl, 1 mM EGTA, 1 mM DTT, 1 mM MgCl₂, 37 °C) + 1 μM CaM.

^bPyrene-actin fluorescence

^cCalculated

^dDetermined from a linear fit of the data at low ATP concentrations

^eLight scattering in the presence of mantATP

^fMantATP

^gPhosphate-binding protein.

The rate of dissociation of myo1b^IQ from pyrene-actin (k₊₆; Scheme 1) was measured by competition with 50-fold excess of unlabeled actin (Figure 1). The time course fit a single exponential function with a rate k₊₆ = 0.0044 ± 0.00010 s^-1 (Table I). The actomyo1b^IQ dissociation constant (K₆) calculated from the dissociation and association rates (k₊₆/k_-6) is K₆ = 0.54 ± 0.024 nM (Table I).

ATP-Induced Population of the Weakly-Bound States

Pyrene-actin fluorescence was used to measure the rate of ATP binding and population of the weakly bound states at 10 – 37 °C. Mixing actomyo1b^IQ with ATP resulted in a transient increase in pyrene-actin fluorescence. No lag phase was present, and the transients were best fit to the sum of two exponential rates with positive amplitudes (Figure 2). The rates of the fast phases were hyperbolically related to the ATP concentration (Figure 3, left column), whereas the rates of the slow phases were independent of ATP concentrations greater than 500 μM (Figure 3, center column).

Figure 2. Temperature dependence of ATP binding to actomyo1b^IQ.

Pyrene-fluorescence transients obtained by mixing 1.0 μM actomyo1b^IQ with 60 μM ATP at 10 – 37 °C.

Figure 3. MgATP induced population of weakly bound actomyo1b^IQ states.

Pyrene-fluorescence transients obtained by mixing 1.0 μM actomyo1b^IQ with various ATP concentrations at 10 – 37 °C were fitted to double exponential functions (k_obs= A_fast(1-e^-kfast·t) + A_slow(1-e^-kslow·t)). The rates of the (left column) fast phases and (center column) slow phases are plotted as a function of ATP concentration. (Right column) Normalized amplitudes of the (●) fast and (■) slow phases are plotted as a function of ATP concentration. The solid lines through the data in the left column are the best fits of the rates of the fast phases to eq. 3.

Geeves et al (14) modeled the fast phase of the increase in pyrene-actin fluorescence as ATP binding to the AM state and subsequent population of the AM.ATP state (K₁′k₊₂′), and proposed that the slow phase reports the transition from a nucleotide-insensitive AM state to a AM′ state that can bind ATP (k_+α) as follows:

where A* represents the unquenched fluorescent state of pyrene-actin. We analyzed the ATP dependence of the fast phase as:

$$k_{\text{obs}}=\frac{k_{+2}\prime \left[\text{ATP}\right]}{\frac{1}{K_1\prime }+\left[\text{ATP}\right]}$$ (eq.3)

where, K₁′ is a rapid equilibrium and k₊₂′ is a rate-limiting isomerization to the high fluorescence AM.ATP state. Values for K₁′ and k₊₂′ at 10 – 37 °C are given in Table 1. K₁′ is relatively insensitive to temperature, while k₊₂′ varies > 80-fold between 10 – 37 °C. An Arrhenius plot of K₁′k₊₂′ is linear and yields an activation energy (E_a) of 111 kJ/mol (Figure 4; Table 3).

Figure 4. Temperature dependence of ATP binding and ADP release.

Arrhenius plots of the natural log of the rates of (top) ATP binding (K₁′k₊₂′) and (center) ADP release (k₊₅′) versus inverse temperature (283 - 310 K) for (●) myo1b^IQ, (■) myosin-II (28), (♦) myosin-V (30), and (×) myosin-VI (30). The center plot also includes the temperature dependence of (○) k_+α for myo1b^IQ Solid lines are linear fits of the data to the Arrhenius equation (eq. 1) yielding E_a's given in Table 3. (Bottom) van't Hoff plot of K_α showing non-linearity at temperatures > 31 °C. The solid line is a linear fit of the 283 - 304 K data to the van't Hoff equation (eq. 2), yielding ΔH° = 81 kJ/mol.

Table 3.

Thermodynamic Parameters for ATP Binding, ADP Release, and k_+α

Temperature Dependence of ATP Binding
	Ea for K1′k+2′ (kJ/mol)	Ea for k+2′ (kJ/mol)
aMyo1bIQ	111	124
bMyosin-II	42.4	N.D.
cMyosin-V	35.8	74.9
cMyosin-VI	47.5	33.8
Temperature Dependence of k+5′ and k+α′
	Ea (kJ/mol)
aMyo1bIQ (k+ α)	89.1
aMyo1bIQ (k+ 5′)	103
cMyosin-V (k+5′)	83.3
cMyosin-VI (k+5′)	58.6

^aThis study.

^bData from Millar and Geeves (28).

^cData from Robblee et al (30).

At high ATP concentrations (> 500 μM), the rate of the slow phase reports the isomerization of AM to AM′ (k_+α), and the ratio of the amplitudes (Figure 3, right column) of the fast phase to the slow phase reports the equilibrium constant between AM and AM′ (14). Values for K_α, k_+α, and k_-α at 10 – 37 °C were determined by averaging points acquired at ATP concentrations > 1 mM at each temperature (Table 2). K_α varies ∼10-fold, while k_+α ranges from 0.53 s^-1 at 10 °C to 13 s^-1 at 37 °C (Table 2). An Arrhenius plot of k_+α is linear with an E_a of 89.1 kJ/mol (Figure 4; Table 3). At low ATP concentrations, the rate of the slow phase shows an apparent ATP concentration dependence. This dependence is due the fact that the slow rate of ATP binding at low ATP concentrations is ≤ k_+α.

Table 2.

Temperature Dependence of ATP Binding and ADP Release^a

	37 °C	31 °C	25 °C	18 °C	10 °C
1/K1′ (μM)	330 ± 25	420 ± 15	380 ± 10	260 ± 26	250 ± 53
k+2′ (s-1)	500 ± 15	240 ± 3.7	82 ± 0.86	23 ± 0.85	5.7 ± 0.28
K1′k+2′ (μM-1s-1)b	1.5 ± 0.12	0.57 ± 0.022	0.22 ± 0.062	0.088 ± 0.0094	0.023 ± 0.0050
Kα	3.7 ± 0.65	5.6 ± 0.25	3.2 ± 0.077	1.3 ± .024	0.55 ± 0.092
k+α (s-1)	13 ± 1.0	9.3 ± 1.0	4.3 ± 0.35	1.7 ± 0.023	0.53 ± 0.0071
k-α (s-1)b	3.5 ± 0.67	1.7 ± 0.19	1.3 ± 0.11	1.3 ± 0.030	0.96 ± 0.16
k+5′ (s-1)	6.7 ± 0.064	3.9 ± 0.036	1.8 ± 0.014	0.59 ± 0.0041	0.16 ± 0.0011

^aKMg25 (10 mM MOPS (pH 7.0), 25 mM KCl, 1 mM EGTA, 1 mM DTT, 1 mM MgCl₂) plus 1 μM CaM.

^bCalculated

ATP Hydrolysis

Binding of mantATP to myo1b^IQ does not result in a fluorescence change when the mant fluorophore is excited directly (13). However, we detect a fluorescence change when the mantATP is excited by energy transfer from the intrinsic tryptophans of myo1b^IQ. The rate of the fluorescence transient is mantATP dependent at concentrations < 50 μM, with a maximum rate of 41 ± 4.9 s-1 (Figure 5). We propose this maximum rate to be the rate of ATP hydrolysis (k₃^app = k₊₃ + k_-3):

Figure 5. Rate of ATP hydrolysis by myo1b^IQ as measured by mantATP fluorescence.

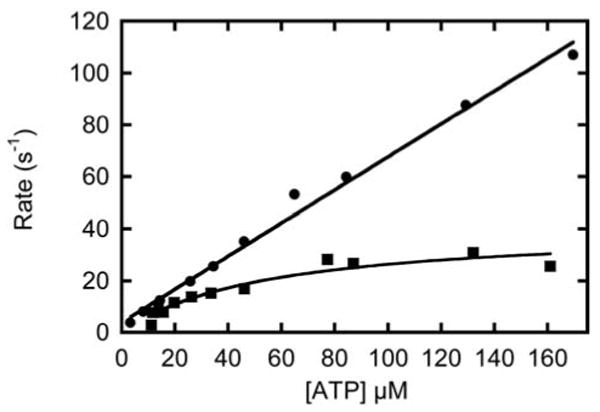
(■) MantATP concentration dependence of the rate of change in mant fluorescence upon binding and fluorescence energy transfer from the intrinsic tryptophans of myo1b^IQ at 37 °C. (●) Rate of actomyo1b^IQ dissociation as a function of mantATP as measured by light scattering at 37 °C.

where M.ADP.P_i* is the high fluorescence state.

The increase in mant fluorescence is not due to the ATP binding (K₁′k₊₂′) or actomyo1b^IQ dissociation (k₈) steps. We monitored the rate of mantATP-induced actomyo1b dissociation by light scattering and found the dissociation rate to be linearly related to all mantATP concentrations tested (Figure 5). A linear fit of the data yields a rate of mantATP binding (K₁′k₊₂′ = 0.64 ± 0.02 μM^-1s^-1; Table 1). This mantATP-induced dissociation is ∼ 2-fold slower than ATP-induced dissociation as measured by pyrene-actin fluorescence (1.5 ± 0.081 μM^-1s^-1; Table 1).

Phosphate Release

Fluorescently-labeled phosphate-binding protein (P_iBP) was used to measure directly the rate of phosphate release (k₊₄′) in sequential-mix, single-turnover, stopped-flow experiments (11, 22, 24, 26). Myo1b^IQ was mixed with ATP, aged 7 s to allow for ATP binding and hydrolysis, and mixed with actin (Figure 6). After the 7 s ageing time, we expect all ATP to bound to myosin and hydrolyzed, with the M.ADP.P_i state as the predominant intermediate (Scheme 1). P_iBP was included with the myo1b^IQ and the actin to prevent transients due to phosphate released during the aging time or phosphate contamination in the actin. In the absence of actin, the rate of phosphate release was too slow to measure on the time-scale of the experiment (< 0.01 s^-1). However, the time courses of phosphate release were single exponentials at all actin concentrations tested and did not show lag or rapid-burst phases (Figure 6). The absence of a linear phase confirmed that the experiments report a single turnover. The actin concentration dependence of the observed rate (k_obs) was modeled as:

Figure 6. Steady-state ATPase rate and phosphate release from myo1b^IQ.

(Top, ●) Actin dependence of the steady-state ATPase rate of myo1b^IQ in KMg25 measured using the NADH-coupled assay at 37 °C. Data is from (21). (Top, ■) Actin dependence of the rate of phosphate release (k₄′) from 2.5 μM myo1b^IQ in the presence of 0 – 80 μM actin, 1.25 μM ATP, and 5 μM P_iBP (concentrations after mixing). The solid line is a fit of the data to eq. 4. Each point is the average of 1 – 3 transients. (Bottom) Time course of transient P_i release from 2.5 μM myo1b^IQ after mixing with 1.25 μM ATP, aging for 7 s, and mixing with 40 μM actin in a sequential mix, single turnover experiment in KMg25 at 37 °C. The smooth curve is a single exponential fit to the data (k_obs= A(1-e^-k·t)).

$$k_{\text{obs}}=\frac{k_{+4}\prime \left[\text{Actin}\right]}{K_9+\left[\text{Actin}\right]}$$ (4)

where K₉ is a rapid equilibrium step and k₊₄′ is irreversible in the absence of free phosphate (Scheme 1) (27). The actin-dependent rate of phosphate release is hyperbolic with K₉ = 53 ± 9.8 μM and k₊₄′ = 0.58 ± 0.056 s^-1. The maximum rate of phosphate release (k₊₄′) is the same as the maximum steady-state rate of ATP turnover (V_max = 0.6 ± 0.1 s^-1), and the affinity of the M.ADP.P for actin (K₉) is the same as the K_ATPase determined in steady-state experiments (50 ± 20 μM; Figure 6) (21). Therefore, the P_i release step is the rate-limiting step in the steady-state ATPase cycle.

ADP Release

The rate of ADP release (k₊₅′) was determined by ATP-induced dissociation of myo1b^IQ from pyrene-actin at 10 – 37 °C:

When myo1b^IQ active-sites are saturated with ADP, ATP binding is rate-limited by the slow dissociation of ADP (13, 22). ADP (30 μM final concentration) was incubated with 150 nM pyrene-actomyo1b^IQ (final concentration) and mixed to 1 mM ATP (Figure 7, top). Transients were acquired on a split time-scale to ensure a fast phase was not being overlooked. Transients at 30 μM ADP were best fit by single exponential functions and had rates that ranged from 0.16 s^-1 at 10 °C to 6.7 s^-1 at 37 °C (Figure 7; Table 2). An Arrhenius plot of the data is linear and yields an E_a of 103 kJ/mol (Figure 4; Table 3). The rates and temperature dependence of k₊₅′ are similar to those determined for k_+α (Tables 2 & 3).

Figure 7. ADP release from actomyo1b^IQ.

(Top) Temperature dependence of the rate of the pyrene-actin fluorescence increase after mixing 1 mM ATP with 0.15 μM actomyo1b^IQ equilibrated with 30 μM ADP. Transients were acquired at 10, 18, 25, 31, and 37 °C. The first 50 ms of the traces were acquired at a higher sampling rate, resulting in larger scatter of the points. Transient acquired in the presence of 30 μM ADP were best fit by single exponential functions. (Bottom) Normalized amplitude of the slow phase obtained by fitting pyrene transients to double exponential functions as a function of ADP concentration at 37 °C. The solid line is a fit of the data to a hyperbola.

The affinity of actomyo1b^IQ for ADP (K₅′) was determined at 37 °C (Figure 7, bottom). In the presence of non-saturating concentrations of ADP, the transient is the sum of two exponential rates. The rate of the slow component reports the rate of ADP release (k₊₅′), and the fast phase represents ATP binding to the nucleotide free sites (K₁′k₊₂′). The affinity of the actomyo1b^IQ for ADP was determined by monitoring the change in the relative amplitude of the slow phase (Figure 7, bottom; (15)). A hyperbolic fit to the data yields an affinity, K₅′ = 0.84 ± 0.068 μM (Table 1).

Discussion

ATP Binding

We confirmed previous results (13-15) showing the apparent second-order rate constant for ATP binding to actomyo1b^IQ to be much slower than other characterized myosins at ambient temperature (Table 2). Actomyo1b^IQ binds ATP ∼30-fold slower than skeletal muscle myosin-II at 18 °C (Figure 4; (28)). However, at 37 °C, myo1b^IQ binds ATP only 5-fold slower than skeletal muscle myosin-II, and binds ATP faster than long- and short-tail myosin-I isoforms from Acanthamoeba (9) and Dictyostelium (12, 29) at the physiological temperatures of these organisms.

An Arrhenius plot of the rate of ATP binding (K₁′k₊₂′) to actomyo1b^IQ yields an E_a of 111 kJ/mol, which is 2.5-fold greater than determined for myosins-II and -VI and 3-fold greater than determined for myosin-V (Figure 4; Table 3). This monstrous temperature dependence is the greatest reported for any myosin and highlights the importance of determining rate constants at physiological temperature when correlating kinetics with biological function. The isomerization step (k₊₂′) is responsible for the temperature dependence of the overall reaction, as is reflected in the similar activation energies for the steps associated with K₁′k₊₂′ and k₊₂′ (Table 3).

The equilibrium constant K₁′ changes less than 2-fold between 10 – 37 °C (Table 2), supporting the assignment of the AM(ATP) state as a collision complex. This property is similar to the initial binding steps of myosins –II and –V, but differs from myosin-VI, which has ∼ 15-fold weaker K₁′ (30). The initial ATP binding step for myosin-VI is not a true collision complex, but is best modeled by a rapid isomerization between a nucleotide-sensitive state and a nucleotide-insensitive state, similar to the much slower transition (k_α; Scheme 1) reported for myo1b (30). The sequence of “loop 1” of the myo1b motor domain has been shown to modulate this transition (15), thus it is plausible that this region also plays a role in regulating a similar transition in other myosins.

AM to AM′ transition

The maximum rate of ATP binding (k₊₂′) is 143-fold faster than the transition from the nucleotide accessible state (AM′) to the nucleotide inaccessible state (AM) at 37 °C (k_-α; Table 1). Therefore, the AM state (Scheme 1) is not significantly populated during steady-state ATP hydrolysis.

The rates and equilibrium constants that define the AM to AM′ transition depend on the temperature to a lesser extent than ATP binding (Figure 4; Table 3). A van't Hoff plot of K_α is linear from 10 – 31 °C with a break occurring at 31 °C (Figure 4). The slope between 10 – 31 °C yields an enthalpy (ΔH°) of 81 kJ/mol. There is high experimental confidence in the 37 °C point, since it is the result of multiple transients acquired at two ATP concentrations. Thus, the non-linearity in the plot is likely due to a change in the standard molar heat capacity (ΔC_P°) of actomyo1b^IQ. Changes in ΔC_P° indicate a significant conformational change in the protein as it approaches physiological temperatures (30).

ATP Hydrolysis

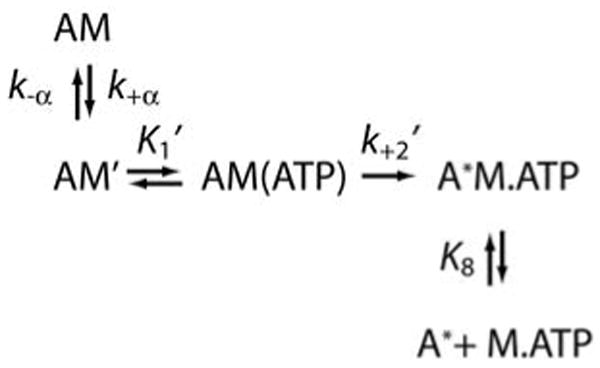
We propose that the change in fluorescence of mantATP, excited by fluorescence resonance energy transfer, is due to a conformational change in the myosin that positions the active site to catalyze ATP hydrolysis (Scheme 4). Muscle myosins show a similar change in fluorescence as a result of an environmental change around tryptophan 510 (31, 32), and an equivalent tryptophan is present in myo1b. We were unable to measure a change in tryptophan fluorescence directly in the presence of actin because of the low signal to noise at 37 °C and the presence of a high fluorescence background from the actin.

Scheme 4.

The observed fluorescence change is not due to mantATP binding (K₁′k₂′) or actomyo1b^IQ dissociation (k₈), since light scattering measurements indicate that the rate does not saturate at high mantATP concentrations (Figure 5). Additionally, this fluorescence change is not reporting a conformational change due to phosphate release (k₊₄′), since it is > 10-fold faster than the rate-limiting step. Therefore, the fluorescence change is most likely the conformational change that limits the rate of ATP hydrolysis (31, 32).

Phosphate Release

The actin-concentration dependence of phosphate release (K₉ = 53 ± 9.8 μM and k₊₄′ = 0.58 ± 0.056 s^-1; Table 1) is identical to the actin-concentration dependence of the steady-state ATPase activity (K_ATPase = 50 ± 20 μM and V_max = 0.6 ± 0.1 s^-1; (21)). Therefore, phosphate release is the rate-limiting step, and the predominant steady-state intermediates are the M.ADP.P_i and AM.ADP.P_i states.

The rate of phosphate release from actomyo1b^IQ is much slower than other characterized myosins, even when one considers physiological temperatures. For example, phosphate release from activated Acanthamoeba myosin-Ic = 24 s^-1 (26), myosin-V > 100 s^-1 (22, 33), and skeletal muscle myosin-II = 75 s^-1 (24). It is not clear why myo1b evolved to have a slow rate of phosphate release, but it is likely that the motor is kinetically tuned to optimally sense tension allowing for force-dependent changes in its duty ratio (see below).

ADP Release

The rate of ADP release (k₊₅′) from myo1b^IQ is slow at all assayed temperatures (Table 2). An Arrhenius plot yields an E_a of 103 kJ/mol, which is comparable to other myosins that have slow rates of ADP release (Figure 4; Table 3), suggesting that the ADP release mechanisms for these myosins are similar.

The kinetic rates and E_a of the AM to AM′ transition are remarkably similar to the rates and E_a of ADP release (Tables 2 and 3), suggesting a similar structural change is responsible for both transitions. Recent work provides evidence that a common structural element of myo1b modulate both the rate of ADP release and k_α (15). Therefore, it is likely that k₊₅′ and k_+α are reporting the same structural transition, which in the case of ADP release, includes a rotation of the myo1b lever arm. As pointed out by Geeves et al (14), in the presence of a load that resists lever arm rotation, the rate of k_-α may increase and k_+α may decrease to such an extent that the AM state becomes a predominant steady-state intermediate (see below).

Duty ratio

The duty ratio is defined as the fraction of the total ATPase cycle time that an individual motor is attached to actin (16). We can calculate the duty ratio of myo1b at 37 °C using the rate constants obtained in our kinetic analysis (Table 1). Since the rate of ADP release limits exit from the strong binding states, and the rate of P_i release limits the rate into the strong binding states (and all other rates are significantly faster), the duty ratio of myo1b under high ATP and actin concentrations can be defined as

$$\text{duty ratio}=\frac{k_{+4}\prime }{k_{+4}\prime +k_{+5}\prime },$$ (5)

which yields a duty ratio of 0.08. Therefore, at physiological ATP (2.2 mM) and ADP (12 μM) concentrations (34) at 37 °C in the absence of load, we expect the M.ADP.P_i and AM.ADP.P_i states to be the predominant steady-state intermediates with the mole fraction of the AM.ADP and AM′ states to be less than 0.1. This finding is consistent with previous reports that myosin-I isoforms are low duty ratio motors (for review, (16)).

Generally, myosins with low duty ratios work at high concentrations to move rapidly relative to actin filaments (e.g., skeletal muscle myosin-II), while those with high duty ratios work in low numbers to move processively along actin filaments (e.g., myosin-V). However, it has been proposed that the attachment lifetimes of some myosin-I isoforms, including myo1b, are highly sensitive to load, with resistive loads proposed to dramatically increase the actin attachment lifetime (13) and duty ratio (10). This prediction is based on the slow rate of ADP release and the ∼ 30° rotation of the long lever arm that occurs after the force-generating powerstroke that accompanies ADP release (35).

If we assume a rigid myo1b lever arm, and we assume that the powerstroke must be completed before ADP is released, we estimate the effect of force on the duty ratio of myo1b (36-38),

$$k_{+5,\text{force}}\prime =k_{+5}\prime \text{exp}\left[\frac{-\text{Fd}}{k_{b}T}\right]$$ (6)

where k_+5,force′ is the rate of ADP release in the presence of external force, F is the external force, d is the distance the end of the lever arm travels upon release of ADP, and k_bT is thermal energy (4.3 pN·nm at 37 °C). Assuming d = 5.5 nm (35), a plot of the duty ratio as a function of force shows that the duty ratio of myo1b is greater than 0.5 at resisting forces as low as 2 pN. If d = 5.5 nm is an underestimate, and is equal to 10 nm under high calmodulin concentrations (21), the duty ratio is ∼0.5 at 1 pN and > 0.8 at 2 pN (Figure 8). Although this simulation is a rough estimate of the force-dependence of the duty ratio, it supports the proposal that myo1b (and likely myo1a and myo1c) are motors well designed for tension maintenance and tension sensing (10, 13, 35, 39). It is interesting to note that alternative splicing within the myo1b lever arm results in isoforms with four, five, or six IQ motifs, and thus may be a mechanism for tuning the strain-dependence of the myo1b duty ratio (21). Depending on the stiffness of the lever arm, more energy may be required to rotate the longer splice isoforms to a position that allows ADP to be release, and thus may slow exit from the strong binding state (13).

Figure 8. Calculated duty ratio as a function of force.

Duty ratios of myo1b calculated as a function of force for two different values of d (see eqs. 5 & 6 and text). Positive forces correspond to pulling back on the lever arm, and negative forces correspond to pushing the lever arm forward.

Recent single-molecule investigations show that the lifetimes of actin-bound myosin intermediates are affected by loads imposed on the lever arm (36-38). Because the myo1b lever arm is 2-3 fold longer than the myosin-II lever arm, and the rate of ADP release from myo1b is significantly slower than from myosins -II and –V, we predict that low resisting forces will more dramatically increase the lifetimes of the strong-binding states of myo1b than myosins-II or -V.

Relationship to other myosin-I isoforms

Myosin-I isoforms can be broadly divided into long-tail and short-tail classes based on the sequences of their motor and tail domains (16). Both classes follow a common ATPase pathway and have low duty ratios (< 0.1), but rate constants that define the pathways vary by > 10-fold. Based on previous studies, we predicted that all short-tail isoforms have slow rate constants (long intermediate lifetimes), and all long-tail isoforms have fast rate constants (short intermediate lifetimes) (11). These kinetic differences provide insight into the function of the isoforms. For example, the long lifetimes of the force-bearing intermediates of the short-tail isoforms are likely important for proposed tension-sensing and structural roles (16).

A recent report shows Dictyostelium myosin-IE (Dmyo1e), a short-tail isoform, has rate constants significantly faster at 20 °C than vertebrate short-tail isoforms measured at the same temperature (12). We show in this study that many of the myo1b^IQ rate constants are of similar magnitude to Dmyo1e when the rates are compared at the respective physiological temperatures of each organism. For example, ATP binding to and ADP release from actomyo1b^IQ at 37 °C are within 4-fold of Dmyo1e at 20 °C. Given these similarities, large kinetic differences are still present. Most notably, phosphate release from actomyo1b^IQ at 37 °C is 15-fold slower than the steady-state ATPase rate of Dmyo1e.

Given the variation in rate constants within the short-tail subclass, it does not appear that one can predict precisely the lifetimes of the biochemical intermediates based on the myosin-I subclass alone. However, it is clear that all characterized short tail isoforms have a relatively slow rate of ADP release, a nucleotide-insensitive actin-bound state, and a low ADP coupling ratio (K₅′/K₅; (40)) as measured previously for myo1b (13), supporting the prediction that these isoforms are tuned for tension-sensing or tension-maintenance (10, 11, 13, 39).

Scheme 2.

Scheme 3.

Scheme 5.

Abbreviations

A

Actin

AM

actomyosin

CaM

calmodulin

Dmyo1e

Dictyostelium myosin-IE

mantATP

2′-deoxy-methyanthraniloyl-labeled ATP

M

myosin

myo1b^IQ

expressed myo1b protein construct containing the motor domain and a single IQ motif with bound calmodulin

P_iBP

fluorescently labeled phosphate binding protein