Abstract
The effectiveness of chemotherapeutic drugs in tumors is reduced by multiple effects including drug diffusion and variable susceptibility of local cell populations. We hypothesized that quantifying the interactions between drugs and tumor microenvironments could be used to identify more effective anti-cancer strategies. To test this hypothesis we created a mathematical model that integrated intracellular metabolism, nutrient and drug diffusion, cell-cycle progression, cellular drug effects, and drug pharmacokinetics. To our knowledge, this is the first model that combines these elements and has coupled them to experimentally derived parameters. Drug cytotoxicity was assumed to be cell-cycle phase specific, and progression through the cell cycle was assumed to be dependent on ATP generation. The model consisted of a coupled set of nonlinear partial differential, ordinary differential and algebraic equations with an outer free boundary, which was solved using orthogonal collocation on a moving grid of finite elements. Model simulations showed the existence of an optimum drug diffusion coefficient: a low diffusivity prevents effective penetration before the drug is cleared from the blood and a high diffusivity limits drug retention. This result suggests that increasing the molecular weight of the anti-cancer drug paclitaxel from 854 to approximately 20,000 by nano-particle conjugation would improve its efficacy. The simulations also showed that fast growing tumors are less responsive to therapy than are slower tumors with more quiescent cells, demonstrating the competing effects of regrowth and cytotoxicity. The therapeutic implications of the simulation results are that 1) monolayer cultures are inadequate for accurately determining therapeutic effects in vitro, 2) decreasing the diffusivity of paclitaxel could increase its efficacy, and 3) measuring the proliferation fraction in tumors could enhance the prediction of therapeutic efficacy.
Keywords: Cell cycle, Drug penetration, Chemotherapy, Pharmacokinetics and Tumor growth model
1. Introduction
The effectiveness of most chemotherapeutic drugs is dependent on the distribution of local microenvironments in tumors (Brown, 2002; Sutherland, 1988; Tannock, 1986). There are two major properties of these microenvironments that reduce therapeutic efficacy: low drug concentrations due to diffusion resistance and reduced responsiveness of cancer cells to the administered drug (Grantab et al., 2006; Jain, 1999; Lankelma, 2002; Minchinton and Tannock, 2006; Tannock, 1986; Tannock, 2001; Tannock et al., 2002). A model containing both of these phenomena could address whether drug concentration gradients affect cell susceptibility. Additionally, understanding the interaction of these barriers to therapy will enable development of novel strategies to overcome them (Jain, 1996).
Resistance to interstitial diffusion is known to significantly reduce drug efficacy in tumors (Au et al., 2002; Grantab et al., 2006; Lankelma, 2002; Nederman and Carlsson, 1984; Nicholson et al., 1997; Tannock et al., 2002). Many potential therapeutic agents that kill cancer cells in monolayer culture flasks do not effectively reduce tumor growth when tested in mice (Olive and Tuveson, 2006; Suggitt and Bibby, 2005). This reduced efficacy can be attributed in part to drug transport limitations. The anticancer drug paclitaxel (Pac) is known to have gradients in tissues that affect its efficacy (Au et al., 2002; Grantab et al., 2006; Nicholson et al., 1997). Experiments with multicellular layer cultures have shown that drug transport through tumor tissue poses a substantial barrier to chemotherapeutic effectiveness for even fast penetrating drugs like 5-fluorouracil (5FU) (Nederman and Carlsson, 1984; Tunggal et al., 1999). Diffusion resistance in tumors is compounded by the chaotic vascular network which has large intercapillary distances compared to normal tissue and therefore more cellular regions distant from the blood supply (Jain, 1999; Konerding et al., 1999).
The responsiveness of cancer cells to chemotherapeutics strongly depends on the cell’s position in the cell cycle (Shah and Schwartz, 2001). Most anticancer agents only target proliferating tumor cells and do not affect poorly nourished quiescent cells that are distant from vasculature (Jackson, 1989; Tannock, 1986). More specifically, many therapeutics affect cells in specific cell-cycle phases. For example, 5-fluorouracil targets cells in S phase (Daniel et al., 2003; Tanaka et al., 2000) and paclitaxel inhibits microtubule formation, which is toxic to cells in the G2 and M phases (Nogales, 2000; Zhao et al., 2005)
Cell-cycle progression is divided into different phases (Fig. 1) namely, G0, G1, S, G2 and M, each characterized by the different functions necessary for progression through cell division under different environmental conditions. In three-dimensional tissue the growth rate and the transition rates through the cell-cycle phases depend on local nutrient availability and the amount of cellular energy (ATP) provided by intracellular metabolism (Costello and Franklin, 1994; Venkatasubramanian et al., 2006). Nutrient availability is controlled by diffusion of nutrients through successive layers of cells in the tissue. When supplied with sufficient nutrients, cells will replicate rapidly and more cells will be in the S, G2 and M phases. In environments with less nutrients, cells will spend more time in G1 and may enter G0 (Carlsson, 1977; Darzynkiewicz et al., 1980; Dethlefsen et al., 1980). This effect has been demonstrated experimentally: at the outer, well-nourished edge of spheroids, the population of cells in the S, G2 and M phases has been shown to be higher than in the interior of spheroids, where the relative population of G1 cells is higher (Carlsson, 1977; Freyer, 1998; LaRue et al., 2004; Wibe et al., 1981). This organization is also seen in tumors grown in mice. The relative population of rapidly growing cells has been shown to be greater near blood vessels than deep within tumor tissue (Sutherland, 1988).
Figure 1.
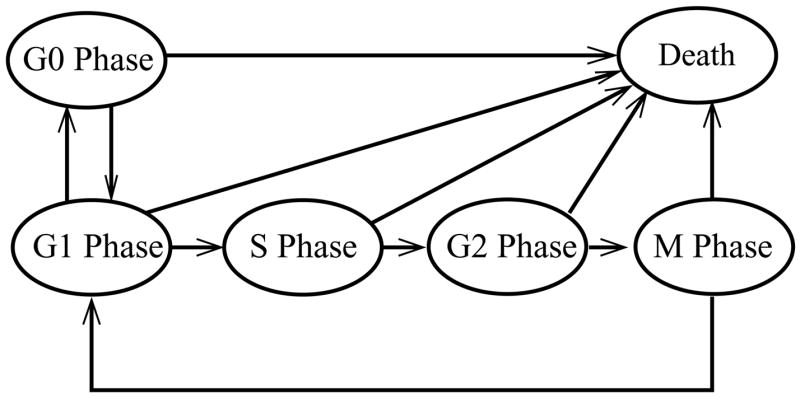
Cell-cycle model incorporated in the spheroid growth model. The entire spheroid volume was assumed to be comprised of either dead cells or cells in the different phases of the cell cycle: G0, G1, S, G2 and M. Each line signifies a transition from of one cell-cycle phase to another. In good nutrient conditions cells will proliferate by traversing from G1 to S to G2 to M to G1. In the final transition from M to G1 phase cells replicate. In good nutrient conditions quiescent G0 cells can become proliferating by entering the G1 phase. In moderately poor nutrient conditions G1 cells will traverse to the quiescent, G0 phase. In acutely poor nutrient conditions (or in the presence of a cytotoxic drug) cells from all cell-cycle phases will die.
When investigating drug efficacy, the effects of drugs on normal cells in the body cannot be ignored. If only the local tumor environment is considered, the obvious treatment solution would be continuous administration of cytotoxic drugs at very high concentrations. This problem is encountered when interpreting drug studies in monolayer cultures: most compounds show efficacy against cancer cells but are systemically too toxic for clinical use (El-Khoueiry and Lenz, 2006; Kearns et al., 1995; Kim and Tannock, 2005). In practice all cancer therapies are toxic to normal cells at some concentration and must be administered in periodic cycles (Kim and Tannock, 2005). For example, paclitaxel is typically administered for 24 hours every 3 weeks (Perez, 1998) and 5-fluorouracil is administered for 24 hours every week (Leichman, 1999; Thomas and Zalcberg, 1998). These intervals allow for normal cells in the body and the immune system to recover between treatments (Kim and Tannock, 2005).
To adequately account for the effects of the body and the cardiovascular system, pharmacokinetics must also be included. The concentration of a drug in the blood cannot be directly controlled. Once an intravenous (IV) injection has been started a lag exists until the concentration in the blood reaches a maximum. Throughout the infusion, drug is constantly being cleared from the blood via the action of the liver and the kidneys which metabolize and excrete it (Gianni et al., 1995; Lau et al., 2001). Pharmacokinetics can be accurately described mathematically using two and three compartment models (Kearns et al., 1995; Terret et al., 2000).
We have developed a tumor model that incorporates spatial heterogeneity, drug diffusion, drug pharmacokinetics, cell-cycle-phase transitions and the diffusion of multiple nutrients to address the hypothesis that understanding the interactions between drugs and the heterogeneous microenvironments in tumors can be used to formulate effective therapeutic strategies. The current model describes the growth of in vitro multicellular tumor spheroids and in vivo avascular tumor nodules. Energy metabolism is described using our previously developed spheroid model for the diffusion of glucose, oxygen, and lactate and the associated generation of ATP (Venkatasubramanian et al., 2006). The tumor model consists of a coupled set of nonlinear partial differential, ordinary differential and algebraic equations with a free outer boundary. An iterative calculation procedure with spatial discretization and a moving grid was used to numerically solve the model equations. Model parameters were estimated from experimental data available in the literature. The components of the model were validated with a range of simulations that were compared to experimental observations.
2. Previous Tumor Models
Previous mathematical studies designed to understand the effect of cell-cycle-specific or non-specific drugs on tumor growth (Table 1) can be broadly divided into two categories: (1) models that considered the tumor as a homogeneous population of cells without spatial heterogeneity and (2) models that incorporated spatial heterogeneity, drug diffusion, and other transport effects.
Table 1.
Summary of tumor growth and drug cytotoxicity models. Models are classified into two categories 1) homogeneous models (no spatial heterogeneity) and 2) transport based models (explicitly incorporation of spatial heterogeneity)
| Author(s) | Elements Included | Result/Discovery |
|---|---|---|
| Homogeneous Models | ||
|
| ||
| Levasseur et al., 1998 | Integrated experiments ands modeling | Altering the time of exposure to the agents can be used to modulate drug effect, response heterogeneity, and drug resistance. |
| Monolayer simulation | ||
| Gardner, 2000 | Cell death | An optimal, finite duration of drug exposure maximizes cell kill. |
| Cell-cycle phases | ||
| Basse et al., 2003; Basse et al., 2004 | Cell death | Flow-cytometric data was analyzed to obtain transition rate parameters between different cell-cycle phases and apoptosis. |
| Cell-cycle progression | ||
| Population balance | ||
| Parameter estimation | ||
| Panetta, 1997 | Proliferating and quiescent cell populations Paclitaxel cytotoxicity | Frequent drug infusion (once every 1 or 2 weeks) is more effective for paclitaxel than the conventional infusion (once in 3 weeks). |
|
| ||
| Transport-Based Models | ||
|
| ||
| Jackson and Byrne, 2000 | Tumor growth | Tumors with well-vascularized peripheries and large avascular centers respond best to treatment. |
| Pharmacokinetics | ||
| Drug cytotoxicity | ||
| Tumor regression | ||
| Jackson, 2003 | Tumor growth | Long-term therapeutic response is sensitive to the threshold |
| Pharmacokinetics | drug concentration required to initiate apoptosis. | |
| Cellular permeability has a stronger effect on the efficiency of long-term treatment than drug sequestration. | ||
| Tzafriri et al., 2005 | Interstitial drug transport | An optimized intratumoral drug release rate from paclitaxel- loaded microspheres was of determined that maximizes killing tumor cells. |
| Lankelma et al., 2000 | Interstitial drug transport | Doxurubicin takes as long as 200 hrs to penetrate to the center of tumors. |
| As great as a 15-fold difference in drug concentration exists at the periphery and center of tumor islets. | ||
| Kuh et al., 1999 | Interstitial drug transport | High tumor cell density is a barrier to paclitaxel penetration. |
| Apoptosis induced by paclitaxel enhances drug penetration. | ||
| Drug accumulation is saturable. | ||
| Bertuzzi et al., 2003 | Effects of oxygen on proliferation and death | New insight was found regarding complex treatment-related events, including cell re-oxygenation and repopulation. |
| Volume reduction due to dead cells disintegration | ||
| Cytotoxicity of radiation and drugs | ||
| Proliferating and quiescent cell populations | ||
| Ward and King, 2003 | Tumor growth | Multicellular spheroids have an enhanced survival rate compared to monolayer cultures. |
| Drug cytotoxicity | ||
The homogenous models included more sophisticated mechanisms describing the cell cycle and drug effects than the spatially distributed models (Table 1). Most of these models were based on experiments with cells grown in monolayer cultures and did not include nutrient or drug transport. The effects of drug concentration and exposure time on monolayer cultures have been described by both phenomenological Hill coefficient models (Levasseur et al., 1998) and mechanistic models that incorporate cell-cycle phases (Gardner, 2000). These drug-effect models predicted that chemotherapeutic strategies could be tailored to individuals and suggested that altering drug scheduling may be more effective than dose escalation (Gardner, 2002b). Multiple compartment, cell-cycle-phase models have been developed that were based on cellular DNA content in order to couple with flow-cytometry data (Basse et al., 2003) and predict the effect of paclitaxel on monolayer cultures (Basse et al., 2004). A mathematical model that divided tumor mass into resistive and sensitive cell populations suggested that frequent drug infusion would be more effective in the treatment of breast and ovarian cancer with paclitaxel (Panetta, 1997).
Models incorporating spatial heterogeneity have also been developed to study the effects of drug diffusion and drug-induced cell death in tumors (Table 1). Jackson and Byrne (Jackson and Byrne, 2000) developed a tumor model incorporating vasculature with drug-resistant and drug-sensitive cell types to study the effect of emergent resistance on chemotherapeutic response. A spatio-temporal model of tumor response to sequestered, intracellular doxorubicin predicted that the response to chemotherapy is sensitive to the threshold level of doxorubicin required to initiate apoptosis at the maximum rate (Jackson, 2003). A reaction-diffusion based model that incorporated drug diffusion through tumor interstitium, intracellular uptake, and drug clearance through the microvasculature was used to determine the optimum drug release rate from intratumorally injected microspheres (Tzafriri et al., 2005). Models of doxorubicin (Lankelma et al., 2000) and paclitaxel (Au et al., 2001) transport through tumor tissue, which incorporate intracellular drug binding, predicted that these drugs penetrate slowly and have long retention times in tissue. These previous models individually accounted for spatial heterogeneity, drug transport limitations, cell-cycle progression, and pharmacokinetics. However, to our knowledge no existing tumor models capture all of these effects. Understanding the interaction of these elements is critical to for the design of effective therapeutic strategies.
3. Model structure
The present model is an extension of our previous model that predicted the extent and location of quiescence assuming that cell growth and death are dependant on intracellular energy metabolism (Venkatasubramanian et al., 2006). In this study we have incorporated cell-cycle progression, drug transport, pharmacodynamics and pharmacokinetics to develop a model capable of predicting the effect of heterogeneous microenvironments on drug efficacy. The model consists of cell and mass balance equations formulated in spherical coordinates under the assumption of radial symmetry.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
Equation (1) represents the conservation of cell number within each cell-cycle phase, where ni is the number of cells in the ith cell-cycle phase per unit volume. The six cell phases included G0, G1, S, G2, M and dead cells. The terms on the left hand side of Eq. (1) are the accumulation of cells in each cell-cycle phase and the convective transport of cells due to expansion of tumor tissue, where ν represents the bulk convective velocity of the cell population. The right hand side represents the net change in the number of cells in each phase due to transitions between the phases as well as cell death.
Equation (2) represents a convective flux that is created by volume changes during cell growth ( ) and death ( ) and which results in a gradient in the cell mass velocity (v). The rate of tumor growth is determined by evaluating the cell mass velocity at the periphery (Eq. 3). Cells were assumed to be tightly packed such that void space could be neglected (Eq. 4). Here Vi is the volume of an individual cell in the ith phase. Tissue volume was assumed to be entirely occupied by cells, and drug was assumed to be associated with the cells. The drug transport equation (Eq. 5) accounts for diffusive transport driven by the gradient in drug concentration and convective transport due to cell motion. The apparent drug diffusion coefficient, Dj, represents the combined effect of drug binding, drug uptake, and drug diffusion in the tissue.
Nutrient diffusion was assumed to be balanced by cellular uptake (Eq. 6), where Ck, Dk and Qk are the local concentration, the diffusion coefficient, and the uptake rate of nutrient k, respectively. The model assumes that tumor cells can consume three nutrients: glucose, oxygen and lactate (Venkatasubramanian et al., 2006). Because the molecular weights of the nutrients are small, their transport is assumed to be fast compared to tumor growth. This pseudo-steady state assumption implies that nutrients do not accumulate in the tissue (Venkatasubramanian et al., 2006). The pseudo-steady state assumption was not applied to the drug mass balance (Eg. 4) to account for the possibility that the time scale for drug diffusion is comparable to that for tumor growth.
For all balances, a Neumann-type symmetry condition was imposed at the tumor center. This constraint was implemented as a zero-gradient boundary condition for the cell, nutrient and drug balances, and a zero-velocity boundary condition for the volume balance. The second boundary condition for the drug balance (Eq. 5), is a time-dependent pharmacokinetic function, f(t), that accounts for drug infusion and washout. Nutrient concentrations were assumed to be constant at the tumor periphery and equal to the bulk concentration (Cj,Bulk, Eq. 6). In the following sections the individual components of this model are described in detail.
3.1 Cell metabolism
A description of primary energy metabolism that encompassed glycolysis and the TCA (tricarboxylic acid) cycle was used to calculate local nutrient uptake rates, Qk. Each uptake rate was determined from 1) the availability of the nutrient in the extracellular environment and 2) stoichiometric limitations of intracellular metabolism. The metabolic model was based on the assumption that glucose and oxygen can be consumed and that lactate can be either produced or consumed. The following three lumped reactions describe the metabolic pathways included in the model:
The maximal uptake rates of each nutrient were assumed to follow Michaelis-Menten-like functions, which describe the enzymatic control of glucose uptake and the saturation of oxygen and lactate uptake at high concentrations (Helmlinger et al., 2002).
| (7) |
Actual uptake rates (QGluc, QOx and QLac) were limited by the stoichiometry of intracellular metabolism (Eq. 8), which was based on three simple assumptions: 1) cells consume glucose when it is available, 2) oxygen uptake rate is limited by the maximal oxygen uptake rate or by the combined maximal uptake rates of the two carbon sources, and 3) lactate can be consumed as a carbon source when the concentration of glucose is low and the concentration of oxygen is high. These assumptions produced the following rules for the actual uptake rates:
| (8) |
ATP production was determined by considering the formation and oxidation of pyruvate and assuming that the rate of the TCA cycle was equivalent to the oxygen uptake rate. The conversion of glucose to pyruvate, the conversion of lactate to pyruvate, and the oxidation of pyruvate were assumed to produce 8, 3, and 15 ATP molecules, respectively. The ATP generation rate was approximated from the three uptake rates and simplified using the third expression of Eq. (8) as follows:
| (9) |
These relationships and assumptions are described in more detail in our previous publication (Venkatasubramanian et al., 2006). The amount of available energy (ATP) is subsequently used to determine the rates of cell-cycle transitions, cell growth and cell death.
3.2 Cell-cycle transitions
The population of live cells in the tumor was divided into fractions corresponding to the different cell-cycle phases: G0, G1, S, G2 and M (Fig. 1). Cell balances (Eq. 1) describe the number density of cells in each phase as a function of radial position and time. The transition rates between the phases are described by kinetic expressions dependent on the local ATP generation rate (Eq. 10).
| (10) |
The transition rates between the phases are given by the following terms:
| (11) |
Here σ is the basal survival rate (Venkatasubramanian et al., 2006). All transitions through the cell cycle increase with increasing ATP production (μ), whereas the transitions to G0 and death increase with decreasing ATP production (μ̂).
There are two possible fates for G1 cells depending on energy availability. Under favorable environmental conditions (high ATP generation rates), G1-phase cells will enter S phase and commence cell division. Under unfavorable conditions (low ATP generation rates), G1-phase cells will enter the quiescent G0 phase. If a G0 cell returns to favorable conditions, it will reenter G1 and continue to replicate through the cell cycle. Actively proliferating cells will progress sequentially through the G1, S, G2 and M phases (Eq. 10). With available energy, M-phase cells divide and produce two G1 cells. Under unfavorable conditions or when exposed to therapeutics, cells in all phases will die (Eq. 10).
Simulations were started with a spherical tissue mass the size of a single cell in G1 phase, which produced the following initial condition:
| (12) |
The units of ni are cells per unit volume. It was assumed that cells in different phases had different volumes.
| (13) |
Because the model describes the evolution of cell populations rather than individual cells, the volumes in Eq. (13) represent the average volumes of cells in each cell-cycle phase. Progression through the cell cycle was assumed to produce a linear increase in the average cell volume, with typical lengths of the different cell-cycle phases used to estimate the cell volumes. Accordingly, the values listed in Table 2 satisfy the following constraints: 1) the average volume of G1 phase cells is greater than one-half the volume of M phase cells; and 2) the average volume of G2 phase cells is greater than average volume of S phase cells. Furthermore, quiescent cells have been reported to have one-half the volume of proliferating cells (Bauer et al., 1982).
Table 2.
Model parameters and their literature sources
| Symbol | Description | Value | Source/Constraint |
|---|---|---|---|
| Nutrient transport and metabolism | |||
|
| |||
| DGluc | Glucose diffusion coefficient | (Casciari et al., 1992) | |
| DOx | Oxygen diffusion coefficient | (Mueller-Klieser and Sutherland, 1984) | |
| DLac | Lactate diffusion coefficient | (Casciari et al., 1992) | |
| CGluc | Glucose concentration in the bulk | 5.5 mM | (Casciari et al., 1992) |
| COx | Oxygen concentration in the bulk | 0.21 mM | (Casciari et al., 1992) |
| CLac | Lactate concentration in the bulk | 0 mM | (Venkatasubramanian et al., 2006) |
| KGluc | Glucose uptake saturation constant | 4.0×10−2 nM | (Casciari et al., 1992) |
| KOx | Oxygen uptake saturation constant | 4.64×10−3 mM | (Casciari et al., 1992) |
| KLac | Lactate uptake saturation constant | 5.65×10−4 mM | (Venkatasubramanian et al., 2006) |
| Maximum glucose uptake | (Casciari et al., 1992) | ||
| Maximum oxygen uptake rate | (Casciari et al., 1992) | ||
| Maximum lactate uptake rate | (Venkatasubramanian et al., 2006) | ||
|
| |||
| Cell-cycle phase related parameters | |||
|
| |||
| Maximum rate of transition from G1 to G0 phase | 4.0×10−2 hr−1 | (Freyer and Schor, 1989) | |
| Maximum rate of transition from G1 to G0 phase | 4.0×10−2 hr−1 | Fixed to be the same as | |
| Maximum rate of transition from G1 to S phase | 1.2×10−1 hr−1 | (Wibe et al., 1981) | |
| Maximum rate of transition from S to G2 phase | 1.08×10−1 hr−1 | (Wibe et al., 1981) | |
| Maximum rate of transition from G2 to M phase | 4.6×10−1 hr−1 | (Wibe et al., 1981) | |
| Maximum rate of transition from M to G1 phase | 9.8×10−1 hr−1 | (Wibe et al., 1981) | |
| KG1,G0 | Critical ATP production rate, G1-G0 transition | (Freyer and Schor, 1989) | |
| KG0,G1 | Critical ATP production rate, G0-G1 transition | (Freyer and Schor, 1989) | |
| KG1,S | Critical ATP production rate, G1-S transition | Larger than KG0,G1 | |
| KS,G2 | Critical ATP production rate, S-G2 transition | Less than KG0,G1 | |
| KG2,M | Critical ATP production rate, G2-M transition | Less than KG0,G1 | |
| KM,G1 | Critical ATP production rate, M-G1 transition | 0 | Mitosis assumed to be energy independent |
| δS | Ratio of the volume of S phase cell to G1 phase cell | 1.52 | (Tyson and Novak, 2001) |
| δG2 | Ratio of the volume of G2 phase cell to G1 phase cell | 1.72 | (Tyson and Novak, 2001) |
| δM | Ratio of the volume of M phase cell to G1 phase cell | 1.89 | (Tyson and Novak, 2001) |
| δG0 | Ratio of the volume of G0 phase cell to G1 phase cell | 0.61 | (Freyer and Schor, 1989) |
|
| |||
| Death parameters due to nutrient deprivation | |||
|
| |||
| Maximum rate death from any living phase ‘i’ due to nutrient deprivation | 14.2×10−2 hr−1 | (Venkatasubramanian et al., 2006) | |
| Ki,D | Critical ATP production rate for ith phase-D transition | (Venkatasubramanian et al., 2006) | |
| δD | Ratio of the volume of initially formed dead cell to G1 phase cell | 0.30 | (Venkatasubramanian et al., 2006) |
| σ | Basal survival rate | 0.9 | (Ward and King, 1997) |
| Volume loss rate of dead cells | 0.487 | Fixed so as to obtain a saturated size of 1 mm | |
|
| |||
| Drug related parameters | |||
|
| |||
| DPAC | Paclitaxel diffusion coefficient | (Nicholson, 1997) | |
| D5FU | 5-fluorouracil diffusion coefficient | (Tunggal, 1999) | |
| Maximum death rate of G2 and M phase cells due to paclitaxel | 3.3×10−1 hr−1 | (Au et al., 1998) | |
| Paclitaxel death rate saturation constant | 6.225 nM | (Au et al., 1998) | |
| Maximum death rate of S cells due to 5-fluorouracil | 7.76×10−2 hr−1 | (Kufe and Major, 1981; Ueda et al., 1997) | |
| S-phase specific death rate saturation constant for 5-fluorouracil | 0.1 μM | (Kufe and Major, 1981; Ueda et al., 1997) | |
| Cell-cycle phase non-specific death rate due to 5-fluorouracil | 4.6×10−1 hr−1 | (Kufe and Major, 1981; Ueda et al., 1997) | |
| Cell-cycle phase non-specific death rate saturation constant for 5-fluorouracil | 503.9 μM | (Kufe and Major, 1981; Ueda et al., 1997) | |
|
| |||
| Pharmacokinetic parameters | |||
|
| |||
| Paclitaxel | |||
|
| |||
| dPAC | Paclitaxel dosage concentration | 69.3 μM | (Gianni et al., 1995) |
| k21 | First order rate constant for return from 2nd to 1st compartment | 1.4 hr−1 | (Gianni et al., 1995) |
| Vm | Maximum transport rate from the 1st to the 2nd compartment | 17.7 μM/hr | (Gianni et al., 1995) |
| Km | Transport saturation constant from the 1st to 2nd compartment | 0.23 μM | (Gianni et al., 1995) |
| VmO | Maximum clearance rate of paclitaxel from the 1st compartment | 29.9 μM/hr | (Gianni et al., 1995) |
| KmO | Clearance saturation constant from the 1st compartment | 7.0 μM | (Gianni et al., 1995) |
| Vmm | Maximum metabolism rate from the 1st compartment | 1.61 μM/hr | (Gianni et al., 1995) |
| Kmm | Metabolism rate saturation constant from the 1st compartment | 60.4 μM | (Gianni et al., 1995) |
| k13 | First order transport rate constant from 1st to 3rd compartment | 2.6 hr−1 | (Gianni et al., 1995) |
| k31 | First order transport rate constant to 1st from 3rd compartment | 0.6 hr−1 | (Gianni et al., 1995) |
|
| |||
| 5FU | |||
|
| |||
| d5FU | 5-fluorouracil dosage concentration | 2.16 mM | (Terret et al., 2000) |
| Vm | Maximum clearance rate of from the 1st compartment. | 1260 mg/hr | (Terret et al., 2000) |
| Km | Clearance rate saturation constant from the 1st compartment | 6.05 mg/L | (Terret et al., 2000) |
| k12 | First order transport rate constant from 1st to 2nd compartment | 5.35 hr−1 | (Terret et al., 2000) |
| k21 | First order transport rate constant from 2nd to 1st compartment | 5.69 hr−1 | (Terret et al., 2000) |
Tumor expansion was assumed to be driven by the relative rates of growth and death, which results in generation and destruction of volume, respectively.
| (14) |
All in tumor volume changes, ϕ, are continuous, because each discrete volume difference between two phases (Vi − Vj) is multiplied by a continuous phase transition rate, μ. The final term in the volume loss expression represents degradation of necrotic material as described below.
3.3 Tumor growth saturation
Long term growth of tumors is primarily attributed to angiogenesis which creates nutrient rich microenvironment (Durand, 1990; Folkman, 1971). The present model and most other tumor models do not consider angiogenesis. Such models without explicit expressions for volume loss result in tumors with perpetually increasing volume (Venkatasubramanian et al., 2006; Ward and King, 1997). A mechanism for the degradation of necrotic debris was included in the present model to account for growth saturation observed in spheroids (Durand, 1990). The cell population was assumed to be comprised of both live and dead cells. Dead cells are created instantaneously following cell death and have a fixed volume VD. Necrotic material is assumed to degrade linearly with a constant rate of μD,loss, which resulted in the following expression for dead cell formation (Eq. 1):
| (15) |
Here, nD is the number density of dead cells. No dead cells were present in the tumor initially.
| (16) |
3.4 Saturated tumor initial condition
The initial condition for the drug concentration depended on the goal of the simulation. Three different types of simulations were run to determine the effects of chemotherapeutics on 1) cancer cells grown as a monolayer, 2) cancer cells grown as multi-cellular spheroids, and 3) cancer cells in human tumors. The monolayer and spheroid simulations were run to compare to previous experimental observations. The simulations with human tumors were run to predict therapeutic efficacy of different treatment strategies. For the simulation of monolayer cultures, cells were assumed to grow at their maximal rate under the assumption of negligible nutrient depletion in the external media. All transport terms in the model were eliminated and the cells were assumed to be exposed to a uniform drug concentration.
| (17) |
All simulations with spheroids and tumors started with a saturated spherical tumor mass at steady state. The initial condition was changed to be a saturated spheroid to expedite simulations.
| (18) |
The difference between the spheroid and tumor simulations was the peripheral drug boundary conditions. For spheroids, drug was added to and removed from the system as a pulse function with duration tpulse to mimic the addition and removal of drug containing medium from the culture.
| (19) |
3.5 Pharmacokinetics
For simulations of drug effects on human tumors the drug concentration at the periphery was given by a pharmacokinetic model. Multi-compartment models are an empirical method used to describe the clearance of drug from the body by absorption, metabolic degradation, and excretion. The pharmacokinetics of 5-fluorouracil and paclitaxel were determined in clinical trials to best fit standard two- and three-compartment models, respectively (Gianni et al., 1995; Terret et al., 2000). In these models the central compartment describes the blood plasma which is assumed to be well mixed. The peripheral compartments have slower distribution and include organs and tissues that are poorly perfused. Here, the drug concentration at the periphery of the tumor is equivalent to the plasma concentration, which is given by the concentration in the central compartment.
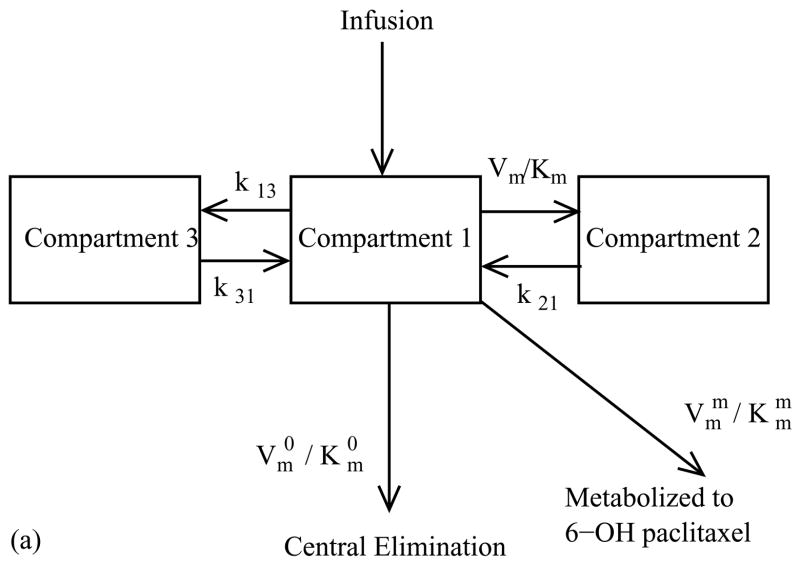
The pharmacokinetic of paclitaxel was found to fit best to a three compartment model (Gianni et al., 1995) with a central compartment containing the tumor and two peripheral compartments (Fig. 2a). Drug exchange between the first and second compartments was first-order and linear, while exchange between the first and third components was non-linear and saturable according to Michaelis–Menten kinetics. Paclitaxel was eliminated from the system by two mechanisms: a nonlinear, saturable clearance mechanism and irreversible, nonlinear metabolism into 6-a-hydroxypaclitaxel (Gianni et al., 1995). These exchanges and degradations were modeled with a set of ordinary differential equations.
Figure 2.
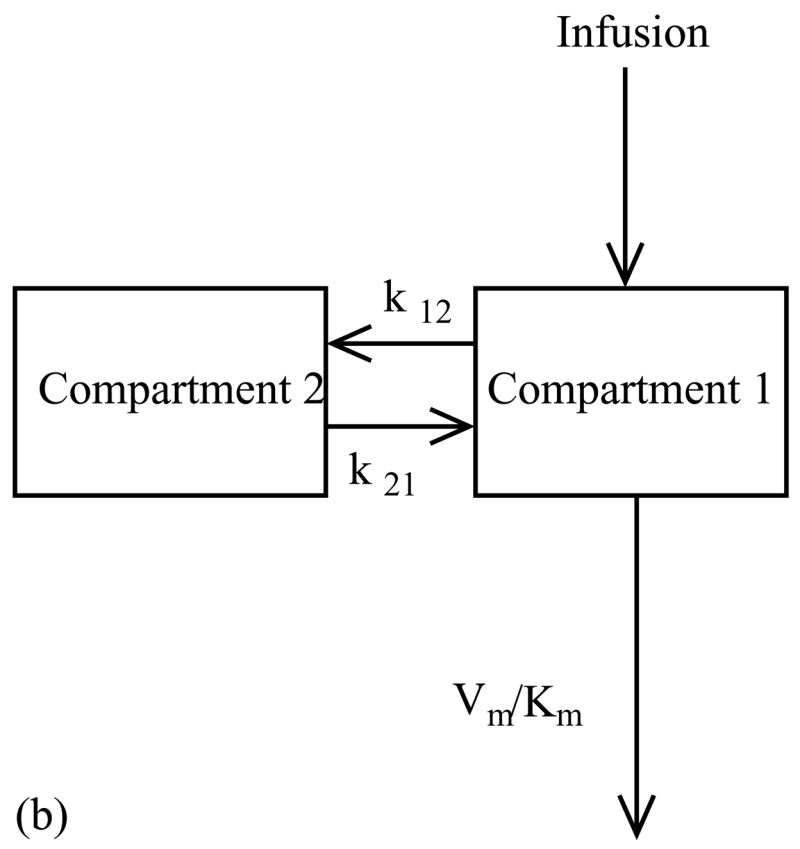
Multi-compartment pharmacokinetic models for (a) Paclitaxel and (b) 5-fluorouracil. (a) In the three compartment model for paclitaxel exchange between the first and second compartments is first-order and linear, and exchange between the first and third components follows Michaelis–Menten kinetics. Paclitaxel is eliminated from the system by non-linear clearance and non-linear metabolism into 6-a-hydroxypaclitaxel. (b) In the two compartment model for 5-fluorouracil exchange between the two compartments is first-order and linear and clearance follows Michaelis–Menten kinetics.
| (20) |
where, H(t) is the unit step function switching at time t=0 and dPAC is the dosage concentration of the administered drug. The drug concentrations in the first, second and third compartments are C1, C2 and C3 respectively; the first order rate constants for exchange between the first, second and third compartments are k12, k31 and k13. The Michaelis–Menten rate constants for the transfer from the first to the third compartment, the clearance by the kidneys, and metabolism into 6-a-hydroxypaclitaxel are Vm and Km, VmO and KmO, and Vmm and Kmm, respectively.
The pharmacokinetics of 5-fluorouracil was previously found to best fit a two compartmental model (Fig. 2b) with constant linear rates of exchange between the compartments and a non-linear saturable rate of elimination (Terret et al., 2000).
| (21) |
For both drugs the concentration at the tumor periphery was given by the concentration in the central compartment.
| (22) |
3.6 Drug cytotoxicity
The cytotoxic effects of paclitaxel and 5-fluorouracil on cells were modeled using Monod-type functions. These two drugs affect cells in different cell-cycle phases. Paclitaxel is cytotoxic to cells in G2 and M phases, and 5-FU is S phase specific at low concentrations and cell-cycle-phase non-specific (CCNS) at higher concentrations. At low concentrations 5-fluorouracil intercalates into DNA, and at high concentrations it misincorporates into RNA (Tanaka et al., 2000). The effects of drug-induced death were assumed to be additive to the metabolic rates, which was implemented by adding terms to the cell-cycle phase expressions in Eq. (1).
| (23) |
| (24) |
In Eq. (23) and Eq. (24), and are the rates of death of G2/M phase cells due to paclitaxel, S phase cells due to 5-fluorouracil, and cell-cycle nonspecific death due to 5-fluorouracil, respectively. The effect of each drug was investigated individually during the simulations.
4. Parameter Estimation
The parameters used in the model (Table 2) were obtained in three ways: 1) they were extracted directly from the literature, 2) they were calculated from experimental data in the literature, or 3) they were estimated based on known physiological behavior. The pharmacokinetic parameters for paclitaxel and 5-fluorouracil (Table 2) were obtained from human trials as reported by Gianni et al., 1995 and Terret et al., 2000, respectively. The volume of dead cells (VD) was assumed to be 50% of the quiescent cell volume (VG0), and the rate of volume loss (μD,loss) was manually adjusted to produce a saturated spheroid with a radius of 1 mm.
4.1 Estimation of cell-cycle parameters
The maximum transition rates ( ) between the proliferating cell-cycle phases were estimated from the length of time cells spend in each phase during exponential growth in monolayer culture. Wibe et al. found that transition times for each phase were TG1 = 7.9, TS = 7, TG2 = 2.1 and TM = 1 hrs (Wibe et al., 1981). The fraction of cells in each phase (g1, s, g2 and m) were calculated from the transition times using Steel’s formula (Montalenti et al., 1998).
| (25) |
The maximal transition rates were estimated from the cell-cycle-phase balances, the phase fractions, and the average doubling time (TD) assuming that the fraction of cells in each cell-cycle phase reached steady state in exponentially growing monolayer cultures.
| (26) |
At steady state
| (27) |
The maximum transition rate from G0 to G1 ( ) was estimated from spheroid dissociation experiments (Freyer and Schor, 1989), where quiescent cells were dissociated from the interior of spheroids and grown in monolayers adequately supplied with nutrients. Compared to proliferating cells, quiescent cells experienced a lag period (TLag = 25 hr) before growing exponentially (Freyer and Schor, 1989). If the inner spheroid region was assumed to be entirely composed of quiescent cells, the length of this lag was dependant on the transition rate from G0 to G1.
| (28) |
No experiments could be found in the literature that study the maximum transition rate from G1 to G0 ( ), so this parameter could not be calculated. This rate was assumed to be equivalent to the maximum transition rate from G0 to G1, which is reasonable because both transitions require the expression and inhibition of similar cell-cycle genes.
The transition rates between each phase were described with Monod-type kinetics. Saturable, hyperbolic expressions were used because each rate must have a maximum value ( ) but diminish to zero at low ATP production rates. Little is known about the saturation constants (Kfrom to), but their relative values and their orders of magnitude could be estimated (Table 2). M phase was assumed to be short and not controlled by energy availability (KM,G1 = 0). At intermediate energy availability, the G1 phase was assumed to elongate (Rossow et al., 1979), i.e. cells could not continue around the cycle, but also not become quiescent (KG1,S > KG1,G0). Once entering the cell cycle, cells would continue their progression with reduced dependence on energy availability (KS,G2 < KG1,G0). Together these assumptions produce the relation, KS, G2 < KG1, G0 < KG1, S. Finally, the saturation constant for the transition from G1 to G0 (KG1,G0) was estimated to match the percentage of quiescent cells previously observed in spheroids (Freyer and Schor, 1989) and the remaining saturation constants (KG1, S and KS,G2) were adjusted in accordance to the above relation. The cell volume in each phase was estimated by assuming that cell volume increases linearly throughout the cycle (Tyson and Novak, 2001). The volume of G0 cells was obtained from Freyer and Sutherland (Freyer and Sutherland, 1980).
4.2 Drug diffusivity
Drug transport was modeled using effective diffusion coefficients that represent the combined effects of extracellular diffusion and transmembrane transport. The diffusion of anti-cancer drugs is also known to be affected by intracellular binding and degradation (Lankelma et al., 2000). Detailed models have been developed that account for these effects, but their accuracy depends on estimation of many unknown parameters (Kuh et al., 2000; Kuh et al., 1999; Lankelma et al., 2000). The effective diffusion coefficients used in this model were estimated using data extracted from multi-cellular layer experiments, in which a layer of cells is grown on a collagen coated Teflon membrane between two compartments (Grantab et al., 2006; Nicholson et al., 1997; Tannock et al., 2002; Tunggal et al., 1999). A known amount of drug is added to one compartment and the concentration is measured in both compartments as a function of time. The following equations were used to fit these data.
| (29) |
The drug concentrations and volumes of the two compartments are CA, CB, VA, and VB. The compartments were assumed to be well mixed and the diffusion resistances were ascribed to be the multicellular layer and the Teflon membrane. Additional parameters in Eq. (29) are Dcell, the effective diffusion coefficient; Lcell, the width of the multicellular layer; Kmem, the mass transfer coefficient of the membrane; A, the cross-sectional area and; Cint, the concentration at the interface of the multicellular layer and the membrane. Data from experiments performed on Teflon membrane without multicellular layers were used to estimate the parameter, Kmem which describes the resistance solely due to membrane. This parameter was used further to fit to the remaining experimental data in order to estimate the parameter describing the resistance due to the multicellular layer (Dcell). Because the diffusivity of paclitaxel may be cell-type dependent (Nicholson et al., 1997; Tannock et al., 2002), the effect of a broad range diffusivities was investigated.
4.3 Drug cytotoxicity parameters
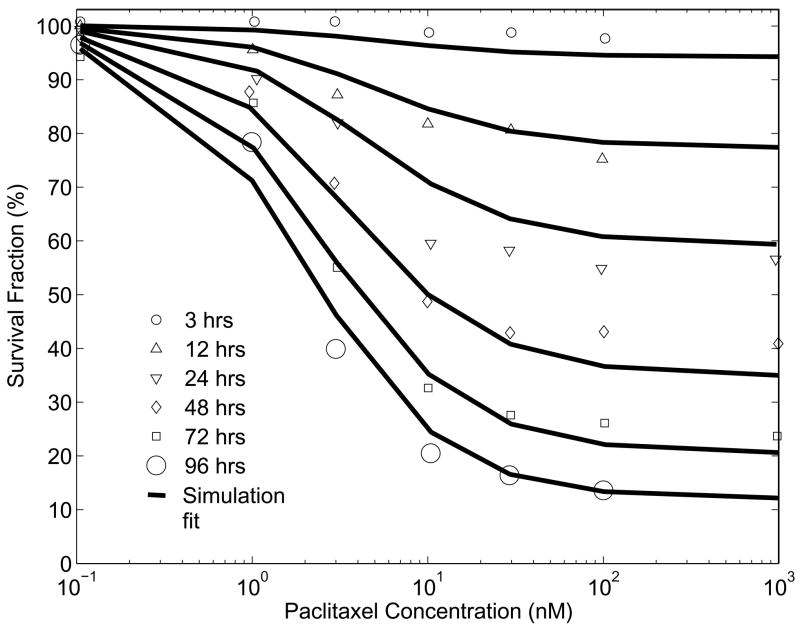
The rate parameters for drug-induced cell death ( and ) were estimated from dose-escalation experiments for paclitaxel (Zhao et al., 2005) and 5-fluorouracil (Tanaka et al., 2000) where, monolayers of cells were exposed to increasing concentrations of drug and the surviving fraction was measured as a function of time (Fig. 3). A monolayer of cells was simulated by eliminating all transport terms from the model, which included Eqs. (2, 3, 5, 6) and the local velocity term in Eq. (1). The concentrations of nutrients were assumed to be constantly high, which caused cells to pass through the cell-cycle at the maximum rates. The rates of drug-induced cell death were assumed to be dependant on the extra-cellular drug concentration according to Eq. (23). As described above, paclitaxel was assumed to be toxic only to G2 and M phase cells (Zhao et al., 2005) and 5-fluorouracil was assumed to be toxic to S phase cells at low concentrations and all cells at high concentrations (Tanaka et al., 2000). Drug induced cell death parameters were estimated using the constrained optimization function fmincon (Matlab 7.0) by minimizing the mean square error between the survival fractions in experiment and simulation.
Figure 3.
Paclitaxel monolayer dose escalation data and simulation results from death rate parameter estimation. Survival fraction is the fraction of living cells after treatment with drug (of a particular concentration for a specific exposure time), compared to the number of living cells in the absence of drug.
Survival fractions were reported for paclitaxel concentrations ranging from 0.01 nM to 10 μM and for exposure times from 3 to 96 hrs ((Au et al., 1998); reported in Fig. 3). The dose response curves obtained using the model, fit well to these reported values (Fig. 3). Consistent with experiments, a plateau was observed in the survival fraction at high drug concentrations and the survival fractions at this plateau decreased with exposure time (Au et al., 1998). The model nicely fit similar survival fraction data for 5-fluorouracil (Tanaka et al., 2000).
4.4 Numerical solution
The tumor model consisted of a coupled set of nonlinear partial differential, ordinary differential, and algebraic equations with a free outer boundary. All equations were non-dimensionalized to improve problem scaling. The following non-dimensional variables were used:
| (30) |
The original model was reduced to a set of algebraic equations and ordinary differential equations in time by spatial discretization using the method of orthogonal collocation on finite elements. At each time point, the spatial domain was mapped to a domain of unit length using a moving grid scheme. The local velocity of the tumor perimeter, v(R), was assigned to the outermost grid point to maintain a moving boundary (Crank, 1984). A unique velocity was assigned to each interior grid point to ensure that it remained stationary with respect to the outermost point.
| (31) |
Here θ̑j corresponds to the dimensionless number densities for each cell-cycle phase and to the dimensionless drug concentration in the spheroid at grid point ‘j’.
The grid point locations were generated by dividing the unit domain into equispaced finite elements and selecting a finite number of grid points within each element as roots of the appropriate Jacobi polynomial (Finlayson, 1980). First the unit domain was divided into 20 finite elements, each containing 3 internal collocation points. A finer grid was implemented at the tumor periphery to capture steep drug concentration profiles typically observed for slow diffusing drugs. In particular, the last peripheral element was further divided into 5 smaller elements, each with 3 internal collocation points.
The discretized equations were solved simultaneously using the differential-algebraic equation (DAE) solver DASPK 2.0 (Brown et al., 1994; Brown et al., 1995). DASPK options were used to exploit the considerable sparsity of the Jacobian matrix and to calculate a consistent set of initial conditions for the DAE system. A constant time step, Δt = 0.005 days, was used for all simulations.
5. Results and Discussion
5.1 Cell-cycle phases in spheroids
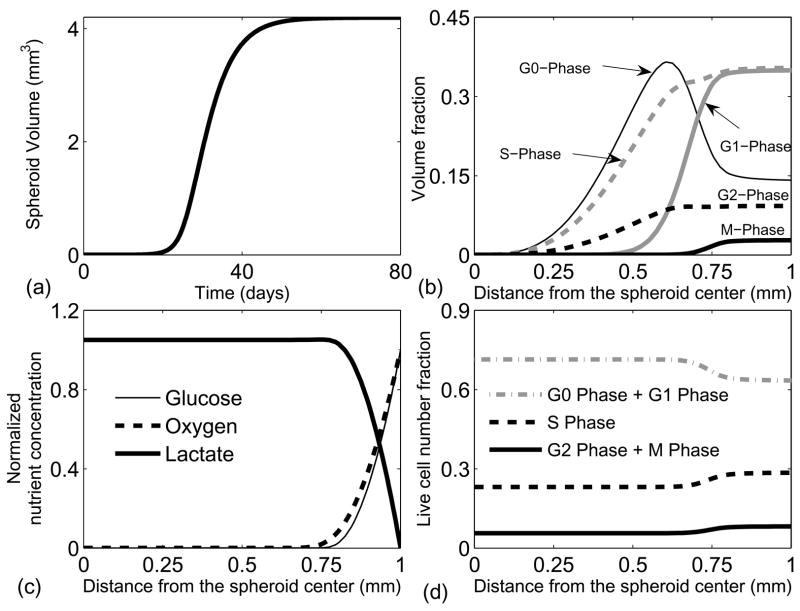
The cell-cycle phase distribution in the different regions of a spheroid was simulated to test the validity of the model. Spheroid growth was initiated with a spherical tissue mass the size of a single cell and progressed in the absence of drug. Growth was characterized by a slow exponential phase followed by a linear growth phase, and terminated with a saturated spheroid with a radius of 1 mm (Fig. 4a). These growth phases are consistent with spheroid growth experiments (Durand, 1990), and can be explained by investigating local growth rates and nutrient concentrations. When the spheroid was small, all cells were exposed to high nutrient concentrations and grew at their maximum exponential rate. As the spheroid grew larger, nutrient limitations appeared in the spheroid core causing growth cessation and death. The tradeoff between growth at the periphery and death in the center resulted in linear growth. As the spheroid grew even larger, degradation of necrotic debris in the center balanced volume generation at the periphery, and the growth of the spheroid saturated (Fig. 4a). In the small spheroid there were no spatial variations in the distribution of cells in the cell-cycle phases, and the fractions of cells in each phase were equivalent to the fractions present in monolayer cultures. As the spheroid grew, the overall cell population became more quiescent as the fraction of cells in G0 increased and the fraction of cells in the proliferating phases (G1, S, G2 and M) decreased (Table 3).
Figure 4.
Spheroid growth and saturation in the absence of a drug. (a) Growth simulation from a single cell in G1-phase to a saturated spheroid of 1mm radius. Spheroid volume initially exhibits an exponential increase, followed by a linear increase, and finally reaching a saturated steady state. (b) Cell-cycle phase volume fractions in a saturated spheroid. More cells are present in the quiescent G0 phase towards the spheroid center. (c) Nutrient profiles of key nutrients, glucose and oxygen. Glucose and oxygen are only available till 250–300 microns from the spheroid periphery, and lactate is present throughout. Lactate is not consumed in the interior because of the lack of oxygen. (d) Cell-cycle-phase fractions of live cells as a function of distance from the spheroid center. This simulation result is qualitatively similar to experimental data reported by Freyer et al. (Freyer, 1998).
Table 3.
Fraction of cells in different cell-cycle phases of monolayer cultures and spheroids at 10th day, 30th day and at saturation. As the spheroid grows, a slow and gradual increase in the fraction of cells in the quiescent G0 phase is accompanied by a corresponding decrease in G1, S, G2 and M phase cells.
| Spheroid at T = 10 days | Spheroid at T = 30 days | Saturated spheroid | |
|---|---|---|---|
| G0 phase fraction | 0.14 | 0.19 | 0.195 |
| G1 phase fraction | 0.35 | 0.27 | 0.24 |
| S Phase fraction | 0.35 | 0.325 | 0.3 |
| G2 Phase fraction | 0.09 | 0.085 | 0.08 |
| M Phase fraction | 0.025 | 0.02 | 0.015 |
In the saturated spheroid, the fraction of cells in each phase was dependent on the radius (Fig. 4b) because of nutrient gradients (Fig. 4c). Glucose and oxygen were only present in a region approximately 250 μm from the spheroid edge and the lactate concentration increased towards the interior (Fig. 4c). These nutrient gradients created three distinct regions: a peripheral region where cells traversed the cell-cycle phases at the maximum rates, an intermediate region where the rates between the phases were affected by available energy, and a central region where the cell cycle stopped and cells in all phases died (Fig. 4b–c).
In the peripheral region of the saturated spheroid, the fraction of cells in each cell-cycle phase was constant and equal to the fraction in monolayer cultures (Fig. 4b). In the transition region, cells in G1 began to enter G0 (Fig. 4b). In this region, cells stalled in G1, resulting in a slight decrease in the S phase fraction (Fig. 4b). Cells also stalled in S and G2, which completely eliminated M phase cells 350 μm from the exterior, because the transition to G1 from M is independent of nutrient availability. The transition of cells from G1 to G0 resulted in the complete absence of G1 cells beyond 600 μm from the spheroid edge. Cells in G0 increased towards a maximum in the intermediate region and decreased beyond 400 μm as the rate of death surpassed the transition rate from G1. In the central region, cells in all the remaining phases (G0, S and G2) died because of severe nutrient limitations.
These transitions match measured cell-cycle fraction in spheroids (Freyer and Sutherland, 1980) showing that the fraction of live cells in G0/G1 increased and the fraction of live cells in S and G2/M decreased towards the center. Wibe et al. identified cells that were stalled in S, G2 and G0 in the core of spheroids (Wibe et al., 1981). Our simulation results were qualitatively consistent with these observations (Fig. 4d).
5.2 Drug effects on spheroid growth
Simulations of spheroid cultures were useful because they gave the theoretical limits of drug treatment by eliminating the effects of pharmacokinetics. In addition, predicted drug effects could easily be validated in the laboratory. The effect of drug treatment on saturated spheroids was simulated to determine the critical drug concentration necessary for complete tumor clearance and to compare the relative effects of dosage and exposure time. In physical spheroid experiments, drug concentrations cannot be changed as a function of time, but only in a step-wise fashion by replacing culture medium. Spheroid cultures were simulated by eliminating all pharmacokinetic terms and holding the drug concentration at the periphery (Cj) constant for a fixed period of time (tpulse) in Eq. (19).
When spheroids were exposed to fixed concentrations of paclitaxel (1, 5, 10 and 50 nM), one of two different behaviors were observed: 1) spheroids shrank slightly and saturated at a smaller size, or 2) spheroids were completely eliminated (Fig. 5a). In these simulations, drug diffusion limitations were only present at early times and all regions were exposed to almost constant drug concentrations thereafter. At low drug concentrations (1nM), death due to drug exposure was balanced by cell growth, which resulted in stabilization at a smaller spheroid radius (Fig. 5a). At higher concentrations (5nM), the rate of death due to drug exposure was close to its maximum value ( ). At this rate, death overpowered growth and the spheroids shrank until they disappeared completely (Fig. 5a). The critical concentration of paclitaxel that enables complete elimination of the spheroid was 1.6nM. This concentration is close to the IC50 of 2 nM, which is the concentration that kills 50% of cells grown in monolayer cultures after 96 hrs (Au et al., 1998). Knowledge of this theoretical limit is useful because if an average concentration of 1.6nM is not maintained throughout a tumor, it is impossible to completely eliminate the tumor.
Figure 5.
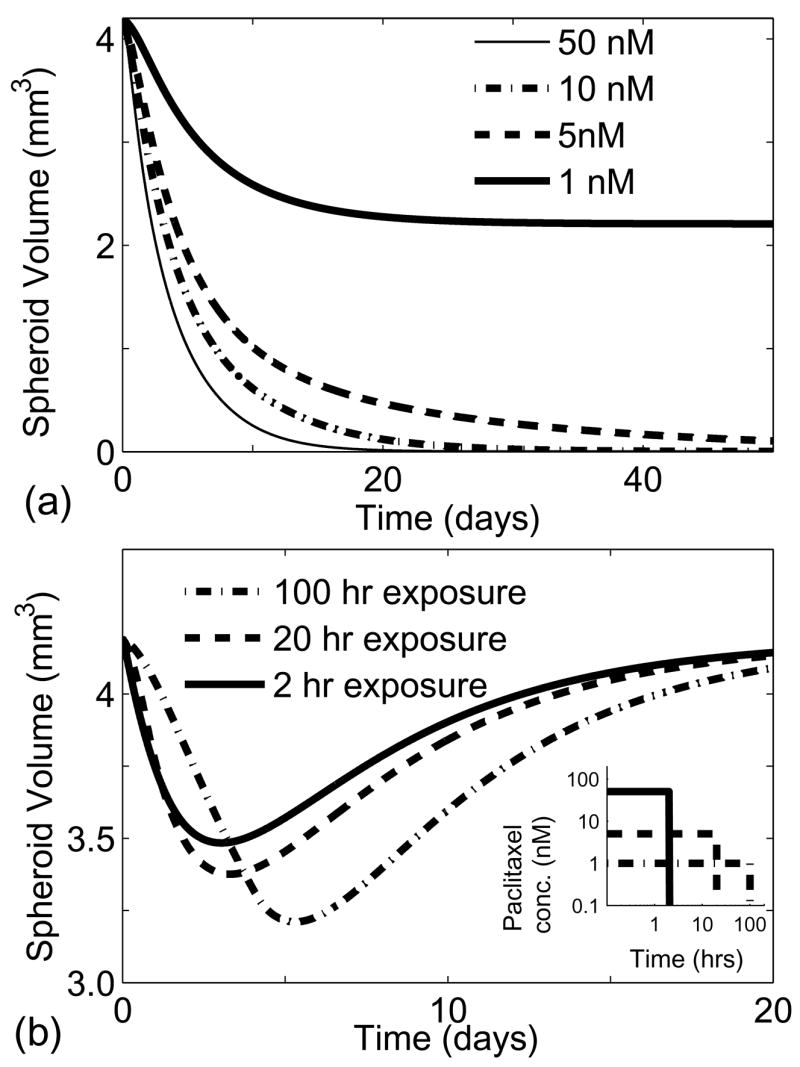
Effect of drug exposure on spheroids. (a) Drug response of spheroids exposed to a constant paclitaxel concentration. Spheroids were completely eliminated when exposed to concentrations greater that 1.6 nM. (b) Comparison of concentration and exposure times on spheroid growth for a fixed area under the curve (AUC) of 0.09 μmol·hrs. Longer exposure and lower concentrations had a greater effect on spheroid volume.
To determine the relative importance of drug concentration and exposure time, spheroids were exposed to different drug concentrations such that the product of exposure time and drug concentration, also known as the area under the curve (AUC), was held constant (Fig. 5b). The exposure times ranged from 1.8 hrs for the highest concentration (50 nM) to 90 hrs for the lowest concentration (1nM). Each of the investigated paclitaxel concentrations were within the clinically relevant range (Gianni et al., 1995). More spheroid shrinkage was seen at lower concentrations because longer exposure ensured complete drug penetration (Fig. 5b). Longer exposure also ensured that drug encountered more cells passing through the responsive cell-cycle phases. This result that longer exposure yielded greater tumor shrinkage is consistent with previously reported models with cell-cycle phase specific drugs (Panetta, 1997; Shochat et al., 1999).
5.3 Drug effects on tumor growth
The effects of paclitaxel and 5-fluorouracil on human tumors in vivo were simulated by adding pharmacokinetics to the tumor growth model. The time dependence of drug concentrations in the blood plasma and at the tumor periphery was obtained by solving the multi-compartment models (Eq. 20 and 21). In the clinic, the dosage ranges for paclitaxel and 5-fluorouracil are 135–275 mg/m2 (Perez, 1998) and 1600–2800 mg/m2 (Leichman, 1999; Thomas and Zalcberg, 1998), respectively. In the simulations, dosages of 225 and 2100 mg/m2 were used for paclitaxel and 5-fluorouracil respectively, which correspond to dosage concentrations of 69.3 μM and 2.16 mM for the average patient. Single 24 hr infusions were simulated for both drugs.
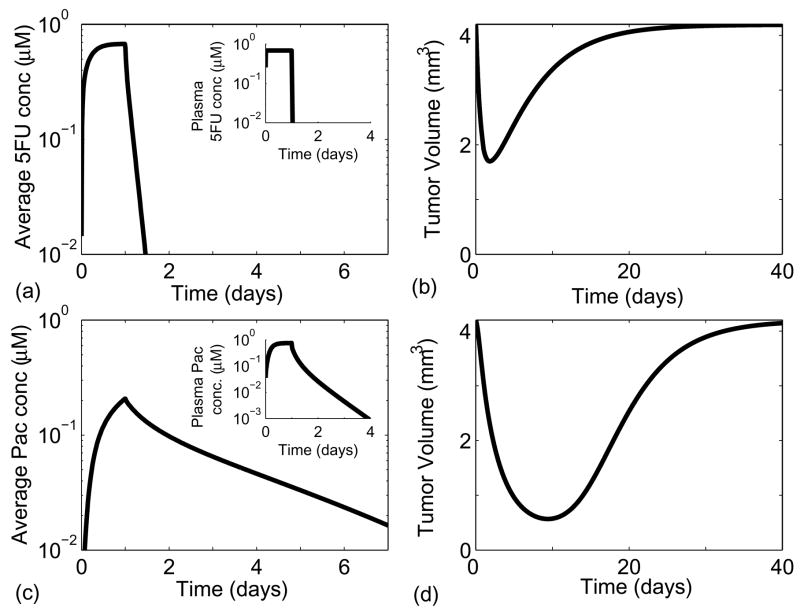
Paclitaxel was present in tumor tissue at physiologically relevant concentrations for longer than 5-fluorouracil (Fig. 6a and 6c), despite the fact that the effective diffusion of paclitaxel is an order of magnitude lower than that of 5-fluorouracil. This behavior was caused by the slow clearance of paclitaxel from the plasma; drug was present in the plasma at relevant concentrations for approximately 60 hrs after infusion (inset Fig. 6c). By contrast, 5-fluorouracil was cleared from the blood within an hour after infusion (inset Fig. 6a).
Figure 6.
Effects of 5-fluorouracil (a and b) and paclitaxel (c and d) on simulations of tumor growth. Pharmacokineticsg were incorporated by varying drug concentration at the tumor periphery according to the solution of the multi-compartmental models. Both drugs were administered intravenously for 24 hours. Figures (a) and (c) show the average tissue concentration of paclitaxel and 5-fluorouracil, respectively. The insets in figures (a) and (c) show the drug concentration in plasma as a function of time. Due to slow diffusion and clearance paclitaxel is retained in the tumor for longer than 5-fluorouracil. Figure (b) and (d) show the extent of spheroid shrinkage following the administration of 5-fluorouracil and paclitaxel, respectively.
Administration of paclitaxel caused similar reduction in the tumor volume compared to 5-fluorouracil, despite its lower toxicity and cell-cycle specificity. Both drugs initially caused tumors to decrease in volume (Fig. 6b and 6d). As the drugs washed out, cells began to proliferate and the tumors regrew to their original volumes. Tumors treated with paclitaxel and 5-fluorouracil reached their minimum volumes in ten and three days, respectively (Fig. 6b and 6d). This difference was primarily caused by the greater retention of paclitaxel, which in turn was due to its slower diffusion and clearance. In addition, the cell-cycle specific action of 5-fluorouracil required a relatively high concentration that was not maintained throughout most of the tumor. This result shows that a drug such as paclitaxel that exhibits lower cytotoxicity in monolayer cultures can be more effective in tumor tissues than a drug such as 5-fluorouracil with higher toxicity due to the effects of drug diffusion and clearance.
5.4 Effect of diffusion coefficient on tumor growth
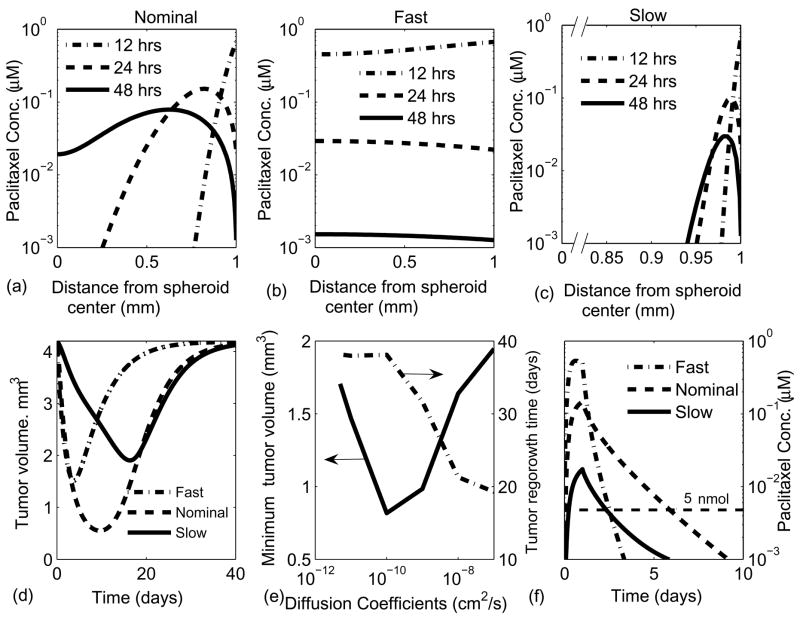
The effect of transport limitations on chemotherapeutic efficacy was determined by perturbing the paclitaxel diffusion coefficient by four orders of magnitude from the nominal measured coefficient (1.1×10−9 cm2/s). The effects of a fast (10−7 cm2/s) and a slow (10−11 cm2/s) diffusing drug were simulated for a 24 hr infusion and using the three compartment paclitaxel pharmacokinetic model.
For the nominal diffusion case, the drug concentration 12 hours after infusion was high at the periphery and low at the center (Fig. 7a). As the plasma concentration dropped with time (24 and 48 hours), a maximum formed in the concentration profile indicating that drug was simultaneously diffusing into the tumor center and being transported back into the blood. With increasing time the gradients completely reversed direction and drug slowly cleared from the entire tumor. For the fast diffusing drug, the gradients were considerably flatter and the drug concentration mirrored the plasma concentration in all regions of the tumor (Fig. 7b). For the slow diffusing drug, the gradients were much steeper and drug never reached the central region of the tumor (Fig. 7c).
Figure 7.
Effect of different effective diffusion coefficients on drug response in tumors. The results are shown for 3 different cases with effective diffusion coefficients: 10−7 cm2/s, 10−9 cm2/s and 10−11 cm2/s; that are referred to as fast diffusion, nominal diffusion and slow diffusion, respectively. (a–c) Spatial drug profile at 12, 24 and 48 hrs after a 24 hour infusion for (a) nominal diffusion coefficient, (b) fast diffusion coefficient and (c) slow diffusion. As the diffusion is decreases from fast to slow, drug concentration gradients become steeper and maximum concentration in the tumor was lower. (d) Effect of diffusion on the extent of tumor shrinkage and the time of recovery. (e) A maxima in tumor shrinkage was found for a diffusion coefficient around 10−10 cm2/s. Beneath a diffusion coefficient at 10−10 cm2/s, regrowth time reached a plateau. (f) Effect of diffusion on the average paclitaxel concentration in tumors. The nominal diffusion coefficient had the greatest retention.
By varying the drug diffusion coefficient an optimum was found that resulted in the greatest drug efficacy. For all values of the diffusion coefficient, tumor volume decreased when drug was present at the highest concentrations and the tumors regrew as the drug was washed out (Fig. 7d). The fast and slow diffusing drugs did not decrease tumor volume as much as nominal paclitaxel (Fig. 7d). Regrowth took comparable times for the slow diffusing drug and nominal paclitaxel (Fig. 7d). As the drug diffusion coefficient decreased, a maximum was reached in the extent of tumor shrinkage and the time for regrowth reached a plateau (Fig. 7e). This plateau existed because slow diffusing drugs had lower retention times. The maximum in tumor shrinkage occurred because the diffusion coefficient had competing effects on drug efficacy: as the diffusion coefficient decreased, the initial concentration decreased and the drug retention time increased (Fig. 7f). Fast diffusing drugs rapidly penetrated the tumor but were washed out quickly. Slow diffusing drugs did not penetrate efficiently but were retained in the tissue much longer. For the fast, nominal, and slow diffusion cases, drug remained at a physiologically relevant concentration (> 5nM) for 2, 5, and 2 days, respectively (Fig. 7f).
The optimum diffusion coefficient was determined to be ~1×10−10 cm2/s (Fig. 7e), which is an order of magnitude less than that of paclitaxel. The drug transport equation (4) was derived using an effective diffusion coefficient that implicitly accounts for more complex phenomena such as intracellular drug binding and degradation. Precise quantitative predictions would be affected by the incorporation of these effects. However, the qualitative behavior of the model would most likely be unaffected. This result suggests that the efficacy of paclitaxel could be improved by decreasing the diffusion coefficient by conjugation to a particle or vesicle, for example. The diffusion coefficient through tumor tissue is inversely correlated to the molecular weight (D α 1/(MW)3/4 (Swabb et al., 1974)), suggesting that increasing the molecular weight of paclitaxel to approximately 20,000 molecular weight units would increase its efficacy.
5.5 Kinetic drug resistance
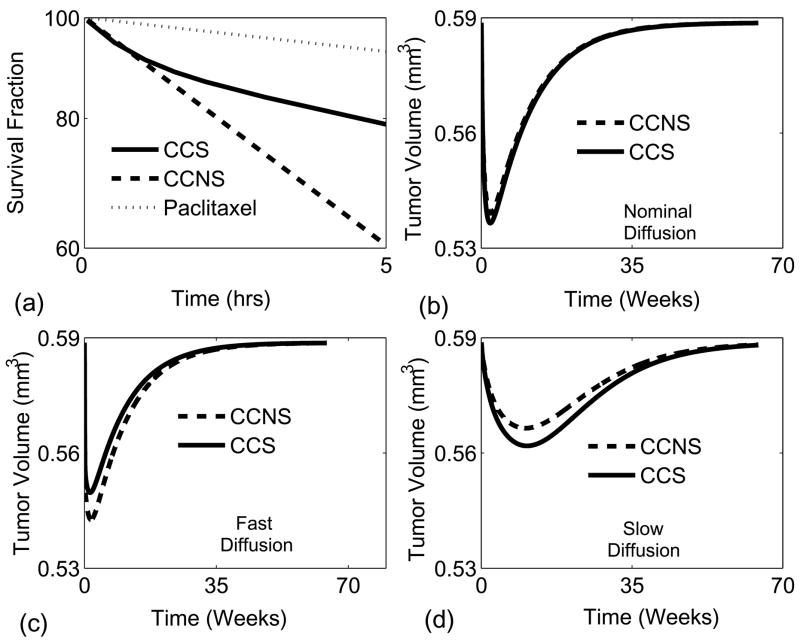
Kinetic drug resistance is the reduction in efficacy of a cell-cycle specific drug due to a limited number of cells in the susceptible cell-cycle phase. We hypothesized that tracking cell-cycle phases in three dimensional tissues would give better a prediction of drug efficacy. To investigate the possible role of kinetic resistance two artificial cases were created in which the death rate was increased five-fold and the proliferation rate was decreased three-fold. The first, cell-cycle specific (CCS) model tracked all cell-cycle phases as described earlier. The second, cell-cycle non-specific (CCNS) model contained only proliferating (G1/S/G2/M), quiescent (G0) and dead cells. In the CCS model paclitaxel killed only G2 and M cells, whereas in the CCNS model all proliferating (G1/S/G2/M) cells were killed. The linear death rate for the CCNS model was matched to the initial death rate of the CCS model.
Kinetic resistance causes a biphasic pattern of cell death in monolayer culture, in which the population initially diminishes quickly as all susceptible cells die, followed by a slower period in which cell death is limited by the rate of cell transition into the susceptible phase (Fig. 8a). However, biphasic cell death was not observed for the nominal paclitaxel, because the rate of drug-induced cell death was proportional to the rate of proliferation (Fig. 8a). The proportionality of these rates caused cells in the susceptible phases to be continuously replenished and prevented drug from significantly affecting the cell-cycle phase fractions. Because of this minimal effect in the nominal case, the death and proliferation rates were adjusted in the artificial CCS and CCNS models to accentuate the biphasic pattern and the role of kinetic resistance (Fig. 8a).
Figure 8.
Kinetic resistance had a minimal effect in three dimensional tumors. (a) Cytotoxicity of paclitaxel for cell-cycle specific and cell-cycle non-specific drugs as a function of exposure time. Death and proliferation rates were increased 5 fold and decreased 3 fold, respectively, for the CCS and CCNS drugs. The response is linear for the CCNS drug and biphasic for the CCS drug. (b–d) Comparison between the administration of the CCS and CCNS drugs on tumors with (b) nominal diffusion, (c) fast diffusion and (d) slow diffusion.
At nominal drug diffusion coefficients the difference between the CCNS and CCS cases was small (Fig. 8b). When the diffusion coefficient was increased the CCNS model over-predicted the rate of tumor reduction (Fig. 8c), which parallels the effects observed in monolayer culture (Fig. 8a). However, when the diffusion coefficient was decreased, the CCNS model under-predicted the rate of tumor reduction (Fig. 8d).
The simulation identified slight differences in the cell-cycle phase profiles of the CCS and CCNS models, and showed that a cell-cycle non-specific model could reasonably predict tumor reduction for cases of altered growth and diffusion. Kinetic resistance did not appreciably affect drug efficacy for two reasons: 1) kinetic resistance is intrinsically a minor effect that does not alter the initial rate of cell death, which is the major cause of drug-induced death in tumors; and 2) cell-cycle transition times were considerable faster than the nominal rates of growth, death, and diffusion, which prevented drugs from having long-term effects on cell-cycle phase populations. These results suggest that explicitly tracking different cell-cycle phases is not essential for predicting drug effects in solid tumors, and also suggest that designing cell-cycle targeting drugs may not offer unique advantages to cell-cycle non-specific drugs.
5.6 Effect of proliferation fraction on tumor growth
The effect of the tumor proliferation fraction on the efficacy of chemotherapy was simulated to determine the response of tumors with less proliferating cells respond. The proliferation fraction of a tumor is defined as the ratio of cells in the cycling phases (G1, S, G2 and M) to the total number of living cells. Tumors have been identified with a wide range of proliferation fractions from 1 to 70% (Gardner, 2002a). This large distribution is associated with considerable difference in cell-cycle times (30 to 60 hours), apoptotic cell fractions (0.1% to 4%); and S-phase fractions (1 to 40%) (Gardner, 2002a). The proliferation fraction has important implications on therapy because most chemotherapeutic agents are only effective on the proliferation cells.
The effect of a series of 24 hr paclitaxel infusions was simulated for two tumors with different proliferation fractions. The nominal tumor simulated above represents a fast growing tumor with a high proliferation fraction (63%; Table 4). A slow growing tumor was created by increasing the maximum transition rate from G1 to G0 ( ) by a factor of 10. Since was found to have the greatest effect on the proliferation fraction, only this one parameter was perturbed to minimize cross parameter effects. The resultant slow-growing tumor had a proliferation fraction of 17% and saturated radius of 0.54mm (Table 4). The S-phase fraction, another indicator of tumor growth, was considerably different between the two tumors (26 compared to 7%; Table 4)
Table 4.
Proliferation metrics of nominal tumor and slow growing tumors
| Nominal tumor | Slow growing tumor | |
|---|---|---|
| Proliferation fraction | 63 % | 17 % |
| G0 phase fraction | 37 % | 83 % |
| S phase fraction | 26 % | 7 % |
| Saturated size (radius) | 1mm | 0.54mm |
Overall volume reduction was greater for the slower growing tumor after several rounds of paclitaxel administration, even though the fast growing tumor had a greater volume reduction immediately following the first infusion (Fig. 9). Administration of paclitaxel in a three week cycle was sufficient to completely eliminate the slow growing tumor (Fig. 9b) but was not able to clear the fast growing tumor (Fig. 9a). This unanticipated result that successive paclitaxel administration was more effective on slow growing tumors was primarily attributed to tumor regrowth. After the first infusion, regrowth began after twelve days for the slow growing tumor, compared to nine days for the fast growing tumor (Fig. 9). For the slow growing tumor, the rate of drug-induced death was greater than the rate of regrowth, even though the death rate was considerably less than that of the fast growing tumor. In the fast growing tumor, the rate of regrowth was able to overcome the death induced by paclitaxel. This observation that regrowth is a major hindrance to chemotherapy is supported by clinical trials showing that slow growing tumors are more responsive to chemotherapy (Choyke et al., 1987; Kim and Tannock, 2005).
Figure 9.
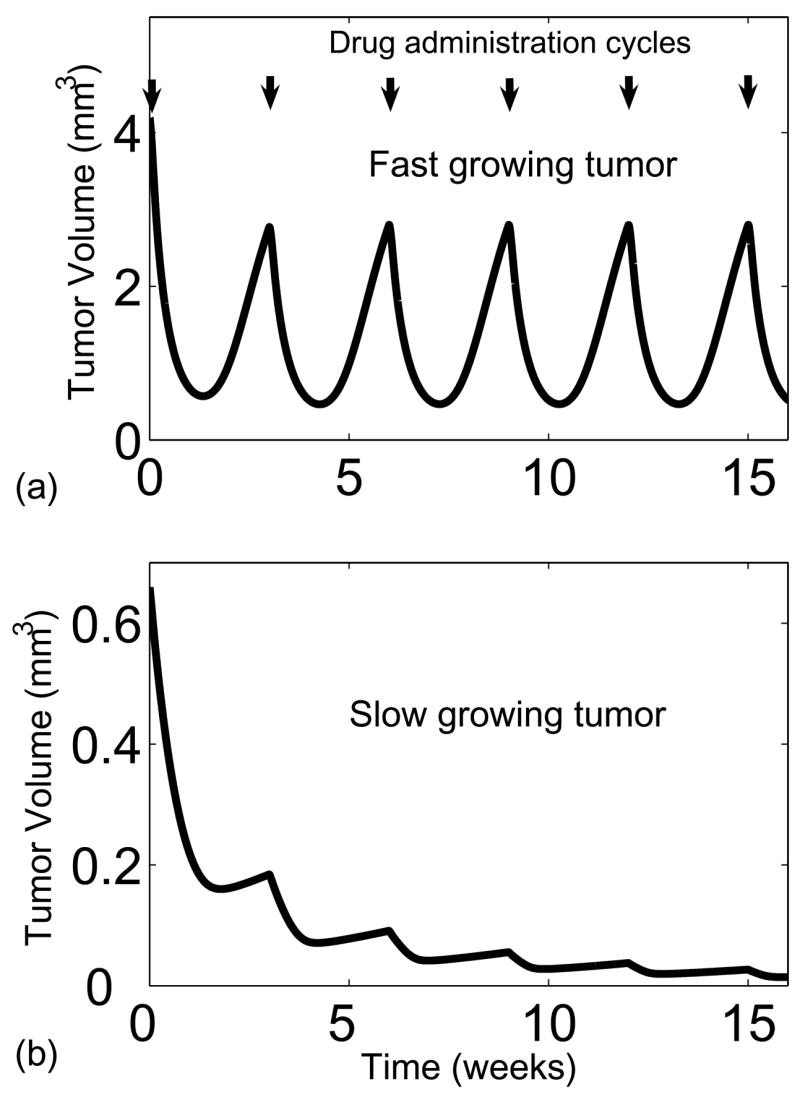
Effect of multiple paclitaxel infusions spaced every 3 weeks on (a) a fast growing and (b) a slow growing tumor. Paclitaxel was more effective against the slow growing tumor even though drug had a greater initial effect on the fast growing tumor. The greater proliferative fraction caused the tumor to regrow faster in the time between two successive drug administrations.
6. Conclusions
A tumor growth model has been developed that incorporates cell metabolism, molecular diffusion, cell-cycle specific drug cytotoxicity, and multi-compartment pharmacokinetics. The model was able to predict the distribution of cell-cycle phases that have been previously experimentally observed in tumors. The simulated effects of two drugs with different transport characteristics, paclitaxel and 5-fluorouracil, demonstrated the balance between drug diffusion, clearance, and cytotoxicity. Hypothetical drugs with intermediate diffusion coefficients had greater efficacy than fast or slow diffusing drugs demonstrating that the transport through tissue is a trade off between penetration and retention. The simulations showed that cell-cycle heterogeneity had a small but identifiable effect, suggesting that cell-cycle targeting drugs may not offer unique advantages to all cell-cycle nonspecific drugs. The model simulations also showed that slow growing tumors are more responsive to chemotherapy because regrowth between drug administrations cannot compete with drug toxicity even though cells are less responsive to drugs due to a lower proliferation fraction.
These simulation results have important therapeutic implications. The results demonstrate the importance of diffusion, and suggest that three-dimensional cultures are useful for determining therapeutic effects in vitro (Kasinskas and Forbes, 2006; Kasinskas and Forbes, 2007; Kim and Forbes, 2007) that cannot be determined in monolayer cultures. The prediction that reducing diffusivity of paclitaxel increases its efficacy should be investigated by measuring the effects of drugs conjugated to nano-particles (Han et al., 2006; Hong et al., 2006). The results also imply that quantifying the proliferation fraction in the tumors of cancer patients would enhance prediction of therapeutic efficacy. This prediction could be investigated in a clinical setting by measuring proliferation and quiescence in tumor biopsies.
Acknowledgments
This work was supported by the National Institute of Health (Grant No. 1 R21 CA112335-01A1), the National Science Foundation (Grant No. DMI-0531171), and the Rays of Hope (Springfield, MA)
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Au JL, Jang SH, Wientjes MG. Clinical aspects of drug delivery to tumors. J Control Release. 2002;78:81–95. doi: 10.1016/s0168-3659(01)00488-6. [DOI] [PubMed] [Google Scholar]
- Au JL, Jang SH, Zheng J, Chen CT, Song S, Hu L, Wientjes MG, Kuh HJ. Determinants of drug delivery and transport to solid tumors: Computational model of intracellular pharmacokinetics of paclitaxel. J Control Release. 2001;74:31–46. doi: 10.1016/s0168-3659(01)00308-x. [DOI] [PubMed] [Google Scholar]
- Au JL, Li D, Gan Y, Gao X, Johnson AL, Johnston J, Millenbaugh NJ, Jang SH, Kuh HJ, Chen CT, Wientjes MG. Pharmacodynamics of immediate and delayed effects of paclitaxel: role of slow apoptosis and intracellular drug retention. Cancer Res. 1998;58:2141–8. [PubMed] [Google Scholar]
- Basse B, Baguley BC, Marshall ES, Joseph WR, van Brunt B, Wake G, Wall DJ. A mathematical model for analysis of the cell cycle in cell lines derived from human tumors. J Math Biol. 2003;47:295–312. doi: 10.1007/s00285-003-0203-0. [DOI] [PubMed] [Google Scholar]
- Basse B, Baguley BC, Marshall ES, Joseph WR, van Brunt B, Wake G, Wall DJ. Modelling cell death in human tumour cell lines exposed to the anticancer drug paclitaxel. J Math Biol. 2004;49:329–57. doi: 10.1007/s00285-003-0254-2. [DOI] [PubMed] [Google Scholar]
- Bauer KD, Keng PC, Sutherland RM. Isolation of quiescent cells from multicellular tumor spheroids using centrifugal elutriation. Cancer Res. 1982;42:72–8. [PubMed] [Google Scholar]
- Bertuzzi A, D’Onofrio A, Fasano A, Gandolfi A. Regression and regrowth of tumour cords following single-dose anticancer treatment. Bull Math Biol. 2003;65:903–31. doi: 10.1016/S0092-8240(03)00054-5. [DOI] [PubMed] [Google Scholar]
- Brown J. Tumor microenvironment and the response to anticancer therapy. Cancer Biol Ther. 2002;1:453–8. doi: 10.4161/cbt.1.5.157. [DOI] [PubMed] [Google Scholar]
- Brown PN, Hindmarsh AC, Petzold LR. Using Krylov methods in the solution of large-scale differential-algebraic systems. SIAM Journal on Scientific Computing. 1994;15:1467–1488. [Google Scholar]
- Brown PN, Hindmarsh AC, Petzold LR. DASPK; Santa Barbara, Ca: 1995. [Google Scholar]
- Carlsson J. A proliferation gradient in three-dimensional colonies of cultured human glioma cells. Int J Cancer. 1977;20:129–36. doi: 10.1002/ijc.2910200120. [DOI] [PubMed] [Google Scholar]
- Casciari JJ, Sotirchos SV, Sutherland RM. Mathematical modelling of microenvironment and growth in EMT6/Ro multicellular tumour spheroids. Cell Prolif. 1992;25:1–22. doi: 10.1111/j.1365-2184.1992.tb01433.x. [DOI] [PubMed] [Google Scholar]
- Choyke P, Zeman R, Gootenberg J, Greenberg J, Hoffer F, Frank J. Thymic atrophy and regrowth in response to chemotherapy: CT evaluation. American Journal of Roentgenology. 1987;149:269–272. doi: 10.2214/ajr.149.2.269. [DOI] [PubMed] [Google Scholar]
- Costello LC, Franklin RB. Bioenergetic theory of prostate malignancy. Prostate. 1994;25:162–6. doi: 10.1002/pros.2990250308. [DOI] [PubMed] [Google Scholar]
- Crank J. Free and moving boundary problems. Clarendon Press; New York: 1984. [Google Scholar]
- Daniel B, Harkin D, Johnston P. 5-Fluorouracil: mechanisms of action and clinical strategies. Nature Review Cancer. 2003;5:330–338. doi: 10.1038/nrc1074. [DOI] [PubMed] [Google Scholar]
- Darzynkiewicz Z, Traganos F, Melamed MR. New cell cycle compartments identified by multiparameter flow cytometry. Cytometry. 1980;1:98–108. doi: 10.1002/cyto.990010203. [DOI] [PubMed] [Google Scholar]
- Dethlefsen LA, Bauer KD, Riley RM. Analytical cytometric approaches to heterogeneous cell populations in solid tumors: a review. Cytometry. 1980;1:89–108. doi: 10.1002/cyto.990010202. [DOI] [PubMed] [Google Scholar]
- Durand RE. Multicell spheroids as a model for cell kinetic studies. Cell Tissue Kinet. 1990;23:141–59. doi: 10.1111/j.1365-2184.1990.tb01111.x. [DOI] [PubMed] [Google Scholar]
- El-Khoueiry AB, Lenz HJ. Should continuous infusion 5-fluorouracil become the standard of care in the USA as it is in Europe? Cancer Invest. 2006;24:50–5. doi: 10.1080/07357900500449694. [DOI] [PubMed] [Google Scholar]
- Finlayson BA. Nonlinear analysis in chemical engineering. McGraw-Hill International Book Co; New York: 1980. [Google Scholar]
- Folkman J. Tumor angiogenesis: therapeutic implications. N Engl J Med. 1971;285:1182–6. doi: 10.1056/NEJM197111182852108. [DOI] [PubMed] [Google Scholar]
- Freyer JP. Decreased mitochondrial function in quiescent cells isolated from multicellular tumor spheroids. J Cell Physiol. 1998;176:138–49. doi: 10.1002/(SICI)1097-4652(199807)176:1<138::AID-JCP16>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]
- Freyer JP, Sutherland RM. Selective dissociation and characterization of cells from different regions of multicell tumor spheroids. Cancer Res. 1980;40:3956–65. [PubMed] [Google Scholar]
- Freyer JP, Schor PL. Regrowth kinetics of cells from different regions of multicellular spheroids of four cell lines. J Cell Physiol. 1989;138:384–92. doi: 10.1002/jcp.1041380222. [DOI] [PubMed] [Google Scholar]
- Gardner SN. A mechanistic, predictive model of dose-response curves for cell cycle phase-specific and -nonspecific drugs. Cancer Res. 2000;60:1417–25. [PubMed] [Google Scholar]
- Gardner SN. Cell cycle phase-specific chemotherapy: computational methods for guiding treatment. Cell Cycle. 2002a;1:369–74. doi: 10.4161/cc.1.6.258. [DOI] [PubMed] [Google Scholar]
- Gardner SN. Modeling multi-drug chemotherapy: tailoring treatment to individuals. J Theor Biol. 2002b;214:181–207. doi: 10.1006/jtbi.2001.2459. [DOI] [PubMed] [Google Scholar]
- Gianni L, Kearns CM, Giani A, Capri G, Vigano L, Lacatelli A, Bonadonna G, Egorin MJ. Nonlinear pharmacokinetics and metabolism of paclitaxel and its pharmacokinetic/pharmacodynamic relationships in humans. J Clin Oncol. 1995;13:180–90. doi: 10.1200/JCO.1995.13.1.180. [DOI] [PubMed] [Google Scholar]
- Grantab R, Sivananthan S, Tannock IF. The penetration of anticancer drugs through tumor tissue as a function of cellular adhesion and packing density of tumor cells. Cancer Res. 2006;66:1033–9. doi: 10.1158/0008-5472.CAN-05-3077. [DOI] [PubMed] [Google Scholar]
- Han G, You CC, Kim BJ, Turingan RS, Forbes NS, Martin CT, Rotello VM. Light-regulated release of DNA and its delivery to nuclei by means of photolabile gold nanoparticles. Angew Chem Int Ed Engl. 2006;45:3165–9. doi: 10.1002/anie.200600214. [DOI] [PubMed] [Google Scholar]
- Helmlinger G, Sckell A, Dellian M, Forbes NS, Jain RK. Acid production in glycolysis-impaired tumors provides new insights into tumor metabolism. Clin Cancer Res. 2002;8:1284–91. [PubMed] [Google Scholar]
- Hong R, Han G, Fernandez JM, Kim BJ, Forbes NS, Rotello VM. Glutathione-mediated delivery and release using monolayer protected nanoparticle carriers. J Am Chem Soc. 2006;128:1078–9. doi: 10.1021/ja056726i. [DOI] [PubMed] [Google Scholar]
- Jackson RC. The problem of the quiescent cancer cell. Adv Enzyme Regul. 1989;29:27–46. doi: 10.1016/0065-2571(89)90092-7. [DOI] [PubMed] [Google Scholar]
- Jackson TL. Intracellular accumulation and mechanism of action of doxorubicin in a spatio-temporal tumor model. J Theor Biol. 2003;220:201–13. doi: 10.1006/jtbi.2003.3156. [DOI] [PubMed] [Google Scholar]
- Jackson TL, Byrne HM. A mathematical model to study the effects of drug resistance and vasculature on the response of solid tumors to chemotherapy. Math Biosci. 2000;164:17–38. doi: 10.1016/s0025-5564(99)00062-0. [DOI] [PubMed] [Google Scholar]
- Jain R. Delivery of molecular medicine to solid tumors. Science. 1996;271:1079–80. doi: 10.1126/science.271.5252.1079. [DOI] [PubMed] [Google Scholar]
- Jain R. Transport of molecules, particles, and cells in solid tumors. Annual Review of Biomedical Engineering. 1999;1:241–263. doi: 10.1146/annurev.bioeng.1.1.241. [DOI] [PubMed] [Google Scholar]
- Kasinskas RW, Forbes NS. Salmonella typhimurium specifically chemotax and proliferate in heterogeneous tumor tissue in vitro. Biotechnol Bioeng. 2006;94:710–21. doi: 10.1002/bit.20883. [DOI] [PubMed] [Google Scholar]
- Kasinskas RW, Forbes NS. Salmonella typhimurium lacking ribose chemoreceptors localize in tumor quiescence and induce apoptosis. Cancer Res. 2007;67:3201–9. doi: 10.1158/0008-5472.CAN-06-2618. [DOI] [PubMed] [Google Scholar]
- Kearns CM, Gianni L, Egorin MJ. Paclitaxel pharmacokinetics and pharmacodynamics. Semin Oncol. 1995;22:16–23. [PubMed] [Google Scholar]
- Kim BJ, Forbes NS. Flux analysis shows that hypoxia-inducible-factor-1-alpha minimally affects intracellular metabolism in tumor spheroids. Biotechnol Bioeng. 2007;96:1167–82. doi: 10.1002/bit.21205. [DOI] [PubMed] [Google Scholar]
- Kim JJ, Tannock IF. Repopulation of cancer cells during therapy: an important cause of treatment failure. Nat Rev Cancer. 2005;5:516–25. doi: 10.1038/nrc1650. [DOI] [PubMed] [Google Scholar]
- Konerding MA, Malkusch W, Klapthor B, van Ackern C, Fait E, Hill SA, Parkins C, Chaplin DJ, Presta M, Denekamp J. Evidence for characteristic vascular patterns in solid tumours: quantitative studies using corrosion casts. Br J Cancer. 1999;80:724–32. doi: 10.1038/sj.bjc.6690416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kufe DW, Major PP. 5-Fluorouracil incorporation into human breast carcinoma RNA correlates with cytotoxicity. J Biol Chem. 1981;256:9802–5. [PubMed] [Google Scholar]
- Kuh HJ, Jang SH, Wientjes MG, Au JL. Computational model of intracellular pharmacokinetics of paclitaxel. J Pharmacol Exp Ther. 2000;293:761–70. [PubMed] [Google Scholar]
- Kuh HJ, Jang SH, Wientjes MG, Weaver JR, Au JL. Determinants of paclitaxel penetration and accumulation in human solid tumor. J Pharmacol Exp Ther. 1999;290:871–80. [PubMed] [Google Scholar]
- Lankelma J. Tissue transport of anti-cancer drugs. Curr Pharm Des. 2002;8:1987–93. doi: 10.2174/1381612023393512. [DOI] [PubMed] [Google Scholar]
- Lankelma J, Fernandez Luque R, Dekker H, Schinkel W, Pinedo HM. A mathematical model of drug transport in human breast cancer. Microvasc Res. 2000;59:149–61. doi: 10.1006/mvre.1999.2218. [DOI] [PubMed] [Google Scholar]
- LaRue KE, Khalil M, Freyer JP. Microenvironmental regulation of proliferation in multicellular spheroids is mediated through differential expression of cyclin-dependent kinase inhibitors. Cancer Res. 2004;64:1621–31. doi: 10.1158/0008-5472.can-2902-2. [DOI] [PubMed] [Google Scholar]
- Lau C, Mole ML, Copeland MF, Rogers JM, Kavlock RJ, Shuey DL, Cameron AM, Ellis DH, Logsdon TR, Merriman J, Setzer RW. Toward a biologically based dose-response model for developmental toxicity of 5-fluorouracil in the rat: acquisition of experimental data. Toxicol Sci. 2001;59:37–48. doi: 10.1093/toxsci/59.1.37. [DOI] [PubMed] [Google Scholar]
- Leichman CG. Schedule dependency of 5-fluorouracil. Oncology (Williston Park) 1999;13:26–32. [PubMed] [Google Scholar]
- Levasseur LM, Slocum HK, Rustum YM, Greco WR. Modeling of the time-dependency of in vitro drug cytotoxicity and resistance. Cancer Res. 1998;58:5749–61. [PubMed] [Google Scholar]
- Minchinton AI, Tannock IF. Drug penetration in solid tumours. Nat Rev Cancer. 2006;6:583–92. doi: 10.1038/nrc1893. [DOI] [PubMed] [Google Scholar]
- Montalenti F, Sena G, Cappella P, Ubezio P. Simulating cancer-cell kinetics after drug treatment: Application to cisplatin on ovarian carcinoma. Physical Review E. 1998;57:5877–5887. [Google Scholar]
- Mueller-Klieser WF, Sutherland RM. Oxygen consumption and oxygen diffusion properties of multicellular spheroids from two different cell lines. Adv Exp Med Biol. 1984;180:311–21. doi: 10.1007/978-1-4684-4895-5_30. [DOI] [PubMed] [Google Scholar]
- Nederman T, Carlsson J. Penetration and binding of vinblastine and 5-fluorouracil in cellular spheroids. Cancer Chemother Pharmacol. 1984;13:131–5. doi: 10.1007/BF00257130. [DOI] [PubMed] [Google Scholar]
- Nicholson KM, Bibby MC, Phillips RM. Influence of drug exposure parameters on the activity of paclitaxel in multicellular spheroids. Eur J Cancer. 1997;33:1291–8. doi: 10.1016/s0959-8049(97)00114-7. [DOI] [PubMed] [Google Scholar]
- Nogales E. Structural insights into microtubule function. Annu Rev Biochem. 2000;69:277–302. doi: 10.1146/annurev.biochem.69.1.277. [DOI] [PubMed] [Google Scholar]
- Olive KP, Tuveson DA. The use of targeted mouse models for preclinical testing of novel cancer therapeutics. Clin Cancer Res. 2006;12:5277–87. doi: 10.1158/1078-0432.CCR-06-0436. [DOI] [PubMed] [Google Scholar]
- Panetta JC. A mathematical model of breast and ovarian cancer treated with paclitaxel. Math Biosci. 1997;146:89–113. doi: 10.1016/s0025-5564(97)00077-1. [DOI] [PubMed] [Google Scholar]
- Perez EA. Paclitaxel in Breast Cancer. Oncologist. 1998;3:373–389. [PubMed] [Google Scholar]
- Rossow PW, Riddle VG, Pardee AB. Synthesis of labile, serum-dependent protein in early G1 controls animal cell growth. Proc Natl Acad Sci U S A. 1979;76:4446–50. doi: 10.1073/pnas.76.9.4446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah MA, Schwartz GK. Cell cycle-mediated drug resistance: an emerging concept in cancer therapy. Clin Cancer Res. 2001;7:2168–81. [PubMed] [Google Scholar]
- Shochat E, Hart D, Agur Z. Using computer simulations for evaluating the efficacy of breast cancer chemotherapy protocols. Mathematical Models & Methods in Applied Sciences. 1999;9:599–615. [Google Scholar]
- Suggitt M, Bibby MC. 50 years of preclinical anticancer drug screening: empirical to target-driven approaches. Clin Cancer Res. 2005;11:971–81. [PubMed] [Google Scholar]
- Sutherland R. Cell and environment interactions in tumor microregions: the multicell spheroid model. Science. 1988;240:177. doi: 10.1126/science.2451290. [DOI] [PubMed] [Google Scholar]
- Swabb EA, Wei J, Gullino PM. Diffusion and convection in normal and neoplastic tissues. Cancer Res. 1974;34:2814–22. [PubMed] [Google Scholar]
- Tanaka F, Fukuse T, Wada H, Fukushima M. The history, mechanism and clinical use of oral 5-fluorouracil derivative chemotherapeutic agents. Curr Pharm Biotechnol. 2000;1:137–64. doi: 10.2174/1389201003378979. [DOI] [PubMed] [Google Scholar]
- Tannock I. Experimental Chemotherapy and Concepts Related to the Cell Cycle. International Journal of Radiation Biology. 1986;49:335–355. doi: 10.1080/09553008514552581. [DOI] [PubMed] [Google Scholar]
- Tannock I. Tumor physiology and drug resistance. Cancer and Metastasis Reviews. 2001;20:123–132. doi: 10.1023/a:1013125027697. [DOI] [PubMed] [Google Scholar]
- Tannock IF, Lee CM, Tunggal JK, Cowan DS, Egorin MJ. Limited penetration of anticancer drugs through tumor tissue: a potential cause of resistance of solid tumors to chemotherapy. Clin Cancer Res. 2002;8:878–84. [PubMed] [Google Scholar]
- Terret C, Erdociain E, Guimbaud R, Boisdron-Celle M, McLeod HL, Fety-Deporte R, Lafont T, Gamelin E, Bugat R, Canal P, Chatelut E. Dose and time dependencies of 5-fluorouracil pharmacokinetics. Clin Pharmacol Ther. 2000;68:270–9. doi: 10.1067/mcp.2000.109352. [DOI] [PubMed] [Google Scholar]
- Thomas DM, Zalcberg JR. 5-fluorouracil: a pharmacological paradigm in the use of cytotoxics. Clin Exp Pharmacol Physiol. 1998;25:887–95. doi: 10.1111/j.1440-1681.1998.tb02339.x. [DOI] [PubMed] [Google Scholar]
- Tunggal JK, Cowan DS, Shaikh H, Tannock IF. Penetration of anticancer drugs through solid tissue: a factor that limits the effectiveness of chemotherapy for solid tumors. Clin Cancer Res. 1999;5:1583–6. [PubMed] [Google Scholar]
- Tyson JJ, Novak B. Regulation of the eukaryotic cell cycle: molecular antagonism, hysteresis, and irreversible transitions. J Theor Biol. 2001;210:249–63. doi: 10.1006/jtbi.2001.2293. [DOI] [PubMed] [Google Scholar]
- Tzafriri AR, Lerner EI, Flashner-Barak M, Hinchcliffe M, Ratner E, Parnas H. Mathematical modeling and optimization of drug delivery from intratumorally injected microspheres. Clin Cancer Res. 2005;11:826–34. [PubMed] [Google Scholar]
- Ueda M, Kumagai K, Ueki K, Inoki C, Orino I, Ueki M. Growth inhibition and apoptotic cell death in uterine cervical carcinoma cells induced by 5-fluorouracil. Int J Cancer. 1997;71:668–74. doi: 10.1002/(sici)1097-0215(19970516)71:4<668::aid-ijc25>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- Venkatasubramanian R, Henson MA, Forbes NS. Incorporating energy metabolism into a growth model of multicellular tumor spheroids. J Theor Biol. 2006 doi: 10.1016/j.jtbi.2006.03.011. [DOI] [PubMed] [Google Scholar]
- Ward JP, King JR. Mathematical modelling of avascular-tumour growth. IMA J Math Appl Med Biol. 1997;14:39–69. [PubMed] [Google Scholar]
- Ward JP, King JR. Mathematical modelling of drug transport in tumour multicell spheroids and monolayer cultures. Math Biosci. 2003;181:177–207. doi: 10.1016/s0025-5564(02)00148-7. [DOI] [PubMed] [Google Scholar]
- Wibe E, Lindmo T, Kaalhus O. Cell kinetic characteristics in different parts of multicellular spheroids of human origin. Cell Tissue Kinet. 1981;14:639–51. doi: 10.1111/j.1365-2184.1981.tb00849.x. [DOI] [PubMed] [Google Scholar]
- Zhao J, Kim JE, Reed E, Li QQ. Molecular mechanism of antitumor activity of taxanes in lung cancer (Review) Int J Oncol. 2005;27:247–56. [PubMed] [Google Scholar]