The Paradoxical Thermodynamic Basis for the Interaction of Ethylene Glycol, Glycine, and Sarcosine Chains with Bovine Carbonic Anhydrase II

Abstract

This paper describes a systematic study of the thermodynamics of association of bovine carbonic anhydrase II (BCA) and para-substituted benzenesulfonamides with chains of oligoglycine, oligosarcosine, and oligoethylene glycol of lengths of 1-5 residues. For all three of these series of ligands, the enthalpy of binding became less favorable, and the entropy less unfavorable, as the chain length of the ligands increased. The dependence on chain length of the enthalpy was almost perfectly compensated by that of the entropy; this compensation resulted in dissociation constants that were independent of chain length for the three series of ligands. Changes in heat capacity were independent of chain length for the three series, and revealed that the amount of molecular surface area buried upon protein-ligand complexation did not increase with increasing chain length. Taken together, these data refute a model in which the chains of the ligands interact hydrophobically with the surface of BCA. To explain the data, a model is proposed based on decreasing “tightness” of the protein-ligand interface as the chain length of the ligand increases. This decreasing tightness, as chain length increases, is reflected in a less favorable enthalpy (due to fewer van der Waals contacts) and a less unfavorable entropy (due to greater mobility of the chain) of binding for ligands with long chains than for those with short chains. Thus, this study demonstrates a surprising example of enthalpy/entropy compensation in a well-defined system. Understanding this compensation is integral to the rational design of high-affinity ligands for proteins.

Introduction

This paper characterizes the thermodynamics of association of bovine carbonic anhydrase II (BCA, EC 4.2.1.1) with ligands designed to test the interplay between enthalpy and entropy of binding. The ligands used were para-substituted benzenesulfonamides (p-H₂NSO₂C₆H₄CONRR’) of structure 1,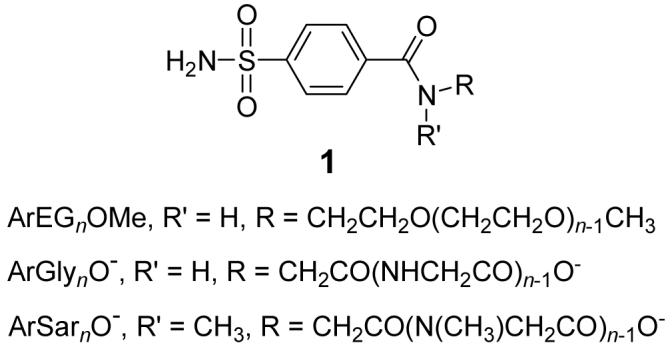where R’ = H or CH₃; the variable part of these ligands were the R groups—oligoethylene glycol (ArEG_nOMe), oligoglycine (ArGly_nO^-), or oligosarcosine (ArSar_nO^-) chains, where n = 1-5. We were interested in these families of ligands for three reasons:

1. Oligoethylene glycol (EG_n), oligoglycine (Gly_n), and oligosarcosine (Sar_n) chains are commonly used as linkers in the design and synthesis of multivalent ligands.^1-6 Understanding why these flexible linkers can be effective as components in high-avidity ligands (when simple considerations of entropy predict that they would not be^{2, 7}) will aid in the design of multivalent ligands (Figure 1).

2. The system of BCA and p-H₂NSO₂C₆H₄CONHR is the simplest one that we know for studying protein-ligand interactions.^8-10 BCA has been well-defined structurally using biophysical tools (particularly X-ray crystallography).^{9, 10} It binds most para-substituted benzenesulfonamides with the same geometry (the ionized sulfonamide nitrogen, ArSO₂NH^-, binds to the Zn^II co-factor, and the phenyl ring interacts directly with a hydrophobic pocket of the enzyme) (Figure 2); this geometry is independent of the nature of R. This consistent mode of binding allows us to consider the interaction of R (here, the oligomeric chain) with the surface of BCA with high confidence that we know how the phenyl ring (and thus, R) is positioned in the active site. Thus, this system perturbs a known interaction, rather than probing an undefined and/or variable one. Perturbation approaches are often the simplest ones to use in working on complicated problems.

3. We previously measured the dissociation constants (K_d) for two of the series of ligands (ArEG_nOMe and ArGly_mO^-, n = 1-5 and m = 1-6), and found an entirely unexpected result: these values of K_d were approximately independent of chain length for both series (ArEG_nOMe, K_d ∼ 0.16 μM and ArGly_mO^- , K_d ∼ 0.33 μM) and similar to that for unsubstituted benzenesulfonamide (K_d ∼ 0.20 μM).¹¹ We had anticipated that values of K_d for sulfonamides with EG_n and Gly_n chains would decrease monotonically with increasing chain length (reflecting an increase in the hydrophobic surface area buried upon protein-ligand complexation) and level off when the number of residues in the chain exceeded the depth of the conical cleft of the enzyme (∼15 Å). (This type of behavior characterizes the interaction of CA with para-substituted benzenesulfonamides where R are alkyl chains;^{11, 12} for HCA, K_d decreases from 83 nM for R = methyl to 1.3 nM for R = n-hexyl and 1.2 nM for R = n-heptyl.¹¹) The insensitivity of K_d to chain length that we observed was particularly difficult to rationalize because the interaction of the chains for ArGly_mO⁻ with the protein was sufficiently strong to decrease the NMR T₂ relaxation times of the α (or methylene) protons of the first three residues of these chains to < 25 ms (the value for these residues when free in solution was 230 ms).¹³ The chains were also sufficiently ordered that we were able to locate the first three residues of the chains (of both the ArGly_mO^- and ArEG_nOMe series) in contact with a hydrophobic patch (the so-called “hydrophobic wall”) of CA in X-ray structures of the protein-ligand complexes (Figure 2).^{14, 15} The principal inference from these studies was that the first three residues of the chains for ArEG_nOMe and ArGly_mO^- interacted in a similar fashion (apparently through hydrophobic contacts) with the hydrophobic wall of CA, but that—counter to our expectations—this interaction had no effect on the value of K_d.

Figure 1.

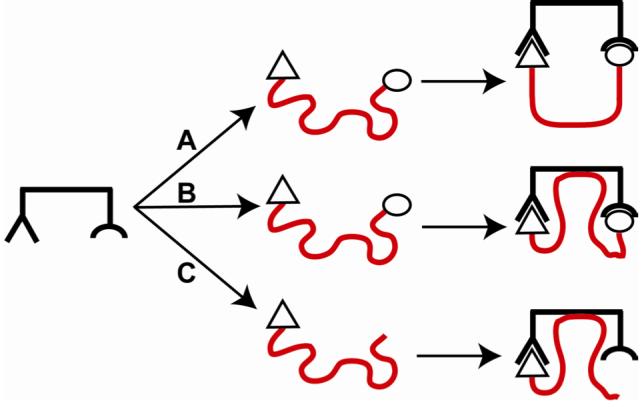
Binding of a bivalent ligand containing a flexible linker (shown in red) to a bivalent receptor. (A) We expect the binding process to suffer from an entropic penalty due to the loss in conformational entropy of the linker, which has fewer allowed conformations after complexation than before. (B) The linker could interact with the receptor, and provide a favorable enthalpy that could partially compensate for the unfavorable conformational entropy. (C) The ligand contains only one binding element and the “linker”. We study this type of structure in this paper to examine directly the interaction of the “linker” (or chain) on the binding of the ligand to the receptor.

Figure 2.

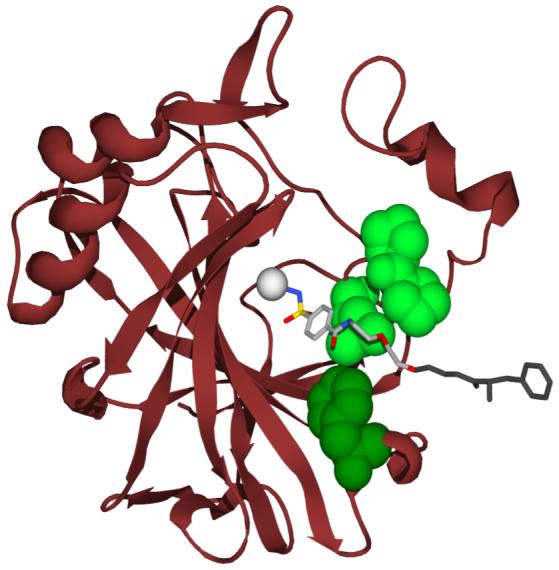
Model for the interaction of p-H₂NSO₂C₆H₄CONH(CH₂CH₂O)₂CH₂CH₂NHCOPheNH₃⁺ (ArEG₃PheNH₃⁺) with HCA II based on the deposited X ray crystallographic coordinates (PDB: 1CNY).¹⁴ HCA has been depicted as a ribbon diagram with the hydrophobic residues that are within van der Waals contact distance of the ligand rendered as space-filling models, and the catalytically essential Zn(II) depicted as a gray sphere. The ligand has been rendered as a ball- and-stick model. The light green space-filling residues, Leu-198, Pro-201, and Pro-202, constitute the so-called “hydrophobic wall” of CA, and form the majority of contacts (both hydrophobic and van der Waals) with the oligoethylene glycol linker of the ligand. The dark green residue, Phe-131, has a significant amount of hydrophobic surface buried in the complex with the ligand. The last glycol unit, and the Phe residue of the ligand, were both disordered, and thus not visualized in the crystal structure. They have been modeled them using stereochemical constraints, and are shown in dark gray. This model was created with POV-Ray.

To explain these results, we proposed a form of enthalpy/entropy compensation^16-21 and hypothesized that longer chains interacted more favorably enthalpically with the surface of BCA (due to greater van der Waals contacts, etc.)²² than shorter ones, but that this interaction was disfavored entropically due to the larger number of degrees of conformational freedom that were restricted to allow such an interaction to occur (Figure 3A).^{13, 15, 23} We found it astonishing that perfect compensation was working with two very different types of chains, especially in light of the aforementioned experimental observation that increasing the length of the chain for para-substituted benzenesulfonamides with alkyl chains decreased K_d.

Figure 3.

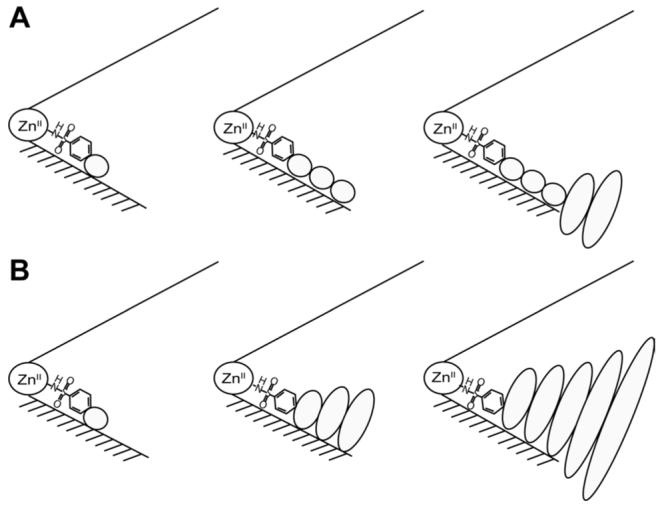
Two models for the interaction of the chains of arylsulfonamide ligands (containing one, three, and five residues) with the surface of carbonic anhydrase. This schematic represents the catalytic cleft of the enzyme as a cone with the Zn^II co-factor at the apex. The bottom surface (shaded) of the cleft is the “hydrophobic wall” of the enzyme. Schematic of (A) hydrophobic effect model and (B) interface mobility model. Ellipses depict the residues of the ligand; the sizes of the ellipses are roughly proportional to the mobility of the individual residues.

Enthalpy/entropy compensation—the positive correlation between enthalpy and entropy of a physicochemical process as a variable of the system is modulated (that minimizes the variation of the free energy of binding)—is a phenomenon that is ubiquitous in biological systems,^16-18 and has been discussed theoretically.^19-21 The qualitative explanation for enthalpy/entropy compensation centers on the inverse relationship between the amount of mobility (ΔS°) at a protein-ligand interface and the strength of the interaction (ΔH°) between protein and ligand at this interface.^{17, 20} Dunitz proposed a theoretical model for this phenomenon in which the protein-ligand complex is approximated as a potential energy well; the entropy of the complex can be estimated from the vibrational energy level spacing, which depends on the force constant of the well.¹⁹ Assuming a Morse potential for the well, the force constant is proportional to the enthalpy of binding.²⁴ Using these approximations, the model generates an enthalpy/entropy compensation curve in which the entropy of the complex decreases monotonically with increasing exothermicity of complexation, but becomes less sensitive to enthalpy when it is very favorable (ΔH° ∼ -20 kcal mol^-1). While the model predicts a curved compensation curve, the compensation is roughly linear over small changes in enthalpy (ΔΔH° ≤ 10 kcal mol^-1). Thus, this theoretical model suggests an origin for the compensation between enthalpy and entropy, based on mobility of the protein-ligand complex. Williams and co-workers have provided experimental support for this idea of interfacial mobility by demonstrating that a glycopeptide dimer interface (a model for a protein-ligand interface) becomes tighter (the physical separation of monomers decreases) with increasing exothermicity of the dimerization. ^{17, 25} The increasing exothermicity was compensated by an increasingly unfavorable entropy, which presumably reflected the decreasing mobility at the tighter dimer interface.

Isothermal titration calorimetry (ITC) is the premier technique for separating free energy of binding into enthalpic and entropic components.²⁶ When the dissociation constant (K_d) is in the range of nM to mM, this technique is able to measure K_d and enthalpy of binding (ΔH°) directly, and entropy of binding (ΔS°) from the relation: ΔS° = (ΔH° - ΔG°) / T.^{26, 27,28} (Because ITC directly measures the heat released upon titration of protein with ligand, it avoids the artifacts of van’t Hoff analysis arising from, for example, the temperature-dependence of enthalpy of binding and/or of the change in specific heat capacity, the large errors in measured parameters due to extrapolations from limited temperature ranges, and the thermal instability of proteins ^29-31,32

In this paper, we used ITC to separate the free energies of binding of the ArEG_nOMe and ArGly_nO^- ligands, as well as those of the previously uncharacterized ArSar_nO^- series, into their enthalpic and entropic components. The objective of this work was to test our hypothesis of enthalpy/entropy compensation. Our intent was to characterize the interaction of these chains with the surface of BCA, in order to further our understanding of the interaction between these classes of chains and proteins. Again contrary to our expectations, these calorimetric data clearly demonstrate that the enthalpy of binding becomes less favorable as the length of the chain increases, while the entropy of binding becomes less unfavorable for all of the series studied. The changes in enthalpy and entropy of binding with chain length (total variation of 1-2 kcal mol^-1, or 10-15%) perfectly compensate one another (making K_d insensitive to chain length) for all three series of ligands studied. On the basis of these data, and of measurements of heat capacities, we now rationalize the behavior of this system using a model in which the interface between the ligand and the hydrophobic wall of the protein becomes less intimate (less “tight”) as the length of the chain increases (Figure 3B). The decreasing tightness of the interface (with increasing length of the chain) results in increasing mobility of the chain of the ligand in the complex, and in decreasing magnitude of the unfavorable entropy of binding. In parallel, the decreasing tightness of the interface results in fewer van der Waals contacts between the ligand and protein, and in decreasing exothermicity of binding.

These results provide a particularly well-defined example of enthalpy/entropy compensation. The binding of three series of oligomeric ligands, which are systematically varied by extending their chain length, with a model protein provides as simple a system as we know with which to examine enthalpy/entropy compensation. Understanding how to circumvent or to exploit this compensation is a key principle in the design of high-affinity ligands for proteins.^{2, 16}

Results

Synthesis of Ligands

ArCO ₂^- and ArCONHMe (Ar = p-H₂NSO₂C₆H₄-) were commercially available. We synthesized ArGly_nO^-, ArEG_nOMe, and ArSar₁O^- (1, n = 1-5) as previously described.¹³ Briefly, the ligands were synthesized by allowing the N-hydroxysuccinimidyl ester of p-carboxybenzenesulfonamide to react with the amino terminus of the appropriate oligomer. We synthesized ArSar_nO^- (1, n = 2-5) through conventional solid-phase methods using the Fmoc-protection strategy (see Experimental section).

Validation of ITC: Measurement of Dissociation Constants

The concentration of BCA was determined by UV spectrophotometry.³³ High purity (≥95%) of the enzyme was ensured by capillary and gel electrophoresis,⁸ and high activity (90-95%) of it was determined by the binding of ethoxzolamide (a selective, stoichiometric ligand that quenches the intrinsic fluorescence of Trp residues of CA when it binds^{34, 35}). The concentration of ligand was determined by quantitative ¹H NMR (see Experimental section). Turnbull and Daranas have recently demonstrated that the value of K_d estimated from curve-fitting of ITC data is insensitive to the concentrations of ligand and protein (when the two are varied by 15%).²⁷ We discuss the influence of the concentrations of ligand and protein on the estimated enthalpy of binding, and our analysis of error for all thermodynamic parameters in the next section. ITC provides the stoichiometry of binding as a fitting parameter; this experimental parameter serves as an internal check on the relative accuracy of the concentrations of protein and ligand. These stoichiometries were 1.00 ± 0.05 for all of the ligands studied here; they validate our methods to estimate the concentrations of both components.

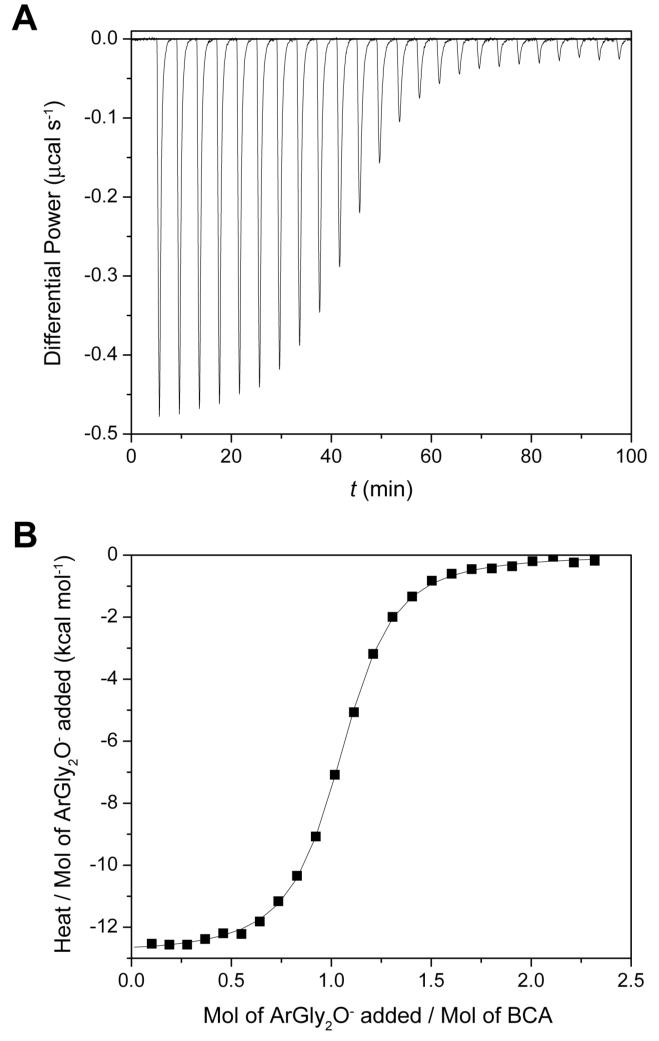
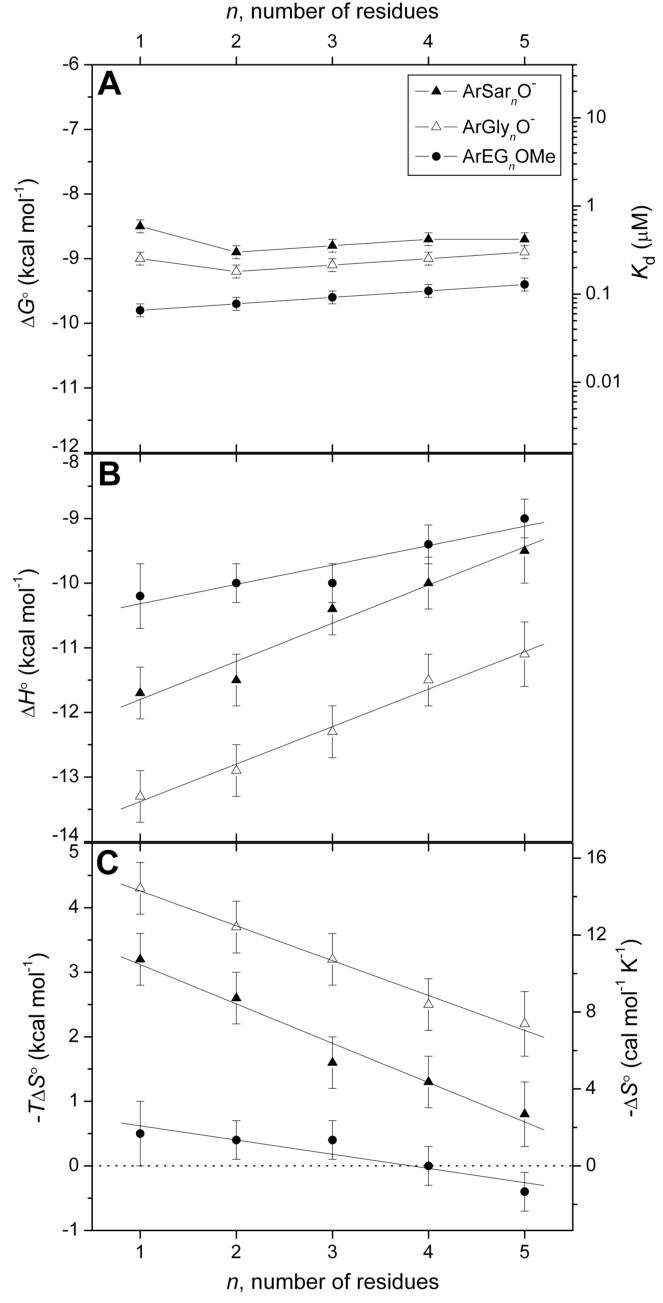
Figure 4 shows a representative thermogram from ITC with the associated curve fitting.²⁶ The dissociation constants from the fitting procedure for ArEG_nOMe and ArGly_nO^- are in good agreement with those we reported previously¹³ (Table 1); these earlier values of K_d were obtained using a fluorescence competition assay and are thus independent. The agreement between the two validates both the ITC methodology and the values of K_d. We have confirmed the previously reported insensitivity of K_d to chain length (n) for ArGly_nO^- (K_d ∼ 0.23 μM) and ArEG_nOMe (K_d ∼ 0.10 μM), and have reported for the first time that the ArSar_nO^- series also exhibits this insensitivity of K_d towards chain length (K_d ∼ 0.40 μM) (Figure 5A).

Figure 4.

A representative ITC experiment showing the titration of arylsulfonamide ligand into a solution of bovine carbonic anhydrase II (BCA). The sample cell contained 10.0 μM BCA in 20 mM sodium phosphate buffer pH 7.5 and 0.6% DMSO-d₆ (v/v) (to solubilize the arylsulfonamide and to allow for NMR quantitation, see Experimental Section). The injection syringe contained 103 μM ArGly₂O^- (1) in the same buffer. One injection of 2.0 μL preceded 24 injections of 12.0 μL. The interval between injections was 4 min. (A) Data after baseline correction. (B) Data after peak integration, blank subtraction, and normalization to moles of injectant. The solid line shows a sigmoid fit to a single-site binding model (with the first datum omitted). The dissociation constant (K_d = 0.20 μM), enthalpy of binding (ΔH° = -12.6 kcal mol^-1), and stoichiometry of binding (N = 1.02) were the fitting parameters in the analysis. See Experimental Section for details.

Table 1.

Thermodynamic parameters for the binding of arlysulfonamide ligands (of structure 1) to bovine carbonic anhydrase II (BCA) in 20 mM sodium phosphate pH 7.5 with 0.6% (v/v) DMSO-d₆ at 298 K

Ligand	n	Kd μM	lit Kda μM	ΔH° kcal mol-1	ΔS° cal mol-1 K-1	ΔCp cal mol-1 K-1
ArCO2-	--	0.50 ± 0.02	0.27b	-14.8 ± 0.5	-21.0 ± 1.5	--
ArCONHMe	--	0.20 ± 0.01	0.083c	-10.8 ± 0.4	-5.5 ± 1.5	--
ArEGnOMe	1	0.068 ± 0.004	0.10d	-10.2 ± 0.5	-1.5 ± 1.5	-40 ± 8
	2	0.085 ± 0.005	0.13d	-10.0 ± 0.3	-1.3 ± 1.0	--
	3	0.10 ± 0.01	0.16d	-10.0 ± 0.3	-1.4 ± 1.0	-47 ± 8
	4	0.12 ± 0.01	0.21d	-9.4 ± 0.3	+0.1 ± 1.0	--
	5	0.13 ± 0.01	0.21d	-9.0 ± 0.3	+1.3 ± 1.0	-40 ± 20
ArGlynO-	1	0.26 ± 0.01	0.30d	-13.3 ± 0.4	-14.6 ± 1.4	-24 ± 2
	2	0.20 ± 0.01	0.26d	-12.9 ± 0.4	-12.5 ± 1.3	--
	3	0.23 ± 0.01	0.33d	-12.3 ± 0.4	-10.9 ± 1.4	-18 ± 10
	4	0.25 ± 0.01	0.37d	-11.5 ± 0.4	-8.4 ± 1.2	--
	5	0.29 ± 0.02	0.37d	-11.1 ± 0.5	-7.3 ± 1.8	-20 ± 7
ArSarnO-	1	0.62 ± 0.03	--	-11.7 ± 0.4	-10.7 ± 1.2	-43 ± 10
	2	0.30 ± 0.01	--	-11.5 ± 0.4	-8.8 ± 1.2	--
	3	0.34 ± 0.01	--	-10.4 ± 0.4	-5.4 ± 1.2	-45 ± 16
	4	0.41 ± 0.02	--	-10.0 ± 0.4	-4.4 ± 1.3	--
	5	0.45 ± 0.02	--	-9.5 ± 0.3	-2.9 ± 1.0	-49 ± 23

^aLiterature values of dissociation constants for the binding of arylsulfonamides to BCA or human carbonic anhydrase II (HCA).

^bMeasured with HCA in Taylor, P. W.; King, R. W.; Burgen, A. S. V. Biochemistry 1970, 9, 2638-2645.

^cMeasured with HCA in ref 11.

^dMeasured with BCA in ref 13.

Figure 5.

Variation in (A) free energy of binding and dissociation constant, (B) enthalpy of binding, and (C) entropy of binding with the number of residues in the chain for arylsulfonamide ligands of structure 1. Error bars are discussed in the text (see Results section). Linear fits to the data in (B) and (C) are shown. The observed fitting parameters (slope in kcal mol^-1 residue^-1, y-intercept in kcal mol^-1) are as follows: for (B), ArGly_nO^- (0.58 ± 0.04, -14.0 ± 0.1), ArSar_nO^- (0.59 ± 0.07, -12.4 ± 0.2), ArEG_nOMe (0.30 ± 0.06, -10.6 ± 0.2); for (C), ArGly_nO^- (-0.54 ± 0.03, 4.8 ± 0.1), ArSar_nO^- (-0.61 ± 0.06, 3.7 ± 0.2), ArEG_nOMe (-0.22 ± 0.05, 0.8 ± 0.2). Uncertainties were given by the linear least-squares fitting procedure. The horizontal dashed line in (C) separates favorable (-TΔS° < 0) from unfavorable (-TΔS° > 0) entropy of binding.

Analysis of Experimental Uncertainty

Several authors have advised caution in the interpretation of thermodynamic results (particularly enthalpy/entropy compensation relationships) due to random errors in the estimation of enthalpy and entropy of binding.³² Thus, we carried out a careful analysis of error.

In ITC, the heat released upon titration of one binding partner with another is normalized to the number of moles of titrant added (Figure 4B). Thus, the estimated value of ΔH° is inversely proportional to the concentration of titrant (here, the arylsulfonamide), because the quantity of titrant added is proportional to the concentration of titrant. For this reason, fractional errors in the estimated value of ΔH° are almost equal to fractional errors in the estimation of concentration of the arylsulfonamide.²⁷ Errors in the concentration of the component in the sample cell (here, BCA) do not affect the estimated value of ΔH°,²⁷ but are instead reflected in deviations of the binding stoichiometry from unity (see previous section). To reduce the uncertainty in concentration of ligand, we used quantitative ¹H NMR to estimate this concentration relative to maleic acid as internal standard. We assumed an uncertainty of 3% from this method of quantitation from literature reports.³⁶ To arrive at an uncertainty for values of ΔH°, we propagated the error in concentration of ligand (taken as 3% of the estimated value of ΔH°) with the largest variation of an individual experiment from the mean value of 2-4 replicate measurements of ΔH°, assuming that the error in concentration of ligand and error in measurement were independent.

For errors in values of K_d for all of the ligands, we used the maximum variation of an individual measurement from the mean of 2-4 replicate measurements. Errors in values of ΔS° were estimated by propagating the errors in values of ΔH° and K_d, assuming that the two errors were independent. Changes in heat capacity (ΔC_p) were determined by measuring ΔH° as a function of temperature over the range T = 288-308 K (see section on Changes in Heat Capacity). Errors in values of ΔC_p were estimated by the error in slopes of linear plots of ΔH° vs. T that were given by the least-square fitting procedure.

Table 1 gives the measured thermodynamic parameters with their associated uncertainties.

The Trends in Enthalpy and Entropy Were Opposite to Those We Expected

We predicted that as the chain of the ligand became longer (i.e., as n increased), ΔH° would become more favorable (due to increasing area of contact between the chain and the hydrophobic wall of the enzyme), and TΔS° more unfavorable (due to entropic restrictions to motion of the chain resulting from proximity to the wall).²³ The result that we observed was counter to this hypothesis: ΔH° became less favorable, and TΔS° less unfavorable, with increasing chain length (Figures 5B and 5C). It is especially remarkable that we observe the same counterintuitive result for three, structurally different chains; this similarity gives us confidence that the result is correct, and not an artifact.

This result poses the central conundrum of this paper: why does the enthalpy of interaction of the chains become less favorable, and the entropy less unfavorable, as the chain becomes longer? We discuss the experimental results in the following sections and then present two possible models to rationalize the data in the Discussion section.

There Was No Clear Discontinuity in Thermodynamic Properties When the Chain Exceeds the Presumed Length of the Hydrophobic Wall of the Enzyme

There was no discontinuity in plots of ΔH° and TΔS° with chain length (n) for any of the series of ligands (Figures 5B and 5C) when the length of the chain exceeded the depth of the conical cleft (15 Å, n ∼ 2-3) of BCA (Figure 2).^{14, 15} The plots were linear (within error) over the length studied, and did not meet our initial expectation that ΔH° and TΔS° would plateau once there were a sufficient number of residues in the chain for additional residues to be outside the active site. This result suggests that there is still an interaction of the chain with BCA when n > 3, and that this interaction is similar for residues in ligands with short (n < 3) chains and for those in ligands with long (n ≥ 3) chains.

This finding seems incompatible with evidence describing binding of ArGly_nO^- to BCA as measured by NMR relaxation times. These data indicated that values of T₂ (120 ms) of residues separated by more than three residues from the phenyl ring, were significantly larger than those (T₂ < 25 ms) of the three residues closest to the phenyl ring; this result suggests a small amount of interaction of these distal residues with the protein.¹³ There was a difference between T₂ for these residues farther from the phenyl ring, and T₂ (230 ms) for residues of the free, uncomplexed ligand; there is, thus, apparently some interaction with BCA of the residues farther than three residues from the phenyl ring.

Molecular dynamics simulations indicated that the benzyl ester in ArGly₃OBn (the benzyl moiety is in a similar position in this ligand as the fourth and fifth residues of ArGly₅O^-) and the pendant amino acid in ArEG₃NHR (R = Gly, Phe) could both interact with the surface of CA in certain conformations of the ligands.^{37, 38} These simulations, thus, support the calorimetric data and suggest a possible interaction with CA of residues farther than three residues from the phenyl ring.

We believe that there is an interaction with the protein of residues of ArGly_nO^- and ArEG_n OMe (and also ArSar_nO^-) where n ≥ 3. We cannot, however, discriminate between the interactions with CA of residues close to the ring (n < 3) and those farther from the ring (n > 3) based on thermochemistry.

Oligoglycine (Gly_n), Oligosarcosine (Sar_n), and Oligoethylene glycol (EG_n) Chains Have Similar Interactions with the Hydrophobic Wall of CA

Qualitatively, the trends for both ΔH° and TΔS° with chain length (n) for the ArGly_nO⁻, ArSar_nO⁻, and ArEG_nOMe ligands roughly parallel one another (Figure 5B and 5C). To assess these trends quantitatively, we constructed linear fits to the plots; the slopes were similar for all three series. The similarity in slopes of the series suggests that the three chains interact similarly with the surface of BCA.

While the best-fit lines of ΔH° (and −TΔS°) to chain length (n) for the three series were roughly parallel (i.e., they had similar slopes), they were off-set (i.e., they had different y-intercepts). These different y-intercepts reflect differences in ΔH° and -TΔS° between the three series that depend on the nature of the first residue (the residue adjacent to the phenyl ring). The addition of subsequent (n > 1) residues (either Gly, Sar, or EG) changes the thermodynamics of binding by roughly the same amount (since the slopes of the best-fit lines were the same). These results suggest that the interactions with the hydrophobic wall of CA of Gly_n, Sar_n, and EG_n chains (beyond the first residue) are thermodynamically similar.

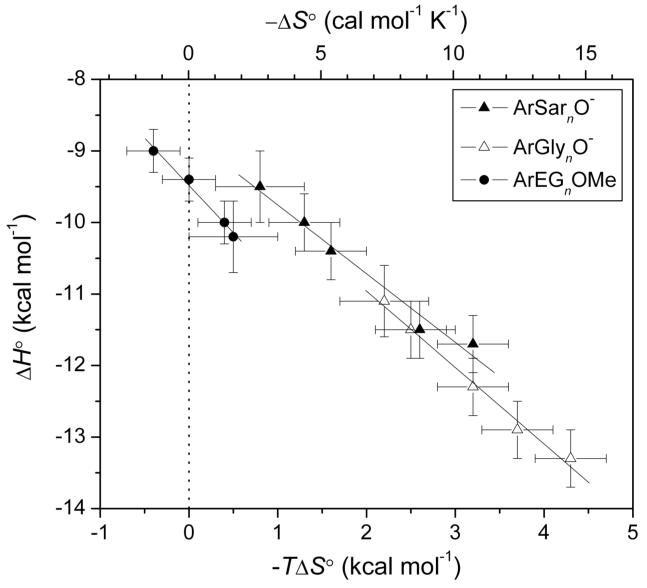
Plots of ΔH° vs. TΔS° (enthalpy/entropy compensation plot) for the three series have slopes near unity, and thus show almost perfect compensation between ΔH° and TΔS° (Figure 6).

Figure 6.

An enthalpy/entropy compensation plot: variation of the enthalpy of binding with the entropy of binding for ligands of structure 1 with n ≥ 1. Error bars are as in Figure 5. The solid lines are linear fits to the data sets and have the following slopes: -0.96 ± 0.08 (ArSar_nO^-), -1.07 ± 0.07 (ArGly_nO^-), and -1.32 ± 0.09 (ArEG_nOMe). Uncertainties were given by the linear least-squares fitting procedure. The dotted vertical line separates favorable (-TΔS° < 0) from unfavorable (-TΔS° > 0) entropy of binding.

Changes in Heat Capacity Provide Information about Buried Molecular Surface Area

The change in heat capacity (ΔC_p) has been termed the “signpost” for the hydrophobic effect; it is negative for the binding of hydrophobic molecules in water.^{22, 39} Models of protein-ligand binding have been proposed that correlate ΔC_p with buried molecular surface area (both polar and nonpolar).^40-42 Sturtevant⁴³ has discussed additional contributions to ΔC_p upon protein-ligand complexation: positive contributions (hydrogen bond formation, increase in number of vibrational modes of the protein from relaxing of structure), negative contributions (exposure of electrostatic charges, reduction in number of vibrational modes of the protein from stiffening of the protein), and neutral contributions (conformational mobility from, for instance, an increase in the number of accessible conformations).

We measured changes in heat capacity (ΔC_p) for n = 1, 3, and 5 for the different series in order to clarify the nature of the interactions of these chains with BCA. We measured the variation of ΔH° with temperature over the range 288-308 K⁴⁴ and used the definition of ΔC_p in eq 1, where T is the temperature in K and ΔH°(T) is the enthalpy of binding at temperature T.

$$\Delta C_p\left(T\right)={\left(\frac{\partial \Delta H°\left(T\right)}{\partial T}\right)}_p$$ (1)

Assuming a constant change in heat capacity over this temperature range, this relation simplifies to eq 2, where ΔH°(0) is the enthalpy of binding at T = 0 K.

$$\Delta H°\left(T\right)=T\Delta C_p+\Delta H°\left(0\right)$$ (2)

Simple linear regression of eq 2 affords ΔC_p.

We titrated the ligand with protein under conditions in which >99.5% of the added protein would be bound by ligand in order to obtain an estimate of ΔH° from a single injection. We averaged at least seven injections, and determined uncertainties (standard deviations of these injections) of < 0.2 kcal mol^-1 (see Experimental section for further information). Table 1 lists values for ΔC_p obtained from linear fits to these data. The values of ΔC_p are small, do not vary with chain length within each series, and vary only slightly among the series. For benzenesulfonamide, ΔC_p has been reported to be +25 cal mol^-1 K^-1.⁴⁵ These results suggest that ΔC_p is dominated by the benzenesulfonamide group with some influence of the first residue of the chain.

At first glance, these results seem to contradict a model in which the chains of the ligand interact hydrophobically with the surface of BCA (ΔC_p should become more negative with increasing chain length in such a model). In the next section, we explore contributions to ΔC_p (listed at the beginning of this section) that could rationalize the data with such a model. We also introduce another theoretical model, and discuss its compatibility with the experimental data.

Discussion

Two Possible Thermodynamic Models

We can imagine two possible models that are consistent with the trends of ΔH° and -TΔS° with chain length (Figure 5): i) one based on hydrophobic interactions (Figure 3A), and ii) one based on interfacial mobility (mobility of the protein-ligand interface) (Figure 3B). We conclude that the second model is the only one consistent with the experimental data.

Overview of Hydrophobic Effect Model

The model based on hydrophobic interactions (Figure 3A) postulates that the interaction of Gly_n, Sar_n, and EG_n chains with CA is due to the classical hydrophobic effect^{22, 39}, the association of hydrophobic molecules in aqueous solution. At temperatures near 298 K, the hydrophobic effect occurs with a favorable entropy (-TΔS° < 0) and a negligible enthalpy (ΔH° ∼ 0). This model rationalizes the data by proposing that as the chain of the ligand gets longer, the amount of nonpolar surface area that becomes buried upon complexation increases; this increasing buried surface area is manifested as a favorable contribution to -TΔS°. For this hypothesis to explain the data, the contribution of the hydrophobic effect to the observed TΔS° must be greater than the unfavorable contribution of restricting the modes of motion of the chain. In this model, the decreasing magnitude of ΔH° (decreasing exothermicity) with increasing chain length could have several origins: i) loss of hydrogen bonds between the unassociated form of the ligand (or of the protein) upon complexation, ii) unfavorable conformations (e.g., eclipsed bonds) of the chain in the complex, and/or iii) destabilization of placing a lone pair of electrons on the chain into contact with the hydrophobic wall of CA. We discuss below how none of these possibilities can adequately explain the trend of ΔH° with chain length for the three series of ligands.

Overview of Interfacial Mobility Model

The second possible model (interfacial mobility model) (Figure 3B) postulates that the interface between protein and the chain of the ligand becomes “looser” (less tight) with increasing chain length. This decreasing tightness of the interface is reflected in a less unfavorable TΔS° (due to greater mobility of the chain) and a correspondingly less favorable ΔH° (due to fewer van der Waals contacts between the protein and ligand) as the length of the chain increases. Enthalpy and entropy perfectly compensate and there is no change in the observed K_d.

In this model, the decreasing tightness of the interface arises because more distal residues (those farther from the phenyl ring) of the chain destabilize the binding of more proximal residues (those closer to the phenyl ring). To explain the data, this model requires that residues that are bound “tightly” in ligands with a short chain be destabilized by more distal residues in ligands with a long chain; if these distal residues did not interact with more proximal residues of the chain or with the protein (and were oriented into solution), ΔH° and TΔS° would become independent of chain length at that point.

Residues that are farther (more distal) from the phenyl ring are plausibly more mobile than those that are closer (more proximal) to the ring. The conical catalytic cleft of CA could force a destabilizing interaction (e.g., torsional or steric strain) of these mobile, distal residues with the bound form of more proximal residues. The protein-ligand complex would relax to a more stable state in which the destabilization is alleviated, by decreasing the tightness of the interface between the more proximal residues and the cleft of CA. The thermodynamics discussed above would then follow.

Evaluation of Both Models In Light of the Experimental Data

Since both models can adequately explain the trends in entropy (and, to a lesser extent, in enthalpy) with chain length, we consider their ability to explain the remaining thermodynamic data. We consider both models, in turn, with respect to the following experimental observations: i) the chain-length independence of ΔC_p, ii) the decreasing magnitude of ΔH° (decreasing exothermicity) with increasing chain length, iii) the similar trends of ΔH° and -TΔS° with chain length for the different series of ligands, and iv) the lack of a discontinuity in plots of ΔH° and -TΔS° with chain length. We first consider the “hydrophobic effect” model (Figure 3A); we conclude that this model is inconsistent with these data.

The Hydrophobic Effect Model is Inconsistent with the Thermodynamic Data

First, ΔC_p was independent of chain length for all three series of ligands; the hydrophobic effect model predicts that ΔC_p would depend on buried molecular surface area (and thus, on chain length). The correlation between ΔC_p and buried molecular surface area of Spolar and Record⁴¹ is given in eq 3a and that of Murphy and Freire⁴² in eq 3b:

$$\Delta C_p=0.32\Delta A_{\mathrm{np}}-0.14\Delta A_{\mathrm{p}}$$ (3a)

$$\Delta C_p=0.45\Delta A_{\mathrm{np}}-0.26\Delta A_{\mathrm{p}}$$ (3b)

where ΔA_np is the change in nonpolar surface area upon protein-ligand complexation (ΔA_np < 0 for the burial of surface area upon complexation), and ΔA_p is the change in polar surface area. We discuss the ArGly_nO^- ligands in detail, because there are X-ray crystal structures and NMR relaxation data for CA-ligand complexes of this series.^{13, 15} We expect that the conclusions regarding the validity of this model drawn from ArGly_nO^- will be applicable to ArSar_nO^- and ArEG_nOMe, because all of the ligands behave similarly in the thermodynamics of their interactions with BCA (Figure 5).

Given the surface area buried by each Gly residue from the X-ray crystal structures (49 Ų Gly^-1),¹⁵ and assuming that the entire interface was nonpolar (as observed in the X-ray crystal structure)¹⁵, we would expect a difference in ΔC between ArGly₃O^- and ArGly₁O^- to be in the range of -31 to -44 cal mol^-1 K^-1 (from eqs 3a and 3b, respectively). Even with the errors of the data, the experimentally observed difference (+6 ± 12 cal mol^-1 K^-1) was much larger than this value, and of opposite sign. A difference of ΔC_p ∼ 0 can be obtained if a significant fraction of the buried surface area were polar (although the CA-Gly interface was completely nonpolar in the X-ray crystal structure¹⁵). Polar surface area at the interface would provide a positive contribution to ΔC_p (from eqs 3a and 3b, respectively); a difference of ΔA_p = -68 to -62 Ų (ΔA_np = -30 to -36 Ų) between ArGly₃O^- and ArGly₁O^- yields ΔΔC_p ∼ 0 for ΔΔA_np + ΔΔA_p = -98 Ų (eq 3). Spolar and Record⁴¹ have proposed eq 4 to relate the buried nonpolar surface area with the entropy of binding from hydrophobic effect contacts (ΔS°_HE) (at T = 298 K):

$$\Delta S{°}_{\mathrm{HE}}=-0.083\Delta A_{\mathrm{np}}$$ (4)

Using the larger (in magnitude) value for the difference in ΔA_np of -36 Ų (from eq 3b), gives a difference in ΔS°_HE of ∼ +3.0 cal mol^-1 K^-1 between ArGly₃O^- and ArGly₁O^-. This value is close to the experimentally observed difference in ΔS° of +3.7 cal mol^-1 K^-1 (Table 1), but this experimentally observed value must also take into account the conformational restriction of the additional rotors in two Gly residues between ArGly₃O^- and ArGly₁O^- (ΔS°_conf ∼ -9 cal mol^-1 K^-1)^{2, 7}. Thus, ΔS°_HE must be greater than ΔS° by ∼9 cal mol^-1 K^-1; this model is inconsistent with the data from ΔC_p.

Second, the hydrophobic effect model cannot explain compellingly why ΔH° decreases in magnitude (becomes less favorable) with increasing chain length (n). Van der waals contacts—which the interactions between Gly and hydrophobic wall of CA seem to be—are expected to be favorable enthalpically, and should make a favorable contribution to ΔH° that increases with chain length.^{22, 23, 46} Unfavorable conformations of the different chains in the CA-ligand complex seem unlikely, given the flexible nature of the chains⁴⁷ and the lack of eclipsed or other unfavorable conformations in the crystal structure.^{14, 15} The removal of hydrogen bonds either within (intramolecular) or between (intermolecular) ligand molecules upon complexation with the enzyme could explain the trend of ΔH° with chain length. We would not, however, expect such hydrogen bonds to be present in the uncomplexed ligand because the chains we studied were short and flexible, and the high dielectric constant of the aqueous buffer should disfavor such weak, electrostatic interactions.²² Further, it strains coincidence that the amount and/or strength of bonding (within or between) uncomplexed ligand molecules would be the same for the different chains studied, or that the unfavorable conformations of the chains would be unfavorable by the same amount for the different chains (possibilities that are required to explain the similar variation of ΔH° with chain length for the different series, see Figure 5).

Third, we consider the most perplexing issue with this model: its inability to explain why there were similar trends in plots of ΔH°, and -TΔS°, with chain length for the three different types of chains (Figures 5A and 5B). For instance, sarcosine has more hydrophobic surface area than glycine due to the N-Me substituent, but behaves similarly thermodynamically. Ethylene glycol is very different structurally than either of the peptidyl chains, but again behaves similarly.

Finally, the observation that residues that extend past the conical cleft of BCA (residues beyond the third one) and are oriented into solution, as evidenced by X-ray crystal structures^{14, 15} (Figure 2) and NMR relaxation¹³ data, still exert the same influence on the thermodynamics of binding as residues that directly interact with the hydrophobic wall of the enzyme is incompatible with this model. There is no plateau (or discontinuity) in plots of ΔH° and -TΔS° with chain length that would be predicted from this model (Figure 5).

The Interfacial Mobility Model Is Consistent with the Thermodynamic Data

We now consider the interfacial mobility model (Figure 3B) in the context of the four pieces of experimental data; we believe that this model is compatible with the data. First, the independence of ΔC_p on chain length within each series, and the modest variation of ΔC_p among the series, are readily explained by this model: ΔC_p is dominated by the benzenesulfonamide group with some influence from the first residue the chain. Subsequent residues (n > 1) interact weakly with the hydrophobic wall of the enzyme and do not influence ΔC_p.

Second, as discussed above, the interfacial mobility model can explain the observation that ΔH° becomes less favorable (less exothermic) as chain length increases.

Third, this model can explain the similar trends of both ΔH° and -TΔS° with chain length of the different series of ligands. In this model, these similar trends (Figure 5) are due to similar destabilization of the binding of residues of the chain by more distal residues (those farther from the phenyl ring). This effect could arise because the constrained orientation of the conical cleft of the enzyme forces the mobility of the distal residues of the chain to destabilize the binding of more proximal residues through, for example, steric or torsional strain. The complex then relaxes by decreasing the tightness of the interface between the more proximal residues of the chain and the hydrophobic wall of CA. This observation does not require that the chains interact directly with the hydrophobic wall of CA in a similar manner (consistent with the different structures and flexibilities of these chains).

Finally, the interfacial mobility model can explain why residues that extend past the presumed length of the wall (those farther than three residues from the phenyl ring, n > 3) can still affect the thermodynamics of interaction. This model can rationalize this observation because these residues, which do not directly interact with the wall, can still destabilize the bound form of more proximal residues that do interact with the wall. A direct interaction of these residues (where n > 3) with the enzyme is not required in this model. We anticipate that the thermodynamic parameters of interaction (ΔH° and TΔS°) will plateau when the chain is sufficiently long that additional destabilization of the binding of more proximal residues (that do interact with the wall) by more distal ones cannot occur; this required length would seem to be greater than of the ligands studied here (n = 5). The interfacial mobility model (Figure 3B) is, thus, consistent with all of the experimental data.

The Mechanism of the Interfacial Mobility Model Is Unclear

The exact mechanism of the interfacial mobility model remains unclear. While we have presented the model as involving destabilization of the binding of residues of the chain by more distal residues, the model could involve destabilization in the protein itself as a result of binding of ligand. Williams and co-workers have recently discussed how enthalpy/entropy compensation could originate from a loosening of protein structure that is coupled to ligand binding.^{17, 48, 49} Ligands with long chains could destabilize interactions within the protein itself (perhaps through a weakening of hydrogen bonds in the protein in a process that does not require gross conformational changes in the structure of the protein). We have no evidence for or against this model, and so cannot comment on the contribution of it, if any, to our system.

Conclusions

This paper establishes that ligands with oligosarcosine chains exhibit the same insensitivity of K_d to chain length as the previously reported oligoglycine- and oligoethylene glycol-containing ligands. We have dissected the thermodynamics of binding of these three series of ligands. While we anticipated that the enthalpy of binding would become more favorable with increasing chain length, and that the entropy of binding more unfavorable,²³ the results were exactly opposite to these expectations. That is, increasing the chain length (number of residues) of these ligands monotonically reduced the favorable enthalpy of binding and decreased the entropic cost of binding. Surprisingly, the different chains seem to behave as slight variations on a general theme with similar variations of enthalpy and entropy with chain length. Our results have thus revealed an unexpected example of enthalpy/entropy compensation in these structurally unrelated chains. We have proposed a model that explains these data. This model requires that the mobility of the chain of the ligand in the protein-ligand complex increases with increasing chain length, and that there be an active destabilization of the binding of residues of the chain that are closer to the phenyl ring by residues of the chain that are farther from the phenyl ring (Figure 3B).

A common approach to rational drug design invokes the principle of additivity: the thermodynamics of binding of a ligand to a protein are assumed to be equal to the sum of the thermodynamics of binding of the individual components of the ligand (with an appropriate entropic benefit of linking the different components together).^{17, 50-53} Williams and co-workers have discussed a complication to this approach by the concept of “negative cooperativity” an interface that displays negative cooperativity is one in which the multiple interactions between a ligand and a protein are mutually incompatible.^{17, 48, 49} At a negatively cooperative interface, the enthalpy of binding is less favorable, while the entropy of binding is less unfavorable, in the combined interaction than in the separate, individual interactions.² Our results suggest an even more extreme situation than negative cooperativity: the enthalpy of the combined interaction can be, not only less favorable than the sum of the independent interactions, but also less favorable than even one of the interactions. According to our model (Figure 3B), this less favorable total enthalpy is due to destabilization of one of the interactions by another. Our results, thus, demonstrate that an additive approach can reach completely incorrect conclusions due to this influence of one component (interaction) on the binding of another.

One of the guiding principles in rational drug design has been the design of ligands that fill the active site of an enzyme in order to increase the number of interactions between protein and ligand.⁵¹ Our results suggest that appending substituents to a parent ligand in an attempt to increase affinity for a target receptor might actually be deleterious for the enthalpy of binding, due to the destabilization of the binding of the parent ligand to the enzyme by the appended moiety (as opposed to simple steric strain between the appended moiety and the protein). While in our case the free energy of binding is not affected by the added groups (the longer chains), it is possible that in certain cases, a smaller, more carefully designed ligand, might bind with a lower free energy of binding to a target protein than a larger ligand (even one that does not merely encounter steric repulsion with residues of the active site of the protein).

One of the tenets in the design of multivalent ligands has been to avoid flexible (conformationally mobile) linkers due to the high cost in conformational entropy that would occur on complexation (Figure 1). Our results suggest that flexible linkers might also be disadvantageous from an enthalpic standpoint, because the linker (or chain) could destabilize the interaction of the ligand with the protein (relative to the ligand lacking the chain or linker). Our model (Figure 3B) predicts that rigid linkers would be able to avoid this enthalpic destabilization due to their reduced mobility, which is the origin of the destabilization between residues of the chain. This hypothesis remains to be tested.

The lowest free energy for the CA/arylsulfonamide complexes is achieved by optimizing the entropy (mobility) of the system at the expense of the enthalpy (fewer van der Waals contacts). We find it surprising that an alternative solution in which the magnitude of the enthalpy is optimized (more van der Waals contacts by increasing the tightness of the interface) at the expense of the entropy (lower conformational mobility) is apparently not available to the system. We cannot address the issue of whether the preference for optimization of entropy is directed by the catalytic cleft (or other structural aspects) of CA, or is an innate property of the interaction of these types of chains with hydrophobic patches.

The most surprising result from our investigation is the near perfect compensation between enthalpy and entropy (Figure 6) for the three series of ligands. At this stage, we do not understand clearly and intuitively why the significant changes in enthalpy (with chain length) are perfectly balanced by changes in entropy. The fact that we observe this compensation for three different series of ligands suggests that it is a general phenomenon (at least within these series). It could, therefore, characterize weak interactions of other types of chains with hydrophobic patches.

In summary, our results demonstrate how poorly we understand protein-ligand interactions, even in relatively simple systems with extensive biophysical characterization. More, and extensive, calorimetric investigations of well-characterized protein-ligand pairs will, we believe, be required to elucidate the origin of enthalpy/entropy compensation and further our ability to exploit this phenomenon in the rational design of high-affinity ligands.

Experimental Section

General Methods

Chemicals were purchased from Aldrich, Fluka, TCI, and Bachem. Bovine carbonic anhydrase II (pI 5.9) was obtained from Sigma. N-Hydroxybenzotriazole (HOBt) and (benzotriazol-1-yloxy)tris(dimethylamino)phosphonium hexafluorophosphate (BOP) were purchased from Advanced Chemtech (Louisville, KY). NMR experiments were carried out on a Varian Inova 500 MHz. Isothermal titration calorimetry was performed using a VP-ITC microcalorimeter (MicroCal). Analytical HPLC was run on a Varian instrument with a C18 column 5 μm (4.6 × 250 mm) from Vydac using a linear gradient of water with 0.1% TFA (A) followed by acetonitrile containing 0.08% TFA (B), at a flow rate of 1.2 mL/min (UV detection at 214 and 254 nm). Preparative reverse-phase HPLC was performed using a Varian Prostar HPLC system equipped with a C18 column 5 μm (10 × 250 mm) from Vydac at a flow rate of 6 mL min^-1 with UV detection at 214 nm.

General Procedures

p-H₂NSO₂C₆H₄CO(NHCH₂CO)_nOH (ArGly_nO^-), p-H₂NSO₂C₆H₄CONH(CH₂CH₂O)_nCH₃ (ArEG_nOMe), and p-H₂NSO₂C₆H₄CON(CH₃)CH₂COOtBu were prepared according to the general procedure of Jain et al.¹³

General Procedure for the Syntheses of p-H₂NSO₂C₆H₄CO(N(CH₃)CH₂CO)_nOH (ArSar_nO^-) (n = 2, 3, 4 and 5). Peptide Synthesis and Characterization

The ArSar_nO^- peptides were synthesized by Fmoc chemistry by the stepwise solid-phase methodology. Assembly of the protected peptide chains was carried out on a 50 μmol scale starting from Fmoc-Sar-Trityl resin. The Fmoc group was removed using 25% piperidine in DMF (1 × 5 min, 1 × 15 min) with agitation by nitrogen. The resin was then filtered and washed with DMF (6 × 3 min). For each coupling step, a solution of the Fmoc-amino acid (5 equiv), BOP (5 equiv), and HOBt (5 equiv) in DMF and DIEA were added successively to the resin, and the suspension was mixed for 10 min. A double coupling was performed sequentially. Monitoring of the coupling reaction was performed with chloranil test. After removal of the last Fmoc protecting group, the resin was washed with DMF, and reacted with 4-carboxybenzenesulfonamide (5 equiv) with BOP (5 equiv), HOBt (5 equiv), and DIEA (5 equiv) in DMF for1 h. The resin was washed with CH₂Cl₂, Et₂O and dried under nitrogen. Cleavage of the peptide from the resin was performed by treatment with a mixture of trifluoroacetic acid, water, and dithiothreitol (90%:5%:5%). After precipitation in cold ether and centrifugation, the peptide was solubilized in water and lyophilized. The crude peptide derivative was purified by HPLC (linear gradient, 0-70% B, 40 min) and lyophilized.

¹H NMR of p-H₂NSO₂C₆H₄CON(CH₃)CH₂COOtBu and p-H₂NSO₂C₆H₄CO(N(CH₃)CH₂CO)_nOH (ArSar_nO^-)

Due to the presence of cis (and trans) isomers for these sarconsine-containing compounds,⁵⁴ resonances become challenging to assign when there is more than one Sar residue in the chain. For all of the ligands in this series, we have assigned the resonances in the aromatic region to protons of the cis and trans isomers for the Sar residue nearest to the phenyl ring. For ArSar₁O^- , we have assigned the resonances for the aliphatic (methylene and N-methyl) protons to these conformations. For ligands with more than one Sar residue in the chain, we have reported the aliphatic resonances as ranges corresponding to the protons of all of the residues (and conformations) of the chain.

p-H₂NSO₂C₆H₄CON(CH₃)CH₂COOtBu

HPLC t_R 13.05 min (linear gradient, 0-100% B, 20 min); ¹H NMR (500 MHz, DMSO-d₆) δ 7.91 (d, J = 8.3 Hz, 2H trans), 7.86 (d, J = 7.8 Hz, 2H cis), 7.60 (d, J = 8.3, 2H trans), 7.48 (m, 2H cis, 2H sulfonamide), 4.15 (s, 2H trans), 3.92 (s, 2H, cis), 3.00 (s, 3H cis), 2.92 (s, 3H trans), 1.46 (s, 9H trans), 1.38 (s, 9H cis); HRMS m/z found 329.1174 (M+H)⁺, calcd 329.1171.

p-H₂NSO₂C₆H₄CON(CH₃)CH₂COOH (ArSar₁O^-)

p-H₂NSO₂C₆H₄CON(CH₃)CH₂COOtBu (100 mg, 304 μmol) was dissolved in 5 mL of trifluoroacetic acid and stirred for 30 min at room temperature. The solution was evaporated to dryness. Recrystallization from 3 mL of deionized hot water yielded a crude white powder (42 mg, 154 μmol, 51%). HPLC t_R 8.61 min (linear gradient, 0-100% B, 20 min); ¹H NMR (500 MHz, DMSO-d₆) δ 7.88 (d, J = 8.3 Hz, 2H trans), 7.84 (d, J = 8.3 Hz, 2H cis), 7.58 (d, J = 8.3, 2H trans), 7.46 (m, 2H cis, 2H sulfonamide), 4.15 (s, 2H, trans), 3.92 (s, 2H, cis), 2.98 (s, 3H, cis), 2.91 (s, 3H, trans); HRMS m/z found 273.0542 (M+H)⁺, calcd 273.0545.

p-H₂NSO₂C₆H₄CO(N(CH₃)CH₂CO)₂OH (ArSar₂O^-)

HPLC t_R 8.69 min (linear gradient, 0-100% B, 20 min); ¹H NMR (500 MHz, DMSO-d₆) δ 7.88 (d, J = 8.3 Hz, 2H trans), 7.80 (m, 2H cis), 7.57 (d, J = 8.3, 2H trans), 7.46 (m, 2H cis, 2H sulfonamide), 4.39 - 3.98 (4H, 4.39 (s), 4.25 (s), 4.18 (s), 4.15 (s), 4.02 (s), 3.98 (m)), 3.04 - 2.80 (6H, 3.04 (s), 2.94 (s), 2.85 (m), 2.80 (m)); HRMS m/z found 344.0914 (M+H)⁺, calcd 344.0916.

p-H₂NSO₂C₆H₄CO(N(CH₃)CH₂CO)₂OH (ArSar₃O^-)

HPLC t_R 8.77 min (linear gradient, 0-100% B, 20 min); ¹H NMR (500 MHz, DMSO-d₆) δ 7.88 (d, J = 7.8 Hz, 2H trans), 7.81 (m, 2H cis), 7.57 (m, 2H trans), 7.45 (m, 2H cis, 2H sulfonamide), 4.39 - 3.95 (6H, 4.39 (m), 4.24 (m), 4.13 (m), 4.01 (m), 3.97 (m), 3.95 (s)), 3.02 - 2.72 (9H, 3.02 - 2.91 (m), 2.86 - 2.72 (m)); HRMS m/z found 415.1289 (M+H)⁺, calcd 415.1287.

p-H₂NSO₂C₆H₄CO(N(CH₃)CH₂CO)₄OH (ArSar₄O^-)

HPLC t_R 8.94 min (linear gradient, 0-100% B, 20 min); ¹H NMR (500 MHz, DMSO-d₆) δ 7.88 (d, J = 7.8 Hz, 2H trans), 7.80 (m, 2H cis), 7.57 (d, J = 6.8, 2H trans), 7.45 (m, 2H cis, 2H sulfonamide), 4.40 - 3.83 (m, 8H), 3.03 - 2.69 (m, 12H); HRMS m/z found 486.1658 (M+H)⁺, calcd 486.1658.

p-H₂NSO₂C₆H₄CO(N(CH₃)CH₂CO)₅OH (ArSar₅O^-)

HPLC t_R 9.06 min (linear gradient, 0-100% B, 20 min); ¹H NMR (500 MHz, DMSO-d₆) δ 7.88 (d, J = 7.8 Hz, 2H trans), 7.80 (m, 2H cis), 7.57 (d, J = 8.3, 2H trans), 7.45 (m, 2H cis, 2H sulfonamide), 4.38 - 3.81 (m, 10H), 3.03 - 2.70 (m, 15H); HRMS m/z found 557.2031 (M+H)⁺, calcd 557.2029.

NMR Quantitation of Stock Solutions of Arylsulfonamide Ligands

Arylsulfonamide ligands were prepared gravimetrically to ∼20 mM in DMSO-d₆. Stock solutions were diluted 1:10 with 2.00 mM maleic acid in DMSO-d₆, prepared gravimetrically. Proton resonances due to the arylsulfonamide were normalized relative to that of maleic acid (allowing a 10 s delay between pulses) to determine accurately the concentration of the stock solutions.

Isothermal Titration Calorimetry

In order to determine values of ΔH° and K_d, ∼10 μM BCA II (concentration determined by UV spectrophotometry, ε₂₈₀ = 57,000 M^-1 cm^-1)³³ in 20 mM sodium phosphate buffer pH 7.5 (with 0.6% DMSO-d₆) was titrated with ∼110 μM arylsulfonamide ligand (concentration determined by ¹H NMR) in the same buffer at T = 298 K. Twenty-five 12.0 μL injections were preceded by one 2.0 μL injection, which was omitted for data analysis. After subtraction of background heats, the data were analyzed by a single-site binding model using the Origin software (provided by Microcal) with the values of binding stoichiometry, ΔH°, and K_d allowed to vary to optimize the fit. Measurements were conducted 2-4 times. For measurements of ΔC_p, solutions of arylsulfonamide > 1 mM (> 1000K_d) in 20 mM sodium phosphate pH 7.5 were titrated with at least seven 10 μL injections of ∼100 μM BCA (concentration determined by UV spectrophotometry) in the same buffer. The individual peaks were averaged, subtracted by the heat of dilution of protein into buffer alone (without ligand), and normalized to the number of moles of BCA added to yield an estimate of ΔH°. These measurements were conducted at 288, 298, and 308 K. Linear-regression analysis of ΔH° vs. T gave an estimate of °C_p.