Multimodal Pressure Flow Analysis: Application of Hilbert Huang Transform in Cerebral Blood Flow Regulation

Abstract

Quantification of nonlinear interactions between two nonstationary signals presents a computational challenge in different research fields, especially for assessments of physiological systems. Traditional approaches that are based on theories of stationary signals cannot resolve nonstationarity-related issues and, thus, cannot reliably assess nonlinear interactions in physiological systems. In this review we discuss a new technique “Multi-Modal Pressure Flow method (MMPF)” that utilizes Hilbert-Huang transformation to quantify dynamic cerebral autoregulation (CA) by studying interaction between nonstationary cerebral blood flow velocity (BFV) and blood pressure (BP). CA is an important mechanism responsible for controlling cerebral blood flow in responses to fluctuations in systemic BP within a few heart-beats. The influence of CA is traditionally assessed from the relationship between the well-pronounced systemic BP and BFV oscillations induced by clinical tests. Reliable noninvasive assessment of dynamic CA, however, remains a challenge in clinical and diagnostic medicine.

In this brief review we: 1) present an overview of transfer function analysis (TFA) that is traditionally used to quantify CA; 2) describe the a MMPF method and its modifications; 3) introduce a newly developed automatic algorithm and engineering aspects of the improved MMPF method; and 4) review clinical applications of MMPF and its sensitivity for detection of CA abnormalities in clinical studies. The MMPF analysis decomposes complex nonstationary BP and BFV signals into multiple empirical modes adaptively so that the fluctuations caused by a specific physiologic process can be represented in a corresponding empirical mode. Using this technique, we recently showed that dynamic CA can be characterized by specific phase delays between the decomposed BP and BFV oscillations, and that the phase shifts are significantly reduced in hypertensive, diabetics and stroke subjects with impaired CA. In addition, the new technique enables reliable assessment of CA using both data collected during clinical test and spontaneous BP/BFV fluctuations during baseline resting conditions.

I. Introduction

Previous works have demonstrated that fluctuations in physiological signals carry important information reflecting the mechanisms underlying control processes and interactions among organ systems at multiple time scales. A major problem in the analysis of physiological signals is related to nonstationarities (statistical properties such as mean and standard deviation vary with time), which is an intrinsic feature of physiological data and persists even without external stimulation.^1–3 The presence of nonstationarities makes traditional approaches assuming stationary signals not reliable. To resolve the difficulties related to nonstationary behavior, concepts and methods derived from statistical physics have been applied in the studies of different control mechanisms including locomotion control,^4–6 cardiac regulation,^{7, 8} cardio-respiratory coupling,^9–11 renal vascular autoregulation,¹² cerebral blood flow regulation,^13–16 and circadian rhythms.^17–19 One of the innovative approaches applied to physiological studies is Hilbert Huang transform (HHT) ²⁰. The HHT is based on nonlinear chaotic theories and has been designed to extract dynamic information from nonstationary signals at different time scales. The advantages of the HHT over traditional Fourier-based methods have been appreciated in many studies of different physiological systems such as blood pressure hemodynamics ²¹ , cerebral autoregulation ^{13, 15, 16}, cardiac dynamics ²², respiratory dynamics ²³,and electroencephalographic activity²⁴. In this review, we focus on the computational challenge on the quantification of interactions between two nonstationary physiologic signals. To demonstrate progress in resolving the generic problem related to nonstationarities, we review the recent applications of nonlinear dynamic approaches based on HHT to one specific physiological control mechanism—cerebral blood flow regulation.

Cerebral autoregulatory mechanisms are engaged to compensate for metabolic demands and perfusion pressure variations under physiologic and pathologic conditions.^{25, 26} Dynamic autoregulation reflects the ability of the cerebral microvasculature to control perfusion by adjusting the small-vessel resistances in response to beat-to-beat blood pressure (BP) fluctuations by involving myogenic and neurogenic regulation. Reliable and noninvasive assessment of cerebral autoregulation (CA) is a major challenge in medical diagnostics. Transcranial Doppler ultrasound (TCD) enables assessment of dynamic CA during interventions with sudden systemic BP changes induced by the Valsalva maneuver (VM), head-up tilt and sit-to-stand test in various medical conditions.^{13, 26–34} Conventional approaches typically model cerebral regulation using mathematical models of a linear and time-invariant system to simulate the dynamics of BP as an input to the system, and cerebral blood flow as output. A transfer function is typically used to explore the relationship between BP and cerebral blood flow velocity (BFV) by calculating gain and phase shift between the BP and BFV power spectra.^{26, 35–40} Many studies have shown that transfer function can identify alterations in BP-BFV relationship under pathologic conditions such as stroke, hypertension, and traumatic brain injuries that are associated with impaired autoregulation. ^{26, 35–39, 41–43} This Fourier transform based approach, however, assumed that signals are composed of superimposed sinusoidal oscillations of constant amplitude and period at a pre-determined frequency range. This assumption puts an unavoidable limitation on the reliability and application of the method, because BP and BFV signals recorded in clinical settings are often nonstationary and are modulated by nonlinearly interacting processes at multiple time-scales corresponding to the beat-to-beat systolic pressure, respiration, spontaneous BP fluctuations, and those induced by interventions.

To overcome problems in CA evaluations related to nonstationarity and nonlinearity, several approaches derived from concepts and methods of nonlinear dynamics have been proposed. ^{13–16, 44–47} A novel computational method called multimodal pressure-flow (MMPF) analysis was recently developed to study the BP-BFV relationship during the Valsalva maneuver (VM).¹³ The MMPF method enables evaluation of autoregulatory dynamics based on instantaneous phase analysis of BP and BFV oscillations induced by the intervention (a sudden reduction of BP and BFV followed by an increase in both signals). The MMPF applies an empirical mode decomposition (EMD) algorithm to decompose complex BP and BFV signals into multiple empirical modes.²¹ Each mode represents a frequency-amplitude modulation in a narrow frequency band that can be related to a specific physiologic process. For example, this technique can easily identify BP and BFV oscillations induced by the VM (0.1-0.03 Hz, i.e., period ~10 to 30 sec). Using this method; a characteristic phase lag between BFV and BP fluctuations corresponding to VM was found in healthy subjects, and this phase lag was reduced in patients with hypertension and stroke.¹³ These findings suggested that BFV-BP phase lag could serve as an index of CA. However, intervention procedures, such as the VM, introduce large intracranial pressure fluctuations and also require patients’ active participation. As a result, such procedures are not applicable under various clinical conditions, such as in acute care settings.

It has been hypothesized that CA can be evaluated from spontaneous BP-BFV fluctuations during resting conditions.^14–16 This hypothesis has been motivated by the facts that i) CA is a continuous dynamic process so that it should always engage to regulate cerebral blood flow; and ii) BP and BFV display spontaneous fluctuations at different time scales^{38, 39, 48–50} even during resting conditions. Since spontaneous BP and BFV fluctuations can be entrained by respiration or other external perturbation over a wide frequency range [0.05-0.4 Hz] ^{51, 52} and the dominant frequency of spontaneous BP fluctuations varies among individuals over time and under different test conditions, reliable measures of the nonlinear BFV-BP relationship without pre-assuming oscillation frequencies and waveform shapes are needed. These requirements are well satisfied by the MMPF algorithm which extracts intrinsic BP and BFV oscillations embedded in the original signals and quantifies instantaneous phase relationship between them. If the MMPF is sensitive and can provide reliable estimation of autoregulation using spontaneous BP and BFV fluctuations, it is expected that, similar to BP and BFV oscillations introduced by the VM, spontaneous BFV and BP oscillations during resting conditions should also exhibit specific phase shifts.

In this review, we present an overview of the transfer function analysis (TFA) that was traditionally used to quantify CA (Sec. II) and of the MMPF method and its modifications (Sec. III). In Sec. IV, we introduce a newly developed automatic algorithm for the improved MMPF method as well as engineering aspects that will potentially lead to a fully automated analysis without expert input. In Sec. V, we review previous applications of MMPF in clinical studies,^{15, 16} in which the ability and reliability of the method in assessing the CA from spontaneous BP-BFV fluctuations during resting conditions were evaluated (Sec. V). Specifically, we discuss the MMPF results in three pathological conditions that are associated with cardiovascular complications affecting cerebrovascular control systems (stroke, hypertension and diabetes). ^53–57 Our previous studies have shown altered CA in these conditions.^{15, 16, 58} Additionally, a comparison of the MMPF and the TFA results in the study of type 2 diabetes was discussed. In Sec. VI, we discuss why nonlinear dynamic approaches such as the MMPF can more reliably quantify nonlinear relationship between nonstationary signals.

II. Transfer Function Analysis

Transfer function analysis which has been widely used in the CA assessment ^{35, 59} is based on Fourier transform. BP and BFV signals are decomposed into multiple sinusoidal waveforms in order to compare the amplitudes and phases of BP and BFV components at different frequencies. The coherence representing the degree of similarity in the variation (phase or amplitude) of two signals within specific frequencies, then, can be evaluated through the cross-spectrum. In general, a strong coherence indicates dysfunction of CA.

The BP and BFV time series are first linearly detrended and divided into 5000- point (100-sec) segments with 50% overlap. The Fourier transform of BP, denoted as S_p(f) , and BFV, denoted as S_V(f) , are calculated for each segment with a spectral resolution of 0.01Hz, and were used to calculate the transfer function

$$H(f)=\frac{S_p(f){\mathrm{S*}}_V(f)}{|S_p{(f)|}^2}=G(f)e^{j\varphi (f)}$$ (1)

where S_V^*(f) is the conjugate of S_V(f); |S_p(f)|² is the power spectrum density of BP; G(f)=|H(f)| is the transfer function amplitude (gain); and ϕ(f) is the transfer function phase at a specific frequency f. The amplitude and the phase of the transfer function reflect the linear amplitude and time relationship between the two signals. The reliability of these linear relationships can be evaluated by C(f), coherence that ranges from 0 to 1:

$$C(f)=\frac{{|S_P(f)S_V^{*}(f)|}^2}{|S_P{(f)|}^2|S_V{(f)|}^2}$$ (2)

A coherence value close to 0 indicates the lack of linear relationship between BP and BFV signals and, therefore, the linear relationship between BP and BFV estimated by the transfer function is not reliable. The absence of linear relationship between BP and BFV is usually assumed to reflect the nonlinear influence of CA.

Average coherence, gain, and phase are calculated in the frequency range below 0.07Hz in which the CA is assumed to be most effective ^{35, 39}. For comparison with the MMPF results, the same transfer function analysis is also performed in the same frequency range as the observed dominant spontaneous oscillations in BP and BFV.

III. Multimodal Pressure-Flow Method

The main concept of the MMPF method is to quantify nonlinear BP-BFV relationship by concentrating on intrinsic components of BP and BFV signals that have simplified temporal structures but still can reflect nonlinear interactions between two physiologic variables. The MMPF method includes four major steps: 1) decomposition of each signal (BP and BFV) into multiple empirical modes; 2) selection of empirical modes for (dominant) oscillations in BP and corresponding oscillations in BFV; 3) calculation of instantaneous phases of extracted BP and BFV oscillations; and 4) calculation of biomarker(s) of CA based on BP-BFV phase relationship.

The improved MMPF method provides a more reliable estimation of BP-BFV phase relationship by implementing a noise assisted EMD, called ensemble EMD (EEMD)⁶⁰, to extract oscillations embedded in nonstationary BP and BFV signals. The EEMD technique can ensure that each component does not consist of oscillations at dramatically disparate scales, and that different components are locally non-overlapping in the frequency domain. Thus, each component obtained from the EEMD may better represent fluctuations corresponding to a specific physiologic process. To demonstrate such an advantage of the EEMD, we will apply the method to extract dominant spontaneous BP-BFV oscillations during baseline resting conditions, and compare the results to those obtained from the traditional EMD method.

A. Empirical mode decomposition

To achieve the first major step of MMPF, we originally utilized the empirical mode decomposition (EMD) algorithm, developed by Huang et al. ²¹ to decompose the nonstationary BP and BFV signals into multiple empirical modes, called intrinsic mode functions (IMFs). Each IMF represents a frequency-amplitude modulation in a narrow band that can be related to a specific physiologic process ²¹.

For a time series x(t) with at least 2 extremes, the EMD uses a sifting procedure to extract IMFs one by one from the smallest scale to the largest scale

$$\begin{array}{lll}x(t)\hfill & =\hfill & c_1(t)+r_1(t)\hfill \\ \hfill & =\hfill & c_1(t)+c_2(t)+r_2(t)\hfill \\ \hfill & ⋮\hfill & \hfill \\ \hfill & =\hfill & c_1(t)+c_2(t)+\cdots +c_n(t)\hfill \end{array}$$ (3)

Where c_k(t) is the k-th IMF component and r_k(t) is the residual after extracting the first k IMF components $\{\text{i.e.}{r}_k(t)=x(t)-{\displaystyle \sum _{i=1}^k{c}_i(t)\}}$ Briefly, the extraction of the k-th IMF includes the following steps:

1. Initialize h₀(t)=h_i−1(t)=r_k−1(t) (if k=1, h₀(t)=x(t)), where i=1;

2. Extract local minima/maxima of h_i−1(t) (if the total number of minima and maxima is less than 2, c_k(t)= h_i−1(t) and stop the whole EMD process);

3. Obtain upper envelope (from maxima) and lower envelope (from minima) functions p(t) and v(t) by interpolating local minima and maxima of h_i−1(t), respectively;

4. Calculate $h_i(t)=h_{i-1}(t)-\frac{p(t)+v(t)}{2}$;

5. Calculate the standard deviation (SD) of $\frac{p(t)+v(t)}{2}$;

6. If SD is small enough (less than a chosen threshold SD max, typically between 0.2 and 0.3) ²¹, the k-th IMF component is assigned as c_k (t) = h_i(t) and r_k (t) = r_k−1(t) − c_k (t); Otherwise repeat steps (ii) to (v) for i+1 until SD<SDmax.

The above procedure is repeated to obtain different IMFs at different scales until there are less than 2 minima or maxima in a residual r_k−1(t) which will be assigned as the last IMF (see the step ii above).

B. Ensemble Empirical Mode Decomposition (EEMD)

For signals with intermittent oscillations, one essential problem of the EMD algorithm is that an intrinsic mode could comprise of oscillations with very different wavelengths at different temporal locations (i.e., mode mixing). The problem can cause certain complications for our analysis, making the results less reliable. To overcome the mode mixing problem, a noise assisted EMD algorithm, namely the Ensemble Empirical Mode Decomposition (EEMD), has been proposed ⁶⁰. The EEMD algorithm first generates an ensemble of data sets obtained by adding different realizations of white noise to the original data. Then, the EMD analysis is applied to these new data sets. Finally, the ensemble average of the corresponding intrinsic mode functions from different decompositions is calculated as the final result. Shortly, for a time series ) x(t), the EEMD includes the following steps:

1. Generate a new signal y(t) by superposing to x(t) to a randomly generated white noise with amplitude equal to certain ratio of the standard deviation of x(t) (applying noise with larger amplitude requires more realizations of decompositions)

2. Perform the EMD on y(t) to obtain intrinsic mode functions;

3. Iterate steps (i)–(ii) m times with different white noise to obtain an ensemble of intrinsic mode function (IMFs)

   $$\{c_k{}^1(t),k=1,2\dots n\},\{c_k{}^2(t),k=1,2\dots n\},\dots ,(c_k{}^m(t),k=1,2\dots n\};$$

4. Calculate the average of intrinsic mode functions $\{\overline{c_k(t)},k=1,2,n\}\text{where}\overline{c_k(t)}=\frac{1}{m}{\displaystyle \sum _{i=1}^m{c}_k^i}(t)$.

The last two steps are applied to reduce noise level and to ensure that the obtained IMFs reflect the true oscillations in the original time series x(t). In this study, we repeats decomposition m times (m>=200) to make sure the noise is reduced to negligible level.

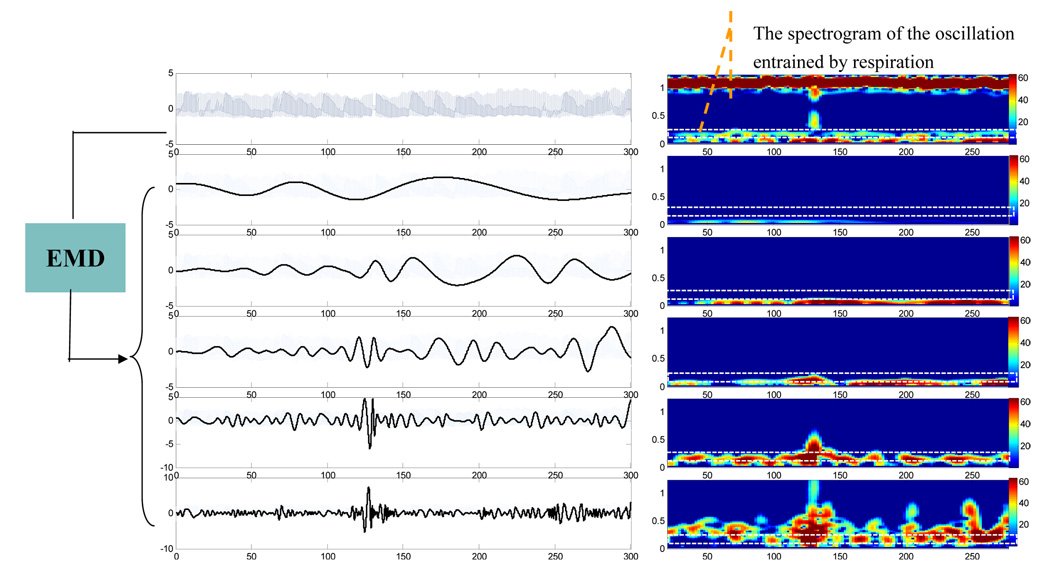
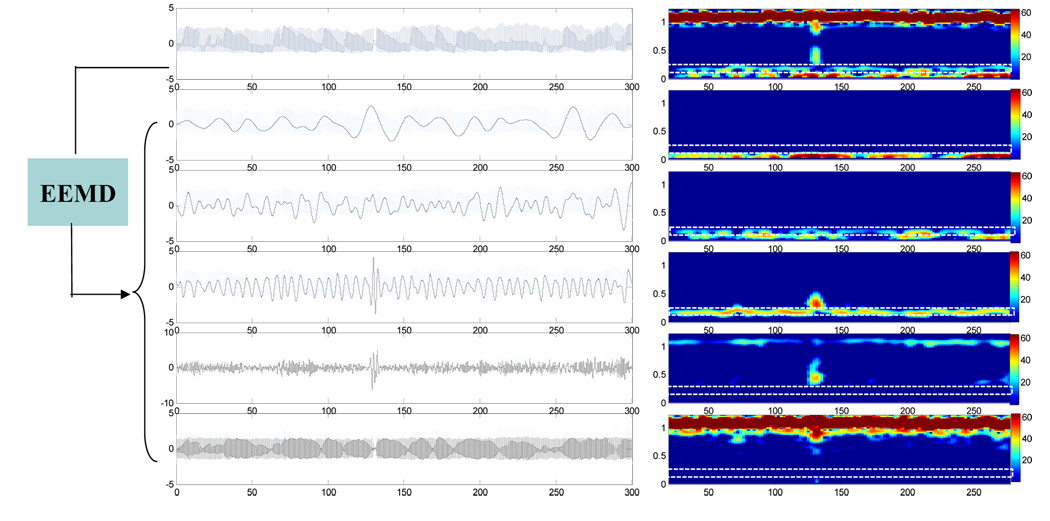
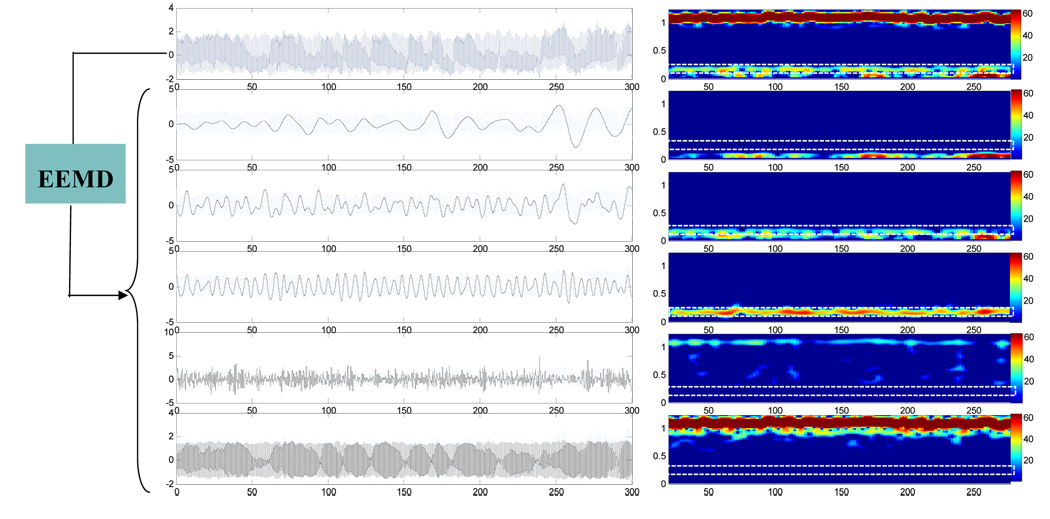
To illustrate the mode mixing problem, we applied both EMD and EEMD to BP signal of a healthy subject. Figure 1 shows the results of the EMD. The left-side panels of Fig. 1 show the original BP signal (the top plot) and the decomposed IMFs (modes 9–5 from the second to the bottom plots). For each plotted signal on the left side of Fig. 1, the corresponding short-time Fourier transform (STFT) spectrogram was obtained by applying Fourier transform in overlapped Gaussian sliding windows (the window size is 40 seconds and 2 second shift between two successive windows), and was plotted using color mapping on the right side of Fig. 1. As shown in the rectangle area of the STFT spectrograms of raw BP signals (marked using white line, the top panel of the right side in Fig. 1), the instantaneous frequency of spontaneous oscillation entrained by the respiration is time dependent over the range of 0.18~0.3Hz. Both mode 5 and mode 6 IMFs from the EMD contain parts of respiration induced oscillations in BP at different time, i.e., no single IMF mode can reflect respiration influence consistently throughout the entire time series. In contrast, as shown in Fig. 2, the mode 7 IMF from the EEMD can fully represent the respiratory oscillations in BP, as indicated by the same STFT spectrogram of the IMF as the original BP signals in the frequency range of 0.18-0.3Hz. Using the EEMD, we also extracted the respiration induced oscillations in the simultaneously recorded BFV signal of the same subject (Mode 7 IMF in Fig. 3).

Figure 1.

(Left Panel) A raw BP signal and its decomposed empirical modes (i.e., c₅–c₉ components from bottom to top) obtained by the EMD method. (Right Panel) The corresponding short-time Fourier transform (STFT) spectrograms of the signals in Left Panel. The spectrogram was obtained using Gaussian sliding window with time duration of 40 seconds, shifted 2 seconds between successive evaluations and then plotted using color map.

Figure 2.

(Left Panel) The same BP signal as shown in Fig. 1 and its decomposed empirical modes (i.e., c₅–c₉ components from bottom to top) obtained by the EEMD method. (Right Panel) The corresponding short-time Fourier transform (STFT) spectrograms of the signals in Left Panel. The spectrograms were calculated and plotted using the same procedure discussed in Fig. 1. The noise ratio for EEMD method is 0.2.

Figure 3.

(Left Panel) A raw BFV signal and its decomposed empirical modes (i.e., c₅–c₉ components from bottom to top) obtained by the EEMD method. (Right Panel) The corresponding short-time Fourier transform (STFT) spectrograms of the signals in Left Panel. The spectrograms were calculated and plotted using the same procedure discussed in Fig. 1. The noise ratio for EEMD method is 0.2.

As shown in our simulation, EEMD ensures the decompositions to compass the range of possible solutions in the sifting process and to collate the signals of different scales in the proper IMF naturally. It produces a set of IMFs, each displaying a time-frequency distribution without transitional gaps. With the elimination of the mode mixing problem, the EEMD can better extract intrinsic mode(s) corresponding to specific physiologic mechanisms.

C. Mode selection

The second step of the MMPF is to choose an IMF for the BP and the corresponding IMF for the BFV signal. The choice seems rather subjective and any mode within the interested frequency range can be used. The following criteria are proposed for this step in order to improve reliability and robustness of MMPF results. The most important one is to ensure that the two chosen IMFs are matched, i.e., the extracted fluctuations in BP and BFV correspond to the same physiologic process. In addition, it is better to choose BP component that has reproducible patterns to minimize variability among different trials. For example, the initial MMPF study used the BP and BFV oscillations induced by interventions such as VM ¹³, and recent studies used the spontaneous BP and BFV oscillations entrained by respiration.^{15, 16} We will discuss these applications of the MMPF and its performance in Sec. IV.

D. Hilbert transform

The third major step of the MMPF analysis is to obtain instantaneous phases of the extracted BP and BFV oscillations (i.e. the IMFs correspond to specific physiology process). Note that the extracted BP and BFV oscillations are not stationary, i.e., their amplitude and frequency vary over time. Such nonstationary oscillations can be better characterized by analytical methods that can quantify the amplitude and phase (or frequency) at any given moment. Therefore, the MMPF uses Hilbert transform to obtain instantaneous phases of BP and BFV oscillation. Unlike the Fourier transform, Hilbert transform does not assume that signals are composed of superimposed sinusoidal oscillations with constant amplitude and frequency. Thus, the instantaneous phases obtained from Hilbert transform are more suitable for the assessment of the nonlinear relationship between complex oscillations ⁶¹.

In order to obtain instantaneous phases with appropriate physical meaning, Hilbert transform requires that an oscillatory signal should be symmetric with respect to the local zero mean and the numbers of zero crossings and extreme should be the same. The intrinsic mode function derived from the EMD method satisfies this requirement (see Sec. III A). For a time series s(t) its Hilbert transform is defined as

$$\tilde{s}(t)=\frac{1}{\pi }P{\displaystyle \int \frac{s(t\text{'})}{t-t\text{'}}dt\text{'}}$$ (4)

Where P denotes the Cauchy principal value. Hilbert transform has an apparent physical meaning in Fourier space: for any positive (negative) frequency f, the Fourier component of the Hilbert transform s̃(t) at this frequency f can be obtained from the Fourier component of the original signal s(t) at the same frequency f after a 90° clockwise (anticlockwise) rotation in the complex plane, e.g., if the original signal is cos(ωt), its Hilbert transform will become cos(ωt−90°)=sin(ωt). For any signal s(t), the corresponding analytic signal can be constructed using its Hilbert transform and the original signal:

$$S(t)\equiv s(t)+i\tilde{s}(t)=A(t)e^{i\phi (t)}$$ (5)

Where A(t) and φ(t) are the instantaneous amplitude and instantaneous phase of s(t), respectively.

In particular, the instantaneous BP and BFV phases are calculated on a sample by sample basis. The BP-BFV phase shift for each subject is calculated as the average of instantaneous differences of BFV and BP phases over the entire baseline. The instantaneous BP-BFV phase shift is averaged over a prolonged time period to provide statistically robust phase estimates.

E. MMPF autoregulation indices

The last step of the MMPF is to derive indices of CA from the instantaneous phases of BP and BFV oscillations. It is believed that CA leads to fast recovery of BFV in response to BP fluctuations and, thus, the phases of BFV oscillations are advanced compared to BP phases. For simplicity of statistical analysis, originally the phase shift at the minimum and maximum of these two signals is used as the index of CA ¹³. To provide statistically more robust phase estimates, the BP-BFV phase shift for each subject can be calculated as the average of instantaneous differences of BFV and BP phases over the course of the VM or spontaneous oscillations.¹⁶

IV. Computer-Assisted Program for MMPF Analysis

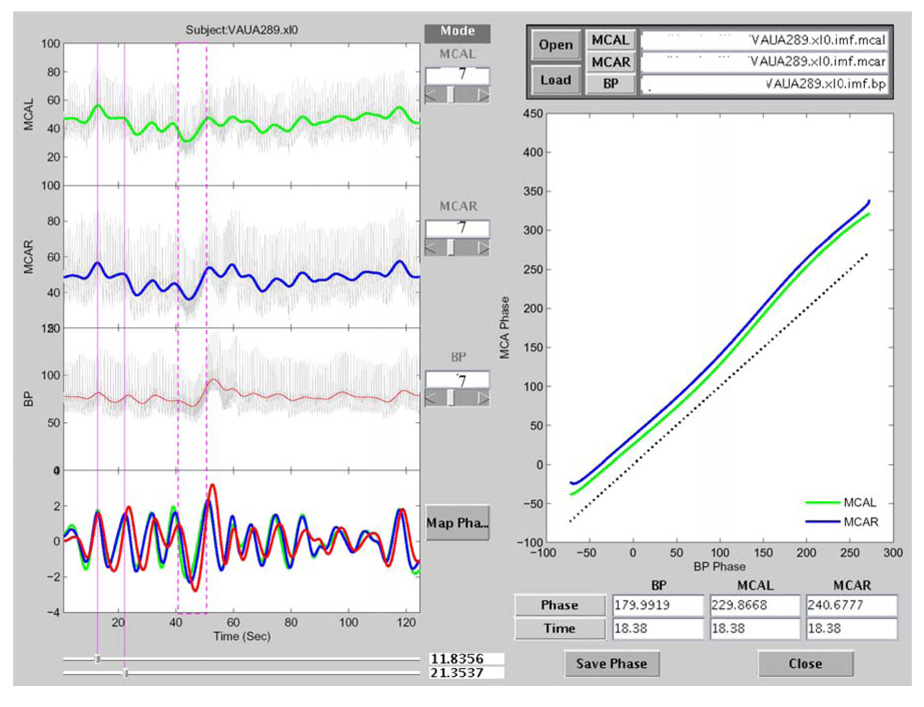
To implement steps C–E in the MMPF analysis, a software package was developed to load the decomposed intrinsic modes of BP and BFV signals, to allow the selections of BP and BFV components, and to calculate the MMPF autoregulation index (Fig. 4). In previous version of the MMPF software, the selection of BP and BFV components had been done manually, i.e., a researcher will pick an intrinsic mode after visualizing all components decomposed by the EMD or EEMD. The manual selection is useful, but it requires fully understanding the MMPF algorithm and all technical details of the program execution. Moreover, the manual selection needs human inputs and it is time consuming. Therefore, the best solution would be to enable a program-based automatic selection according to the defined criteria for mode selection, described in Sec. III C. As a first step to achieve this goal, we have designed a computer-assisted program to select the respiratory-modulated oscillation from the decomposed IMF modes. In this program, the STFT spectrogram analysis, a well-known method of time frequency analysis, is performed for all decomposed modes (right panel of Fig. 2 and Fig. 3). For each mode, the instantaneous mean frequency for each sliding window is obtained. The IMF with the mean frequency oscillating mostly in a selected frequency range (e.g., 0.1~0.4 Hz for spontaneous oscillations during baseline conditions) is automatically picked as the default mode to be used for the assessment of autoregulation. With the illustrated spectrograms, the default mode can also be manually verified or modified to ensure that the automated selection is appropriate. The same procedure is used to obtain both spontaneous oscillations in BP and the corresponding oscillations in BFV. Finally, the instantaneous BP and BFV phases are calculated using Hilbert transform on a sample by sample basis. The instantaneous BP-BFV phase shift for each subject is averaged over 5 minutes and is used as an index of the dynamic CA.

Figure 4.

Screen copy of the MMPF analysis software (adapted from Ref. 15). The data shown in this plot are from a healthy subject. The top three panels on the left show BFV (left side and right side) and BP signals, respectively. The colored curves in these panels show the results after removing faster fluctuations from the original signals. The bottom left panel shows the corresponding intrinsic modes for these three signals (red: BP; blue: BFV on right side; green: BFV on left side). The vertical red dashed box (around 40–50 seconds) identifies part of the VM period. The spontaneous oscillations in these signals during resting conditions prior to the VM can also be visualized. One of these oscillations (around 14–22 seconds) is identified by two vertical red lines. The result of the BP-BFV phase shift analysis of this period is plotted in the right panel. A reference line (dotted black line), indicating synchronization between BP and BFV, is shown in this panel for easy comparison. The result is representative of normal autoregulation where BFV leads BP (by about 50 degrees in phase).

V. Performance of Improved MMPF

A. Assessment of autoregulation in healthy control, hypertensive and stroke subjects during resting condition

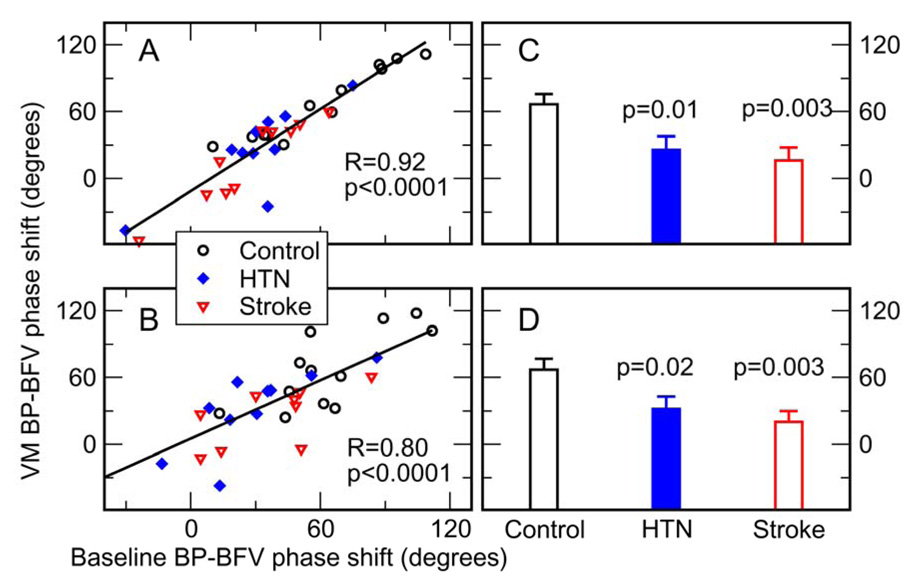
To test whether the MMPF can evaluate the dynamics of CA from spontaneous BP-BFV fluctuations during supine rest, our recent study compared the BP-BFV phase shifts obtained from BP and BFV oscillations introduced by the VM and from spontaneous BP-BFV oscillations during supine baseline.¹⁵ Data of 12 control, 10 hypertensive and 10 stroke subjects during VM and baseline resting condition were analyzed using the improved MMPF method. Spontaneous oscillations (period: mean±SD, 15.7±9.2 seconds) in the same frequency range as the VM oscillations (17.7±7.9 seconds, pair t-test p=0.37) were chosen. BP-BFV phase shifts during spontaneous oscillations (ranging from ~−60 to 120 degrees) were highly correlated to those obtained from VM oscillations (left side middle cerebral arteries R=0.92, p<0.0001; right side R=0.80, p<0.0001) (Figure 5). Consistently, the paired-t test showed that the average BP-BFV phase shifts during baseline were statistically the same as the values during the VM (p>0.47). These results indicate that the MMPF method can enable reliable assessment of CA dynamics and its impairment under pathologic conditions using spontaneous BP-BFV fluctuations.

Figure 5.

Comparison of the BP-BFV phase shift during two different conditions and between control, hypertensive (HTN), and stroke groups. (A–B) (adapted from Ref. 15). For each subject in this study, BP-BFV phase shifts for left (A) and right (B) side middle cerebral arteries (MCA) were measured during the Valsalva maneuver (VM) and during supine baseline conditions. The straight line is the linear regression fit of the data. The phase shifts during VM and baseline showed a strong correlation (left R=0.92, p<0.0001; right R=0.8, p<0.0001). (C–D). BP-BFV phase shifts during VM were smaller in hypertensive and stroke groups than in control group in both left and right MCAs (HTN: left p=0.01, right p=0.02; Stroke: left p=0.003, right p=0.003).

B. Measurement of cerebral autoregulation dynamics based on spontaneous oscillations entrained by respirations in diabetic subjects

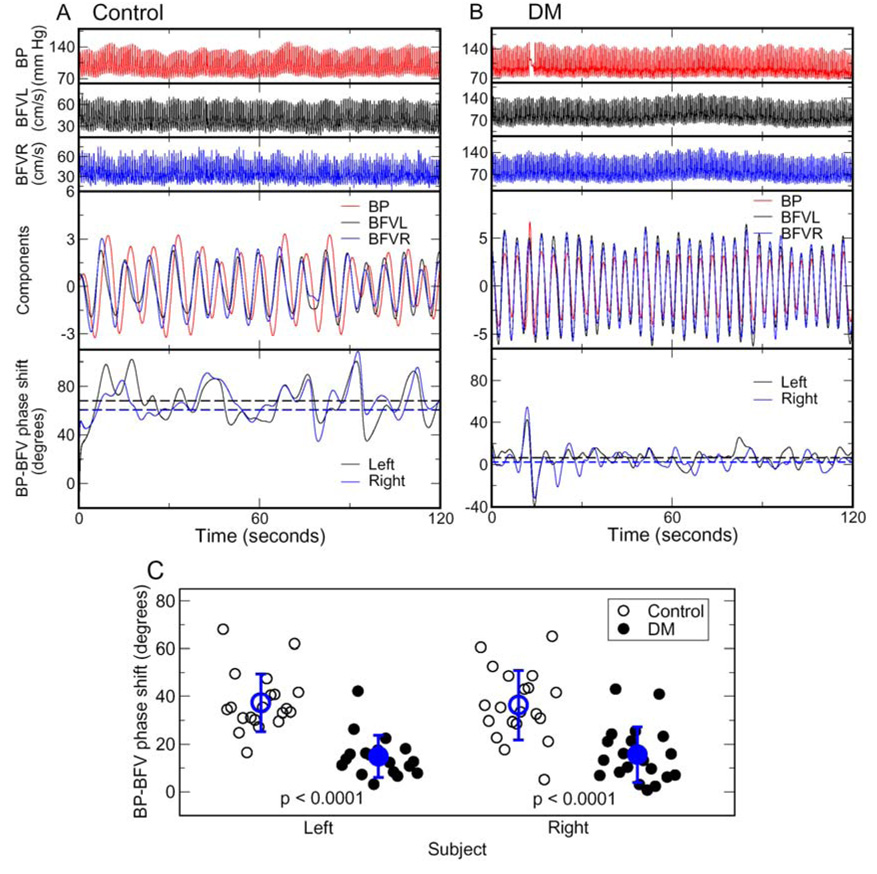
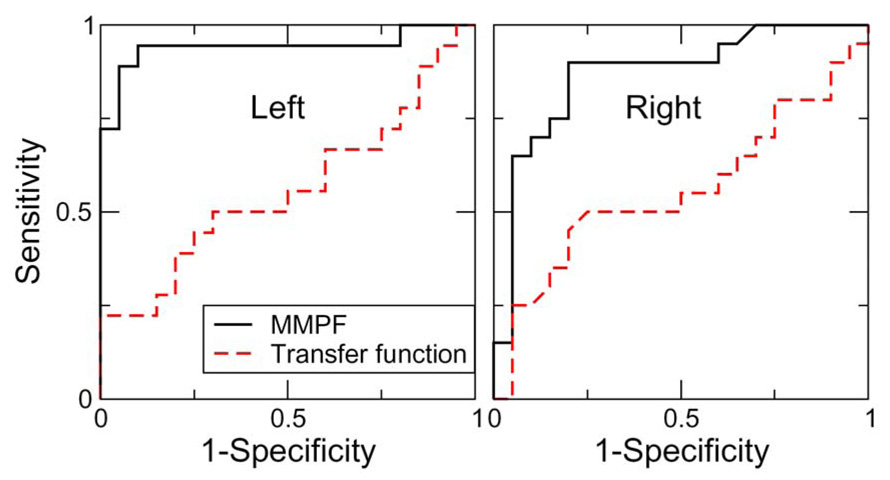
In our recent study ¹⁶, the MMPF method was applied to study the relationship between spontaneous BP-BFV oscillations at the respiratory frequency (~0.1–0.4Hz) in healthy (control) and diabetic subjects. The results showed that in healthy subjects, there were also specific phase shifts between spontaneous BP and BFV oscillations over this frequency range (0.1–0.4Hz) and that the phase shifts were significantly reduced in patients with type 2 diabetes, indicating altered dynamics of BP-BFV relationship, and thus impairment of vasoregulation in diabetic subjects (Fig.6). In contrast, the transfer function analysis was unable to show any significant group differences of phase shifts between BP and BFV signals at the frequency <0.07Hz in which CA is traditionally studied, as well as over the frequency range of 0.1–0.4Hz (see Table 1). The sensitivity and specificity of the MMPF and transfer function measures were compared using receiver operating characteristic (ROC) analysis ⁶² by comparing the areas under the ROC curves (AUC) between the control and diabetes groups. The ROC analysis showed that the AUC of MMFP-based phase shifts (left: 0.94±0.04; right: 0.87±0.06) are larger than those obtained by applying transfer function analysis (left: 0.56±0.09, p<0.001; right: 0.56±0.09, p=0.003) (Fig. 7), indicating that the BP-BFV phase shifts may serve as a more sensitive biomarker for the Diabetes Mellitus (DM) group than the traditional transfer function phase.

Figure 6.

Spontaneous oscillations of blood pressure (BP) and cerebral blood flow velocity (BFV) in (A) a 72-year-old healthy control woman and (B) a 52-year-old man with type 2 diabetes during supine baseline. Figure 6A was adapted from Ref. 16. BP, left and right BFVs (Panels 1 to 3 in A and B) were decomposed into different modes using ensemble empirical mode decomposition algorithm, each mode corresponding to fluctuations at different time scale. The components corresponding to respirations at frequency ranging from ~0.1 to 0.4Hz (the forth panels in A and B) were extracted and used for the assessment of BP-BFV relationship. Instantaneous phases of BP and BFV oscillations (solid lines in the bottom panels of A and B) were obtained using the Hilbert transform. There were large time/phase delays in BP oscillations compared to the BFV oscillations. For each subject, the average BFV-BP phase shift (horizontal dashed lines in bottom panels of A and B) was obtained as the average of instantaneous BFV-BPV phase shifts during the entire 5-min supine baseline. (C) Phase shifts between spontaneous oscillations of BP and BFV were much smaller in diabetes group than in healthy control group (p<0.0001). The group averages of control and diabetes are shown in blue symbols with error bars as the standard deviations. There was no significant difference in phase shifts between left and right blood flow velocities in both control and diabetes groups.

Table 1.

Transfer function results. Adapted from Ref 16.

Group	0.01— 0.07Hz			0.1—0.4Hz
	Control (n=20)	Diabetes(n=20)	p	Control (n=20)	Diabetes (n=20)	p
Coherence (left)	0.47±0.12	0.54±0.15	0.12	0.71±0.13	0.60±0.18	0.05
Coherence (right)	0.45±0.11	0.50±0.17	0.25	0.70±0.12	0.58±0.17	0.02
Gain (left)	0.67±0.42	0.67±0.42	0.98	1.07±0.27	0.68±0.34	0.0003
Gain (right)	0.65±0.43	0.59±0.36	0.64	1.01±0.33	0.63±0.34	0.0006
Phase (left)	36.9±32.1	44.3±32.5	0.49	20.6±8.8	19.5±10.4	0.73
Phase (right)	44.6±29.9	38.5±39.4	0.57	21.3±11.8	22.2±9.6	0.79

P values indicate between group comparisons.

Figure 7.

Receiver operating characteristic (ROC) curves for the DM prediction using BP-BFV phase shifts obtained from the MMPF method and using transfer function phases (0.1–0.4Hz) (adapted from Ref. 16). The y axis is the sensitivity, representing the percentage of DM subjects identified; and the x axis is 1-specificity; i.e., the percentage of control subjects that are incorrectly identified as DM subjects. The areas under the ROC curves (AUC) closer to 1.0 for BP-BFV phase shifts indicates that the MMPF measure serve as a better discriminator between the control and DM groups than traditional transfer function analysis.

VI. Discussion & Conclusion

Assessment of Nonlinear Interactions between Nonstationary Signals

Quantification of nonlinear interactions between two nonstationary signals presents a computational challenge in different research fields, especially for assessments of physiological systems. The computational approaches, based on traditional theories and methods, cannot resolve nonstationarity-related issues and be used reliably to study these systems. One possible and promising approach is to utilize and adopt concepts and methods derived from nonlinear dynamics that are designed to explore nonlinear interactions in nonstationary systems. In the last two decades, nonlinear dynamic approaches have been applied in many different biological fields such as cardiovascular system, respiration, locomotor activity, and neuronal activity in brain ^{11, 14, 63,64}. It has been gradually accepted that nonlinear dynamic methods can provide new information about the control mechanisms of physiological systems that may be difficult to be characterized using traditional approaches. In this review, we aim to demonstrate the point by discussing recent advance in the field of cerebral blood flow regulation and the contribution of a nonlinear dynamic approach as represented by the multimodal pressure flow method (as discussed in the following sections). Though the MMPF method has been mainly applied to assess the cerebral autoregulation, the concept of this approach is generally applicable for other physiological controls that involve interactions between two nonstationary signals. Designing and improving these approaches is crucial to tackle the generic problem related to nonstationarity.

Assessment of autoregulation from spontaneous BP and BFV oscillations

Autoregulatory responses are assessed by challenging cerebrovascular systems using interventions such as the VM, thigh cuff deflation and the head-up tilt ^{26–31, 65}. However, these intervention procedures may introduce large intracranial pressure fluctuations and require patients’ active cooperation. Therefore, they are not generally applicable in acute care clinical settings. In recent studies, an improved MMPF method was introduced to quantify the BP-BFV relationship in healthy, hypertensive and stroke subjects during supine resting conditions¹⁵. The results support the notion that autoregulation is a dynamic process and is always engaged even during resting conditions. Dynamic autoregulation is needed for continuous adjustment of cerebral perfusion in response to variations of autonomic cardiovascular and respiratory control (e.g., respiration, heart rate, blood pressure, vascular tone). Furthermore, applying the method to healthy and diabetic subjects, we showed that cerebral vasoregulatory processes that control pressure-flow relationship can operate at shorter time-scales (<10 seconds) than previously suggested (Fig. 6).

In this review we also introduced new results that present a significant improvement of MMPF method by introducing an automated mode selection algorithm that is based on time–frequency analysis. This approach allows objective mode selection based on time-frequency measures. Thus, the MMPF software is now more user-friendly and does not require computational knowledge to implement the MMPF technique for clinical evaluations.

Unlike traditional Fourier transform based approaches, the MMPF method does not assume the BP and BFV as superimposed sinusoidal oscillations of constant amplitude and period at a preset frequency range. Instead, the method adopts a new adaptive signal processing algorithm, EEMD, to extract dominant spontaneous oscillations that are actually embedded in the BP and BFV fluctuations. Since spontaneous oscillations that are related to a specific physiology process are usually nonstationary (i.e., statistical properties such as mean levels and oscillation period vary over time and change for different subjects), the conventional filters that are based on Fourier or wavelet theories are not reliable or valid for the extraction of embedded spontaneous oscillation from the BP and BFV signals. In this paper, we demonstrated that the EEMD can accurately extract oscillations associated with respirations from nonstationary BP and BFV signals. This result indicates that the EEMD can serve as a blind time-variant filter to extract the embedded nonstationary oscillations adaptively. Studying spontaneous BP and BFV oscillations extracted by the EEMD method revealed advanced phases in BFV compared to those in BP, i.e., flow oscillations preceded systemic pressure oscillations. These BP-BFV phase shifts were similar to those observed during the VM at the BP minimum and maximum ¹³. Such positive phase shift has also been reported using Fourier transform methods during head-up tilt, and is interpreted as the faster recovery of BFV caused by the compensation of cerebral vasoregulation.³⁰ In our study, we showed that BP-BFV phase shifts of spontaneous oscillation for hypertensive, stroke subjects were significantly reduced when compared to healthy subjects as shown by previous studies during the VM.¹³ Therefore, the BP-BFV phase shifts derived from the spontaneous oscillations can also be used as the indicator of dynamic CA.

Frequency dependence of cerebral autoregulation

It has been proposed that autoregulatory mechanisms act as a highpass filter—cybernetic model,^{35, 37} being more active at lower frequencies (<0.1Hz) and less effective for faster spontaneous fluctuations and at respiration frequency. Though there is no established physiologic neural pathway that can account for the highpass filter mechanism, the frequency dependent influence of CA has been supported by many studies that are based on the transfer function analysis.^{39, 40, 42, 66} It is important to note that coherence, gain, and phase of transfer function are continuous functions of frequency and do not exhibit an apparent transition point at a specific frequency. Thus, the frequency-dependent influence of CA, as suggested by the model and transfer function results, does not indicate a cutoff frequency beyond which CA has no influence on blood flow regulation. Nevertheless, many studies used ~0.1Hz as an upper frequency boundary for the transfer function analysis, such choice of frequency range for the estimation of CA seems rather arbitrary. Since previous studies showed that blood flow level after induced sudden blood reduction can be restored within 3–6 seconds (corresponding to 0.16–0.33Hz in frequency domain),^{67, 68} there is no reason to refute that CA can modulate the relationship of BP and BFV at frequencies faster than 0.1Hz. Indeed, there were already studies indicating that BP and BFV oscillations at frequencies faster than 0.1Hz may also provide useful information on CA.^{14, 69}

Moreover, the transfer function analysis is based on Fourier transform that implicitly assumes stationary signals composed of sinusoidal oscillations of constant amplitude and period. However, real-world recordings, such as BP and BFV signals, are usually nonstationary and exhibit dynamic changes over time (e.g. shifts of respiratory frequencies, occurrence of spontaneous waves, etc). Therefore, a single transfer function may not be sensitive enough to identify the influences of CA on relationship between the BP and BFV oscillations at all time scales.

It is intriguing that the MMPF analysis revealed a specific phase shift between BP and BFV oscillation in the frequency range of ~0.1–0.4Hz in control subjects, and this phase shift was significantly reduced in diabetic subjects. These findings strongly support that CA is a continuous dynamic process, influencing BP-BFV relationship over a frequency range (>0.1Hz) that is beyond previously ranges recognized. However, transfer function analysis could not identify this alteration in BP-BFV phase relationship in diabetic subjects in this frequency range, suggesting that inherent nonlinearities of CA may be better described by nonlinear methods such as the MMPF and multivariate coherence–an approach that takes into account contributions of other inputs, e.g., pressure and cerebrovascular resistances.⁴⁶

Comparison of the MMPF method and traditional CA approaches

The observation that transfer function analysis (TFA) cannot, but the MMPF can, show difference in phase relation between systemic BP and BFV in type 2 diabetes, may lead to following explanations: 1) TFA quantifies pressure and flow relationship in a specific frequency range , while MMPF is not frequency dependent. Therefore, these two methods may quantify different aspects of underlying mechanisms responsible for blood flow regulation. 2) Sensitivities of these two methods are different so that their performances in a small sample size of subjects can be different. As shown by previous studies, both TFA and MMPF can identify alterations in blood flow regulation in pathologic conditions such as stroke, hypertension, and traumatic brain injuries that are associated with impaired autoregulation. These findings indicate that both methods can quantify CA using BP and cerebral BFV, but do not explain different results in diabetic patients. The second possibility comes from the fact that TFA usually focuses on the frequencies below 0.1Hz while MMPF does not assume frequency range, i.e., MMPF extracted dominant oscillations that are truly embedded in data. Thus, the optimal frequency range to distinguish the difference between controls and diabetics in blood pressure and blood flow relationship is not known. In this study, we found that there were no group differences in TFA results in the frequency range 0.01–0.07 Hz (in which CA was traditionally believed to affect pressure and flow relationship). The frequency of dominant oscillations in blood pressure and flow extracted by MMPF was from 0.1 to 0.4Hz. However, BP-BFV phase obtained from TFA for the frequency range 0.1–0.4 Hz showed no difference between controls and diabetic subjects, either (see Table 1). This finding refutes the notion that the differences in results detected by TFA and MMPF are merely due to differences in frequency range. Therefore, the differences in sensitivity of both methods offer explanation for discrepancy in the CA estimates in diabetic patients. Consistently, we found that the BP-BFV phase shift had a better performance in discriminating between control subjects and subjects with type 2 diabetes (Fig. 7). The different results obtained from the two analyses may not be surprising because the BP-BFV phase shifts of transfer function analysis are based on the Fourier transform which is not applicable to nonstationary BP and BFV signals and nonlinear BP-BFV relationship. Comparisons of the MMPF and the TFA performance was done only using data obtained from patients with type 2 diabetes. It would be desirable to further establish reliability and repeatability of these methods in other pathological conditions that are known to impair cerebral autoregulation.

This review was focused on the MMPF method. There are other approaches from nonlinear dynamics such as phase synchronization technique,¹⁴ multiple multivariate coherence ⁴⁶, and general Volterra-Wiener approaches ^{44, 45, 47} that have been used to quantify cerebral autoregulation but could not be covered in this short review. More systematic studies are necessary to evaluate advantages and disadvantages of these innovative methods during different physiological and pathological conditions.

In conclusion, CA dynamics can be reliably estimated from spontaneous BP and BFV fluctuations during baseline resting conditions, and the BFV-BP phase shift obtained by the improved MMPF method is a sensitive and reliable measure of blood flow regulation and can be potentially used to monitor autoregulation in subjects with cerebromiscrovascular diseases

Abbreviations

MMPF

Multimodal Pressure Flow method

EMD

empirical mode decomposition

EEMD

ensemble empirical mode decomposition

IMF

intrinsic mode functions

BP

blood pressure

BFV

blood flow velocity

VM

Valsalva maneuver

TCD

transcranial Doppler

CA

cerebral autoregulation