Firing synchronization and temporal order in noisy neuronal networks

Abstract

Noise-induced complete synchronization and frequency synchronization in coupled spiking and bursting neurons are studied firstly. The effects of noise and coupling are discussed. It is found that bursting neurons are easier to achieve firing synchronization than spiking ones, which means that bursting activities are more important for information transfer in neuronal networks. Secondly, the effects of noise on firing synchronization in a noisy map neuronal network are presented. Noise-induced synchronization and temporal order are investigated by means of the firing rate function and the order index. Firing synchronization and temporal order of excitatory neurons can be greatly enhanced by subthreshold stimuli with resonance frequency. Finally, it is concluded that random perturbations play an important role in firing activities and temporal order in neuronal networks.

Introduction

After the famous papers by Watts and Strogatz (1998) and by Barabási and Albert (1999), complex systems started to be described within the framework of complex networks. It is well known that a single neuron in the vertebrate cortex connects to more than 10,000 postsynaptic neurons via synapses forming a complex network (Gerstner and Kistler 2002). The emergent property of this dynamical system is that a set of neurons will synchronize and fire impulses simultaneously. In the context of neuroscience, this emergent property is used to implement quite sophisticated and highly specialized "logical" functionalities such as memorization with Hebbian learning, and recognition of patterns (or memories).

During the past decades, synchronization phenomena of coupled systems (Pecora and Carroll 1990; Rosenblum et al. 1996; Shuai and Durand 1999; Rulkov et al. 1995) have been extensively studied in various fields of science, such as circuits (Chua et al. 1993), engineering (Li and Chen 2003) and biophysics (Jirsa 2008; Heinzel et al. 2007) etc. The observations of synchronous neural activity in the central nervous system (Gray et al. 1989; Eckhorn and Bauer 1988) suggest that neural activity is a cooperative process of neurons and synchronization plays a vital role in information processing in the brain, for example, in processing information from different sensory systems to form a coherent and unified perception of the external world.

Noise exists widely in natural systems, such as in physics, chemistry, biology, economy and engineering. The phenomena of stochastic resonance (SR) (Neiman et al. 1998; Longtin and Chialvo 1998) and coherence resonance (CR) (Longtin 1997; Baltanás and Casado 2002) have been extensively studied over the last two decades. Actually, in neural systems, noise arises from intrinsic and extrinsic sources, such as the random switching of ion channels, the quasi-random release of neurotransmitter by the synapse, and most important random synaptic input from other neurons. Noise was traditionally seen as a disturbance which limits the accuracy of information transfer, while it is true that intrinsic noise presented in excitable cells can play a relevant role in signal detecting and processing (Casado 2003). However, intracellular recordings from cortical neurons in vivo exhibit large and rapid fluctuations of the membrane potential from many synaptic events (Jagadeesh et al. 1992). Hence, the effects of noise on neuronal networks should be studied extensively so as to get better insight into complex collective rhythms and the cooperative operations of neural firing.

All of the results presented in the study of synchronization in population of interacting nonlinear oscillators can be applied to understand some key issues in neuroscience. Noise-induced complete synchronization of two uncoupled identical Hindmarsh–Rose neurons was reported in He et al. (2003). However, the authors only presented the result when neurons exhibited chaotic bursting. The synchronization behaviour of a pair of Hodgkin-Huxley neurons due to the existence of conductance (channel) noise was studied in the excitable region, in which neurons were incapable to fire spontaneously in the absence of noise (Casado 2003; Casado et al. 2003). The effect of noise on coupled nonidentical excitable Morris–Lecar neurons was discussed in Postnov et al. (2000), in which the noise intensity was considered as a frequency mismatch parameter and the connection between noise-induced synchronization phenomenon of oscillators and coherence resonance effect was presented. However, spiking and bursting, with regular or chaotic dynamic behaviour, are two main firing patterns for a single neuron. In this article, we will discuss noise effects on firing synchronization (including complete synchronization and phase synchronization) of coupled spiking or bursting neurons.

Since neurons are known to be noisy analogue units, noisy neurons coupled via synapses can carry out complex and advanced collective activities and cognitive operations with high reliability (Izhikevich 2000). The coherence of an array of Morris–Lecar neurons coupled via chemical synapses was studied with the noise level changed (Balenzuela and Garcĺa-Ojalvo 2005). Results showed that chemical synapses were more efficient than gap junctions in enhancing coherence at optimal noise (known as array-enhanced coherence resonance). Perc studied the effect of spatio-temporal additive noise on the spatial dynamics of excitable neuronal media (Perc 2005). It was shown that there existed an optimal noise intensity at which spatial coherence resonance was maximal. Effects of small-world connectivity on noise-induced temporal and spatial order in neural media were also investigated in Perc (2007). They found that the introduction of long-range couplings induced disorder of noise-induced patterns observed by exclusive diffusive connectivity of spatial units. Indeed, spatio-temporal dynamics in spatially extended systems with the support of noise are one of the most flourishing and fascinating topics of research in the field of nonlinear science. We will also discuss noise effects on firing synchronization and temporal order in a noisy map neuronal network as a prototype.

An outline of this paper is given as follows. Noise-induced complete synchronization and frequency synchronization in coupled noisy neurons with the effects of noise coupling are presented in section “Firing synchronization in coupled noisy neurons”. Section “Firing synchronization and temporal order in a square lattice noisy neuronal network” investigates firing synchronization resonance and temporal order in a noisy map neuronal network with subthreshold stimuli. Finally, conclusion and discussion are given in section “Conclusion and discussion”.

Firing synchronization in coupled noisy neurons

Synchronous neuronal firing has been suggested as particularly relevant for neuronal signal transmission and coding. And Firing synchronization is the simplest spatial pattern in neuronal networks. After achieving the firing synchronization, neurons in the network will fire simultaneously (complete synchronization) or their phases have some relations (phase synchronization). In this section, we mainly discuss the effects of the noise on firing synchronization of coupled neurons in networks, without considering the effect of network structure.

Hindmarsh–Rose neuron model

The three-variable Hindmarsh–Rose (HR) model of action potential (Hindmarsh and Rose 1984) was proposed as a mathematical representation of the firing behaviour of neurons, and it was originally introduced to give a bursting type with long interspike intervals (ISIs) of real neurons. It can be used to simulate spiking/bursting and chaos phenomena in real neurons. The equations of HR model are given as follows:

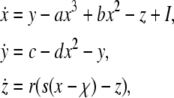1

where x represents the membrane action potential, y is a recovery variable associated with the fast current, Na⁺ or K⁺, and z is a slow adaptation current such as Ca²⁺; and a, b, c, d, r, s and χ are constants; I is the external direct current. In the following numerical simulations, let a = 1.0, b = 3.0, c = 1.0, d = 5.0, r = 0.006, s = 4.0, χ = −1.6 and choose I as a control parameter to produce various firing patterns.

Complete synchronization

When one deals with coupled oscillators, complete synchronization appears as the equality of the state variables while evolving in time. In neural systems, a neuron connected to another group of neurons may receive a common input signal, which often approaches a Gaussian distribution as the result of integration of many independent synaptic currents. In general, when two neurons start from different initial conditions, the spike timings of them may not coincide finally, that is, complete synchronization may not be achieved. However, when a suitable randomly fluctuating injection current is applied to them, the spike timings is possible to be driven into synchronization, which is called noise-induced synchronization.

As for how to evaluate complete synchronization of coupled noisy neurons, we begin with a general system with temporal evolution governed by the following equation:

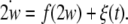Here 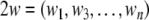is an n-dimensional state vector, 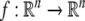is a vector function and 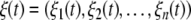with ξ_i(t) being the Gaussian white noise (GWN) with the statistical property 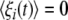and 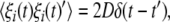where D is the noise intensity and δ(·) is the Dirac delta-function. Through a bidirectional electrical coupling between subsystems, we obtain a coupled system as follows:

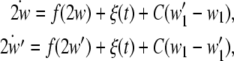2

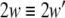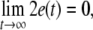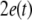in which C ≥ 0 is the coupling strength, as a special case, C = 0 means no coupling between subsystems. In this framework, complete synchronization is defined as the identity between the trajectories of subsystems. Then the existence of complete synchronization requires that the synchronization manifold is asymptotically stable, or equivalently, where is the synchronization error defined by 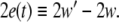This stability property usually can be justified by using the stability analysis of the following linearized system for small 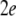and weak noise:

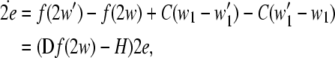3

where 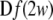is the Jacobian matrix of the vactor field f evaluated onto the trajectory of any subsystem of the synchronous coupled system, and the coupling matrix H is a constant n × n matrix, in which the element H₁₁ = 2C and all the others are equal to zero. This linearized Eq. 3 has the same form as that of the corresponding noise-free system, while the trajectory of 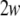here is different from that of the noise-free system. Based on the linearized dynamics, Lyapunov exponents are well defined similar to that in the deterministic case, and two neurons will reach complete synchronization when the largest Lyapunov exponent becomes negative.

Consider a network of two electrically coupled identical noisy HR neurons. The model is described by the following equations:

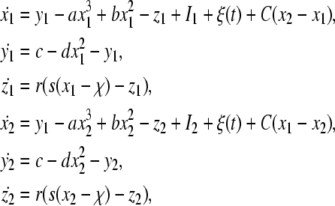4

in which the external direct current I₁ = I₂ = I is chosen as a control parameter, the term C(x₁−x₂) (or C(x₂−x₁)) represents the coupling term and C is the coupling strength, and ξ(t) is GWN with the noise intensity D. In what follows, we consider two situations, that is, complete synchronization of both uncoupled and coupled neurons with common noise. Complete synchronization of two uncoupled identical HR neurons forcing by a common GWN was also reported by He et al. (2003), where neurons only exhibited chaotic firing. However, here we focus on how firing patterns (including spiking and bursting) influence synchronization of both uncoupled and coupled neurons.

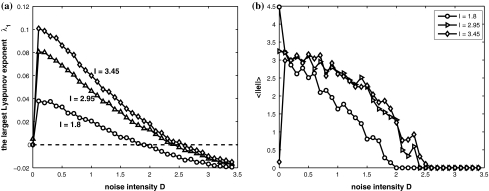
Firstly, consider two uncoupled identical HR neurons driven randomly by a common GWN, with the model given by (4) for C = 0. We change the value of the parameter I to obtain different firing patterns of neurons. Especially, choose I = 1.8 for period-2 bursting, I = 3.45 for period-2 spiking, and I = 2.95 for chaotic firing pattern. Then we calculate the largest Lyapunov exponent λ₁ as a function of the noise intensity D for these values of I. In parallel, the average synchronization error between two neurons defined by 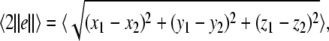in which the brackets denote time averaging, is also computed. It is seen that λ₁ undergoes a transition from positive to negative at a critical noise intensity from Fig. 1a and the synchronization error vanishes beyond this critical value from Fig. 1b. Therefore, complete synchronization can be achieved due to appropriate noise even though there is no coupling between two HR neurons.

Fig. 1.

Noise-induced complete synchronization of two uncoupled identical HR neurons driven by GWN. (a) The largest Lyapunov exponents λ₁ versus the noise intensity; (b) the mean synchronization error 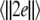versus the noise intensity for I = 1.8 (○), I = 2.95 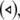and I = 3.45 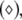respectively

Secondly, coupled neurons are often subjected to a common random forcing of GWN. Thus it is interesting to study the effect of interplay between noise and coupling of neuronal systems to complete synchronization. In Shi and Lu (2005), we have considered complete synchronization of two coupled HR neurons and derived the critical values of the coupling strength for different firing patterns with external current being varied. For weak coupling strength (such as C = 0.1), two coupled identical HR neurons cannot reach complete synchronization in the absence of noise. Hence, we further consider the effect of noise to complete synchronization in these weakly coupled HR neurons here.

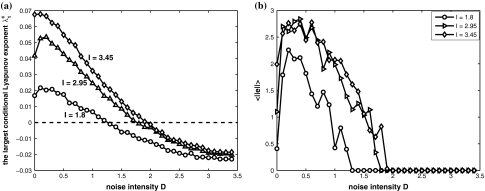
Consider system (4) of two electrically coupled HR neurons driven by a common GWN for C = 0.1. The largest conditional Lyapunov exponent λ^c₁ and the average synchronization error 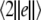as functions of the noise intensity D are calculated for different external direct currents as shown in Fig. 2. It can be seen that λ^c₁ undergoes a transition from positive to negative at a critical noise intensity, and the synchronization error vanishes beyond this critical value. Therefore, appropriate noise may also induce complete synchronization in coupled neurons.

Fig. 2.

Noise-induced complete synchronization of two coupled identical HR neurons driven by GWN. (a) The largest conditional Lyapunov exponents 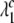versus the noise intensity; (b) the mean synchronization error 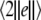versus the noise intensity for I = 1.8 (○), I = 2.95 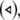and I = 3.45 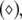respectively. Here, the coupling strength C = 0.1

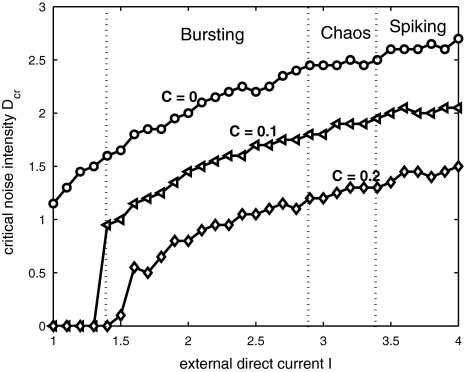
It is also seen from Fig. 2 that the critical noise intensity increases with the increase of the external direct current. The relations between the critical noise intensity and the external direct current for different couplings are shown in Fig. 3. It is seen that the critical noise intensity for coupled neurons decreases with the coupling strength being increased. This implies that coupling between neurons can enhance the sensitivity of synchronization to noise.

Fig. 3.

The critical values of the noise intensity for complete synchronization of two uncoupled neurons (○) or two coupled neurons 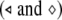and with a common GWN versus the external direct current

Taking account of the variation of the firing activities of the HR neuron with respect to the external direct current in Shi and Lu (2005), in which the firing pattern of a single HR neuron may transit from bursting to spiking with the current I being increased. It is shown in Fig. 3 that the critical noise intensity of bursting neurons for noise-induced synchronization is less than that of spiking neurons under the same coupling. In fact, this can be explained by that burst synchronization of neurons only concerns the time evolution of slow-varying variables, but spike synchronization concerns that of whole variables, including both the slow-varying and fast-varying variables. Therefore, complete synchronization in bursting patterns is easier to realize than that in spiking patterns in general, no matter whether noise exists.

Frequency synchronization

Nonidentity is common in neurons, and it is important to study the synchronization phenomena of coupled nonidentical neurons. Due to the nonidentity of neurons, coupled neurons may be feasible to achieve phase synchronization or frequency synchronization, rather than complete synchronization.

If ϕ₁(t) is the phase of an oscillator and ϕ₂(t) is the phase of another oscillator coupled with the first one, then m:l phase synchronization can be formalized as |mϕ₁(t)−lϕ₂(t)| < {const, where m and l are integers. m:l frequency Synchronization is defined as frequency entrainment, provided that the frequencies of two oscillators are in rational relation, that is, |mω₁−lω₂| = 0, where m and l are the same as above. It can be shown that they are equivalent in certain sense.

For neurons stimulated by noise, the random fluctuation causes stochastic firing and the spike sequences may be influenced randomly. Under this situation, spikes are counted when the upstroke of the voltage variable reaching a given threshold value, say x = 0.8 here. Then the residence time between two successive spiking events is given by the sequence T_j = τ_j+1−τ_j, called interspike intervals, where τ_j is the time of the j-th spike. Correspondingly, the mean firing period of a stochastic spike sequence is defined by

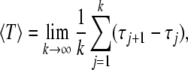and the mean firing frequency by 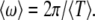With this definition, the simplest case of 1:1 frequency synchronization of two stochastic neurons for m = l = 1 is investigated later. Similar to the above subsection, we will discuss two situations in what follows.

Firstly, we explore the frequency synchronization of uncoupled noisy nonidentical HR neurons. The equations are given as follows:

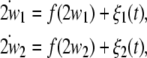5

where 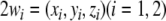denotes the state variables of the i-th HR neuron governed by (1), and 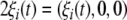with ξ_i(t) being GWN applied to the i-th neuron. The nonidentity between neurons is concerned by the differences between the external currents I₁ and I₂ as well as the noise intensities D₁ and D₂ of two neurons.

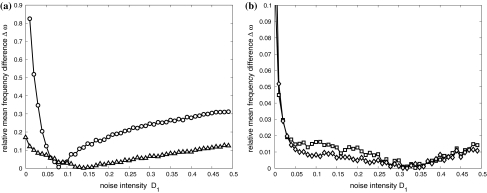
Fix D₂ = 0.05 for the second neuron while let D₁ for the first neuron changeable. Taking account of versatility of neuronal firing patterns, we choose the external currents I₁ = 1.25, I₂ = 1.3 for excitable states; I₁ = 1.45, I₂ = 1.5 for periodic bursting states; I₁ = 3.0, I₂ = 3.05 for chaotic firing states and I₁ = 3.6, I₂ = 3.65 for periodic spiking state, respectively. The dependence of the relative mean frequency difference 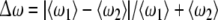on the noise intensity D₁ is plotted in Fig. 4. It is shown that mean frequency locking occurs in a very narrow interval of D₁ for different firing patterns. It is obvious that the critical noise intensity (about D₁ = 0.15) for bursting neurons to reach frequency synchronization is smaller than that (about D₁ = 0.3) for spiking neurons. Therefore, similar to complete synchronization, noise-induced frequency synchronization in bursting patterns is also easier to realize than that in spiking patterns.

Fig. 4.

The diagrams of the relative mean frequency difference 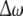versus the noise intensity D₁ for uncoupled HR neurons with different firing patterns. (a) excitable state (○) and periodic bursting 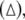(b) chaotic firing 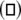and periodic spiking 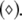Here D₂ = 0.05

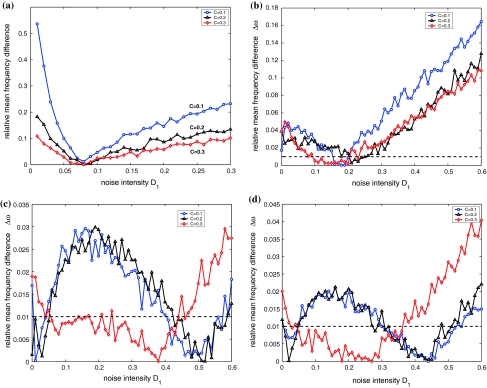
Secondly, we consider the frequency synchronization of weakly coupled noisy nonidentical HR neurons. From numerical simulations, if there is no noise, two neurons with the above firing patterns could not achieve frequency locking when the coupling strength C is less than 0.3. When noise is taken into account, the variation of the relative mean frequency difference with respect to the noise intensity D₁ is calculated for D₂ = 0.05 and I₁, I₂ chosen above. The coupling strength is fixed at C = 0.1, 0.2, 0.3, respectively. In all simulation results of Fig. 5, frequency locking is considered to be realized when the relative mean frequency difference is less than 0.01. It is evident that with the coupling strength being increased, the range of the noise intensity in which frequency synchronization occurs becomes larger for all firing patterns. It is also clear that when C = 0.3, the dependence of the mean frequency difference on the noise intensity may change greatly, see Fig. 9c and d.

Fig. 5.

The diagrams of the relative mean frequency difference 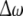versus the noise intensity D₁ for coupled HR neurons for different firing patterns. (a) Excitable state, (b) periodic bursting, (c) chaotic firing and (d) periodic spiking. Here D₂ = 0.05

Fig. 9.

Variations of the autocorrelation function c(τ) for the corresponding noise-induced patterns in Fig. 8 are shown in the upper and lower rows, respectively. The noise level D is (a) 0.0005, (b) 0.003, (c) 0.008. Here, the diffusive coefficient σ = 0.0025

Firing synchronization and temporal order in a square lattice noisy neuronal network

The Rulkov map neuronal network model

We consider an ensemble of identical 2D Rulkov map neurons diffusively coupled with nearest neighbours. The coupling implies the interaction of electrical synapses among neurons. The noisy Rulkov map neuronal network in a square lattice of size N × N is given by

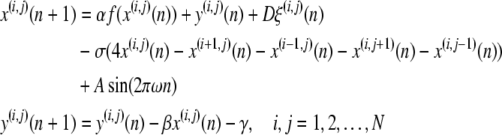6

where x^(i,j)(n) is the membrane potential of the (i,j)-th neuron, y^(i,j)(n) is considered as the variation of ion concentration , representing the fast and slow dynamics, respectively. The slow evolution of y^(i,j)(n) is due to the small values of parameters β and γ, with β = γ = 0.001 in this paper. n Is the discrete time, and α is a model control parameter. 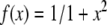is a nonlinear function, D denotes the noise level and ξ^(i,j) is the Gaussian white noise for the (i,j)-th neuron. σ is the diffusive coefficient. A and ω are the amplitude and frequency of the external stimulus, respectively. In this study, the periodic boundary condition is applied, thus setting x^(0,j)(n) = x^(N,j)(n), x^(N+1,j)(n) = x^(1,j)(n), x^(i,0)(n) = x^(i,N)(n), x^(i,N+1)(n) = x^(i,1)(n).

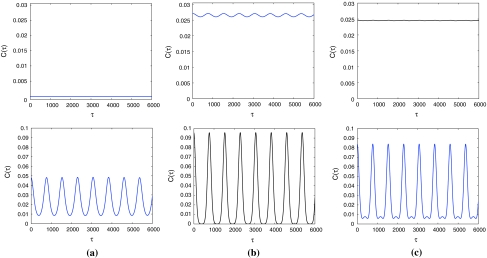
When a single neuron in the excitable steady state responds to suitable fluctuation of noise, it may fire stochastic periodic cycles, which has been extensively studied as stochastic resonance or coherence resonance for neuron models (Ray and Sengupta 2006; Neiman and Sung 1996; Miyakawa et al. 2003; Lee and Kim 1999; Plesser and Geisel 2001). Until recently, Jiang investigated resonances for the Rulkov map neuron model (Jiang 2005). It was shown that the excitable Rulkov map neuron may display both stochastic and coherence resonances, in response to periodic stimuli in the presence of different additive and parametric noises. Here, for a clear vision of this phenomenon, temporal evolutions for three different noise levels are shown in Fig. 6. It is observed in Fig. 6a that the noise level D is too small to evoke large amplitude excitations. For intermediate values of D, neurons start to produce large amplitude spikes with periodic-like firing as seen in Fig. 6b. If D is further increased, the number of spikes in a given time interval increases; however, larger D can increase the overall disorder in firing as shown in Fig. 6c. Hence, there exists an optimal D at which the noise-induced response of the Rulkov map neuron is well pronounced but still largely ordered. This phenomenon is known as coherence resonance in the Rulkov map neuron (Pikovsky and Kurths 1997).

Fig. 6.

Time series of the Rulkov map neuron for different noise levels without periodic stimuli. The noise level D is (a) 0.001, (b) 0.02, (c) 0.1

Firing synchronization and temporal order

Here we consider collective spatio-temporal dynamics in this Rulkov map neuronal network.

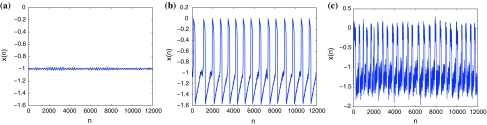
At first we briefly show the effect of noise on spatial patterns in this network. Without external stimuli, characteristic spatial rasters of x in a network of 128 × 128 size are presented in the upper row of Fig. 7 for different noise levels at a given discrete time n. As illustrated in the upper of Fig. 7a, under small noise levels, neurons cannot excite spikes to depict evident spatial structures. Nevertheless, under intermediate noise, noise-induced patterns emerge in the lattice, orderly propagating in the shape of beautiful circular waves as shown in the upper of Fig. 7b. With the noise level being increased further, ordered spatial patterns are destroyed by stronger noisy perturbations and then replaced by disordered random portraits as observed in the upper of Fig. 7c. More details about these spatial patterns resulted from spatial coherence resonance by noise can be referred to reference (Perc 2005).

Fig. 7.

Noise-induced spatial patterns in the Rulkov map neuronal network without subthreshold stimuli are shown in the upper row, and that with subthreshold stimuli are shown in the lower row. The values of x(i,j) are depicted at the point (i, j) in a 128  ×  128 square grid network at given time. The noise level D is (a) 0.0005, (b) 0.003, (c) 0.008. Here, the diffusive coefficient σ = 0.0025

If neurons in this Rulkov map neuronal network are subjected to the same subthreshold stimulus with A = 0.00125 and ω = 0.00130, which is close to natural frequency of the Rulkov neuron. Noise-induced spatial rasters of x at a given time in the network with subthreshold stimuli are shown in the lower row of Fig. 7. Compared with the upper row of Fig. 7b, it is obvious that the beautiful circular structure is distorted by subthreshold stimuli as shown in the lower of Fig. 7b but much more neurons are in the firing state. It can be seen later that this phenomenon is related to firing synchronization caused by subthreshold stimuli in this network.

Now we focus on the collective temporal behaviour of this Rulkov map neuronal network, especially firing synchronization and temporal order. In order to describe the dynamics of neuronal firing synchronization in this network, a firing rate function 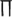is defined as follows. We call a Rulkov map neuron in firing state when its membrane potential x exceeds the threshold value x_th = −0.2. Suppose that m neurons are firing at a given discrete time n, then we define the firing rate function 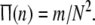This statistical function can simply measure the fraction of firing neurons in the network. Actually, 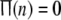means that none of neurons in this network is perturbed strongly enough for x to exceed the threshold x_th at given time n; while 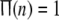indicates that all neurons are in firing state simultaneously at given time n, which implies global synchrony with the best temporal order in this network.

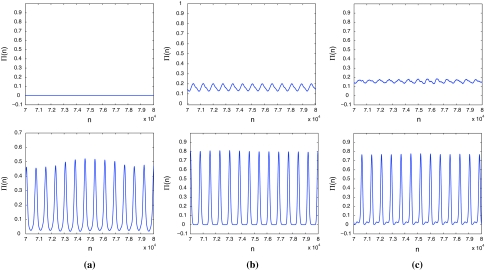
Corresponding the noise-induced spatial patterns in the upper row of Fig. 7, the temporal variations of the firing rate function are studied for different noise levels in Fig. 8. It is noticed in the upper of Fig. 8a that 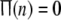and then no neuron is in firing state for very weak noise. Noise-induced firings can be observed for stronger noise with the maximum value 0.2 of the firing rate function in the upper row of Fig. 8. This means that at most 20 percent of neurons can fire simultaneously due to noise without external stimuli. Moreover, the firing temporal order at intermediate noise levels (see the upper of Fig. 8b) is better that at larger noise levels (see the upper of Fig. 8c).

Fig. 8.

Firing rate functions corresponding to the noise-induced spatial patterns in Fig. 7. The noise level D is (a) 0.0005, (b) 0.003, (c) 0.008. Here, the diffusive coefficient σ = 0.0025

Now we consider the ability of subthreshold stimuli to enhance firing synchronization and temporal order. The neurons in this network are subjected to the same subthreshold stimulus with ω = 0.00130 as before. Compared with the upper row of Fig. 8, the maximum value of the firing rate function is apparently increased as well as its periodicity shown in the lower row of Fig. 8. This implies that firing synchronization and temporal order can be greatly enhanced in the presence of subthreshold stimuli. Moreover, the firing rate function varies periodically at intermediate noise levels with the value higher than that for smaller or larger noise levels. For example, The maximum firing rate is 0.8 for D = 0.003 , which means that up to 80 percent of neurons can fire simultaneously; while it is at most 0.5 and 0.76 for D = 0.0005 and for 0.008, respectively. Consequently, there exists an optimal noise level with maximal firing synchronization and temporal order of neurons firing when subthreshold stimulus is turned on.

Based on the firing rate function, the autocorrelation function c(τ) is introduce as

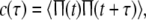7

where 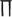is the firing rate function, τ the time delay, and 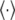denotes the average over time. If 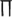is a periodic function of t, then c(τ) is also periodic to the same extent. c(τ) can be used in quantitative description of the firing temporal order; that is, larger amplitude and periodicity of c(τ) indicate higher temporal order of neurons; on the contrary, small-amplitude irregular oscillations of c(τ) indicate lower temporal order of neurons.

The temporal variation of the autocorrelation function c(τ) of this Rulkov map neuronal network without external stimuli is shown in the upper row of Fig. 9. Spiky and periodic variation of c(τ) at intermediate noise levels can be observed in the upper of Fig. 9b, which corresponds to higher temporal order of firing in this network. On the contrary, small amplitude fluctuation of c(τ) in the upper of Fig. 9c shows lower temporal order in this network.

When neurons are subjected to the subthreshold stimulus with ω = 0.00130, it should be noticed that periodic variation with large amplitude of c(τ) can be observed in the lower row of Fig. 9, regardless of the noise level. Then this subthreshold stimulus can clearly enhance the firing synchronization and temporal order of excitatory neurons in this network. Similar investigation has been conducted for subthreshold stimuli with different frequencies. Hence, it is shown that firing synchronization and temporal order can be greatly enhanced only when the stimulus frequency is very close to ω = 0.00130.

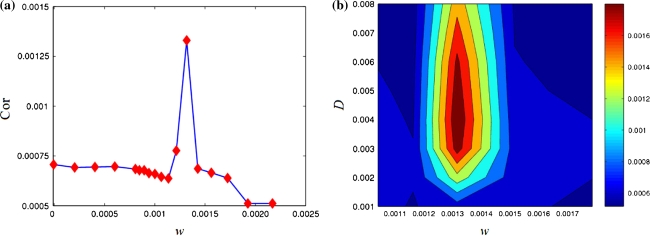
For better understanding temporal order, a characteristic quantity, the order index, is introduced by means of the autocorrelation function and defined as 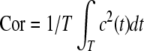(see Pikovsky and Kurths 1997). It is well-known that the more ordered this neuronal network is, the larger is its order index. Therefore, the order index can be used to measure the degree of temporal order in this neuronal network. Figure 10a shows the dependence of the order index on the frequency of subthreshold stimulus ω with fixed noise level D = 0.002. It is found that the order index has an abrupt peak when the subthreshold stimulus frequency is near ω = 0.00130, which is the natural frequency of the Rulkov map neuron. For smaller or larger stimulus frequencies, the order index is drastically decreased, resulting in a destruction of temporal order among neurons. This fact reveals the resonance essence of the enhancement of firing synchronization and temporal order by subthreshold stimuli.

Fig. 10.

(a) Dependence of the order index 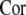on the frequency of subthreshold stimulus ω, (b) variation of the order index 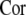with respect to the frequency ω of subthreshold stimulus and the noise level D. The colorbar shows the value of the order index

An overall inspection of the results of the order index for various D and ω are shown in Fig. 10b. It is obvious that for different values of D only when the stimulus frequency is very close to ω = 0.00130 the temporal order in the this network can be resonantly pronounced. More importantly, it is found that there exists an island at the center of Fig. 10b, where the order index reaches its maximum. Hence, the existence of the optimal noise and the resonance frequency for firing synchronization and temporal order support a complementary role of noise and external stimuli for the temporal dynamics in this network. However, as mentioned in the lower of Fig. 7b before, ordered noise-induced spatial patterns may be destroyed by subthreshold stimuli.

Conclusion and discussion

The effects of noise on firing synchronization of coupled neurons and a square lattice map neuronal network are investigated. Both complete synchronization and frequency synchronization in uncoupled and coupled noisy neurons can be achieved under suitable noise. The dependence of the critical noise intensity for noise-induced synchronization on the external current and the coupling strength is discussed. It is also found that it is easier to realize synchronization for bursting neurons than spiking ones. This fact implies the important role of bursting activities in information transfer in neuronal systems.

Furthermore, collective response of firing activities in a spatially extended noisy neuronal network is studied. Noise-induced firing synchronization and temporal order in the network can be greatly enhanced by subthreshold stimuli with the resonant frequency of neurons and reach maximum at an optimal noise level. However, as mentioned before, the enhancement of synchronization resonance by subthreshold stimuli is realized at the cost of the destruction of noise-induced ordered spatial patterns.