Olfactory system gamma oscillations: the physiological dissection of a cognitive neural system

Abstract

Oscillatory phenomena have been a focus of dynamical systems research since the time of the classical studies on the pendulum by Galileo. Fast cortical oscillations also have a long and storied history in neurophysiology, and olfactory oscillations have led the way with a depth of explanation not present in the literature of most other cortical systems. From the earliest studies of odor-evoked oscillations by Adrian, many reports have focused on mechanisms and functional associations of these oscillations, in particular for the so-called gamma oscillations. As a result, much information is now available regarding the biophysical mechanisms that underlie the oscillations in the mammalian olfactory system. Recent studies have expanded on these and addressed functionality directly in mammals and in the analogous insect system. Sub-bands within the rodent gamma oscillatory band associated with specific behavioral and cognitive states have also been identified. All this makes oscillatory neuronal networks a unique interdisciplinary platform from which to study neurocognitive and dynamical phenomena in intact, freely behaving animals. We present here a summary of what has been learned about the functional role and mechanisms of gamma oscillations in the olfactory system as a guide for similar studies in other cortical systems.

Introduction

Oscillations in the electrical activity of the brain have been known and explored since the early days of neurophysiology. Since many of the observed phenomena derive from investigations on animals’ sensory systems, much research in the area has been devoted to understanding oscillations in this context, both in the early and late stages of processing (Gray et al. 1989; Freeman 1991; Joliot et al. 1994; Tallon et al. 1995; Kay and Freeman 1998). Furthermore, since the time of Galileo’s studies on the pendulum in the seventeenth century (Galilei 1638; Acheson 1997), oscillatory phenomena have been fascinating researchers because they indicate dynamical systems, in which repetitive or periodic fluctuations of a variable develop over time generating a behavior that can be studied with mathematical tools. In the case of the brain, neural oscillations often reflect the behavior of cellular networks and, as such, they offer the researcher an occasion to explore the temporal evolution of interconnected neuronal groups during cognitive tasks. Thus, brain oscillations constitute a unique opportunity for interdisciplinary research to explore, at once, cognitive, neurobiological and dynamical phenomena. An adequate framework to study oscillations is then a critical tool for understanding the neurophysiological basis of an animal’s cognitive processing.

What we now know as gamma oscillations of the local field potential (LFP) were recorded in the olfactory bulb (referred hereafter simply as bulb or OB) of hedgehogs more than sixty years ago by Lord Edgar Douglas Adrian in England (Adrian 1942). Since then, gamma oscillatory activity has been studied extensively, with particular detail in the case of the mammalian OB. As a result, most of the cellular and network processes underlying these oscillations are now well established for this sensory system. In addition to the elucidation of these biophysical mechanisms, a large amount of research has started to provide insight about the physiological role of these oscillations.

This review presents the basic notions of olfactory system organization, a brief account of the historical and conceptual development of gamma oscillations, and a description of the corpus of research, both experimental and theoretical, about these oscillations in the context of mammalian olfactory systems.

Olfactory system organization

Airborne odorant molecules enter the nasal cavity upon inhalation and partition between the air and the mucus depending on their physicochemical features. Odorants dissolved in the mucus bind to odorant receptors and activate olfactory receptor neurons (ORNs), the primary sensory neurons of the olfactory system. ORNs are unique in that they make direct contact with chemicals in the environment and project directly to cortical neurons in the forebrain (the OB). In rodents, the majority of ORNs express only one type of receptor protein (Chess et al. 1994; Malnic et al. 1999; Rawson et al. 2000; Serizawa et al. 2000, 2004), and ORNs expressing the same receptor type converge to the same pair of glomeruli on opposing sides of a single OB (Mombaerts et al. 1996). A few large zones can be distinguished in the olfactory epithelium, where ORNs expressing the same receptor class are relatively confined. However, within each zone, cells expressing different receptors are scattered throughout and intermingled (Ressler et al. 1993). ORN projection to the OB is organized in what has been called rhinotopic and odotopic maps (Schoenfeld and Knott 2004). The rhinotopic organization refers to rostrocaudal air channels in the nasal cavity that contain neurons projecting to rostrocaudally-oriented areas of the OB. In addition, the central (medial) channels are mapped onto the dorsal OB, whereas more peripheral (lateral) channels are mapped onto the ventral bulb. Regarding the odotopic organization, ORN populations (expressing a particular receptor) are assorted in patches distributed along the central-peripheral axis within the olfactory epithelium, and project to specific positions in the OB (Schoenfeld and Knott 2004).

Odorant-elicited action potentials propagate along ORN axons, which project to the OBs, a pair of bean-shaped structures located anteriorly in the brain. In macrosmatic animals such as rodents and dogs, they constitute the most rostral part of the brain and comprise a large part of the telencephalon. On the contrary, primates are microsmatic mammals, in which the neocortex has developed to such extent that it overshadows the OBs. Carnivora and ruminants, on the other hand, constitute an intermediate group between these two extremes.

The OBs are composed of three-layered paleocortex, consisting mainly of three cell types: an excitatory projection neuron population, the mitral and tufted (M/T) cells (the principal cells of the bulb), that receive input from the ORNs, and two interneuron populations. Roughly speaking, glomeruli appear as a collection of sphere-like structures of neuropil covering most of the surface of the bulbs.

ORN terminals, which are glutamatergic, synapse in the glomeruli onto the apical dendritic tufts of M/T cells. Glomeruli are surrounded by a diverse interneuron population, the juxtaglomerular cells, composed of many different cellular types. It is now known that juxtaglomerular cells can both excite and inhibit activity of M/T cells and each other (Kosaka and Kosaka 2005; Wachowiak and Shipley 2006), although this was originally proposed by Walter Freeman and colleagues, as a result of physiological studies (Siklos et al. 1995). Within the glomeruli, M/T cell dendrites can also excite each other via glutamate spillover (Isaacson 1999). Juxtaglomerular cells can also affect the release of glutamate from the ORN axon terminals via presynaptic GABAergic and dopaminergic mechanisms (Hsia et al. 1999; Wachowiak et al. 2005; Vucinic et al. 2006). Deep to the glomerular layer are the external plexiform layer, containing mostly fibers and synapses, then the M/T cell layer, containing mostly the M/T cell bodies, the internal plexiform layer, and finally the granule cell layer in the center of the bulb. Granule cells are a large population of GABAergic interneurons that form reciprocal dendrodendritic synapses with M/T cells in the external plexiform layer, an important synapse in the generation of oscillations. Mutual inhibition, an interaction that can generate oscillatory behavior in the hippocampus (Whittington et al. 2000) has been postulated to exist between granule cells, because these cells express GABA receptors, and as a result of computational studies (Freeman 1979; Linster and Gervais 1996). M/T cells project their long axons outside of the OB to many parts of the olfactory and limbic systems and also form axodendritic synapses with OB granule cells via axon collaterals (Fig. 1).

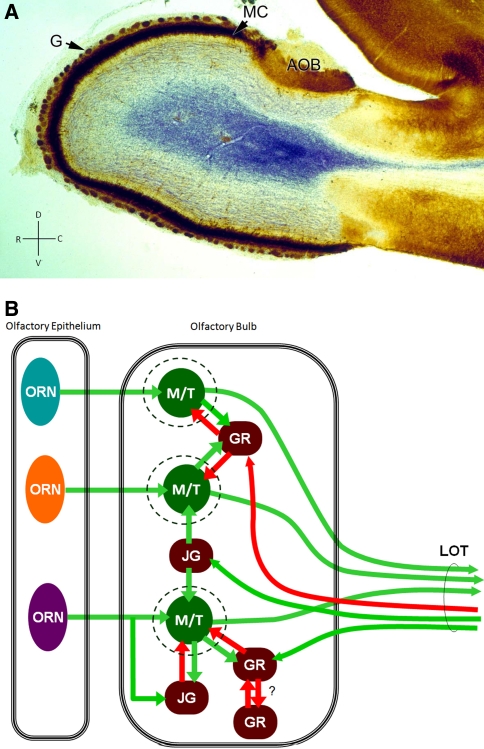
Fig. 1.

Neuronal layers, types and circuitry of the OB. (a) Sagittal section through a rodent OB. The olfactory nerve has been removed, although in the anterior surface of the bulb some remnants can be seen. Glomerular (G) layer and mitral cell (MC) layer are seen clearly. Axons of mitral cells are stained in blue (Nissl stain). AOB: Accessory OB. D, V, R, C: Dorso-Ventral and Rostro-Caudal axes. (b) Main components of the OB neuronal network. Not all the described interactions are shown. Green and red arrows represent excitatory and inhibitory synaptic interactions, respectively. A mutual inhibition relationship has been proposed by some authors between granule cells. ORN: Olfactory receptor neuron; M/T: Mitral and Tufted cells; GR: granule cell; JG: juxtaglomerular cell; LOT: Lateral olfactory tract. (a) taken from (Elsaesser and Paysan 2007) (publisher: BioMed Central)

Synaptic input to the OB from the brain is glutamatergic and GABAergic from many parts of the olfactory and limbic systems. Most of this input comes in onto the granule cells, but some reaches up into the glomerular layer (Shepherd et al. 2004). Modulator systems of all types project to the OB and affect synapses at all levels: serotonin from the raphe nuclei, noradrenaline from the locus coeruleus (Takeuchi et al. 1982), histamine and oxytocin from the hypothalamus (Inagaki et al. 1988; Yu et al. 1996), and acetylcholine from the horizontal nucleus of the diagonal band of Broca (Senut et al. 1989; Linster et al. 1999). Most of the dopamine in the OB comes from a population of juxtaglomerular cells (Halasz et al. 1977), but in sheep (and probably in other mammals) there is a small projection of neurons from the ventral tegmentum to the OB granule cell layer (Levy et al. 1999).

The OB projects to a set of brain structures collectively known as the primary olfactory cortex, with three main groups: the anterior olfactory nucleus, the rostral olfactory cortex and the lateral olfactory cortex (Shipley et al. 1995). Within the latter there is one of the most studied regions, the pyriform cortex (also spelled “piriform”) which receives very dense inputs from OB M/T cells in its anterior portion (anterior pyriform cortex) and weaker projections in its posterior portion (posterior pyriform cortex). Like the bulb, it is composed of paleocortex, with two populations of pyramidal cells. Bulb M/T cells project to many other parts of the limbic system, including the entorhinal cortex and amygdala. The OB receives inputs from most of the areas to which it projects, providing a rich anatomical substrate for complex dynamics.

Olfactory bulb gamma oscillations

Short historical review

The work of Lord Adrian in England (Adrian 1942) is usually regarded as the first one that described what we now call gamma oscillations. He subsequently recorded LFPs from the OB of anesthetized cats, rabbits, and hedgehogs (Adrian 1950), and reported two different kinds of what he called potential oscillations: one type was elicited by olfactory stimuli (which he called ‘induced’) and the other was spontaneously evoked (‘intrinsic’). The frequency of the induced oscillations varied in different experiments, lying in the 40–60 Hz range. Adrian found that these oscillations were associated with increased firing of M/T cells and noticed some correlation with the respiratory cycle.

About the same time a clinical group in the US showed that similar oscillations were induced in the OB of a human subject (Sem-Jacobsen et al. 1953) after the application of several odorants to the nostrils (liliac perfume, oil of lemon, benzene, coffee, tincture of valerian and others). The tip of the electrode was located in the vicinity of the bulb and the odorant-induced oscillations were found to appear in successive bursts of activity of 28–32 Hz in frequency and, contrary to Adrian’s findings, were absent at all stages of barbiturate anesthesia. Nevertheless, the authors were aware of Adrian’s work and noted the similarity between both types of oscillations, in one of the first reports of sensory-evoked electroencephalogram (EEG) oscillatory activity in humans.

Nearly a decade later, a Chilean-Mexican research group (Lavin et al. 1959; Hernandez-Peon et al. 1960) reported oscillations recorded from the OB of alert, unrestrained cats. They found that when cats were alerted by several stimuli (visual, acoustic, somatic or gustatory), oscillatory bursts in the range of 34–48 Hz were elicited. They dubbed these bursts of activity ‘arousal discharges’, since they were related to the alert state and were absent during anesthesia.

Walter J. Freeman, from the University of California at Berkeley (Freeman 1975; Freeman and Skarda 1985) also studied this oscillatory activity in the OB of awake cats and rabbits (35–90 Hz, centered around 40 Hz). Continuing on Adrian’s findings, he showed that the oscillations were synchronized to each inspiration, that is, bursts of gamma activity were correlated to air inflow over olfactory sensory neurons in the mucosa. Each burst begins shortly after inspiration and terminates during expiration. This is illustrated in Fig. 2.

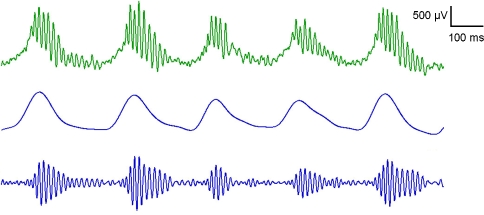
Fig. 2.

Gamma and theta LFP oscillations recorded from the OB of an awake, freely behaving rat. The top (green) trace shows raw LFP recording (1–475 Hz). Middle trace shows recording filtered between 1–12 Hz, revealing the Theta oscillation. Bottom trace displays the recording filtered between 65–100 Hz, showing the gamma oscillation. The theta oscillation can be used as a proxy for the animal’s respiration cycle, where the rising phase of the oscillation corresponds to inspiration and the falling phase to expiration. Note the correlation between the theta phase and the onset of gamma bursts. Upward deflection corresponds to positive polarity

Freeman’s research established gamma oscillations as a fundamental functional signal in the brain and proposed that this oscillatory activity serves a physiological role in olfactory perception. He developed a multi-site recording device that he used to record the LFP oscillations at the surface of the bulb of awake rabbits, measuring simultaneously from 64 electrodes. He discovered that odorant-evoked oscillations displayed the same frequency over broad regions of the bulb’s surface, and suggested that odor quality is likely to be encoded in the spatial amplitude pattern of activity following olfactory stimulation (Freeman and Schneider 1982; Di Prisco and Freeman 1985). Freeman and his colleagues found that the spatial pattern of activation corresponded primarily to the ‘meaning’ of the stimulus, being stable only once the particular odorant was associated with positive or negative reinforcement. Furthermore, when a rabbit learned a new odor-association pair, this changed the representations of previously learned odorants (Freeman 1991). These studies established a perceptual and cognitive structure for gamma oscillations, but proof of their functionality still remained.

Where does the name ‘gamma’ come from? Freeman and Bressler used the name ‘gamma rhythm’ for the first time in 1980 (Bressler and Freeman 1980), to designate activity in the range of 35–90 Hz recorded from the olfactory system (OB, anterior olfactory nucleus and pyriform cortex) of cats, rabbits and rats. Freeman claims to have coined the name ‘gamma waves,’ in analogy with the well known range of high-frequency electromagnetic radiation (Freeman 1991). Nevertheless, the name ‘gamma resonance’ was used previously by Erol Başar and Çiğdem Özesmi to refer to 60–80 Hz oscillations in the hippocampus of awake cats (Basar and Ozesmi 1972).

Gamma oscillations, as defined exclusively by their frequency range, have been found in several brain regions in both animals and humans (Buzsaki and Draguhn 2004). In humans, an early study reported bursts of 50 Hz activity in intracranial recordings from the temporoparietal lobes in response to photic stimulation (Chatrian et al. 1960). Shortly after this, the same group reported that similar activity (40–45 Hz) could be elicited by different kinds of sensory stimulation: auditory, painful, tactile, proprioceptive and olfactory (Pérez-Borja et al. 1961). Since then, several independent groups have shown gamma activity in different brain systems, not only LFP oscillations but also at more macroscopic (EEG) and microscopic (cellular) levels. Some examples are: mammalian thalamocortical networks (Steriade et al. 1996), hippocampus (Traub et al. 1998), auditory and visual systems (Gray et al. 1989; Joliot et al. 1994; Tallon et al. 1995), invertebrate ganglia (Schutt and Basar 1992), primate motor cortex (Donoghue et al. 1998), and many others.

Cellular mechanisms

How do OB gamma oscillations arise? What are the events at the cellular level that explain the potential fluctuations in the gamma frequency range?

These oscillations are observed as fluctuations of the LFP, an extracellular potential that arises from the current loops generated when the membrane potential of neurons changes. The usual analysis of electrical potential of neurons considers inward and outward currents, that is, charge flow through the neuronal membrane; to understand LFPs it is necessary to consider as well the movement of charge along the membrane. These extracellular and intracellular currents form loops that go through the membrane twice. When a dendritic terminal is depolarized, inward current flows, ions enter the cell at one point and exit to the extracellular space at some distant point, where the current is attracted to the original site of entrance. Hence, from the point of view of the extracellular space, we can consider different segments of the neuron as current sinks (if at these points current leaves the extracellular space and enters the cell) or sources (if current exits the cell to the extracellular space). The particular spatial organization and dynamical evolution of sinks and sources in a certain neuronal group is the generator of the LFP. Thus, the LFP is often referred to as the measure of input to a set of neurons, as it is associated with the flow of ions into or out of the cells at the postsynaptic side of the synapses. However, it also represents the state of the neural population and can be a surrogate measure for firing probability, as described below.

In the mammalian olfactory system, a central feature in the generation of oscillations is the reciprocal dendrodendritic synapse between M/T and granule cells in the OB (Shepherd 1972); this synapse can be considered as a physical realization of a negative feedback loop between these two kinds of cells. Stimulation of ORNs in the mucosa by odorants or airflow (Grosmaitre et al. 2007) generates action potentials that travel along the olfactory nerve and arrive at glomeruli, releasing glutamate and depolarizing the apical dendrites of M/T cells. This depolarization spreads along the cell membrane producing mainly two events: one, the (eventual) firing of action potentials that will travel along the lateral olfactory tract and excite pyramidal cells in the olfactory cortex, and two, depolarization of neighboring granule cells, which results in the local release of GABA from the interneuron, causing a disexcitation of the M/T cells and a consequent inhibition of the latter. In conditions of repetitive firing of olfactory nerve fibers onto M/T cells, this cycle repeats itself, giving rise to gamma oscillations.

In one of the earlier mathematical models of electric potential distribution in brain tissue, Wilfrid Rall and Gordon Shepherd reconstructed the LFP in the OB evoked by stimulation of the lateral olfactory tract (Rall and Shepherd 1968), using previous theoretical methods and experimental results (Rall 1962, 1964; Phillips et al. 1963; Rall et al. 1966). They found that this depolarization of M/T cells generated, sequentially, an extracellular current running radially from glomerular to deeper layers, and then a new extracellular current, lasting longer, running in the opposite direction (radially outward). These findings were compatible with a mechanism in which every time the M/T cell was excited (in this case the excitation was antidromically evoked, but it was equivalent to the case of M/T cell excitation by olfactory nerve terminals; see Fig. 3), this resulted in depolarization of granule cell dendrites, which in turn conveyed inhibition back to M/T cell dendrites (Fig. 4). Rall and Shepherd highlighted the crucial importance of this synapse in the physiological operation of the bulb and realized that this interaction offered a mechanism for the generation of the LFP oscillatory activity.

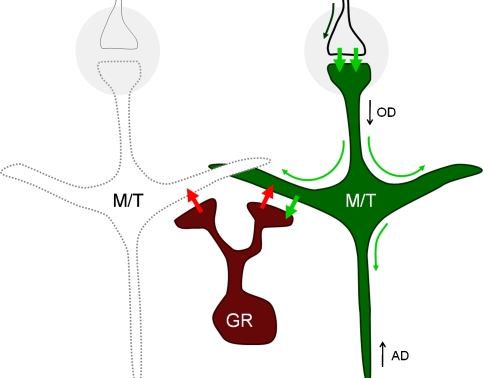
Fig. 3.

Reciprocal dendrodendritic synapse between M/T and granule cells. Action potentials from ORNs arrive at glomeruli (gray circles) and excite (short green arrows) M/T cells. This depolarization propagates from the postsynaptic membrane through the entire cell (long green arrows), resulting in excitation of granule cells through glutamate liberation at the dendrodendritic synapse. The excitation of granule cells causes them to liberate GABA (red arrows), eliciting recurrent and lateral inhibition of M/T cells. Note that due to the geometry of the arrangement, the same dynamical interactions can be elicited by antidromic activation of M/T cells. GR: granule cell. OD, AD: antidromic and orthodromic directions. After Rall et al. (1966)

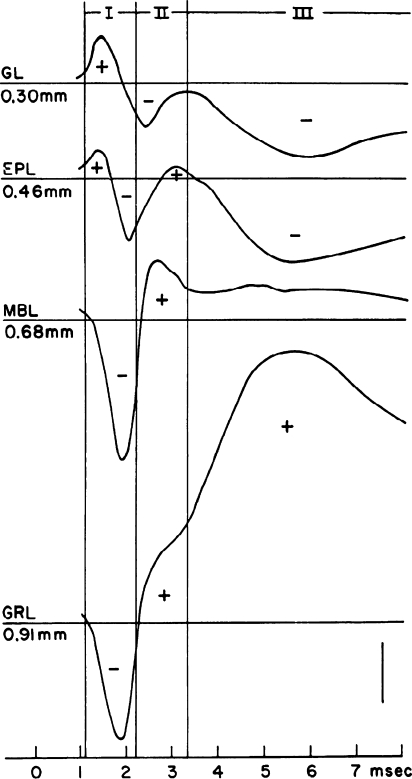
Fig. 4.

Antidromically evoked LFPs in the rabbit OB at different depths (indicated in mm). Animal was anesthetized. GL: glomerular layer; EPL: External plexiform layer; MBL: Mitral layer; GRL: granule cell layer. From Rall and Shepherd (1968), used with permission

If we now turn to extend these considerations to the OB network, we need to note that due to the widespread distribution of dendrodenritic contacts, activated M/T cells excite granule cells that also make contact with other M/T cells, and hence the activity of the interneuron results not only in recurrent but also in lateral inhibition (Fig. 3), a feature that may play an important role in the generation of widespread gamma oscillations (Bathellier et al. 2006). Thus, a plausible network mechanism could be as follows: odorant molecules binding to receptors excite a particular subset of olfactory sensory neurons, which results in the activation of a corresponding subset of M/T cells in the bulb; this subset fires and produces a stream of inhibitory postsynaptic potentials spread throughout the whole network, which prevents subsequent firing for a brief lapse due to the activation of the inhibitory interneurons. After this period, a new subset of M/T cells (that may or may not overlap with the previous one) is stimulated and fires again, which restarts the cycle. In addition to this process, lateral inhibition at the level of glomeruli has been described to occur, as a result of the activity of the short axon cells, a process that displays the structure of a center-surround inhibition among glomeruli, which could also contribute to the olfactory-evoked spatial patterns of activation of M/T cells (Aungst et al. 2003).

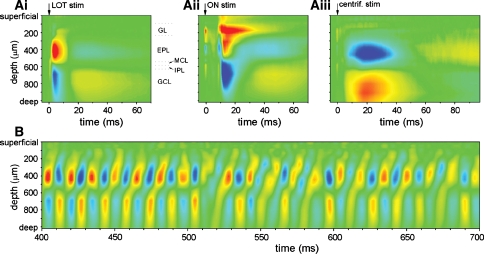
Since LFPs are generated by extracellular currents that connect inward and outward cell membrane currents, the only way to infer the underlying synaptic currents that support the field potential is to record at different sites along the length of the neural axis, and use these data to estimate the sources and sinks of current, a procedure called current source density (CSD) analysis (Mitzdorf 1985). Earlier studies used electrical stimulation and the oscillatory evoked potential to measure the response at successive 100 μm depths (Martinez and Freeman 1984) but newer methods allow precise monitoring of the signal simultaneously at equally spaced depths with multisite probes. Using this technique, it has been shown that indeed the dynamic interaction between M/T and granule cells generates the gamma oscillations (Neville and Haberly 2003). In urethane-anesthetized rats, LFPs were recorded under several conditions: antidromic stimulation of M/T cells, electrical stimulation of the olfactory nerve, stimulation of pyramidal cells in pyriform cortex, and odorant stimulation. This study found that during odor-evoked gamma oscillations there was a repeated pattern of alternating source-sink pairs in the external and internal plexiform layers, a finding consistent with the abovementioned negative feedback loop between M/T and granule cells (Fig. 5).

Fig. 5.

Current source-density CSD analysis of LFP gamma oscillations in the OB of anesthetized rats. Current sources (blue tones) and sinks (red tones) are shown under different conditions. Recording depths are shown in each plot, and the corresponding cell layers are labeled in Ai. The top plots show results obtained by using three different kinds of M/T stimulation: antidromic, by stimulation of the lateral olfactory tract (Ai), orthodromic, by stimulation of the olfactory nerve (Aii), and centrifugal, by stimulation of pyriform cortex (Aiii). B shows the temporal evolution of the sources and sinks during a gamma oscillation. From Neville and Haberly (2003), used with permission

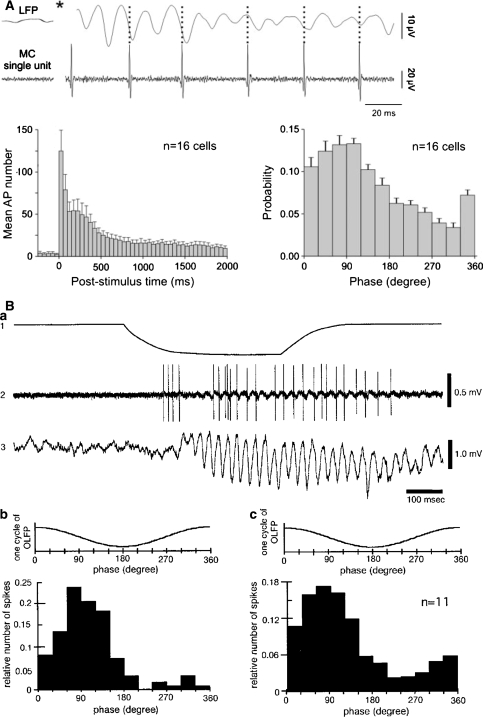
What is the relationship between the firing of individual neurons and the LFP gamma oscillation? Experimental results (Eeckman and Freeman 1990; Kashiwadani et al. 1999; Buonviso et al. 2003; Bathellier et al. 2006) have shown two important features: (1) there is a consistent phase relationship between M/T cell spiking activity and the LFP, namely, that firing usually occurs in the descending phase of the LFP oscillation (when positive is up), and (2) M/T cells do not fire in every single oscillation cycle (Fig. 6). Therefore, the frequency and power of the gamma oscillation can be used as a measure of the firing probability of a M/T cell during these LFP events (Eeckman and Freeman 1990).

Fig. 6.

Relationship between M/T spiking activity and LFP oscillation phase. (A) Mice OB slices, electrical stimulation of the olfactory nerve. The top traces show the simultaneous recording of extracellular action potentials from a M/T cell and LFPs, highlighting the relationship between the spiking time and the LFP phase. The star indicates the time of the stimulation. In the bottom plots, results are summarized for sixteen cells, showing the mean action potential number in a post stimulus time histogram (left) and M/T spike firing probability for different LFP phases. (B) Urethane-anesthetized rabbits, odorant stimulation. The top trace in (a) shows the duration of stimulation, the middle trace shows M/T spiking activity and bottom trace displays the LFP simultaneously measured. (b and c) show the relationship between M/T spiking activity and LFP phase, in (b) for one cell and in (c) for eleven cells. OLFP: Oscillatory LFP. (A) from Bathellier et al. (2006) and (B) from Kashiwadani et al. (1999), used with permission

While it may be tempting to equate an increase in gamma power with an increase in neural synchrony, the use of the term ‘synchrony’ is ambiguous in this context. Gamma oscillations represent the probability of a mitral cell firing or the summed probability of neurons in the neighborhood firing. These oscillations are not a readout of the firing rate of the local neural population, and they do not represent the pattern of firing of a given cell on a single inhalation. The phase at which a given neuron fires is close to a quarter cycle from the negative peak of the oscillation, and this might suggest that since neurons are firing in a tighter time window they must be more synchronous with each other. However, tighter locking of the local neurons’ firing times with the 90 degree phase mark of single gamma cycles will result in larger gamma oscillations but little or no increase in the coincident firing of any two neurons. This is because for the vast majority of the time, these two neurons are not synchronous with each other. While the target neurons (e.g., pyriform cortex pyramidal cells) receive more coincident input, the neurons providing this input are not more synchronous with each other. Thus, the power of the gamma band oscillatory signal represents the degree of cooperativity in the local population. While oscillations are often used to refer to synchrony among neurons, synchrony in this case is better described as between an individual neuron and the population level oscillation. Undoubtedly some neurons within the population will be synchronous at some points during the oscillation, but this likely contributes little to the power and precision of the gamma oscillation.

Functional role of the gamma oscillation

As described above, in the early- and mid-1980s, Freeman and colleagues showed that there was a relationship between the OB gamma oscillation and associative learning of odors (Freeman and Schneider 1982; Di Prisco and Freeman 1985). While this was compelling evidence for the importance of gamma oscillations, it fell short of describing a functional role. Until recently, there was no direct corroboration that specific disruption of oscillatory activity leads to changes in behavior. However, several recent studies now support the gamma oscillation as a functional mechanism in olfactory processing.

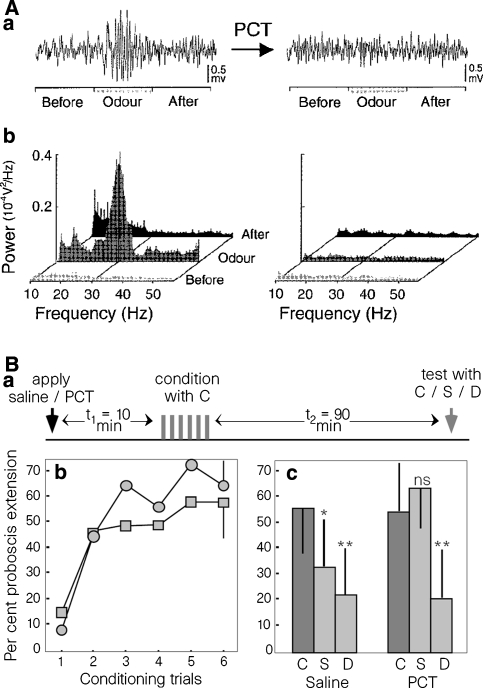
The first studies that addressed this relationship were done in honeybees and locusts (Stopfer et al. 1997; MacLeod et al. 1998). Each time a locust’s or honeybee’s antenna is presented with an odorant, a characteristic LFP oscillation (20–30 Hz) is evoked. This oscillation is recorded from the calyx of the mushroom bodies but represents coordinated activity in projection neurons of the antennal lobe (the analog of the vertebrate OB). These oscillations are specific for odorants, since they are not evoked by air. Superfusion of the brain with picrotoxin, a GABA_A receptor antagonist, abolished the oscillations by desynchronizing projection neurons (without altering their slower activity patterns, i.e., a selective alteration of the synchrony) and decreased the ability of similarly treated honeybees to discriminate the similar (hexanol and octanol) but did not affect the discrimination of the different (hexanol and geraniol) odorants (Fig. 7). In the locust system this treatment was also shown to reduce oscillations and to alter the responses of the targets of the antennal lobe neurons without changing the slow temporal structure of the antennal lobe neurons’ responses to odorants (MacLeod et al. 1998). Together, these studies showed that the insect analog of the gamma oscillation played a functional role in fine but not coarse odor discrimination.

Fig. 7.

Picrotoxin abolition of odor-induced gamma LFP oscillations and olfactory discrimination impairment in honeybees. (A) Traces in (a) show the LFP signal during the presentation of the odor with (left) and without (right) previous application of picrotoxin (PCT). Power spectra correspondent to traces in (a) are shown in (b). (B) In (a) is shown the experimental training and testing protocol for the discrimination. (b) shows the conditioning protocol and the bees’ learning (in this paradigm, the odor is the unconditioned stimulus and it is paired with the proboscis extension, which corresponds to a conditioned response). (c) shows the behavioral differences between saline- and PCT-treated animals. C and S correspond to similar odors (aliphatic alcohols differing only in chain length) and D is the terpene geraniol. Note that PCT-treated bees cannot discriminate between C and S. Reprinted by permission from Macmillan Publishers Ltd.: Nature 390:70–74 (6 November 1997), copyright 1997

In the olfactory system of rodents, evidence came from experiments with mice lacking the ß3 subunit of the GABA_A receptor (ß3−/− mice) (Nusser et al. 2001). Granule cells in the OB express only the ß3 variant of the ß subunit on their GABA_A receptors, whereas other cells in the OB express other beta subunits. Since it is known that inhibitory interneuron activity is essential for the generation of LFP oscillatory activity, ß3−/− animals constituted an excellent model to study the behavioral correlates of modified gamma oscillations.

As judged against controls, ß3−/− animals displayed enhanced OB LFP gamma oscillations (Fig. 8) and increased synaptic inhibition in M/T cells, as reflected in the analysis of the amplitude and frequency of their inhibitory postsynaptic currents. Behaviorally, mutant animals exhibited, compared to control littermates (ß+/+), a better ability to discriminate between similar monomolecular alcohols. In addition, ß3−/− mice performed worse than controls when discriminating between alcohol mixtures. As a whole, these results showed that the alteration of the olfactory network gamma oscillations in a mammal had a profound and complex impact on its olfactory behaviors.

Fig. 8.

Enhanced LFP gamma activity in the OB of ß3−/− mice. (A) Data shows four examples of raw tracings of OB LFP signals recorded from freely behaving animals during exploration of their cage. Gamma oscillations are seen in bursts of activity, much more prominent in the case of the mutant animals. From Nusser et al. (2001), used with permission. (B) Power spectra of OB LFP signals during exploratory behavior. Note the increase in power centered around 65 Hz for mutant animals. From Kay (2003), used with permission

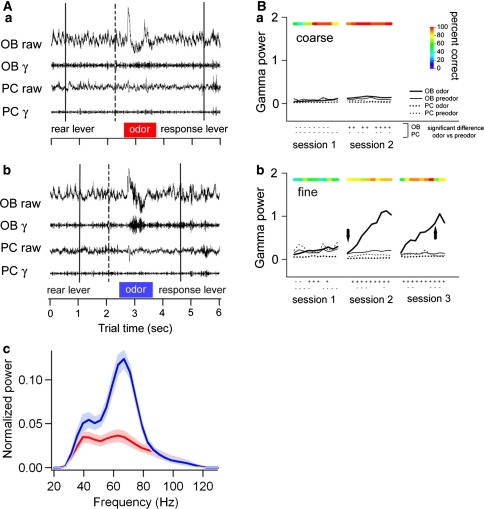
Recently, the role of gamma oscillations was assessed in a previously untested situation: during intrinsic dynamical modulation of the olfactory network associated with a learning process (Beshel et al. 2007). Rats were trained to discriminate between pairs of similar and dissimilar odorants, and LFPs were recorded from the OB and the pyriform cortex. OB gamma oscillations were found to selectively increase in amplitude according to task demands, with fine odor discrimination associated with augmented gamma power in contrast to coarse discrimination (Fig. 9a). Furthermore, the power evolved during sessions, increasing across trials, after the rats reached criterion performance in the task, and they reset at the beginning of a new session (Fig. 9b). This study showed for the first time that animals can modulate the amount of gamma oscillatory activity dependent on the type of pattern discrimination needed. Interestingly, the enhancement in this case was not tightly coupled to performance levels, but had a slow time course such that once rats reached criterion performance, gamma oscillations would begin at low levels and steadily increase in power throughout the 2 hours of a test session over about 200 odor identification trials. This was accompanied by an enhanced evoked potential and suppression of gamma oscillations in the pyriform cortex. These phenomena suggest a cholinergic mechanism, as they resemble similar effects associated with application of cholinergic agonists in frog olfactory bulb (Hall and Delaney 2001), rat pyriform cortex (Chabaud et al. 1999), computational models (Liljenstrom and Hasselmo 1995; Borgers et al. 2005), and cat visual cortex (Rodriguez et al. 2004); this theory has not yet been tested in the olfactory system.

Fig. 9.

Intrinsic modulation of olfactory gamma LFP oscillation power in rats, matching the tasks demands. (A) LFP recordings during an olfactory discrimination task, showing OB (OB) and pyriform cortex (PC) raw signals (1–475 Hz) and gamma-filtered signal (65–100 Hz). (a) Corresponds to a ‘coarse’ discrimination task (dissimilar odorants) and (b) corresponds to a ‘fine’ discrimination (very similar odorants). (c) Shows the power spectra of the odor delivery period for the gamma band (indicated with colored bars in a and b) for both conditions. Note the enhanced power for the ‘fine’ condition. (B) Evolution of gamma power within sessions, for coarse and fine discriminations. From Beshel et al. (2007), used with permission

Different kinds of gamma

Gamma oscillations have been noted in many cortical areas and behavioral settings. Since the first investigations, the high frequency activity dubbed ‘gamma’ comprised a fairly large range of frequencies even within single species, varying among reports, but ranging usually between 30 and 100 Hz. Such a wide range is likely to contain activity resultant from different network processes and synaptic interactions. Here we present some of the evidence available concerning experimental efforts to discriminate between the processes underlying gamma activity.

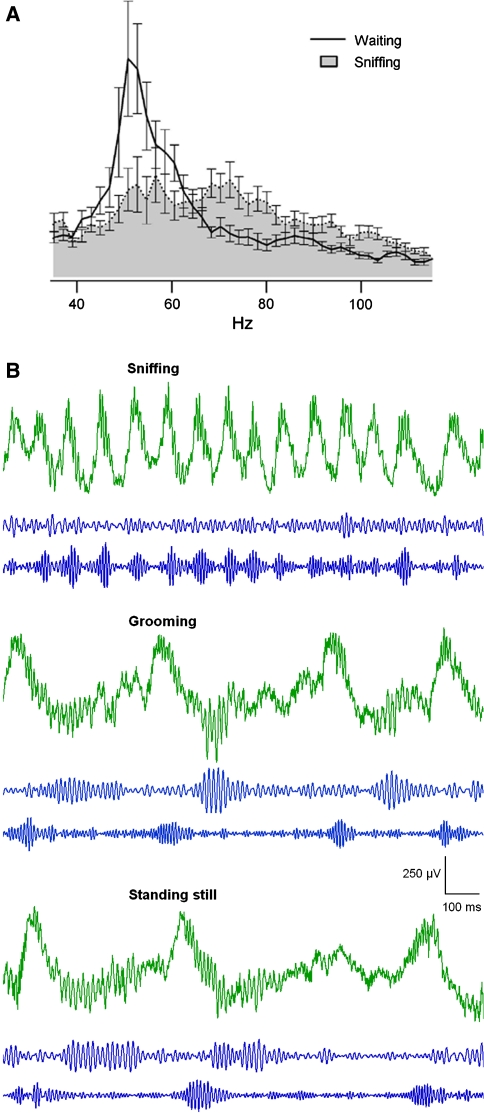
Recording LFPs from awake, freely behaving rats and mice, Kay was able to discern two different kinds of gamma activity, which were correlated with different behaviors and seemed to be associated with different synaptic pathways in the bulb (Kay 2003). The animals were trained to discriminate between two odorants, and consistently displayed low frequency gamma (35–65 Hz) during the waiting period, when they were alert and motionless (Fig. 10a). This low gamma sub-band (dubbed ‘gamma 2’) was completely absent during the odor sampling period. Gamma 2 oscillations were found to appear simultaneously in the OB and in the pyriform cortex of the rats. In contrast, throughout the sniffing period, the activity corresponded to the well described, inspiration-synchronized bursts of high frequency gamma (65–100 Hz), which were named ‘gamma 1.’ An important difference between these two kinds of activity was not only the frequency range, but also their relation to the animal’s respiration cycles: the onset of gamma 1 (‘classic’ gamma) bursts was tightly locked to inspiration, whereas gamma 2 activity did not display this correlation and occurred between inhalations during periods of slow breathing in attentive behavior. Moreover, gamma 2 activity was found to be absent in ß3−/− mice and in anesthetized rodents, and is distinctly and selectively displayed during particular behaviors, such as grooming, drinking and attentive states (Rojas-Líbano and Kay, unpublished observations. See Fig. 10b). Despite these observations, nothing is known about the functionality of these oscillations.

Fig. 10.

Two different kinds of gamma oscillatory activity in the rat. (a) Power spectra from OB LFP recordings during an olfactory discrimination task. During the waiting period (prior to odor presentation) there is a low-frequency component of gamma activity, centered around 50 Hz, that is absent during odor sampling (‘sniffing’); from Kay (2003), used with permission. (b) LFP activity recorded from freely moving animals during three different behaviors. Green traces: raw data; middle traces: data filtered between 35–65 Hz (‘gamma 2’); bottom traces: data filtered between 65–100 Hz (‘gamma 1’). Note that during sniffing behavior the theta frequency is much higher (about 8 Hz) than during grooming or standing still (about 1 Hz). Note as well the absence of gamma 2 bursts during sniffing. Upward deflection corresponds to positive polarity

This subdivision of the gamma band in the olfactory system points out the necessity of knowing the cellular and synaptic sources of oscillations and their systemwide coherence patterns. While fast oscillations have been noted in several brain regions, these studies are primarily phenomenological, and little is known about the synaptic origins of these signals. Without current source density studies, such as those described above, or combined single unit and LFP recordings, little can be known about how the different types of gamma oscillations within and between cortical areas and in different behavioral states are related.

Computational models of the olfactory system

The olfactory system with its prominent oscillatory activity was one of the first cortical systems to be addressed computationally. We present some of these models as examples of what has been done in the field, and our selection is by no means exhaustive. Many more examples can be found in the literature (Wilson and Bower 1992; Linster and Gervais 1996; Hendin et al. 1998; Davison et al. 2003; Simoes-de-Souza and Roque 2004).

Early models of the oscillatory evoked potential

The earliest mathematical descriptions of an olfactory oscillatory evoked potential came from Freeman (1961, 1964). These models of the pyriform cortex used interactions between excitatory and inhibitory populations of neurons as a basis for a negative feedback circuit in a classical harmonic oscillator circuit. This approach was the foundation of Freeman’s later work, representing neural populations as computational entities, described in greater detail below. Following closely on Freeman’s early computational efforts was work by Rall and Shepherd (described above in the “Cellular mechanisms” section) (Rall and Shepherd 1968), which addressed oscillations as interactions between single cells using the Hodgkin–Huxley approach. This model was conceptually similar to the Freeman model, focusing again on negative feedback interactions, but it addressed the cellular components explicitly in compartmental fashion. As already mentioned, the authors pointed out that this synaptic interaction provided a putative mechanism to explain oscillatory population behavior.

The concept of mass action

A basic intuition in the building of Freeman’s models was the necessity to reconcile two views: the classical neurophysiological one, represented by Charles Sherrington, that considers the nuclei or groups of neurons to be the fundamental module of the nervous system (Sherrington 1906), and the more computational view, represented by McCulloch-Pitts’ logical neurons (McCulloch and Pitts 1943), where the single cell level, with its all-or-none behavior, holds the key to understanding the mode of operation of the system. On the other hand, the methodological inspiration for action by groups of neurons can be found in non-equilibrium thermodynamics (Nicolis and Prigogine 1977; Prigogine 1978), where a set of mathematical tools was developed to deal with systems formed by high numbers of stochastically interacting elements. A central feature of these systems is the emergence of macrostates, which are global and coherent patterns of activity, provided that a continuous supply of energy is delivered to the system. Freeman referred to the application of this mathematical and physical insight to neural systems as the concept of mass action.1

The general strategy, initially developed by Freeman (1975 and his earlier papers that gave rise to this book), was as follows: the fundamental units for modeling are the so called neural sets, which are groups of neurons related by shared anatomical connectivity patterns. These sets can be thought as modules arranged in a hierarchy, designated (from lower to higher levels) KO, KI, KII, KIII, …, with each hierarchical level characterized by a particular connectivity pattern or topology. The definition of a KO set, in Freeman’s words, is

…any set of neurons numbering from 10³ to 10⁸ having a common source of input and a common sign of output (+ or e, excitatory; − or i, inhibitory), and having no functional interconnections. […] The set is not defined by a particular input but by a range of possible inputs from the common source. (Freeman, 1975, p. 26)

Correspondingly, KO sets are the basic modules of the model, and a KI set is defined as a set having a common input, the same kind of output (excitatory or inhibitory), and dense connectivity within the set. KII sets are constituted of two interconnected KI sets. Thus, for the olfactory system, a KII set, containing KI and KO sets, models each of the main components: OB, anterior olfactory nucleus, and pyriform cortex, with the entire set of interconnected structures forming the complete KIII set (Freeman 1987). Differential equations representing the temporal evolution of macrostates of each of these sets are constructed, and the variables and parameters used do not necessarily have a direct correspondence to usual neuronal variables (e.g., time constants, conductances, etc.) The solutions of the differential equations that constitute the model contain the basic features of the olfactory system EEG, including the characteristic bursts of gamma activity, not as causal entities but as the emergent set of macrostates that represent coordinated activity from the underlying neural masses. One of the major successes of this model was the introduction of spontaneous and sensory induced oscillatory states and the roles that feedback can play in shaping the OB’s response in sensory discrimination. This model displayed four basic features also present in olfactory neural oscillations, namely a) oscillatory activity had the same dominant frequency everywhere in the bulb, b) the local mitral cell population’s oscillation phase led that of the granule cells’ by a quarter cycle, c) there was a non-zero phase gradient field across the bulb, and d) the oscillatory burst rode on a baseline shift phase-locked with sniff cycles.

Oscillations within networks of individual neurons

Several models address gamma oscillations at the level of interactions between individual neurons, and we describe two such models here, one based more on theoretical principles (Li and Hopfield 1989) and the other tied more closely to physiological detail (Bathellier et al. 2006).

Li and Hopfield (1989) constructed a model of the OB, using the concept of simple harmonic oscillators, the units of which were mitral and granule cells, topologically arranged as one or two dimensional rings. The model assumed a direct connection between ORNs and mitral cells and included no glomerular processing. The input from ORNs to mitral cells was modeled by a function that increased linearly during inhalation and decreased exponentially during exhalation. A fixed centrifugal input directed to granule cells was also included. The state of activity of each neuron was described by variables for mitral and granule cells, resembling the membrane potential, and therefore the output of the cells could be described as functions of their internal states. In this way, the bulb model was conceived as having equations of motion, which are the dynamical description of the state variables that include the connectivity between the cells and the time constants for each cell. In response to input, the system generates oscillations that are completely dependent on the input, since in its absence, weak incoherent oscillatory activity is observed.

This model is conceptually similar to Freeman’s model, but like Rall and Shepherd’s model, it focuses in its structure on single cells rather than neural populations. In addition, the authors performed a mathematical analysis of their equations and found that mitral and granule cells can be conceived as a group of coupled non-linear damped oscillators, which nonetheless behave linearly for small amplitudes. The study showed that the oscillations did not depend on the number of cells, and the ‘macroscopic’ oscillatory modes could grow, because a group of coupled oscillators is not always stable. In their view the EEG waves are considered an epiphenomenon in that they do not carry information, and information is found at the level of single cells. This model was extended by Li (Li 1990), introducing a changing centrifugal input that could also modulate OB responses. This showed that the sensitivity of the bulb could be shaped by the centrifugal input, and this could be responsible for simultaneous adaptation (relative to some odor) and enhanced sensitivity (to a different one).

A more recent model is particularly interesting for the present discussion because it aimed not only to reconstruct the processing and recognition of odorants by the olfactory system, but it also explored specifically the cellular and synaptic mechanisms underlying the generation of gamma oscillations (Bathellier et al. 2006). It is a network model, in which physiological data (i.e., neuronal conductances, capacitances, time constants, equilibrium potentials, and currents) are used to build single-compartment models of the cells with Hodgkin–Huxley voltage dependent kinetics. As is usual, the dynamical variable is the membrane potential, and the equation for mitral cells takes the form of a differential equation based on the main currents flowing through the cell membrane (e.g., different channels for Na⁺, K⁺, etc), including an input current (modeling the ORN synapse onto mitral cells) and a synaptic current (representing GABAergic input). Other factors include membrane resistance and capacitance and the reversal potential of leak currents. All the voltage-dependent currents are described by classic gating variables, which in turn are described by differential equations. The study addresses lateral inhibition (mediated by granule cells) and/or lateral excitation between mitral cells as possible coupling modalities. More stable oscillations arise with lateral inhibition than lateral excitation, and the frequency of the oscillation can be modified by varying the time constants of the inhibitory events. This in itself helps to make specific predictions on the roles that various neuromodulators may play in shaping OB gamma oscillations, since the effect of many of these is to alter the strength and time course of inhibitory events at the dendrodendritic synapse. Thus, in this model as well, lateral inhibition between mitral cells, mediated by granule cells, emerges as a central feature in the generation of LFP gamma oscillations.

In summary, all of these modeling efforts over almost 50 years come back to the reciprocal interaction between excitatory and inhibitory populations in producing sensory induced oscillations in the olfactory system. This arguably makes the olfactory circuit the best understood of all cortical oscillatory networks.

Applications to other cortical gamma oscillations

As gamma oscillations are observed in other sensory and motor systems, it is important to turn to the depth of research in the olfactory system as a guide for describing these oscillations at multiple levels. Without knowing the synaptic, cellular and system dynamical properties of these phenomena, the term gamma assumes association with other systems only by virtue of frequency. Since frequencies for homologous phenomena can vary among species (Bressler and Freeman 1980), it is crucial that these oscillations be described at multiple levels to assess their functionality and even the definition of the term gamma in each context. For example, this is important in evaluating the analogous odor-evoked oscillations in insect systems, as they frequently occupy the 20–30 Hz band (similar in frequency to mammalian beta oscillations), but show several similarities with what we have described here as OB gamma oscillations. Analogously, frogs show an odor evoked “fast” oscillation at about 10 Hz (within the range of the theta and even the EEG alpha bands), with the same set of cellular determinants as the mammalian odor-evoked gamma oscillations. Furthermore, within the rodent OB we have also described a different set of gamma band oscillations (‘gamma 2’) that are not evoked by stimuli and appear to rely on inhibition of granule cells (Kay 2003).

Thus, taking the olfactory system as a guide we urge researchers of sensory evoked oscillations in other systems to evaluate (1) phase relationships between principal neurons and the LFP oscillation; (2) the synaptic sources of the oscillations, using current source density measures; (3) the role of pattern discrimination overlap in functionality of oscillations; and (4) the influences of centrifugal feedback and lateral inhibition in the size and coordination of gamma oscillations. We propose that to truly be analogous to OB sensory-evoked gamma oscillations they should be similar on these four criteria, independent of the frequencies involved.

Conclusion

Brain oscillations reflect the dynamical evolution of neuronal networks. Under certain conditions, interconnected groups of cells generate periodic fluctuations in the extracellular potential that have patterned temporal structure in which distinct states can be identified and defined; because of this they can be studied as dynamical systems. Moreover, due to the reliability of oscillatory recording in experimental animals, the relationship between these neuronal oscillations and an animal’s behavioral and cognitive processes can be studied in the laboratory, creating an interdisciplinary arena that brings together concepts and methods gleaned from neurobiology, mathematics, psychology, computational modeling, and cognitive science.

For mammals and certainly for humans, olfaction plays a crucial role in perception and is deeply linked to emotional and learning and memory processes. The particularities of the mammalian olfactory system organization make it well suited for the analysis of oscillations, and a vast corpus of research in the past half century has been devoted to understanding them in this context. Therefore, detailed information is available from the olfactory system about the cellular processes and synaptic interactions that generate these oscillations, making them easier to interpret and to manipulate than in many neocortical systems, where most aspects of the neuronal mechanisms that produce the oscillations are unknown. Several lines of research, including behavioral neurophysiology and computational modeling, have also started to elucidate the role of the oscillations in sensory processing, providing integrative insights about the neurobiological correlates of cognitive phenomena.