Simulating water with the SCCDFTB method: from molecular clusters to the liquid state

Abstract

The recently developed self-consistent-charge density functional tight binding (SCCDFTB) method provides an accurate and inexpensive quantum mechanical solution to many molecular systems of interests. To examine the performance of the SCCDFTB method on (liquid) water, the most fundamental yet indispensable molecule in biological systems, we have reported here the simulation results of water in sizes ranging from molecular clusters to the liquid state. The latter simulation was achieved through the use of the linear scaling divide-and-conquer approach. The results of liquid water simulation indicated that the SCCDFTB method can describe the structural and energetics of liquid water in qualitative agreement with experiments, while the results of water clusters suggested potential future improvements that may apply to the SCCDFTB method.

Introduction

Results of simulations of liquid water with simple molecular mechanics models have shown remarkable agreement between modeled and experimentally determined properties of water. This was first shown by the work of Rahman and Stillinger with the ST2 model.¹ Subsequently, Berendsen and Jorgensen and their coworkers respectively introduced the SPC ² and TIP3P ³ models, that each had just the three atomic masses as centers of force and two adjustable parameters, the repulsive LJ parameter for interactions between oxygen atoms of neighboring water molecules, and the partial charge of the model’s hydrogen atoms. The best values of these parameters were found by requiring energy and density of the model to match experimental values. Once this had been done, properties such as radial distribution function, diffusion coefficient, excess free energy and dielectric constant were found to be in approximate agreement with measured values. In all these models, and several subsequently introduced modifications,^4,5 the atomic partial charges are fixed, and the polarization of water molecules under the influence of the charge distribution provided by surrounding molecules in the liquid is accounted for by making the model molecular dipole moment significantly higher than that measured for water molecules in the vapor. While various polarizable water models have been proposed,^6–9 they have found little application in simulations of aqueous solutions, especially of systems with biological relevance, whereas the fixed-charge models are widely used.

As an alternative to improving such molecular mechanics models, one may consider using an approach in which the energy and forces are based on a formulation of quantum mechanical (QM) description. The major obstacles in the application of quantum mechanics are the small size of a sample to reasonably well represent liquid water and the long computer runs that are required to equilibrate the sample and collect statistically significant results. Thus, the QM Hamiltonian used must be sufficiently simplified to allow the calculations with available compute power, and, to be useful in practice, sufficiently sophisticated to capture the interactions between water molecules at least as well as is the case for the simple molecular mechanics models. These requirements can be fulfilled by a large class of semi-empirical quantum mechanical methods, in particular a recently developed SCCDFTB method showed excellent performance on many biological molecular systems.

The SCCDFTB method takes roots in density functional based tight binding theory. ^10–13 The accuracy and efficiency of the method are achieved through several key approximations. (1) The charge density fluctuations are approximated by atomic charge fluctuations, which lead to a quadratic term of charge-charge interactions and thus provide a self-consistence scheme on the basis of charge transfer. (2) The Kohn-Sham orbital are built on the basis set of optimized minimal atomic orbital. (3) The repulsive terms are approximated by two-body interactions which were empirically fitted to DFT calculations, specifically the PBE functional in the current form,¹⁴ of a set of training molecules. As a result, the SCCDFTB method shows good accuracy over a variety of molecular systems. Recent applications of SCCDFTB method on peptide, protein, and DNA systems reported significantly improved accuracy as compared with classical molecular mechanics force fields. ^15–24

Our focus in this report is to examine the ability of the SCCDFTB method in describing the water system. We carried out linear scaling divide-and-conquer SCCDFTB simulations on the liquid water system. The results indicated that the SCCDFTB can describe liquid water in qualitative agreement with experiments. The analysis of the calculations of water clusters furthermore pointed to possible future improvements that could enhance this method.

Methods and Computational Details

To model the liquid state of water, 360 water molecules in a cubic box of 22.1049 × 22.1049 × 22.1049 ų were used in the constant-volume molecular dynamics simulations at 298 K. The density of water was set to the experimental measurement of 997.07 kg/m³. The divide-and-conquer method was used to carry out the full quantum mechanical calculation of this system.^15,25–28 The whole system was naturally divided into 360 subsystems; each subsystem comprised of one central water molecule and a buffer region of other water molecules whose atoms were within 5.5 Å of the central water molecule. The buffer list was updated every 16 integration steps. At each MD step, the energies and gradients were computed after SCF calculations with at least four iterations. The SCF convergence criterion was set to 10⁻⁷ hartree (= 6.275 × 10⁻⁵ kcal/mol).

The MD integration step was 1 fs. Ewald summation was not applied; interactions between two water molecules were completely turned off if the atomic distances between the two exceed 9 Å. This particular setup was adopted here because it was also commonly used in the simulations of classical water models, ⁵ even though dual/longer cutoffs with Ewald summation might be necessary for the simulation of biomolecular systems. The temperature of the system was held at 298 K by Berendsen thermostat.²⁹ The temperature relaxation time was set to 0.1 ps. 64 ps MD simulations were performed with the last 56 ps used for analysis.

For the calculation of water clusters, systems with the number of water molecules varying from 2 to 20 were investigated. The (H₂O)_N structures from the Cambridge Cluster Database ³⁰ were used as the initial conformation.³¹ Those structures had been optimized at RHF/6-31G(d,p) level and were thought to be the best-known energy-minima at that level of theory.

For each water cluster, the molecular structure was minimized with the SCCDFTB method using limited-memory BFGS (LBFGS) algorithm;^32,33 the energies were then computed and compared with ab initio results. Afterwards, the molecular system was heated up to 350 K and a MD simulation of 100 ps was carried out with the SCCDFTB method. With the integration time step of 1 fs, the structures were saved every 20 steps. The saved structures were subjected to a LBFGS minimization until the maximal gradient component is less than 0.01 kcal/mol/Å. Usually the minimization took about a thousand steps. Those conformations with lowest energies were the subject of detailed analysis. Even though this heating-cooling procedure might not sample the complete phase space, it was expected to sufficiently sample the regions typically experienced in ordinary molecular dynamics simulations.

Previous work indicated that the γ function of the SCCDFTB method plays a vital role in the correct description of hydrogen-bonded systems.¹³ The original form of the γ function consists of two terms

$${\gamma }_{\alpha \beta }=\frac{1}{r_{\alpha \beta }}-S_{\alpha \beta }$$ (1)

where r_αβ is the distance, and S_αβ is the short-range corrections term between two nuclei α and β. It was found that this simple form, while correctly predicting the structures and energies of many molecules, reproduces poorly the hydrogen-bond interaction in the gas phase. As an example, the SCCDFTB calculated binding energy of water dimer is considerably lower than ab initio result. To treat the anomaly of hydrogen-bond, a modified γ function was introduced

$${\gamma }_{\alpha \beta }=\frac{1}{r_{\alpha \beta }}-S_{\alpha \beta }f(r_{\alpha \beta })$$ (2)

Here the function f(r_αβ) was brought in to damp the short-range interactions. ¹³ As a result, γ function becomes more positive in the short range and leads to stronger polarization for the atoms forming H-bonds. In the current study, the two γ functions were both employed in an effort to investigate their influences in liquid water. Specifically, the damping function in the modified γ function takes the form of

$$f(r_{\alpha \beta })=exp\left[-{\left(\frac{u_{\alpha }+u_{\beta }}{2}\right)}^4{r}_{\alpha \beta }^2\right]$$ (3)

The program Sigma combined with the SCCDFTB code was employed for the simulation of water clusters.^16,34 To simulate liquid water, a divide-and-conquer version of the standalone SCCDFTB code was used, which was modified from a version previously used for the QM/MM simulation of the crambin molecule in water. ¹⁵

Results and Discussion

One of the most important properties of liquid is the radial distribution function (RDF). The oxygen-oxygen RDF is the characteristic property of the liquid state simulation of water models. In Fig. 1 we depict the oxygen-oxygen RDF of the simulations of liquid water with and without the modified γ function for the H-bond interactions, in comparison with experimental measurement from neutron diffraction experiments. ³⁵ When the original γ function was used, the first solvation shell appears at distances exceeding experimental measurement, with the peak positioning at 2.84 Å. The use of modified γ function significantly improves the results as to shift the peak position of the RDF back to 2.75 Å. Integrating over the first peak of the RDF gives the number of water molecules in the first solvation shell, which is approximately 4.5 for experimental data, 8.7 for the original γ function, and 6.7 for the modified γ function. Indeed with the modified γ function the SCCDFTB method provides better description for the short-range interaction as the curve overlaps with experimental data for distance less 2.70 Å. However, there appears to be too many neighboring water molecules forming an enlarged first solvation shell. In the microscopic level of structure, the tetrahedral H-bond pattern of water was disrupted as on average more than four nearby water molecules now form H-bonds with one water molecule.

Figure 1.

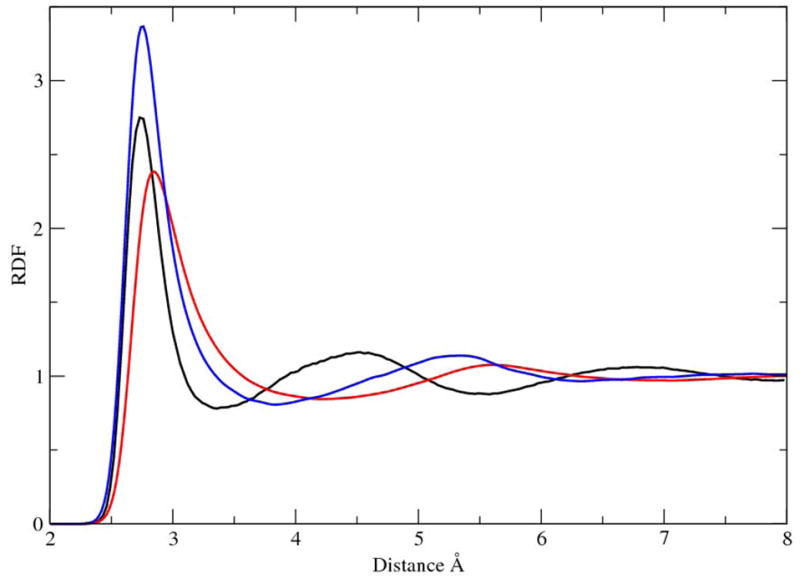
Comparison of the oxygen-oxygen RDF functions. Black: experimental measurement; ³⁵ red, SCCDFTB method with the original γ function; blue, SCCDFTB with the modified γ function for the H-bond.

Several factors may contribute to the simulation results of liquid water, including the tight binding scheme, the minimal basis set, the simplified point charge interaction, and finally, the fitted parameters in the SCCDFTB method. In particular the parameters of the SCCDFTB method have been derived using the PBE functional which suggests that any deficiency in the PBE functional will be inborn with the SCCDFTB method. Previous CPMD simulations with the PBE functional also indicted an “over-structured” first solvation shell,³⁶ in agreement with our observations here. The further difference between the first RDF peak of the CPMD simulations and of the SCCDFTB simulations might be attributed to the approximations adopted in the SCCDFTB method. One should also note that like many other functionals, the PBE functional does not have the long-range dispersion effect which may also contribute to the current results. Even though an empirical correction term likely will improve the results,^15,37,38 it is not expected to improve the structure of first solvation shell of liquid water because of the long-range character of the dispersion interactions.

Obviously it is difficult to decompose the effects of all these factors to examine individual contributions for solution simulations. Some insights may be gained through an easier route. We turn to the water clusters which have been under extensive theoretical study and analysis.^{30,31,39–48} Specifically for clusters of no more than 20 water molecules, broad phase space searching has been carried out to determine the global minimal conformations at the ab initio HF, DFT, or MP2 level.^{31,45,49–52} Even though the ab initio calculations at the HF/6-31G(d,p) level may not necessarily determine the precise structures and energetics of the water clusters in gas phase and furthermore may not be extrapolated to the properties in the condensed phase, they at least provided a reliable reference for our calculations. In fact the same tendency has been repeatedly observed in ab initio calculations at different level of theories and with different basis sets. ^31,45,49,50

Figure 2 depicts the variation of binding energies with respect to the number of water molecules in the clusters. The results showed again that the modified new γ function substantially improves the calculation of binding energies, as compared with the ab initio results. For those ab initio-determined structures, the binding energies with the new γ function are in fact quite close to the HF/6-31G(d,p) calculations. From this perspective, one might wonder if the simulation of liquid water could have been further improved or if there were other factors may also be attributed to the results. For example, the interaction model and the parameters of the SCCDFTB method were derived and examined with respect to the structures and energetics of training molecules at/around their common equilibrium states, in other words, a small region of the phase space close to the equilibrium conformations. Given the complexity of the multi-body interactions, especially in the case of water molecules, one wonders if such interaction models and parameters can still reproduce as well the structures and energetics in other parts of the high-dimension phase space.

Figure 2.

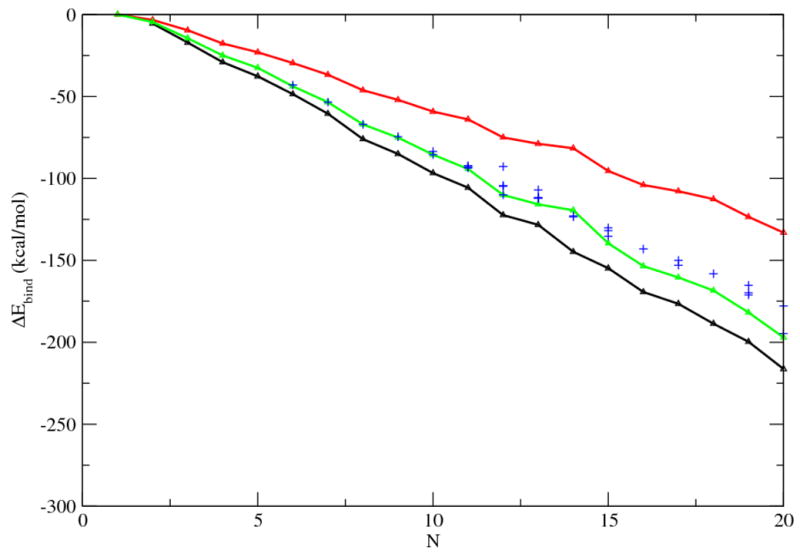
Binding energies of the water cluster vs the number of water molecules. Black line, results from HF/6-31G(d,p) calculations; red line, SCCDFTB energies with the original γ function; green line, SCCDFTB energies with the modified γ function for the H-bond; blue plus, SCCDFTB energies with the modified γ function for a set of DFT optimized structures. ⁴⁵ For the latter three, the structures were re-minimized with the corresponding SCCDFTB methods prior to the calculation of energies.

To explore this question, the two-step heating-cooling procedure was used to explore the energy minimum states of water clusters. For our ultimate interests in the liquid water, the attention here is the water clusters with N, the number of water molecules, larger than 8. Table I lists the energies of five lowest minimum-energy states determined with this approach. For most water clusters, the energies of the starting ab initio structures remain the lowest. However, for N = 10, 11, 13, 14, and 18, the SCCDFTB method identified lowest energy conformations different from those determined with the HF/6-31G(d,p) method.

Table I.

Five lowest SCCDFTB energies of (H₂O)_N, N=9 through 20, identified in the heating-cooling process. The energies are in kcal/mol.

N	ΔEbinda
9	−75.085	−74.979	−74.677	−74.644	−74.579
10	−85.782	−85.517	−85.438	−85.384	−85.312
11	−95.894	−95.690	−95.667	−95.312	−94.972
12	−110.107	−110.089	−107.459	−107.413	−106.613
13	−118.180	−117.558	−116.537	−116.223	−115.795
14	−127.540	−127.129	−126.980	−126.349	−126.275
15	−139.591	−138.745	−136.955	−136.723	−136.048
16	−153.532	−149.177	−148.727	−147.347	−146.643
17	−160.466	−159.756	−159.096	−158.490	−158.162
18	−172.066	−171.937	−171.394	−169.798	−169.589
19	−181.816	−181.761	−178.524	−178.124	−178.103
20	−197.040	−189.571	−189.570	−189.522	−188.910

^aThe five lowest energies are in the ascending order. The structures with numbers in bold are identical to the structures obtained by minimization of the SCCDFTB energy with as starting point the minimum-energy (HF/6-31G(d,p)) structures.

For the (H₂O)₁₀ cluster, the lowest-energy structures from two methods are shown in Fig 3. The HF/6-31G(d,p) method identified a structure with two parallel layers of five-member rings as the most stable conformations. (Fig 3a) The SCCDFTB method identified a conformation in which eight water molecules form a cube, and the other two stay on the top of one side of the cube to form a “handle”. (Fig 3b) Even though it looks like this structure is very similar to the second-lowest-energy conformation in the HF/6-31G(d,p) calculations, ³¹ (Fig 3c) there are clear differences between them. The pattern of hydrogen bonds between the cube and the handle is unmistakably different. In the HF/6-31G(d,p) structure, (Fig. 3c) the four water molecules in the middle layer each has one O-H bond pointing to the next neighbor, and the other O-H bond in turn pointing to above or below the current layer in a circular “up-down-up-down” pattern. In the SCCDFTB structure, (Fig. 3b) those four water molecules, while maintain the same intra-layer H-bond pattern as each again points one O-H bond to the next neighbor, have the other O-H bonds point to other layers in a pairwise “up-up-down-down” pattern. As a result, one may note the unusual triangles between the handle (top layer) and the cube in the SCCDFTB structure, (Fig 3b) i.e., water molecules 1, 2, and 3, and 4, 5, and 6. The relative positions of the three water molecules in each triangle indicate unusual H-bonds between them.

Figure 3.

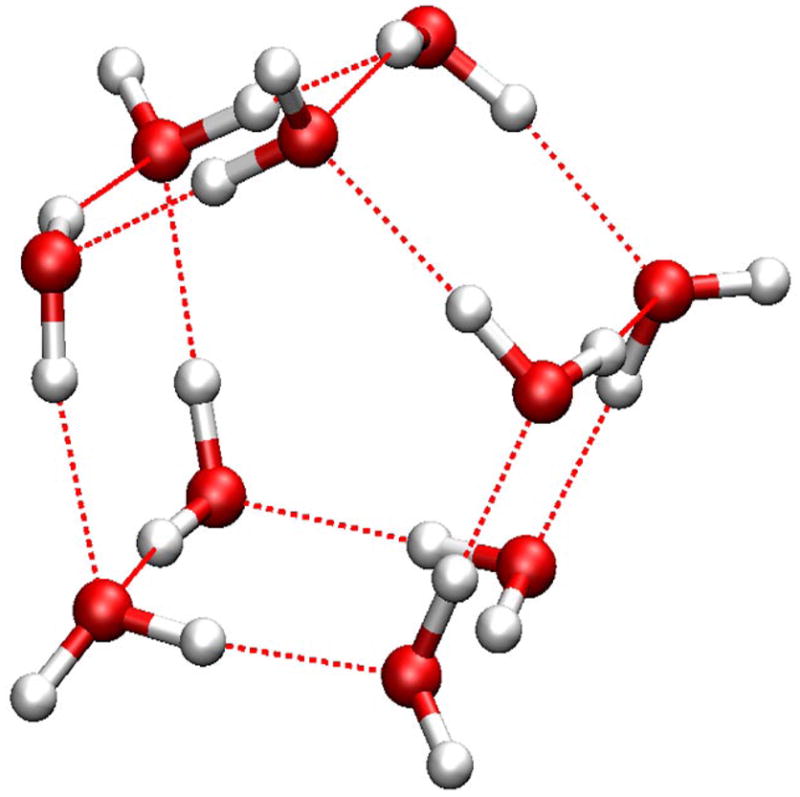
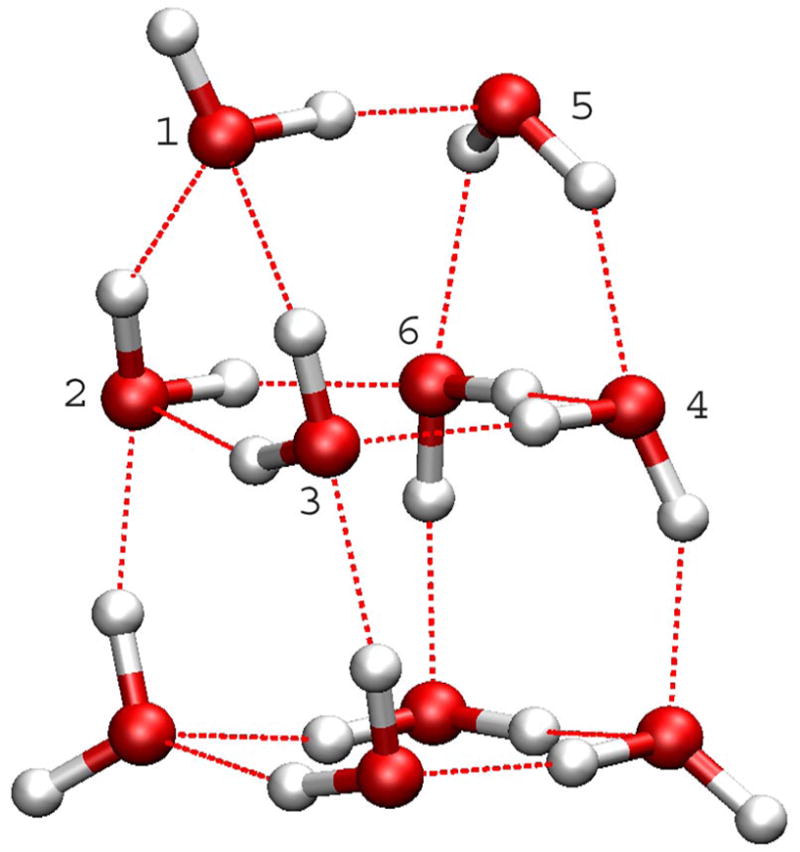
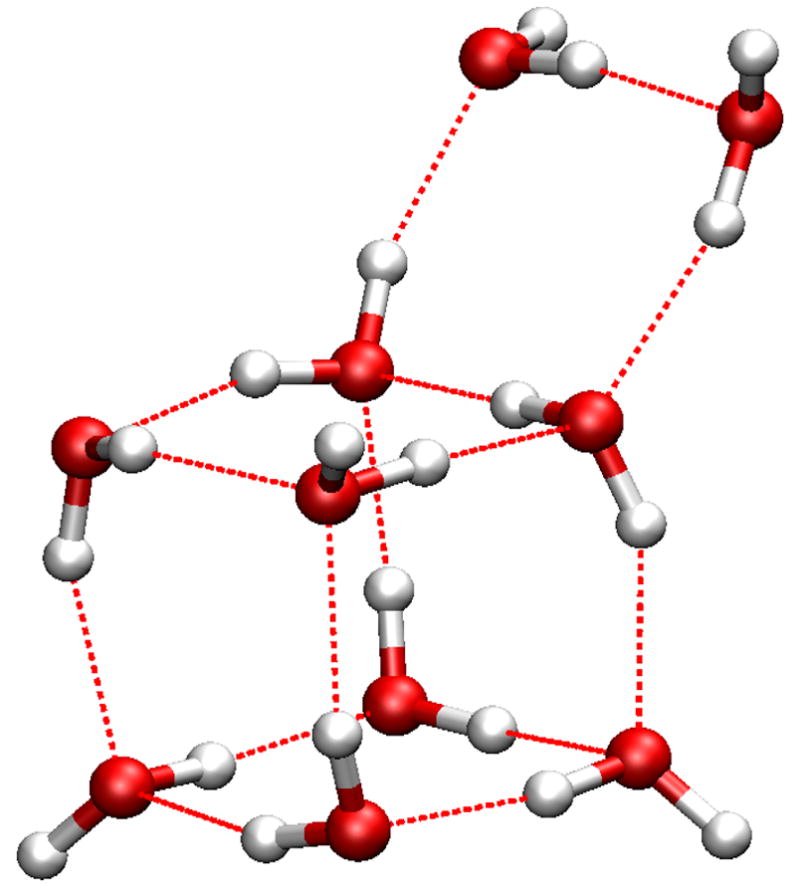
Minimized structures of the (H₂O)₁₀ cluster: a) the structure in the Cambridge Cluster Database after minimization with the SCCDFTB method; b) the lowest-energy structure identified in the heating-cooling procedure with the SCCDFTB method; c) the second-lowest-energy structure from HF/6-31G(d,p) optimization. ³¹

For the (H₂O)₁₁ cluster, the lowest-energy structures from two methods are shown in Fig 4. As an extension to the (H2O)₁₀ structure, the HF/6-31G(d,p) structure is a two parallel layer of pentamers with the 11^th water molecule forming H-bond with a corner. (Fig 4a) The SCCDFTB structure, (Fig 4b) more like the second most stable structure in HF calculations, is a cuboid with one corner missing. The three water molecules in the bottom form an obtuse triangle, which is an acute triangle in the corresponding HF/6-31G(d,p) structure. (Fig 6. in ref 31)

Figure 4.

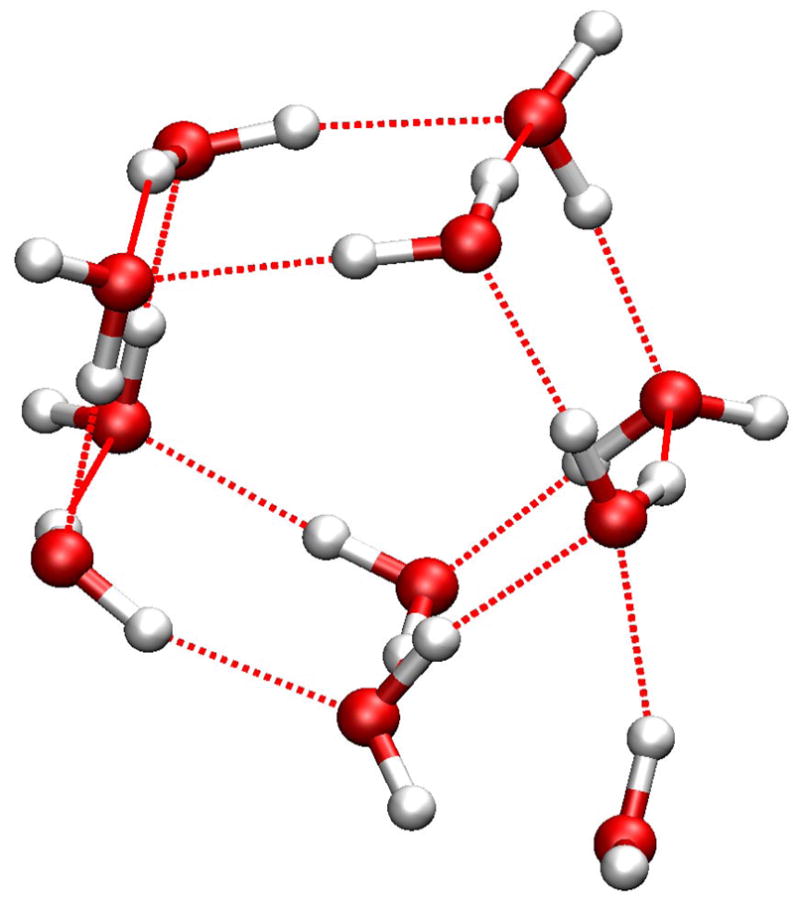
Minimized structures of the (H₂O)₁₁ cluster: a) the structure in the Cambridge Cluster Database after minimization with the SCCDFTB method; b) the lowest-energy structure identified in the heating-cooling procedure with the SCCDFTB method. The three water molecules on the bottom form an obtuse triangle as indicated by the blue dotted lines.

Figure 6.

Minimized structures of the (H₂O)₁₄ cluster. CPK model in red (oxygen) and white (hydrogen) is the structure minimized from the Cambridge Cluster Database; CPK model in blue is the lowest-energy conformation identified with the SCCDFTB method h.

For the (H₂O)₁₃ cluster, the lowest-energy structures from two methods are shown in Fig 5. Both structures were formed with a cuboid plus an extension of one water molecule. In the HF/6-31G(d,p) structure, the additional water molecule only formed one H-bond with a corner of the cuboid. In the SCCDFTB structure, this water formed two H-bonds with an edge of the cuboid, which again led to an unusual triangular structure of water cluster, similar to the H-bonded triangle in the structure of (H₂O)₁₀ cluster. (Figure 3b)

Figure 5.

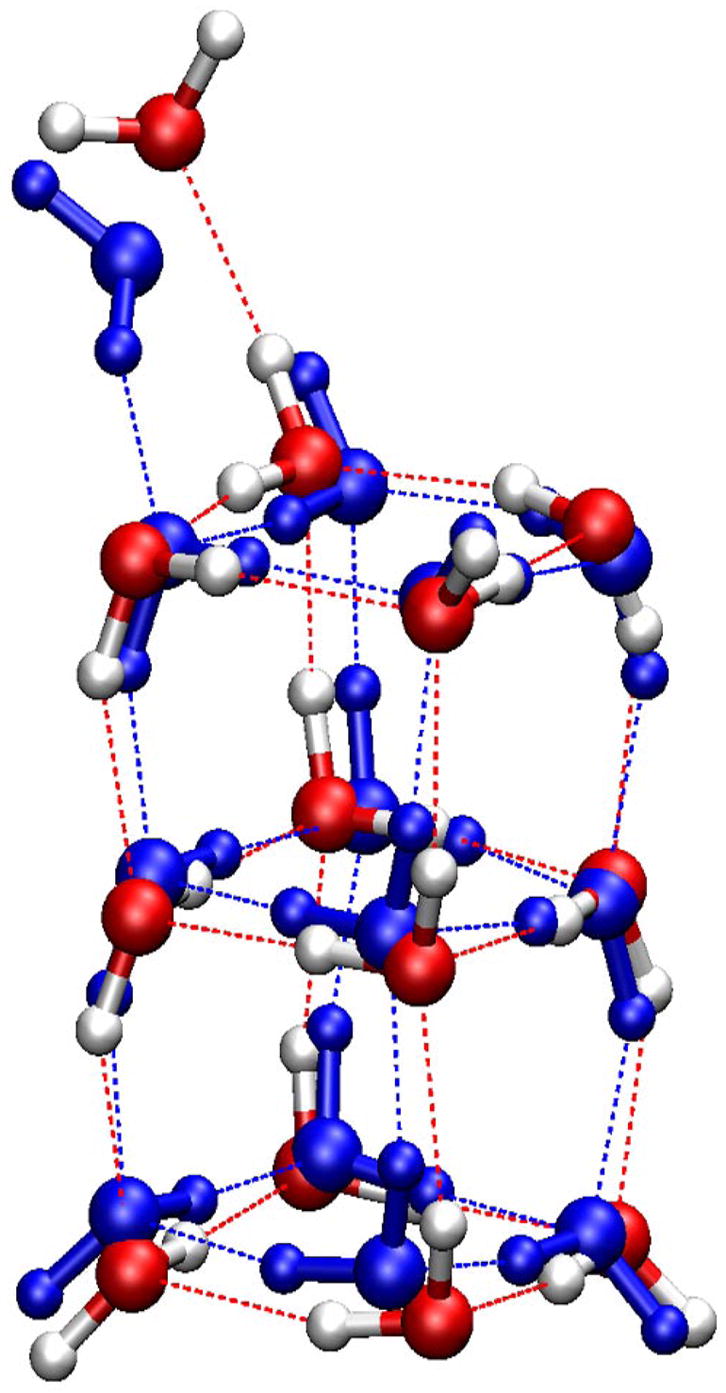
Minimized structures of the (H₂O)₁₃ cluster. CPK model in red (oxygen) and white (hydrogen) is the structure minimized from the Cambridge Cluster Database; CPK model in blue is the lowest-energy conformation identified with the SCCDFTB method.

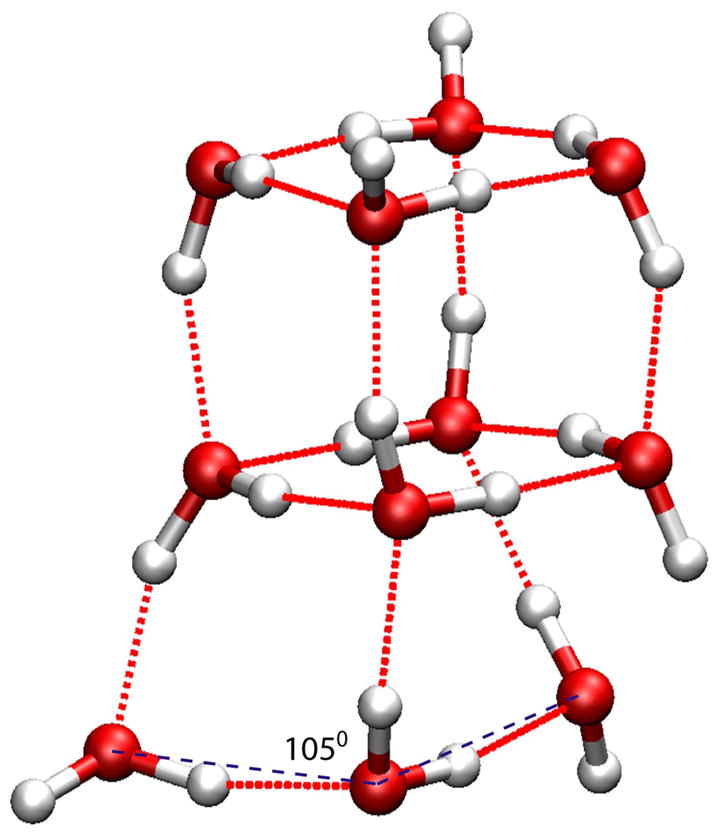
For the (H₂O)₁₄ cluster, the lowest-energy structures from two methods are shown in Fig 6. The overall structures are surprisingly similar to each other, except that the size of the SCCDFTB structure is slightly smaller than the HF/6-31G(d,p) structure. The most important difference is the H-bonding pattern of the four/five-member rings at the top: in the SCCDFTB structure, there are two OH bonds at the top free of H-bond; in the HF/6-31G(d,p) structure, the OH bonds of the top level are all saturated by H-bonds.

For the (H₂O)₁₈ cluster, the lowest-energy structures from two methods are shown in Fig 7. The biggest difference is the relative position of the two water molecules on the top: in the SCCDFTB structure, the two top water molecules formed a closed “basket handle” and resembled the SCCDFTB structure of (H₂O)₁₀ cluster; in the HF/6-31G(d,p) structure, the two water molecules only interacted with an edge of the stacked water cubes. In both the (H₂O)₁₈ and (H₂O)₁₀ clusters, it seems there is a tendency of forming three/four-member ring structure of water molecules in the SCCDFTB method, which partially explains the extra stabilization of the lowest-SCCDFTB-energy structures identified here.

Figure 6.

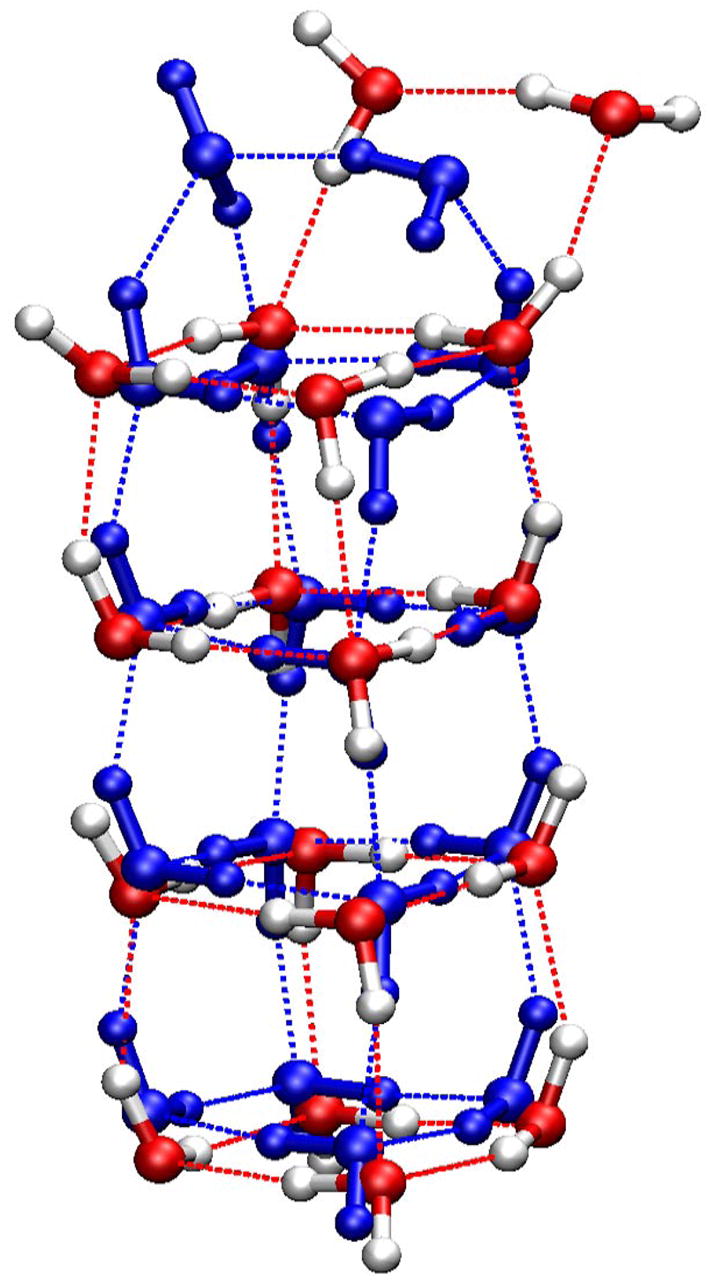
Minimized structures of the (H₂O)₁₈ cluster. CPK model in red (oxygen) and white (hydrogen) is the structure minimized from the Cambridge Cluster Database; CPK model in blue is the lowest-energy conformation identified with the SCCDFTB method.

A recent DFT study also reported a set of minimum energy structure for water clusters. ⁴⁵ For those structures reported, we also computed the binding energies using the SCCDFTB method with new γ function. (Fig. 2) All but the (H₂O)₁₄ cluster have energy higher or equal to that of the structures optimized in HF/6-31G(d,p) calculations. This may again indicate that the SCCDFTB method over-stabilizes small ring of water molecules appeared in the HF/6-31G(d,p) calculations instead of large five/six-member rings which are abundant in the DFT calculations.

For those lowest-energy conformations identified by the SCCDFTB method for the (H₂O)_N cluster, N=10, 11, 13, 14, and 18, we further re-minimized them by the HF/6-31G(d,p) method to examine if those structures are stable in ab initio methods. The energies of the re-minimized conformations are reported in Table II. The SCCDFTB structures are indeed stable with the HF/6-31G(d,p) method. However, the value and rank of energies are evidently different from SCCDFTB calculations. One surprising result is that the (H₂O)₁₁ and (H₂O)₁₃ structures identified with the SCCDFTB method have HF/6-31G(d,p) energy even slightly lower than that of the lowest-energy structure in the original HF/6-31G(d,p) calculations. This result might be attributed to much broader sampling of the phase space in the SCCDFTB simulations carried out here, which also highlights the important role SCCDFTB can play as a bridge between inaccurate molecular mechanics force fields and accurate but expensive high-level ab initio methods. To accurately measure the relative stabilities of those conformations, further calculations with a more rigorous QM method might be needed, however.

Table II.

Comparison of the HF/6-31G(d,p) binding energies between the lowest-energy conformations identified with SCCDFTB method and HF/6-31G(d,p) method for (H₂O)_N, N=10, 11, 13, 14, and 18. The energies are in kcal/mol.

N	ΔEbind(SCCDFTB)a	ΔEbind(HF)b
10	−93.97	−96.75
11	−105.89	−105.69
13	−130.33	−128.33
14	−141.05	−144.78
18	−187.59	−188.64

^aThe energies were computed by re-minimizing the lowest-SCCDFTB-energy structures with the HF/6-31G(d,p) method.

^bThe original lowest binding energies reported in ref 31.

Combining the analysis of the structures in both the simulations of the liquid water and the water clusters, one general observation is that the SCCDFTB method has a tendency of forming three/four-member ring of water clusters, therefore, more than four water molecules can settle in the limited space of the first solvation shell. Even though the exact reasons responsible for this tendency cannot be concluded here, obviously a better description for the H-bond interaction is desired. To reach this goal, several improvements of the SCCDFTB method might be helpful, including: using of larger basis sets, adding multipolar interactions other than point charges, and refitting the SCCDFTB parameters to a better DFT functional.

For other conformations with their energies listed in Table I, further analysis of the corresponding structures reveals additional interesting observations. Contrary to the ab initio calculation in which a limited number of minimum energy conformations with significant energy differences have been found for each cluster, the SCCDFTB method determined many more minimum energy conformations, most of which were only slightly different in energies, such as the (H₂O)₉ cluster shown in Table I. Examining the structures indicated that often those structures differed only by a subtle change of the conformation, e.g., a flipping of a non-hydrogen-bonded O-H bond between the axial and equatorial positions. If those structures were minimized again with ab initio methods, most of them eventually converged to the same small ensemble of minimum energy conformations identified in the original ab initio calculations.³¹ In other words, it appears that the surface of the SCCDFTB calculation may be discontinuous and thus many artificial minimum energy states showed up. This result might be attributed to the tabulated parameters in the SCCDFTB method which were designed to speed up the speed of computations.

Conclusion

Using the SCCDFTB method, we have carried out full quantum mechanic simulation of liquid water with the divide-and-conquer method. The simulation results, although still distant from perfection, gives qualitatively correct description of shell-structured liquid water. Analysis of the simulation of the liquid water and the conformational search of the water clusters reveal the deficiency of the SCCDFTB method, as well as the directions to improve the SCCDFTB method.