Polarizable Empirical Force Field for Aromatic Compounds Based on the Classical Drude Oscillator

Abstract

The polarizable empirical CHARMM force field based on the classical Drude oscillator has been extended to the aromatic compounds benzene and toluene. Parameters were optimized for benzene and then transferred directly to toluene, with parameters for the methyl moiety of toluene taken from the previously published work on the alkanes. Optimization of all parameters was performed against an extensive set of quantum mechanical and experimental data. Ab initio data was used for determination of the electrostatic parameters, the vibrational analysis, and in the optimization of the relative magnitudes of the Lennard-Jones parameters. The absolute values of the Lennard-Jones parameters were determined by comparing computed and experimental heats of vaporization, molecular volumes, free energies of hydration and dielectric constants. The newly developed parameter set was extensively tested against additional experimental data such as vibrational spectra in the condensed phase, diffusion constants, heat capacities at constant pressure and isothermal compressibilities including data as a function of temperature. Moreover, the structure of liquid benzene, liquid toluene and of solutions of each in water were studied. In the case of benzene, the computed and experimental total distribution function were compared, with the developed model shown to be in excellent agreement with experiment.

Introduction

Aromatic compounds, of which benzene may be considered the parent, play a central role in the chemical industry as well as in biological systems. These include a series of hydrocarbons known as the benzene series, formed by the substitution of methyl groups, CH₃, for the hydrogen atoms of the benzene molecule. Based on their general importance, aromatic compounds have been subjected to a multitude of studies in all phases: crystalline, liquid and gaseous. The use of spectroscopic methods is ubiquitous, and different techniques ranging from neutron scattering^1–4, and nuclear spin resonance⁵ to both linear^6–9 and non-linear^10–15 spectroscopies have been applied to study this class of compounds.

A current trend is the use of spectroscopic techniques in condensed phases, with the spectroscopic intensities, line shapes and widths related to the structure and dynamics of the liquids.^6–15 In fact, in the condensed phase it is these properties, together with the line position, that are particularly sensitive to both the static and dynamic environment of a given molecule. Understanding such properties requires probing the structure and motion of the fluid at a molecular level, information that can typically only be obtained from theoretical approaches. The availability of information from computational studies may be used retrospectively to interpret the spectroscopic parameters.

First-principles ab initio calculations^16,17 have been extensively used to study both ground and excited state properties in the gas phase. A recent review of the latest developments in ab initio computational studies of aromatic compounds can be found in ref 18. Going beyond gas phase theoretical studies via ab initio methods are a variety of condensed phase simulation studies of aromatic compounds using molecular dynamics (MD)^4,19–29 or Monte-Carlo^30,31 methods often based on empirical force fields, typically making use of nonpolarizable or additive models.^27,32–34 These models have proved their usefulness by accurately reproducing a variety of experimental observables including phase change properties, free energies of solvation, transport properties and structural properties of the fluids or solids. Examples of additive models include the CHARMM,³⁵ GROMOS,³⁶ OPLS,³² and AMBER³⁷ force fields, among others. The majority of these force fields have been optimized based on the reproduction of experimental enthalpies of vaporization and densities, as pioneered by Jorgensen.³⁸ Further improvements in additive models have included the incorporation of free energies of hydration in the target data^39–41 and MacKerell and co-workers have introduced a protocol for Lennard-Jones (LJ) parameter optimization using a combined ab initio/empirical approach that provides better balanced LJ parameters.³⁹ Such advances are expected to further improve the accuracy of additive force fields, although the limitation associated with the additive approximation in the treatment of electrostatics will hinder significant further development of such models.

Empirical models of aromatic molecules using non-additive, polarizable models are still scarce in the literature and, to date, have not demonstrated any substantial changes in the molecular properties over the traditional additive force fields.^34,42 These studies made use of fluctuating charge models to treat the explicit polarizability. Heats of vaporization and molecular volumes were used for the optimization of those force fields; however, additional validation of the models using a wider range of condensed phase properties was not performed.

The present study is a continuation of our ongoing effort towards development of a polarizable empirical force field for biological molecules. In the present model electronic polarizability is introduced via a classical Drude oscillator,^43–50 which allows for the nonadditivity to be treated via auxiliary particles attached to the atomic centers of the system. An extended Lagrangian for use in MD simulations using the Drude model has been presented⁵⁰ and water models, referred to as SWM4-DP⁵¹ and SWM4-NDP⁵², have been developed and shown to reproduce a variety of experimental condensed phase properties including the dielectric and self-diffusion constants. In these water models the polarizability is treated via the use of a Drude particle on only the oxygen, laying the groundwork for a force field that includes polarizability only on non-hydrogen atoms. Beyond development of the water models, Drude based force fields for ethanol⁵³ and alkanes⁵⁴ have been presented. In addition, a general method for the determination of the partial atomic charges and polarizabilities has been presented and applied to develop a preliminary model of DNA that was shown to be stable in a 1 ns MD simulation that included explicit solvent and sodium counterions.⁵⁵

In the present paper, a novel force field for the aromatic compounds benzene and toluene based on a polarizable potential energy function in the context of the classical Drude oscillator is presented. It is shown that a variety of experimental and QM target data are accurately reproduced by the force field, including condensed phase properties. In addition, to better put the present force field in the context of previously published CHARMM additive force fields, results from the CHARMM22 (C22) force field are presented.³⁵

Computational Methods

QM calculations were performed with the Gaussian 03 suite of programs.⁵⁶ Geometry optimizations were performed at the MP2(fc)/6-31G(d) level of theory. This level of theory provides molecular geometries consistent with available gas phase experimental data (see the Supporting Information) and it has been previously utilized during optimization of the latest version of the latest all-atom additive CHARMM force field (CHARMM27).^57,58 QM calculations of the molecular electrostatic potentials (ESP) were performed on MP2 optimized geometries using the B3LYP hybrid functional^59,60,61 and the correlation-consistent double-ζ Dunning aug-cc-pVDZ basis set,⁶² as previously discussed.⁵⁴ Single-point energy B3LYP calculations were performed with the tight convergence criteria producing the target QM ESP maps. QM calculations on the complexes with rare gas atoms were performed at the MP3/6-311++G(3d,3p) level³⁹ and vibrational analysis was performed at the MP2/6-31G* level followed by scaling of the frequencies by 0.9434.⁶³ Potential energy distributions of the normal modes were performed as previously published.⁶⁴

Empirical force field calculations were performed with the program CHARMM.^65,66 The simple functional form of the potential energy function from the pairwise additive CHARMM all-atom force field⁶⁶ was used with polarizability introduced using the classical Drude oscillator model with some modification. In the classical Drude oscillator model the polarizability is introduced by adding massless charged particles attached to polarizable atoms (e.g., only non-hydrogen atoms in the present model) via a harmonic spring with the force constant k_D. The partial atomic charge of a polarizable atom q is redistributed between the Drude particle and atomic core. The sign of the charges on Drude particles q_D has minimal impact due to the point dipole approximation; q_D is chosen to be negative by analogy with the electron charge.⁶⁷ The magnitudes of q_D can be unambiguously determined from the atomic polarizabilities using the relationship α =q_D²/k_D. The charge on the atomic core q_c is determined by subtracting the Drude charge from the charge on the atom-Drude pair q, such that each atom-Drude pair forms a dipole q_D·d, where d is the displacement vector going from the atom to its Drude particle. Thus, the electrostatic energy term in the additive potential energy function was modified to include interactions between atomic cores and Drude particles, and the term describing the self-energy of a polarizable atom via the harmonic term 1/2k_D·d² was added to the potential energy function.⁶⁷

All nonbonded electrostatic interactions involving Drude particles are treated in the same way as electrostatic interactions between real atoms, i.e., via the Coulomb law. For atoms excluded from the nonbonded lists (i.e., 1–2 and 1–3 covalent pairs), the electrostatic term is modified to allow 1–2 and 1–3 screened dipole-dipole interactions, as suggested by Thole.⁶⁸ The screening is implemented through the smearing of the charge on the Drude particle and real atom. Then the screened dipole-dipole interactions are calculated via interactions between a smeared charge with a Slater distribution (using the screening parameter 2.6 in all our calculations) and a point charge.⁵³

Partial atomic charges and atomic polarizabilities for the Drude polarizable force field for the aromatic compounds were determined from restrained fitting to QM response ESP maps, as per previous protocol.⁶⁷ Briefly, the ESP grid points were located on concentric non intersecting Connolly surfaces around the molecules. To determine both atomic polarizabilities and partial atomic charges from the single fitting procedure, a series of perturbed ESP maps was generated, representing the electronic response of the molecule in the presence of a background point charge of magnitude +0.5e placed on Connolly surfaces along chemical bonds and in the gaps between the initial perturbation charges to achieve nearly equidistant coverage of the molecular shape. Five alternating Connolly surfaces of perturbation charges and grid points were generated with size factors 2.2 (charges), 3.0 (grid), 4.0 (charges), 5.0 (grid), and 6.0 (charges), where the size factor multiplied by the vdW radius of the corresponding atom determines its distance from the corresponding surface. Fitting was performed using parabolic restraints to the initial values of both the charges and polarizabilities with the weighting factor of 10⁻⁵ Å⁻². Additionally, a flat well potential with the half-width of 0.1 was used for atomic polarizabilities. Fitting to the same charge and polarizability values was imposed for chemically equivalent atoms.

Molecular dynamics (MD) simulations were performed at 1 atm pressure using the new velocity Verlet integrator⁵⁰ implemented in CHARMM. The SWM4-NDP model⁵² was used in all calculations involving water. All simulations were performed by default at 298.2 K for both benzene and toluene. Temperature dependence studies of the enthalpies of vaporization were also conducted and the values of the temperatures appear in the text. For these temperatures experimental data for the substances in the liquid phase at 1 atm pressure is available. A Nosé-Hoover thermostat with a relaxation time of 0.1 ps was applied to all real atoms to control the global temperature of the system. A modified Andersen-Hoover barostat with a relaxation time of 0.1 ps was used to maintain the system at constant pressure. Condensed-phase MD simulations were performed using periodic boundary conditions and SHAKE to constrain covalent bonds involving hydrogens.⁶⁹ Electrostatic interactions were treated using particle-mesh Ewald (PME) summation⁷⁰ with a coupling parameter 0.34 and a 6^th order spline for mesh interpolation. Nonbond pair lists were maintained out to 14 Å, and a real space cutoff of 12 Å was used for the electrostatic and Lennard-Jones terms. Long-range contributions to the van der Waals terms were corrected for as previously described.^71,72 The extended Lagrangian double-thermostat formalism⁵⁰ was used in all polarizable MD simulations where a mass of 0.4 amu was transferred from real atoms to the corresponding Drude particles. The amplitude of their oscillation was controlled with a separate low-temperature thermostat (at T = 0.1 K) to ensure that their time course approximates the SCF regimen.⁵⁰

Operational parameters for the MD simulations using the extended Lagrangian formalism included 1.0 fs time steps and force constants of 500 kcal/(mol·Å²) on the Drude particles. Tests of larger force constants, up to 800 kcal/(mol·Å²) were conducted and yielded virtually identical results. All simulations of the neat fluids requiring periodic boundary conditions were performed typically with cubic boxes containing 128 molecules. This is the case of all simulations leading to computation of densities, enthalpies of vaporization, self-diffusion coefficient, isothermal compressibilities, specific heat capacities and the dielectric constants. Larger boxes of 256 molecules were used to study the dynamics of the pure liquids in order to be able to recover the full layered structure of the liquids as required for analysis of radial or spatial distribution functions. Simulations requiring dissolution of benzene or toluene in water were conducted in cubic boxes containing 128 water molecules. This was used, for example, in the computational determinations of the free energies of hydration and in the analysis of hydration through the use of radial or spatial distribution functions. The same protocol was used for the simulations with the polarizable and C22 force fields, with the TIP3P water model⁷³ used in the additive force field calculations. The total length and the number of simulations used in the parametrization work varied according to the observable being simulated and the stage of the parameterization work. During the optimization stages, in particular during optimization of LJ parameters using condensed phase simulations, a high rate of turnover was required in order to probe many combinations of LJ parameters. In this case simulations to compute enthalpies of vaporization were performed with total lengths of 500 or 700 ps, of which the final 200 and 400 ps were used for analysis. Free energies of hydration were carried out initially with runs of 10ps for equilibration and 30 ps for analysis. Validation of the newly developed parameters made use of longer simulation times, as follows; (a) densities, enthalpies of vaporization, coefficient of self-diffusion, isothermal compressibilities, specific heat capacities and the dielectric constants were obtained from simulations of 1 ns of which the last 600 ps were taken for analysis. Each property was run multiple times using different random number seeds to assign the initial velocities, as noted, and the results averaged; (b) simulations for the computation of the free energies of solvation were run for a total of 130 ps with the first 30 ps used for equilibration and the final 100 ps for the production run. Coordinates sets from the trajectories were saved every 0.1 ps in the case of the dielectric constants and every 0.5 ps otherwise when required.

Additional properties as required for both optimization and validation of the presented model were calculated as follow. The density (ρ) is the total mass over the current volume averaged over the simulations,

$$\rho =\langle \frac{\mathit{mass}}{V}\rangle$$ (1)

Experimental densities as a function of temperature were taken from refs ^74,75. The error bar of ρ equals the corresponding standard deviation.

Heats of vaporization, ΔH_vap, were determined from differences of averages of the potential energy of the molecules in the condensed phase, <U_liquid>, and the average potential energy of a molecule in the gas phase, <U_gas>. These values were corrected for the different volumes between the liquid and gas phases by the term RT.⁷⁶ The complete expression to compute the heats of vaporization is:

$$\mathrm{\Delta }{H}_{\mathit{vap}}=-\frac{\langle U_{\mathit{liq}}\rangle }{N_{\mathit{mol}}}+\langle U_{\mathit{gas}}\rangle +RT$$ (2)

One assumption of this expression is the equivalence of the sum of the kinetic and vibrational energies in the gas and liquid phases.⁷⁷ Calculation of the gas phase energies, U_gas, was done using Langevin dynamics in the SCF approximation. The same Drude force constant and masses used in the condensed-phase simulations were used along with infinite nonbonded cutoffs. A friction coefficient of 5.0 ps⁻¹ was applied to all atoms except for Drude particles. The gas-phase simulations were performed on one monomer for 2 ns.

Calculation of the self-diffusion coefficient (D_s) requires computation of the mean square displacement (MSD) of the center-of-mass (COM) of all molecules according to the equation, where D_PBC is the apparent self-diffusivity for the periodic boundary condition:

$$D_{\mathit{PBC}}=\underset{t\to \infty }{lim}\frac{1}{6}\frac{\partial }{\partial t}\langle MS{D}_{\mathit{COM}}\rangle$$ (3)

The computed values of D_s were corrected for system size effects using the hydrodynamic model of Yeh and Hummer⁷⁸ of a particle surrounded by a solvent with a viscosity, η,

$$D_S=D_{\mathit{PBC}}+\frac{K_{B}T\xi }{6\pi \eta L}$$ (4)

Isothermal compressibilities were calculated from

$${\beta }_T=-\frac{1}{V}{\left(\frac{\partial V}{\partial P}\right)}_T=\frac{\langle \delta V^2\rangle }{V{K}_{B}T}$$ (5)

where V is the volume, 〈δV²〉 are volume fluctuations and K_B is the Boltzmann’s constant.

The specific heat capacity (C_p) at constant pressure was calculated with five production runs at different temperatures, 293.2, 298.2, 303.2, 308.2 and 313.2. The total energy 〈U_tot〉 and the volume 〈V〉 were averaged over time. The pressure used in the following formula is the target value of the barostat (P = 1 atm). A linear fit of the plot (〈U_tot〉 + P〈V〉) vs T was used to calculate C_p.

$$C_P=\frac{1}{N_{\mathit{mol}}}{\left(\frac{\partial \langle U_{\mathit{total}}\rangle +P\langle V\rangle }{\partial T}\right)}_{T=300K,P=\mathit{atm}}$$ (6)

The static dielectric constant ε of the pure compounds was calculated from the dipole moment fluctuations of the box using

$$\epsilon ={\epsilon }_{\infty }+\frac{4\pi }{3{\langle V\rangle }_{(f)}{k}_B{T}^{\ast }}\left({\langle M^2\rangle }_{(f)}-{\langle M\rangle }_{(f)}^2\right)$$ (7)

where M is the total dipole moment of the box, <V> is the average volume of the box, and ε_∞ is the high-frequency or optical dielectric constant ε_∞.⁷⁹ Time series of M were obtained from 4 independent simulations of 600 ps using data from the last 400 ps of each simulation and then concatenated into one large time series, which was used for the ε calculation from eq 7. The values of ε were then averaged over the last 200 ps of this combined time series when they reached a plateau in all simulations. The high-frequency optical dielectric constant, ε_∞ can be estimated from the Clausius-Mossotti equation, which relates ε_∞ to the molecular polarizability.^51,80 However, we used a more direct way of calculating ε_∞ from classical fluctuations of induced dipoles as a measure of total polarizability of the box as was proposed by Neumann and Steinhauser⁸¹ and recently used by Lamoureux et al.⁵¹ ε_∞ was calculated from the dipole fluctuations of the box associated with the movement of Drude oscillators according to Langevin dynamics at temperature T* for 10 frozen nuclear configurations extracted from regular molecular dynamics simulations using the equation

$${\epsilon }_{\infty }=1+\frac{4\pi }{3{\langle V\rangle }_{(f)}{k}_B{T}^{\ast }}\left({\langle M^2\rangle }_{(f)}-{{\langle M\rangle }_{(f)}}^2\right)$$ (8)

where <…>_(f) indicates an average over induced-dipole fluctuations only.⁵¹ It was previously found that the choice of T* is irrelevant for the calculation of ε_∞ since nuclear positions are fixed⁵¹ and thus T* was chosen to be 0.1 K as for the low temperature thermostat used in the extended Lagrangian molecular dynamics simulations (see above). For additive CHARMM force field simulations ε_∞ was set to 1 since no electronic degrees of freedom are explicitly modeled in this case.

Free energies of hydration were computed through free energy perturbation (FEP)⁸² using the protocol of Deng and Roux.⁸³ In the FEP method, the free energy change ΔG corresponding to the change in the potential energy from U_i to U_j can be determined as an average over the ensemble of configurations generated with the potential energy U_i, according to eq 9:

$$\mathrm{\Delta }G=-kTln{\langle exp\left(-\frac{U_j-U_i}{kT}\right)\rangle }_{(U_i)}$$ (9)

Since this technique is valid only when the perturbation is small, in practice intermediate potential energy surfaces U(λ) are constructed where λ is a coupling parameter such that U(λ=0) = U_i and for U(λ=1) = U_j.⁸³ The free energy of hydration was calculated as a sum of nonpolar and electrostatic components. The nonpolar part was decomposed into dispersion and repulsion contributions using the method of Weeks, Chandler and Andersen (WCA).⁸⁴ All atomic and Drude charges of the solute were set to 0 when calculating the nonpolar contribution. The slowly varying dispersion term was calculated with the linear coupling scheme with the coupling parameter ζ according to equation 10 with ζ varied from 0 to 1 in increments of 0.1. Indexes μ and v represent solute and solvent, respectively.

$$U_{uv}^{\mathit{nonpolar}}(\xi )=U_{uv}^{\mathit{repul}}+\xi U_{uv}^{\mathit{disper}}$$ (10)

The repulsive term was transformed to a soft-core potential and calculated in multiple stages.⁸³ The staging parameter, s, was set to 0.0, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 and 1.0. The electrostatic part was also calculated using the standard linear coupling scheme with a coupling parameter λ. The parameter λ varied from 0 to 1 in increments of 0.1. The states with λ=0 and λ=l correspond to the fully discharged and charged solute, respectively. The free energy contributions from simulations run using different staging parameters were summed. The weighted histogram analysis method (WHAM)⁸⁵ was used to obtain the free energies from the simulations. The solvation free energies were computed as a sum of the electrostatic, dispersive, and repulsive contributions. Each term was obtained as a difference in the free energy of the solute in water and in a vacuum.

Results and Discussion

Optimization and validation of the force field

Optimization of the benzene model was based on both QM and experimental data. Internal parameters were optimized to reproduce geometries and vibrational spectra from both QM and experimental data.⁸⁶ Electrostatic parameters were from QM ESP maps while the LJ parameters were based on the density and the heat of vaporization of neat benzene and the free energy of solvation of benzene at room temperature. As generally done in the CHARMM force fields optimization was performed in an iterative manner as required due to the interdependence of the different terms in the energy function.^39,58,87 The process is nicely illustrated in Figure 1 of ref 58, where a flowchart of the various steps involved in the optimization process in presented.

Validation of the newly developed parameters for benzene and applied to toluene used various thermodynamic and transport properties including the densities and heats of vaporization as a function of temperature, the self diffusion coefficient, the isothermal compressibility, specific heat capacity and the dielectric constants.

Determination of electrostatic parameters

Determination of the electrostatic parameters, the charges and polarizabilities, is the first step in the parametrization protocol of the Drude polarizable force field. Initial values of the partial atomic charges and polarizabilities were taken from the C22 additive all-atom force field³⁵ and from adjusted Miller’s atomic hybrid polarizabilities (ahp) values, respectively.⁸⁸ Benzene is a highly symmetric molecule and all six CH groups are equivalent thus restraining the charges to be of equal magnitudes and different signs on the C and H atoms. However, on toluene the optimized charges do not need to maintain electroneutrality on the methyl or CH groups, though the values of chemically identical atoms are restrained to be equivalent. The fitted values of atomic polarizabilities were scaled to reflect the reduced polarization expected for the condensed media and/or to correct for the systematic underestimation of experimental molecular polarizabilities by B3LYP calculations. Polarizabilities were scaled by 0.724 as in refs ⁵¹ and ⁵³.

Initial calculations were undertaken using the scaled polarizabilities and the full charges. However, in the case of benzene it was observed that the polarization response in MD simulations of the monomer in the gas phase was unstable. This led to catastrophic failure, which is attributed to the symmetry of the benzene molecule causing problems in the charge fitting procedure. To overcome this problem it was necessary to scale the partial atomic charges by 0.7 for benzene, yielding charged comparable to toluene (Table S3 of supporting information). No such scaling was performed for toluene. As will be shown below this adjustment lead to some decreases in the ability of the model to reproduce gas-phase target data associated with the benzene dimer and benzene-rare gas interactions; however, the model with the scaled charges lead to good agreement with a variety of condensed phase data. Also, as unscaled charges were used with toluene, the application of the force field to other aromatic species will be performed using charges directly from the fitting procedure.

Initial assessment of the quality of the fitted electrostatic parameters was done by comparing computed dipole or quadrupole moments and polarizabilities with QM and/or experimental results (Table 1). Benzene has a null dipole moment at the equilibrium geometry and comparison was to the quadrupole moment. Included in Table 1 are results for benzene without and with scaling of the charges. Concerning the benzene quadrupole moment, charge scaling of the charges lead to improved agreement with the various target data, with the level of agreement being significantly better than CHARMM22. The improved agreement of the polarizable model is expected due to the need to overestimate the quadrupole in the additive model as required to reproduce the condensed phase effects. For toluene, the polarizable model overestimates the experimental dipole while CHARMM22 significantly underestimates the dipole. The latter result appears to be associated with the charge assignment approach used in the CHARMM22 force field where standard charges for the aromatic and aliphatic groups are used without further optimization.⁸⁹

Table 1.

Dipole (in Debye) and quadrapole moments (in au) for different models of benzene and toluene. (1 au ≈ 4.4866 × 10⁻⁴⁰ C·m² ≈ 1.3450 Buckingham)

Method	μ	θαα	θββ	θχχ	Ref
Benzene
Drudea	0	2.67	2.67	−5.34
Drudeb	0	3.58	3.58	−7.15
C22	0	4.50	4.50	−9.00
Zeeman		3.25	3.25	−6.50	119
Zeeman		3.16	3.25	−6.32	120
X-Ray		3.20	3.20	−6.40	121
Birefringence		3.16	3.16	−6.31	122
Birefringence		3.23	3.23	−6.46	123
Toluene
Drudeb	0.420	−4.47	2.18	2.29
C22	0.122	−5.17	2.57	2.59
Experimentc	0.375				109

^aPolarizable model with unsealed charges.

^bPolarizable model with charges scaled by 0.7.

^cMethodology unknown

Optimization of Internal Parameters

Optimization of the internal parameters was done by reproducing target data on the geometry and vibrational spectra of benzene. Internal parameters for toluene were transferred from benzene and complemented with previously determined parameters for the methyl group.⁵⁴ Target data for the geometries included the optimized structure of benzene at the MP2/6-31G(d) level along with a survey of the Cambridge Structural Database (CSD),⁹⁰ with the results shown in Table S1 of the Supporting Information. Direct transfer of the internal parameters from the additive model was appropriate, since the optimized geometries for both models are equivalent. This is true for all bond, angle and torsion parameters, except one. This is also evident from the good agreement with the target experimental⁸⁶ and scaled MP2/6-31G(d) spectra shown in Table S2 of the Supplementary Information. The list of all parameters used in this work is shown in Table S3 of the Supplementary Information.

Optimization of Lennard-Jones Parameters

LJ parameters were optimized iteratively based on a procedure described in detail in ref 39. It involves two steps: the relative and absolute optimizations. The relative procedure, aimed at yielding parameters in which the relative values of the LJ parameters for different atom types (e.g., carbon and hydrogen in the aromatic ring of benzene) were able to reproduce relative ab initio minimum interaction energies and geometries for different rare gases to model compound interactions, was initially applied. Target data for this optimization includes RMS fluctuations about average differences or ratios between the QM and empirical models for selected interaction orientations between He and Ne. The absolute optimization procedure is included to ensure that the values of the LJ parameters yield condensed-phase properties, such as enthalpies of vaporization and free energies of solvation, in good agreement with experiment at 298.2 K. The newly developed parameters were validated by comparing computed and experimental thermodynamic and transport properties at different temperatures. Thermodynamic properties included enthalpies of vaporization, free energies of solvation, isothermal compressibilities and heat capacities at constant pressure. Diffusion coefficients computed at several temperatures were the only transport property computed in this work.

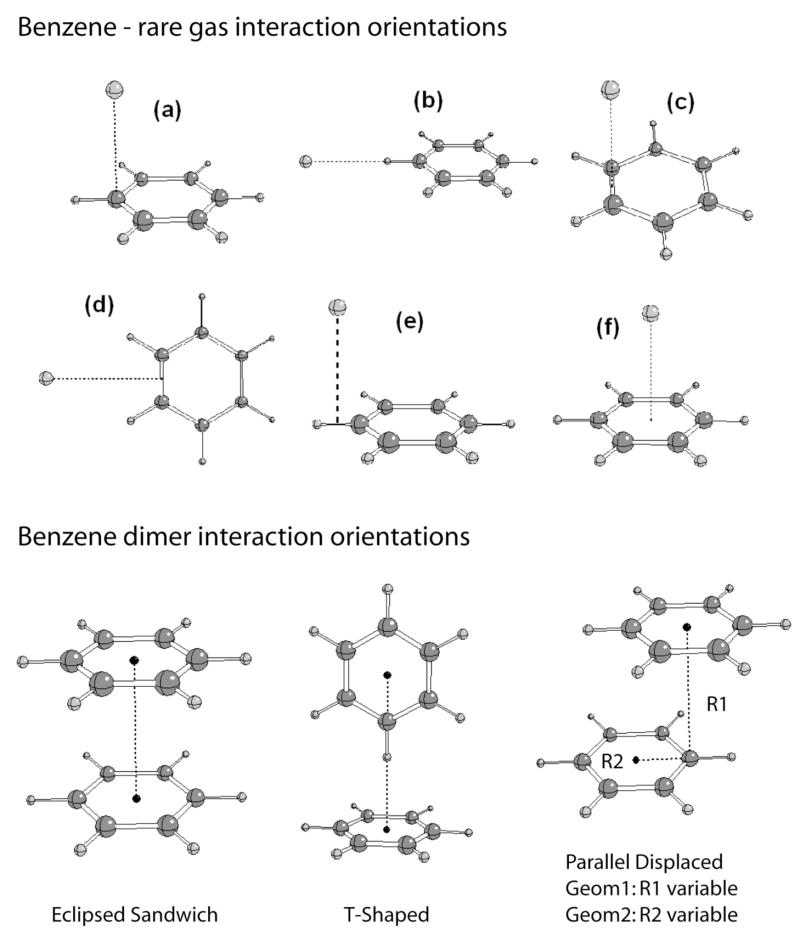
Presented in Table 2 are the RMS fluctuations about the average differences and ratios between the QM and empirical models for the interactions with the rare gases. Data are based on the interaction orientations shown in Figure 1. In Table S4 of the Supporting Information absolute values for the individual interactions are presented. RMS fluctuations of both the ratios and differences of the rare gas interactions are generally similar for the polarizable models in which the charges are unscaled and scaled. Such a small change is expected given that the use of rare gas atoms is designed to primarily probe repulsion/dispersion interactions. Importantly, the fluctuations are systematically improved in the polarizable force field as compared to the additive model, although by a small margin. This indicates that the use of the improved electrostatic model that includes polarizability allows for a better balance of the LJ parameters of carbon and hydrogen, with the relatively small improvement with respect to CHARMM22 indicative of the quality of the additive model.

Table 2.

RMS fluctuations about the average differences and ratios between the QM and CHARMM minimum interaction energies and distances for the benzene-rare gas interactions.^*

	Rmin(Å)		Emin (kcal/mol)
Complex	Drude	C22	Drude	C22
	Difference
Benzene/Hea	0.1292	0.1325	0.0211	0.0243
Benzene/Heb	0.1243		0.0239
Benzene/Nea	0.0564	0.0564	0.0684	0.0708
Benzene/Neb	0.0577		0.0651
	Ratio
Benzene/Hea	0.0478	0.0492	0.1907	0.1962
Benzene/Heb	0.0482		0.1827
Benzene/Nea	0.0167	0.0190	0.0874	0.0891
Benzene/Neb	0.0171		0.0823

^*RMS fluctuations were calculated as in Yin and MacKerell.³⁹

^aPolarizable model with unsealed charges.

^bPolarizable model with charges scaled by 0.7.

Figure 1.

Interaction orientations of benzene with the rare gases and of the benzene dimer.

Energies and geometries for the interaction of benzene dimers were also incorporated in the optimization of the LJ parameters. Calculations of binding energies and geometries of benzene dimers have been actively studied using quantum mechanical methods. In the past five years alone 12 studies have been published.^91–102 Reference data for the present work was taken from CCSD(T) calculations extrapolated to the complete basis set limit by Sinnokrot and Sherrill, probably the most accurate study published to date.⁹⁶ Three geometries were considered in ref 96 namely: staggered, T-shaped and laterally displaced geometries (Figure 1). This yields 4 target interaction orientations since the laterally displaced geometry is described by two distances and two geometries with each of the distances being individually frozen during optimization of the dimer. Comparison of the polarizable model with unscaled charges shows the overall agreement to be satisfactory, with the staggered geometry being slightly to favorable with the remaining interactions underestimated. Differences in the distances vary significantly, being to short for the staggered orientation and significantly to long for the second laterally displaced orientation. The use of scaled charges leads to the balance of the interaction energies becoming significantly worse, with the staggered and T-shaped orientations significantly overestimated and underestimated, respectively. However, the two displaced orientation interaction energies are in good agreement with the QM and minimum interaction energy differences being better balanced. The CHARMM22 results are similar to the unscaled polarizable results, with a reasonable balance of the interaction energies but poorer balance of the distances as a function of the interaction orientation.

Heats of vaporization and molecular volumes for toluene and benzene are shown in Table 4 for both the additive and polarizable models. For both benzene and toluene the Drude model reproduces the experimental target data within 2% of the experimental value, our targeted limit. Noteworthy is the good agreement observed for toluene since no special optimization of LJ or internal parameters was performed relative to benzene. Only the electrostatic parameters were determined as described above. Transferability of parameters is a key aspect of a force field and the current combination of LJ and internal parameters yield satisfactory condensed phase properties when applied to toluene. The same set of parameters has been used as the basis of a polarizable model of heteroaromatic molecules, including pyridine and pyrimidine, and yielded results of the same quality.¹⁰³ As will be shown below, the model also yields excellent agreement at temperatures above room temperature, which were not considered in the optimization procedure, highlighting the quality of the Drude model and the developed parameter set.

Table 4.

Comparison of empirical and experimental heats of vaporization and densities of neat benzene and toluene

		Drude		C22		Experimental dataa
	T(K)	Vm(Å3)	ΔHvap	Vm(Å3)	ΔHvap	Vm(Å3)	ΔHvap
Benzene	298.2	147.46±0.71	8.01±0.03	151.97±0.72	7.53±0.03	148.00	8.08
Benzene	353.3	159.29±1.09	7.33±0.04	166.01±0.83	6.74±0.04	158.40b	7.34c
Toluene	298.2	175.64±0.38	9.12±0.04	180.43±0.19	8.47±0.05	176.51	9.08
Toluene	383.8	195.81±0.85	7.83±0.04	203.85±1.52	7.31±0.02	195.06b	7.93c

Experimental data from ref109.

From eqs 4–11.4a and 4–11.5 of ref124.

Experimental data from ref125.

Free energies of hydration of benzene and toluene for both the polarizable Drude model and C22 are compared with experimental results in Table 5. The results for both force fields are good, with the polarizable model performing better in the case of benzene and worse for toluene. Better agreement for benzene is expected due to the free energy of solvation being considered during parameter optimization; the satisfactory level of agreement for toluene supports the transferability of the model.

Table 5.

Comparison of experimental and calculated free energies of solvation in aqueous solution for benzene and toluene

	Benzene				Toluene
	Drude	C22	Expt.		Drude	C22	Expt.
ΔGrep	14.61±0.11	12.73		ΔGrep	17.00±0.21	14.69
Δ Gdisp	14.24±0.09	−12.05		ΔGdisp	16.32±0.07	−13.82
ΔGnp	0.37±0.20	0.68		ΔGnp	0.68±0.21	0.87
ΔGel	−1.43±0.06	−1.80		ΔGel	−2.00±0.02	−1.69
ΔGsol	−1.06±0.22	−1.12	−0.86	ΔGsol	−1.32±0.21	−0.83	−0.89

A number of additional pure solvent properties were calculated to validate the model. Dielectric constants are shown in Table 6. As is evident the agreement of the Drude model with experiment is very good. The basis of this level of agreement are the ε_∞ values which are due to the presence of polarizability in the model. The omission of explicit polarizability in the additive CHARMM force fields inherently disallows the proper treatment of the dielectric, as previously discussed for the alkanes.⁵⁴

Table 6.

Comparison of experimental and calculated dielectric constant of liquid benzene and toluene

	Dielectric constant (a)		Heat capacity (cal·mol−1K−1)
	Benzene	toluene	benzene	toluene
Expt.	2.2825	2.3790	32.49	37.59
Drude	2.1369(ε∞) 2.1799 (ε)	2.3374 (ε∞) 2.5642 (ε)	38.50±0.35	46.38±0.35
C22	1.0247 (ε)	1.0369 (ε)	40.95±0.28	51.84±6.78

^aExperimental data from ref 109

Computed and experimental heat capacities are given in Table 6. For both satisfactory results are obtained for the polarizable models of both benzene and toluene. For both models the absolute values of the calculated and experimental heat capacities are somewhat overestimated; however the model is able to reproduce the difference between benzene and toluene with an error of 2.3 cal·mol⁻¹·K⁻¹.

Results for the computed isothermal compressibility of benzene and toluene are shown in Table 7. The polarizable model slightly underestimates the experimental values for both benzene and toluene and the calculated toluene value is slightly higher than benzene in contrast to experiment, though the precision of the calculated values is larger than the differences in the average values. C22 performed better than the Drude model, except at the highest temperatures. The isothermal compressibility is the only property where the additive model clearly outperforms the polarizable model.

Table 7.

Comparison of experimental and calculated isothermal compressibilities of liquid benzene and toluene. Units are Gpa⁻¹

	Temperature (K)	Drude	C22	Exp.a
Benzene	288.2	0.693±0.214	0.842±0.179	0.907
Benzene	298.2	0.825±0.124	0.976±0.099	0.969
Benzene	313.2	0.877±0.135	1.129±0.085	1.098
Benzene	328.2	1.112±0.096	1.386±0.138	1.178*
Toluene	273.2	0.745±0.162	0.667±0.058	0.784
Toluene	298.2	0.872±0.300	0.882±0.110	0.915
Toluene	325.7	1.269±0.107	1.389±0.053	1.092*

^aaverage of experimental values from ref126.

^*experimental value obtained at 323.2 K

The performance of the polarizable empirical force field was also validated by computing the self-diffusion coefficients of the pure liquids. The results are shown in Table 8. Both the polarizable and additive models are in excellent agreement with experiment. This includes the temperature dependence of the calculated values following the experimental trends for both molecules.

Table 8.

Comparison of experimental and calculated self-diffusion coefficients of liquid benzene and toluene

		Drude	C22	Exp
	T(K)	105·D (cm2·s−1)	105·D (cm2·s−1)	105·D (cm2·s−1)
Benzene	288.2	1.85±0.16	1.85±0.18	1.85a
Benzene	298.2	2.26±0.14	2.17±0.17	2.20
Benzene	313.2	2.95±0.41	2.70±0.15	2.79
Benzene	328.2	3.45±0.18	3.66±0.52	3.66
Toluene	273.3	1.38±0.12	1.35±0.12	1.54
Toluene	298.2	1.97±0.17	2.08±0.18	2.28
Toluene	325.7	3.35±0.13	3.35±0.11	3.22

Structure of liquid benzene and toluene

A common method of studying the structure of neat liquids and solutions is to calculate radial distribution functions (RDFs), g(r), between different interaction sites. These quantities, sometimes designated as “pair correlation functions,” can be combined to obtain the probable structure of dimer configurations and structures of solvation spheres and intermolecular interactions including hydrogen bonds. RDFs can also be used to calculate coordination numbers by integrating over the RDFs in order to obtain an average number of neighbors as a function of distance. Experimental atom–atom radial distributions are available as Fourier-transformed partially resolved structure factors from neutron or x-ray diffraction studies.¹⁰⁴ For example, the benzene liquid structure has been determined by Narten^105,106 and recently Tassaing and co-workers have studied the structure of liquid and supercritical benzene by neutron diffraction.¹⁰⁷

The total radial distribution function for the polarizable and additive models, denoted as g_inter as in ref 107 are shown in Figure 2. The curves are nearly identical to the experimental data of Cabaço and co-workers⁴ obtained from incoherent neutron diffraction experiments. Both the polarizable and additive models reproduce the experimental data nearly perfectly. However, previous computer simulations have shown that this is the case with the overwhelming majority of simulation conditions,^108,47–50 suggesting that reproduction of this property is relatively trivial.

Figure 2.

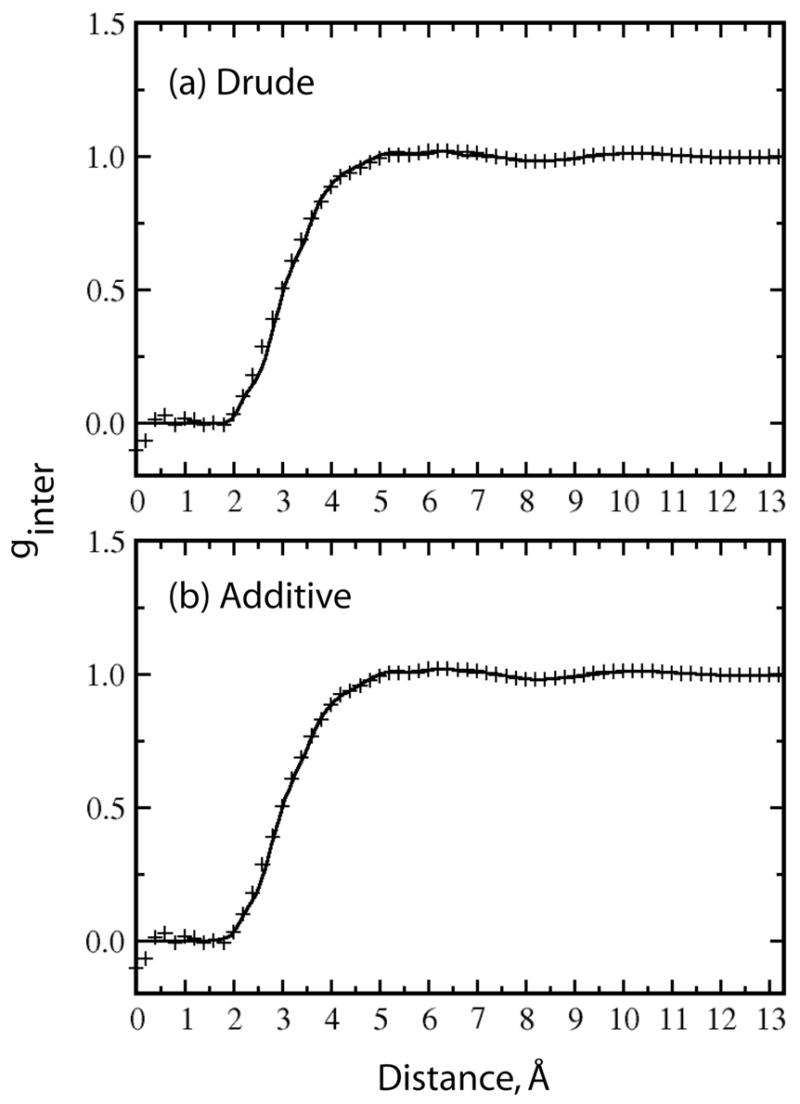
Computed intermolecular pair correlation function g_inter(r)· g_inter(r) was calculated from the pair radial distribution functions: g_CC, g_CH and g_HH through the expression g_inter(r) = 0.25·g_CC+0.50·g_CH+0.25·g_HH. Calculated data shown as a solid line and experimental data from Cabaço and coworkers in reference ¹⁰⁴ presented as crosses.

More detailed comparison of the new polarizable and CHARMM22 models was performed via comparison of the RDFs for the centers of mass of benzene and toluene, as shown in Figure 3. The RDFs are similar for both the additive and polarizable models, showing long-range order extending up to the third shell. The distribution of the first neighbors has a maximum at about 5.6 Å with a contact distance between molecular centers of mass of about 3.7 Å. However, there are subtle differences in the RDFs with the Drude model having the initial rise in first peak at shorter distances than CHARMM22 with the maximum of the first peak at a slightly larger distance. This suggests the Drude model to have a somewhat softer interaction surface for the benzene-benzene interactions as may be expected due to the inclusion of polarizability.

Figure 3.

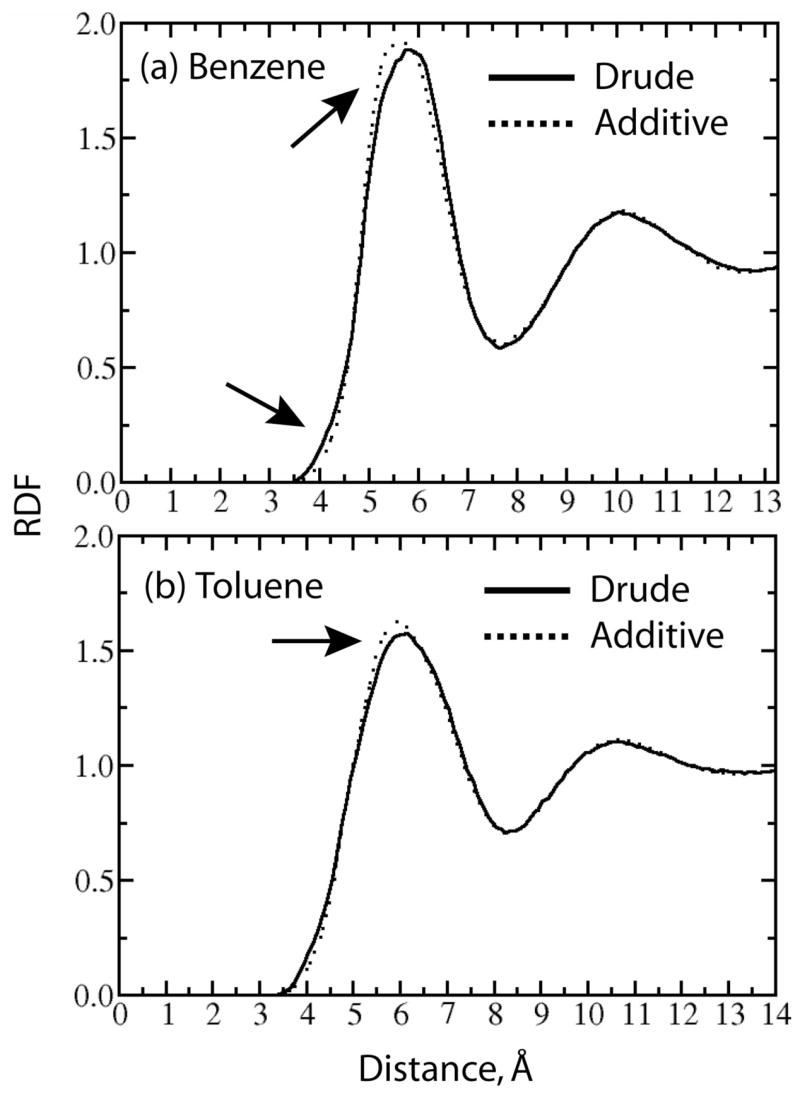
Radial distribution functions between the center of mass of benzene (a) or toluene (b) and that of surrounding molecules for the polarizable (solid line) and additive (dotted line) models of the pure solvents. Important features of the two curves are indicated by the arrows, (x axis: distance in Å; y axis: normalized intensity).

Further exploration of the cage structures in pure benzene and toluene were performed via computation of the spatial distribution functions G(r,θ), defined in equation 11 as

$$G(r,\theta )=\frac{1}{N\rho }\langle \sum _{i=j}\delta (r-r_{ij})\delta (\theta -{\theta }_{ij})\rangle$$ (11)

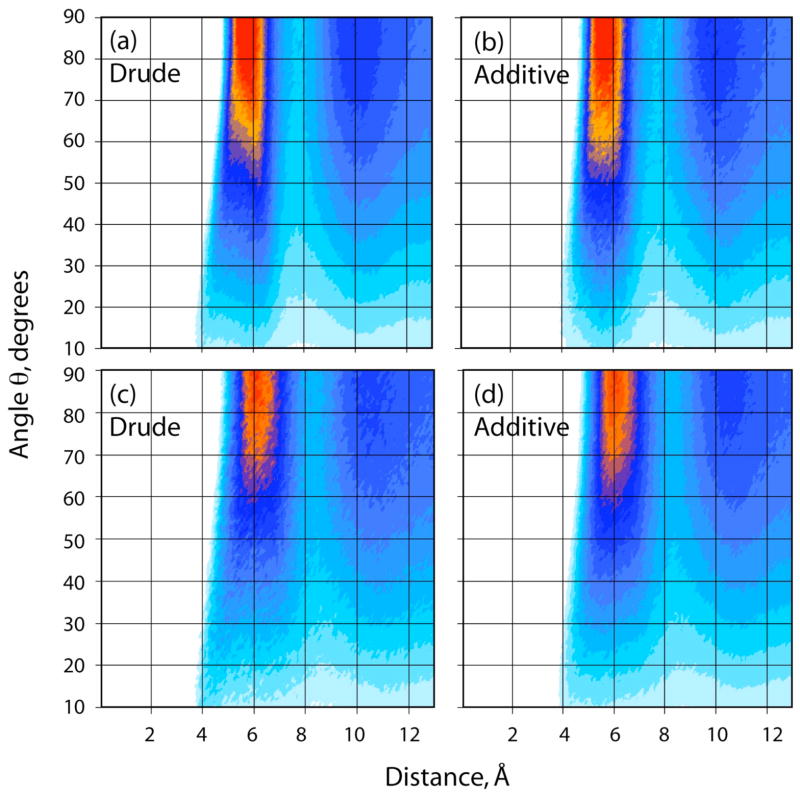
where ρ is the density of the sample. The angular part, (θ), is defined by the angle between the separation vector and a vector perpendicular to the aromatic ring with the origin at the center of the ring. A geometrical description of the coordinate system is shown in Figure 4. The G(r, θ) function gives the orientational correlation of a pair of molecules i and j having their centers of mass at a distance r_{i j} and the angle between their main symmetry axes equal to θ_ij. The representations of G(r, θ) of benzene are shown as contour plots in Figures 5a and 5b for the polarizable and C22 models, respectively. Unlike the crystal, the first coordination shell of the liquid reveals, on average, no uniquely preferred orientation. Both T-shaped orientations (Figure 6a) corresponding to the region of 4 – 6 A and 0 to 40° and sandwich or parallel displaced types of arrangements (Figure 6b) can occur. The parallel arrangements are favored as evidenced by the maxima of the G(r, θ) function occurring between the 60 and 90° in both the polarizable and additive force fields, though this is related to the increase in the number of possible benzene-benzene interactions that may occur. At distances less than 4.7 Å the T-shaped orientation is favored for obvious steric reasons due to the close packing. Again, the overall distributions for the two models are similar, although the distribution of the first peak (i.e. From 4 to 7 Å) is broader and less symmetric in the polarizable model. Thus, while both models reproduce the experimental RDFs with satisfactory accuracy (Figure 2), there are subtle differences suggesting that the polarizable model is giving a somewhat different picture of the atomic details of the interactions in liquid benzene.

Figure 4.

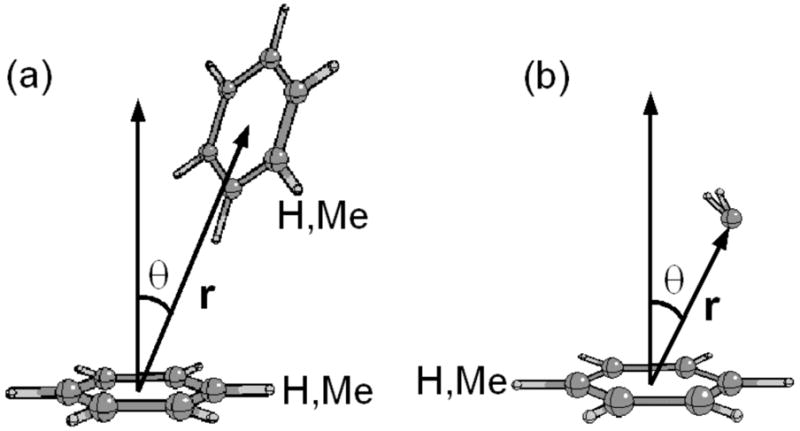
Illustration of the coordinate system used to compute the spatial distribution functions. r is the separation vector between the center-of-mass of a benzene or toluene molecule and the center-of-mass of another benzene or toluene or the oxygen atom of a water molecule. θ is the angle between r and the vector perpendicular to the plane of the aromatic ring from the center-of-mass.

Figure 5.

Spatial distribution functions of liquid benzene and toluene. Plots (a) and (b) are for the polarizable and additive models of benzene and plots (c) and (d) are for the polarizable and additive models of toluene. The coordinate system is illustrated in Figure 4. The gradation of colors, going from areas of less to higher probabilities is white < pale blue < dark blue < orange < red.

Figure 6.

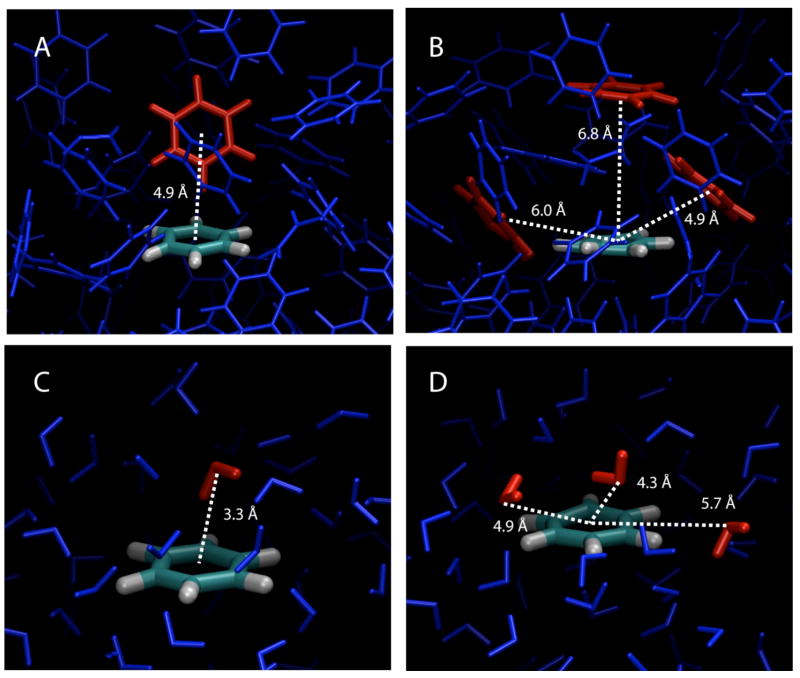
Illustration of typical interactions occurring between benzene molecules (panels a and b) and between benzene and water (panels c and d). Panel (a) represents benzene-benzene T-shaped type of interaction (Figure 1) and (b) shows benzene-benzene interactions similar the eclipsed sandwich and parallel displaced orientations from the polarizable pure benzene simulation. Panel (c) represents a water interacting with the centroid of the benzene ring corresponding to the region of 3.3 Å and 10 – 20° in Figure 8 and (d) shows typical interactions of water around the edge of the benzene ring corresponding to the region of 4 – 6 Å and 40 to 90° in Figure 8 from the polarizable benzene-water simulation.

In toluene the overall G(r, θ) distributions (Figures 5c and 5d) are similar to that of benzene. However, the area of accumulation at 6 Å from 50 to 90° is broader than in benzene, although the maxima occupy similar regions. This is due to the presence of the methyl group leading to the sampling of a wider range of orientations similar to the parallel displaced orientation seen in Figures 1 and 6b. An impact from the inclusion of polarization is visible by comparing Figures 5c and 5d. This region from 4 to 8 Å and 10 to 50° is slightly more diffuse in the polarizable model, consistent with that seen in benzene.

Aqueous Solutions of Benzene and Toluene

Aqueous hydration of organic compounds has received a great deal of attention. Polar and apolar groups have different solubilities in water and this has been linked to many diverse phenomena in chemistry and biology.^51–58 While hydrophobic interactions are expected to be important in dissolving benzene and toluene in water, it should be kept in mind that toluene has a small dipole moment of 0.375 D¹⁰⁹ and that benzene possesses a considerable molecular quadrupole moment, which is involved in Coulombic interactions. Also, there is experimental evidence for attraction between the π-electrons of benzene and the hydrogen atoms of water in a hydrogen-bond like configuration.¹¹⁰ Further, the aromatic structure of benzene imparts a negative partial charge on its face and a positive partial charge around its edges. Based on these properties the ability of benzene to act as a hydrogen bond acceptor was predicted in the 1980s.¹¹¹ Since that time, experiments have shown that benzene does indeed form hydrogen bonds with water (see ref 112 and refs therein). In addition, details of the water-benzene interaction have been investigated using Monte Carlo^113,114 and MD^115–117 simulations of a single benzene molecule in solution. These theoretical studies also show that water molecules prefer to adopt a hydrogen-bonding interaction with the faces of the benzene ring. In one study a hydration sphere of approximately 23 water molecules around benzene was observed with two water molecules found on each side of the benzene plane.¹¹⁸ These results are consistent with the higher relative solubility of benzene over that of other hydrocarbons.

Figure 7a shows the RDF curves between the center of mass of benzene and the oxygen atoms of the water molecules. Differences between the polarizable and additive models are indicated by arrows. An interesting feature is a shoulder at the distance of 3.5 Å. This feature is due to direct interactions of the benzene carbon and water hydrogen atoms. The shoulder is higher and more structured in the additive force field versus the polarizable model. This again suggests the polarizable model to be somewhat softer than the additive model, yielding a slightly different atomic picture of the interactions of benzene with its environment. There is also a small shift of the large peak in Figure 7a to smaller separations in the polarizable force field. In addition, the rift separating the peaks at 5.1 and 7.6 Å is more pronounced with the polarizable force field. These results suggest that while the polarizable model is softer with respect to contact interactions it also yields a more well defined preference for water molecules to populate the region associated with the first benzene-water peak as compared to the additive model.

Figure 7.

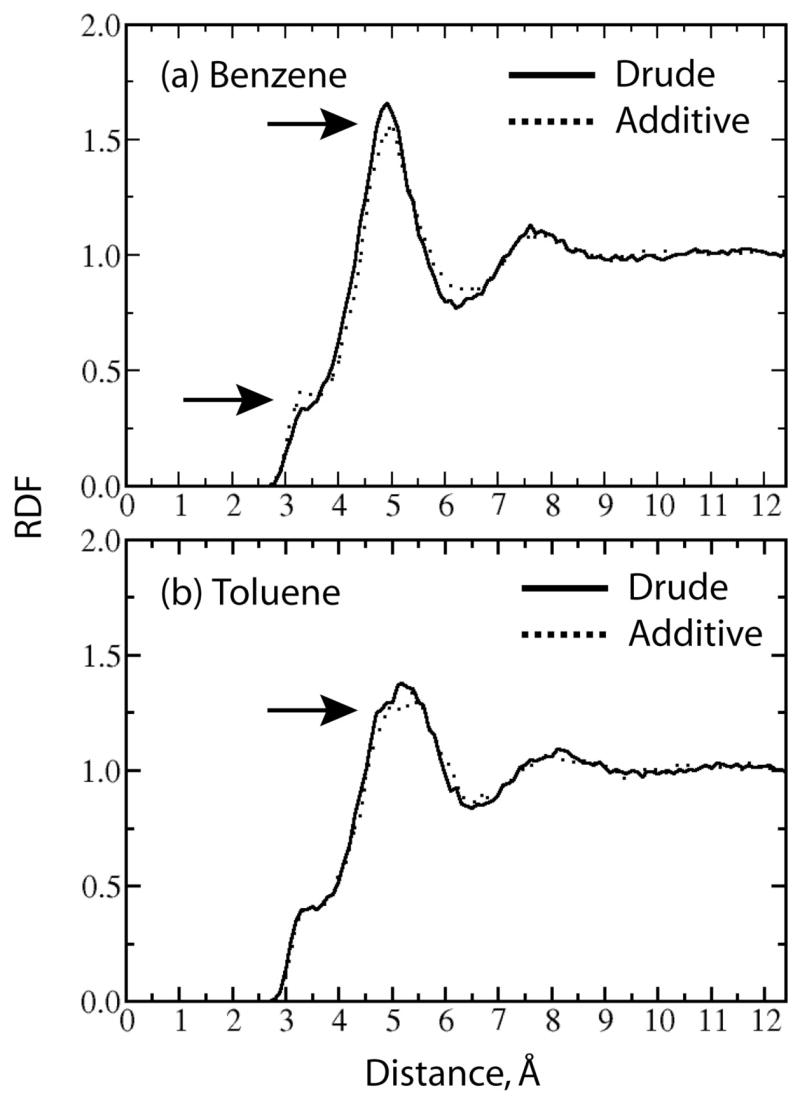
Radial distribution functions between the centers of mass of benzene (a) or toluene (b) and the oxygen atoms of the water molecules for the polarizable (solid line) and additive (dotted line) models. Arrows indicate relevant features in the plots, (x axis: distance in Å; y axis: normalized intensity).

In toluene the difference between polarizable and additive force fields is less evident, particularly in the region of the shoulder at 3.5 Å (Figure 7b). However, similar to benzene, the first peak is more structured in the polarizable model and the minima at ~6.5 Å more pronounced. For the remaining distances the structure of water around toluene remains largely identical for the two models.

Further insight into the distribution of the water molecules around a single molecule of benzene was obtained by using combined distribution functions of both the radial and angular coordinates of the separation vector, as performed above for the pure solvents based on equation 11. The coordinate system defining the distributions is shown in Figure 4, with the resulting distributions presented as contour plots for the polarizable and additive CHARMM calculations of both benzene (Figure 8a and b) and toluene (Figure 8c and d). Red corresponds to areas of high accessibility to water and white to areas where water is excluded. Looking at the results for benzene the following features are evident:

Figure 8.

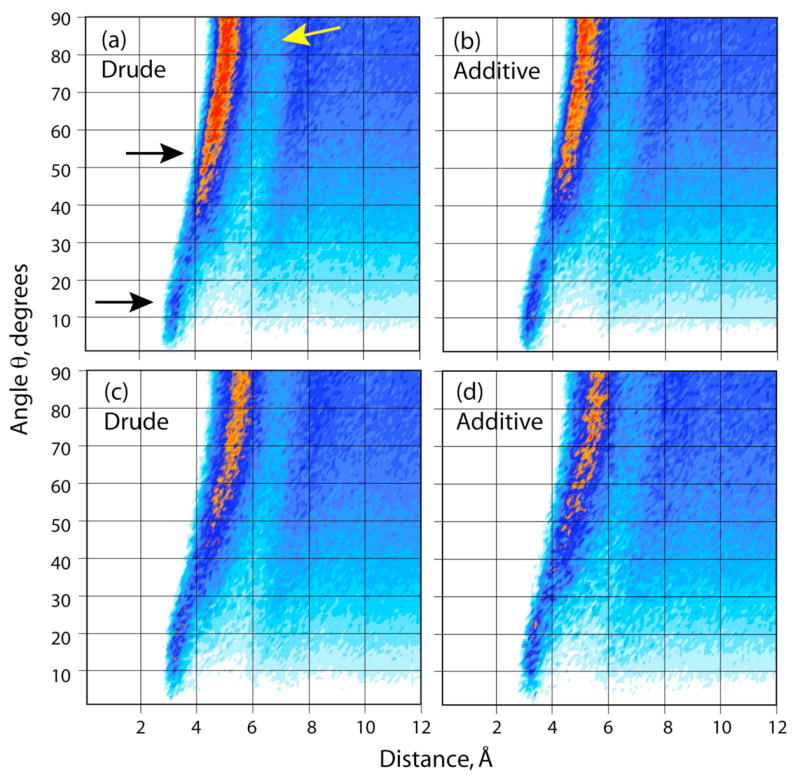
Spatial distribution functions of aqueous solutions of benzene and toluene. Plots (a) and (b) are for the polarizable and additive models of benzene in water. Plots (c) and (d) are for the polarizable and additive models of toluene in water. The coordinate system is illustrated in Figure 4. The gradation of colors, going from areas of less to higher probabilities is white < pale blue < dark blue < orange < red.

Water in the immediate vicinity of benzene lay above and below the C_h symmetry plane, as seen in Figure 6c. This region from 3 to 4 Å and from 0 to 30° is seen to be somewhat broader and slightly more populated in the additive mode. This is consistent with the higher peak observed at 3.5 Å in Figure 7a. These observations are the result of polarization above the molecular plane, which biases the water molecules to lie above the carbon atoms.

The bulk of water molecules stay in regions approximately parallel to the molecular plane over the carbon and hydrogen atoms (Figure 6d) and out to an edge-on orientation with the ring. This corresponds to the orange/red areas of Figure 8 from 40 to 90°. Water is somewhat more structured in the case of the polarizable force field and stays in a narrower area. The increased structure of the water molecules observed with the polarizable force field is further indicated by the area between 6–7 A and 60–90 °, which is more depleted in Figure 8a (yellow arrow).

In the case of toluene the contour plots for the polarizable and additive models (Figure 8c and d) are consistent with the RDF plots of Figure 7b. The contact region from 3 to 4 Å is similar for the two models, with the population of the highly sampled region directly above the face of the ring slightly more well-defined in the polarizable model.

Conclusions

Presented is a polarizable model of benzene based on the classical Drude oscillator formalism. The model was optimized to reproduce a variety of gas and condensed phase target data. Transferability of the optimized parameters was tested via their application to toluene, with the methyl parameters transferred from previously published alkane parameters. The quality of the resulting toluene model in treating various condensed phase properties supports the transferability of the parameters. Additional validation of the developed force field was performed via calculation of additional condensed phase data, including dielectric constants, self-diffusion coefficients, heat capacities, isothermal compressibilities and radial distribution functions. While many of the structural based properties are similar for the presented polarizable and additive models, there are differences in the atomic details of the interactions in the condensed phase. These differences along with the general improvement of the polarizable model in reproducing condensed phase properties and its ability to reproduce the experimental dielectric constant, which is not possible in the additive force field, indicates that the model will be useful for force field based studies of benzene and related compounds. In addition, the availability of aromatic parameters lays the groundwork for the development of a Drude-based polarizable model for biological molecules.

Supplementary Material

si20070209_123. SUPPORTING INFORMATION.

Four tables including geometries, vibrations, force parameters and interactions with rare gases are presented.

Table 3.

Benzene dimer minimum interaction energies and geometries

Orientation	Interaction Energies, kcal/mol			Distances, Å
Polar	QM	Empirical	Diff	QM	Empirical	Diff
Sandwiched	−1.81	−1.91	−0.10	3.90	3.75	−0.15
T-Shaped	−2.74	−2.40	0.34	5.00	5.11	0.11
P-Displaced 1	−2.78	−2.28	0.50	3.60	3.60	0.00
P-Displaced 2	−2.78	−2.36	0.42	1.60	2.10	0.50
Polar, 0.7 scaled charges
Sandwiched	−1.81	−2.62	−0.81	3.90	3.70	−0.20
T-Shaped	−2.74	−2.07	0.67	5.00	5.15	0.15
P-Displaced 1	−2.78	−2.69	0.09	3.60	3.58	−0.02
P-Displaced 2	−2.78	−2.70	0.08	1.60	1.39	−0.21
C22
Sandwiched	−1.81	−1.85	−0.04	3.90	3.76	−0.14
T-Shaped	−2.74	−2.15	0.59	5.00	5.15	0.15
P-Displaced 1	−2.78	−2.12	0.66	3.60	3.63	0.03
P-Displaced 2	−2.78	−2.19	0.59	1.60	2.10	0.50

Interaction orientations in Figure 1.