How is spatial context learning integrated over signal versus noise? A primacy effect in contextual cueing

Abstract

Over repeated exposure to particular visual search displays, subjects are able to implicitly extract regularities that then make search more efficient—a phenomenon known as contextual cueing. Here we explore how the learning involved in contextual cueing is formed, maintained, and updated over experience. During an initial training phase, a group of signal first subjects searched through a series of predictive displays (where distractor locations were perfectly correlated with the target location), followed with no overt break by a series of unpredictive displays (where repeated contexts were uncorrelated with target locations). A second noise first group of subjects encountered the unpredictive displays followed by the predictive displays. Despite the fact that both groups had the same overall exposure to signal and noise, only the signal first group demonstrated subsequent contextual cueing. This primacy effect indicates that initial experience can result in hypotheses about regularities in displays—or the lack thereof—which then become resistant to updating. The absence of regularities in early stages of training even blocked observers from learning predictive regularities later on.

A major goal of visual processing is to recover information about the structure of the natural environment. Such information comes in several forms. Perhaps most intuitively, visual processing involves recovering the local visual features of objects, and the way those objects and features are arranged into visual scenes. A considerable amount of regularity in visual input, however, is also statistically distributed in both space and time. Accordingly, the visual system also appears to automatically extract regularities in spatial layouts and temporal sequences—including subtle regularities that may not be available to conscious report. Here we focus on determining just how and when such learning is triggered, maintained, and updated over time, focusing on contextual cueing.

CONTEXTUAL CUEING

The phenomenon of contextual cueing was originally demonstrated in the spatial domain using visual search tasks (Chun & Jiang, 1998). Subjects searched for target shapes in a field of distractor shapes with half of the trials involving a small set of spatial layouts that were frequently repeated. In these trials, the layout of the distractors predicted the target location (though not its identity). In the other half of the trials, in contrast, the distractor layouts were not repeated, and were not associated with any particular target location. Such experiments yielded the phenomenon of contextual cueing: Search response times grew faster over time for the repeated layouts. Critically, this learning occurs without intent or even conscious awareness of the regularities. Since this initial demonstration, a growing body of research has explored just which factors support such learning (see Chun, 2003).

STATISTICAL LEARNING

Studies of contextual cueing have typically focused on the response-time benefits that accrue due to the encoding of statistical regularities, but additional research conducted under the rubric of “statistical learning” (Saffran, Aslin, & Newport, 1996) has shown that such learning can also be expressed in other ways, including simple familiarity judgements, even when no explicit task is involved during encoding. In the spatial domain, for example, a pair of shapes that appear in correlated locations (within more complex displays) will come to be associated, so that this pair will later seem more familiar to observers than an arbitrary pairing of shapes—even if all individual shapes had been experienced equally often (Fiser & Aslin, 2001, 2002b). Visual statistical learning of this type also occurs in the temporal domain, where observers encounter a sequence of shapes, one at a time, and become implicitly familiarized with subtle regularities in the order with which the shapes are presented (Fiser & Aslin, 2002a; see also Olson & Chun, 2001). Other recent studies of temporal visual statistical learning have blurred the distinction between contextual cueing and statistical learning, showing that the same statistical regularities can give rise to both enhanced familiarity judgments and response-time benefits (Turk-Browne, Jungé, & Scholl, 2005). In this situation, the underlying learning is presumably the same in each case, and is simply being expressed in different ways.

THE CURRENT STUDY: HOW IS SPATIAL CONTEXT LEARNING INTEGRATED OVER SIGNAL VERSUS NOISE?

Previous research on spatial contextual cueing has explored several factors that constrain what is learned (e.g., only locally proximate layouts, or only attended items; Jiang & Chun, 2001; Olson & Chun, 2002). Here, in contrast, we explore an equally important question that to our knowledge has not received any direct study: Is contextual cueing sensitive to the order in which predictive information is presented? In particular, suppose that subjects encounter a sequence that contains both (1) signal trials, in which distractor locations are predictive of target positions, and (2) noise trials, in which there is no such relationship. Holding constant the statistical information that is encountered in the overarching sequence, does the order of exposure to these two subsequences impact what is learned? This is exactly the experimental design that we employ in the present study.

We can distinguish at least three possible answers to this question, each of which has some intuitive support:

1. Such learning may simply be continuous. Since subjects are not even typically aware of the underlying regularities (Chun, 2003; Chun & Jiang, 1998), they do not choose to begin (or to stop) learning them. Rather, the learning that underlies contextual cueing may simply happen, all the time. If in fact contextual cueing is an automatic process, then it would certainly be helpful for it to operate on all available regularities. Thus, the order in which signal and noise subsequences are encountered may not affect what is learned at the end of the overall sequence.

2. Such learning may indeed operate continuously, but be biased to jettison older regularities. The visual environment, after all, can change, and regularities that used to apply may no longer hold. Thus, it might make more sense for contextual cueing to prioritize more recently encountered regularities. This might give rise to a recency effect that would predict better learning when signal follows noise, compared to when noise follows signal.

3. In direct opposition to the previous possibility, such learning may actually weigh earlier information more heavily than recent information. Though contextual cueing seems to operate automatically and effortlessly, it may in fact require substantial underlying resources. As a result, it may simply be wasteful for such learning to operate continuously—especially with regard to spatial layouts in the real world. After such layouts are learned, they may often be stable, such that it would yield no further benefits to keep learning those same layouts over and over. Conversely, if processing experience fails to uncover any regularities, it might not be economical for the visual system to continue searching for them. Rather, it might make more sense to give up when it is possible to reliably determine that no strong regularities are present. These considerations might give rise to a primacy effect, wherein contextual cueing is dominated by initially encountered information—so that learning is better when signal precedes noise, compared to when noise precedes signal.

A critical task in the study of any cognitive or perceptual process is to determine when that process does and does not operate. It seems to us that each of the three possible conflicting outcomes in this regard for contextual cueing is reasonably plausible, and that none is a straw man. As a result, we designed the present study to determine which of these possibilities is true, but we did so without any single theoretically motivated prediction about the outcome.

METHOD

Participants

Forty-six students at Yale University participated for pay. Twenty-three subjects were run in the signal first condition and twenty-three were run in the noise first condition. Data from two subjects (one in each condition) were excluded from the analysis because their overall error rates were greater than 3 standard deviations above the mean for the search task. All observers were naïve to the purpose of the experiment and had normal or corrected-to-normal acuity.

Apparatus

The experiment was programmed in Matlab using the Psychophysics Toolbox extensions (Brainard, 1997), and was conducted on a Macintosh computer with a 17-inch screen. Subjects viewed the display without restraint from approximately 57 cm.

Stimuli

Throughout the experiment subjects searched through displays of randomly rotated distractor “L”s (oriented 0, 90, 180, or 270 deg), and responded to the orientation of the single rotated target “T”. Each “L” subtended approximately 2.0 deg, and the point of contact between the longer and shorter bars was offset towards centre by 0.15 deg, to increase search difficulty. The two possible targets were “T”s (subtending 2.0 deg) rotated by either 90 or 270 deg, and exactly one was present on every search trial.

For each subject we generated 24 distinct context displays that were constant throughout the experiment and presented once in every block. Each display contained 12 items, three in each quadrant of the screen. Each item was placed into one of 12 evenly distributed potential locations within each quadrant (yielding 48 possible distractor locations), and was then randomly jittered by 0.0–0.5 deg. During the initial training phase (described below), these 24 context displays were each presented in signal blocks and in noise blocks. In signal blocks, each of the 24 displays was always paired with a specific unique target location, chosen randomly (at the beginning of the experiment) from a subset of 32 possible locations. The target replaced a distractor item in the same quadrant, keeping a total of 12 items in each display. In noise blocks, each of the same 24 displays was always paired with a new target location on every trial. These locations were in fact the same 24 target positions from the signal blocks, but were now presented on each trial in a way that was uncorrelated with distractor layout. A sample search display is depicted in Figure 1.

Figure 1.

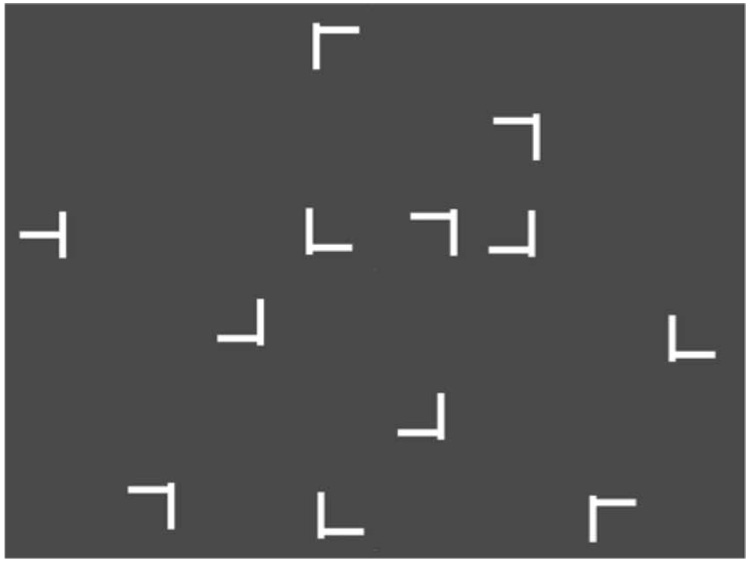
A sample search array containing 1 target “T” and 11 distractor “L”s forming a spatial context.

Design and procedure

Subjects were instructed to respond as quickly and accurately as possible to the target “T” on each trial by pressing one of two keys to indicate its orientation. No mention was made of any layout repetitions, or of any distinct phases within the experiment. If an incorrect response was made, or if no response was made after 7 s, the word “error” appeared for 500 ms superimposed on the search display, and the experiment advanced to the next trial. After a correct response, the experiment advanced immediately. All subjects initially completed 24 practice trials, the results of which were not recorded.

Training phase (Epochs 1–4)

Subjects in the signal first condition initially completed 18 blocks (analysed below as three epochs) of search, with each block including 24 trials: each of 24 unique contexts paired consistently with its constant target location. These repeated correlations between context and target locations form the “signal” that may be learned. These 24 trials were presented in a different random order in each block. Subjects then completed six blocks (one epoch) of search with each block containing the same 24 contexts paired with random target locations. Subjects in the noise first condition received these two training phases in the reverse order: One epoch of noise followed by three epochs of signal. Unlike most previous contextual cueing studies, which intermix predictive and nonpredictive trials within blocks (though see Chua & Chun, 2003), this design requires blocking all predictive trials together and all nonpredictive trials together.

Test phase (Epoch 5)

After all signal and noise blocks had been encountered, learning was tested for all subjects in an identical test phase. There was no overt break between training and test. This test phase consisted of a single epoch (six blocks of 24 trials) of search using the same 24 contexts. During this final epoch, however, the 24 contexts were split into two sets of 12. The first test-predictive set was identical to the signal trials during training; this set maintained the predictive pairings between target locations and distractor layouts that had been previously encountered. The second test-unpredictive set was newly constructed in the same manner as the Noise trials during training, with uncorrelated target and distractor locations. The target locations assigned for the test-unpredictive set were chosen to be equated to the targets of the test-predictive set in terms of eccentricity and quadrant of the display. The 12 test-predictive and 12 test-unpredictive trials were presented intermixed in a different random order for each of the six blocks of this phase.

RESULTS

The raw mean response times for each epoch of the experiment are presented in Table 1 (for signal first subjects) and Table 2 (for noise first subjects). These values were calculated only from correct trials. Error rates were low, averaging 1.4% with a range of 0.1–4.2%.¹

TABLE 1.

Mean response times (in ms) by epoch for signal first subjects

	Category
	Signal			Noise	Training	Test
Epoch	1	2	3	4	1–4	5
Test-unpredictive (TU)	1830	1608	1449	1491	1595	1444
Test-predictive (TP)	1942	1668	1497	1491	1650	1368
TU–TP					−55	76

TABLE 2.

Mean response times (in ms) by epoch for noise first subjects

	Category
	Noise	Signal			Training	Test
Epoch	1	2	3	4	1–4	5
Test-unpredictive (TU)	1892	1721	1539	1475	1657	1504
Test-predictive (TP)	1944	1717	1585	1508	1689	1505
TU–TP					−32	−1

We submitted the data to a three-factor mixed design analysis of variance, with trial type (test-predictive vs. test-unpredictive) and experimental phase (training vs. test) as within-subject factors, and condition (signal first vs. noise first) as a between-subjects factor. This analysis revealed a robust main effect of experimental phase, F(1, 42)= 156.470, p <.001, but no main effect of trial type, F(1, 42) = 0.022, p =.882, or condition, F(1, 42) = 0.607, p =.440. There was a significant interaction between experimental phase and trial type, F(1, 42) = 15.267, p <.001, but no other significant two-way interactions: Experimental phase and condition, F(1, 42) = 2.452, p =.125; trial type and condition, F(1, 42) =.456, p =.503. To determine the nature of the interaction between experimental phase and trial type, we tested for effects of trial type separately for the two experimental phases. When collapsed over all observers, there was no effect for the test phase, i.e., Epoch 5, t(43) = 1.414, p =.164. Unexpectedly, however, there was a reliable effect of trial type for training, i.e., Epochs 1–4, t(43) = 2.373, p=.022: Test-predictive trials were 44 ms slower than test-unpredictive trials. This last effect was surprising, since by design these two classes of trials should be similar during the training phase. However, wide variance in the actual displays may have introduced differences in the ease of searching through those particular displays themselves, regardless of any contextual cueing. Such differences may have loomed especially large in the present study: Since there were only ever 12 distractor configurations that were unpredictive at test (vs. 360 such trials in the original contextual cueing studies), even a few especially easy or difficult displays could readily skew the results, as they were repeated so often. However, our analyses below take into account these display differences between conditions.

Crucial for our main hypothesis, the three-way interaction between condition, trial type, and experimental phase was significant, F(1, 42) = 5.820, p =.020. To clarify the nature of this interaction, we computed the effects of trial type and experimental phase separately for signal first and noise first subjects. For the signal first subjects, there was a main effect of experimental phase, F(1, 21) = 109.653, p <.001, no main effect of trial type, F(1, 21) = 0.153, p =.70, but a significant interaction, F(1, 21) = 17.017, p <.001. The noise first subjects showed a similar pattern, but without an interaction: Experimental phase, F(1, 21) = 54.594, p <.001; trial type, F(1, 21) =.310, p =.584; interaction, F(1, 21) = 1.352, p =.258.

Another way to highlight the difference in contextual cueing between signal first and noise first subjects is to directly compare the effect of trial type in the test phase, after factoring out the unexpectedly significant differences observed in the training phase. These normalized comparisons (graphed in Figure 2) are the clearest measure of contextual cueing in our study; they yielded significant contextual cueing for signal first subjects, t(21) = 4.125, p <.001, but not for noise first subjects, t(21) = 1.16, p =.258, and these values were significantly different, t(21) = 2.313, p =.031.

Figure 2.

Contextual cueing advantage at test, normalized from training, for both signal first and noise first groups.

DISCUSSION

The primary result of this study was that contextual cueing was observed in the signal first subjects, but not the noise first subjects, despite the fact that both groups had the same overall exposure to statistical regularities. This indicates that the learning that underlies contextual cueing does not operate continuously. Previous discussions have noted that such learning may be subject to capacity limits in terms of the spatial scope of associations (Brady & Chun, 2006; Olson & Chun, 2002), but to our knowledge this is the first demonstration that contextual cueing is also subject to temporal limits. In particular, our results clearly indicated a primacy effect in contextual cueing. This suggests that implicit contextual learning may have an intrinsic endpoint—resulting in a type of functional hypothesis about regularities in displays (or the lack thereof) that then becomes resistant to further updating. This is apparent both in the failure to extract regularities from a signal preceded by noise, and in the persistence of contextual cueing from an initial signal through subsequent intervening noise. Moreover, since similar primacy effects are observed in temporal visual statistical learning of nonspatial correlations over time (Catena, Scholl, Isola, & Turk-Browne, 2006), this may be a general feature of statistical processing in the mind.

A key goal for further research on this primacy effect will be to determine just how and when it can be overcome. At one (implausible) extreme, such effects could be global: An implicit “conclusion” about the statistical structure that is or is not present in a display could effectively “turn off” learning for all other spatial regularities in the environment. This would be highly maladaptive: Just because there are no regularities over here doesn’t mean there aren’t important regularities over there. At the other extreme, such “conclusions” could be highly specific to particular aspects of the displays: Learning may still be reengaged even after initial training if the stimuli are now presented in new locations, new colours, new sizes, etc. This possibility may be more plausible: In fact, some contextual cueing is “hyperspecific” in that it does not transfer to stimuli with different visual features, even when the differences are extremely subtle (Jiang & Song, 2005). In future work, it will be important to determine whether such subtle changes can not only foil the expression of learning, but can also reengage learning after previous encounters with statistical noise.

Primacy effects have been well documented in experimental psychology (e.g., Nickerson, 1998), in contexts ranging from the formal consideration of contingency information (e.g., Yates & Curley, 1986) to the formation of personality impressions (e.g., Anderson & Jacobson, 1965; Hendrick & Costantini, 1970). Some such experiments have even demonstrated primacy effects using designs that were very similar to that used here, wherein covariation information is identical for all subjects, but evidence in support of a causal relationship was present only early or late in the initial stimuli (Dennis & Ahn, 2001). In nearly all of these experiments, however, the affected judgements were explicit and conscious—and may in fact arise from the intentional consideration of some factors before others (e.g., Klayman & Ha, 1987).

In contrast, the primacy effect observed in this experiment was presumably implicit. Numerous contextual cueing studies have confirmed that subjects are almost never aware of the predictive nature of repeated displays, or even of the repetitions themselves (e.g., Chun, 2003; Chun & Jiang, 1998), even when blocked designs were used (Chua & Chun, 2003). Thus, the present experiment indicates that such primacy effects can also arise from incidental visual processing in the absence of a covert strategy.