Structure-Specific Statistical Mapping of White Matter Tracts

Abstract

We present a new model-based framework for the statistical analysis of diffusion imaging data associated with specific white matter tracts. The framework takes advantage of the fact that several of the major white matter tracts are thin sheet-like structures that can be effectively modeled by medial representations. The approach involves segmenting major tracts and fitting them with deformable geometric medial models. The medial representation makes it possible to average and combine tensor-based features along directions locally perpendicular to the tracts, thus reducing data dimensionality and accounting for errors in normalization. The framework enables the analysis of individual white matter structures, and provides a range of possibilities for computing statistics and visualizing differences between cohorts. The framework is demonstrated in a study of white matter differences in pediatric chromosome 22q11.2 deletion syndrome.

1 Introduction

In recent years there has been increased interest in neuroimaging statistical mapping techniques that are structure-specific. The underlying belief is that analysis that takes into account the unique properties of specific anatomical structures and focuses its attention on these structures can be more sensitive than analysis performed over the whole brain. Furthermore, analysis that restricts its attention to structures of interest produces inferences that are also structure-specific. Such inferences can be communicated and visualized more effectively than whole-brain results, since they can be described and presented in the context of well-known structures. Thus, for instance, a significant cluster at the tail of the hippocampus is easier to describe and visualize than a cluster at a certain position in Talairach space. Another key feature of structure-specific analysis is the ability to combine or average data along anatomically meaningful directions while respecting the boundaries between structures, as opposed to uniform smoothing over the whole brain.

Structure-specific analysis requires a suitable representation for the anatomical structures of interest, and the main aim of this paper is to provide a representation that is particularly well-suited for analyzing white matter structures in diffusion MRI studies. White matter tracts (fasciculi) are thin, sheet-like or tube-like structures, and as such can be effectively described using skeletons. This fact is leveraged in the tract-based spatial statistics (TBSS) approach (Smith et al., 2006), although there skeletons are derived for the entire white matter region and no distinction between white matter structures is made. In this paper we propose to use the continuous medial representation (cm-rep) (Yushkevich et al., 2006b) to model individual white matter tracts. The advantage of using cm-reps, as opposed to skeletonization, is that the skeleton of the structure of interest is represented by a parametric surface. A parametric representation of the skeleton allows us to perform manifold-based statistical analyses similar to those used in cortical flat-mapping (e.g., (Thompson et al., 2001; Fischl et al., 1999)).

One of the main motivations for representing white matter tracts using parametric geometrical models is to offer an alternative to smoothing in situations where it is necessary to increase the sensitivity of statistical analysis at the cost of specificity. Whereas isotropic smoothing reduces the locality of detectable statistical differences equally in all directions, geometrical models provide a way to combine and collapse data in the context of the structure of interest, making it possible to reduce the locality along “less interesting” directions while maintaining specificity along the directions that are more meaningful. One way to apply such shape-based averaging is to reduce the dimensionality of a volumetric dataset to a two-manifold that is representative of the overall shape of the dataset. For thin structures, the skeleton is an ideal manifold onto which to project volumetric data because the skeleton captures the overall shape of the structure.

In this paper, the new structure-specific analysis framework is used to model major fasciculi with sheet-like geometry: the corpus callosum (CC), corticospinal tract (CST), inferior longitudinal fasciculus (ILF), superior longitudinal fasciculus (SLF), inferior fronto-occipital fasciculus (IFO) and uncinate fasciculus (UNC). The framework is demonstrated by application to statistical mapping of white matter tracts in chromosome 22q11.2 deletion syndrome (DS22q11.2), which encompasses most cases of DiGeorge and Velocardiofacial syndromes amongst others. Cluster analysis performed on the medial surfaces of white matter tracts yields a number of statistically significant findings indicating that DS22q11.2 is associated with bilateral differences in diffusivity in three of the fasciculi.

The paper is organized as follows. Section 2 reviews current approaches to white matter analysis and motivates the medial-based structure-specific mapping framework. The methods employed by the framework, including atlas-building, model initialization, fitting and statistical analysis, are described in Section 3. A demonstration of the method in the context of the DS22q11.2 study is presented in Section 4.2. The discussion in Section 5 focuses on the next steps in the implementation of the structure-specific analysis framework, such as direct automatic fitting of medial tract models to diffusion tensor imaging (DTI) data.

2 Background

The traditional approach to structure-specific analysis of diffusion imaging data has been to identify regions of interest and integrate diffusion-based measurements over these regions, forming a small number of statistical features (Horsfield and Jones, 2002). The advent of fiber tracking algorithms (Mori et al., 2002) has made it possible to map out DTI-based statistical features along the length of fiber bundles. A number of authors (Jones et al., 2005b; Corouge et al., 2006; Lin et al., 2006; Maddah et al., 2007) identify bundles of fibers with similar shape and make inferences on the base of bundle centerlines; this approach is well-suited for tubular structures, but larger sheet-like structures like the corpus callosum have to be divided into several tubular bundles. Our approach is designed to analyze sheet-like structures as a whole, and is highly complementary to bundle-based methods: one could use our models for sheet-like fasciculi and bundle-based analysis for tube-like fasciculi.

Cascio et al. (Cascio et al., 2006) and Sun et al. (Sun et al., 2007) collapse DTI-derived features onto the midsagittal cross-section of the corpus callosum and perform analysis in this two-dimensional space. Such structure-specific approaches are powerful because they take advantage of the specific geometry of the corpus callosum. However, the dimensionality reduction accomplished by these methods is very distinct from our approach: in the former, DTI data are averaged or combined along the length of fibers and projected onto a flat region on the midsagittal plane, while in our approach this data is collapsed onto a manifold representative of the overall shape of a white matter tract.

Another approach to white matter analysis involves adapting voxel-based and deformation-based morphometry (Ashburner and Friston, 2000) to diffusion data. Whole-brain morphometry is tailored for exploratory analysis, and serves different needs than structure-specific methods. A common approach is to normalize the subjects’ structural images (T1, T2, or in some cases, fractional anisotropy (FA) images derived from diffusion-weighted MRI) to a standard whole-brain template (e.g., (Eriksson et al., 2001)). More recently, specialized deformable registration methods for diffusion data have been developed (Zhang et al., 2006; Cao et al., 2005). Voxel-based morphometry in DTI has been applied in a large number of studies. One of the concerns raised about the standard VBM approach in DTI data is that structure boundaries and within-structure directional information are not taken into account during smoothing and analysis (Jones et al., 2005a). The tract-based spatial statistics (TBSS) framework for DTI morphometry addresses this limitation by incorporating the geometric properties of white matter tracts in the analysis. This is achieved by using registration to compute a “mean FA” image, thresholding this image, computing the skeleton of the thresholded region, projecting the subjects’ FA values onto the skeleton, and performing statistical analysis on the skeleton. TBSS leverages the fact that the skeleton is a natural representation for white matter structures, which are thin sheet-like or tube-like objects. One of the limitations, however, is that by operating on the mean FA image, TBSS ignores orientation information, which can lead to fasciculi that have different orientation but similar anisotropy being combined together into a single structure. Thus the skeleton computed by TBSS may not correspond to the skeletons of the individual fasciculi at such locations. Recent work by Kindlmann et al. (2007) overcomes this limitation to some extent by formulating a way to automatically detect surfaces that separate adjacent fasciculi with differing fiber orientations, and providing a way to estimate the skeletons of adjacent fasciculi separately.

Our paper also represents white matter structures medially. However, unlike TBSS, we use medial models to represent specific white matter structures of interest, rather than all of white matter. In order to distinguish between adjacent tracts, we derive segmentations of individual fasciculi using fiber tractography. The use of parametric medial models with predefined topology simplifies statistical analysis and makes it possible for the rich collection of statistical tools and visualization approaches developed in the cortical flat-mapping literature to be applied to white matter studies. This is illustrated by the manifold-based cluster analysis presented at the end of this paper.

3 Methods and Materials

3.1 Analysis Framework Overview

The main aim of this paper is to give a proof-of-concept demonstration of a new model-based framework for representing major fasciculi and analyzing associated DTI data. This framework includes three main components: segmentation, modeling and statistical analysis. These components leverage prior work in atlas-based segmentation, deformable medial modeling and non-parametric statistical analysis. Prior to describing these components in detail, we note that alternative approaches to each of them are available and emphasize that the focus of this paper is on demonstrating the framework as a whole rather than on the implementation of each of its components.

In the current implementation, segmentation, modeling and analysis all take place in atlas space. That is, all DTI images in a study are normalized to a common atlas, which is derived from the images themselves. Working in atlas space facilitates the segmentation and modeling of white matter structures. An alternative, discussed in Sec. 5, is to perform segmentation, modeling and analysis in subject space. The main difference between these approaches is in the way that inter-subject correspondences are computed (on the basis of image-based normalization in the atlas-based approach, or on the basis of shape in subject-space analysis).

3.2 Normalization to a DTI Atlas

The DTI atlas is constructed by normalizing all DTI images in a study to a common average image. A number of techniques for computing an unbiased average image from a cohort of images have been proposed (Thompson and Toga, 1997; Guimond et al., 2000; Joshi et al., 2004; Avants and Gee, 2004). We use a similar approach (Zhang et al., 2007b) that leverages a new deformable DTI registration algorithm (Zhang et al., 2006), in which image similarity is computed on the basis of full tensor images, rather than scalar features. When measuring similarity between tensor images, it is essential to take into account the fact that when a transformation is applied to a tensor field, the orientation of the tensors is changed. A unique property of our registration algorithm is the ability to model the effect of deformation on tensor orientation as an analytic function of the Jacobian matrix of the deformation field. By using full tensor information in the similarity metric, the method aligns white matter regions better than scalar-based registration methods, as demonstrated by Zhang et al. (2007a) in a task-driven evaluation study.

When building the atlas, the initial average image is computed as a log-Euclidean mean (Arsigny et al., 2006) of the input diffusion tensor images. The average is then iteratively refined by repeating the following procedure: register the subject images to the current average, then compute a refined average for the next iteration as the Euclidean mean of the normalized images. This procedure is repeated until the average image converges.

To allow asymmetry analysis and to simplify the modeling of bilateral fasciculi, a symmetric average is constructed by simply applying the above averaging procedure to the non-symmetric population average and its mirror image across the midsagittal plane (the midsagittal plane is estimated automatically by solving a three-parameter rigid registration problem, similar to (Ardekani et al., 1997)). The images of the subjects are then registered to the symmetric average. The combination of the symmetric average image and the warps from the average to each of the subject’s DTI images forms the symmetric DTI atlas. This atlas captures the correspondences between the white matter regions of different subjects as well as between left and right hemispheres of each subject.

3.3 Tract Segmentation

Six major fasciculi (CC, CST, IFO, ILF, SLF, UNC) were segmented in the white matter atlas using an established protocol by Wakana et al. (2004), which is based on fiber tracking. The FACT fiber tracking algorithm (Mori et al., 1999) was applied to the DTI white matter atlas with the FA threshold of 0.15 and an inner product threshold of 0.7, which prevents angles larger than 45° during tracking. A fiber was tracked from the center of any voxel with a FA > 0.2. Fibers of interest were extracted using a multiple region of interest (ROI) based approach (Conturo et al., 1999; Mori et al., 2002). Two types of ROIs were defined: those through which all fibers in a tract must pass, and those through which none of the fibers may pass. Since in this paper, a 2D manifold-based model of fasciculi is employed, only those fasciculi that have a major portion that is sheet-like were segmented. Fasciculi that are more appropriately represented by tubular models, such as the tapetum of the CC, the cingulum, the fornix and the optic tract were not segmented. Fasciculi in the cerebellum and brain stem were not considered either. Only the arcuate portion of the SLF, which can be tracked consistently, was segmented. Binary 3D segmentations of individual fasciculi were generated by labeling voxels in the white matter atlas through which at least one fiber passed. The binary segmentations were further edited using ITK-SNAP (Yushkevich et al., 2006a) by one of the authors (HZ) to remove extraneous connections: the portion of the CST extending to the cerebellum was removed; regions that can not be disambiguated between CC and CST were attributed to both structures. Fig. 4–Fig. 9 show the binary segmentations for the six selected fasciculi. The segmentation of all six fasciculi required less than two hours of user time, and no slice-by-slice or voxel-by-voxel editing was performed.

Fig. 4.

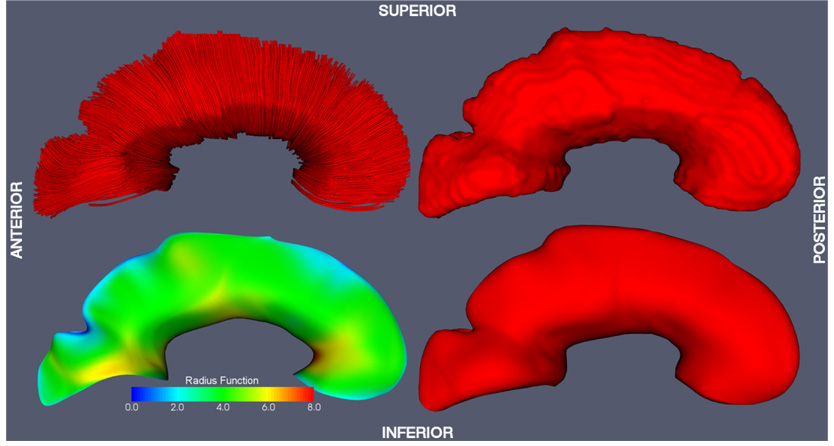
Corpus callosum (CC) model-fitting result. Top left: fiber tracking and fiber labeling result. Top right: binary segmentation derived from the fiber tracking result. Bottom left: the skeleton surface of the cm-rep model fitted to the binary segmentation. The color map along the skeleton surface plots the radius scalar field R, i.e., the local thickness of the model. Bottom right: the boundary surface of the cm-rep model.

Fig. 9.

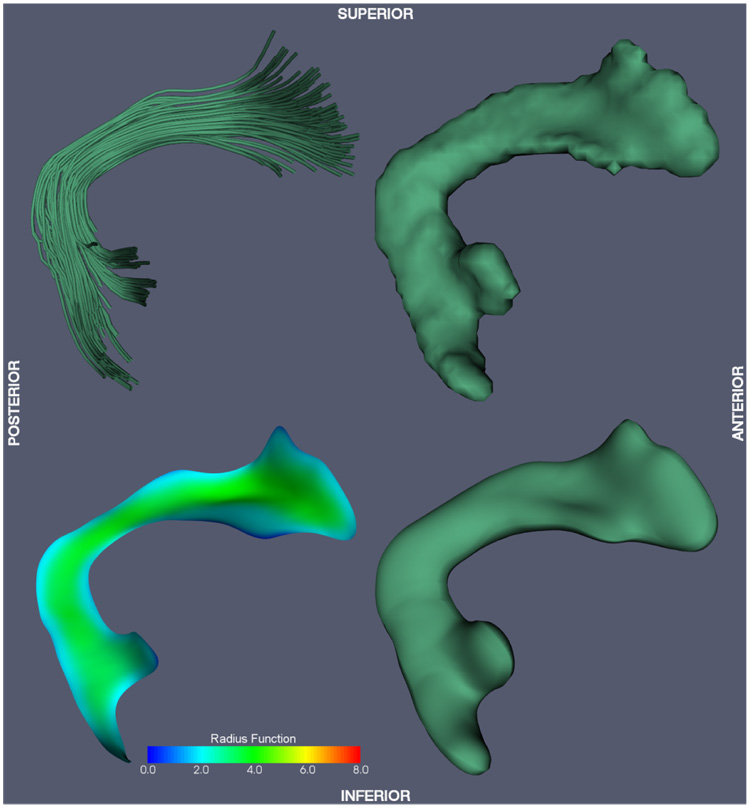
Superior longitudinal fasciculus (SLF) model-fitting result.

3.4 Geometrical Modeling of Major Fasciculi

Geometrical modeling of the fasciculi involves fitting deformable medial models (cm-reps) to binary segmentations of the fasciculi in atlas space. These models describe the skeleton ¹ and the boundary of a geometrical object as parametric digital surfaces with predefined topology. Furthermore, the models describe the geometrical relationship between the skeleton and the boundary, such that deformations applied to the model’s skeleton can be propagated to the model’s boundary. The medial models used in this paper have skeletons consisting of a single surface patch, i.e., non-branching skeletons. For most fasciculi, a single-surface model appears sufficient, as our fitting results demonstrate.

The deformable medial model is constructed as follows. We start with an initial mesh representation of the skeleton, denoted S₀. The mesh S₀ is triangular, which allows maximum flexibility for modeling complex skeleton shapes. Each vertex i in the mesh S₀ is a tuple {m_0,i, R_0,i}, where m_0,i ∈ ℝ³ is the coordinate of the vertex and R_0,i ∈ ℝ⁺ is the radius value, which describes the local thickness of the model. The initial mesh S₀ is fairly sparse (see Fig. 3d). Loop subdivision (Loop and DeRose, 1990) is used to derive a sequence of successively finer meshes S₁, S₂,…, which converge to a continuous limit surface as k → ∞. In practice, only two or three levels of subdivision are used when modeling the skeleton surface. In order to deform a medial model to optimize some cost function, we change the values of m_0,i and R_0,i in the sparse mesh S₀. The corresponding deformation of the finer-level meshes is simply a linear function of the update to the sparse mesh.

Fig. 3.

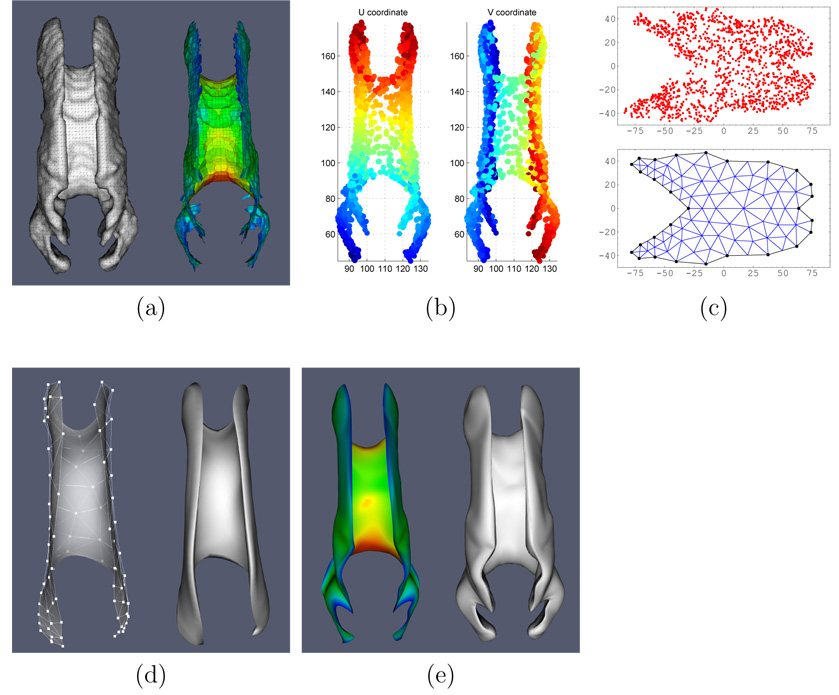
Model building and fitting, illustrated for the CC. a. The boundary and the pruned skeleton of the binary segmentation of the CC (in atlas space). The color map plots the distance from the skeleton to the boundary, i.e., thickness. Red indicates greatest thickness (at the genu and splenium); blue indicates places where the CC is thinnest. Note that the skeleton is not a manifold since it may contain any number of branches. b. The two-dimensional embedding of the skeleton using maximal variance unfolding (Weinberger and Saul, 2006). The two plots use color to show the u and v parameters assigned to each point on the skeleton. Blue represents low u, v values and red represents higher u, v. c. A scatter plot of the skeleton’s points in u, v space and, underneath, the conforming constrained Delaunay triangulation of the region containing the points. d. The initial cm-rep model for the corpus callosum: on the left is the skeleton surface with the control mesh displayed as a wireframe; on the right is the boundary surface derived by inverse skeletonization. e. The result of fitting the cm-rep model to the binary segmentation (the skeleton and the boundary of the model are shown). Again, thickness is plotted in color.

Let S_k be the mesh representing the skeleton of a deformable medial model at subdivision level _k. The boundary of the medial model is derived analytically from the skeleton using inverse skeletonization, i.e. finding a closed surface mesh b_k whose Blum skeleton is approximately S_k. The boundary surface mesh has sphere topology and consists of two halves, each of disk topology. These halves lie on the opposite sides of the skeleton and share a common edge. The boundary halves are denoted ${\mathbf{b}}_k^{-}\text{and}{\mathbf{b}}_k^{+}$ (see Fig. 2) and are given by the following inverse skeletonization expression (Damon, 2004, 2005; Yushkevich et al., 2006b):

$${\mathbf{b}}^{\pm }=\mathbf{m}+R{\overrightarrow{U}}^{\pm },$$ (1)

$${\overrightarrow{U}}^{\pm }=-{\nabla }_{\mathbf{m}}R\pm \sqrt{1-{\Vert {\nabla }_{\mathbf{m}}R\Vert }^2}{\overrightarrow{N}}_{\mathbf{m}},$$ (2)

where ${\overrightarrow{N}}_{\mathbf{m}}$ denotes the unit normal to the skeleton and ∇_mR is the Riemannian gradient of R on the manifold m. The normal and the Riemannian gradient at node i are approximated from the ring of neighboring nodes using the expression for the tangent vectors to the limit surface of Loop subdivision, as given by Xu (2004).

Fig. 2.

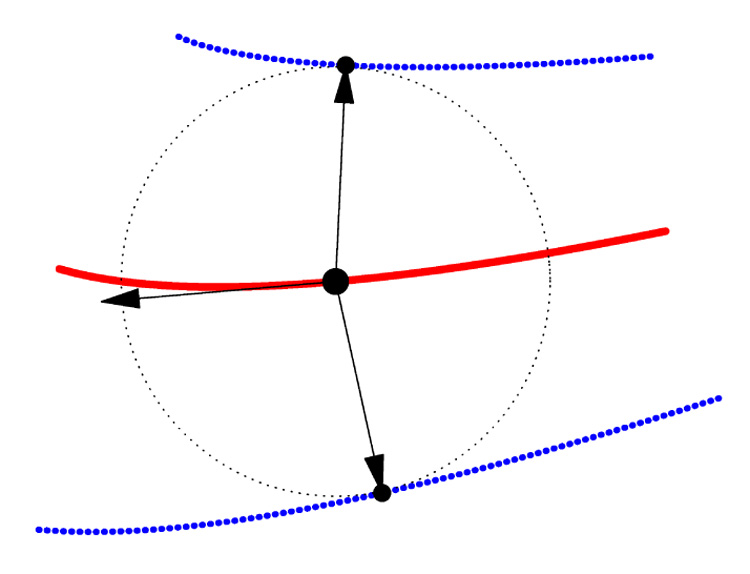
Two-dimensional diagram of medial geometry. The red curve represents the medial surface (skeleton) m. The circle has radius R, given by the radial scalar field on m. The boundary, shown in blue, consists of two parts, b⁺ and b⁻, derived from the skeleton and radial scalar field by inverse skeletonization (1). The vector ∇_mR lies in the tangent plane of m and points in the direction of greatest change in R.

The arrows pointing from m to b⁺ and b⁻ are called spokes.

The inverse skeletonization of a skeleton surface S : Ω → ℝ³ yields a surface of spherical topology whose skeleton is S only if S satisfies a set of sufficient conditions (Damon, 2004, 2005; Yushkevich et al., 2006b). These conditions include the following equality constraint at each point along the edge of the skeleton surface:

$$\Vert {\nabla }_{\mathbf{m}}R\Vert =1\text{on}\partial \mathrm{\Omega }.$$ (3)

In previous work, this constraint has been satisfied in different ways: by adapting the domain Ω such that (3) is satisfied along ∂Ω (Yushkevich et al., 2003); by defining R as a solution of a Poisson partial differential equation with the boundary condition identical to (3) (Yushkevich et al., 2006b) or by using specially designed subdivision rules for quadrilateral meshes to model the surface m (Terriberry and Gerig, 2006). In this paper, we simply admit skeleton meshes S_k that slightly violate the equality constraint (3) and correct these solutions by local adjustment. During fitting, a penalty is imposed on (‖∇_mR‖ − 1)² along edge nodes in the mesh S_k, which forces ‖∇_mR‖ to be very close to 1. The correction procedure consists of simply applying (1) as if ‖∇_mR‖ were actually equal to 1 at edge nodes. While this approach may not be as elegant as the previous ones, it behaves well in practice and leads to a very efficient fitting algorithm. The remaining sufficient conditions of inverse skeletonization are inequality constraints and are handled in this paper the same way as in (Yushkevich et al., 2006b), i.e., by using additional penalty terms during model fitting.

Now, as we apply deformations to the nodes of the sparse-level skeleton S₀, we can use inverse skeletonization to generate a boundary of the medial model at subdivision level k. Furthermore, the correspondence between points on the skeleton and boundary points established by (1) allows us to parameterize the region enclosed by the boundary, as discussed in Sec. 3.5. Overlap between the medial model and a binary image can be computed efficiently. Thus, fitting a model to a binary segmentation of a fasciculus is an optimization problem where overlap between the model’s interior and the segmentation is maximized and the penalty terms required for inverse skeletonization to be well-posed are minimized. Model fitting is discussed in greater detail in (Yushkevich et al., 2006b).

3.4.1 Automatic Model-Building for Initialization

Prior to fitting a deformable medial model to a target structure, an initial model must be generated. While it is possible to begin with a simple stock model, the freedom to choose an arbitrary domain Ω makes it possible to build data-driven initial models. With the freedom to define cm-reps over arbitrary domains comes the problem of finding the right domain and the right mesh configuration for a particular anatomical structure. We accomplish this by essentially flattening the skeleton of the structure, under constraints that minimize local distortion.

Automatic domain generation and model building employ the following pipeline. Given a binary image of the structure of interest, we first compute the Voronoi skeleton of the structure using qhull (www.qhull.org) and use simple heuristics (similar to (Näf et al., 1996)) to prune away the least salient branches. Unlike earlier work on automatic medial model initialization (Styner et al., 2003), we do not require the Voronoi skeleton to be pruned down until it becomes a manifold. Instead, we use the Maximum Variance Unfolding (MVU) technique (Weinberger and Saul, 2006) which finds a two-dimensional embedding of the skeletons’ vertices that minimally distorts the distances between neighboring vertices. The two-dimensional embedding assigns a pair of coordinates (u_i, v_i) ∈ ℝ² to each of the vertices x_i in the skeleton. A manifold can then be fitted to the skeleton by fitting low-degree polynomial surfaces to the data x_i(u_i, v_i), y_i(u_i, v_i), z_i(u_i, v_i). The domain Ω is computed as a region homeomorphic to a disc in ℝ² that encloses all of the points (u_i, v_i). This is achieved by rasterizing the scatter plot of (u_i, v_i) and applying dilation and erosion operations. To produce a quality triangulation of Ω, we sample a set of 20–40 points along its boundary and use the meshing program triangle to produce conforming constrained Delaunay triangulations (Shewchuk, 1996). The initialization pipeline is illustrated in Fig 3 using the CC as the example.

3.5 Shape-Based Coordinate System

A key property of medial models is the ability to parameterize the entire interior of the model using a shape-based coordinate system. Let us refer to the vectors $R{\overrightarrow{U}}^{\pm }$ with tail on the medial surface m as spokes. If m is a continuous surface and the constraints of inverse skeletonization are met, the spokes span the interior of the model, i.e., the region enclosed by the surface b⁻ ∪ b⁺. Every point inside this region can belong to only one spoke. Let us use coordinates (u, v) to describe where the tail of a spoke is on the medial surface, and use the coordinate ξ ∈ [−1, 1] to describe a location along a spoke (when ξ > 0, it references the spoke $R{\overrightarrow{U}}^{+},$ and when ξ < 0, it references the spoke $R{\overrightarrow{U}}^{-}$). Then every point x on the model’s interior can be assigned a set of coordinates (u, v, ξ), as follows:

$$\mathbf{x}(u,v,\xi )=\{\begin{array}{ll}\mathbf{m}(u,v)+\xi R(u,v)U^{+}(u,v)\hfill & \text{if}\xi \ge 0\hfill \\ \mathbf{m}(u,v)-\xi R(u,v)U^{-}(u,v)\hfill & \mathrm{o}/\mathrm{w}.\hfill \end{array}$$ (4)

This assignment is unique, except when (u, v) ∈ ∂Ω, in which case the spokes $R{\overrightarrow{U}}^{+}\text{and}R{\overrightarrow{U}}^{-}$ coincide. This 3D parametrization of the model is a powerful tool, as it allows us to analyze data on the interior of structures in a shape-based coordinate system.

3.6 Statistical Analysis on Medial Manifolds

This section describes one of many possible ways to perform structure-specific white matter analysis in cm-rep coordinate space. We assume a simple scenario, where we are interested in analyzing differences between two groups of subjects. To further simplify the analysis, we restrict our attention only to the differences in the apparent diffusion coefficient (ADC). ADC is a scalar measurement of overall diffusivity equal to the mean of the eigenvalues of a diffusion tensor.

The key feature of our statistical analysis approach is the projection of tensor-derived quantities lying on the interior of a fasciculus onto its medial manifold. This projection results in a dimensionality reduction along the spoke direction, i.e., the direction orthogonal to the boundary of the fasciculus. Like smoothing, dimensionality reduction increases sensitivity at the cost of decreased specificity. However, unlike isotropic Gaussian smoothing, data reduction along spoke directions respects the boundaries between structures. Furthermore, isotropic Gaussian smoothing causes equal loss of specificity in all directions, while, arguably, dimensionality reduction along spokes in thin sheet-like fasciculi causes loss of specificity along the least interesting direction.

We propose and compare two approaches to dimensionality reduction; other approaches are also possible. In both approaches, we map the three-dimensional field of diffusion tensors D(x) defined over the image domain to two-dimensional tensor fields defined over the medial manifold of each fasciculus. For each fasciculus, this mapping is achieved by sampling diffusion tensors along spokes RU^±(u, v) and deriving a single tensor D̃(u, v) for each point on the medial manifold. Such a two-dimensional tensor field is computed for each fasciculus in each subject.

The first strategy is an adaptation of the dimensionality reduction strategy used in TBSS (Smith et al., 2006) and will be referred to as the ‘Max-FA’ strategy. In this strategy, we select the diffusion tensor that has the largest FA of all the tensors sampled along the pair of spokes:

$$\begin{array}{ll}\stackrel{\sim }{D}(u,v)=D(\mathbf{x}(u,v,{\xi }^{*}(u,v))),\hfill & \text{where}\hfill \\ \hfill & {\xi }^{*}(u,v)=\text{arg}\underset{\xi \in [-1,1]}{\text{max}}\text{FA}(D(\mathbf{x}(u,v,\xi ))).\hfill \end{array}$$ (5)

In TBSS, this strategy is adopted to correct for registration errors in atlas building. Since FA tends to be larger on the interior of fasciculi, by searching for the position with the largest FA value along vectors which extend from the interior to the fasciculus boundary, one may recover intersubject correspondences distorted by imperfect registration (Smith et al., 2006). However, there is a slight but important difference between our ‘Max-FA’ approach and TBSS. The latter computes the skeleton of the entire white matter region (defined by an FA threshold) and so the search for the maximum FA value may span multiple fasciculi if they are not separated by voxels with low FA. Our approach searches within the interior of each fasciculus, as defined by our tracking-based segmentation protocol. The effects of this difference are examined in Sec. 4.2.

The second proposed strategy is to compute the average tensor along each pair of spokes. Following Arsigny et al. (2006), we compute the tensor average using the log-Euclidean formulation:

$$\stackrel{\sim }{D}(u,v)=\text{exp}[\frac{1}{2}{\displaystyle {\int }_{-1}^1\text{log}D(\mathbf{x}(u,v,\xi ))}\mathrm{d}\xi ].$$ (6)

This strategy assumes that the registration quality is sufficiently high and uses averaging as the way to increase sensitivity of the analysis at the cost of specificity in the spoke direction, which is assumed to be of least interest. A third strategy, which is not studied here, is not to perform dimensionality reduction, but to generate statistical maps in the full u, v, ξ coordinate system. This approach has the advantage of greatest specificity.

The analysis of statistical feature maps defined over manifolds has been studied extensively in the neuroimaging literature and many of the techniques previously proposed for cortical surface analysis can be directly applied to the analysis of white matter differences on medial manifolds of fasciculi (e.g., (Thompson et al., 2001; Fischl et al., 1999)). As an illustration, we analyze the ADC differences between two groups using non-parametric cluster-based analysis with family-wise error rate (FWER) correction (Nichols and Holmes, 2002). First, we compute a two-sample t-test at each point on the medial manifold of each fasciculus. Then, given an arbitrary threshold t₀, the set of clusters with t > t₀ is extracted. In this context, a cluster C ∈ Ω is a simply connected subset in the domain of the medial manifold that satisfies t(u, v) ≥ t₀ for all (u, v) ∈ C. We record the mass of each cluster C, defined as

$$\text{mass}(C)={\displaystyle {\int }_{C}t(u,v)\mathrm{d}A}.$$

We compare the mass of each cluster to the histogram of maximal cluster masses generated from a large number of identical experiments in which the labels of the subjects are randomly permuted. This histogram lookup yields a corrected p-value for each cluster. The histogram of cluster masses is pooled over all structures of interest, so that the FWER correction takes into account the number of structures that we examine.

4 Experimental Evaluation

4.1 Evaluation Experiment: Subjects and Imaging Protocol

We demonstrate the proposed structure-specific white matter analysis paradigm in an ongoing study of DS22q11.2 conducted at the Department of Psychiatry and Behavioral Science, M.I.N.D. Institute of University of California, Davis. DS22q11.2 is associated with reduced brain volume, and in particular, has been linked to morphological changes in white matter (Eliez et al., 2000; Kates et al., 2001; Simon et al., 2005). We are interested in testing the hypothesis that white matter structure is different between children with DS22q11.2 and typically developing children (TD).

The participants in the study include 18 normally developing children and 13 children with DS22q11.2. Diffusion-weighted and structural MRI were acquired for each participant on a 3 Tesla Siemens Trio scanner. A single-shot, spin-echo, diffusion-weighted echo-planar imaging (EPI) sequence was used for the diffusion-weighted MRI. The diffusion scheme was as follows: one image with minimum possible diffusion gradient, referred to as the b = 0 image, followed by twelve images measured with twelve non-collinear and non-coplanar diffusion encoding directions isotropically distributed in space (b = 1000s/mm²). Additional imaging parameters for the diffusion-weighted sequence are: TR = 6500 ms, TE = 99 ms, 90° flip angle, number of averages = 6, matrix size = 128 × 128, slice thickness = 3.0 mm, spacing between slices = 3.0 mm, 40 axial slices with in-plane resolution of 1.72 × 1.72 mm.

Diffusion-weighted images were corrected for motion and eddy-current artifacts using the method described in (Mangin et al., 2002), prior to extracting brain parenchyma with the Brain Extraction Tool (Smith, 2002). Diffusion tensor images were then reconstructed from the diffusion-weighted images using the standard linear regression approach (Basser et al., 1994). Finally, the resulting tensor volumes were resampled to a voxel space of 128 × 128 × 64 with voxel dimensions equal to 1.72 × 1.72 × 2.5mm³. The resampled volume, with axial dimension equal to a power of 2, is better suited for registration algorithms that require the construction of standard multi-resolution image pyramids.

4.2 Results

The pipeline described in Sec. 3 was applied to all 31 images in the study. First, a symmetric unbiased population atlas was constructed using image registration; this atlas is illustrated in Fig. 1. A qualitative assessment of registration accuracy is presented in Fig 11, which shows the DTI images from eight subjects warped into the space of the atlas. No large-scale registration errors are evident, although there are small-scale differences.

Fig. 1.

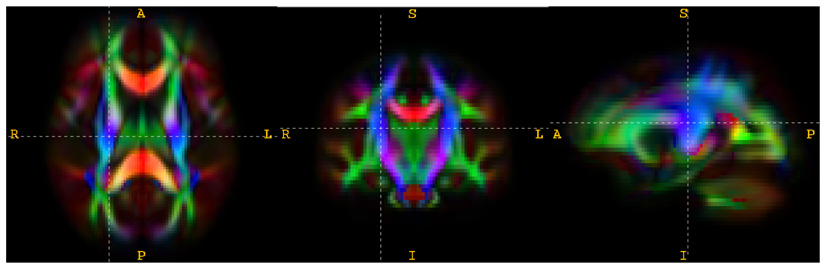
Three orthogonal views through the right CST in the white matter atlas constructed from 31 subjects (13 children with DS22q11.2 and 18 typically developing children). The standard color-coding scheme for visualizing the principal direction of diffusion is used: red for left-right, green for anterior-posterior and blue for inferior-superior. The intensity is scaled by FA.

Fig. 11.

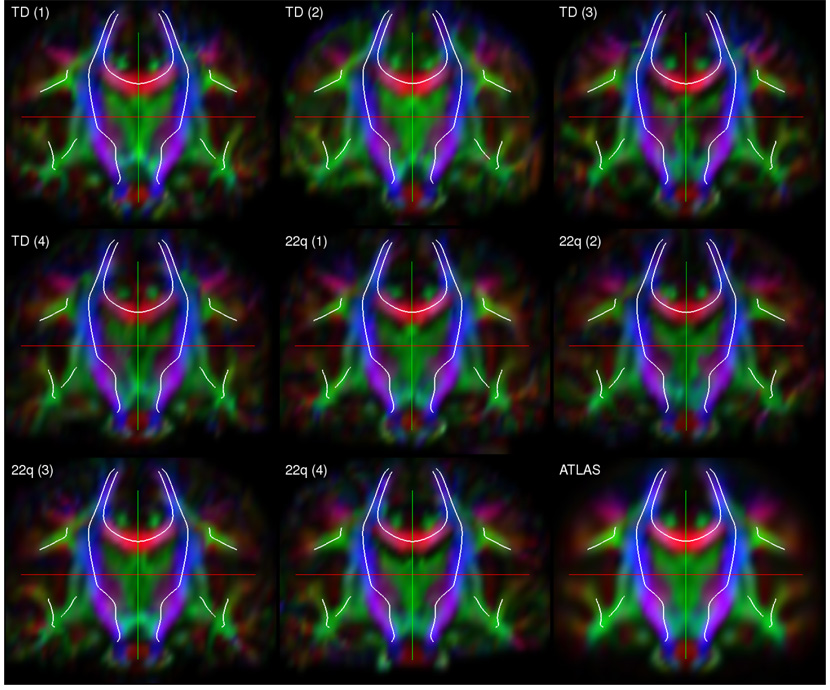
Visual assessment of registration accuracy. Each plot above shows a coronal slice through one of the subjects’ DTI images registered to the DTI atlas, except for the last plot, which shows the atlas itself. The projection of the medial models of the fasciculi into the cut plane are shown as white curves in each plot. These curves are exactly the same across all nine plots and are provided as a reference.

Fiber tracking and tract labeling were used to segment six fasciculi of interest in atlas space. Fiber tracking results and the corresponding binary segmentations are shown in top row of Fig. 4–Fig. 9. Medial models that were fit to each of the binary segmentations are shown in the bottom row of Fig. 4–Fig. 9. The model fitting accuracy for the six fasciculi is listed in Table 1, in terms of Dice overlap between the binary segmentation of a fasciculus and the fitted cm-rep model, as well as root mean square displacement from the boundary of the fitted cm-rep to the boundary of the binary segmentation. The fitting accuracy is high (~0.95 Dice overlap) for five of the six fasciculi. For the ILF, fitting accuracy is lower (0.90 Dice overlap), due to branching fibers in the posterior part of the fasciculus (Fig. 8). Fitting this structure more accurately would require extending our medial modeling approach to allow multi-manifold skeletons, which is the subject of ongoing research. A combined view of the six fasciculi and the medial models fitted to them is shown in Fig. 10.

Table 1.

Accuracy of cm-rep model fitting to binary segmentations of the six selected fasciculi, in terms of Dice overlap and root mean square boundary displacement (RMSBD).

Fasciculus	Dice Overlap	RMSBD (mm)
CC	0.957	0.332
CST	0.954	0.285
ILF	0.902	0.320
SLF	0.944	0.246
IFO	0.950	0.226
UNC	0.951	0.219

Fig. 8.

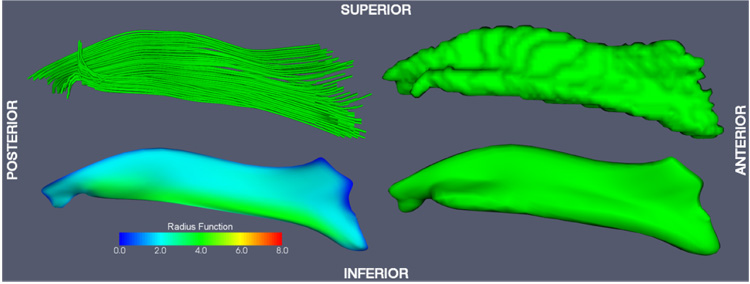
Inferior longitudinal fasciculus (ILF) model-fitting result.

Fig. 10.

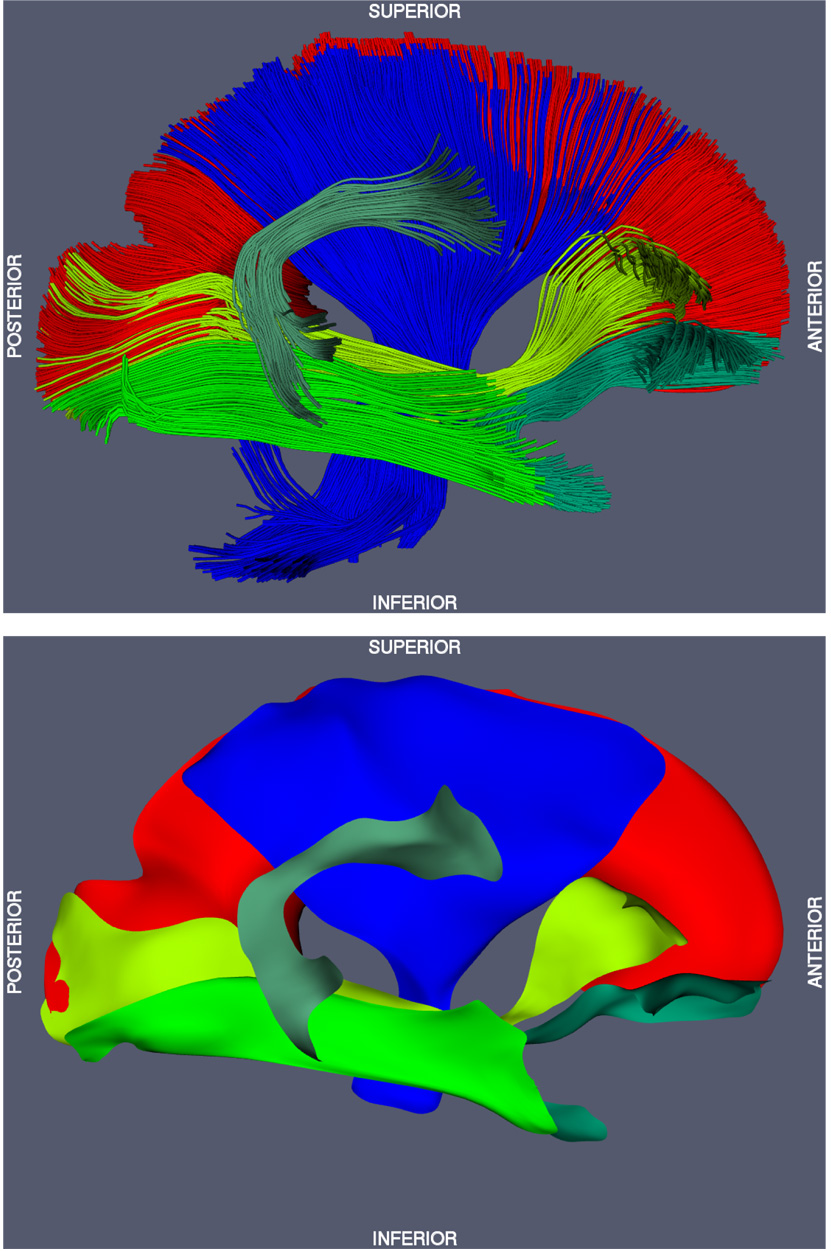
Top: fiber tracking results for the six selected fasciculi. Bottom: skeletons of the cm-rep models fitted to the six selected fasciculi.

Fig. 12 plots the distribution of thickness along the medial models fitted to each of the fasciculi. Thickness is also shown as a color map in Fig. 4–Fig. 9. The CC and CST are the thickest fasciculi, with thickness reaching 16mm. ILF is the thinnest, with maximal thickness below 9mm. The voxel size of our DTI data is 1.72mm × 1.72mm × 3.0mm. Hence, the dimensionality reduction strategies proposed above do indeed combine data from multiple voxels.

Fig. 12.

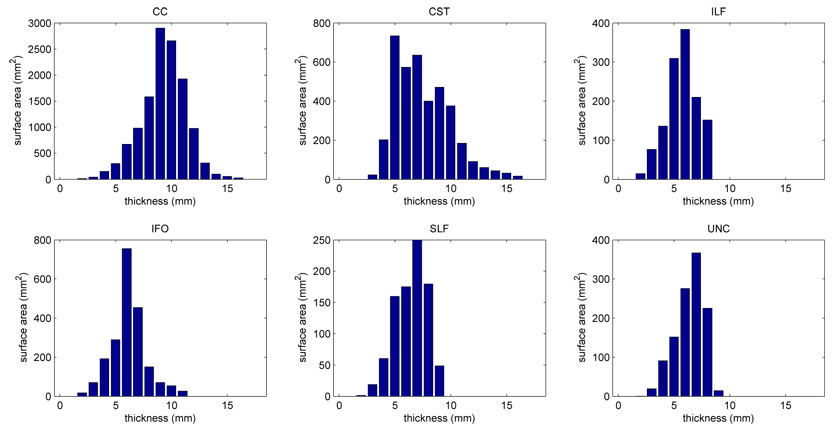
Thickness profiles of the medial models fitted to the six fasciculi in atlas space. The bars in the thickness profiles represent the surface area of the region on the medial manifold where the thickness falls within the range [i − 0.5, i + 0.5] for i = 0, 1,…, 18. Thickness is defined as the diameter of the maximal inscribed ball centered at the given point on the medial axis (i.e., thickness is twice the radius function R(u, v)).

For each fasciculus, we tested the hypothesis that ADC is greater in TD than in DS22q11.2. This hypothesis was tested using both ‘Max-FA’ and tensor averaging dimensionality reduction strategies. In each case, a t-map was generated over the medial manifold of each fasciculus. These t-maps are plotted in three dimensions in Fig. 13 as color maps over the medial manifolds. An alternative visualization in the top row of Fig. 14 displays the t-maps in the two-dimensional u, v domain of each fasciculus, making it easy to display the results of hypothesis testing on a single page. Note that the two-dimensional projection of each fasciculus roughly resembles the shape of the fasciculus in three dimensions, making it easier to interpret the two-dimensional t-maps. The 2D visualization is also an effective tool for comparing the results of different studies or different contrasts within a study.

Fig. 13.

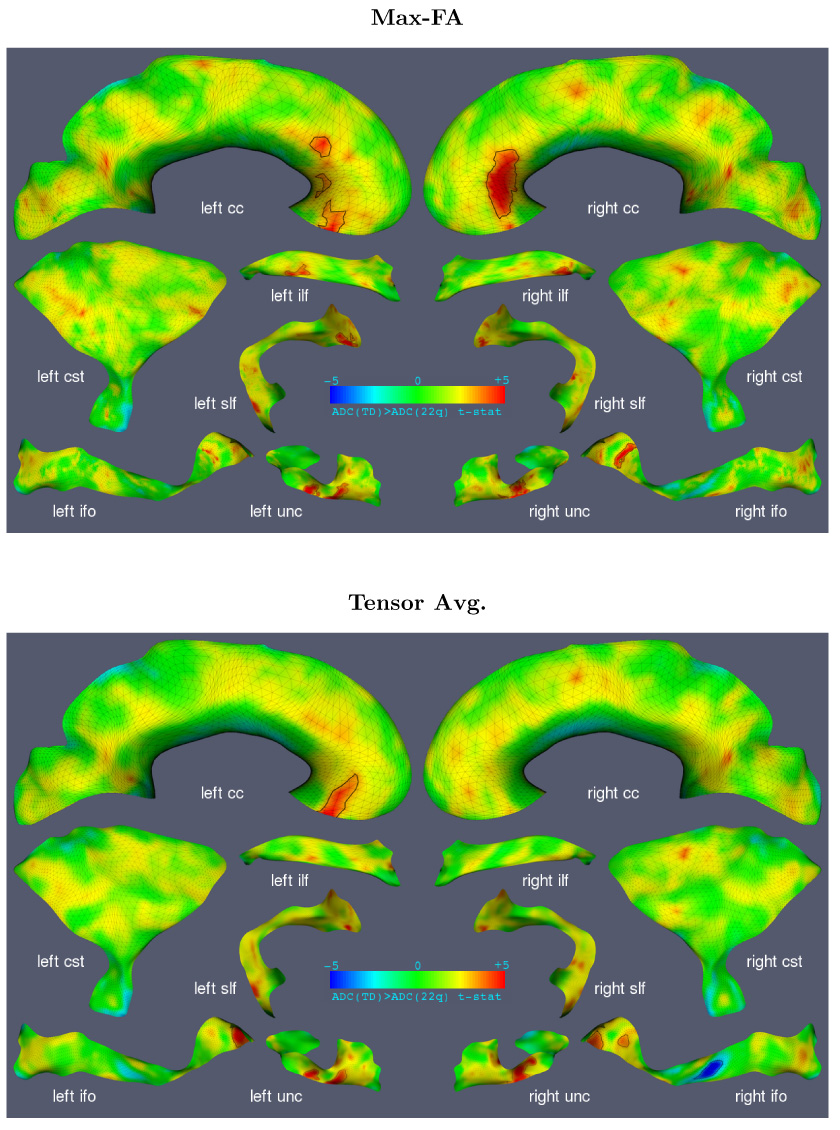
Results of cluster analysis comparing ADC between DS22q11.2 and TD, displayed in three dimensions. The medial models are colored by the t-score for the hypothesis ADC(TD) > ADC(DS22q11.2). Statistically significant clusters are marked by a black outline. Results for both dimensionality reduction strategies (Max-FA and tensor averaging) are shown.

Fig. 14.

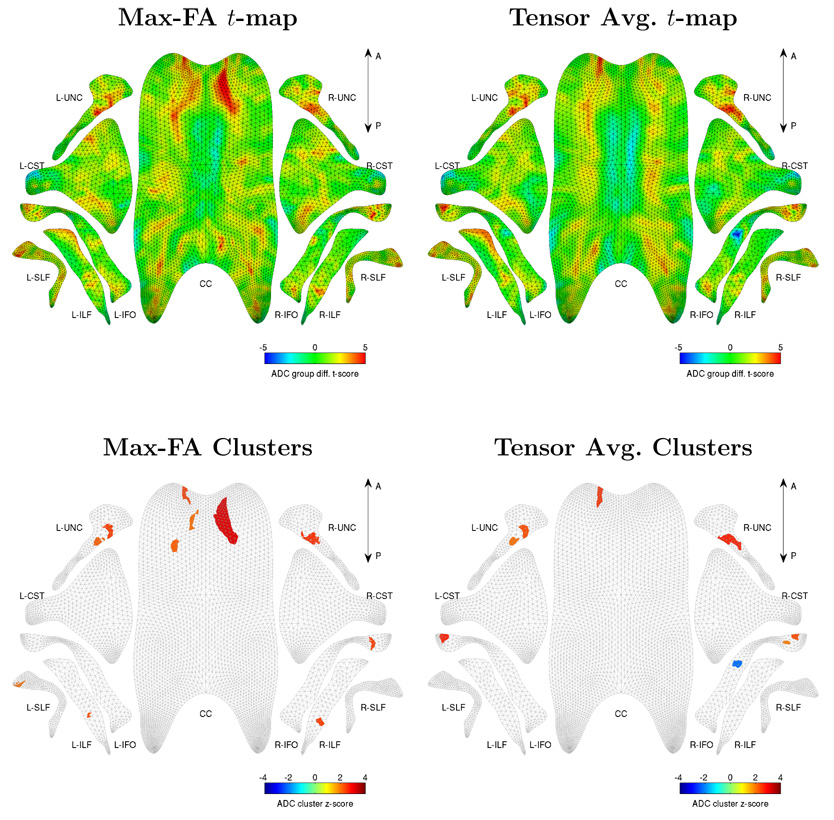
A statistical analysis of ADC differences between TD vs. DS22q11.2, computed using two different dimensionality reduction strategies (MaxFA and tensor averaging, see Sec. 3.6) and visualized in two dimensions. Top row: t-maps for the TD vs. DS22q11.2 group comparison (t > 0 indicates greater ADC in TD, and vice versa). The t-map in each plot is the same as in Fig 13, but is projected onto a 2D domain, allowing the t-maps associated with all 11 fasciculi to be viewed simultaneously. Bottom row: a similar visualization of the statistically significant clusters in ADC comparison (clusters thresholded at t = ±3.40 with FWER-corrected p-value below 0.05). The 2D domain for each fasciculus is displayed as a gray mesh (see Fig. 3c), and the significant clusters are displayed in color. Red clusters correspond to increased ADC in DS22q11.2, and blue clusters correspond to increased ADC in TD.

To find the regions where ADC differences between TD and DS22q11.2 groups are statistically significant, we performed permutation-based cluster analysis with 10000 random permutations. The cluster threshold t₀ was set to 3.40, corresponding to an uncorrected p-value of 0.001. The sets of clusters computed for each contrast and each dimensionality reduction strategy are shown in a two-dimensional flattened view in the bottom row of Fig. 14. The clusters detected using tensor averaging dimensionality reduction are listed in Table 2 and the clusters detected with ‘Max-FA’ are listed in Table 3. The results consistently point to ADC differences in CC, IFO and UNC. However, the study is ongoing and we intend to report the complete results, including FA differences, in a separate clinically-oriented paper.

Table 2.

Statistically significant clusters for the ADC comparison between DS22q11.2 and typical development (TD), using the tensor averaging dimensionality reduction strategy. Clusters are defined as connected regions with |t| > 3.40 on the fascicular medial manifold. For each cluster, four values are shown. The first value is the surface area of the cluster on the medial manifold. Next, t̄ is the average value of the t-statistic inside the cluster. Positive values of t indicate greater ADC in TD than in DS22q11.2. Third, the FWER-corrected p-value of the cluster is given (the correction treats pointwise hypothesis testing across all 11 fasciculi as a single multiple comparison problem). Last, ${\overline{t}}_{\text{maxfa}}$ gives the average over the cluster of the t-map computed using the ‘MaxFA’ dimensionality reduction strategy. The difference between t̄ and ${\overline{t}}_{\text{maxfa}}$ gives an indication of how sensitive the cluster is to the choice of dimensionality reduction.

Fasciculus	Cluster Location	Area, mm2	t̄	pcorr	${\overline{t}}_{\text{maxfa}}$
cc	l. anterior	82.9	3.89	0.0096	3.42
left ifo	anterior	88.8	4.49	0.0085	3.11
left unc	anterior medial	54.7	4.23	0.0184	3.99
left unc	medial	34.4	4.14	0.0346	4.13
right ifo	mid-fasciculus	58.4	−4.44	0.0266	−1.26*
right ifo	anterior	26.0	3.60	0.0492	4.16
right ifo	anterior	48.3	3.84	0.0213	2.98
right unc	medial	103.7	4.19	0.0070	3.62

^*indicates the clusters where this difference is most striking.

Table 3.

Statistically significant clusters for the ADC comparison between DS22q11.2 and TD, using the ‘MaxFA’ dimensionality reduction strategy. See caption in Table 2 for details.

Fasciculus	Cluster Location	Area, mm2	t̄	pcorr	${\overline{t}}_{\text{tenav}}$
cc	l. anterior	50.7	3.75	0.0162	3.66
cc	l. anterior	23.9	3.52	0.0427	2.38
cc	l. anterior	34.0	3.79	0.0274	2.92
cc	r. anterior	208.9	4.49	0.0015	1.71*
left ilf	posterior	40.4	3.80	0.0213	2.39
left unc	anterior medial	53.2	4.07	0.0149	4.18
left unc	medial	34.5	4.17	0.0268	4.08
left slf	inferior	26.4	4.15	0.0372	3.06
right ilf	posterior	49.9	4.10	0.0164	2.52
right ifo	anterior	48.3	4.25	0.0169	3.32
right unc	medial	74.4	3.99	0.0090	4.16

More clusters are obtained using the ‘MaxFA’ strategy than using tensor averaging. In particular, a large cluster is detected in the right genu of the CC, for which there is no equivalent in the clusters generated by tensor averaging. However, looking at the differences between lists of clusters can be deceptive because a cluster’s presence or absence can be sensitive to small differences in the topography of the t-map from which the cluster is generated. A more fair assessment when comparing t-maps generated by two strategies is to examine the t-values from different strategies over the extent of the same cluster. This comparison is made in Tables 2 and Table 3. For each cluster, the average t in the ‘native’ t-map is reported (i.e., the same t-map that was used to generate the cluster), along with the average t in the ‘opposite’ t-map. In all cases, the native |t̄| > 3.40 since 3.40 is the clustering threshold. For almost all clusters, the opposite t̄ is also fairly large, indicating agreement between the two strategies. The two exceptions are the cluster for the tensor averaging strategy located in the right IFO $({\overline{t}}_{\text{tenav}}=-4.44,{\overline{t}}_{\text{maxfa}}=-1.26)$ and the cluster for ‘MaxFA’ strategy located in the right genu of the CC $({\overline{t}}_{\text{maxfa}}=4.49,{\overline{t}}_{\text{tenav}}=1.71).$

Fig. 15 helps explain why the two strategies can produce different t-maps. It looks at the aforementioned cluster in the right IFO, and examines where the tensors with maximal FA are in relation to the medial manifold of the fasciculus. It turns out that over the region of the cluster, the tensors with maximal FA are located not along the medial manifold but towards the end of the spokes that point in the direction of the adjacent ILF, which passes very close to the IFO. The tensors in the ILF have larger FA than tensors in the IFO, and the ‘MaxFA’ strategy chooses the former. Thus, although it seems to produce larger and more numerous clusters, the ‘MaxFA’ strategy can also fail to detect statistically significant differences in places where one fasciculus passes close to another.

Fig. 15.

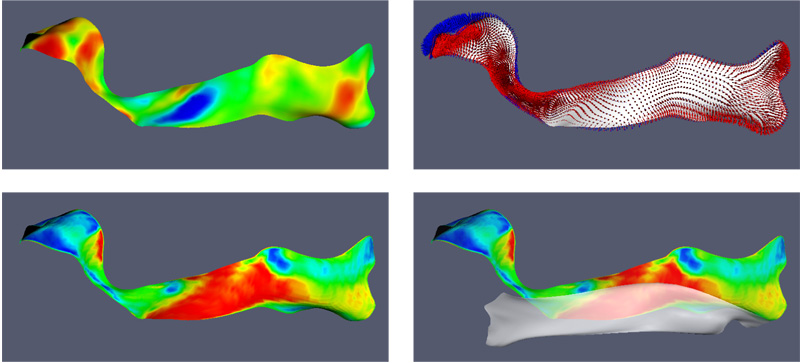
Closer examination of the cluster in the right IFO that appears under the tensor averaging strategy but has no equivalent under the ‘MaxFA’ strategy. Top left: the t-map for the ADC(TD) vs. ADC(DS22q11.2) comparison produced by the tensor averaging strategy (this is the same t-map as in Fig. 13). The cluster of interest is the blue spot in the t-map (increased ADC in DS22q11.2). Top right: the spokes along the medial manifold of the right IFO. Each spoke is a line segment extending from the medial manifold to the corresponding (and also nearest) point on the boundary (see Fig. 2). Spoke RU⁺ is shown in red and spoke RU⁻ in blue. Bottom left: a color map showing where the ‘MaxFA’ strategy samples the DTI image in relation to the medial manifold of the right IFO. Red indicates that the tensor with maximal FA is located at the end of spoke RU⁺ (on average over all 31 subjects) and blue indicates that the tensor with maximal FA is at the end of RU⁻. Green indicates that the tensor with maxFA is, on average, located along the medial manifold. Bottom right: the medial manifold of the right ILF is shown next to the right IFO. The two fasciculi pass close to each other. The ‘MaxFA’ strategy appears to be sampling tensors from the right ILF, which has greater FA values, and causes the statistically significant differences in the adjacent IFO to be missed.

The other cluster that is inconsistent between the two strategies is located in the right genu of the CC. As Fig. 16 shows, this cluster is located where the CC is adjacent on one side to the lateral ventricles. Unlike in the case of the right IFO, there is no systematic shift in the position of the diffusion tensor with maximal FA along the spokes in that area of the CC; on average, the position of the maximal FA tensor is right on the medial manifold. It is likely that the low sensitivity of the tensor averaging strategy is due to the partial volume effects between the CC and adjacent highly isotropic gray and CSF structures.

Fig. 16.

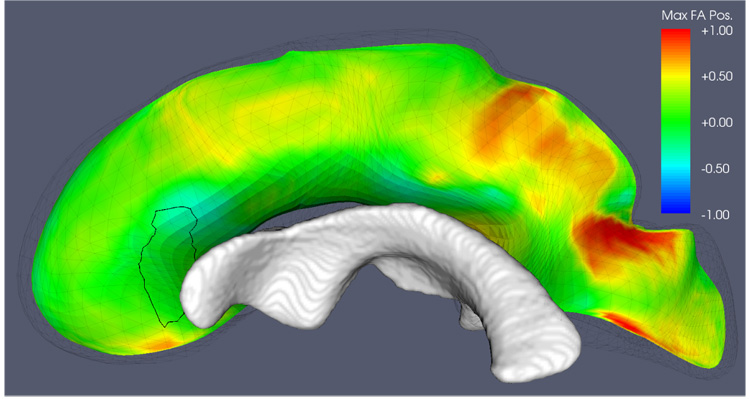
A closer look at the cluster in the right anterior CC that appears under the ‘MaxFA’ strategy but has no equivalent under the tensor averaging strategy. The location of the cluster in question is outlined on the medial surface of the CC. The medial manifold is colored by the relative position along the spokes of the tensor with maximal FA. Positive values (red) indicate that on average, the maximal FA tensor is located on the side of the medial manifold away from the midsagittal plane;. negative values indicate that maximal FA tensors tend to be located one the side facing the midsagittal plane; and values close to zero indicate no bias in the location of the maximal FA tensor. The lateral ventricle is in close proximity to the cluster, which may help explain why tensor averaging, which is more prone to partial volume errors, is less sensitive in this region.

5 Discussion and Conclusions

This work demonstrates the feasibility of using deformable medial models for structure-specific statistical mapping of DTI data in major white matter fasciculi. The cornerstone of this approach is the shape-based parametrization of the fasciculi. Medial models are a natural representation for thin sheet-like structures because the medial manifold effectively summarizes the overall shape of structures and presents an ideal target for dimensionality reduction. Collapsing tensors by taking the average along spokes is an attractive alternative to spatial smoothing of DTI data. Both approaches trade specificity for sensitivity by averaging data from multiple locations, but spoke-based averaging also reduces data dimensionality and explicitly strives to ensure that averaging is applied within the structure of interest, not across its boundaries. However, since averaging takes place in atlas space and normalization is never perfect, there is still a possibility for tensor data outside of the structure of interest to be included in the analysis. The TBSS-inspired approach of summarizing data along the spokes by selecting the tensor with maximal FA is also feasible in our framework and, as shown above, can lead to increased sensitivity, albeit at the cost of potentially missing significant differences in areas of adjoining fasciculi.

The use of skeletons in DTI analysis was pioneered by Smith et al. (2006) in the the TBSS approach. Our approach is distinct from TBSS in several important ways. First, our approach is directed at statistical mapping of individual fasciculi, while TBSS aims to draw inferences about white matter as a whole. In TBSS, deterministic skeletonization is applied to the set of all voxels with above-threshold fractional anisotropy. This results in a skeleton consisting of hundreds or thousands of branches, some of which may be spurious and sensitive to noise. In contrast, the cm-rep approach yields a single approximating medial surface for each of the six selected fasciculi. This simple parametric representation allows statistical mapping of individual fasciculi and provides an easy and attractive way to visualize and interpret statistical differences. It establishes a canonical two-dimensional coordinate space for the fasciculi (Fig. 14), where the results from different white matter studies can be compared.

There are a number of ways to improve the proposed analysis framework. The framework can be extended to incorporate fasciculi for which the sheet-like model is inappropriate, such as the cingulum and the fornix. The tube-based geometrical tract model developed by Jones et al. (2005b); Corouge et al. (2006); Lin et al. (2006); Maddah et al. (2007) is particularly well-suited for modeling these structures, and can be used in parallel with our approach.

In the current experiment, cm-rep models were fit to tract segmentations in template space. The dimensionality reduction of tensor data along spokes also occurs in template space, meaning that in subject space the averaging takes place along curves that are not guaranteed to extend from the medial axis to the boundary, since the deformations yielded by registration algorithms do not preserve the geometrical relationship between the boundaries and skeletons of structures. An alternative approach is to fit cm-rep models to tract segmentations in subject space. This can be achieved by warping the binary segmentations from the template to each of the subjects, and fitting a cm-rep model to each of these warped segmentations. In this way, the registration component would be leveraged to align the boundary a structure, while the normalization of the structure’s interior would be based on the geometrical correspondences generated by cm-rep fitting.

Reliance on expert-driven segmentation of the fasciculi is another limitation. Although the segmentation of the fasciculi in atlas space requires less than two hours of expert time, performing segmentation in subject space would be prohibitively expensive for many studies. Furthermore, the simple six-parameter tensor-based representation of diffusion in our dataset and simple streamline-based fiber tracking employed by FACT limit the accuracy with which white matter tracts can be segmented. For instance, the data near the cortex is too noisy to accurately model the cortical projections of the fasciculi. However, the limitations of segmentation method do not preclude us from performing statistical analysis, as long as it is safe to assume that the segmentation error is independent of the differences between cohorts in a study. Recent advances in DTI segmentation (Lenglet et al., 2006; O’Donnell and Westin, 2007; Awate et al., 2007) and higher resolution imaging may indeed make it possible to more accurately label fasciculi in atlas space, as well as in individual subject images, and to do so automatically or with minimal user interaction. However, given the fact that deformable medial models are themselves a very powerful segmentation tool (Pizer et al., 1999; Joshi et al., 2002), a truly attractive approach would be to fit the deformable medial models employed in this paper directly to DTI data, rather than to segmentations obtained with other techniques. This would require incorporating tensor-based and connectivity-based likelihood metrics into cm-rep fitting, as well as training shape priors for each of the fasciculi. In addition to shape, priors may incorporate the variation in the angle between spokes of the medial model and the principal direction of diffusion in the underlying DTI data. Model-based segmentation of the fasciculi is one of the key long-term aims of our research.

The statistical methods used in this paper represent just one of many possible approaches to structure-specific inference. For example, instead of permutation-based cluster analysis, one could use point-wise hypothesis testing with false discovery rate correction (Benjamini and Yekutieli, 2001). It is also possible to subdivide the fasciculi according to cortical regions to which individual fibers connect, and to compute region-wise statistics. Instead of using features derived from diffusion tensors averaged along spokes, multivariate analysis may be applied, where each point on the medial manifold is associated with a tuple of diffusion tensors. Such a framework would be more sensitive to group differences occurring on opposite sides of the medial manifold.

In conclusion, we have presented a novel structure-specific framework for analyzing white matter differences between populations. The technique can be seen both as a model-based structure-specific alternative to the TBSS method (Smith et al., 2006) and as an extension of the cortical flat mapping paradigm to white matter structures. The six sheet-like fasciculi in the human brain are modeled using deformable medial models, which allows the diffusion tensor data associated with these structures to be projected onto parametric manifolds or even flattened to a two-dimensional domain. This approach simplifies white matter analysis and provides a compelling way to present results of white matter studies.

Fig. 5.

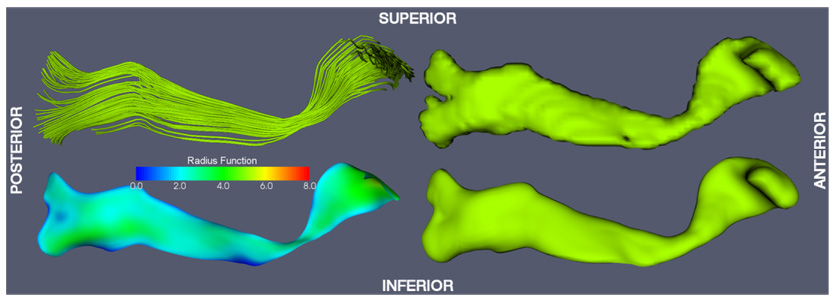
Inferior fronto-occipital fasciculus (IFO) model-fitting result.

Fig. 6.

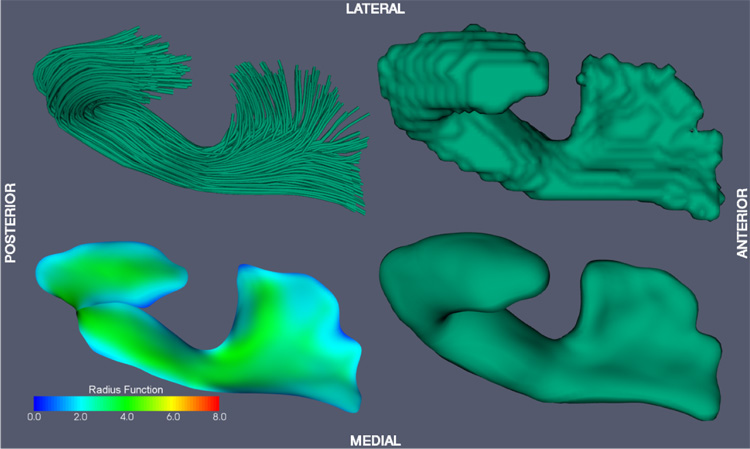
Uncinate fasciculus (UNC) model-fitting result.

Fig. 7.

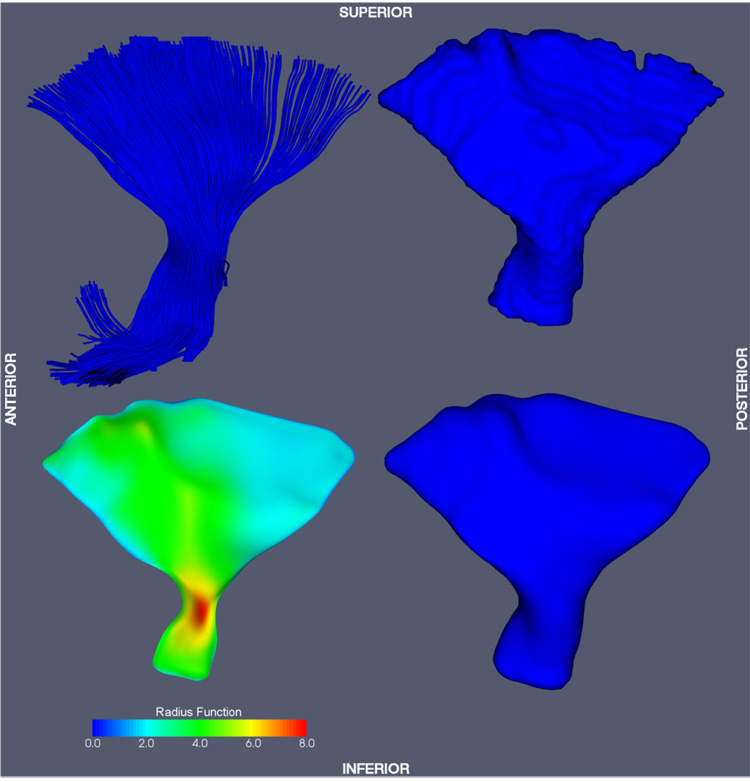
Corticospinal tract (CST) model-fitting result.