Alternans of cardiac calcium cycling in a cluster of ryanodine receptors: a simulation study

Abstract

Mechanical alternans in cardiac muscle is associated with intracellular Ca²⁺ alternans. Mechanisms underlying intracellular Ca²⁺ alternans are unclear. In previous experimental studies, we produced alternans of systolic Ca²⁺ under voltage clamp, either by partially inhibiting the Ca²⁺ release mechanism, or by applying small depolarizing pulses. In each case, alternans relied on propagating waves of Ca²⁺ release. The aim of this study is to investigate by computer modeling how alternans of systolic Ca²⁺ is produced. A mathematical model of a cardiac cell with 75 coupled elements is developed, with each element contains L-type Ca²⁺ current, a subspace into which Ca release takes place, a cytoplasmic space, sarcoplasmic reticulum (SR) release channels [ryanodine receptor (RyR)], and uptake sites (SERCA). Interelement coupling is via Ca²⁺ diffusion between neighboring subspaces via cytoplasmic spaces and network SR spaces. Small depolarizing pulses were simulated by step changes of cell membrane potential (20 mV) with random block of L-type channels. Partial inhibition of the release mechanism is mimicked by applying a reduction of RyR open probability in response to full stimulation by L-type channels. In both cases, systolic alternans follow, consistent with our experimental observations, being generated by propagating waves of Ca²⁺ release and sustained through alternation of SR Ca²⁺ content. This study provides novel and fundamental insights to understand mechanisms that may underlie intracellular Ca²⁺ alternans without the need for refractoriness of L-type Ca or RyR channels under rapid pacing.

up to 50% of deaths seen in heart failure are sudden and likely, therefore, to be due to cardiac arrhythmias. In heart failure, up to 40% of patients exhibit a phenomenon known as mechanical alternans (19), when the force of contraction of the heart alternates between strong and weak. A related phenomenon is microvolt T-wave alternans, detectable in the ECG (1) and considered to be especially arrhythmogenic. Many cardiac arrhythmias are thought to be due to irregularity of Ca²⁺ handling (11, 30, 36) by the sarcoplasmic reticulum (SR), the main source of Ca²⁺ for cardiac contraction. Systolic Ca²⁺ release occurs via Ca²⁺-induced Ca²⁺ release (CICR), triggered by Ca²⁺ entry on L-type Ca²⁺ channels (3). In mechanical alternans, large and small contractions follow each other (10, 13, 27) due to alternation of systolic Ca²⁺ (21, 40). In isolated cardiac cells, alternans of systolic Ca²⁺ is associated with alternans of cell shortening (16). Systolic Ca alternans are also associated with alternans of action potential duration (6, 22, 31) and alternans of the T-wave of the ECG (31).

Changes in amplitude and timing of Ca release during systole can influence the action potential shape by acting on Ca-sensitive currents, e.g., Na/Ca exchange (NCX) causing ECG abnormalities and the arrhythmogenicity of systolic Ca alternans.

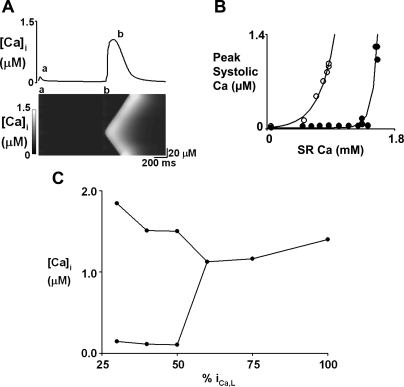
Previous work in our laboratory has focused on intracellular Ca²⁺ concentration ([Ca²⁺]_i) alternans and suggests that SR Ca content fluctuation is key to cardiac alternans (7). We found that, in rat ventricular myocytes, small (20 mV) depolarizing pulses produced alternans of the amplitude of the Ca²⁺ transient. Confocal measurements of [Ca²⁺]_i showed the larger transients involved waves of CICR. In addition, SR Ca²⁺ content alternated in phase with the alternans of Ca²⁺ transient amplitude. During alternans of systolic release, we found that the relationship between Ca²⁺ transient amplitude and SR Ca²⁺ content was extremely steep. We attributed this steeper relationship to the dependence on Ca wave propagation, as this requires a “threshold” SR Ca²⁺ content (8).

The work presented here attempts to build a theoretical framework to describe the observations of Ca²⁺ release profiles measured by confocal microscopy and to investigate detailed mechanisms underlying the emergence of Ca²⁺ alternans. The simulation results support conclusions from experiments that alternans can arise due to propagation of waves of Ca²⁺ release, and that this results from a large increase in the gain of the feedback controlling SR Ca²⁺ content. This study provides a novel and fundamental insight into a mechanism underlying the genesis of systolic Ca²⁺ alternans that does not require refractoriness of L-type Ca or ryanodine receptor (RyR) channel.

METHODS

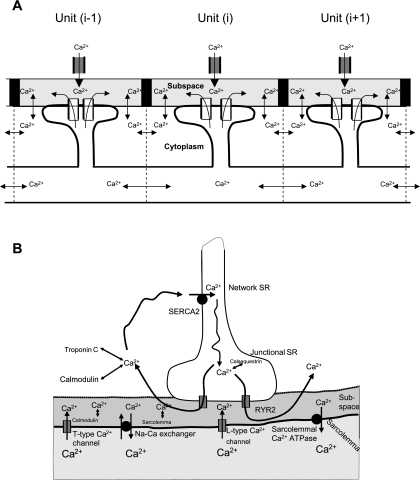
Our model consists of a cluster of coupled RyRs for a cardiac cell (see Fig. 1A). The cell has a length of 150 μm, which is discretized into 75 units along the longitudinal direction. Each unit encompasses 2 μm in the longitudinal dimension, and the entire cell depth and height in other dimensions. The spatial resolution of 2 μm is similar to the longitudinal distance between adjacent Ca²⁺ release units of cardiac cells (1.94 ± 0.31 μm) (5) and is fine enough to produce stable numerical solutions for Ca²⁺ waves in the model. Each element has a cluster of unitary voltage-gated L-type Ca²⁺ channels (contributing to global L-type Ca²⁺ channel current in each element; hereafter referred to as L-type Ca²⁺ channel), a subspace under the sarcolemma, a cytoplasmic space, and a cluster of SR RyR channels (contributing global SR RyR channel release in each element; hereafter referred to as RyR channel) (see Fig. 1B). For each element, mathematical equations (see appendix) were developed to model Ca²⁺ cycling. Interelement coupling is via Ca²⁺ diffusion from subspaces to cytoplasmic spaces and via network SR spaces. In simulations, we have taken two approaches: 100-ms depolarizing pulses at 1 Hz from a holding potential of −40 mV were used to activate L-type channels to open in each element. In the first approach, the depolarizing pulse was from −40 to 0 mV, and we partially inhibited the Ca²⁺ release mechanism by increasing the threshold of RyR Ca²⁺ release to mimic the decreased sensitivity of RyR by tetracaine, as suggested by a previous study (15). In the second approach, the depolarizing pulse was small, from −40 to −20 mV. To simulate the decreased global L-type Ca²⁺ current in the cell in response to such a small stimulus pulse (7), the L-type Ca²⁺ current was blocked (setting to zero) in some elements randomly chosen from the cell, but remained the same as in the control for the nonblocked elements. Thus Ca²⁺ release was activated at only a few elements, with L-type Ca²⁺ current being fully activated. In simulations, the population of blocked elements varies (say 40 out of 75 elements) to produce different levels of L-type Ca²⁺ current amplitude reduction in the cell.

Fig. 1.

A: schematic model of a cluster of coupled ryanodine receptors (RyRs) in a cardiac cell. The cell has a length of 150 μm, with 75 elements, giving 2-μm spatial resolution. Coupling of these elements is via Ca²⁺ diffusion between neighboring cytoplasmic and network sarcoplasmic reticulum (SR) spaces, as described in the appendix. B: schematic model of Ca²⁺ cycling for each element of the cluster illustrated in A. Three main Ca²⁺ cycling processes were modeled, which included 1) Ca²⁺ entry by L-type Ca²⁺ channel and Ca²⁺-induced Ca²⁺ release (CICR); 2) Ca²⁺ removal by Na/Ca exchanger and ATP-dependent Ca²⁺ pump; and 3) Ca²⁺ diffusion and Ca²⁺ binding to its buffers.

Development of equations: table and choices of parameters.

We assume the global L-type Ca channel current (produced by a cluster of unitary L-type channels in each element) and intracellular Ca²⁺ cycling of RyRs have the same kinetics for all elements and are described by whole cell equations similar to the approach used in the study of Shiferaw and Karma (34). The equations of Ca²⁺ cycling were modified from the model developed by Kurata et al. (20) with parameters and equations derived from experimental data of ventricular myocytes and used in the Luo-Rudy (26) model of guinea pig ventricular myocytes. In the model, some parameters, such as the volumes of cell, subspace, cytoplasm, network SR, and junctional SR, were adjusted (3) to fit the rat ventricular cell in our experiments. Despite being simple, the model captures most general features of cardiac Ca cycling necessary for CICR wave propagation, which enables us to unravel the major determinants responsible for systolic Ca²⁺ alternans, i.e., propagation of CICR waves and steep relationship between RyR release and the SR Ca content. Detailed glossary and equations are given in the appendix.

The cardiac myocyte is a spatially extended object, within which Ca²⁺ diffuses. Our previous experimental results suggest Ca²⁺ diffusion is crucial during systolic Ca²⁺ alternans (7, 9). Spatially extended models have been developed to study Ca²⁺ sparks and waves (38). To simulate Ca²⁺ wave propagation and Ca²⁺ release alternans, we developed a more detailed model of Ca²⁺ spatial diffusion. It includes Ca²⁺ diffusion from the subspaces to myoplasmic spaces and between network SR spaces of neighboring elements. The diffusion parameters were chosen in such a way that the propagation of CICR waves matches our experimental data; these parameters are close to those used in previous studies (14, 15, 17, 20, 23, 26, 28, 32, 34, 35, 37, 38). Detailed comparisons of model parameter values with those of literature-based and other models are given in Table 1.

Table 1.

Comparison of parameters used in the model with experimental data and other models

Parameters	Model Value	Literature-Based or Other Model Values	Ref. No.
tCa diff (time constant for Ca diffusion from subspace to cytoplasmic space)	0.04 ms	0.04 ms	23
		0.05–0.6 ms	37
		0.04 ms	20
		0.0007 ms	32
		0.0007 ms	38
		0.005 ms	14
		2 ms	34
		26.7 ms	28
τCa i diff (time constant for Ca diffusion between neighboring cytoplasmic spaces)	4 ms	5 ms	34
τCa up diff (time constant for Ca diffusion between neighboring network SR spaces)	600 ms	100 ms	34
Estimated Ca diffusion coefficient in the cytoplasmic space	10.0 × 10−6 cm2/s	1.0 × 10−6 cm2/s	23
		4.0 × 10−6 cm2/s	2
		7.0 × 10−7 to 7.9 × 10−6 cm2/s	37
		1.5 × 10−6 to 3.0 × 10−6 cm2/s	34
Measured Ca propagation velocity	0.212 mm/s	0.05–15 mm/s	2
τtr (time constant for Ca diffusion from network SR to junctional SR)	60 ms	1–100 ms	35
		50 ms	34
		60 ms	20
		180 ms	26
		34.48 ms	17
		10 ms	38
		3 ms	14
		0.5747 ms	28
		0.005 ms	32

SR, sarcoplasmic reticulum.

RESULTS

Spatially uniform model.

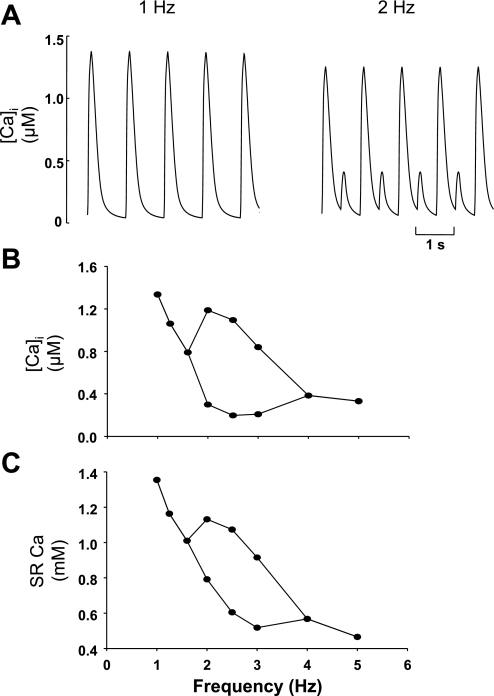
Several models of Ca handling in cardiac muscle have been shown to produce systolic Ca alternans (18, 35, 37). Typically, these models lack a spatial dimension, and alternans is produced by raising the pacing frequency. We thought it important to show that our model can also produce similar behavior. Thus the traces in Fig. 2A show simulations run at 1 and 2 Hz in a single element of our model, i.e., there are now no other elements into which Ca can diffuse. At 1-Hz pacing, the Ca transient is uniform, with no variability from pulse to pulse. However, when the pacing frequency is raised to 2 Hz, clear, large alternans of systolic Ca are present. The full frequency dependence is shown in Fig. 2B, where the Ca transient amplitude is plotted as a function of the frequency of stimulation (the stimulus pulse is the same for all stimulus frequency, e.g., from −40 to 0 mV, with a duration of 100 ms). At a frequency of 2 Hz, alternans is maximal, but, as the stimulation frequency increases further, the ratio of alternans decreases until it reaches 1 again at 4 Hz. The plot (Fig. 2C) below shows how the SR Ca content varies with stimulation frequency. It decreases dramatically with the increase of stimulus rate, due to more frequent Ca release from the SR and less time interval for Ca being taken back to the SR between two successive stimuli.

Fig. 2.

Simulations from a single Ca²⁺ release unit showing the effects of pacing frequency. For all stimulus frequency, the stimulus pulse has the same amplitude (from −40 to 0 mV) and duration (100 ms). A: time traces of cytoplasmic Ca²⁺ transient at 1 Hz (left) and 2 Hz (right). Ca²⁺ release is uniform from pulse to pulse at 1 Hz, but shows clear alternans at 2 Hz. B: Ca transient amplitude as a function of frequency; bifurcation leads to cytoplasmic Ca²⁺ transient alternans. C: associated SR Ca²⁺ content. [Ca²⁺]_i, intracellular Ca²⁺ concentration.

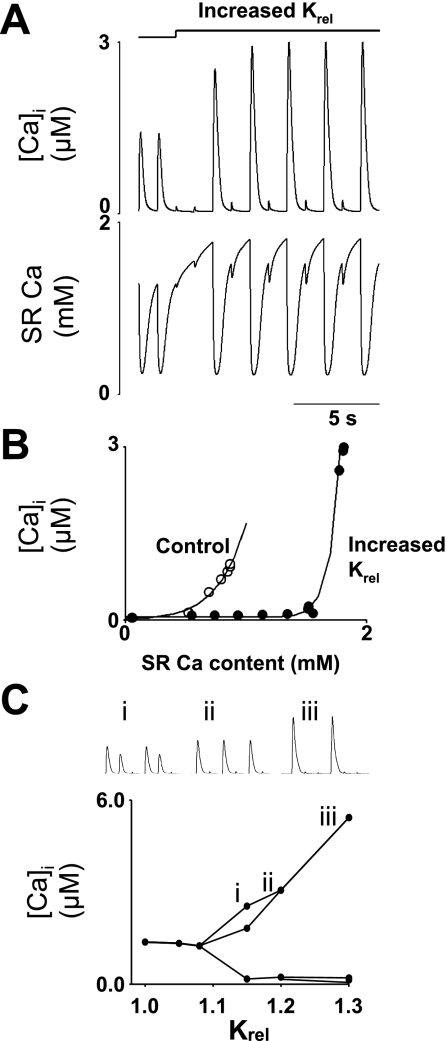
The other maneuver we have used in this study to elicit alternans is an increase of the half-maximal subspace [Ca²⁺] for Ca²⁺ release from junctional SR (K_rel) (the subspace [Ca²⁺] required to stimulate RyR to open is raised by 20%) to mimic inhibition of CICR. In the uniform model (functionally equivalent to a single release site version of the model: Fig. 3A), there are two control stimuli, and raising K_rel leads to alternans following two very small systolic transients. Junctional SR Ca²⁺ content (below) shows each control stimulus depletes the SR, followed by a refilling period. After raising K_rel, the period with very small transients allows the SR to fill to the point where alternans can occur. Before small releases, SR content is less than before large releases. The plot in Fig. 3B shows how alternans is produced. There are two plots of SR Ca²⁺ release vs. SR Ca²⁺ content under control conditions (open symbols) and with K_rel raised (solid symbols). These plots follow SR filling from the empty state (not shown). It is clear that, when K_rel is raised, a higher SR Ca²⁺ content is reached (which requires more refilling time after a large release), and the steepness of the relationship is increased [the fitted lines have the formula systolic Ca = a + b(SR Ca)ⁿ; in control n = 3.5, rising to 15.0 when K_rel is raised]. This extra steepness of this relationship allows large changes of released Ca²⁺ for relatively minor changes of diastolic SR content. The plot in Fig. 3C shows how the Ca transient amplitude (at 1 Hz) changes with increasing K_rel. The 1:1 alternans that we illustrate throughout this study is, in fact, only seen in a narrow range of K_rel values, around 1.2 times control: at lower values, two large releases accompany one small, and, at higher values, there are two small releases for each large. Examples of the Ca transients at each of the three values of K_rel plotted (1.15, 1.2, and 1.3) are shown above.

Fig. 3.

Model-generated Ca²⁺ alternans by increasing half-maximal Ca²⁺ subspace concentration for Ca²⁺ release from junctional SR (K_rel) to mimic tetracaine. Ca transients were produced by a sequence of 1-Hz, 100-ms depolarizing pulses from a holding potential of −40 to 0 mV. K_rel was increased uniformly by 20% after the first 2 pulses. Ca²⁺ alternans developed after a period of Ca release inhibition after K_rel was increased. A: traces of cytoplasmic Ca²⁺ transients (top) and SR Ca²⁺ (bottom). B: relationship between SR Ca content and systolic Ca in the cytoplasmic space for control (○) and increased K_rel (•) conditions as SR Ca recovers from empty state. Solid line was produced by curve fitting of systolic Ca = a + b(SR Ca)ⁿ, where n = 3.5 for control and rises to 15.0 for increased K_rel. C: systolic Ca as a function of K_rel. Bifurcation leads to cytoplasmic Ca²⁺ alternans. Increase in K_rel results in various patterns of cytoplasmic Ca²⁺ alternans, such as 2:1 (i), 1:1 (ii), or 1:2 (iii) as shown in the inset.

The effect of adding a spatial dimension.

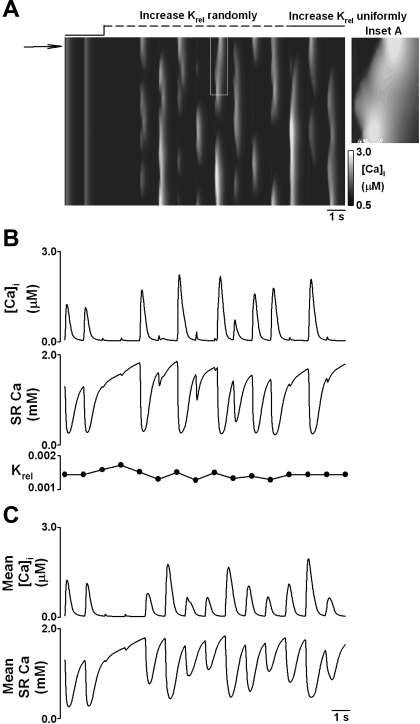
Introduction of a spatial dimension allows us to increase K_rel in a random pattern across the 75 release unit array. On average, the increase of K_rel is the same as in Fig. 3, but now it varies among the 75 release units randomly. This pattern of raised threshold also changes with each stimulus, to mimic in a simplified manner the random nature of CICR inhibition in RyR clusters. The line scan in Fig. 4A shows two control stimuli followed by two very small transients after K_rel is raised. Raising K_rel by an average of 20% is indicated by the line above the line scan. The line is initially dashed to indicate randomly changing K_rel; thereafter, the solid line indicates a uniformly raised value. Raising K_rel fragments the release profile, and local alternans follows. In agreement with our experimental data (9), large releases are associated with miniwaves of Ca²⁺ release (see inset A). Previously we have suggested that, associated with such behavior, there would be local variations in SR Ca²⁺ content caused by variations of local release and efflux. The model can give us this information; Fig. 4B shows local alternans of systolic Ca at the point marked by the arrow in Fig. 4A, the middle panel shows SR Ca²⁺ content from this area. During local alternans, SR Ca is relatively higher locally before large releases than before small releases. As the extent of alternans varies across the cell, the degree of alternans averaged over the whole cell is somewhat smaller that that shown in B (c.f., Fig. 4, B and C).

Fig. 4.

Model-generated Ca²⁺ alternans by increasing K_rel nonuniformly across the 75 element array. Ca²⁺ transients were produced by a sequence of 1-Hz, 100-ms depolarizing pulses from a holding potential of −40 to 0 mV. K_rel was increased in a random pattern by an average of 20% across the cell after the first 2 pulses (indicated above the line scan). The pattern in which K_rel was raised also varied at random from stimulus to stimulus. The line above the line scan becoming solid indicates that K_rel is uniformly 20% above the control level. A: line scan of cytoplasmic Ca²⁺ transient across the cell. After increase of K_rel, localized and fragmented Ca²⁺ alternans developed after a short period of Ca²⁺ release inhibition. Inset A: propagation of local Ca²⁺ wave for the region marked by white box. B, top: traces of cytoplasmic Ca²⁺ recorded from one element marked by the arrow. Middle: associated trace of SR Ca²⁺ from the same element. Bottom: trace of K_rel in the same element. C, top: trace of mean cytoplasmic Ca²⁺ averaged across the cell. Bottom: trace of SR Ca²⁺ averaged across the cell.

Cytoplasmic Ca²⁺ transients produced by small depolarizations.

Another experimental method that produces alternans is the use of small depolarizations (7). In the model, a series of small stimulus pulses lead to sustained alternans of cytoplasmic Ca²⁺ transients (e.g., Fig. 5A). However, the degree of alternans averaged over the whole cell is much greater than in Fig. 4. This is because either none of the cell releases Ca²⁺ (a in Fig. 5A), or all of the cell responds (b in Fig. 5A), i.e., there is no out-of-phase alternation taking place to reduce the overall degree of alternans. However, unlike Figs. 2 and 3, where similarly large alternans is present in the dimensionless model, the large release involves Ca²⁺ wave propagation (Figs. 5A and 7A), very similar to our experimental data (7). The steepness of the relationship between systolic Ca²⁺ and SR Ca²⁺ is also increased in this alternans. The fitted lines in Fig. 5B have n set to 3.5 in control (open symbols) and 18.4 during small depolarizations (solid symbols).

Fig. 5.

Model-generated Ca²⁺ alternans by small depolarizing pulses. The model is stimulated by a series of 1-Hz, 100-ms pulses from a holding potential of −40 to −20 mV. In addition, 40 out of 75 individual units of L-type Ca²⁺ channel current (I_Ca,L) were randomly blocked. A, top: cytoplasmic Ca²⁺ averaged across model of cell. Bottom: line scan images of cytoplasmic Ca²⁺ across cell that correspond to the transients marked a and b above. B: relationship between SR Ca²⁺ content and systolic Ca²⁺ in the cytoplasmic space for control (○) and small-pulse (•) conditions as the model recovers from the empty state. Solid line was produced by curve fitting of systolic Ca = a + b(SR Ca)ⁿ; n = 3.5 for control and 18.4 for small-pulse depolarization. C: systolic Ca as a function of I_Ca,L amplitude in the whole cell; bifurcation leads to cytoplasmic Ca²⁺ alternans. In simulations, different populations of elements are randomly chosen from the 75 units for block, producing different I_Ca,L amplitude in the cell (%I_Ca,L).

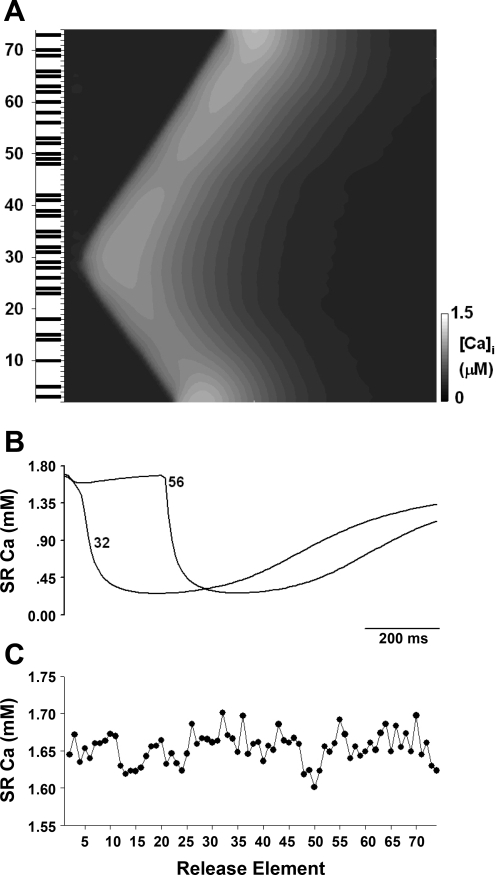
Fig. 7.

A: propagation of cytoplasmic Ca²⁺ wave produced by localized CICR in response to I_Ca,L trigger (with the same condition as in Fig. 6) and spatial diffusion of Ca²⁺. Solid bars: elements with fully active I_Ca,L channels. B: SR Ca²⁺ transients for some local elements 32 and 56. C: spatial distribution of SR Ca²⁺ content at end diastole.

In Fig. 5, A and B, 40 out of 75 elements in the cell are chosen randomly to have their L-type Ca current blocked. The remained current in the whole cell is 46% of control. Further studies have also been conducted to explore the general relationship between Ca²⁺ release and the reduction in the amplitude of L-type channel current in the whole cell via varying the number of blocked elements. The graph in Fig. 5C shows the full relationship between the remained averaged global L-type current (as percentage of control) in the whole cell and Ca release. A decrease of L-type channel current means the number of sites where CICR can take place decreases. At small current values (<60% of control), there is large alternans. At the current values between 30 and 50% of control, there is 1:1 alternans. With L-type currents <30% and between 50 and 60%, the alternans pattern produced is complicated and does not follow the 1:1 pattern shown in Fig. 5A (somewhat similar to the situation in Fig. 3C). Finally, >60% of L-type current amplitude alternans disappears.

Two phases of Ca²⁺ release.

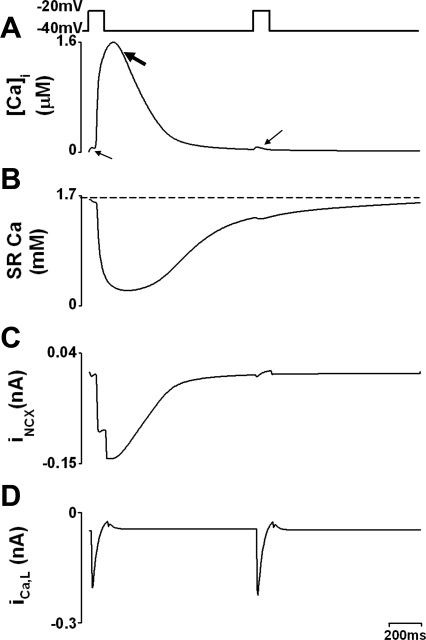
The model also reproduces the biphasic release we see experimentally when using small pulses. The trace of systolic Ca²⁺ in Fig. 6A shows two successive stimuli each demonstrating a small, initial release (marked by small arrow). A second phase of release (produced by wave propagation; marked by big arrow) follows in the first stimulus. Again, this fits well with data from cells under similar experimental conditions. Both phases are due to CICR: the first represents release stimulated by L-type Ca channel activity, and the second, propagating CICR.

Fig. 6.

Ca²⁺ content and efflux during Ca²⁺ alternans produced by small depolarization pulses with 40 out of 75 elements blocked. A: [Ca²⁺] in cytoplasmic space. Biphasic Ca release is obvious with a small initial release evoked by stimulus (small arrow) followed by a big release (large arrow). B: Ca²⁺ content in the SR. C: Na/Ca exchanger current (I_NCX). D: I_Ca,L.

SR Ca²⁺ content, NCX current, and Ca²⁺ transient.

Alternans following small depolarizations also relies on changes of SR Ca content; Fig. 6 shows SR Ca²⁺ content (averaged over all release units) and efflux via NCX current during large and small Ca²⁺ transients. A large Ca²⁺ transient was associated with a large SR Ca²⁺ release (i.e., junctional SR content falls more; Fig. 6B) and more Ca²⁺ removal by NCX (Fig. 6C), while a small Ca²⁺ transient was associated with less Ca²⁺ release and less Ca²⁺ removal by NCX. The dashed line in Fig. 6B illustrates that, before the small release, SR Ca²⁺ is lower than before the large release. This, too, is consistent with experimental observations (7). The L-type currents in Fig. 6D indicate that changes in SR Ca²⁺ are solely responsible for changes in systolic release as trigger Ca²⁺ is unchanged between large and small releases.

One question is: where is release triggered by L-type channel openings and where is it propagated following small depolarizations? Obviously, triggered release will only be possible where L-type Ca current is activated. The solid bars in Fig. 7A show the elements at which the L-type Ca channels open on this particular stimulus; where release is initiated (sites 28 and 29 and 31 and 32), there is full opening of L-type channels in the element. However, such L-type openings do not always trigger Ca release, e.g., sites 48, 49, and 50 and 56 and 58 have L-type openings but no CICR follows. These sites had to wait for the arrival of the wave initiated at sites 31 and 32 to release Ca.

One possible explanation for failure of L-type channels to trigger CICR is suggested by Fig. 7, B and C. Figure 7B shows changes in SR Ca at two different sites from the line scan, i.e., sites 32 and 56. At site 32, there is an early release of Ca due to activation of L-type Ca channels; at site 56, Ca release fails initially but is activated later by the arrival of the wave. Although sites 32 and 56 seem to have the same initial SR Ca content, Fig. 7C shows the initial values in more detail for each site, and it is clear that site 32 has a marginally higher content, making it more likely to release.

DISCUSSION

Our previous work has shown two maneuvers that produce local and global alternans of systolic Ca²⁺ release in ventricular cells (7, 9). Reducing RyR open probability in voltage-clamped cells with, e.g., tetracaine or acidic intracellular pH, produces alternans of systolic release that remains local, i.e., different parts of the cell show alternans out of phase with each other. Decreasing the amplitude of the L-type Ca current produces alternans that involve the whole cell. We have suggested that alternans is due to increased steepness of the relationship between SR Ca²⁺ content and release of Ca²⁺ (a measure of the gain of Ca release). Increased steepness in both local and global alternans is due to the appearance of waves, as these rely on the SR reaching a threshold Ca²⁺ content (8). This ought to lead to an essentially infinitely steep relationship: above threshold, waves occur and release is large; below threshold, there are no waves and release is small. In this paper, we present simulations of this behavior to determine the important factors underlying generation of alternans of systolic Ca release. Our major finding is that the fragmented Ca²⁺ wave propagation and steep relationship between SR Ca²⁺ content and release of Ca²⁺ play a major role in the genesis of Ca²⁺ alternans at low-stimulus frequency (1 Hz) without the need for refractoriness of L-type Ca or RyR channels. The alternans sustains through alternation of SR Ca²⁺ content. This is different from the mechanism underlying the genesis of Ca²⁺ alternans at rapid pacing, as reported by Shiferaw and Karma (34), where refractoriness of ion channels and electrical action potentials are involved to produce instable Ca diffusion, leading to symmetry breaking.

The simulations we have done here can reproduce all features of systolic Ca²⁺ alternans, local and global, that we have seen in cells. The two types of alternans we find share several features in common: on a large Ca transient, initial release is stimulated by L-type Ca current in only a few sites; the released Ca²⁺ initiates a propagating wave by inducing further SR Ca²⁺ release in regions that did not respond to the initial depolarization. Such a large Ca release locally ensures that the SR remains depleted at the next stimulus.

In the model, the reduced open probability of RyR can be produced by increasing the parameter K_rel (the subspace Ca required to open the RyR, i.e., RyR Ca sensitivity). In Fig. 3, we increased K_rel by 20%; this produces 1:1 alternans of systolic release. The plot in Fig. 3B shows why alternans has occurred; there is a greatly increased steepness of the relationship between Ca²⁺ release and diastolic SR Ca²⁺ content compared with the control. Thus for a small reduction of Ca²⁺ in the SR at end diastole, there is a very large reduction in systolic release. However, in this case, the increased steepness in this plot does not rely on wave propagation, as there is no spatial dimension in the model.

In our studies of raising K_rel, we have concentrated on a value of 1.2 times control, as this produces an alternans ratio of 1:1, i.e., for each large transient, there is a small transient. However, it is clear from Fig. 3C that other patterns of alternans are possible. In all cases, the cell is maintaining Ca flux balance, i.e., the amount of Ca that enters the cell must also leave. However, it is clear that the number of stimulation cycles required to make this balance can vary. How altering K_rel changes the pattern of alternans is not yet clear and warrants further studies.

Fragmentation of the release profile seen in cells when tetracaine or acid pH is applied can be reproduced in the full version of the model (75 release units in contact by diffusion between neighboring element's cytoplasmic spaces) by applying a random pattern of increase of K_rel across the array of release units. Although L-type channel opening is uniform across the array, Ca²⁺ wave propagation was initiated at a limited number of release sites (Fig. 4A). If a region of the cell is not stimulated to release Ca by an L-type channel opening, it may then be able to support wave propagation. If Ca release takes place (triggered either way), on the next stimulus the SR in this region is depleted of Ca²⁺ (Fig. 4B) and so does not respond to either stimulus or arrival of a wave. This reliance on SR Ca does not, however, reflect a luminal effect (24), as no “sensor” of SR Ca content inside the SR has been built into the model, although it may reflect a change in the feedback of the CICR mechanism. Released Ca feeding back to activate more CICR will be more evident if SR Ca content is high.

Application of increased K_rel in a random pattern across the cell requires explanation. Conditions throughout the cell are unlikely to be entirely uniform in experiments as they are in the model. Although other possibilities may exist, in real cells, fragmentation of the release profile might occur through small, local variations of SR Ca²⁺ due to, e.g., spontaneous sparks and/or local differences in K_rel. In each case, a spatially inhomogeneous response of the SR to L-type current would be expected to result. The mechanism we propose for depletion and refilling of the SR would then maintain such inhomogeneity. This is confirmed in Fig. 4A, at the point where the dashed line (marking raised K_rel) becomes solid, the random changes of K_rel cease, i.e., K_rel is raised by 20% uniformly across the array. Despite this, the fragmented release profile is maintained.

As in real cells, at the whole cell level, the degree of alternans in the model is rather small during local alternans (Fig. 4C). This results from the lack of synchrony of release, i.e., regions alternating to a lesser extent or out of phase partially balance each other. This is just as we saw in experiments on rat ventricular myocytes in the presence of tetracaine and acidic pH (9).

We can now ask why it is that, in real cells, alternans is not uniform, but is produced by propagation of miniwaves? It is clear from Fig. 3 that uniform alternans is possible (75 release units together with a uniform increase of K_rel would also produce uniform alternans); however, if we compare the SR Ca values produced by the model required for uniform alternans with those when miniwaves produce alternans, we see that alternans in a single unit requires higher SR Ca levels (1.81 vs. 1.56 mM). Thus there are two probable factors that combine to prevent the appearance of uniform alternans in the cell: conditions are unlikely ever to be sufficiently uniform to allow them to develop, and, in any case, alternans due to miniwaves will develop at a lower SR Ca, thereby preventing SR Ca rising high enough.

Small depolarizations and alternans.

When alternans are produced by reducing the number of L-type Ca channels that respond to depolarization, rather than the number of RyR that respond to L-type current, the degree of alternans at the whole cell level is greater in both cells and the model (Fig. 5). In this case, a few elements with activated L-type channels trigger SR Ca release. This released Ca diffuses to neighboring sites, where it activates CICR. This two-stage process leads to the biphasic Ca²⁺ release in Fig. 6, averaged over the whole cell. The time taken for the second phase to rise is dictated by the propagation velocity of the wave of CICR.

In the model, the number of release sites responding to small depolarization pulse is reduced by the imposition of a block of L-type channel current locally in some of elements (see Limitations of the model), which are randomly chosen from the 75 release elements in the array, giving a different pattern of L-type channel activation with each stimulus. The different pattern of L-type channel activation on each stimulus results in different initiation sites for Ca release (not shown). However, the pattern of L-type channel opening is not the only influence on where RyR openings result, as many L-type channel openings do not produce SR release (Fig. 7). Where release triggered by L-type Ca channels is absent or small, SR Ca content is low at the time of stimulation, e.g., site 56. The model has no luminal site that could confer extra sensitivity of the release unit at high Ca content. Thus it appears that Ca released can feed back to stimulate further release, if SR content is high.

The importance of SR Ca content.

As we have reported before, during alternans, large releases deplete the SR due to greater activation of Ca²⁺ efflux pathways. This can be seen in Fig. 6, where the large NCX current depletes the SR of Ca. By the time of the next stimulus, the junctional SR has not completely refilled. This small depletion of the SR means no wave propagation is possible, and a small release results. As little efflux is activated by this small release, the SR is able to refill back to the level able to support wave propagation, and a large release results once again on the next cycle. A similar explanation of alternans can be used on a local scale to explain the simulations of the effects of tetracaine or acid pH. The large releases cause either global (Fig. 6B) or local (Fig. 4B) SR depletion, depending on how inhibition of RyR opening is applied. This depletion leads to reduced release of Ca and prevents wave propagation. Obviously, for local depletions of SR Ca to be able to influence the amount of Ca released, it requires that the depletion persist long enough. The intercoupling between neighboring SR release sites allows for local depletion to persist sufficiently long to maintain alternans.

The actual shape of the relationship between systolic [Ca] and frequency is interesting: when alternans first appears, the ratio is large, but, as frequency increases, the alternans ratio declines until systolic [Ca] is once again uniform from beat to beat. Associated with these changes is a fall of SR Ca content, which suggests that alternans is only possible over a narrow range of SR Ca content. Perhaps as SR Ca content falls, the steepness of the relationship between SR Ca release and diastolic SR Ca content falls too low to provide sufficient depletion of the SR in any one cycle. Obviously, real cells exhibit alternans when frequency is raised. In the past, our laboratory has produced models of alternans that rely on a very steep relationship between SR Ca²⁺ release and SR Ca²⁺ content (12). Such a model produces alternans (e.g., Figs. 2 and 3 in this study); however, we now consider any approach that does not include a spatial element incomplete, as it cannot produce behavior that involves propagation of waves. It would be interesting in future simulations to impose some heterogeneity on the model (perhaps by application of a resting frequency of sparks to produce small variations of SR Ca content) to determine whether this will cause the Ca release profile to fragment at higher frequencies and allow miniwaves of Ca release and alternans to appear.

A recent report has shown (29) that, although present in the majority of cells studied, systolic Ca alternans can result without apparent alternans of SR Ca content. The simulations presented here, however, are intended to address the situation where the release of Ca from the SR is compromised, either by inhibition of CICR or limitation of L-type Ca current. It is entirely possible that the mechanism put forward here of fragmentation of the Ca release profile, followed by propagation of waves, is not the only one capable of leading to systolic Ca alternans. It would be interesting in the future to model the conditions required for such alternans, independent of SR Ca content.

Limitations of the model.

The present model has several limitations. In the present study, the SR Ca release was modeled by quasi-steady-state approximation of RyR gating kinetics; however, this seems reasonable considering the rapid activation (0.07–0.27 ms) (42) and extremely slow inactivation of the RyR gate (43) compared with the L-type Ca channel and the low stimulus frequency (1 Hz). In simulations, the mechanism of reversible SR uptake was not incorporated in the model. However, simulations with an alternative reversible SR uptake equation (33) (see Eq. A18.1 in appendix) show similar results. We have made no attempt here to model electrophysiological consequences of systolic Ca²⁺ alternans, although it is clear from our previous work and here (Fig. 6) that currents generated as a result of the changes in Ca²⁺ release would be expected to alter action potential shape and/or duration. The model includes no influence of SR Ca content on the behavior of the Ca release channel (25); this is thought to play a role in control of Ca release, but should, if present, accentuate the effects of local differences of SR Ca content on Ca release. Importantly, the model uses whole cell behavior of L-type current in each of the elements rather than the behavior of single unitary L-type channels. As a result, the changes of voltage used in this paper reduce current flow through the L-type channel of each release unit rather than increase unitary channel current. Finally, the model is a one-dimensional simulation of a cell and, therefore, lacks the three-dimensional complexities of a whole cell, such as t-tubule networks (39) and spatial distribution of L-type current (4) and NCX current (41). Each of these limitations needs to be addressed in future studies.

Despite these limitations, the model demonstrates that propagation of waves of CICR following fragmentation of the systolic Ca release profile is able to produce systolic Ca alternans. In addition, the model highlights the importance of interactions between local SR Ca content, L-type Ca channel activity, and sensitivity to Ca of the Ca release channel of the SR in sustaining this behavior.

GRANTS

Work on this paper was funded in part by grants from the British Heart Foundation and Biotechnology and Biological Sciences Research Council.

APPENDIX

Glossary

F

Faraday constant

I

Ionic current

R

Universal gas constant

SR

Sarcoplasmic reticulum

t

Time

T

Absolute temperature

V

Membrane potential (in mV)

Ionic channel currents.

I_Ca,L

L-type Ca²⁺ channel current

I_Ca,P

Sarcolemmal Ca²⁺ pump current

I_NaCa

Na⁺/Ca²⁺ exchanger (NCX) current

Cell geometry.

V_cell

Cell volume

V_i

Myoplasmic volume available for Ca²⁺ diffusion

V_rel

Volume of junctional SR (Ca²⁺ release store)

V_sub

Subspace volume

V_up

Volume of network SR (Ca²⁺ uptake store)

Ionic concentrations.

[Ca²⁺]_i

Myoplasmic Ca²⁺ concentration

[Ca²⁺]_o

Extracellular Ca²⁺ concentration

[Ca²⁺]_rel

Ca²⁺ concentration in junctional SR

[Ca²⁺]_sub

Subspace Ca²⁺ concentration

[Ca²⁺]_up

Ca²⁺ concentration in network SR

[Mg²⁺]_i

Intracellular Mg²⁺ concentration

[Na⁺]_i

Intracellular Na⁺ concentration

[Na⁺]_o

Extracellular Na⁺ concentration

Equilibrium (reversal) potentials.

E_Ca,L

Apparent reversal potential of I_Ca,L

Sarcolemmal ionic currents.

d_L

Activation gating variable for I_Ca,L

d_L,∞

Steady-state d_L

d_NaCa

Denominator constant for I_NaCa

f_L

Inactivation gating variable for I_Ca,L

f_L,∞

Steady-state f_L

g_Ca,L

Maximum I_Ca,L conductance

k_NaCa

Scaling factor for I_NaCa

y_NaCa

Position of Erying rate theory energy barrier controlling voltage dependence of I_NaCa

α

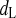
Opening rate constant of d_L

α

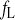
Opening rate constant of f_L

β

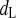
Closing rate constant of d_L

β

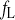
Closing rate constant of f_L

τ

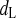
Time constant of d_L

τ

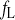
Time constant of f_L

Ca²⁺ diffusion flux.

J_{Ca diff}

Ca²⁺ diffusion flux from subspace to myoplasm

J_{Ca i diff}

Ca²⁺ transfer flux between neighboring myoplasm

J_{Ca up diff}

Ca²⁺ transfer flux between neighboring network SR

τ_{Ca diff}

Time constant for Ca²⁺ diffusion from subspace to myoplasm

τ_{Ca i diff}

Time constant for Ca²⁺ diffusion between neighboring myoplasmic units

τ_{Ca up diff}

Time constant for Ca²⁺ diffusion between neighboring network SR units

SR function.

J_rel

Ca²⁺ release flux from junctional SR to subspace

J_tr

Ca²⁺ transfer flux from network SR to junctional SR

J_up

Ca²⁺ uptake flux from myoplasm to network SR

K_rel

Half-maximal [Ca²⁺]_sub for Ca²⁺ release from junctional SR

K_up

Half-maximal [Ca²⁺]_i for Ca²⁺ uptake by Ca²⁺ pump in network SR

P_rel

Rate constant for Ca²⁺ release from junctional SR

P_up

Rate constant for Ca²⁺ uptake by Ca²⁺ pump in network SR

τ_tr

Time constant for Ca²⁺ transfer from network SR to junctional SR

Ca²⁺ buffering.

[CQ]_tot

Total calsequestrin concentration

[CM]_tot

Total calmodulin concentration

k_{b CM}

Ca²⁺ dissociation constant for calmodulin

k_{b CQ}

Ca²⁺ dissociation constant for calsequestrin

k_{b TC}

Ca²⁺ dissociation constant for troponin-Ca complex

k_{b TMC}

Ca²⁺ dissociation constant for troponin-Mg complex

k_{b TMM}

Mg²⁺ dissociation constant for troponin-Mg complex

k_{f CM}

Ca²⁺ association constant for calmodulin

k_{f CQ}

Ca²⁺ association constant for calsequestrin

k_{f TC}

Ca²⁺ association constant for troponin

k_{f TMC}

Ca²⁺ association constant for troponin-Mg complex

k_{f TMM}

Mg²⁺ association constant for troponin-Mg complex

[TC]_tot

Total concentration of troponin-Ca complex

[TMC]_tot

Total concentration of troponin-Mg complex

f_CMi,_∞

Fractional occupancy of calmodulin by Ca²⁺ in myoplasm

f_{CMi rate}

Derivative of f_CMi with respect to (WRT) time: df_CMi/dt

f_CMs,∞

Fractional occupancy of calmodulin by Ca²⁺ in subspace

f_{CMs rate}

Derivative of f_CMs WRT time: df_CMs/dt

f_CQ,∞

Fractional occupancy of calsequestrin by Ca²⁺

f_{CQ rate}

Derivative of f_CQ WRT time: df_CQ/dt

f_TC,∞

Fractional occupancy of the troponin-Ca site by Ca²⁺

f_{TC rate}

Derivative of f_TC WRT time: df_TC/dt

f_TMC,∞

Fractional occupancy of the troponin-Mg site by Ca²⁺

f_{TMC rate}

Derivative of f_TMC WRT time: df_TMC/dt

f_TMM,∞

Fractional occupancy of the troponin-Mg site by Mg²⁺

f_{TMM rate}

Derivative of f_TMM WRT time: df_TMM/dt

Equations

Sarcolemmal ionic current.

L-TYPE Ca²⁺ CHANNEL CURRENT.

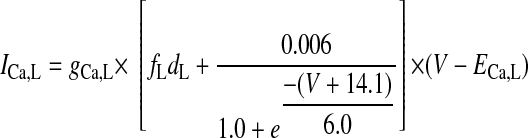(A1)

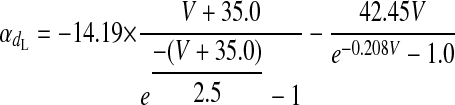(A2)

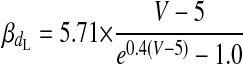(A3)

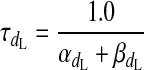(A4)

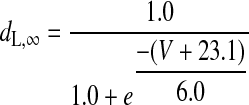(A5)

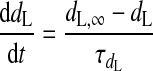(A6)

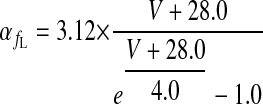(A7)

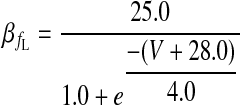(A8)

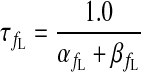(A9)

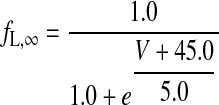(A10)

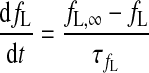(A11)

BACKGROUND, PUMP, AND EXCHANGER CURRENTS.

(A12)

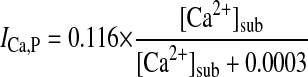(A13)

Intracellular Ca²⁺ dynamics.

Ca²⁺ DIFFUSION FLUX.

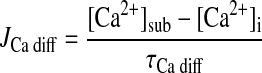(A14)

Ca²⁺ DIFFUSION FLUX BETWEEN NEIGHBORED ELEMENTS.

For each coupled element array, indexed by k (k varies between 1 and 75):

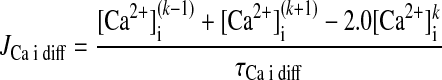(A15)

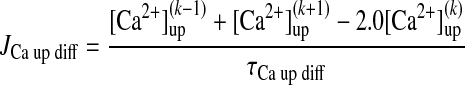(A16)

Ca²⁺ HANDLING BY SR.

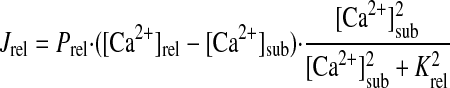(A17)

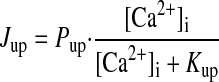(A18)

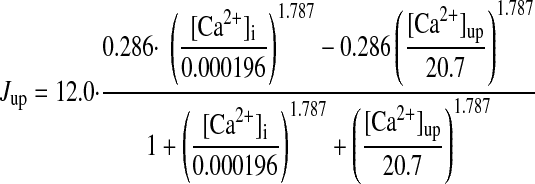(A18.1)

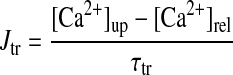(A19)

INTRACELLULAR ION CONCENTRATIONS.

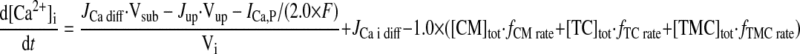(A20)

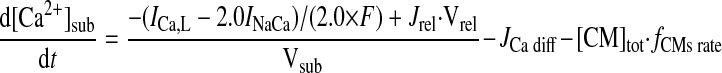(A21)

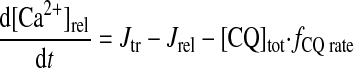(A22)

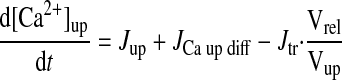(A23)

Ca²⁺ BUFFERING.

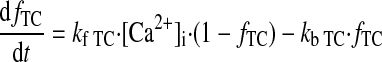(A24)

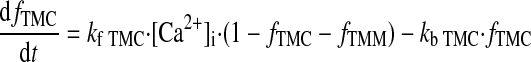(A25)

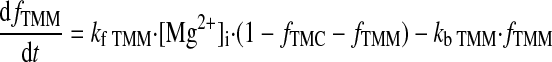(A26)

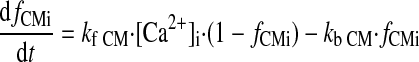(A27)

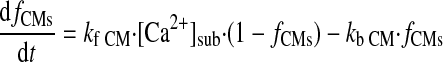(A28)

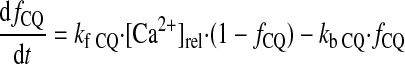(A29)

Model constants.

See Table 2 for model parameters and values.

Table 2.

Model parameters and values

Model Parameters	Values
[Ca2+]o, mM	2
[CM]tot, mM	0.045
[CQ]tot, mM	10
dNaCa	0.0001
ECa,L, mV	46.4
F, C/M	96,484.6
gCa,L	0.06588648
kb CM, ms−1	0.542
kb CQ, ms−1	0.445
kb TC, ms−1	0.446
kb TMC, ms−1	0.00751
kb TMM, ms−1	0.751
kf CM, mM−1·ms−1	227.7
kf CQ, mM−1·ms−1	0.534
kf TC, mM−1·ms−1	88.8
kf TMC, mM−1·ms−1	227.7
kf TMM, mM−1·ms−1	2.277
kNaCa	0.883584 × 10−5
Krel, mM	0.0012
Kup, mM	0.00045
[Mg2+]i, mM	2.5
[Na+]i, mM	8
[Na+]o, mM	140
Prel, ms−1	1.8
Pup, mM/ms	0.005
R, J·mol−1·K−1	8.314472
T, Kelvin	310
[TC]tot, mM	0.031
[TMC]tot, mM	0.062
Vcell, pl	36.8
Vi, pl	13
Vrel, pl	0.2352
Vsub, pl	2.4
Vup, pl	1.624
τtr, ms	60
τCa diff, ms	0.04
τCaidiff, ms	4
τCa up diff, ms	600
yNaCa	0.5

See Glossary for definition of terms.