Decomposition of indwelling EMG signals

Abstract

Decomposition of indwelling electromyographic (EMG) signals is challenging in view of the complex and often unpredictable behaviors and interactions of the action potential trains of different motor units that constitute the indwelling EMG signal. These phenomena create a myriad of problem situations that a decomposition technique needs to address to attain completeness and accuracy levels required for various scientific and clinical applications. Starting with the maximum a posteriori probability classifier adapted from the original precision decomposition system (PD I) of LeFever and De Luca (25, 26), an artificial intelligence approach has been used to develop a multiclassifier system (PD II) for addressing some of the experimentally identified problem situations. On a database of indwelling EMG signals reflecting such conditions, the fully automatic PD II system is found to achieve a decomposition accuracy of 86.0% despite the fact that its results include low-amplitude action potential trains that are not decomposable at all via systems such as PD I. Accuracy was established by comparing the decompositions of indwelling EMG signals obtained from two sensors. At the end of the automatic PD II decomposition procedure, the accuracy may be enhanced to nearly 100% via an interactive editor, a particularly significant fact for the previously indecomposable trains.

there is a clear and present need for an accurate, fast, and easy to use electromyographic (EMG) signal decomposition technology for the field of motor control and motor disorders. By accurately decomposing the EMG signal into its constituent motor unit action potential trains (MUAPTs), it is possible to image the firing behavior of motor units. Understanding the normal and abnormal behavior of motor unit control is fundamental to seeking surgical, pharmacological, and exercise-based interventions. Other important applications of accurate decomposition technology exist in areas such as aging, exercise physiology, space medicine, and ergonomics, where it is of interest to understand whether the control of muscles is altered as a consequence of aging, exercise, exposure to microgravity, fatigue, and excessive and prolonged force production.

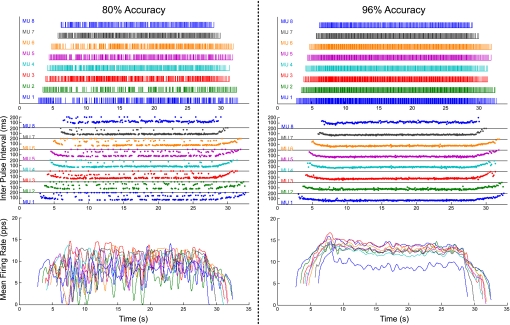
To usefully serve a significant numbers of applications, an EMG signal decomposition system should be able to achieve high levels of decomposition accuracy and speed. However, speed must not be attained at the expense of accuracy or completeness. Decomposition systems that produce only two or three MUAPTs or that produce incomplete or insufficiently accurate results are of limited value to the scientific and clinical communities. To emphasize the importance of accuracy, two different decompositions of the same EMG signal are presented in Fig. 1 : one with 80% accuracy and the other with 96% accuracy. Figure 1, top, presents the firing times of the individual decomposed MUAPTs, Fig. 1, middle, presents the same data with the interpulse interval plotted vertically; and Fig. 1, bottom, presents the firing rates of the motor units. It is clear that the decomposition of 80% accuracy provides a confused representation of the firing rates of motor units, whereas the decomposition of 96% accuracy provides an orderly expression of the firing rates of the motor units where the common fluctuation and hierarchal organization of the firing rates of the motor units is evident. (The method for measuring the accuracy of the decomposition will be addressed in methods.) Clearly, the 80% result would not be acceptable in many practical applications even if the corresponding decomposition program were speedier than the one that produced the 96% result.

Fig. 1.

Decomposition results for 80% accuracy (left) and 96% accuracy (right) of the same underlying indwelling electromyographic (EMG) signal. In each case, there is a “bar plot” (top) showing the firing times for the decomposed motor unit action potential trains (MUAPTs), a “dot plot” (middle) showing the interpulse intervals for the decomposed MUAPTs, and a plot of the firing rate curves (bottom) derived for the 8 decomposed MUAPTs.

The complex task of accurately decomposing the EMG signal has been an alluring goal for numerous investigators over the past four decades. Dominant among the pioneering attempts were the works of Gerstein and Clark (17), Simon (44), Keehn (23), and Glaser and Marks (18). Applications to separate the indwelling EMG signals did not appear until a full decade later when the works of LeFever and De Luca (25, 26), LeFever et al. (27), Andreassen (4), Guiheneuc et al. (19), Mambrito and De Luca (30), McGill et al. (33), and Broman (6) became known. Later, other researchers published various attempts at decomposing the indwelling EMG signal (8, 15, 16, 29, 34, 41, 46, 47, 52) and its surface counterpart (13, 21, 24). Although previous approaches to decomposing the indwelling EMG signal have yielded significant successes, there is ample need for improvements. For example, the PD I system of LeFever and De Luca (26) has a fully automatic mode that has a typical accuracy of ∼65% (30). Furthermore, it requires time-consuming user-interactive editing of its results (up to 15 min/s of EMG signal with as few as 6 MUAPTs) to accurately resolve some of the complex superpositions and to accurately pinpoint motor unit recruitment and derecruitment times. Even then, user-assisted PD I typically attains 100% accuracy for at most eight concurrent MUAPTs within an indwelling EMG signal (30). A more recent system, the interactive EMGLAB program (34), is also predicated on the availability of time-consuming user intervention. In this case, the input signal is processed in 2-s segments, and each segment has to be “inspected manually to complete the decomposition and verify the results.” Signals with 9–12 decomposable MUAPTs are claimed to require manual effort on the order of 10–20 min/s of signal (34). Another recent system, EMG-LODEC (52), utilizes “supervised classification” of signal segments judged to not involve MUAP superpositions. The supervision in the classification process relies on the cognition and skills of an experienced human operator. That system is also limited by the fact that it cannot automatically resolve more than two overlapping MUAPs because “the computation time is prohibitive for more [overlapping MUAPs].” Unsupervised classification was utilized in another recent system (16), but it also was unable to accurately resolve complex superpositions involving the overlap of several MUAPs each. A significant accuracy drop-off is thus observed with this system when more than eight MUAPTs are involved (16).

In this paper, we describe practically and conceptually significant improvements to the precision decomposition technique of PD I that was originated by LeFever and De Luca and underwent refinements over a period of 2.5 decades. As a result of our recent improvements, a new system, PD II, has been implemented. PD II represents a significant advance over existing decomposition methods for indwelling EMG signals: 1) it decomposes even relatively low-amplitude MUAPTs with superior accuracy and speed, and 2) it manages the complexities of force-varying contractions with significantly greater success.

These characteristics of PD II were largely enabled by the incorporation of sophisticated signal processing and artificial intelligence technologies into its design. Some of these improvements have been summarized in recent conference publications (20, 36–40).

BACKGROUND

It has been nearly three decades since the foundations of the original precision decomposition technique were laid down in the PD I system. This system was specifically designed to enable physiological experiments for the motor control community. It has been described previously (6, 12, 25, 26, 30). The PD I technique has been useful for decomposing indwelling EMG signals during isometric contractions and has been used in numerous physiological studies by our group as well as by others (1–3, 10, 11, 14, 22, 31, 32, 42, 45, 49).

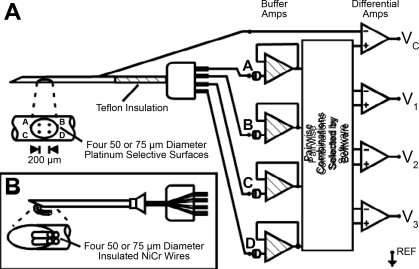
PD I decomposes indwelling EMG signals detected with a quadrifilar needle sensor (9–11) or a quadrifilar wire sensor (12) (see Fig. 2 for details). Three differential channels of EMG signals are used from these sensors. The shape of an action potential is represented differently on each channel due to the different orientation of the detection surfaces on the sensor and the source of the action potential.

Fig. 2.

Details of the quadrifilar needle sensor and how we used it to obtain 3 differential channels (V₁, V₂, V₃) of EMG signal and 1 cannula-derived signal (V_c) for spike-triggered averaging. Inset: details of a quadrifilar wire sensor that we sometimes used instead of the needle sensor.

The PD I technique consists of identifying action potentials in the indwelling EMG signal and assigning them to specific motor units by classifying the shapes and amplitudes of the action potentials. The assignments of the action potentials are made via a maximum a posteriori probability (MAP) algorithm on the basis of template matching and the probability of firing of the individual motor units being tracked. Artificial intelligence techniques are used to track slight modifications in the shapes of the action potentials and for addressing superposition of action potentials. The PD I algorithm is typically able to automatically decompose five MUAPTs and occasionally up to eight MUAPTs in the indwelling EMG signal with an accuracy of 60–70% (10, 11). The technique has provisions for using an interactive editor program to obtain a decomposition accuracy of 100% in some EMG signal records.

Challenges for improved decomposition of EMG signals.

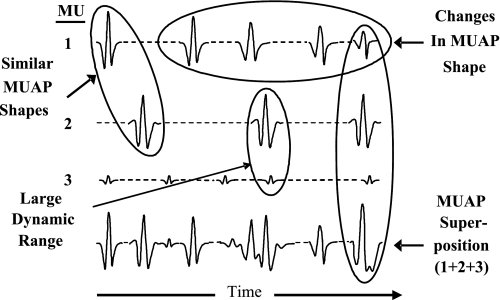
For a decomposition technology to be more useful to the researcher or clinician than PD I, it must possess the accuracy and completeness characteristics described in the Introduction. More specifically, its algorithms must be able to deal with four major complexities that occur within the signal. These complexities are shown in Fig. 3, and they are 1) superposition of action potentials from different motor units, 2) large dynamic range of the amplitudes among the action potentials of different motor units of interest, 3) shape changes across the different action potentials of each motor unit (due to slight movement between the sensor and muscle fibers and/or intracellular processes), and 4) similarity of shape at various times among the action potentials of different motor units. These phenomena often also act in concert with each other to make the decomposition task all the more difficult. In methods, we present the algorithms for our improved precision decomposition technique, which we refer to as PD II.

Fig. 3.

Illustration of various categories of challenges that arise in the decomposition of EMG signals: similar motor unit action potential (MUAP) shapes, changes in MUAP shape, large dynamic range in MUAP amplitudes, and superposition of MUAPs. MU, motor unit.

Knowledge-based system development.

The classifiers used in the PD II system have their theoretical foundations in statistical signal processing, pattern recognition, and graph search. However, these classifiers have many parameters associated with them that have to be “tuned” for the overall system to give the desired level of decomposition performance. In developing PD II, we were particularly concerned that this tuning should be performed by the system itself rather than be left to the system user. It was also important that the tuning be entirely signal dependent rather than be influenced by any input from the user regarding the signal source (e.g., identification of the source muscle). For developing such a self-tuning system, we decided to utilize a knowledge-based artificial intelligence framework previously developed by us, which we call Integrated Processing and Understanding of Signals (IPUS). (28, 35). A C++ software platform (50) was used to incorporate the IPUS framework within PD II development. The IPUS framework permits the system designer to conveniently define specialized rules (the entire collection of these rules constitute a “knowledge base”) that are used at run time to decide how to tune the algorithm parameters in response to various statistics computed from the signal. For example, one of the rules associated with the MAP classifier in PD II continuously updates a statistic for how many MUAPT candidates per detection are being generated for application of the MAP criterion; if the statistic takes on a specified value, the rule causes an increase in the value of one of the classifier parameters so as to relax the criterion for candidate generation.

METHODS

There are three major classification methodologies underlying the PD II system. The first is the MAP classifier, whose design is based on making the decision as to which MUAPT is “most likely” to have given rise to a newly observed MUAP. The MAP receiver is most error prone 1) when the MUAP shape of a particular MUAPT changes too rapidly and 2) when there is superposition between two or more MUAPTs. The first problem in PD II is dealt with via the integration (INT) classifier, and the second problem is dealt with via the superposition (SUP) classifier.

The theoretical foundation of the MAP classifier of PD II is the same as that for the MAP classifier used in PD I. The INT classifier is based on the innovative application of the concept of similarity/dissimilarity pursuit (5) to the problem of deciding whether the MAP classifier has classified different parts of the same MUAPT as two or more different MUAPTs. The key innovation behind the SUP receiver is the application of statistical utility maximization (48) to the problem of resolving complex superposition between two or more MUAPs.

MAP classifier.

There are three key concepts involved in the structuring of this classifier. The first concept is that of identifying each signal segment that could correspond to a MUAP or a contiguous superposition of MUAPs. The second concept is to apply a preliminary shape criterion (PSC) to rule out MUAPTs from a segment on the basis that the MUAP shapes for those MUAPTs are distinctly different from the segment data. The third concept is to apply the MAP classification criterion (MAPCC) to select the “most likely” match to the segment data from among the MUAPTs whose MUAP shapes have not been ruled out by the PSC. Further details of the classifier are given below.

The MAP classifier generates MUAPT classifications (represented via symbols u₁,u₂,…,u_m) that are supported by the underlying EMG signal after it has been broken down into segments determined to contain signal amplitudes within an order of magnitude of the maximum signal level. After identification (via peak detection within signal segments) of candidate MUAP data vector ρ̄, the MAP classifier assigns it to one of the MUAPT classifications, say u_j, provided the data meet a PSC and a MAPCC. The PSC requires that

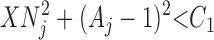(1)

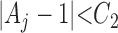(2)

where the values C₁ and C₂ are algorithm parameters, and

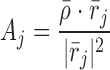(3)

while

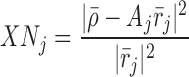(4)

where r̄_j represents a “template” for the “central peak” of the jth MUAPT. The dot product is carried out after alignment of the template peak (at 2.5 times the original sampling rate) with the data peak. If the PSC is satisfied by u_j, the MAPCC requires that

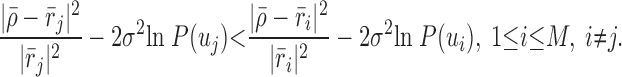(5)

In Eq. 5, σ² is the noise level (an algorithm parameter) and P(u_j) is an algorithm parameter that represents the a priori probability that MUAP data ρ̄ supports classification u_j. If MUAP data ρ̄ does not support one of the prior symbols, the MAP classifier declares data ρ̄ as support for a new MUAPT classification. Once the entire EMG signal has been analyzed, a “symbol filtering” stage rejects MUAP classifications that are determined to be weakly supported by the signal data. The symbol filtering is primarily based on results from an “extended PSC” to each instance of classified MUAP data. The extended PSC is the same as the PSC except that it replaces r̄_j in Eqs. 3 and 4 by a significantly longer version of the template beyond its “central peak” to include “side lobes.”

INT classifier.

A situation that is problematic for PD I algorithms involves motor units whose action potentials have similar shapes (see Fig. 3). Although it attempts to distinguish such shapes from each other, the PD I algorithm often inadvertently discriminates between action potential shapes that belong to the same motor unit but that experience significant shape change due to relative muscle fiber-to-sensor displacements. In the database of challenging EMG signals that we have used for algorithm evaluation, this type of phenomenon affects almost 50% of the decomposed action potential trains. The INT classifier of PD II was developed to address such situations.

The algorithm parameters associated with the MAP classifier have their values assigned in a manner that minimizes the fraction of classifications that are unreliable. However, to avoid false alarms, the MAP classifier often produces different MUAPT classifications for different MUAP subgroups of the same underlying MUAPT. The INT classifier of PD II is designed to integrate different classifications corresponding to the same underlying MUAPT. Further details of the INT classifier are given below.

Define a set S of MUAPT classifications produced by the MAP classifier. The goal of the INT classifier is to produce another set (S′) of MUAPT classifications such that any underlying MUAPT has at most one MUAPT classification corresponding to it in S′. Each element in S′ is either an element of S or it is obtained via an “integration” operation, say ⊕, applied to a subgroup of S. We adopt the notation u_1,2 = u₁ ⊕ u₂ to represent a MUAPT classification that includes each MUAP of classification u₁ in S as well as each MUAP of classification u₂ in S but includes no MUAP of any of the other MUAPT classifications in S. More generally, assuming S = {u₁,u₂,…u_N}, we can define an integration operation as resulting in u_i1,i2…,ik= u_i1 ⊕ u_i2 ⊕ u_i3 ⊕ … ⊕ u_ik, where i_j ≠ i_k, ∇ ≠ k. The INT classifier can now be defined as a greedy algorithm (5) for similarity/dissimilarity pursuit that on each iteration seeks to place in S′ an element û = u_{î1,î2…,îk} such that

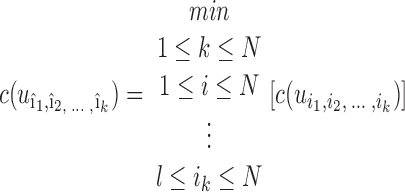(6)

and to remove the elements u_î1…u_îk from S. The function c(u) is an estimated integration “cost” that is the sum of an inclusion measure and an exclusion measure. The inclusion measure relates to the degree of interelement dissimilarity within u. The exclusion measure relates to the cross-element similarity between the elements of u and the elements of S not in u.

SUP classifier.

The most significant signal dynamic taking place in the EMG context is the superposition of different action potentials (see Fig. 3). The overlap between superimposed MUAPTs would not be statistically significant if different MUAP shapes were statistically uncorrelated with each other. However, most MUAP shapes have a certain degree of correlation. The SUP receiver is designed to explicitly take these correlations into account while estimating a “likelihood” statistic for each MUAP shape. These “likelihood” values are then utilized within a statistical utility maximization procedure (48) for deciding which MUAPs are actually present. Details of the likelihood estimation process are given below.

To address the superposition phenomenon, the SUP classifier applies an “iterative correlation procedure” to the kth candidate data ρ̄_k where one or more weak classifications were rejected by the MAP classifier. This procedure is designed to estimate likelihood values for possible MUAP classifications. The SUP classifier then uses statistical utility maximization (48) to identify MUAP classifications that it deems to be definitely supported by the kth candidate data ρ̄_k. Denoting the template of the ith MUAPT by the vector s̄_i, the SUP classifier estimates the likelihood of the ith MUAPT to be supported by the kth candidate data as:

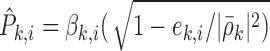where

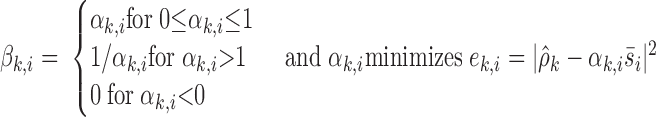(7)

If P̂_k,j = P̂_k,j and P̂_k,j is above a threshold, the SUP classifier subtracts s̄_j from ρ̄_k and iteratively repeats this process. If there have been m subtractions in ρ̄, the SUP classifier also adjusts the corresponding likelihood values to compensate for subtraction noise by multiplying them with (α_i)^m where α_i is a statistic for the amplitude of the ith MUAPT relative to the maximum-amplitude MUAPT. Because multiple likelihood values may be calculated for each MUAPT, the SUP classifier uses the maximum value among them when using utility maximization to identify the MUAP classifications that it deems to be definitely supported by the data, ρ̄_k.

Accuracy criterion.

When one proposes to decompose a signal whose composition is not known a priori, it is incumbent on the proponent to prove that the decomposition is performed accurately. One obvious approach for proving accuracy would be to construct mathematically a signal of known components (MUAPTs) and then proceed to decompose the synthesized signal into the constituent action potentials and check the veracity of the outcome. Two decades ago, Mambrito and De Luca (30) showed that, if the shapes of the action potentials remain invariant throughout the contraction, this approach is not sufficiently challenging, even when white noise having amplitude 40% of the average amplitude of the action potentials was added to the signal. The challenges presented by real signals and identified in previous sections represent important complexities that must be dealt with. In addition, the algorithms must be able to cope with other unforeseen signal components that are occasionally presented by real data due to abrupt displacements of the sensor with respect to the source of the action potentials. Consequently, we used the two-source technique (30) to establish the accuracy of PD II signal decompositions, as was originally done for PD I in 1984.

Two quadrifilar needle sensors were inserted ∼1 cm into the tibialis anterior muscle and 1 cm apart. The subject had no known neurological disorders. (The subject read and signed an informed consent form approved by the Institutional Review Board of Boston University.) It was expected that some of the motor units would contribute signals to both sensors and others to only one sensor, depending on the proximity of the muscle fibers to the separate sensors. The EMG signal from each sensor was automatically decomposed via PD II and then independently further processed with the assistance of an interactive editor. As in the case of PD I, it was found that a subset of the MUAPTs in the two decompositions had firing times in lock step with each other. The precise coincidence of 97.6% of action potentials in those trains from the two signals proves that PD II accurately decomposes both signals since the probability that PD II makes exactly the same errors in both signals is extremely small.

The establishment of the accuracy of interactively edited PD II decomposition results paves the way for using them as “benchmarks” for assessing the accuracy of the fully automatic PD II decompositions. When a fully automatic decomposition algorithm produces its estimates for the firing times of a MUAPT, two types of errors can occur with respect to the benchmark: false negatives and false positives. A false negative occurs when the algorithm fails to find a particular MUAPT firing in a segment indicated by the benchmark. A false positive occurs when the algorithm declares a firing to have occurred in a segment where the benchmark indicates that no firing of that MUAPT actually took place. The accuracy of the algorithm on the ith MUAPT [A(i)] is defined in this paper as:

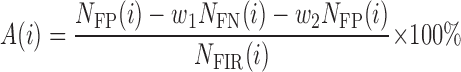(8)

where N_FIR(i), N_FN(i) , and N_FP(i) are the number of firings, false negatives, and false positives for the ith MUAPT and weights (w₁ and w₂) that may be assigned values other than unity as required for the evaluation.

The accuracy numbers for automatic decomposition algorithms in the remainder of this paper were computed on the basis of previous work (8). The benchmarks were set via interactive editing of the decomposition results produced by the automatic signal decomposition algorithms. The weights (w₁ and w₂) were both set to unity. The decomposition accuracy of any multi-MUAPT contraction was computed as the average of the accuracies with respect to each individual MUAPT. The rationale behind this is that each MUAPT in the decomposition has equal importance regardless of the number of firings within it.

RESULTS

The hallmark of PD II's design is reflected in its capacity to automatically produce under realistic conditions indwelling EMG signal decompositions that do not require extensive interactive editing to assure 100% accuracy. Realistic conditions include contractions ranging from those that are barely perceivable to those that approach maximum voluntary contraction (MVC) levels. These in turn give rise to phenomena such as complex MUAP superpositions, MUAPs with relatively low amplitudes and/or multimodal shapes, rapid MUAP shape changes that are either continuous or erratic, and MUAP firing rates that change either continuously or erratically. On a database of six realistic indwelling EMG signals reflecting the entire range of these conditions, PD II was experimentally found to automatically decompose an average of 9.5 MUAPTs per signal with an average accuracy of 86.0%. This is in contrast to PD I, which on the same database decomposed an average of 7.5 MUAPTs per signal with an average accuracy of 65.2%. All of the MUAPTs decomposed by PD I were also successfully decomposed by PD II. The greater accuracy of PD II on these MUAPTs means that 60% fewer errors have to be dealt with during interactive editing to raise the accuracy level to clinically or scientifically acceptable levels. Furthermore, the 86% accuracy of the automatic PD II system also applies to low-amplitude MUAPTs that are completely missed by systems such as PD I. Such MUAPTs, which suffer disproportionately from superposition with larger amplitude MUAPTs, have thus become amenable for the first time to scientific and/or clinical analyses.

These levels of performance are also reflective of the results obtained in numerous other decompositions that we have performed on indwelling EMG signals outside of the database. Importantly, PD II was successful in decomposing the indwelling EMG signal from ∼80% of the signals that we attempted to decompose from a variety of contractions of the types shown in Table 1. In this section, details of the indwelling EMG signal database and of the fully automatic decomposition results on it are presented.

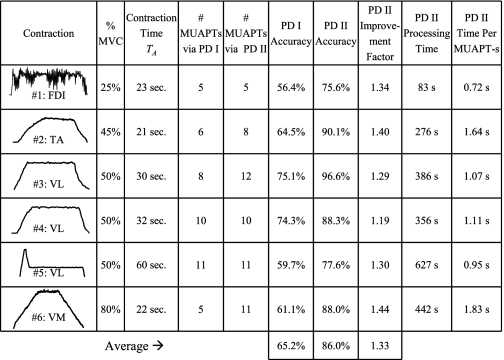
Table 1.

Performance of PD 1 and PD II on the EMG signal database

FDI, first dorsal interosseous; TA, tibialis anterior; VL, vastus lateralis; VM, vastus medialis; MUAPT, motor unit action potential train.

EMG signal database.

The EMG signal database that we used for evaluating precision decomposition algorithms was obtained from six different experiments in which subjects were asked to perform various types of muscle contractions. (All of the subjects read and signed an informed consent form approved by the Institutional Review Board of Boston University.) In each case, the three-channel indwelling EMG signal from the quadrifilar needle sensor was sampled at 20 kHz, using an analog anti-aliasing fourth-order Butterworth filter with a 3-dB cutoff at 9.5 kHz. Subsequently, a 1-pole high-pass filter with a 3-dB cutoff at 1 kHz was applied to the digital EMG signal to keep individual action potential durations as short as possible while retaining the information that experimentally has been found to provide a sufficient discrimination capability.

Contraction 1 in the database is that of the first dorsal interosseous muscle. The subject carrying out the contraction attempted to produce an isometric trapezoidal force profile with a plateau at the 25% MVC level. However, an erratic force profile was actually produced because of the presence of tremor. The entire contraction lasted 23 s. The three-channel indwelling EMG signal for this contraction was primarily selected because the presence of tremor tends to induce erratic firing rates in the constituent MUAPTs.

Contraction 2 in the database is that of the tibialis anterior muscle. The subject in this case attempted and managed to produce an isometric trapezoidal force profile with a plateau at approximately the 45% MVC level. The entire contraction lasted 21 s. The four-channel indwelling EMG signal for this contraction was primarily selected because its decomposition using the previous PD I version and interactive editing indicated the presence of a MUAPT that undergoes erratic shape changes during certain portions of the contraction.

Contraction 3 in the database is that of the vastus lateralis (VL) muscle. The subject in this case attempted and managed to produce an isometric trapezoidal force profile with a plateau at approximately the 50% MVC level. The entire contraction lasted 30 s. The three-channel indwelling EMG signal for this contraction was primarily selected because its decomposition using PD I and interactive editing indicated the presence of at least eight decomposable MUAPTs, several of which are bimodal (that is, they have satellite potentials), and thus give rise to complex superpositions.

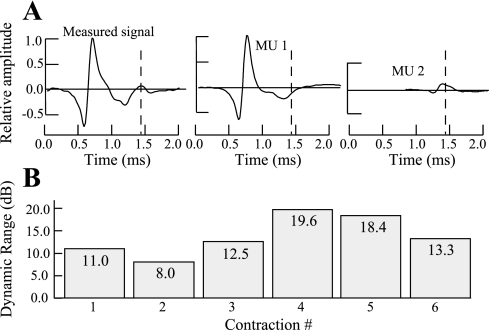
Contraction 4 in the database is that of the VL muscle. The subject in this case attempted and managed to produce an isometric trapezoidal force profile with a plateau at approximately the 50% MVC level. The entire contraction lasted 32 s. The three-channel indwelling EMG signal for this contraction was primarily selected because its decomposition using the previous PD I version and interactive editing indicated the presence of at least 10 decomposable MUAPTs whose amplitudes spanned a dynamic range of 19.6 dB, the largest in our database.

Contraction 5 in the database is that of the VL muscle. The subject in this case attempted and managed to produce an isometric nontrapezoidal force profile with plateaus at approximately the 20% and the 50% MVC level. The entire contraction lasted 60 s. The three-channel indwelling EMG signal for this contraction was primarily selected because of its nontrapezoidal profile and because it was part of an ∼10-min-long signal epoch corresponding to a series of 10 consecutive contractions performed by the subject for a study designed to evaluate the effects of fatigue.

Contraction 6 in the database is that of the vastus medialis muscle. The subject in this case attempted and managed to produce an isometric trapezoidal force profile with a plateau at approximately the 80% MVC level. The entire contraction lasted 22 s. The four-channel indwelling EMG signal for this contraction was primarily selected because of its high force level.

Overall accuracy comparisons on database.

The average decomposition accuracy of PD II algorithms is 86.0% over the entire database compared with an average of 65.2% for PD I algorithms. (Note that, for some decompositions, the accuracy of PD I reached ∼80%. These decompositions, which were further processed by an interactive editor, were used to provide the data for our previous publications.) On our database of challenging indwelling EMG signals, PD II's automatic algorithms yielded an improvement by a factor of 1.33 over the decomposition accuracy of PD I's automatic algorithms. In Table 1, we present a comparison of decomposition accuracies achieved by the two systems on different signals within our database. The improvement factor for different signals ranges from 1.19 to 1.44 with an average of 1.33. The improvement factor of 1.19 was on a signal (contraction 4) in which the dynamic range of decomposed MUAP amplitudes was 19.6 dB compared with dynamic ranges of 8.0 dB (contraction 2), 11.0 dB (contraction 1), 12.5 dB (contraction 3), 13.3 dB (contraction 6), and 18.4 dB (contraction 5) with respective improvement factors of 1.40, 1.34, 1.29, 1.44, and 1.30. The improvement factor of 1.34 is particularly impressive for the nonisotonic characteristics of contraction 1.

Table 1 also indicates the processing time for each of the contractions in our EMG signal database. The processing was carried out on a Dell Inspiron 9300 laptop with a 2-GHz Pentium M processor and with 512 megabytes of RAM. As shown in Table 1, the processing time per decomposed MUAPT is of the same order as the contraction time.

Table 2 shows the accuracy values attained after the final application of each of the three PD II classifiers. The MAP classifier in PD II is on average found to produce an accuracy of 63.0% on this database. This is lower than the accuracy achieved via PD I (which has its own version of MAP classifier) because the MAP classifier in PD II includes symbol processing for rejecting weak classifications. Subsequent classifiers replace those weak classifications by more accurate classifications. First, the INT classifier takes the average accuracy to 68.2%. Second, the SUP classifier boosts the average accuracy to 86.0%.

Table 2.

Contribution of PD II classifiers to performance on the EMG signal database

Contraction No.	MAP Algorithm Accuracy	INT Algorithm Accuracy	SUP Algorithm Accuracy
1	45.6%	52.9%	75.6%
2	61.7%	69.5%	90.1%
3	75.3%	75.9%	96.6%
4	74.1%	75.2%	88.3%
5	60.1%	71.5%	77.6%
6	61.4%	63.9%	88.0%
Average	63.0%	68.2%	86.0%

MAP, maximum a posteriori probability; INT, integration; SUP, superposition.

Accurate resolution of complex superpositions.

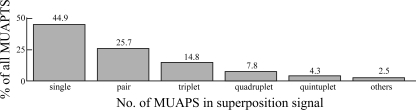
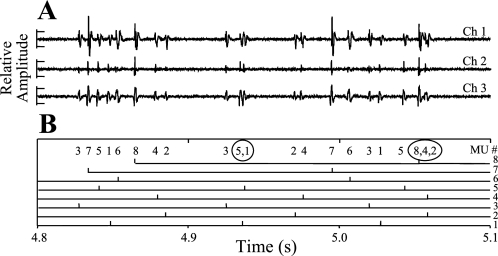
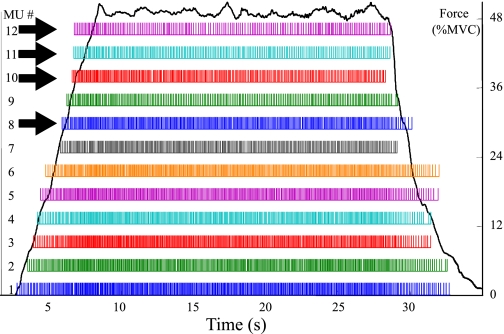
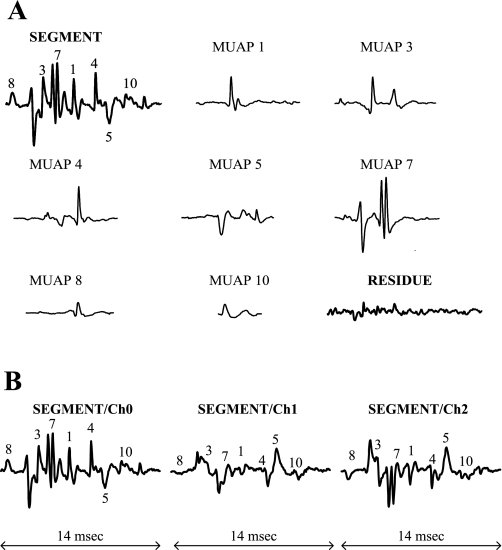
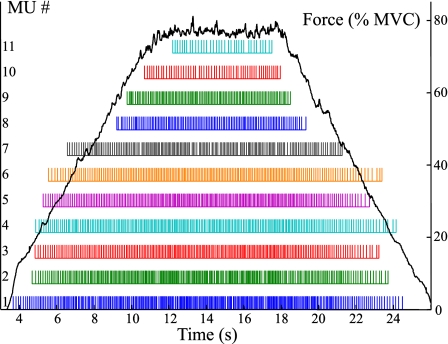
The occurrence of complex superpositions among the MUAPs of different motor units is among the foremost challenges of any EMG decomposition system. The pervasiveness of such superposition phenomena in our database of indwelling EMG signals is illustrated in Fig. 4. It is seen that, although 44.9% of the firings of the decomposable motor units occur by themselves, the remainder are in superposition with at least one other MUAP. More specifically, 25.7% of the decomposable MUAPs occur in superposition pairs, 14.8% in superposition triplets, 7.8% in superposition quadruplets, 4.3% in superposition quintuplets, and 2.5% in superpositions of sextuplets or more MUAPs. The difficulty in resolving even relatively simple cases of superposition can be appreciated via the example waveforms shown in Fig. 5A. These three waveforms represent 0.3 s of three channels of indwelling EMG data collected near the beginning of a contraction. The detection times of MUAPs and the classification of their corresponding motor units, numbered 1 through 8, were determined via PD II, and they are illustrated in Fig. 5B. The contraction level rises from 18.75% MVC at the beginning of these data to 21.55% MVC at the end. Two motor units (7 and 8) are recruited during this interval. Motor units 1 and 5 are a superimposed pair at ∼4.93 s, and motor units 2, 4, and 8 are a superimposed triplet at 5.06 s. The occurrence of the MUAP of motor unit 2 within the triplet is particularly difficult to visually ascertain from the waveforms. However, its presence can be confirmed via subtraction of the motor unit templates from the data in question. PD II is found to be highly successful in not only resolving such superpositions but also significantly more complicated ones that arise at higher %MVC levels. For example, consider the case of contraction 3 in our database where PD II yielded the highest accuracy level of 96.6%. Figure 6 shows results for 12 motor units as they were decomposed by PD II without any interactive editing by a human operator. Four of the decomposed MUAPTS (solid arrows in Fig. 6) were not decomposable via PD I. Superimposed on Fig. 6 is an experimentally measured “force profile” of the contraction that the subject performed during data acquisition. In performing the decomposition of Fig. 6, PD II had to successfully deal with a variety of complex superpositions among the MUAPs of the 12 decomposed motor units. In one case, the SUP classifier of PD II succeeded in accurately decomposing (without the need of any interactive editing by a human operator) a superposition of seven MUAPs. As shown for channel 0 in Fig. 7, the SUP classifier decomposed the three-channel indwelling EMG signal segment into seven MUAP components. The channel 0 residue obtained when the seven MUAPs are subtracted from the original segment is shown in Fig. 7A; all three channels (0, 1, and 2) of the original segment are shown in Fig. 7B.

Fig. 4.

Percentage of MUAPS in our indwelling EMG database that are involved in no superposition (singles) or in superpositions involving 2 MUAPs each (pairs), 3 MUAPs each (triplets), and so forth.

Fig. 5.

A: 3 channels (ch) of a short portion (0.3 s) of an indwelling EMG signal collected near the beginning of a contraction whose level rises from 18.75% to 21.55% MVC. B: firing times of 8 of the motor units extracted by fully automatic PD II from the same short portion of indwelling EMG signal. PD II successfully identified the recruitment of motor units 7 and 8 over this portion of the signal. It also successfully resolved the superposition triplet involving motor units 8, 4, and 2 ∼0.26 s into the signal portion.

Fig. 6.

Bar plot showing the firing times of 12 MUAPTs that were decomposed by fully automatic PD II when applied to the 30-s indwelling EMG signal for contraction 3 (from the vastus lateralis muscle) in our database. The MUAPTs indicated by arrows were not decomposable via PD I.

Fig. 7.

PD II automatically decomposed the 14-ms SEGMENT waveform into 7 MUAP waveforms. A: channel 0 of the SEGMENT, channel 0 of each of the 7 MUAP templates, and channel 0 of the RESIDUE waveform resulting from subtraction of the 7 MUAP waveforms from the SEGMENT waveform. B: all 3 channels of the SEGMENT. In A and B, each number on the SEGMENT waveform indicates the relative position of the major peak of the corresponding MUAP waveform.

Accurate decomposition of multiphase MUAPs.

It can also be observed from Fig. 7 that several of the MUAPs involved in contraction 3 have a multiphase characteristic. This is a testament to the ability of the SUP classifier in PD II to handle the complexities associated with multiphase MUAPs.

Accurate determination of recruitment times.

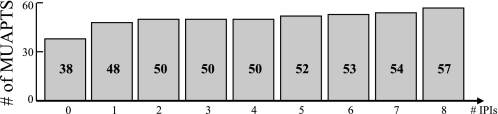
A critical element in carrying out indwelling EMG signal decomposition is the capability of accurately determining the recruitment times of each of the motor units. The bar plot for contraction 3 in Fig. 6 has been verified to reflect the actual recruitment times (via an interactive editor) for 9 of the 12 motor units. In the case of motor units 10-12, the recruitment times indicated by the bar plot are off from the actual recruitment times by 1 inter pulse interval IPI each (an error of n IPI's means the first n firings were missed by the decomposition program). In general, as indicated in Fig. 8, we find that 38 of the 57 MUAPTs decomposed via PD II on our indwelling EMG database had no error in their recruitment times; another 10 MUAPTs had a recruitment error of just 1 IPI each. In other words, 84.2% of the MUAPTs had their recruitment times determined to within an accuracy of 1 IPI. This is particularly significant because the recruitment of motor units occurs when the contraction level is being increased. During such transitions, the indwelling EMG sensor is likely to experience displacement relative to the muscle fibers, thus giving rise to shape changes in the detected action potentials.

Fig. 8.

Number of MUAPTs (out of a total of 57 in our indwelling EMG database) whose recruitment times are determined by fully automatic PD II to within a specified number (on the horizontal axis) of interpulse intervals for the corresponding motor unit.

Accuracy in tracking shape changes.

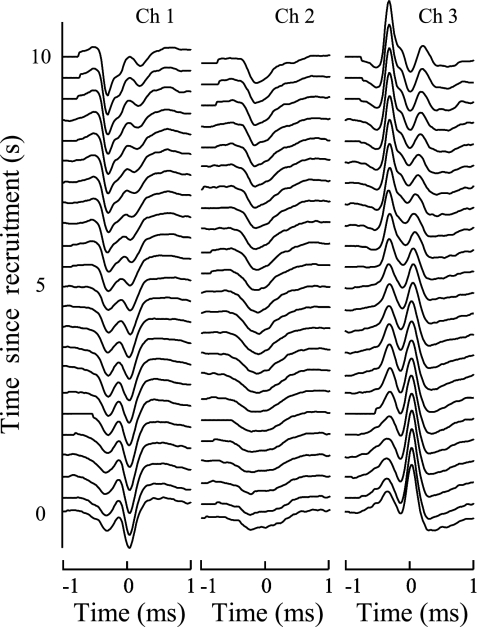
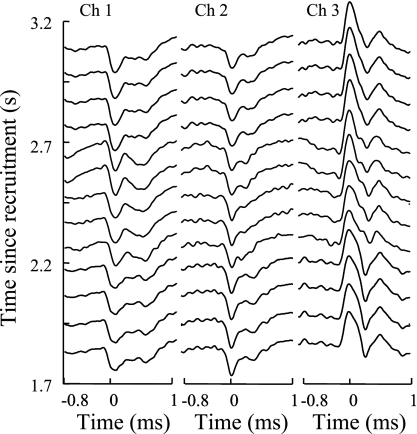
The ability of PD II to track shape changes is in part due to the adaptive nature of its MAP classifier and in part due to the INT classifier. In Fig. 9, we show the shape changes that take place in the three-channel action potentials of motor unit 1 of contraction 3 during a portion of its recruitment period. The MAP classifier of PD II easily tracked the relatively smooth changes. In Fig. 10, we show the shape changes that take place in the three-channel action potentials of motor unit 6 of contraction 3 during a portion of its recruitment period. In this case, there is an interval of ∼0.5 s during which the action potentials experience an abrupt change in shape (in the region highlighted by the use of thicker lines). In this case, the MAP classifier declares the action potentials within the 0.5-s period to be the firings of a new motor unit. However, the INT classifier of PD II is able to associate them back to motor unit 6.

Fig. 9.

Smoothly evolving shape of the MUAPs of motor unit 1 in contraction 3 over its first 10 s.

Fig. 10.

Abrupt shape change in the MUAPs of motor unit 6 of contraction 3 from ∼2.2 to ∼2.7 s and highlighted via bolder lines.

Accuracy on low-amplitude MUAPs.

Another important feature of PD II is its ability to resolve superpositions among motor units that have significant differences in amplitude. In Fig. 11A, we show a successful decomposition of an indwelling EMG signal segment from contraction 5 as a superposition of two action potentials with disparate amplitudes. Similar superpositions are also resolved across our indwelling EMG database, where the dynamic range of amplitudes (see Fig. 11B) of the various action potentials decomposed by PD II can be as high as 19.6 dB.

Fig. 11.

A: indwelling EMG signal segment from our database that was decomposed via fully automatic PD II into 2 MUAPs for motor unit 1 (MU1; high amplitude) and motor unit 2 (MU2; low amplitude), respectively. B: dynamic range (in dB) of amplitudes spanned by the MUAPs decomposed by PD II for each contraction in our EMG database.

Accuracy in tracking firing-rate perturbations.

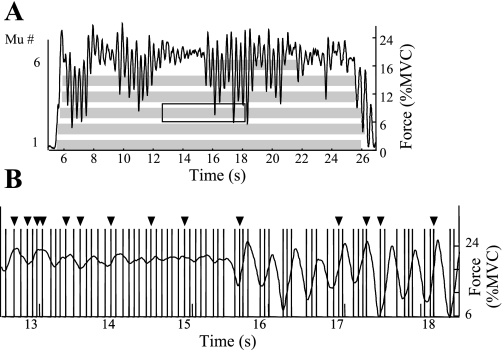
Figure 12 provides an illustration of the ability of PD II to track highly variable IPIs in a situation where the subject from whom the indwelling EMG signal was detected exhibits significant tremor. Figure 12A shows an abstracted bar plot for contraction 1 and highlights a section that is the focus of the rest of the figure. Figure 12B shows all the bars for the highlighted section. The 14 bars pointed to by the solid triangles were produced by the SUP classifier as add-ons to the preexisting bars produced by the INT classifier. It is apparent that the SUP classifier made a significant difference in this section yet produced no false positives despite variations in IPI that correlate well with the superimposed force profile.

Fig. 12.

A: abstracted bar plot for contraction 1 from our indwelling EMG database. This contraction was obtained from the first dorsal interosseous of a cerebellar patient. B: bar plot in detail for the boxed region in A. Bars pointed to by the solid triangles were produced as add-ons by the SUP classifier.

Accuracy at high MVC levels.

Yet another attribute of PD II is its ability to perform well even at high %MVC levels. For example, in the case of contraction 6, the subject achieved 80% MVC level for almost 10 s. The indwelling EMG signal in such cases is characterized by the presence of a greater number of active motor units. PD II was able in this case to decompose 11 motor units (as compared with 5 motor units in the case of PD I) quite accurately because of its enhanced capacity for resolving complex superpositions. The bar plot for contraction 6 is shown in Fig. 13.

Fig. 13.

Bar plot for the firing times obtained via fully automatic PD II on a signal corresponding to contraction 6 (from the vastus medialis) in our database in which a force level of 80% MVC was reached.

Accuracy for multicontraction signal epochs.

Contraction 5 in our indwelling EMG database was part of a multicontraction signal epoch that lasted ∼11 min. Although we included just one of those contractions in our indwelling EMG database, the other contractions were also decomposed via PD II with a similar degree of accuracy. Also, PD II is generally able to track the same motor unit when it appears in different epochs. In fact, it is able to do so for more motor units than PD I because of its greater accuracy.

DISCUSSION

The PD II system reported in this paper, in many respects, satisfies most of the objectives that define a pragmatic and useful decomposition system. In its present form, and with the assistance of an interactive editor, the system can be usefully applied to decompose most indwelling EMG signals from attempted isometric contractions that are apt to be employed when studying problems in the field of motor control. However, for the system to be employed in the clinical environment, it will be necessary to improve the typical accuracy in the automatic mode from 86% to at least 96%. The reason for this level of accuracy may be seen in Fig. 1. At this level, the need for an interactive editor is completely eliminated, thereby providing useful and accurate results in a matter of minutes. The interactive editor presently imposes a level of expertise and substantial time demands on the user, up to a few hours per minute of signal in low accuracy cases, a condition that is not likely to be accepted in busy clinical environments. Shortcomings of PD II that presently have to be addressed via the interactive editor fall into three major categories. First, there is the failure of PD II in some instances to differentiate between similarly shaped action potentials of two different motor units when either is involved in severe superposition with the action potentials of other motor units. Second, there is the failure of PD II in some instances to detect a low-amplitude action potential because of “masking” by an action potential that is several times higher in amplitude. Finally, there is the inability of PD II to sometimes distinguish correctly between similarly shaped action potentials of two different motor units when one of them undergoes shape changes that make its action potential much closer in shape to that of the action potential of the other motor unit.

The present form of PD II represents a substantial improvement in performance over our previous version (PD I) and that of other recently published works (16, 34, 41, 52). In contrast to these works, PD II does not require significant user interaction to systematically identify motor unit recruitment and derecruitment for a large set (>10) of concurrently active motor units, to resolve superpositions of up to seven MUAPs, to decompose signals from dramatically changing MUAP shapes, to decompose signals from erratic force contractions, and to decompose a large set of motor units from contraction levels as great as 80% MVC. Furthermore, PD II has been found to perform reliably in achieving its accuracy levels not just on the database of indwelling EMG signals presented in this paper but also on a large number of other indwelling EMG signals with characteristics similar to those of the signals in our indwelling EMG database. The reliability with which the PD II system is able to perform automatic decompositions at impressive accuracy levels is such that we did not hesitate to successfully give a real-time demonstration of the capabilities of an earlier version of the system in a workshop (with over 60 attendees) at the 2004 International Society of Electrophysiology and Kinesiology Conference (Boston, MA). The present version of the system is even more accurate and can more reliably produce those levels of accuracy across a broad range of indwelling EMG signals.

The foundational strength of PD II lies in its ability (provided via IPUS) to carry out knowledge-based searches for signal-dependent operating points for its parameterized classifiers. No other reported system has such a capability. Given the complex nature of the automatic decomposition problem, it seems inevitable to us that any practical solution would have to possess some type of parameter-tuning capability to minimize and ultimately eliminate the need for interactive editing of the automatic results. Although the present version of PD II uses parameterized classifiers built on the original MAP classifier of PD I, there is nothing to preclude the use of other parameterized classification approaches [e.g., convolutional mixtures analysis (21), wavelet analysis (52), or genetic algorithms (16)] within the same framework and hence to enhance the respective performance levels of those methods as well.

The main advantage of our PD II system is that it allows the exploration of the behavior of the nervous system during a variety of contractions, thus enabling a more fertile and more comprehensive assessment of the motor control properties of the motor units. Examples of such investigations where we have used the PD II system can be found in recent publications by Adam and De Luca (1, 2). In these two works, our group followed the firings of motor units throughout a sequence of muscle contractions up to exhaustion; in so doing, our group studied for the first time the behaviors of individual motor units throughout the full course of a fatiguing contraction. Another application can be found in Roark et al. (42), in which our group was able to collect and study motor unit firings from the laryngeal muscles. In this study, the data collection was difficult and tenuous, yielding a limited number of data records. It was important that the decomposition succeed in decomposing the available data because of the limited access to the patients that were studied and the complexity of the recording technique. A similarly challenging decomposition was successfully accomplished in cerebellar stroke patients who were unable to provide well-behaved contraction in the first dorsal interosseous muscle when tested. In a recent paper by Sauvage et al. (43), our group decomposed the indwelling EMG signal and provided insight regarding the role of the cerebellum in the control of motor units.

GRANTS

This work was supported in part by National Institutes of Health Bioengineering Research Partnership Grant HD-38585 from the National Center for Medical Rehabilitation Research of the National Institute of Child Health and Human Development.