Navigating networks by using homophily and degree

Abstract

Many large distributed systems can be characterized as networks where short paths exist between nearly every pair of nodes. These include social, biological, communication, and distribution networks, which often display power-law or small-world structure. A central challenge of distributed systems is directing messages to specific nodes through a sequence of decisions made by individual nodes without global knowledge of the network. We present a probabilistic analysis of this navigation problem that produces a surprisingly simple and effective method for directing messages. This method requires calculating only the product of the two measures widely used to summarize all local information. It outperforms prior approaches reported in the literature by a large margin, and it provides a formal model that may describe how humans make decisions in sociological studies intended to explore the social network as well as how they make decisions in more naturalistic settings.

Much of the current interest in small-world networks has drawn inspiration from the now classic work of Travers and Milgram (1). Their 1969 study asked individuals to deliver letters to designated persons by passing them through chains of first-name acquaintances. That study, as well as more recent work (2), shows that surprisingly short paths exist between pairs of nodes in real-world social networks.

However, the existence of such paths is only one of the interesting findings of the study. Kleinberg (3) notes that the study contains a second finding of fundamental algorithmic importance: People are able to find short paths even though they know very little about the target individual or the network. Both Kleinberg and a variety of subsequent researchers have addressed the question of how such network navigation is possible.

That work identifies two network characteristics that can guide navigation. The first is homophily—the tendency of attributes of connected nodes to be correlated. People tend to be acquainted with other people who live in the same geographical area or who have the same occupation. The second is the existence of high-degree nodes. Some people have a large number of acquaintances and act as hubs that connect different social circles.

Both of these characteristics are widely observed in real-world networks, and both lead directly to navigation algorithms. Consideration of homophily gives rise to a navigation algorithm that passes messages to the neighbor that is the most similar to the target node (e.g., an acquaintance who lives in Boston, if the target person lives in Boston) (3–6), whereas consideration of degree gives rise to an algorithm that favors the neighbor with the highest degree (7).

In contrast to previous work, we cast the navigation problem as a task of decision making under uncertainty, in which the desired decision is to forward the message to the neighbor with the minimum expected distance to the target. We show how the desired decision may be approximated by using a single criterion—the probability that the neighbor links directly to the target—which may be estimated by a simple product of the homophily and degree information. Our formulation directly implies an algorithm that we call expected-value navigation (EVN). Earlier algorithms are special cases of EVN when only homophily or degree information is present.

We show that, across a wide range of synthetic and real-world networks, EVN performs as well as or better than the best previous algorithms. More importantly, in the majority of cases where previous algorithms do not perform well, EVN synthesizes whatever homophily and degree information can be exploited to identify much shorter paths than any previous method.

These results have implications for understanding the functioning of current and prospective distributed systems that route messages by using local information. These systems include social networks routing messages, referral systems for finding informed experts, and also technological systems for routing messages on the Internet, ad hoc wireless networking, and peer-to-peer file sharing.

Formulation

We formulate the navigation problem as a probabilistic decision-making task in which the objective is to minimize the length of the path traveled by the message. We assume that each node knows about its immediate neighbors—including their identity, degree, and attributes—but is unaware of the rest of the network. At the source node, and subsequently at each node along the path, the optimal decision rule (given the limited information) is to forward the message to the neighbor from which the message will reach the target in the smallest number of hops, assuming that all future nodes will make their decision similarly by using local information. Although a recurrence relation may, in principle, govern the optimal decision rule, it is not apparent how this can be formulated in a way that would suggest an effective navigation method.

Instead, we suggest that an effective (although not necessarily optimal) decision would be to forward the message to the neighbor with the minimum expected distance to the target, where distance from node s to node t is the length of the shortest path from s to t. We can express this quantity, the expected value of the distance d_st from neighbor s to target t, as a weighted sum of all possible distances:

Computing this expectation is daunting but, fortunately, not necessary. Effective decision making requires only identifying the neighbor that minimizes the expectation. To perform this comparison, we propose to use only the first term in the series, which calculates the probability of a distance of one. The relative values of this first term may be an accurate estimator of the relative values of the entire expectation, because the terms in the series are correlated, and this correlation increases with increasing homophily. For example, given a relatively high probability of a distance of one, we expect a relatively high probability of a distance of two. In general, the greater the first term, the lower the whole expectation, so the resulting decision rule is to select the neighbor with the highest probability of linking directly to the target. This probability is influenced by both homophily and degree. The more similar the neighbor is to the target and the higher the degree of the neighbor, the greater the probability that the neighbor links directly to the target. In directed networks, we express this relationship by making the simplifying assumption that the links originating at s were created independently, with the same probability (q_st) of terminating at t. When the network exhibits homophily, q_st is a function of the similarity between nodes s and t. The number of links from s to t (n_st) then follows a binomial distribution with probability of success q_st and k_s trials, where k_s is the out-degree of s. Using the Poisson approximation to the binomial, we can compute the first term of Eq. 1:

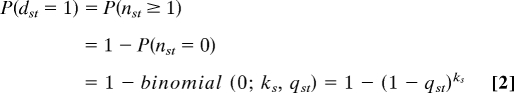In undirected networks, we obtain the same result, similarly assuming that the links were placed independently. In this case, we use q_st to denote the probability that, given that a link borders node s, it connects node s to node t.

Because only a relative ordering is necessary for effective navigation, the resulting decision rule is remarkably simple: Select the neighbor that maximizes the product of a degree term (k_s) and a homophily term (q_st). If the network shows no homophily, this is equivalent to selecting the neighbor with the highest degree. On the other hand, if all nodes have equal degree, it is equivalent to selecting the neighbor most similar to the target. An algorithm follows directly from this rule that we call EVN.

Evaluation

We evaluated EVN experimentally on a collection of synthetic and real-world networks, comparing its performance to three other navigation methods: (i) similarity-based navigation, which selects the neighbor most similar to the target node in attribute value, (ii) degree-based navigation, which selects the neighbor with the highest out-degree, and (iii) random navigation. EVN assigns previously visited neighbors zero probability of linking directly to the target—otherwise they would have terminated the search by forwarding to the target. Consequently, EVN ignores visited neighbors if there is at least one unvisited neighbor; it selects randomly among all neighbors otherwise. We used this treatment of visited neighbors with all navigation methods because it consistently outperformed alternative methods of handling visited neighbors, including avoiding only the last visited node or ignoring previous visits. We recorded the performance of global search as a ceiling; when the individual nodes know the entire network structure, a breadth-first search easily identifies the shortest path, if one exists.

Synthetic Networks.

We controlled homophily using a single attribute on each node, distributed uniformly in the interval [0, 1]. For a link originating at node s, the probability of linking to node t was proportional to the preference between the two nodes, f_st = (max{∣a_s − a_t∣, 0.01})^−r, where a_s and a_t are attribute values on nodes s and t, and r is a homophily parameter. When r is zero, the graph shows no homophily: A link originating from a given node is equally likely to end at any other node. As r grows, links become more likely to connect nodes with similar attribute values. The max term puts a bound on the preference values. In its absence, the preference between two nodes may be arbitrarily large because two attribute values may be arbitrarily close. In applying similarity-based navigation, we considered all neighbors within 0.01 of the target to be equally close, to account for the presence of this max term. The EVN decision rule^† was to maximize k_sf_st.

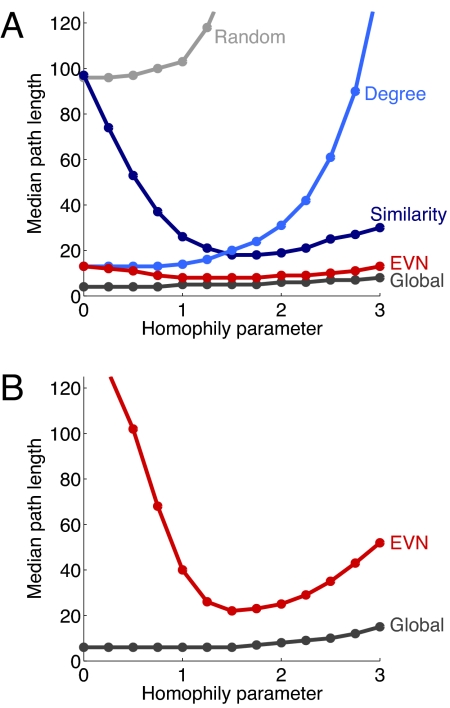
Figs. 1A and 2 show results on networks in which out-degree followed a (truncated) power-law distribution. Specifically, the probability of out-degree k was proportional to k^−β for k ≤ 100, zero otherwise. In such networks, most nodes have only a few edges, but a few nodes have much higher degree. High-degree nodes become more likely with decreasing β, which we refer to as the degree parameter.

Fig. 1.

Median path lengths on power-law networks with degree parameter 1.5 (A), on Poisson networks with λ = 3.5 (B). The graphs show performance on 5,000 randomly selected search tasks on 30 randomly generated 1,000-node networks. “Global” indicates the median path lengths obtained with complete knowledge of the network. Navigation methods not shown in B resulted in median path lengths higher than the values shown on the graph.

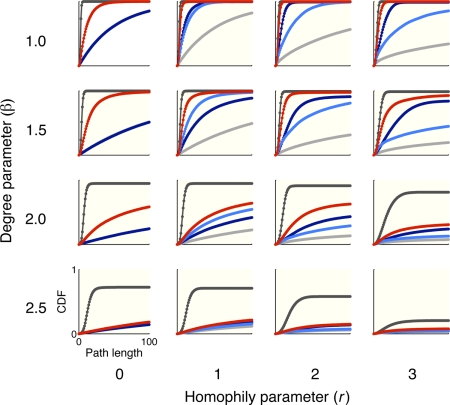
Fig. 2.

Empirical CDF (cumulative distribution function) of path length in power-law networks as a function of degree and homophily parameters. Each plot shows the proportion of searches completed within a given path length. The x axis in each plot ranges from 0 to 100; the y axis ranges from 0 to 1. The color-coding is the same as in Fig. 1. When the homophily parameter is 0, the network shows no homophily. Consequently, EVN performs identically to degree-based navigation, whereas similarity-based navigation performs identically to random navigation. Even with global search, the proportion of completed searches does not always reach 1 because the networks are not necessarily fully connected.

Fig. 1A shows median path lengths with degree parameter 1.5. In these networks, most node pairs were connected through short paths, but random navigation was not effective in identifying them. Degree-based navigation was effective for small values of the homophily parameter, but with increasing homophily, links become more likely to connect nodes that are similar, so high-degree nodes become less effective as hubs that connect different regions of the graph. Similarity-based navigation showed a different trend, performing best for medium values of homophily, consistent with findings presented by Kleinberg (3). Low homophily is not effective in guiding the search, whereas high homophily creates a graph structure that does not contain many short paths. In contrast, EVN was effective for all values of the homophily parameter. It performed as well as or better than the other algorithms, the improvement was usually substantial, and its performance was close to that of global search. Fig. 2 shows cumulative path-length distributions as a function of degree and homophily parameters. These plots show similar trends across networks with different degree parameters, but with increasing degree parameter, high-degree nodes become less likely, resulting in performance decrements in both local and global search. In all cases, EVN equals or exceeds the performance of the other local search algorithms. In the majority of cases, characterized by both nonzero homophily and some variation among nodes in out-degree, EVN systematically outperforms the other local search algorithms by a wide margin.

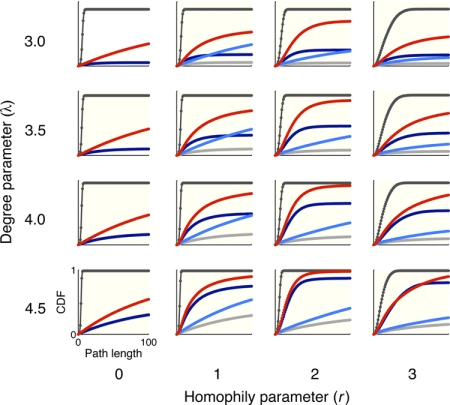
Figs. 1B and 3 show results on networks in which out-degree followed a (truncated) Poisson distribution. Specifically, the probability of out-degree k was proportional to ^λke^−λ/k! for k ≤ 100, zero otherwise. Compared with power-law networks, Poisson networks show much less variation in their out-degree and therefore are less suitable for local search.

Fig. 3.

Empirical CDF (cumulative distribution function) of path length in Poisson networks as a function of degree and homophily parameters. Each plot shows the proportion of searches completed within a given path length. The x axis in each plot ranges from 0 to 100; the y axis ranges from 0 to 1. The color-coding is the same as in Fig. 1.

Fig. 1B shows median path lengths when λ = 3.5. The expected out-degree in these networks approximately equals the expected out-degree in power-law networks with degree parameter 1.5, but the performance of local search is quite different, as expected. Neither homophily nor degree was able to successfully guide navigation by itself,^‡ but using both sources of information yielded qualitatively different results, particularly for intermediate values of the homophily parameter. Fig. 3 shows that, in general, using both sources of information leads to comparable or shorter path lengths, in many cases drastically improving performance. When the homophily parameter is zero, local search performance is poor because the corresponding networks have neither the high-degree nodes nor the homophily structure to guide the search. Search performance improves with increasing λ (or, equivalently, expected out-degree) and is best for intermediate ranges of homophily.

We conducted similar experiments in synthetic networks with undirected edges. These experiments provided qualitatively similar evidence concerning EVN′s ability to synthesize homophily and degree information to efficiently direct messages to their destination.

Citation Network.

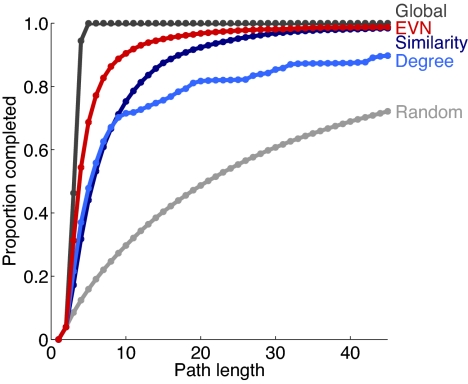
In addition to the synthetic networks described above, we examined the effectiveness of EVN in a real-world network: a citation network in which the nodes were papers in the theoretical high-energy physics (hep-th) area of arXiv.org, an on-line archive of research papers. We included papers that were published in 1995–2000 and that were cited by more than 50 other papers. We placed an undirected link between two papers if one of them referred to the other. The network included 833 nodes and 13,267 links. We defined node similarity using the words that appear in paper titles and abstracts. The results, shown in Fig. 4, are qualitatively similar to those obtained in synthetic networks.

Fig. 4.

Performance on the hep-th citation network. We represented the title and abstract of each paper as a weighted-term vector using TFIDF (term frequency × inverse document frequency) weighting and defined paper similarity as cosine correlation between these term vectors (8). We discretized this continuous similarity measure and, for each discrete value it took, estimated q_st from the network. Cumulative path-length distributions in 10,000 randomly selected search tasks are shown.

Poisson Approximation to the Binomial.

The Poisson approximation to the binomial, which we have used to obtain Eq. 3, is appropriate when the success probability is small, and the number of trials is large. In the search tasks we address, the success probability (q_st) is likely to be very small—it is the probability of linking to a specific node among a large number of choices—but the number of trials (k_s) is not necessarily large. Repeating our experiments using Eq. 2 yielded almost identical path-length distributions.^§ In all experiments reported earlier, the number of searches completed within a given path length was within 98.2–103.5% of those obtained by using Eq. 2. The accuracy of the Poisson approximation has important consequences. The product form of the decision rule has the desirable property that the choice between neighbors s and v is not sensitive to the individual values of q_st and q_vt but only to their ratio. In other words, individual q_st estimates need not be absolutely accurate. It is sufficient to accurately estimate their ratio.

EVN Approximation to Expected Distance.

EVN approximates expected distance using only the probability of a path of length one. It uses this estimate to rank a set of nodes with respect to their expected distance to a given target node. We conducted a limited test of this approximation on our synthetic networks with power-law degree distribution. In tens of thousands of randomly generated networks, we computed distance between all node pairs and obtained an empirical estimate of expected distance to target as a function of out-degree and similarity to target. We then compared navigation decisions made with EVN to those made by using expected distance.

We first performed pairwise comparisons, sampling node out-degree and similarity-to-target uniformly among all possibilities. Table 1 shows the proportion of pairwise comparisons in which EVN′s ranking was identical to the ranking obtained by expected distance. This proportion ranged between 0.92 and 1.00 for different settings of the homophily and degree parameters, indicating a high degree of accuracy.

Table 1.

Proportion of EVN decisions that are consistent with using expected distance

Degree parameter (β)	Homophily parameter (r)
	0	1	2	3
1.0	1.00 (1.00)	0.95 (0.75)	0.98 (0.75)	0.97 (0.72)
1.5	1.00 (1.00)	0.95 (0.72)	0.98 (0.77)	0.96 (0.86)
2.0	1.00 (1.00)	0.93 (0.77)	0.98 (0.85)	0.95 (0.93)
2.5	1.00 (1.00)	0.91 (0.83)	0.97 (0.92)	0.95 (0.92)

For each setting of the homophily and degree parameters, expected distance from a given node to a target node was estimated as a function of node degree and attribute difference from the target node. Node degree was a discrete value ranging from 1 to 100. Attribute difference was a continuous value ranging from 0 to 1; it was discretized in increments of 0.05, starting at 0.025, to obtain estimates of expected distance. Expected distances for intermediate values were computed by using linear interpolation based on two closest points. The table shows outcomes of pairwise comparisons among all possible nodes, where a node could have any out-degree value, and its attribute difference from the target node could take any of the discretized values of this variable. The numbers in parentheses show outcomes of comparisons among eligible neighbors in actual navigation tasks. Values are rounded to the nearest hundredth.

We then examined the actual forwarding decisions made on navigation tasks used to obtain Fig. 2, looking only at those cases in which there were at least two eligible neighbors to which the message could be forwarded. We compared EVN‘s choice to the node that would be selected by using expected distance. When the two nodes were identical or their expected distances to target differed by <0.1 hop, we called it a conforming choice. The numbers in parentheses in Table 1 show the proportion of conforming choices. This proportion was greater than 0.7 in all of our experimental settings. We expect these proportions to be lower than the proportions obtained in pairwise comparisons because they typically show comparisons among more than two nodes, sometimes as many as 100 nodes, with lower settings of the degree parameter generally resulting in comparisons among a larger number of nodes.

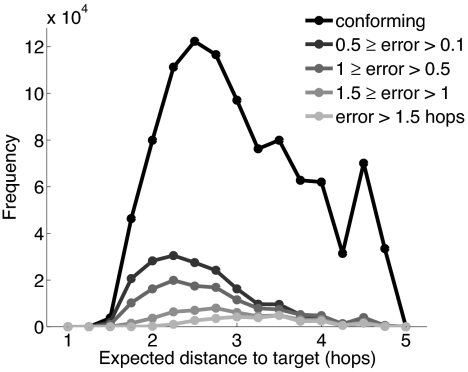
Fig. 5 shows the frequency and magnitude of the errors that EVN made when the homophily parameter was 1.0 and the degree parameter was 1.5. This is one of the experimental settings in which the proportion of conforming choices was at its lowest. The figure shows errors in terms of the difference in expected distance between EVN′s choice and the eligible neighbor with the lowest expected distance to the target. The majority of the errors were made when the message was relatively close to the target node. The magnitude of the errors was usually small. With different homophily and degree parameters, the relative magnitude and distribution of errors were qualitatively similar.

Fig. 5.

Frequency and magnitude of errors in power-law networks with homophily parameter 1.0 and degree parameter 1.5. Errors are the differences in expected distance to target between EVN′s choice and the eligible neighbor with the lowest expected distance to target. Conforming choices have, at most, 0.1 hop error. We examined only the decisions in which at least two eligible neighbors were present.

Considering that the expected distances are approximate values, these results should be viewed as suggestive. However, they do support our hypothesis that EVN ranking decisions are generally close to those that would be obtained by the full expectation.

Conclusion

Our results show that a simple product of degree and homophily measures can be quite effective in guiding local search. In contrast to the equation for the full expectation, the simple product is a plausible calculation for unaided human decision-makers. This suggests that future studies should pay greater attention to the extent to which degree is used by human subjects navigating in social networks. Substantial evidence exists that subjects use homophily when navigating (2, 9). When surveyed (2), subjects only rarely indicate that they use number of friends as the primary rationale for selecting a neighbor. However, whether it is an important secondary rationale, and the extent to which it might influence decision making, remains an open question.