Water Dynamics in Nafion Fuel Cell Membranes: the Effects of Confinement and Structural Changes on the Hydrogen Bond Network

Abstract

The complex environments experienced by water molecules in the hydrophilic channels of Nafion membranes are studied by ultrafast infrared pump-probe spectroscopy. A wavelength dependent study of the vibrational lifetime of the O-D stretch of dilute HOD in H₂O confined in Nafion membranes provides evidence of two distinct ensembles of water molecules. While only two ensembles are present at each level of membrane hydration studied, the characteristics of the two ensembles change as the water content of the membrane changes. Time dependent anisotropy measurements show that the orientational motions of water molecules in Nafion membranes are significantly slower than in bulk water and that lower hydration levels result in slower orientational relaxation. Initial wavelength dependent results for the anisotropy show no clear variation in the time scale for orientational motion across a broad range of frequencies. The anisotropy decay is analyzed using a model based on restricted orientational diffusion within a hydrogen bond configuration followed by total reorientation through jump diffusion.

I. Introduction

In recent years, evidence of global warming and the depletion of global oil reserves have spurred research and development of alternative fuels and energy sources. One fuel that has seen increased interest due to its potential as a zero emissions energy source is hydrogen. Hydrogen powered vehicles using Polymer Electrolyte Membrane Fuel Cells (PEMFCs) have been demonstrated by a number of auto manufacturers and hydrogen powered buses are in service in several cities.

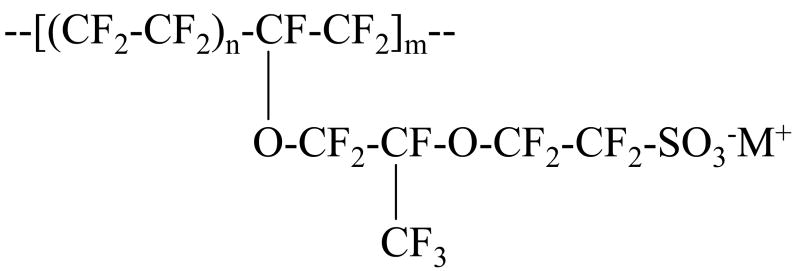
Nafion (a product of Du Pont) is the most common membrane separator used in PEMFCs due to its chemical and thermal stability and its high proton conductivity. It is a polymer, consisting of a long chain fluorocarbon backbone with pendant, sulfonic acid terminated, polyether side chains. The repeat structure of Nafion is shown in figure 1. The extreme difference in the polarity of the fluorocarbon backbone and the sulfonic acid side chains causes segregation of the membrane into hydrophobic and hydrophilic aggregates.^1-4 Hydrogen fuel cells operate through the oxidation of hydrogen gas at the anode to protons and the reduction of the protons with oxygen to water at the cathode. The electrons lost by the hydrogen gas at the anode are available to do work and the water produced at the cathode can either be expelled as exhaust or used to maintain the hydration of the membrane. It is the ability of Nafion to conduct protons from the anode to the cathode of a fuel cell that is its most important practical characteristic, and it is the water absorbed inside the membrane that enables this proton conduction.

Figure 1.

Repeat structure of Nafion. n can vary between 5 and 14 but for 1100 EW Nafion, n = 7. m is typically on the order of 1000.

The importance of the hydrophilic regions of Nafion for proton conduction has inspired a great deal of research over the past three decades since its development in the early 1970s. Early work centered on characterizing the structure and physical properties of Nafion membranes, focusing primarily on the structure of the hydrophilic domains.^5-7 X-ray scattering studies led to a model for the internal morphology of the membrane based on a hydrophilic region consisting of clusters of ionic groups in a reverse micellar type structure connected by small channels.^5,6 One of the first experiments to look directly at the water inside Nafion membranes was presented by Falk, who used steady state IR spectroscopy of H₂O, D₂O and HOD to study the properties of water in Nafion.⁸ IR spectra show that water experiences a range of environments in Nafion and that the hydrogen bond network in Nafion is weaker than in bulk water.^8,9 Based on his IR spectra, Falk proposed that the internal structure consisted of a tortuous network of interconnected channels with significant local heterogeneity.⁸ While the reverse micellar model persisted through much of the 1990s, later small-angle neutron scattering studies and small-angle X-ray studies led to a new model consisting of fibrillar aggregates of hydrophobic polymer with the hydrophilic side chains protruding radially outward.^1,3,4 These tubular aggregates stack together, forming hydrophilic domains consisting of irregular channels that can grow or shrink depending on the water content of the membrane. While the early X-ray scattering studies included the connectivity of the reverse micellar clusters as an ad hoc addition to explain the conductivity of protons and water through the membrane, the fibrillar model unambiguously includes the heterogeneity observed in the environments experienced by the water molecules. Recent molecular dynamics (MD) simulations of the structure of Nafion have provided additional support for a more random structure of interconnected channels.¹⁰

Often, the properties of Nafion are studied at various degrees of hydration from dry to fully hydrated. Scattering experiments show that the hydrophilic domains swell with increased hydration. NMR^11,12, IR⁹, and MD simulations^10,13 show that the pendant side chains in the hydrophilic domains can rearrange as the hydration increases. Ultimately, the practical question in terms of fuel cell operation is: how does the swelling and rearrangement of the hydrophilic domains affect the mechanism for proton transport through Nafion?

Because proton transport is intimately connected to hydrogen bond network structural rearrangement, the answer to this question requires a detailed study of the dynamics of water molecules in Nafion as a function of hydration. Several experiments have probed the dynamics of water including NMR,^14-16 quasielastic neutron scattering,¹⁷ MD simulation,¹⁸ and time resolved IR spectroscopy.⁹ NMR experiments have measured both proton and water diffusion to determine the amount of proton diffusion due to vehicular transport vs. Grotthüs shuttling. Results from these experiments show that an increase in hydration results in an increase in Grotthüs proton transport. Neutron scattering experiments have measured the fast, local diffusion of water molecules and show that the length scales for diffusion increase with increasing hydration. The MD simulation was conducted at a single hydration level but showed evidence for both Grotthüs and vehicular proton transport. While these experiments provide useful macroscopic and microscopic pictures of water and proton movement, on a fundamental level, diffusion of protons and water molecules depends on the reorganization of the hydrogen bond network of water. A useful technique for directly interrogating the hydrogen bond network of water is ultrafast infrared spectroscopy.^19-30

Here, we present an IR pump-probe study of the dynamics of water absorbed in Nafion membranes at four hydration levels. IR spectroscopy of dilute HOD in H₂O or D₂O provides a direct probe of the hydrogen bond network and dynamics of water.^24,27 The local environment of an HOD molecule is reported by its linear IR spectrum³¹ and its vibrational lifetime. Vibrational relaxation is sensitive to both local fluctuating forces acting upon an excited vibrational mode and the availability of lower frequency accepting modes to dissipate the energy.³² Changes in the local environment can alter the fluctuating forces and shift the energy levels of the accepting modes, altering the vibrational lifetime. Although it is difficult to pinpoint the cause of a change in the vibrational lifetime, the fact that it is sensitive to local effects allows the identification of multiple ensembles based on differences in the vibrational lifetime at different frequencies.

Global rearrangements of the hydrogen bond network are reflected in the time dependent orientational anisotropy, which is a measure of the reorientational motions of the water molecules. Reorientation requires the concerted motion of several water molecules and involves the reorganization of the hydrogen bond network through the breaking and forming of hydrogen bonds. This requirement causes the anisotropy to be sensitive to the characteristics of the hydrogen bond network as a whole rather than the local environment of an O-D oscillator. The detailed wavelength dependent study of the vibrational lifetime and orientational relaxation presented below provides insights into both the local and long range dynamics of water contained in the hydrophilic domains of Nafion.

II. Experimental Procedures

Nafion-117 samples were purchased from Fuelcellstore.com in the acid form. Samples were converted to the sodium form by soaking in 1 M sodium chloride solution for 24 hours followed by a deionized water rinse and were used without further purification. A home built humidity control system was used to equilibrate the samples under constant relative humidity conditions. Relative humidity on a scale of 0 to 1 is equivalent to the activity of water, which is defined as the ratio of the partial pressure of water in the air to the partial pressure of water saturated air at a given temperature. Dry air (dew point - 100 °C) is bubbled through a water reservoir containing dilute (<5%) HOD in H₂O. The reservoir is maintained at various constant temperatures to produce relative humidities ranging from 0 to 100% (activities from 0 to 1). The humidified air purges a Plexiglas box with a humidity meter to monitor the relative humidity and glove ports for sample manipulation and preparation. The number of water molecules per sulfonate group, λ, was determined by measuring the mass uptake of a Nafion membrane as a function of water activity. Mass uptake measurements were made with a balance placed inside the Plexiglas humidity box. Samples were prepared at water contents varying from λ = 1 to 7.5 for pump-probe experiments. Samples equilibrated under 0% relative humidity still contained approximately one water per sulfonate, (λ = 1). These samples will be referred to as “dry” Nafion. All samples prepared in the humidity system were sealed in sample cells between 3 mm thick CaF₂ windows separated by a 200 μm Teflon spacer. The long term stability of the samples was monitored by FT-IR spectroscopy to ensure that the cells were air tight. All experiments were performed at 25 °C.

The laser system used in these experiments consists of a home-built Ti:Sapphire oscillator and regenerative amplifier operating at 1 kHz which pump an OPA and difference frequency stage to produce ∼70 fs, ∼4 μm IR pulses. Pulses are split into pump and probe pulses with the probe's polarization set to ∼45° relative to the pump. After the sample, the components of the probe with polarization parallel and perpendicular to the pump are selected to avoid depolarization effects due to optics in the beam path.³³ Polarizers set to parallel and perpendicular are rotated into the beam using a computer controlled filter wheel. Scans alternate between parallel and perpendicular to reduce effects of long term laser drift between the two polarizations. After the polarizers, a half wave plate rotates the polarization of each component to 45° prior to the entrance slit of a 0.25 m monochromator so that both parallel and perpendicular polarization scans experience the same diffraction efficiency from the monochromator grating. The spectrally resolved pump-probe signal is detected by a 32 element HgCdTe detector (Infrared Associates). Great care is taken to ensure that the probe intensity for both parallel and perpendicular components is the same on a given pixel of the array detector to avoid the consequences of the mildly nonlinear response of HgCdTe with increasing intensity.³⁴ The pump-probe signal is determined in part by the slope of the detector response curve at a given probe intensity. Maintaining the same probe intensity for both parallel and perpendicular polarizations ensures that the slope of the detector response is the same for both components and that the measured pump-probe signal is representative of the dynamics of the system under study, rather than the nonlinearity of the detector. With an accurate measurement of I_|| and I_┴ vibrational population relaxation, P(t) (lifetime) is obtained using,

$$P(t)=I_{\parallel }+2I_{\perp }$$ (1)

and the orientational relaxation, r(t) (anisotropy) is given by,

$$r(t)=\frac{I_{\parallel }-I_{\perp }}{I_{\parallel }+2I_{\perp }}=\frac{2}{5}{C}_2(t)$$ (2)

where C₂ (t) is the second Legendre polynomial orientational correlation function.

III. Results and Discussion

A. Vibrational Lifetimes

Recently, the vibrational lifetime of dilute HOD in H₂O absorbed in Nafion was measured for the first time.⁹ The measurement of the vibrational lifetime as well as the IR spectrum of water in Nafion provided evidence for multiple ensembles of water molecules in Nafion. While the IR spectra at all hydration levels could be fit using a weighted sum of two fixed spectral components, the vibrational lifetime showed evidence that the characteristics of the two ensembles was changing with hydration. The vibrational lifetime measurements in this earlier study were conducted only at the peak of the absorption spectrum for each sample.

Here we report a complete wavelength dependent study of the vibrational lifetime at each hydration. In all of the samples studied, the deposition of heat from vibrational relaxation causes a long time signal that does not decay on the time scale of our experiment. This effect has been well documented both in bulk water^24,27 and in reverse micelles.^20,29 In the sample studied here, the long term off-set signal ranges from about 10% (highest hydration) to 1 or 2% (lowest hydration) of the initial amplitude. The vibrational lifetime can be extracted from the total signal by invoking a kinetic model for the deposition of energy following vibrational relaxation. The data presented here have been corrected for this heating contribution using the procedures developed previously.^24,27

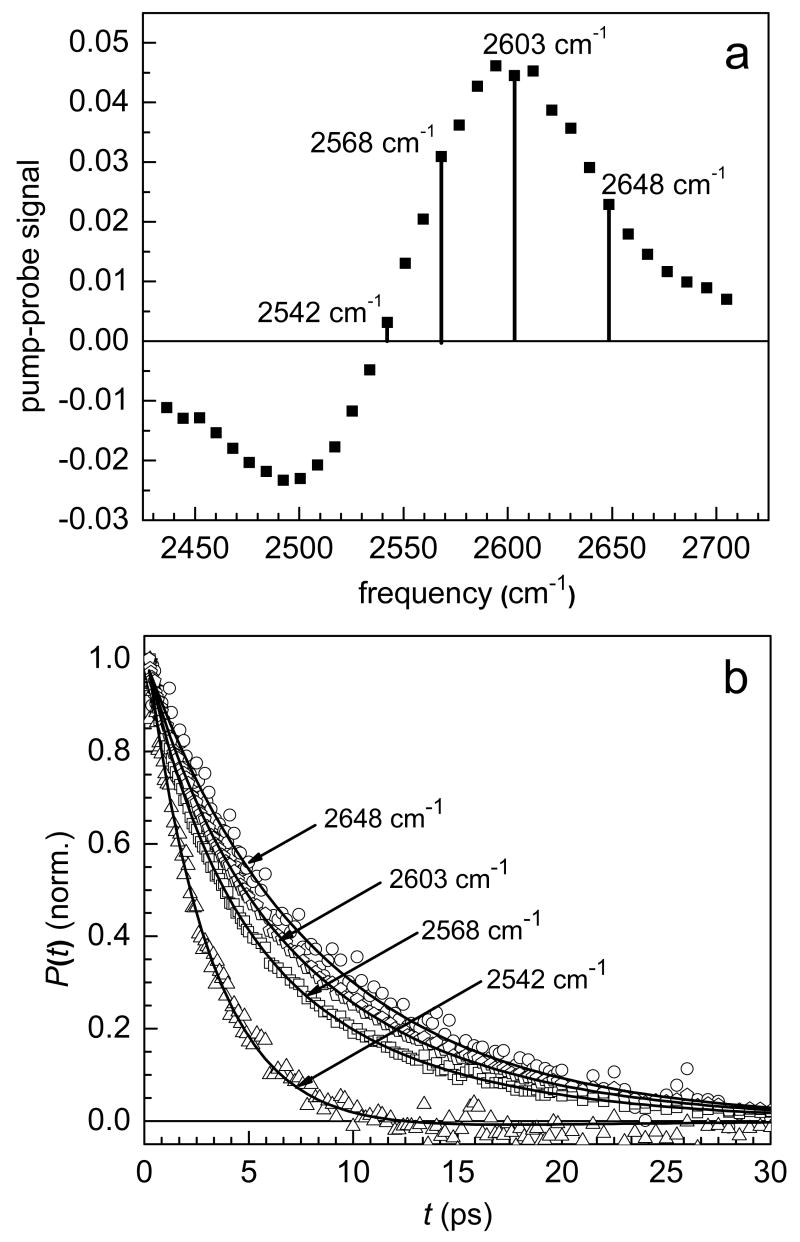
Figure 2a shows the pump-probe spectrum of λ = 3 Nafion at 0.2 ps. The pump-probe spectrum consists of a positive signal (bleach) in the 0-1 region and a negative signal (induced absorption) in the 1-2 region. Four different frequencies are marked at various locations in the 0-1 region of figure 2a. Figure 2b shows normalized plots of the vibrational lifetime at these four frequencies. It is clear that the vibrational lifetime decay is much faster on the red (low frequency) side of the 0-1 region than it is on the blue (high frequency) side.

Figure 2.

a. Pump-probe spectrum of λ = 3 Nafion at 0.2 ps. b. Population dynamics (vibrational lifetimes) at four different frequencies in the 0-1 corresponding to the frequencies labeled in a. The solid lines are biexponential fits to the data at each frequency with the time constants fixed at τ₁ = 3.2 ps and τ₂ = 8.6 ps. Only the relative amplitude of the two components is varied.

The vibrational lifetime increases monotonically from the red side to the blue side across the 0-1 transition and is fit well by a biexponential at all wavelengths. Interestingly, the vibrational lifetime can be fit at all wavelengths in the 0-1 (and also in the 1-2) using two fixed time constants. This is strong evidence that water in λ = 3 Nafion experiences two very different environments. Although the magnitude of the transition dipole moment in water is frequency dependent,³⁵ at a given frequency, the water molecules contributing to the signal should have the same transition dipole moment. Therefore, the relative amount of water in each environment can be extracted from the amplitudes of the two exponentials. For a normalized population decay we have:

$$P(t)=a{e}^{-t/{\tau }_1}+(1-a)e^{-t/{\tau }_2},$$ (3)

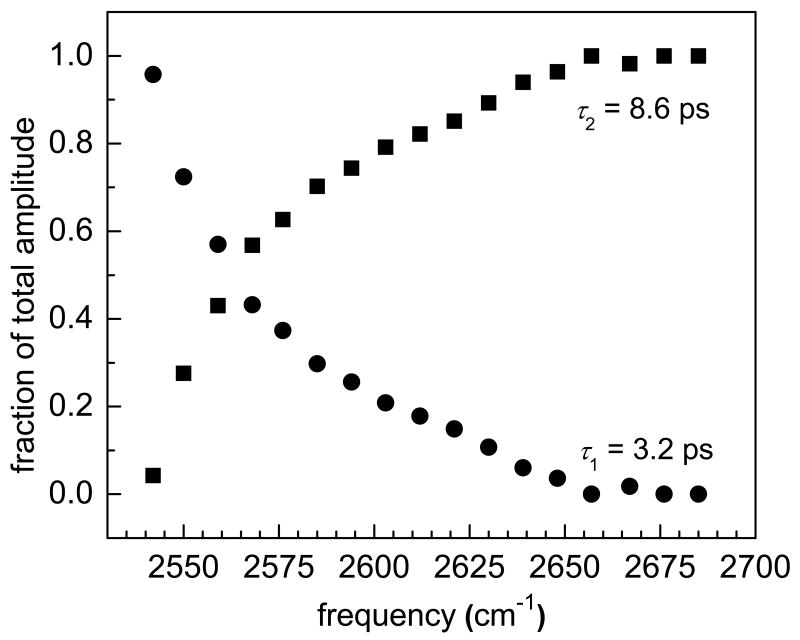
where a is the fraction of water molecules in environment 1 with vibrational lifetime τ₁ and (1-a) is the fraction of water molecules in environment 2 with vibrational lifetime τ₂. In λ = 3 Nafion, τ₁ = 3.2 ps and τ₂ = 8.6 ps. The solid lines in figure 2b are fits to the data using these two time constants. Figure 3 shows the relative amount of water in each environment at each frequency in the 0-1 region of the spectrum. On the blue side, the vibrational lifetime is a single exponential with a time constant of 8.6 ps. In this region, only one ensemble of water molecules contributes to the pump-probe signal. Moving toward lower frequencies, the fraction of water molecules with a vibrational lifetime of 3.2 ps increases until on the red side of the 0-1 transition the data are fit well by a single exponential with a time constant of 3.2 ps. In the intermediate wavelengths, both ensembles contribute to the signal.

Figure 3.

The fraction of the total amplitude in each component of the vibrational population decay at frequencies in the 0-1 region of λ = 3 Nafion.

Evidence for multiple hydrogen bond environments has been observed in several other systems including reverse micelles,²⁰ and mixtures of water with ions or other solutes.^26,36,37 In these systems, water may either hydrogen bond to another water molecule, or it may interact with the head group of the reverse micelle or one of the solute ions or molecules. Wiersma and coworkers showed that the components of the vibrational lifetime of water molecules in mixtures with acetonitrile depended on the mole fraction of water present in the mixture.³⁷ At low water content, water molecules were essentially isolated from one another and could only hydrogen bond to acetonitrile molecules. As the amount of water in the sample increased, the size of the water clusters grew, changing the vibrational lifetimes of both the water-water and water-acetonitrile bonded subensembles. This change was attributed to an increase in the bulk-like characteristics of the water clusters as well as the increased probability that a water molecule interacting with acetonitrile would be able to rapidly break its hydrogen bond and form a new hydrogen bond with a water molecule, leading to a faster pathway for vibrational relaxation. AOT reverse micelles are another system that consists of multiple ensembles of water.²⁰ In the case of AOT, it has been shown that increasing the size of the water pool does not change the time constants for vibrational relaxation but simply increases the relative fraction of molecules in a bulk-like environment.²⁰ A core/shell model was used to describe the data. In this model, the characteristics of water molecules interacting with the head group interface (shell) do not change as the size of the reverse micelle changes. The fact that this model works well for all sizes of reverse micelles is a strong indication that the structure of the interfacial region does not change with reverse micelle size.

Nafion is similar in many ways to AOT reverse micelles. In fact, early models of Nafion invoked a reverse micellar structure for the hydrophilic regions. Nafion has sulfonate terminated side chains, much like the surfactant AOT. In the present experiments, the counter ion used for the sulfonate groups in Nafion was Na⁺, which is the same counter ion used in experiments on AOT reverse micelles. However, the results for the vibrational lifetime have some important and interesting differences. If the hydrophilic regions of Nafion simply grew larger with increased hydration, maintaining the structure of the interface, one would expect the vibrational lifetime of water in Nafion to follow a trend similar to water in AOT reverse micelles. In other words, the two time constants describing the vibrational relaxation of “core” water and interfacial water should remain constant, with only the relative amounts of each environment changing at different hydrations. Instead, both components of the vibrational lifetime of water in Nafion change as the hydration level is increased. Table 1 contains the results of global fits to the vibrational lifetime data of the four different hydration levels of Nafion studied in this experiment. At each hydration level, the relative amount of each component at a given wavelength follows a similar trend to the results for λ = 3 Nafion shown in figure 3. It is useful to note that the lifetime of the O-D stretch of HOD in bulk water is 1.7 ps, and is single exponential.²⁰ The τ₁ component in Nafion is approaching the bulk water value at the highest hydration level studied.

Table 1.

Population relaxation times for the two components of the vibrational lifetime at different hydrations.

	τ1 (ps)	τ2 (ps)
λ = 1	5.1	11
λ = 3	3.2	8.6
λ = 5	2.3	6.5
λ = 7.5	2.0	5.9

The change in both components of the vibrational lifetime as the hydration level of the membrane increases bears some resemblance to the results for acetonitrile/water mixtures, yet it is clear that the hydrophilic regions of Nafion cannot be viewed as a simple binary solution. Based on neutron and X-ray scattering data, the network of hydrophilic regions is made possible by the irregular stacking of fiber-like aggregates of the fluorocarbon backbone.³ The sulfonate terminated side chains are tethered to these fibers and constrained sterically, both by adjacent side chains and the packing of the surrounding fluorocarbon fibers. MD simulations¹⁰ show that the side chains tend to lie flat against the hydrophobic backbone with only the sulfonate groups penetrating into the hydrophilic domain, but due to the relatively large spacing between adjacent side chains (7 –(CF₂-CF₂)- groups for an 1100 EW sample of Nafion), a great deal of space can exist between adjacent sulfonate groups. In other words, the walls of the hydrophilic domain are not a smooth array of sulfonate groups like the walls of an AOT reverse micelle. At low hydration levels, water absorbed into the membrane and forming a hydrogen bond with a sulfonate group may be trapped against the hydrophobic backbone on the opposite side of the hydrophilic domain due to the irregularity of the polymeric structure and the spaces between sulfonate groups. Linear IR spectroscopy shows that a small portion of the water molecules in Nafion experience an extremely hydrophobic environment.^8,9 Yet, as the hydration level increases, the number of water molecules experiencing this type of environment decreases, indicating a rearrangement of the hydrophilic domains to reduce the contact between water and fluorocarbon.⁹ This restructuring of the hydrophilic domains is most likely due to a rearrangement of the pendant side chains to form more thermodynamically stable water clusters. MD simulations¹³ and NMR experiments¹² provide evidence for this interpretation.

Several important conclusions can now be drawn based on a comparison between the results for the vibrational lifetime of water in Nafion, acetonitrile/water mixtures, and AOT reverse micelles. While the hydrophilic domains of Nafion may seem similar to AOT reverse micelles in many respects, the change in the vibrational lifetime with changing water content indicates that the hydrophilic domains restructure, in contrast to the interfacial region of AOT. The sulfonate groups in AOT reverse micelles have very little mobility because they are constrained by the close packing of the surfactant molecules. In Nafion, the side chains are clearly not constrained to the extent that they are in AOT and are therefore able to rearrange to some degree. Acetonitrile molecules in binary mixtures of acetonitrile/water have essentially complete mobility to rearrange in order to form the most stable water cluster possible. Clearly, the ability of the sulfonate terminated side chains in Nafion to rearrange is intermediate between the fixed structure of the head groups in AOT reverse micelles and the free reorganization that is possible in a binary acetonitrile/water solution. The side chains in Nafion have some ability to reorganize to produce more thermodynamically stable water clusters but this restructuring is constrained by the structure of the fluorocarbon backbone and the packing of the polymer's hydrophobic aggregates.

B. Orientational Relaxation

Unlike the vibrational lifetime, orientational relaxation, which is measured through the time resolved anisotropy, has a concrete physical connection to the motions of water molecules. A great deal of experimental effort has been devoted to studying the orientational motions of water molecules.^20,24,27,28 The breaking and forming of hydrogen bonds, which is central to the reorientation of a water molecule, is an important step in both translational diffusion and proton transfer. In Nafion, both translational motion and proton transfer are critical for fuel cell performance, and understanding how the orientational motions of water molecules change as the amount of water in the membrane varies is fundamental in modeling these processes.

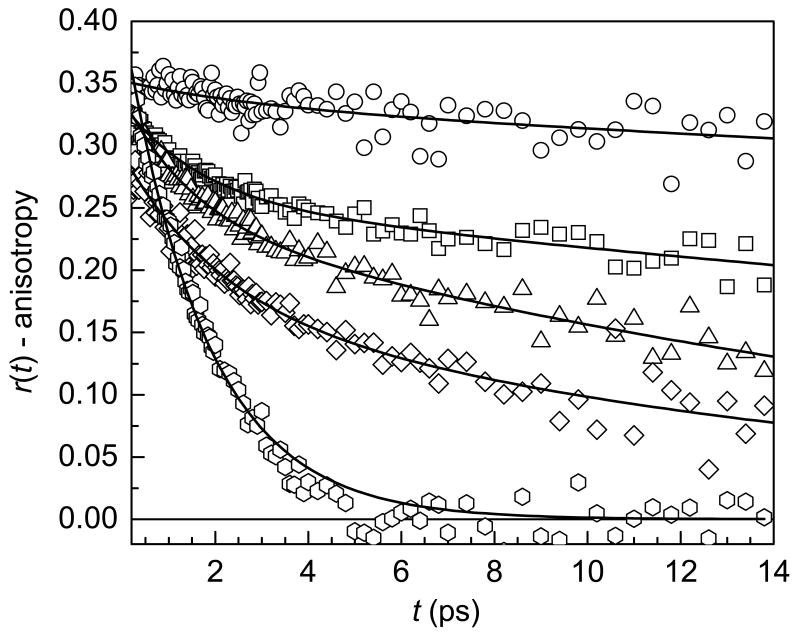
Anisotropy decays collected at the peak of the absorbance spectrum for each sample are shown in figure 4 along with the anisotropy decay of bulk water for comparison. Clearly, the anisotropy decays become significantly slower as the hydration level of the membrane decreases, and none of the curves (except water) can be fit by a single exponential decay. Following ultrafast inertial motion (tens of femtoseconds), the anisotropy of bulk water decays as a single exponential with a decay time of 2.6 ps.^20,27 Experiments probing the reorientation of water molecules confined in AOT reverse micelles yield biexponential decays for the anisotropy (following an inertial component), which are attributed to the disruption of the hydrogen bond network by confinement effects.^20,21,38,39 In AOT reverse micelles, the orientational dynamics become slower as the size of the reverse micelle decreases, following a similar trend to that shown in figure 4 for Nafion. Slowing of the anisotropy decay has also been observed in other binary mixtures of water as well as in solutions of water with ions.^19,40 Water molecules in the first solvation shell of an anion have slower orientational dynamics, but the presence of anions has little effect on the dynamics of the water in general. These results show that a significant disruption of the hydrogen bond network must occur for the orientational dynamics of water to be affected.

Figure 4.

Anisotropy decays at the peak of the absorption spectrum for λ = 1 (circles), 3 (squares), 5 (triangles), and 7.5 (diamonds). The anisotropy decay of bulk water (hexagons) is shown for comparison. Solid lines are fits to the data. All Nafion samples were fit using biexponential decays. Water was fit using a single exponential decay.

Several groups have measured the anisotropy decays of bulk water^24,27,28 and confined water.^19-21,38,39 Recently an MD simulation provided a physically useful interpretation of the anisotropy decay for bulk water.⁴¹ The experimentally measured anisotropy decay of bulk water is fit well by a single exponential with a time constant of 2.6 ps.^20,27 Usually the physical model employed for the orientational dynamics of molecules in liquids is Gaussian diffusion, which is the origin of the Debye-Stokes-Einstein (DSE) equation. The DSE equation is based on the reorienting molecule taking random, infinitesimal steps, and yields a single exponential decay with a decay time related to the orientational diffusion constant. For bulk water this model can be used to fit the data. However, a model based on infinitesimal diffusion does not take into account an important property of water: its tetrahedral hydrogen bond network. The directionality of the interactions between water molecules within the tetrahedral framework of the hydrogen bond network means that hydrogen bonds must be broken and new bonds formed for complete reorientation to occur.

A significant body of literature exists for modeling the orientational motions of molecules in solution. Early on, several authors realized the shortcomings of the Gaussian diffusion model in describing the orientational motions of small molecules in solution. Ivanov's jump diffusion model⁴² and Gordon's J and m diffusion models⁴³ were two of the earliest. These models developed expressions for the orientational correlation function for finite steps. Tao and Szabo developed models for the rotational motion of macromolecules,^44,45 and Szabo extended the model to describe a general case of restricted orientational diffusion.⁴⁶

The biexponential decay of the anisotropy observed for water in AOT has been described using a model based on restricted orientational diffusion or “wobbling in a cone.”^20,21 In the wobbling in a cone model, the motions of the molecules are restricted at short times to lie within a cone of half-angle θ_c. This motion is diffusive in nature, but rather than proceeding to sample the entire sphere, it is restricted by the boundary conditions of the cone. After this initial wobbling period, the slow, long time decay of the anisotropy is attributed to full sampling of the rest of orientational space.

The MD simulations of Laage and Hynes highlighted the well established tetrahedral nature of the hydrogen bond network of water.⁴¹ Based on this physical picture for the microscopic structure of water, Laage and Hynes found that the orientational motions of water molecules are better described by a jump diffusion model based on Ivanov's approach,⁴² in which the jumps correspond to the rearrangement of hydrogen bonds among water molecules.⁴¹ From a physical point of view, this description makes sense; complete orientational randomization of the hydroxyl transition dipole cannot only involve many infinitesimal random steps but should also involve the breaking and forming of hydrogen bonds. Energetically a water molecule will not break a hydrogen bond without virtually immediately forming a new hydrogen bond.⁴⁷ The MD simulations show that the hydrogen bond switching process involves the transient formation of a bifurcated hydrogen bond to reduce the energetic penalty for switching hydrogen bond partners. This bifurcated hydrogen bond is the transition state in the large amplitude orientational jump that leads to the formation of a new local hydrogen bond configuration.⁴¹ In the simulation, the average angular amplitude of the jump was determined to be 60°. This is far from the diffusive limit, yet this model also produces a single exponential decay for the orientational correlation function (anisotropy).^41,42 The time constant, τ, for the anisotropy decay measured in the IR pump-probe experiment (second Legendre polynomial correlation function) given by the jump diffusion model is

$$\tau =\frac{{\tau }_j}{\left(1-0.2\frac{sin2.5{\theta }_0}{sin{\theta }_0/2}\right)},$$ (4)

where τ_j is the time between jumps, and θ₀ is the jump angle.

In Nafion, the anisotropy decay does not fit to a single exponential. Unlike the vibrational lifetime, biexponential behavior does not imply that the anisotropy is produced by two subensembles.²⁰ In fact, it has been shown that two subensembles with different orientational relaxation rates and overlapping spectra will not produce a biexponential decay of the anisotropy.²⁰ Here the time scales of the two components of the anisotropy decay differ by a large enough amount that it is possible to propose a reasonable physical underpinning for the different mechanisms that give rise to the decays. The physical picture of the microscopic structure of water can guide the interpretation. The motions of the O-D bond in an O-D----O hydrogen bond are restricted by the hydrogen bond potential energy surface. The lowest energy, corresponding to the shortest hydrogen bond length, occurs when the O-D bond lies directly along the line between the two oxygen atoms in the hydrogen bond. At room temperature, water molecules have enough energy to sample substantial portions of the hydrogen bond potential energy surface. In MD simulations one of the characteristics used to define the existence of a hydrogen bond is the angle between the O-D bond and the O-O axis being less than 30°.⁴¹ This definition permits a significant amount of orientational space to be sampled without breaking a hydrogen bond. Therefore, it is reasonable to assume that over some range of angles, the orientational motion of the O-D bond will be caused by thermal fluctuations of the intact hydrogen bond network and will be essentially diffusive in nature. The only restriction on the motion of the O-D in this regime is the increase in potential energy as it moves away from the O-O axis. In contrast, a large amplitude fluctuation in the orientation of the O-D bond can only be achieved through a rearrangement of the hydrogen bond network by breaking and forming new hydrogen bonds.

With this physical picture in mind it is possible to combine the wobbling in a cone model applied previously (short time dynamics) with the jump diffusion model (long time dynamics) for water reorientation. Since the large amplitude jump reorientations depend on changes in the coordination of water molecules in the first and second solvation shell of the HOD molecule it is safe to assume that the wobbling motion of the O-D bond within the hydrogen bond potential is statistically independent from the jumps.⁴¹ For statistically independent processes, the overall orientational correlation function can be factored into correlation functions for the two separate processes.⁴⁶

$$C_2(t)=C_w(t)C_j(t)$$ (5)

Where C₂(t) is the overall correlation function measured by the anisotropy decay (r(t) = 0.4C₂(t)), C_w(t) is the correlation function for the wobbling motion, and C_j (t) is the correlation function for the jump diffusion. From Lipari and Szabo, the correlation function for the motion with the intact hydrogen bond is given by:

$$C_w(t)=S^2+\left(1-S^2\right)e^{-t/{\tau }_w}$$ (6)

Here, S is known as the generalized order parameter which describes the degree of restriction and τ_w is the time constant for the orientational motion. In the context of the wobbling in a cone model, S can be related to the cone angle by:

$$S=\frac{1}{2}(cos{\theta }_c)(1+cos{\theta }_c).$$ (7)

The wobbling diffusion constant is not determined solely by τ_w but also depends on θ_c. The expression for wobbling angular diffusion constant, D_w is⁴⁵

$$D_w=\frac{x_w^2{(1+x_w)}^2\{ln[(1+x_w)/2]+(1-x_w)/2\}}{{\tau }_w(1-S^2)[2(x_w-1)]}+\frac{(1-x_w)(6+8x_w-x_w^2-12x_w^3-7x_w^4)}{24{\tau }_w(1-S^2)},$$ (8)

where x_w = cosθ_c. In the limit of θ_c = 180°, i.e., there is no restriction to the orientational diffusion, S² = 0 and D_w = 1/6τ_w, as expected from the Debye-Stokes- Einstein treatment of Gaussian angular diffusion. The correlation function for jump reorientation is simply:

$$C_j(t)=e^{-t/\tau }$$ (9)

Where τ is the jump diffusion time constant for the second Legendre polynomial.

The total correlation function can then be expressed as

$$C_2(t)=\left(S^2+\left(1-S^2\right)e^{-t/{\tau }_w}\right)e^{-t/\tau }$$ (10)

The cone angle, θ_c, can be extracted from the amplitude of the long time component of the anisotropy decay, which has time constant τ_L = τ. Since jump diffusion may contribute slightly to the decay of the anisotropy at early times, τ_w is related to the two measured time constants by:

$${\tau }_w={\left({\tau }_S^{-1}-{\tau }_L^{-1}\right)}^{-1},$$ (11)

where τ_s is the short time component of the anisotropy decay, which follows the ultrafast inertial decay. Table 2 lists the measured amplitudes, A_s and A_L, and time constants, τ_w and τ, for the anisotropy decay at the four hydration levels as well as the cone angles, θ_c and the cone diffusion constants, D_w. Separating the jump rate, 1/τ_j, from the jump angle, θ₀, is not possible from the measurement of τ because there are two unknowns in the equation (see equation 4). However, to obtain an idea of the time scale of τ_j, the value obtained for θ₀ from the MD simulations of bulk water⁴¹ can be used. Then, from equation 4, τ_j = 0.8 τ. Thus, the values reported for τ in Table 2 are closely related to the jump time, which can be interpreted as the time scale for hydrogen bond network rearrangement.

Table 2.

Orientational relaxation parameters: A_S is the short component amplitude, τ_w is the wobbling time constant, θ_c is the cone angle, A_L is the long component amplitude, and τ is the jump diffusion time constant.

	AS	τw (ps)	θc	Dw (ps-1)	AL	τ (ps)
λ = 1	0.02 ± 0.02	3*	20°±4°	0.003	0.33 ± 0.02	∞
λ = 3	0.08 ± 0.01	1.8 ± 0.2	31°±2°	0.03	0.25 ± 0.01	63 ± 10
λ = 5	0.10 ±0.01	1.3 ± 0.2	33°±2°	0.03	0.24 ± 0.01	22 ± 2
λ = 7.5	0.12 ± 0.02	1.9 ± 0.4	42°±3°	0.03	0.17 ± 0.02	17 ± 3
water					0.34 ± 0.01	2.6 ± 0.1

^*The amplitude of this component is so small that it is difficult to determine the time constant. 3 ps is approximately the correct value. The value is not significantly faster than this, but could be slower.

There are several trends in the anisotropy parameters reported in Table 2. First, the amplitude of the short time component, A_S, increases with increased hydration leading to larger cone angles for higher hydration levels. This implies that the water molecules are able to sample more of their orientational space on a fast time scale. At the lowest hydration level, λ = 1, virtually no reorientation occurs after the small amplitude short time component. When the τ_w and θ_c are combined (equation 8), the wobbling diffusion constants, D_w, are all the same for the higher hydration levels within experimental error. The λ₁ value is much smaller. While the wobbling diffusion constants are the same except of the lowest hydration same, the long time component, τ, becomes significantly faster for the higher hydration levels. If the angular displacements that water molecules make during a jump are similar at each of the hydrations, the increase in the decay of the long component indicates that the jump rate is increasing with increased hydration. In the case of λ = 1, so little water is present in the membrane that it is never possible to find a new hydrogen bond acceptor, so no jumps occur on the time scale of the experiment. Finally, none of the anisotropy decays extrapolate to 0.4 at time t = 0 due to a fast inertial component that occurs in the first ∼100 fs. This component's amplitude is determined by the difference from 0.4 of the sum of A_L and A_S. A direct measurement of the inertial decay constant was not possible in these experiments because of the large non-resonant contribution to the signal around t = 0 caused by the temporal overlap of the pulses.

Given the current detailed understanding of water dynamics, the orientational motions of water molecules are not a local phenomenon. Complete reorientation requires the breaking and forming of hydrogen bonds, which depends on the concerted motion of several water molecules to lower the energy barrier of the hydrogen bond transition state. Although the local reorientational event requires the participation of water molecules in the first and second solvation shells of the reorienting molecule, the ability of these two molecules to accept a hydrogen bond depends on the dynamics of their own solvation shells. The necessity for cooperative motion means that the anisotropy is sensitive to the hydrogen bond dynamics of a group of water molecules, not the local environment of a single water molecule. The short time scale wobbling in a cone motion is also determined by the nature of the hydrogen bond network bonded to the wobbling OD hydroxyl group under observation.

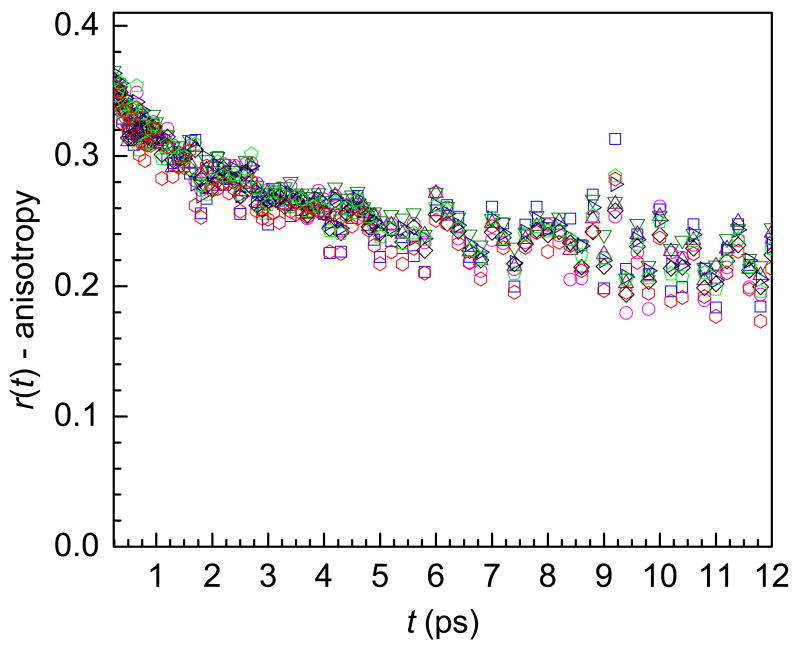
A wavelength dependent study shows no change in the anisotropy with frequency. Figure 5 displays the anisotropy decays at 8 wavelengths for λ = 3 Nafion over a 62 cm^-1 range in the 0-1 from 2568 cm^-1 to 2630 cm^-1. For comparison, the amplitude of the two components of the vibrational lifetime changed by ∼30% in the same range (see figure 3).

Figure 5.

Anisotropy decays for λ = 3 at eight frequencies ranging from 2568 cm^-1 to 2630 cm^-1. Within experimental error there is no frequency dependence.

The lack of wavelength dependence provides strong evidence that the orientational dynamics of water in Nafion are sensitive to global characteristics of the hydrogen bond network rather than the local effects that determine the absorption frequencies and vibrational lifetimes.²⁰

IV. Concluding Remarks

Wavelength dependent studies of the vibrational lifetime at four different hydration levels provide evidence for two ensembles of water molecules whose characteristics change with the amount of water in the membrane. The changes in the vibrational lifetimes of water with hydration level show that the hydrophilic domains of Nafion do not have a consistent interfacial structure independent of the level of hydration in contrast to AOT reverse micelles. Instead, the pendant side chains which anchor the sulfonate groups to the fluorocarbon backbone are labile enough to rearrange and stabilize water clusters as the amount of water increases.

Unlike the vibrational lifetime, the anisotropy is sensitive to the global structural rearrangements of the changing hydrogen bond network. A model based on wobbling in a cone diffusion within a molecule's original hydrogen bond configuration followed by large angle jump diffusion provides a useful approach for visualizing the physical processes responsible for reorientation. This model is particularly interesting at the lowest hydration level, λ = 1, where no jumps are possible due to the low water content. These highly immobilized water molecules are probably hydrogen bonded to one or more sulfonate oxygens with no other mobile water molecules nearby to provide new hydrogen bond partners. At higher hydration levels, the wobbling diffusion constants are independent of the hydration level, but the time constant for jump diffusion becomes significantly faster indicating an increased ability for hydrogen bond network rearrangement to occur. Hydrogen bond rearrangement is necessary for proton transfer. In fuel cells, the performance of polymer electrolyte membranes like Nafion depends on the dynamical properties of the water inside the membranes. Understanding how the changing environment of the water molecules affects their structural dynamics provides a key tool for unraveling the mechanisms for the transfer and transport of protons in fuel cell membranes.