A Biophysical Model of Synaptic Plasticity and Metaplasticity Can Account for the Dynamics of the Backward Shift of Hippocampal Place Fields

Abstract

Hippocampal place cells in the rat undergo experience-dependent changes when the rat runs stereotyped routes. One such change, the backward shift of the place field center of mass, has been linked by previous modeling efforts to spike-timing–dependent plasticity (STDP). However, these models did not account for the termination of the place field shift and they were based on an abstract implementation of STDP that ignores many of the features found in cortical plasticity. Here, instead of the abstract STDP model, we use a calcium-dependent plasticity (CaDP) learning rule that can account for many of the observed properties of cortical plasticity. We use the CaDP learning rule in combination with a model of metaplasticity to simulate place field dynamics. Without any major changes to the parameters of the original model, the present simulations account both for the initial rapid place field shift and for the subsequent slowing down of this shift. These results suggest that the CaDP model captures the essence of a general cortical mechanism of synaptic plasticity, which may underlie numerous forms of synaptic plasticity observed both in vivo and in vitro.

INTRODUCTION

Understanding the mechanisms by which the brain represents and stores temporal sequences is a fundamental problem that has wide relevance across the nervous system. Such mechanisms may 1) allow the organism to learn to associate neutral stimuli that precede (and therefore predict) a behaviorally relevant stimulus and to ignore stimuli that are uncorrelated with the relevant stimulus; 2) allow sensory systems to tune their response profiles on the basis of the spatiotemporal, statistical regularities of their inputs; 3) allow the formation of stimulus–response chains that translate sensory perception into behavioral output; and 4) allow the storage and retrieval of memories of sequences, a hallmark of episodic memory.

The postulate promulgated by Hebb (1949) that the connection from neuron A to neuron B would be strengthened if neuron A “repeatedly or persistently takes part in firing” neuron B implies a temporal-order rule for spike firing. The synapse from neuron A to neuron B should strengthen only if the firing of neuron A precedes the firing of neuron B; if neurons A and B fired simultaneously or if neuron A fired after neuron B, then neuron A could not have caused neuron B to fire. Hebb further theorized that this postulate would cause groups of neurons to organize into cell assemblies, with recurrent excitatory connections causing the assembly to fire in a coordinated fashion. Finally, when one cell assembly formed and consistently preceded the firing of another cell assembly, the connections from assembly A to assembly B would strengthen selectively, such that the activation of assembly A (by sensory input, for example) could cause the subsequent activation of assembly B (which could activate assembly C, and so on) with no further external input necessary to drive the system. Hebb called this sequential activation of cell assemblies a “phase sequence.”

Subsequent discovery of the phenomenon of long-term potentiation (LTP) has led support to these notions (Bliss and Lømo 1973). In particular, the discovery that activity of the presynaptic cell must precede the activity of the postsynaptic cell to produce LTP demonstrated the causal nature of the synaptic potentiation (Levy and Steward 1983). More recently, the phenomenon of spike-timing–dependent plasticity (STDP), in which pairs of pre- and postsynaptic spikes can cause LTP or LTD (long-term depression), depending on whether the presynaptic or postsynaptic spike occurred first, respectively (Bi and Poo 1998; Markram et al. 1997), further strengthened the notion that the sequential order of neuronal firing can be reflected in the pattern of weights stored in the synaptic matrix of the network.

Numerous models have utilized the temporally asymmetric nature of LTP induction to create representations of neuronal sequences to solve various temporal-sequence–dependent tasks. Levy (1989, 1996) used such rules to solve hippocampus-related tasks such as Pavlovian trace conditioning and spatial path disambiguation. Blum and Abbott (1996) used temporally asymmetric LTP in a model of Morris water-maze learning, in which the learning rule created a representation in which learned paths toward the escape platform were encoded in the synaptic weight matrix of a network of hippocampal place cells. The model of Blum and Abbott made the strong prediction that, if an animal made repeated trajectories along a stereotyped path, the place fields of the neurons would shift backward (in the direction opposite to the animal's motion) as the result of the asymmetric LTP induction. This prediction was confirmed experimentally by Mehta and colleagues (1997, 2000), who showed that the center of mass (COM) of place fields shifted backward and the shape of the place field could become negatively skewed, under some conditions, as a rat ran repeated laps on a narrow track. A subsequent study demonstrated that the backward shift depended on N-methyl-d-aspartate receptors (NMDARs) (Ekstrom et al. 2001). A firing-rate model of STDP was able to capture both the asymmetric changes of the weight distribution onto the postsynaptic cell and the asymmetric expansion of the output (i.e., the place field) of the cell (Mehta et al. 2000). Yu et al. (2006) subsequently demonstrated that an integrate-and-fire network model could also show the backward-shift phenomenon.

STDP is one of many induction protocols that cause NMDAR-dependent changes in synaptic strength, and the above-discussed models used a learning rule that explicitly simulated variants of this one induction protocol. Different learning rules describe other forms of LTP/LTD induction (e.g., 100-Hz stimulation, 1-Hz stimulation, and theta-burst stimulation; Bliss and Lømo 1973; Dudek and Bear 1992; Larson et al. 1986), and a complete account of plasticity at these synapses requires a rule (or set of rules) that incorporates all these known forms of plasticity induction. Shouval and colleagues (2002) proposed a biophysical model that uses postsynaptic Ca²⁺ concentration as a signal that can account for all of these different forms of plasticity. The calcium-dependent plasticity (CaDP) model replicated the effects of tetanic stimulation, low-frequency stimulation, theta-burst stimulation, and STDP. Moreover, it made a novel prediction that there were actually two regions of LTD in the STDP curve, not just one, because postsynaptic spikes that occurred at a long interval after a presynaptic spike actually caused LTD. This prediction has been confirmed experimentally in at least some synapses (Nishiyama et al. 2000; Wittenberg and Wang 2006). An additional consequence of the CaDP model is that STDP plasticity curves are frequency dependent (Shouval et al. 2002), as observed experimentally (Markram et al. 1997; Sjostrom et al. 2001).

The CaDP model, in combination with a model of metaplasticity, is able to reproduce the experience-dependent formation of selective receptive fields, as found experimentally in visual cortex (Yeung et al. 2004). The purpose of the present study was to determine whether this model could also reproduce the backward-shift effect of hippocampal place cells—a phenomenon and system it was not designed to address. We found that the CaDP model, with no substantial changes from previous work on visual cortex, could indeed reproduce the backward-shift effect of place fields. Moreover, the model solved a problem of previous place-field shift models, in that the dynamics of the model significantly slowed down the backward shift after a number of laps, in agreement with experimental data, rather than allowing the shift to continue indefinitely.

METHODS

Model structure

A feedforward model was constructed with 1,000 input cells (the input layer) and one output cell receiving weighted inputs from the input layer (Fig. 1A ). All of the input cells had identical, nonplastic, Gaussian place fields and the centers of these place fields were evenly distributed along a circular track with a circumference of 2 m. During all the simulations presented here, the rat ran around the track at a constant speed of 0.5 m/s. We have varied this speed within the range of 0.25–1 m/s and found no qualitative change in the shifting of place fields. The width (at half-maximum) of the input place fields was set at 0.3 m, which was derived from empirical data (Lee et al. 2004; Mehta et al. 1997, 2000) and had been used in our previous model (Yu et al. 2006). The place field's magnitude at a given location determined the probability that the respective input cell would generate a spike

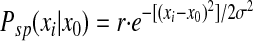(1)

where r is a scaling factor that controls the firing rate of input cells (set so that the maximal input firing rate was 10 Hz; Lee et al. 2004), x₀ is the center of the place field, x_i is the current position of the rat, and σ determines the width of the place field (full width at half-height = 2.355σ). Total synaptic input to the postsynaptic cell was generated randomly by

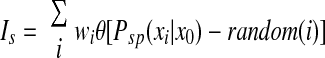(2)

where w_i is the synaptic weight from input cell I, random(i) is generated independently for each input by a uniform random generator between 0 and 1, and θ is the Heaviside function, which has the value 0 if its argument is <0 and 1 if its argument is >0. The current is given in milliamperes and the synaptic weights (w_i) are given directly in units of current.

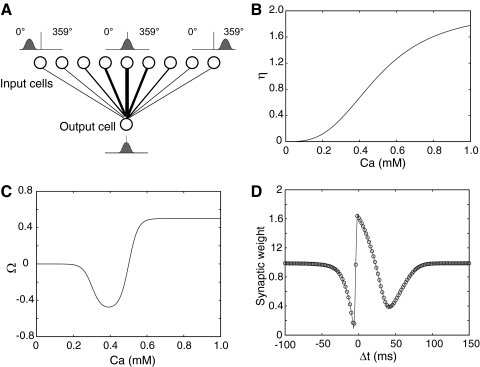
FIG. 1.

Model structure and calcium-dependent plasticity (CaDP) learning rule (Shouval et al. 2002; Yeung et al. 2004). A: the feedforward model consisted of 1,000 presynaptic cells (only 9 cells illustrated here) and a single postsynaptic output cell. The output cell received weighted inputs from every input cell. The centers of the place fields of the input neurons were evenly distributed along a circular track (2-m circumference), which is graphically illustrated here as a straight line, for simplicity, with 360 discrete, 1° bins. The lines between the input layer and the output cell represent synaptic connections and the thickness of the lines indicates the strength of the synaptic weights. B: the [Ca²⁺]-dependent η function that determines the learning rate. The total learning is a product of both the Ω and the η functions. C: the Ω function that determines the direction and amplitude of plasticity. When postsynaptic [Ca²⁺] is low (<0.2 mM), there is no plasticity and the synaptic weight stays at baseline. When [Ca²⁺] is in the middle range (∼0.2–0.5 mM), the synaptic weight is weakened (long-term depression [LTD]). When postsynaptic [Ca²⁺] is high (>0.5 mM), the synaptic weight is strengthened (long-term potentiation [LTP]). D: the spike-timing–dependent plasticity (STDP) curve generated by the CaDP learning with 1-Hz pairing. A presynaptic spike train and a postsynaptic spike train, each at 1 Hz and with a total of 50 spikes, were paired at the time difference specified in the x-axis (Δt >0, presynaptic spike occurred before postsynaptic spike; Δt <0, presynaptic spike occurs after postsynaptic spike). The final synaptic weights were normalized to the baseline level, which is 1.

The output cell is a leaky integrate-and-fire neuron that receives weighted inputs from all of the 1,000 input cells and generates a spike once the membrane potential (V) crosses the firing threshold (−50 mV)

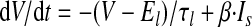(3)

where V is the membrane potential; E_l is the leak current equilibrium potential (−60 mV); τ_l is the time constant for this leak current (25 ms; Song et al. 2000); I_s is the synaptic input current; and β, in units of Ω/ms, is a scaling factor that controls the total synaptic input level to ensure that the peak firing rate of the output cell is in the frequency range of 10–100 Hz found in the experiments (Lee et al. 2004; Mehta et al. 2000). If V reaches the firing threshold of −50 mV, a postsynaptic spike is generated and a back-propagating action potential BPAP(t) is inserted with a total amplitude of 100 mV; 75% of this value decays rapidly (τ_f^B = 3 ms) and the remainder decays slowly (τ_s^B = 25 ms). The BPAP is an important component of this model, in that it controls the amount of calcium that flows into the spine (Shouval et al. 2002).

CaDP learning rule

The synaptic weights are plastic and subject to the CaDP learning rule (Shouval et al. 2002; Yeung et al. 2004), in which postsynaptic [Ca²⁺] determines synaptic plasticity. Synaptic weights are updated as

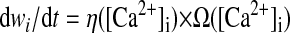(4)

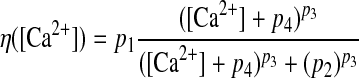(5)

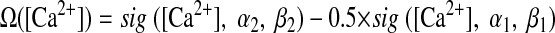(6)

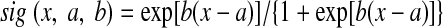(7)

where η([Ca²⁺]) is a calcium-dependent learning rate (Fig. 1B) and Ω([Ca²⁺]) is a U-shaped function of calcium that determines the direction and amplitude of plasticity (Fig. 1C). Equations 5–7 define the functional form of η and Ω (Fig. 1, B and C), with the parameters (p₁, p₂, p₃, p₄) = (2, 0.5, 3, 0.00001) and (α₁, β₁, α₂, β₂) = (0.3, 40, 0.5, 40).

The STDP curve generated by the CaDP model at 1-Hz pairing is shown in Fig. 1D. Different from the “standard” STDP curve described in previous experimental and modeling papers (Bi and Poo 1998; Song et al. 2000; Yu et al. 2006), this STDP curve has a second LTD window in the pre-post region (Δt >0) that peaks around +40 ms. The existence of this second LTD window is supported by recent reports in hippocampal slice studies (Nishiyama et al. 2000; Wittenberg and Wang 2006) and has an important impact on the present results (see following text).

Calcium influx

The local NMDAR-mediated calcium concentration follows a first-order linear differential equation

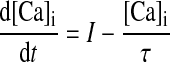(8)

where I is the NMDAR calcium current and τ = 20 ms is the calcium passive decay time constant (Markram et al. 1995; Sabatini et al. 2002). The current I depends on the association between presynaptic spike times and the postsynaptic depolarization level as I = g_mf(t, t_pre)H(V), where f describes the dynamics of the glutamate–receptor interaction, H describes the voltage-dependent magnesium block of the NMDAR, and g_m determines the NMDAR conductance. If we measure calcium concentration in micromoles (μM), then the units of g_m are in μM/(ms mV). However, it is best to view the calcium concentration as a unitless, phenomenological variable. On a presynaptic spike, f reaches its peak value of 1, and then 70% of this value decays with a fast time constant (τ_f^N = 50 ms), and the remainder decays with a slower time constant (τ_s^N = 200 ms). H describes the voltage dependence of the NMDAR (Jahr and Stevens, 1990).

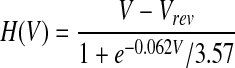(9)

with a reversal potential for calcium V_rev = 130 mV. The contribution of the local depolarization to the H-function is negligible compared with the contribution of the BPAP, so here we use V = V_rest + BPAP(t).

Metaplasticity

Like other Hebbian-type plasticity rules, the CaDP rule by itself is not stable. Metaplasticity is a homeostatic mechanism that has been used with the CaDP model to regulate membrane activity (Yeung et al. 2004). Metaplasticity controls postsynaptic calcium, and thereby the activity level of the postsynaptic neuron, through a slow, activity-dependent regulation of NMDAR conductance (g_m). Metaplasticity is implemented through a voltage-dependent kinetic model of NMDAR insertion and removal

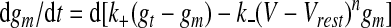(10)

where the total NMDAR conductance, g_t (−3 × 10⁻³), sets the upper limit on g_m; k₊ (8 × 10⁻⁵) is the insertion rate; k₋(V − V_rest)ⁿ is the removal rate (k₋ = 8 × 10⁻⁷); n = 2 is an exponent; and d is a factor controlling the rate of metaplasticity (Yeung et al. 2004). Units for k₊ are [1/ms] and for k₋ are [1/ms mV²]. There are significant experimental indications that, in cortex, reduced activity increases the time constant of NMDARs and increased activity reduces this time constant (Carmignoto and Vicini 1992; Philpot et al. 2001; Quinlan et al. 1999; Rao and Craig 1997). This type of change is qualitatively similar to the rule assumed here, in that there is a negative feedback of the total charge influx through NMDARs. There are also indications that changing the activity levels in culture can cause a change in the total number of NMDARs (Watt et al. 2000).

Initial conditions

Initially the output neuron is connected to the input neurons by a Gaussian function such that the output cell initially forms a place field. Each input place cell is defined by its own central location, x₀, which is different for each input cell. For the output cell, we define its center as location j in the input space and, using this notation, the initial weights w_i are connected according to the rule

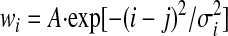(11)

where the normalization factor was set to obtain a peak output firing rate of 10 Hz. The model results are not sensitive to the exact details of the starting conditions and place fields can develop even if the initial weights are random (see results).

RESULTS

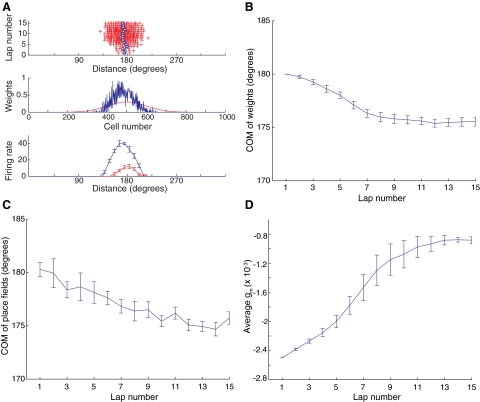
The model assumes a simple architecture of a single hippocampal cell that receives input from an array of place fields (Fig. 1A). The place fields are arranged on a circular track, which is linearized in discrete, 1° bins from 0 to 359° in Fig. 1A. Initial connections between the input and output cells were typically set as a smooth Gaussian, producing an output cell with a localized place field. In simulations, as the animal moves along the track, a CaDP rule modifies the synaptic connections between the input cells and the simulated hippocampal cell. These simulations replicate the backward shift of hippocampal place fields. Figure 2 A (top) shows the locations on the track where spikes were fired by the output neuron for a single run on the model in which 15 laps were simulated. Each cross corresponds to a single spike and the blue circles denote the center of mass (COM) of the spikes for each lap. After some initial forward and backward shifts over the first four laps, when the firing was relatively weak and subject to stochastic fluctuation in spiking, the firing grew stronger and shifted back steadily in laps 5–8 before stabilizing. The middle graph plots the initial (red) and final (blue) values of the synaptic weights from the input cells onto the output neuron. The initial weights formed a Gaussian distribution, but after 15 laps, the weights were stronger, more sharply distributed, and shifted backward from the initial distribution. The weight vector was depressed or “trimmed” on the right shoulder because the corresponding input cells on average fired later than the output cell and therefore received LTD due to the first LTD window in the STDP curve (Fig. 1D). The weight vector was also trimmed on the left shoulder because these input cells fired earlier than the output cell with timing that, on average, fell into the second LTD window of the STDP curve. Because the weight vector was trimmed on both shoulders due to LTD and grew only near the middle (biased toward the left) due to LTP, the total weight vector was sharpened while shifting backward.

FIG. 2.

Backward shift of synaptic weight distribution and place field of the output cell. A, top: raster plots of spikes generated by the output cell in each lap. The blue circles indicate the center of mass (COM) for each lap. Middle: the synaptic weight before (red) and after (blue) the model ran 15 laps. The synaptic weight vector was initially Gaussian and centered in the middle of the track, but it shifted backward and became more sharply tuned after 15 laps. Bottom: shows that the place field of the output cell shifted backward and the peak firing rate grew after 15 laps. Because the spiking in the model was a stochastic process, the initial and end-place fields were averaged over 10 different runs with corresponding weight vectors fixed to the values obtained at the start and end of the 15 training laps, respectively (error bars denote the SEs). B: average backward shifts of the synaptic weight vector over 10 different simulations. Note the fast shifts at the beginning and the slow shifts toward the end. C: average backward shifts of the COM of the place field over 10 different simulations. Due to stochasticity in the model, the curve is noisier than that of the weight vector and the trend is less clear. D: average N-methyl-d-aspartate receptor (NMDAR) conductance over 10 different simulations. The growth of the firing rates in the output neuron caused the decrease (in absolute value) of NMDAR conductance.

In experiments, place fields are not measured in terms of their synaptic weights, but in terms of the firing patterns of the place cell. The bottom graph of Fig. 2A shows the mean shape of the simulated place fields, averaged over 10 runs of the simulation, at the first (red) and last (blue) laps. The place fields show a strong strengthening and asymmetric expansion in the direction opposite to the rat's travel (i.e., backward), in agreement with the physiological data (Ekstrom et al. 2001; Lee et al. 2004; Mehta et al. 1997, 2000; Yu et al. 2006). On average, the COM of the distribution of synaptic weights onto the output cell began to shift backward from the very start of the simulation (between laps 1 and 2) before apparently reaching asymptote around laps 7 and 8 (Fig. 2B). Similarly, the COM of the place fields, on average, also shifted backward from the beginning of the simulation (Fig. 2C).

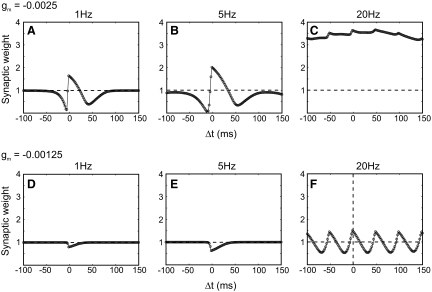
Concomitant with the asymmetric strengthening of the synaptic weights onto the output cell was a decrease in the NMDAR conductance (Fig. 2D), as the result of the increased firing of the postsynaptic cell. This homeostatic mechanism, which was previously incorporated into the CaDP model to rein in runaway plasticity (Yeung et al. 2004), was also the reason that the backward shift slowed down significantly. The CaDP model at low frequencies acts like a causal STDP rule and causes the backward shift of place fields, as described earlier. However, as observed experimentally, causality matters less at high frequencies and plasticity is controlled primarily by the pre- and postsynaptic firing rates (Shouval et al. 2002; Sjostrom et al. 2001). This loss of causality is demonstrated in Fig. 3, A–C, which shows the STDP curves produced by the model at a constant NMDAR conductance level of g_m = −0.0025. Without metaplasticity, increases in postsynaptic firing rate (Fig. 3C) would have eliminated the backward shift. That is, all spike-time pairings would have induced LTP and no LTD, resulting in a symmetric expansion of the place field in both directions. However, due to the metaplasticity mechanism in the model (Fig. 2D), the NMDAR conductance is decreased as the firing rate increases (to g_m ≈ −0.00125). In Fig. 3, D–F, we show the resulting STDP curves at this new conductance level. At low frequencies no LTP is observed and only a slight LTD remains, whereas at 20 Hz significant bidirectional plasticity remains, but without the sharp transition at Δt = 0. The reduced plasticity at low frequencies and the reduced asymmetry at higher frequencies eliminate the place-field expansion as the firing rates increase and critically slow down the backward shift.

FIG. 3.

Effect of variation in spike frequency and NMDAR conductance on the STDP curves generated by the CaDP learning rule. A–C: when the NMDAR conductance (g_m) is high (−0.0025) and spike-pair frequency is low (1 or 5 Hz), the STDP curve has both spike-timing–dependent LTP and LTD regions. At a high pairing rate (20 Hz), there is only LTP and STDP is almost lost. (Multiple peaks occur at 20 Hz because of the periodicity of the high rate of stimulation.) The dashed line denotes the baseline. D–F: when the NMDAR conductance (g_m) is low (−0.00125) and the spike-pair frequency is low (1 or 5 Hz), there is only LTD, which accounts for the continuous depression of the “shoulders” of the weight vector (compare Figs. 2A and 4A). At high pairing frequency (20 Hz), there are both LTP and LTD regions. However, the STDP curve under these conditions becomes more symmetric around the Δt = 0 time point, compared with the standard STDP curve (high g_m, low firing rate). Combined with smaller LTP and LTD peaks, the STDP becomes much weaker. As the firing rate grows even higher (40 Hz), the STDP will continue this trend and eventually be eliminated (not shown).

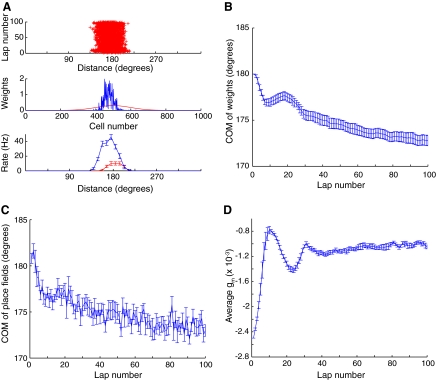
To demonstrate the dynamic interactions between the homeostatic mechanisms and the backward shift, the simulations were allowed to run for 100 laps (Fig. 4). The synaptic weight distribution sharpened considerably between laps 1 and 100 and the place field became stronger and shifted backward (Fig. 4A). Figure 4B shows that the COM of the weight distribution shifted backward rapidly over the first 7 to 8 laps, and then gradually shifted forward again for the next 12 laps, before resuming a more gradual backward shift that slowed down in the later laps. Similarly, the COM of the place field shifted back rapidly, then shifted forward gradually for a number of laps, before resuming a more gradual backward shift. Interestingly, the original report of the backward shift by Mehta et al. (1997; see Fig. 2B of that paper) demonstrated such a transient, forward shift in the COM in the later laps of the 17 laps recorded in that experiment. The reason for the reversals in direction of change of the weight distribution was the different time courses of the STDP (w_ij) and the homeostatic plasticity (g_m). Initially, the STDP caused the weights to change in a way that produced the backward shift. As the firing rates increased, the magnitude of g_m decreased until it eventually put a brake on the increase in firing (Fig. 4D). At this point, g_m began to increase and, since the firing rate was already high, the STDP curve favored a forward shift of the weights. Eventually, g_m reached a stable level around lap 35 and the model parameters were such that the synaptic weight changes reached a steady state with few overall changes to the distribution thereafter.

FIG. 4.

Model stability. This figure is plotted as in Fig. 2 except that the model was run with 100 instead of 15 laps. Note that although the rate of change is critically slowed down in later iterations, a slow gradual shift continues throughout the simulation. Such a small shift might be hard to detect experimentally. Although the place field continues to shift, its overall shape, magnitude and width are similar to the place field after 15 iterations (Fig. 2A). Note that significant oscillations are observed during these long runs because of the different time constants of fast STDP and slow metaplasticity.

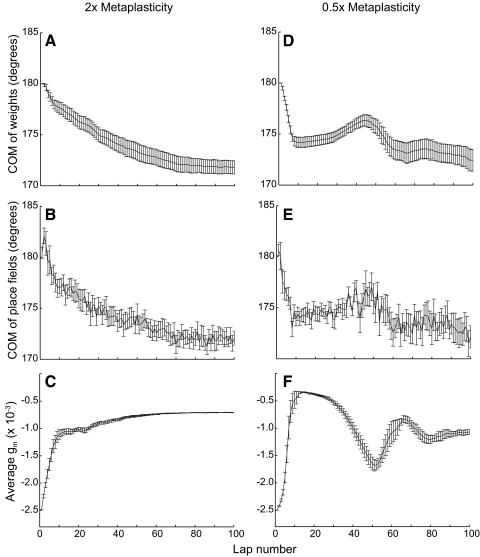
It is interesting to note that the reversals in the direction of the COM shift (Fig. 4B) coincided with the oscillations in the magnitude of the NMDAR conductance (Fig. 4D). To demonstrate that the changes in these two variables are related and to demonstrate that the overall behavior of this model is robust, we varied the metaplasticity parameters. We altered the rate of metaplasticity by simultaneously multiplying both k₊ and k₋ by a factor of 2 or 0.5 (Fig. 5). This manipulation did not change the possible dynamical fixed points and thus the basic trend of a backward shift was similar to that of Fig. 4. However, the dynamical rate of change to g_m was significantly altered and so were the resulting dynamics of the shift. For the faster dynamics (Fig. 5, A–C) the oscillations of g_m were eliminated, as were the reversals in the directions of the shift. For the slower dynamics (Fig. 5, D–F) the oscillations of g_m were increased, as were the oscillations in the directions of shift. In addition to showing how the place-field dynamics depend on the parameters of metaplasticity, these results demonstrate that the performance of the model is qualitatively robust over a large parameter range. Therefore although the precise system dynamics (and specifically the oscillations) depend on the details of the metaplasticity model and even on its parameters, the basic phenomenon—the slowdown of the backward shift—is independent of the specific parameters and, possibly, even independent of the precise formulation of metaplasticity, as long as a negative feedback is produced through the regulation of plasticity.

FIG. 5.

A change in the parameters of metaplasticity does not alter the basic trend of backward shifts. When the k₊ and k₋ (NMDA receptor insertion and removal rate constants) used in metaplasticity were changed to 2× (A–C) or 0.5× (D–F) of the original value, the basic trend of backward shifts remained the same. The most significant change was the amplitude of oscillation (compare A to D) because the manipulation changed the time constant of metaplasticity.

To test how sensitive the model is to other parameters, we independently varied some of the important parameters of CaDP and observed whether such manipulations significantly changed the performance of the model. Table 1 shows the range of these parameters within which the model behaved similarly to that shown in Figs. 2 and 4. Changes in total NMDAR conductance or in the shapes of the η curve and the Ω curve (Fig. 1) did not qualitatively alter the results (data not shown). The speed of metaplasticity was characterized by the parameter d, which multiplies both k₊ and k₋ and therefore changes the convergence rate of metaplasticity (normally d = 1). We found that d can range from 0.25 to 4 without qualitatively changing the simulation results.

TABLE 1.

Sensitivity of the model to some important parameters

Parameter	gt	α2	p1	p2	d	β1, β2
Function	Total NMDAR conductance	LTP threshold	Learning rate	Learning rate	Metaplasticity	Ω function
Tested range	2.5–4.5 × 10−3	0.45–0.65	1–5	0.5–0.6	0.25–4	20–80

The input rate throughout these simulations was set with a peak of 10 Hz. We tested whether the model was sensitive to changes in the input firing rates. As the input rate increased, so did the stable output rate and, for moderate increases in input rates, the shift in place field location was maintained. However, for a large increase in the input rate (40 Hz, with the standard parameters; data not shown) there was no longer a shift, although there was still a plasticity-dependent change in the shape of the place fields. The dependence of the shift on the input rate is consistent with our discussion about the impact of rates on the shape of spike-timing–dependent plasticity, as illustrated in Fig. 3.

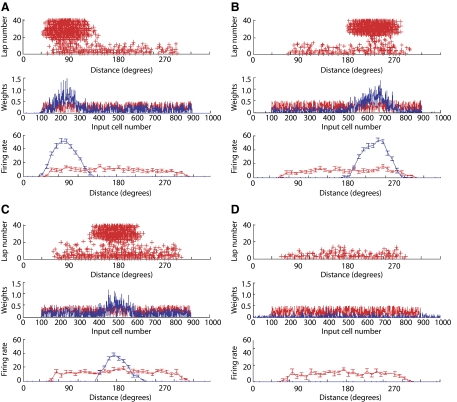
All the simulations described to this point were started from an initially well structured place field of the output neuron (Fig. 1A). However, if simulations are started from a nonstructured place field, this model often generates well-structured place fields. Figure 6 shows the results of 4 different simulation runs in which the initial connections between the input cells and the output cell were random. In three of these simulations, well-structured place fields developed over the course of the simulations and, in one simulation, the development of the place field failed. Overall, structured place fields developed in 16/20 simulation runs. Although in experimental data place fields do not form from such random, nonspecific firing patterns (Frank et al. 2004), the ability to develop structured place fields from a random initial state demonstrates that the model is robust in terms of its relative insensitivity to starting conditions.

FIG. 6.

De novo place field formation. Initial weights were generated randomly (0–0.5) from input cells 100–900. The model was then run for 40 laps with CaDP learning rules. Out of a total of 20 simulations, 16 developed spatial tuning (place fields) at different locations with different shapes and peak amplitudes. Three examples are given here (A–C). In 4 cases the weight vectors eventually “died out” or disappeared after 20–30 laps and an example is given here (D). The conventions are the same as in Figs. 2A and 4A.

DISCUSSION

The backward shift in place fields has been explained by the causal nature of STDP curves, which exhibit a sharp transition between LTD and LTP as a function of the difference between pre- and postsynaptic spike times. Previous simulations using timing-dependent plasticity rules have indeed demonstrated this backward shift (Blum and Abbott 1996; Mehta et al. 2000; Yu et al. 2006). However, because the causal nature of STDP is preserved throughout these simulations, there is no reason that these backward shifts would terminate or even slow down, in the absence of additional mechanisms. The backward shift observed experimentally, however, does slow down and seems to terminate or asymptote (Ekstrom et al. 2001; Lee et al. 2004; Mehta et al. 1997, 2000; Yu et al. 2006). Furthermore, in previous models of the backward shift, plasticity was based on an abstract and frequency-independent model of STDP. The assumption of frequency independence is not consistent with experiments that have shown that the STDP curves are frequency dependent (Markram et al. 1997; Sjostrom et al. 2001) and that at high frequencies LTP dominates. Previous papers have described calcium-dependent plasticity rules that can account for various induction protocols, including the frequency dependence of STDP (Abarbanel et al. 2003; Rubin et al. 2005; Shouval et al. 2002). When such plasticity rules are coupled with metaplasticity, they can produce selective receptive fields (Yeung et al. 2004).

In this study we use the CaDP model of synaptic plasticity in combination with a model of metaplasticity, a combination that was previously used to simulate receptive field plasticity in visual cortex (Yeung et al. 2004). Here we applied this combination to simulations of place field plasticity in the hippocampus. The results showed a robust backward shift in the place field COM, accompanied by an increase in firing rates, as observed experimentally (Lee et al. 2004; Mehta et al. 1997; Yu et al. 2006). We also find that this backward shift of the place field COM critically slows down as a result of metaplasticity. We have obtained these results without assuming any additional stopping mechanisms, by simply applying a model previously developed to account for visual cortex plasticity to simulations of place field plasticity. The general trends in these simulations—such as backward shifts, increase in firing rates, sharpening of place fields, and termination of shift—are robust to significant parameter changes. For some parameters, the results exhibit damped oscillations in the place field locations that are coupled to oscillations in the value of the NMDAR conductance. Such oscillations may also be present in some experimental results (see Fig. 2B of Mehta et al. 1997), but they are not a robust prediction of our model, since they are parameter dependent. Nonetheless, damped oscillations are characteristic of many coupled systems of dynamical equations; for example, they are exhibited in the BCM (Bienenstock–Cooper–Munro; Bienenstock et al. 1982) rule when the time constant of the sliding modification threshold is significantly slower than the plasticity time constants (Cooper et al. 2004).

Although the CaDP model produces a robust backward shift in the place field COM, we do not find the emergence of a significant negative skew in the shape of the place fields. Indeed, the development of a negative skew is experimentally variable as well, seemingly dependent on a number of parameters such as the brain region and perhaps the nature of the experimental task (Huxter et al. 2003; Lee et al. 2004; Mehta et al. 1997, 2000; Yu et al. 2006), as well as on the precise definitions of the place-field boundaries (Mehta et al. 2000). For example, Lee et al. (2004) reported the development of negative skewness in CA3 place fields but not in simultaneously recorded CA1 place fields. The second LTD region present in the deterministic CaDP model at positive Δt (Fig. 1D) likely results in a trimming of the left-hand flank of the place field as the shift develops. Therefore the second LTD window is a likely factor preventing the emergence of a negative skew in the model. If the second LTD window were not present, or if it were significantly smaller, a greater negative skew might develop, as shown in previous models using a standard STDP curve with a single LTD window (Mehta et al. 2000; Yu et al. 2006). It has been previously shown that stochastic synaptic transmission (Shouval and Kalantzis 2005) or an additional veto mechanism (Rubin et al. 2005) can reduce or eliminate the second LTD window in a calcium-dependent model. Including stochastic synaptic transmission or a veto mechanism is therefore likely to result in the emergence of a negative skew, but stochasticity or additional veto mechanisms are beyond the scope of this paper. Nonetheless, these considerations suggest that the development of negative skewness in place fields may be related to the conditions under which a second region of LTD is present physiologically in the STDP curve.

Although the general trends in this model are robust, the precise dynamics of individual simulations are very different. The variability between the dynamics of individual simulations depends on the precise system parameters, the initial conditions, and the randomness of specific simulations. Such variability of the dynamics of place-field shifts is also observed experimentally. For example, Lee and Knierim (2007) showed that, although at a population level there may be a consistent backward trend in COM shifts in CA3 or CA1, there is a large amount of variability at the single-neuron level. Some place fields can shift forward, others can shift backward, and others remain stable. Interestingly, there appears to be a greater coherence of shifting in the place fields of CA3 cells and in the tuning curves of head direction cells compared with the place fields of CA1 cells, which may reflect the influence of network dynamics of the two former regions forcing a more coherent population response to the variable synaptic changes occurring at the single-cell level (Lee et al. 2004; Yu et al. 2006).

Metaplasticity is an experience-dependent change in synaptic plasticity (Abraham and Bear 1996) and various forms of metaplasticity have been observed experimentally. An appropriate choice of a metaplasticity model (Yeung et al. 2004) can serve as a negative feedback mechanism that is similar to the sliding threshold of the BCM rule (Bienenstock et al. 1982). Such a metaplasticity mechanism is also able to account for some forms of synaptic scaling (Turrigiano 1999; Yeung et al. 2004). The form of metaplasticity used here, adopted from Yeung et al. (2004), was implemented as a voltage-dependent change in the NMDAR conductance. There is evidence that properties of NMDAR conductance are activity dependent (Bellone and Nicoll 2007; Carmignoto and Vicini 1992; Philpot et al. 2001) and these changes may contribute to metaplasticity. However, a similar negative feedback could be implemented by other specific mechanisms as well, such as activity-dependent changes in calcium buffer concentration or spine shape, and these different mechanisms are likely to produce qualitatively similar results.

In summary, the present study adopted a model of synaptic plasticity that was originally derived and tested against visual cortex data (Yeung et al. 2004) and applied the model to the phenomenon of the asymmetric expansion of hippocampal place fields. With no significant changes in parameters, the model was able to replicate the backward shift of place fields. Moreover, the combination of CaDP and metaplasticity automatically solved a problem with previous models (Mehta et al. 2000; Yu et al. 2006) by causing the backward shifting to slow down after a number of laps, consistent with the experimental data. Similar receptive field shifts occur in visual cortex (Fu et al. 2002; Yao and Dan 2001) and hippocampus (Ekstrom et al. 2001; Lee et al. 2004; Mehta et al. 1997, 2000; Yu et al. 2006) as the result of appropriate spike-timing manipulations. Because the CaDP model can account for physiological data from both in vitro and in vivo preparations, it may capture the essence of a general cortical mechanism of synaptic plasticity (Shouval et al. 2002).

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke Grant P01 NS-038310.