Privileged Coding of Convex Shapes in Human Object-Selective Cortex

Abstract

What is the neural code for object shape? Despite intensive research, the precise nature of object representations in high-level visual cortex remains elusive. Here we use functional magnetic resonance imaging (fMRI) to show that convex shapes are encoded in a privileged fashion by human lateral occipital complex (LOC), a region that has been implicated in object recognition. On each trial, two convex or two concave shapes that were either identical or different were presented sequentially. Critically, the convex and concave stimuli were the same except for a binocular disparity change that reversed the figure–ground assignment. The fMRI response in LOC for convex stimuli was higher for different than that for identical shape pairs, indicating sensitivity to differences in convex shape. However, when the same stimuli were seen as concave, the response for different and identical pairs was the same, indicating lower sensitivity to changes in concave shape than convex shape. This pattern was more pronounced in the anterior than that in the posterior portion of LOC. These results suggest that convex contours could be important elements in cortical object representations.

INTRODUCTION

A central challenge of visual neuroscience is to determine the neural code for object shape. It is widely thought that visual processing occurs in a hierarchy along the occipital and temporal lobe: cells in the primary visual cortex (V1) respond preferentially to simple features such as oriented lines (Hubel and Wiesel 1959), whereas neurons in higher stages of the hierarchy, including V2 and V4, respond selectively to more complex stimuli such as oriented contour segments (Pasupathy and Connor 1999) or Cartesian, hyperbolic, and radial gratings (Gallant et al. 1992). However, half a century after Hubel and Wiesel's seminal studies, it remains unknown exactly how objects are represented in the highest, object-selective stages of this hierarchy, such as inferotemporal cortex (IT) in monkeys (Tanaka et al. 1991) and lateral occipital complex (LOC) in humans (Malach et al. 1995).

What is encoded in these regions? Previous work has suggested roles for a variety of stimuli and features: real-world objects such as hands or faces (Desimone et al. 1984; Perrett et al. 1979, 1982; Tsao et al. 2006); combinations of complex shapes (Tanaka et al. 1991); intuitive object parts (Hayworth and Biederman 2006); nonaccidental features (Kayaert et al. 2003); and simple shape dimensions such as taper and axis curvature (Kayaert et al. 2005). Here we test the hypothesis that convex shapes are encoded in a privileged fashion in high-level visual cortex; specifically, that LOC is more sensitive to changes in convex than in concave shapes.

This hypothesis is motivated by both theoretical and psychophysical studies. First, a number of theories of object recognition suggest that human observers encode shapes in terms of their constituent “parts” (Biederman 1987; Hoffman and Richards 1984; Kimia et al. 1995; Marr and Nishihara 1979). Parts, in turn, usually coincide with convex maxima of the shape contour (Hoffman and Richards 1984; Koenderink and van Doorn 1982; Norman et al. 2001; Siddiqi and Kimia 1995). Thus convexities are good candidates for basic units of shape description.

Second, psychophysical studies have shown that convex curvature appears to be processed in a privileged fashion by the human visual system: Rubin (1915) first pointed out that observers favor figure/ground interpretations that emphasize convex projections over concave indentations. Moreover, recognition performance (Biederman 1987; Braunstein et al. 1989; Driver and Baylis 1995) and perceptual judgments of location (Bertamini 2001) and shape similarity (Subirana-Vilanova and Richards 1996) are more accurate for convex than for concave features.

Based on these considerations, we asked whether LOC exhibits higher sensitivity for convex contours than that for concave contours. We used functional magnetic resonance imaging (fMRI) adaptation to measure sensitivity to stimulus differences for convex and concave stimuli. Critically, the convex and concave stimuli were identical except for a binocular disparity change that reversed the figure–ground assignment of the stimulus. We found that LOC is more sensitive to changes in convex than in concave shape. This finding suggests that convex shapes may play a privileged role in the neural representations underlying object recognition.

EXPERIMENT 1: SENSITIVITY TO CONVEX VERSUS CONCAVE SHAPE

Methods

PARTICIPANTS.

Participants were 16 members of the MIT community (10 female, 6 male). All gave informed consent and had normal or corrected-to-normal vision. The fMRI data of 4 participants were excluded either because regions of interest (ROIs) could not be identified in the localizer scans (3) or because of excessive head motion (1). Importantly, these subjects were excluded before analysis of the conditions of interest (convex vs. concave trials).

STIMULI.

Localizer scans.

The lateral occipital complex (LOC) was localized as the region that responded more strongly to grayscale images of intact objects than to images of scrambled objects (P < 10⁻⁶), as described previously (Grill-Spector et al. 1998). The fusiform face area (FFA; Kanwisher et al. 1997) was defined as the region responding more to faces than to objects (P < 10⁻⁶). The parahippocampal place area (PPA; Epstein and Kanwisher 1998) was defined as the region responding more to scenes than to objects (P < 10⁻⁶). The retinotopic ROI was defined based on activation at the occipital pole in a contrast between all stimulus conditions versus baseline in the localizer scans (P < 10⁻⁶; Williams et al. 2007).

Experimental scans.

To match the low-level properties of convex and concave stimuli, we generated displays (1,024 × 768 pixels = 26 × 19°; viewing distance 114 cm) in which a curved contour separated two image regions, both appearing behind a circular aperture (10° diameter; Fig. 1). Displays were rendered stereoscopically (using red/blue glasses) such that the region surrounding the aperture was at −0.2° disparity and thus appeared near. Inside the aperture, the region on one side of the contour was set at 0° disparity and the other side at a far disparity of 0.3°. Thus the region on one side of the contour appeared closer to the viewer and thus as the figure; the region on the other side of the contour appeared farther from the viewer and thus as the background. Because contours are assigned to the figure region (Driver and Baylis 1995), the same display could then be switched between having convex versus concave shape by reversing only the disparity of the two regions (Fig. 1; Driver and Baylis 1995). Throughout, the terms “convex” and “concave” stimuli refer to displays in which the convex or the concave side of the contour, respectively, is seen as in front and thus as a figure. All surfaces were random-dot patterns. The center of the aperture contained a fixation cross. The fixation cross was at −0.2° disparity, like the surface defining the aperture. Thus it “floated” above both the figure and the ground and, crucially, it appeared at the same disparity for the “convex” and “concave” conditions. This matching of fixation across conditions decreases the likelihood of confounds through differential fixation and, in a separate experiment (described in the following text), we confirmed that subjects did actually fixate in all conditions. It is also unlikely that subjects made differential vergence eye movements across the conditions, since nonhuman primate experiments have shown minimal influence of background disparity on vergence during fixation (Cumming and Paker 2000), although in principle this possibility cannot be discounted (Allison et al. 2004). However, even then such vergence effects would be of greater concern in dorsal areas and are likely to have little or no influence on the ventral areas in which we were interested (Culham et al. 1998; Quinlan and Culham 2007).

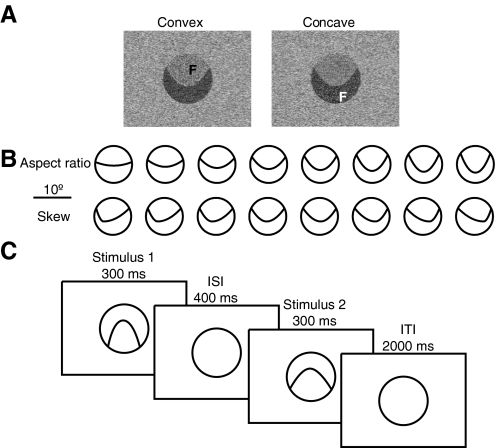
FIG. 1.

A: example of convex and concave stimuli. A curved stereo- and luminance-defined contour separated 2 image regions, both appearing behind a circular aperture. The region on one side of the contour appeared closer to the viewer and thus as the figure (“F”) and the region on the other side of the contour appeared farther from the viewer and thus as the background. The same display could be convex or concave depending on which side of the contour was the figure. B: aspect ratio and skew were parametrically varied. The 2 stimuli on each trial were either identical, or 1, 2, or 4 steps removed from each other in this stimulus space. Each individual stimulus occurred equally often in each of these 4 conditions, so any differences in response between conditions reflect the relationship only between the 2 stimuli in a trial, not the specific stimuli themselves. Orientation (top/bottom of the aperture) and brightness were counterbalanced. C: time sequence for a trial.

Due to the unobstructed view afforded by the custom-built surface coil that we used (see following text), the binocular field of view (i.e., the overlap between the left- and right-eye views) was as large as the display itself (i.e., 26 × 19°). Preexperiment testing showed that all subjects could effortlessly see the depth structure in all parts of the stimuli.

Aspect ratio and skew were varied parametrically in the stimuli. Aspect ratio was defined as width of the contour with respect to its length (and is thus commensurate with “curvature” in the context of these stimuli) and skew as the location of the vertex with respect to the base. Each could assume one of eight possible values (Fig. 1B). Since convex and concave stimuli were identical except for the stereo flip, there was no difference between convex and concave stimuli in terms of aspect ratio or skew.

We fully counterbalanced the low-level properties of the stimuli as follows. First, to counterbalance stereo, the figure region was always at 0° disparity and the background region was always at a far disparity of 0.3°; thus the “convex” side of the contour appeared at 0° disparity on half of the trials and at 0.3° disparity on the other half of trials. Similarly, the “concave” side of the contour appeared at 0° disparity on half of trials and at 0.3° disparity on the other half of trials. Thus neither convex nor concave stimuli appeared at different average disparities.

Second, the figure region appeared in the upper part of the display for half of the convex stimuli and in the lower part for the other half of convex stimuli; similarly, the figure region appeared in the upper part of the display for half of the concave stimuli and in the lower part for half of the concave stimuli. This counterbalancing rules out any effects of orientation.

Third, the mean luminance of the surface defining the aperture was 50% and that of the two image regions (figure and ground) were 40 and 60%. To fully counterbalance luminance, the figure region was at 40% luminance for half of the convex trials and at 60% luminance for the other half of the convex trials; similarly, the figure region was at 40% luminance for half of the concave trials and at 60% luminance for the other half of the concave trials. Thus luminance was fully counterbalanced across convex and concave stimuli.

Finally, we sought to exclude any possible effects of surface area. If, for instance, the surface area and therefore the onset transient of a convex stimulus were larger than that of a concave stimulus, this difference might confound some of our findings. For this reason the contour divided the aperture in two exactly identical subregions in terms of area; thus the surface area of the “concave” side of the contour was the same as the surface area of the “convex” side of the contour. This control also rules out any confounds from the fact that the random-dot pattern changed in the figure region when the figure came on, but not in the ground region.

PROCEDURE.

To assess neural sensitivity to convex and concave stimuli in object-selective brain regions, we used event-related fMRI adaptation in humans (Kourtzi and Kanwisher 2001). In this paradigm, a higher response to two successively presented different stimuli than to successively presented identical stimuli indicates sensitivity to that stimulus difference. Adaptation can therefore provide a measure of sensitivity to a given stimulus dimension: if a cortical region is sensitive to a particular stimulus dimension (e.g., contour curvature), a stimulus change in this dimension leads to a higher response than no change; conversely, if the region is insensitive to that dimension, no increase in response is observed to the “identical” case. This paradigm is thus well suited to address our question: is LOC sensitive to changes in contour curvature? In particular, does this sensitivity differ when the same contour is seen as convex versus concave?

Because effect sizes in event-related fMRI studies are typically small, the adaptation method is most useful when tested in an independently defined region of interest. Here we focused on the lateral occipital complex (LOC), a cortical region that has been implicated in object recognition (Grill-Spector et al. 2000) and in the representation of object shape (Malach et al. 1995). This region has been further divided into a posterior region (often termed LO) and an anterior region at the posterior end of the fusiform gyrus (pFs) (Grill-Spector et al. 2001; Hayworth and Biederman 2006).

Each participant was run in one session of about 2 h, consisting of eight experimental scans and three to four LOC localizer scans. Stimuli were presented using the Psychophysics Toolbox (Brainard 1997) and Matlab (The MathWorks, Natick, MA).

The localizer scans were run as described previously (Grill-Spector et al. 1998). The experimental scans were event related and each scan contained 64 stimulus trials and 24 fixation trials. The near surround and the far background of the aperture were continuously present. On each stimulus trial we presented two “figures” at 0° disparity against the far-disparity background, for 300 ms each, with an interstimulus interval (ISI) of 400 ms and an intertrial interval (ITI) of 2 s (Fig. 1C). Both stimuli on each trial had the same orientation, lightness, and were both concave or both convex. The stimulus pairs on each trial were either identical or differed from each other in either aspect ratio or skew in steps of one, two, or four units of aspect ratio or skew (Fig. 1B). Thus we used one “identical” condition and three “different” conditions, for both the convex and the concave conditions. Each condition appeared 16 times in one run, for a total of 128 times during the entire experiment.

The space of eight stimuli (for each aspect ratio and skew) was assigned to the conditions as follows. In the identical condition, each stimulus was used twice per run (i.e., each run contained two trials on which, say, stimulus 1 was repeated). In each of the one-, two-, and four-step conditions, each stimulus also appeared twice per run: once as the first stimulus of the pair, once as the second. For the one-step condition, the possible stimulus pairs used were as follows: (1, 2), (3, 4), (5, 6), (7, 8) and the same pairs in reverse order; for the two-step condition, the stimulus pairs were (1, 3), (2, 4), (5, 7), (6, 8), plus reversal; for the four-step condition, the pairs were (1, 5), (2, 6), (3, 7), (4, 8), plus reversal.

Thus each individual stimulus appeared equally often in each of the four conditions, and equally often as the first and as the second stimulus in a trial. Within each scan, the lightness (light/dark) and polarity (convex/concave) of all figures was the same; also, within each scan the figures varied either only in aspect ratio or only in skew. The orientation of the figure varied randomly across trials.

Subjects performed a same-different task in the scanner: they were required to press one of two buttons when the two shapes in a trial were identical and the other button if they were different. The mapping of the responses to the buttons was counterbalanced across subjects, such that half of subjects responded “left-same/right-different,” whereas the other half of subjects responded “left-different/right-same.”

FUNCTIONAL IMAGING.

fMRI scanning was performed on a 3T Siemens Trio Scanner (Siemens, Erlangen, Germany) at the MGH/MIT/HMS Athinoula A. Martinos Center for Biomedical Imaging (Charlestown, MA). A gradient echo single-shot pulse sequence was used (experimental scans: TR = 1.5 s; localizer scans: TR = 2 s; TE = 30 ms). Twenty-five slices were collected with a custom-built eight-channel phased array surface coil. Slices were oriented roughly perpendicular to the calcarine sulcus and covered most of the occipital and posterior temporal lobes, as well as some of the inferior parietal lobes. Slices were 3 mm thick, with a 10% gap, and had an in-plane resolution of 3 × 3 mm.

DATA ANALYSIS.

Data analysis was performed using FS-FAST (http://surfer.nmr.mgh.harvard.edu) and fROI (http://froi.sourceforge.net). Before statistical analysis, images were motion corrected (Cox and Jesmanowicz 1999) and the data from the blocked localizer scans (not the event-related scans) were smoothed (3-mm full width at half-maximum Gaussian kernel).

The LOC was defined as the set of contiguous voxels in the central occipitotemporal cortex that showed significantly stronger activation (P < 10⁻⁶, uncorrected; this threshold is stricter than the commonly used P < 10⁻⁴ and is close to the Bonferroni-corrected threshold of P < 10⁻⁷) to intact objects (Malach et al. 1995) than to scrambled versions of the same objects. Within the LOC, two subregions were defined as described previously (Grill-Spector et al. 1998): a posterior and lateral part, the lateral occipital region (LO), and an anterior and ventral part, the posterior fusiform gyrus (pFs). The retinotopic ROI was defined as the set of voxels at the occipital pole and bordering the calcarine sulcus that were significantly active (P < 10⁻⁶, uncorrected) in the LOC localizer scans, but did not overlap with LOC. Because the stimuli were presented at the fovea, different retinotopic areas (V1–V4) could not be distinguished due to the merging of the representations at the foveal confluence (Dougherty et al. 2003).

For the blocked localizer scans, statistical maps were calculated by correlating the signal time course with a gamma function (delta = 2.25, tau = 1.25) for each voxel convolved with the block time course. For the event-related scans, the hemodynamic response was extracted using a deconvolution analysis, without any assumptions about the shape of the response. The time course of the fMRI response of each experimental scan was extracted by averaging the data from all voxels within each of the independently defined ROIs. Statistical analysis was performed on the peak activation of the hemodynamic response function. Standard ANOVA statistics are reported, except where Mauchly's test of sphericity was rejected and therefore a Greenhouse–Geisser test was required.

Results

BEHAVIORAL DATA.

In agreement with previous results (Driver and Baylis 1995), behavioral performance on the same–different task was faster and more accurate for convex compared with concave stimuli: reaction times (RTs) were significantly shorter on “convex” than on “concave” trials [mean ± SE: convex 948 ± 27 ms, concave 999 ± 28 ms; F_(1,15) = 7.78, P < 0.02, repeated-measures ANOVA], and perceptual sensitivity as measured by d′ was greater for convex than for concave stimuli [mean ± SE: convex 3.24 ± 0.13, concave 3.09 ± 0.13; F_(1,15) = 6.86, P < 0.02; Table 1]. The RT effect was the same when the reaction times were first log-transformed [F_(1,15) = 9.86, P < 0.01]. However, note that this effect was much smaller than that reported by Driver and Baylis (1995); these authors found an error rate difference of 15 percentage points between convex and concave conditions, whereas ours was only 2 percentage points (86 vs. 84%).

TABLE 1.

Behavioral performance on the same–different task in experiment 1

	Concave				Convex
	Identical	1 Step	2 Steps	4 Steps	Identical	1 Step	2 Steps	4 Steps
A. Reaction time (RT), ms
RT	1,032	1,072	977	916	988	1,006	926	874
SE	31	28	27	33	30	24	27	27
B. d′

	1 Step	2 Steps	4 Steps	1 Step	2 Steps	4 Steps
d′	2.22	3.24	3.83	2.33	3.45	3.94
SE	0.09	0.13	0.16	0.11	0.15	0.13

Values are means and SE of reaction time (A) and d′ (B). Participants had to indicate whether the two contours in a trial were the same or different (2AFC).

FMRI DATA.

A greater blood oxygen level–dependent (BOLD) response to any of the three different conditions compared with the identical condition indicates neural sensitivity to the stimulus change in the different condition. If sensitivity in LOC is greater for changes in convex than in concave stimuli, we would expect the difference in response between the different and identical conditions to be larger for convex than for concave stimuli.

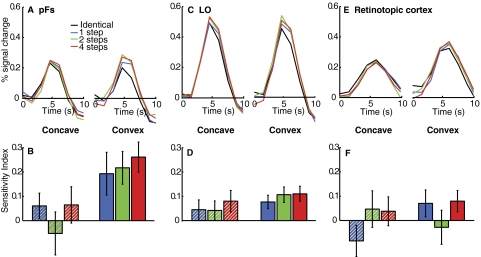
Since we observed no differences between changes in aspect ratio and skew, we collapse across these conditions in the following. ROI analysis in the anterior portion of LOC, pFs, revealed a stronger response for each of the different compared with the identical conditions for convex stimuli, indicating sensitivity to changes in part shape in this region [F_(3,33) = 8.95, P < 0.001; Fig. 2A]. Crucially, however, there was little difference between the different and identical conditions for concave stimuli [F_(3,33) = 0.68, P = 0.57; Fig. 2A]. Thus in pFs sensitivity was greater to changes in convex than in concave shapes. In LO, a similar pattern was observed, although the difference between the convex and concave conditions was smaller than that in pFs [convex: F_(3,33) = 6.64, P < 0.001; concave: F_(3,33) = 2.04, P = 0.13; Fig. 2C].

FIG. 2.

Functional magnetic resonance imaging (fMRI) results, experiment 1. Hemodynamic response curves in anterior lateral occipital complex (LOC) (posterior fusiform gyrus [pFs], A), posterior LOC (LO, C), and retinotopic cortex (E) are shown separately for concave (left panels) and convex stimuli (right panels). A higher response for different than that for identical conditions indicates sensitivity to the stimulus difference. Sensitivity index for pFs (B), LO (D), and retinotopic cortex (F). A high index indicates high sensitivity to changes in the stimulus. Greater sensitivity for convex than concave shapes was found in pFs, but not in either LO or retinotopic cortex.

To quantify these results, we computed a standard sensitivity index by subtracting the average percentage signal change of the peak response in the identical condition from that of each of the different conditions, and normalizing by their sum (Avidan et al. 2002). A high index (≤1) indicates strong sensitivity. In pFs, the sensitivity index was significantly higher for convex than for concave stimuli [F_(1,11) = 9.52, P < 0.02; Fig. 2B], confirming greater sensitivity for changes in convex than in concave shape in this region. In contrast, in LO we found no main effect of convexity [F_(1,11) = 0.84, P = 0.38; Fig. 2D], even though the index was greater than zero for the “convex” conditions, but failed to reach significance for the “concave” conditions (convex: t₁₁ = 3.85, P < 0.01; concave: t₁₁ = 1.62, P = 0.13). The two-way interaction between convexity and ROI on the sensitivity index was significant [F_(1,11) = 9.48, P < 0.02]. Thus sensitivity to changes in convex shape was greater than sensitivity to changes in concave shape in pFs, and this effect was significantly greater than that in LO.

This result cannot be due to the higher proportion of incorrect trials in the concave condition because the fMRI results were not different when incorrect trials were excluded from the analysis. To further control for a possible effect of task difficulty, we equated the reaction times of the “convex” and “concave” conditions: for each subject, we excluded the “concave” trials with the slowest reaction times and the “convex” trials with the fastest reaction times, until the average reaction times for both conditions were matched. Only “correct” trials were considered in this analysis. Using only this subset of trials, the fMRI results of the original analysis remained unchanged, ruling out task difficulty as a source of our results. Experiment 2 controlled for task difficulty experimentally (see following text).

No effect of convexity was found in retinotopic cortex [F_(1,11) = 2.91, P = 0.12; Fig. 2, E and F], ruling out a low-level basis of the effect observed in pFs. Convex stimuli tended to elicit stronger activation than concave stimuli in retinotopic cortex (Fig. 2E), presumably because the figure was always at the fixation cross (and thus covered the fovea) for convex but not concave stimuli (Van Essen et al. 1984); however, this difference cannot account for the adaptation effect found in pFs. That we observed no sensitivity to different versus identical stimuli in either the convex or concave conditions in retinotopic cortex is likely due to the fact that receptive fields are small in this region and fMRI short-term adaptation studies often do not find adaptation in this region (Fang et al. 2005, 2007).

Figure 2A shows that the release from adaptation in pFs was of similar magnitude for stimulus changes of one, two, and four steps. Accordingly, there was no main effect of the number of steps in pFs in the sensitivity index [Greenhouse–Geisser, F_(1.13,12.43) = 1.07, P = 0.33]. The same was true for LO and retinotopic cortex [LO: F_(2,22) = 1.97, P = 0.16; retinotopic: F_(2,22) = 2.17, P = 0.14]. Furthermore, there was no interaction between the number of steps and convexity in any ROI [pFs: F_(2,22) = 0.57, P = 0.57; LO: F_(2,22) = 0.20, P = 0.82; retinotopic: F_(2,22) = 0.60, P = 0.56]. These results are consistent with the findings of Fang et al. (2005, 2007) that short-term fMRI adaptation (used here) is sensitive to the existence of a stimulus change but not its magnitude.

The higher sensitivity for convex than for concave shape in pFs but not in LO was not dependent on the use of the sensitivity index, but was confirmed by a three-way interaction of ROI (pFs vs. LO), convexity, and number of steps [F_(3,33) = 3.11, P < 0.05]. Planned comparisons on the mean peak response revealed a significant two-way interaction of convexity and number of steps (identical vs. one step vs. two steps vs. four steps) in pFs, but not in LO [pFs: F_(3,33) = 2.38, P < 0.05: LO: F_(3,33) = 0.34, P = 0.80].

EXPERIMENT 2: CONTROL FOR FOVEAL STIMULATION AND TASK PERFORMANCE

In experiment 1, participants fixated on a fixation cross at the center of the aperture. Because the stimuli were designed so that the areas on each side of the contour were identical, the center of the aperture necessarily always coincided with the “convex” side of the contours. Therefore the visual transient associated with the appearance and disappearance of the shapes occurred at the fovea for convex stimuli and off the fovea for concave stimuli. The higher sensitivity for convex stimuli observed in experiment 1 could therefore be explained by higher cortical sensitivity to changes in the figure at the fovea than in the periphery. This possibility is consistent with the higher activation of retinotopic cortex by convex than by concave stimuli in experiment 1.

To address this potential confound, we conducted a control experiment that was identical to experiment 1, except that the fixation cross contained within the aperture was located 3.75° above the center and 1.25° below the border of the aperture along the vertical meridian on one half of trials and 3.75° below the center and 1.25° above the border of the aperture on the other half of trials. Participants were instructed to fixate on the cross and therefore fixation was on the “concave” side of the contour on half of the trials and on the “convex” side on the other half. This manipulation allowed us to address the effect of fixation location on the result obtained in experiment 1.

Second, in experiment 1 we obtained the well-known behavioral effect of superior performance for convex compared with concave stimuli (Driver and Baylis 1995). In principle this difference could explain the fMRI results. This possibility is unlikely since it would require an interaction of task difficulty with neural adaptation; furthermore, as noted earlier, the behavioral difference between the convex and concave conditions was very small in terms of the error rate (a difference of two percentage points). However, we nevertheless sought to control for this possible confound. To this end, we included only the “identical” and “4 steps different” conditions in experiment 2. Experiment 1 had shown these conditions to be equally difficult for convex and concave shapes (Table 1). Furthermore, the omission of the two intermediate conditions from experiment 1 made up f or the power lost by the two additional conditions created by the fixation requirement (fixation on convex vs. fixation on concave).

Methods

PARTICIPANTS.

Participants were 12 members of the MIT community (7 female, 5 male). The fMRI data of 2 participants were excluded because of excessive head motion.

STIMULI AND PROCEDURE.

The stimuli and procedures were identical to those in experiment 1, except for the change in the location of the fixation cross and the omission of the “1 step different” and “2 steps different” conditions, as described earlier. Thus this experiment had four trial types: convex versus concave, crossed with identical versus different (4 steps).

FUNCTIONAL IMAGING AND DATA ANALYSIS.

Functional imaging parameters and data analysis procedures were identical to those described in experiment 1, except that the scanning was performed on the 3T Siemens Trio Scanner at the Martinos Center at MIT. Because of the change in scanner, two additional head coils were used: a custom-built 32-channel coil (five subjects) and a Siemens 12-channel birdcage coil (three subjects). The remaining four subjects were scanned with the eight-channel surface coil used in experiment 1.

EYE-TRACKING.

Eye-tracking was performed in a separate session, using an I-SCAN RK-464 infrared system with a sampling rate of 240 Hz. Four of the participants of experiment 2 were seated 75 cm from a screen and performed the same task as in the scanner for four runs, with the order of conditions and stimuli identical to those they had experienced in the scanner. They were not explicitly instructed to fixate, but rather to perform the task exactly as they had done during the fMRI scan.

Results

BEHAVIORAL DATA.

Participants again performed a same–different task on the pair of stimuli on each trial. In contrast to experiment 1, performance between the “convex” and “concave” conditions did not differ in either d′ [mean ± SE: convex 3.80 ± 0.29, concave 3.74 ± 0.25, F_(1,10) = 0.06, P = 0.81; Table 2] or reaction time (RT) [mean ± SE: convex 898 ± 109 ms, concave 1,001 ± 130 ms, F_(1,10) = 2.86, P = 0.12]. Fixation location (up/down) had no effect on performance [RT: fixation on figure: 945 ± 118 ms; fixation on ground: 954 ± 120 ms; F_(1,10) = 0.66, P = 0.44; d′: fixation on figure: 3.74 ± 0.30; fixation on ground: 3.80 ± 0.25; F_(1,10) = 0.56, P = 0.47]. Fixation location and convexity did not interact [RT: F_(1,10) = 1.52, P = 0.25; d′: F_(1,10) = 0.02, P = 0.90]. Again the results did not change when the RTs were first log-transformed [convex vs. concave: F_(1,10) = 3.01, P = 0.11; fixation on figure vs. ground, F_(1,10) = 0.35, P = 0.59].

TABLE 2.

Behavioral performance on the same–different task in experiment 2

	Concave		Convex
	Fixation on Figure	Fixation on Ground	Fixation on Figure	Fixation on Ground
A. Reaction time (RT), ms
RT	993	1,010	898	899
SE	127	132	109	109
B. d′
d′	3.71	3.78	3.77	3.83
SE	0.28	0.23	0.32	0.27

Values are means and SE of reaction time (A) and d′ (B).

FMRI DATA.

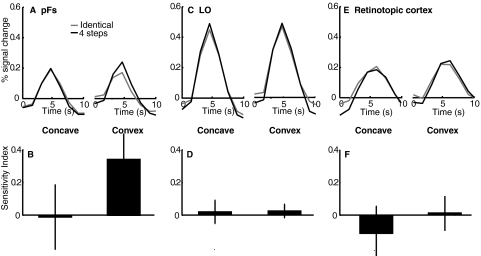
As in experiment 1, an ROI analysis in pFs showed stronger activation for the “different” compared with the “identical” condition on “convex” trials, but not on “concave” trials, demonstrating greater sensitivity to changes in convex than in concave shapes in pFs (Fig. 3A). The sensitivity index was significantly higher for convex than for concave stimuli in pFs [F_(1,7) = 6.47, P < 0.05; Fig. 3B] and an ANOVA on the mean peak response showed an interaction of convexity and identical versus different conditions in pFs [F_(1,7) = 3.87, P < 0.05]. Critically, this effect did not interact with fixation location in either the mean peak response or the sensitivity index [mean peak response: F_(1,7) = 0.002, P = 0.97; sensitivity index: F_(1,7) = 0.33, P = 0.58; Supplemental Figs. S1 and S2],1 indicating that the result of experiment 1 is independent of fixation location.

FIG. 3.

fMRI results, experiment 2. Hemodynamic response curves in anterior LOC (pFs, A), posterior LOC (LO, C), and retinotopic cortex (E) are shown separately for concave (left panels) and convex stimuli (right panels). Sensitivity index for pFs (B), LO (D), and retinotopic cortex (F).

As in experiment 1, LO did not show greater sensitivity to convex than to concave stimuli: there was no interaction between convexity and identical versus different conditions in the mean peak response [F_(1,7) = 0.19, P = 0.68; Fig. 3C] and no main effect of convexity in the sensitivity index [F_(1,7) = 0.11, P = 0.75; Fig. 3D]. In contrast to experiment 1, LO did not show a release from adaptation for different versus same trials (mean peak response: convex, t₇ = 0.99, P = 0.35; concave, t₇ = 1.23, P = 0.26; sensitivity index: convex, t₇ = 0.04, P = 0.97; concave, t₇ = 1.21, P = 0.27).

The difference between pFs and LO was confirmed in the mean peak response by a three-way interaction of ROI (pFs vs. LO), convexity, and step size (identical vs. different) [F_(1,7) = 10.90, P < 0.05]; and in the sensitivity index by a two-way interaction of ROI and convexity [F_(1,7) = 10.30, P < 0.05].

Thus we draw the same conclusions as from experiment 1: that there is greater sensitivity for convex than for concave shape in anterior LOC, but not in posterior LOC, while controlling for fixation location. The absence of a performance difference between the “convex” and “concave” conditions in this experiment rules out task difficulty as a source of the results. To further corroborate this independence, we again matched the reaction times between “convex” and “concave” conditions, as described earlier, and obtained the same results.

In retinotopic cortex, the sensitivity index did not show an effect of convexity or fixation location [convexity: F_(1,7) = 0.08, P = 0.79; fixation: F_(1,7) = 0.05, P = 0.83; interaction: F_(1,7) = 1.23, P = 0.30]. This again replicates the findings of experiment 1.

In addition, experiment 2 allowed us to address the higher mean signal for convex compared with concave stimuli in retinotopic cortex found in experiment 1. We hypothesized that this main effect was due to the fact that participants in experiment 1 fixated the center of the aperture, where the disparity change occurred (Schira et al. 2004). Therefore convex stimuli appeared at fixation and concave stimuli away from fixation, possibly resulting in a higher mean signal for convex than for concave stimuli. If this had been the reason for the main effect in experiment 1, we would predict a higher mean signal in experiment 2 for fixation on the figure compared with fixation on the background. This difference was obtained [F_(1,7) = 9.67, P < 0.05] and it suggests that fixation location explains the higher mean signal for convex than for concave stimuli found in retinotopic cortex in experiment 1. However, this effect cannot explain the adaptation effect found in pFs in either experiment. Moreover, no main effect for fixation location was found in the peak activation in pFs or LO [pFs: F_(1,7) = 3.18, P = 0.11; LO: F_(1,7) = 1.03, P = 0.34].

Thus controlling for fixation location and task difficulty abolished the main effect of “convex” versus “concave” conditions in retinotopic cortex, but did not alter the results in LO and pFs.

EYE-TRACKING EXPERIMENT.

To confirm that participants could maintain stable fixation throughout the experiment, four of the participants of experiment 2 repeated four runs of the fMRI experiment outside the scanner while their eye movements were being recorded. The fMRI results of these participants matched the mean result and the stimulus presentation during eye-tracking for each participant was exactly the same as that during fMRI. All participants fixated extremely well. The average deviation from fixation was 0.34° (SE 0.15°) across a given run, and no run showed a deviation that was statistically different from fixation. The average deviation was well below the distance between the fixation cross and the contour, which was 2.5° on average and 1.5° at a minimum. Importantly, the average deviation from fixation was not different for “convex” and “concave” conditions, and for fixation on and off the figure region (mean deviation from fixation across a run: convex, fixation on figure: 0.29 ± 0.20°; convex, fixation on ground: 0.35 ± 0.21°; concave, fixation on figure: 0.34 ± 0.10°; concave, fixation on ground: 0.36 ± 0.10°).

The average SD of the eye position in a given run was 0.85° (SE 0.14°). Taking into account a 0.34° average deviation from fixation, this implies that participants' fixation remained on the correct side of the contour 99.5% of the time. This is a conservative estimate because it does not make an allowance for measurement error. Furthermore, the SD of the eye position was indistinguishable for convex versus concave stimuli, and fixation on figure versus fixation on ground (SD of fixation across a given run: convex, fixation on figure: 0.85 ± 0.16°; convex, fixation on ground: 0.85 ± 0.14°; concave, fixation on figure: 0.86 ± 0.14°; concave, fixation on ground: 0.85 ± 0.12°). Thus differential fixation performance or eye movements cannot explain our results across different conditions.

FURTHER ROIS

To test whether the greater sensitivity for convex than for concave shapes we observed in anterior LOC was specific to object-selective cortex, we defined two additional ROIs: the fusiform face area (Kanwisher et al. 1997) and the parahippocampal place area (Epstein and Kanwisher 1998). In the fusiform face area (FFA), which is anatomically adjacent to pFs, we observed a weakly significant effect of convexity in the sensitivity index in experiment 1 [convexity: F_(1,10) = 3.67, P < 0.05]. However, this effect was not confirmed by the ANOVA on the peak signal rather than the sensitivity index [interaction convexity × number of steps: F_(3,30) = 0.53, P = 0.66]. Furthermore, when we controlled for fixation location and task difficulty in experiment 2, FFA showed no effect of greater sensitivity to convex than to concave shapes either in the sensitivity index [convexity: F_(1,7) = 0.56, P = 0.48] or in the peak response [interaction convexity × identical/different: F_(1,7) = 0.26, P = 0.62].

Similarly, we observed no effect of greater sensitivity to convex than to concave shapes in PPA. In experiment 1, PPA showed no main effect of convexity in the sensitivity index [convexity: F_1,9 = 0.04, P = 0.84] and in the peak signal [interaction convexity × identical/different: F_(1,9) = 1.97, P = 0.14]. Similarly, in experiment 2, PPA showed no effect of greater sensitivity for convex than for concave shapes in the sensitivity index [convexity: F_(1,7) = 0.89, P = 0.38] or in the peak signal [interaction convexity × identical/different: F_(1,7) = 1.61, P = 0.24].

These results indicate that the greater sensitivity to convexities than to concavities we observed in both experiments is indeed specific to object-selective areas and anterior LOC (pFs) in particular.

DISCUSSION

The aim of our study was to test whether privileged representation of convex shapes could serve as a coding principle in object-selective brain regions at the top end of the cortical visual hierarchy. Indeed we found greater sensitivity to changes in convex than in concave shape in LOC, a region that has been implicated in object recognition (Grill-Spector et al. 2000). This effect was restricted to the anterior portion of LOC, pFs, and was not observed either in the posterior portion, LO, or in retinotopic cortex. It was found in each of two experiments and was independent of fixation location, eye movements, and task performance. The greater sensitivity to convex than to concave shape is particularly striking considering that the two stimulus sets were identical except for a disparity change.

Thus we can provide a partial answer to the question of the neural code for object shape: convex curvature appears to be processed in a privileged fashion in object-selective cortex; we therefore propose that convex contour segments could be important elements in cortical object representations.

This conclusion is consistent with psychophysical studies showing a behavioral advantage for convexities over concavities in a variety of shape-discrimination tasks (Bertamini 2001; Biederman 1987; Braunstein et al. 1989; Driver and Baylis 1995; Subirana-Vilanova and Richards 1996); it is also consistent with extant models of shape decomposition that assign a privileged role to “parts” (Biederman 1987; Hoffman and Richards 1984; Kimia et al. 1995; Marr and Nishihara 1979). More generally, our findings suggest that the neural representation of object shape is not simply a collection of raw image fragments (Ullman et al. 2002), but instead depends strongly on figure–ground assignment (see also Gilaie-Dotan et al. 2002; Kourtzi and Kanwisher 2001).

Furthermore, our findings complement and extend previous fMRI and electrophysiological studies. First, a recent fMRI study has found higher mean activation (as opposed to higher sensitivity, reported here) for convex than for concave stimuli (objects vs. holes of the same shape) in LOC (Vinberg and Grill-Spector 2008). These results underscore the importance of convex stimuli in object-selective cortex; however, they differ from our findings since we did not observe a convex > concave main effect. We speculate that this discrepancy may be due to the fact that the convex stimuli in Vinberg and Grill-Spector's study were “object-like,” whereas the concave stimuli were “holes”; our convex and concave stimuli did not differ in this fashion and this may account for the absence of a main effect in LOC with our stimuli.

Second, electrophysiological studies have shown that macaque area V4 contains more cells that respond to convex than to concave stimuli (Pasupathy and Connor 1999, 2001). Our findings are in agreement with this work in that they suggest privileged encoding of convexities compared with concavities. However, these authors find no differential tuning for convex and concave stimuli in V4 (see Fig. 7 in Pasupathy and Connor 2001, which shows no reliable correlation between the convexity of the stimulus and the SD of the fitted neuronal response). Also, the larger number of convex cells found by Pasupathy and Connor would predict stronger activation for convex than for concave shapes, which our study did not find. These discrepancies could be due to differences in cortical area (LOC/IT vs. V4), species (human vs. macaque), and/or method (single-unit recording vs. fMRI adaptation). As pointed out earlier, the present study could not separately examine V4 or other retinotopic regions because these regions cannot be distinguished from each other at the foveal confluence (Dougherty et al. 2003). However, our experiments do suggest an answer to what might be found in retinotopic regions: we find higher sensitivity for convexities than for concavities in anterior LOC, but not in posterior LOC; the dissociation between these two subregions of LOC is statistically significant in both independent replications herein. Since posterior LOC is anterior and downstream of retinotopic regions, the absence of an effect in this region suggests that the convexity advantage does not emerge within retinotopic regions, and not even in the first stages of object-selective cortex, but rather only at higher stages of object-selective cortex (anterior LOC). More generally, our finding of sharper tuning for convex than for concave stimuli in pFs, but not in LO, corroborates prior evidence for a hierarchy of visual processing, with representations of simple stimuli, such as oriented bars in early visual areas, and higher-level shape representations in more anterior regions (Dehaene et al. 2005; Grill-Spector et al. 2001; Hayworth and Biederman 2006; Tanaka et al. 1991).

A potential challenge to our results is the recent finding that single-cell responses can exhibit less-than-complete adaptation to two different stimuli even if the initial firing rate for the two stimuli is indistinguishable (Sawamura et al. 2006). This finding suggests that fMRI adaptation can overestimate the sharpness of the underlying neuronal tuning curves. However, our main result is the relative strength of adaptation for convex versus concave shapes, specifically greater release from adaptation for convex than for concave shape changes. This finding is independent of any general overestimation of the strength of tuning arising from the use of the adaptation method (Sawamura et al. 2006). Similarly, one might argue that our results are potentially confounded by the fact that the degree to which object-selective cortex exhibits adaptation depends on the nature of the task performed (Murray and Wojciulik 2004). However, the same argument expressed earlier applies here: our main finding is an interaction between the magnitudes of adaptation in the convex versus the concave conditions, and this finding is not vulnerable to the confound described. Moreover, task performance did not differ between the convex and concave conditions in experiment 2, also arguing against task dependence of our effect. Finally, our results did not change when we excluded incorrect trials from the analysis, and when we equated the reaction times of the “convex” and “concave” conditions in both experiments by excluding trials until the average reaction times were matched (data not shown). Thus task difficulty can be ruled out as a source of the results of our experiments. However, whether similar results would be obtained with a completely different task remains a subject for future study.

Notwithstanding the importance of convexities in shape representation demonstrated here, concavities have also been shown to play a role in object recognition: part-based object recognition theories posit segmentation into parts at concave minima (Hoffman and Richards 1984; Koenderink and van Doorn 1982; Marr and Nishihara 1978; Siddiqi and Kimia 1995), and psychophysical evidence points toward an advantage for concave stimuli in visual search and change detection tasks (Barenholtz et al. 2003; Cohen et al. 2005; Hulleman et al. 2000; Humphreys and Müller 2000). However, these findings are not inconsistent with our results. Instead, they suggest that convexities and concavities are important at different stages in object recognition. Specifically, the process of extracting shape descriptions might consist of an early figure–ground segmentation stage, an intermediate stage at which the figure is divided at its concave minima, and a final stage of representation of the resulting convex parts. One might thus speculate that earlier cortical regions may show greater sensitivity to concavities than to convexities. This prediction could not be tested in detail here because all stimuli were presented at the fovea where retinotopic areas cannot be distinguished. However, no differential sensitivity to convexities versus concavities was observed in our retinotopic ROI, suggesting that if a concavity advantage exists in retinotopic areas, it is not widespread.

In summary, we have demonstrated privileged representation of convex compared with concave shapes in human object-selective cortex (anterior LOC), indicating that convexity may play an important role in the neural code for object shape that we use to distinguish one object from another. The present results raise many new questions for future research. Do other cortical regions show higher specificity for concavities, making them candidates for the neural substrate of shape segmentation at concave minima? Given that curvature polarity depends on figure–ground assignment, how and where in cortex is figure–ground assignment achieved (Lamme 1995; Qiu and von der Heydt 2005; Schira et al. 2004)? Finally, how do cortical representations of convexities and concavities interact with representations of other shape features that are thought to be important in coding object shape, such as nonaccidental properties (Kayaert et al. 2003)? The methods used here should enable us to make progress in answering these questions, which are at the very core of the problem of object recognition.

GRANTS

This research was supported by National Eye Institute Grants EY-13455 to N. Kanwisher and EY-16187 to M. S. Livingstone, National Center for Research Resources Grant P41-RR-14075, and the Mental Illness and Neuroscience Discovery Institute. J. Haushofer was supported by the Boehringer-Ingelheim Foundation and the German National Merit Foundation.