NMR evidence of a sharp change in a measure of local order in deeply supercooled confined water

Abstract

Using NMR, we measure the proton chemical shift δ, of supercooled nanoconfined water in the temperature range 195 K < T < 350 K. Because δ is directly connected to the magnetic shielding tensor, we discuss the data in terms of the local hydrogen bond geometry and order. We argue that the derivative −(∂ ln δ/∂T)_P should behave roughly as the constant pressure specific heat C_P(T), and we confirm this argument by detailed comparisons with literature values of C_P(T) in the range 290–370 K. We find that −(∂ ln δ/∂T)_P displays a pronounced maximum upon crossing the locus of maximum correlation length at ≈240 K, consistent with the liquid-liquid critical point hypothesis for water, which predicts that C_P(T) displays a maximum on crossing the Widom line.

Unlike most fluids, water displays anomalies in thermodynamical properties such as compressibility, isobaric heat capacity, and thermal expansion coefficient, and their explanation on molecular basis remains a challenge (1–3). One hypothesis that has received support from various theoretical studies (4–7) is the liquid-liquid (LL) critical point hypothesis, but a proper test can be obtained only by studying the properties of liquid water well below its homogeneous nucleation temperature, T_H = 231 K. This is made possible by confining water inside nanoporous structures so small that the liquid cannot freeze.

Among recent findings concerning water's dynamical properties at these low temperatures are (8–13): a fragile-to-strong crossover and the violation of the Stokes-Einstein relation, related to the crossing of the Widom line and to the existence of a low-density-liquid-like (LDL-like) local structure. The Widom line is the locus of maximum correlation length in the one-phase region beyond the liquid-liquid critical point, where thermodynamic response functions take their maximum values (12, 13). Scattering experiments (using neutrons and x-rays) have given precise values of the pair correlation function (PCF), providing important benchmarks for testing models of its structure. The PCF represents only an isotropically averaged measure of structure. Thus, in many cases, PCFs may not faithfully reproduce the subtle hydrogen bond geometry responsible for water's thermal anomalies. Our goal in this study is to provide additional information on the local hydrogen bond geometry and, in particular, the average number of the possible configurations of the local molecular hydrogen bonding geometry, by measuring the NMR proton chemical shift δ. If a water molecule in a dilute gas is taken to be an isolated-state reference, the chemical shift δ accounts for the change of the value of the magnetic shielding with respect to that of such a reference. Hence the chemical shift is related to the “non-dilute” or “virial” interaction of a water molecule with its surroundings, providing a picture of the intermolecular geometry (14–19). Originally, it has been proposed, especially in the high temperature regime, that δ represents the number of hydrogen bonds (HB), N_HB, with which a water molecule is involved at a certain temperature (20–22). Nowadays it is accepted that, especially after a lot of theoretical and experimental studies, the proton chemical shift of water is a function not only of the number of HB but also of the intermolecular distances and angles: i.e., 〈N_HB〉 (16). Thus, a careful study of δ vs. T gives details of the thermal evolution of the water configurations especially in the supercooled regime where there is the onset of complex clustering phenomena [percolation-like (23, 24)] just driven by the HB interaction (25–30).

We propose here an approach for which the T derivative of the chemical shift can give an estimate of the configurational specific heat and measure the water proton chemical shift as a function of temperature by studying confined water in two different systems recently used to measure water thermodynamical parameters under deep supercooling conditions: (i) a micelle-templated mesoporous silica matrix, comprised of quasi-1D cylindrical tubes (MCM-41-S) (8–13, 31), and (ii) the hydration water in the protein lysozyme in the temperature range 180 K < T < 360 K, a system also the object of detailed studies by using both theoretical and experimental approaches (32–37).

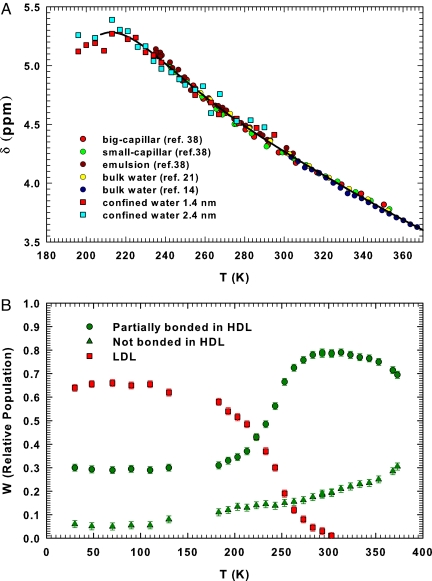
Fig. 1A shows our δ(T) data in MCM samples, after correcting for the magnetic susceptibility χ(T) = χ₀ρ(T). Fig. 1A also shows, from the work of Hindman (21), all of the experimentally available δ(T) data in the temperature range of stable bulk liquid water, and the δ values from T = 350 K down to 235 K, of three different samples: large (80–120 μm) and small (10–20 μm) capillaries, and water confined in an emulsion (38). Although for the δ data of refs. 21 and 38, the reference material was CH₄, all measured values, after the proper correction, nicely fall onto a single master curve, whereby the reference system is a water molecule in a diluted gas in supercritical conditions (14). Fig. 1A reports such a situation in the range 180 K < T < 370 K and shows agreement between our data and the previous δ(T) measurements. We see that the behavior of these literature data (circles) is characterized by a continuous increase on decreasing T that becomes more pronounced in the lower temperature region. At lower T the situation changes: on decreasing T there is a round-off in δ(T) with a possible maximum at ≈215 K. Because different experiments quote (with respect to the isolated water molecule) δ = 7.4 ppm for a single crystal of hexagonal ice I_h (39), our data show that δ(T) does not evolve in a simple monotonic way from the liquid to the ice phase. The continuous increase in the proton chemical shift with T decreasing down to the supercooled regime, has been originally interpreted in terms of a cooperative increase in HB formation rate. Thus, there is a continuous development of a considerable degree of short-range order or “clustering.” In addition, because the T region <225 K is dominated by the LDL local structure (11), this confirms the idea that this liquid-water phase has a local geometry different from the high-density liquid (HDL) local structure prevalent in the stable liquid regime.

Fig. 1.

The proton chemical shift and the relative populations of water. (A) Proton chemical shift of water, δ, as a function of temperature. Literature data are plotted as circles, and the present data are plotted as squares symbols. The line is a guide for the eye. (B) The relative population of the high density liquid (HDL) and the low density liquid (LDL) water contributions obtained from the Raman and FTIR spectral analysis versus temperature. The HDL and the LDL data are plotted as green and red symbols, respectively. For HDL, the contributions of partially bonded 1 < N_HB < 3 (circles) and not bonded N_HB = 0 (triangles) water molecules are reported separately. As can be observed, these latter two contributions have opposite behaviors on increasing T >300 K.

The recently measured relative population of the two main local structures, LDL-like and HDL-like (11, 40), in the region 30 K < T < 373 K, provides a qualitative explanation for the observed δ(T) (Fig. 1A). From a structural point of view, the temperature range can be divided into three intervals:

• ℛ_HDL (T > 250 K) dominated by molecules with local HDL geometry.

• ℛ_LDL (T ≲ 220 K) dominated by local LDL geometry and an intermediate region in which the population of these local geometries are comparable:

• ℛ_int (220 K ≲ T < 250 K).

Visual inspection of δ(T) shows three different behaviors as temperature decreases in the three different regions: (i) a continuous increase in ℛ_HDL, (ii) an inflection point at ≈250 K with a sudden change in the derivative in the ℛ_int interval, and finally (iii) a flattening at ≈220 K followed by a slow decrease in the ℛ_LDL region. These results support a picture in which the main role is played by the LDL and HDL local geometric structure, characterized by different local electronic distributions, thus by different local environments of the hydrogen atom. A proper analysis of their fractional weights allows us to calculate the absolute value of water density ρ(T) in the range 30 K < T < 373 K. In addition to the well known maximum at 277 K, there appears a minimum in ρ(T) at 203 ± 5 K (40). Moreover, the coefficient of thermal expansion α_ρ = −(∂ρ/∂T)_P, related to the cross-correlation between the entropy and volume fluctuations, shows a well defined maximum on crossing the Widom line T_W (P). In the first interval ℛ_HDL, in which the normal liquid region (273–353 K) and a region of moderate supercooling lie, δ(T) increases as T decreases. Both the normal liquid and the supercritical regions have been considered from both the theoretical and experimental points of view to explain as the proton chemical shift reflects the properties of the local order (14, 16, 17) in regions in which there is a direct relation between δ(T) and the average number of hydrogen bonds 〈N_HB〉, in which a water molecule is involved: δ(T) ∝ 〈N_HB〉. On the basis of the thermal evolution of the LDL and HDL local structures (Fig. 1B), we consider that such a situation holds also in the other two temperature regions, ℛ_int and ℛ_LDL, where there is the progressive build-up of the expanded tetrahedral HB network with decreasing temperature.

The chemical shift δ(T) is related to the number of possible configurations of the water molecules in the HB network. Considering that this number is inversely proportional to 〈N_HB〉, according to the entropy definition we can assume S ≈ −k_B ln〈N_HB〉. Therefore, the temperature derivative of the measured fractional chemical shift,

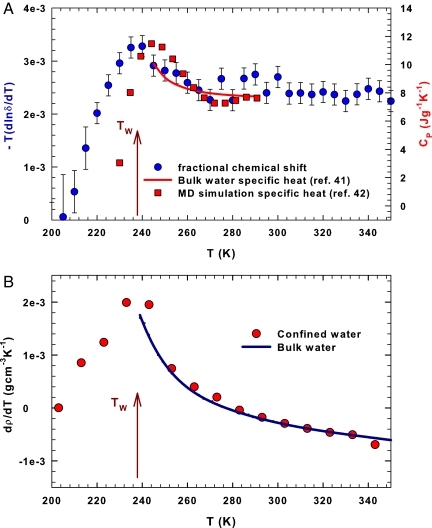
should be proportional to the constant pressure specific heat C_P(T) (being C_P = T(∂S/∂T)_P), a quantity never experimentally measured in the deep supercooled regime <250 K for liquid bulk water. Fig. 2A reports (Left) the derivative −T∂ ln δ(T)/∂T obtained from the δ(T) data of Fig. 1A. Also shown are the C_P(T) values measured in bulk water in the interval 244.5 K < T < 290 K (41) and the same quantity obtained by means of a simulation study from the TIP5P model of water for 210 K < T < 290 K (Right) (42). All these data display an analogous thermal behavior. In fact, within the error bars, there is good agreement between the C_P data. The “configurational” specific heat obtained from the measured δ and the C_P(T) calculated in simulation display maxima at about the same temperature (≃235 K) of the maximum in (∂ρ/∂T)_P (40) upon crossing the Widom line temperature, T_W (Fig. 2B) (10, 13, 43). We stress that whereas (∂ρ/∂T)_P is directly related to the cross-correlation between the entropy and volume fluctuations 〈(ΔSΔV)〉, C_P is proportional to the square of the entropy fluctuations. We stress that very recent calorimetric data on water confined in silica gel, which cover the range 100 K < T < 300 K, show a behavior that agrees with our results (44).

Fig. 2.

Measured thermodynamical response functions of water. (A) The temperature derivative of the measured fractional chemical shift −T∂ ln δ(T)/∂T (blue symbols, Left), the specific heat at constant pressure, C_P (Right), measured in bulk water in the supercooled regime (red line, ref. 41), and C_P calculated for the TIP5P model of water (red squares, ref. 42). (B) The temperature derivative of the water density (40). The arrows indicate the Widom line temperature T_W .

To confirm the validity of our approach and the obtained results, we consider δ of the hydration water proton for lysozyme at the hydration level h = 0.3, a condition in which only one monolayer of water is supposed to be on the surface of each protein. We have explored the temperature range 200 K < T < 370 K for the following reasons: (i) in such a system, water dynamics display the fragile-to-strong cross-over phenomena (FSC) observed in confined and simulated water (32, 42); in particular, the cross-over temperature T_W is nearly coincident among these water confined forms (32, 42); (ii) another phenomenon governing biological properties of proteins occurs at high temperatures, just below the onset of protein denaturation. In the first case, the FSC is entirely due to the complete development of the LDL water phase (i.e., of the HB tetrahedral network) located just at the Widom line (32, 42).

A protein is in the native state up to a given temperature and evolves, on increasing T, into a region characterized by a reversible unfolding-folding process. This latter phenomenon depends on the chemical nature of the protein and the solvent. For water-lysozyme it occurs in the range 310 K < T < 360 K. Above 355 K, lysozyme denatures irreversibly. For h = 0.12, calorimetric measurements (33) show a broad peak in C_P. The process rate constant varies with T according to an Arrhenius law with an activation energy typical of the HB strength (33), so hydration water appears to play a determinant role also for this transition. In particular, all of the observed data of an experiment characterized by the peak in C_P at T = 346 K are consistent with the point of view that the first step of denaturation of a small one-domain globular protein like lysozyme is a reversible conformational (unfolding) transition, and the second step is irreversible. Thus, a dramatic change in the protein structure is driven by the HBs between the protein and its hydration water. This latter quantity is strictly related to δ.

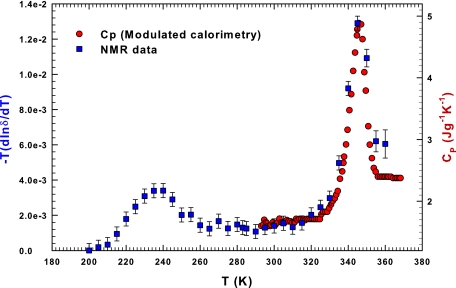
Fig. 3 shows in a double scale plot (−T∂ ln δ(T)/∂T)_P for lysozyme hydration water and the right-hand side of the figure reports C_P measured in the temperature region including the reversible unfolding-folding process. One sees that (−T∂ ln δ(T)/∂T) displays two maxima, the first on crossing the Widom line T_W(P) as proposed by experiments and simulation studies on hydrated proteins (32, 42) and the second at a temperature nearly coincident with the associated protein denaturation process. The first maximum, at ≈240 K, i.e., the same temperature as that of confined water, is a proof that both are due to the same structural change of water. In fact, at T_W the LDL phase dominates water properties (11, 34). Finally, the agreement between δ and C_P, aside from different prefactors, supports the physical idea that both C_P and δ are measures of the temperature derivative of an entropy-like quantity. Because δ is related to orientational local order, as opposed to other translational local order, our finding is consistent with the possibility that the contribution of the orientational disorder to entropy is dominant. Our work is also consistent with molecular dynamics simulations using the TIP5P model, which demonstrate that in protein hydration water and in bulk water, dQ/dT has a maximum at the crossing of the Widom line T_W(P) (35).

Fig. 3.

Test of the argument that the logarithmic temperature derivative of the proton chemical shift is related to the specific heat. The figure, reporting data coming from the water-protein (lysozyme) system, shows a detailed comparison between the present NMR data and previous C_P data (33).

In conclusion, the present study introduces NMR proton chemical shift measurements as a new method for estimating the configurational part of the heat capacity C_P(T) that results from the hydrogen bonding of the water molecules. Because the NMR technique also gives the chemical shift of each sample nucleus with non-zero spin, such an approach may be applicable to more complex materials.

Methods

It is widely known that the chemical shift δ is an assumed linear response of the electronic structure of a system under investigation to an external magnetic field B₀, as B(j) = (1 − δ_j)B₀, where j is an index identifying the chemical environment (45, 46). It is measured in an NMR experiment by the free induction decay (FID),^‖ and specifically, it is related to the magnetic shielding tensor σ, which in turn relates to the local field experienced by the magnetic moment of the observed nucleus. The magnetic shielding tensor σ, strongly dependent on the local electronic environment, is a useful probe of the local geometry and, in particular, for the hydrogen bond structure for water and aqueous systems and solutions (47). Of interest to us are the isotropic parts, σ_iso ≡ Tr(σ/3), and the shielding anisotropy Δσ ≡ σ₃₃ − (σ₁₁ + σ₂₂)/2, where σ₁₁, σ₂₂, and σ₃₃ are the three principal components of σ. σ_iso is experimentally obtained via the measured proton chemical shift relative to a reference state through the relation (48).

Here, χ is the magnetic susceptibility, and the factor A depends on the sample shape and orientation: A = 1/3 for a spherical sample. Because the magnetic field exerted on a proton is B₀[1 + (4π/3)χ(T)], the resonance frequency is ω(T) = γH₀[1 − σ(T) + (4π/3)χ(T)], where γ is the proton gyromagnetic ratio. Thus, the deviation of σ(T) from a reference value gives δ(T). Because the magnetic susceptibility per water molecule, χ₀, can be assumed to be T and P independent, χ(T) is simply given by χ₀ρ(T), where ρ(T) is the density at a temperature T. In the liquid and gas phases, ω(T) and ρ(T) can be obtained directly from the experiment. Considering that water molecules in the gas phase at 473 K are isolated, we can set δ_g(473 K) = 0, where g indicates the gas. Thus, δ(T) = (ω(T) − ω_g)/ω_g − (4π/3)χ₀(ρ(T) − ρ_g). Thus, δ(T) can be determined from ω(T) and ρ(T). Hence, an isolated water molecule in a dilute gas can be taken to be the reference for δ, so that δ represents the effect of the interaction of water with the surroundings providing, in particular, a rigorous picture of the intermolecular geometry (14). In liquid water, the shielding tensor is isotropically averaged by fast molecular tumbling, so the NMR frequency provides information only on σ_iso. In addition, the Δσ contribution escapes detection because ¹H relaxation is heavily dominated by the strong magnetic dipole field from nearby protons (49). However, δ is directly related to the average number of local configurations in which a water molecule is involved (14–17). The water proton chemical shift has been studied in the same confined geometry used in the previous experiments. The confining substrate is a micelle-templated mesoporous silica matrix MCM-41-S comprised of quasi-1D cylindrical tubes arranged in a hexagonal structure, synthesized by using the zeolite seeds method (8–11). We study two different samples having tube diameters of d = 2.4 nm and 1.4 nm. Both have hydration levels of h ≃ 0.5 g of H₂O per gram of MCM-41-S. We perform static NMR experiments at ambient pressure P in the temperature interval 195 K < T < 293 K by using a Bruker AVANCE NMR spectrometer operating at 700 MHz proton resonance frequency. At h ≃ 0.5 both samples are fully hydrated and the measured δ(T) are, within the experimental uncertainty of ±0.05 ppm, pore size independent. As can be observed in Fig. 1A, at lower T there is a round-off in δ(T) with a possible maximum at ≈215 K. However, such a situation (which is not relevant to the present study) deserves special care, so we planned a magic angle spinning (MAS-NMR) experiment. The second studied system consists of the first-shell hydration water of lysozyme. In that case we have used hen egg white lysozyme obtained from Fluka (L7651 three times crystallized, dialysed, and lyophilized) and used without further purification. Samples were dried, hydrated isopiestically and controlled by means of a precise procedure (32). We used protein-water samples with hydration levels h = 0.3. The configurational heat capacity, obtained from δ(T) by means of Eq. 1, is plotted on the left-hand sides of Figs. 2A and 3. The comparison with respect to the measured C_P values is made by means of a double scale plot (on the right-hand side of these figures). The only difference is one adjustable parameter: the amplitude of the signal.