Dynamic Simulation of Three Dimensional Architectural and Mechanical Alterations in Human Trabecular Bone during Menopause

Abstract

A three dimensional (3D) computational simulation of dynamic process of trabecular bone remodeling was developed with all the parameters derived from physiological and clinical data. Contributions of the microstructural bone formation deficits: trabecular plate perforations, trabecular rod breakages, and isolated bone fragments, to the rapid bone loss and disruption of trabecular microarchitecture during menopause were studied. Eighteen human trabecular bone samples from femoral neck (FN) and spine were scanned using a micro computed tomography (μCT) system. Bone resorption and formation were simulated as a computational cycle corresponding to 40-day resorption/160-day formation. Resorption cavities were randomly created over the bone surface according to the activation frequency, which was strictly based on clinical data. Every resorption cavity was refilled during formation unless it caused trabecular plate perforation, trabecular rod breakage or isolated fragments. A 20-year-period starting 5 years before and ending 15 years after menopause was simulated for each specimen. Elastic moduli, standard and individual trabeculae segmentation (ITS)-based morphological parameters were evaluated for each simulated 3D image. For both spine and FN groups, the time courses of predicted bone loss pattern by microstructural bone formation deficits were fairly consistent with the clinical measurements. The percentage of bone loss due to trabecular plate perforation, trabecular rod breakage, and isolated bone fragments were 73.2%, 18.9% and 7.9% at the simulated 15 years after menopause. The ITS-based plate fraction (pBV/BV), mean plate surface area (pTb.S), plate number density (pTb.N), and mean rod thickness (rTb.Th) decreased while rod fraction (rBV/BV) and rod number density (rTb.N) increased after the simulated menopause. The dynamic bone remodeling simulation based on microstructural bone formation deficits predicted the time course of menopausal bone loss pattern of spine and FN. Microstructural plate perforation could be the primary cause of menopausal trabecular bone loss. The combined effect of trabeculae perforation, breakage, and isolated fragments resulted in fewer and smaller trabecular plates and more but thinner trabecular rods.

INTRODUCTION

The human skeleton is renewed continuously via the bone remodeling process through one’s entire life. This process consists of a coupling of bone resorption by osteoclasts and bone formation by osteoblasts through basic multicellular units (BMUs). For women in menopause, increased BMU activities result in accelerated trabecular bone loss and disruption of trabecular architecture, which leads to postmenopausal osteoporosis in millions of patients in the U.S. alone. It is believed that the depletion of estrogen during menopause accounts for a reduction of restraints on osteoclasts and incurs the increased bone remodeling activities via additional new BMUs sites within the bone [1-3]. Even though the predominance of bone resorption over bone formation is observed in menopausal osteoporosis, the underlying mechanisms of bone loss via increased BMUs are not well understood.

Many theoretical modeling and computational simulations have been proposed to investigate the dynamic behavior of bone remodeling [4-7]. Hernandez et al. [6] developed a kinetic model of BMUs activities to evaluate bone mass change at menopause. Although the study was based on one dimensional (1D) continuum model, it was able to predict the time course of bone loss during menopause that was consistent with clinical data [8] under the assumption of a maintained increase in bone remodeling activation, or a transient increase in bone remodeling activation but with a local deficit between bone formation and bone resorption (i.e., the amount of bone formation is less than the bone resorption at a local remodeling site), or their combinations [6]. The local bone formation deficit simulated in their model was metabolic such that the anabolic bone formation lags behind the catabolic bone resorption. We will classify this type of bone formation deficit as a metabolic deficit.

As high resolution imaging methodologies such as micro computed tomography (μCT) become more accessible, the study of trabecular bone remodeling simulation begins to take into account of the influence of cellular activities on two-dimensional (2D) or three-dimensional (3D) trabecular bone architecture [9-12]. Van der linden et al. first introduced a 3D computational simulation of bone remodeling based on μCT images of human trabecular bone [11, 13]. Their model involved both the local metabolic deficit between bone formation and bone resorption, and disconnected trabeculae during each remodeling cycle. In their paper, the bone formation deficit due to microstructural changes (such as disconnected trabeculae) was first introduced [11]. We will classify this type of bone formation deficits as a microstructural deficit. The study showed that the metabolic bone formation deficit accounted for 69-96% of bone loss in post-menopausal osteoporosis [11]. However, if the local metabolic imbalance between bone resorption and formation was the primary reason for the loss of trabecular bone during menopause, the increased remodeling activities during menopause would result in a relatively unaltered trabecular network with thinner individual trabeculae. Based on the well established studies on osteoporosis, this is not the case because the trabecular bone architecture undergoes a dramatic transformation with aging [14], especially in females [15].

In 1983, Parfitt et al. examined age-related changes in the trabecular plate thickness as well as the trabecular plate density. Their study suggested that a reduction in the plate density would be a more significant predictor of trabecular bone loss than a decrease in the plate thickness [16]. The authors proposed that the successive cycles of bone remodeling could quickly lead to a focal perforation of a trabecular plate and progressive enlargement of the perforation ultimately convert trabecular plates to trabecular rods. In vivo studies also showed perforations in trabecular plates and breakages of trabecular rods as the dominant patterns of trabecular bone loss in addition to local metabolic bone formation deficit [17]. Therefore, the perforation of trabecular plates could be an important mechanism that is responsible for the imbalanced bone turnover. Thus, the incorporation of trabecular plate perforation as one of the microstructural bone loss mechanisms would be essential for an accurate prediction of the change of trabecular bone mass, architecture and strength during menopause.

In the present work, we developed a 3D computational modeling approach to simulate the dynamic process of trabecular bone remodeling during menopause with all the parameters derived from recently published clinical data [18]. We proposed that the reduction in the bone mass and mechanical competence during menopause is resulted from the microstructural bone formation deficit to repair the architectural change of trabecular network (plate perforation, rod breakage, and isolated fragments broken off from the main architecture) caused by bone resorption (Figure 1). While bone resorption cavities were simulated to randomly locate at bone surface, bone formation was assumed to be governed by the microstructure of remodeling sites. If resorption happens at a thick trabecular plate or rod where resorption cavity does not cause an architectural change, then the bone resorption and formation is balanced (i.e., there is no metabolic or microstructural bone formation deficit); in contrast, for a thin trabecula where resorption cavity leads to an architectural change such as perforation or disconnection, bone formation would fail to refill this resorption (i.e., microstructural bone formation deficit). To test our hypothesis, we applied the simulation on 3D μCT images of human trabecular bone samples obtained from the spine and femoral neck (FN). A rigorous 3D digital topological analysis (DTA) technique was applied to identify three types of local architectural changes caused by resorption cavities: perforated holes in trabecular plates, broken trabecular rods, and isolated bone fragments broken off from the main architecture (Figure 1). The time course of average bone volume changes for both the spine and FN groups during menopausal bone remodeling simulation were compared with the previous clinical data from menopausal patients [8] to validate the feasibility of this simulation approach. The bone loss due to each type of microstructural deficit was also quantified to explore the contributions of different microstructural bone loss mechanisms to menopausal osteoporosis. In addition, the changes in architecture of trabecular bone were evaluated using both standard and individual trabeculae segmentation (ITS)-based morphological analyses [19, 20]. The latter new morphological analysis technique has been able to quantify 3D architectural changes of trabecular bone at the individual trabeculae level [20]. Furthermore, the changes in elastic properties of trabecular bone during simulated menopause were evaluated using finite element analysis (FEA). Finally, the influences of remodeling cycle and resorption cavity dimensions on the prediction of bone loss and contributions of microstructural deficits were examined in subsets of samples in both spine and FN groups (Appendix I).

Figure 1.

Examples of bone loss mechanisms due to perforation of a trabecular plate (A-B), broken trabecular rod (C-D), and isolated bone fragments (E-F) caused by random bone resorption.

Materials and Methods

Trabecular Bone Sample Preparation and μCT Imaging

Based on previous published protocols [21-24], nine cylindrical human vertebral trabecular bone samples were obtained from eight lumbar vertebrae (L3 and L4, 67.6±16.0 year-old and 6 males/2 females) and nine cylindrical human femoral neck (FN) trabecular bone samples were obtained from eight proximal femurs (63.1±13.2 year-old and 5 males/3 females). Because of the lack of relatively dense trabecular bone samples in female subjects, samples from male subjects were used to represent the healthy pre-menopausal trabecular bone (BV/TV>0.1). The axis of each trabecular bone core was aligned with the principal orientation of trabeculae. The subjects were screened to exclude metabolic bone diseases or bone cancer, and X-ray radiographs were taken to ensure that there was no evidence of damage or other bone pathologies. Each specimen with central gage length of 15 mm was scanned by a μCT system, VivaCT 40 (SCANCO Medical AG, Bassersdorf, Switzerland), at 21μm nominal isotropic resolution. Then the central ∼4×4×4 mm cubical sub-volume equivalent to 191×191×191 voxels was extracted along main anatomic directions from each reconstructed image. A global thresholding technique was applied to binarize gray-scale μCT images where the minimum between the bone and bone marrow peaks in the voxel gray values histogram was chosen as the threshold value. A previous study suggested that predictions of apparent mechanical and microstructural properties of trabecular bone using a high-resolution and 16-bit microCT image are independent of thresholding techniques and agree well with experimental measurements [25]. Subsequently, the isolated voxels or disconnected voxel-clusters were removed from binarized μCT images by the principal component analysis [26, 27]. The resulting μCT images were used for simulation of bone remodeling.

Simulation of Bone Remodeling During Menopause

In the simulation, a computational cycle represented a 40-day period. A complete bone remodeling cycle was simulated to start with one computational cycle (40-day resorption period) followed by four computational cycles (160-day formation period). These values were based on the measurements from young healthy individuals, i.e., a 42-day resorption phase and 152-day reversal and mineralization phases, reported by Eriksen et al. [28]. During each computational cycle (40-day), a certain number of hemispherical resorption cavities (42 μm deep and 126 μm in diameter) were formed and randomly placed over the bone surface (Figure 2). The reported resorption cavity depth in the literature varies from ∼20 to 60 μm depending on the methodology used [29-32]. In this study, the resorption cavity depth was set to be 42 μm, approximating the mean wall thickness (37.7∼38.1 μm) found in the transilial biopsies of normal peri-menopausal females [18]. The number of resorption cavities was strictly determined by the current total bone surface area, mean surface area of the resorption cavity, and remodeling activation frequency (Ac.f) during each resorption cycle. The determination of Ac.f was based upon a recently published clinical study where Ac.f was measured in transilial bone biopsy specimens from 50 healthy premenopausal women before (49.4±1.9 years) and 1 year after menopause (54.6±2.2 years), in 34 healthy women 13 years past menopause (60.0±7.6 years), and in 89 women with untreated osteoporosis (67.0±7.2 years) [18]. The simulated Ac.f in bone remodeling increased linearly from 0.13/year at 5 years before menopause to 0.24/year at 2 years after menopause, and continued increasing until it reached 0.37/year at 7 years after menopause, after which it remained at the same elevated level [18]. A period of 20 years, starting 5 years before and ending 15 years after menopause, was simulated for each sample in both spine and FN groups.

Figure 2.

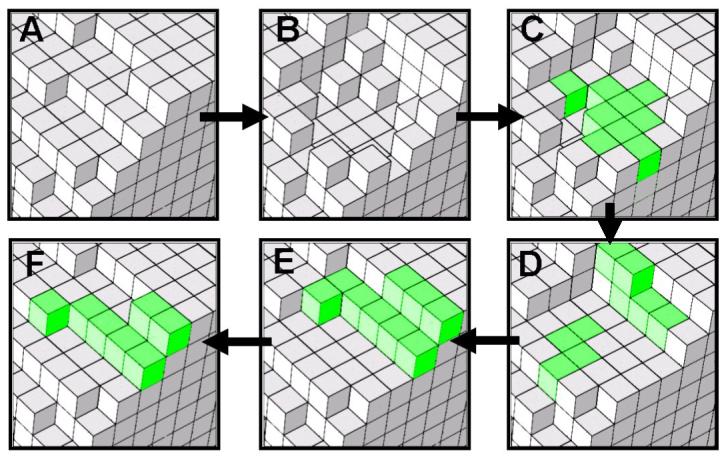
A simulated full remodeling cycle (200 days) where the resorption cavity does not cause architectural change and is refilled in four layers: (A) day 0: bone surface, (B) day 40: resorption cavity, (C) day 80: first-layer refill (new bone formation shown in green), (D) day 120: second-layer refill, (E) day 160: third-layer refill and (F) day 200: fourth-layer refill of bone formation. At day 200 (F), bone surface becomes the same as day 0 (A).

Unlike the random bone resorption, bone formation was coupled with bone resorption and the microstructural bone formation deficits depended on the local microstructural alterations of remodeling sites (perforations or breakages) in our simulation. The challenge lay in how to identify the local trabecular plate perforations or trabeculae breakages at each remodeling site in a rigorous and automated fashion. During the creation of each resorption cavity, the to-be-removed voxel went through a digital topological detection [33] under the current topological configuration to identify whether the removal of the voxel would cause a topological change on its 26-neighbor (neighboring voxels with face (6), edge (12), and vertex (8) connections) [26, 33, 34]. If the removal of the voxel were to change the current topology by creating a tunnel in its 26-neighbor [26, 33, 34], then the resorption cavity would be characterized by the perforation mechanism (Figure 1). On the other hand, if the removal of the voxel were to change the object number in its 26-neighbor [26, 33, 34], then the resorption cavity would be related to the breakage mechanism (Figure 1). Under the hypothesis of the microstructural bone formation deficit, the resorption cavity causing a perforation or breakage of a trabecula was not refilled in the followed formation period. Otherwise, all the resorption cavities were refilled through a four-layer recovery in the following 160-day formation period. i.e., there was no metabolic or microstructural bone formation deficit (Figure 2). The recovery of each layer was completed during one computational cycle (40-day). At the end of each computational cycle, isolated voxels or voxel-clusters caused by breakage or perforation of trabeculae were removed by the principal component analysis [26, 27]. The bone loss due to different mechanisms (plate perforation, rod breakage, and isolated fragments) was quantified and recorded at the end of each computational cycle.

The degree of mineralization was assumed to be constant and homogeneous for each trabecular bone specimen. Thus the relative change of bone mineral density (BMD) can be derived from the change of bone volume. The time-course of average bone loss of both spine and FN groups were compared with those reported in a clinical longitudinal study which was based on a 9.5-year observation of 54 normal menopausal women (entry age: 49.2±1.9 years) [8].

The algorithms for the simulation system were written in Microsoft Visual C⁺⁺ (Microsoft Inc., Redmond, WA, USA) and implemented on a Dell XPS PC workstation (Dell Inc., Round Rock, TX, USA).

3D Standard Morphological Analysis

To study the influence of the simulated menopausal bone remodeling on the 3D architecture of trabecular bone, the standard morphological parameters such as the trabecular number (Tb.N*), trabecular thickness (Tb.Th*), trabecular spacing (Tb.Sp*), structure model index (SMI), and connectivity density (Conn.D) were determined for each sample at the simulation time points of -5, 0, 5, 10 and 15 years from the occurrence of menopause using the standard morphological analysis software on the VivaCT 40 system (Bassersdorf, SCANCO Medical AG, Switzerland). The SMI is a measurement of the bone’s degree of rod-likeness in the form of an index ranging from 0 to 3 [35]. The Conn.D is a quantitative description of the trabecular connection [36, 37], which increases with the presence of perforations and decreases with breakages.

Individual Trabecula Segmentation (ITS)-Based Morphological Analyses

Recently, a new morphological analysis technique has been developed, in which the evaluation of trabecular structure is based on truly decomposed “individual” trabecular plates and rods [20]. To explicitly quantify the microstructural change of trabecular plates and rods, we applied the ITS-based morphological analyses to evaluate the morphological parameters for trabecular plates and rods separately. The following morphological parameters were reported for each bone sample at the time points -5, 0, 5, 10 and 15 years from the beginning of menopause in the simulation: plate tissue fraction (pBV/BV, the total volume of plate bone voxels divided by the total volume of bone voxels), mean trabecular plate thickness (pTb.Th, mm, the average thickness of trabecular plates), mean trabecular rod thickness (rTb.Th, mm, the average diameter of trabecular rods), trabecular plate and rod number density (pTb.N and rTb.N, 1/mm, the cube root of the total number of trabecular plates or rods divided by the bulk volume), mean trabecular rod length (rTb.ℓ, mm, the average length of trabecular rods), and mean trabecular plate surface area (pTb.S, mm², the average surface area of trabecular plates).

Finite Element Analysis (FEA)

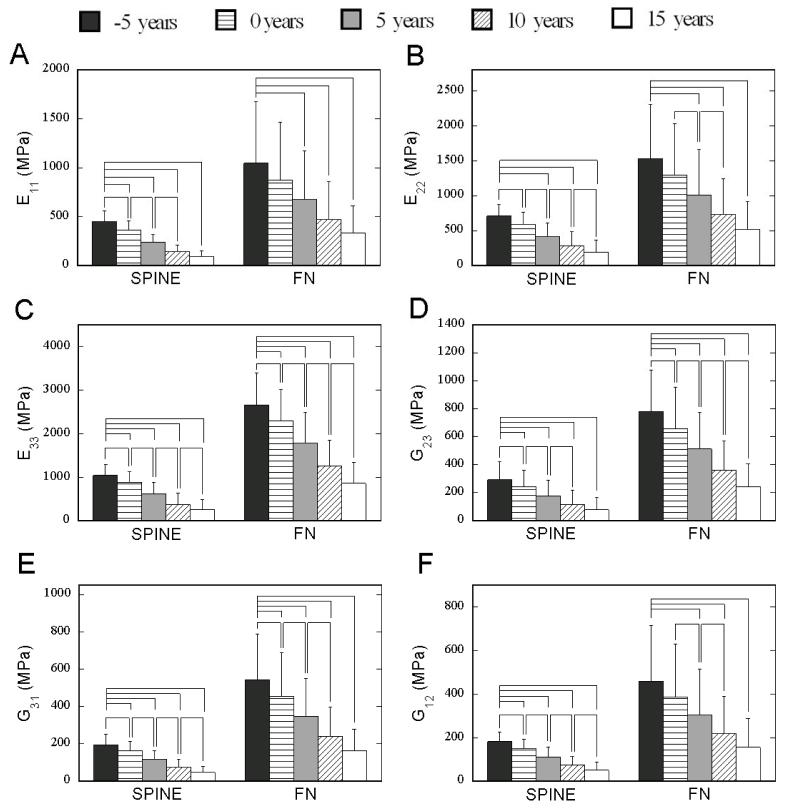
For each sample, simulated 3D images at the time points of 5 years before, 0, 5, 10 and 15 years after menopause (Figure 3) were converted to a set of voxel-based FE models by converting each voxel to an 8-node brick element. The trabecular bone tissue was modeled as an isotropic, linear elastic material with a Young’s modulus (E_s) of 15 GPa and a Poisson’s ratio of 0.3 for all models [38]. An element-by-element pre-conditioned conjugate gradient solver [39] was used for six μFE analyses on each model, representing three uniaxial compression tests along three orthogonal imaging axes and three uniaxial shear tests. Anisotropic stiffness matrix was first determined based on the results from above analyses, then a new coordinate system representing best orthotropic symmetry was calculated using an optimization procedure [40]. Transformation of anisotropic stiffness matrix to new coordinate yielded an orthotropic stiffness tensor [41]. Elastic moduli (three Young’s moduli, E₁₁<E₂₂<E₃₃ and three shear moduli, G₂₃, G₃₁, G₁₂,) were then derived from the orthotropic stiffness tensor.

Figure 3.

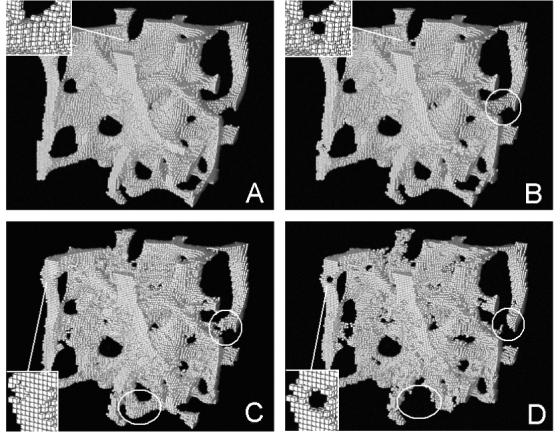
Simulations of a trabecular bone sample from the spine at (A) 5 years before menopause, (B) 0, (C) 5, and (D) 10 years after menopause. Note the perforation of a trabecular plate in the insets, the breakage of a trabecular rod in the circles, and the loss of a trabecula in the ellipses.

Statistical Analyses

All the statistical analyses were performed using KaleidaGraph 3.6 software (Synergy Software, Reading, PA) on a PC workstation. To explore quantitatively the microscopic bone loss mechanism during menopause, paired Student t-tests were performed to compare the relative change of BV/TV due to different bone loss mechanisms: plate perforation, rod breakage, and isolated fragments at the time points -5, 0, 5, 10 and 15 years from the beginning of menopause. As spine and FN groups experienced similar bone loss mechanisms, data was pooled together and the baseline was chosen as the beginning of the simulation, which corresponded to the 5 years before the menopause. To determine the time effect on the changes of morphological properties of trabecular bone during 20-year simulation, a one-way analysis of variance (ANOVA) with repeated measures was performed for the standard and ITS-based morphological parameters from both spine and FN groups, respectively. Then, a Tukey Honestly Significance Difference (HSD) post hoc test was performed to detect the significant change in each parameter relative to the previous time point as well as relative to the baseline value. We also conducted ANOVA and HSD tests for each of the six elastic moduli: E₁₁, E₂₂, E₃₃, G₂₃, G₃₁, and G₁₂ to determine the time effect on the changes in mechanical properties during the simulation.

Result

The original trabecular bone image was shown to gradually change from an intact structure into more porous and destructed one during the simulation of bone remodeling (Figure 3). In addition, the insets of Figure 3 clearly showed a trabecular plate being perforated. The procedure of trabecular rod breakage was also illustrated stepwise in Figure 3b, Figure 3c and Figure 3d (highlighted in circle): a hole was first created on the surface of a trabecular rod (Figure 3b to Figure 3c) and enlarged until breakage of the rod (Figure 3c to Figure 3d). From Figure 3c to Figure 3d, a portion of trabecula at the bottom of figures (highlighted in ellipse) was completely resorbed.

At the simulation of 15 years after menopause, the bone loss due to the trabecular plate perforation, trabecular rod breakage, and isolated bone fragments was 73.2%, 18.9% and 7.9% of the total bone loss, respectively. The statistical results showed significant difference among the three bone loss mechanisms (plate perforation > rod breakage > isolated fragments, p<0.001) at the time points 0, 5, 10 and 15 years after the menopause (Figure 4).

Figure 4.

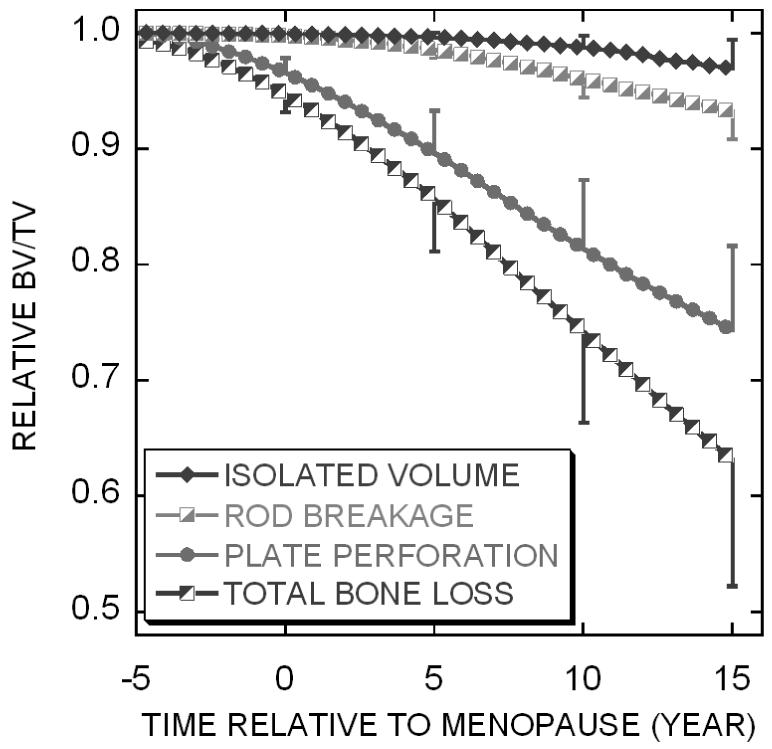
The relative BV/TV change (mean ± standard deviation) due to different types of bone loss in the menopausal bone remodeling simulation.

At the beginning of the simulation, the averaged BV/TV of spine and FN group were 0.12±0.01 and 0.23±0.08, respectively. Based upon the clinical study, a baseline was chosen to be approximately four years before menopause for both simulation results and clinical measurements. For both spine and FN groups, the time courses of the predicted bone loss pattern were consistent with the corresponding clinical measurements [8] (Figure 5).

Figure 5.

Predicted (mean ± standard deviation) spine (left) and femur (right) relative BV/TV change compared with the corresponding clinical BMD data from Recker et al. [8].

A significant effect of time was detected within both spine and FN groups for all the standard and ITS-based morphological parameters with the only exception of the ITS-based parameter rTb.ℓ in the FN group. Conn.D in both spine and FN groups significantly increased from 5 years before to 5 years after menopause and reached a plateau in the later years (Figure 6A). A continuous and significant increase relative to previous time point was detected in SMI of spine group starting at 5 years after menopause and starting at the year of menopause in the FN group (Figure 6B). In contrast, a significant decrease was found in ITS-based pBV/BV of spine group during first 10 years and a continuous and significant decrease was detected in pBV/TV of FN group throughout the 20-year simulation (Figure 6C). The change in both SMI and pBV/BV indicated a transition of plate-like structure to more rod-like structure.

Figure 6.

Changes in standard and ITS-based morphological parameters at the simulated year before or after menopause for both spine and FN groups. Bracket indicates significant difference (p<0.05).

Tb.Th* of spine and FN groups decreased significantly relative to the baseline, and a continuous and significant decrease relative to the previous time point was detected in Tb.Th* of FN group until 10 years after menopause (Figure 6D). On the other hand, no continuous change relative to the previous time point was detected in ITS-based pTb.Th of both FN and spine groups (Figure 6E). In contrast, a continuous and significant decrease was detected in rTb.Th until 5 and 10 years after menopause in spine group and FN group, respectively (Figure 6F).

Tb.N* of both spine and FN groups significantly increased in the first 10 years and reached a plateau in the later years (Figure 6G). However, ITS-based results showed a significant decrease of pTb.N in the later years of simulation and a significant increase of rTb.N until 5 or 10 years after menopause (Figure 6H and Figure 6I). In general, there was no significant change in Tb.Sp* of both spine and FN group. ITS-based pTb.S, which indicates the average surface area of trabecular plates, significantly decreased in both spine and FN groups, especially in the early years (Figure 6K). On the other hand, rTb.ℓ, the average length of trabecular rods, showed a significant decrease in spine group at the time of menopause while remained constant in FN group (Figure 6L).

Young’s moduli and shear moduli of both spine and FN groups decreased significantly during the 20-year simulation of menopausal bone remodeling (Figure 7).

Figure 7.

Changes in mechanical properties at the simulated year before or after menopause for both spine and FN groups. Bracket indicates significant difference (p<0.05).

Discussion

Previous investigations have pursued a 3D simulation of trabecular bone remodeling on a trabecular level for parametric studies of effects of resorption cavities [11, 13, 42]. Adapting the similar modeling philosophy, the present study used a rigorous DTA technique to simulate microscopic bone loss mechanisms due to the microstructural bone formation deficit during menopausal bone remodeling in 3D μCT images of human trabecular bone. Under the assumption of random bone resorption and microstructural bone formation deficit, the primary bone loss targeted at the thinnest trabecular sites due to three bone loss mechanisms: trabecular plate perforation, trabecular rod breakage, and isolated fragments of trabecular bone. In previous work, Tayyar et al. simulated bone remodeling after menopause using a simplified 3D structural model and reported that up to 40% bone loss was due to perforation during menopause [9]. In μCT based 3D simulation, Van der linden et al. found the contribution of broken trabeculae varied between 1% to 20% [11]. These studies considered and evaluated only one of the two microstructural bone loss mechanisms, the plate perforation or rod breakage, and attributed the rest of bone loss to the metabolic bone formation deficit. The current study specifically considered only the bone formation deficit due to microstructural alterations such as plate perforation and rod breakage. The simulation results suggested that it would be possible to predict the clinical time course of bone loss during post-menopausal osteoporosis based exclusively on the hypothesis of microstructural bone formation deficit. Based on this assumption, results also suggested that trabecular plate perforation accounted for more than 70% of total bone loss. This data was consistent with the in vivo evidence that the etiology of bone loss in patients proceeds via a transition from trabecular plates to rods, and eventual breakage of the rod elements [14]. Furthermore, the sensitivity study (Appendix I) confirmed that trabecular plate perforation was the dominant microstructural bone loss mechanism despite the variations in remodeling cycle and resorption cavity dimensions.

The disruption of trabecular architecture caused by focal resorption explains the change of several morphological parameters of trabecular bone. Accumulated plate perforations over time may change the trabecular plates into connected trabecular rods and result in continuous reduction in pBV/BV and increase in SMI. However, the trabecular plate perforation and trabecular rod breakage have opposite effects on Conn.D: the plate perforation increases Conn.D while the rod breakage decreases it. Therefore, at the beginning of simulation Conn.D increased due to plate perforation. At the later years of simulation, the antagonistic effects of plate perforation and rod breakage in Conn.D canceled each other.

Standard morphological analyses showed decreased Tb.Th* and increased Tb.N* in both spine and FN groups after menopausal bone remodeling. Interestingly, the changes of ITS-based trabecular thickness and number were different in plates and rods. For instance, the changes of pTb.N and rTb.N were even in opposite directions (Figure 6). According to the results of ITS-based morphological analyses, the simulated bone loss severely impaired trabecular rod thickness, but not trabecular plate thickness. However, the number and the mean surface area of trabecular plates decreased, implying fewer and smaller trabecular plates resulted from menopausal bone remodeling. On the other hand, more trabecular rods were generated by the perforation of trabecular plates and the breakage of trabecular rods, without significant change in rod length. Standard morphological parameters cannot adequately indicate the architectural changes in the sense that plate- and rod-associated parameters change differently. In contrast, the ITS-based morphological parameters are based on the measurements of individual trabecular plates and rods and thus are able to detect the subtle changes of both trabecular types.

It should be noted that no significant change occurred in Tb.Sp of both groups, which contradicted the results of existing studies that Tb.Sp increase is associated with postmenopausal bone loss. As our main focus is on menopausal bone remodeling, other age-related bone loss factors, such as the metabolic bone formation deficit (difference between the amount of bone formed and resorbed at each remodeling site) were not considered. By including metabolic bone formation deficit, we will expect a significant increase in Tb.Sp, as well as a more significant decrease in Tb.Th associating with bone loss.

In this study, we performed FE analysis to evaluate the elastic mechanical properties of trabecular bone, which has become a prevailing method for quantification of mechanical properties of trabecular bone [39, 41, 43-45]. Excellent agreements were shown between the experimental data and the predicted apparent modulus, apparent compressive, tensile strengths, and failure strains across anatomic sites [25, 46-49]. Therefore, it is appropriate in the scope of the current study for assessing the mechanical consequence of trabecular bone loss.

With decreasing bone volume, significant reductions in Young’s moduli (E₁₁, E₂₂ and E₃₃) and shear moduli (G₂₃, G₃₁ and G₁₂) were found (Figure 7). In the previous study, Guo et al. simulated effects of trabeculae thinning and trabeculae loss in idealized 3D plate and rod models [50]. Their results showed a respective 5.5% and 9.7% loss in Young’s modulus for plate model and rod model under trabeculae thinning with 5% decrease in BV/TV. In contrast, the percent reduction in Young’s modulus under random trabeculae loss with 5% decrease in BV/TV was 2.3∼33.7% for rod model and 14.7% for plate model. In this study, at the fifth year of simulation (the year of menopause), the approximate 5% drop of BV/TV corresponds to 15%∼20% decrease in Young’s moduli for both spine and FN groups (Figure 5 and Figure 7). This result is comparable to that of the idealized model with random trabeculae loss since the primary cause of the current simulation of menopausal bone loss is due to the perforation and breakage, instead of trabeculae thinning.

Unlike previous parametric studies, all the modeling parameters of the current simulation were based on pathophysiological findings and clinical data [18]. The simulation successfully predicted the menopausal bone loss patterns of spine and FN, which were observed from the BMD measurements of peri-menopausal patients [8]. It should be noted that bone resorption cavity depth and activation frequency used in the simulation were based on the longitudinal histomorphometric measurements of the same group of peri-menopausal patients [18]. Nevertheless, some caution is advised with respect to the influence of resorption cavity dimensions and bone resorption/formation period on the bone loss prediction. The sensitivity study (Appendix I) showed that the variation of bone remodeling simulation parameters had a significant impact on bone loss predicted. Therefore accurate remodeling parameter selection is critical to the simulation results.

Certain limitations should be taken into consideration. First, the entire trabecular bone structure was digitized by an image resolution of 21 μm. Given 42 μm as the resorption depth, the current image resolution may not be sufficient to represent certain intermediate status of resorption cavities through bone formation. Second, the procedure of formation of each resorption cavity was only simulated by four stages (Figure 2) while in reality it could last several days and has any possible geometry. Thirdly, to evaluate the efficacy of the remodeling simulation, we chose trabecular bone specimens from spine and FN and compared the simulated bone loss with that from the published clinical study conducted on pre-menopausal patients [8]. To make it comparable, we intended to choose the specimen which can represent the broad range of bone densities from healthy and pre-menopausal women. However, due to the lack of female donors at the age of pre-menopause, we included several specimens from male donors with a desired bone density instead of taking the specimens from female donors in their peri- or post-menopausal stage with low bone density. A recently published paper by Khosla et al. suggests that “over life, women undergo loss of trabeculae with an increase in Tb.Sp, whereas men begin young adult life with thicker trabeculae and primarily sustain trabecular thinning with no net change in Tb.N or Tb.Sp” [15]. Therefore, due to the lack of appropriate pre-menopausal female controls, we selected elder male subjects as surrogates because we considered that these male subjects had relatively intact trabecular microstructure, which might be comparable to the pre-menopausal females. We expect that the inclusion of these male subjects will not change our major conclusion that (1) microstructural plate perforation is the primary cause of menopausal trabecular bone loss and (2) the combined effect of trabeculae perforation, breakage, and isolated fragments resulted in fewer and smaller trabecular plates and more but thinner trabecular rods. However, the difference remains between the simulation and clinical groups. The prediction of the time course of menopausal bone loss pattern of the spine and FN could change due to subjects selection and this should be considered when making comparisons between the simulation and clinical results (Figure 4).

It is widely believed that trabecular bone mass and structure adapts to the mechanical environment [51]. Several computational models have been developed to interpret the influence of local mechanical stimuli to bone remodeling and suggested that the change of mechanical environment affects trabecular bone’s density, architecture, alignment and mechanical properties [52-56]. A recent study by Hernandez et al. evaluated the effects of resorption cavities on trabecular bone strength using μCT based FE models. It was discovered that cavities which were targeted at regions of high strain caused far more pronounced reductions in strength and stiffness than randomly added cavities [42]. In the present study, although resorption cavities were distributed randomly over trabecular bone surface, bone loss only occurred at the weakest regions where perforation or disconnection was likely to take place. These regions may have very high possibility to be under high strain. However, in the future, it would be important to directly incorporate the influence of mechanical stimuli in the simulation to examine its effects on menopausal bone remodeling.

In the present work, for the first time, we evaluated contributions of different microstructural bone loss mechanisms to the morphological and mechanical properties of human trabecular bone during menopause. The results suggested that plate perforation played a far more important role on bone loss than other mechanisms. Strictly based on histomorphometric data from clinical study, the current simulation successfully predicted the pattern of relative bone loss consistent with measurement from peri-menopausal patients [8]. With the development of high resolution human in-vivo μCT system, it is promising that this simulation could possibly provide a patient-specific prediction of BV/TV and bone morphology based on a current μCT scan of trabecular bone. Based on the same simulation system, effects of various treatment of osteoporosis, such as antiresorptive drugs, parathyroid hormone (PTH) and estrogen replacement, could be evaluated either by modifying the remodeling parameters (Ac.f, resorption depth, etc.) with respect to the physiological effects of the treatment, or by including additional related mechanisms such as the degree of mineralization and the positive focal bone balance (i.e., the amount of bone formation is greater than the amount of bone resorption at a local remodeling site). To achieve the above goals, in vivo animal or even patient studies would be necessary to verify the current simulation approach.

Appendix I: Influences of Remodeling Cycle and Resorption Cavity Dimensions on the model prediction in bone volume

In order to investigate the sensitivity of the remodeling simulation to the model parameters, three specimens from each group (BV/TV: 0.13±0.02 in spine and 0.25±0.06 in FN) were randomly selected. In the baseline parameter setting, the remodeling cavity was simulated as a hemispherical pit which was 42 μm in depth and 126 μm in diameter and the remodeling cycle consisted of a 40-day resorption followed by a 160-day formation. In each sensitivity simulation, either the remodeling cycle, the resorption depth, or the resorption diameter was varied. The resulted predictions of bone loss at 0, 5, 10 and 15 years after menopause were compared with those predicted using the baseline parameters. First, the influence of remodeling cycle on bone loss prediction was examined. Four sets of parameters were used: 40-day resorption/120-day formation, 40-day resorption/200-day formation, 30-day resorption/120-day formation, and 50-day resorption/200-day formation. In the latter two cases, the duration ratio between resorption and formation was fixed to that in the baseline case (1:4). The effect of resorption depth was tested by changing it from 42 μm to 21 and 63 μm. Finally the impact of resorption diameter was examined by varying it from 126 μm to 84 and 168 μm.

With a fixed 40-day resorption period, an increase in bone formation period reduced bone loss in both spine and FN groups; on the other hand, a decrease in bone formation period caused increased bone loss in the spine group but a minimal change in the FN group. With a fixed 1:4 resorption-to-formation period ratio, an increase in resorption period reduced bone loss and a decrease in resorption period raised the bone loss in both spine and FN groups. The resorption cavity dimension had a significant influence on the bone loss prediction: an increase in resorption depth or diameter accelerated the predicted bone loss while a decrease in either one reduced bone loss in both spine and FN groups (Table A1).

The predicted percentage of bone loss due to plate perforation, rod breakage, or isolated fragments under various conditions of the remodeling cycle and resorption cavity dimensions was shown in Table A2. Changes in any remodeling parameter did not affect the conclusion that (1) trabeculae perforation dominated all the microscopic bone loss mechanisms; (2) trabecular rod breakage was the secondary cause of the bone loss, and (3) the isolated bone fragments had the minimal effect on the total trabecular bone loss.

Table A1.

Predicted relative BV/TV change of spine and FN groups under the baseline parameter setting and under the change of remodeling parameters (remodeling cycle and resorption cavity dimension)

	Spine				FN
Year After Menopause	0	5	10	15	0	5	10	15
Baseline Setting*	4.6±1.5%	12.3±4.0%	21.8±6.6%	31.9±9.2%	4.4±0.5%	11.1±1.1%	19.8±2.0%	28.2±2.8%
40 Day Resorption, 120 Day Formation	4.5±1.1%	13.0±3.1%	23.6±5.3%	34.9±6.2%	4.3±0.2%	11.0±0.7%	19.7±1.7%	28.4±2.8%
40 Day Resorption, 200 Day Formation	4.3±0.9%	10.4±2.5%	18.7±4.3%	27.2±6.6%	3.9±0.1%	9.1±0.4%	15.6±1.2%	22.4±2.0%
30 Day Resorption, 120 Day Formation	6.2±1.9%	16.1±3.9%	28.6±6.8%	40.3±8.3%	5.3±0.3%	13.4±0.8%	23.5±2.0%	33.4±2.9%
50 Day Resorption, 200 Day Formation	3.4±0.8%	8.9±1.9%	16.7±4.0%	23.5±5.4%	3.3±0.2%	8.1±0.6%	13.8±1.0%	19.7±1.9%
21 μm Resorption Depth	2.1±0.7%	6.5±1.7%	13.3±3.3%	20.9±4.5%	1.9±0.2%	5.5±0.3%	10.5±0.5%	16.1±0.8%
63 μm Resorption Depth	7.6±1.7%	21.1±4.0%	39.1±5.1%	53.6±5.4%	6.5±0.3%	17.3±1.1%	31.2±2.5%	44.7±3.7%
84 μm Resorption Diameter	3.2±0.8%	8.0±1.9%	13.7±3.7%	20.1±5.3%	3.4±0.1%	7.8±0.4%	12.9±1.0%	18.1±1.5%
168 μm Resorption Diameter	4.1±1.1%	12.1±2.7%	24.1±5.9%	35.9±7.1%	3.8±0.2%	10.3±0.5%	19.5±1.7%	29.5±2.5%

^*Baseline setting: 40-day resorption followed by 160-day formation; resorption cavity: 42 μm in depth and 126 μm in diameter.

Table A2.

Predicted percentage of spine and FN bone loss due to various mechanisms under the baseline parameter setting and under the change of remodeling parameters (remodeling cycle and resorption cavity dimension) at 15 years after menopause

	Spine			FN
Bone Loss Mechanisms	Plate Perforation	Rod Breakage	Isolated Fragments	Plate Perforation	Rod Breakage	Isolated Fragments
Baseline Setting*	73.3±4.4%	18.9±1.4%	7.7±3.1%	77.0±0.4%	18.7±0.7%	4.3±3.3%
40 Day Resorption, 120 Day Formation	70.9±5.8%	19.3±1.3%	9.8±6.3%	76.6±0.5%	19.6±0.5%	3.8±2.2%
40 Day Resorption, 200 Day Formation	76.1±5.7%	17.6±1.1%	6.3±4.7%	79.1±0.3%	18.3±0.3%	2.5±2.1%
30 Day Resorption, 120 Day Formation	73.3±4.5%	18.9±1.5%	7.7±5.2%	72.2±0.6%	20.1±0.4%	7.7±1.7%
50 Day Resorption, 200 Day Formation	72.9±3.5%	21.5±1.4%	5.6±2.2%	80.2±0.2%	17.4±0.3%	2.4±2.3%
21 μm Resorption Depth	74.7±5.0%	20.2±1.5%	5.0±3.7%	75.9±0.1%	20.5±0.5%	3.6±4.4%
63 μm Resorption Depth	63.8±3.8%	22.4±2.6%	13.7±6.1%	71.6±1.2%	23.7±0.3%	4.6±0.5%
84 μm Resorption Diameter	77.8±3.7%	17.2±1.1%	5.0±2.6%	80.0±0.2%	17.1±0.3%	2.9±2.0%
168 μm Resorption Diameter	70.0±4.2%	21.7±1.7%	8.2±4.0%	75.2±0.5%	21.7±0.4%	3.1±1.7%

^*Baseline setting: 40-day resorption followed by 160-day formation; resorption cavity: 42 μm in depth and 126 μm in diameter.