Multiplicity of DNA Single-Strand Breaks Produced in pUC18 Exposed to the Direct Effects of Ionizing Radiation

Abstract

The transition of plasmid DNA from a supercoiled to an open circle conformation, as detected by gel electrophoresis, affords an extraordinarily sensitive method for detecting single-strand breaks (SSBs), one measure of deoxyribose damage. To determine the yield of SSBs, G(ssb), by this method, it is commonly assumed that Poisson statistics apply such that, on average, one SSB occurs per supercoiled plasmid lost. For the direct effect, at a large enough plasmid size, this assumption may be invalid. In this report, the assumption that one SSB occurs per pUC18 plasmid (2686 bp) is tested by measuring free base release (fbr), which is also a measure of deoxyribose damage in films prepared under controlled relative humidity so as to produce known levels of DNA hydration. The level of DNA hydration, Γ, is expressed in mol water/mol nucleotide. The yield of free base release, G(fbr), was measured by HPLC after exposure of the films to 70 kV X rays and subsequent dissolution in water. It is well known that damage in deoxyribose leads to SSBs and free base release. Based on known mechanisms, there exists a close correspondence between free base release and SSBs, i.e., G(fbr) ≅ G(ssb). Following this assumption, the SSB multiplicity, m(ssb), was determined, where m(ssb) was defined as the mean number of SSBs per supercoiled plasmid lost. The yield of lost supercoil was determined previously (S. Purkayastha et al., J. Phys. Chem. B 110, 26286–26291, 2006). We found that m(ssb) = 1.4 ± 0.2 at Γ = 2.5 and m(ssb) = 2.8 ± 0.5 to 3.1 ± 0.5 at Γ = 22.5, indicating that the assumption of one SSB per lost supercoil is not likely to hold for a 2686-bp plasmid exposed to the direct effect. In addition, an increase in G(fbr), upon stepping from Γ = 2.5 to Γ = 22.5, was paralleled by an increase in the yield of trapped deoxyribose radicals, G_dRib(fr), also measured previously. As a consequence, the shortfall between SSBs and trapped radicals, G(diff) = G(ssb) − G_dRib(fr), remained relatively constant at 90–110 nmol/J. The lack of change between the two extremes of hydration is in keeping with the suggestion that non-radical species, such as doubly oxidized deoxyribose, are responsible for the shortfall.

INTRODUCTION

The direct effect of ionizing radiation occurs when ionizations take place in the target molecule itself. In biological systems, the target of interest is DNA. These ionizations create sites of single electron loss (holes) that lead predominantly to strand breaks plus oxidized purines and to sites of single electron addition that lead predominantly to reduced bases (1–3). The same products are also formed by the ionization of water in the solvation shell of DNA, either through the capture of electrons ejected from the solvent shell or by transfer of holes generated in it (4, 5). DNA damage originating from ionization of this solvent shell plus that from ionization of the DNA itself is called direct-type damage (6).

Thus, when quantifying the yield of direct-type DNA damage, the solvation shell is included in the target mass. The degree of DNA hydration, designated as Γ, is expressed in moles of water per mole of nucleotide residue. In fully hydrated DNA, Γ lies in the range 20–22. This amount of water approximately doubles the target mass for direct-type damage. While experimental data indicate that direct-type damage for low-LET radiation may account for 30 to 50% of the total DNA damage in a living cell (7, 8), heuristic arguments suggest the contribution may be greater than 50% (9). But despite its importance, determining the yields of direct-type DNA damage has proven to be a challenge because in the experimental systems designed to produce only direct-type DNA damage, the product yields are typically below 0.1%. This explains the long-term use of particularly sensitive analytical methods such as EPR spectroscopy in this area.

Low product yields can be overcome by using plasmid DNA as the target. The introduction of a single-strand break (SSB) in a supercoiled plasmid produces a conformational change of the entire molecule that is easily detected by gel electrophoresis. In the 2686-bp plasmid pUC18, for example, from the point of view of detection, a strand break is amplified by 2 × 2686, i.e. about 5000-fold. Therefore, this approach has been used for measuring direct-type SSBs in solid-state samples (10–14) and in aqueous solutions by extrapolation to higher scavenging capacities (7, 8, 15).

Previously we studied films of plasmid pUC18 at different hydration levels between Γ = 2.5 and 22.5 (12). To elucidate the mechanisms underlying direct-type DNA damage, we quantified the radiation chemical yields (or G values) of trapped free radicals, GΣ (fr), single-strand breaks, G(ssb), double-strand breaks, G(dsb), and base damage. Base damage was detected as strand breaks formed after incubation with the base excision repair endonucleases, endonuclease III (Nth) and formamidopyrimidine-DNA N-glycosylase (Fpg), an approach used in other systems (16–19). In our work we found it difficult to reconcile changes in base damage yields with changes in the yield of trapped free radicals. As the hydration level, Γ, was increased from 2.5 to 22.5, the yield of base radicals increased, as expected, by 2.4-fold while the yield of base damage unexpectedly decreased by 3.2-fold (12). Because base damage yields should correlate directly with the yields of their precursor base radicals (1), we hypothesized that the divergence between them was caused by an artifact introduced by using an SSB assay to measure base damage (12).

The analysis assumes a Poisson distribution of SSB events (and of their base damage precursors before conversion to breaks by enzyme incubation) so that the apparent break yield can be derived from measurement of the fraction of supercoiled (i.e., containing no breaks) plasmid. The applicability of Poisson statistics at this level is routinely assumed to be valid in model systems that employ plasmid targets in solution (19–22). However, because the water content of homogeneous solutions is too large to model direct-type effects, it is necessary instead to study DNA in the solid state. In addition, a characteristic feature of the spatial distribution of ionization events from all types of ionizing radiations is that they tend to be clustered together on the nanometer scale into regions called spurs, blobs and short tracks (23, 24). It is therefore possible that multiple strand breaks are produced within the same plasmid and that the total number of individual SSB events per plasmid is greater than that assumed by the level of Poisson statistics employed. This effect had been observed in a related system where DNA damage was produced in a plasmid target by high-LET radiation (25). Thus this multiplicity argument can reconcile the disagreement we observe between radical and product yields, and invoking it is consistent with the known properties of ionizing radiation.

To quantify multiplicity, we have measured the release of free unaltered bases from the plasmid films. Unmodified bases are released from the plasmid after the damage of the deoxyribose group to which they are bound. The free base assay has been used as an estimate of the indirect damage to deoxyribose (and therefore of strand break formation) for many years (23, 26, 27), predating the use of plasmids. A good correlation between SSBs and free base release is expected because the predominate pathway to SSBs is through hydrogen abstraction from the deoxyribose by hydroxyl radicals (23), and, with only minor exceptions, these carbon-centered radicals lead to SSBs and free base release (28).

For direct damage to the DNA backbone, the degree of correlation between free base release and strand breaks is not as well established. In this work we assume that the yield of free base release is approximately equal to the yield of strand breaks, G(sb) = G(ssb) + 2 G(DSB) ≅ G(fbr). Because G(ssb) ≫ G(DSB), the approximation G(ssb) ≅ G(fbr) also holds. This assumption is based on both direct and indirect evidence. Direct evidence comes from studies of d(CGCGCG)₂ crystals. The measured yields of strand break products (29) were used to calculate the lower limit for the yield of SSBs upon irradiation at room temperature, G(ssb) ≥ 110 ± 20 nmol/J. The yield of free base release (30) was found to be G(fbr) = 124 ± 8 nmol/J. The G(fbr)/G(ssb) ratio was less than or equal to 1.1 ± 0.2. Indirect evidence comes from the knowledge that ionization of the DNA backbone, through the direct effect, results in neutral carbon-centered radicals produced by deprotonation of the backbone radical cations (2, 31). Because other radical cation reactions, such as release of base, are predictably unfavorable and have not been observed, the majority of deoxyribose damage proceeds through one of the five neutral carbon radicals (32). As stated above, with only minor exceptions, these radicals are known to lead to SSBs and free base release (28). Based on this evidence, it is anticipated that G(fbr)/G(sb) will prove equal to 1.0 to within better than ±20% and quite possibly within a few percent.

Here we report the yields of unaltered free base release, G(fbr), measured using films of plasmid pUC18 prepared at the same time and from the same stock as films prepared in our earlier work (13). Assuming that G(fbr) provides an estimate of the strand break yield, we determine the multiplicity of strand breaks in pUC18.

METHODS

Film Preparation

Solid-state films of pUC18 (2686 bp) were equilibrated to hydration levels of Γ ~ 2.5 and 22.5 using the same batch of pUC18 and prepared at the same time as for the samples used in ref. (12). The procedure for preparing the films has been described previously (13, 14). The films were stored for ~1 year at room temperature.

Irradiation and Dosimetry

The DNA samples were irradiated at room temperature, under air, and inside Suprasil quartz tubes (wall thickness of ~0.15 mm). X rays were generated by a Varian/Eimac OEG-76H tungsten-target tube operated at 70 keV and 20 mA. The samples and X-ray tubes were enclosed in a lead-lined box with 20 mm between the sample and the X-ray window. The X-ray beam was filtered by a 40-μm-thick aluminum foil.

The dose rate at the face of the quartz tubes was 2.2 kGy/min, measured by FTW-60 series radiochromic film (Far West Technology, Inc., Goleta, CA). The wall of the sample tube attenuated the beam by 51 ± 6%, measured by EPR-based alanine-pellet dosimetry (6), resulting in a sample dose rate of 1.1 kGy/min. The variance in attenuation by the quartz wall is negligible. Since the same quartz sample tubes and same sample sizes were used previously in the measurement of SSBs, the sample container cannot be a significant variable in the comparison of free base release with SSBs. Additionally, it is important to note that, based on product yields measured previously² (13, 30), variations between different types of sample containers, plastic and quartz, indicate that our dosimetry was consistent from one sample holder to another. Furthermore, we have measured the attenuation of the X-ray beam by the sample itself using EPR-based Teflon dosimetry (33). For the DNA films used in this study, which weighed 140–180 μg, self attenuation is less than 2%; i.e., the dose is effectively uniform over the entire sample volume.

HPLC

After irradiation at room temperature, pUC18 films were dissolved immediately in a known volume of aqueous 50 mM sodium acetate (pH 6.8) containing 10 μM uracil and then stored at 4°C for 24 h. Prior to HPLC, the samples were incubated at 75°C for 30 min. This was done to follow the protocol used previously to measure the yield of total SSBs (13), where it was found that heat-labile sites accounted for 22 to 33% of the total SSB yield. It is noteworthy, however, that this heat treatment has little impact on the yield of free base release. The solution either (1) was filtered through Nanosep^® 3K Omega ultrafiltration device (Pall Co., East Hills, NY), retaining fragments >~5 bp (i.e., 3000 MW cutoff), at 5600g for 20 min at room temperature or (2) was treated with spermine to a final concentration of 20 mM to precipitate the DNA. In protocol 1, the filtrate was assayed by HPLC, while in protocol 2, 100% ethanol was added to bring the solution to 85–90% ethanol (v/v). The solution was then kept at room temperature for 3–4 h, and the precipitate was pelleted at 5600g for 20 min at room temperature. The precipitate was decanted and washed twice with 50 μl of cold 85% ethanol. After the supernatant was lyophilized (or vacuum dried), the residue was dissolved in nuclease-free water (using the same volume that was used when the films were dissolved initially), and then assayed by HPLC. Protocols 1 and 2 have been applied to other genomic DNA (unpublished data), and both protocols gave the same results.

The solution, at pH 6.8, was fed to a Waters Alliance^™ HPLC system equipped with a 2690 solvent delivery system, Waters 996 PDA detector, and an auto sampler. The unaltered free base was separated on a Phenomenex Columbus C-18 reverse-phase column (4.6 ± 250 mm, 5 μm bead size, 110 D pore size) at 303 K using 40 mM ammonium acetate (pH 6.8) as a mobile phase and by applying a linear gradient of 0.9–10% acetonitrile over 25 min. The unaltered free bases were detected by their absorbance at 254 nm and were quantified by comparison with uracil as an internal standard as described in ref. (30). Waters Millennium^® software was used to integrate the chromatographic peaks.

RESULTS

The radiation-induced release of the unaltered free bases, cytosine (Cyt), guanine (Gua), thymine (Thy), and adenine (Ade), was measured using HPLC. Figure 1 compares the chromatograms for doses of 0, 40 and 50 kGy delivered to pUC18 films hydrated to Γ = 2.5 and 22.5. As shown in Fig. 2, the increase in free base was a linear function of dose over the range of 0–90 kGy. For each of the four bases, the chemical yields were calculated from the slope of the linear least-squares fit to the data at doses of ≤ 90 kGy. For the yield of total free base release, G(fbr), the line was fitted to data points obtained by summing over the four individual bases at each dose. The chemical yields of the four bases and total base release are given in Table 1.

FIG. 1.

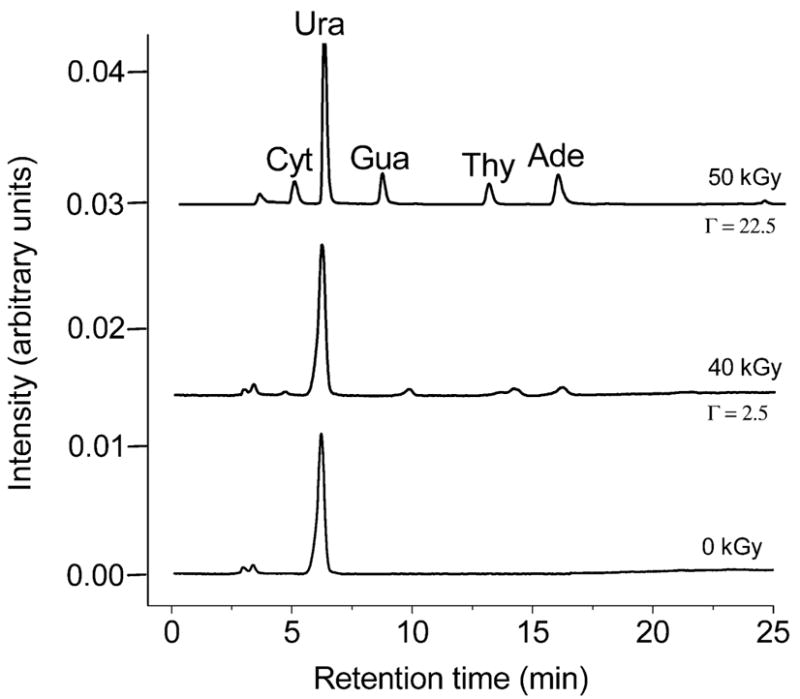
HPLC chromatograms (monitored at 254 nm) are shown for pUC18 films incubated at Γ = 2.5 and 22.5 and X-irradiated with 40 kGy and 50 kGy, respectively. For a dose of 0 kGy, a Γ = 2.5 film is shown; the Γ = 22.5 is effectively the same. Cyt = cytosine, Gua = guanine, Ade = adenine, Thy = thymine, and Ura = uracil; the latter was used as an internal standard. Note that in comparing peak intensities, it is important to take into account the difference in target mass between Γ = 2.5 and Γ = 22.5.

FIG. 2.

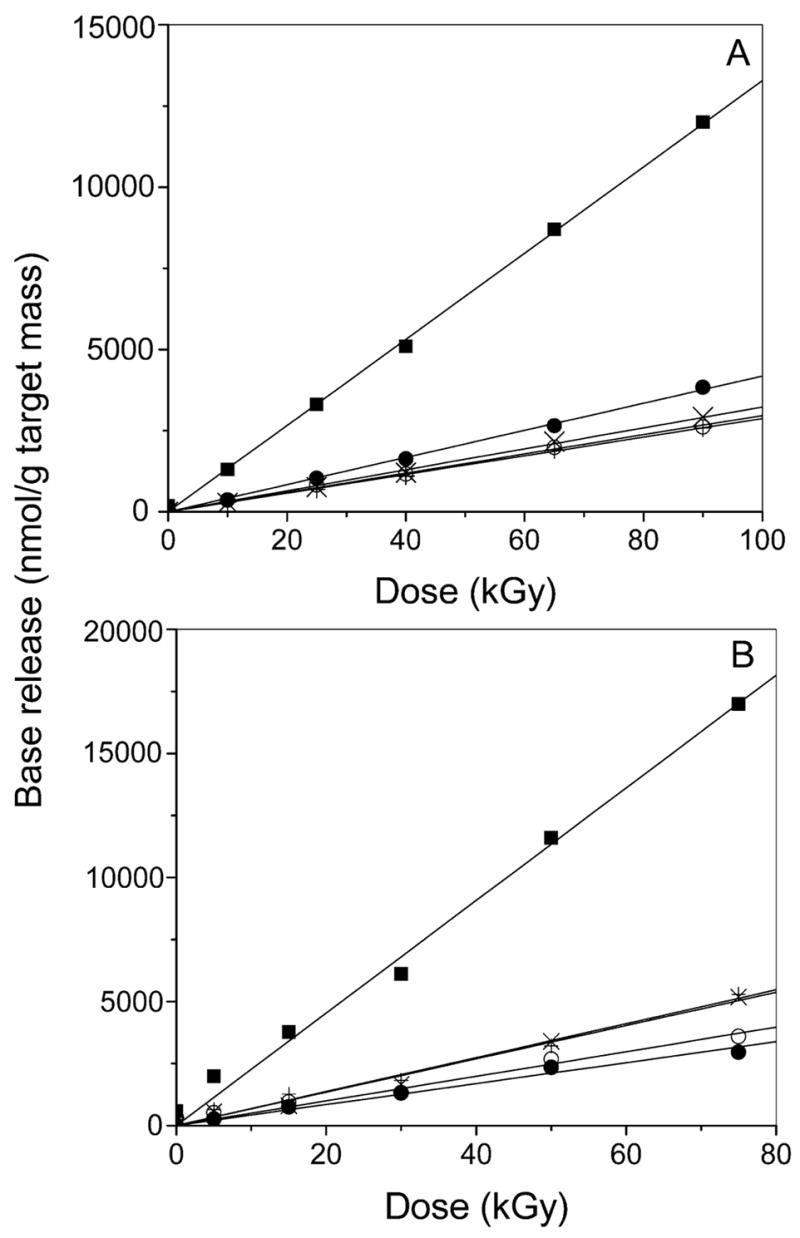
Dose–response curves for the release of cytosine (●), guanine (○), thymine (×), adenine (+), and total free base (■) from X-irradiated pUC18 films at room temperature under Γ = 2.5 (panel A) and Γ = 22.5 (panel B). The solid line shows the linear least-squares fit to the data for ≤ 90 kGy. Note that here free base release is plotted using the target mass, i.e., the mass of DNA plus its solvent shell, as in our previous work (13).

TABLE 1.

Radiation Chemical Yields in nmol/J for Free Base Release in pUC18 Plasmid DNA Films and Calculation of the Multiplicity of Single-Strand Breaks

Γ	G(Cyt)	G(Gua)	G(Thy)	G(Ade)	G(fbr)	G(sc-loss)a	m(fbr)b
2.5 ± 0.2	41 ± 1	29 ± 1	34 ± 1	30 ± 1	134 ± 4	92 ± 16	1.5 ± 0.3
22.5 ± 1.1	46 ± 2	47 ± 7	64 ± 9	55 ± 5	212 ± 21	66 ± 8	3.2 ± 0.5

^aG(sc-loss) values were reported under G total(ssb) in Table I of ref. (13).

^bFree base release multiplicity = m(fbr) = G(fbr)/G(sc-loss).

We found that the yield of total free base release, G(fbr), increased by 60% as the hydration was increased from a Γ of 2.5 to 22.5, where “total” refers to prompt plus heat-labile sites. This is in contrast to our previous measurements of total SSB yields (13), which were based on the loss of supercoiled pUC18; these values are given under G(sc-loss) in Table 1. G(sc-loss) decreased by 30% over the same hydration range.

The free base release multiplicity, m(fbr), is defined as the mean number of free base released per supercoil lost, m(fbr) = G(fbr)/G(sc-loss). Values of m(fbr) are given in the last column of Table 1. In calculating m(fbr), it was assumed that yields of free base release can be compared with the loss of supercoil, even though the irradiation was at room temperature for the former and 4 K for the later. Evidence that the yield of free base release is insensitive to irradiation temperature comes from the study of d(CGCGCG)₂ (30); also, the loss of supercoil appears to be insensitive to irradiation temperature based on G(sc-loss) being the same for pUC18 at Γ = 2.5 X-irradiated at 4 K and room temperature.² Under this assumption, the free base release multiplicity was found: m(fbr) = 1.5 ± 0.3 at Γ = 2.5 and m(fbr) = 3.2 ± 0.5 at Γ = 22.5. Because the solvation shell is part of the target mass, the target mass doubles in going from Γ = 2.5 to 22.5. It is noteworthy that, when the target mass doubled, the multiplicity doubled.

DISCUSSION

Single-Strand Break Multiplicity

The values of single-strand break multiplicity, m(ssb), can be calculated from the experimentally determined values of m(fbr) using the assumption of G(fbr)/G(ssb) = 1, which is discussed in the Introduction. In calculating m(ssb), we first separate out the possibility that a small amount of free base release may be generated via the indirect effect in the Γ = 22.5 samples. This allows for an estimate of G_dir(fbr), the yield of free base release due to the direct effect alone. At Γ = 22.5, an indirect effect due to OH radicals formed in the water lying beyond the inner shell of Γ ≤ 10 (4, 5) is expected. If all of the OH radicals formed in the outer shell lead to deoxyribose damage, then the OH radical yield, G(OH^●), would equal the yield of free base release produced indirectly, G_indir(fbr). By subtraction of the OH radical yield, G(fbr) − G(OH^●), the lower limit for the yield of free base release due to direct-type damage, G_dir(fbr), is obtained (column 2, Table 2). This is the lower limit because competing reactions of the OH radical, such as H₂O₂ formation and base attack, result in G_indir(fbr) − G(OH^●). The upper limit assumes that no OH radicals attack the DNA backbone.

TABLE 2.

Comparative Radiation Chemical Yields in nmol/J for Trapped Deoxyribose Radicals, Free Base Release and Direct SSBs

Γ	G(OH●)a	Gdir(fbr)b	G(dsb)c	Gdir(ssb)d	m(ssb)e	Gdir(ssb)/G(dsb)	GdRib(fr)f	G(diff)g
2.5 ± 0.2	0	134 ± 4	4.8 ± 0.9	124 ± 4	1.4 ± 0.2	26 ± 5	33 ± 5	91 ± 4
22.5 ± 1.1	23	>189 ± 21	3.5 ± 0.5	>182 ± 21	>2.8 ± 0.5	>52 ± 10	79 ± 12	>103 ± 21
		<212 ± 21		<205 ± 21	<3.1 ± 0.5	<59 ± 10		<126 ± 21

^aA yield of 70 nmol/J (5) was applied to the water target mass, which consists of the water lying beyond the hole transfer layer: Γ-10 = target mass = 12.5 waters/nucleotide for Γ = 10.

^bG_dir(fbr) ≥ G(fbr) − G(^●OH) and ≤G(fbr).

^cValues from ref. (12).

^dG_dir(ssb) = G(fbr) − 2 × G(dsb), assuming each SSB of the DSB gives a free base release.

^eSSB multiplicity = m(ssb) = G_dir(ssb)/G(sc-loss).

^fG_dRib(fr) values were reported in Table I of ref. (13).

^gShortfall = G(diff) = G_dir(ssb) − G_dRib(fr).

Another source of free base release, although minor, is DSBs. Each DSB should correlate with the release of two bases. Therefore, G_dir(ssb) = G_dir(fbr) − 2 × G(DSB), which is greater than or equal to G(fbr) − G(OH^●) − 2 × G(dsb). Column 4 of Table 2 gives the values of G_dir(ssb), and division by G(sc-loss) from Table 1 gives the values of m(ssb): 1.4 ± 0.2 at Γ = 2.5 and 2.8 ± 0.5 to 3.1 ± 0.5 at Γ = 22.5.

The SSB multiplicity is found to be greater than one, supporting our previous proposal (12) that the induction of direct-type SSBs in plasmid DNA cannot be measured accurately using an analysis based on a Poisson process that assumes an average of one SSB per plasmid. In general the SSB yield determined by the release of unmodified bases, G(fbr), exceeds the SSB yield, G(ssb), calculated by applying a simple level of Poisson statistics to the loss of supercoiled pUC18. This inequality increases as the multiplicity increases.

A multiplicity greater than 1.0 is consistent with known properties of radiation tracks and the size of pUC18. The radius of pUC18 at gamma 22.5, assuming a density of 1.4 g/ml and a spherical shape, would be 10 nm. For an average spur of 62.5 eV in water, LaVerne and Pimblott (34) find $\sigma ({\text{e}}_{\text{aq}}^{-})=2.23\text{nm}$ and, based on a Gaussian distribution, 60% of the radicals are within a radius of σ and 98% within 2σ. About six primary radicals are generated by a 60 eV energy deposition. The radius of a spherical plasmid is about five times larger that the spur radius, and the volume is larger by two orders of magnitude. Therefore, a single spur has a high probability of being contained within a single molecule and, given the relative scale, more than one spur per molecule is probable. From this perspective, to avoid a multiplicity greater than 1.0, an asymmetric shape is required, a shape whereby pUC18 folding upon itself is minimized. Under the slow evaporation methods used in forming our films, intramolecular aggregation is favored over intermolecular aggregation. While the idealized shape of a sphere overestimates the actual volume/surface ratio, the relative volumes of the plasmid and cluster argue that one would expect m(ssb) to be greater than 1.0.

Ratio of SSBs to DSBs

The ratio of G_dir(ssb) to G(dsb), where G_dir(ssb) is now based on free base release measurements, is given in column 7 of Table 2. The value of 26 ± 5 for Γ = 2.5 is high compared to values reported previously (10, 13, 35, 36) that were determined by loss of supercoil in plasmids under low hydration conditions and gave ratios ranging from 7 to 19. We suggest that literature values for G_dir(ssb)/G(dsb) based on solid-state plasmid samples are most likely smaller than the actual values. While this discrepancy is small at the lowest hydration level of Γ = 2.5, it increases when DNA is fully solvated. As the multiplicity increases, the additional SSBs are not accompanied by any additional loss of supercoiled plasmid. Consequently, the G_dir(ssb)/G(dsb) ratio had appeared to be independent of Γ (10, 13). We now report that this is not the case; the value of the ratio increases with increasing Γ. The increase, primarily due to the increase in G_dir(ssb), reflects an increase in non-clustered damage relative to clustered damage. We believe this has important implications for understanding how track expansion is influenced by DNA hydration.

Comparison of Free Base Release with Free Radical Trapping

Unaltered free base release is a direct consequence of deoxyribose oxidation. Fbr generated by the indirect effect is initiated by OH radical attack, which results in hydrogen abstraction from one of the five deoxyribose carbons, and free base release generated by the direct effect is initiated by one-electron loss from the DNA followed rapidly by deprotonation from one of the five deoxyribose carbons. These five carbon-centered radicals, whether formed through the direct or indirect effect, are unstable intermediates that lead to free base release (27–29, 37). In the solid state, deoxyribose radicals generated by the direct effect can be stabilized at low temperatures, and the yields of these trapped radicals can be measured.

Yields of deoxyribose radicals trapped, G_dRib(fr), previously reported in pUC18 films irradiated at 4 K (13), are presented in column 8 of Table 2. It is of interest to compare G_dRib(fr) with SSBs due to direct-type damage, G_dir(ssb). As seen in Table 2, the increase in G_dir(ssb) is comparable to the increase in G_dRib(fr). This finding differs from our earlier observation (13) in which G(ssb) [more accurately called G(sc-loss)] actually decreased. The increase in SSBs with increased free radical trapping is consistent with current mechanistic models for strand breaks (31).

It was noted previously that the yield of deoxyribose radicals trapped in pUC18 at Γ = 2.5 is insufficient to account for the yield of SSBs (13). In that work, no explanation could be offered as to why this shortfall, G(diff) = G_dir(ssb) = G_dRib(fr), appeared to shrink to zero as the DNA hydration was increased to Γ = 22.5. It is now clear that G(diff) does not shrink to zero; this was an artifact stemming from what now appears to be the incorrect assumption that m(ssb) = 1. In light of the values of G(diff) reported in the last column of Table 2, we find that the shortfall is relatively independent of DNA hydration. Also, it is notable that the G(diff) values observed here for pUC18 films are comparable to the values, ranging from 60 to 100 nmol/J, measured in films of oligodeoxynucleotides (30, 38). The persistence of the shortfall from Γ 2.5 to 22.5 is consistent with our working hypothesis that there exists a non-radical species such as doubly oxidized deoxyribose that is responsible for the shortfall (13, 30).

Detection of Base Damage by SSB Induction

As we have argued previously (12), attempts to use the plasmid system to detect base damage by using base excision repair enzymes to produce strand breaks almost certainly resulted in measured yields that are much smaller than the actual yields. Now this can be readily understood. The yield of direct-type base damage is about three times the yield of free base release in an oligodeoxynucleotide at Γ = 2.5 (38). Using this same multiplier for pUC18 at Γ = 2.5, the yield of SSBs generated from base damage would be ~3 × 1.4 = ~4.2, and the sum of base damage plus SSBs gives m = ~4.2 + 1.4 = ~6. At Γ = 22.5, the multiplicity of base damage plus SSBs increases to ~13. It is important to recognize that these multiplicities reflect the number of damages produced in an entire plasmid and not the number of damages stemming from a single ionization cluster within the plasmid. These findings indicate that when enzymatically induced SSBs are used to detect direct-type base damage in plasmid DNA, the majority of the base damage is missed.

Plasmid Size

If strand break multiplicity in pUC18 leads to values of G(ssb) that are less than G(sc-loss), then measurements of G(sc-loss) in a larger plasmid should result in an even larger discrepancy. In our earlier study (14), we were surprised to find that G(ssb) measured in pEC films was 40% less than G(ssb) measured in pUC18 films. It was difficult to explain why the larger 10,810-bp DNA should behave differently than the smaller 2686-bp DNA. A straightforward explanation for this unexpected result would be that m(ssb), for two plasmids of different size, will be larger for the larger plasmid. When using loss of supercoil as a measure of SSBs, the number of SSBs missed in pEC would have been greater than the number of SSBs missed in pUC18.

CONCLUSIONS

The free base release multiplicity, defined as the mean number of free bases released per supercoil lost, increased from m(fbr) = 1.5 ± 0.3 at Γ = 2.5 to m(fbr) = 3.2 ± 0.5 at Γ = 22.5. Using free base release, we estimate the single-strand break multiplicity, m(ssb), to be 1.4 ± 0.2 at Γ = 2.5 and 2.8 to 3.1 at Γ = 22.5. Because m(ssb) > 1.0, direct-type SSBs in plasmid DNA cannot be measured accurately using an analysis based on a Poisson process that assumes an average of one SSB per plasmid. Therefore, the calculated yield of direct SSBs, G_dir(ssb), is found to be larger than reported previously, particularly at Γ = 22.5.

The ratio of SSB yield to DSB yield increased at the higher level of hydration, going from 26 ± 5 at Γ = 2.5 to 52-59 ± 10 at Γ = 22.5.

An increase in yield of trapped deoxyribose radicals, G_dRib(fr), upon stepping from Γ of 2.5 to 22.5, was paralleled by an increase in G_dir(ssb). But the shortfall, G(diff) = G_dir(ssb) − G_dRib(fr), changed little, remaining in the range of 90–110 nmol/J.