Abstract
CXC and CC chemokines are involved in numerous biological processes, and their function in situ may be significantly influenced by heterodimer formation, as was recently reported, for example, for CXC chemokines CXCL4/PF4 and CXCL8/IL8 that interact to form heterodimers that modulate chemotactic and cell proliferation activities. Here we used molecular dynamics simulations to determine relative association free energies (overall average and per residue) for homo- and heterodimer pairs of CXC (CXCL4/PF4, CXCL8/IL8, CXCL1/Gro-α, and CXCL7/NAP-2) and CC (CCL5/RANTES, CCL2/MCP-1, and CCL8/MCP-2) chemokines. Even though structural homology among monomer folds of all CXC and CC chemokines permits heterodimer assembly, our calculated association free energies depend upon the particular pair of chemokines in terms of the net electrostatic and nonelectrostatic forces involved, as well as (for CC/CXC mixed chemokines) the selection of dimer type (CC or CXC). These relative free energies indicate that association of some pairs of chemokines is more favorable than others. Our approach is validated by correlation of calculated and experimentally determined free energies. Results are discussed in terms of CXC and CC chemokine function and have significant biological implications.
Chemokines are small (8-12 kDa) homologous proteins that are involved in many biological processes, ranging from chemotaxis (1) and degranulation of different types of leukocytes (2) to hematopoiesis (3) and angiogenesis (4, 5). They are generally subdivided into four subfamilies based on relative positioning of the first two of four highly conserved cysteine residues: CXC, CC, C, and CX3C (6). In the largest chemokine subfamilies, CC and CXC, the first two cysteines are adjacent (CC motif) or separated by a single nonconserved amino acid (CXC motif), respectively. The C chemokines lack the first and third of the conserved cysteines, and the CX3C chemokines have three amino acids between the first two cysteine residues. The sequence identity between chemokines varies from less than 20% to over 90%. Nevertheless, chemokines from different subfamilies adopt essentially the same monomer folds. Each monomer has a flexible N-terminal domain, followed by an N-terminal loop, a three-stranded antiparallel β-sheet region, and a prominent C-terminal α-helix (7).
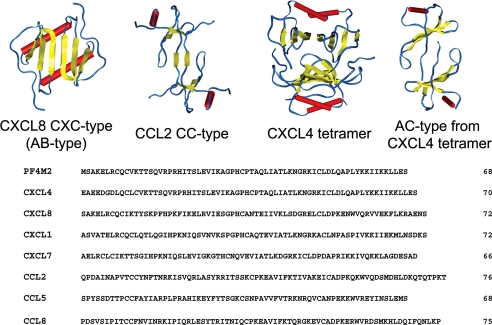
All chemokines oligomerize into dimers, and some also into tetramers (8, 9). Three-dimensional folds of dimers are similar among members of a subfamily. However, despite having strikingly similar monomer folds, CXC and CC monomers associate differently (7). The more globular CXC-type (previously called AB-type (10)) dimer is formed by extension of the three-stranded β-sheet from each monomer into a six-stranded β-sheet, on top of which are the two C-terminal α-helices, running antiparallel, as illustrated for CXCL8/IL82 (11) in Fig. 1. In contrast, CC chemokines form elongated end-to-end type dimers through contacts between their N termini, as shown for CCL2/MCP-1 (12) in the same figure. For CC-type dimers, the two C-terminal helices run almost perpendicular to each other on opposite sides of the molecule. CXC-type dimers can also associate to form tetramers, as exemplified with CXCL4/PF4 (10) in Fig. 1. Tetramerization has also been observed for CXCL7/NAP-2 (13) but not for CXCL8/IL8 or CXCL1/Gro-α.
FIGURE 1.
Structures and amino acid sequences of CXC and CC chemokines. The folded structures of homodimers of CXC chemokine CXCL8 (11) and CC chemokine CCL2 (12) are illustrated to exemplify three-dimensional structures of all CXC and CC chemokine homo-oligomers. The structure of the tetramer of CXCL4 (10) is also shown, along with the CXCL4 AC-type dimers as explained in the text. The amino acid sequences of CXC (PF4M2, CXCL8, CXCL4, CXCL1, and CXCL7) and CC (CCL5 and CCL2) chemokines are shown at the bottom of the figure.
CXC and CC chemokine quarternary structure is determined primarily by which amino acid residues are present at the particular inter-subunit interface (7, 14). Therefore, monomers of different chemokines may be mutually substitutable if the arrangement of individual residues at a given monomer-monomer interface in a heterodimer is energetically and sterically more favorable than that in either homodimer. Indeed, we showed recently, using NMR and surface plasmon resonance, that at least three members of the CXC family, CXCL4, its N-terminal chimera PF4M2 (15), and CXCL8, readily exchange subunits to form heterodimers that exhibit similar equilibrium dimerization constants (Kd) as observed for homodimers (16, 17). It has also been shown that CC chemokines, CCL3/MIP-1α and CCL4/MIP-1β, CCL2, and CCL8/MCP-2, can form heterodimers (18). Moreover, it has been suggested that heterodimerization between members of CXC and CC subfamilies can also occur as follows: chemokine CXCL4 and CC chemokine CCL5/RANTES (19), as well as CC secondary lymphoid tissue chemokine (CCL21/SLC) and CXC B cell attracting chemokine-1 (CXCL13/BCA-1) (20). The functional result is that heterodimerization dramatically modulates the biological activities of these chemokines. For example, the presence of angiogenic CXCL8 in solution with anti-angiogenic CXCL4 increases the anti-proliferative activity of CXCL4 against endothelial cells (16). The co-presence of CXCL4 and CXCL8, in turn, attenuates the CXCL8-mediated rise in intracellular calcium in a myeloid progenitor cell line and enhances CXCL8-induced migration of bone marrow-derived pro-B-cells (Baf/3) (16, 17).
This investigation, which was motivated by these studies (16, 17), explores the energetic basis for heterodimerization of CXC and CC chemokines. Here we used the molecular mechanics and Poisson-Boltzmann surface area (MM-PBSA) approach to calculate binding free energies (21-23) and to predict which pairs of CXC and CC chemokines would likely form in solution. Free energy calculations from MD simulations have been used in various biological applications (24-28), thus establishing their usefulness to better understand protein-protein associations (29). The MM-PBSA approach has emerged recently as a rapid computational approach that is broadly applicable to molecular systems that differ substantially in structure and/or are of comparable size, such as protein-protein complexes (21, 23, 28, 29). Here we investigated formation of chemokine complexes by evaluating absolute binding free energies and comparing them to experimentally determined values.
EXPERIMENTAL PROCEDURES
Molecular Dynamics Simulations—Molecular dynamics (MD) simulations were performed for homodimers (CXCL8, CXCL4, CXCL1, CXCL7, CCL5, CCL2, and CCL8), heterodimers (CXCL4/CXCL8, PF4M2/CXCL8, CXCL4/CXCL1, CXCL4/CXCL7, CXCL8/CXCL1, CXCL8/CXCL7, and CXCL1/CXCL7; two types of CCL2/CCL5, CCL2/CCL8, CCL2/CXCL8, CCL5/CXCL8, CCL2/CXCL4, and CCL5/CXCL4; and two complexes with CCL5 mutants, CCL5(E26A)/CXCL4 and CCL5(44AANA47)/CXCL4) and homotetramers of CXCL4 and PF4M2. Starting protein structures for molecular dynamics simulations were built based on x-ray or NMR structures taken from the Protein Data Bank (30) without change. The corresponding Protein Data Bank entries were 1RHP, 1PFM, 1IL8, 1MSG, 1NAP, 1RTO, 1DOM, and 1ESR. The tetramer of CXCL4 is formed as a sandwich of dimers (AB and CD). Therefore, the homodimer of CXCL4 for the simulation was obtained by deleting one of the dimers (CD) from x-ray-derived tetramer. Heterodimers of CXCL4/CXCL8 (or other CXC chemokines) were formed by replacing one of the monomer subunits from an AB-type dimer of native CXCL4 with a monomer subunit from CXCL8 after superimposing the CXCL4 and CXCL8 homodimer. For CXCL4/CXCL8, a heterodimer of AC-type (adjacent monomers from dimers forming a sandwich) was also built by replacing C subunit of CXCL4 with a monomer subunit from CXCL8. For CCL2/CXCL8 and CCL5/CXCL8, two types of heterodimers were built, CXC-type (using CXCL8 homodimer as a template) and CC-type (using CC chemokine partner homodimers as a template).
Fig. 1 shows the three-dimensional structures of CXCL4 tetramer, CXC (or AB)-type and AC-type dimers of CXCL4 derived from tetramer, and CC-type dimer exemplified by CCL2. All initial structures were built using the Insight II program (Biosym Technologies Inc., San Diego). Hydrogen atoms were added to the crystal structure using HBUILD module of the CHARMM program (31). The ionization state of the system was set at pH 5.0, the pH value used in our experimental studies (16). At this pH, the net charge on monomers was +9 for CXCL4, +6 for CXCL8, +8 for CXCL1, +7 for CXCL7, +6 for CCL5, +7 for CCL2, and +5 for CCL8. Amino acid sequences of these chemokines are shown in Fig. 1. Although native CXCL4 and CXCL7 have 70 amino acid residues, coordinates for the first 6 residues in CXCL4 and first 4 residues in CXCL7 are not provided in the PDB files. Therefore, truncated CXCL7 has been used in this study, and absent N-terminal residues in CXCL4, which are important in forming CC-type heterodimers, have been added based on homology modeling using PF4M2.
MD simulations were performed using the c29b2 version of CHARMM (31). After an initial equilibration of 0.005 ns, we performed a 1-ns trajectory simulation for each hetero- and homodimer. The time step in the simulations was 1 fs. Coordinates were saved at 1-ps time intervals, resulting in a total of 1000 configurations for analysis. All complexes were simulated in boxes of 74 × 63 × 63 Å3 or 70 × 65 × 65 Å3 with explicit solvent molecules described by the TIP3P model, along with periodic boundary conditions. To make the total charge of the box 0, chloride ions were added to neutralize the system. Simulations were carried out using the CHARMM 22 all-hydrogen force field (32) with a dielectric constant of 1. 2000 steps of steepest descent minimization, followed by gradual heating to 300 K, and 5000 steps of system equilibration preceded each simulation run. The temperature during runs was maintained at 300 K. van der Waals (vdW) interactions were truncated at 13 Å using a shifted smoothing function, whereas electrostatic interactions were calculated using the Particle Mesh Ewald method (33). The SHAKE method was employed to constrain bond lengths involving hydrogen atoms (34).
Free Energy Calculations—The MM-PBSA method combines an
explicit molecular mechanical (MM) model for the solute with a continuum
Poisson-Boltzmann method for the solvation free energy. In this method, a
molecular dynamics simulation is initially performed on a protein complex
solvated explicitly using periodic boundary conditions. Then the solvent is
removed, and the binding free energy, ΔG, is calculated for
each time increment according to Equation
1,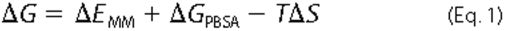
where ΔEMM is the change in molecular mechanical energy upon binding; ΔGPBSA is the change in solvation energy, and TΔS is the entropic contribution to binding. An estimate of the vibrational entropic contribution to the binding energy can be done by using normal mode (NM) analysis (35).
Strictly speaking, when oligomerization is considered, separate trajectories for each monomer and oligomer should be acquired and analyzed. However, we assumed that the conformation of the monomer subunit in both free and bound states is the same and estimated ΔG from snapshots over the trajectory of the complex only. Therefore, energetic contributions from bonds, angles, and torsion angles are essentially not considered.
Chemokine dimerization or tetramerization was described by the following
set of equilibria shown in Equation
2,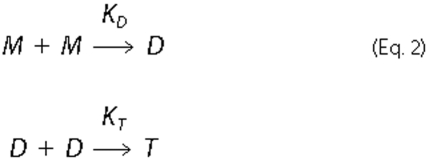
M, D, and T indicate monomer, dimer (homo- or hetero-), and tetramer (CXCL4
only) states, respectively. The following thermodynamic cycle (Equation 3) was
used to evaluate the free energy of dimer or tetramer formation in water,
 ,
,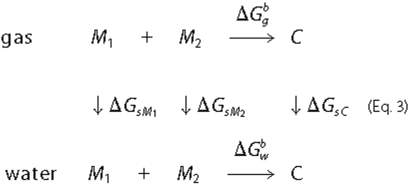
Here 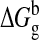 is the free
energy of dimer or tetramer formation in the gas phase.
ΔGsM1,
ΔGsM2, and
ΔGsC are the free energies of solvation
for molecule 1 (M or D), molecule 2 (M or D), and for the complex (D or T),
respectively.
is the free
energy of dimer or tetramer formation in the gas phase.
ΔGsM1,
ΔGsM2, and
ΔGsC are the free energies of solvation
for molecule 1 (M or D), molecule 2 (M or D), and for the complex (D or T),
respectively. 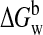 was
determined as the sum shown in Equation
4,
was
determined as the sum shown in Equation
4,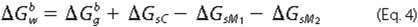
All energy calculations were performed using the MM-PBSA approach (21-23) and the CHARMM program (31). Comparisons were then made between homo-oligomers and hetero-oligomers.
In the MM-PBSA method,
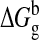 is calculated from
molecular mechanics interaction energies shown in Equation
5,
is calculated from
molecular mechanics interaction energies shown in Equation
5,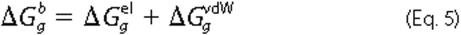
Here 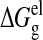 is the
electrostatic free energy, and ΔGgvdW is
the vdW interaction free energy between two molecules in the gas phase. Only
complexes, and not monomers, were simulated; therefore, only nonbonded
contributions to the free energy have been considered.
is the
electrostatic free energy, and ΔGgvdW is
the vdW interaction free energy between two molecules in the gas phase. Only
complexes, and not monomers, were simulated; therefore, only nonbonded
contributions to the free energy have been considered.
The solvation free energy was determined as the sum of electrostatic (ΔGelg) and non-electrostatic (ΔGnon-elg), terms as indicated in Equation 6,
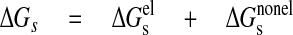 |
(Eq.6) |
The electrostatic contribution to the solvation free energy,
ΔGel, was calculated using the finite difference
Poisson-Boltzman method with the PBEQ module in CHARMM
(31). Both
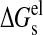 and
and
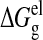 were calculated
simultaneously in two steps. For the initial Poisson-Boltzmann calculation,
the grid size was set to 1.0 Å. For the second step, the grid size was
decreased to 0.45 Å, and the box was filled 85%. The dielectric constant
for the interior of protein is usually considered to be in the range from 2 to
4. For this study it was set to 2, and the dielectric constant of water was
set to 80.
were calculated
simultaneously in two steps. For the initial Poisson-Boltzmann calculation,
the grid size was set to 1.0 Å. For the second step, the grid size was
decreased to 0.45 Å, and the box was filled 85%. The dielectric constant
for the interior of protein is usually considered to be in the range from 2 to
4. For this study it was set to 2, and the dielectric constant of water was
set to 80.
The non-electrostatic contribution to the solvation free energy includes vdW interactions between solute and solvent, ΔGvdW, and is the free energy required to create the solute cavity in the solvent, ΔGcav. The vdW and cavity terms were represented by a linear function of the total solvent-accessible surface area shown in Equation 7,
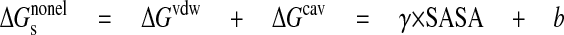 |
(Eq.7) |
where γ = 0.00542 kcal/(mol·Å2), and b = 0.92 kcal/mol (36). For the solvent-accessible surface area calculation, the radius of the probe sphere was set to 1.4 Å.
Contributions to the binding free energy per residue were calculated as the difference in energy of a given residue in the monomer from that in the dimer (dimerization) or in the dimer and in the tetramer (tetramerization). Electrostatic and non-electrostatic contributions were considered separately, using the approach described above.
Vibrational entropy was estimated from normal mode analysis using VIBRAN module of CHARMM program (31). The estimation was based on 40 snapshots taken from the last 800 ps of the trajectory (500 ps for tetramers) with an even interval.
RESULTS
CXC Heterodimers of CXCL4 and CXCL8—To validate our MD-based approach, we first investigated CXC chemokines CXCL4 and CXCL8, because heterodimerization between them has been demonstrated experimentally, and structural evidence as to how they associate as heterodimers is available (16). Three observations from these calculations on CXCL4 and CXCL8 support our approach as follows: 1) the time dependence of root mean square deviations (r.m.s.d.) for backbone heavy atoms; 2) time-averaged fluctuations per residue; and 3) expected free energy variations of residues at the homo- and heterodimer interfaces.
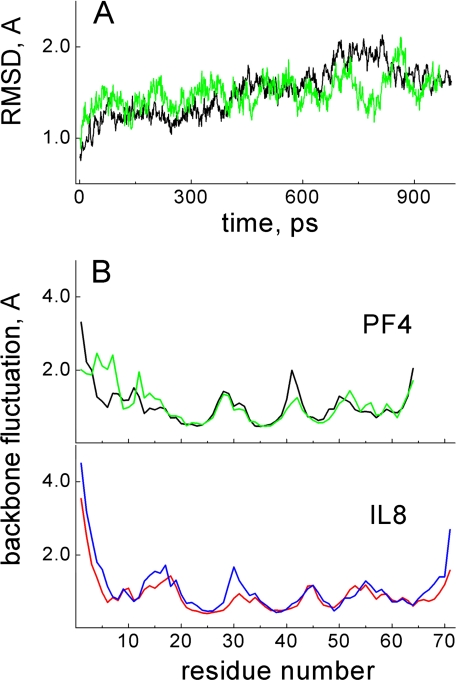
Fig. 2A illustrates the time dependence of r.m.s.d. for backbone heavy atoms (averaged) of CXCL4 subunit in homodimer (black) and heterodimer with CXCL8 (green). Because the first six N-terminal residues (and last four C-terminal residues) in each dimer deviated substantially from their initial positions compared with other residues during MD simulations, these more flexible residues were not included in the r.m.s.d. values reported. Initial r.m.s.d. values for all structures (Fig. 2A) leveled out at about 200-300 ps (500 ps for CXCL4 tetramer, data not shown), and then fluctuated within less than 0.5 Å over the remainder of the simulation. The relative constancy of r.m.s.d. values over the last 700-800 ps of the trajectory suggests formation of stable homo- and heterodimers.
FIGURE 2.
Backbone averaged r.m.s.d. values and per residue fluctuations. A, from an MD simulation (1-ns trajectory), r.m.s.d. values averaged over backbone heavy atoms are shown for CXCL4 subunit in the homo-(black) and heterodimers (green). B, time-averaged backbone Cα fluctuations are plotted per residue for the CXCL4 homodimer (black) and for the CXCL4 subunit in the CXCL4/CXCL8 heterodimer (green). Time-averaged backbone Cα fluctuations are plotted per residue for the CXCL8 homodimer (blue) and for the CXCL8 subunit in the CXCL4/CXCL8 heterodimer (red). Fluctuations were averaged over the last 800 ps of the 1 ns trajectory.
Structural stability is further supported by viewing time-averaged fluctuations per residue, as plotted in Fig. 2B for CXCL4 and CXCL8. Here the amplitude of fluctuations correlates well with elements in the folded structures of these CXC chemokines. For example, residues experiencing the largest fluctuations are located within the more flexible N and C termini and the loops, whereas residues within the less flexible, well structured regions (three-stranded β-sheet and C-terminal α-helix) show considerably smaller r.m.s.d. values (less than 1 Å) (37-41). This correlation supports the idea that our calculations reflect actual structural effects. Moreover, time-averaged fluctuations reflect essentially the same trends as observed experimentally (11, 37-41). Additionally, fluctuational amplitudes are essentially the same for homodimers and heterodimers, further supporting thermodynamic stability of the CXCL4/CXCL8 heterodimer.
Calculated free energies are given in Table 1, and electrostatic and non-electrostatic contributions to these free energies are plotted per residue in Fig. 3, e.g. for CXCL4 and CXCL8 homodimers and heterodimers. For comparison, experimentally determined free energies are provided in Table 2. Although these calculated free energies are comparable with those determined using MM-PBSA approach with other proteins (28, 29), it is readily apparent that the calculated energies far exceed those determined experimentally. Clearly this discrepancy lies in the limits of the calculated energies, as we will discuss later under “Discussion.” Nevertheless, trends in these energies can be compared. In this regard, although hydrophobic interactions contribute the most and about equally to the energetics of CXCL4 and CXCL8 homodimer formation, electrostatic interactions contribute more to the energetics of homodimer formation for CXCL8 than for CXCL4. In fact, homodimerization of CXCL4 is electrostatically unfavorable, with a total electrostatic contribution to the binding free energy of +5.54 kcal/mol for the homodimer and +12.3 kcal/mol for the homotetramer (Table 1).
TABLE 1.
Calculated binding free energies
Calculated binding free energies and individual contributions from electrostatic (el) and non-electrostatic (nonel) terms. The column NM gives an estimate of the vibrational entropic contribution to the binding energy determined using normal mode analysis. All energies are averaged over last 500 or 800 ps of 1-ns trajectories and are expressed in kcal/mol.
 |
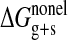 |
NM |
ΔGcalc |
||
|---|---|---|---|---|---|
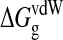 |
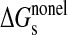 |
||||
| Homodimers (tetramers where noted) CXC | |||||
| CXCL4/PF4 | 5.54 | −31.6 | −4.14 | 9.30 | −20.9 |
| PF4M2 | 4.22 | −30.4 | −4.27 | 10.7 | −19.8 |
| CXCL4/PF4 (tetramer) | 12.3 | −35.5 | −9.48 | 9.22 | −23.5 |
| PF4M2 (tetramer) | 21.9 | −42.7 | −11.3 | 10.7 | −21.4 |
| CXCL8/IL8 | −16.5 | −25.3 | −3.33 | 8.81 | −36.3 |
| CXCL1/Gro-α | 3.47 | −32.3 | −4.24 | 8.84 | −24.2 |
|
CXCL7/NAP-2
|
1.05
|
−31.1
|
−4.27
|
11.7
|
−22.7
|
| CC | |||||
| CCL2/MCP-1 | 2.18 | −39.8 | −4.36 | 10.4 | −31.5 |
| CCL5/RANTES | −4.07 | −35.8 | −4.57 | 9.57 | −34.9 |
|
CCL8/MCP-2
|
−7.16
|
−40.4
|
−5.27
|
9.18
|
−43.7
|
| Heterodimers, CXC | |||||
| CXCL4/CXCL8 | −1.78 | −32.7 | −4.14 | 8.01 | −29.7 |
| PF4M2/CXCL8 | 0.69 | −32.8 | −4.67 | 9.12 | −27.7 |
| CXCL4/CXCL1 | 2.13 | −33.4 | −4.35 | 10.1 | −25.5 |
| CXCL4/CXCL7 | −0.22 | −25.7 | −3.79 | 8.70 | −21.0 |
| CXCL8/CXCL1 | −1.39 | −36.9 | −5.16 | 8.78 | −34.7 |
| CXCL8/CXCL7 | −6.42 | −23.2 | −4.01 | 11.3 | −22.3 |
|
CXCL7/CXCL1
|
1.54
|
−36.7
|
−4.78
|
9.31
|
−30.7
|
| Heterodimers, CC | |||||
| CCL2/CCL5 (CXC) | −2.37 | −26.9 | −4.30 | 8.69 | −24.7 |
| CCL2/CCL5 (CC) | −0.18 | −40.5 | −4.70 | 9.18 | −36.2 |
| CCL2/CCL8 (CXC) | −1.37 | −42.4 | −5.52 | 8.91 | −40.4 |
|
CCL2/CCL8 (CC)
|
−1.69
|
−42.5
|
−5.12
|
9.15
|
−40.2
|
| Heterodimers, CXC-CC mixed | |||||
| CXCL4/CCL5 (CXC) | 4.31 | −26.8 | −3.99 | 8.91 | −17.6 |
| CXCL4/CCL5 (CC) | −25.5 | −28.5 | −4.12 | 9.00 | −49.1 |
| CXCL4/CCL5 E26A (CC) | −9.83 | −25.9 | −4.01 | 9.15 | −30.6 |
| CXCL4/CCL5 44AANA47 (CC) | 0.01 | −22.3 | −3.21 | 8.97 | −16.5 |
| CXCL4/CCL2 (CXC) | −3.91 | −33.4 | −4.69 | 8.82 | −33.2 |
| CXCL4/CCL2 (CC) | 1.70 | −24.8 | −3.50 | 9.21 | −17.4 |
| CXCL8/CCL2 (CXC) | −3.49 | −38.9 | −5.47 | 8.82 | −39.1 |
| CXCL8/CCL2 (CC) | 3.30 | −33.9 | −3.92 | 8.97 | −25.5 |
| CXCL8/CCL5 (CXC) | 1.58 | −34.3 | −4.52 | 10.2 | −27.0 |
| CXCL8/CCL5 (CC) | −0.70 | −34.1 | −4.27 | 9.05 | −28.7 |
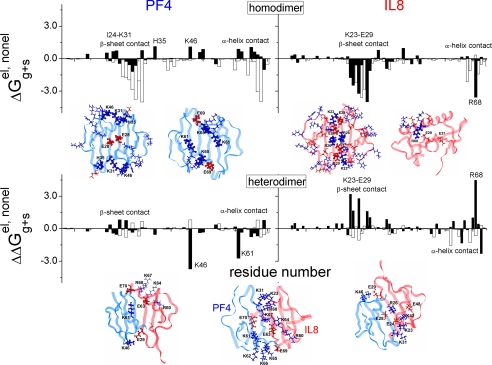
FIGURE 3.
Binding free energies per residue for CXCL4 and CXCL8 homo- and heterodimers. Calculated free energies are plotted per residue for CXCL4 homodimers, CXCL8 homodimers, CXCL4 in CXCL4/CXCL8 heterodimers, and CXCL8 in CXCL4/CXCL8 heterodimers. Electrostatic (solid bars) and non-electrostatic (open bars) contributions to the free energy are shown. These contributions are calculated as the difference between contributions to the free energy of heterodimer and homodimer formation. Consequently, residues that have positive contributions are energetically unfavorable, whereas those residues that demonstrate a negative contribution are energetically favorable. Some residues most affected by subunit-subunit interactions in each respective dimer are labeled. Structures of CXCL4 and CXCL8 homo- and heterodimers are shown as insets below each respective panel, with two views each for CXCL4 and CXCL8 homodimers, and three views for the CXCL4/CXCL8 heterodimer. CXCL4 subunit is shown in blue and CXCL8 subunit is shown in red in each complex.
TABLE 2.
Experimental binding free energies
Experimentally determined dissociation constants for CXC and CC chemokine homo- and heterocomplexes and free energies were calculated using the equation ΔG = -RT InKd. Numbers in parentheses correspond to those in our reference list.
| Homo- or heterodimers (tetramers where noted) | Experimental conditions | Kd, exp, × 10−6m | ΔGexpa |
|---|---|---|---|
| kcal/mol | |||
| CXCL4/PF4 | Low salt,b pH 5.0, 30 °C, NMR | 90 (9, 56, 57) | −5.6 |
| PF4M2 | Low salt,b pH 5.0, 30 °C, NMR | 500 (13) | −4.6 |
| CXCL4/PF4 (tetramer) | Low salt,b pH 5.0, 30 °C, NMR | 3 (9, 56, 57) | −7.7 |
| PF4M2 (tetramer) | Low salt,b pH 5.0, 30 °C, NMR | 10 (13) | −6.9 |
| CXCL8/IL8 | 20 mm sodium phosphate, 150 mm NaCl, pH 7.4, 37 °C, titration microcalorimetry | 18 (±6) (58) | −7.2 |
| Phosphate-buffered saline, pH 7.4, 8 °C, ultracentrifugation | 21 (±10) (59) | −6.0 | |
| 20 mm sodium phosphate, 150 mm NaCl, pH 7.4, 25 °C, ultracentrifugation | 14 (±4) (58) | −6.6 | |
| Phosphate-buffered saline, pH 7.2, 37 °C, sedimentation | 4 (±2.2) (60) | −7.7 | |
| 50 mm phosphate, pH 5.7, 20 °C, sedimentation | <0.1 (60) | −9.4 | |
| Phosphate-buffered saline, pH 7.4, 20 °C, chemical cross-linking | 0.77 (±0.37) (61) | −8.2 | |
| CXCL1/Gro-α | 50 mm sodium phosphate, 100 mm NaCl, pH 5.0, 20 °C, ultracentrifugation | 43 (±14) (62) | −5.9 |
| 50 mm sodium phosphate, 100 mm NaCl, pH 7.0, 20 °C, ultracentrifugation | 4 (±3) (62) | −7.2 | |
| 20 mm Tris-HCl, pH 5.0, 40 °C, ultracentrifugation | 769 (±176) (63) | −4.5 | |
| 20 mm Tris-HCl, pH 5.0, 200 mm salt, 40 °C, ultracentrifugation | 59 (±4) (63) | −6.1 | |
| No salt, pH 5.0, 40 °C, NMR | 435 (63) | −4.8 | |
| CXCL7/NAP-2 | 50 mm sodium phosphate, 100 mm NaCl, pH 5.0, 20 °C, ultracentrifugation | 102 (±36) (62) | −5.4 |
| 50 mm sodium phosphate, 100 mm NaCl, pH 7.0, 20 °C, ultracentrifugation | 53 (±20) (62) | −5.7 | |
| Low salt, pH = 5.0, 30 °C, NMR | 75 (13) | −5.7 | |
| 250 mm NaCl, pH 7.0, 30 °C, NMR | 300 (13) | −4.9 | |
| Phosphate-buffered saline, pH 7.4, 20 °C, chemical cross-linking | 0.32 (±0.07) (61) | −8.7 | |
| CCL2/MCP-1 | Phosphate-buffered saline, pH 7.4, 8 °C, ultracentrifugation | 33 (±18) (59) | −5.8 |
| CCL5/RANTES | 25 mm acetate, pH 3.7, 35 °C, NMR | 35 (64) | −6.3 |
| CXCL4/CXCL8 | Biacore | 0.04 (17) | −9.8 |
| 20 mm NaCl, pH 5.0, 40 °C, NMR | 1 (16) | −8.6 | |
| PF4M2/CXCL8 | 20 mm NaCl, pH 5.0, 40 °C, NMR | 0.7 (16) | −8.8 |
| CXCL4/CCL5 (CC) | Biacore | 0.8 (19) | −8.1 |
| CXCL4/CCL5 E26A (CC) | Biacore | 3.8 (19) | −7.2 |
| CXCL4/CCL5 44AANA47 (CC) | Biacore | Not observed (19) |
Free energies are recalculated from experimentally derived dissociation constants taking into account the temperature, at which experiments were carried out.
Low salt means less than 20 mm equivalents of NaCl.
For CXCL4 homodimer formation, it was originally proposed that proximity of the two interfacial Glu-28 glutamates would be electrostatically unfavorable (10). Proximity of the two glutamates is illustrated in the CXCL4 CXC-type dimer structure inserts to Fig. 3. However, this is not the case, as positively charged residues are distributed around both glutamates. In fact, our results show that CXCL4 homodimerization is electrostatically unfavorable because of proximity of positively charged residues His-35, Lys-46, Lys-61, Lys-65, and Lys-31 which oppose each other at the homodimer interface. The side chain conformation of Lys-31, for example, changes significantly during the simulation because of electrostatic repulsion from Lys-46 on the opposing subunit. On the other hand, favorable electrostatic interactions occur between Glu-69 on one subunit and helix residues Lys-61 and Lys-65 on the other. Nevertheless, hydrophobic interactions among interfacial β-strand residues Ile-24, Leu-27, and Val-29 and C-terminal helix residues Tyr-60, Ile-64, Leu-67, and Leu-68, which become less accessible to water molecules when in the dimer state, drive CXCL4 homodimer formation.
In contrast to the situation with CXCL4, electrostatic interactions are favorable for CXCL8 homodimer formation (Fig. 3, top right panel), with a total electrostatic contribution of -16.5 kcal/mol (Table 1) compared with +5.5 kcal/mol for the CXCL4 homodimer. The net charge on the CXCL8 monomer is +6 at pH 5. However, the total number of charged amino acid residues is 26 (10 acidic and 16 basic), unlike CXCL4 which has 17 (4 acidic and 13 basic residues). The distribution of these residues in CXCL8 is such that all charged groups at the interface between subunits (Lys-23, Glu-24, Arg-26, and Glu-29) benefit energetically from dimerization. This is visualized in the CXCL8 structure inserts to Fig. 3. Even though two arginines (Arg-26) are brought close together in the dimer, the symmetric distribution of positively and negatively charged residues creates the favorable surroundings. In addition, C-terminal helix residue Arg-68 in the homodimer is positioned in a more electrostatically favorable environment, proximal to Glu-29 and Glu-E37 from two β-strands of the other subunit.
For CXCL4/CXCL8 heterodimer formation, there are significant changes in energetic contributions. In this case, CXCL4 gains electrostatically and loses non-electrostatically (in the tetramer), whereas CXCL8 loses electrostatically and gains non-electrostatically (Table 1). These changes drive heterodimerization. The per residue free energies for CXCL4/CXCL8 heterodimer formation are plotted for individual CXCL4 and CXCL8 subunits in the lower part of Fig. 3, and three different views of the structure of this heterodimer are illustrated below these plots. As with homodimer formation, the most significant changes occur at the interface between subunits, because overall conformations of each chemokine monomer remain essentially the same. From the CXCL4 subunit side, Lys-46 and Lys-61 show the largest gain in electrostatic energy, because in the CXCL4 homodimer Lys-46 is situated near Lys-31, whereas in the heterodimer it is proximal to Glu-29 and Glu-37 of the CXCL8 subunit (Fig. 3, bottom, left-most structure) in the CXCL4/CXCL8 heterodimer. This now favorable electrostatic interaction promotes CXCL4/CXCL8 heterodimerization. A similar case presents itself for Lys-61, which in the CXCL4 homodimer is grouped with three other lysines (Lys-62, Lys-65, and Lys-66) and a glutamate (Glu-69) on the adjacent monomer. In the CXCL4/CXCL8 heterodimer, Lys-61 is now proximal to additional negatively charged group (Glu-63) from the C-terminal helix of CXCL8 (Arg-60, Glu-63, Lys-64, Lys-67, Arg-68, and Glu-70) (middle structure). This association creates a favorable electrostatic environment. CXCL4 residues His-35 and Arg-49 also benefit energetically from disruption of the CXCL4 homotetramer, where His-35 is close to Arg-49 from an opposing subunit. In the CXCL4/CXCL8 heterodimer, both residues are in a more electrostatically favorable environment. In addition, CXCL4 residues Arg-20, Arg-22, His-23, and Lys-50 and all four C-terminal lysines (Lys-61, Lys-62, Lys-65, and Lys-66) gain electrostatic energy in the CXCL4/CXCL8 heterodimer. These highly favorable associations drive CXCL4 tetramer disruption and CXCL4/CXCL8 heterodimer formation. Experimentally, CXCL4/CXCL8 heterotetramers have not been observed, at least up to protein concentrations in the millimolar range (16).
From the CXCL8 side, C-terminal residues Glu-63 and Glu-70 of CXCL8 also favor heterodimer formation, because they are brought into proximity with four lysines and only one glutamate of the CXCL4 C-terminal helix (Lys-61, Lys-62, Lys-65, Lys-66, and Glu-69; Fig. 3, bottom, middle structure). On the other hand, CXCL8 residues Lys-23, Arg-26, and Glu-9 (Fig. 3, right-most structure) do not contribute favorably to heterodimer formation because of a loss in the balance of electrostatic charge in the CXCL8 homodimer. Thus, in the heterodimer, Lys-23 (CXCL8) is near Lys-31 (CXCL4), rather than Glu-29 in the CXCL8 homodimer, and even though Glu-29 still has a positively charged neighbor in the heterodimer (Lys-46 of CXCL4), Lys-46 is at a greater distance apart. In addition, Arg-68 of CXCL8 in the heterodimer loses its neighbor Glu-29 to the less favorable interaction with Lys-31 of CXCL4.
These environmental changes among residues of CXCL4 and CXCL8 subunits in the heterodimer result in quaternary structural shifts. In the heterodimer, CXCL4 and CXCL8 subunits are closer together and are oriented slightly differently from those in each homodimer. In particular, the C-terminal helix of the CXCL8 subunit is closer to the C-terminal helix from the CXCL4 subunit, because of more favorable non-electrostatic contributions from residues at the contact interface (in particular, Pro-53, Gln-59, Val-62, and Leu-66). These quaternary structural shifts, however, have little, if any, effect on the overall conformation of each monomer subunit. As mentioned above, NMR experimental investigations have provided evidence only for formation of the CXC-type CXCL4/CXCL8 heterodimer (16, 17). In fact, if we calculate energies for another CXCL4 homodimer type that could form in solution, namely a β-sheet sandwich AC-type dimer (10) (see Fig. 1), time-averaged fluctuations for residues located at the inter-subunit interface are substantially larger than those for AB-type (CXC-type) homodimers, whereas fluctuations for residues located within the loops/turns and termini are essentially the same. Larger fluctuations at the interface indicate that AC-type dimers would be less stable than AB-type dimers, which is consistent with these NMR data, as well as with previous conclusions based on the x-ray structure of native CXCL4 (10).
CXC Heterodimers with CXCL1/Gro-α and
CXCL7/NAP-2—Structural homology among all CXC chemokines suggests
that other combinations will also form heterodimers. Having validated our
approach with CXCL4 and CXCL8, we extended the study to two other CXC
chemokines, CXCL1 and CXCL7. Binding free energies for CXCL1 and CXCL7
homodimer formation are given in Table
1, along with those for heterodimer formation with each other, as
well as with CXCL4 and CXCL8. As for CXCL4 and CXCL8 discussed above, binding
energies are high compared with those determined experimentally
(Table 2). Reasons for this lie
in limitations to our approach and will be detailed under
“Discussion.” For now, one should consider that although
calculated values are not absolute, comparisons or trends between/among
calculated free energies do provide a realistic picture. Ideally, formation of
heterodimers is deemed likely when the binding energy of heterodimerization is
less than binding energies for each or at least one of corresponding
homodimers, i.e.
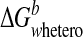 ≤
≤
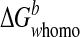 . In this regard, CXCL1
should readily form heterodimers with CXCL4 and CXCL8, whereas it has a lower
probability to form heterodimers with CXCL7. The least likely heterodimers to
form among this group of CXC chemokines are CXCL8/CXCL7 and CXCL4/CXCL7.
. In this regard, CXCL1
should readily form heterodimers with CXCL4 and CXCL8, whereas it has a lower
probability to form heterodimers with CXCL7. The least likely heterodimers to
form among this group of CXC chemokines are CXCL8/CXCL7 and CXCL4/CXCL7.
Because CXCL7 and CXCL1 have 70-80% sequence homology with CXCL4, similar per residue conclusions regarding homodimer formation of CXCL7 and CXCL1 can be made, as was discussed above for CXCL4. The primary difference is that electrostatic contributions to the binding free energy are more favorable for dimerization of CXCL7 and CXCL1 than for CXCL4. In CXCL7 like CXCL4, repulsive effects from negatively charged glutamates positioned at the inter-subunit interface are quelled by surrounding positively charged residues, whereas in CXCL1 that interface is composed entirely of non-polar residues that allow closer packing of side chains.
Structural insight into why CXCL1 and CXCL7 form heterodimers with CXCL4 and CXCL8 comes from analysis of per residue contributions to the free energy, as illustrated in supplemental Fig. 1 for heterodimers CXCL4/CXCL1 (A), CXCL4/CXCL7 (B), CXCL8/CXCL1 (C), and CXCL8/CXCL7 (D). When CXCL8 is paired with CXCL1 or CXCL7, charged residues Lys-23, Arg-26, Glu-24, and Glu-29 of CXCL8 (positioned at the inter-subunit interface) oppose heterodimer formation. This follows from the electrostatic nature of CXCL8 homodimerization, as discussed above. By placing these charged residues of CXCL8 in more unfavorable electrostatic surroundings, any CXC chemokine partner perturbs the symmetry of charge distribution found in the CXCL8 homodimer. Lys-23, Arg-26, Glu-29, and Arg-68 all display the most positive free energy values. On the other hand, Lys-60 of CXCL1 (or Lys-56 and Lys-62 of CXCL7) which is (are) proximal to Glu-63 and Glu-69 from CXCL8 in the heterodimer, compensate partially for this. Alternatively, charged residues from both CXCL4 and CXCL1 (or CXCL7), although being less influential electrostatically, do contribute mostly positively to CXCL4/CXCL1 (or CXCL4/CXCL7) heterodimer formation. Although less important to CXCL4/CXCL1 heterodimer formation, nonelectrostatic contributions to the free energy from CXCL8 are significant, favoring CXCL8/CXCL1 heterodimerization.
CC Heterodimers—As with CXC chemokines, structural homology among all CC-chemokine monomers makes CC heterodimer formation likely. To explore this, we performed the same free energy calculations on three CC chemokines, CCL5, CCL2, and CCL8. CCL2 and CCL8 form homodimers solely via contacts among N-terminal hydrophobic residues that form a short anti-parallel β-sheet (see Fig. 1). In CCL5, in addition to hydrophobic residues between Thr-7 and Tyr-14, charged residues Asp-6 and Arg-47 also contribute to homodimerization. Our calculations indicate that formation of a CCL5/CCL2 CC-type heterodimer is energetically favorable, with a ΔGw = -36.2 kcal/mol for the heterodimer, compared with -31.5 kcal/mol for CCL2 homodimer and -34.9 kcal/mol for CCL5 homodimer (Table 1). On the other hand, formation of a CXC-type CCL5/CCL2 heterodimer is, as expected, energetically much less favorable (-24.7 kcal/mol; see Table 1), due primarily to the presence of two proximal arginines (Arg-29 and Arg-30) in the middle of first β-strand that would be involved in intersubunit contacts in the CXC-type dimer, as well as in the vicinity of Lys-44, Lys-49, and Arg-24. A high content of positively charged residues on their C-terminal helices also makes formation of the CXC-type heterodimer of these two CC chemokines electrostatically unfavorable. Based on calculated free energies, CCL2 would also form a heterodimer with CCL8. ΔGw for the heterodimer is -40.3 kcal/mol, compared with -31.5 kcal/mol for the CCL2 homodimer and -43.7 kcal/mol for the CCL8 homodimer. Formation of the CCL2/CCL8 heterodimer has been confirmed experimentally (42). However, although our calculated values indicate that either type of heterodimer, CC or CXC, could form, Crown et al. (43) concluded that formation of the CC-type heterodimer is more probable.
CXC and CC Mixed Chemokine Heterodimers—Because the protein backbone fold of any CC chemokine monomer is overall the same as that of any CXC chemokine monomer, we hypothesized that CC and CXC chemokines could form CXC/CC mixed heterodimers. If so, a related question would be which type of dimer, CXC-type or CC-type, would be more energetically favored. To address these questions, MD simulations and free energy calculations were performed on the following CXC/CC mixed heterodimers for both CXC-type and CC-type dimer motifs: CXCL4/CCL5, CXCL4/CCL2, CXCL8/CCL5, and CXCL8/CCL2.
Binding free energies (Table 1) are favorable for formation of CXC-CC mixed heterodimers of CXCL4/CCL5, CXCL4/CCL2, and CXCL8/CCL2 but not of CXCL8/CCL5. Furthermore, for these pairs of CXC-CC mixed heterodimers, the CXC-type dimer is favored for CXCL4/CCL2 and CXCL8/CCL2, whereas the CC-type dimer is favored for CXCL4/CCL5. Selection of a CXC-type or CC-type dimer depends on the particular residues at each respective inter-subunit interface.
Per residue energies are exemplified for CXC-type and CC-type heterodimers of CXCL8/CCL2 and CXCL8/CCL5 in supplemental Fig. 2. In the energetically favored CXC-type CXCL8/CCL2 heterodimer (Fig. 2A), N-terminal residues of CCL2 (that normally interact at the CC-type dimer interface) lost energy, whereas CCL2 β-strand residues Ala-26 to Ser-33 at the CXC-type dimer interface gained energy. For the CXCL8 subunit, the N terminus was neutral, whereas interfacial β-strand residues lost energy (primarily electrostatic). In the CC-type CXCL8/CCL2 heterodimer (Fig. 2B), N-terminal residues of CXCL8 actually gained considerable energy, whereas β-strand residues Lys-23 to Glu-29 of CXCL8 lost even more energy (electrostatic and non-electrostatic) than when in the CXC-type heterodimer. Favorable per residue energies for the CCL2 subunit in the CXC-type heterodimer, were lost in the CC-type heterodimer. Overall, energetically the formation of CC-type heterodimers from both the side of CXCL8 and CCL2 was less favorable than the formation of CXC-type heterodimer. This was even obvious from the trajectories themselves (Fig. 2A). In the CC-type CXCL8/CCL2 heterodimer, residues within the well structured β-sheet and C-terminal α-helix of CXCL8 fluctuated significantly, whereas in the CXC-type heterodimer, they were essentially the same as those in the CXCL8 homodimer. For the CCL2 subunit, per residue fluctuations did not differ significantly for either CC-type or CXC-type heterodimers, although they were generally somewhat lower in the CXC-type. Therefore, selection of heterodimer type was influenced more by CXCL8.
As mentioned above, the CXCL8/CCL5 heterodimers would likely not form as either CXC- or CC-type dimers. This is because the CCL5 homodimer is stabilized primarily by interactions among noncharged N-terminal residues that form a short intersubunit β-sheet and by electrostatic interactions between Asp-6 of one monomer and Arg-47 (third β-strand) of the other. These favorable interactions are disrupted when CXCL8 replaces one of the CCL5 subunits in either CXC- or CC-type heterodimer. Although CXCL8 Asp-4 might replace CCL5 Asp-6, the CXCL8 N terminus is shorter, leaving CXCL8 Asp-4 more distant from CCL5 Arg-47 in a CC-type heterodimer. In addition, proximity of CXCL8 Lys-3 and Arg-6 to CCL5 Arg-47 would electrostatically oppose heterodimerization. Furthermore, charged residues Lys-23, Glu-24, Arg-26, and Glu-29 at the CXCL8 homodimer interface lose their favorable electrostatic environment when in either CXC- or CC-type CXCL8/CCL5 heterodimer. In particular, close proximity of CCL5 Glu-26 and CXCL8 Glu-29 in a CXC-type heterodimer would be significantly electrostatically repulsive.
Although it is improbable that CXCL8 and CCL5 would form CXC- or CC-type heterodimers, we cannot rule out formation of an CXCL8/CCL5 heterodimer that has some novel dimeric structure. During the course of MD simulations for both CC- and CXC-type CXCL8/CCL5 heterodimers, we noted that the mutual orientation of these two monomer subunits tended to deviate significantly, unlike another pair of chemokines we investigated. For the CC-type heterodimer, the subunits reoriented themselves in a way that Asp-4 of CXCL8 moved closer to Arg-47 of CCL5, and Asp-6 of CCL5 moved closer to Lys-11 of CXCL8. For the CXC-type heterodimer, Asp-4 of CXCL8 also moved toward Arg-47 of CCL5, whereas the two subunits moved further apart because of electrostatic repulsion between Glu-26 of CCL5 and Glu-29 of CXCL8. A much longer simulation and/or experimental evidence would be necessary for further insight into what heterodimer structure, if any, would form in this case.
Comparison with Experimentally Determined Free Energies—For a number of CXC and CC chemokines, experimentally determined equilibrium dissociation constants (and therefore free energies) are available in the literature. These Kd values and related free energies are listed in Table 2, along with the solution conditions and experimental techniques used to determine them. For some of these chemokines, multiple Kd values have been reported (all those known are listed in Table 2), and these can vary considerably depending upon such experimental variables as temperature, pH, and salt concentration. We chose to perform our calculations at what would approximate low salt and pH 5 with acidic residues being negatively charged and basic residues being positively charged (histidine residues, assumed to all have a pKa of 6, would be mostly positively charged). Many experimental Kd values for chemokines (Table 2) were determined either at pH 5 and low salt, or at about pH 7 and 200-250 mm ionic strength.
In general, experimental Kd values increase significantly with increasing pH and ionic strength. However, because free energies vary as the natural logarithm of Kd, a 10-fold difference in Kd is about a 2.3-fold difference in free energy. In Table 2, there are only a few instances where fair comparisons (i.e. using the same experimental technique, under otherwise the same solution conditions) can be made, and in these cases, either changing the pH from 5 to 7 or the ionic strength from about 20 to 200 mm results in about a 0.5-1.5 kcal/mol decrease in free energy. This is not a major factor when considering trends in our calculated free energies.
Experimental Kd values listed in Table 2 are perhaps even more varied because of the technique used to determine them. The most reliable and consistent Kd values seem to be those derived from NMR, calorimetry, and ultracentrifugation, whereas those derived from Biacore and chemical cross-linking appear to be overestimated in comparison.
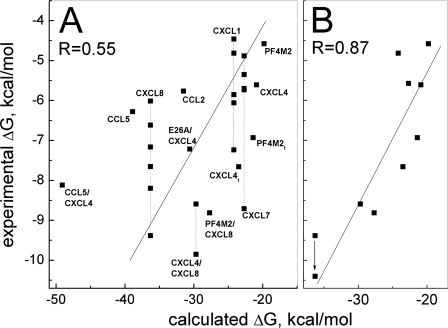
Nevertheless, if we plot all experimentally determined free energies shown in Table 2 versus the respective calculated free energies (Table 1), we have the correlation plot shown in Fig. 4A that has a linear regression coefficient R = 0.55. Although this R value seems low, it reflects the relatively large variation in experimentally determined free energies for reasons discussed above, i.e. pH, ionic strength, and experimental technique. For example, free energies reported for CXCL8 (IL8) dimer formation range from -6.0 to -9.4 kcal/mol (Table 2).
FIGURE 4.
Correlation between calculated and experimentally determined binding free energies. A, all experimentally derived free energies available in the literature and determined at rather diverse experimental conditions and by different methods are plotted versus calculated free energies. Solid line shows a linear fit of the data, yielding a linear regression coefficient R = 0.55. B, experimental values determined at solution conditions similar to those at which we carried out simulations, i.e. at low salt (< 20 mm) and at pH 5.0-7.0 are shown. A linear fit to the data (solid line) gives R = 0.87.
For a fairer and more reasonable comparison between calculated and experimental values, one should use experimental values determined at the same, or at least similar, solution conditions. In this regard, the largest subset of the experimentally determined free energies (Table 2) is that determined at low salt (≤20 mm equivalents of NaCl) and pH 5, i.e. CXCL4 (PF4) and PF4-M2 (both dimer and tetramer), CXCL8 (IL8), CXCL1 (Gro-α), CXCL7 (NAP-2), and mixed chemokines CXCL4/CXCL8 and PF4M2/CXCL8. For IL8, however, the lowest salt concentration for which experimental data are available is 50 mm phosphate buffer; therefore, we adjusted the reported free energy from -9.4 to -10.4 kcal/mol because it has been reported that adding this much salt to solution will lower the free energy of CXC chemokine dimerization by about 1 kcal/mol (13). Fig. 4B gives the resulting correlation plot, which has R = 0.87, indicating a relatively good correlation between experiment and theory. However, even if we do not adjust this value, the R value remains relatively high at 0.83.
Our approach is further validated by separately analyzing association free energies determined for chemokines under different solution conditions. Under high salt conditions, for example, averaged free energies are -6.9 + 0.8 kcal/mol for CXCL8 (IL8), -5.9 + 1.3 kcal/mol for CXCL1 (Gro-α), and -5.3 + 0.4 kcal/mol for CXCL7 (NAP-2) compared with calculated values (Table 1) of -36.3, -24.2, and -22.7 kcal/mol, respectively. Note that this trend is similar to that illustrated in Fig. 4B, i.e. a lower experimental value is associated with a lower calculated value.
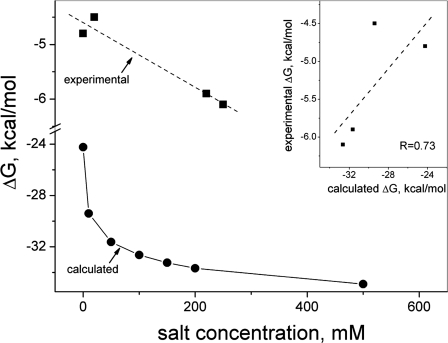
To expand upon this point, we calculated free energies as a function of ionic strength for CXCL1 (Gro-α, Fig. 5) for which experimental free energies have been reported at several salt concentrations (Table 2). As expected due to electrostatic screening effects, free energies decrease rapidly at lower salt concentrations and varied less at higher salt concentrations. In addition, only the Poisson-Boltzmann term (not unexpectedly) was affected by changes in ionic strength, whereas the van der Waals term was relatively independent of ionic strength. Experimental free energies for CXCL1 are plotted at the top of Fig. 5, and the inset shows the correlation between calculated and experimental values. Even though at lower ionic strength free energies are more variable, the correlation is relatively good with R = 0.73.
FIGURE 5.
Binding energies as a function of ionic strength. Experimental (squares) and calculated (circles) binding energies at different concentrations of salt are shown for CXCL1. Lines represent the best fit of data. The inset shows the correlation between calculated and experimental values.
To address the issue of pH variations, we also calculated free energies for CXCL1 at what would approximate the charge state of the protein at pH 7 by changing the ionization state of histidine residues (CXCL1 dimer has four histidines). In doing so, the calculated free energy decreased by 1.7 kcal/mol. Regardless of the accuracy of the calculation, the trend again parallels that observed experimentally (Table 2), where the free energy goes from -5.9 kcal/mol (pH 5) to -7.2 kcal/mol (pH 7). The same is true for CXCL7 (NAP-2), where the difference in calculated free energy is a net negative increase of about 1 kcal/mol to be compared with an experimental free energy change from -5.4 kcal/mol at pH 5 to -5.7 kcal/mol at pH 7 (Table 2).
Furthermore, trends in our calculated free energies for mutants of CCL5 (Rantes) in heterophylic interactions with CXCL4 (PF4) (19) also correlate with experimentally determined free energies. In this case, CCL5 mutant 44AANA47 was reported not to interact with CXCL4, whereas mutant E26A was shown to interact with CXCL4 more weakly (Kd = 3.8 × 10-6 m; ΔG =-7.86 kcal/mol) than wild-type CCL5 (Kd = 0.8 × 10-6 m; ΔG =-8.84 kcal/mol). This same trend is followed by our calculated free energies, i.e. -49.1 kcal/mol for wild-type CCL5, -30.6 kcal/mol for mutant E26A, and -16.6 kcal/mol for mutant 44AANA47.
This having been said, CCL5 is somewhat exceptional in that it forms larger oligomers (tetramers and above) at higher pH and low salt (42). This is the reason why experimental free energies (as well as the NMR solution structure) were determined at around pH 4. However, in the absence of any high resolution structure of these higher oligomer states, we could not calculate free energies for any higher order hetero-oligomer state. The same can be said for CCL5 mutant E26A, which can form tetramers of unknown high resolution structure (42). The most that our calculations say about CCL5 is that this CC chemokine is favored or is not favored to form heterodimers with another CC or CXC chemokine.
DISCUSSION
Our previous work in this area demonstrated experimentally that CXCL4 and CXCL8 associate as heterodimers as the cause for functional modulation of their individual activities (16, 17). The present results extend our knowledge on chemokine heterodimerization and indicate that heterodimer formation is thermodynamically favored among many other pairs of CXC chemokines (CXCL4, CXCL8, CXCL1, and CXCL7) as well as CC chemokines (CCL5, CCL2, and CCL8), and mixed CXC/CC chemokines. These findings are consistent with various reports in the literature as follows: 1) Biacore data from von Hundelshausen et al. (19) who showed that CXCL4 forms a heteromeric complex with CCL5; 2) immunoprecipitation results from Paoletti et al. (20) who proposed that CXCL13 and CCL21 might form a heteromeric complex; and 3) recent studies of Crown et al. (43) who studied heterodimerization between CCR2 receptor ligands and found that especially strong heterodimerization is observed between CCL2 and CCL8.
Conservation among the folded monomer structures of all of these CXC and CC chemokines generally allows heterodimerization, and alignment of specific pairs of amino acid residues at the dimer interface of individual monomers appears to primarily dictate the level of thermodynamic stability and selection of dimer type (CXC or CC). This is especially true for CXC-CC mixed heterodimers, where placement of specific amino acid residues (positively/negatively charged, polar, or hydrophobic) within β-strand 1 and/or within the N terminus determines selection of CXC-type or CC-type heterodimers. This study also provides insight into which specific residue interactions (i.e. electrostatic and non-electrostatic contributions to the free energy on a per residue basis) promote homodimer and heterodimer formation. This information cannot easily be determined experimentally. In general, heterodimerization is mediated primarily by non-electrostatic interactions, with the exception of CXCL8 and CCL5 where electrostatic forces contribute significantly to the binding free energy. Per residue free energies range up to about -3 kcal/mol, and although these values are relatively large on a per residue basis, they do correlate structurally, i.e. the largest values are associated with those residues directly involved at the inter-dimer interface. This, in turn, increases our level of confidence in the predictive values from these calculations.
Nevertheless, even though two of the highly energetically favorable heterodimers (CXCL4/CXCL8 and CXCL4/CCL5) have been observed experimentally (16, 19) consistent with trends in our calculated binding free energies (Table 1), our calculated values are unrealistically large in magnitude compared with those determined experimentally (Table 2). The main reason for these differences lies in the limitations of the computational approach. Use of a direct computational approach to correlate the experimental and calculated absolute binding free energies of macromolecular complexes remains quite challenging, even today. Although rigorous approaches, such as free energy perturbation and thermodynamic integration, have been shown to be applicable in the study of ligand binding (44, 45), they are not very well suited for the study of large protein complex formation. Application of the end point free energy approach, such as the linear interaction model (46) within the implicit solvation model framework (21), has improved both efficiency and accuracy of these calculations. However, universal application of these computational methods remains limited by our understanding of the balance among various energy contributions to the total free energy of the system studied (21, 47). These works have demonstrated that the balance among various energy contributions depends on the nature of the system, and the successful application of these methods requires regressionary scaling of these energy contributions to obtain accurate correlation with experiments. For protein association studies where the corresponding electrostatic and non-electrostatic energy terms can be significantly different (as is the case at hand), a regression type approach becomes difficult. In our present study of chemokine heterodimer formation, we evaluated absolute binding free energies based on the MM-PBSA method (21, 48). Even though recent models have attempted to estimate various entropic contributions (49-51), extension of these conformational sampling based methods toward macromolecular assembly becomes problematic. Our calculation of the absolute binding free energy was based on simulation of the protein complex alone. As such, the conformational entropic contribution of the monomeric protein was not taken fully into account, leading to higher-than-expected values.
Regardless of the limitation of the theoretical framework, calculated binding free energies are useful to predict formation of chemokine heterodimers when they are compared within this series of chemokine complexes. From the perspective of CXCL4, for example, heterodimers with CXCL8 are more energetically favored than CXCL4 homo-oligomers. On the other hand, the CXCL4/CXCL8 heterodimer is less energetically favorable than the CXCL8 homodimer. Nevertheless, CXCL4/CXCL8 heterodimers will still form in equilibrium with homodimers, and given the fact that serum concentrations of CXCL4 are generally much higher than those of CXCL8, especially when platelets are activated as in the case of platelet aggregation and wound healing, mass action will shift the association equilibrium much in favor of the CXCL4/CXCL8 heterodimer. Therefore, biology should respond to the relative concentrations of respective pairs of CXC and CC (and possibly other) chemokine monomers.
This expanded view of CXC and CC chemokine heterodimerization presents a new way to think about chemokines in situ and about how they may function (52, 53). A number of reports have found that various combinations of CXC and CC chemokines, although not all of them, can act synergistically (19, 20, 52-55). Overall, observed functional effects from mixed chemokines depend not only on the particular combination of chemokines but also on the biological assay and cell type used in that assay. In certain instances, we can correlate modulation of biological activities with the potential to form heterodimers, i.e. our relative free energies (Table 1). In this regard, we recently showed that heterodimerization of CXCL8 and CXCL4 increases the anti-proliferative effect from CXCL4 on endothelial cells in culture, as well as modulates the chemotactic effect from CXCL8 on Baf3 cells (16). The highly favorable free energy for formation of CXCL4/CXCL8 heterodimers (Table 1) is consistent with our previous experimental observation that CXCL4/CXCL8 heterodimers form in solution (16). Furthermore, combination of CXCL4 and CCL5 causes significant enhancement of monocyte arrest on the endothelium (19), and the CXCL4/CCL5 heterodimer is also highly thermodynamically favored. Furthermore, the chemotactic activity of CXCL8 on neutrophils is enhanced upon addition of chemokines CXCL4 and CCL2 (53), and the calculated association free energies for combination of this pair is also relatively highly favorable. On the other hand, addition of CXCL7 to CXCL8 exhibits no effect on CXCL8-mediated cell migration (29, 34), and formation of CXCL7/CXCL8 heterodimers is calculated to be much less energetically favorable (Table 1).
Correlations with experiment (e.g. Fig. 4) increase the level of confidence in the predictive value of our calculated free energies, and even though further experimental evidence, both structural and functional, is required to validate all of our predictive findings and relate these to actual in vivo situations, our results do suggest significant biological implications. CXC and CC chemokines are involved in numerous biological processes where specific chemokines may be up-regulated or down-regulated depending on various biological stimuli. At the very least, the change in concentration of any one chemokine (due e.g. to inflammation) certainly would result in re-shuffling via mass action of most, if not all, chemokine homodimer and heterodimer populations that are co-localized at a particular site in situ, and this could have dramatic consequences biologically. Because of this, the potential for heterodimerization should be taken into account when presenting/discussing any experimental results involving CXC and CC chemokines.
Supplementary Material
Acknowledgments
We thank Minnesota Supercomputing Institute (University of Minnesota) for providing computer resources.
This work was supported, in whole or in part, by National Institutes of Health NRSA training Grant HL 07062 (to I. V. N.). The costs of publication of this article were defrayed in part by the payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 U.S.C. Section 1734 solely to indicate this fact.
The on-line version of this article (available at http://www.jbc.org) contains supplemental Figs. 1 and 2.
Footnotes
The abbreviations used are: IL8, interleukin 8; PF4, platelet factor 4; PF4-M2, N-terminal chimera of PF4; Gro-α, growth-related protein α; NAP-2, neutrophil-activated protein 2; RANTES, regulated on activation, normal T cells expressed and secreted; MCP, monocyte chemotactic protein; r.m.s.d., root-mean-square deviation; MM-PBSA, molecular mechanics and Poisson-Boltzmann surface area; vdW, van der Waals.
References
- 1.Baggiolini, M. (1998) Nature 392 565-568 [DOI] [PubMed] [Google Scholar]
- 2.Mackay, C. R. (2001) Nat. Immunol. 2 95-101 [DOI] [PubMed] [Google Scholar]
- 3.Youn, B. S., Mantel, C., and Broxmeyer, H. E. (2000) Immunol. Rev. 177 150-174 [DOI] [PubMed] [Google Scholar]
- 4.Belperio, J. A., Keane, M. P., Arenberg, D. A., Addison, C. L., Ehlert, J. E., Burdick, M. D., and Strieter, R. M. (2000) J. Leukocyte Biol. 68 1-8 [PubMed] [Google Scholar]
- 5.Koch, A. E., Polverini, P. J., Kunkel, S. L., Harlow, L. A., DiPietro, L. A., Elner, V. M., Elner, S. G., and Strieter, R. M. (1992) Science 258 1798-1801 [DOI] [PubMed] [Google Scholar]
- 6.Zlotnik, A., and Yoshie, O. (2000) Immunity 12 121-127 [DOI] [PubMed] [Google Scholar]
- 7.Clore, G. M., and Gronenborn, A. M. (1995) FASEB J. 9 57-62 [DOI] [PubMed] [Google Scholar]
- 8.Clark-Lewis, I., Kim, K. S., Rajarathnam, K., Gong, J. H., Dewald, B., Moser, B., Baggiolini, M., and Sykes, B. D. (1995) J. Leukocyte Biol. 57 703-711 [DOI] [PubMed] [Google Scholar]
- 9.Mayo, K. H., and Chen, M. J. (1989) Biochemistry 28 9469-9478 [DOI] [PubMed] [Google Scholar]
- 10.St Charles, R., Walz, D. A., and Edwards, B. F. (1989) J. Biol. Chem. 264 2092-2099 [PubMed] [Google Scholar]
- 11.Clore, G. M., Appella, E., Yamada, M., Matsushima, K., and Gronenborn, A. M. (1990) Biochemistry 29 1689-1696 [DOI] [PubMed] [Google Scholar]
- 12.Handel, T. M., and Domaille, P. J. (1996) Biochemistry 35 6569-6584 [DOI] [PubMed] [Google Scholar]
- 13.Yang, Y., Mayo, K. H., Daly, T. J., Barry, J. K., and La Rosa, G. J. (1994) J. Biol. Chem. 269 20110-20118 [PubMed] [Google Scholar]
- 14.Czaplewski, L. G., McKeating, J., Craven, C. J., Higgins, L. D., Appay, V., Brown, A., Dudgeon, T., Howard, L. A., Meyers, T., Owen, J., Palan, S. R., Tan, P., Wilson, G., Woods, N. R., Heyworth, C. M., Lord, B. I., Brotherton, D., Christison, R., Craig, S., Cribbes, S., Edwards, R. M., Evans, S. J., Gilbert, R., Morgan, P., Randle, E., Schofield, N., Varley, P. G., Fisher, J., Waltho, J. P., and Hunter, M. G. (1999) J. Biol. Chem. 274 16077-16084 [DOI] [PubMed] [Google Scholar]
- 15.Mayo, K. H., Roongta, V., Ilyina, E., Milius, R., Barker, S., Quinlan, C., La Rosa, G., and Daly, T. J. (1995) Biochemistry 34 11399-11409 [DOI] [PubMed] [Google Scholar]
- 16.Nesmelova, I. V., Sham, Y., Dudek, A. Z., van Eijk, L. I., Wu, G., Slungaard, A., Mortari, F., Griffioen, A. W., and Mayo, K. H. (2005) J. Biol. Chem. 280 4948-4958 [DOI] [PubMed] [Google Scholar]
- 17.Dudek, A. Z., Nesmelova, I., Mayo, K., Verfaillie, C. M., Pitchford, S., and Slungaard, A. (2003) Blood 101 4687-4694 [DOI] [PubMed] [Google Scholar]
- 18.Guan, E., Wang, J., and Norcross, M. A. (2001) J. Biol. Chem. 276 12404-12409 [DOI] [PubMed] [Google Scholar]
- 19.von Hundelshausen, P., Koenen, R. R., Sack, M., Mause, S. F., Adriaens, W., Proudfoot, A. E., Hackeng, T. M., and Weber, C. (2005) Blood 105 924-930 [DOI] [PubMed] [Google Scholar]
- 20.Paoletti, S., Petkovic, V., Sebastiani, S., Danelon, M. G., Uguccioni, M., and Gerber, B. O. (2005) Blood 105 3405-3412 [DOI] [PubMed] [Google Scholar]
- 21.Kollman, P. A., Massova, I., Reyes, C., Kuhn, B., Huo, S., Chong, L., Lee, M., Lee, T., Duan, Y., Wang, W., Donini, O., Cieplak, P., Srinivasan, J., Case, D. A., and Cheatham, T. E., III (2000) Acc. Chem. Res. 33 889-897 [DOI] [PubMed] [Google Scholar]
- 22.Srinivasan, J., Miller, J., Kollman, P. A., and Case, D. A. (1998) J. Biomol. Struct. Dyn. 16 671-682 [DOI] [PubMed] [Google Scholar]
- 23.Wang, W., and Kollman, P. A. (2000) J. Mol. Biol. 303 567-582 [DOI] [PubMed] [Google Scholar]
- 24.Gilson, M. K., Given, J. A., Bush, B. L., and McCammon, J. A. (1997) Biophys. J. 72 1047-1069 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Warshel, A. (2002) Acc. Chem. Res. 35 385-395 [DOI] [PubMed] [Google Scholar]
- 26.Warshel, A. (2003) Annu. Rev. Biophys. Biomol. Struct. 32 425-443 [DOI] [PubMed] [Google Scholar]
- 27.Lazaridis, T., and Karplus, M. (2003) Biophys. Chem. 100 367-395 [DOI] [PubMed] [Google Scholar]
- 28.Xu, Y., and Wang, R. (2006) Proteins 64 1058-1068 [DOI] [PubMed] [Google Scholar]
- 29.Gohlke, H., Kiel, C., and Case, D. A. (2003) J. Mol. Biol. 330 891-913 [DOI] [PubMed] [Google Scholar]
- 30.Bernstein, F. C., Koetzle, T. F., Williams, G. J., Meyer, E. F., Jr., Brice, M. D., Rodgers, J. R., Kennard, O., Shimanouchi, T., and Tasumi, M. (1977) J. Mol. Biol. 112 535-542 [DOI] [PubMed] [Google Scholar]
- 31.Brooks, B. R., Bruccoleri, R. E., Olafson, B. D., States, D. J., Swaminathan, S., and Karplus, M. (1983) J. Comput. Chem. 4 187-217 [Google Scholar]
- 32.MacKerell, A. D., Jr., Bashford, D., Bellott, M., Dunbrack, R. L., Jr., Evanseck, J., Field, M. J., Fischer, S., Gao, J., Guo, H., Ha, S., Joseph, D., Kuchnir, L., Kuczera, K., Lau, F. T. K., Mattos, C., Michnick, S., Ngo, T., Nguyen, D. T., Prodhom, B., Reiher, W. E., III, Roux, B., Schlenkrich, M., Smith, J., Stote, R., Straub, J., Watanabe, M., Wiorkiewicz-Kuczera, J., Yin, D., and Karplus, M. (1998) J. Phys. Chem. 102 3586-3616 [DOI] [PubMed] [Google Scholar]
- 33.Darden, T. A., York, D. M., and Pedersen, L. G. (1993) J. Chem. Phys. 98 10089-10092 [Google Scholar]
- 34.Ryckaert, J. P., Ciccotti, G., and Berendsen, H. J. C. (1977) J. Comp. Physics 23 327-341 [Google Scholar]
- 35.Case, D. A. (1994) Curr. Opin. Struct. Biol. 4 285-290 [Google Scholar]
- 36.Sitkoff, D., Sharp, K. A., and Honig, B. (1994) J. Phys. Chem. 98 1978-1988 [Google Scholar]
- 37.Grasberger, B. L., Gronenborn, A. M., and Clore, G. M. (1993) J. Mol. Biol. 230 364-372 [DOI] [PubMed] [Google Scholar]
- 38.Ye, J., Mayer, K. L., and Stone, M. J. (1999) J. Biomol. NMR 15 115-124 [DOI] [PubMed] [Google Scholar]
- 39.Ye, J., Mayer, K. L., Mayer, M. R., and Stone, M. J. (2001) Biochemistry 40 7820-7831 [DOI] [PubMed] [Google Scholar]
- 40.LiWang, A. C., Cao, J. J., Zheng, H., Lu, Z., Peiper, S. C., and LiWang, P. J. (1999) Biochemistry 38 442-453 [DOI] [PubMed] [Google Scholar]
- 41.Cornell, W., Abseher, R., Nilges, M., and Case, D. A. (2001) J. Mol. Graph. Model. 19 136-145 [DOI] [PubMed] [Google Scholar]
- 42.Shaw, J. P., Johnson, Z., Borlat, F., Zwahlen, C., Kungl, A., Roulin, K., Harrenga, A., Wells, T. N., and Proudfoot, A. E. (2004) Structure (Lond.) 12 2081-2093 [DOI] [PubMed] [Google Scholar]
- 43.Crown, S. E., Yu, Y., Sweeney, M. D., Leary, J. A., and Handel, T. M. (2006) J. Biol. Chem. 281 25438-25446 [DOI] [PubMed] [Google Scholar]
- 44.Beveridge, D. L., and DiCapua, F. M. (1989) Annu. Rev. Biophys. Biophys. Chem. 18 431-492 [DOI] [PubMed] [Google Scholar]
- 45.Straatsma, T. P., and McCammon, J. A. (1992) Annu. Rev. Phys. Chem. 43 407-435 [Google Scholar]
- 46.Aqvist, J., Medina, C., and Samuelsson, J. E. (1994) Protein Eng. 7 385-391 [DOI] [PubMed] [Google Scholar]
- 47.Sham, Y. Y., Chu, Z. T., Tao, H., and Warshel, A. (2000) Proteins 39 393-407 [PubMed] [Google Scholar]
- 48.Swanson, J. M., Henchman, R. H., and McCammon, J. A. (2004) Biophys. J. 86 67-74 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Luo, H., and Sharp, K. (2002) Proc. Natl. Acad. Sci. U. S. A. 99 10399-10404 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Villa, J., Strajbl, M., Glennon, T. M., Sham, Y. Y., Chu, Z. T., and Warshel, A. (2000) Proc. Natl. Acad. Sci. U. S. A. 97 11899-11904 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Karlsson, M., Martensson, L. G., Karlsson, C., and Carlsson, U. (2005) Biochemistry 44 3487-3493 [DOI] [PubMed] [Google Scholar]
- 52.Weber, C., and Koenen, R. R. (2006) Trends Immunol. 27 268-273 [DOI] [PubMed] [Google Scholar]
- 53.Gouwy, M., Struyf, S., Catusse, J., Proost, P., and Van Damme, J. (2004) J. Leukocyte Biol. 76 185-194 [DOI] [PubMed] [Google Scholar]
- 54.Broxmeyer, H. E., Sherry, B., Cooper, S., Lu, L., Maze, R., Beckmann, M. P., Cerami, A., and Ralph, P. (1993) J. Immunol. 150 3448-3458 [PubMed] [Google Scholar]
- 55.Gouwy, M., Struyf, S., Mahieu, F., Put, W., Proost, P., and Van Damme, J. (2002) Mol. Pharmacol. 62 173-180 [DOI] [PubMed] [Google Scholar]
- 56.Chen, M. J., and Mayo, K. H. (1991) Biochemistry 30 6402-6411 [DOI] [PubMed] [Google Scholar]
- 57.Mayo, K. H. (1991) Biochemistry 30 925-934 [DOI] [PubMed] [Google Scholar]
- 58.Burrows, S. D., Doyle, M. L., Murphy, K. P., Franklin, S. G., White, J. R., Brooks, I., McNulty, D. E., Scott, M. O., Knutson, J. R., Porter, D., Young, P. R., and Hensley, P. (1994) Biochemistry 33 12741-12745 [DOI] [PubMed] [Google Scholar]
- 59.Paolini, J. F., Willard, D., Consler, T., Luther, M., and Krangel, M. S. (1994) J. Immunol. 153 2704-2717 [PubMed] [Google Scholar]
- 60.Lowman, H. B., Fairbrother, W. J., Slagle, P. H., Kabakoff, R., Liu, J., Shire, S., and Hebert, C. A. (1997) Protein Sci. 6 598-608 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Schnitzel, W., Monschein, U., and Besemer, J. (1994) J. Leukocyte Biol. 55 763-770 [DOI] [PubMed] [Google Scholar]
- 62.Rajarathnam, K., Kay, C. M., Dewald, B., Wolf, M., Baggiolini, M., Clark-Lewis, I., and Sykes, B. D. (1997) J. Biol. Chem. 272 1725-1729 [DOI] [PubMed] [Google Scholar]
- 63.Hanzawa, H., Haruyama, H., Konishi, K., Watanabe, K., and Tsurufuji, S. (1997) J. Biochem. (Tokyo) 121 835-841 [DOI] [PubMed] [Google Scholar]
- 64.Skelton, N. J., Aspiras, F., Ogez, J., and Schall, T. J. (1995) Biochemistry 34 5329-5342 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.