Time Series Analysis of Spontaneous Upper-Extremity Movements of Premature Infants With Brain Injuries

Abstract

Background and Purpose: Comparisons of spontaneous movements of premature infants with brain injuries and those without brain injuries can provide insights into normal and abnormal processes in the ontogeny of motor development. In this study, the characteristics of spontaneous upper-extremity movements of premature infants with brain injuries and those without brain injuries were examined with time series analysis.

Subjects: Participants were 7 premature infants with brain injuries and 7 matched, low-risk, premature infants at the age of 1 month after term.

Methods: A triaxial accelerometer was used to measure upper-extremity limb acceleration in 3-dimensional space. Acceleration signals were recorded from the right wrist when the infant was in an active, alert state and lying in the supine position. The recording time was 200 seconds. The acceleration signal was sampled at a rate of 200 Hz. The acceleration time series data were analyzed by nonlinear analysis as well as linear analysis.

Results: The nonlinear time series analysis indicated that spontaneous movements of premature infants have nonlinear, chaotic, dynamic characteristics. The movements of the infants with brain injuries were characterized by larger dimensionality, and they were more unstable and unpredictable than those of infants without brain injuries.

Discussion and Conclusion: As determined by nonlinear analysis, the spontaneous movements of the premature infants with brain injuries had the characteristics of increased disorganization compared with those of the infants without brain injuries. Infants with brain injuries may manifest problems with self-organization as a function of the coordination of subsystems. Physical therapists should be able to support interactions among the subsystems and promote self-organization of motor learning through the individualized provision of various sensorimotor experiences for infants.

Researchers and clinicians have been interested in studying the development of infants’ spontaneous movements as a basis for understanding the development of motor coordination and the generation of voluntary movements. A mathematical framework has lagged behind the traditional qualitative approach to the study of motor systems,¹ but a mathematical understanding essentially adds to the base of knowledge of how a system works. On a more practical level, this understanding supports the ability to predict the future behavior of a motor system. The ability to predict this behavior, in turn, is crucial to the ability to control the behavior or the motor dysfunction. In this study, our main focus was to add to the mathematical understanding of the arm movement profiles of premature infants with brain injuries (BI) and those without BI.

A brief description of the mathematical and dynamic system terms that are used in this article is presented in the Appendix.^2–13 A glossary of technical terms is included to describe additional mathematical terms.

Dynamic system theory provides a way to conceptualize motor development. In this conceptualization, motor behavior emerges from the dynamic cooperation of many subsystems.¹⁴ The subsystems consist of intrinsic factors, such as muscle strength (force-generating capacity), body weight, postural support, and the infant's mood and brain development, and extrinsic factors, such as the environmental conditions and specific task requirements.^15,16 The dynamic system approach emphasizes that movement self-organizes as a result of interactions of the participating subsystems in developmental and real time.¹⁴ The dynamic system approach differs from traditional behavioral-maturationist and reflex-based descriptions of motor behavior.¹⁵ Reflex-based descriptions of development explicitly refer to the role of the nervous system in behavioral development, with an emphasis on the hierarchical nature of the nervous system. In contrast, from the dynamic system perspective, motor development is not prescriptive, hierarchical, or attributed solely to maturation of the central nervous system (CNS).¹⁶ Rather, the subsystems self-organize to produce movement and do not depend a priori on the existence of instructions embodied in one hierarchically important subsystem (such as the CNS).

Thelen and colleagues^17–19 studied how intentional reaching arises from infants’ ongoing, intrinsic movement dynamics and how first reaches become successively adapted to the task. They suggested that the infant CNS does not contain programs that detail hand trajectory, joint coordination, and muscle activation patterns. Rather, these patterns are the consequences of the natural dynamics of the system and the active exploration of the match between those dynamics and the task. On the basis of dynamic system theory, they showed that infants’ movements and changes in movements may be viewed as self-organizing dynamic systems. The differences between the traditional behavioral-maturationist and dynamic system perspectives carry implications for therapeutics and clinical evaluations in physical therapy. In the dynamic system view, there is no single cause or predetermined model, be it genetic, neurological, cognitive, or environmental, for behavioral changes, and changes in movements with age cannot be attributed solely to maturation of the CNS.

In this study, we examined whether spontaneous (as distinguished from intentional) arm movements of premature infants have characteristics of nonlinear dynamics. Premature infants are known to be at higher risk for motor impairment, but reliable, specific identification and prediction of the extent of impairment remain elusive.^20,21 However, it is important to establish whether premature infants’ spontaneous movements can be described by deterministic chaos and, therefore, possess some significant order versus being described as random, nonmeaningful, and unpredictable motion. An underlying order conferred by deterministic chaos would reflect on the ability of the system to adapt or respond to learning through exploration and suggests that the subsystems, including the environmental context in which this learning and adaptation occur, could make a difference in the outcome. We also sought to clarify whether arm movement pattern differences between premature infants with BI and those without BI could be detected and described quantitatively by analysis of time series data. The comparison data are useful in understanding how the trajectories of infants’ arm movements are perturbed by BI, as assessed quantitatively by the loss of predictability and complexity of movement. We tested the following 2 hypotheses:

1. The acceleration time series of upper-extremity spontaneous movements of premature infants demonstrate characteristics of nonlinear dynamics.

2. The motor characteristics of infants with BI significantly differ from those of infants without BI, as indicated by increased disorganization of motor control.

Method

Participants

The characteristics of the study participants are shown in Table 1. The participants were premature infants who were admitted to the neonatal intensive care unit at (Hamamatsu City Hospital, Shizuoka, Japan). A premature infant was defined as one born before 37 weeks of gestation (pregnancy). Seven premature infants (5 males and 2 females) with BI constituted the group of infants with BI in this study. Brain injuries included periventricular leukomalacia (PVL) and intracranial hemorrhage. Periventricular leukomalacia was defined as increased echogenicity in the periventricular region with cyst formation on serial cranial ultrasound examinations. Infants who developed cysts of 3 mm or more in diameter in the periventricular white matter were diagnosed as having cystic PVL. Serial ultrasound scans were performed by pediatric clinicians at discharge from the neonatal intensive care unit. Low-risk infants (group of infants without BI in this study) were included on the basis of the following criteria: matched with infants with BI for sex, birth weight (within 100 g), and gestational age (within 1 week) and born without complications of congenital heart disease, abnormal CNS manifestations, chromosomal aberrations, or lung disease. There were no statistically significant differences between the 2 groups in terms of background characteristics. Informed consent was provided by the participants’ parents.

Table 1.

Characteristics of Study Participants^a

^aAPGAR=appearance, pulse, grimace, activity, and respiration; F=female; M=male; IVH=intraventricular hemorrhage; PVL=periventricular leukomalacia.

^bThe maximum size of the cyst in the recording for each infant was described as small (≤5 mm in diameter), moderate (6–14 mm), or large (≥15 mm). Intracranial hemorrhage was defined according to the grading system described by Papile et al (Papile LA, Burstein J, Burstein R, Koffler H. Incidence and evolution of subependymal and intraventricular hemorrhage: a study of infants with birth weights less than 1,500 gm. J Pediatr. 1978;92:529–534), as follows: grade I=subependymal hemorrhage with no IVH, grade II=IVH with no ventricular dilatation, grade III=IVH with ventricular dilatation, and grade IV=IVH with parenchymal hemorrhage.

Equipment

A triaxial accelerometer (Motion Recorder MVP-A304Ac DigiTrac)^* was used to measure limb acceleration in 3-dimensional space. In this configuration, x-data correspond to anterior-posterior movements of the arm (in the perpendicular horizontal direction), y-data correspond to abduction and adduction movements of the arm (in the horizontal direction), and z-data correspond to elevation movements of the arm (in the vertical direction). The monitor weighed 4 g, and its dimensions (width, depth, and height) were 20, 12.5, and 7.5 mm. The monitor did not require manipulation during use. The acceleration signal was sampled at a rate of 200 Hz (1/0.005 second, 8 bit), and data were stored in the system memory of the monitor until data collection was complete. Digitized data were transferred to a computer for subsequent processing with analysis software.

Procedure

We recorded spontaneous upper-extremity movements at 1 month postterm age by using the triaxial accelerometer. Acceleration signals were recorded from the right wrist when the infant was in an active, alert state and lying in the supine position. The infant's state was defined by use of the Neonatal Behavioral Assessment Scale as described by Brazelton and Nugent.²² During the active, alert state, the infant moves frequently and is more energetic with eye movements and vocalization. If the infant was in a crying or sleep state, the recordings were postponed. The recordings were obtained between feedings, during active wakefulness, when spontaneous movements were present. A small motion sensor (accelerometer) was taped to the infant's hand just below the right wrist, similar to a wrist band. Infants rested on a firm crib mattress that was 5 cm thick. Infants were undressed or wore diapers that did not interfere with their freedom of movement or with the visualization of their arms and legs. The recording time was 200 seconds, as recommended for the characteristics of this accelerometer.^23,24 This duration of recording is also consistent with that used in previous kinematic studies of infant limb movements.^25–27 Neonates spend the majority of their time in quiescent states,²⁸ thus limiting the opportunities to capture a sustained 200-second segment of spontaneous generalized movements (GMs). For the purpose of this study, we did not repeat the trial. There was no manipulation of the infant during the recording phase. Measurements were obtained in the hospital or outpatient clinic 1 month after birth by the same investigator each time.

Data Analysis

Power spectrum analysis.

The power spectrum is a representation of the magnitudes of the various frequency components. We estimated the power spectrum of the acceleration signal for each axis by using the maximum entropy method (MEM). The MEM estimates the spectrum that is most random or has the maximum entropy of any power spectrum consistent with the measured data. The MEM provides better resolution for a short data acquisition.²⁹ The MEM is also called the “all-poles method” or “autoregressive method.”

Estimation of embedding parameters.

In practice, time delay embedding is routinely used as the first step in the analysis of experimentally observed nonlinear dynamic systems.³⁰ This method is used to reconstruct the m-dimensional state space with the delay coordinates. We calculated the optimal embedding dimension by using a false-nearest-neighbor (FNN) method.³¹ The optimal embedding dimension is a description of the number of dimensions needed to unfold the structure of a given dynamic system in space.

The main idea of the FNN method is that for deterministic systems, points that are close in the state space stay close under forward iteration. If the embedding dimension for reconstructing an attractor is too small, points may appear as close neighbors purely through projection effects. If, on the other hand, the embedding dimension is large enough, then FNNs are fully rejected and only real close neighbors are resolved. Larger dimensionality in the fluctuations of a system may indicate a higher degree of freedom.

The first concern is determining a good choice for delay times. The autocorrelation function provides important information about reasonable delay times, and the false-neighbor statistic can provide guidance about the proper embedding dimension. The autocorrelation function is an estimate of the additional correlation between the data at time τ and the data at time (t−τ). We chose 250 milliseconds as the delay time in this study because a reasonable choice is the first zero of the autocorrelation function.

Maximal Lyapunov exponent.

The hallmark of deterministic chaos is the sensitive dependence of future states on the initial conditions. An initial small perturbation will grow exponentially, and the growth rate is called the Lyapunov exponent. We estimated the maximal Lyapunov exponent by using the algorithm introduced by Kantz.³² In that algorithm, the average expansion rate is estimated as a function of the time span. If the average expansion rate shows a robust linear increase in some range of the time span, its slope is an estimate of the maximal Lyapunov exponent. The lack of a robust linear region can result from several factors (eg, noise, undersampled time series, and small embedding dimension). Noise reduction was performed by use of the method described by Schreiber and Schmitz³³ and Schreiber³⁴; this method was also used to add random noise to the original data. The estimate of the maximal Lyapunov exponent was computed from the slope in 5 dimensions.

Testing for nonlinearity with surrogate data.

The idea of surrogate data analysis is to create an ensemble of different realizations of the null hypothesis that the data should be generated by a linear stochastic process and to apply statistical testing to reject this null hypothesis. If this null hypothesis cannot be rejected, the results of a nonlinear analysis (eg, the system has chaotic dynamics) must be regarded as spurious. Significant differences between the original time series and their surrogate data would indicate that the fluctuations observed in the acceleration time series of spontaneous movements were not randomly derived and might provide evidence that chaotic dynamic systems generate the dynamics of infants’ spontaneous movements. In this study, we generated the surrogate data by using a technique known as the amplitude-adjusted Fourier transform algorithm.³⁵ The surrogate data created by the amplitude-adjusted Fourier transform algorithm had the same power spectrum and amplitude distribution as the original time series. For statistical testing, we used the prediction errors from locally constant predictions.³⁰ In a previous study of full-term infants, we showed that when the state space is reconstructed with 5 or 6 embedding dimensions, the nonlinear characteristic can be observed clearly.²³ Therefore, testing for nonlinearity with surrogate data was performed in 5 dimensions. The linear and nonlinear time series analyses were performed with the TISEAN package.^30,35,36

For comparison of the 2 groups (with BI and without BI), statistical analyses were performed with the Mann-Whitney U test for the optimal embedding dimension and with the Student t test for the maximal Lyapunov exponent, depending on the distribution of each variable of interest.

Results

Power Spectrum Analysis

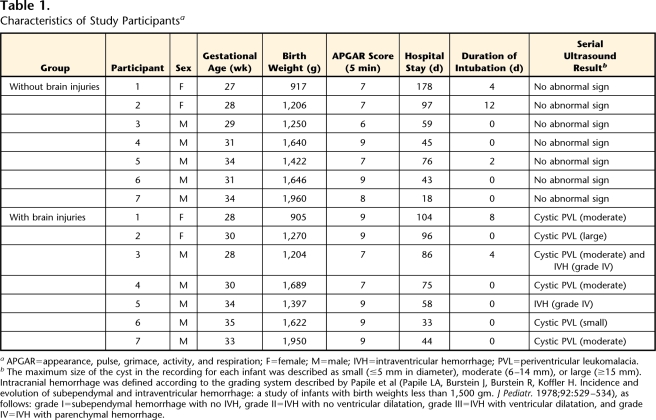
Figure 1 illustrates typical patterns of power spectra (2 optimal cases) in a log-log plot. Each spectral curve has a peak at a frequency of about 1 Hz. This finding suggests that the characteristic period of the spontaneous movement is about 1 minute. The tail of the spectral curve seems to follow the power law f⁻², a finding that may be associated with randomness in the high-frequency range. These results were shown for all participants. It can be interpreted from these results that spontaneous movements are random movements in a linear analysis.

Figure 1.

Typical patterns of power spectra in log-log plots for case (participant 1) without brain injury (left) and case (participant 1) with brain injury (right).

Testing for Nonlinearity With Surrogate Data

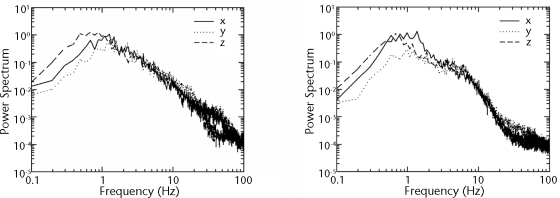
Table 2 shows a quantification of the predictability of both the original and the surrogate data in embedding dimension 5. The prediction errors of the original data were smaller than those of the surrogate data in all infants without BI and in 5 infants with BI. However, in 2 infants in the BI group (infants 1 and 5), the prediction errors of the original data were larger than those of the surrogate data. These results indicate that the fluctuations observed in the acceleration time series in some infants with BI did not have characteristics of chaos, suggesting that spontaneous movements of infants with BI had characteristics of randomness.

Table 2.

Testing for Nonlinearity With Surrogate Data in 5 Dimensions

^aThe prediction errors of the original data were larger than those of the surrogate data.

Optimal Embedding Dimension

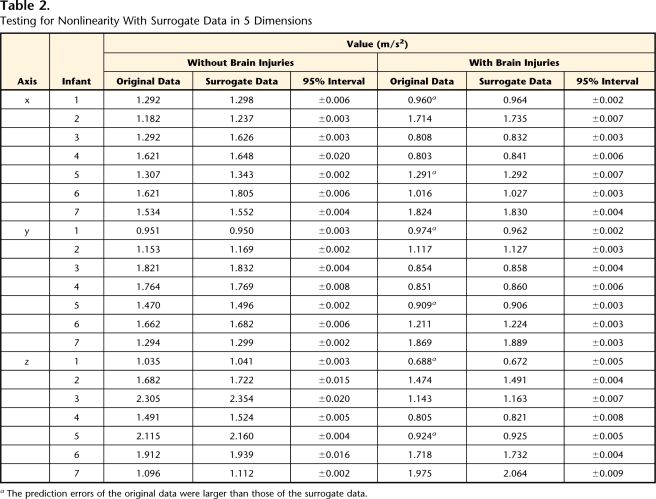
Table 3 shows a comparison between the optimal embedding dimension values of infants without BI and those of infants with BI. The optimal embedding dimension values for infants with BI were 7 (x-axis), 8 (y-axis), and 8 (z-axis), indicating a larger optimal dimension for these infants than for infants without BI, whose values were 6, 7, and 6, respectively. These results indicate that the fluctuations observed in the acceleration time series in infants with BI showed larger dimensionality than those in infants without BI.

Table 3.

Comparison of the Optimal Embedding Dimension Values Calculated With the False-Nearest-Neighbor Method

^aValues are median (range).

^bAs determined with the Mann-Whitney U test.

Maximal Lyapunov Exponent

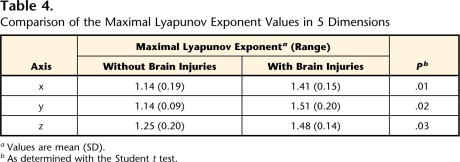
Table 4 shows a comparison of the maximal Lyapunov exponent values in 5 dimensions by a least-squares method. For all infants, the maximal Lyapunov exponent values were positive, indicating that the system was chaotic. Infants with BI also had significantly higher values for all axes than those without BI. These results indicate that the fluctuations observed in the acceleration time series in infants with BI were more locally unstable and unpredictable than those in infants without BI.

Table 4.

Comparison of the Maximal Lyapunov Exponent Values in 5 Dimensions

^aValues are mean (SD).

^bAs determined with the Student t test.

Discussion

In this study, we compared the dynamics of spontaneous upper-extremity movements between infants without BI and infants with BI by using time series analysis. We recorded infant arm movements as time series data by using a triaxial accelerometer and analyzed the data by linear and nonlinear methods.

We examined whether spontaneous arm movements of infants show characteristics of nonlinear dynamics. From the power spectrum analysis with the MEM, it appeared that spontaneous arm movements were largely a linear, random process in both infants with BI and those without BI. This result suggested that the infants’ spontaneous movements had characteristics of randomness in the high-frequency range. Also, in tests for nonlinearity with the surrogate data, the original data were always significantly smaller than those of their surrogate counterparts in infants without BI. Furthermore, the maximal Lyapunov exponent values were positive in both infants with BI and infants without BI. The positive exponent provided evidence that chaotic dynamic systems generated the dynamics of the infants’ spontaneous movements. Overall, the nonlinear time series analysis suggested that the infants’ spontaneous movements were characterized by nonlinear dynamics, whereas the linear analysis (power spectrum analysis) appeared to indicate a largely linear, random process. These results revealed that the fluctuations observed in the original time series were distinguishable from linear noise, indicating that the original time series data were not randomly derived. Therefore, infants’ spontaneous movements are not meaningless motion but are deterministic chaos, with a significant embedded order.

In previous studies, researchers applied chaotic dynamics to reveal the self-organized mechanisms in motor control.^37–39 In these studies, self-organization was the principle underlying the formation of coordinative structures. Our results support these findings. They suggested that motor development orients the processes of self-organization on the basis of chaotic dynamics, which might reflect processes of subsystems such as the CNS, sensory perception, musculoskeletal system, and the environment.

Self-generated arm movements have been proposed as providing the sensorimotor experiences by which infants learn the arm control required for purposeful reaching.^40–43 Bhat and colleagues^44–47 determined how groups of nonreaching, nearly reaching, and newly reaching infants changed the kinematics of their spontaneous arm movements in the presence of a toy. They proposed that important organismic constraints influence arm movements throughout the prereaching period and provide a foundation for the overlay of task-related constraints leading to the emergence of purposeful reaching. Infants provided with opportunities to produce a wider range of arm movements contacted toys earlier than control infants.⁴⁸ With the emergence of reaching, infants begin to independently explore and physically manipulate their environment. Thus, the emergence of reaching influences motor, social, perceptual, and cognitive development.

We next compared the motor behavior characteristics of infants with BI and infants without BI. Our results revealed that the spontaneous arm movements of infants with BI were more disorganized (showed larger dimensionality, more instability, and more unpredictability), suggesting underlying problems with self-organization processes for coordination. As determined by tests for nonlinearity, the original data were larger than those of their surrogate data (95% interval) in 2 infants in the BI group. This result might signify that in some infants with BI, the fluctuations observed in the original time series were not distinguishable from linear noise, nonlinear noise, or both, suggesting that spontaneous movements of infants with BI have characteristics of a disorganized motor system. The maximal Lyapunov exponent values for infants with BI were significantly higher than those for infants without BI for all segments. Because the Lyapunov exponent is a measure of the local stability of a dynamic system and its dependence on initial conditions, this result indicated that the arm movements of infants with BI were more locally unstable and unpredictable than those of infants without BI. The FNN values can be thought of as a measure of the number of active degrees of freedom and as a guide to the number of variables that are contributing to the observed behavior of the system. An FNN analysis describes the minimum number of variables that are related to the control of early human motor development, as the neurobehavioral system evolves over time, and that are required to form a valid state space from a given time series. Infants with BI had significantly larger embedding dimensions than those without BI for all axes. This result suggested that fluctuations of spontaneous movements of infants with BI showed larger dimensionality, indicating a higher degree of freedom, than those of infants without BI. Larger dimensionality in the fluctuations of a system may also be an indicator of reduced organization into synergy, representing randomness of behavior. Also, infants 1 and 6 with BI had very different characteristics (Tab. 1). Clinically, infant 1 was at higher risk for long-term motor impairment. This infant also had higher maximal Lyapunov exponent and FNN values.

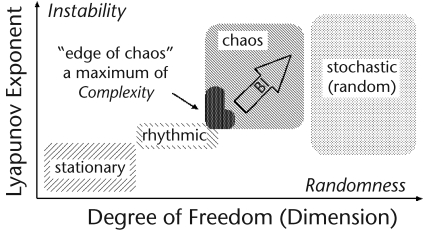
We should emphasize that complexity must be distinguished from randomness in the terminology of complex systems. Higher Lyapunov exponent values for infants with BI do not always indicate more complexity. Although systems with large dimensionality (ie, those with a high degree of freedom) may be random, complex behavior can be produced by systems with small dimensionality, and many variables do not necessarily create complexity. Instead, complexity is created by nonlinearity, which causes self-organization, adaptation, and emergent behavior. The relationship between the Lyapunov exponent and the degree of freedom is illustrated in Figure 2 in the Appendix. A system has the greatest complexity near the transition from ordered to chaotic behaviors. This area of parameters is called the “edge of chaos,” where it is thought that the complexity is maximal and the system is optimized for adaptation and information processing.^49–51 Therefore, in this study, it can be interpreted that infants with BI lost complexity in their arm movements (higher Lyapunov exponent and degree of freedom).

Figure 2.

Illustration of the relationship between the Lyapunov exponent and the degree of freedom.

The results obtained from the comparison of infants with BI and infants without BI demonstrated that spontaneous movements of infants with BI were more disorganized than those of infants without BI. According to the degree-of-freedom problem posited by Bernstein,⁵² self-organization is the principle underlying the formation of coordinative structures.^37,39 The movement characteristics of infants with BI, such as larger dimensionality, more instability, and more unpredictability, indicated disorganization of the self-organization processes for coordination. Our results suggest that premature infants with BI may have difficulties with self-organization processes. The processes involved in motor coordination and the generation of voluntary movements may be disrupted or compromised in infants with BI.

The findings in this study are congruent with the results of observational as well as kinematic studies. By clinical assessment, GMs—as defined by Prechtl and coworkers⁵⁴—are characterized by complexity, variation, and fluency. If the nervous system is impaired, then GMs lose their complex and variable character and become monotonous and of poor quality.⁵⁴ Abnormal GMs are characterized by a reduction in complexity, variation, and fluency. There is substantial evidence that the presence of markedly abnormal movements (ie, GMs that are virtually devoid of complexity, variation, and fluency) reflects on the presence of serious brain dysfunction.^55–57 Ohgi et al⁵⁸ also suggested that infants with PVL displayed uncoordinated, spontaneous movements, such as jerky, overshooting, and poor-quality repertoires. Furthermore, Fetters et al⁵⁹ performed kinematic analyses of kicking movements of both full-term and premature infants with a white matter disorder. They suggested that premature infants with a white matter disorder demonstrated aberrant patterns of coordination evident through both the temporal and the spatial characteristics of the kicks.

The results of this study lead to some clinical implications for the practice of physical therapy for infants with disabilities. Our results indicated that premature infants with BI may have difficulties with self-organization processes. Physical therapy should support self-organization through interactions of multiple subsystems (such as the CNS; vision, hearing, sensory-tactile, musculoskeletal, and joint systems; and the environment), as cooperation among many interacting systems contributes to motor performance and development. It will be important to provide infants with opportunities to engage in adaptive problem solving for movement-related tasks, so as to reinforce learning through feedback systems for sensory-perceptual-motor information.⁶⁰

The limitations of this study include the small sample size and the quantification of movements at only one time point. Because of the latter limitation, we cannot make inferences about the infants’ developmental trajectories. Future investigations with this methodology should include more subjects and repeated measures over time (follow-up in weeks or months) to monitor these developmental processes.

Conclusion

Our results indicate that upper-extremity spontaneous movements of premature infants have characteristics of nonlinear dynamics. Our findings reveal that motor development orients the processes of self-organization on the basis of chaotic dynamics, which might reflect interactions among subsystems, such as the CNS, sensory perception, musculoskeletal system, and the environment. Furthermore, spontaneous arm movements of infants with BI are characterized by more disorganization than those of infants without BI. Infants with BI may have problems with self-organization as a function of the coordination of subsystems. Assessment and early intervention in physical therapy should be focused on a combination of mechanical, neurologic, cognitive, and perceptual factors in addition to environmental contributions, specific to both the task and the context of the infant's actions (sensorimotor experiences). Physical therapists should be able to support interactions among the subsystems and promote self-organization of motor learning through the individualized provision of varied sensorimotor experiences for the infant.

Appendix.

Decryption of Mathematical and Dynamic System Terms and Glossary of Technical Terms

A brief description of the mathematical and dynamic system terms used in the article is presented. A glossary of technical terms is included to describe additional mathematical terms. The descriptions may be overly simplistic or underwhelming to readers, depending on familiarity with the terms, but a comprehensive explanation of terms is clearly not possible in the format of this article. Several textbooks and publications are available for reference under the keywords “nonlinear analysis” and “dynamic systems.”

We begin by introducing the term dynamic system, by which we mean a system that can be defined by a set of variables whose values change over time.² Motor behavior is a complex dynamic system that evolves over time. The variables that describe the course of the behavior of the system as a function of time are known as state variables, because collectively they describe the state of the system at any given time. The state variables trace out trajectories over time in a state space. The state space is simply an imaginary map of all of the possibilities open to the system. These possibilities may range from 2 points in a coin toss, as in heads or tails, to a multitude of points in other systems.

Dynamic systems can be classified and described according to the concepts of randomness anddeterminism. A random system is ruled to some extent by chance. Given complete information on the dynamics and initial state, it is not possible to predict precisely the future course of a random system, although it may be possible to determine the statistics of the future course—that is, to calcu-late the likelihood of the system being in particular states at specific times. A deterministic system is the opposite of a random system. With a deterministic system, given perfect knowledge of the initial conditions and the system dynamics, the future behavior for all time points can be determined. Systems may have a mixture of deterministic and random properties.

Additional terms used to describe dynamic systems are linearity and nonlinearity. A linear system is defined by 2 properties: scaling and superposition. Scaling means that, if a given input produces a given output, then doubling the size of the input will double the size of the output, and so on, for any arbitrary scaling of the input. Superposition means that, if one input produces a given output and a different input produces another output, providing the sum of these 2 inputs to the system will produce as output the sum of the 2 individual outputs. A nonlinear system does not satisfy the conditions of scaling and superposition. That is, the variables to be solved cannot be written as a linear sum of independent components. In the real world, a true linear system does not exist. Most physical and physiological systems are inherently nonlinear.

We next draw readers’ attention to the terms used to categorize different system behaviors. Several terms are used to categorize system behaviors, but we focus on the terms random and chaotic. As the term implies, random behavior is unpredictable. However, the question of randomness is a relative one. Given a time series or other data set, the data are no longer random but are fixed. There are potential admixtures of random and deterministic properties in systems. Chaos arises from a deterministic system but is so complex in appearance that it may be mistaken for randomness. The 3 defining features of chaos are appearance of random behavior, sensitive dependence on initial conditions, and determinism. The classic notion of the “butterfly effect” describes the sensitive dependence on initial conditions in chaos theory. From Lorenz's work on weather prediction stemmed the notion that a butterfly flapping its wings in one city today can influence the weather thousands of miles away a week from now.³ The importance of this notion is that a potentially simple deterministic system can produce complex behavior and that, if the underlying system is deterministic, then it follows rules, revealing ways to understand and control the system.

Mathematical analysis of complex dynamic systems, such as motor behavior, is best approached with nonlinear analysis, which takes the time series into account. Nonlinear time series analysis has been applied in several studies to the analysis of motor behavior development. Heath and colleagues⁴,⁵ demonstrated that nonlinear dynamic analysis techniques allowed researchers to determine the information complexity of temporal data by use of physiological and psychological measurements. Newell and Vaillancourt⁶ discussed the utility of nonlinear analysis in motor learning.

Dynamic systems involving spontaneous movements cannot be linear and are expected to invoke nonlinear rules. The technical terms for nonlinear time series analysis cannot be adequately covered in this article, but the reader is referred to the glossary of technical terms and the references as needed. Within the glossary, it is emphasized that irregular motion is not always random but can be deterministic chaos. This point is essential to understanding the results presented in this article. The set of techniques used in nonlinear time series analysis are based on an examination of the structural characteristics of a time series embedded in an appropriately constructed state space.⁷ The characteristics of that state space then can be examined to gain insight into motor control. For establishment of the state space from data, time delay embedding is usually used. This technique involves establishing a state space representation of the system by use of current and delayed values from the time series. The dimension of the reconstructed state space is called the embedding dimension. The maximal Lyapunov exponent provides an indication for the predictability of a dynamic system. The surrogate data method is a test for nonlinearity.

Glossary of Technical Terms

Nonlinear Time Series Analysis: Nonlinear time series analysis is useful when linear data analysis fails to mathematically describe or characterize the observed data adequately. In the paradigm of linear data analysis, a small cause always leads to a small effect, and irregular behavior of the system is regarded as the result of random external input to the system. If it is thought that the irregular behavior is attributable to some internal factors, nonlinear time series analysis must be used.

Nonlinear time series analysis is based on the theory of dynamic systems. The evolution rule of the dynamic system is a deterministic rule, in which only one future state follows the current state. The concept of deterministic chaos (see below) has proven to be fruitful in the understanding of irregular temporal behavior in systems that do not seem to be inherently stochastic (random).⁸

Deterministic Chaos: In general terms, chaos means a situation in which everything is disorganized and completely out of control. In mathematics and physics, however, deterministic chaos stands for aperiodic, long-term behavior in a deterministic system. Deterministic chaos is often referred to as chaos for brevity. Chaos exhibits highly sensitive dependence on initial conditions. Starting from very close initial conditions, a chaotic system very rapidly moves to different states. This amplification of small errors is called local instability. Because of local instability, the long-term behavior of a chaotic system is impossible to predict and appears to be random, although the short-term behavior is predictable. There is sometimes confusion between chaos and randomness, but there are some fundamental differences. Randomness originates from stochastic noise. On the other hand, a chaotic system has a simple rule so that it can be synchronized or controlled.⁹,¹⁰ Chaos can be distinguished from randomness by estimating the degree of freedom (dimension) and Lyapunov exponent, as explained below.

Embedding Dimension and Degree of Freedom: For a deterministic system, a state space is a space in which all possible states of the system are represented. Thus, a point in this space specifies the state of the system and vice versa. In the theory of dynamic systems, degree of freedom is defined as the dimension of the state space, which is equal to the number of variables necessary to describe the state of the system. In experiments, one cannot always measure all of these variables. Thus, the orbit in the state space cannot often be observed directly. In this situation, time delay embedding coordinates are useful for reconstructing the state space. According to the Takens embedding theorem, one can reconstruct the state space with the time delay embedding coordinate (x_{t−(m−1)τ}, x_{t−(m−2)τ}, … x_t−τ, x_t), where x_t is a value measured at moment t. The number of m is called the embedding dimension; the time τ is referred to as the delay. There are some methods that can be used to find optimal values for the embedding parameters m and τ.⁸ One of them is the false-nearest-neighbor method, which identifies whether a certain embedding dimension is sufficient for the reconstruction of a state space. Although the optimal embedding dimension and the degree of freedom are mathematically different concepts, they often have similar values in practice. Within the framework of the theory of dynamic systems, a stochastic system has an infinite dimension (ie, the degree of freedom is also infinite). When synchronization happens in a rhythmic or chaotic system, the degree of freedom decreases because the behavior of some variables is described by the other variables in the synchronized situation. Similarly, self-organization is realized by a reduction in the degree of freedom.

Maximal Lyapunov Exponent: Chaotic systems display exponential sensitive dependence on initial conditions. Consider 2 nearby initial conditions and imagine that they evolve forward in time. When the separation between the 2 orbits at the initial time is small enough, the separation grows exponentially over time. The maximal Lyapunov exponent represents the exponential rate of the divergence. Thus, for a chaotic system, the maximal Lyapunov exponent is positive. For rhythmic motion (limit cycle), it is 0. For stationary behavior, it is negative. A higher Lyapunov exponent means that the system is more unstable and more unpredictable. For a stochastic system, the maximal Lyapunov exponent is not well defined. If a deterministic system is perturbed by random noise (eg, measurement error), the maximal Lyapunov exponent diverges. Several methods have been developed to estimate the Lyapunov exponent of an underlying deterministic system.⁸ We applied the Kantz algorithm.

Complexity and Randomness: The relationship between the Lyapunov exponent and the degree of freedom is illustrated in Figure 2. The left bottom border in the chaos region is called the “edge of chaos,” where it is thought that the complexity is maximal and the system is somehow optimized for adaptation and information processing.¹¹–¹³ Note that complexity is distinguished from randomness in terms of the study of complex systems. Although models with large dimensionality (ie, those with a high degree of freedom) may be random, complex system behavior can be produced by models with small di-mensionality, and many variables do not necessarily create complexity. Instead, complexity is created by nonlinearity, which causes self-organization, adaptation, and emergent behavior.

Surrogate Data Method: Surrogate data are used to determine whether the results from nonlinear time series analysis are statistically true. Surrogate data are created to have the same power spectrum and amplitude distribution as the observed time series. The surrogate data method tests the observed time series against the null hypothesis that it results from a linear, stochastic process. If the null hypothesis is rejected, this test supports the notion that the system that produces the time series is nonlinear. If the null hypothesis is not rejected, the outcome is not statistically significant.