Quantitative FRET Analysis by Fast Acquisition Time Domain FLIM at High Spatial Resolution in Living Cells

Abstract

Quantitative analysis in Förster resonance energy transfer (FRET) experiments in live cells for protein interaction studies is still a challenging issue. In a two-component system (FRET and no FRET donor species), fitting of fluorescence lifetime imaging microscopy (FLIM) data gives the fraction of donor molecules involved in FRET (f_D) and the intrinsic transfer efficiency. But when fast FLIM acquisitions are used to monitor dynamic changes in protein-protein interactions at high spatial and temporal resolutions in living cells, photon statistics and time resolution are limited. In this case, fitting procedures are not reliable, even for single lifetime donors. We introduce the new concept of a minimal fraction of donor molecules involved in FRET (mf_D), coming from the mathematical minimization of f_D. We find particular advantage in the use of mf_D because it can be obtained without fitting procedures and it is derived directly from FLIM data. mf_D constitutes an interesting quantitative parameter for live cell studies because it is related to the minimal relative concentration of interacting proteins. For multi-lifetime donors, the process of fitting complex fluorescence decays to find at least four reliable lifetimes is a near impossible task. Here, mf_D extension for multi-lifetime donors is the only quantitative determinant. We applied this methodology for imaging the interaction between the bromodomains of TAF_II250 and acetylated histones H4 in living cells at high resolution. We show the existence of discrete acetylated chromatin domains where the minimal fraction of bromodomain interacting with acetylated H4 oscillates from 0.26 to 0.36 and whose size is smaller than half of one micron cube. We demonstrate that mf_D by itself is a useful tool to investigate quantitatively protein interactions in live cells, especially when using fast FRET-FLIM acquisition times.

INTRODUCTION

Fluorescence-based methods encompass different disciplines and a vast number of technical approaches. Among the different fluorescence-based applied methodologies, Förster resonance energy transfer (FRET) (1) stands alone as a technique that permits one to investigate molecular processes with nanometer resolution (2). During the last 40 years, FRET has been used to understand a great variety of molecular interactions, both in vitro and in vivo. Advances in different photonic imaging techniques and the development of fluorescent probes, and particularly fluorescent proteins (3,4), have raised FRET microscopy to the level of dominance in the field. Protein-protein interactions in living cells can be directly monitored using FRET. This aspect is critical to improve our understanding of different processes occurring in vivo (biochemical protein cascades) and if it is done quantitatively, to build or improve biological mathematical models (5).

A quantitative parameter of FRET is the quantum yield of the energy transfer process (E). E provides information on the distance and/or the mutual orientation of the two dipoles in the interaction under study. It depends on the rate constants of the donor fluorescence de-excitation, which in turn are related to the fluorescence lifetime of the donor alone and the donor involved in FRET, τ_D and τ_F, respectively. Donor fluorescence lifetime decreases due to energy transfer in the excited state and the percentage of the decrease is equal to E. The determination of FRET efficiency by fluorescence lifetime measurements is advantageous in living cell studies since the fluorescence lifetime is independent from fluorophore concentration and the excitation light path, parameters that are unknown in cells under the microscope.

Other quantitative FRET techniques based on steady-state intensity allow determination of the apparent FRET efficiency, E_app (6–13). E_app depends directly on the product of two parameters: the intrinsic FRET efficiency value (E) and the fraction of the donor that undergoes FRET (f_D, using the notation of Hoppe et al. (6)). In this respect, others have shown (14) that steady-state intensity-based approaches are not able to obtain f_D out of E_app. To determine f_D, the intrinsic FRET efficiency (E) must be calculated independently.

Fluorescence lifetime imaging microscopy (FLIM) is a well-established technique to determine the fluorescence kinetics of the donor emission for FRET measurements (15–17). In FLIM, analysis of fluorescence decays by mean lifetime does not require a high number of measured photons. But, for a two-component system (free and bound donor), the mean fluorescence lifetime depends on E and f_D, which are impossible to resolve separately. To simultaneously obtain f_D and E values from the fit, fluorescence decay analysis must be done with two components or more, and data has to be acquired with the highest number of photon counts so that statistics are robust enough to reduce fitting imprecisions. This is particularly true when only a small fraction of the donor is interacting with the acceptor. By using the time-correlated single-photon counting (TCSPC) method for a single-lifetime donor, E and f_D can be obtained from the fit of fluorescence decay using a double-exponential model (15–17). TCSPC allows a high temporal resolution of the fluorescence kinetics (few tens of picoseconds) and offers the possibility to attain high photon statistics. Several minutes of data acquisition are, however, necessary to obtain sufficient photon statistics per pixel. Such long acquisition times are not compatible with high spatiotemporal resolution of quantitative FRET images. Although some studies propose different approaches to deal with these quantitative aspects (18–22), the development of a technique to follow the relative amount of interaction between two proteins at high spatial and temporal resolutions in living cells is still a challenge for FRET-based microscopy.

In this work, we present a method that provides a way to monitor dynamic changes in protein-protein interactions at high spatial and temporal resolutions in living cells. Here, considering a two-component system with a narrow distribution of E, we introduce the new concept of the minimal percentage of donor molecule involved in FRET (mf_D). This novel approach is biologically interesting because it retrieves information about a known threshold of interacting donor protein. One advantageous property of mf_D is that it only depends upon experimental data: it does not require E determination from a fit, which is impossible when fast acquisitions are required for monitoring dynamic changes. We also show that if the donor fluorescence decay is multiexponential (multi-lifetime donor), this minimal value of FRET, mf_D, can also be obtained and is the only biological parameter that can be directly determined. Combining multifocal multiphoton excitation and a fast-gated charge-coupled device (CCD) camera (TriM-FLIM system), we applied this methodology for imaging the interaction between the bromodomain of the transcriptional factor TAF_II250 and acetylated histones H4 in living cells at high resolution. Two types of donors were used, green fluorescent protein (GFP, single lifetime) or cyan fluorescent protein (CFP, multiple lifetimes). Similar mf_D values were obtained, taking into account the dark species of the red acceptor (S. Padilla-Para, M. Coppey-Moisan, and M. Tramier, unpublished data, (23–25)). We show the existence of discrete acetylated chromatin domains where the minimal fraction of bromodomain interacting to acetylated H4 oscillates from 0.26 to 0.36 and whose size is smaller than half a micron cube.

MATHEMATICAL BACKGROUND

Single-lifetime donor systems with two components

Considering a fluorescence decay i(t), the mean fluorescence lifetime is defined as

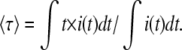(1)

To analyze data coming from a discrete sampling, the mean lifetime is directly calculated by applying Eq. 1. For a time-gated stack of images, we have

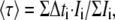(2)

where Δt_i corresponds to the time delay after the laser pulse of the i^th image acquired and I_i to the pixel intensity map in the i^th image.

In the case of a single lifetime donor system with two components in which there is a fraction of donor which undergoes FRET (f_D) and a fraction which does not (1-f_D), the fluorescence decay of the donor i(t), is defined as

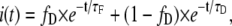(3)

where τ_D is the corresponding single donor lifetime and τ_F stands for the corresponding FRET lifetime. If we solve Eq. 1 using Eq. 3, we obtain the expression

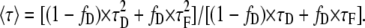(4)

Isolating f_D and normalizing the last expression dividing by τ_D we find an expression that accounts for the fraction of donor in interaction:

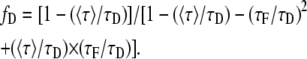(5)

Minimal fraction of interacting donor

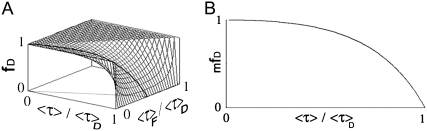
The surface which represents f_D as a function of 〈τ〉/τ_D and τ_F/τ_D is presented in Fig. 1 A. For each value of τ_F/τ_D there is a corresponding parabola exhibiting a minimum. We introduce the concept of minimal fraction of donor undergoing FRET (mf_D), which corresponds to the function describing each one of these minimums. Mathematically, f_D depends on two variables (τ_F/τ_D and 〈τ〉/τ_D) and can be minimized following τ_F/τ_D. The partial derivative (∂f_D/∂(τ_F/τ_D)) is zero for τ_F = 〈τ〉/2. Replacing τ_F by 〈τ〉/2 in Eq. 5 gives

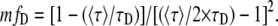(6)

Fig. 1 B shows the behavior of mf_D as a function of 〈τ〉/τ_D. mf_D retrieves information about the minimal threshold of donors engaged in FRET in a related system. That is to say, mf_D provides instantaneous knowledge about the minimal extent of the interaction under study. This is particularly relevant in biology because without knowing the intrinsic transfer efficiency (since mf_D does not require previous τ_F knowledge), quantitative data related to the relative concentration is immediately at hand.

FIGURE 1.

Surface plot of f_D for a single lifetime donor system with two species. (A) f_D surface plotted as a function of 〈τ〉/τ_D and τ_F/τ_D using Eq. 5. (B) mf_D versus 〈τ〉/τ_D related to the minimization of f_D as a function of τ_F/τ_D (τ_F = 〈τ〉/2) using Eq. 6. Note that the surface plotted in panel A presents an observable minimum, which corresponds to the curve plotted in panel B.

Extension to multi-lifetime donor systems

Now, considering the general case in which we have a multi-lifetime donor, the donor fluorescence decay, i_D(t), is defined as

(7)

where a_i are the preexponential factors and τ_Di the corresponding donor lifetimes. If there is FRET, each donor lifetime τ_Di is shortened to the corresponding FRET lifetime (τ_Fi) while a_i remains unchanged. Since the preexponential factors are related to the relative concentration of each species, we can consider that they remain the same when FRET occurs. The donor fluorescence decay upon FRET, i_F(t), can be expressed as

(8)

For a two-component system with multi-lifetime donor, we can write the expression for the complex intensity decay as

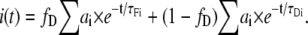(9)

In the above expression, f_D still represents the fraction of donor that undergoes FRET. If we solve Eq. 1 using Eqs. 7 and 9, we obtain the next expression for the mean lifetime:

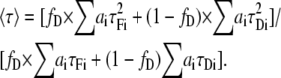(10)

To introduce the mean lifetime of the donor alone, 〈τ〉_D, and the donor that undergoes FRET, 〈τ〉_F, Eq. 1 is solved using Eqs. 7 and 8, and one obtains

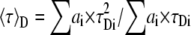(11)

and

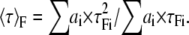(12)

Using Eqs. 11 and 12 in Eq. 10 and isolating f_D, the next expression is easily found as

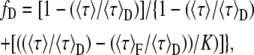(13)

with

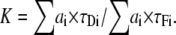(14)

Observe that Eq. 13 is an extension of Eq. 5. In the particular case of single lifetime donor, 〈τ〉_F = τ_F, 〈τ〉_D = τ_D, and K = τ_D/τ_F, and Eq. 13 becomes Eq. 5.

Equation 13 cannot be easily applied because in the majority of cases the discrete lifetimes (τ_Di and τ_Fi) are unknown. But, following the same procedure as for the single lifetime donor, we can introduce mf_D (the minimization of f_D). This time, f_D depends on three variables (〈τ〉_F/〈τ〉_D, 〈τ〉/〈τ〉_D and K). To obtain the minimal fraction of donor undergoing FRET for multi-lifetime donor systems (mf_D), we minimize f_D as a function of K and 〈τ〉_F/〈τ〉_D. Since τ_Di ≥ τ_Fi, Eq. 14 gives K ≥ 1. ∂f_D/∂K > 0 then f_D is minimal for K = 1. For the second parameter (〈τ〉_F/〈τ〉_D), since the partial derivative of Eq. 13, ∂f_D/∂(〈τ〉_F/〈τ〉_D) > 0, the minimal amount of percentage of FRET corresponds to the value of f_D for the minimal value of 〈τ〉_F/〈τ〉_D, which is 0. Then, for the two-species model with a multi-lifetime donor system, mf_D is a simplification of Eq. 13 using K = 1 and 〈τ〉_F/〈τ〉_D = 0:

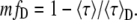(15)

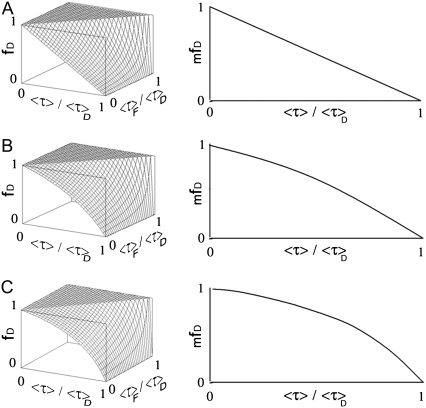
To graphically visualize the minimization, f_D was plotted as a function of 〈τ〉_F/〈τ〉_D and 〈τ〉/〈τ〉_D giving values of K = 1, 2, or 3 using Eq. 13 (Fig. 2, left panel). After minimization following 〈τ〉_F/〈τ〉_D (〈τ〉_F/〈τ〉_D = 0), the corresponding mf_D for each value of K are presented in the right panel. As demonstrated above, the value for K that makes f_D to be minimal is 1. Note that, in this case, mf_D grows linearly as a function of 〈τ〉/〈τ〉_D (Fig. 1 A, right panel), as expected (Eq. 15).

FIGURE 2.

Surface plot of f_D for a multi-lifetime donor system with two species. (Left panel) f_D versus 〈τ〉/〈τ〉_D and 〈τ〉_F/〈τ〉_D using Eq. 13 for K = 1 (A), 2 (B), or 3 (C). (Right panel) corresponding mf_D versus 〈τ〉/〈τ〉_D related to the minimization of f_D as a function of 〈τ〉_F/〈τ〉_D (〈τ〉_F/〈τ〉_D = 0). Surface and curve in panel A are lower than the surfaces and curves presented in panels B and C. It corresponds to the minimization of f_D following K. For the curve in panel A (〈τ〉_F/〈τ〉_D = 0 and K = 1), mf_D is linear as defined by Eq. 15.

The two ways to minimize the f_D function for single or multi-lifetime donor systems are very different. In the case of single lifetime donor, the shape of the f_D surface directly provides a way to find mf_D. In this case, when τ_F = 〈τ〉/2, mf_D = f_D. Inversely, for multi-lifetime donors, f_D minimization leads to K and 〈τ〉_F values impossible to attain simultaneously (K = 1: FRET does not occur and 〈τ〉_F = 0: maximum value of FRET). This relies on the fact that K and 〈τ〉_F are interdependent parameters. This apparent contradiction does not affect the mathematical meaning of mf_D, which always corresponds to a minimization of the f_D function, but in a more stringent manner than for the single-lifetime donor case. Thus in those systems, mf_D is always smaller compared to f_D. Nevertheless, mf_D plays an important biological role because it accomplishes the task of giving a quantitative interacting protein threshold for a complex multiexponential system when an approach using the complete description of FRET kinetics (fluorescence decay multi-exponential fitting using more than four lifetimes) is a nonrealistic option.

MATERIALS AND METHODS

Plasmid constructs

Fluorescent fusion proteins were cloned in pEGFP-C1 (Clontech, Mountain View, CA) and “pmCherry-C1.” To generate pmCherry-C1, the mCherry coding sequence was transferred from pRSETB-Cherry (a generous gift from Dr. Tsien, University of California at San Diego) into a Clontech vector backbone (26). In mCherry-H4 construct, H4 cDNA (IMAGE:2130477) is cloned in mCherry-C1 vector using Xhol and SalI sites of the MCS. In pEGFP-bromodomain (BD) module construct, the BD sequence is obtained from Kanno et al. (27) and contains the amino acids 1207–1872 of TAF_II250. This sequence is cloned in the p-mCherry vector using EcoRI and KpnI sites of the MCS. CFP-BD and YFP-H4 were also obtained from Kanno et al. (27).

Solution and cell culture

Rhodamine 6G (Rd) and acridine orange (AO) (dye content 99%) were obtained from Sigma Aldrich (Stenheim, Germany). Initial solutions 10⁻⁵ M for Rd and AO were adjusted by dilution measuring their corresponding pure fluorescence decays so that similar intensity decay amplitudes were found for the final solutions, i.e., equal intensity for the first gated image of each acquisition. Using these final solutions, the fraction of Rd compound in each mixture corresponds to the fraction of the lifetime amplitude for each one of the resulting 11 solutions.

HEK293 cells were cultured in Dulbecco's modified Eagle's medium containing 10% fetal bovine serum (PAA Laboratories GmbH, Pasching, Austria). The cultures were incubated at 37°C in a humidified atmosphere of 5% CO₂. HEK293 cells were seeded on 32-mm round glass coverslip at a density of 2 × 10⁵ cells. When cells were ∼70% of confluence, they were transfected with a total amount of 1 μg of expression vectors using Nanofectin I (PAA). Twenty-four hours after transfection, cells were incubated with 2.5 mM of Sodium Butirate. Twelve hours after we had spiked Sodium Butirate, coverslips were mounted in an open observation chamber with special DMEM-F12 to prevent fluorescence from the medium (DMEM-F12 without Phenol red, B12 vitamin, Riboflavin and supplemented with 20 mM HEPES and L-Glutamine from PAA).

Time domain picosecond fluorescence lifetime microscopy and data analysis

Space-resolved fluorescence lifetimes were obtained by taking advantage of simultaneous acquisition of time and space information by a time- and space-correlated single-photon counting (TSCSPC) detector (quadrant anode detector, EuroPhoton, Berlin, Germany), as described previously (16). The mode-locked titanium sapphire laser (Millennia 5W/Tsunami 3960-M3BB-UPG kit, Spectra-Physics, Les Ulis, France) was tuned to 960 nm to obtain wavelengths of 480 nm after frequency doubling for GFP excitation and a 535AF45 emission filter was used.

The acquired fluorescence decays were deconvoluted with the instrument response function and fitted by a Marquardt nonlinear least-square algorithm using Globals Unlimited software (Laboratory for Fluorescence Dynamics; University of California at Irvine) with a one- or two-exponential theoretical model.

FRET efficiency, E, was calculated as

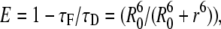(16)

where R₀ is the Förster radius, r the distance between donor and acceptor, τ_D fluorescence lifetime of the donor, and τ_F the FRET lifetime. The R₀ for the GFP/mCherry couple was calculated from

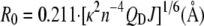(17)

with

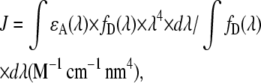(18)

where n is the refractive index, Q_D the fluorescence quantum yield of the donor, κ the parameter related to the orientation of donor and acceptor, ɛ_A(λ) the acceptor absorption spectrum, and f_D(λ) the donor emission spectrum. To calculate R₀ = 47 Å for the GFP/mCherry, we took the refractive index of the protein (1.33), a κ² of (2/3), the emission spectrum and quantum efficiency of the GFP (0.6) from Peter et al. (17), the mCherry absorption spectrum with a maximum molar extinction coefficient of 72,000 M⁻¹ cm⁻¹ from Shaner et al. (28).

Multifocal multiphoton fluorescence lifetime imaging microscopy and data analysis

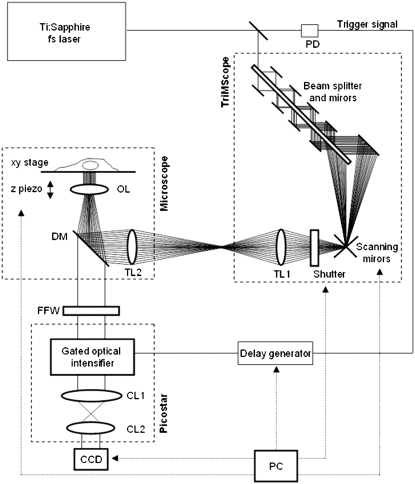
The two-photon picosecond FLIM system (TriM-FLIM) combines multifocal multiphoton excitation (TriMscope, LaVisionBiotec, Bielefeld, Germany) and a fast-gated CCD camera (PicoStar, LaVisionBiotec) (Fig. 3), as described elsewhere (29). Two-photon multifocal excitation was carried out using the TriMScope connected to an inverted microscope (IX 71, Olympus, Tokyo, Japan). A mode-locked Ti:Sa laser at 800, 850, and 950 nm for the excitation of cyan fluorescence protein (CFP), mixture of AO and Rd and green fluorescent protein (GFP), respectively (Spectra Physics, Évry, France) is split into 2–64 beams by utilizing a 50/50 beam splitter and mirrors. The set of beams is passing through a 2000 Hz scanner before illuminating the back aperture of a ×60 NA 1.2 infrared water immersion objective (Olympus, Tokyo, Japan). A line of foci is then created at the focal plane, which can be scanned across the sample, making a pseudo wide-field illumination. A filter wheel of spectral filters (535AF45 for GFP and mixture of AO/Rd and 480AF30 for CFP) is used to select the fluorescence imaged onto a fast-gated light intensifier connected to a CCD camera (PicoStar). The gate of the intensifier (adjusted at 1 ns and 2 ns depending on the experiment) is triggered by an electronic signal coming from the laser and a programmable delay box was used to acquire a stack of time-correlated images. The intensifier plays the role of a very fast shutter and, for each delay (from 0 to 10 ns or from 0 to 8 ns) the intensified signal corresponds to photons coming from a particular region of the fluorescence decay (1-ns or 2-ns gate width, respectively). The acquisition time of the CCD camera was adjusted considering the fluorescence signal level (generally from 0.5 to 3 s). All instrumentation was controlled by IMspector software developed by LaVisionBiotec.

FIGURE 3.

TriM-FLIM setup. The scheme describes the optical path of the excitation source and the different components of the system. The excitation source is a two-photon Ti:Sapphire fs laser, tunable from 700 nm to 950 nm. Part of the laser is sent to a fast photodiode (PD) and the signal, which is used to trigger the gated optical intensifier, passes through a delay generator. The laser then enters the TriMScope. The laser beam goes through the combination of beam splitter and mirrors generating 64 beams which are scanned and directed into the objective lens (OL) by passing through tube lens (TL1 and TL2). The fluorescence signal from the sample is selected by a dichroic mirror (DM) and a fluorescence filter inserted into a wheel (FFW) and directed to the PicoStar constituted by a gated optical intensifier (photocathode, multichannel plates, and phosphor screen) and an optical coupling system (CL1 and CL2). The image is then acquired by a CCD camera. A PC controls the scanning mirrors, the excitation shutter, the delay generator, the CCD camera, the FFW, and the microscope (xy stage and z piezo) using IMspector software.

Analysis of the data was done using ImageJ (W. S. Rasband, ImageJ, U.S. National Institutes of Health, Bethesda, Maryland, http://rsb.info.nih.gov/ij/). Raw images were first smoothened by a 3 × 3 mask to decrease the noise. Equation 2 was applied on background-subtracted stacks of time-gated images to recover mean lifetime images. Equation 5 was applied on mean lifetime images using fixed values of τ_D and τ_F to recover f_D. Equations 6 and 15 were applied on mean lifetime images using fixed value of 〈τ〉_D and τ_D to recover mf_D for single lifetime donor and multi-lifetime donor, respectively. The routine Igor (Wave Metrics, Lake Oswego, OR) was used to fit the fluorescence decay corresponding to the stack of images obtained with the TriM FLIM system.

RESULTS AND DISCUSSION

Determination of bromodomain and acetylated histone H4 interaction by FRET using single-photon counting

Acetylation of histones correlates with gene activation and can be recognized by chromatin-associated proteins containing bromodomains. The bromodomain is a module of ∼110 amino acids that is conserved in many chromatin-associated proteins including histone acetyltransferases. TAF_II250 is a component of the basal transcription factor TF_IID, and its double bromodomain (BD) module binds to an acetylated H4 peptide in vitro (30–32) and in vivo as demonstrated by the flow cytometric adaptation of FRET (27). These methods, however, cannot provide quantitative measurements of the histones acetylation nor determine the spatial distribution in the nucleus. We tagged the TAF_II250 double BD module with GFP (GFP-BD) and the histone H4 with the red fluorescent protein, mCherry-H4 (mCherry) to quantify and visualize histone acetylation in living cells by FRET imaging.

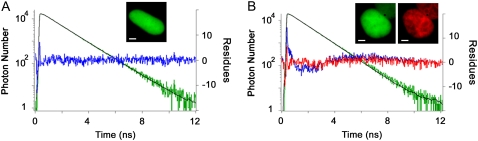
FRET was first determined by using time-domain picosecond fluorescence lifetime microscopy commonly used in the laboratory (16,26,33–35). Fluorescence decay images (GFP-BD in the presence and in the absence of mCherry-H4) were acquired by using the TSCSPC set up and a representative experiment is presented in Fig. 4. As expected, both fusion proteins colocalize in the nucleus with a diffuse pattern for GFP-BD and a chromatin pattern for mCherry-H4. The fluorescence decay of GFP-BD expressed alone extracted from the whole nucleus is well fitted by a single exponential as the residues behave linearly over the time window (τ_D = 2.58 ± 0.02 ns, n = 48). In contrast the fluorescence decay of GFP-BD coexpressed with mCherry-H4 does not exhibit a monoexponential decay as the residue curve of the single-exponential fit is not linear anymore. The addition of a second shorter fluorescence lifetime is necessary and corresponds to the proof of FRET (τ_F = 0.65 ± 0.05 ns, n = 53) in each individual cell analyzed. Thanks to the 10³ time channels and the 120 ps of full width at half-maximum of the instrument response function (16), the precision on the determination of τ_F is accurate (only 0.05 ns, n = 53). This τ_F value corresponds to a FRET efficiency E = 0.75 and to a distance between GFP and mCherry chromophores of 39 Å (by taking R₀ of 47 Å, see Materials and Methods). This is compatible with the distance between the N-terminal of H4 and the N-terminal of BD, which was deduced from the size and the conformation of the crystallized form of the bromodomain (31). These results are obtained because high photon statistics (∼3.10⁶ counted photons) are reached by binning all the pixels of each nucleus to keep an acceptable acquisition time (3 min). The fraction of the short lifetime component (f_D) is variable from cell to cell (f_D up to 0.33 with a mean value of 0.19, 25% of cells present no FRET signal). Here, FRET is determined for each individual cell analyzed but information regarding each pixel of the image is missing.

FIGURE 4.

GFP-BD interaction with acetylated mCherry-H4 in the nucleus of HEK293 live cells using a single-photon counting method. (A) Steady-state intensity image of GFP-BD expressed alone in HEK293 cell (green). The corresponding GFP-BD fluorescence decay (green curve) extracted from the whole nucleus is fitted by a single exponential (black line, τ_D = 2.59 ns) and the residues are presented (blue curve). (B) Steady-state intensity images of GFP-BD (green) and mCherry-H4 (red) coexpressed in HEK293 cells. The corresponding GFP-BD fluorescence decay (green curve) extracted from the whole nucleus is fitted by a single- (τ = 2.46 ns) and a biexponential model (τ_D = 2.59 ns fixed and τ_F = 0.65 ns) and residues are presented (blue curve and red curve, respectively). Note that the fluorescence decay is better fitted with a biexponential model as shown by residues. Scale bar = 2 μm.

mf_D as pixel-by-pixel quantitative tool for fast time domain FLIM acquisition

Using single-photon counting detection, acquisition times must be long enough so that sufficient counted photons are at hand to have a good precision fit. From the above experiment, 3 min were necessary to quantify the average FRET throughout the nucleus. However, to obtain quantitative information on a pixel-by-pixel basis, the acquisition time needs to be increased to several tens of minutes. Under these conditions, chromatin movement is not negligible. The results would correspond to the average of all dynamic processes that occur during the acquisition time, thus the measured FRET spatial location would be averaged. To be able to follow fast dynamic variations related to protein interactions in living cells with high spatial resolution, the acquisition time has to be as short as possible.

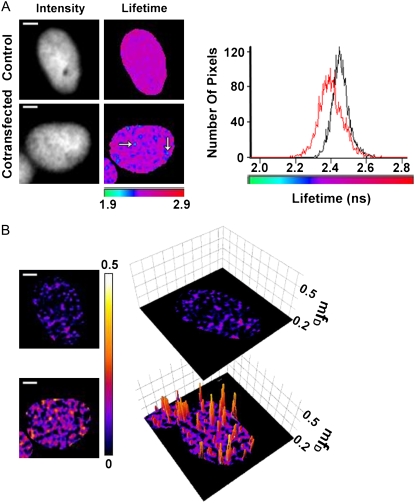
We investigated the impact of fast acquisitions on f_D and mf_D with the same biological example (GFP-BD and mCherry-H4) using the TriM-FLIM system. A windowing scheme using only five time-gated images was used so that very fast acquisition times were achieved (between 3 and 12 s for one stack, depending on the fluorescence intensity level of the sample). The gate width was 2 ns with a total time window of 10 ns. Taking into account the gain of the light intensifier and the full well-capacity of the CCD camera, ∼100 photons were acquired for each pixel of the image stack. The mean lifetime calculated for each pixel using Eq. 4 was then determined by the arrival time statistics of these 100 photons. Fig. 5 shows a representative experiment of a cell expressing GFP-BD alone and expressing GFP-BD in the presence of mCherry-H4. The mean lifetime of the GFP-BD decreased globally from 2.45 ns in the absence of the acceptor, to 2.40 ns in the presence of mCherry-H4. The decrease can be seen in a comparison of the two lifetime histograms of GFP-BD alone and GFP-BD in the presence of mCherry-H4 (Fig. 5 A). Moreover, the histogram of GFP-BD in the presence of mCherry-H4 presents a higher distribution of lifetime heterogeneity which corresponds to pixel-by-pixel FRET heterogeneity (see arrows in Fig. 5 A). These measured differences are characteristic of the presence of FRET and the decrease in the donor lifetime is statistically significant for the whole population of cells analyzed (from 2.44 ± 0.01 ns to 2.40 ± 0.01 ns, n = 30). The GFP-tagged bromodomain of TAF_II250 interacts with the mCherry-tagged histone H4 and thus reveals the acetylated H4 chromatin domain in the nucleus of living cells, in accordance to our results using a single-photon counting method. Interestingly, a small decrease in the mean lifetime can be related to a relevant fraction of donor undergoing FRET (see the shape of the curve at the vicinity of 〈τ〉/τ_D = 1 shown in Fig. 2). Note that the difference between the two lifetimes of the donor alone obtained with single-photon counting (2.58 ns) and TriM-FLIM (2.44 ns) are not comparable since the two methods of calculating the lifetime are not identical; the first one derives from a fit and the second one is obtained from a direct calculation of mean lifetime (Eq. 4). In fact, the lifetimes arising from these two different calculations are never compared. The comparisons are always made on values coming from the same calculation procedure.

FIGURE 5.

FLIM and mf_D images of GFP-BD interaction with acetylated mCherry-H4 in the nucleus of HEK293 live cells using TriM-FLIM system at fast acquisition times. (A) Intensity and FLIM images of GFP-BD expressed alone as control (upper panel) or with mCherry-H4 as cotransfection (lower panel) in HEK293 live cells using the TriM-FLIM system at 950 nm excitation and 535AF45 emission filter with five time-gated images. Intensity images were obtained by summing the time-gated stack. FLIM images were obtained by using Eq. 2 in a pixel-by-pixel manner. The corresponding lifetime histograms are presented in the right panel (black for control and red for cotransfection). White arrows show two chromatin domains in which GFP-BD mean lifetime decreases significantly. The mean lifetime averaged throughout the nucleus decreased from 2.45 ns for the control to 2.40 ns for the cotransfection. Scale bar = 2 μm. (B) (Left panel) mf_D images of control and cotransfection obtained by using Eq. 6 with τ_D = 2.45 ns. (Right panel) Three-dimensional representation of the corresponding mf_D images using a threshold limit given by the control (0.2). Scale bar = 2 μm.

To quantify protein interactions by f_D, τ_F has to be obtained from the fit of the fluorescence decay of the donor in the presence of the acceptor. From the stack of five time-gated images acquired by the TriM-FLIM, a fluorescence decay corresponding to the nucleus is extracted. But the number of photons collected in this fast acquisition mode and the number of time points (five time-gated images) does not provide enough statistical information to obtain reliable τ_F values. Double-exponential fits converge to zero for the short lifetime, or the preexponential factor, or to the same lifetimes for both components. These τ_F values are not consistent and do not allow f_D determination directly from this experiment.

To overcome these difficulties, we introduce the new concept of mf_D. Mean lifetimes for GFP-BD in the presence and absence of mCherry-H4 are still reliable; therefore calculation of mf_D is possible. mf_D gives the minimal fraction of interacting GFP-BD and two-dimensional topology maps were obtained directly from the mean lifetime images using Eq. 6 (Fig. 5 B). In addition, a three-dimensional representation of mf_D images using a threshold limit given by the control is included to highlight the differences between control and FRET images (Fig. 5 B). The average value of mf_D throughout the nucleus determined from 30 independent acquisitions varies between 0.03 and 0.13 with a mean value of 0.06. Using this fast acquisition mode, the spatial resolution map of mf_D is ∼0.2 μm³ (the size of the voxel). The mf_D punctuated nuclear pattern in Fig. 5 B reveals the existence of eight discrete acetylated chromatin domains whose size is resolution-limited, and thus smaller to half one micron cube. In these domains, the minimal fraction of GFP-BD interacting with acetylated mCherry-H4 oscillates from 0.26 to 0.36. This image demonstrates that fast acquisitions can be made without losing the possibility of performing quantitative analysis if mf_D is the parameter chosen to characterize the system.

Comparison of f_D and mf_D

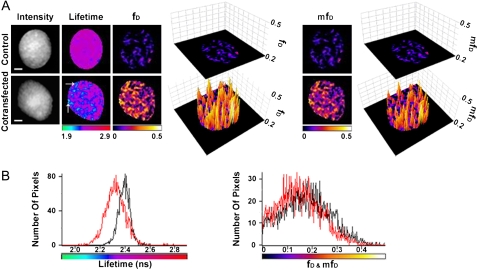
The same FRET example was used to measure and compare f_D and mf_D in cells coexpressing GFP-BD and mCherry-H4. Aiming to recover τ_F by fluorescence decay fitting, we increased the number of time points and the time resolution of the TriM-FLIM acquisition by increasing the number of gates and decreasing the time width of each gate (11 time-gated images with 1 ns time width). This last windowing scheme has the consequence to increase by a factor of four the acquisition time for two reasons: 1), the time width is decreased by a factor of two, decreasing the fluorescence signal and increasing the exposure time of each gated-image by the same factor; and 2), the number of images to be acquired is more or less twofold (11 time-gated images instead of five). In this case, mean fluorescence lifetime images (GFP-BD in the presence and absence of mCherry-H4) are presented in Fig. 6 A. The mean lifetime of the GFP-BD decreased globally from 2.41 ns in the absence of the acceptor, to 2.34 ns in the presence of mCherry-H4, thus indicating FRET. Note that the two mean lifetime histograms present the same characteristics as for the five time-gated acquisition (Fig. 6 B, left panel) and that the decrease in the donor lifetime corresponds to the decrease obtained with the fast acquisition mode (five time-gates images). This decrease is statistically significant for the whole population of cells analyzed (from 2.40 ± 0.02 ns to 2.37 ± 0.02 ns, n = 33).

FIGURE 6.

FLIM, f_D and mf_D images of GFP-BD interaction with acetylated mCherry-H4 in the nucleus of HEK293 live cells using the TriM-FLIM system with 11 time-gated images. (A) Intensity, FLIM, f_D, and mf_D images of GFP-BD expressed alone as control (upper panel) or with mCherry-H4 as cotransfection (lower panel) in HEK293 live cells using the TriM-FLIM system at 950 nm excitation and 535AF45 emission filter with 11 time-gated images. Intensity images were obtained by summing the time-gated stack. FLIM images were obtained by using Eq. 2 in a pixel-by-pixel manner. White arrows show two chromatin domains in which GFP-BD mean lifetime decreases significantly. The mean lifetime averaged throughout the nucleus decreased from 2.41 ns for the control to 2.34 ns for the cotransfection. f_D and mf_D images were obtained by using Eq. 5 (with τ_D = 2.41 ns and τ_F = 0.65 ns) and Eq.6 (with τ_D = 2.41 ns), respectively. Three-dimensional representations of the corresponding f_D and mf_D images using a threshold limit given by the control (0.2) are also presented. Scale bar = 2 μm. (B) (Left panel) Corresponding lifetime histograms of control (black curve) and cotransfection (red curve). (Right panel) Comparison of f_D (black) and mf_D (red) histograms of the cotransfected cell (mean f_D of 0.13 and mean mf_D of 0.11).

With the intention to determine f_D, the FRET lifetime (τ_F) was calculated from the biexponential fit of the fluorescence decay of the donor in the presence of the acceptor from the stack of 11 time-gated images acquired by the TriM-FLIM (τ_F = 0.65 ± 0.59 ns, n = 33). The donor lifetime was fixed at τ_D = 2.40 ns, which was derived from the monoexponential fit of the donor alone. The mean value obtained for τ_F matches the FRET lifetime found with the single-photon counting method. The large τ_F standard deviation would come from both: 1), the difference of acquisition time and then photon statistics; and 2), the difference in the number of fitted data points (10³ time channels for single photon counting, and only 11 here). From the mean lifetime two-dimensional maps obtained with the TriM-FLIM system, and using Eq. 5 with the τ_F value determined above, two-dimensional f_D maps were calculated (Fig. 6 A). Alternatively, mf_D two-dimensional topology maps were obtained directly from the mean lifetime two-dimensional maps using Eq. 6 (Fig. 6 A). In addition, a three-dimensional representation of both f_D and mf_D images using a threshold limit given by the control is included to reveal the differences between control and FRET images (Fig. 6 A). Both f_D and mf_D images are very similar and present the same pattern while FRET occurs with a very close mean value of f_D (0.13) and mf_D (0.11). The two histograms are also superimposed in Fig. 6 B (right panel). The underestimation of the amount of donor which undergoes FRET when taking mf_D relative to f_D is only 15% in this example.

mf_D as a function of τ_F and f_D

Previous knowledge of τ_F obtained by fitting the fluorescence decay of BD-GFP in the presence of mCherry-H4 using a double-exponential model (with the TriM-FLIM system using 11 time-gated images) allowed us to compare mf_D with f_D. But in this case, the comparison is restricted to a singular example. In this section, we explore mf_D in a more general context. mf_D behavior has been tested 1), as a function of transfer efficiency fixing f_D; 2), all over the f_D range fixing τ_F; and 3), all over the f_D range for an interval of transfer efficiency from 0.2 to 0.8.

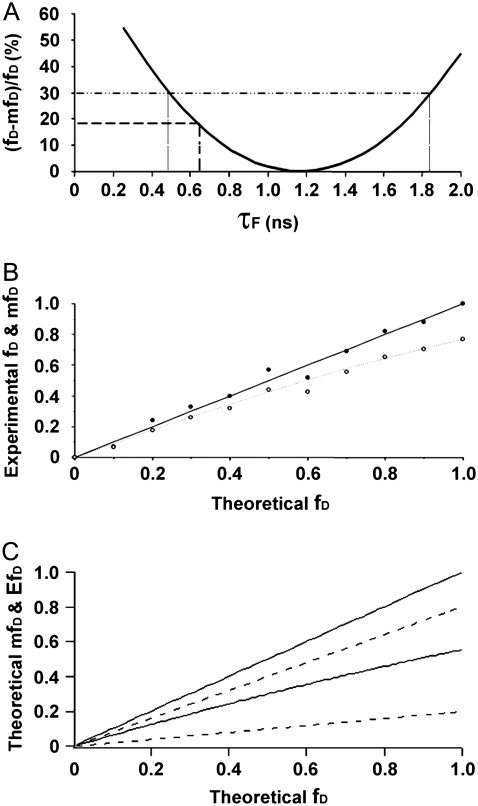
We have calculated the theoretical underestimation ((f_D − mf_D)/f_D) for the final experiment to compare mf_D and f_D as a function of τ_F (Fig. 7 A). Equations 5 and 6 were used fixing the value of τ_D = 2.41 ns and 〈τ〉 = 2.34 ns. As expected, for τ_F = 0.65 ns, we found a value of 17% (Fig. 7 A, dashed line). The slight difference between 15% determined above (Fig. 6) and 17% arises from the different type of data used to calculate the underestimation (mean histogram values of f_D and mf_D versus mean lifetime values). Interestingly enough, for a relatively small underestimation (for example, <30%), τ_F covers a large range of values (from 0.5 ns to 1.9 ns) (Fig. 7 A, dotted lines). The particular shape of the f_D surface (very flat around the minimum) allows for very good approximations of f_D using mf_D calculation for systems in which τ_F values fall close to 〈τ〉/2. In our biological example, the proportion of donor-tagged protein in interaction with the acceptor-tagged protein is smaller than 0.5, and the intrinsic FRET efficiency is not very different from 0.5. This makes τ_F similar to 〈τ〉/2, and f_D can be replaced by mf_D.

FIGURE 7.

The mf_D behavior as a function of τ_F and f_D. (A) Underestimation of f_D by mf_D as a function of τ_F for GFP-BD interaction with acetylated mCherry-H4 (11 time-gated experiments). Equations 5 and 6 were used, fixing the value of τ_D = 2.41 ns and 〈τ〉 = 2.34 ns. The dashed line placed at τ_F = 0.65 ns defines the underestimation made for this biological example (17%). The pointed line at 30% of underestimation defines a range of τ_F lifetimes from 0.5 ns to 1.9 ns; in this range mf_D happens to be very close to f_D. (B) Comparison between f_D and mf_D for a single-lifetime donor system in vitro. Mean lifetime measurements of solutions of AO and Rd with different fractions (from 0 to 1 with an increment of 0.1) were carried out under the TriM-FLIM system at 850 nm excitation and 535AF45 emission filter. f_D (solid dots) and mf_D (open dots) were calculated using Eq. 5 (with τ_D = 3.47 ns and τ_F = 2.25 ns) and Eq. 6 (with τ_D = 3.47 ns), respectively, and plotted versus theoretical f_D. The black straight line represents the theoretical value of AO percentage whereas the dashed line stands for the theoretical mf_D curve (see text for calculation details). (C) Theoretical mf_D and Ef_D behavior all over the f_D range for an interval of transfer efficiency from 0.2 to 0.8 (see text for calculation details). The range of indetermination of mf_D (region between the solid lines) for a given f_D is narrower than the one corresponding to Ef_D (region between the dashed lines).

Aiming to study the mf_D behavior over the f_D range, a set of 11 solutions with different proportions of acridine orange (AO) and rhodamine-6G (Rd) (from 0 to 1 in AO fraction with a periodic decrease of 0.1 in Rd fraction) was investigated. The idea was to mimic a two-component model with a single-lifetime donor system using solutions containing two dyes of different lifetimes varying their ratio. The short lifetime of AO (2.25 ns) represents τ_F while the long lifetime of Rd (3.47 ns) stands for τ_D. Acquisitions were carried out on the TriM-FLIM system using 11 time-gated images. We used Eq. 5 to determine f_D, the fraction of AO in mixtures of AO/Rd in solution from the mean fluorescence lifetime images obtained by the TriM-FLIM system (Fig. 7 B, solid dots). The solid straight line represents the real percentage of AO when preparing the solutions (theoretical f_D). Since the solid dots superimpose the solid straight line, the measured f_D values for all the solutions are in agreement with the theoretical value. Using the same experimental data, Eq. 6 was applied to get mf_D (Fig. 7 B, open dots). The theoretical mf_D value was also calculated by using the theoretical mean lifetime of each mixture determined from Eq. 4 (Fig. 7 B, dotted line). Experimental and theoretical mf_D values are very close to each other. As expected, the value for mf_D in every solution is below the f_D value. For AO fraction from 0 to 0.5, slight differences between the solid and open dots are shown in Fig. 7 B. In fact, in this case, f_D and mf_D are alike. In solutions where the AO fraction exceeds 0.5, the mean lifetime of the solution begins to decrease gradually (from 2.96 to 2.25 ns) making f_D and mf_D diverge. For pure AO solution (f_D = 1), we found an mf_D value of 0.78, which corresponds to the maximal difference. For systems with high fraction of donor engaged in a FRET process, mf_D is not as close to f_D. However, mf_D gives quantitative information about the minimal percentage of FRET regardless of its efficiency.

Finally, mf_D behavior was theoretically studied over the f_D range for an interval of transfer efficiency from 0.2 to 0.8, considering a two-component system with single lifetime donor (Fig. 7 C). From Eq. 4, 〈τ〉/τ_D can be expressed as a function of f_D and E. By substituting this last expression into Eq. 6, we determined mf_D as a function of E and f_D. Using an interval of E from 0.2 until 0.8, the region of possible mf_D values was plotted as a function of f_D (region between the two solid lines). Although mf_D must be understood as an independent parameter, we were interested in testing its performance together with the apparent FRET efficiency (E_app = Ef_D), the parameter measured in quantitative FRET methods based on the “3-filter-cube” (6–14). The region of possible Ef_D values as a function of f_D was plotted on the same figure using the same E interval (region between the two dashed lines). When looking at Fig. 7 C one realizes that the range of mf_D and Ef_D possible values grows together with f_D. It can also be seen that the range of indetermination of mf_D for a given f_D is narrower than the one corresponding to Ef_D. Since mf_D is directly derived from f_D the correspondence between both parameters is quite accurate even for a long E range. Although “3-filter-cube” measurements provide a more detailed information concerning other interesting parameters (the fraction of acceptor molecules engaged in FRET (f_A) and the molar ratio of donor-to-acceptor (R)), the range of indetermination of the measured E_app (= Ef_D) is wider than for mf_D. In other words, from our study, based on donor FLIM measurements, f_A and R are ignored, but we do take into account E as a variable, and mf_D is a way to obtain the minimal fraction of proteins interacting independently of E.

mf_D as a quantitative tool for multi-lifetime donor systems

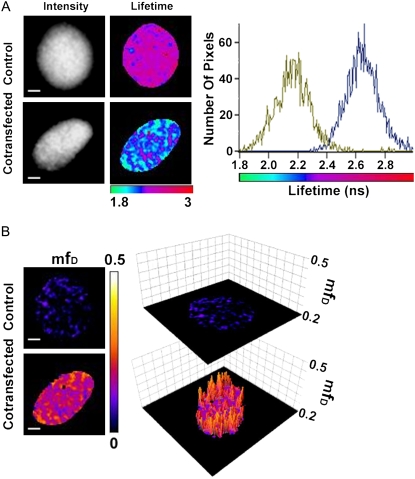
Contrary to GFP, CFP does not exhibit a monoexponential fluorescence decay (17,26,35). With the intention to exemplify a two-component model with a multi-lifetime donor system, the CFP/YFP FRET couple was used. Fusion proteins of CFP-BD and YFP-H4 (obtained from (27)) were coexpressed in cells to measure BD and acetylated H4 interaction. The fitting process of the CFP fluorescence decay in a FRET-FLIM experiment to find a minimum of four reliable lifetimes is very complicated (26,35), and clearly f_D cannot be determined. Then, the only way to characterize quantitatively protein interactions is to apply multi-lifetime extension of mf_D introduced in Eq. 15. A representative acquisition of a Trim-FLIM experiment (11 time-gated images) is shown (Fig. 8). The mean lifetime of CFP-BD in the presence of YFP-H4 decreased considerably compared to CFP-BD alone (from 2.64 ns to 2.20 ns), showing clearly that FRET occurred within the system. The two lifetime histograms of CFP-BD alone and CFP-BD in the presence of YFP-H4 confirm this decrease (Fig. 8 A). Fig. 8 shows mf_D two-dimensional topology maps directly obtained from the mean lifetime images using Eq. 15. A three-dimensional representation of mf_D images using a threshold limit given by the control is also presented to demonstrate the difference between the control and FRET images. For the whole nucleus, the FRET image gives an average mf_D value of 0.17. Hence, at least 17% of CFP-BD is bound to acetylated YFP-H4. The use of mf_D is an attempt to find quantitative results, as fitting in a multiexponential environment is a very difficult task.

FIGURE 8.

FLIM and mf_D images of CFP-BD interaction with acetylated YFP-H4 in the nucleus of HEK293 live cells using TriM-FLIM system. (A) Intensity and FLIM images of CFP-BD expressed alone as control (upper panel) or with mCherry-H4 as cotransfection (lower panel) in HEK293 live cells using the TriM-FLIM system at 800 nm excitation and 480AF30 emission filter with 11 time-gated images. Intensity images were obtained by summing the time-gated stack. FLIM images were obtained by using Eq. 2 in a pixel-by-pixel manner. The corresponding lifetime histograms are presented in the right panel (blue for control and green for cotransfection). The mean lifetime averaged throughout the nucleus decreased from 2.64 ns for the control to 2.20 ns for the cotransfection. Scale bar = 2 μm. (B) (Left panel) mf_D images of control and cotransfection obtained by using Eq. 15 with 〈τ〉_D = 2.64 ns. (Right panel) Three-dimensional representation of the corresponding mf_D images using a threshold limit given by the control (0.2). Scale bar = 2 μm.

The average value of mf_D throughout the nucleus determined with the single-lifetime donor system (GFP-BD and mCherry-H4) varies between 0 and 0.13 with a mean value of 0.06 when taking both five and 11 time-gated images experiments (n = 63). In comparison, for the multi-lifetime donor system (CFP-BD and YFP-mCherry) we obtain values of mf_D, which vary from 0.05 to 0.17 with a mean of 0.11 (n = 5). The linear growth of mf_D as a function of 〈τ〉/τ_D should give an inferior value of mf_D in multiexponential models compared to the value for the single-lifetime models. Surprisingly, this is not the case. The explanation for this phenomenon is the existence of a dark state in mCherry (S. Padilla-Para, M. Coppey-Moisan, and M. Tramier, unpublished data, (23–25)). In systems composed by the GFP-mCherry couple, the proportion of FRET should be doubled due to the fact that those dark states can cause an underestimation in the analysis by a factor of two (24) or more (S. Padilla-Para, M. Coppey-Moisan, and M. Tramier, unpublished data). This means that the mf_D obtained for the multi-lifetime donor, i.e., 0.11, is smaller than the real amount of interacting protein in the above examples (the amount of GFP-BD interacting with mCherry-H4) which is equal or superior to 0.12 (two-times the mean value of mf_D for a single-lifetime donor). The advantage of using a single-lifetime donor system in the frame of mf_D determination is better estimations with regard to the real f_D values. Other features, such as the stability of GFP (which is not as sensitive as CFP to photobleaching (26)), must also be taken in consideration when choosing a FRET couple.

CONCLUSION

It has been shown that the GFP-BD fluorescence decays in living cells under the microscope by using the TCSPC method are significantly different in GFP-BD monotransfected cells and in mCherry-H4 and GFP-BD cotransfected cells. The GFP-BD fluorescence decay alone is fitted to a single lifetime, while the GFP-BD fluorescence decay in presence of mCherry-H4 has a better fit with two exponentials, as shown by the comparison of residues of each fit in Fig. 4. The short lifetime (τ_F = 0.65 ± 0.05 ns) likely corresponds to the GFP-BD molecules interacting with mCherry-H4 since this fluorescence lifetime could never be observed in the absence of the mCherry-tagged histone. The mean f_D value per nucleus is 0.19 and varies from cell to cell, from no detectable interaction to a maximum value of 0.33.

To get a high f_D resolution spatial map of the GFP-BD in interaction with mCherry-H4 we compared the fluorescence decays acquired with TCSPC and time-gated CCD. Interestingly, the decays obtained with 11 gates (20 s of time acquisition) can still be fitted with two lifetimes. The value found for τ_F is similar to those determined from the fit of TCSPC decay but the standard error is bigger (τ_F = 0.65 ± 0.59 ns instead of τ_F = 0.65 ± 0.05 ns). In contrast, the decays obtained with a faster acquisition time (down to 3 s) by using only five time-gated images can no longer be fitted to a double-exponential model. The GFP-BD mean lifetime histogram is, however, significantly shifted to the short lifetime in the presence of mCherry-H4, which unveils the occurrence of FRET.

The mathematical development presented in Materials and Methods introduces the new concept of minimal fraction of donor engaged in FRET (mf_D) for a two-component system. For protein interaction studies, this parameter gives the minimal fraction of donor-tagged protein in interaction with acceptor-tagged protein for the corresponding biological system. Interestingly, the subnuclear pattern of mf_D and f_D obtained with the time-gated CCD system using 11 gates are quite similar. In contrast to the TCSPC data, where the f_D value per nucleus is inferior to 0.33, the f_D and mf_D high resolution spatial maps obtained with the time-gated CCD system reveals the existence of higher values (up to 0.49) in several chromatin domains corresponding to one or few pixels. This emphasizes the importance of fast acquisitions to avoid fluorescence decay average over different chromatin domains due to chromatin movements or other dynamical processes during the acquisition time.

The acquisition time invested in a FLIM measurement is then a paramount factor when considering a dynamical biological system. Here we show that mf_D makes it possible to quantify protein interactions with a strong reduction of the acquisition time down to 3 s. Moreover, mf_D provides information about potentially interacting pairs, independent of the transfer efficiency. The mf_D values, obtained from two independent experiments where the protein interaction under study is not the same, can be compared. This property is especially suitable for a comparative study of a donor protein interaction with two acceptor partners having different transfer efficiency. Furthermore, mf_D images could be treated to obtain the number of interacting particles (relative concentration) in the form of two-dimensional maps. This could simply be done by multiplying the mf_D two-dimensional topology map by the amplitude of the corresponding fluorescence decay at time zero (the first gated-image). The resulting images would offer the possibility to obtain information about the spatiotemporal correlation of the interacting particles under study.

The classical analysis FLIM technique in which the fluorescent decay is fitted to each pixel of a related image is still challenging because of the complexity of the decay of some fluorescent proteins and the intrinsic difficulty of the calculation of the fit for every pixel. In the case of a multi-lifetime donor system (for example, a system in which CFP plays the role of donor), it is almost impossible to determine f_D, as fluorescence decay analysis with more than two discrete lifetimes is always difficult (17,26,35). Here, mf_D extension is the only quantitative determinant. The experiment performed with a time-gated CCD system using 11 gates for a multi-lifetime donor system (CFP-BD alone and in the presence of YFP-H4 in living cells) gave an average value of mf_D throughout the nucleus which varies from 0.05 to 0.17 with a mean value of 0.11 (n = 5). It has been shown that mf_D results using GFP and CFP donor are almost identical if one takes into account the red acceptor dark states (23–25).

Another attempt to solve the problems arising from the classical FLIM quantitative analysis based on fitting is the phasor approach (PA) (21,22,36). PA simplifies the process of analysis of FLIM images by changing the histogram of time delays in a vector with two components (phase and modulation) which is represented in a polar plot. The advantage of this analysis technique is the absence of fitting calculations. Although no values for the lifetimes of the system are provided by the PA analysis, this technique gives quantitative information regardless of the system under investigation (single or multiple lifetime donors). Moreover, PA allows differentiation between autofluorescence and FRET. But, since PA is based on the analysis of a two-dimensional histogram of the whole cell, it does not provide a direct determination of the f_D image in a pixel-by-pixel manner. We found this way of analyzing data complementary to the method proposed here.

The mf_D approach is then an interesting concept for FRET-FLIM experiments because 1), it offers the possibility to obtain immediately quantitative information related to the relative concentration of interacting donor; 2), it can be obtained without fitting so that fast acquisitions can be performed; 3), it provides better spatiotemporal resolution than other approaches based on longer acquisition times; and 4), it can be used for both single- and multi-lifetime systems. For all these reasons we believe that mf_D is a simple fast and precise quantitative parameter when studying protein interaction in living cells.