Direct Modeling of X-Ray Diffraction Pattern from Contracting Skeletal Muscle

Abstract

A direct modeling approach was used to quantitatively interpret the two-dimensional x-ray diffraction patterns obtained from contracting mammalian skeletal muscle. The dependence of the calculated layer line intensities on the number of myosin heads bound to the thin filaments, on the conformation of these heads and on their mode of attachment to actin, was studied systematically. Results of modeling are compared to experimental data collected from permeabilized fibers from rabbit skeletal muscle contracting at 5°C and 30°C and developing low and high isometric tension, respectively. The results of the modeling show that: i), the intensity of the first actin layer line is independent of the tilt of the light chain domains of myosin heads and can be used as a measure of the fraction of myosin heads stereospecifically attached to actin; ii), during isometric contraction at near physiological temperature, the fraction of these heads is ∼40% and the light chain domains of the majority of them are more perpendicular to the filament axis than in rigor; and iii), at low temperature, when isometric tension is low, a majority of the attached myosin heads are bound to actin nonstereospecifically whereas at high temperature and tension they are bound stereospecifically.

INTRODUCTION

Low angle x-ray diffraction is a well-established and powerful tool for studying the structural changes responsible for muscle contraction (1). The spatial (2) and time (3) resolution of this method is better than for any other structural method used to investigate the structure-function relationship of actin-myosin interactions in contracting muscles. However, the quantitative interpretation of the x-ray diffraction data from muscle requires appropriate mathematical models. All models are based on the known structures of the actin and myosin filaments and consider changes in the structure of the myosin molecule, particularly in the globular region of the molecule, the myosin head (also called subfragment 1, or S1), which binds to actin and which is the site of ATPase activity. Until recently, such models dealt with only one or a few x-ray reflections (2–8) and were not designed for the quantitative explanation of the whole diffraction pattern from contracting muscle, although several articles successfully explained the diffraction pattern of relaxed muscle where myosin heads do not interact with actin (9–13). Gu and colleagues (14) successfully modeled a set of actin and myosin layer lines in experiments where only weakly bound acto-myosin·ATP complexes are formed. Modeling of a set of actin, myosin, and actin-myosin layer lines was carried out by Yagi et al. (15,16) for simulation of structural responses to step length changes in contracting muscle.

A few years ago, a direct modeling approach was proposed for simulation of the whole two-dimensional (2D) x-ray diffraction pattern from skeletal muscle in rigor where all myosin heads are bound to actin. The approach makes use of a high-resolution model of the acto-S1 rigor complex (17) as well as parameters that define the actin labeling pattern by myosin heads and filament disorder in sarcomeres. The resulting model was tested against experimental data and provided a good fit without recourse to local or global optimization of model parameters (18).

Here we extend this approach to the diffraction patterns of contracting muscle. The quantitative interpretation of the active pattern is more difficult than for the rigor pattern. In contracting muscle, the estimates of the fraction of myosin heads stereospecifically bound to actin range from 5% (19) up to 75% (6). Little is known about the structure of the actin-S1 complex during contraction. Also, the shape of myosin head changes upon binding of nucleotide and ATP hydrolysis so that the “neck”, or the light chain domain (LCD, also called “lever arm”), of the head tilts by several tens of degrees with respect to the catalytic domain (CD), probably resulting in an axial movement of the interdigitating filaments (20,21). In contracting muscle, a mixture of myosin heads with different tilt of the lever arm is expected, but the distribution of the heads among different conformational states is unknown. Besides, some myosin heads in contracting muscle are attached to actin nonstereospecifically (22–27). We shall use the term stereospecific binding of a myosin head to actin to mean that the CD has a fixed, rigid position on the actin site it is bound to. Nonstereospecific attachment means that the CD of bound myosin heads may take up different axial or azimuthal angles with respect to actin. Nevertheless, these attached heads contribute to the observed fiber stiffness. Direct inspection of electron microscopy tomograms revealed such nonstereospecific heads in contracting insect flight muscles (28). The model should account for the effect of the lever arm tilting and should account for the contribution of stereo- and nonstereospecifically attached heads as well as of actin and regulatory proteins of the thin filaments, troponin and tropomyosin, to the intensities of different x-ray reflections. We performed systematic calculations of the diffraction pattern of muscle as a function of the number of myosin heads bound to actin, the configuration of the heads, and of the azimuthal and axial angles of their attachment. The model calculations were compared to diffraction patterns collected from single fibers or bundles of three permeabilized fibers from fast rabbit muscle at the plateau of isometric contraction before and after temperature jumps (T-jumps) from 5°C to 30°C.

The aim of the work was to develop a quantitative understanding of the influence of different model parameters on the diffraction pattern and to determine robust features of the pattern that can be unambiguously interpreted in terms of the behavior of myosin heads in contracting muscle.

MATERIALS AND METHODS

Experimental data

Bundles of muscle fibers were dissected from psoas muscle of rabbit killed by pentobarbitone intravenous overdose and neck dislocation. After permeabilization, single fibers or bundles of three fibers were dissected and mounted in the setup described by Bershitsky et al. (29). Before activating, the fibers or bundles were partially cross-linked with 10 mM 1-ethyl-3-[3-dimethylamino)propyl]-carbodiimide (EDC) at 15°C for 5–6 min to preserve their structural and mechanical stability (27). Contraction was activated by bathing the fiber or bundle in the following solution: (in mM) 100 3-[N-morpholino]-propanesulfonic acid, 5 MgATP, 10 CaEGTA, 20 phosphocreatine, 200 units/ml creatine phosphokinase, 10 mM dithiothreitol (all chemicals from Sigma-Aldrich, St. Louis, MO), with an ionic strength of 0.15 M, pH 7.1 at 20°C. T-jumps from ∼5°C to ∼30°C (range 27.5–32°C) were produced by passing a 1 ms-long alternating current pulse (30 kHz, 2 kV) along the length of the muscle bundle while it was suspended in a wet, cold atmosphere within the experimental trough (30).

The experiments were carried out at the European Synchrotron Radiation Facility (ID02 station, ESRF, Grenoble, France) at a wavelength of 0.0995 nm, using FReLoN 2D charge-coupled device detectors. In one set of experiments where x-ray diffraction patterns were collected before and after the T-jumps from ∼5°C to ∼30°C, the sample-to-detector distance was 2.4 m. The detector operated in a 1024 × 1024 pixel mode and the x-ray beam dimensions at the sample were 400 μm horizontally and 250 μm vertically (full width at half-maximum). In another set of experiments where the diffraction patterns collected from several segments of a long single muscle fiber in the relaxed state, in rigor, and during isometric contraction at 28–30°C were compared, the camera length was 2.5 m, the detector operated in a 1024 × 256 pixel mode, and the full width at half-maximum beam size was 250 × 250 μm, along and across the sample. Segments of a single fiber or bundles of three permeabilized fibers (bundle diameter 120–150 μm) were mounted at a sarcomere length of 2.4 μm between a force transducer and a motor. In the first set of experiments, two 5 ms long time frames at the plateau of contraction at 5°C and 30°C were taken and used for analysis. Tension developed by a bundle increased by a factor of 3.1 ± 0.4 after the T-jump. In the second set of experiments, x-ray diffraction patterns were collected from three segments of one single muscle fiber (diameter 100 μm) in the relaxed state, in rigor, or after EDC cross-linking during steady-state post-T-jump contraction at 30°C during 100 ms long time frames.

The x-ray exposure of each bundle before and after each T-jump was the same, so that data obtained from all runs of the experimental protocol in five different bundles before and after the T-jumps were added together after background subtraction, flat field correction, and averaging over four symmetric quadrants without any further normalization. In another set of experiments with single muscle fiber segments, the data collected in each state (relaxed, rigor, or high-temperature isometric contraction) were added together and then normalized for exposure in each state. As the fiber diameter was uniform and the x-ray beam at ESRF was quite stable, no further normalization was made.

Diffraction data were analyzed using bsl (CCP13 suite) and BS (written by Natalia Koubassova, available at http://muscle.imec.msu.ru/bs_1.htm) software as described (29). The layer line intensities were extracted from the patterns as described by Koubassova and Tsaturyan (18).

When experimental data were compared to calculated diffraction intensities, a scaling parameter λ minimizing the R-factor was used. The R-factor was calculated as follows.

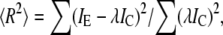where I_E and I_C are the experimental and calculated intensities of the most bright layer lines TN1 + A1, M3, M6 = A5, A6. The R-factor and the scaling factor λ were determined for either a pair of diffraction patterns (one experimental and one calculated) or for two pairs of diffraction patterns (two experimental and two calculated). In the last case, both experimental patterns were collected from the same specimens and scaled for time of x-ray exposure. The summation in this case was made over diffraction intensities in both pairs of patterns. The simultaneous fit of two diffraction patterns was performed for either active and rigor patterns collected from one single fiber (see Fig. 3) or for patterns collected from several bundles of contracting fibers at low and high temperature in two time windows of the same duration before and after the T-jumps (see Fig. 8).

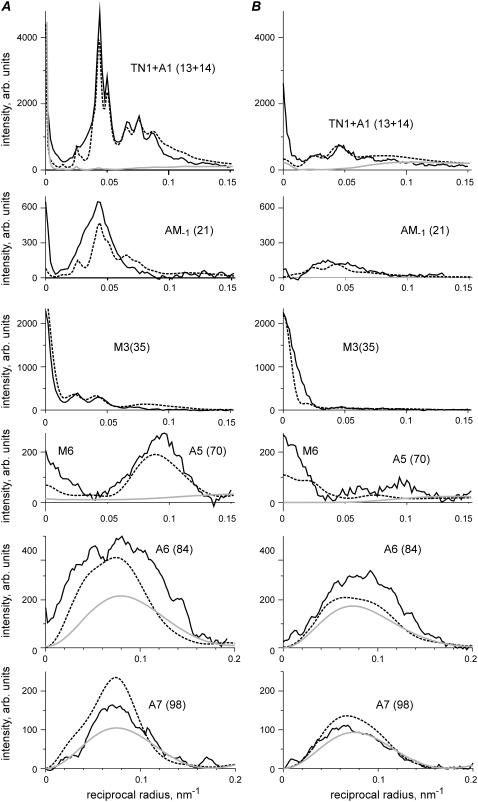
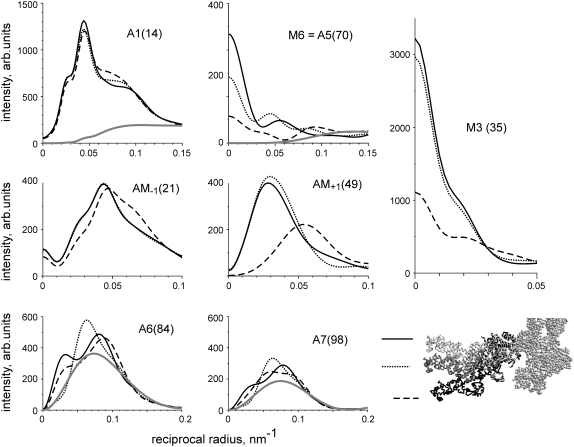
FIGURE 3.

Comparison of experimental (solid lines) and calculated (dashed lines) layer line intensities in rigor (A) and during active contraction at ∼30°C (B) for the same experimental data set as in Fig. 2. Layer lines are labeled on the corresponding panels. Numbers in brackets show the indices of the calculated layer lines in a 500.5 nm long unit cell. As the patterns were collected from a single muscle fiber and normalized for the x-ray exposure in each state, the intensities of different reflections in rigor and during active contraction can be compared quantitatively. Calculations were made for the following parameter sets: (A) e = 0.25, f(S) =1, d_max = 2 nm, Δr_A = 2 nm, Δz_A = 2 nm, Δr_T = 3.5 nm, Δz_T = 6 nm, Ψ_ax = 0, Ψ_az = 0, rigor configuration; (B) e = 0.5, f(S) = 0.4, d_max = 4 nm, Δr_A = 3.5 nm, Δz_A = 1.5 nm, Ψ_ax = 0, Ψ_az = -10°, prepower stroke configuration. Gray lines show the calculated intensities of actin layer lines in the relaxed state, f(S) = f(N) = 0; no bound heads. Both calculated diffraction patterns were multiplied for the same scaling factor λ = 0.56 providing a minimal R-factor of 0.099.

FIGURE 8.

Calculated (dashed lines) and observed (solid lines) intensities of some layer lines during isometric contraction at ∼5°C (A) and ∼30°C (B). Data from 90 temperature jumps in experiments with five bundles of three muscle fibers performed as described (27), the total exposure at each temperature 450 ms. Meridional part on AM₋₁ layer line on experimental data is labeled M4 as the quality of this data set did not allow resolving them. All calculated intensities were scaled by the same factor. Layer lines are labeled. Model parameters in A: e = 0.5, f(S) = 0.13, f(N) = 0.27 (Ψ_az = 60°, Ψ_ax = 0); Δr_A = 3.5 nm, Δz_A = 1.5 nm; in B parameters are the same as in Fig. 3 B.

Modeling

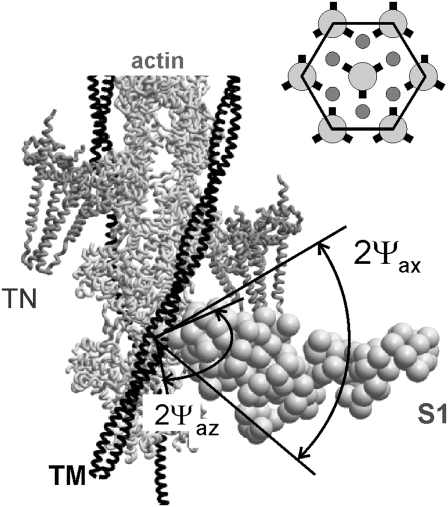
The structure of the A-band used in our model is described as follows. A 500.5 nm-long superlattice unit cell consists of three myosin filaments and six actin filaments. All actin filaments have the same orientation, whereas the central and peripheral myosin filaments in a unit cell have different orientation producing a superlattice (Fig. 1, inset). Actin filaments were considered as left-handed 13₆ helices and myosin filaments were modeled as right-handed three-stranded helices with successive crowns of myosin heads rotated by 120° (31,32). The axial distance between neighbor actin monomers is 2.75 nm; the pitch of the actin helix is 35.75 nm; the pitch of the myosin helix is 42.9 nm with 14.3 nm axial distance between myosin backbone origins of crowns of myosin heads. Troponin molecules were assumed to be bound to every seventh actin monomer in each of two strands of the actin pseudotwofold helix. Tropomyosin had the same 38.5 nm axial repeat as troponin. The repeat is equal to the height of 14 actin monomers. To account for the observed difference in spacing of the actin and troponin x-ray reflections, the pitch of the actin helix in the model was shorter than the troponin-tropomyosin repeat.

FIGURE 1.

Arrangement of a unit cell used in the model. A segment of thin filament, including actin monomers, tropomyosin strand, TM, and 2 troponin molecules, TN, with a stereospecifically attached myosin head, S1. The head is in the so-called active configuration with its light chain domain LCD tilted by 50° axially toward the M-line compared to rigor conformation (17), Z-line toward the bottom of the figure. Nonstereospecifically attached myosin heads can bind actin at various angles in the planes perpendicular (azimuthal plane) and parallel (axial plane) to the filament axis. Axial and azimuthal attachment angles of these heads are assumed to be uniformly distributed within ranges ±Ψ_ax and ±Ψ_az, respectively. (Inset) hexagonal unit cell in the projection perpendicular to the filament axis. Actin filaments are shown as small circles, all in the same orientation. The orientation of the myosin filaments is indicated by the positions of the origins of the myosin heads (short thick lines).

The thin and thick filaments were considered to be rigid, i.e., inextensible, unbendable, and untwistable. The only types of lattice disorder considered were transverse and axial disorders of the thin filaments whereas the axes of the filaments remained parallel to the fiber axis. As the conformation and distribution of the detached heads are uncertain and their contribution to the x-ray diffraction pattern is significant for myosin reflections, but not for actin layer lines, we did not consider their contribution to the diffraction pattern in this work. Any contribution to the layer line intensities from C-protein, titin, and other sarcomere proteins was neglected.

High resolution structures of actin and of the myosin heads were taken from Holmes et al. (17). Tropomyosin and troponin structures were taken from the recent model of Pirani et al. (33). Tropomyosin was azimuthally rotated from its “blocked” state by −25°, to the position found to be characteristic for actively contracting muscle (33,34). The rotation angle was assumed to be the same during active contraction at low and high temperature and in rigor. In the current model, attached myosin heads were in either the stereospecifically, S, or nonstereospecifically, N, bound state. CDs of the stereospecifically bound heads were fixed on the actin filament, whereas the LCDs were allowed to tilt axially and azimuthally with respect to the CD (Fig. 1). The preforce-generating configuration of the myosin head was modeled by a 50° axial tilt of the LCD with respect to the CD to a state nearly perpendicular to the filament axis. Nonstereospecifically attached heads were allowed to bind actin at different angles, whereas the position of LCD with respect to CD was fixed. For these heads, we assumed uniform random distribution of attachment angles in axial and azimuthal planes within certain limits, ±Ψ_ax and ±Ψ_az, respectively (Fig. 1). The structures of nonstereospecifically attached actin-S1 complexes were obtained by rolling S1 on the surface of actin filament with respect to a point inside actin subdomain 1.

The actin labeling pattern in a unit cell was determined using the principle of minimal elastic distortion energy (18). According to this principle, a myosin head binds the actin monomer on one of the six surrounding thin filaments for which the elastic distortion energy, 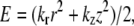is the lowest. The energy E is associated with the binding. It is determined by axial, z, and transverse, r, displacements of the head-tail (S1-S2) junction of a myosin head from its “resting” position on the backbone of the thick filament and by axial and transverse stiffness, k_z, k_r. If the stiffness ratio e = k_r/k_z of an attached myosin head and the fraction f of these heads are specified, the labeling pattern of the unit cell is determined uniquely by an iterative procedure. Firstly, “the best” actin monomer and the elastic distortion energy associated with the binding to this monomer are calculated for each of 630 myosin heads in the unit cell. The actin monomers to which troponin molecules are bound were considered as “occupied” and not eligible for the head binding. Then the bound heads are sorted in ascending order of elastic energy and the 630 × f best of them bind actin monomers. In the case when two or more myosin heads are conflicting for one actin monomer, the head with the smaller energy binds it. Then the procedure is repeated for the remaining myosin heads and actin monomers until the number of attached heads reaches f × 630.

During contraction, tension induces significant filament disorder so that the crystal-like lattice sampling observed in rigor muscle largely disappears and the remaining sampling can adequately be accounted for by consideration of a single superlattice unit cell. Two disorder parameters, Δr_A, Δz_A, describe the root mean-squared transverse and axial disorder of the actin and myosin filaments in a unit cell. Parameters of transverse and axial disorder of the second kind, Δr_T, Δz_T, were used to describe disturbance of the actin-myosin lattice in rigor. The loss of crystallinity during active contraction was simulated by infinitely high Δr_T and Δz_T. Calculations of the layer line intensities were carried out as described previously (Appendix A, (18)). Attached myosin heads contribute to the thin filament Fourier transforms where l is the number of the layer line and i is the number of the actin filament in the unit cell (i = 1, … , 6).

Fourier transforms of the thin filaments without myosin heads were calculated using high-resolution structures of troponin, tropomyosin, and actin (Fig. 1) for each of six filaments using a detailed model where each residue was a scattering center. The transforms were stored in tables and added to where l was a multiple of 13 or 14. The atomic model of the myosin head was substituted by a low-resolution model consisting of 145 spheres of 1 nm radius each (Fig. 1). The scattering power of each sphere was proportional to the total number of electrons in the atoms lying within the sphere. The distal parts of bound myosin heads were allowed to bend toward their origin on the surface of the thick filament (18). The displacement of the C-terminus of S1 was limited by a certain value d_max.

The intensity I_l of the layer lines produced by a superlattice unit cell was calculated as the azimuthally averaged square of the Fourier transform taking into account disorder of the filaments:

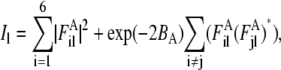where * denotes complex conjugate and B_A is the “thermal” factor describing the deviation of thin filaments from their ideal position in the unit cell (35):

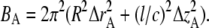The effect of model parameters on the calculated x-ray intensities was studied. The values providing a better fit to the data were chosen as follows. The stiffness ratio parameter, e, determines the ratio of the total intensities of the A1, M3, and actin-myosin beating layer lines, AM₋₁, AM₊₁. The best e values were found to be 0.25 for rigor and 0.5 for the diffraction patterns of contracting muscle. The orientation of myosin heads during isometric contraction was also varied to better describe the shape of the A1 and A6 actin layer lines. A 10° azimuthal tilt with respect to the rigor orientation was found to improve the A6 shape. A global search of the parameters describing lattice disorder and the fraction of myosin heads stereospecifically bound to actin during isometric contraction was performed to fit both rigor and active patterns simultaneously.

RESULTS

Experimental diffraction patterns

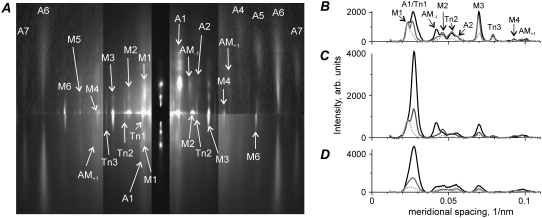
Two-dimensional low angle x-ray diffraction patterns collected from a single permeabilized muscle fiber in three different physiological states—relaxed, rigor, and during active contraction at 30°C—are shown in Fig. 2 A. Meridional intensity profiles obtained by radial integration of these three diffraction patterns are plotted in Fig. 2, B–D. Integration was performed in three off-meridional radial ranges: 1,0 row line (B, 0.025–0.043 nm⁻¹); 1,1 plus 2,0 row lines (C, 0.043–0.061 nm⁻¹); and a region that contains the 2,1, 3,0, 2,2, and 3,1 row lines (D, 0.061–0.1 nm⁻¹).

FIGURE 2.

(A) X-ray diffraction patterns obtained from three segments of a single muscle fiber in the relaxed state (upper left quadrant), in rigor (upper right quadrant), and during active contraction at ∼30°C (both lower quadrants). The intensity of each pattern was scaled for fiber exposure in each state (300 ms, 700 ms, and 1200 ms, for relaxed, rigor, and active states, respectively) and symmetrically averaged; higher intensity is white, lower intensity is black. The equator is vertical and the meridian is horizontal. A vertical metal strip in front of the detector attenuates the equatorial reflections ∼10-fold and prevents saturation of the detector; the inner part of the patterns at the meridional spacing of <0.087 nm⁻¹ was attenuated by a factor of 3 to visualize strong and weak reflections on one diagram; meridional and layer line reflections mentioned in the text are labeled. (B–D) Meridional profiles of the off- meridional intensity for the same three diffraction patterns as in A in the regions of radial integration of 0.025–0.043 nm⁻¹ (1,0 row line), 0.043–0.061 nm⁻¹ (1,1 and 2,0 row lines), and 0.061–0.1 nm⁻¹ (2,1, 3,0, 2,2, and 3,1 row lines), respectively; background subtracted. Gray dotted, black, and gray solid lines correspond to relaxed, rigor, and active states, respectively; the position of some layer lines is labeled in B.

During isometric contraction and especially in rigor, the intensities of all actin layer lines increased compared to the pattern in relaxed muscle. The increase in the intensities of the actin layer lines results from an increase in electron density of the actin helix due to the myosin heads bound to actin. The first actin layer line, A1, has a spacing of (∼36.4 nm)⁻¹ in rigor that shifts to (∼36.9 nm)⁻¹ during high-temperature isometric contraction. In both these states, A1 remains clearly separated from the neighboring myosin layer line M1 at (∼43 nm)⁻¹. Only at a high reciprocal radii higher than 0.06 nm⁻¹, the M1 and A1 layer lines overlap (Fig. 2 D) due to “arching” caused by imperfect alignment of the thin and thick filaments.

At a reciprocal radii of 0.025–0.06 nm⁻¹, the A1 intensity in relaxed fiber was negligible compared to its value during active isometric contraction at near physiological temperature and especially compared to rigor where A1 is maximal (Fig. 2, B and C). The total A1 intensity integrated in this radial range in relaxed fiber was less than 5% of that during active contraction. At a higher reciprocal radii of 0.06–0.1 nm⁻¹, the A1 intensity in the relaxed state was more substantial, but still much lower than that in contracting muscle (Fig. 2 D). During contraction at near physiological temperature, the contribution of the thin filaments themselves to the total integrated A1 intensity is negligible compared to that of bound myosin heads, especially if a narrow integration range of 0.025–0.06 nm⁻¹ is used.

The meridional troponin meridional reflections TN1, TN2, and TN3 have spacings close to a multiple of (∼38.5 nm)⁻¹ in all three physiological states. The intensities of the troponin reflections do not change much when myosin heads bind actin in rigor or during active contraction (Fig. 2 A). The presence of the (38.5 nm)⁻¹ troponin reflection gives an x-shape to the A1 layer line in rigor and during isometric contraction (Fig. 2 A). The second actin layer line, A2, at ∼(18.2 nm)⁻¹ in rigor is separated from the second troponin meridional reflection, TN2, at ∼(19.2 nm)⁻¹ (Fig. 2, A and B). These data show that the crossover period of the actin helix that controls the spacing of the A1 and A2 layer lines is somewhat shorter than the axial distance between consequent troponin molecules bound to every 7th monomer on each pseudotwofold strand of the actin helix. For this reason, we modeled the actin filament as a 13₆ left-handed rather than a 28₁₃ helix where the troponin-tropomyosin and actin axial periods are the same.

The meridional M3 myosin reflection was weak in the low temperature relaxed state, a characteristic of such patterns for mammalian muscles. In rigor and especially during active contraction, the M3 intensity increased. Its radial width during active contraction was higher than in the relaxed or rigor state, indicating an increase in axial disorder of the second kind of the myosin filaments (35,36). The intensity of the M6 myosin meridional reflection was low in relaxed muscle fiber and became brighter in rigor and especially during active contraction (Fig. 2 A), showing a significant contribution of attached myosin heads to its intensity.

Myosin off-meridional layer lines became slightly weaker when relaxed muscle fibers went into rigor or developed active tension. However, Fig. 2 A shows that some myosin reflections, especially the so-called forbidden meridional reflections M1 and M2, remained quite bright in rigor where all myosin heads are believed to be strongly bound to actin. During active contraction, the meridional M1 and M2 intensities became much weaker than in the relaxed or rigor states.

The beating actin-myosin layer lines AM₋₁ at ∼(24 nm)⁻¹ and AM₊₁ at ∼(10.3 nm)⁻¹ arise from the ∼14.5 nm modulating caused by the binding of myosin heads to actin and specifically originate from myosin heads bound to actin (37,38,18). In rigor, the AM₋₁ intensity is very high. During high-temperature isometric contraction, AM₋₁ is seen as a low-angle shoulder on the cluster of reflections between 0.04 nm⁻¹ and 0.056 nm⁻¹ that also contains M2, TN2, and A2 (Fig. 2 B). Like the AM₋₁ layer line, AM₊₁ is absent in the relaxed muscle, but is clearly seen in rigor and during active contraction (Fig. 2, A–C). In our patterns, AM₊₁ is separated from the neighboring myosin layer line M4 at ∼(10.9 nm)⁻¹. The AM₊₁ intensity during active contraction is close to that in rigor (Fig. 2, A–C), although not more than a half of myosin heads are bound to actin in contracting muscle (39).

Comparison of calculated and observed diffraction patterns

The intensity profiles of some layer lines in two calculated diffraction patterns are shown in Fig. 3 together with the experimental data of Fig. 2. The binding patterns of myosin heads on the actin filaments for rigor and actively contracting muscle were calculated with the stiffness ratio parameter e = 0.25 and e = 0.5, respectively, as described in Materials and Methods. The pattern for fibers in rigor was calculated assuming that all myosin heads are stereospecifically bound to actin in the same configuration as that suggested by Holmes et al. (17). The diffraction pattern for actively contracting fibers was calculated assuming that 40% of myosin heads are attached stereospecifically, f(S) = 0.4, with their “neck” domains tilted by 50° with respect to the catalytic domains. Additionally, the catalytic domain of the heads was tilted azimuthally by −10° with respect to actin to improve the shape of the calculated A6 and A7 actin layer lines (see below). The necks were subject to elastic bending as described in Materials and Methods. The remaining 60% of myosin heads were assumed to be detached, and their contribution to the layer line intensities was not taken into account.

Although as mentioned above (Fig. 2 A) the A1 layer line and TN1 meridional reflection had different but close spacings in the rigor and active diffraction patterns, we were unable to separate them and draw two separate intensity profiles. For this reason, we compared the experimentally determined intensity of the combined TN1 + A1 layer line with the sum of calculated intensities of the 13th and 14th layer lines (Fig. 3).

The model reproduces the main features of the experimental patterns. In rigor, all actin-based layer lines, A1–A7, and the beating actin-myosin layer lines AM₊₁, AM₋₁, are very intense, and the intensity of the myosin layer lines (except the meridional M3 and M6 reflections) is low. In contracting muscle, the intensities of the actin and of the actin-myosin layer lines are significantly lower and those of the myosin layer lines are somewhat higher than in rigor. Again there is a very bright meridional reflection on the M3 layer line and a bright meridional spot on M6 in both the calculated and experimental diffraction patterns of contracting muscle.

The model quantitatively reproduces the relative values of the total intensities of the brightest layer lines in rigor and during isometric contraction and simulates reasonably well the intensity distributions along these layer lines (Fig. 3). The total 〈R²〉 value for both patterns taken together was 9.9%, whereas for the rigor and active patterns separately it was 8.9% and 11.9%, respectively. The scaling factor λ was 0.56 for both patterns taken together, 0.59 for the rigor pattern alone, and 0.53 for the active pattern alone.

The main discrepancies between the calculated and observed patterns are as follows. The model underestimates the observed M6 intensity compared to both experimental patterns probably because a part of the M6 intensity originates from some structures of the thick filaments, which are different from myosin heads (see Discussion). The calculated A6 intensity is somewhat lower whereas that of A7 is somewhat higher than their observed values in rigor and in active diffraction patterns. The same discrepancy is seen for relaxed diffraction patterns and those calculated for thin filaments without bound myosin heads where the calculated ratio of the total A7 and A6 intensities is 0.42 whereas the experimentally observed value for this ratio in relaxed muscle fibers was only 0.23–0.25 (data not shown). The discrepancy remains even when troponin and tropomyosin are excluded from the model of the thin filaments. So the underestimation of the A6 intensity and the overestimation of the A7 intensity is a feature of the current F-actin model. Also, the calculated M3 intensity profile is narrower than the experimental one, probably because of the lack of contribution of detached myosin heads to this reflection. These heads were not taken into account in our calculations.

The effect of the configuration of stereospecifically bound myosin heads on the layer line intensities

The effect of the tilt of the light chain domains (or lever arms) of myosin heads stereospecifically bound to actin on the calculated intensities of some layer lines is shown in Fig. 4. Myosin heads with their LCDs in the postpower stroke (rigor-like) configurations or tilted by 30° or 50° to mimic a prepower stroke state were attached to actin according to the principle of minimal elastic distortion energy. The actin binding pattern of myosin heads to actin filaments was the same for all three sets of calculations. The fraction of stereospecifically bound heads was also the same, 40% (f(S) = 0.4) in all three cases.

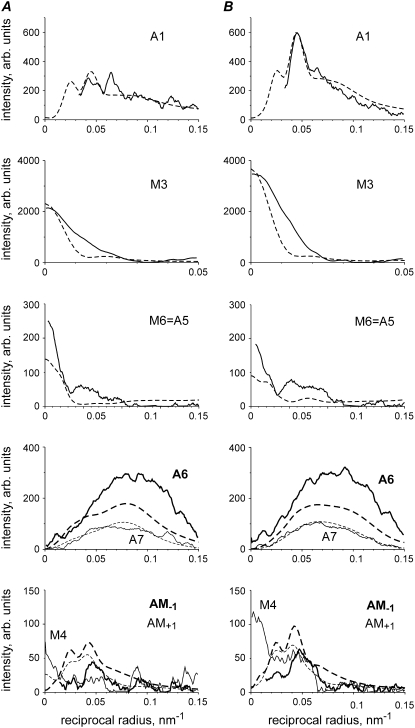
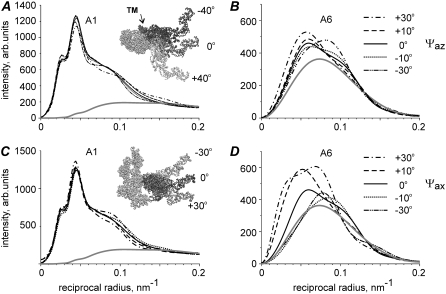
FIGURE 4.

Calculated dependence of the profiles of some bright layer lines on the axial tilt of the LCD of the stereospecifically attached myosin head. Layer lines are labeled on the corresponding panels. Numbers in brackets show the indices of the layer lines in the 500.5 nm long unit cell. Dashed lines correspond to the rigor-like configuration of the myosin head (black S1 in the bottom right panel), dotted lines correspond to the 30° axial tilt of LCD toward the M-line, solid lines correspond to “active” configuration where the LCD is tilted by 50° axially toward the M-line (white S1 in bottom right panel) and gray lines are calculated intensities of the actin layer lines without any bound heads. Calculations were made for the following parameter set: e = 0.25, f(S) = 0.4, d_max = 0, Δr_A = 3 nm, Δz_A = 4 nm, Ψ_ax = 0, Ψ_az = 0, prepower stroke.

The A1 intensity is insensitive to the lever arm tilt. Its total intensity changed by <5% for a 50° lever arm tilt from the rigor-like conformation (Fig. 4). Similarly, the beating layer line AM₋₁ did not change much upon tilting and its total intensity remained almost constant despite the change in the shape of stereospecifically attached heads.

In contrast, the M3 intensity was high when the LCDs of the heads were approximately perpendicular to the filament axis and decreased sharply when the lever arm moved toward the Z-line of sarcomeres to a rigor configuration. The calculated M6 intensity is also quite sensitive to the lever arm tilt (Fig. 4). The intensity distribution along the high order actin and actin-myosin layer lines was found to be very sensitive to the lever arm tilt. Specifically, the shape of the A6 and A7 actin layer lines and the position of the intensity peak on the A5 actin layer line changed markedly when the LCD was tilted by 30° or by 50° with respect to the rigor positions. Interestingly, the total intensity of the AM₊₁ layer line changed upon tilting by a factor of 2. The position of its peak also moved from 0.055 nm⁻¹, characteristic for the rigor-like conformation to 0.025–0.03 nm⁻¹ in the preforce-generating states (Fig. 4).

We also tested the effect of the azimuthal and axial rigid-body rotation of the stereospecifically bound myosin heads on the intensities of the brightest inner and outer actin layer lines, A1 and A6, respectively (Fig. 5). Again the A1 intensity was not sensitive to the angle of stereospecific binding of S1 to actin, and its total integrated intensity did not change by >7% upon ±30° rotations in both directions.

FIGURE 5.

Calculated dependence of the profiles of A1 and A6 layer lines on the azimuthal (A and B) and axial (C and D) tilt of the stereospecifically attached myosin head. Insets on the panels show the configuration of stereospecifically attached head used for calculations that correspond to the drawn lines. Ψ_az = 0°, Ψ_ax = 0° (solid lines) correspond to the active or prepower stroke configuration where the LCD is tilted by 50° axially toward the M-line from the rigor-like configuration of S1. Insets on A and C panels show the directions of rotation in two planes: the actin axis is perpendicular to the plane of the figure in A and vertical in C with the Z-line toward the bottom of the figure. TM (dark gray) in A indicates the position of tropomyosin. The whole S1 was rotated azimuthally or axially by rolling on the actin surface, by maintaining the binding end of S1 on the rigor-binding surface of actin as much as possible. Gray lines are calculated intensities of actin layer lines without bound heads. Calculations were made for the following parameter set: e = 0.25, f(S) = 0.4, d_max = 0, Δr_A = 3 nm, Δz_A = 4 nm.

The shape of the A6 layer line and its total intensity are highly sensitive to rotation of the stereospecifically bound myosin heads on the actin surface (Fig. 5). Azimuthal rotation shifts the position of the intensity peak of this layer line. As the position of the peak during isometric contraction remains at the same reciprocal radius as in the relaxed state, a −10–15° rotation of the heads allows one to improve the model fit of the A6 intensity in contracting muscle. For this reason, we tilted bound myosin heads by −10° for the calculations presented in Figs. 3 and 8. The calculated A6 intensity was dramatically affected by the axial tilt of CD. Even a −10° rotation changed its total intensity by >25% (Fig. 5).

The effect of the number of stereospecifically bound myosin heads on the layer line intensities

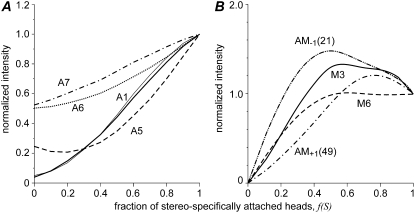
The dependence of the calculated total intensities of some layer lines on the number of stereospecifically bound heads is shown in Fig. 6. The total intensity of the first actin layer line, I_A1, is nearly proportional to the fraction of stereospecifically bound heads, f(S), although somewhat lower than linear function. As some contribution of regulatory proteins to A1 was found at higher reciprocal radii, we plotted the A1 intensity integrated in the regions of 0.015–0.06 nm⁻¹ and 0.015–0.1 nm⁻¹ separately. No significant difference was found between the two plots after their normalization for the maximal intensity at f(S) = 1 (Fig. 6 A). As mentioned above, the A1 intensity is insensitive to tilt of the LCD with respect to the CD or to the rotation of whole stereospecifically attached myosin head about actin surface, so that the I_A1 plot in Fig. 6 A remains the same for different configurations of the stereospecifically attached head considered in the model.

FIGURE 6.

Calculated dependence of the intensities of the brightest actin and myosin layer lines on the fraction of stereospecifically attached heads, f(S). (A) Intensities of the first actin layer line A1 (thick and thin solid lines), off-meridional A5 (dashed), A6 (dotted), and A7 (dash-dotted) actin layer lines. (B) The intensities of M3 (solid lines), AM₋₁ (dash-dot-dot), M6 (dashed) and AM₊₁ (dash-dotted) layer lines. Two regions of integration are shown for A1 in A: long (0.014 nm⁻¹; 0.1 nm⁻¹), thick line, and short (0.014 nm⁻¹; 0.6 nm⁻¹), thin line. The latter interval was used in experimental data analysis to minimize the contributions of actin, troponin, and tropomyosin. All intensities are shown normalized for their values at f(S) = 1. The other model parameters, except f(S), were the same as in Fig 3 B.

The dependence of the normalized M3 intensity on f(S) is complex. It increases with f(S) while it is <0.5 and decreases at higher f(S). The M3 intensity strongly depends on axial filament disorder. The normalized intensity of the M6 meridional reflection and those of the AM₋₁ and AM₊₁ beating layer lines also reached maxima at intermediate f(S). This is not surprising, as the beating layer lines arise from a 14.5 nm myosin-based axial modulation of the actin binding pattern by myosin heads. When the most “convenient” actin sites that correspond to the 14.5 nm repeat are already occupied by bound myosin heads, the next head is forced to bind to a less “convenient” actin site and the modulation becomes less pronounced.

The intensities of the high order actin layer lines A5, A6, and A7 increase with f(S) in different ways. The off-meridional intensity of the A5 actin layer line above the background level increases nearly proportionally to the square of the fraction of stereospecifically bound heads. In rigor, f(S) = 1, the A6 and A7 intensities increase by a factor of ∼2 above their level in the relaxed state, f(S) = 0. The increase with f(S) approximately follows a square law for A6 and a linear relationship for A7 (Fig. 6). It should be mentioned that the A5, A6, and A7, AM₊₁ layer lines are very sensitive to tilt of the LCD, attachment angles of the head, and to the amount of bending of the LCD, i.e., on d_max. For this reason, the plots describing the dependence of the normalized integrated intensities of these layer lines on f(S) change upon change in each of these parameters and may differ substantially from those shown in Fig. 6, A and B.

Diffraction by nonstereospecifically bound myosin heads

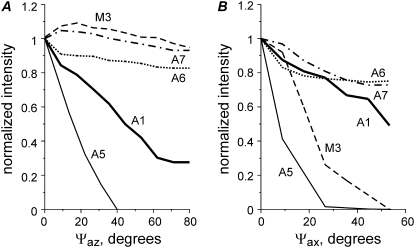
We simulated the nonstereospecific attachment of myosin heads to actin by random assignment of azimuthal and axial angles of attachment of a myosin head to an actin monomer within the limits ±Ψ_az and ±Ψ_ax. The dependence of the calculated intensities of some layer lines on the limits of the attachment angles is shown in Fig. 7. The calculated A1 intensity is not very sensitive to axial disorder, but decreases sharply with increasing azimuthal disorder. When Ψ_az reaches 60–70°, I_A1 drops to ∼0.3 of its value for stereospecific binding although the same 40% fraction of myosin heads remains bound to actin. An even stronger dependence on azimuthal disorder was found for the calculated off-meridional intensity of the fifth actin layer line A5 (Fig. 7 A). Less sensitivity to Ψ_az was found for A6 and A7. On the other hand, a more pronounced decrease in the intensities of A6 and A7 was found when the axial angle of the head attachment Ψ_ax was varied (Fig. 7 B). Axial disorder leads to a sharp decrease in the calculated intensity of the M3 and M6 myosin meridional reflections and of the off-meridional A5 intensity and to a smaller extent in the A1 intensity.

FIGURE 7.

Characteristics of nonstereospecific binding. Calculated changes in the intensities of some layer lines on the width of the distribution of the attached, nonstereospecifically bound heads in azimuthal (A) and axial (B) planes. f(N) = 0.4. A1, solid thick line; M3, dashed line; A5, solid thin line; A6, dotted line; and A7, dash-dotted line. Calculated intensity values are averaged for five runs (with different random choice of the attachment angles) and normalized for their values in the case of stereospecific binding (Ψ_az = Ψ_ax = 0).

Modeling the effect of temperature

Increasing the temperature of contracting rabbit muscle fibers from ∼5°C to ∼30°C leads to an ∼3-fold increase in isometric tension. As the tension rise occurs without changes in instantaneous stiffness (40,30), it was proposed that the increase in temperature is accompanied by a transition of nonstereospecifically bound myosin heads to a stereospecifically bound state (24,27). To check the consistency of this assumption, we compared 2D x-ray diffraction patterns collected from the same muscle fibers during isometric contraction at ∼5°C and ∼30°C with diffraction patterns calculated according to our model. The high temperature pattern was calculated with f(S) = 0.4, f(N) = 0. The low temperature diffraction pattern was simulated by the model with f(S) = 0.13, f(N) = 0.27, Ψ_az = 60°, and Ψ_ax = 0°, i.e., the effect of temperature was simulated by assuming that 40% of myosin heads are attached to actin at both temperatures, but all attached heads are bound to actin stereospecifically at the higher temperature, and only one-third of them are bound stereospecifically at the lower temperature. The results of calculations of the intensities of some layer lines are shown in Fig. 8. The model reproduces many features of the experimental diffraction patterns at both high and low temperature. Specifically, the calculated intensity profiles of the A1, M3, and A7 layer lines are similar to the experimental ones. The experimental A6 intensity is somewhat higher and those of the AM₋₁, AM₊₁ layer lines are lower than the calculated intensities, although the intensity distributions along the layer lines were very similar. The spatial resolution of the T-jump experiments was lower than that in the experiments shown in Figs. 2 and 3. For this reason we were unable to separate the M4 meridional reflection from the AM₊₁ beating layer line, which are shown together in the bottom panel of Fig. 8.

DISCUSSION

Modeling is used here to simulate observed experimental diffraction patterns and also to investigate systematically the effect of changes in model parameters on the features of the diffraction pattern, thus providing useful insight into the origin and behavior of the main x-ray reflections.

Model quality

A direct modeling approach previously tested by the quantitative description of x-ray diffraction on muscle fibers in the rigor state is expanded here to diffraction by contracting muscles. The approach is based on the available high resolution structures of actin, troponin, and tropomyosin and of the myosin head on physically plausible parameterization of the actin-myosin binding pattern (18). The model reasonably well reproduces the 2D diffraction pattern of isometrically contracting mammalian muscle fibers (Figs. 3 and 8). Two parameters in the model, the fraction of bound heads, f, and the stiffness ratio, e, fully determine the binding patterns of myosin heads to actin monomers in a superlattice unit cell in the overlap region of a sarcomere. Parameter e controls the trade-off between axial and azimuthal mismatch when a myosin head binds to the most “convenient” actin monomer.

The actin binding pattern calculated using the principle of minimal elastic distortion energy has two types of myosin-based modulation (18). Apart from the well-known ∼14.3 nm, or M3, modulation (41,37,15,16), there is also a strong ∼7.2 nm, or M6, modulation that determines the relatively high intensity of meridional M6 myosin reflection in the diffraction pattern of rigor and actively contracting muscle (Fig. 2; (18,38)). The ∼14.3 nm axial distance between neighboring crowns of myosin heads produces the main M3 repeat of the binding of myosin heads to actin. The second, ∼7.2 nm, harmonic of this repeat should be present in the binding pattern. The dispersion of the binding sites is quite high due to the ∼5.5 nm distance between neighboring actin monomers commensurable with the 14.3 nm myosin repeat. For this reason, the M6 harmonic in any one-dimensional model of actin labeling by bound myosin heads is low.

Our model and the principle of minimal elastic distortion account for the three-dimensional (3D) structure of the actin-myosin lattice and explain the high degree of the M6 modulation. The lower is e the higher is the 14.3 nm modulation and the lower is the 7.2 nm modulation. For high e values, this modulation can be even more pronounced than M3 (18). The M3 modulation produces the actin-myosin beating layer lines at (∼24 nm)⁻¹ and (∼10.4 nm)⁻¹, AM₊₁ and AM₋₁, respectively (Fig. 2; (37,38,18)). The M6 modulation is responsible for the meridional reflection at ∼7.2 nm and also contributes to the off-meridional intensity on the A1, A6, and A7 actin layer lines (38,18). In our calculations, the model parameters e = 0.25 for rigor and e = 0.5 for active contraction were chosen to match the observed M3, M6, AM₊₁, and AM_-1 intensities. The choice is not unique as the meridional intensities depend not only on e, but also on axial disorder of the actin and myosin filaments, and have a contribution from the detached heads. Although some structures of the thick filaments different from bound myosin heads probably contribute to the M6 intensity (8), high sensitivity of the M6 intensity to changes in muscle length (8) is evidence of a substantial head contribution to this intensity. Therefore the binding of myosin heads to actin has a strong modulation with a ∼7.2 nm repeat that is accounted for by our model.

Although our model reproduces the main features of the observed 2D x-ray diffraction pattern of muscle fibers contracting at ∼30°C, the intensity of some calculated layer lines differs from their experimental values. The observed A6 intensity is substantially higher than the calculated one (Figs. 3 and 8) whereas that of A7 is either overestimated (Fig. 3) or fitted reasonably well. We suggest that the main reason for this is the quality of the existing models of the thin filament structure, which overestimates the observed ratio of 0.23–0.25 for the total integral A7 and A6 intensities in relaxed muscle fibers. Our model does not reproduce the “forbidden” M1 and M2 myosin meridional reflections, which are quite bright in rigor and relaxed patterns and are much less intense during active contractions (Fig. 2). These reflections probably originate from breaking the threefold symmetry of the thick filaments due to the presence of C-protein (9), which is not taken into account in our model.

The radial width of the M3 myosin meridional reflection is underestimated by the current model (Figs. 3 and 8) although a minimal degree of crystallinity of the actin-myosin filament lattice (single superlattice unit cell) was used for modeling diffraction from actively contracting muscle. Calculations taking into account the contribution of detached myosin heads to the M3 intensity provide a better fit to the M3 reflection (data not shown). However, we decided to omit any contribution of the detached myosin heads to the diffraction pattern as one needs too many additional unknown parameters to describe their structural properties.

In the model suggested by Yagi et al. (15,16), the actin binding pattern was modeled by a random labeling of myosin heads along actin filament with a 14.5 nm modulation. This model simulated the intensities of the A1, M3, and AM₊₁ layer lines and was the first to point out the dependence of the AM₊₁ intensity on the axial tilt of LCD of attached myosin heads. The actin binding pattern was defined by two parameters. One of these, the binding probability, has the same meaning as the fraction of attached myosin heads, f, in our model. The second parameter, the standard deviation from the exact M3 modulation, is different from the stiffness ratio e used in our model because the principle of minimal elastic distortion energy in the 3D actin-myosin lattice influences not only the M3 modulation, but also the M6 modulation. As the Yagi et al. model does not account for the packing of the actin and myosin filaments in the 3D filament lattice in the A-band of sarcomeres and for the contribution of the detached heads in the diffraction pattern, it could not explain the presence of the meridional peak on M6. Also the A1, A6, and A7 intensities, which contain contribution from the 7.2 nm modulation (18), were probably underestimated.

During isometric contraction, the crystal-like lattice sampling on the diffraction pattern is less pronounced than in rigor (Fig. 2). The decrease in crystallinity probably results from active forces that impose significant disorder of the filament lattice in both axial and transverse directions. The amount of the disorder is such that the model with a single superlattice unit cell consisting of six actin and three myosin filaments can account for the amount of sampling seen in the experimental patterns (Figs. 3 and 8).

The intensity of A1 actin layer line as a measure of the fraction of stereospecifically attached heads

Calculations show that the total intensity of the A1 actin layer line, I_A1, is not sensitive to either a tilt of the LCDs of stereospecifically bound myosin heads (Fig. 4) or to a variation in the azimuthal and axial angles of stereospecifically bound heads (Fig. 5). Only an unrealistically high tilt of the whole myosin head is capable of inducing changes in I_A1 of >10%. The calculated I_A1 was shown to be insensitive to the disorder of the filament lattice in sarcomeres as this only affects the intensity distribution and lattice sampling (18).

During active isometric contraction at near physiological temperature and in rigor, the contribution of actin filaments to the A1 intensity is substantial only on the meridian (where TN1 reflection is seen, Figs. 2 and 3) and at high reciprocal radii of >0.06 nm⁻¹ (Fig. 2). In the off-meridional region of 0.025–0.06 nm⁻¹ where the contribution of bound myosin heads to the A1 intensity is maximal, the contribution of the actin filaments to A1 intensity is negligibly small (Fig. 2, C and D). Our model reproduces the data, showing only a small actin component of A1 in this radial range (Fig. 3). Even after integration in a wider radial range of 0.014–0.1 nm⁻¹, the contribution of the thin filaments themselves to A1 remains small (Fig. 6).

Calculations presented in Fig. 6 demonstrate that I_A1 normalized for its value in rigor (where all myosin heads are strongly attached to actin) increases nearly proportionally with the fraction of stereospecifically bound head, f(S). These results show that in the conditions when all attached myosin heads are bound to actin stereospecifically, normalized I_A1 can be used as a robust measure of the fraction of attached heads. The contribution of the nonstereospecifically attached heads to the I_A1 depends on the degree of disorder of attachment angles (Fig. 7) and may not be negligible. For this reason, I_A1 provides a lower estimate of f(S), so that the total fraction of bound heads can be higher than the estimate based on I_A1 if a significant fraction of the heads is bound nonstereospecifically. During isometric contraction at ∼30°C, I_A1 is ∼30% of its rigor value (Fig. 3). We believe that in these conditions, the fraction of nonstereospecifically attached heads is small, therefore 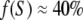(Fig. 3). A similar value was obtained from mechanical measurements in single frog and rabbit muscle fibers by Linari et al. (39,42). Our estimate is much higher than the value of 5% estimated from the A1 intensity in mouse diaphragm muscle contracting at room temperature (19) and somewhat smaller than 55–75% derived from the intensities of A6 and A7 layer lines in rabbit psoas muscle (6). The normalized calculated A1 intensity depends not only on f(S), but also on the stiffness ratio parameter, e, that can be estimated but not measured precisely from experimental diffraction patterns. Reasonable estimates of e are in the range of 0.25–0.5. For these e values, ambiguity in the estimate for f(S) derived from the I_A1 value is within ±5%. More accurate estimates can be obtained from the normalized sum of the I_A1 and the total intensities of the actin-myosin beating layer lines, AM₊₁ and AM₋₁, that is equal to f(S) with ±3% accuracy, for f(S) in the range of 0.1–0.4 (data not shown). Experimentally, the measurement of the beating layer line intensities is more difficult than that of I_A1, as these reflections are much less intense and the layer lines partially overlap with neighboring M2 and M4 myosin layer lines, respectively. For these reasons, the spatial resolution and the signal/noise ratio of the x-ray diffraction experimental data need to be high to measure the AM₊₁, AM₋₁ intensities reliably.

As mentioned previously, the calculated I_A1 does not follow the square law suggested by a simple theory (43) mainly due to the 7.2 nm modulation (38,18). As a result, the dependence of I_A1 on f(S) is somewhat intermediate between a linear and a square relation (Fig. 6).

The calculated M3 intensity increases with f(S) for a low fraction of bound heads and decreases when it approaches its maximal value in rigor (Fig. 6). The reason for this bell-shaped behavior is an increase in dispersion of the actin binding sites from the 14.3 nm myosin-based modulation with an increase in the actin occupancy: as the more “convenient” actin monomers are occupied, the dispersion from the M3 repeat increases.

A feature that we can learn from the modeling is that the intensities of the higher order actin layer lines A5, A6, and A7 cannot be used for quantitative estimate of the fraction of stereospecifically attached heads, as these intensities are sensitive to the shape of bound heads (Figs. 4 and 5) and, more importantly, they decrease markedly when a small (up to 2 nm) disorder is imposed to the “neck” domains of bound heads. As the disorder and the shape of the heads are unknown a priori, one should be careful in interpreting these intensities in terms of the number of myosin heads bound to actin or changes in their configuration.

Nonstereospecifically attached heads and temperature-induced changes in the diffraction pattern from contracting muscle

The result of calculations of the effect of myosin head disorder on layer line intensities (Fig. 7) does not agree with the common belief that the disorder mainly affects the intensities of the high angle layer lines and not the low angle ones (10,19). This is true for axial and radial disorder for which the thermal factor is 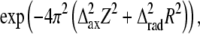where 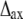and 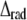are the root mean-squared axial and radial disorder, respectively, and Z and R are the axial and radial coordinates in reciprocal space (35), respectively. For these types of disorder, the intensity decreases sharply with an increase in the number of the layer line (proportional to Z) and along a layer line at higher reciprocal radius R. The results of calculation presented in Fig. 7 B agree well with this theory.

The effect of azimuthal disorder is different for different Fourier-Bessel terms, which contribute to the intensity of a layer line, and for this reason the results of our calculations do not follow the simple rule “the higher order the higher the effect of disorder” (Fig. 7 A). This can be explained as follows. The thermal factor for azimuthal disorder with respect to the filament axis can be expressed as 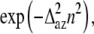where 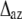is the root mean-squared azimuthal disorder and n is the order of the Bessel function J_n of the first kind that gives a contribution to the lth layer line intensity via a Fourier-Bessel term F_ln. For this reason, azimuthal disorder mainly depresses the contribution of the Bessel functions with high 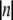such as A1 and A5, where the main contribution comes from J₂ and J₃, respectively, whereas the effect of the disorder on higher order layer lines, A6 and A7, is much less pronounced because the main Fourier-Bessel term for these layer lines is J₁.

It has been known for a long time that the increase in temperature of contracting muscle induces an increase in the force it produces. This increase in temperature and isometric force was found to be accompanied by an increase in I_A1 (24), which occurs simultaneously with force (27). As the increase in temperature does not induce a significant increase in instantaneous fiber stiffness (40,30,44) and in the intensity of the equatorial 1,1 x-ray reflection (25), we proposed that the rise of the A1 intensity with temperature is due to a transition of nonstereospecifically attached myosin heads to a stereospecifically bound state, and that this transition is an essential part of force generation. Results of our calculations (Fig. 8) show that the main changes in the x-ray diffraction pattern of contracting muscle fibers upon increase in temperature can indeed be explained by such transition. A quantitative agreement between the low I_A1 (∼10% of its rigor value) observed during isometric contraction at ∼5°C and results of calculation with 40% of myosin heads attached can only be achieved with relatively high (±60°) azimuthal disorder of nonstereospecifically attached heads (Fig. 8). This range is somewhat wider than that found by Taylor et al. ((28), full range 86°) from analysis of the averaged tomogram of contracting insect flight muscle. An attempt to account for the contribution of nonstereospecifically bound heads to the diffraction pattern was made by Iwamoto et al. (45), who used stretched rabbit muscle fibers soaked with endogenous S1, which were then cross-linked to actin with EDC. In rigor, cross-linked S1s strongly enhanced all actin layer lines, whereas in the presence of ATP, no contribution of endogenous myosin heads to these layer lines was seen, suggesting a wide distribution of the attachment angles of myosin heads to actin despite covalent links between them.

The A1 intensity tightly correlates with isometric force in intact and permeabilized fibers from muscles of both cold- and warm-blooded animals. In intact frog muscle contracting at 8°C, normalized I_A1 is ∼0.15 (41). A slightly smaller I_A1 (0.12) was reported for single permeabilized muscle fibers from the frog contracting at the lower temperature of 5-6°C. I_A1 increased in parallel with tension to 0.24 and 0.36 when temperature rose to ∼17°C and ∼30°C, respectively (24). A similar although smaller increase in I_A1 was found in intact frog muscle fibers over a narrower temperature range (46). In the experiments with rabbit muscle fibers presented here, temperature sensitivity of isometric force was more pronounced: more than a threefold rise over a temperature range of 5–30°C compared to less than a twofold rise for frog muscles. Correspondingly, the increase in normalized I_A1 with temperature was also more marked; it rose from 0.08 to 0.3.

Fig. 8 shows the results of simultaneous fit of the pre- and post-T-jump diffraction patterns of actively contracting muscle with the model where the fractions of stereo- and nonstereospecifically attached myosin heads change with temperature according to hypothesis suggested by Ferenczi et al. (27). The fraction of stereospecifically bound heads increased with temperature by a factor of 3, from 13% to 40%, proportionally to isometric tension, whereas the total number of attached heads was 40% independent of temperature. The fact that the model reproduces changes in the intensities of the A1, M3, A5, A6, and A7 layer lines induced by an increase in temperature (Fig. 8) supports the “roll and lock” model of force generation by myosin heads (27). The transition from nonstereo- to stereospecifically bound state of the heads during the normal process of cross-bridge cycling is consistent with the types of kinetic models derived from measurements of ATPase activity in contracting fibers (47) in which attached cross-bridges undergo conformational changes linked to the release of products of hydrolysis, P_i and ADP.

The shape of stereospecifically attached heads during isometric contraction

Although the intensity of the brightest actin line, A1, is insensitive to the orientation of the light chain domain of stereospecifically bound myosin heads, the intensities of the high order layer lines change depending on the lever arm tilt (Fig. 4). Among them, the beating actin-myosin layer line AM₊₁ at ∼(10.3 nm)⁻¹ is of specific interest as its intensity changes by ∼2-fold and the position of the peak of the intensity shifts markedly when the LCDs of myosin heads go from a preforce-generating to a rigor-like position (Fig. 4). The experimental intensity distribution along this layer line is close to that calculated for the “active” configuration of LCD (Fig. 8), showing that the necks of a majority of myosin heads in contracting muscle are more perpendicular to the actin filament than in rigor. The position of the off-meridional peak of the intensity of the A5 layer line at ∼(7.2 nm)⁻¹ is also sensitive to the LCD orientation (Fig. 4). Comparison of observed and calculated intensity profiles (Fig. 8) again shows that the necks of a majority of stereospecifically bound heads are in a position close to that in preforce-generating head configuration. However, the choice of the preforce-generating configuration of myosin head is not unique and has an axial range of ∼10°. For example, 40° tilt of the myosin head also can be used for fitting experimental data. The 40–50° interval of the LCD angles is compatible with the results of the experiments with quick length changes of intact frog fibers, where the average configuration of the myosin head in isometric contraction was modeled by tilting and bending of the LCD so that the C-terminus of the head was displaced by 7 nm along the actin filament axis compared with the rigor-like conformation (48). Our active configuration is also close to the preforce-generating conformational state of scallop S1 (21).

Using the A6 and A7 actin layer lines for determining the shape of stereospecifically bound heads is more ambiguous, as actin filaments themselves as well as nonstereospecifically bound myosin heads contribute significantly to these layer lines (Figs. 4, 6–8). These intensities are also very sensitive to small variation of attachment angles (Fig. 5).

It should be mentioned that the x-ray diffraction modeling shows the features of the majority of myosin heads, and does not exclude a small fraction of myosin heads in other conformations, for example at the end of the power stroke.

SUMMARY

We show here that the main features of the whole 2D x-ray diffraction pattern from contracting muscle fibers can be quantitatively simulated by a model based on the available high resolution structures of actin and of the myosin head. Only two additional parameters are required to fully describe the actin binding pattern in the 3D actin-myosin filament lattice in the A-band of a sarcomere. The total integral intensity of the first actin layer line A1 is insensitive to a tilt of the light chain domains of myosin heads and to lattice disorder, and for these reasons can be used as a robust measure of the fraction of myosin heads stereospecifically bound to actin and presumably producing active force. This fraction is ∼40% during isometric contraction at near physiological temperature. At low temperature, a majority of myosin heads are bound to actin nonstereospecifically. The light chain domains of a majority of myosin heads stereospecifically bound to actin during isometric contraction are in a position more perpendicular to the filament axis than in rigor as revealed by the intensity distribution along the A5 and AM₊₁ layer lines.