Abstract
The cause of the anomalous mole fraction effect (AMFE) in calcium-selective ion channels is studied. An AMFE occurs when the conductance through a channel is lower in a mixture of salts than in the pure salts at the same concentration. The textbook interpretation of the AMFE is that multiple ions move through the pore in coordinated, single-file motion. Instead of this, we find that at its most basic level an AMFE reflects a channel's preferential binding selectivity for one ion species over another. The AMFE is explained by considering the charged and uncharged regions of the pore as electrical resistors in series: the AMFE is produced by these regions of high and low ion concentration changing differently with mole fraction due to the preferential ion selectivity. This is demonstrated with simulations of a model L-type calcium channel and a mathematical analysis of a simplistic point-charge model. The particle simulations reproduce the experimental data of two L-type channel AMFEs. Conditions under which an AMFE may be found experimentally are discussed. The resistors-in-series model provides a fundamentally different explanation of the AMFE than the traditional theory and does not require single filing, multiple occupancy, or momentum-correlated ion motion.
INTRODUCTION
In vivo, ion channels perform a variety of functions like gating and selecting the ions to be conducted. In vitro, these functions are tested under different conditions and theories are used to infer their physical basis. One of the oldest and best-known of these physical inferences is from the mole fraction experiment. In the classic form of this experiment, the channel conductance is measured with a mixture of two ion species X and Y in the baths. The total concentration of the mixture ([X] + [Y]) is fixed while the mole fraction [X] / ([X] + [Y]) is changed. For most channels, the conductance changes monotonically between the two endpoint conductances of pure X and pure Y in the baths. For some channels, however, the channel conductance of the mixture is less than the endpoint conductances. This anomalous mole fraction effect (AMFE) is usually interpreted as multiple ions moving through the pore in a single file.
Takeuchi and Takeuchi were the first to measure an AMFE in crayfish muscle (1); the conductance-versus-mole-fraction curve had a minimum in mixtures of Cl− with CNS−,  and I−. The AMFE has since been found in more channels (reviewed by Hille (2)). This article focuses on calcium channels, where some of the largest AMFEs have been observed. For example, Almers et al. (3) and Almers and McCleskey (4) found that Ca2+ blocked Na+ current by 90% in the L-type calcium channel (3,4). In a similar experiment, Ca2+ blocked Na+ current by 50% in the ryanodine receptor (RyR) calcium channel, and Ca2+ blocked Cs+ current by 60% (5).
and I−. The AMFE has since been found in more channels (reviewed by Hille (2)). This article focuses on calcium channels, where some of the largest AMFEs have been observed. For example, Almers et al. (3) and Almers and McCleskey (4) found that Ca2+ blocked Na+ current by 90% in the L-type calcium channel (3,4). In a similar experiment, Ca2+ blocked Na+ current by 50% in the ryanodine receptor (RyR) calcium channel, and Ca2+ blocked Cs+ current by 60% (5).
A theoretical explanation of the AMFE using a chemical kinetics model (6) is still taught in textbooks (2). In this model, the selectivity filter of the channel has multiple binding sites for permeating ions that are separated by energy barriers over which the ions must hop. Because the selectivity filter is narrow and a binding site can only hold one ion, ions must move through in a single file. Therefore, current is produced by the correlated motion of the ions through the filter. In the barrier model, the presence of an AMFE indicates a queue of multiple ions moving through the pore (a multi-ion channel). The absence of an AMFE is generally interpreted as the channel containing only one ion or less at a time. Mole fraction experiments are routinely interpreted with this model, to the point where multi-ion channel is synonymous with the presence of an AMFE. A cursory search of PubMed and the literature of calcium channels reveals many recent examples of this presumed equivalence (7–18).
From this point of view, a mole fraction experiment is then a very powerful tool to determine whether there is, at most, only one ion in the selectivity filter at a time or there are several ions. There are, however, several problems with this interpretation, especially in the realm of calcium channels. First, barrier models themselves have been the subject of much debate and do not include the physics known to occur in electrolytes in confining geometries (19–29). Moreover, detailed analyses of particle simulations inside channels (including calcium channels) have found that energy profiles change substantially with all experimental conditions, both on the atomic timescale (30,31) and at steady state (5,22–24,32,33). Second, the general conclusion that an AMFE implies a multiply occupied, single-file pore has been experimentally disproved; several AMFEs have been observed in 50 Å-wide synthetic nanopores in plastic—where there is clearly no single filing or correlated ion motion (34). Moreover, an ion channel model without single filing predicted all the AMFE results known in RyR before the experiments confirmed them (5,35). Third, another model showed that—at least in principle—it is possible to have AMFEs with significantly less than one ion in the channel and without single filing (36). At the very least, the interpretation of an AMFE is model-dependent, and an AMFE must be interpreted with the model that includes the physics that best describes all the properties of that particular channel.
In this article, we examine the AMFE for channels with negative protein charges in the selectivity filter. These kinds of channels tend to be calcium-selective. Examples include the EEEE locus of the L-type channel (37,38) and the DDDD locus of the RyR (39–41). A theory of the AMFE in these channels has been presented by Nonner et al. (36) and this article builds on their results.
Nonner et al. (36) described their ions as point charges moving in the electrostatic mean-field, the simplest model of ions within the Nernst-Planck (NP) description of diffusive ion flux (a simplification called the Poisson-Nernst-Planck, PNP, model). They found that the AMFE was the result of localized, ion-specific binding within the pore; that is, ion species X is bound more tightly in one subregion of the channel than ion species Y. Adjacent to the binding region, a depletion zone is formed. In the depletion zone, ion concentrations (of one or both ion species) are small and therefore electrical resistance is high. This high-resistance region in series with the low-resistance binding region produces the AMFE because these resistances change differently with mole fraction. We call this the resistors-in-series model.
This idea was recently tested in 50 Å-diameter synthetic nanopores in plastic (34). These pores have a significant AMFE in mixtures of Ca2+ and monovalent cations. The experiments were described with NP theory coupled with Monte Carlo (MC) simulations of finite-sized ions (NP+MC). The results were consistent with those of Nonner et al. (36) for point-sized ions: preferential binding of one ion species over the other in the center of the pore produced the AMFE because the resistance of the highly Ca2+-selective center changed differently with mole fraction than the nonselective ends of the pore.
Here, we apply a similar NP+MC approach to a model L-type calcium channel and reproduce two AMFEs known from experiment. Both AMFEs are explained with the resistors-in-series model. In the Appendix, we perform a separate mathematical analysis of a very simplified PNP model with point-charge ions and show the importance of depletion zones and which variables affect the high-resistance region. Our results suggest that the resistors-in-series model is a viable alternative to the traditional AMFE model.
THEORY AND METHODS
Two different kinds of mole fraction experiments
Two types of experimental protocols have historically been used to produce AMFEs:
Classical mole fraction experiment. This is the experiment described in the Introduction: ion species X and Y are mixed together with [X] + [Y] fixed while the mole fraction [X]/([X] + [Y]) is changed. Both baths are identical and current or conductance is recorded as a function of mole fraction.
Added-salt experiment. In this experiment, [Y] is kept fixed and current or conductance is recorded as [X] is increased. This experiment is very similar to the classical experiment when the channel has a high affinity for X so that at the minimum [X] is low compared to [Y]. In some cases, X is only added to one side of the channel while [Y] is the same in both baths. This has been done in both the L-type (3,4) and RyR (5) calcium channels because high [Ca2+] on the cytosolic side of these channels decreases their open probability.
In this article, we analyze both of these experiments.
Conductance from the Nernst-Planck equation
To compute ion current, we assume that the ions move diffusively; that is, the current is described by the NP equation
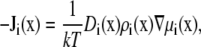 |
(1) |
where 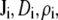 and
and 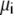 are the local flux density, diffusion coefficient, density, and electrochemical potential, respectively, of ion species i. The value k is the Boltzmann constant and T is the temperature. Equation 1 can be reduced to a one-dimensional approximation by assuming that the ions move perpendicularly across equi-concentration/potential surfaces of area A that can be approximated as spherical shells perpendicular to the protein and long-axis of the channel (28,42,43):
are the local flux density, diffusion coefficient, density, and electrochemical potential, respectively, of ion species i. The value k is the Boltzmann constant and T is the temperature. Equation 1 can be reduced to a one-dimensional approximation by assuming that the ions move perpendicularly across equi-concentration/potential surfaces of area A that can be approximated as spherical shells perpendicular to the protein and long-axis of the channel (28,42,43):
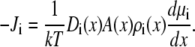 |
(2) |
Ji is now the flux of species i, not the flux density, and is a constant. Inside the selectivity filter (−5 Å < x < 5 Å in Fig. 1) the area A is the cross-sectional area of the pore, but outside the selectivity filter the ions are assumed to flow perpendicular to spherical shells (with area A) that are perpendicular to both the protein/membrane and the long-axis of the pore (see Fig. 1 of (43)). We average over these shells. This same one-dimensional NP approach was used to model RyR permeation and AMFEs (5,35). The selectivity filter of RyR was modeled by the same eight half-charge oxygens used here and its radius was only 0.5 Å wider than the radius of our model L-type channel. We believe that this shows that the one-dimensional NP theory is a reasonable approach for the very similar channel we have in this article.
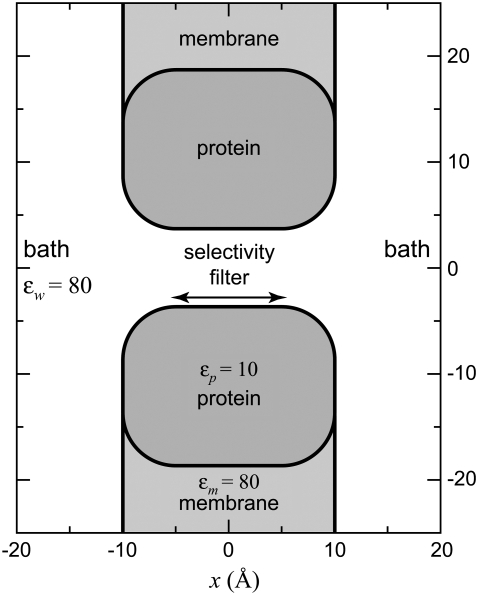
FIGURE 1.
The model L-type channel pore used in the MC simulations. A cross section of the cylindrical simulation cell is shown. The selectivity filter and the baths have a dielectric constant ɛw of 80 and the protein a dielectric constant ɛp of 10. The dielectric constant of the membrane ɛm is 80, but this is only for computational convenience; setting ɛm = 2 does not affect the ion binding within the pore, but significantly increases the computation time of the simulations (32). The figure focuses on the channel and does not show the entire baths; the size of the simulation box is much larger than indicated in the figure.
Equation 2 can be integrated from bath to bath across the channel:
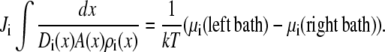 |
(3) |
In this article, we assume that both baths are identical so the electrochemical potential difference between the baths in Eq. 3 is only the applied voltage V,
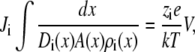 |
(4) |
where the right bath is electrically grounded. If we further assume that V is small so that current/voltage curves are linear, the channel conductance g is given by
 |
(5) |
where the sum is over all permeant ion species and the Ri values are the resistances to current flow for ion species i. These resistances are given by
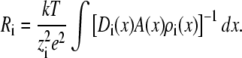 |
(6) |
Here, the integral is from bath to bath. We will use Eqs. 5 and 6 to analyze the AMFE.
But, before considering the AMFE, Eqs. 5 and 6 already give some insights into ion channel conductance:
The conductance of each ion species i depends on the integral of the reciprocal of Di(x)A(x)ρi(x). Even if one assumes that the diffusion coefficients and area are constant throughout the channel, the concentration profiles of the ions are generally very complex with many peaks and valleys (32,33,44–46). Because the reciprocal of the concentration profile determines the conductance, the low-concentration regions are weighted differently than the high-concentration regions. This can be interpreted by considering ion flux as going through resistors in series: a low-concentration region is a high-resistance element in series with low-resistance elements formed by high-concentration regions, as pointed out by Nonner et al. (36). Similarly, regions with a small diffusion coefficient and/or small cross-sectional area can form high-resistance elements. The net resistance of any region must, however, take into account the full product Di(x)A(x)ρi(x), rather than just any individual factor.
Conductance can be computed from equilibrium calculations/simulations, as long as the current/voltage relation is linear. In that case, the conductance is constant and the output of Eq. 5 is the same for all applied voltages (including zero). The concentration profiles will be different for different voltages, but the sum of the reciprocal of the resistances Ri will be the same for all voltages. We will use this observation to compute conductances for a model of the L-type calcium channel from equilibrium MC simulations.
To compute conductance, the ions' diffusion coefficients are needed in addition to the ions' concentration profiles. In the baths, experimental values are known and in the selectivity filter, one can assign a constant diffusion coefficient as a first approximation. The connection between the two regions of the system is, however, less clear. For simplicity, we will assume that flux is limited only in the selectivity filter and that the channel atria are negligible. We will show that this simplification reproduces the experimental AMFEs and then discuss why the atria may (to first order) be ignored. With this approximation, Eq. 5 becomes
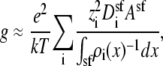 |
(7) |
where 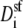 is the diffusion coefficient of species i in the selectivity filter and Asf is the cross-sectional area of the selectivity filter.
is the diffusion coefficient of species i in the selectivity filter and Asf is the cross-sectional area of the selectivity filter.
This still leaves the selectivity filter diffusion coefficients 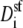 as free parameters. To reduce the number of open parameters even more, we only consider normalized currents. Here, we normalize with the conductance at 0 Ca2+. Then, the normalized conductance from Eq. 7 only depends on the ratio of the diffusion coefficients
as free parameters. To reduce the number of open parameters even more, we only consider normalized currents. Here, we normalize with the conductance at 0 Ca2+. Then, the normalized conductance from Eq. 7 only depends on the ratio of the diffusion coefficients 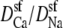 (or
(or 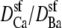 ). This is our only open parameter.
). This is our only open parameter.
This treatment of the diffusion coefficients is obviously very approximate. For example, we assume that there is no radial or axial dependence within the selectivity filter because any other assumption would require a theory of diffusion coefficients inside a highly-charged, densely-packed cylinder. We are not aware of such a theory. In addition, diffusion coefficients of ions inside a highly-charged channel have, to our knowledge, not been computed from molecular dynamics. Below, we either show how different values change our results or we determine them by fitting to a single experimental data point. Therefore, the values we compute are best interpreted as effective diffusion coefficients in this one-dimensional theory.
Monte Carlo simulations of a model L-type calcium channel
We present two sets of AMFE calculations based on Eq. 5, one with PNP (i.e., point-charge ions) and one based on MC simulations of a model L-type calcium channel. The PNP channel model we use has been previously described (28). This analysis is presented in the Appendix.
Here we only describe the model L-type calcium channel and the MC simulations used to compute binding selectivity in it. Details of both the model (46) and the simulations (32,44) have been described previously. In these kinds of equilibrium simulations, particles are moved to minimize the free energy of the system so that spatial correlations among ions are computed, but momentum correlations are ignored.
The geometry of the model L-type calcium channel is shown in Fig. 1. The channel is modeled only as the selectivity filter, a 10 Å-long cylinder that is 7 Å in diameter. The selectivity filter contains eight oxygens with a −1/2 charge (O1/2– ions) used to model the COO− terminal groups of the four glutamates (the EEEE locus) that give the L-type channel its selectivity properties (37,38). These oxygens are free to move inside the selectivity filter, but are confined within it by hard-wall potentials. This approximates the relatively free motion of tethered terminal COO− groups inside the permeation pathway. This representation of glutamates (and aspartates) has been very successful in reproducing experimental data (5,33,35,42,44–49).
In the simulations, ions are charged, hard spheres with Pauling diameters of 1.98 Å for Ca2+, 1.90 Å for Na+, 2.70 Å for Ba2+, 3.62 Å for Cl−, and 2.80 Å for O1/2–; they are not adjustable parameters. Water is a dielectric material with dielectric constant 80. The dielectric constant is the same inside the selectivity filter; anywhere the ions move the dielectric constant is 80. Surrounding the selectivity filter is a protein with a low dielectric constant with value 10. The dielectric constant of the membrane is taken to be 80 for computational convenience; using a lower value increases computation time, but does not affect selectivity at all (32).
The Metropolis MC simulations we use are designed for equilibrium systems so we only consider identical (symmetric) baths and zero applied voltage. While this is a restriction on what can be simulated, it allows us to directly simulate the micromolar Ca2+ concentrations necessary to study the L-type calcium channel. This is possible with a combination of the grand canonical ensemble and biased ion moves between the big baths and the small selectivity filter (32,44). In a grand canonical MC step, either a randomly-selected ion is moved to a new (possibly biased) position within the simulation cell or a charge-neutral group of 1 Ca2+ and 2 Cl− are created or deleted within the simulation cell (with a bias given to the selectivity filter). For any ion move/creation/deletion, the charge induced on the water/protein dielectric boundary is explicitly computed and used to compute the electrostatic component of the system energy (32). Each ion move/creation/deletion is accepted with a probability that ensures microscopic reversibility, as previously described (32,44).
This model of a calcium channel is a very reduced version of the real thing. The channel has been stripped down to the minimum amount of physics needed to have micromolar Ca2+ versus Na+ selectivity (32,46). This previous work also established many of the model parameters (e.g., dielectric constants, length, size, and shape of the pore) and we do not change them here. This reduced model leaves out many things like highly complex possible ion motions and interactions seen in all-atom simulations whose impact will have to be explored.
The model also leaves out water molecules and uses 80 as the dielectric constant inside the pore, although it is probably <80. The choice of 80 is driven by the inaccuracy of Born energy approximations of ions crossing dielectric boundaries and the computational complexity of a better approximation. However, the very close proximity of the dielectric 10 protein to the permeating ions does give a Born-like penalty to an ion entering the channel. Because of this, the dielectric values described here should only be considered effective parameters.
To test the sensitivity of our results, we performed simulations with a dielectric of 40 for the electrolyte. We found that the general pattern of ion distribution is insensitive to this model assumption. Because both the cation/cation and cation/glutamate interactions are equally increased, the ion binding pattern needed for the AMFE (discussed below) is unchanged; Ca2+ binds only in the center of the pore and Na+ is distributed throughout the pore (data not shown). Changing the pore diameter or the protein dielectric constant also do not affect this pattern of binding (32,46). Therefore, the microscopic interpretations we make are still likely to be valid when parameters are changed or more atomic detail is added.
While a more detailed model with a different dielectric coefficient inside the pore is necessary, this is the first—and so far only—model of a calcium channel in which particle simulations have directly simulated micromolar Ca2+ affinity (46,50). This model is a first step to a more detailed model of a calcium channel, but even this simple model reproduces the experimentally measured AMFEs of the L-type calcium channels with only one open parameter per experiment. While this is not sufficient by itself, it does indicate that this model—and its physics of selectivity and the AMFE—are worth studying further.
Reduced models like this are very useful because they include less atomic detail than molecular dynamics simulations so they are computationally much faster. Therefore, they can explore how the free energy landscape changes over a large set of experimental conditions. Despite their reduced physics, these models also explain a great deal of experimental data (5,32,33,35,44–46,48,51).
Role of flexible glutamates
NP approaches (Eq. 1) have been demonstrated to fail in narrow channels like the potassium channel, especially for point-charge ions (52). In that article, Corry et al. showed that ion flux is diffusive (i.e., the NP equation is valid) if the pore radius is larger than two screening (Debye) lengths. This ensures that the pore contains a sufficiently large sample of both cations and anions for ion screening to occur. Because our selectivity filter contains mobile carboxyl groups at very high concentration (46), permeant cations are screened very effectively and the screening length is always <1.25 Å (49,53). Therefore, our 3.5 Å pore radius is well within the diffusive limit. This is also consistent with the success of an NP model with hard-sphere ions in predicting all the AMFEs in the RyR calcium channel (5,35) (see also Fig. 2). With an 8 Å wide selectivity filter, the model RyR pore is only 1 Å wider than the model pore used here.
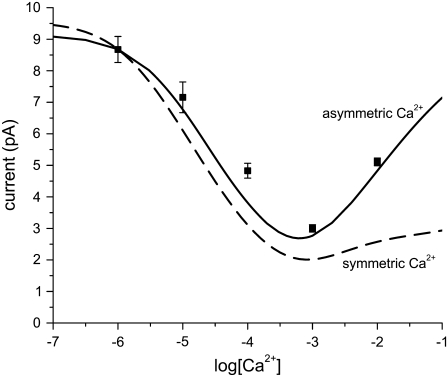
FIGURE 2.
Illustrating the effect of adding salt symmetrically versus asymmetrically. The calculations are made with the PNP/Density Functional Theory model of RyR by Gillespie (5). This model reproduces RyR permeation data in >100 different ionic solutions. It also predicted all the AMFEs of RyR (5,35). Both baths contain 100 mM CsCl, and CaCl2 is added either asymmetrically in the lumenal bath (solid line) or symmetrically (dashed line), and the current at −20 mV applied potential is plotted versus [Ca2+]. The asymmetric (solid) curve reproduces the experimental data (symbols) (5), but because millimolar Ca2+ reduces the open probability of RyR, the experiment cannot be done under symmetric conditions.
The screening of Ca2+ by the glutamates has been shown to drive the Ca2+ versus monovalent selectivity in RyR (5). We have also computed the importance of this screening with two kinds of selectivity filters (data not shown). In each pore, one Ca2+ is fixed in place at the center of the selectivity filter and another Ca2+ is brought in from the bath. The first filter has four immobile glutamates outside of the permeation pathway (inside the protein, which has a dielectric constant of 10 like the protein used in this article). In this pore, the approaching Ca2+ is electrostatically repelled from the pore when its center is 4 Å away from the edge of the filter. The second filter is the one used in this article. Its mobile carboxyl groups screen the two Ca2+ from each other so that the approaching Ca2+ is not repelled until its center is already ∼1 Å inside the filter.
RESULTS
The main focus of this article is a model of the L-type calcium channel developed with our co-workers (46). In addition, in the Appendix we also analyze a simpler model to explore the roots of the AMFE. This PNP model uses point-charge ions (not the hard-sphere ions used in the rest of the article) for which a mathematical analysis is possible. With this model, we find:
The presence of an AMFE reflects the preferential selectivity of the channel for one of the cations. That is, the AMFE occurs only when the mole fraction of one ion species in the pore is larger than its mole fraction in the bath.
The AMFE involves the resistances of all regions within the channel and how they change with mole fraction.
The ion diffusion coefficients are important contributors to the resistance of each channel region. In fact, having the endpoint conductances (at mole fractions 0 and 1) too far apart can eliminate the AMFE.
We find these general principles to hold for the AMFE in the model L-type calcium channel with ions modeled as charged, hard spheres.
The L-type channel is modeled only as the selectivity filter surrounded by a low-dielectric protein sheath (Fig. 1) and has micromolar Ca2+ affinity like the L-type calcium channel (46). Here, we apply the conductance equation (Eq. 5) to the concentration profiles computed from the MC simulations to reproduce two experimental AMFEs of the L-type channel: Ca2+ block of Na+ current (3,4) and Ca2+ versus Ba2+ AMFE (4,7,54).
Ca2+ block of Na+ current
The micromolar Ca2+ affinity of the L-type calcium channel is defined by the added-salt experiment of Almers et al. (3) and Almers and McCleskey (4), where Ca2+ was added to 32 mM Na+ on the external side of the muscle fibers; the internal solutions contained 32 mM Cs+. This asymmetric adding of Ca2+ increases the high-[Ca2+] (i.e., upswing) conductance (compared to symmetric conditions) because the driving force of Ca2+ increases as [Ca2+] increases on only one side of the membrane (e.g., by ∼200 mV for 1 μM Ca2+ on one side and 10 mM Ca2+ on the other). This is illustrated in Fig. 2 with a model of ion permeation through RyR that can compute current in asymmetric conditions. Ca2+ is added asymmetrically (solid line) or symmetrically (dashed line) to Cs+ in RyR; both cases have an AMFE, but the minimum is less pronounced in symmetric conditions. Since our MC simulations require symmetric baths, we expect that our theory will not reproduce the high-[Ca2+] part of the conductance curve ([Ca2+] > 1 mM), but the micromolar block of Na+ current should be unaffected.
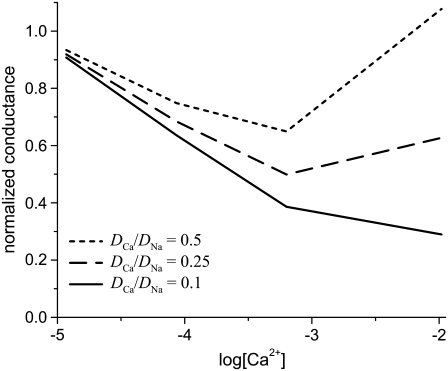
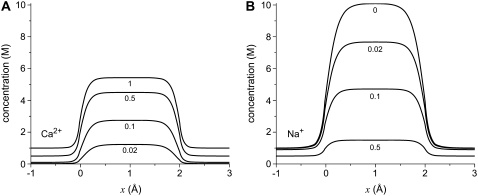
Fig. 3 shows the ion concentrations of Na+ and Ca2+ as CaCl2 is added to 30 mM NaCl. By substituting these profiles into Eq. 7 and integrating over the selectivity filter (−5 Å < x < 5 Å), we compute the AMFE shown in Fig. 4. The experimental data are shown for comparison (symbols). Three values of 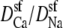 are used: 0.5, 0.25, and 0.1. The only effect of the diffusion coefficients is to change the high-[Ca2+] part of the conductance curve; the computed normalized conductances up to 10 μM Ca2+ are independent of the relative diffusion coefficients. All three curves show that the Na+ current is half-blocked by 1 μM Ca2+. Also, in all three curves the minimum occurs at [Ca2+] = 100 μM. These values agree with the experimental values and are independent of any adjustable parameters.
are used: 0.5, 0.25, and 0.1. The only effect of the diffusion coefficients is to change the high-[Ca2+] part of the conductance curve; the computed normalized conductances up to 10 μM Ca2+ are independent of the relative diffusion coefficients. All three curves show that the Na+ current is half-blocked by 1 μM Ca2+. Also, in all three curves the minimum occurs at [Ca2+] = 100 μM. These values agree with the experimental values and are independent of any adjustable parameters.
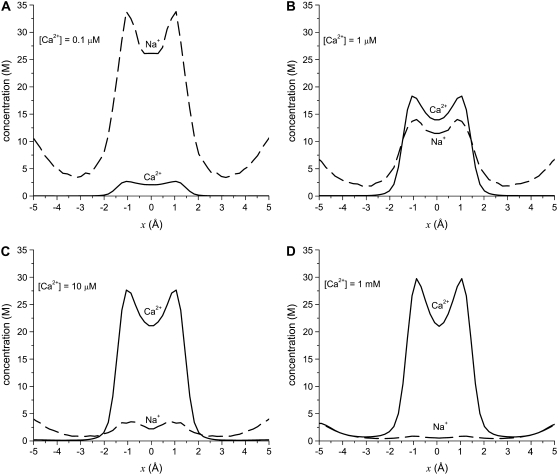
FIGURE 3.
Concentration profiles of the model L-type calcium channel for Ca2+ (solid lines) and Na+ (dashed lines) from equilibrium MC simulations. The baths contains 30 mM NaCl and CaCl2 is added to both baths: (A) 0.1 μM Ca2+, (B) 1 μM Ca2+, (C) 10 μM Ca2+, and (D) 1000 μM = 1 mM Ca2+.
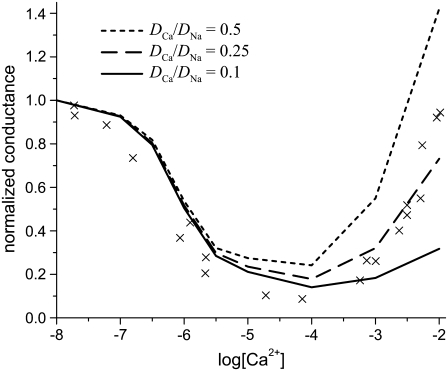
FIGURE 4.
The Na+/Ca2+ AMFE computed from the MC simulations of the model L-type calcium channel. The baths contain 30 mM NaCl, and CaCl2 is added to both baths. The conductances are normalized with the [Ca2+] = 0 conductance. Three different values of the relative diffusion coefficients are considered: 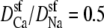 (dotted line), 0.25 (dashed line), and 0.1 (solid line). The experimental data of Almers et al. (crosses) is shown for comparison (3).
(dotted line), 0.25 (dashed line), and 0.1 (solid line). The experimental data of Almers et al. (crosses) is shown for comparison (3).
When 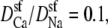 the minimum normalized conductance is 14%, compared to 9% for the experiment. Larger values of
the minimum normalized conductance is 14%, compared to 9% for the experiment. Larger values of 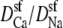 are inconsistent with the experimental data, even though the values 0.5 and 0.25 seem to reproduce the upswing arm of the curve. This is, however, misleading, as described above. On the other hand,
are inconsistent with the experimental data, even though the values 0.5 and 0.25 seem to reproduce the upswing arm of the curve. This is, however, misleading, as described above. On the other hand, 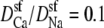 is consistent with the relatively flat upswing expected under the symmetric bath conditions (Fig. 2). This large difference between Na+ and Ca2+ diffusion coefficients has been consistently found in all one-dimensional Nernst-Planck models of calcium channels (5,28,35,55) and probably reflects (qualitatively at least) a real difference between Na+ and Ca2+ diffusion through a channel. In the selectivity filter, the Na+ and Ca2+ are surrounded by mobile, negatively-charged carboxyl groups that hinder the motion of both ions, but their greater electrostatic attraction to Ca2+ causes greater drag on Ca2+. (This kind of momentum transfer between cations and oxygens is explicitly computed in molecular and Brownian dynamics simulations, but must be parameterized in the NP approach since it does not include momentum conservation (56,57).)
is consistent with the relatively flat upswing expected under the symmetric bath conditions (Fig. 2). This large difference between Na+ and Ca2+ diffusion coefficients has been consistently found in all one-dimensional Nernst-Planck models of calcium channels (5,28,35,55) and probably reflects (qualitatively at least) a real difference between Na+ and Ca2+ diffusion through a channel. In the selectivity filter, the Na+ and Ca2+ are surrounded by mobile, negatively-charged carboxyl groups that hinder the motion of both ions, but their greater electrostatic attraction to Ca2+ causes greater drag on Ca2+. (This kind of momentum transfer between cations and oxygens is explicitly computed in molecular and Brownian dynamics simulations, but must be parameterized in the NP approach since it does not include momentum conservation (56,57).)
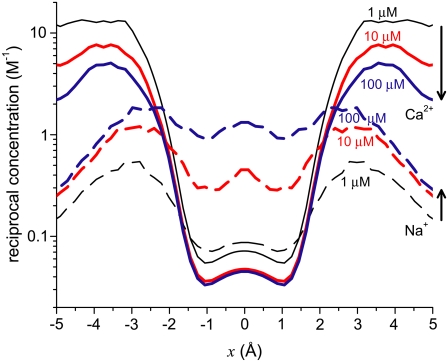
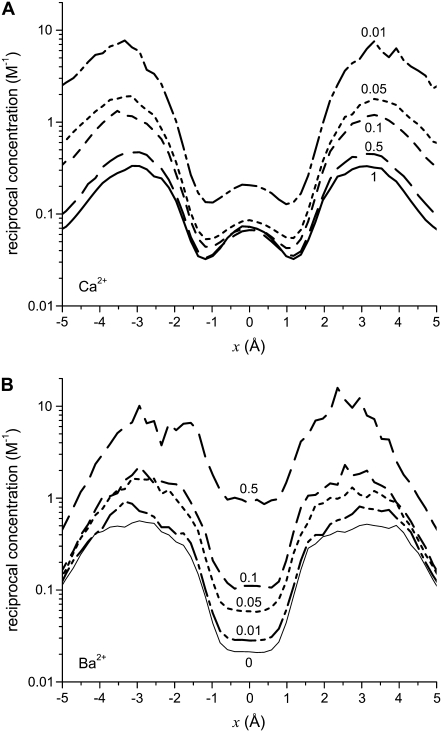
To analyze this AMFE, we start with the reciprocal of the ion concentrations (1/ρi(x)) that determine the resistance for each ion species in Eq. 7 (Fig. 5). For both Ca2+ (solid lines) and Na+ (dashed lines), the reciprocal concentration (and therefore the resistance) is low in the middle of the selectivity filter (−1 Å < x < 1 Å). For Ca2+, however, the reciprocal concentration sharply increases in the outer regions of the filter (1 Å < |x| < 5 Å), whereas this effect is much smaller for Na+. The origin of this can be seen in the ion profiles (Fig. 3): Ca2+ is present in the filter at high concentrations only in the center and otherwise the Ca2+ concentration is very small; the Na+ concentration is lower in the outer regions of the filter than in the middle, but still in the molar range.
FIGURE 5.
Profiles of the reciprocal concentrations (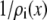 ) shown in Fig. 3 for Ca2+ (solid lines) and Na+ (dashed lines). (Black) 1 μM Ca2+; (red) 10 μM Ca2+; and (blue) 100 μM Ca2+. The arrows indicate increasing [Ca2+] for the Ca2+ and Na+ curves.
) shown in Fig. 3 for Ca2+ (solid lines) and Na+ (dashed lines). (Black) 1 μM Ca2+; (red) 10 μM Ca2+; and (blue) 100 μM Ca2+. The arrows indicate increasing [Ca2+] for the Ca2+ and Na+ curves.
The origin of the AMFE lies here. Ca2+ accumulates in the channel, but it binds only in the middle and is depleted elsewhere. Therefore, while there is a lot of Ca2+ in the pore, it does not contribute to the overall conductance because of the very high resistance of the depletion regions (1 Å < |x| < 5 Å). Na+ continues to conduct, but because it has been displaced by Ca2+, there is less Na+ present in the pore and therefore Na+ conductance decreases. This then explains why the diffusion coefficient ratios 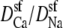 are unimportant when [Ca2+] < 10 μM: there is no Ca2+ current at low [Ca2+] even though Ca2+ occupies the pore. This also explains why more of the channel did not have to be taken into account in the analysis: a large depletion zone of an ion species in one part of the channel will stop the flux of that ion species no matter how much of the rest of the system is modeled. Here the important depletion zone forms inside the selectivity filter.
are unimportant when [Ca2+] < 10 μM: there is no Ca2+ current at low [Ca2+] even though Ca2+ occupies the pore. This also explains why more of the channel did not have to be taken into account in the analysis: a large depletion zone of an ion species in one part of the channel will stop the flux of that ion species no matter how much of the rest of the system is modeled. Here the important depletion zone forms inside the selectivity filter.
The same depletion and binding patterns are also found in a 10 Å-wide version of our L-type selectivity filter (46) that also exhibits an AMFE (Fig. 6). In this wider pore, there is no single-filing of ions, which we cannot explicitly rule out in the 7 Å-wide pore. The AMFE is less pronounced and occurs at higher [Ca2+] because this wide channel has a lower Ca2+ affinity than the more narrow pore (46), but the basic physics of the AMFE is the same in both the 7 Å- and 10 Å-wide pores.
FIGURE 6.
Na+/Ca2+ AMFE in a 10 Å-wide version of the pore in Fig. 1. CaCl2 is added to 100 mM NaCl. Three different values of the relative diffusion coefficients are considered: 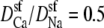 (dotted line), 0.25 (dashed line), and 0.1 (solid line). Density profiles for this channel have been published previously (46).
(dotted line), 0.25 (dashed line), and 0.1 (solid line). Density profiles for this channel have been published previously (46).
Ca2+ versus Ba2+ AMFE
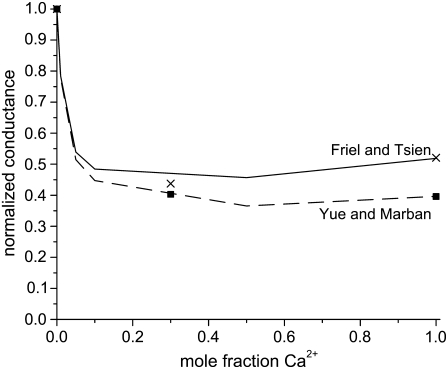
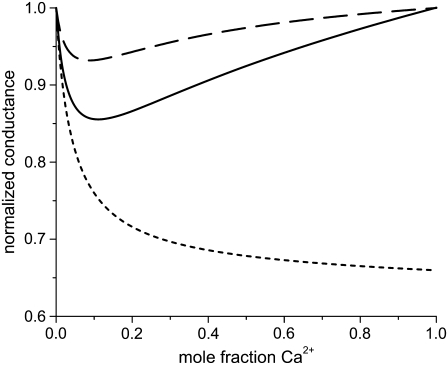
Almers and McCleskey (4) also found an AMFE for mixtures of Ba2+ and Ca2+ in the L-type calcium channel with a classic mole fraction protocol (except that the mixture solutions were only added to the external side of the muscle fiber). [Ba2+] + [Ca2+] was held constant at 10 mM. Almers and McCleskey used whole-cell recordings where gating and permeation cannot be unambiguously separated. Later, Friel and Tsien (54) and Yue and Marban (7) repeated this experiment with single-channel recordings and got conflicting results. Friel and Tsien found an AMFE, but a less pronounced one than Almers and McCleskey. Yue and Marban did not find an AMFE. The difference was attributed to the two groups using channels from different cell types (7). Using our model of the L-type calcium channel we show below that the Ca2+/Ba2+ AMFE depends critically on the ratio of the diffusion coefficients of the two ions: a small variation in this ratio makes or breaks this AMFE.
We simulated this mole fraction experiment in symmetric baths and applied Eq. 7 to compute the AMFE shown in Fig. 7 (lines). The figure shows two curves. The solid line reproduces the experiments of Friel and Tsien (crosses) and the dashed line the experiments of Yue and Marban (squares). We use the same concentration profiles in Eq. 7 to compute both curves. However, each group measured different conductance ratios at mole fraction 1; Friel and Tsien measured 0.53, while Yue and Marban measured 0.4. This required diffusion coefficient ratios 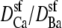 of 0.280 and 0.214 to fit these results at mole fraction 1. The rest of the curve is computed without any adjustable parameters and is essentially a prediction of the model.
of 0.280 and 0.214 to fit these results at mole fraction 1. The rest of the curve is computed without any adjustable parameters and is essentially a prediction of the model.
FIGURE 7.
The Ca2+/Ba2+ AMFE computed from the MC simulations of the model L-type calcium channel. The baths contain mixtures of Ba2+ and Ca2+ so that [Ba2+] + [Ca2+] = 10 mM. The conductances are normalized with the [Ca2+] = 0 conductance. Two different values of the relative diffusion coefficients are considered: 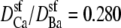 (solid line) and 0.214 (dashed line). These were chose to reproduce the experimental currents in pure Ca2+ measured by Friel and Tsien (54) and Yue and Marban (7). The experimental data of Friel and Tsien (crosses) and Yue and Marban (squares) are shown for comparison.
(solid line) and 0.214 (dashed line). These were chose to reproduce the experimental currents in pure Ca2+ measured by Friel and Tsien (54) and Yue and Marban (7). The experimental data of Friel and Tsien (crosses) and Yue and Marban (squares) are shown for comparison.
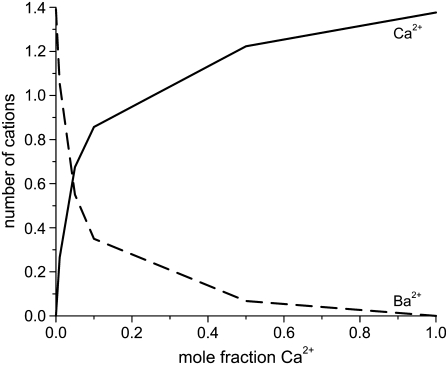
In both cases, we find that <10% Ca2+ dramatically reduces the current, which was found by all three groups (4,7,54). This reduction in current is mirrored by the highly-preferential binding of Ca2+ (i.e., the number of Ca2+ ions in the selectivity filter changes superlinearly with mole fraction). This is shown in Fig. 8. In a mixture of only 10% Ca2+, 75% of the Ba2+ has already been displaced from the selectivity filter. By Eq. 7, it is the reciprocal of each ion concentration that determines its conductance. This is shown in Fig. 9 for this experiment. The preferential binding of Ca2+ causes the reciprocal of the Ca2+ concentration at the center of the pore to saturate by a mole fraction of 0.1. Therefore, the resistance to Ca2+ flow in the center of the pore saturates. In the outer regions of the selectivity filter, the reciprocal of the Ca2+ concentration does not saturate. For Ba2+, the reciprocal of the concentration changes more in the center of pore than in the outer regions. These different characteristics produce the AMFE.
FIGURE 8.
The number of Ca2+ (solid line) and Ba+ (dashed line) in the selectivity filter as a function of Ca2+ mole fraction.
FIGURE 9.
Profiles of the reciprocal concentrations (1/ρi(x)) for (A) Ca2+ and (B) Ba+. The mole fraction of Ca2+ is indicated for each curve.
While the theory reproduces both results, our results do depend on the diffusion coefficient ratio 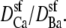 This is expected. In fact, it was a prediction of the analysis in a recent article on AMFEs in wide synthetic nanopores: AMFEs can disappear if the mole fraction 0 and 1 endpoint conductances are too dissimilar (34). This is also discussed in the Appendix.
This is expected. In fact, it was a prediction of the analysis in a recent article on AMFEs in wide synthetic nanopores: AMFEs can disappear if the mole fraction 0 and 1 endpoint conductances are too dissimilar (34). This is also discussed in the Appendix.
The AMFE for Ca2+/Ba2+ mixtures in the L-type channel seems to be on this cusp. Intuitively, the farther apart the endpoint conductances are, the more the current must be depressed to observe an AMFE (34). This is seen in the result of Friel and Tsien (54): there is an AMFE, but it is shallow. Our results suggest that the smaller current ratio of the channel measured by Yue and Marban (7) was enough to make the AMFE too shallow to measure. Such slightly different conductance properties are common in variants of the same channel type from different animal species.
Because this model of the L-type calcium channel has micromolar Ca2+ selectivity (Fig. 4) and because it also reproduces the Ca2+/Ba2+ AMFE curves (excluding the endpoints) without any adjustable parameters (Fig. 7), we conclude that this model holds promise as a model of the L-type channel and should be studied further.
DISCUSSION
Resistors-in-series model
To examine the AMFE, Nonner et al. (36) used numerical solutions of the PNP equations; they showed that localized ion-specific binding could produce an AMFE by creating depletion zones of low ion concentration. Low ion concentration, in turn, corresponds to high resistance to ion flow that limits the overall series conductance. Our analysis confirms their result: depletion of ions in some regions of the channel causes the AMFE in this model because the resistances of each region change differently with mole fraction. The Ca2+/Ba2+ AMFE and the analysis in the Appendix shows, however, that localized binding differences among the ions are not necessary for the AMFE (Fig. 9; and see Fig. 12).
FIGURE 12.
Concentration profiles of the PNP model for (A) Ca2+ and (B) Na+ at zero applied voltage. The mole fraction of Ca2+ for each line is indicated. [Na+] + [Ca2+] = 1 M in both baths.
This article and a recent article on AMFEs in synthetic nanopores (34) have extended this resistors-in-series model by showing that at its most basic level the AMFE reflects the preferential binding of one ion species over another. This interpretation is consistent with experiments where the conductance versus mole fraction curve is not linear, but does not have a minimum (i.e., the curve is monotonic). The analysis in the Appendix shows this, and the dotted line later in Fig. 11 is an example. From such a curve one can infer that the pore preferentially conducts Ca2+ because a small amount of Ca2+ disproportionately moves the conductance toward the pure Ca2+ conductance and away from the pure Na+ conductance. Ca2+ must, of course, be in the pore for it to be conducted. Therefore, a nonlinear, monotonic curve indicates that one species is preferentially bound by the pore, as described previously (58). The analysis in this article then shows that preferential ion binding also produces the minimum in mole fraction experiments. That is, preferential binding causes all nonideal mole fraction behavior, whether there is a minimum or not.
FIGURE 11.
An AMFE computed with one-dimensional PNP where normalized conductance versus the mole fraction of Ca2+ (η) is shown. The selectivity filter is 20 Å long and 8 Å in diameter and connected to the baths by two 10 Å-long conical atria as described previously (28,35). The fixed charge of the protein is a −10 M volume charge in the selectivity filter. In the baths are a mixture of monovalent cation (Na+), divalent cation (Ca2+), and monovalent anion. The total cation concentration [Na+] + [Ca2+] is constant at 1 M. For the solid and dashed lines, the diffusion coefficients were chosen so that at η = 0 and η = 1 the conductances were equal. (Solid line) The diffusion coefficients in the baths are 10 times larger than in the selectivity filter for both Na+ and Ca2+; 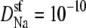 and
and 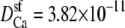 m2/s. (Dotted line) The diffusion coefficients in the baths are 10 times larger than in the selectivity filter for both Na+ and Ca2+ (like for the solid line), but now the diffusion coefficients for Ca2+ were chosen so that there was no AMFE;
m2/s. (Dotted line) The diffusion coefficients in the baths are 10 times larger than in the selectivity filter for both Na+ and Ca2+ (like for the solid line), but now the diffusion coefficients for Ca2+ were chosen so that there was no AMFE; 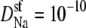 and
and 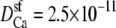 m2/s. (Dashed line) The diffusion coefficients in the baths and selectivity for Ca2+ were the same as for the solid line, but now
m2/s. (Dashed line) The diffusion coefficients in the baths and selectivity for Ca2+ were the same as for the solid line, but now 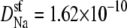 and
and 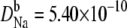 m2/s, so that for Na+ the diffusion coefficients in the baths are only three times larger than in the selectivity filter.
m2/s, so that for Na+ the diffusion coefficients in the baths are only three times larger than in the selectivity filter.
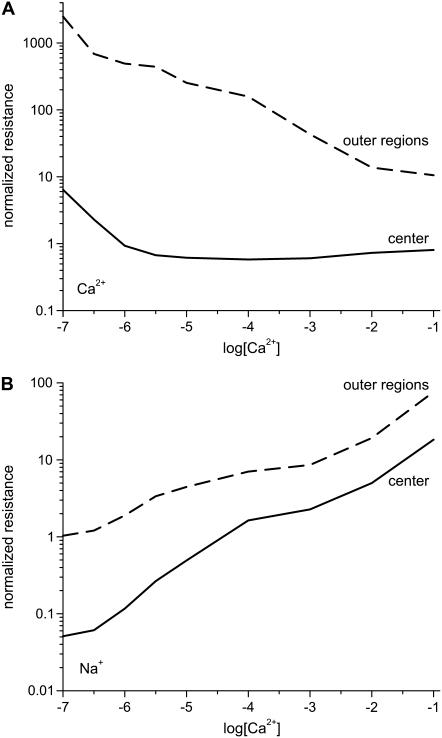
The integrated Nernst-Planck equation (Eqs. 5 and 6) we used here allows us to examine how—because of the preferential ion binding—the resistances of the high- and low-concentration zones change with mole fraction and how these changes produce the AMFE. As a specific example, we consider the block of Na+ current by Ca2+ in our model L-type channel. Fig. 10 shows the resistances of Ca2+ (Fig. 10 A) and Na+ (Fig. 10 B) in the center of the channel (−1 Å < x < 1 Å) (solid lines) and the outer regions of the selectivity filter (1 Å < |x| < 5 Å) (dashed lines). Specifically, the resistances Ri for ion species i are given by
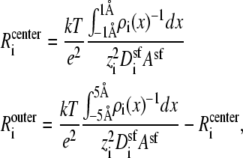 |
(8) |
and the total conductance of the channel g given by Eq. 7 is
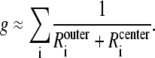 |
(9) |
FIGURE 10.
Normalized resistances of the center (solid line) and outer regions (dashed line) of the model L-type calcium channel (Eq. 8). The resistances are normalized to the full-channel resistance of Na+ with [Ca2+] = 0. (A) Resistances for Ca2+. For the curves shown, 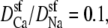 but changing this parameter only moves both curves up or down the log scale by the same constant. (B) Resistances for Na+.
but changing this parameter only moves both curves up or down the log scale by the same constant. (B) Resistances for Na+.
How [Ca2+] changes the ions' resistances in different regions of the channel is hard to predict. Fig. 10 shows that the resistance of Ca2+ in the channel center is constant for [Ca2+] > 3 μM. At the same time, the resistance of Ca2+ in the outer portions of the selectivity filter steadily decreases as [Ca2+] increases. Because Ca2+ tends to accumulate only in the very center of the channel until [Ca2+] becomes large (Fig. 3), the resistance in the outer regions is much larger than in the center (Fig. 10 A, dashed line). Therefore, even though Ca2+ is accumulating in the center of the pore, there is very little Ca2+ current contributing to the total ionic current; the total channel resistance for Ca2+ is dominated by the high resistance of the outer regions. It is not until there is millimolar Ca2+ in the bath that Ca2+ accumulates in the outer regions of the selectivity filter (Fig. 3 D). In that case, the resistances for Ca2+ in the center and the outer regions start to become comparable (Fig. 10 A).
On the other hand, the resistances of Na+ in both regions are both monotonically increasing with [Ca2+] because Ca2+ is displacing Na+ throughout the selectivity filter (Fig. 3). This lowers Na+ concentration, increases Na+ resistance, and decreases Na+ current. The ratio of center to outer region resistances is not nearly as large for Na+ as for Ca2+ because Na+ accumulates more evenly throughout the pore, not just in the center like Ca2+ (Fig. 3). By Eq. 8, these changes in resistances are due to changes in the ion binding within the different regions of the channel.
The liquidlike selectivity filter
The preferential ion binding needed to produce the AMFE requires that one ion species is present in the selectivity filter in a proportion greater than its mole fraction in the bath. This causes the resistance of that ion in the selectivity filter to change more rapidly than in the other regions of the pore. In the model L-type calcium channel described here, the selectivity arises from a balance of electrostatic interactions of ions (permeating cations as well as glutamate oxygens) and excluded-volume effects due to the crowding of many ions into the small selectivity filter—the charge/space competition theory of selectivity (5,32,33,35,44–51,58–61).
The specific pattern of binding and depletion zones is a balance of these physical forces, not chemistry. The center of our selectivity filter is certainly a binding site for cations because of the negative charges of the four glutamates (Fig. 3). But, because the glutamates are flexible, they rearrange to screen the permeating cations. The average positions of the cations and glutamates (e.g., with Ca2+ only in the center and Na+ more uniformly distributed, Fig. 3) are those that balance these forces to bring the system to its lowest free energy. Even for Ca2+ versus Na+ competition, it is not only the electrostatic forces that determine the preferential Ca2+ binding. Ion size also plays an important role (5,62); because the glutamate oxygens accumulate at the edges of the filter at high concentration (32,44,46), Ca2+ is excluded almost completely and Na+ concentration is significantly depressed. Secondary binding sites also appear at the entrance of the filter to screen the still-negative net charge of the filter. (Note that these binding sites are outputs of the simulations, not inputs like in barrier models.) For Ca2+-versus-Ba2+ competition, where the cations have the same charge, both ions are equally attracted to the negatively-charged pore, and ion size is the only thing that determines the preferential Ca2+ binding.
The key to making the binding and depletion zones are three properties of the glutamates: they are closely packed in the permeation pathway; they are flexible; and they take up a substantial amount of space.
Because the glutamates are in the pore lumen, the permeating cations can get closer, sharply reducing the large repulsive energy among the densely-packed glutamates.
Because the glutamates are flexible, they are subject to the same forces as the permeant cations so they rearrange to screen the permeating cations, lowering the energy of the system even more; the glutamates create a liquidlike environment where ions move diffusively.
Because the glutamates take up space, ions must compete for limited space in the selectivity filter. This crowded environment allows the pore to select between ions of the same valence and amplifies divalent versus monovalent selectivity (5,32,33,35,44–51,58–61).
When the glutamates are fixed in place outside of the permeation pathway, then they satisfy none of these properties. In that case, previous studies have shown that the high Ca2+ affinity of the pore disappears (50). Moreover, the Ca2+/Ba2+ AMFE would not be explained because such a model cannot discriminate between ions of the same valence (63) while a crowded selectivity filter with flexible glutamates has a strong preference for Ca2+ (Fig. 8).
The competing forces on the ions inside the liquidlike selectivity filter (with its tethered, but flexible glutamates) must be present in more detailed simulations of this kind of calcium channel. But, by reducing the physics in the model calcium channel to its bare essentials, it is easier to understand how the binding and depletion zones and the AMFE come about.
Criteria for predicting AMFEs in experiments
Both this article and a recent article (34) point to a set of criteria that are necessary to observe an AMFE in experiments:
The channel has different affinities for the ions. The channel should have a relatively high affinity for one ion species over the other. By our analysis, the AMFE is a reflection of differences in ion affinity. We experimentally tested this hypothesis for wide a pore in an earlier article (34). In this article, this is illustrated in Figs. 3, 8, and later in Fig. 13.
The endpoint conductances should be approximately equal. In a classic mole fraction experiment, the conductances at mole fractions 0 and 1 should be approximately equal. In an added-salt experiment, the conductances of no added salt and some high concentration of added salt should be approximately equal. Intuitively, if the endpoint conductances of the graph are far apart, the conductance must be depressed much more than if the endpoints are equal; that is, the AMFE must be much larger to be noticeable. We experimentally verified the relationship between endpoint conductances and AMFE depth in an earlier article (34). In this article, this is illustrated in Figs. 4, 7, and later in Fig. 11 and where different diffusion coefficients produced very different AMFEs—or no AMFE at all—but did not change the affinity of the channel for either ion species.
FIGURE 13.
The number of Ca2+ and Na+ in the pore as a function of Ca2+ mole fraction η computed with the PNP model under the conditions of Fig. 12. The dotted lines are 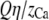 and
and 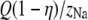 where Q = 6 is the number of negative protein charges in the selectivity filter. If the solid lines were the same as the dotted lines, then the channel would not preferentially select one cation over the other; their proportion in the channel would be the same as in the baths. Here
where Q = 6 is the number of negative protein charges in the selectivity filter. If the solid lines were the same as the dotted lines, then the channel would not preferentially select one cation over the other; their proportion in the channel would be the same as in the baths. Here 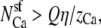 indicating the Ca2+ is preferentially bound by this channel.
indicating the Ca2+ is preferentially bound by this channel.
These two criteria were used to predict the Na+/Cs+ AMFE in RyR (35). Previous studies had shown that highly-charged channels prefer small cations, unless dehydration/resolvation effects are important (44,60,61). Because Na+ is smaller than Cs+ (2 Å in diameter versus 3.4 Å), RyR has a higher affinity for Cs+ than Cs+ (5). Moreover, in 250 mM symmetric baths, the conductance of Na+ is 480 pS and the conductance of Cs+ is 520 pS—almost the same. Therefore, Na+ and Cs+ satisfy both criteria.
Several classic mole fraction experiments had previously been performed on RyR, but no AMFE was found before the Na+/Cs+ AMFE predicted by the RyR model (35). Two of these experiments—which did not produce an AMFE—were Li+ versus K+ (16) and Ca2+ versus Mg2+ (17). In retrospect, neither of these experiments met both of the criteria and therefore now it is possible to see why they did not produce an AMFE. For example, Li+ is smaller than K+ (1.33 Å in diameter vs. 2.76 Å) and therefore RyR has a higher affinity for Li+ (5). However, in 250 mM symmetric baths, the conductance of Li+ is 200 pS and the conductance of K+ is 800 pS—a fourfold difference. Therefore, to observe an AMFE, Li+ would have had to reduce conductance by >75%. In comparison, Na+ reduces current ∼10% in Na+/Cs+ mixtures. For Ca2+ versus Mg2+ the situation is reversed: the conductances of RyR in pure Ca2+ and Mg2+ are very similar, but RyR does not preferentially select one over the other.
CONCLUSION
The textbook theory of the AMFE describes multiple ions moving through a channel by jumping over static energy barriers. The channel is narrow so that ions move through in a single file and the ions' motions are correlated; one ion cannot move to the next well until the ion occupying that well leaves (2,6). If all the assumptions are true, this model produces an AMFE. The validity of barrier models is, however, a matter of debate since they do not include the physics known to occur in electrolytes in confining geometries (19–29).
The resistors-in-series model is an alternative mechanism that reproduces a substantial amount of experimental AMFE data (5,34,35). Here, we have shown this not only with our model calcium channel, but also with a 10 Å-wide version of the same pore and a mathematical analysis. The combination of the charge/space competition model of ion binding and a diffusive NP model of ion current are fundamentally different than the hopping mechanism. The charge/space competition model of ion binding computes how the barriers and wells change with mole fraction based on the physics of confined electrolytes. In turn, these local changes in ion binding change the local resistance to ion current, producing the AMFE.
The binding of ions in the pore is a balance of electrostatic attraction of cations into the negatively-charged pore and the space that they take up in the crowded selectivity filter. In this sense, the ions' average positions in the pore are correlated because they cannot overlap. This kind of position correlation determines the binding and depletion zones. In the resistors-in-series model, the ions are not momentum-correlated, however; the NP equation does not conserve momentum so one ion gaining or losing velocity from another ion cannot be the root cause of current in the NP approach.
Most importantly, the AMFE in the resistors-in-series model also does not a priori require single filing of ions; single-filing is an output of our simulations. While we cannot explicitly rule out single-filing in the 7 Å wide model L-type calcium channel presented here, the same theory explains the AMFE in several cases where ions can pass each other. These include 50 Å-wide synthetic nanopores (34); a 10 Å-wide, non-single-filing version of our model pore (Fig. 6); models with point-charge ions (Appendix and (36)); and models where radial homogeneity was assumed (5,28,35).
In light of these results, an AMFE should not immediately be interpreted as implying that multiple ions move through the pore in a single file. The resistors-in-series model implies that it reflects the preferential binding of one ion species over another.
Acknowledgments
The authors are grateful to Bob Eisenberg for helpful discussions and pointing us to relevant literature. Other useful comments on the manuscript from Wolfgang Nonner are also gratefully acknowledged. The authors thank Prof. Michael Fill (Rush University Medical Center) for making the experimental data shown in Fig. 2 available.
The authors were supported through National Institutes of Health grant No. GM076013 (Robert Eisenberg, PI). D.G. was also supported by National Institutes of Health grant No. AR054098 (Michael Fill, PI). D.B. was also supported by the Hungarian National Research Fund (OTKA grant No. K63322).
APPENDIX: A SIMPLIFIED MODEL TO ILLUSTRATE IDEAS
In this Appendix, we do a mathematical analysis of a simple PNP model with point-charge ions. In the main text we model ions more realistically with Pauling radii, but the point-charge model is amenable to mathematics so that the root of the AMFE for this model can be understood with explicit equations.
We consider a very simple cation-selective channel: a long pore (e.g., 20 Å) with a region of large, uniform, negative space charge (e.g., −10 M) to represent the negatively-charged amino acids of the channel protein. The ions are modeled as point charges moving in the electrostatic mean-field (i.e., modeled with regular PNP) so that they can easily pass each other. Because the pore is long, in the center of the pore the negative protein charge is neutralized by the permeant cations. This simplification allows us to analyze the AMFE in this example. A short selectivity filter without charge neutrality is considered in the main text with the model L-type calcium channel.
Classic mole fraction experiment in the simplified model
Fig. 11 (solid line) shows that this model exhibits an AMFE. The relative diffusion coefficients of the cations have been chosen so that both of their conductances are equal in pure NaCl and CaCl2 solutions; if the endpoint conductances are sufficiently different, there is no AMFE (Fig. 11, dotted line). In the analysis that follows, we assume equal endpoint conductances to simplify the algebra.
Fig. 12 shows the concentration profiles of the monovalent cations (call them Na+) and the divalent cations (call them Ca2+) at different mole fractions (0%, 2%, 10%, 50%, and 100% Ca2+) in a classic mole fraction experiment. With zero applied voltage, the concentration profiles have a plateau in the pore, a simplification that can be used in Eq. 5 to understand the origin of the AMFE. Specifically, we assume that each profile is piecewise constant with values 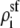 in the selectivity filter of the channel and the bath concentration
in the selectivity filter of the channel and the bath concentration 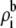 elsewhere. We assume that the anion does not contribute to the current. Briefly we note that the “localized ion-specific binding” of Nonner et al. (36) is not required for the AMFE. In this example (and with the Ca2+ versus Ba2+ AMFE), both ion species bind to the same region of the pore and there is no local binding.
elsewhere. We assume that the anion does not contribute to the current. Briefly we note that the “localized ion-specific binding” of Nonner et al. (36) is not required for the AMFE. In this example (and with the Ca2+ versus Ba2+ AMFE), both ion species bind to the same region of the pore and there is no local binding.
The integral for each ion species i in Eq. 6 is an electrical resistance. In this simplified example, the resistance integral can be divided into the resistance from the selectivity filter and the rest of the system (i.e., everything but the selectivity filter); these regions are (generally non-Ohmic) resistors in series,
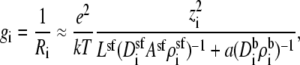 |
(10) |
where Lsf and Asf are the length and area of the narrow part of the selectivity filter, respectively (20 Å and 50.24 Å2 in this example). Also,
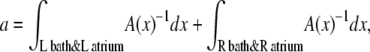 |
(11) |
where the integrals are over the entire system except the selectivity filter itself (i.e., both baths and atria connecting the baths to the channel). We have also used that the diffusion coefficient and concentration of species i take one value in the selectivity filter (superscript sf) and another in the baths (superscript b). The cross-sectional area of the selectivity filter was taken as the constant Asf.
Equation 10 already reveals one origin of the AMFE: the resistance of the atria and baths. If the channel atria and baths are neglected by assuming that they have a much lower resistance than the selectivity filter—a common simplifying assumption (58)—then the assumption that Na+ and Ca2+ have the same conductance when they are the only cations means that 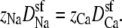 Since the selectivity filter is charge-neutral in this particular example, we have
Since the selectivity filter is charge-neutral in this particular example, we have
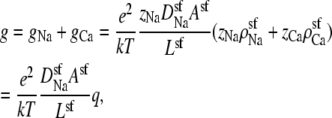 |
(12) |
where –q is the negative protein charge concentration in the selectivity filter (−10 M in this example). Equation 12 then states that g is constant for all mole fractions since all of the parameters in it are constants. That is, neglecting the resistances of the atria and baths in the analysis cannot produce an AMFE. Next we show that including these atrial and bath resistances in the analysis does produce an AMFE—but only if the pore preferentially binds one ion species over the other.
If the mole fraction of Ca2+ in the baths is η, then 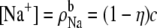 and
and 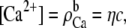 where c is the fixed bath concentration [Na+] + [Ca2+]. In the simplified channel considered in this example,
where c is the fixed bath concentration [Na+] + [Ca2+]. In the simplified channel considered in this example,
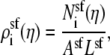 |
(13) |
where 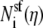 is the number of ion of species i in the pore as the Ca2+ mole fraction η changes. Asf Lsf is the volume of the selectivity filter. This approximation is only possible because, in this particular example, the ion concentrations are approximately constant in the selectivity filter (Fig. 12); it is not true in general and not true for the model L-type channel in the main text (Fig. 3). Then the channel conductance as a function of Ca2+ mole fraction η (Eq. 10) can be written as
is the number of ion of species i in the pore as the Ca2+ mole fraction η changes. Asf Lsf is the volume of the selectivity filter. This approximation is only possible because, in this particular example, the ion concentrations are approximately constant in the selectivity filter (Fig. 12); it is not true in general and not true for the model L-type channel in the main text (Fig. 3). Then the channel conductance as a function of Ca2+ mole fraction η (Eq. 10) can be written as
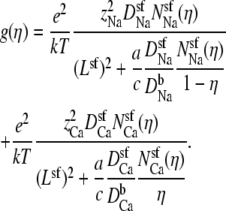 |
(14) |
First, we consider the case where the channel does not have a higher affinity for one cation than the other. Then the number of ions in the pore is proportional to its bath concentration: 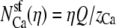 and
and 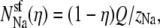 where Q is the number of negative protein charges in the selectivity filter (six, in this example). Then,
where Q is the number of negative protein charges in the selectivity filter (six, in this example). Then,
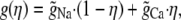 |
(15) |
where
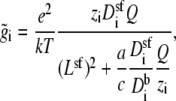 |
(16) |
so that g is a linear function of η. Because the conductances with η = 0 and η = 1 are equal (that is, 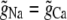 ), g is actually constant as η is varied. There is no AMFE if the channel does not preferentially select one ion species over the other.
), g is actually constant as η is varied. There is no AMFE if the channel does not preferentially select one ion species over the other.
With some algebra it is also possible to show that g has a minimum if Ca2+ preferentially displaces Na+ from the selectivity filter with increasing Ca2+ mole fraction η (i.e., if 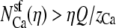 ). The preferential selectivity of Ca2+ over Na+ (Fig. 13)—in combination with the atrial resistances—produces the AMFE seen in Fig. 11. A similar analysis for this channel with two cations with the same valence gives the same result: an AMFE occurs (i.e., g has a minimum) if and only if one of the cation species is preferentially selected by the channel and the atrial resistances are considered in the analysis.
). The preferential selectivity of Ca2+ over Na+ (Fig. 13)—in combination with the atrial resistances—produces the AMFE seen in Fig. 11. A similar analysis for this channel with two cations with the same valence gives the same result: an AMFE occurs (i.e., g has a minimum) if and only if one of the cation species is preferentially selected by the channel and the atrial resistances are considered in the analysis.
Nonner et al. (36) noted that in their analysis an AMFE occurred even if one ion species is repelled from some portion of the pore (36). This result is consistent with our findings. Suppose that ion species X has mole fraction η in the bath. Preferential selectivity of X means that 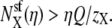 Charge neutrality in the selectivity filter implies that
Charge neutrality in the selectivity filter implies that 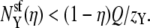 If X is now repelled from the pore so that
If X is now repelled from the pore so that 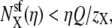 then
then 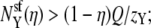 Y is now the preferentially selected species. In general, it is only the difference in repulsion between the two species that is important (5), and it is the least repelled ion that is preferentially selected.
Y is now the preferentially selected species. In general, it is only the difference in repulsion between the two species that is important (5), and it is the least repelled ion that is preferentially selected.
Several aspects of the AMFE are revealed by this example that we also found in the more complex system we analyzed in the main text:
The presence of an AMFE reflects the preferential selectivity of the channel for one of the cations.
The AMFE involves the resistances of all regions within the channel and how they change with mole fraction. In a highly-charged pore like in those considered in this article, the selectivity filter may be the region where the flux is limited so that
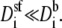 However, the pore's high charge makes
However, the pore's high charge makes 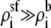 to counteract the disparity in the diffusion coefficients (Eq. 10). This makes the resistance of the channel access regions of comparable size to that of the selectivity filter. While the selectivity filter still has the highest resistance, the resistance of the access regions is not so much less that they can be ignored. The resistances of each region varies with mole fraction differently, producing the AMFE. In this particular simplified example, the access region resistance change was proportional to
to counteract the disparity in the diffusion coefficients (Eq. 10). This makes the resistance of the channel access regions of comparable size to that of the selectivity filter. While the selectivity filter still has the highest resistance, the resistance of the access regions is not so much less that they can be ignored. The resistances of each region varies with mole fraction differently, producing the AMFE. In this particular simplified example, the access region resistance change was proportional to 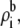 while the selectivity filter resistance was buffered by the protein charge in the selectivity filter (Eq. 10).
while the selectivity filter resistance was buffered by the protein charge in the selectivity filter (Eq. 10).The channel geometry and the ion diffusion coefficients are important contributors to the resistance of each channel region (see Eq. 6). As pointed out by Nonner et al. (36), the diffusion coefficients cannot, by themselves, cause the AMFE. This is because, in equilibrium, the diffusion coefficients do not determine ion binding, the origin of the AMFE; when Ji = 0 for all species in Eq. 2, the diffusion coefficients divide out. The depth of the AMFE, however, depends on the geometry and diffusion coefficients, as illustrated in Fig. 10 (dashed line). There the resistance of the selectivity filter to Na+ has been reduced with a larger diffusion coefficient, reducing the depth of the AMFE. Therefore, the depth of the AMFE is not an indicator of how much the channel selects one ion species over another by binding. This idea has been verified experimentally (34).
Added-salt experiment in the simplified model
The analysis described above can also be applied to the added-salt version of the mole fraction experiment. When [Na+] is constant and [Ca2+] is increased from 0, Eq. 14 becomes
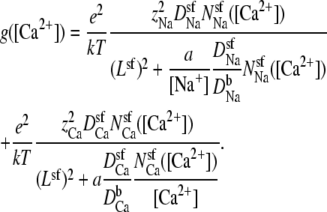 |
(17) |
It is straightforward to show that g can only decrease if 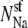 decreases as [Ca2+] increases; that is, observing an AMFE means that the Ca2+ is displacing the Na+. The converse is not true, however: the absence of an AMFE does not imply that Na+ is not being displaced; gNa may decrease, but increasing [Ca2+] always increases gCa, possibly enough to make the total conductance (g = gNa + gCa) increase as [Ca2+] increases. Only when the AMFE is actually present can conclusions be drawn: an AMFE in the added-salt experiment—like the classic mole fraction experiment—reflects a preferential binding of one ion species over the other.
decreases as [Ca2+] increases; that is, observing an AMFE means that the Ca2+ is displacing the Na+. The converse is not true, however: the absence of an AMFE does not imply that Na+ is not being displaced; gNa may decrease, but increasing [Ca2+] always increases gCa, possibly enough to make the total conductance (g = gNa + gCa) increase as [Ca2+] increases. Only when the AMFE is actually present can conclusions be drawn: an AMFE in the added-salt experiment—like the classic mole fraction experiment—reflects a preferential binding of one ion species over the other.
Editor: Ron Elber.
References
- 1.Takeuchi, A., and N. Takeuchi. 1971. Anion interaction at the inhibitory post-synaptic membrane of the crayfish neuromuscular junction. J. Physiol. 212:337–351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hille, B. 2001. Ion Channels of Excitable Membranes. Sinauer, Sunderland, MA.
- 3.Almers, W., E. W. McCleskey, and P. T. Palade. 1984. A non-selective cation conductance in frog muscle membrane blocked by micromolar external calcium ions. J. Physiol. 353:565–583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Almers, W., and E. W. McCleskey. 1984. Non-selective conductance in calcium channels of frog muscle: calcium selectivity in a single-file pore. J. Physiol. 353:585–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gillespie, D. 2008. Energetics of divalent selectivity in a calcium channel: the ryanodine receptor case study. Biophys. J. 94:1169–1184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hille, B., and W. Schwarz. 1978. Potassium channels as multi-ion single-file pores. J. Gen. Physiol. 72:409–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Yue, D. T., and E. Marban. 1990. Permeation in the dihydropyridine-sensitive calcium channel. Multi-ion occupancy but no anomalous mole-fraction effect between Ba2+ and Ca2+. J. Gen. Physiol. 95:911–939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mironov, S. L. 1992. Conformational model for ion permeation in membrane channels: a comparison with multi-ion models and applications to calcium channel permeability. Biophys. J. 63:485–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ravindran, A., H. Kwiecinski, O. Alvarez, G. Eisenman, and E. Moczydlowski. 1992. Modeling ion permeation through batrachotoxin-modified Na+ channels from rat skeletal muscle with a multi-ion pore. Biophys. J. 61:494–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tabcharani, J. A., J. M. Rommens, Y. X. Hou, X. B. Chang, L. C. Tsui, J. R. Riordan, and J. W. Hanrahan. 1993. Multi-ion pore behavior in the CFTR chloride channel. Nature. 366:79–82. [DOI] [PubMed] [Google Scholar]
- 11.Sabovcik, R., J. Li, P. Kucera, and B. Prod'hom. 1995. Permeation properties of a Ca2+-blockable monovalent cation channel in the ectoderm of the chick embryo: pore size and multioccupancy probed with organic cations and Ca2+. J. Gen. Physiol. 106:149–174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ismailov, I. I., V. G. Shlyonsky, O. Alvarez, and D. J. Benos. 1997. Cation permeability of a cloned rat epithelial amiloride-sensitive Na+ channel. J. Physiol. 504:287–300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Linsdell, P., J. A. Tabcharani, and J. W. Hanrahan. 1997. Multi-ion mechanism for ion permeation and block in the cystic fibrosis transmembrane conductance regulator chloride channel. J. Gen. Physiol. 110:365–377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Qu, Z., and H. C. Hartzell. 2000. Anion permeation in Ca2+-activated Cl− channels. J. Gen. Physiol. 116:825–844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Winters, C. J., and T. E. Andreoli. 2002. Cl channels in basolateral TAL membranes. XVII. Kinetic properties of mcClC-Ka, a basolateral CTAL Cl− channel. J. Membr. Biol. 186:159–164. [DOI] [PubMed] [Google Scholar]
- 16.Lindsay, A. R., S. D. Manning, and A. J. Williams. 1991. Monovalent cation conductance in the ryanodine receptor-channel of sheep cardiac muscle sarcoplasmic reticulum. J. Physiol. 439:463–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tinker, A., and A. J. Williams. 1992. Divalent cation conduction in the ryanodine receptor channel of sheep cardiac muscle sarcoplasmic reticulum. J. Gen. Physiol. 100:479–493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sather, W. A., and E. W. McCleskey. 2003. Permeation and selectivity in calcium channels. Annu. Rev. Physiol. 65:133–159. [DOI] [PubMed] [Google Scholar]
- 19.Cooper, K., E. Jakobsson, and P. Wolynes. 1985. The theory of ion transport through membrane channels. Prog. Biophys. Mol. Biol. 46:51–96. [DOI] [PubMed] [Google Scholar]
- 20.Cooper, K. E., P. Y. Gates, and R. S. Eisenberg. 1988. Diffusion theory and discrete rate constants in ion permeation. J. Membr. Biol. 106:95–105. [DOI] [PubMed] [Google Scholar]
- 21.Cooper, K. E., P. Y. Gates, and R. S. Eisenberg. 1988. Surmounting barriers in ionic channels. Q. Rev. Biophys. 21:331–364. [DOI] [PubMed] [Google Scholar]
- 22.Eisenberg, R. S. 1996. Computing the field in proteins and channels. J. Membr. Biol. 150:1–25. [DOI] [PubMed] [Google Scholar]
- 23.Eisenberg, R. S. 1996. Atomic biology, electrostatics and ionic channels. In New Developments and Theoretical Studies of Proteins. R. Elber, editor. World Scientific. Philadelphia, PA.
- 24.Eisenberg, R. S. 1999. From structure to function in open ionic channels. J. Membr. Biol. 171:1–24. [DOI] [PubMed] [Google Scholar]
- 25.Hänggi, P., P. Talkner, and M. Borokovec. 1990. Reaction-rate theory: fifty years after Kramers. Rev. Mod. Phys. 62:251–341. [Google Scholar]
- 26.Eisenberg, R. S., M. M. Kłosek, and Z. Schuss. 1995. Diffusion as a chemical reaction: stochastic trajectories between fixed concentrations. J. Chem. Phys. 102:1767–1780. [Google Scholar]
- 27.Chen, D., L. Xu, A. Tripathy, G. Meissner, and B. Eisenberg. 1997. Permeation through the calcium release channel of cardiac muscle. Biophys. J. 73:1337–1354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Nonner, W., and B. Eisenberg. 1998. Ion permeation and glutamate residues linked by Poisson-Nernst-Planck theory in L-type calcium channels. Biophys. J. 75:1287–1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nonner, W., D. P. Chen, and B. Eisenberg. 1999. Progress and prospects in permeation. J. Gen. Physiol. 113:773–782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chung, S.-H., T. W. Allen, M. Hoyles, and S. Kuyucak. 1999. Permeation of ions across the potassium channel: Brownian dynamics studies. Biophys. J. 77:2517–2533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Corry, B., T. W. Allen, S. Kuyucak, and S.-H. Chung. 2001. Mechanisms of permeation and selectivity in calcium channels. Biophys. J. 80:195–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Boda, D., M. Valiskó, B. Eisenberg, W. Nonner, D. J. Henderson, and D. Gillespie. 2006. The effect of protein dielectric coefficient on the ionic selectivity of a calcium channel. J. Chem. Phys. 125:034901. [DOI] [PubMed] [Google Scholar]
- 33.Boda, D., W. Nonner, M. Valisko, D. Henderson, B. Eisenberg, and D. Gillespie. 2007. Steric selectivity in Na channels arising from protein polarization and mobile side chains. Biophys. J. 93:1960–1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gillespie, D., D. Boda, Y. He, P. Apel, and Z. S. Siwy. 2008. Synthetic nanopores as a test case for ion channel theories: the anomalous mole fraction effect without single filling. Biophys. J. 95:609–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gillespie, D., L. Xu, Y. Wang, and G. Meissner. 2005. (De)constructing the ryanodine receptor: modeling ion permeation and selectivity of the calcium release channel. J. Phys. Chem. B. 109:15598–15610. [DOI] [PubMed] [Google Scholar]
- 36.Nonner, W., D. P. Chen, and B. Eisenberg. 1998. Anomalous mole fraction effect, electrostatics, and binding in ionic channels. Biophys. J. 74:2327–2334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Yang, J., P. T. Ellinor, W. A. Sather, J.-F. Zhang, and R. Tsien. 1993. Molecular determinants of Ca2+ selectivity and ion permeation in L-type Ca2+ channels. Nature. 366:158–161. [DOI] [PubMed] [Google Scholar]
- 38.Ellinor, P. T., J. Yang, W. A. Sather, J.-F. Zhang, and R. Tsien. 1995. Ca2+ channel selectivity at a single locus for high-affinity Ca2+ interactions. Neuron. 15:1121–1132. [DOI] [PubMed] [Google Scholar]
- 39.Gao, L., D. Balshaw, L. Xu, A. Tripathy, C. Xin, and G. Meissner. 2000. Evidence for a role of the lumenal M3–M4 loop in skeletal muscle Ca2+ release channel (ryanodine receptor) activity and conductance. Biophys. J. 79:828–840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wang, Y., L. Xu, D. A. Pasek, D. Gillespie, and G. Meissner. 2005. Probing the role of negatively charged amino acid residues in ion permeation of skeletal muscle ryanodine receptor. Biophys. J. 89:256–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Xu, L., Y. Wang, D. Gillespie, and G. Meissner. 2006. Two rings of negative charges in the cytosolic vestibule of type-1 ryanodine receptor modulate ion fluxes. Biophys. J. 90:443–453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gillespie, D. 1999. A Singular Perturbation Analysis of the Poisson-Nernst-Planck system: Applications to Ionic Channels. Rush University, Chicago, Illinois. [DOI] [PMC free article] [PubMed]
- 43.Gillespie, D., W. Nonner, and R. S. Eisenberg. 2002. Coupling Poisson-Nernst-Planck and density functional theory to calculate ion flux. J. Phys. Condens. Matter. 14:12129–12145. [Google Scholar]
- 44.Boda, D., D. Henderson, and D. D. Busath. 2002. Monte Carlo study of the selectivity of calcium channels: improved geometry. Mol. Phys. 100:2361–2368. [Google Scholar]
- 45.Boda, D., D. Busath, B. Eisenberg, D. J. Henderson, and W. Nonner. 2002. Monte Carlo simulations of ion selectivity in a biological Na+ channel: charge-space competition. Phys. Chem. Chem. Phys. 4:5154–5160. [Google Scholar]
- 46.Boda, D., M. Valiskó, B. Eisenberg, W. Nonner, D. J. Henderson, and D. Gillespie. 2007. Combined effect of pore radius and protein dielectric coefficient on the selectivity of a calcium channel. Phys. Rev. Lett. 98:168102. [DOI] [PubMed] [Google Scholar]
- 47.Nonner, W., D. Gillespie, D. J. Henderson, and B. Eisenberg. 2001. Ion accumulation in a biological calcium channel: effects of solvent and confining pressure. J. Phys. Chem. B. 105:6427–6436. [Google Scholar]
- 48.Miedema, H., M. Vrouenraets, J. Wierenga, D. Gillespie, B. Eisenberg, W. Meijberg, and W. Nonner. 2006. Ca2+ selectivity of a chemically modified OmpF with reduced pore volume. Biophys. J. 91:4392–4400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Nonner, W., L. Catacuzzeno, and B. Eisenberg. 2000. Binding and selectivity in L-type calcium channels: a mean spherical approximation. Biophys. J. 79:1976–1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Boda, D., W. Nonner, D. Henderson, B. Eisenberg, and D. Gillespie. 2008. Volume exclusion in calcium selective channels. Biophys. J. 94:3486–3496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Miedema, H., A. Meter-Arkema, J. Wierenga, J. Tang, B. Eisenberg, W. Nonner, H. Hektor, D. Gillespie, and W. Meijberg. 2004. Permeation properties of an engineered bacterial OmpF porin containing the EEEE-locus of Ca2+ channels. Biophys. J. 87:3137–3147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Corry, B., S. Kuyucak, and S.-H. Chung. 2000. Tests of Continuum theories as models of ion channels. II. Poisson-Nernst-Planck theory versus Brownian dynamics. Biophys. J. 78:2364–2381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Waisman, E., and J. L. Lebowitz. 1970. Exact solution of an integral equation for the structure of a primitive model of an electrolyte. J. Chem. Phys. 52:4307–4309. [Google Scholar]
- 54.Friel, D. D., and R. W. Tsien. 1989. Voltage-gated calcium channels: direct observation of the anomalous mole fraction effect at the single-channel level. Proc. Natl. Acad. Sci. USA. 86:5207–5211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Chen, D., L. Xu, B. Eisenberg, and G. Meissner. 2003. Calcium ion permeation through the calcium release channel (ryanodine receptor) of cardiac muscle. J. Phys. Chem. B. 107:9139–9145. [Google Scholar]
- 56.Berry, S. R., S. A. Rice, and J. Ross. 2000. Physical Chemistry. Oxford, New York.
- 57.Lundstrom, M. 2000. Fundamentals of Carrier Transport. Cambridge University Press, New York.
- 58.Gillespie, D., and R. S. Eisenberg. 2002. Physical descriptions of experimental selectivity measurements in ion channels. Eur. Biophys. J. 31:454–466. [DOI] [PubMed] [Google Scholar]
- 59.Eisenberg, B. 2003. Proteins, channels and crowded ions. Biophys. Chem. 100:507–517. [DOI] [PubMed] [Google Scholar]
- 60.Boda, D., D. D. Busath, D. J. Henderson, and S. Sokolowski. 2000. Monte Carlo simulations of the mechanism of channel selectivity: the competition between volume exclusion and charge neutrality. J. Phys. Chem. B. 104:8903–8910. [Google Scholar]
- 61.Boda, D., D. Henderson, and D. D. Busath. 2001. Monte Carlo study of the effect of ion and channel size on the selectivity of a model calcium channel. J. Phys. Chem. B. 105:11574–11577. [Google Scholar]
- 62.Valiskó, M., D. Boda, and D. Gillespie. 2007. Selective adsorption of ions with different diameter and valence at highly-charged interfaces. J. Phys. Chem. C. 111:15575–15585. [Google Scholar]
- 63.Corry, B., T. Vora, and S.-H. Chung. 2005. Electrostatic basis of valence selectivity in cationic channels. Biochim. Biophys. Acta Biomembr. 1711:72–86. [DOI] [PubMed] [Google Scholar]