Cylindrical Illumination Confocal Spectroscopy: Rectifying the Limitations of Confocal Single Molecule Spectroscopy through One-Dimensional Beam Shaping

Abstract

Cylindrical illumination confocal spectroscopy (CICS) is a new implementation of single molecule detection that can be generically incorporated into any microfluidic system and allows highly quantitative and accurate analysis of single fluorescent molecules. Through theoretical modeling of confocal optics and Monte Carlo simulations, one-dimensional beam shaping is used to create a highly uniform sheet-like observation volume that enables the detection of digital fluorescence bursts while retaining single fluorophore sensitivity. First, we theoretically show that when used to detect single molecules in a microchannel, CICS can be optimized to obtain near 100% mass detection efficiency, <10% relative SD in burst heights, and a high signal/noise ratio. As a result, CICS is far less sensitive to thresholding artifacts than traditional single molecule detection and significantly more accurate at determining both burst rate and burst parameters. CICS is then experimentally implemented, optically characterized, and integrated into separate two microfluidic devices for the analysis of fluorescently stained plasmid DNA and single Cy5 labeled oligonucleotides. CICS rectifies the limitations of traditional confocal spectroscopy-based single molecule detection without the significant operational complications of competing technologies.

INTRODUCTION

Single molecule detection (SMD) allows the study of molecular properties without the bias of ensemble averaging. Although methods using scanning probe, resonant, and electrical sensors are being developed (1), it can also be performed using confocal spectroscopy, an optical detection method in which a collimated laser beam is focused into a diffraction-limited spot ∼1 fL in volume and used to excite single fluorescent molecules. Although biomolecules are often tethered to solid substrates for in depth study of molecular dynamics, continuous flow systems offer higher throughput and are the preferred embodiment for quantitative applications. From herein, SMD will refer to confocal spectroscopy of molecules in free solution under continuous flow. SMD is ideally suited as a platform for the detection of rare biomolecules such as nucleic acids (2–5), proteins, and small ligands (6), the characterization of biomolecular interactions and molecular processes (7,8), DNA sizing (9), and pathogen detection (10).

Although in principle, SMD can be highly quantitative, its current implementations limit its accuracy, throughput, and practical applicability. The minute size of the SMD observation volume enables high signal/noise ratio detection of even single fluorescent molecules due to highly suppressed background levels. However, the diffraction-limited observation volume that enables SMD also significantly hampers its application in quantification and burst parameter determination. Because the observation volume in standard SMD is typically much smaller than the channel used for molecular transport, a condition of low mass detection efficiency is created where the large majority of molecules escape detection. We define the mass detection efficiency as the total proportion of molecules flowing through the channel that are detected. These mass detection efficiencies are usually 1% or less (11). For example, assuming that 1), all molecules passing within the observation volume are detected; 2), a radially symmetric, ellipsoidal, confocal observation volume with 1/e² radii of 0.5 × 1 μm; and 3), detection within a 100 μm ID microcapillary, the resultant mass detection efficiency would be <0.05%. This necessitates extended data acquisition times and increased sample volumes for the detection of rare molecules (12). In addition, because the observation volume profile is Gaussian in shape and highly nonuniform, a molecule's specific trajectory through the detection region will have a large influence on the emitted and collected fluorescence bursts, adding significant variability and uncertainty to not only the burst parameters but also their rate of detection.

The majority of approaches to rectify these short-comings have centered around controlling molecular trajectory using either hydrodynamic (13,14) or electrokinetic (11,12,15) forces as well as nanochannel confinement (16–18). These approaches have limitations in their practical application due to effectiveness, throughput limitations, and ease of use. We report a confocal spectroscopy platform that enables highly quantitative, continuous flow, single molecule analysis with high uniformity and high mass detection efficiency called cylindrical illumination confocal spectroscopy (CICS). CICS is designed to be a highly sensitive and high throughput detection method that can be generically integrated into all microfluidic systems without additional microfluidic components.

Rather than use a minute, diffraction limited point, CICS uses a sheet-like observation volume that can entirely span the cross section of a microchannel. It is created through the one-dimensional (1-D) expansion of a standard diffraction-limited detection volume from ∼0.5 fL to 3.5 fL using a cylindrical lens. Large observation volume expansions in three dimensions (3-D) (>100× increase in volume) have been carried out previously to directly increase mass detection efficiency and to decrease detection variability by reducing the effects of molecular trajectory (4,9,19–21) However, these approaches often still require molecular focusing and/or unnecessarily compromise sensitivity because observation volume expansion in the direction of molecular travel is superfluous. For example, much pioneering work has been carried out by Goodwin et al. in reducing detection variability through a combination of 3-D observation volume expansion (1 pL) and hydrodynamic focusing (9,21). Although highly sensitive and uniform, these flow cytometry based methods use an orthogonal excitation scheme that is ill suited to incorporation with microfluidic systems. Chou et al. (20), on the other hand, have carried out a 3-D observation volume expansion to increase uniformity in an epi-fluorescent format for DNA sizing in a polydimethylsiloxane (PDMS) microfluidic device. The large size of the observation volume (375 fL) reduces signal/noise ratio and limits sensitivity to the detection of large DNA fragments (>1 kbp). Rather than a large 3-D expansion, a smaller 1-D expansion can be used to increase mass detection efficiency and increase detection uniformity while having a reduced effect on signal/noise ratio and detection sensitivity. One-dimensional beam shaping using cylindrical lenses has been applied recently in selective plane illumination microscopy (22), confocal line scan imaging (23), imaging-based detection of DNA (24), and fluorescence detection of electrophoretically separated proteins (25) but has not been explored thoroughly in SMD. We present CICS as a confocal SMD method in which the trade-off between observation volume size, signal/noise ratio, detection uniformity, and mass detection efficiency can be easily modeled and optimized through 1-D beam shaping.

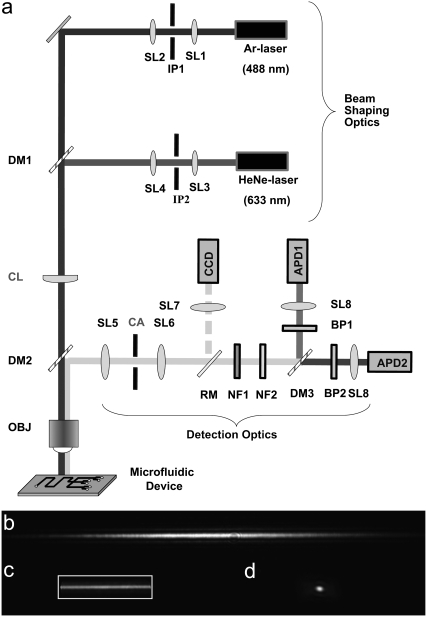
As depicted in Fig. 1 a, high signal/noise detection is enabled by the combination of a cylindrical lens with a novel, microfabricated confocal aperture. The cylindrical lens is used to expand the illumination volume laterally in 1-D (along the x direction or width) while remaining diffraction is limited in the y direction to maximize signal/noise ratio (Fig. 1 b). A confocal aperture is used to limit light collection to only the center section of the illumination volume (Fig. 1 c). The microfabricated confocal aperture is neither round nor slit-like as in typical SMD but is rectangular and mimics the shape of the CICS observation volume. Whereas typical pinholes are nominally sized to the 1/e² radius of the diffraction limited illumination volume (26), the CICS aperture is designed to occlude a much larger proportion of the illumination volume; <30% of the illumination volume in the x direction is allowed to pass, such that a uniform, sheet-like observation volume is created. The final CICS observation volume is designed to be slightly larger than the accompanying microchannel to span the entire cross section for uniform detection with near 100% mass detection efficiency, rectifying the limitations of traditional SMD without the drawbacks of molecular focusing or nanochannel confinement. This enables the resultant fluorescence bursts to not only be discrete but also so uniform they become digital in nature, ensuring accurate and robust quantification analysis.

FIGURE 1.

(a) Schematic diagram of the key optical components in the CICS system. Reflected images of the illumination volume in (b) CICS with no aperture, (c) CICS after the 620 × 115 μm rectangular aperture, and (d) standard SMD with no pinhole. The standard SMD illumination volume resembles a football that extends in and out of the plane of the page whereas the CICS observation volume resembles an elongated sheet or plane that also extends in and out of the page. The CICS observation volume is expanded in 1-D using a cylindrical lens (CL) and then filtered using a rectangular aperture (CA). In the absence of a confocal aperture in b, the CICS illumination profile is roughly Gaussian in shape along the x, y, and z axis, chosen to align with the width, length, and height of a microchannel, respectively. The addition of the confocal aperture in c, depicted as a rectangular outline, allows collection of fluorescence from only the uniform center section of the illumination volume. Abbreviations: APD, avalanche photodiode; BP, bandpass filter; CA, confocal aperture; CCD, CCD camera; CL, cylindrical lens; DM, dichroic mirror; IP, illumination pinhole; NF, notch filter; OBJ, objective; RM, removable mirror; and SL, spherical lens.

CICS is shown to be superior to traditional SMD in accurate quantification and precise burst parameter determination. First, the limitations of traditional SMD and the potential benefits of CICS are theoretically explored using a combination of semigeometric optics modeling and Monte Carlo simulations. CICS is optimized for a 5 × 2 μm microchannel (w × h) and theoretically shown to have near 100% mass detection efficiency and <10% relative standard deviation (RSD) in the uniformity of detected fluorescence. Then, these models are validated using experimentally acquired observation volume profiles. Finally, CICS is implemented and demonstrated in two microfluidic systems through the detection of fluorescently stained DNA in a silicon device and a PDMS device and the detection of single Cy5 dye molecules in a PDMS device.

MATERIALS AND METHODS

Numerical simulation—observation volume

The observation volume (OV) profiles of confocal spectroscopy systems and their effects have been well explored in fluorescence correlation spectroscopy and SMD (27–33). We adopt a simple semigeometric optics approach used previously by Rigler et al. (31) and Qian and Elson (32) to theoretically model and guide the design of the CICS system (see Theory T1 in the Supplementary Material, Data S1).

The code for simulation of the OV profiles was written in MATLAB (The MathWorks, Natick, MA). In both simulations, the total observation volume, 10 × 10.2 × 12 μm (x × y × z), was discretized into 0.05 × 0.15 × 0.05 μm (x × y × z) elements. The OV function was evaluated at each element and stored in a 3-D array for analysis. The image space, 8 × 8 μm, was discretized into 0.02 × 0.02 μm elements. The constants used for standard SMD simulation were: w_o = 0.5 μm, p_o = 75 μm, M = 83.3, n = 1.47, λ = 525 nm, NA = 1.35, and r_o = 0.5 μm. The constants used for CICS simulation were: x_o = 25 μm, y_o = 0.5 μm, z_o = 5 μm, p_o = 300 μm, M = 83.3, n = 1.47, λ = 525 nm, NA = 1.35, and r_o = 0.5 μm.

Numerical simulation—Monte Carlo

Once the OV profiles are calculated, Monte Carlo simulations can be used to model the stochastic procession of molecules through the observation volume and the Poisson photoemission and detection process. This method is used to produce simulated single molecule trace data that can be analyzed in a manner identical to experimental data. During each time step, molecules are generated at random initial locations according to the concentration and propagated a distance in the y direction according to the flow velocity (see Theory T2 in the Supplementary Material, Data S1).

The Monte Carlo simulation was implemented in MATLAB. Each fluorescent molecule has no volume and is assumed to be a point emitter. The models simulate 4 and 8 kb dsDNA stained at a 5:1 bp/dye ratio. The nominal DNA concentration was 1 pM unless otherwise indicated. A constant flow profile of v = 1.5 mm/s was used in all simulations. Diffusion is ignored, and molecules travel in the y direction only. A 0.1 ms time step was used, and all simulations were run for 100 s. Two data traces, one with and one without Poisson fluctuations in the photoemission and photodetection process, are stored, allowing accurate determination of mass detection efficiency. The signal/background ratio (SBR = average burst height/average background) was adjusted to match experimental data. In standard SMD, the simulation approximates the flow of molecules in a channel significantly larger than the observation volume. For CICS, a channel of 10.2 × 5 × 2 μm (l × w × h) was simulated.

CICS instrumentation

All data were acquired with a custom-built, dual laser, dual detection channel, single molecule spectroscopy system capable of both traditional SMD and CICS with 488 nm and/or 633 nm laser illumination and detection at 520 nm and 670 nm. The beam from a 488-nm Ar-ion laser (Melles Griot, Carlsbad, CA) was expanded, collimated, and filtered using two doublet lenses (f = 50 mm and f = 200 mm; Thorlabs, Newton, NJ) and a 150-μm pinhole (Melles Griot, Carlsbad, CA) arranged as a Keplerian beam expander. The beam from a 633-nm He-Ne laser (Melles Griot) is also expanded and filtered using similar optics. The two beams are spatially aligned using beam steering mirrors mounted on gimbals (U100-G2K; Newport, Irvine, CA) and combined using a dichroic mirror (z633RDC; Chroma Technology, Rockingham, VT). The laser powers are individually adjusted using neutral density filters (Thorlabs). In CICS mode, a cylindrical lens (f = 300 mm; Thorlabs) is used to shape the beam into a sheet and focused into the back focal plane of the microscope objective. The laser is then tightly focused by a 100× oil-immersion (1.4 NA) objective (100× UPlanFl; Olympus, Center Valley, PA). The fluorescence is collected by the same objective and spectrally separated from the excitation light using a second dichroic mirror (z488/633RPC, Chroma Technology). It is passed through a confocal aperture, further separated into two detection bands by a third dichroic mirror (XF2016; Omega Optical, Brattleboro, VT) and filtered by bandpass filters (520DF40 and 670DF40; Omega Optical) before being imaged onto silicon avalanche photodiodes (SPCM-CD2801 and SPCM-AQR13; PerkinElmer Optoelectronics, Fremont, CA) with f = 30 mm doublet lenses (Thorlabs). Holographic notch filters (HNPF-488.0-1 and HNPF-633.0-1; Kaiser Optical Systems, Ann Arbor, MI) are also used to reduce the background from scattered light. Using an f = 150 mm doublet tube lens (Thorlabs), the total magnification at the pinhole is ∼83×. For standard SMD, a circular pinhole (Melles Griot, Carlsbad, CA) is used but for CICS, a rectangular, microfabricated confocal aperture is used. Data is collected from the avalanche photodiodes by a PC using a PCI6602 counter/DAQ card (National Instruments, Austin, TX) that is controlled using software written in Labview (National Instruments). Samples are positioned using a combination of a computer controlled, high resolution piezoelectric flexure stage (P-517.3CL; PI, Auburn, MA) and a manual XYZ linear stage (M-462; Newport, Irvine, CA). The entire system was built on a pneumatically isolated optical table (RS2000; Newport).

Microfabricated confocal aperture

The confocal aperture is fabricated from a 4-inch silicon wafer (300-μm thick, (1,0,0), SSP, p-type). 60-μm thick SPR220-7 (Rohm and Haas Electronic Materials, Marlborough, MA) is patterned using a triple spin coat and used as a masking material for a through wafer inductively coupled plasma/reactive ion etch (Trion Phantom RIE/ICP). The etch simultaneously forms the rectangular aperture and releases the die as a 9.5-mm diameter disk that can be mounted into a XYZθ-stage (RSP-1T and M-UMR5.25; Newport;) for alignment. Apertures of 620 × 115 μm and 630 × 170 μm were used. Because the alignment of the aperture is critical to the observation volume uniformity, a RetigaExi CCD (QImaging Corporation, Surrey, BC, Canada) is used to guide the alignment. Image analysis is performed using IPLab (BD Biosciences Bioimaging, Rockville, MD).

Single molecule trace data analysis

Data analysis is performed using software written in Labview. A thresholding algorithm is first used to discern fluorescence bursts from background fluctuations. The threshold can be set either at a constant value or in proportion to the background fluctuation levels. The identified bursts can then individually analyzed for burst width, burst height, and burst size after a background correction is carried out. No smoothing algorithms are applied.

OV profile acquisition

OV profile analysis was carried out on the 488-SMD and 488-CICS systems. The experimental OV profiles were acquired by scanning a 0.24-μm yellow-green CML fluorescent bead (Invitrogen, Carlsbad, CA) through the OV using a high resolution piezoelectric stage (PI) and recording the resultant fluorescence intensity as a function of position. A low excitation laser power of 0.008 mW/cm² was used to minimize photobleaching. The fluorescent beads were diluted to a concentration of 2 × 10⁶ beads/mL using DI water. A 5-μL drop of the diluted bead solution was placed onto a No. 1 thickness glass coverslip (Fisher Scientific, Pittsburgh, PA) and allowed to dry. Then, the beads were covered with a thin layer of PDMS (Dow Corning, Midland, MI) for protection (34). Beads were imaged from the backside through the glass. A rough 100 × 100 μm (x × y) scan was used to locate individual beads. Once an isolated bead was found, it was scanned in 0.15 × 0.15 × 0.15 μm (x × y × z) steps over a 4 × 4 × 8 μm volume for standard SMD and in 0.25 × 0.15 × 0.15 μm steps over a 12 × 6 × 10 μm volume for CICS. The fluorescence intensity was binned in 1-ms intervals and averaged over 25 ms at each point.

pBR322 DNA preparation

For 488-SMD and 488-CICS analysis, pBR322 DNA (4.3 kbp; New England BioLabs, Ipswich, MA) was stained with PicoGreen (Invitrogen) using the protocol developed by Yan et al. (35). The DNA was diluted to100 ng/mL in TE buffer and stained with 1 μM PicoGreen for 1 h in the dark. It was then further diluted down to 1 pM in TE buffer for measurement. For 633-SMD and 633-CICS analysis, pBR322 DNA was stained with TOTO-3 (Invitrogen). The DNA was diluted to 100 ng/mL in TE buffer and stained with TOTO-3 at a 5:1 basepair/dye ratio for 1 h in the dark. It was then further diluted down to 1 pM in TE buffer for measurement.

Cy5 oligonucleotide preparation

Single Cy5 5′ end-labeled 24 bp ssDNA (Cy5-5′-AAGGGATTCCTGGGAAAACTGGAC-3′; Integrated DNA Technologies, Coralville, IA) was resuspended in DI water and diluted to 1 pM concentration in filtered TE buffer for measurement.

633-SMD/Cy5 analysis in a microcapillary

A flow cell was fabricated using 100 μm ID fused silica microcapillary tubing (Polymicro Technology, Phoenix, AZ). A syringe pump (PHD2000; Harvard Apparatus, Holliston, MA) was used to drive the Cy5 labeled oligonucleotide through the flow cell at a volumetric flow rate of 1 μL/min. The input laser power was 0.185 mW/cm², and a 1 ms photon binning time was used. A typical trace consists of 300 s of data.

488-CICS pBR322 /PicoGreen-DNA analysis in silicon microfluidics

For 488-CICS analysis of pBR322 DNA, the cylindrical lens is inserted into the beam path, and the circular pinhole is swapped for a 620 × 115 μm rectangular confocal aperture. A microfluidic device was fabricated from silicon. First, 500 × 5 × 2 μm (l × w × h) channels were etched into a 4-inch, 500-μm thick, SSP, p-type, (1,0,0) silicon wafer using reactive ion etching and photoresist as a masking material. After etching, 0.8-mm through-wafer fluidic vias were drilled into the silicon substrate using an abrasive diamond mandrel. Then, the channels were sealed by anodic bonding of 130 μm thick borosilicate glass (Precision Glass and Optics, Santa Ana, CA). Finally, Nanoport (Upchurch, Oak Harbor, WA) fluidic couplings were epoxied to the backside. A syringe pump was used drive sample through the device at a typical volumetric flow rate of 0.001 μL/min such that the flow velocity is comparable to that of standard SMD. A 0.1 ms bin time was used. A typical trace consists of 300 s of data. The input laser power was 0.08 mW/cm².

633-CICS and 633-SMD/TOTO-3-DNA and Cy5 oligonucleotide analysis in PDMS microfluidics

For 633-CICS analysis of both TOTO-3-stained pBR322 DNA and Cy5, a 630 × 170 μm confocal aperture was used. Standard soft-lithography techniques (36) were used to create 500 × 5 × 2 μm (l × w × h) PDMS channels bonded to #1 glass coverslips (Fisher Scientific). A syringe pump was used drive sample through the device at a volumetric flow rate of 0.001 μL/min such that the flow velocity is comparable to that of standard SMD. A 0.1-ms bin time was used in the pBR322 DNA analysis whereas a 1-ms bin time was used in the Cy5 oligonucleotide analysis. A typical trace consists of 300 s of data. Illumination powers of 1.85 mW/cm² and 0.057 mW/cm² were used for CICS and SMD analysis of pBR322 DNA, respectively. Illumination powers of 3.7 mW/cm² and 0.185 mW/cm² were used for CICS and SMD analysis of Cy5 oligonucleotide, respectively.

RESULTS

Observation volume modeling

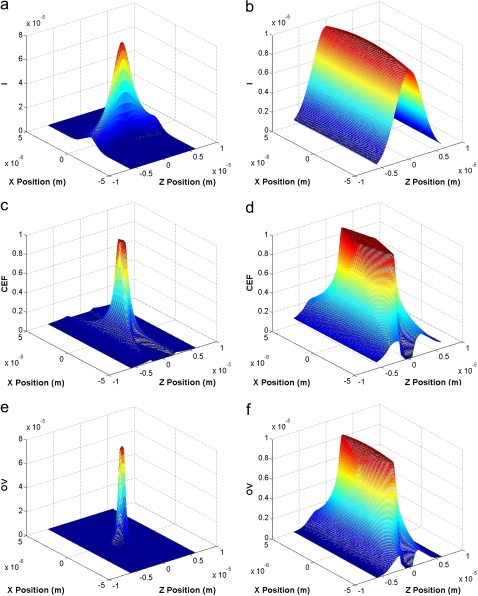
Individual molecules that traverse the observation volume of CICS are detected uniformly irrespective of location or trajectory whereas fluorescent signals that are detected using traditional SMD are a strong function of molecular trajectory. It is this enhancement in observation volume uniformity that enables CICS to be significantly more accurate, precise, and quantitative than traditional SMD. A semi-geometric optics model is used to theoretically compare the OV profiles of CICS with traditional SMD. Fig. 2 shows the calculated illumination, collection efficiency, and OV profiles for standard SMD and CICS.

FIGURE 2.

Illumination, I (top), collection efficiency, CEF (middle), and observation volume, OV (bottom), profiles of traditional SMD (left) and CICS (right) calculated using a semigeometric optics model. The profiles are illustrated as xz plots. Traditional SMD has a small OV profile that varies sharply in the x and z directions whereas the CICS OV profile has a smooth plateau region that varies minimally. The units of illumination profile and OV profile are arbitrary units (AU).

The increased uniformity of CICS is created by two key modifications to the standard confocal spectroscopy system. Standard SMD has a diffraction limited illumination profile that is radially symmetric and has a 1/e² radius of ∼0.5 μm (Fig. 2 a). By using an appropriate cylindrical lens, this radius can be elongated in 1-D to ∼25 μm to form a sheet of excitation light rather than a point (Fig. 2 b). Because the illumination profile is expanded in 1-D perpendicular to flow only, noise from background is minimized whereas uniformity and mass detection efficiency are increased. Standard SMD also uses a small pinhole (∼100 μm) such that the collection efficiency decays sharply at regions away from the confocal point (Fig. 2 c). In CICS, a large pinhole or aperture (∼600 μm) is used such that fluorescence can be collected uniformly from the entire 7 × 2 μm (w × h) center plateau region (Fig. 2 d). However, with a standard pinhole the stray light is no longer optimally apertured due to the geometric discrepancy between the circular pinhole and the sheet-like illumination. For optimal results, a microfabricated rectangular aperture is used as described subsequently.

As shown in Fig. 2 e, the result of the diffraction limited illumination profile and the sharply decaying collection efficiency is that traditional SMD has an OV profile that is nearly Gaussian in shape and varies sharply with position. Molecules that traverse the center of the observation volume result in much larger fluorescence bursts than molecules that travel through the edges, creating a train of highly variable single molecule bursts due to the typically random distribution of molecules in solution. This intrinsic variability makes accurate determination of burst parameters or burst frequency difficult. Conversely, due to the broad illumination profile and the uniform collection efficiency, Fig. 2 f shows that the OV profile of CICS has a large plateau region of ∼7 × 2 μm (w × h) where both excitation and detection occur in an extremely uniform manner. Over this plateau region, the detected fluorescence intensity is expected to have <10% RSD due to optical variation. Unlike standard SMD that requires nanochannel confinement (e.g., 0.35 × 0.25 μm, w × h) to achieve comparable performance (37), CICS can be carried out within a much larger microchannel (5 × 2 μm, w × h, >100× increase in cross-sectional area). Because the optimal microchannel is slightly smaller than the CICS observation volume, digital fluorescence bursts will be detected with near 100% mass detection efficiency.

Monte Carlo simulations

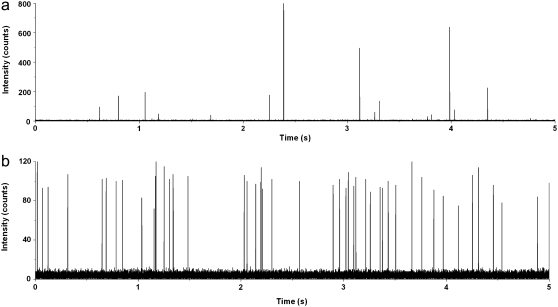
To further explore the effects of the observation volume nonuniformity and molecular trajectory, the Monte Carlo method is used to generate simulated single molecule traces based on the theoretical OV profiles in Fig. 2. Fluorescent molecules are generated at random initial locations and propagated through the observation volume according to the flow profile. During each time step, the fluorescence signal arising from all molecules within the observation volume as well as the background signal is integrated. Fig. 3, a and b, respectively, depict two simulated traces for a proto-typical embodiment of traditional SMD carried out within a channel that is larger than the observation volume and CICS carried out within a 5 × 2 μm (w × h) microchannel. As expected, traditional SMD shows a smaller number of highly variable bursts due to the nonuniform OV profile whereas CICS shows a larger number of highly uniform bursts that appear digital due to the smooth plateau region.

FIGURE 3.

Simulated single molecule trace data of (a) standard SMD and (b) CICS performed using Monte Carlo simulations and the theoretical OV profiles. CICS displays a significant increase in burst rate and burst height uniformity over traditional SMD. An increase in background noise is also evident. The bin time was 0.1 ms.

The burst rate of CICS increases in direct proportion to the 1-D expansion. The large enhancement in mass detection efficiency is achieved through the combination of this increase in burst rate due to the observation volume expansion and the use of a microchannel that is size-matched to the observation volume. The mass detection efficiency can be accurately analyzed in the simulation through a comparison of all randomly generated molecules against those detected after thresholding. When a discrimination threshold of 30 counts is applied, the mass detection efficiency of CICS within the 5 × 2 μm channel (w × h) is 100% with no false positives or false negatives due to the digital nature of the fluorescence bursts. If the channel size is further increased to 7 × 3 μm (w × h), the mass detection efficiency remains at 100% but the burst height variability increases from 13% RSD to 26% RSD, illustrating the tradeoff between observation volume size, throughput, and detection uniformity (data not shown).

In fact, the variability in burst height is no longer dominated by nonuniformity in the OV profile but rather the Poisson photoemission and detection process. Although the uniformity can be improved by changing the collimation optics and aperture should a larger observation volume be necessary, there will be a concurrent decrease in signal/noise ratio that is unavoidable. Further improvements must be found by increasing the fluorescence intensity through higher illumination powers or from longer photon binning times instead of optical modifications.

In contrast, because traditional SMD is performed usually within a channel that is much larger than the observation volume, it has an extremely low mass detection efficiency. For example, given a 100-μm ID microcapillary, the mass detection efficiency is <0.05% under the same threshold. This low mass detection efficiency is due to a combination of the minute observation volume, observation volume nonuniformity, thresholding artifacts, and Poisson fluctuations. The large majority of molecules (>99.6%) escape detection because of the size mismatch between the observation volume and the microcapillary. The remainder of the molecules (∼0.3%) are missed because their corresponding fluorescence bursts reside below the threshold and are indistinguishable from background fluctuations. To obtain 100% mass detection efficiency using standard SMD, nanochannel confinement or molecular focusing of molecules to a stream width of ≪1 μm would be necessary.

Detailed analysis of the Monte Carlo data shows that when thresholding algorithms are used to discriminate fluorescence bursts from background fluctuations, as is common practice, the quantification accuracy of traditional SMD is compromised due to thresholding artifacts. The burst rate is defined as the rate at which fluorescence bursts are detected and is proportional to the concentration of molecules in the sample as well as the sample flow rate and mass detection efficiency. The burst height is then defined as the maximum number of photon counts per bin time emitted by a molecule during a transit event. It is related to the brightness of the molecule, the observation volume uniformity, the flow rate, and photon binning time. The wide distribution of burst heights in standard SMD causes the burst rate and determined burst parameters to vary widely with the specific threshold applied as shown in Table 1. As the threshold is increased, the smaller bursts are progressively excluded, gradually decreasing the burst rate and shifting the average burst height upward. Accurate determination of the absolute burst rate and burst height is extremely difficult because it is nearly impossible to distinguish between small fluorescence bursts arising from molecules that traverse the periphery of the observation volume and random background fluctuations. In contrast, because CICS bursts are uniform in size, they are much more robust when used with thresholding algorithms. The applied threshold can vary over a wide range without affecting either the burst rate or determined burst parameters. This is due to the digital nature of the fluorescence bursts. The average burst height determined using CICS remains extremely constant as the threshold is varied from 20 to 70 counts, increasing only 4% whereas the average burst height determined using traditional SMD increases 100%.

TABLE 1.

Thresholding artifacts in traditional SMD versus CICS

	Traditional SMD		CICS
Threshold (counts)	Burst rate/100 s	Burst height (counts)	Burst rate/100 s	Burst height (counts)
20	421	149 ± 199	958	101 ± 24
30	305	197 ± 216	906	105 ± 14
40	257	227 ± 223	906	105 ± 14
50	224	254 ± 226	906	105 ± 14
60	206	272 ± 229	906	105 ± 14
70	183	298 ± 229	903	105 ± 14

Analysis of 100-s Monte Carlo simulation data. The digital nature of fluorescence bursts acquired using CICS allows the system to be robust against thresholding artifacts. However, quantitative burst parameters determined using traditional SMD are highly sensitive to the specific threshold applied. Bin time, 0.1 ms.

Matters are further complicated when molecules of varying brightness need to be quantified using the burst rate. Two populations of molecules of equal concentration but different brightness levels can give significantly different burst rates even if the same threshold is applied, necessitating precise calibration for each molecular species. These effects are illustrated in Table 2. The simulated DNA is stoichiometrically stained such that the number of incorporated dye molecules and, hence, brightness increases linearly with DNA length. Although the total quantity of DNA is conserved in all cases, the burst rate of standard SMD can vary by almost 40% when presented with only a 2× increase in DNA length. With standard SMD, it is impossible to determine concentration based on burst rate alone. Prior knowledge of the sample composition is necessary to provide an accurate reference standard. When an unknown mixture of molecules of varying brightness is present, such calibrations are often unfeasible as it becomes impossible to independently separate the effects of brightness and concentration. CICS, however, is highly robust even when quantifying mixtures of molecules as shown in Table 2. A constant quantity of DNA is reflected even in the presence of varying mixtures. The burst rates differ by <5% in the same situation, implicating that concentration can be determined blindly based on burst rate alone.

TABLE 2.

Single molecule burst rates in varying DNA mixtures

	1 pM 4 kbp	1 pM 8 kbp	0.5 pM 4 kbp +0.5 pM 8 kbp	0.25 pM 4 kbp + 0.75 pM 8 kbp
Traditional SMD	305	420	381	410
CICS	915	928	948	922

Simulated burst rate of DNA mixtures taken using traditional SMD and CICS. The burst rate of traditional SMD varies as relative proportions of the two DNA components are varied although the total concentration is conserved in all cases. The CICS burst rate remains consistent across the mixtures. The applied threshold was 30 counts. Bin time, 0.1 ms.

These Monte Carlo simulations have shown theoretically that the 1-D expansion of the observation volume and increase in observation volume uniformity provide the basis for CICS to achieve 100% mass detection efficiency within a microchannel and to perform highly accurate and robust burst parameter analysis. CICS rectifies the limitations of traditional SMD while still preserving single molecule sensitivity.

Experimental observation volume mapping

The OV profiles of the 488-SMD and the 488-CICS systems were acquired by rastering a submicron fluorescent bead through the observation volume and recording the collected fluorescence intensity as a function of position. Fig. 4, a and b, show xz plots that track the theoretical predictions of Fig. 2. Standard SMD has a small, sharply decaying OV profile that can be accurately modeled using a 3-D Gaussian approximation. Excellent fits to Gaussian functions were obtained resulting in measured 1/e² radii of 0.33, 0.44, and 0.99 μm in the x, y, and z directions, respectively; this leads to an observation volume size of 0.6 fL (see Figs. S1, a, c, and e, in the Supplementary Material, Data S2). However, the observation volume is not perfectly symmetrical and contains some aberrations. These are likely due to artifacts caused by optical aberrations, misalignment of optical components, mechanical drift and instability of the scanning stage, and photobleaching of the fluorescent bead.

FIGURE 4.

OV profiles of (a) traditional SMD and (b) CICS acquired using a submicron fluorescent bead. The CICS observation volume resembles traditional SMD in the z direction but is elongated in the x direction such that it can span a typical microchannel.

The CICS system, on the other hand, shows a much larger, elongated observation volume that is fairly uniform in the center section. The OV profile of CICS mirrors that of traditional SMD in the y- (y₀ = 0.25 μm) and z directions (z₀ = 1.18 μm) but is elongated in the x direction (x_uniform ∼7 μm) as designed (see Fig. S1, Data S2). This is further illustrated in Fig. 1, b–d, where a CCD is used to take images of the standard SMD and CICS illumination volumes using a reflective interface held perpendicular to the optical axis. In Fig. 1 b, the 1/e² radius of the illumination volume in the x direction (width) is stretched to 12.1 μm using an f = 300 mm cylindrical lens (see Fig. S2, Data S2). In Fig. 1 c, a 620 × 115 μm confocal aperture limits light collection to only the center 7 μm where the illumination is most uniform (see Fig. S3, Data S2). Over this region there is an ∼6% RSD and 15% maximum variation in illumination intensity. Because the characteristic dimensions of the observation volume are larger than the 5 × 2 μm (w × h) microchannel used to transport molecules, near 100% mass detection efficiency is expected as theoretically predicted (38). For analysis using 633-CICS, the confocal aperture was increased to 630 × 170 μm (w × h) to increase signal intensity and reduce the axial dependence of collection uniformity.

Despite the general agreement, the experimental CICS OV profile lacks the distinct plateau present in the theoretical simulations. This is expected as the sharp plateau is a limitation of the semigeometric optics approximation used. In practice, the sharp cutoff in collection efficiency defined by the aperture is replaced by a smooth decay. In addition, the dependence of the OV profile in the z-dimension is much sharper than that predicted by the model. This can possibly be rectified through the use of a lower numerical aperture (NA) microscope objective or larger confocal aperture. Finally, there is additional nonuniformity introduced by diffraction, optical aberrations, misalignment, and experimental error that are not accounted for in the theoretical simulations. Similar point spread functions have recently been reported in confocal line scanning applications (23,39). Together, these effects increase the nonuniformity over theoretical predictions. Further improvements in uniformity can still be had through the incorporation of an objective with a higher degree of aberration correction, improved optical alignment, increased mechanical stability, and minor refinements in optical design.

DNA analysis

For the preliminary demonstration of CICS, analysis was performed on bright, multiply stained pBR322 DNA molecules. Initially, a silicon-based microfluidic chip containing 5 × 2 μm microchannels was used to precisely transport molecules through the uniform 7 × 2 μm CICS observation volume. 488-CICS was first used to analyze PicoGreen stained pBR322 DNA. The experimental trace (see Fig. S4, Data S2) is characterized by a large number of uniform fluorescence bursts and shows strong similarities to the simulated trace of Fig. 3 b. It has a high burst rate of 1955 bursts/300 s when a detection threshold of 22 counts is applied and average burst height of 33.0 ±10.4 counts (RSD = 31%). However, accompanying the large increase in burst rate and uniformity is a substantial increase in background. The large increase in background is greater than that expected from the observation volume expansion alone. The close proximity of the glass-water interface at the top of the channel and the opaque silicon at the bottom of the 2-μm high microchannel creates large amounts of scattered light, significantly increasing background levels and leading to a low SBR of 6 (SBR = average burst height/average background). This scatter background is more effectively rejected by the smaller pinhole in standard SMD than the larger, rectangular aperture in CICS. To prevent the background from swamping out the fluorescent bursts, the illumination power was limited to only 0.08 mW/cm². Therefore, in the subsequent experiments a transition to a glass-PDMS devices was made.

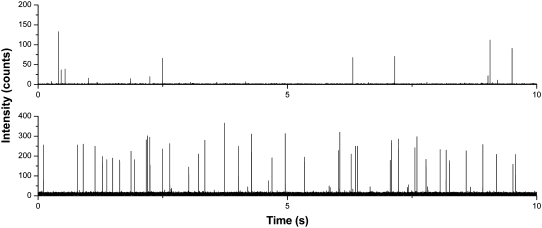
To compare CICS with SMD, a second microfluidic device of identical geometry to the first was fabricated out of PDMS and glass using soft lithography. The transparent PDMS-glass materials have lower scatter background than the opaque silicon used previously. Red excitation (633 nm) with far red detection (670 nm) was found to have a lower average background and fewer spurious fluorescent bursts when used with PDMS devices than blue excitation (488 nm) with green detection (520 nm). It is believed that this can be attributed to the PDMS autofluorescence (40–42) as well as the large number of organic contaminants and impurities that fluoresce in green. As a result, TOTO-3 stained pBR322 DNA was analyzed rather than the previous PicoGreen-stained DNA. The low scatter background enabled 633-CICS to be run at 1.85 mW/cm² rather than the low 0.08 mW/cm² used previously in 488-CICS. To achieve comparable illumination power densities at the observation region, 633-SMD was operated at 0.059 mW/cm² to account for the >30× decrease in illumination volume size (see Figs. S5 and S6, Data S2). Fig. 5 shows two single molecule traces taken using 633-SMD (top) and 633-CICS (bottom). These traces closely resemble the Monte Carlo data in Fig. 3. The CICS traces show a higher burst rate, more uniform fluorescent bursts, and a slightly higher background than the SMD traces. Standard SMD, at a discrimination threshold of 10 counts, shows 336 bursts in a 300-s period with an average burst height of 51.5 ± 44.6 counts (RSD = 87%). It is difficult, though, to set a threshold where both false negative and false positive bursts are minimized Setting the threshold at the standard μ + 3σ level, which gives a 99.7% confidence interval, would lead to an average of 9000 false positive peaks when acquiring data over a 300-s period with a 0.1 ms bin time. Thus, it is necessary to use a significantly higher threshold at the cost of an increased number of false negatives. Because there is no optimal threshold setting, it is difficult to determine the accuracy of the absolute burst rate and burst parameters.

FIGURE 5.

Experimental single molecule trace data of TOTO-3 stained pBR322 DNA taken using SMD (top) and CICS (bottom). The CICS experimental data shows a high burst rate and burst height uniformity that parallels the results of the Monte Carlo simulations. The bin time was 0.1 ms.

CICS burst data, on the other hand, is much less sensitive to thresholding artifacts as predicted by the model. Using a threshold of 100 counts, 1278 fluorescent bursts were detected over a 300-s period where the average burst height was 211.6 ± 56.6 counts (RSD = 27%). When the threshold is varied over a wide range of 65–135 counts, the number of detected bursts decreases only 11% whereas in standard SMD the burst rate decreases by 44% over a much smaller range of 6–14 counts (see Fig. S7, Data S2). The price to pay for the increased uniformity and burst rate is a correlated reduction in SBR. Although the 633-CICS SBR of 22 is much improved over the previous 488-CICS results performed within the silicon devices due to the decreased scattering background in the PDMS devices, it is still less than SBR of 271 obtained using 633-SMD. This reduction in SBR using CICS is fairly consistent but slightly more than that expected from the ∼7× linear expansion in observation volume size.

Because the channel dimensions of the silicon and PDMS devices are identical, the burst height uniformities are expected to be similar as is seen. However, they are ∼10% greater than that which was theoretically predicted. Further uniformity improvements can be expected if the axial dependence (z direction) is reduced through lower NA collection optics such as a 1.2 NA water immersion objective. The remainder of variability can be attributed to factors such as variability in staining efficiency, fluctuations in the illumination intensity, instabilities in the flow velocity, and the Poiseuille flow profile.

Two significant drawbacks of the PDMS devices that were not encountered using the silicon devices were frequent flow instabilities and long transient times when changing flow velocities. This can likely be attributed to the elastic nature of the PDMS and the less robust nature of the fluidic couplings. These effects become apparent as short time scale fluctuations in the burst rate (∼ seconds), longer time scale drift (∼ tens of minutes), and sudden spikes in burst rate. They are exacerbated by the intrinsic difficulty in controlling such low flow rates (0.001 μL/min) as well as the high flow resistance of the small microchannels. From the optical characterizations and simulations, it is evident that the 7 × 2 μm observation volume is sufficient to span the entire 5 × 2 μm microchannel. Although based on the uniformity of the burst height histogram (see Fig. S8, Data S2), it is evident that nearly all the molecules are flowing through the uniform center section of the observation volume. This implies that the large majority of molecules within the channel are in fact being detected. Thus, we believe the decreased burst rate can be largely attributed to flow variability.

Although the observation volume here was expanded ∼7×, which corresponded to an ∼10× decrease in SBR from standard SMD, it can be tailored to almost any size using the correct combination of cylindrical lens and aperture. The required signal/noise ratio and observation volume uniformity will dictate the maximum focal volume expansion that can be carried out while maintaining adequate sensitivity.

Single fluorophore sensitivity

CICS was tested to see if single fluorophore sensitivity was preserved despite the observation volume expansion. Cy5-labeled 24 bp ssDNA was diluted to 1 pM, flowed through the PDMS microfluidic device, and analyzed using both traditional SMD and CICS. CICS was run at 3.7 mW/cm² whereas SMD was carried out at 0.185 mW/cm². A longer photon binning time (1 ms vs. 0.1 ms) was used in the single fluorophore Cy5 experiments to increase signal levels. When standard SMD is carried out within a large capillary, Cy5 fluorophores can be detected with a SBR of 13 and 89% RSD in burst height (threshold = 8 counts, average burst height = 18.0 ± 16.1 counts). Whereas when standard SMD is carried out within the microchannel, the scatter background is increased due to the close proximity of the glass-water and water-PDMS interfaces resulting in a slightly reduced SBR of 10 (see Fig. S9, Data S2) whereas burst height RSD remains at a comparable 90% (average burst height = 36.7 ± 32.9 counts) when a threshold of 14 is applied. In comparison, CICS is significantly more uniform (see Fig. S9, Data S2). The average Cy5 burst height was 120.8 ± 58.9 counts, which corresponds to a RSD of 49% (threshold = 254 counts). This burst uniformity is expected to be decreased when compared to the pBR burst uniformity because of the decreased brightness of the single Cy5 fluorophore. CICS showed an SBR of 1.6 that was 6× lower than the standard SMD SBR, consistent with the 7× increase in observation volume size. This illustrates the trade-off in uniformity, burst rate, and SBR that can be easily predicted and engineered using CICS. For single fluorophore analysis, the current 7 × 2 μm OV/5 × 2 μm microchannel combination is likely the largest expansion that can be performed while retaining single fluorophore sensitivity. But for brighter molecules such as fluorescent beads, quantum dots, or multiply labeled DNA or proteins, it is expected that even larger microchannels may be used for increased throughput.

Single fluorophore mass detection efficiency

As discussed previously, single Cy5 fluorophores are readily detected by both standard SMD and CICS. The estimation of mass detection efficiency requires an accurate determination of the absolute burst rate, which is in turn highly influenced by the specific threshold applied. The optimal threshold balances the proportion of false positive bursts against the proportion of false negative bursts in the attempt to minimize the influence of both. However, when analyzing dim molecules such as single fluorophores where the fluorescent fluctuations are not fully resolved from the background fluctuations (i.e., the distribution of fluorescent fluctuations overlaps the distribution of background fluctuations), this becomes extremely difficult because every threshold chosen will introduce an inordinate number of either false positives or false negatives. We adapt the method of Huang et al. (25) to extrapolate the true burst rate from that determined after thresholding. Given the applied flow rate (0.001 μl/min) and nominal concentration (1 pM), an average of ∼3011 molecules are expected to flow through the channel during each 300-s period. Using standard SMD, 232 molecules can be detected leading to a mass detection efficiency of 7.5% (see Fig. S10, Data S2). This burst rate appears somewhat lower than expected. Under CICS analysis, on the other hand, 3467 molecules can be detected (see Fig. S11, Data S2). Although this number is slightly greater than the expected number of molecules, this difference may be attributed to errors in flow rate due to pump calibration, instabilities in flow as discussed previously, pipetting errors in sample preparation, and inaccuracies in the data analysis method.

The large mass detection efficiency increase in CICS is achieved through the combination of two effects, a decrease in the size of the transport channel and a matched 1-D increase in observation volume size. Standard SMD mass detection efficiencies (<1%) are low because the transport channel (diameter ∼100 μm) is typically much larger than the SMD observation volume (diameter ∼1 μm). Because the mass detection efficiency describes the relative proportion of detected molecules, a reduction in transport channel size increases mass detection efficiency without a concurrent increase in burst rate whereas an increase in observation volume size increases both mass detection efficiency and burst rate. As the channel size is reduced to below the observation volume size, the mass detection efficiency is maximized whereas the absolute burst rate is progressively reduced. Using the previous method, standard SMD carried out in a 100-μm diameter capillary achieves a mass detection efficiency of only 0.04% (see Fig. S12, Data S2). By substituting a 5 × 2 μm microchannel, the mass detection efficiency is increased to 7.5% whereas the absolute burst rate is actually reduced by 5× because the low microchannel height limits the effective size of the observation volume. This 7.5% roughly correlates to the overlap in cross-sectional area between the SMD observation volume size and the microchannel, but is slightly lower than the 10–15% expected, likely due to flow instabilities, a slight misalignment of the channel to the observation volume, and inaccuracy in the estimation method. To increase mass detection efficiency to near 100% using standard SMD, a nanochannel must be used (38). However, CICS further increases mass detection efficiency by matching the 5 × 2 μm microchannel with an optimized 1-D observation volume expansion. This leads to a 15× increase in absolute burst rate over standard SMD in a microchannel and near 100% mass detection efficiency. The observation volume in CICS can be easily tailored to span a given channel geometry with the correct choice of optics and aperture using the methods previous described.

Burst size distribution analysis

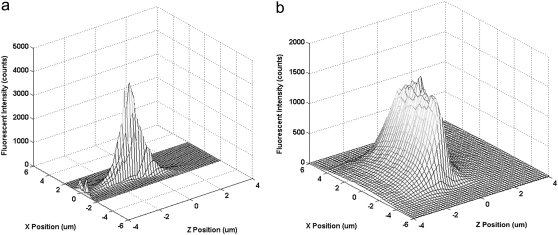
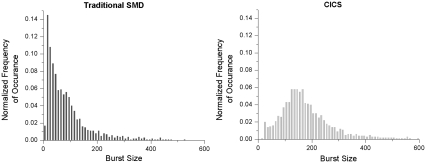
Not only is CICS more accurate in quantification and burst parameter determination, the greatly enhanced uniformity enables single molecule assays that cannot be carried out using traditional SMD. For example, burst size distribution analysis uses the distribution of individual fluorescence burst intensities to determine the size of a molecule. As shown in Fig. 6, the Gaussian OV profile of standard SMD does not allow a clear distinction of the pBR DNA population from the background fluctuations. However, the same DNA shows a clear population centered around 151 counts when analyzed using CICS. Thus, the average burst size can be more accurately determined without being skewed by background fluctuations. In fact, the digital fluorescence bursts even obviate the need for smoothing algorithms such as Lee filtering when processing such data (43). Using CICS, it is possible to carry out a burst size distribution assay on a mixture of DNA molecules and individually identify the constituents of that mixture as well as their individual concentrations. Such an assay would be impossible using standard SMD. Future work will investigate the benefits of CICS in a variety of single molecule assays.

FIGURE 6.

Burst size distribution analysis histograms of PicoGreen-stained pBR322 DNA taken using standard SMD (left) and CICS (right). In standard SMD, the DNA peak is not resolved from the noise fluctuations due to the Gaussian OV profile whereas CICS shows a clearly discernible peak due to the high uniformity of the OV profile.

CONCLUSION

In conclusion, through careful modeling and implementation, CICS has been engineered to alleviate the subtle shortcomings of traditional SMD that make it difficult to apply in a widespread manner. CICS significantly enhances uniformity and mass detection efficiency while still preserving single fluorophore sensitivity, allowing more accurate and precise determination of single molecule parameters than traditional SMD. It can be operated with higher throughput and with less complication than competing technologies using molecular focusing and molecular confinement. In addition, its quantification accuracy is further reinforced by its robustness against thresholding artifacts. Finally, because CICS uses an epi-fluorescent arrangement, it is easily used with all types of microfluidic devices including those with opaque substrates such as silicon. This makes it an ideal detection platform that can be generically combined with all microfluidic systems. Because the mass detection efficiency, detection uniformity, and signal/noise ratio can be accurately predicted, it can be easily optimized for any microfluidic channel size and application. CICS has great potential in applications such as clinical diagnostics, biochemical analysis, and biosensing where accurate quantification of the molecular properties of rare biomolecules is necessary.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.