Micro-Macro Link in Rheology of Erythrocyte and Vesicle Suspensions

Abstract

We report on the rheology of dilute suspensions of red blood cells (RBC) and vesicles. The viscosity of RBC suspensions reveals a previously unknown signature: it exhibits a pronounced minimum when the viscosity of the ambient medium is close to the value at which the transition from tank-treading to tumbling occurs. This bifurcation is triggered by varying the viscosity of the ambient fluid. It is found that the intrinsic viscosity of the suspension varies by about a factor of 4 in the explored parameter range. Surprisingly, this significant change of the intrinsic viscosity is revealed even at low hematocrit (5%). We suggest that this finding may be used to detect blood flow disorders linked to pathologies that affect RBC shape and mechanical properties. This opens future perspectives on setting up new diagnostic tools, with great efficiency even at very low hematocrit. Investigations are also performed on giant vesicle suspensions, and compared to RBCs.

Understanding blood rheology both in vivo and in vitro is important both at the fundamental and practical levels. Blood is a complex fluid (1–3), the rheology of which is dictated by red blood cells (RBCs), whose volume fraction (hematocrit, H) is ∼45% of normal human blood.

Blood exhibits several non-Newtonian behaviors, such as shear thinning (decrease of viscosity with shear rate) or thixotropic effect (decline of viscosity after cessation of shearing). The non-Newtonian nature of blood expresses the intimate coupling between the microscales, at the level of RBCs, and the global scale of the flow. A general modeling of blood rheology based on the dynamics at the microscopic scale still presents a significant challenge, although some key points in blood rheology have been identified (1–3) (e.g., the Fahraeus-Lindquist effect in blood vessels, the role of RBC deformation in rheology, etc.).

We have performed an experimental study on a dilute suspension where the cell/cell adhesion is absent. Hydrodynamic interactions among cells are weak and rouleaux formation is inhibited thanks to removal of plasma proteins.

We also report on the viscosity of giant unilamellar vesicle suspensions (GUV). Drawing a comparison between vesicle and RBC suspensions may provide a way for identifying the role of the cytoskeleton on rheology.

A key parameter in this study is the viscosity ratio λ = η_in/η_out, where η_in and η_out are the viscosities of the internal (hemoglobin solution for RBC) and external fluids. A parameter that can be adjusted for GUVs, and that can vary for RBCs due to pathologies, is the reduced volume 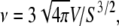where V is the volume and S the surface area of the membrane (ν = 1 for a spherical object and ∼0.6 for a normal RBC). Alternatively, one may use the dimensionless excess area Δ = 4π(ν^−2/3 – 1) (Δ = 0 for a sphere and ∼5. for a normal RBC).

RBCs and vesicles under shear flow exhibit several dynamical behaviors: i), tank-treading (TT) (4,5): the cell (and vesicle as well) makes a fixed angle with the flow direction while its (fluid) membrane undergoes a tank-treading like motion; ii), tumbling (TB) (6,7), which occurs above a certain viscosity contrast; and iii), vacillating-breathing (8) for vesicles (oscillation of the long axis about the flow direction, accompanied with breathing of the shape) and for RBC (9). Other more complex dynamics have also been predicted (10). The question of the impact of these microscopic dynamics on the overall rheology naturally arises.

A major experimental result reported here is a minimum of the intrinsic viscosity of RBC suspensions in the vicinity of the TT-TB transition. This reveals a qualitative change due to the link between microscopic and macroscopic dynamics. The position of the minimum should depend on structural and mechanical properties, which are different for healthy and pathological cells.

Viscosities of diluted RBC and vesicle suspensions were measured as a function of the viscosity ratio λ between the inner and outer fluids (relative to the vesicle or erythrocyte membrane). All chemicals were purchased from Sigma-Aldrich (Saint Quentin Fallavier, France) and used without any further purification.

Microscopic observations were performed on an Olympus (Rungis, France) IX 71 inverted microscope in phase contrast (GUVs and RBC) or bright field (RBC) modes.

Erythrocyte samples were provided by the CHU (Centre Hospitalier Universitaire) of Grenoble, France, from hematologically healthy donors. Phosphate-buffered saline (PBS) with pH 7.4 and osmolarity 290 ± 10 mOsm/kg or PBS dextran (D1037, D4751, and D4626 from Sigma) solutions were used as suspending media. The cytoplasmic viscosity of RBCs is determined on the basis of the mean corpuscular hemoglobin concentration (11).

For GUVs, a range of λ between 0.2 and 4 was explored. Vesicles were prepared from dioleoyl phosphatidylcholine (P-6354 from Sigma) in sucrose in 1:4 glycerol-water mixture (for λ < 1) or glucose-dextran aqueous solution (for λ > 1) by electroformation (12). Samples were then diluted in an outer medium (glucose and dextran solution in a 1:4 glycerol-water mixture or a sucrose aqueous solution), which is slightly hyperosmotic to deflate vesicles, and has a different viscosity to vary λ.

Viscosity measurements were made at the constant temperature of 22°C with different instruments: a stress-controlled Bohlin Gemini 150 rheometer (Malvern Instruments, Orsay, France) with a cone-plate geometry (60 mm diameter, 2° angle), a LS30 low-shear rheometer (Contraves, Orsay, France) with a cylinder-Couette geometry used for cases where the solvent viscosity is between 2 and 7 mPa.s, and a Schott (Mainz, Germany) capillary viscometer for viscosities between 1 and 10 mPa.s.

For RBCs, the final hematocrit was checked by counting cells in a sample placed in a 100 μm deep polydimethylsiloxane observation chamber. During the injection of RBC samples in that chamber, we could also check that the two regimes of RBC dynamics (TT and TB) were microscopically observed for λ < 2 and λ > 2 (13,14).

For vesicles, after the viscosity measurement, the sample was placed in the observation chamber and a statistical measurement of the vesicle population (vesicle diameter, number) was done using ImageJ software.

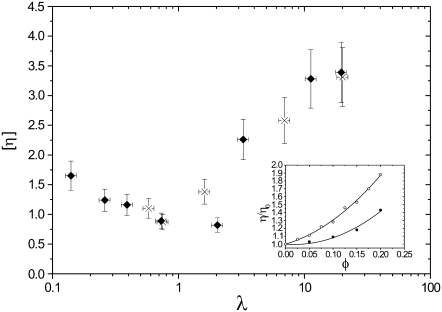
For RBCs, several measurements were made at different hematocrit values to check the applicability of dilute suspension theories (15–17). The results are shown in the inset of Fig. 1 for two viscosity ratios in the TT and TB regimes. Nonlinear effects due to hydrodynamic interactions among RBCs are no longer negligible when the volume fraction φ reaches 10%. Therefore, we restricted our study to volume fractions φ < 10%. For all viscosity measurements shown thereafter, each data point is the result of averaging between 2 and 6 different samples and 5 and 10 measurements for each sample, and error bars shown in Fig. 1 include the dispersion of these measurements, the error on the measurement of volume fractions, and the precision of viscosity measurements.

FIGURE 1.

Intrinsic viscosity [η] versus viscosity ratio λ for RBCs with φ = 5% (♦) and φ = 7.5% (×). (Inset) Viscosity (relative to solvent viscosity) versus volume fraction for suspensions of red blood cells in (○) PBS buffer (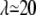), and (•) in 20% dextran (D1037) solution in PBS ().

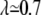In the dilute limit, the variations of suspension viscosities compared to the viscosity of the suspending medium are proportional to the volume fraction. We present intrinsic viscosities defined by

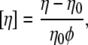(1)

where η₀ is the solvent viscosity and φ the volume fraction of particles.

Fig. 1 shows the measured intrinsic viscosities [η] as a function of the viscosity ratio λ for RBCs with 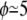%, and 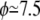%. Remarkably, the intrinsic viscosity decreases until the viscosity ratio λ reaches the range 1–3, then sharply increases. This change of regime corresponds to the transition from TT to TB that is observed at high shear rates when the relative viscosity is increased. In the TT regime, when approaching the transition to TB, the particle's long axis becomes increasingly aligned with the flow, leading to smaller viscous dissipation. In the TB regime, a larger fluid volume is disturbed, leading to an increase of the viscosity.

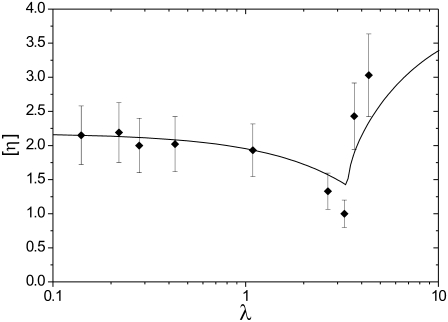
The same measurements were made for lipid vesicles for 2.5% < φ < 12% as shown in Fig. 2. We have also checked when vesicles exhibit TB or TT. Vesicle samples are usually much more polydisperse than RBCs: vesicle size varies between 5 and 100 μm with a peak between 15 and 20 μm, and reduced volume varies between 0.9 and 1 (corresponding to excess areas between 0 and 1) in the same sample. However, despite this dispersity, the viscosity of vesicle suspensions follows the general trend of RBC suspensions with a slow decrease in the TT regime and a rapid increase after the transition to TB.

FIGURE 2.

Intrinsic viscosity [η] versus viscosity ratio λ for vesicles with 3% < φ < 12%. The solid line shows the analytical results (Eqs. 1–3) for vesicles with excess area Δ = 0.5.

Recently, an expression for the viscosity in the TT regime has been derived for quasi-spherical vesicles (8):

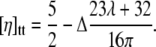(2)

The viscosity decreases upon increasing λ, in agreement with the experimental results. In the TB regime, there was no analytical result available yet. The numerical study has shown (18) that the viscosity increases with λ in the TB regime. We have derived an analytical result for the viscosity in the TB regime. This is possible in the small capillary number limit where a direct transition (i.e., not preceded by the VB mode) from TT to TB occurs (the capillary number is defined as 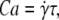where 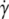is the shear rate and τ is the relaxation time of the vesicles; we may also regard this number as the Deborah number usually invoked in the complex fluid literature). By taking the low Ca limit of the instantaneous viscosity of tumbling vesicles in suspension (15) and averaging over orientations, one gets

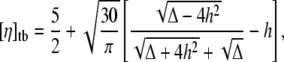(3)

with 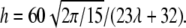Tumbling corresponds to 4h² < Δ (and TT to the opposite limit) (8). The analytical results are shown in Fig. 2 (solid line).

In the case of vesicles, for a fitted excess area of Δ = 0.5, the model reproduces rather well (both qualitatively and quantitatively) the experimental results for vesicles. This corresponds to a reduced volume ν = 0.94, which falls in the range of values measured in the polydisperse sample.

The RBC results seem to follow the same qualitative trend as for vesicles as shown in Fig.1. This shows that, as long as the viscosity is concerned, no qualitative effect due to the cytoskeleton can be deduced. Quantitative effects are, however, quite significant.

This novel result, which shows a clear signature of the microscopic dynamics on RBCs' suspension viscosity, should trigger new studies on blood rheology. Since the TT-TB bifurcation significantly depends on the reduced volume (18), cells from patients suffering from congenital hemolytic anemia (spherocytosis, elliptocytosis), which have significantly larger reduced volumes, should exhibit a transition from TT to TB at a different viscosity ratio. We believe that this information could shed light on blood flow disorders associated with these pathologies and be used as a complementary diagnosis in help identifying RBCs' pathologies. This feature is interesting inasmuch as only 5% of hematocrit already shows ample rheological signatures.