Abstract
Measurements of time-resolved fluorescence anisotropy and fluorescence resonance energy transfer are finding many applications in the study of biological macromolecules as they enable structural properties of the host molecules to be determined in their natural environment. A difficulty in interpreting these experiments is that they both require knowledge of the relative orientation of the fluorophores, a property that is almost impossible to measure. Here we conduct simulations of AlexaFluor488 and AlexaFluor568 attached to two sites on the membrane channel MscL to provide an alternative mechanism for determining the likely configurations and orientational freedom of the fluorophores, as well as the most likely value of the orientation factor κ2 for energy transfer between them. The fluorophores are relatively mobile, and are found to be more so when immersed in bulk water than when they interact with the lipid membrane. The fluorophores never insert deeply into the lipid, despite their hydrophobic linkers and aromatic headgroup structures. Properties such as the fluorescence anisotropy decay can be predicted from simulations of the fluorophores in bulk water that closely match experimental data. In contrast, when the fluorophores were attached to the large MscL protein it was difficult to sample all the possible configurations of the fluorophores due to the computational time required. While this approach is likely to provide useful data on solvent-accessible fluorophores attached to small proteins, simulations lasting >50 ns or the use of biasing forces are required to accurately predict orientation factors for use in energy transfer experiments on larger membrane-bound proteins.
INTRODUCTION
Fluorescence spectroscopy is an important tool for understanding molecular biophysics. Not only can fluorescent tags be used to track the localization of proteins and molecules within cells, they can also be used to probe the operation of individual macromolecules themselves. Fluorophores preferentially absorb and emit light polarized in certain directions due to the presence of transition moments within the molecular scaffold. Tracing the degree to which initially polarized incident light becomes depolarized upon emission, for example, yields information about how much the fluorophore can rotate between absorption and emission. This in turn can be used to examine the mobility or flexibility of the protein to which it is attached. If the fluorophore is held relatively rigidly to the host molecule, then tracking changes in the orientation of the fluorophore can be used to trace conformational changes in the host. Sase et al. (1), for example, were able to follow the axial rotation of actin filaments sliding over myosin fixed to a surface using this approach, while Adachi et al. (2) were able to directly observe the rotary motion of F1-ATPase.
Fluorescence can also be used as a way to measure distances in macromolecular systems by utilizing the process known as fluorescence resonance energy transfer (FRET). In this, one fluorescent molecule (the donor) excited by a photon of light spontaneously transfers its energy to another molecule (the acceptor) by a nonradiative dipole-dipole interaction (3–5). The fraction, or efficiency, of energy transferred depends on the distance between the molecules, and typically takes place over distances of 10–100 Å, depending on the spectral characteristics of the molecules. Thus, if fluorophores are attached to known sites, measurement of the efficiency of energy transfer provides an ideal probe of inter- and intramolecular distances over macromolecular length scales. With this in mind, FRET has been used for measuring the structure and conformational changes within molecules (6–10), interactions between molecules (11,12), and as a powerful indicator of biochemical events (13). A complication is that as well as being dependent on the distance between the fluorophores, the efficiency of energy transfer is also dependent on the relative orientation of the transition moments of the donor and acceptor molecules.
One major difficulty with fluorescence techniques that involve the orientation of the fluorophores is that measuring these orientations and their relation to the host molecule experimentally can be extremely difficult. Indeed, most successful applications involve rigidly binding the fluorophore to a single host molecule, and this host molecule to a surface (1,2). In most applications, however, neither of these is achieved, which can introduce a large degree of uncertainty into the interpretation of any results. In FRET, for example, the relative orientation of the donor and acceptor molecules is used to relate the efficiency of energy transfer to the distance between the molecules via the so-called orientation factor κ2, which can take values between 0 and 4. The difficulties involved in determining the orientations mean that in most cases the molecules are simply assumed to rapidly diffuse through all possible orientations to one another, in which case a value of κ2 = 2/3 can be used (4,14). The use of this value in general situations has been long debated (see, for example, (14,15)), and although it yields reasonable results in many situations, it is at best an approximation whose validity can only be determined by comparison with distance measurements obtained from other means such as from x-ray diffraction.
Recently, techniques have been developed to measure the orientation of fluorophores relative to the host molecule in macroscopically ordered systems such as when the host molecules are embedded in a cell membrane using measurements of the polarization of the emission (16–19) or directly from confocal images (20). However, at best these approaches can only be used to place limits on the possible orientations of the fluorophore relative to the host and cannot easily discriminate between different models of diffusion of the fluorophore orientation.
Computational techniques now provide alternative ways to examine the behavior of large biophysical systems. A recent publication demonstrated that simulation can be helpful in interpreting the results of fluorescence anisotropy experiments (21) by differentiating the effect of fast dynamics of the dye relative to the protein and the slower dynamics of the protein loop itself and the overall tumbling of the molecule. Molecular dynamics simulation has also been used to directly compare the distribution in distances between donor and acceptor pairs attached to a prion repeat protein allowing the dynamics of the protein to be determined in atomic detail (22). More-recent simulations have been used to directly calculate FRET between fluorophores attached to a polyproline linker (23) or involving tryptophan in a tetracycline repressor protein (24). No computational studies have been made, however, to study how the orientation of fluorescent tags added to proteins influence FRET taking place between them. This situation is becoming increasingly common as FRET is used to gather detailed structural information about proteins as they operate (10,25).
Here, we utilize computer simulation to help solve the problem of measuring fluorophore orientations with a specific application to FRET. We examine the orientation of dye molecules attached to an integral membrane protein MscL. This protein forms a safety valve in bacterial cells opening a wide pore under membrane tension to relieve pressure during hypoosmotic stress (26–28). By carefully parameterizing the dyes AlexaFluor488 (AF488) and AlexaFluor568 (AF568) the dye molecules can be simulated when attached to the host protein embedded in a lipid bilayer. This enables the relative orientation of the molecules to be determined during simulations for use in relating FRET efficiency measurements to the distance between the molecules and for comparison with corresponding experimental measurements. The distances between the fluorophores during the simulation can also be compared with values determined in experimental FRET measurements. Although fluorescent proteins are commonly used to label proteins when measuring FRET, we concentrate in this article on the smaller AlexaFluors to complement our experimental studies and, because, small molecule dyes are more commonly used when specific distances are being measured.
METHODS
Structures of the dyes
The structures of the AF488 and AF568 dyes were obtained by performing a sequence of geometry optimizations using the program Gaussian03 (29). Although the dyes are only available as a mixture of 5- and 6-isomers (Invitrogen-Molecular Probes, Eugene, OR), we restricted our study to the 5-isomer, hoping that this would make only a small adjustment to the final orientation of the dye molecule relative to the protein and membrane. An initial guess of each structure based upon a previously reported study of AF488 (21) was first geometry-optimized using Hartree-Fock theory and a 3-21G basis set. The results of this were then fed into a similar calculation using a 6-31G basis set, then a 6-31G* basis set before a final geometry was obtained using the 6-31+G* basis set for consistency with the CHARMM force field. Unlike the previous study of AF488 (21), five CH2 groups were included in the linker to make the structure consistent with that published by Invitrogen-Molecular Probes.
Parameterization of the dyes
The AlexaFluor dyes are comprised of an alkane linker attached to a large aromatic headgroup with an extended π-electron system. For this reason, they pose difficult targets for accurate parameterization for use with classical force-field methods. Fortunately, the headgroups of the dyes are likely to remain relatively planar in most situations. Thus, the overall orientation of the dye relative to the host molecule is most strongly influenced by the behavior of the linker region that is much more similar to well-parameterized molecules, an assertion that is supported by the simulations presented here.
Partial charges on the atoms were determined by fitting the electrostatic potential (i.e., the ESP method) (30,31) on the results of a BLYP density functional calculation utilizing the geometry-optimized structures. Due to the presence of sulfur atoms, a triple-ζ 6-311+G** basis set was used for this purpose. During resonance energy transfer, the donor molecule exists in an excited state before passing its energy to the acceptor molecule. As we are interested in the relative orientation of the molecules during such transfer events, we must calculate partial charges on the donor molecule in its first excited state. Atomic charges were calculated for both the ground and first excited states using time-dependent methods (32), and in all cases these charges were within 0.05 e of each other. Thus, the same set of partial charges could reasonably be used to represent both states. Any slightly asymmetric charges were adjusted to maintain the symmetry of the dye headgroup. Also, the aliphatic hydrogens were assigned a charge of 0.09 and the carbon to which they were attached adjusted to neutralize this as is standard in the CHARMM force field. Unlike in the previous study of AF488 (21), the total charge of each dye was set to −1 (rather than −2) as suggested by Invitrogen-Molecular Probes, and to make the molecule a closed shell system.
The equilibrium bond lengths, bond angles, and dihedral angles were determined from the quantum mechanical structures. Force constants, however, were determined from comparison to atoms with similar chemical environments in the CHARMM27 force field. The van der Waals parameters of the atoms are much less sensitive to the environment and were similarly derived from similar atom types in the force field. Partial charges and bond parameters for the bound form of the AlexaFluor molecules were obtained from quantum mechanical calculations of the AlexaFluor linker to a cysteine residue.
Determination of transition dipole moments
To be able to determine the angle between the transition moments of the dyes to the plane of the membrane as well as the angle between the donor and acceptor transition moments during molecular dynamics simulations, the orientation of these moments within the molecular structure must be determined. Calculations were made on both the entire geometry-optimized AlexaFluor structures, and on just the three-ring headgroup to allow larger basis sets to be used. Excited state calculations were made using both the single excitation CI-singles (33) and time-dependent methods (32) using either Hartree-Fock or density functional theory. Basis sets ranging from STO-3G to 6-311++G** were used for the headgroup calculations, while basis sets up to 6-31G* were examined for calculations on the entire molecule. Calculations were made using both Gaussian03 (29) and MOLPRO (34).
Molecular dynamics simulations
To conduct MD simulations, the imaged structure of the MscL protein (35) (PDB entry 1MSL) was placed within a 120 × 120 Å patch of POPC lipid membrane and solvated in a flexible TIP3 water- and ion-containing box (150 mM NaCl) making sure the entire system remained neutral as illustrated in Fig. 1. The entire system contained ∼170,000 atoms. Molecular dynamics simulations were performed with NAMD (36) using the CHARMM27 all-atom parameter set with a timestep of 1 fs and periodic boundaries. Electrostatic interactions were calculated using the particle-mesh Ewald scheme, while Lennard-Jones interactions are cut-off distance at 12 Å. All simulations were carried out at constant pressure (1 atmosphere) and temperature (310 K).
FIGURE 1.
Simulation system. AlexaFluor488 and AlexaFluor568 (shown in space-filling representation) are attached to residue 42 of the MscL protein (yellow) embedded in a lipid bilayer (light brown), surrounded by water (brown), sodium (purple), and chloride (green) ions. The front half of the lipid, water, and ion atoms have been removed to reveal the protein and dye molecules.
Initially, the MscL protein was equilibrated without dye molecules attached. To do this, the lipid and water was initially energy-minimized for 1000 steps while the protein was held fixed. Then, the protein backbone was fixed and all other atoms were minimized for a further 5000 steps before releasing the backbone and minimizing for a further 1000 steps. After this, harmonic constraints (3 kcal/Å2) were applied to the α-carbon atoms of the protein and the system was heated to 310 K over 3 ps of simulation before simulating for an additional 20 ps. Finally the restraints on the backbone atoms were halved for another 20 ps of simulation before turning all restraints off and simulating the entire system for 3.7 ns.
After this initial equilibration, separate simulations were conducted with AlexaFluor dyes attached at either residue 42 (end of a transmembrane helix) or at residue 55 (periplasmic domain). As the functional protein is pentameric, when one fluorophore is attached to each subunit a total of five fluorophores are included in the simulation. In this case we attach three AF488 molecules and two AF568. To attach the dye molecules, a mutation was introduced into each of the five subunits of the protein to mimic the introduction of a cysteine residue at that position as done experimentally when labeling the protein (10). Then, the dye molecules were positioned with their linkers adjacent to the cysteine residues to which they are attached and the headgroup pointing away from the protein and the dye was joined to the protein with a covalent bond. Water or ions overlapping with the dye were removed from the system. The system was then energy-minimized for 5000 steps before dynamics simulations were run. In addition, simulations were also made in which part of the protein and just one of the dye molecules were simulated as described in detail below.
Separate simulations were also conducted to examine the behavior of the free dye molecules in water. In these, the dye molecule was placed in a 40 Å3 box of water molecules with one Na+ ion to keep the system neutral. Simulations were performed with periodic boundary conditions as described above.
Calculation of fluorescence anisotropy and orientation factor
The fluorescence anisotropy was calculated from the simulations using an approach similar to that described previously, assuming the absorption and emission dipoles are parallel (21). The vector describing the transition moment was saved at every step and the anisotropy as a function of time calculated from
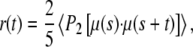 |
(1) |
where P2(x) = (3x2 – 1)/2, μ(s) is the transition moment at the time of excitation and μ(s + t) is the transition moment some time later. The averaging is achieved by taking results using each frame of the simulation as the time of excitation in turn and averaging results for the given time t after this.
The orientation factor κ2 can be easily calculated at any frame of the simulation from the transition moments using
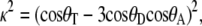 |
(2) |
where θT is the angle between the transition moments of the donor and acceptor, θD is the angle between the donor transition moment and the line connecting the donor and acceptor, and θA is the angle between the acceptor transition moment and this line.
Measures of the mobility of individual fluorophores
The average orientation of the fluorophores relative to the membrane and their mobility cannot be measured experimentally. All that can be determined is the B-factor that depends on both of these quantities (20),
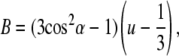 |
(3) |
in which α is the average angle between the fluorophore transition moment and the membrane normal. The quantity u represents a measure of the orientational freedom of the fluorophore with values closer to 1 representing more rigidly held orientations. The value u = 1 implies fixed fluorophore orientations and u = 1/3 completely free orientations. The parameter u does not contain informational about the rate of orientational rearrangement, only the average orientational distribution and cannot be directly related to the fluorescence anisotropy decay r(t). The expression u = 1, however, does imply that the anisotropy is constant r(t) = 2/5.
RESULTS
Structures of the dyes
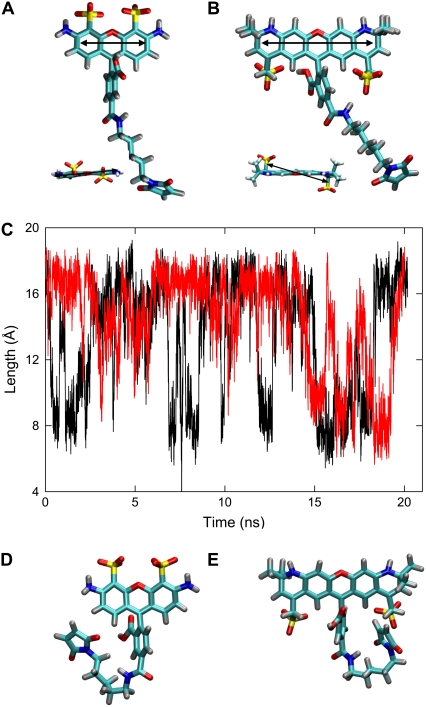
The geometry-optimized structures of the AlexaFluor dyes are shown in Fig. 2, A and B, respectively. Consistent transition moments were obtained using both CIS and TD Hartree-Fock methods for both the entire molecule and the headgroup only (provided the basis set was larger than STO-3G). Surprisingly, using TD DFT with both the BLYP and B3LYP functionals created incongruous results with only very weak transition moments found. The directions of the transition moment found in the Hartree-Fock methods are indicated by the arrows in Fig. 2, A and B. For AF488, this lies roughly in the plane of the headgroup structure; but for AF568, it is slightly skewed due to the off-plane positions of the sulfite groups.
FIGURE 2.
Structures of AlexaFluor dyes. The geometry-optimized structures found in ab initio calculations are shown for (A) AF488 and (B) AF568. The direction of the transition moment is indicated by the arrow. (C) The length of the dyes, measured from the central oxygen in the headgroup to the furthest carbon in the linker is plotted during simulations in which AF488 (black) or AF568 (red) is immersed in water. Compact structures sampled during the molecular dynamics simulations are shown for (D) AF488 and (E) AF568.
AlexaFluor dyes in water
The linker groups in the fluorophores are found to be quite flexible in molecular dynamics simulations. When the fluorophores are placed in a water box they are found to oscillate between two predominant structures as indicated in Fig. 2 C, where the length of the molecule is plotted during the simulation (measured between the oxygen in the center of the headgroup and the carbon at the far end of the maleimide group). In one of these conformations the molecule is fully extended, very similar to the structures found in the ab initio calculations. In the other, the linker bends into a compact U-shape (Fig. 2, D and E) such as to minimize the interaction between the nonpolar linker with the surrounding water. Similar conformations were reported in a previous molecular dynamics simulation of AF488 (21).
It has previously been noted that the decay of fluorescence anisotropy of the dyes, an experimentally measurable property, can be directly predicted from simulations such as conducted in this study. We calculated the fluorescence anisotropy decay of AF488 and AF568 in water, and fitting the decay curves with a single exponential function yields a rotational correlation time of 176 ps for AF488 and 316 ps for the larger AF568 molecule. Notably, the result for AF488 is longer than found in the previous study, and much closer to the experimentally measured value (170 ps). The use of a longer linker group, a different charge on the fluorophore to match the properties suggested by Invitrogen-Molecular Probes, and the use of a different force field (CHARMM as opposed to GROMACS), may explain these differences.
AlexaFluor dyes on MscL
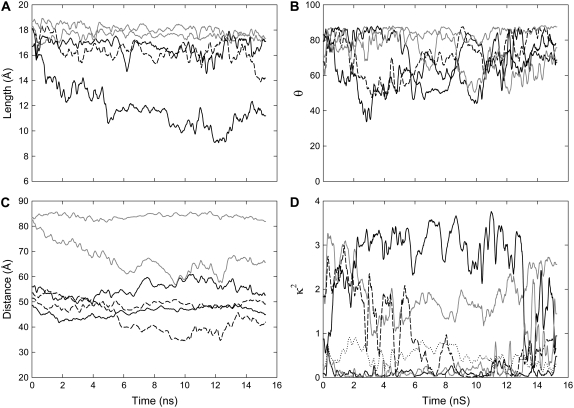
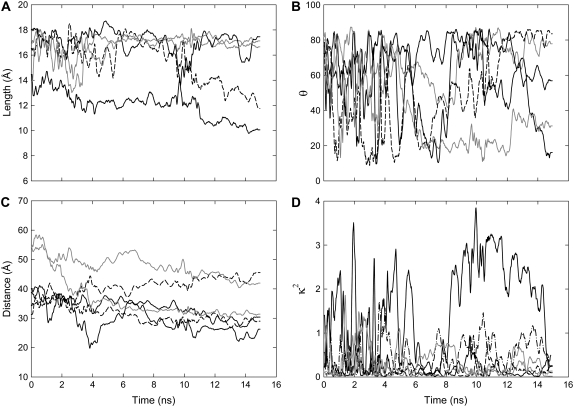
Similar conformational changes of the linker are observed when the dye molecules are bound to the MscL protein as in water, but the timescale of the oscillations between them is much slower. In Fig. 3 A the lengths of the five fluorophores attached to residue 42 are shown, and it is apparent that while four of them remain in the extended conformation for the entire simulation, one AF488 quickly adopts the bent shape. A similar plot is shown in Fig. 4 A when the fluorophores are attached to residue 55. In this case one fluorophore remains in the compact conformation throughout the simulations, but two others also sample this state.
FIGURE 3.
Properties of the fluorophores when attached to residue 42 near the lipid-water interface on MscL. Running average values of the length of the fluorophores (A), and angle between the transition moment and membrane normal (B) are shown during the simulations for each fluorophore, where results for the three AF488 molecules are shown as solid or dashed curves and two AF568s in shading. The running average distance between each of the AF488 and AF568 fluorophore pairs (C) and the orientation factor for transfer between them (D) are shown where the nearest neighbor pairs are shown as solid or dashed lines, and next nearest-neighbor pairs are shown in shading.
FIGURE 4.
Properties of the fluorophores when attached to residue 55 in the periplasmic domain of MscL. All symbols are as for Fig. 3. The relatively common low κ2 values arise from the AlexaFluor headgroups lying perpendicular to one another.
For comparison with measurements of the orientation of fluorophores attached to membrane-bound proteins, we plot the angle of the fluorophore transition moment with respect to the membrane normal in Figs. 3 B and 4 B. When the dyes are attached to site 42, the headgroups remain fairly much in the plane of the membrane throughout the simulation. As this site lies level with the top of the membrane the fluorophores can adopt a relatively stable configuration along the membrane water interface, as can be seen in Fig. 1. This allows the nonpolar linker to sit within the hydrophobic core of the membrane, while the polar headgroups of the fluorophores sit among the lipid headgroups and water. When the fluorophores are attached further from the membrane (Fig. 4 B), no such configurations can arise and they are found to be much more mobile, sampling a number of angles throughout the simulation.
The actual angle of the fluorophore relative to the membrane cannot be measured directly using experimental methods (20). Rather, what can be measured is the so-called B-factor that relates the average angle and the mobility of the fluorophore. In Table 1, we show the average angle, mobility, and B-factor for each of the fluorophores in the two simulations. The mobility, or orientational freedom of the fluorophores is denoted by the parameter u that can range from 0 for completely mobile fluorophores to 1 for fluorophores with a fixed orientation (20). The values of u show that the fluorophores are more mobile when attached to the periplasmic domain in agreement with previous results. Surprisingly, this freedom means that the values of the B-factor are very different for each fluorophore, adopting both positive and negative values, and show greater variation than when the fluorophores are attached to site 42. The B parameter has been measured experimentally for these situations, yielding values of −0.10, −0.19 for AF488 and AF568 attached to site 42 and −0.08, and −0.15 when attached to site 55 (20). The difference between the simulated values and the measured ones, as well as the variation within the results for the different fluorophores, suggests that the simulation has not been conducted for long enough to obtain reliable average values, a point that will be discussed in more detail below.
TABLE 1.
Orientation-related properties of the AlexaFluor dyes
| Site 42
|
Site 55
|
|||||
|---|---|---|---|---|---|---|
| AF | θ | u | B | θ | u | B |
| 1 AF488 | 61 | 0.96 | −0.18 | 53 | 0.86 | 0.046 |
| 2 AF568 | 69 | 0.96 | −0.37 | 69 | 0.96 | −0.38 |
| 3 AF488 | 83 | 0.98 | −0.61 | 47 | 0.90 | 0.22 |
| 4 AF568 | 74 | 0.95 | −0.48 | 71 | 0.96 | −0.42 |
| 5 AF488 | 72 | 0.97 | −0.43 | 39 | 0.90 | 0.48 |
These properties were found during simulations in which they are attached to residue 42 or residue 55 of MscL.
In Figs. 3 C and 4 C, the distance between the AF488 and AF568 pairs is plotted—the property usually measured in FRET experiments. It is notable that these distances do not stay constant during the simulation. When attached at residue 42, the distance between next-nearest neighbors is always larger than that between nearest neighbors, as may be expected. But, the difference in distance between pairs of nearest or next-nearest neighbors can differ by as much as 20 Å. Measurement of the distance between many FRET pairs, as in ensemble measurements, will only yield the average intensities resulting from an average of all fluorophore separations. When the fluorophores are attached to the periplasmic domain, next nearest neighbors at times get closer than nearest neighbors. This results from the system losing its fivefold symmetry, as can be seen in Fig. 5 B. This may have consequences when interpreting FRET data assuming a symmetric protein.
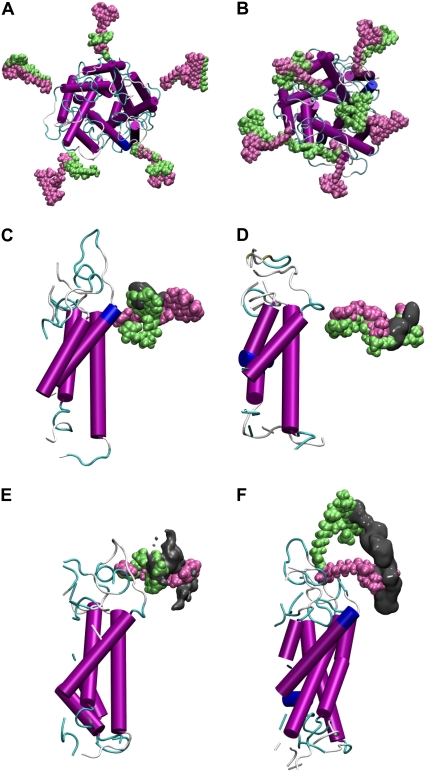
FIGURE 5.
Locations of the fluorophores at the beginning (pink) and end (green) of each simulation. Results are shown for 15-ns simulations when the fluorophores are attached to (A) residue 42 and (B) residue 55. Similar results are shown for simulations of a single fluorophore and only part of the protein: (C) AF488 attached at residue 42 (50-ns simulation); (D) AF568 attached to residue 42 (50-ns simulation); (E) AF488 attached to residue 55 (30-ns simulation); and (F) AF568 attached to residue 55 (30-ns simulation). The volume of space sampled by the central oxygen in the fluorophore headgroup is indicated by the gray surface in the later pictures.
Finally, the instantaneous orientation factor, κ2, which influences resonance energy transfer, is plotted in Figs. 3 D and 4 D. It is evident in our simulations firstly that the κ2 value is often significantly different between different pairs of fluorophores. Secondly, these values change significantly during the simulation, and it is not unusual for the fluorophores to sample the entire range of possible values (0–4) within the short simulation time (15 ns). Given that the fluorescence lifetime of most fluorophores is a few nanoseconds, it is quite likely that their relative orientation will change while the donor is excited, a fact that should be apparent in measurements of fluorescence anisotropy.
The average value of κ2 for each fluorophore pair is shown in Table 2. The MscL protein is made from five identical subunits, meaning that the fluorophores are attached to identical sites. Thus, the fact that differing pairs of fluorophores have very different average κ2 values suggests that the simulations have not been run for long enough to obtain good average values, and that longer simulations are required to directly predict the orientation factor from such simulations. Unfortunately, the size of the simulation makes this computationally demanding.
TABLE 2.
Average κ2 values for energy transfer between AlexaFluor pairs during molecular dynamics simulations
| AF pair | Site 42 | Site 55 |
|---|---|---|
| 1 2 | 0.119 | 1.812 |
| 3 2 | 1.785 | 0.205 |
| 3 4 | 2.650 | 0.650 |
| 5 4 | 0.606 | 0.126 |
| 1 4 | 0.322 | 0.134 |
| 5 2 | 0.416 | 0.277 |
Averages do not include the first 3-ns equilibration time.
Single AlexaFluor dyes on MscL
As simulations of fluorophores attached to the complete MscL pentamer did not allow the average orientation factor (or FRET efficiency) to be determined, two alternative approaches were examined to overcome the computational requirements of long simulations. The first involved conducting simulations on smaller systems containing only one fluorophore while the second approach was to assume that each fluorophore moves independently to increase the ensemble that was being averaged.
Six additional simulations were conducted on smaller systems, each containing just one-fifth of the protein and one fluorophore. Two independent simulations were conducted with each of AF488 and AF568 attached to site 42 (one for 50 ns and one for 25 ns), while one was conducted with each fluorophore attached to site 55 (each 30 ns in length). To do this, a region of the large simulations containing the desired fluorophore along with the surrounding protein, lipid, and water was selected. Atoms within 2 Å of the edge were held by strong harmonic constraints (2 kcal/mol Å2) to maintain the integrity of the system, while the remainder of the atoms could move freely. Snapshots showing the selected protein and fluorophore are shown in Fig. 5.
Simulations on these smaller systems could be conducted for up to 50 ns—significantly longer than any conducted on the entire pentameric system. In Fig. 5, C–F, the position of the fluorophores relative to the protein is shown at the beginning and end of the simulations. The region of space sampled by the central oxygen in the headgroup of each fluorophore is also illustrated by the gray surface, indicating that the fluorophores do move considerably during the simulation. As noted previously, fluorophores attached to the periplasmic domain appear more mobile than those attached at the lipid water interface. This can be quantified by calculating the volume of the surfaces illustrated in Fig. 5 as in Table 3, which shows the periplasmic fluorophores are almost twice as mobile.
TABLE 3.
Mobility of fluorophores and cysteine residue to which they are bound
| Volume of isosurface (Å3)
|
||
|---|---|---|
| Fluorophore | Site 42 | Site 55 |
| AF488 | 25,226 | 58,293 |
| AF568 | 22,560 | 55,052 |
| CYS | 15,917 | 20,242 |
The volume of the surface swept out by the central oxygen atoms in the headgroup of the fluorophores, or the sulfur atom in the cysteine residue in 25 ns of simulation, is shown for each site.
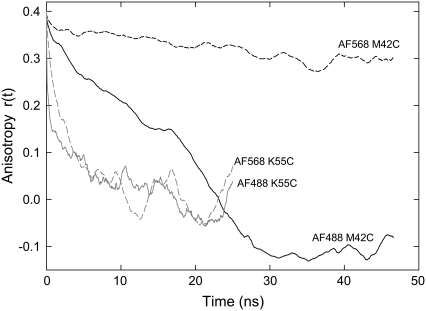
As expected, the fluorophores are much less mobile when attached to MscL than they are when dispersed in water. As a consequence, the timescale for fluorescence anisotropy decay is much larger, as illustrated in Fig. 6. Indeed, when the fluorophores are attached to residue 42 the fluorophore orientation does not change significantly during 50 ns of simulation, thus the timescale for rotational correlation cannot be estimated. The greater rotational freedom of the fluorophores attached to residue 55 does lead to their orientations becoming uncorrelated after long times and a rotational correlation time of 1.8 and 2.7 ns for AF488 and AF568, respectively—much greater than found for the dyes in water.
FIGURE 6.
Fluorescence anisotropy decay curves calculated from simulations of a single fluorophore attached to MscL. Results are shown for AF488 (solid line) and AF568 (dashed line) attached to site 42 (solid color) and site 55 (shaded line).
An interesting question to consider is whether the greater mobility of the fluorophores when attached to residue 55 compared to residue 42 is a consequence of the differing environment of the fluorophores or the mobility of the protein site to which they are attached. To help answer this question the volume of space sampled by the sulfur atom in the cysteine residue to which the fluorophores are bound is also shown in Table 3. Although the residue 55 has slightly greater mobility than residue 42, the difference is much smaller than it is for the fluorophores themselves, suggesting that greater mobility of fluorophores attached to site 55 is due more to their bulk environment than any difference in the underlying protein mobility at that site.
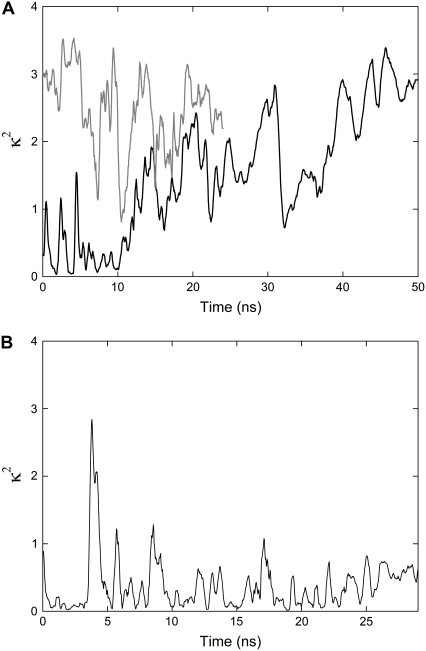
To judge whether the simulations of the smaller systems have enabled long enough simulations to be conducted to collect reliable overage fluorophore orientations, we need to consider how reliably the fluorophores sample their possible conformational space. One way to do this is to note whether the fluorophore length, angle to the membrane, and orientation factor visit the same values many times during the simulation, or continue to adopt new values as the simulation proceeds. Although the distance and orientation factor κ2 cannot be directly determined from simulation of a single fluorophore, this information can be inferred if we assume that the simulations of the donor (AF488) and acceptor (AF568) are offset by 72° with respect to one another as in a pentameric protein. The orientation factor calculated in this way is plotted in Fig. 7. As the fluorophores are more mobile when attached to site 55, it appears as if a reasonable average value for κ2 could be obtained. However, it appears unlikely that a reliable average value could be determined for site 42 as the orientation factor appears to sample new values throughout the entire simulation period.
FIGURE 7.
Running average orientation factor calculated from simulations of just one fluorophore and part of the protein. Results are calculated with fluorophores attached to (A) site 42 and (B) site 55. Results of a second independent simulation for site 42 are also indicated by the shaded line.
Single pot ensemble averaging
The second approach to improve the sampling is to assume that each fluorophore in each simulation moves independently. This means firstly that the relative orientations of different fluorophores in the same simulation, as well as fluorophores in separate simulations, can be utilized by rotating each about the axis of symmetry in the pentameric protein by multiples of 72° as described above. Secondly, the orientation factor can be calculated over all combinations of times, rather than simply calculating it from the orientation of each fluorophore at the same time in the simulation. To do this, the position of each fluorophore at each time step in each simulation was treated equivalently and, after rotation so that each was aligned as if attached to the same protein subunit, added to a large pot containing all the other fluorophore positions and conformations. Averaging the quantities of interest of this large ensemble greatly increases the statistics.
We first consider the average properties of single fluorophores as shown in Table 4. While our simulations data, especially that for site 42, predicts more negative values for the B-factor than found experimentally (−0.08 to −0.19), they do place the average angle relative to the membrane normal in the experimentally determined range.
TABLE 4.
Orientation-related properties of single AlexaFluor dyes
| Site | AF | θ | u | B |
|---|---|---|---|---|
| 42 | 488 | 72 | 0.95 | −0.43 |
| 42 | 568 | 79 | 0.97 | −0.56 |
| 55 | 488 | 64 | 0.91 | −0.25 |
| 55 | 568 | 53 | 0.89 | −0.04 |
These properties were found from the one-pot ensemble averaging.
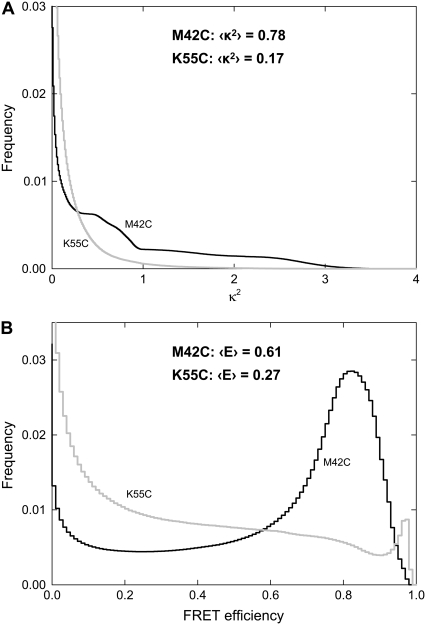
The more interesting quantities to calculate are the average values of the orientation factor and the FRET efficiency for transfer between fluorophores. In Fig. 8 we plot frequency histograms for both of these quantities. It is notable that our results predict that the FRET efficiency of transfer between fluorophores at any instant in time could lie almost anywhere in the possible range from 0 to 1, a consequence of the fact that the fluorophores alter their relative orientation and positions significantly during the simulations. Notably the average FRET efficiency when the fluorophores are attached to site 42 is 0.61 is in perfect agreement with the experimentally determined value of 0.61 ± 0.1. This should be considered somewhat fortuitous given that the measurements of the individual fluorophore orientations described above differ with experimental values. It does, however, suggest that the structural arrangements of the fluorophores seen in these simulations may reflect the positions adopted in reality. The values of κ2, in this case, are larger than the traditionally used value of 2/3, because, as the fluorophores keep some degree of alignment through the simulations, they all remain roughly in the plane of the membrane.
FIGURE 8.
Results from ensemble averaging of the data as described in the text. The frequency at which each value of (A) the orientation factor and (B) the given FRET efficiency arise are indicated with the fluorophores attached to site 42 (solid lines) and site 55 (shaded lines).
In contrast, the orientation factor when the fluorophores are attached to site 55 is significantly lower than the dynamic average value of 2/3. This results in a lower FRET efficiency than seen for site 42, despite the fact that the fluorophores are generally closer together (see Fig. 4). That the FRET efficiency is lower in this case is in agreement with unpublished experimental measurements, although measurements suggest a real value of <0.1.
DISCUSSION
The simulation of fluorophores attached to protein molecules has the prospect of greatly enhancing our understanding of experimental measurements by allowing the prediction of properties such as fluorophore orientations that cannot be measured experimentally. In this case we attach AF488 and AF568 to two different sites on the MscL protein and examine their behavior over many tens of nanoseconds of simulations. One clear conclusion of these simulations is that the fluorophores are relatively mobile, adopting both extended and compact conformations as well as rotating in space. It is also clear that the environment of the fluorophores can greatly influence their mobility. When the dyes are attached near the membrane water interface, they adopt relatively stable configurations with the nonpolar regions interacting with the hydrophobic lipid core, and the polar headgroups with the lipid headgroups and water. When the dyes stick into bulk water, however, they can rotate more freely. Thus, caution must be applied if using measures of the motion of the dyes to directly represent the underlying motion of the host molecule. Surprisingly, there was no evidence of the fluorophores inserting into the lipid core, despite the extended aromatic rings in their structures.
It was hoped that the simulations conducted in this study might be used to predict the likely value of the orientation factor κ2 for use in corresponding FRET experiments. Simulations of the dyes in water in this and a previous study (21) has shown that short molecular dynamics simulations can be used to accurately predict the anisotropy decay, a property that is related to the orientational freedom of the fluorophores. Also, the fact that fluorescence lifetimes are approximately a few nanoseconds gave hope that we would be able to simulate for long enough to accurately predict values for κ2. When attached to the MscL protein, however, the orientational freedom of the fluorophores is reduced and the time required to allow the fluorophore to sample all available configurations is greatly enlarged. This means that long simulations are required to calculate useful average values of the orientation of the transition moments of the fluorophores relative to the plane of the membrane and to each other. Alternatively, given the short length of the excited state compared to the timescale of mobility of the fluorophores, it is possible that FRET measurements could be sampling nonequilibrium configurations. We simulated for up to 50 ns, but were unable to obtain useful values as is apparent in the discrepancies between our predicted B factors and measured values. As a consequence, we were unable to predict the most likely value of κ2 to use when interpreting our experiments.
It is worthwhile reflecting under what conditions the approach developed here will be of use in determining likely orientation factors in situations of biological relevance. The methodology is not straightforward; it requires accurate parameterization of the fluorophores for use in MD simulations, since this has not previously been done for many such molecules. It requires knowledge of the orientation of the transition dipoles within the molecule from experimental measurements or a willingness to calculate these using ab initio methods. Finally it requires long molecular dynamics simulations to derive accurate average properties. The poor sampling arising in our simulations results both from having a large protein that requires a large simulation system, and the interaction of the fluorophores with the lipid that reduces their mobility. Such issues may be less of a problem in small soluble proteins, or could be countered by using greater computational power. This means that an assessment of the solvent accessibility of the fluorophores and the size of the protein may help to determine whether the computational effort involved in simulating it is likely to achieve worthwhile results.
Alternatively, rather than using a brute force approach that requires large simulations times to determine the fluorophore orientations as in this study, biasing forces could be used to make the fluorophores sample a greater range of configurations is a shorter simulation time. Using umbrella sampling (37–39) with the location of the center of the fluorophore headgroup as the reaction coordinate, for example, could enable a probability distribution function for the fluorophore configurations to be determined, from which much better average orientations could be extrapolated.
Although still in its infancy, the use of molecular simulations to better understand and interpret fluorescence experiments holds great promise.
Acknowledgments
Parameter files for the AlexaFluor dyes are available from the authors.
This work is supported by funding from the Australian Research Council, an award under the Merit Allocation Scheme on the Australian Partnership for Advanced Computing National Facility at the Australian National University, and additional computer time from iVEC.
Editor: Helmut Grubmüller.
References
- 1.Sase, I., H. Miyata, S. Ishiwata, and K. Kinosita. 1997. Axial rotation of sliding actin filaments revealed by single-fluorophore imaging. Proc. Natl. Acad. Sci. USA. 94:5646–5650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Adachi, K., R. Yasuda, H. Noji, H. Itoh, Y. Harada, M. Yoshida, and J. K. Kinosita. 2000. Stepping rotation of F1-ATPase visualized through angle-resolved single-fluorophore imaging. Proc. Natl. Acad. Sci. USA. 97:7243–7247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Förster, T. 1959. Transfer mechanisms of electronic excitation. Discuss. Faraday Soc. 27:7–17. [Google Scholar]
- 4.van der Meer, B., G. Coker, and S. Chen. 1994. Resonance Energy Transfer: Theory and Data. VCH, New York.
- 5.Clegg, R. 1996. Fluorescence resonance energy transfer (FRET). In Fluorescence Imaging Spectroscopy and Microscopy. X. F. Wang and B. Herman, editors. Wiley and Sons, New York.
- 6.Haas, E., E. Katchalski-Katzir, and I. Steinberg. 1975. Effect of the orientation of donor and acceptor on the probability of energy transfer involving electronic transitions of mixed polarization. Biochemistry. 17:5065–5070. [DOI] [PubMed] [Google Scholar]
- 7.Lakowicz, J., I. Gryczynski, W. Wiczk, G. Laczko, F. Prendergast, and M. Johnson. 1990. Conformational distributions of melittin in water/methanol mixtures from frequency-domain measurements of nonradiative energy transfer. Biophys. Chem. 36:99–115. [DOI] [PubMed] [Google Scholar]
- 8.Chapman, E., K. Alexander, T. Vorherr, E. Carafoil, and D. Storm. 1992. Fluorescence energy transfer analysis of calmodulin-peptide complexes. Biochemistry. 31:12819–12825. [DOI] [PubMed] [Google Scholar]
- 9.Heyduk, T. 2002. Measuring protein conformational changes by FRET/LRET. Curr. Opin. Biotechnol. 13:292–296. [DOI] [PubMed] [Google Scholar]
- 10.Corry, B., P. Rigby, Z. Liu, and B. Martinac. 2005. Conformational changes involved in MscL channel gating measured using FRET spectroscopy. Biophys. J. 89:L49–L51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hink, M., T. Bisselin, and A. Visser. 2002. Imaging protein-protein interactions in living cells. Plant Mol. Biol. 50:871–883. [DOI] [PubMed] [Google Scholar]
- 12.Parsons, M., B. Vojnovic, and S. Ameer-Beg. 2004. Imaging protein-protein interactions in cell motility using fluorescence resonance energy transfer (FRET). Biochem. Soc. Trans. 32:431–433. [DOI] [PubMed] [Google Scholar]
- 13.Bunt, G., and F. Wouters. 2004. Visualization of molecular activities inside living cells with fluorescent labels. Int. Rev. Cytol. 237:205–277. [DOI] [PubMed] [Google Scholar]
- 14.Remedios, C. D., and P. Moens. 1995. Fluorescence resonance energy transfer spectroscopy is a reliable “ruler” for measuring structural changes in proteins. J. Struct. Biol. 115:175–185. [DOI] [PubMed] [Google Scholar]
- 15.Dale, R., J. Eisinger, and W. Blumberg. 1979. The orientational freedom of molecular probes: the orientation factor in intramolecular energy transfer. Biophys. J. 26:161–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.van der Meer, B., R. P. H. Kooyman, and Y. K. Levine. 1982. A theory of fluorescence depolarization in macroscopically ordered membrane systems. Chem. Phys. 66:39–50. [Google Scholar]
- 17.van Gurp, M., H. van Langen, G. van Ginkel, and Y. Levine. 1988. Angle resolved techniques in studies of organic molecules in ordered systems using polarized light. In Polarized Spectroscopy of Ordered Systems. Kluwer, Dordrecht, the Netherlands.
- 18.van der Heide, U., B. Orbons, H. Gerritsen, and Y. Levine. 1992. The orientation of transition moments of dye molecules used in fluorescence studies of muscle systems. Eur. Biophys. J. 21:263–272. [DOI] [PubMed] [Google Scholar]
- 19.Benninger, R., B. Önfelt, M. Neil, D. Davis, and P. French. 2005. Fluorescence imaging of two-photon linear dichroism: cholesterol depletion disrupts molecular orientation in cell membranes. Biophys. J. 88:609–622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Corry, B., D. Jayatilaka, B. Martinac, and P. Rigby. 2006. Determination of the orientational distribution and orientation factor for transfer between membrane bound fluorophores using a confocal microscope. Biophys. J. 91:1032–1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Schröder, G., U. Alexiev, and H. Grubmüller. 2005. Simulation of fluorescence anisotropy experiments: probing protein dynamics. Biophys. J. 89:3757–3770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gustiananda, M., J. Liggins, P. Cummins, and J. Gready. 2004. Conformation of prion protein repeat peptides probed by FRET measurements and molecular dynamics simulations. Biophys. J. 86:2467–2483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Best, R., K. Merchant, I. Gopich, B. Schuler, A. Bax, and W. Eaton. 2007. Effect of flexibility and cis residues in single-molecule FRET studies of polyproline. Proc. Natl. Acad. Sci. USA. 104:18964–18969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Beierlein, F., O. Othersen, H. Lanig, S. Schneider, and T. Clark. 2006. Simulating FRET from tryptophan: is the rotamer model correct? J. Am. Chem. Soc. 128:5142–5152. [DOI] [PubMed] [Google Scholar]
- 25.Posson, D., C. M. P. Ge, F. Bezanilla, and P. Selvin. 2005. Small vertical movement of a K+ channel voltage sensor measured with luminescence energy transfer. Nature. 436:848–851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Martinac, B. 2004. Mechanosensitive ion channels: molecules of mechanotransduction. J. Cell Sci. 117:2449–2460. [DOI] [PubMed] [Google Scholar]
- 27.Hamill, O., and B. Martinac. 2001. Molecular basis of mechanotransduction in living cells. Physiol. Rev. 81:685–740. [DOI] [PubMed] [Google Scholar]
- 28.Levina, N., S. Totemeyer, N. Stokes, P. Louis, M. Jones, and I. Booth. 1999. Protection of Escherichia coli cells against extreme turgor by activation of MscS and MscL mechanosensitive channels: identification of genes required for MscS activity. EMBO J. 18:1730–1737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Frisch, M. J., G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, and J. A. Pople. 2004. Gaussian 03, Rev. C.02. Gaussian, Wallingford CT.
- 30.Singh, U. C., and P. A. Kollman. 1984. An approach to computing electrostatic charges for molecules. J. Comput. Chem. 5:129–145. [Google Scholar]
- 31.Besler, B. H., K. M. Merz, Jr., and P. A. Kollman. 1990. Atomic charges derived from semiempirical methods. J. Comput. Chem. 11:431–439. [Google Scholar]
- 32.Stratmann, R. E., G. E. Scuseria, and M. J. Frisch. 1998. An efficient implementation of time-dependent density-functional theory for the calculation of excitation energies of large molecules. J. Chem. Phys. 109:8218–8224. [Google Scholar]
- 33.Foresman, J. B., M. Head-Gordon, J. A. Pople, and M. J. Frisch. 1992. Toward a systematic molecular orbital theory for excited states. J. Phys. Chem. 96:135–149. [Google Scholar]
- 34.Werner, H.-J., P. J. Knowles, R. Lindh, F. R. Manby, M. Schütz, P. Celani, T. Korona, G. Rauhut, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, C. Hampel, G. Hetzer, A. W. Lloyd, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklaß, P. Palmieri, R. Pitzer, U. Schumann, H. Stoll, A. J. Stone, R. Tarroni, and T. Thorsteinsson. 2006. MOLPRO, Ver. 2006.1. A package of ab initio programs. http://www.molpro.net.
- 35.Chang, G., R. Spencer, A. Lee, M. Barclay, and D. Rees. 1998. Structure of the MscL homologue from Mycobacterium tuberculosis: a gated mechanosensitive ion channel. Science. 282:2220–2226. [DOI] [PubMed] [Google Scholar]
- 36.Phillips, J., R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. Skeel, L. Kale, and K. Schulten. 2005. Scalable molecular dynamics with NAMD. J. Comput. Chem. 26:1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Torrie, G., and J. Valleau. 1974. Monte Carlo free energy estimates using non-Boltzmann sampling: application to the sub-critical Lennard-Jones fluid. Chem. Phys. Lett. 28:578–581. [Google Scholar]
- 38.Kumar, S., D. Bouzida, R. Swendsen, P. Kollman, and J. Rosenberg. 1992. The weighted histogram analysis method for free energy calculations on biomolecules.1. The method. J. Comput. Chem. 13:1011–1021. [Google Scholar]
- 39.Roux, B. 1995. The calculation of potential of mean force using computer simulations. Comput. Phys. Commun. 91:275–282. [Google Scholar]