Dielectric Cytometry with Three-Dimensional Cellular Modeling

Abstract

We have developed what we believe is an efficient method to determine the electric parameters (the specific membrane capacitance C_m and the cytoplasm conductivity κ_i) of cells from their dielectric dispersion. First, a limited number of dispersion curves are numerically calculated for a three-dimensional cell model by changing C_m and κ_i, and their amplitudes Δɛ and relaxation times τ are determined by assuming a Cole-Cole function. Second, regression formulas are obtained from the values of Δɛ and τ and then used for the determination of C_m and κ_i from the experimental Δɛ and τ. This method was applied to the dielectric dispersion measured for rabbit erythrocytes (discocytes and echinocytes) and human erythrocytes (normocytes), and provided reasonable C_m and κ_i of the erythrocytes and excellent agreement between the theoretical and experimental dispersion curves.

INTRODUCTION

Cell membranes regulate the transport of materials between the cytoplasm and the extracellular environment. Transition in the state of the cell is usually accompanied by changes in the electric parameters of the cytoplasm and the membrane. Thus, quantitative measurement of the electric parameters is important not only for basic biological research but also for clinical diagnosis. Among the various measurement methods available, dielectric spectroscopy, which measures the frequency dependence of complex permittivity ɛ*(ω) (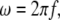 where f is the frequency), enables nondestructive, label-free estimation of the electric parameters. Since the estimation utilizes the dielectric relaxation of the cell suspension due to interfacial polarization, which is sensitive to the structure of the cell (especially cell shape), modeling of cells is very important for analysis of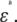

Erythrocytes are commonly employed for diagnosis of diseases, and their shape is susceptible to physiological conditions that cause them to change from biconcave to echinus-like and spherical shapes (1–5). For the spherical erythrocyte (spherocyte), can be represented by an analytical equation for a simple spherical cell model (6,7). Such analytical approaches are, however, applicable only to simple shapes such as spheres and ellipsoids—not to more complicated shapes. Because of a lack of analytical solutions, it has been difficult to determine the electric parameters of even the normocyte (normal erythrocyte) on the basis of the model with high fidelity to its biconcave shape. Hence, we have developed a new numerical method based on rigorous electric-field simulation combined with three-dimensional modeling of an erythrocyte to determine its electric parameters from the experimental 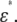With this method, computational effort is drastically reduced by the use of an efficient regression analysis. The method was tested on both rabbit and human erythrocytes with highly anisotropic shapes: discocytes with a biconcave shape, echinocytes from rabbit blood with an echinus-like spinous shape (see Fig. 1 a), and normocytes from human blood.

FIGURE 1.

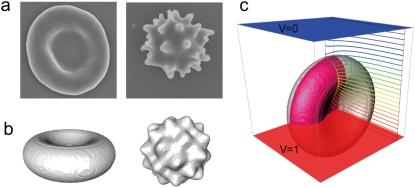
(a) SEM images of the discocyte (left) and the echinocyte (right). (b) The corresponding three-dimensional models for FDM simulation. (c) The eighth part (highlighted in red) of the discocyte model used for the simulation and the calculated isopotential lines at 1.0 × 10⁵ Hz.

METHODS

Sample preparation and characterization

The blood of a healthy rabbit (Oryctolagus cuniculus, ∼15 weeks old) was supplied from Kohjin Bio (Sakado, Japan) 1 day after it was collected in an antiseptic environment. It was immediately mixed with an equal volume of Alsever's solution (anhydrous citric acid 0.55 g/L, anhydrous sodium citrate 8.0 g/L, sodium chloride 4.2 g/L, and glucose 20.5 g/L). The rabbit blood was centrifuged at 500 × g for 10 min (this condition was always used thereafter), and the sediment was suspended in phosphate-buffered saline (PBS) of pH 7.4 at 298 K. In the suspension, more than 90% of the erythrocytes were echinocytes, probably because of the temporal transformation of the normocytes during preservation before the blood was received. To prepare the spherocytes and discocytes, the echinocytes were incubated in PBS of pH 5.3 and 8.5, respectively, for ∼30 min at 298 K until it was confirmed by means of an optical microscope (Axio Imager M1, Carl Zeiss, Jena, Germany) that they had transformed into the intended shape. In addition, normal human erythrocytes collected from a healthy person were washed twice with PBS of pH 7.4 by centrifugation and resuspended in the same PBS. A hematocrit centrifuge (Haematokrit 210, Andreas Hettich, Tuttlingen, Germany) was used to measure the volume fraction P (for the spherocyte, P was also derived from 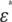using the spherical cell model (7)).

The morphological parameters that characterize the spherocytes, discocytes, and echinocytes were measured using the optical microscope as follows (1): The diameter of a spherocyte is 6.1 ± 0.45 μm (2). The length along the longitudinal axis of a discocyte is 8.0 ± 0.59 μm (3). The top-to-top and valley-to-valley distances between a diagonal pair of spines over the echinocyte surface are 7.8 ± 0.47 and 5.4 ± 0.57 μm, respectively. The shapes of the erythrocytes were also examined using a scanning electron microscope (SEM; S-3000N, Hitachi High-Technologies, Hitachi, Japan). The erythrocytes were fixed by 1% glutaraldehyde for 2 h at 277 K and dehydrated in a graded series of alcohol solutions (50%, 70%, 90%, 95% v/v, and anhydrous ethanol). They were then spread on cover glasses, dried in air, and sputtered with platinum before SEM observation. Because the erythrocytes were considerably reduced in size during the fixation and dehydration processes, we used the optical microscope instead of the SEM to obtain the geometric parameters of the erythrocytes for quantitative analysis.

Dielectric spectroscopy measurement

Dielectric spectra were measured for the rabbit discocytes, echinocytes, and spherocytes, and the human normocytes suspended in PBS of pH 8.5, 7.4, 5.3, and 7.4, respectively, by an impedance analyzer (4294A, Agilent Technologies, Santa Clara, CA) over a frequency range from 1.0 × 10⁴ to 1.1 × 10⁸ Hz at a voltage amplitude of 0.30 V. A capacitor-type cell made of acrylic resin, with two parallel platinum electrodes with spacing of 3.5 mm and diameter of 8 mm, was used. The electric double layers near the electrodes can be viewed as capacitive elements electrically connected in series to the sample solution, which yield parasitic dielectric relaxation in the kHz region. To reduce these electrode polarization effects, therefore, the electrodes were carefully plated with platinum black to increase their surface areas so that the characteristic frequency of the parasitic relaxation would be shifted toward lower frequencies far away from the region that is relevant for cellular dielectric spectroscopy (8,9). Organic compounds can adsorb onto the electrodes during measurement and form thin dielectric layers, which reduces the capacitance of the electric double layers and thus slightly increases the characteristic frequency of the parasitic relaxation. It was found, however, that the characteristic frequency was still low enough to accurately measure the dielectric spectra of erythrocytes. The temperature of the suspension was maintained at 298 K by circulating water around the cell.

Cell modeling

The biconcave shape of discocytes and normocytes has been represented by an empirical equation (10). However, the discontinuity of the curvature at the edges of the longitudinal axis that appears in that equation may cause an erroneous electric potential distribution. Thus, we devised a new equation that represents biconcave shapes similar to those provided by the previous one but resolves the discontinuity problem as follows: Consider four circles that are tangent in pairs. Two of them with radius r are located at symmetric positions on both sides of the x axis, whereas the other two with radius R are located in the same way but on the y axis (R > r). A biconcave enclosed curve consists of the minor arcs of the circles of radius R and the major arcs of the circles of radius r, which is a good approximation for the cross section of the biconcave disk in the x, y plane (the center of the disk is located at the origin) if appropriate values are chosen for r, R, and θ, where θ is the angle between the x axis and the tangential line through the two points of tangency in the first and third quadrants of the x, y plane. Because the size and shape are almost identical between the rabbit discocyte and the human normocyte, we assumed the same shape for them. With the geometric parameters r = 1.28 μm, the thickness of 0.405 μm at the center of the biconcave disk (10), and the diameter of 8.0 μm measured for the rabbit discocyte and human normocyte, simple geometric consideration provides the values of R and θ, that is, R = 3.09 μm and θ = 0.93 radian.

For the echinocyte, even though the number and shapes of the spines varied from cell to cell, the representative shape was modeled as a sphere with its surface modified by sinusoidal functions (11). The distance r from the origin to an arbitrary point on the surface is given by

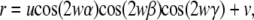where u is the height of the spines, v is the radius of the sphere, w determines the number of spines, and cosα, cosβ, and cosγ are the direction cosines with respect to the x, y, and z axes, respectively. The three constants were determined from the microscope measurement, and u = 0.611 μm, v = 3.30 μm, and w = 3. The simulated models are shown in Fig. 1 with the corresponding SEM images.

Numerical simulation

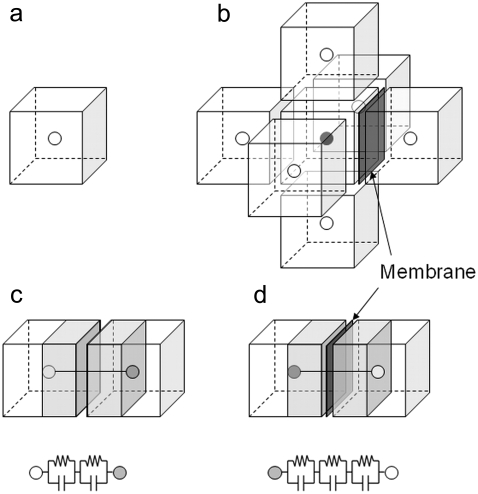
We consider a system that comprises parallel plate electrodes and a cell in a medium (see Fig. 1 c). The 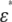of the system is calculated by the numerical technique based on the three-dimensional finite difference method (FDM) as described previously (11,12). The system is divided into 100 × 100 × 100 cubic elements (with size = ∼70 nm). Each element has either the complex permittivity of the cytoplasm or that of the medium, and a grid point at its center (see Fig. 2). The discretized cell model used for calculation consists of the elements with their grid points inside the volume enclosed by the cell surface represented by the function described above. The complex admittance between neighboring grid points is provided by assuming a homogeneous electric field between them. For the boundary between the cytoplasm and the medium, the admittance is represented by a combination of three equivalent circuits corresponding to the cytoplasm, the membrane, and the medium, as shown in Fig. 2 d. The net current that flows into an element through its six neighboring elements is zero. Thus, the simultaneous equations are obtained for electric potentials at all the grid points, which are solved by a successive over-relaxation method under the boundary conditions that the electric potential on the electrode is given and the current through the four sides is zero. Thus, we obtain the electric potential distribution, the current through the electrodes, and the admittance of the system, which can be readily converted to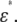

FIGURE 2.

(a) Cubic element with unique complex permittivity for an FDM simulation, in which a grid point for potential calculation is located at the center. (b) The element surrounded by six cubic elements to derive the potential at the center grid point. The figure exemplifies the case in which the cell membrane exists between the center element and the rightmost one. (c) Equivalent circuit model with two parallel capacitance and conductance components, which represents the current path between the center element and the leftmost one in b. (d) Equivalent circuit model for the center element and the rightmost one with additional capacitance and conductance components for the cell membrane.

For the cell model of biconcave shape, the dielectric responses to the electric fields parallel and perpendicular to the axis of rotational symmetry were separately calculated and averaged with relative weights of 1 and 2, respectively. This linear superposition is valid for a dilute suspension, where intercellular interactions are very small (13) (note that the volume fraction of each suspension P is <10%). To reduce computational effort, the eighth part of the system with the center of the cell model at the origin, as exemplified in Fig. 1 c, was used by exploiting the rotational symmetry about the electric field direction. The surface area of the discretized model S₁ as the summation of the surfaces of the elements exposed to the medium is larger than that of the cell model S₂. Because this discrepancy causes overestimation of the total membrane capacitance, the membrane capacitance per unit area C_m was multiplied by S₂/S₁ to correct for this error and then used for simulation.

The cell model used for this study does not take into account the tangential conductance along the cell membrane, which originates from excess positive ions in the diffused electric double layer induced by negatively charged groups of glycolipids on the membrane surface. The thickness and the amount of excess ions in the double layer with respect to the bulk phase can be estimated from the zeta potential of erythrocytes in physiological saline (14) by means of the Guoy-Chapman theory (15); they are ∼0.8 nm and 17%, respectively. Using these parameters and assuming that the mobilities of the ions are the same for the double layer and the bulk phase, dielectric dispersion curves were simulated on the basis of the analytical theory for spherical multiphase systems (16); however, the results were not considered relevant enough to be shown here for this discussion. We have found that the dielectric dispersion curves are not affected by the existence of the diffused electric double layer for physiological conditions with relatively high ionic strength unless an unreasonably large enhancement of the ion mobility (∼10³) in the electric double layer is assumed, and thus we concluded that the surface conductance could be neglected for this study.

RESULTS AND DISCUSSION

The method to accurately calculate 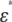for any type of erythrocyte was described in the previous section. Here, we discuss how to determine unknown electric parameters (C_m and the cytoplasm conductivity κ_i in this case) from the experimental 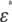of erythrocyte suspensions. In a straightforward method, a number of normalized dielectric dispersion curves ɛ*/P are calculated over wide ranges of C_m and κ_i and fitted to the experimental one to determine the best-fit C_m and κ_i. However, this method is not practical because it requires repeated time-consuming FDM simulations. Hence, we developed what we believe is a more efficient method. First, we calculated ɛ*/P for only 25 sets of C_m and κ_i. Second, we obtained the relaxation amplitude Δɛ and the relaxation time τ by fitting an empirical Cole-Cole function (17)

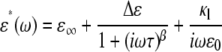(1)

to a simulated dispersion curve for each set of C_m and κ_i, where β is the Cole-Cole parameter, 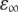is the high-frequency limit of dielectric constant, 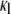is the low-frequency limit of conductivity, and ɛ₀ is the permittivity of vacuum. Finally, Δɛ/P and τ were expressed as a function of C_m and κ_i using the following forms, which are similar to those derived for the spherical cell model at low P (18):

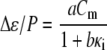(2)

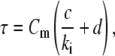(3)

where a, b, c, and d are the regression coefficients.

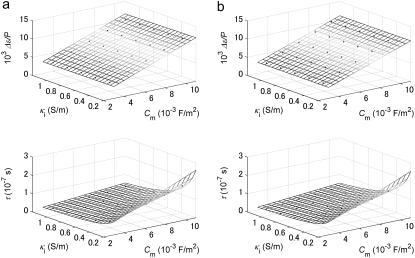
Multiple regression analysis against the calculated data over the 25 sets of C_m and κ_i was performed to determine the coefficients in Eqs. 2 and 3 as follows: a = 1.10 × 10⁶ m²/F, b = 2.86 × 10⁻² m/S, c = 4.52 × 10⁻⁶ m, and d = 1.19 × 10⁻⁶ m²/S for the biconcave erythrocyte; and a = 1.01 × 10⁶ m²/F, b = 1.10 × 10⁻⁴ m/S, c = 4.39 × 10⁻⁶ m, and d = 1.15 × 10⁻⁶ m²/S for the echinocyte. The three-dimensional renderings of Δɛ/P and τ calculated by Eqs. 2 and 3 are shown as a function of C_m and κ_i in Fig. 3 together with the 25 data points. Because the data points are well represented with Eqs. 2 and 3, the application of the equations is verified for at least the discocyte, the echinocyte, and the normocyte.

FIGURE 3.

Three-dimensional renderings of the normalized relaxation amplitude Δɛ/P and the relaxation time τ calculated by Eqs. 2 and 3 as functions of the specific membrane capacitance C_m and the cytoplasm conductivity κ_i for (a) the discocyte and (b) the echinocyte. Also plotted as blue solid circles are the data obtained by fitting Eq. 1 to the simulated dielectric dispersion curves.

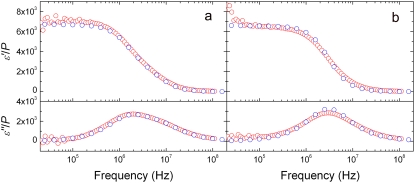
The experimental dielectric dispersion curves were also fitted by Eq. 1. to give Δɛ_exp and τ_exp. Even though the goodness of fit is lower for the discocyte and normocyte than for the spherocyte and echinocyte because of their highly anisotropic shapes, Δɛ_exp andτ_exp were used to characterize the corresponding dispersion. Substituting Δɛ_exp/P and τ_exp into Eqs. 2 and 3, we can calculate C_m and κ_i as shown in Table 1. The values of C_m and κ_i for the rabbit spherocyte were obtained using the analytical equation of the spherical cell model. The value of the cytoplasm permittivity ɛ_i was assumed to be 50, because 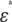is insensitive to ɛ_i for a dilute solution (19). The conductivity of the cell membrane was also assumed to be 10⁻⁷ S/m, because the value does not affect the analysis if it is <10⁻⁶ S/m (this condition holds for a wide variety of nonexcitable cells, including intact erythrocytes (20)). The permittivity and conductivity of the solvent were 78.3 and 1.67 S/m, respectively. We calculated ɛ*/P by the FDM simulation using the values in Table 1 to confirm that the experimental dispersion curves are excellently reproduced for the discocyte, the echinocyte (Fig. 4, a and b, respectively), and the normocyte (not shown).

TABLE 1.

Volume fractions and the electric parameters of the four types of erythrocytes

Erythrocyte type	Sample from	Volume fraction (%)	Membrane capacitance (mF/m2)	Cytoplasm conductivity (S/m)
Spherocyte	Rabbit	5.8	6.33	0.713
Discocyte	Rabbit	7.2	6.68	0.539
Echinocyte	Rabbit	9.0	6.53	0.651
Normocyte	Human	9.8	8.79	0.666

Determined from the experimental dielectric dispersion curves by the analytical approach (the spherocyte) and the numerical approach (the other three types).

FIGURE 4.

Complex permittivities calculated with the optimized membrane capacitance and cytoplasm conductivity (blue circles) compared with the experimental ones (red circles) for (a) the discocyte and (b) the echinocyte. The slight discrepancy between simulation and experiment in the lower-frequency region below ∼10⁵ Hz is due to incomplete elimination of electrode-polarization effects from the experimental data.

Next, we discuss the electric parameters shown in Table 1. The values of C_m are almost the same for all three types of rabbit erythrocytes. This indicates that C_m does not change during the shape transition by pH regulation. Furthermore, these values agree well with those previously obtained for mouse erythrocytes swollen by reducing the osmotic pressure of the suspending medium (C_m = 0.72 mF/m²) (21), and sheep erythrocyte ghosts (C_m = 0.6–0.8 mF/m²) (7). On the other hand, κ_i for the spherocyte is larger than that for the discocyte by 32%. When the discocytes are swollen to be spherical, water likely enters the cytoplasm through the semipermeable cell membrane, and consequently the protein and electrolyte concentrations in the cytoplasm decrease. Thus, the increase in κ_i is determined as a trade-off between the decreases in the intracellular viscosity η_i and the electrolyte concentration c_e. Obviously, c_e is inversely proportional to the cell volume V_c as long as the electrolytes in the medium do not enter the cytoplasm. According to an electron spin resonance study with human erythrocytes whose V_c was changed by pH regulation (22), η_i is proportional to exp(1.215/v_c), where v_c is the relative volume of the cell with respect to that of the discocyte. Thus, c_e and η_i for the spherocyte (V_c = 118 μm³) are respectively 0.80 and 0.78 times as large as those for the discocyte (V_c = 94.1 μm³). Since κ_i is proportional to c_e/η_i, κ_i for the spherocyte should be nearly identical to that for the discocyte. However, this estimation is inconsistent with the experimental result. If we assume no change in c_e and a decrease in η_i by a factor of 0.78, the increment in κ_i becomes 28%, which agrees rather well with the corresponding value of 32% obtained in this study. This may suggest that c_e is nearly kept constant by inflow of electrolytes together with water to the cytoplasm due to alteration of the membrane permeability by the pH change (23).

To verify the above argument about κ_i experimentally, we measured the conductivity of hemoglobin solutions containing KCl and PBS. Hemoglobin from bovine blood (H2500, Sigma-Aldrich, St. Louis, MO) was dissolved in 80 mM KCl at the consensus concentration of 340 mg/mL in erythrocytes, and its conductivity was measured at 10 kHz. The obtained value was 0.594 S/m, which is close to that of κ_i for the discocyte in Table 1. Since the increment in V_c is 25% in the shape change from the discocyte to the spherocyte, four parts of the hemoglobin solution were diluted with one part of PBS. The dilution increased the conductivity by 33%, which is consistent with the increment in κ_i observed in the shape change. Pauly and Schwan (24) measured the values of κ_i for erythrocytes of different species around 100 MHz, where the cell membrane is effectively short-circuited, and found that the hypothetical cytoplasm conductivity estimated from the summation of the limiting conductivities of constituent ions in infinite dilution is ∼3 times larger than the experimental one. They considered that the mobilities of small electrolyte ions decrease in concentrated protein solution because of the strong hydrodynamic and electrostatic interaction between them. Their experimental results support our conclusion above.

Since the method developed in this article is applicable to any type of cell with an arbitrary shape, a wide variety of applications can be considered if it is implemented in the format of modern microbiotechnology. A microarray format, for example, would enable parallel analysis of the responses of cells to various chemical substances through the change in their electric parameters. Also, our efficient numerical method is compatible with high-throughput counting of single blood cells of different shapes flowing one by one in a microfluidic channel, the most common clinical test.