Key Interactions in Integrin Ectodomain Responsible for Global Conformational Change Detected by Elastic Network Normal-Mode Analysis

Abstract

Integrin, a membrane protein with a huge extracellular domain, participates in cell-cell and cell-extracellular-matrix interactions for metazoan. A group of integrins is known to perform a large-scale structural change when the protein is activated, but the activation mechanism and generality of the conformational change remain to be elucidated. We performed normal-mode analysis of the elastic network model on integrin α_Vβ₃ ectodomain in the bent form and identified key residues that influenced molecular motions. Iterative normal-mode calculations demonstrated that the specific nonbonded interactions involving the key residues work as a snap to keep integrin in the bent form. The importance of the key residues for the conformational change was further verified by mutation experiments, in which integrin α_IIbβ₃ was used. The conservation pattern of amino acid residues among the integrin family showed that the characteristic pattern of residues seen around these key residues is found in the limited groups of integrin β-chains. This conservation pattern suggests that the molecular mechanism of the conformational change relying on the interactions found in integrin α_Vβ₃ is unique to the limited types of integrins.

INTRODUCTION

Integrins are one of the metazoan protein families of adhesion receptors that mediate cell-cell and cell-extracellular-matrix interactions (1). In addition to this function, integrins transmit signals bidirectionally across the plasma membrane. Through these functions, integrins play key roles in diverse biological processes including cell migration, development, immune responses, and vascular hemostasis. They are therefore the target of effective therapeutic drugs against thrombosis and inflammation (1).

Integrin is a heterodimer transmembrane protein complex made of α- and β-chains. In mammals, 18 homologous α-chains and eight homologous β-chains are known so far, and different combinations of α- and β-chains have been identified. Integrins are not constitutively active as receptors. On cell surfaces, integrins are usually in a state of low affinity to their ligands (inactive state). By signals from inside the cell, integrins are supposed to be activated and function as receptors (inside-out signaling) (2).

Solution of the crystal structure of the ectodomain of integrin, α_Vβ₃, was a major advance in the study of integrin (3). The crystal structure revealed that the head region was extremely bent over the two nearly parallel tails. Electron microscopy had shown that the integrin had an extended form (4–6), but later, the bent conformation of integrin was also observed. It was then shown that the bent conformation corresponded to the inactive state and the extended conformation to the active state, where integrin has high affinity to its ligand (7). The relationship between two conformations and two functional states is now well demonstrated. However, the transition mechanism between the two conformations is not yet understood.

Here, we studied the conformational changes of integrin ectodomain using normal-mode analysis (NMA) of the elastic network model of the protein. The application of conventional NMA to biomolecules, which employs realistic energy function in contrast to the NMA of the elastic network model, started more than 20 years ago (8–10). Since then, many biomolecules have been studied using NMA. This approach is widely used and has proved very effective for elucidating conformational fluctuations and changes related to biological functions. NMA of the elastic network model of a protein, which is directly related to this work, was first developed by Tirion (11), and the calculated normal modes were shown to faithfully reproduce the B-factors obtained from x-ray crystal structure analysis (12). It requires much fewer computational resources compared to the conventional method, so that the applications to huge macromolecular structures such as ribosomes and virus capsids (13–17) are possible. Here we applied the NMA of the elastic network model to the ectodomain of integrin α_Vβ₃ in the bent form (inactive state). The analysis enabled us to identify the key residues that work as a switch for conformational changes of the integrin ectodomain. Iterative normal-mode calculations demonstrated that the key residues work as a snap to keep the structure in the bent form. The importance of the residues was further verified experimentally.

MATERIALS AND METHODS

Naming scheme for extracellular domains of integrin α_Vβ₃

In this article, we follow the widely used naming scheme for the ectodomain of integrin α_Vβ₃ (see Xiong et al. (3), for example). The α-chain consists of β-propeller (residues 1–438), thigh (439–592), calf-1 (602–738), and calf-2 (739–956) domains. The β-chain consists of PSI (1–54), hybrid (55–108 and 353–432), βA (109–352), EGF-1 and -2 (453–529), EGF-3 (532–562), EGF-4 (563–605), and βTD (606–690) domains. The PSI and EGF-1 and -2 domains are missing in the x-ray crystal structure to which we applied NMAs.

Elastic network model

In the usual treatment of an elastic network model (12,18), each residue in a protein is represented by the C_α atom. If the distance between two C_α atoms is less than the arbitrary chosen cutoff length, R_c (8–12 Å), the two residues are considered to be neighbors and the two C_α atoms are connected by a spring whose equilibrium length is the same as the distance in the initial conformation. Thus, the distance between the two C_α atoms is considered to be the distance between the two residues. The same spring constant C is used for all springs in the network model.

In this study, we defined the distance between two residues in a different way for the reason explained in the Results and Discussion section. We first considered all atoms except for hydrogens, and calculated the distances between all pairs of atoms. The shortest distance between atoms in two different residues was defined as the distance between the two residues, and if it was less than the arbitrary chosen cutoff length, r_c (3–5 Å), the two residues were considered to be neighbors. Once the neighbors were identified, each residue was represented by the C_α atom, and the C_α atoms in the neighbor residues were connected by springs with an arbitrarily chosen spring constant, C. The adjacent C_α atoms along the amino acid chain were automatically connected by this approach. We further introduced springs along the amino acid chain between C_α atoms in nth and (n + 2)th residues and between those in nth and (n + 3)th residues. The former spring restrained the fluctuations of the virtual bond angle formed by C_α atoms in nth, (n + 1)th and (n + 2)th residues, and the latter spring those of the virtual dihedral angle formed by C_α atoms in nth, (n + 1)th, (n + 2)th and (n + 3)th residues.

Normal-mode analysis of the elastic network model

The basic formulation of the NMA of the elastic network model is the same as that for the NMA performed with different coordinate systems and force fields (19–27);

The conformational potential energy of the system is approximated by the multidimensional parabola,

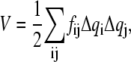(1)

where is the instantaneous fluctuation of the ith generalized coordinate from its equilibrium value and 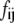is an element of a Hessian matrix, F. The approximation is valid in the vicinity of minimum energy points.

The kinetic energy K is similarly expressed in quadratic form in terms of 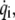the first derivative of 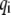with respect to time, and coefficient which is an element of the “mass” matrix, H:

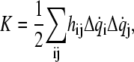(2)

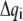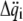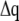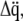If the and are collected in the vectors and respectively, Lagrange's equation of motion is simplified to

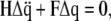(3)

with a solution of the form

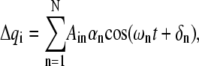(4)

where N is the number of freedom in the system. The constant 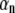and phase angle 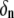are determined from the initial conditions. The coefficient 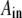is an element of a matrix A which simultaneously diagonalizes H and F; that is, 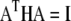and 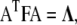where 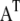denotes the transposition of 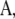I is an identity matrix, and 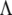is a diagonal matrix with elements

In this study, the conformational potential energy of the elastic network model is expressed in the following form, as was done by Tirion (11):

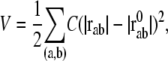(5)

where C is the spring constant, 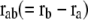is the vector pointing from atom 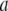to atom 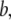and the superscript zero indicates the initial conformation. Thus, the initial conformation has the minimum energy so that the energy minimization process is not necessary. In our treatment, each residue is represented by a C_α atom, an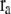d and 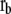are regarded as the positions of residues 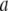and 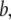respectively. The summation is taken over all pairs of the neighboring residues.

If Eq. 5 is expanded about 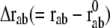and terms higher than second order are ignored, it is simplified to

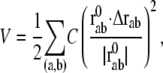(6)

from which the Hessian matrix, F, is easily derived. We report the normalized normal-mode frequencies in the Results and Discussion section, because the normal-mode frequencies, which are obtained by diagonalizing the matrix F, are proportional to the square root of the arbitrarily chosen spring constant, C. Our system is described by the Cartesian coordinate, and thus the mass matrix H is a diagonal matrix with the 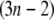th, 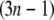th, and 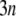th diagonal elements equal to the total mass of the 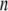th residue.

Comparison of thermal atomic fluctuations

To see how well the calculated values agreed with experimental values, the correlation coefficient was calculated using the equation

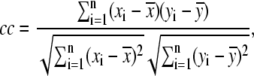(7)

where 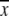is the average of 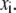In this study, the correlation coefficient between the thermal atomic fluctuations derived from the NMA and those derived from the B-factors of the crystal structure was calculated. In the NMA, the thermal atomic fluctuations are given as a sum of contributions from all normal modes except for the six zero-frequency normal modes corresponding to the rigid body motions as a whole. The thermal atomic fluctuations of the crystal structure are proportional to the square root of the B-factors.

Similarity of two normal modes

We studied the effect of interactions between neighboring residues on the molecular motions to detect the key residues for the conformational changes of integrin. For this purpose, we compared low-frequency normal modes calculated for a model with full interactions to those for a model without specific interactions. The comparison of the two normal modes was made in terms of similarity, defined as

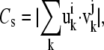(8)

where 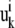and 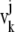are displacement vectors of the 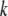th atom in the 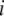th and 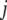th normal modes, respectively, for the two elastic network models. Here, displacement vectors were normalized as

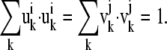(9)

If the value is close to 1, the two normal modes are similar to each other. If it is close to zero, they are dissimilar.

Iterative normal-mode calculations

For the conventional NMA, a time-consuming energy minimization process is necessary before the NMA. For the NMA of the elastic network model, the energy minimization process is not necessary, and the NMA can be applied to any given conformation (28). If atoms in a protein are moved by a small amount from the initial positions along the displacement vectors in a normal mode, a slightly different new structure is generated. If the NMA of the elastic network model is applied to this new structure, another new structure can be obtained. By repeating this process, a series of structures is generated. This approach is often used for building atomic models based on electron microscopy density maps (29–31). Here, we call this series of calculations “iterative normal-mode calculation” and use this approach for forcing the conformational change of integrin from the bent to the extended forms and studying the role of the specific interactions in the conformational change.

The x-ray crystal structure of integrin (Protein Data Bank ID 1jv2 (3)) was used as the initial structure (the 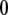th structure). After the 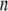th NMA for the 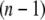th structure, many structures were generated by deforming the 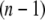th structure along each of the three lowest-frequency normal modes, and the structure with the largest distance between the head region and C-terminal end was chosen as the 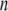th structure. The distance was measured between two C_α atoms in the residues Lys⁸² and Glu⁷⁶⁵ of the α-chain. The deformation was restricted so that the root mean-square displacement (rmsd) of the 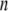th structure from the 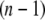th is <0.1 Å. The iterative calculation was terminated when the increment of distance between the head and C-terminal end of a new conformation (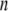th conformation) and that of the previous conformation was <0.1 Å.

Each time a new structure made of C_α atoms was generated by the approach described above, the coordinates of other atoms, which were necessary for updating the network formation, were determined by rigid-body treatment and a least-square fitting procedure (32) as follows. A structure made of a C_α atom in each residue (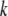th residue) and a few C_α atoms in the nearby residues along the amino acid chain in the x-ray crystal structure was treated as a rigid body and was fitted into the corresponding structure in the newly generated structure by rotational and translational manipulation in the least-square fitting procedure. The same manipulation was then applied to the other atoms in the 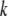th residue of the x-ray crystal structure to get the positions of these atoms in the new structure. This process was repeated for all residues and the coordinates of all atoms in the new structure were obtained.

The purpose of the iterative normal-mode calculation in this study was to clarify the role of specific interactions in the conformational change from the bent to the extended form, in other words, to check whether the specific interactions obstructed the conformational change or not. For this purpose, two different iterative calculations were necessary. In one calculation, the specific interactions were kept, and in the other, they were not. However, the connectivity for the specific interactions could have changed during the iterative normal-mode calculation, because the network formation was to be updated each time a new structure was generated. To avoid this, we did not update the connectivity for the specific interactions during the iteration.

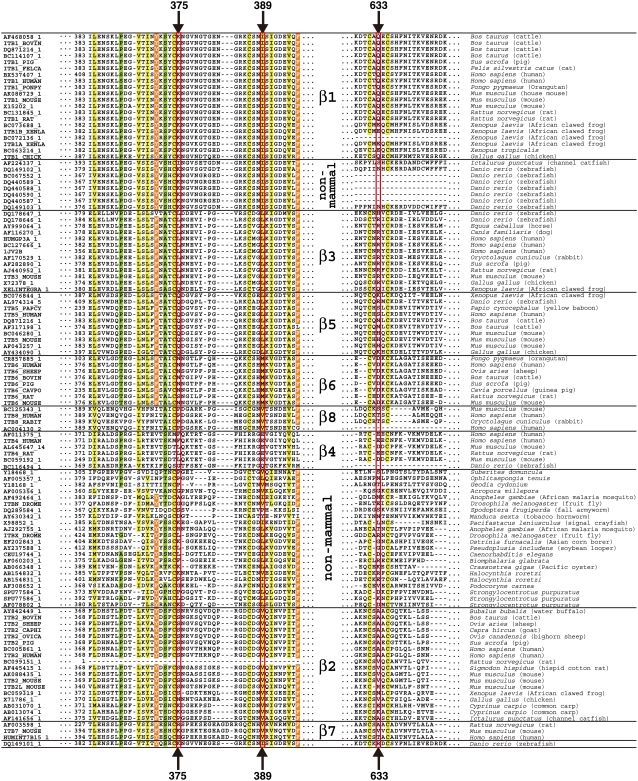
Multiple sequence alignment and conservation pattern of the residues

Homologous amino acid sequences to integrin from Homo sapiens α_Vβ₃ were searched for out of all the amino acid sequences in UniProt (33) and all the translated amino acid sequences in DDBJ (34) by BLAST (35) with default parameters. Sequences derived from pseudogenes and partial sequences were eliminated. Identical sequences in the obtained set of sequences were grouped and only one of the sequences in each group was kept for building multiple sequence alignment. The multiple sequence alignment was built based on the progressive alignment method (36) using the BLOSUM62 matrix (37). Alignment at regions with extremely low sequence identity was manually adjusted based on the heuristic knowledge that cysteine residues should be well conserved and aligned among homologous extracellular domains. Sequences were grouped into clusters based on a phylogenetic tree built by the neighbor-joining method (38), with evolutionary distances calculated by the method of Kimura (39). The threshold for grouping the integrin sequences was set to be consistent with the annotation of sequences based on a previous study (1). Conservation of amino acid residues at positions of concern in each group was manually identified.

Mutation experiment to verify the activation mechanism

We experimentally verified the activation mechanism of integrin predicted by the NMA. We used integrin α_IIbβ₃ instead of α_Vβ₃ for mutation experiments. Although the former is exclusively expressed on platelets and megakaryocytes different from the latter, and is known to use a different mechanism of signaling at the cytoplasmic domain of the α-chain (40), it has a common β₃-chain and binds to common ligands such as fibrinogen, fibronectin, and vitronectin in an RGD-dependent fashion. In addition to these structural and functional similarities, it has been well established that α_IIbβ₃ increases its affinity for fibrinogen by undergoing structural rearrangement upon inside-out signaling (41). Thus, we took advantage of the α_IIbβ₃-fibrinogen interactions to examine the effect of the mutations.

Normal mouse IgG was purchased from Sigma-Aldrich (St. Louis, MO). Anti-α_IIb monoclonal antibody (mAb) PL98DF6 (42) was a generous gift from Drs. J. Ylänne (University of Oulu, Oulu, Finland) and I. Virtanen (University of Helsinki, Helsinki, Finland). Anti-α_IIbβ₃-complex-specific activating mAb PT25-2 has previously been characterized (43). RPE-conjugated goat antimouse polyclonal antibody was purchased from Biosource (Camarillo, CA). The synthetic peptide Gly-Arg-Gly-Asp-Ser (GRGDS) was purchased from Peptide Research Institute (Osaka, Japan). Fluorescein-isothiocyanate (FITC) was purchased from Sigma-Aldrich. Human fibrinogen (Fbg) was purchased from Experimental Cell Research (South Bend, IN).

The full-length cDNAs for integrin α_IIb and β₃ subunits, generous gifts from Dr. Joseph C. Loftus (Mayo Clinic, Scottsdale, AZ), were cloned into the mammalian expression vector pBJ-1, kindly provided by Dr. Mark Davis (University of California, San Francisco, CA). The cDNAs for β₃ mutant L375A, L389A, R404A, R633A, R633del, R404A/R633A, R404A/R633del, and R404A/S674A were created by site-directed mutagenesis using the Transformer Site-Directed Mutagenesis Kit (BD Biosciences, San Jose, CA).

Chinese hamster ovary (CHO-K1) cells were cultured in Dulbecco's modified Eagle's medium (Invitrogen, Carlsbad, CA) supplemented with 10% fetal calf serum (Hyclone, Logan, UT), 1% penicillin and streptomycin (Invitrogen), and 1% nonessential amino acids (Sigma-Aldrich), and maintained at 37°C in a humidified incubator supplemented with 5% Fifty micrograms of α_IIb cDNA construct was cotransfected with 50 μg of β₃ cDNA construct into CHO-K1 cells by electroporation. After 48 h, cells were detached and used for assays.

FITC-labeling of human Fbg is described in detail elsewhere (44). In brief, after adjusting the pH of human Fbg at 1 mg/ml in phosphate-buffered saline to 8.5 with 5% Na₂CO₃, 1/100 volume of 10 mg/ml FITC in dimethylsulfoxide was added and incubated at room temperature for 10 min. FITC-labeled Fbg was separated from free FITC on a PD-10 column (Amersham Biosciences, Uppsala, Sweden) equilibrated with HEPES-buffered saline (10 mM Hepes, 150 mM NaCl, pH 7.4). The concentration and F/P ratio of FITC-labeled Fbg were calculated as previously described (44). Forty-eight hours after transfection, cells were detached with phosphate-buffered saline containing 3.5 mM EDTA and incubated with nonfunctional anti-α_IIb mAb PL98DF6 followed by an RPE-conjugated F(ab′)2 fragment of goat anti-mouse IgG. After washing, cells were incubated with FITC-labeled Fbg at 350 μg/ml with or without 1 mM GRGDS peptide in modified HEPES-Tyrode buffer (5 mM Hepes, 5 mM glucose, 0.2 mg/ml bovine serum albumin, and 1× Tyrode's solution) containing 1 mM and 1 mM for 2 h at 4°C. In some experiments, mAb PT25-2 was included at 10 μg/ml to activate α_IIbβ₃. After washing, fluorescence was measured on FACS Calibur. The median Fbg binding (FL1) to cell populations expressing high α_IIb (FL2 > 500) was calculated. Background binding in the presence of 1 mM GRGDS peptide was subtracted to obtain specific binding. Normalized Fbg binding was calculated by dividing the specific binding by the mean α_IIbβ₃ expression (FL2) of the gated population.

RESULTS AND DISCUSSION

Elastic network model of integrin α_Vβ₃

The first step of the calculation is the formation of the elastic network model based on the x-ray crystal structure of integrin with a specific cutoff length. Motions of residues in this model depend on the number of neighboring residues. Residues with a small number of neighbors can move with less restraint compared to those with many neighbors. The number of the springs in molecules, which connect the C_α atoms in neighboring residues, depends on the cutoff length. Thus, the cutoff length is the most important parameter determining molecular motions.

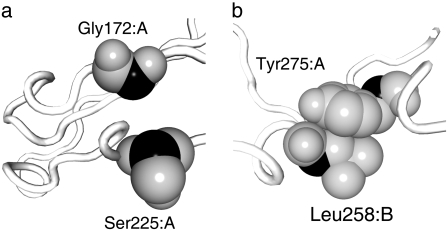
As described in Materials and Methods, our definition of the distance between two residues is different from that in the conventional approach. Fig. 1 demonstrates the difference between the two approaches with a specific example. Two residue pairs in integrin, Gly¹⁷² and Ser²²⁵ in the α-chain, and Tyr²⁷⁴ in the α-chain and Leu²⁵⁸ in the β-chain, are shown in Fig. 1 a and b, respectively. The distances between the two C_α atoms (black) are 7.5 Å in both cases, whereas the shortest interatomic distances between the two residues in Fig. 1, a and b, are 7.0 and 3.3 Å, respectively. In the conventional approach, the two C_α atoms are connected by springs in both cases (assuming R_c > 7.5), whereas in our approach the C_α atoms in the former case are not connected and those in the latter case are connected (assuming 3.3 < r_c < 7.0). Thus, the network formation is more sensitive to the local conformation in our approach.

FIGURE 1.

Two pairs of residues, Gly¹⁷² and Ser²²⁵ in the α-chain (a), and Tyr²⁷⁴ in the α-chain and Leu²⁵⁸ in the β-chain (b) in the x-ray crystal structure of integrin demonstrate the difference between the two approaches used to generate an elastic network model. The C_α atoms are colored in black, other atoms in gray. The backbone is represented by a white tube. In the conventional approach, the two residues in both cases are connected by a spring when the cutoff length, R_c, is >7.5 Å. In our approach, the residues in b are connected, whereas those in a are not, when the cutoff length, r_c, satisfies 3.3 < r_c < 7.0.

A relatively large number of the pairs of residues are similar to the case shown in Fig. 1 a, that is, pairs of residues that have short C_α distances but long interatomic distances. For example, there are 774 pairs of residues in integrin in which the distances between the C_α atoms are between 7.5 and 8 Å, and these are usually regarded as neighboring residues according to the conventional approach. For 197 of these pairs of residues (25%), the shortest interatomic distances are >6 Å, and for 412 pairs (53%), the distances are >5 Å, which means that according to our approach, a fairly large number of the pairs of residues are not regarded as neighboring residues.

In this article, we studied the global conformational change of integrin from the bent to the extended conformation. Before we used our modified approach, we had used the conventional approach to build the elastic network model of the x-ray crystal structure of integrin with normal cutoff length (R_c = 8 Å) and had studied the molecular motions. However, we had not observed the motions that could direct the bent conformation of integrin to the extended one in the lowest-frequency normal modes. Some springs between residues must have hindered such motions. Thus, these springs should have been eliminated to promote the conformational change. We therefore tried to remove such springs from the elastic network model. However, it was not easy to find all such springs by eliminating springs one by one and checking the effect by NMA, because multiple springs could have been involved in the hindrance. Instead, we decreased the cutoff length so that springs representing interactions with longer distances would be eliminated, assuming that these interactions would be weaker and less important for the conformational change. To make this assumption more valid, we defined the distance between two residues as the shortest interatomic distance, as described above. We will discuss the effect of the different definition later.

Dependence of molecular motions on cutoff length, r_c

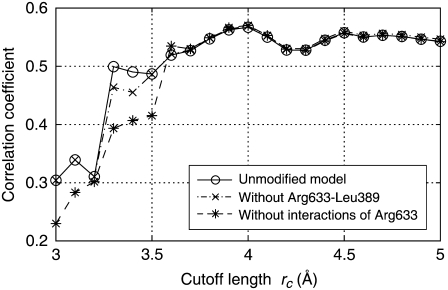
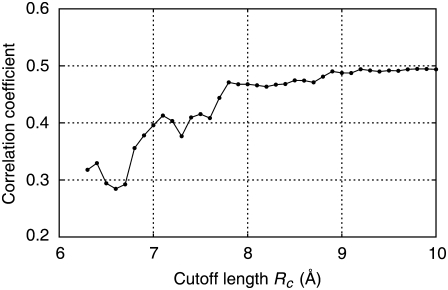
NMAs were carried out for the elastic network models with various cutoff lengths, and the correlation coefficients were calculated based on Eq. 7. In Fig. 2, the calculated coefficients are plotted against the cutoff length as open circles connected by a solid line. The coefficients for cutoff lengths >∼3.6 Å were roughly constant. However, at around r_c = 3.2–3.3 Å, the coefficients dropped abruptly. This cutoff length is roughly equivalent to the hydrogen bond distance, suggesting that the springs representing hydrogen bonds were on the verge of elimination in this range of cutoff lengths. A large correlation coefficient suggests that the molecular motions derived from the calculation are similar to those in the crystal structure, whereas a small coefficient suggests molecular motions that are different. We checked that the small coefficients did not stem from extremely large thermal atomic fluctuations, which are often observed for atoms with a small number of neighbors (data not shown).

FIGURE 2.

Correlation coefficient of the thermal atomic fluctuations derived from NMA and x-ray crystal structural data (B-factor) plotted against the cutoff length. Open circles connected by solid line: unmodified model. “X” symbols connected by dash-dotted line: model without interaction between Arg⁶³³ and Leu³⁸⁹. Asterisks connected by dashed line: model without interactions between Arg⁶³³ and nearby nonbonded residues.

The change of the molecular motions reflects the change of the energy landscape of the molecule, that is, the energy required for the conformational change from the x-ray crystal structure (bent structure) to the other conformations is altered. Thus, the conformational change to the extended one may become easier.

To identify the interactions that contributed to the sudden change of the coefficient, we eliminated the springs one by one by reducing the cutoff length starting from 3.3 Å, and NMA was performed. There were 231 springs that were to be eliminated when the cutoff length was reduced from 3.3 to 3.2 Å. We found the maximum drop in the coefficient when the spring connecting C_α atoms in Leu³⁸⁹ and Arg⁶³³ in the β-chain was eliminated, suggesting that the interaction represented by this spring has a large influence on the molecular motions.

The maximum drop in the coefficient observed when the interaction between Leu³⁸⁹ and Arg⁶³³ was eliminated does not mean that the drastic change in molecular motions would be caused by the elimination of the interaction at any cutoff length. If the longer cutoff length were assumed, other interactions would have had to be eliminated at the same time for the drastic change of the coefficient to occur. Thus, this result only suggests that the interaction between Leu³⁸⁹ and Arg⁶³³ was the one with the shortest distance that contributed to keeping the molecular motions as in the x-ray crystal structure. Indeed, the effect of eliminating the interaction between Leu³⁸⁹ and Arg⁶³³ independent of the cutoff length was limited, as shown in Fig. 2, where the correlation coefficients for the network models without the interaction between Leu³⁸⁹ and Arg⁶³³, irrespective of the cutoff length, are plotted by “X” symbols connected by a dash-dotted line. We found that the effect was enhanced if the interactions of Arg⁶³³ with other nearby residues were simultaneously eliminated. In Fig. 2, the correlation coefficients are plotted by asterisks connected by a dashed line for the network models in which the C_α atom of Arg⁶³³ was not connected to the C_a atoms in the nearby nonbonded residues (including Leu³⁸⁹) by springs. In the latter network models, the correlation coefficients were further deviated from those for the original models with full interactions (open circles) in the wider range of cutoff lengths. This suggests that the interactions of Arg⁶³³ with nearby residues have an influence on the molecular motions.

Change of lowest-frequency normal modes of integrin

The above analysis showed that the correlation coefficients dropped when the interactions of Arg⁶³³ were eliminated. However, it did not tell whether the drop was related to the biologically important conformational change of integrin, that is, the conformational change from the bent to the extended form. In this and the following subsections, we reveal what changed when the correlation coefficient dropped.

The change of the correlation coefficient is due to the change of the normal modes. To see what changed in the normal modes when the correlation coefficient dropped, we compared the lowest-frequency normal modes, which influence the global molecular motions, of the two elastic network models with different correlation coefficients.

The comparison was made for the two network models with and without the springs connecting the C_α atom of Arg⁶³³ to those in the nonbonded neighboring residues at the cutoff length of 3.4 Å (we call the former model A and the latter model B). At this cutoff length, the molecular motions of model A were similar to those in the x-ray crystal structure (Fig. 2, open circles), and by removing the springs of Arg⁶³³, quite a large change in correlation coefficient was observed (asterisks), indicating that the springs were working as a switch for molecular motions.

A comparison of the five lowest-frequency normal modes for models A and B is shown in Table 1. It is clear that the second-, fourth-, and fifth-lowest-frequency normal modes of model B were similar to the first, second, and third modes of model A, respectively. The normal-mode frequencies were relatively close to each other. However, the first and the third modes of model B were not so similar to any of the five modes of model A. This result indicates that the new types of motions emerged once the interactions of Arg⁶³³ with other residues were eliminated.

TABLE 1.

Comparison of the lowest-frequency normal modes of elastic network models A and B

		Model B
	Frequency	0.72	0.73	1.36	1.66	2.01
Model A	1.00	0.25	0.95	0.02	0.01	0.14
	1.52	0.51	0.11	0.20	0.82	0.07
	1.99	0.41	0.00	0.32	0.26	0.78
	2.28	0.45	0.14	0.15	0.28	0.52
	2.58	0.32	0.10	0.56	0.35	0.04

Numbers >0.75 are shown in bold. The normal-mode frequencies are shown as relative values with respect to the lowest frequency of model A.

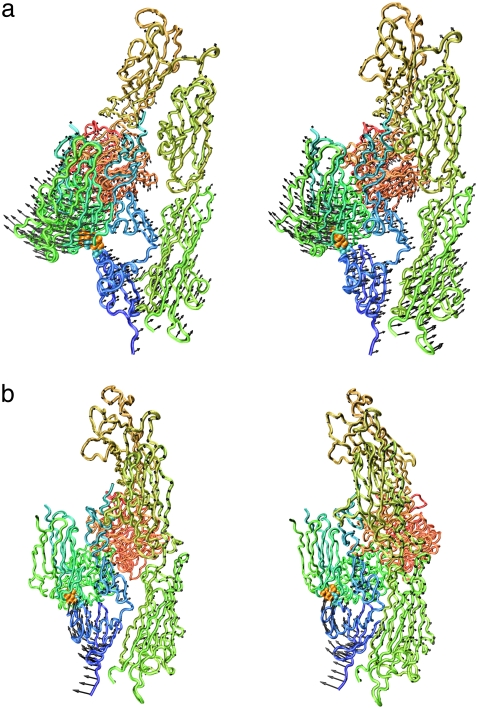
The motion described by the lowest-frequency mode of model B is shown in Fig. 3 a. During this motion, the distance between the hybrid domain (Fig. 3, deep green; see also Figs. 4 and 8 a) and EGF-3 and EGF-4 (Fig. 3, cyan; see also Figs. 4 and 8 a) oscillated. Due to the springs from Arg⁶³³, which connected the βTD (cyan; see also Figs. 4 and 8 a) with the hybrid domain near the head region (drawn beneath the hybrid domain in Fig. 3), the motions of the hybrid domain of model A were restrained, whereas those in model B were not. In this way, eliminating the interactions of Arg⁶³³ enhanced separation (opening motions) of the hybrid domain from the EGF domains. This opening motion might further induce elimination of the interactions between the hybrid domain and the EGF domains, which is shown to be important for the conformational change of integrin, as explained later.

FIGURE 3.

Displacement vectors of C_α atoms of integrin in the lowest- (a) and third-lowest- (b) frequency normal modes of model B (see text) drawn in stereo with the backbone. Leu³⁷⁵, Leu³⁸⁹, and Arg⁶³³ are shown by a space-filling model. The images were generated with a VMD program (62).

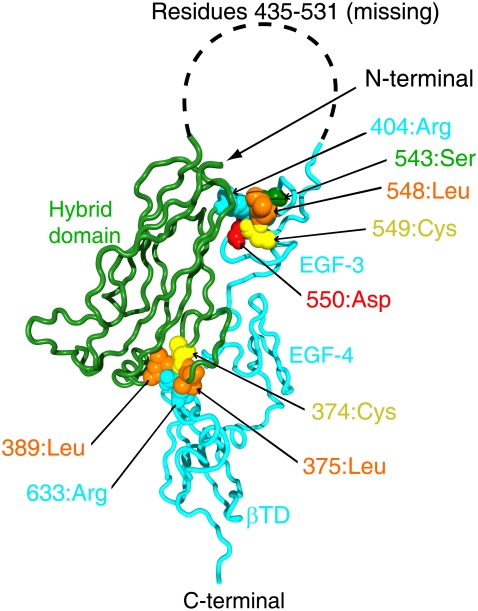
FIGURE 4.

Three-dimensional structure of integrin β₃-chain. Arg⁶³³ and Arg⁴⁰⁴, with their nearby residues, are shown by a space-filling model.

FIGURE 8.

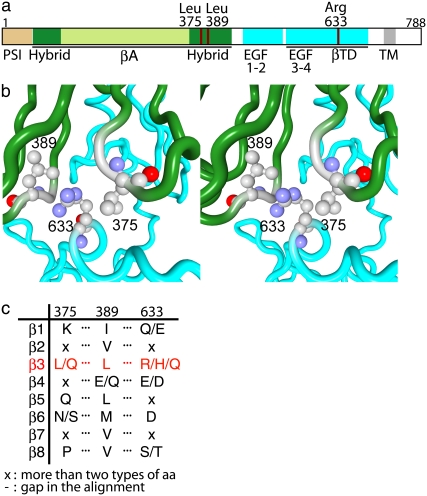
Conservation patterns of amino acid residues among different integrin β-chains at positions corresponding to positions 375, 389, and 633 of H. sapiens integrin β-chain. (a) A diagram of integrin β-chain to show domain organization and the location of residues 375, 389, and 633. Black bars below the diagram indicate regions observed with x-ray crystal structure. (b) Stereo figure of local structure around the three residues, showing that Arg⁶³³ is sandwiched by Leu³⁷⁵ and Leu³⁸⁹. (c) Conservation pattern of residues in the three positions of mammalian integrin β-chain extracted from the multiple sequence alignment in Fig. 9. A slash in the column indicates that the position is occupied by one of the two or three amino acid residues, and x indicates that the position is not conserved in the group.

Role of inside-out signaling to local conformational change

Fig. 4 shows the local conformation around Arg⁶³³ (cyan) in the x-ray crystal structure. The residue Arg⁶³³ belongs to the βTD, and its side chain interacts with residues in the hybrid domain near the head region; the side chain of Arg⁶³³ is sandwiched by two leucine residues, Leu³⁷⁵ and Leu³⁸⁹ (orange), in the hybrid domain (see also Fig. 8 b). Our calculation suggests that the interactions of Arg⁶³³ with nearby residues influences the molecular motions. If the side chain of Arg⁶³³ is moved from the position in the x-ray crystal structure to a position where it is no longer sandwiched by the two residues, the interactions of Arg⁶³³ with nearby residues will be eliminated. Such a motion of the side chain of Arg⁶³³ was observed only in the third-lowest-frequency mode of the network model-B, as is shown in Fig. 3 b. This mode involved the motion of the βTD as a whole. Some external forces should be applied to move βTD and eliminate the interactions of Arg⁶³³, to switch model A into model B.

The x-ray crystal structure we used for NMA lacks the cytoplasmic domains and the transmembrane (TM) domains. Although the 3D structure of these domains is not so clear, there are abundant data indicating that the cytoplasmic domains can regulate integrin activation (45–53). These data show that integrin is activated if the membrane-proximal regions of the α and β cytoplasmic tails are separated, and that the interactions between these segments restrain the integrin in an inactive state. These studies were mainly performed on integrin α_IIbβ₃. The conformational rearrangement in the cytoplasmic domains should be transmitted to the ectodomains through the TM domains. However, little is known about the role of the TM domains in this process. Similar to the case of the cytoplasmic domains, modification of the membrane-proximal regions of ectodomain to inhibit the separation of the α- and β-chains restrains the activation, whereas enhancing the separation promotes activation (6,7,54).

This experimental evidence is consistent with our results. Separation of the membrane-proximal regions of the α and β cytoplasmic tails, caused by binding of proteins such as talin (55–57), will cause rearrangement of the TM domains. This rearrangement will cause the conformational rearrangement of the βTD, which is close to the TM domain. If the rearrangement is similar to that shown in Fig. 3 b, the interactions of Arg⁶³³ with nearby residues will be eliminated, and the conformational change of ectodomain will be promoted. It is interesting to note that the motions shown in Fig. 3 b involve separation of the membrane-proximal regions of the α- and β-chains of the ectodomain, which has been shown to be important for integrin activation (6,7,54).

In Fig. 4, most of the residues involved in the interactions between the hybrid domain and the EGF domains are also indicated by the space-filling model. The amino acid residues that participate in the interactions are the same types as those in the interactions between the βTD and the hybrid domain, and in a similar way; a leucine (orange) and a cysteine (yellow) are adjacent to each other and in contact with the side chain of an arginine (cyan), which connects the two different domains. Compared to Arg⁶³³, Arg⁴⁰⁴ is relatively exposed, and the area participating in the interactions is smaller.

Role of local interactions on the global conformational change

We deformed the x-ray crystal structure of integrin by iterative normal-mode calculations and studied the impact of eliminating the interactions we found above on the global conformational change from the bent to the extended forms. To clarify the set of interactions, we named the interactions between Arg⁶³³ and nearby residues “interaction A”, and those between the hybrid domain and the EGF domains “interaction B”. We performed four types of iterative normal-mode calculations, namely calculation with both A and B, calculation with A and without B, calculation without A and with B, and calculation without either A or B (Table 2). In all calculations, the cutoff length was set to 3.4 Å.

TABLE 2.

Summary of four iterative normal-mode calculations

Calculation No.	Interaction A	Interaction B	Final conformation
1	−	−	Extended
2	−	+	L-shaped
3	+	−	Bent
4	+	+	Bent

Interaction A refers to the interactions of Arg⁶³³ with Cys³⁷⁴, Gly³⁸⁸, and Leu³⁸⁹, and interaction B to those of Arg⁴⁰⁴ with Ser⁵⁴³, Leu⁵⁴⁸, Cys⁵⁴⁹, and Asp⁵⁵⁰ plus the interactions between Glu³⁶⁴ and Ser⁵⁵¹. The plus and minus symbols mean that the springs representing these interactions exist or do not exist, respectively.

There are 25 disulfide bonds in the x-ray crystal structure of integrin. These bonds should not have broken during the iterative calculation. Thus, we kept the 25 springs between the residues that were covalently connected by the S-S bond.

In the x-ray crystal structure, residues between Asp⁴³⁴ and Lys⁵³² in the β-chain were missing. During the iterative calculation, the distance between the two residues could become unrealistically long due to the lack of these residues. To prevent this happening, we added a spring between the C_α atoms in Asp⁴³⁴ and Lys⁵³² whose spring constant was 1/10 that of the normal spring, assuming that the distance between the two residues was easier to change than those between nearby residues.

Two springs were eliminated in the four iterative calculations to enhance the conformational change. They were the spring between Val³³² and Ser⁶⁷⁴ in the β-chain and that between Ser³⁰⁵ in the α-chain and Arg⁵⁶³ in the β-chain. These springs prevented the conformational changes when they were maintained in the calculations. The prevention of the conformational change by the former spring agrees with an experimental result, where the bent conformation was shown to be stabilized if the two residues (Val³³² and Ser⁶⁷⁴) were replaced by cysteines and a disulfide bond was formed (7). Even if the two residues were mutated so that they did not interact with each other, however, the ligand-binding affinity of integrin was not perturbed (T. Kamata, M. Handa, Y. Ikeda, and S. Aiso, unpublished data). Thus, the interactions did not play an active role in conformational change. Furthermore, even when the spring between Val³³² and Ser⁶⁷⁴ was eliminated from the elastic network model for the x-ray crystal structure, new types of global motions, such as those observed when the springs of Arg⁶³³ were eliminated, did not emerge in the lowest-frequency range. These experimental and computational results suggest that the interactions between Val³³² and Ser⁶⁷⁴ need to be eliminated for the conformational change of integrin, but that the elimination does not have the effect of enhancing the conformational change. The spring between Ser³⁰⁵ in the α-chain and Arg⁵⁶³ in the β-chain was eliminated for similar reasons. An experiment to replace a loop region in the α_IIb-chain, which corresponds to the loop including Ser³⁰⁵ in the α_V-chain, with that in the α₅-chain suggested that the interactions between Ser³⁰⁵ and Arg⁵⁶³ do not have an influence on the conformational change (58). Iterative normal-mode calculations showed that the spring needed to be eliminated for the conformational change. However, eliminating the spring from the elastic network model for the x-ray crystal structure had little effect on the lowest-frequency normal modes.

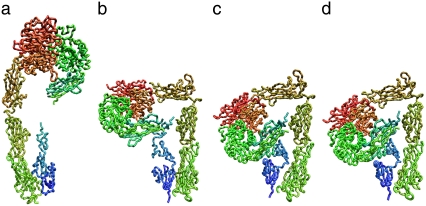
Among the four iterative calculations, integrin fully extended in one case, when the springs for both interactions A and B were eliminated (Fig. 5 a, and Table 2, calculation 1). In calculation 2 of Table 2, the conformational change terminated when the molecule took on an L-shape, as shown in Fig. 5 b. This result demonstrated the importance of eliminating interaction B for the conformational change to the fully extended form. The results of calculations 3 and 4 (Fig. 5, c and d) were quite similar. The corresponding structures (nth structures) during the iterative calculations were also similar to each other (rmsd < 3 Å). This result suggests that eliminating interaction B has a small effect on the conformational change if interaction A is maintained. The four iterative calculations clearly demonstrated that interaction A (interactions involving Arg⁶³³) works as a snap to keep integrin in the bent form.

FIGURE 5.

(a–d) Backbone structures of integrin at the end of iterative normal-mode calculations 1–4, respectively (Table 2).

Comparison with the conventional elastic network model

Our elastic network model differs from the conventional model in the definition of the distance between two residues. We introduced this definition so that the network formation would be more sensitive to the local conformation, as described earlier. Here, to observe the effect of the difference in definition, we carried out the same calculations as those performed to obtain Fig. 2 using the conventional elastic network model. Decreasing the cutoff length tends to destabilize the elastic network model. To avoid this, we modified the conventional elastic network model by introducing springs, irrespective of the cutoff length, along the amino acid chain between C_α atoms in the nth and (n + 2)th residues and between those in nth and (n + 3)th residues, which is the same procedure as in our elastic network model. The calculated correlation coefficients are plotted against cutoff length R_c in Fig. 6. The coefficients were relatively large and roughly constant when the cutoff length, R_c, was >7.8 Å, indicating that the molecular motions derived from the calculations were similar to those in the crystal structure. In our elastic network model, the coefficient took similar values when the cutoff length, r_c, was >3.3 Å, as shown in Fig. 2. There were 8332 springs in the conventional model with R_c = 7.8 Å, and 5512 springs in our elastic network model with r_c = 3.3 Å. The two network models had 5342 springs in common. Thus, the conventional model had 2990 additional springs and our model had 170 additional springs. The former springs correspond to the case shown in Fig. 1 a, but the latter do not correspond to any cases in Fig. 1. In the interactions represented by the latter case, amino acid residues with long side chains, such as Tyr or Arg, were often involved. The correlation coefficient between the thermal atomic fluctuations from the B-factors and those from the elastic network model, which was made from the common 5342 springs, was low (0.28). Thus, these additional springs were necessary in both models to reproduce the molecular motions in the crystal structure. However, there were obviously many more additional springs in the conventional model, suggesting that there were many springs in the conventional model that were not critically important for reproducing the molecular motions in the crystal structure.

FIGURE 6.

Correlation coefficient of the thermal atomic fluctuations derived from NMA and x-ray crystal structural data (B-factor) plotted against the cutoff length, R_c. Conventional elastic network models were used.

Fig. 6 shows that the coefficient decreased noticeably as the cutoff length became shorter than 7.8 Å. However, the decrease was gradual compared to Fig. 2. In Fig. 2, the coefficient decreased by ∼0.2 when the cutoff length was changed from 3.3 to 3.2 Å, whereas in this case, the same amount of decrease was observed only when the cutoff length was changed from 7.8 Å to 6.6 Å. Corresponding to the larger change in cutoff length to achieve the same amount of decrease of the coefficient, the number of the springs eliminated by the change in cutoff length was larger (1495 vs. 231). This result further supports the idea that there were more springs in the conventional elastic network model than in our model that did not critically influence the molecular motions.

The results presented here suggest that the short-distance interactions between two residues in our elastic network model have a potentially greater influence on the molecular motions than those in the conventional elastic network model, and thus that our definition of the distance between two residues is more effective than that in the conventional elastic network model in extracting or sorting such influential interactions, which is the major aim of this study.

Identifying key interactions for conformational change by NMA

Tama et al. (59) performed NMAs of the (conventional) elastic network models of proteins whose open and closed forms were solved by x-ray crystallography. They compared the atomic displacements in the conformational change from open to closed and closed to open forms with those in the normal modes. They found that the elastic network model for the open form generally had a normal mode in which the atomic displacements were close to those in the conformational change, whereas that for the closed form did not. In the case of integrin, there are two forms, that is, the bent form and the extended form. The former corresponds to the closed form, and the latter to the open form. The x-ray crystal structure was solved only for the bent form. Thus, if we consider the study by Tama et al. (59), what we did corresponds to the study to find the normal modes of the closed form of a protein that directed the molecule toward the open form. We found that the normal modes involved in the conformational change were newly generated by reducing the cutoff length until the correlation coefficients dropped drastically. Thus, our approach may be regarded as a possible solution for finding the normal modes of the closed form of a protein that direct the molecular structure toward the open form.

Instead of reducing the cutoff length, we can “manually” eliminate the interactions between domains of the elastic network model so that the extension of the molecule becomes easier. Assuming the cutoff length r_c = 5 Å, we performed NMA of the elastic network model. When all springs between the hybrid domain and the EGF/βTD domains were eliminated from this model, the correlation coefficient dropped from 0.54 (Fig. 2, open circles) to 0.34, and the lowest-frequency normal mode was similar to that shown in Fig. 3 a (with similarity of 0.75). This suggests that the “manual” elimination of interactions has an effect similar to the reduction of the cutoff length. However, without prior knowledge, it is difficult to decide which interactions should be eliminated.

Mutation experiments

Our calculations suggested that the interactions between Arg⁶³³ and the nonbonded nearby residues had to be eliminated for the structural rearrangement of integrin from the bent to the extended form to occur. Our calculations also suggested that the extension of integrin would be enhanced once the interactions were eliminated. To examine our predictions, specific interactions involving Arg⁶³³ were disrupted by mutating amino acid residues involved in the interactions.

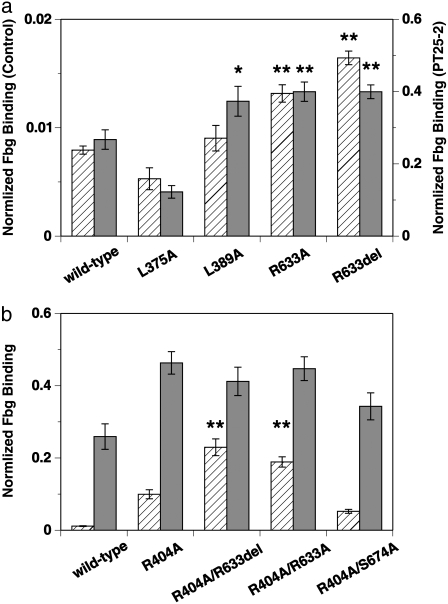
Mutant α_IIbβ₃ was transiently expressed on the mammalian CHO cell surface and FITC-labeled fibrinogen-binding to these cells was examined. As shown in Fig. 7 a, wild-type α_IIbβ₃ expressed on the CHO cell surface was in a low-affinity state and did not bind to fibrinogen significantly unless activated by mAb PT25-2, which brought up the binding by ∼33-fold. It has previously been shown that the mAb PT25-2 binds to the β-propeller domain of α_IIb-chain of integrin in platelets and induces the binding of integrin to fibrinogen (43,60). In contrast to the independent mutation of Leu³⁷⁵ or Leu³⁸⁹ to Ala, where the binding to fibrinogen was not affected so much, mutation of Arg⁶³³ to Ala, or its complete deletion, significantly increased the binding (p < 0.01). Activation with PT25-2 gave similar results, except that the L389A mutation showed a significant increase in binding (p < 0.05). These results indicate that the interactions involving the side chain of Arg⁶³³ are indeed important for constraining α_IIbβ₃ in a low-affinity state, as we predicted.

FIGURE 7.

Average amount of FITC-labeled Fbg bound to CHO cells expressing wild-type or mutated α_IIbβ₃ obtained from six separate experiments. The amount of Fbg in the presence of control antibody (hatched bars) and PT25-2 (shaded bars) is shown separately in arbitrary units with error bars. (a) Results for mutations at the residues involved in the Arg⁶³³-mediated interactions are compared with those for the wild-type. Amino acid residues Leu³⁷⁵, Leu³⁸⁹, and Arg⁶³³ in the β₃-chain were either mutated to Ala (L375A, L389A, and R633A) or deleted (R633del). The amount of Fbg in the presence of the control antibody and PT25-2 is shown in the left and right axes, respectively. Mutants that showed a statistically significant increase in binding from the wild-type are indicated by asterisks: *p < 0.05; **p < 0.01. (b) Results for single mutation of Arg⁴⁰⁴ in the β₃-chain (R404A) and double mutations of Arg⁴⁰⁴ in combination with either Arg⁶³³ (R404A/R633A, R404A/R633del) or Ser⁶⁷⁴ (R404A/S674A) are shown and compared with those for the wild-type. Mutants that showed significant increase in binding from the wild-type are indicated by asterisks: **p < 0.01.

The mutations L375A and L389A did not activate α_IIbβ₃ (actually L375A with PT25-2 deactivated it, with p < 0.01). Because the degree of expression of integrin on the cell surface was not affected by these mutations, it is not probable that the mutations caused global conformational change. To find the reason for the low activation, we checked the thermal fluctuations of side-chain atoms in the arginine residues derived from the B-factor of the x-ray crystal structure. There are 62 arginines in the x-ray crystal structure. In most of the residues, the thermal fluctuations of the side-chain atoms farther away from the C_α atom are larger suggesting the inherent flexibility of the side chain. Due to this flexibility, the side-chain atoms of Arg⁶³³ might be able to find new interaction sites in the mutated residue or in the nearby residues when Leu³⁷⁵ or Leu³⁸⁹ were mutated. In the case of L375A, the newly generated interactions might turn out to be stronger than the original and, as a result, α_IIbβ₃ might be further deactivated.

Our experimental results showed that complete elimination of the interactions involving Arg⁶³³ by deletion was not sufficient to fully activate α_IIbβ₃. According to our calculation, the elimination of Arg⁶³³-mediated interactions alone would allow only halfway extension of integrin (Fig. 5 b); in other words, Arg⁶³³ is the key residue to initiate the extension, but not the key residue to complete the extension. Thus, the results from the mutational studies are consistent with our calculations. The calculation further showed that complete extension would be achieved if the interactions between the hybrid domain and EGF domains involving Arg⁴⁰⁴ were also eliminated (Fig. 5 a). To verify this calculation result, we introduced mutations on both Arg⁴⁰⁴ and Arg⁶³³ at the same time. Arg⁴⁰⁴ was mutated to Ala and Arg⁶³³ was either mutated to Ala or deleted. As a reference, we performed a double mutation on Arg⁴⁰⁴ and Ser⁶⁷⁴, both of which were mutated to Ala, as well as a single mutation of Arg⁴⁰⁴ to Ala. The mutation of Ser⁶⁷⁴ is already known to have little effect on the activation, as discussed above. The results of the double mutations are almost exactly as we expected based on our calculations, as shown in Fig. 7 b. Compared to the single mutation R404A, the double mutations R404A/R633X (where X is A or del) clearly had larger effects (p < 0.01), which is in contrast to the effect of R404A/S674A, where the activity of integrin was not significantly different from the single mutations. The comparison between R404A/R633X and R404A/S674A demonstrates the importance of Arg⁶³³ again. These experimental and computational results suggest that the interactions at multiple interfaces have to be disrupted to achieve full activation as well as full extension.

It was demonstrated that α_Vβ₃ and α_IIbβ₃ integrins are different in their signaling mechanisms (40). This difference may be partially explained by the different interactions between the cytoplasmic α and β tails, in addition to the difference between the molecules that may associate with the specific α cytoplasmic tails. Another report showed that extracellular calf-2/(EGF-4 and βTD) interface interactions affect manganese-induced activation differently in two β₃ integrins (61). These reports suggest that the α/β interface interactions have a significant impact on integrin activation and are responsible for the differential regulation in two β₃ integrins. Thus, the Arg⁶³³ mutations may not necessarily have the same effect on the α_Vβ₃-ligand interaction as on the α_IIbβ₃-fibrinogen interaction observed in this study. However, the primary interdomain interactions that directly constrain α_Vβ₃ integrin to the bent form in the crystal structure will be those of the hybrid domain with EGF and βTD domains, in which the interactions of Arg⁶³³ are included, and not those at the α/β interface. Thus, it is reasonable to assume that disrupting the Arg⁶³³-mediated interactions has similar effects on the activation of α_Vβ₃ as well.

Conservation patterns of residues in key interactions in the integrin β-chain

NMAs and mutation experiments on integrin suggested that the interactions of Arg⁶³³ in the β₃-chain with nearby nonbonded residues work as a snap to keep integrin in the bent form. Among the nearby residues, two leucine residues interact with Arg⁶³³ in an interesting manner, that is, they sandwich the side chain of Arg⁶³³ (Fig. 8 b). We checked the conservation pattern of these residues in homologous integrin β-chain sequences.

From the amino acid sequence databases, 113 sequences homologous to the H. sapiens integrin β₃-chain were retrieved and were clustered into 10 groups by a phylogenetic tree built on a multiple-sequence alignment (Fig. 9). Mammalian integrin β-chains are known to be classified into eight groups based on sequence similarity, ligand specificity, and expressed cells (1). Our results included two clusters of nonmammalian integrin β-chains, and eight other groups were consistent with the previous study. The set of key residues was conserved as Leu/Leu/Arg only in the integrin β₃-chain, and in other β-chains, the evolutionarily corresponding positions were either conserved with different amino acid residues or not conserved (Fig. 8 c).

FIGURE 9.

Multiple-sequence alignment of integrin β-chains. Regions around the residues concerned are shown. The key residues found in the β₃-chain by NMA on H. sapiens integrin α_Vβ₃ and residues at homologous sites are boxed in red. Well conserved residues and cysteine residues in all the chains are highlighted. Identifications of each sequence in Genbank/UniProt/PDB are described on the left and the name of the species that the sequence is derived from is described on the right. The order of amino acid sequences is based on the sequence identity, and a horizontal bar separates groups in β-chains. The alignment around position 633 of β₄- and nonmammal chains was manually adjusted after automatic multiple-sequence alignment.

Arginine has one of the longest aliphatic side chains in 20 amino acids, and hence, possible interactions between Leu and Arg are hydrophobic ones using aliphatic side chains (Fig. 8 b). The conservation patterns of other β-chains are dissimilar to those of the β₃-chain, which suggests that other β-chains may have different molecular mechanisms for the conformational transition or do not undergo a conformational change at all. β₁- and β₂-chains are known to undergo a similar type of bent-to-extended conformational transition, and we surmise that the molecular detail of the mechanism is different from that in β₃-chain.

CONCLUSION

The conformational change of integrin from the bent to the extended forms was studied by NMA of the elastic network model. The calculations revealed the key residues for the conformational change, and their importance was confirmed by the experiment. Multiple sequence alignment showed that the characteristic pattern of residues (Leu/Leu/Arg) was conserved only in the integrin β₃-chain, suggesting that the mechanism of the conformational change from the bent to the extended forms studied here is unique to the chain.

A pathway for the conformational change was speculated from the calculations, which is summarized as follows. The first step is the motion of the βTD as a whole (shown in Fig. 3 b), which is perhaps brought up by a signal from inside the cell (inside-out signaling). This motion involves the displacement of Arg⁶³³ in the β₃-chain, whose side chain is sandwiched by two leucine residues in the x-ray crystal structure. By this motion, the interactions of Arg⁶³³ with nearby nonbonded residues will be eliminated. Once the interactions of Arg⁶³³ are eliminated, the molecular motions change quite drastically. Specifically, the motions of the hybrid domain in the β₃-chain become dominant (Fig. 3 a). The motions will enhance the separation of the hybrid domain from the EGF domains and will contribute to the elimination of the interactions between these domains. If the interactions are eliminated, further drastic conformational change becomes easier, and the molecule will extend (Fig. 5 a).