Elution-Extrusion Countercurrent Chromatography: Theory and Concepts in Metabolic Analysis

Abstract

Elution-extrusion countercurrent chromatography (EECCC) takes full advantage of the liquid nature of the stationary phase in CCC by combining regular chromatographic elution with stationary phase extrusion. EECCC is shown to be a three-stage process consisting of classical elution (I), sweeping elution (II), and extrusion (III). After only two column volumes of solvent, it rapidly yields a high-resolution chromatogram that covers an extended polarity range of solutes. As hydrophilicity/lipophilicity balance is a crucial discriminatory property of analytes in highly complex mixtures such as metabolomic samples, the precise determination of CCC distribution constants (K_D) is vital to the analysis of metabolomes and other complex biological matrices. This work builds the EECCC concept by performing a full theoretical treatment and providing equations for retention volumes, peak widths, resolution factors, and distribution constants. Experimental validation utilizes natural products standards that resemble the zero to infinity range of the polarity continuum. EECCC extends the “sweet spot” of high-resolution in CCC, and provides access to the otherwise practically unapproachable high-K_D portion of the high-resolution chromatograms in CCC. Its improved capabilities of K_D-targeting make EECCC a promising tool for the specific analysis of “small” molecules in complex samples such as in metabolomic fingerprinting and footprinting.

Countercurrent chromatography (CCC) is a liquid chromatography technique that uses a liquid stationary phase.^1-3 Typically, CCC employs biphasic liquid systems to separate solutes. One major advantage of working with a liquid as opposed to a solid stationary phase is that the solutes have access to the whole volume of the stationary phase. Historically, CCC has primarily been used as a preparative separation technique,⁴ in particular for the separation and purification of natural products (5-8 and references therein). Regarding CCC development and application, the entire body of relevant literature indicates a strong preference for separation problems that involve particularly complex samples, mainly of biological origin. Interestingly, this inclination connects CCC to a recently evolving area of analytical chemistry dealing with the analysis of natural metabolites in their entirety, i.e., metabolomics.

It is the combination of the complexity and the presence of “background” matrices that represents the major analytical challenge in the current state of metabolomics research⁹ (and references therein). While, at present, the complexity of the biosynthetic metabolic cocktails can only be roughly approximated, with estimates ranging from 10³ to >10⁵ depending on the organism, any given metabolome undoubtedly represents a mixture of an extremely large number of “small” molecules originating from primary and secondary metabolism of the organism. Moreover, the metabolites greatly differ in molecular weight, structural class, functional group chemistry, and – most importantly for this consideration – in their hydrophilicity/lipophilicity balance. Accordingly, metabolomic mixtures such as crude extracts used in drug discovery programs or as starting materials for analytical purposes present a significant challenge to any analytical technique, including chromatography, sample handling, and sample preparation. Additional challenges in metabolic fingerprinting and footprinting arise from the fact that metabolites span an estimated 7−9 orders of magnitude of concentration.^10,11 Thus, analytical methodology that is capable of “sorting” metabolites/analytes according to one of the above key differential properties, such as hydrophilicity, and doing so in an efficient manner is in high demand.^9,12,13

Along similar lines, when working with highly complex mixtures of analytes, a method for rapid estimation of the hydrophobicity range of a given sample in a particular solvent system is in high demand. In order to address this point, the recently proposed Generally Useful Estimation of Solvent System (GUESS) method allows rapid evaluation of the usefulness of a particular biphasic liquid system in CCC.¹⁴ The GUESS approach has been utilized in the bioassay-guided search for new anti-tuberculosis drugs, a process that can greatly benefit from the use of CCC.¹⁵ Another outcome of the GUESS study was the definition of a “sweet spot” in CCC chromatograms, which is made in terms of a range of solute distribution constants (K_D), and refers to the area where maximum efficiency of CCC is expected to occur.¹⁴ Subsequently, it was shown that in order to allow comparison of CCC chromatograms obtained under various experimental conditions, they shall be plotted with the distribution ratio (K_D), rather than volume or time, on the x-axis. Utilizing a standardized mixture of solutes of widely differing polarities in simplifying resemblance of metabolic mixtures, i.e., the GUESSmix, it could be demonstrated very recently by experiment that chromatograms obtained by elution extrusion CCC (EECCC) do cover a significantly extended polarity range. In addition, EECCC provides an extended “sweet spot” of separation and those offer high-resolution separation of a wider polarity range of analytes. By taking into consideration that the solute distribution ratio spans the full zero to infinite interval, this study went two steps beyond the idea of K_D plots in CCC by introducing the concepts of reciprocal symmetry (ReS) and reciprocal shifted symmetry (ReSS) as graphical representations of EECCC separations.¹⁶

The method of elution-extrusion countercurrent chromatography (EECCC) was proposed in 2003 to extend the hydrophobicity window of a countercurrent separation at will.¹⁷ Subsequent early reports on its application again focus on natural products. E.g., EECCC is currently used routinely for the fast dereplication of metabolites in microbial extracts with antifungal activity in an industrial drug discovery program.¹⁸ The EECCC method can take particular advantage of the liquid nature of the stationary phase in CCC owing to the fact that inside a CCC column solutes are moving in the form of very narrow bands.¹⁹ It is a major strength of EECCC that the narrow band widths present inside the column are preserved, as during the extrusion stage of EECCC the liquid stationary phase is simply pushed out of the presumably inert column. The resulting sharp “extruded” peaks can be fully utilized for subsequent collection and/or detection of the analytes such as natural metabolites.

Since the first description of the EECCC method,¹⁷ inconsistencies have been observed between the documented fundamental theory,¹⁸ reports of practical applications of the EECCC method,^16-19 and experimental observations. While a significant number of sources of systematic errors can be identified for any experimental implementations of CCC, including EECCC, such as errors introduced by the liquid dispensing systems or by dead volumes, these deviations have prompted us to completely re-examine the theory of EECCC. One goal of this study was to explain the systematic biases found in calculated positions of solute peaks that were apparently due to an inexactitude in the equations used to calculate the extrusion volumes. Thus, based on an in-depth re-examination of the theoretical foundations of the EECCC method, independently derived equations have been developed that allow proper prediction of peak position and peak width. This enables more accurate description of analytes/metabolites that fall into the high-K_D portion of the extended EECCC polarity window.

A second goal was to test the new equations experimentally with standard mixtures of natural products, i.e. the GUESSmix, that cover a wide range of polarity and, thus, can serve as a basic model of metabolomic complexity. The objective of this part of the study was to experimentally validate the EECCC method by testing for graphical and numerical K_D matches in ReSS plots of GUESSmix chromatograms. Finally, this work aims to clarify the mechanisms and unify the nomenclature associated with the EECCC technique.

EXPERIMENTAL SECTION

Instrumentation

High-speed countercurrent chromatography (HSCCC) was performed on a Model CCC-1000 J-type instrument (Pharma-Tech Research Corporation, Baltimore, MD, USA). It consisted of a self-balancing three-coil centrifuge rotor and coils wrapped with 1.6 mm internal diameter of PTFE (Teflon) tubing to a volume of 40 mL each. The distance between the coil holder axis and central axis of the centrifuge (R) was 7.5 cm. The β ratio (β_r) varied from 0.73 at the periphery to 0.47 at the center (β_r = r/R where r is the spool radius and R is the rotor radius). The rotation of the horizontally arranged coil assembly relative to the coil winding situated the head at the periphery position of the coil assemblies. Furthermore, the HSCCC system included a Lab-Alliance Series III digital single-piston solvent pump, a Shimadzu SPD-10A UV-vis detector with preparative flow cell, and an ISCO Lab Alliance Foxy Jr. fraction collector. Chromatogram data was collected with a Cole-Parmer 80807−00 modular paperless recorder and transferred in digital form to an Excel spreadsheet.

Thin Layer Chromatography

Collected fractions were reduced in volume and analyzed with TLC at room temperature. Alugram pre-coated 0.20 mm thick silica gel G/UV₂₅₄ aluminum plates (20 × 20 cm; Macherey-Nagel, Germany) were cut to 9.5 cm × 20 cm before spotting. Plates were dipped in the general-purpose reagent: 4% p-anisaldehyde/ 4% sulfuric acid/ 92% acetic acid, drained and heated on a Camag TLC Plate Heater III at 95° C for about 5 minutes. Digital preservation of all TLC chromatograms was achieved with a Canon CanoScan Lide20 scanner.

Chemicals

HPLC grade solvents were purchased from Fisher Scientific or Sigma-Aldrich. GUESSmix component chemicals were purchased from the Sigma Aldrich Fluka group (St. Louis, MO and Milwaukee, WI). Table 1 lists twelve GUESSmix compounds sorted by increasing octanol/water partition coefficients. The biphasic liquid system selected is the mixture of hexane/ethyl acetate/methanol/water in the volume ratio of 4:6:4:6 v/v. Once equilibrated, this system separates in an aqueous lower phase whose composition was determined to be respectively 0.5/20.4/47/32.1 %v/v with a density of 0.879 g/cm³ at 22°C; and an upper phase whose composition was respectively 76.3/20.2/3.3/0.2 %v/v and density of 0.713 g/cm³.²⁰ The stationary phase was the lighter organic phase and the mobile phase was the denser aqueous phase.

Table 1.

Structures and physicochemical properties of the solutes used.

code	Solute	Structure	m.w.	pKa	Log Ko/w	Log KD
r	new coccine red		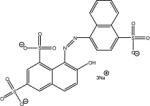C20H11N2O10S3Na3 604.5	trianion	−5.1	(a)
C	caffeine		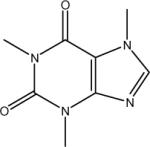C8H10N4O2 194.2	14.0	−0.07	−0.60
V	vanillin		C8H8O3 152.2	10.2	1.21	0.15
M	coumarin		C9H6O2 146.2	n.i.	1.39	0.60
Q	quercetin		C15H10O7 302.2	10.3	1.48	0.27
F	ferulic acid		C10H10O4 194.2	4.4	1.51	−0.07
U	umbelliferone		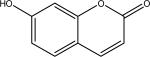C9H6O3 162.2	10.3	1.58	0.06
Z	salicylic acid		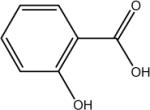C7H6O3 138.1	2.9	2.26	0.78
N	naringenin		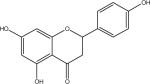C15H12O5 272.3	10.1	2.52	0.65
O	carvone		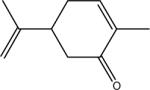C10H14O 150.2	n.i.	3.07	1.38
E	estradiol		C18H24O2 272.4	10.5	3.94	1.04
b	β-carotene		C40H56 537	n.i.	17.6	(b)

n.i. = non ionizable; log K_o/w values were obtained using the Kowwin software (www.syrres.com/esc/est_kowdemo.htm). The Log K_D values were determined in the liquid system hexane/ethyl acetate/methanol/water 4/6/4/6 v/v. a) new coccine red is not retained (K_D = 0); b) β-carotene marks the end of the extrusion step (K_D ∞).

CCC Procedures

Samples of GUESSmix compounds were prepared as previously described in the form of a stock solution with a final concentration of approximately 0.1g/mL of combined compounds.¹² The stock solution was stored at −30° C and warmed to room temperature before use. The GUESSmix compounds were prepared for a chromatography by drying 2.2 mL of the stock solution under forced air, and the resulting residue was then suspended in equal volumes of upper and lower phase of the solvent system. The biphasic mixture of GUESSmix compounds was then filtered and loaded into a 2 mL sample loop.

The solvent system was thoroughly mixed, vented and allowed to separate into two distinct phases before use. The lipophilic lighter stationary phase was initially pumped into the column with no rotation. Then the coils were rotated 1200 rpm as the hydrophilic denser mobile phase was pumped at a flow rate of 1 mL/min entering the column head. In order to observe the volume of stationary phase eluted from the column, the resulting effluent was collected in a graduated cylinder. The hydrodynamic equilibrium was considered to be established when the volumes of the two phases of the eluant were approximately equal. In order to optimize volumetric precision, primarily for the determination of V_M and V_S, and for the subsequent calculation of the chromatograms, preference was given to the method of “injection at equilibrium” over “injection before equilibrium”. While the latter is routinely used in CCC separations, in particular when maximizing sample throughput, K_D values tend to be less consistent due to difficulties in precisely accounting for minor loss of stationary phase that is frequently associated with early eluting analytes. The standard compound mixture was injected on the column, the fraction collector started, and the recorder turned on. All fractions were collected at 3 min/tube. After a predetermined volume (V_CM, also called the switch volume) of aqueous mobile phase had eluted from the column, the organic phase was pumped into the column, marking the beginning of sweep elution and subsequent extrusion, and also entering through the column head. After the lipophilic marker, β-carotene, eluted from the column (120 mL after V_CM) the run was discontinued. The collected fractions were reduced in volume and TLC performed to corroborate the UV-vis data.

THEORY

The Elution-Extrusion Method

As CCC is support-free and utilizes a liquid stationary phase,¹ this liquid nature can be used advantageously to widen the polarity coverage of the method. In fact, Giddings²¹ demonstrated that the broadening of a solute band moving inside a chromatographic column depends only on the band position, X, and the column height equivalent to a theoretical plate, H, being simply expressed as $\sigma =\sqrt{XH}$ , σ being the standard deviation of the Gaussian peak. The peak width at base of a Gaussian band is equal to 4σ. Thus, solutes can be baseline separated inside the column well before leaving it. Utilizing the liquid nature of the stationary phase, it is possible to save significant amounts of solvents by recovering the solutes from the stationary phase, rather than eluting them from the CCC column.¹⁷

Upon injection of the solutes, the first stage in the EECCC method is classical elution (CM = classical mode). After the switch volume V_CM of mobile phase has moved the solutes to their respective positions X_i inside the column, the subsequent stages of the EECCC method are initiated by switching the solvent reservoir of the liquid pump system from mobile phase to stationary phase, i.e., making the formerly stationary phase the mobile liquid. As detailed below, the solutes located inside the column including the “stationary” phase are subsequently pushed out of the column in the form of narrow peaks that show a decreasing peak width as their retention volume increases.¹⁹ The invaluable advantage of the EECCC method is that solutes cannot stay trapped in the column, i.e., full sample recovery can be achieved.

Approaches to the Theory of EECCC

There are two principal ways to derive the theory that describes K_D values of solutes in EECCC: the velocity model (VelMod) and the volumetric model (VolMod). Both models aim to describe solute retention in the CCC column, but they look at the moving analytes from different angles, i.e., the speed and position in the column vs. the volume “eluted” from/pumped into the column. In the following, the theory will first be devised using VelMod, while VolMod will subsequently be taken into account to support it. Finally, experimental evidence using real GUESSmix samples are used to demonstrate the validity of the calculations within the boundaries of experimental error achievable with current instrumentation.

The Velocity Model (VelMod) of Solute Retention in the Elution-Extrusion

The equilibrated CCC column can be considered as a tube of length L, volume V_C, containing a volume V_M of mobile phase, and, consequently, a volume V_S = V_C − V_M of stationary phase. The retention volume, V_R, of a solute i is expressed by the classical equation

$$V_{Ri}=V_M+K_{Di}{V}_S$$ (1)

with K_D, the solute distribution constant or partition coefficient. K_D is the ratio of the equilibrium solute concentration in the stationary phase to the concentration in the mobile phase.

Elution

In the initial period of classical elution, which represents Stage I of the EECCC method, all solutes i move inside the column at a speed u_i:

$$u_i=F\cdot L∕V_{Ri}$$ (2)

with F being the mobile phase flow rate (mL/s). This movement happens at a speed that is slower than the linear velocity of the mobile phase, u_M (Figure 1A):

$$u_M=F\cdot L∕V_M$$ (3)

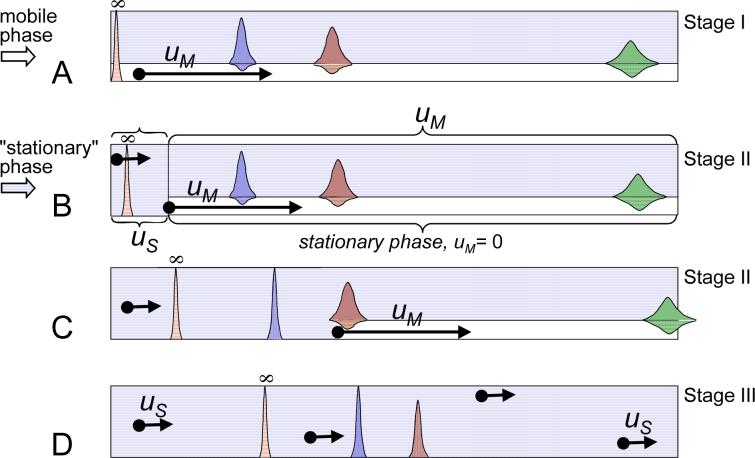
Figure 1.

Schematic representation of the Elution-Extrusion CCC method using the velocity approach (see text). A – The elution period (Stage I). The mobile phase moves with a u_M linear velocity. B – The extrusion period starts. During the following Stage II, i.e, the sweeping elution, the solvent front moves with the mobile phase linear velocity u_M. At the column head, the “stationary” phase moves at the linear velocity u_S. At the same time, the “stationary” phase is really stationary only at those positions ahead of the solvent front. C – During the sweep elution time, the solutes located near the column end are still exposed to elution conditions, partitioning between the two phases as long as they are not passed by the “stationary’ phase solvent front. Only mobile phase exits the column. D – Extrusion (Stage III). The whole column contains only “stationary” phase, and all remaining solutes move at the S phase velocity, u_S. The peak marked with the infinite sign locates the position of carotene, a solute with a very high K_D constant that marks the end of the experiment when leaving the CCC column.

The operator chooses to end the elution stage after the mobile phase volume V_CM (switch volume) has passed through the CCC column. At this point, all solutes i with retention volumes V_Ri lower than V_CM have been eluted from the column. At the same time, the solutes that are still inside the column are located at distances X_i from the column inlet:

$$X_i=L(V_{CM}∕V_{Ri})$$ (4)

Extrusion

Previously¹⁷ it had been overlooked that the “extrusion” part (switch of mobile phase) of the elution-extrusion method, which starts at volume V_CM, actually takes place in two stages that correspond to the two volumes contained in the column, the mobile (V_M) and the stationary phase (V_S) volumes.

The former period is Stage II of the EECCC method. It represents the sweep elution stage, during which a solvent front moves between the two phases inside the CCC column. This movement occurs from the inlet to the outlet and at the mobile phase speed u_M, which is faster than all solute velocities u_i. From the perspective of the outlet, e.g., any hyphenated detector, only mobile phase leaves the column (Figure 1B and 1C). The “stationary” phase volume needed to complete EECCC Stage II is exactly equal to V_M.

During Stage III (“true” extrusion, no elution component, Figure 1D), the remaining volume, V_C − V_M = V_S, of “stationary” phase containing all the solutes in the stationary phase (S phase, Figure 1) is pushed out at a linear velocity:

$$u_S=F\cdot \mathrm{L}∕V_C$$ (5)

It is noteworthy that the stationary phase velocity during Stage II elution was zero.

Solute Position inside the CCC Column

At the beginning of “extrusion”, i.e. volume V_CM or start of Stage II, the liquid phase entering the column is switched from the mobile phase to the (former) stationary phase (thus termed “stationary” phase in this work). Consequently, the solutes are located inside the column at the distances X_i given by eq 4. The solutes are exposed to one of two possible processes at any given point of time: either process 1, where both of the liquid phases are present, then the solutes are partitioned between the two phases and move at speed u_i (eq 2; classical chromatographic elution process); or in process 2, where only the “stationary” phase is present, then the solutes are simply carried along at speed u_S (eq 5; linear transportation process). An important caveat for the further understanding of the theory of “extrusion” (Stages II and III of EECCC) is that the change between the chromatographic elution and linear transport processes does not occur at the same time for all solutes. Rather, a change in velocity process occurs when the solvent front of the Stage II sweeping elution (Figure 1B and 1C) passes the solute. Until that happens, the solute has moved by a relatively small distance, ΔX_i, before getting “caught up” by the solvent front of “stationary” phase. This represents a classical pursuit problem, which is solved by calculating the time required for the solvent front to “catch” solute i as follows:

$$\frac{X_i+\Delta X_i}{u_M}=\frac{\Delta X_i}{u_i}$$ (6)

Using eqs 1, 2 and 3 to express the parameters in eq 6, it becomes:

$$\Delta X_i=X_i\frac{V_M}{K_{Di}{V}_S}.$$ (7)

This means that solute i is located at the distance X_i+ΔX_i when being “caught up” by the S/M solvent front (Figure 1C):

$$X_i+\Delta X_i=\frac{L{V}_{CM}}{K_{Di}{V}_S}$$ (8)

Finally, an important case to consider is the case of solute i that will leave the column without “seeing” the stationary front. This holds true if the distance X_i +ΔX_i exceeds the column length L; an example is the rightmost solute in Figure 1A. In other words, this applies to solutes with K_Di lower or equal to V_CM/V_S, i.e., during extrusion Stage III.

Solute Retention Volumes for Phase III

The solute retention volume for compounds the leave the system in Stage III (pure extrusion), V_EECCCi, corresponds to the two processes actually seen by the solute. During the previous Stage II, sweeping elution: a volume V_CM plus the extra mobile phase volume corresponding to the X_i +ΔX_i dislocation of the solute (Figure 1C). During the actual extrusion, Stage III: transport at speed u_S (eq 5) by the “stationary” phase for the distance L − (X_i +ΔX_i) remaining to be traveled inside the column to reach the column outlet. Adding them yields V_EECCCi as

$$V_{EECCCi}=V_{CM}+(X_i+\Delta X_i)V_M∕L+[L-(X_i+\Delta X_i)]V_C∕L$$ (9)

Combining eqs 8, 9, and the relationship V_S = V_C − V_M, the solute retention volume, V_EECCCi, becomes:

$$V_{EECCCi}=V_{CM}+V_C-V_{CM}∕K_{Di}$$ (10)

for solutes with K_Di ≥ V_CM/V_S, i.e, during EECCC extrusion Stage III.

The Volume Model (VolMod) of Solute Retention in the Elution-Extrusion

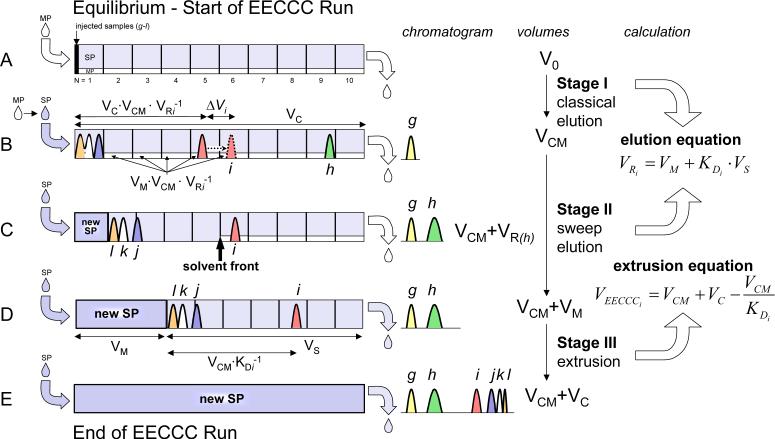
An alternative approach to describing solute location can be made in terms of volume (Figure 2). In an equilibrated CCC column, the volume required to elute solute i by classic elution (V_Ri) is expressed in eq 1. The volume V_CM remains unaltered as the volume of mobile phase that was pumped into the column before switching the solvent supply to “stationary” phase. Hence, once V_CM of mobile phase has been introduced into the column, solute i has moved by the volume V_C·V_CM·V_Ri⁻¹ (equivalent to X_i in the VelMod approach). This means that there is V_M·V_CM·V_Ri⁻¹ of mobile phase behind solute i (Figure 2B). As i keeps traveling by ΔV_i during the sweep stage until there is no more mobile phase behind it, the amount of stationary phase that needs to be pumped is V_M×V_CM×V_Ri⁻¹+ ΔV_i. At the point where no more mobile phase is behind it (Figure 2C), solute i has traveled a column volume represented by term 11

$$V_C\cdot \frac{V_{CM}+\left(\frac{V_M\cdot V_{CM}}{V_{Ri}}\right)+\Delta V_i}{V_{Ri}}$$ (11)

Figure 2.

The EECCC concept using the volume approach and a hypothetical mixture of six solutes, g to l, in a theoretical 10-cell CCC machine. Inside the column, there are denser mobile phase (open mixing zone in the column) and lighter stationary phase (dashed). The droplet with arrow at left indicates solvent inlet, whereas the droplet at right indicates solvent outlet. A) the beginning of the run. All six solutes are at the inlet of column. Mobile phase is being pumped in and eluting. B) After a V_CM volume of mobile phase has been used to separate the 6 solutes with only solute g coming out, the sweep stage begins as the inlet was just switched to stationary phase from mobile phase. Solute i is at V_C×V_CM×V_Ri⁻¹ (ml) from the inlet and has V_M·V_CM·V_Ri⁻¹ (ml) of mobile phase behind it. ΔV_i is the additional volume i will travel during the sweep stage. C) The end of elution for i, all the mobile phase behind is now replaced by new (previously stationary) phase. Hereafter i will NOT be partitioned and will only “slide” in the column. Solute h, which was inside the column at the beginning of the sweep stage, has also been eluted. Solutes j/k/l, which had not been separated at 2B, achieved separation due to further partitioning during the sweep stage. D) The end of the sweep stage, all the mobile phase is now replaced by new stationary phase and the first droplet of stationary phase comes out from the outlet. This is the beginning of extrusion. K_D of any solute came out before this point should be calculated with classical equation (i.e. eq1). E) The end of the run, everything injected in the column has come out in the form of thinner and thinner peaks, even solute l with K_Dl = ∞, the thinnest peak.

Term 11 is the counterpart to X_i+ΔX_i in VelMod approach, and is proportional to the amount of stationary phase pumped into the column during sweep elution, Stage II; hence

$$V_C\cdot \frac{V_{CM}+\left(\frac{V_M\cdot V_{CM}}{V_{Ri}}\right)+\Delta V_i}{V_{Ri}}=\frac{V_C}{V_M}\cdot \left(\frac{V_M\cdot V_{CM}}{V_{Ri}}+\Delta V_i\right)$$ (12)

This is solved as

$$\Delta V_i=\frac{{V_M}^2\cdot V_{CM}}{V_{Ri}(V_{Ri}-V_M)}$$ (13)

Thus, at the point when the first droplet of stationary phase is ready to leave the column (Figure 2D), solute i has traveled a volume represented by term 14

$$V_S\cdot \frac{V_{CM}+\frac{V_M\cdot V_{CM}}{V_{Ri}}+\frac{{V_M}^2\cdot V_{CM}}{V_{Ri}(V_{Ri}-V_M)}}{V_{Ri}}+V_M$$ (14)

This can be simplified to

$$\frac{V_S\cdot V_{CM}}{V_{Ri}-V_M}+V_M$$ (15)

Considering eq 1, term 15 is the same as

$$\frac{V_{CM}}{K_{Di}}+V_M$$ (16)

Hence, under the condition of “extrusion” (Stages II+III) with K_Di>V_CM/V_S, V_EECCCi becomes

$$V_{EECCCi}=V_{CM}+V_M+V_C-(\frac{V_{CM}}{K_{Di}}+V_M)=V_{CM}+V_C-\frac{V_{CM}}{K_{Di}}\mathrm{q}.\mathrm{e}.\mathrm{d}.$$ (10)

Summary of Stages and Solute Retention in the EECCC

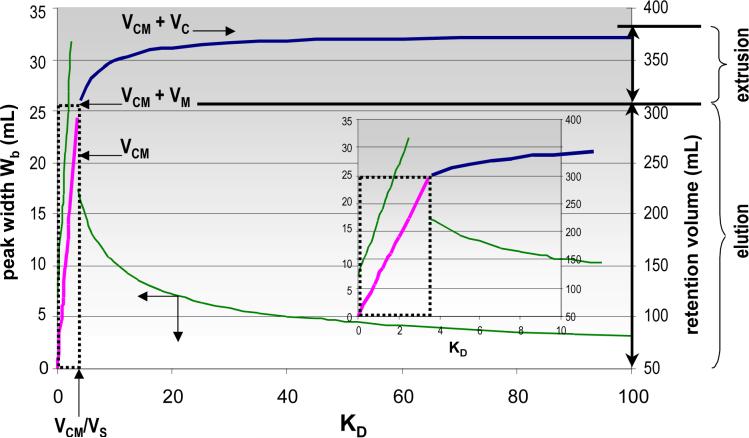
Figure 3 shows that the solute retention volume increases linearly with its distribution constant during elution (Stages I and II), which lasts during the combined volume V_CM + V_M and corresponds to those solutes with K_D ≤ V_CM/V_S. For all solutes with distribution constants above V_CM/V_S, the V_EECCCi retention volume is much smaller than the classical V_R retention as the maximum possible retention volume in EECCC is V_CM + V_C for solutes with K_D = ∞ (Stage III).

Figure 3.

Retention volume (right axis and thick lines) and solute peak width (in volume, left axis and thin lines) plotted versus solute distribution constant in the EECCC method. Values calculated (eq 1, 10 and 22) with V_C = 120 mL, V_M = 50 mL, V_S = 70 mL, V_CM = 254 mL and N = 900 plates. The limit between elution and extrusion occurs for K_D = V_CM/V_S = 254/70 = 3.63 and V_R = V_CM + V_M = 304 mL (dotted area). The inset is an enlargement of the 0<K_D<10 region.

Figure 2 summarizes the three stages of EECCC, how different solutes behave during the process, and which equations to use to calculate solute K_D values over the 0 to ∞ range of the chromatogram. From a practical point of view, the important volumes required to consider during EECCC operation are:

V_S The stationary phase volume retained in the CCC column of known volume V_C; determined at the beginning of the experiment after reaching column equilibrium

V_M The mobile phase volume inside the column; is equal to V_C − V_S

V_CM The mobile phase volume after which the operator switches the supply of flowing liquid phase from mobile to previously stationary phase (designated “stationary” phase); start of EECCC Stage II

V_CM+V_M The volume at which the liquid phase that exits the column changes from mobile to “stationary” phase; start of EECCC Stage III

V_CM+V_C The maximum retention volume for solutes with an infinite K_D; represents the end of the EECCC experiment. The CCC column is filled with fresh stationary phase, and is ready for equilibration in preparation for another experiment.

Solute Distribution Constants

Depending on the processes seen by the solutes (processes 1 vs 2, see above), retention volumes and distribution constants are related differently: For solutes that are exclusively eluted, i.e., with 0 < K_D < V_CM/V_S , only mobile phase exits the column, and K_D can simply be calculated from eq 1 as

$$V_M<V_R<V_{CM}+V_M\to K_D=\frac{V_R-V_M}{V_S}$$ (17)

For solutes that are both eluted and extruded, i.e., with V_CM/V_S < K_D < ∞, the solute retention volume is composed of a mobile phase volume, V_CM + V_M, plus a successive “stationary” phase volume, V_S − V_CM/K_D. Thus, K_D becomes

$$V_{CM}+V_M<V_{EECCC}<V_{CM}+V_C\to K_D=\frac{V_{CM}}{V_{CM}+V_C-V_{EECCC}}$$ (18)

Selectivity

In order to define selectivity, the ratio of the retention volume difference between two solutes over their distribution constant difference, dV/dK_D,⁹ can be established as a selectivity during elution (Stages I and II) as:

$$\mathrm{d}{V}_R∕\mathrm{d}{K}_D=V_S$$ (19)

Thus, selectivity improves as liquid stationary phase retention in the CCC column increases, and the retention volume V_R increases linearly with K_D (Figure 3, elution). During extrusion (Stage III), the difference in extrusion retention volume, dV_EECCC, replaces dV_R, and the selectivity becomes

$$\mathrm{d}{V}_{EECCC}∕\mathrm{d}{K}_D=V_{CM}∕{K_D}^2$$ (20)

Thus, selectivity increases with the volume V_CM at which sweeping and extrusion were initiated, but it decreases quadratically with the K_D value of the solute. For example, the inset in Figure 3 shows that there is a difference in retention volume (= V_S) of about 70 mL between two solutes with K_D of 2 and 3, respectively, after an elution stage that lasted for 254 mL. However, if the two solutes have K_D values of 9 and 10, respectively, the difference is only 2.8 mL. The difference becomes as small as 0.28 mL for two solutes with K_D values as high as 90 and 100, respectively (Figure 3). This underlines the critical importance of the ΔX_i and ΔV_i correction terms of solute position and retention volumes, respectively.

Peak Width and Resolution in EECCC

As a property of the Gaussian curves, the band width at base of a given solute i, W_bi (elution peak width), is simply equal to 4σ under the assumption of strictly Gaussian peak shape.

$$W_{bi}=4V_{Ri}∕\sqrt{N}$$ (21)

The peak widths at base increase linearly with the solute retention volume (Figure 3). Since the CCC column efficiency, N, can be considered constant, it is actually the eluted solute peak width that can be measured to calculate N.

The picture changes when looking at extruded peak widths. Inside the column, the Gaussian peak standard deviation only depends on the position of the solute and (height or) length equivalent of a theoretical plate.¹⁹ Assuming that the peaks are Gaussian and that the Taylor diffusion introduced by the “stationary” phase progressing in tubes is negligible, the extruded peak width expressed in terms of column length is:

$$W_{bi}=4\sigma =4\sqrt{(X_i+\Delta X_i)H}=4L\sqrt{\frac{V_{CM}}{N{K}_{Di}{V}_S}}$$ (22)

or, in volume units:

$$W_{bi}=4\sigma =4V_C\sqrt{\frac{V_{CM}}{N{K}_{Di}{V}_S}}$$ (23)

Accordingly, Figure 3 shows that the width of extruded peaks decreases as the retention volume V_EECCC increases.

Resolution Factor

In chromatography, the resolution factor is defined as the retention volume differences between two successive peaks divided by their average peak width at base:

$$R_S=2\frac{V_{R2}-V_{R1}}{W_{b2}+W_{b1}}$$ (24)

The resolution equation in the classical elution mode is expressed by:

$$R_S=\frac{\sqrt{N}}{4}\frac{K_{D2}-K_{D1}}{\frac{V_M}{V_S}+\frac{(K_{D2}+K_{D1})}{2}}$$ (25)

Equation 25 provides evidence for the critical role of the stationary phase volume in CCC. Unless a CCC column contains a relatively large fraction of stationary phase (noted S_F = V_S/V_C), its ability to separate analytes remain relatively low.¹

The equation describing resolution in extrusion mode can be expressed using eqs. 10, 23 and 24 as:

$$R_S=\frac{\sqrt{N}}{2V_C}\sqrt{V_{CM}}\left(\sqrt{\frac{1}{K_{D1}}}-\sqrt{\frac{1}{K_{D2}}}\right)$$ (26)

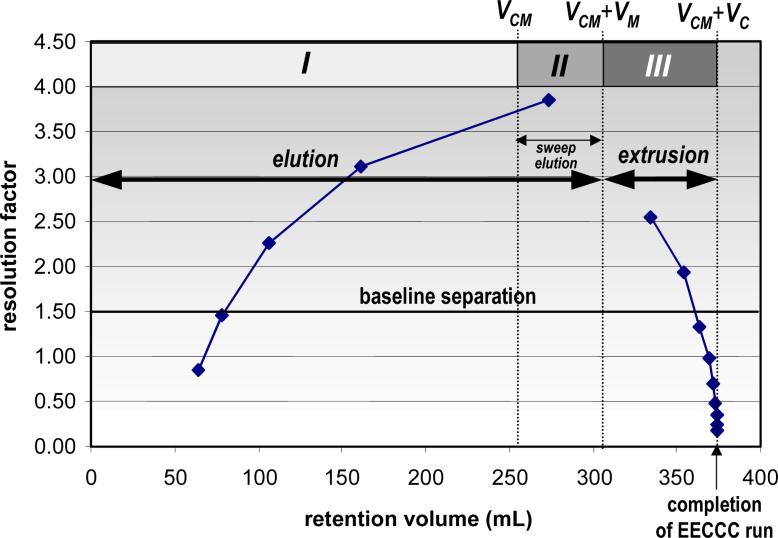
Table 2 lists the retention volumes, peak widths at base, and resolution factors for hypothetical solutes with distribution constants that successively double, a situation that corresponds to a constant Log K_D difference of 0.3. Figure 4 shows that, in this particular situation, while the resolution factors increase, the retention volumes become rapidly prohibitive when working in elution mode. In the extrusion mode, however, the maximum retention volume is known to be V_CM + V_C, and solutes with high K_D values can be analyzed with a feasible volume. The limitation of extrusion results from the fact that the resolution factors decrease rapidly towards the very end of the extrusion (Stage III). In practice, and given the currently available CCC instrumentation, it is reasonable to expect that solutes with K_D > 100 cannot be experimentally distinguished. However, it should be borne in mind that all injected solutes are fully recovered by extrusion and, thus, are amenable to a subsequent CCC separation in a two-phase solvent system of different polarity.

Table 2.

Retention volumes, peak widths and resolution factors of hypothetical solutes

KD	VR	Wb	Rs
0.1	57	7.60
0.2	64	8.53	0.86
0.4	78	10.4	1.46
0.8	106	14.1	2.27
1.6	162	21.6	3.12
3.2	274	36.4	3.84
6.4	334.31	12.05	2.50
12.8	354.16	8.52	1.93
25	363.84	6.10	1.32
50	368.92	4.31	0.97
100	371.46	3.05	0.69
200	372.73	2.16	0.49
400	373.37	1.53	0.34
800	373.68	1.08	0.24
1600	373.84	0.76	0.17

Values in bold correspond to the extrusion step. V_C = 120 mL, V_M = 50 mL, V_S = 70 mL, V_CM = 254 mL and N = 900 plates. The limit between elution and extrusion occurs for K_D = V_CM/V_S = 254/70 = 3.63 and V_R = V_CM + V_M = 304 mL Total elution is V_CM + V_C = 374 mL.

Figure 4.

Resolution factors obtained between two solutes related by a distribution constant ratio equal to two or ΔLog K_D = 0.3. Left curve: elution mode; right curve: extrusion mode. V_C = 120 mL, V_M = 50 mL, V_S = 70 mL, V_CM = 254 mL and N = 900 plates. The last solutes have left the column at volume V_CM + V_C = 254 + 120 = 374 mL, but at this point the resolution factor is nil.

RESULTS AND DISCUSSION

Previous Results Revisited

When the EECCC method was first introduced,¹⁷ a mixture of alkylbenzene derivatives was separated with two CCC columns: one was a hydrodynamic column (HSCCC, as used in the present study) of V_C = 175 mL, the other a hydrostatic column of V_C = 101 mL. The solutes and the two-phase liquid system of heptane/methanol/water 10/9/1 (v/v) were selected, because that system had been extensively studied already and the distribution constants, K_D, were known.²² Table 3 lists the experimental retention volumes obtained from the aforementioned mixture of alkylbenzene derivatives and the corresponding theoretical volumes calculated with eqs 1 and 10. The calculated retention volumes coincided with the experimental values, with errors below 1% for the hydrodynamic column. However, because the ΔX_i (or ΔV_i) solute displacement were missing in the previous computation, this produced a bias that increased dramatically with the solute distribution constant (7.8% and 13.5% for butyl and octylbenzene, respectively; see Table 3). In the case of the hydrostatic column, also called centrifugal partition chromatography, CPC, the errors obtained with eq 10 are also significantly lower than those obtained previously. The fact that a 9% difference remains between theoretical and experimental results obtained earlier can best be explained by shortcomings of the experimental implementation, i.e., mainly instrument design. More generally, in hydrostatic CCC (CPC), it is also possible that a fraction of the mobile phase stays entrapped in the channels of the hydrostatic column. Another potential source of deviation in hydrostatic CCC relates to the choice of normal vs reversed phase mode elution: When extruding with the lighter phase in descending mode, some mixing by convection may occur because flow and centrifugal field forces are pointing in the same direction. In contrast, perturbation inside the cells is unlikely to occur when extruding with the heavier phase in normal phase (ascending) mode as flow and centrifugal field are in opposed. In order to accommodate any of the aforementioned phenomena into the EECCC calculation, it would be necessary to introduce adjustment factors into the calculation of volumes of extruded stationary phase.

Table 3.

Elution-Extrusion of an Alkylbenzene and a Steroid Mixture

compounda	KD	VR exp.	VR ref.17	deviation	VR calc.	Deviation
Hydrodynamic 3-coil CCC column, VC = 175 mL, VM = 80 mL, VS = 95 mL, VCM = 270 mL
benzene	2.0	268	273	+1.9%	270	+0.7%
toluene	3.0	352	346	−1.7%	355	+0.9%
ethylbenzene	4.0	380	386	+1.6%	378	−0.5%
butylbenzene	7.7	412	444	+7.8%	410	−0.5%
octylbenzene	31	436	495	+13.5%	436	0%
Hydrostatic CPC column, VC = 101 mL, VM = 21 mL, VS = 80 mL, VCM = 199 mL
benzene	2.0	184	183	−0.5%	181	−1.6%
toluene	3.0	228	232	+1.7%	233	+2.2%
butylbenzene	7.7	252	287	+14%	274	+8.7%
octylbenzene	31	268	312	+16%	293	+9.3%
Hydrodynamic 1-coil CCC column, VC = 52.2 mL, VM = 21 mL, VS = 31.2mL, VCM = 33 mL19
prednisone	0.12	24.6	-		24.7	+0.4%
prednisolone	0.56	38.6	-		38.5	−0.2%
testosterone	1.4	62.8	-		61.6	−1.9%
estrone	4.6	78	-		78	0%
cholesterol	40	84.6	-		84.4	−0.2%

^aalkylbenzene were separated with the liquid system heptane/methanol/water 5/4/1 v/v with the aqueous lower mobile phase and the heptane lighter stationary and extruding phase. Steroids were separated with the heptane/ethyl acetate/methanol/water 5/6/5/6 v/v liquid system with the aqueous lower mobile phase and the organic lighter stationary and extruding phase.

With regard to the previously presented EECCC separation of a steroid mixture,¹⁸ Table 3 builds on this example by showing the experimental volumes, as correctly represented by eq 10, and, thus, allowing the theoretical modeling of the peak position of the analytes. It is important to note that for the computation volume V_CM needs to be set to 33 mL rather than 54 mL. The latter represents V_CM + V_M, i.e., the volume at which the phase change is seen at the column exit and/or the detector signal.

Concerning the nomenclature of the EECCC method, based on elution and extrusion mechanisms, EECCC separations can be segregated into three stages: classical elution (I), sweeping elution (II) after the liquid phase supply is switched from mobile to stationary phase, and extrusion (III). During Stage II, the solutes are swept by a solvent front that moves at the mobile phase velocity and passes all non-eluted solutes still present in the column. During sweeping time, solutes move by a small distance, and still only mobile phase leaves the column. This small motion of the solutes had been previously overlooked, while introducing a significant bias in the calculation of the CCC solute distribution constants.

GUESSmix EECCC chromatogram

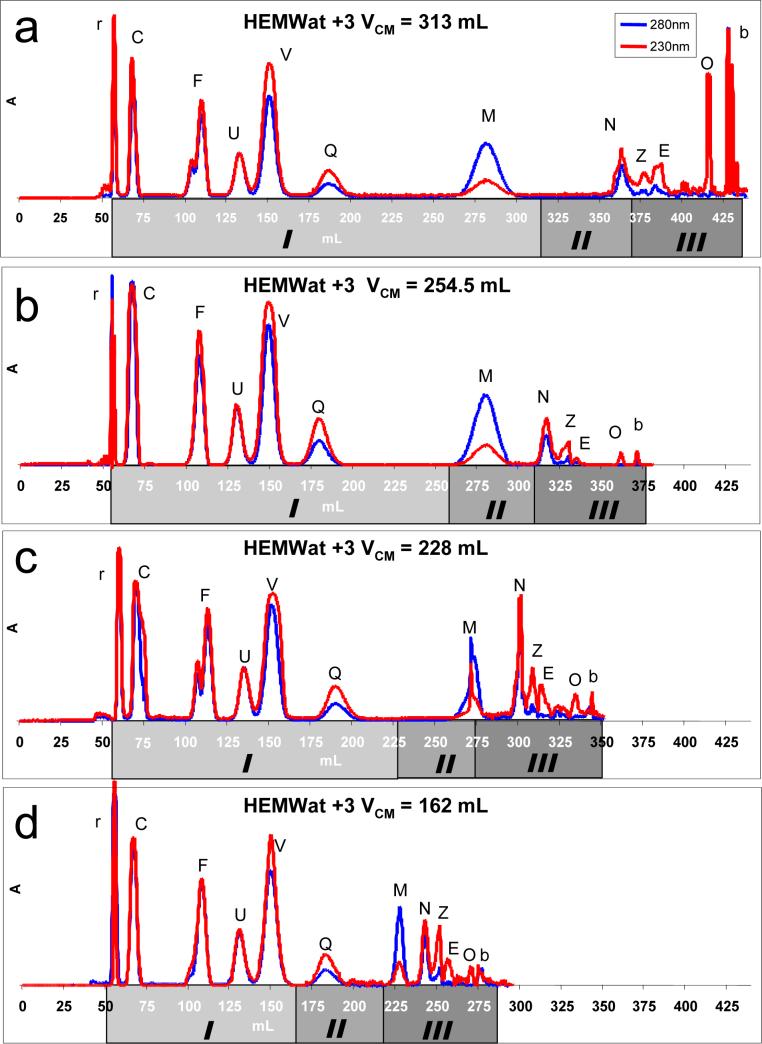
Figure 5 illustrates a series of four EECCC retention volume chromatograms of the same solute mixture and solvent system performed on the same instrument. The stationary phase retention ratio is similar for each run, as indicated by the retention volumes of the red dye marker peak (new coccine red, r). The switch volume, V_CM, however, is different for each chromatogram, as is indicated by the decreasing overall run times. The shading scheme on the x-axis shows the positions of the three elution-extrusion stages (elution – sweep elution – extrusion). Of particular interest are those peaks that are positioned in different elution-extrusion stages in different runs. It is evident that the quercetin (Q) and coumarin (M) peaks have similar peak width and shape in both the classical and sweep elution stages. This observation reinforces the theoretical assertion that these two stages operate under classical elution mechanics. On the other hand, there is a noticeable difference in the peak widths of coumarin (M) and naringenin (N) between those peaks in the classical and/or sweep elution stages and the peaks situated in the extrusion stage. In essence, the peaks are noticeably thinner in the extrusion stage than either the classical or sweeping elution stages. This is fully consistent with the theory presented above. An unusual case occurs in Figure 5c where the coumarin (M) peak is caught between the sweep elution and extrusion stages and becomes somewhat deformed as a result.

Figure 5.

HSCCC separation of the GUESSmix compounds (Table 1) in HEMWat +3 (hexane/ethyl acetate/methanol/ water 4:6:4:6). The experimental parameters for 5a, 5b, 5c, and 5d were V_CM = 313, 254.5, 228, 162 mL (Stage I) and S_F = 0.54, 0.55, 0.52, 0.54 respectively. V_C = 120 mL (Stage II + Stage III), denser aqueous was mobile phase, 2 mL/min, UV detection.

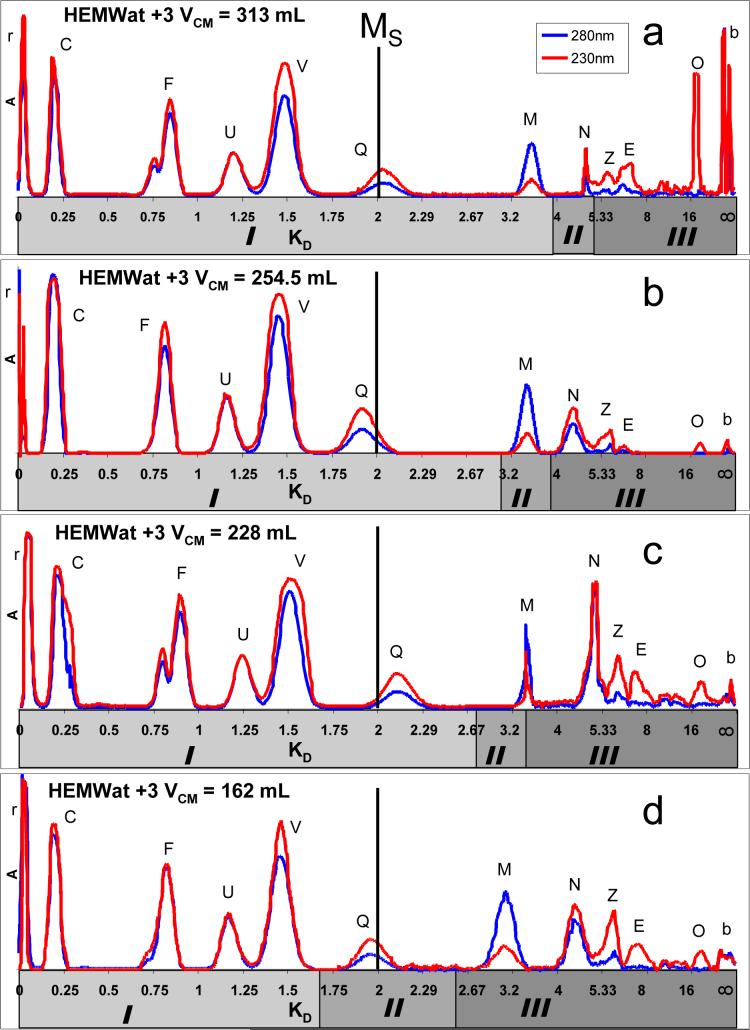
Figure 6 presents an alternate view of the four chromatographic runs by representing them all on Reciprocal Shifted Symmetry (ReSS) plots with a midline at M_s = 2. In these chromatograms the corresponding K_D values of each analyte can be compared. The distribution constants for CCC are considered to be constant for a particular analyte in each particular solvent system independent of other experimental parameters such as stationary phase retention ratio (S_F), and column volume (V_C). The calculated K_D values for each analyte are shown in Table 4. For those compounds with K_D values between 0.25 and 25, the percent error averages at 4.5% and is always less than 7.5%. The shifts in experimentally determined K_D values are a result of errors introduced at various points during the experiment. Potential sources of error include, but are not limited to, stationary phase bleed,⁴ extra-column volume,²³ absence of temperature control, numerous flying lead connections between CCC coils, and the fact that retention volumes are calculated by multiplying time and flow rate. As a result, there are significant sources of systematic errors, among others, that potentially affect the volumetric precision of any CCC experiment with any modern CCC apparatus. Therefore, the achieved precision can be considered being remarkably good, as can be the repeatability of EECCC.

Figure 6.

ReSS plots with a symmetry point at M_S = 2 of the HSCCC separations shown in Figure 5. For Stages I and II volumes, eq 18 is used to relate V_R and K_D; for Stage III, it is eq 19. K_D = 0 to 2 (M_S) are plotted using a linear scale. From K_D >2 to ∞, the linear scale is calculated as M_s (2 − M_s/K_D) = 4 − 4/K_D.

Table 4.

Experimental evidence for the congruence of EECCC K_D values

code	Solute	KD at VCM =				average	st dev.	% std
		313 mL	254.5 mL	228 mL	162 mL
r	new coccine red	0	0	0	0	0	-	-
C	caffeine	0.19	0.21	0.22	0.18	0.20	0.02	10
F	ferulic acid	0.84	0.82	0.90	0.82	0.85	0.04	4.7
U	umbelliferone	1.20	1.15	1.24	1.17	1.19	0.04	3.4
V	vanillin	1.50	1.46	1.51	1.46	1.48	0.03	2.0
Q	quercetin	2.04	1.93	2.14	1.97	2.02	0.09	4.5
M	coumarin	3.51	3.44	3.43	3.00	3.35	0.23	6.9
N	naringenin	4.81	4.43	4.85	4.15	4.56	0.33	7.2
Z	salicylic acid	5.69	5.72	5.85	5.40	5.67	0.19	3.4
E	estradiol	6.80	6.44	6.91	6.75	6.73	0.2	3.0
O	carvone	19.6	20.4	19.0	18.0	19.2	1.0	5.2
b	β-carotene	630	510	460	330	480	150	31

Data obtained with experiments shown in Figures 5 and 6.

CONCLUSIONS

The Rapid 2V_C method in metabolome analysis

For successful CCC analysis of complex samples, such as metabolomic mixtures or other natural products extracts, it is of paramount importance to know rapidly the spectrum of polarity and the polarity distribution of the analytes contained in these complex mixtures. Besides the possibility to use thin-layer chromatography combined with the GUESS approach,¹⁴ such information can also be obtained using the EECCC method with only two column (V_C) volumes of solvent:¹⁸ One column volume of mobile phase for elution in Stage I, and a second column volume of “stationary” phase to sweep elute in Stage II and extrude the column content in Stage III. With V_CM = V_C, solutes with 0 < K_D < V_C/V_S = 1 + V_M/Vs = 1/S_F are eluted by the mobile phase. All other solutes with V_C/V_S < K_D < ∞ are extruded by the “stationary” phase. Bearing in mind that the resolution between peaks has the trend shown by Figure 3, resolution maximizes around the phase change (K_D = V_C/V_S) and drops rapidly once the highly retained solutes with very higher K_D values are extruded from the column. Since the method is rapid, this opens the opportunity to separate the highly retained solutes by using another two-phase liquid system of shifted polarity.

Metabolomic Application of EECCC

As EECCC provides much improved access to precise K_D information of a largely extended range of polarity, shifted towards the more highly retained solutes, much valuable chromatographic information about primary and secondary metabolites can be gained from a single EECCC run. Even for those metabolites that are captured in the high-K_D range of the initial EECCC chromatogram, much helpful information can be gained. Towards this end, the very recently established “polarity relationships” between families of two-phase solvent systems allow the determination of both overlapping and adjacent windows of optimal resolution across the polarity continuum of CCC.²⁴ Thus, EECCC has potential as a portal method to explore this polarity continuum, especially since the separations can be performed in both normal and reverse phase mode. In addition, EECCC allows the prediction of the composition of subsequent two-phase solvent systems that are capable of “moving” these metabolites into the practically usable range of high-resolution separation.

The fact that in CCC both phases are liquids greatly simplifies the chromatographic exchanges of analytes between mobile and stationary phase: only liquid-liquid partitioning is involved. Unlike in HPLC, CCC has no irreversible adsorption, no pore size exclusion, no residual silanol chemistry and similar problems originating from the stationary phase. The liquid nature of the stationary phase allows for manipulations that are impossible when using a solid stationary phase. Extrusion of the liquid stationary phase is one of these unique features, and this study describes how the elution-extrusion method in CCC (EECCC) makes use of this advantage. It is demonstrated how EECCC can be fully modeled in its three stages: straightforward solute partitioning between the immiscible phases when both two phases are present during Stages I and II (elution), followed by the carrying of the solutes when only a single phase is present during Stage III (extrusion step). The equations 1 (Stages I and II) and 10 (Stage III) allow for an accurate prediction of peak positions in EECCC, provided that the distribution constant K_D of the corresponding solutes are known. Conversely, the EECCC method can be used to calculate the distribution constants from the solute retention volumes. With regard to the separation of complex analytes, EECCC offers a widely extended “sweet spot” of high-resolution in CCC, associated with favorable peak widths in the extrusion stage of the chromatograms. Thus, EECCC is proven fit for the purpose of developing applications that serve the separation of complex biological samples, such as in metabolomics, with the ability to target specific analytes based on their K_D ranges or values.