Coordinative Properties of Highly Fluorinated Solvents with Amino and Ether Groups

Abstract

In spite of the widespread use of perfluorinated solvents with amino and ether groups in a variety of application fields, the coordinative properties of these compounds are poorly known. It is generally assumed that the electron withdrawing perfluorinated moieties render these functional groups rather inert, but little is known quantitatively about the extent of their inertness. This paper reports on the interactions between inorganic monocations and perfluorotripentylamine and 2H-perfluoro-5,8,11-trimethyl-3,6,9,12-tetraoxapentadecane, as determined with fluorous liquid-membrane cation-selective electrodes doped with tetrakis[3,5-bis(perfluorohexyl)phenyl]borate salts. The amine does not undergo measurable association with any ion tested, and its formal pK_a is shown to be smaller than -0.5. This is consistent with the nearly planar structure of the amine at its nitrogen center, as obtained with density functional theory calculations. The tetraether interacts very weakly with Na⁺ and Li⁺. Assuming 1:1 stoichiometry, formal association constants were determined to be 2.3 and 1.5 M^-1, respectively. This disproves an earlier proposition that the Lewis base character in such compounds may be non-existent. Due to the extremely low polarity of fluorous solvents and the resulting high extent of ion pair formation, a fluorophilic electrolyte salt with perfluoroalkyl substituents on both the cation and the anion had to be developed for these experiments. In its pure form, this first fluorophilic electrolyte salt is an ionic liquid with a glass transition temperature, T_g, of -18.5 °C. Interestingly, the molar conductivity of solutions of this salt increases very steeply in the high concentration range, making it a particularly effective electrolyte salt.

Introduction

Highly fluorinated liquid phases are the least polar of any known liquid phases.^1,2 Their extreme nonpolarity arises from high local symmetry as well as a lack of polarizability. As an example for just how nonpolar these compounds are, the system of perfluorooctane and octane separates at room temperature into two phases precisely because octane is too polar. On the π* scale of solvent polarity/polarizability, where water is at 1.09 and cyclohexane defines 0, perfluorooctane exhibits the surprisingly low value of -0.41.³ In order to differentiate these extraordinarily nonpolar compounds from conventional organic compounds, Horváth and Rábai coined the term “fluorous”.⁴ In this regard, it is important to note the distinction between these fluorous compounds and the partially fluorinated polymers with high concentrations of very polar ion-exchanger groups (e.g., Nafion or Tosflex). The latter are highly polar, very hydrophilic, and may soak up large amounts of water. Indeed, fluorinated ion-exchanger polymers and fluorous phases are on the very opposite end of the polarity scale.

There are currently a wide range of fluorous solvents readily available. Some of the more commonly used compounds include perfluorinated alkanes, cycloalkanes, trialkylamines, butyltetrahydrofuran, and an array of perfluoropolyethers. These and other fluorous materials are used in a wide variety of industrial and academic applications, such as for drug delivery,⁵ fluorous biphasic catalysis,^4,6,7 microfluidics,⁸ organic synthesis,⁹ fuel cell research,¹⁰ battery technology,¹¹ lubricant technology,¹² or heat transfer applications.¹³ Moreover, there are several amorphous perfluoropolymers with a variety of uses, such as for fiber optical cables, contact lenses and other optical materials.^14-16 Although one would expect that binding of ions and polar compounds to the amino and ether groups in some of these fluorous materials is greatly diminished by the strongly electron-withdrawing nature of the neighboring perfluorinated moieties,^2,6,7,17,18 very little is known about such interactions.

Most of the available literature focuses on highly fluorinated but not perfluorinated compounds. For example, a pK_a of 5.7 was observed for 2,2,2-trifluoroethylamine,¹⁹ which is five units lower than for the corresponding nonfluorinated compound. For a diamine in which the two secondary amines have a CH₂(CF₂)₃ and a CH₂(CF₂)CF₃ substituent, the pK_a was reported to be too low to be measurable by titration in aqueous solution.²⁰ The two methylene groups separating the trifluoromethyl group from the amino group in 3,3,3-trifluoropropylamine already affect the pK_a much less (pK_a 8.7),¹⁹ and ab initio calculations of proton affinities of primary amines with tri-, tetra-, and pentamethylene spacers imply that the trimethylene spacer is quite efficient at reducing the electron withdrawing effect of a perfluoroalkyl substituent.¹⁸ Relative basicities in CDCl₃ are known for trialkylamines with the general structure N[(CH₂)_nRf_m], where Rf_m represents a perfluoroalkyl substituent and n takes a value between 3 and 5.²¹ One of the few reported qualitative observations regarding perfluorinated compounds states that perfluoro(tert-butylamine), which has an amino group with only one fluorinated substituent, gives a crystalline sulfate when treated with small amounts of sulfuric acid, but separates again on slight dilution of the solution.¹⁷ Also, the hydrochloride of this salt is formed in concentrated hydrochloric acid.²¹ However, while the amino groups of perfluorinated trialkylamines are generally assumed to be inert, quantitative information is very sparse. Arguably the most informative result described in the literature is the π* value of solvent dipolarity/polarizability for perfluorotributylamine of -0.36, as measured with solvatochromic dyes.^3,22 A comparison with the π* values of perfluorooctane (-0.41), perfluoroheptane (-0.39), and perfluorodimethyldecalin (-0.33) clearly shows that perfluorotributylamine shares with these pure perfluorocarbons an extremely low polarity. Since several of the solvatochromic test dyes are potential hydrogen bond donors, this low π* value suggests that perfluorotributylamine is a weak base at most.

The reported information about the coordinative properties of perfluoroethers is just as sparse as that about perfluorinated amines. While partially fluorinated crown ethers and cryptands are well known to form complexes with alkali and alkaline earth metal cations²³ as well as anions such as fluoride,²⁴ gas phase studies have shown that perfluorinated crown ethers and cryptands can bind O₂^- and F^-.²⁵ However, it has been speculated that, due to the strong electron withdrawing effect of the CF₂ groups, the base character in perfluorinated macrocycles may be nonexistent.²⁵

Considering the widespread use of these compounds, a more quantitative knowledge of the role of amino and ether groups in perfluorinated materials is highly desirable. We are particularly interested in this question since we expect that receptor-doped fluorous membranes represent a new approach to reduce biofouling²⁶ and may eventually lead to receptor-based chemical sensors that can be implanted long term into the human body. It has been long recognized that biofouling can be caused by specific and nonspecific adsorption to sensor surfaces. To prevent this type of biofouling, the chemical modification of sensor surfaces,²⁷ e.g., with poly(ethylene oxide) chains, and the continuous release of NO from polymeric sensing membranes²⁸ were developed. However, response drifts and the loss of sensor selectivities due to the extraction of synthetic nonionic surfactants²⁹ and naturally occurring electrically neutral hydrophobic compounds^30,31 into receptor-doped polymeric membranes was demonstrated only recently. Examples of this are the decrease in selectivities of a H⁺-selective ISE by up to four orders of magnitude upon exposure to cheese³⁰ and the six-fold increase in Na⁺ interference of the commercially highly successful valinomycin-based K⁺ ISE upon exposure to urine.³¹ Fluorous sensing membranes are expected to eliminate this type of biofouling due to the low solubility of natural hydrophobic compounds in fluorous phases. For example, in hexane at 37 °C, stearic acid has a solubility of 430 mM, but in trans-1,2-bis(perfluorohexyl)ethylene, it has a solubility of only 0.026 mM,³² a decrease of greater than four orders of magnitude.

With a view of such sensing applications, we developed cation-selective electrodes^33,34 that can be readily used to study the interaction of fluorous solvents with different cations.³⁵ It was demonstrated that fluorous sensor membranes can be made from porous Teflon discs impregnated with a solution of a fluorophilic salt dissolved in a fluorous solvent. The cation selectivities exhibited by these fluorous membranes far exceed those of cation exchangers with conventional organic membrane materials. The selectivities of the fluorous receptor-free membranes spanned a range of sixteen orders of magnitude, which is eight orders of magnitude larger than for conventional o-nitrophenyl octyl ether. The high selectivity found in fluorous membranes is a result of the lack of solvation of ions dissolved in fluorous phases, which is further illustrated by the high ion-pair association constants measured in this system.³⁵

While we and others¹⁶ are developing perfluoropolymer systems with higher mechanical strength for analytical applications, the fluorous supported liquid phases remain convenient to characterize sensor systems without the possible complications resulting from the introduction of a perfluoropolymer, such as an effect of functional groups of the polymer on membrane selectivities. Most important for this article, these fluorous supported liquid phases are ideal to study the coordinative properties of fluorous solvents and other fluorous compounds with potentially coordinating groups. In this paper, we report on the interactions between inorganic monocations and the fluorous solvents perfluorotripentylamine and 2H-perfluoro-5,8,11-trimethyl-3,6,9,12-tetraoxapentadecane. To perform some of the potentiometric experiments, a fluorophilic electrolyte salt with perfluoroalkyl substituents on both the cation and the anion was developed. Its properties as an ionic liquid are discussed, and its effect on membrane conductivities is described. An upper limit for the pK_a value of the amine is reported and discussed in view of the molecular structures of perfluorinated trialkylamines, as obtained with density functional theory calculations. Also, binding of Na⁺ and Li⁺ to the highly fluorinated tetraether is discussed.

Results and Discussion

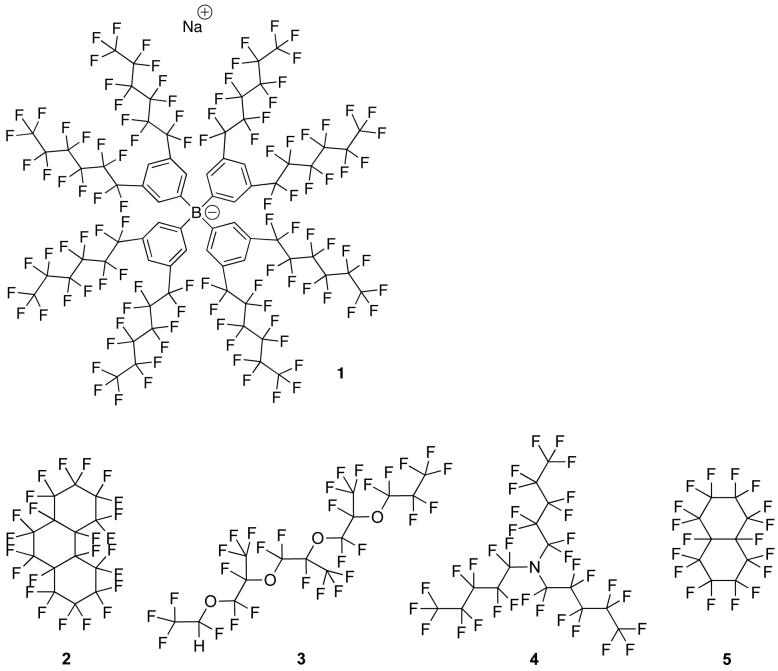
The fluorous liquid-membrane cation-selective electrodes used in this study (see Fig. 1) were prepared from porous Teflon discs impregnated with a solution of the fluorophilic salt sodium tetrakis[3,5-bis(perfluorohexyl)phenyl]borate, 1, in a fluorous solvent. In our first report on this type of sensor,³⁵ the fluorous solvent perfluoroperhydrophenanthrene, 2, was used because its pour point (-20 °C) is below room temperature, and because its boiling point (215 °C) is high enough to prevent evaporation during experiments. Linear perfluorinated alkanes have ranges between their melting and boiling points that are too narrow to be useful, and branched perfluorinated alkanes are not readily available. In this study, 2H-perfluoro-5,8,11-trimethyl-3,6,9,12-tetraoxapentadecane (3), perfluorotripentylamine (4), and perfluorodecalin (5) were used as alternative fluorous solvents. Because of their appropriate melting and boiling points, tetraether 3 (mp, -115 °C; bp, 192-195 °C) and amine 4 (bp, 210-220 °C) were utilized as representatives of fluorous solvents with amino and ether groups, respectively. The bicylic fluorocarbon perfluorodecalin, 5, was used for control experiments.

Figure 1.

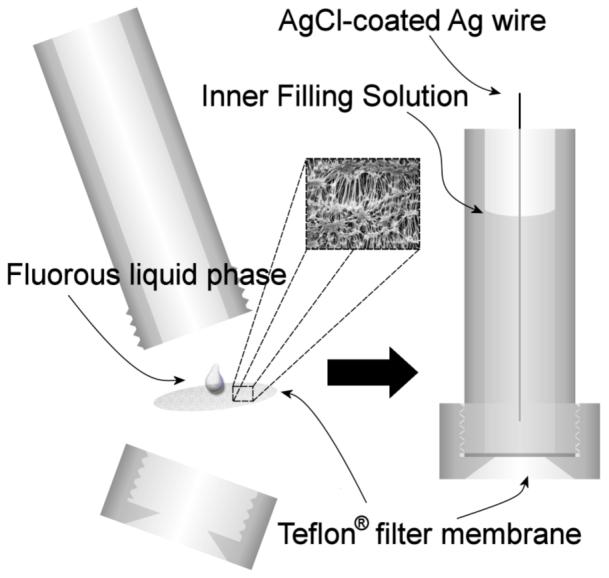
Schematic of a cation-selective electrode based on a fluorous liquid phase supported by an inert porous support.

The dielectric constants, ε, of 2 (2.03), 4 (1.98), and 5 (1.95)³⁶ all fall within a very narrow range, illustrating the very similar character of these solvents. However, these solvents do not dissolve the fluorophilic sodium tetraphenylborate derivative 1 equally well. While the solubilities of 1 in tetraether 3 (0.91 mM) and the two fluorocarbons (2, 1.4 mM; 5, 1.1 mM) are very similar, the solubility of 1 in amine 4 is about one order of magnitude lower (0.074 mM). This difference may be explained by steric reasons, but a definite explanation eludes us. It has important consequences for the potentiometric properties of these fluorous membranes, though. To show this, inert support filters were impregnated with saturated solutions of borate salt 1 in the different fluorous solvents, the thus obtained membranes were conditioned in KCl solutions to permit for K⁺ vs Na⁺ ion exchange over several hours, and the electrical resistances of these membranes were determined. Not surprisingly, the resistance of the membranes based on amine 4 as solvent (1.1 × 10⁴ MΩ) was found to be significantly higher than those of membranes prepared with either one of the two fluorocarbons (2, 1.7 × 10³ MΩ; 5, 4.0 × 10² MΩ) or the tetraether 3 (3.0 × 10¹ MΩ).

It was found that membranes with a resistance greater than 10 GΩ tended to have response times greater than 5 min, which compromised selectivity measurements. In many cases, by the time the membrane potential equilibrated, the cation initially present in the membrane had already exchanged with the interfering ion to such an extent that interfering ions had reached the interface between the fluorous membrane and the inner filling solution of the electrode (see Fig. 1). This could not be tolerated since the potentiometric response under such circumstances is not governed exclusively by the phase boundary potential at the sample/membrane interface. To solve this resistance problem for this study and in view of the development of chemical sensors, we synthesized the first fluorous electrolyte (6). While we did not test higher concentrations, electrolyte salt 6 is soluble in perfluorohexanes, perfluoroperhydrophenanthrene, and perfluorotripentylamine at concentrations up to 10 mM. Indeed, to the best of our knowledge, it is the salt with the highest solubility in perfluorocarbons described yet.

Interestingly, the pure electrolyte salt 6 is an ionic liquid.³⁷ At low temperatures, it does not crystallize but undergoes a transition into a glass. Using differential scanning calorimetry (DSC), the glass transition temperature, T_g, was determined to be -18.5 °C.

As expected, the addition of electrolyte salt 6 (10 mM) to supported fluorous liquid phases lowered their electrical resistances significantly. Membranes prepared from perfluoroperhydrophenanthrene, 2, or from amine 4 exhibited approximately hundred-fold decreases in resistance (2 doped with 1.0 mM 1 and 10 mM 6: 2.3 × 10¹ MΩ; 4 doped with 1.0 mM 1 and 10 mM 6: 5.9 MΩ).

The impedance spectra of membrane filters impregnated with a 10 mM solution of electrolyte salt 6 in perfluoroperhydrophenanthrene provided unanticipated results (see Fig. 2). When Mitex™ filters were used as the solid support,³⁵ the resulting impedance plane plots exhibited a shape resembling—but not perfectly fitting—what would be expected for two equivalent RC circuits in series (Fig 2a). Similar plots have been described elsewhere³⁸ and were attributed to an inhomogeneity in the size of pores of the filter support. In contrast, impedance plane plots of Fluoropore™ filters impregnated with the same solution showed the expected single semicircle resulting from the bulk resistance and capacitance (Figure 2b). Moreover, selectivity measurements performed with Fluoropore™ filters showed a somewhat larger selectivity for tetraalkylammonium cations than Mitex™ filters, suggesting more than architectural differences between the filter types. For these reasons, the Fluoropore™ filters were used for all data reported in this paper except for Fig. 2a.

Figure 2.

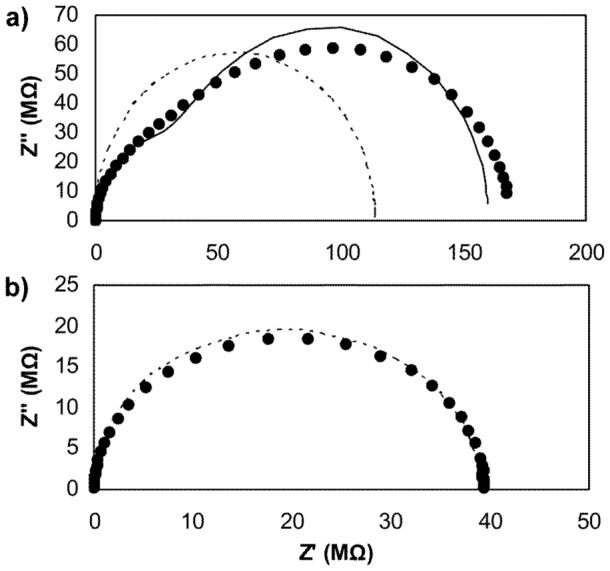
Impedance plane plots of a Mitex™ membrane (a) and a Fluoropore™ membrane (b) impregnated with a solution of electrolyte salt 6 (10 mM) in perfluoroperhydrophenanthrene (2). Dotted line: fit with one RC equivalent circuit. Solid line: fit with two RC circuits in series.

In an attempt to determine the ion-pair formation constant of electrolyte salt 6 in perfluoroperhydrophenanthrene (2), the conductivity was determined as a function of the electrolyte salt concentration. In the lower concentration range, a decrease in molar conductivity is observed as the concentration of 6 increases (see Fig. 3). Indeed, this is expected when the ratio of ions forming ion pairs increases with the electrolyte concentration. However, Figure 3 also shows that, as the electrolyte concentration increases further, the conductivity increases seemingly exponentially and much faster than predicted by the Fuoss-Kraus theory.³⁹ This unusually steep increase may be the result of the formation of large aggregates and ion-hopping, as it has been observed with certain other electrolyte solutions in media of low dielectric constant.⁴⁰ We will investigate this effect more thoroughly and report about it with more detail elsewhere. At this point, it suffices to say that 6 is an excellent electrolyte salt for fluorous solvents.

Figure 3.

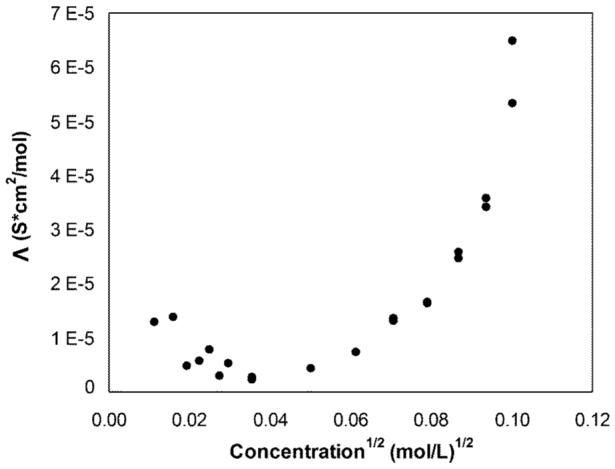
Plot of molar conductivity vs. concentration of electrolyte salt 6 in perfluoroperhydrophenanthrene, 2.

The potentiometric selectivities of five different types of cation-selective membranes based on four different fluorous solvents are shown in Table 1. The Cs⁺ ion serves as the common reference point. To enable an unbiased evaluation of membranes based on amine 4, which could only be used in combination with 10 mM electrolyte salt 6 (see above), the selectivities of membranes based on 2 were determined with and without electrolyte salt. A comparison of the selectivities of the two membrane types based on 2 shows that the effect of the electrolyte salt on the high preference for tetraalkylammonium cations is small, while the effect on the selectivities over the smaller alkali metal cations is somewhat more pronounced. In view of the extremely strong ion pair formation in fluorous phases,³⁵ this is not very surprising. Evidently, the 10 mM excess of anions in the membranes with electrolyte favors ion pair formation with the small alkali metal cations disproportionately.

Table 1.

Potentiometrically Determined Logarithmic Selectivity Coefficients, $\log K_{\mathrm{Cs},\mathrm{J}}^{\mathrm{pot}}$, of Fluorous Liquid-Membrane Cation-Selective Electrodes, Referenced to Cs⁺

membrane composition			$\log K_{\mathrm{Cs},\mathrm{J}}^{\mathrm{pot}}$
solvent	[1] / mM	[6] / mM	N(Bu)4+	N(Pr)4+	NH4+	H+	K+	Na+	Li+
2	1.4	-	+13.1	+11.1	-1.96	-2.35	-2.51	-3.87	-3.92
2	1.0	10	+13.2	+11.4	-1.62	-1.87	-2.03	-3.17	-3.33
4	1.0	10	+13.2	+11.5	-1.49	-1.87	-1.89	-2.79	-3.10
3	0.91	-	+13.4	+11.6	-1.40	-1.81	-1.85	-2.78	-2.99
5	1.1	-	+12.9	+11.4	-1.99	-2.60	-2.74	-3.83	-3.95

Not only the previously reported membranes based on perfluoroperhydrophenanthrene (2),³⁵ but also all four new membrane formulations exhibit selectivities that span a remarkably wide range of at least 16 orders of magnitude. Despite the possibility of specific interactions between the cations and two of the fluorous solvents (see below), the order of selectivities follows the Hofmeister series for all membranes, which agrees with the free energies of hydration of the cations.^34,41 As shown in the following, the adaptation of the phase boundary potential model for the response of potentiometric sensors^34,42 makes it possible to use these experimentally observed potentiometric selectivities to quantify specific interactions of small cations with fluorous solvents, both in macroscopic and molecular terms.

Single ion distribution coefficients⁴³ describing the distribution of an ion i between a fluorous reference phase lacking any coordinating groups and a phase formed by a fluorous solvent with coordinating groups can be derived using the electrochemical potentials, ${\tilde{\mu }}_{\mathrm{i},\mathrm{ref}}$ and ${\tilde{\mu }}_{\mathrm{i},\mathrm{co}}$, of this ion in the two respective phases:

$${\tilde{\mu }}_{\mathrm{i},\mathrm{ref}}={\mu }_{\mathrm{i},\mathrm{ref}}^{\mathrm{o}}+\mathrm{R}T\ln a_{\mathrm{i},\mathrm{ref}}+zF{\Phi }_{\mathrm{i},\mathrm{ref}}$$ (1a)

$${\tilde{\mu }}_{\mathrm{i},\mathrm{co}}={\mu }_{\mathrm{i},\mathrm{co}}^{\mathrm{o}}+\mathrm{R}T\ln a_{\mathrm{i},\mathrm{co}}+zF{\Phi }_{\mathrm{i},\mathrm{co}}$$ (1b)

where Φ_i,ref and Φ_i,co are the electrical potentials and a_i,ref and a_i,co are the ion activities in the respective phases, z is the charge of ion i, and R and T have their usual meanings. The two fluorous phases cannot be equilibrated with one another by direct contact since they are miscible with one another. However, the two fluorous phases could be separated by an aqueous phase containing the ion i, permitting each fluorous phase to get into equilibrium with the aqueous phase. Thereby, equilibration of the two fluorous phases with respect to ion i may be achieved without them having to contact one another directly. For two fluorous phases that are in such an equilibrium, ${\tilde{\mu }}_{\mathrm{i},\mathrm{ref}}$ equals ${\tilde{\mu }}_{\mathrm{i},\mathrm{co}}$, and it can be shown from equations 1a and 1b that

$${\mu }_{\mathrm{i},\mathrm{co}}^{\mathrm{o}}-{\mu }_{\mathrm{i},\mathrm{ref}}^{\mathrm{o}}=\Delta {\mu }_{\mathrm{i},\mathrm{co}∕\mathrm{ref}}^{\mathrm{o}}=\mathrm{R}T\ln \frac{a_{\mathrm{i},\mathrm{ref}}}{a_{\mathrm{i},\mathrm{co}}}+zF({\Phi }_{\mathrm{i},\mathrm{ref}}-{\Phi }_{\mathrm{i},\mathrm{co}})$$ (2)

The ion activities are related to the total concentrations, c_i,ref and c_i,co, in the respective phases by their activity coefficients, γ_i,ref and γ_i,co. Since electroneutrality requires that the total concentration of anionic sites, c_R, in each bulk phase must equal the total concentration of cations, equation 2 can be reformed to:

$$\Delta {\mu }_{\mathrm{i},\mathrm{co}∕\mathrm{ref}}^{\mathrm{o}}=\mathrm{R}T\ln \frac{{\gamma }_{\mathrm{i},\mathrm{ref}}{c}_{\mathrm{R},\mathrm{ref}}}{{\gamma }_{\mathrm{i},\mathrm{co}}{c}_{\mathrm{R},\mathrm{co}}}+zF({\Phi }_{\mathrm{i},\mathrm{ref}}-{\Phi }_{\mathrm{i},\mathrm{co}})$$ (3)

Subtracting $\Delta {\mu }_{\mathrm{i},\mathrm{co}∕\mathrm{ref}}^{\mathrm{o}}$ from a term $\Delta {\mu }_{\mathrm{j},\mathrm{co}∕\mathrm{ref}}^{\mathrm{o}}$, formulated for two analogous fluorous phases with the same ion concentrations but the ion j with the same charge as ion i, gives:

$$\Delta {\mu }_{\mathrm{j},\mathrm{co}∕\mathrm{ref}}^{\mathrm{o}}-\Delta {\mu }_{\mathrm{i},\mathrm{co}∕\mathrm{ref}}^{\mathrm{o}}=\mathrm{R}T\ln \frac{{\gamma }_{\mathrm{i},\mathrm{co}}{\gamma }_{\mathrm{j},\mathrm{ref}}}{{\gamma }_{\mathrm{i},\mathrm{ref}}{\gamma }_{\mathrm{j},\mathrm{co}}}+zF({\Phi }_{\mathrm{j},\mathrm{ref}}-{\Phi }_{\mathrm{j},\mathrm{co}}-{\Phi }_{\mathrm{i},\mathrm{ref}}+{\Phi }_{\mathrm{i},\mathrm{co}})$$ (4)

The term Φ_j,ref-Φ_i,ref equals $(\mathrm{R}T∕z\mathrm{F})\ln K_{\mathrm{i},\mathrm{j}}^{\mathrm{pot},\mathrm{ref}}$, where $K_{\mathrm{i},\mathrm{j}}^{\mathrm{pot},\mathrm{ref}}$ is the potentiometric selectivity coefficient of the fluorous ion-exchanger membrane (for a proof see Supplementary Information).^34,42 In other words, it directly corresponds to the difference between the potentials measured once with that electrode immersed in a solution of ion j and once immersed in a solution of ion i of the same concentration. Since it follows analogously that Φ_j,co-Φ_i,co equals $(\mathrm{R}T∕z\mathrm{F})\ln K_{\mathrm{i},\mathrm{j}}^{\mathrm{pot},\mathrm{co}}$, equation 4 can be reformed to

$$\Delta {\mu }_{\mathrm{j},\mathrm{co}∕\mathrm{ref}}^{\mathrm{o}}-\Delta {\mu }_{\mathrm{i},\mathrm{co}∕\mathrm{ref}}^{\mathrm{o}}=\mathrm{R}T\ln \frac{{\gamma }_{\mathrm{i},\mathrm{co}}{\gamma }_{\mathrm{j},\mathrm{ref}}}{{\gamma }_{\mathrm{i},\mathrm{ref}}{\gamma }_{\mathrm{j},\mathrm{co}}}+\mathrm{R}T(\ln K_{\mathrm{i},\mathrm{j}}^{\mathrm{pot},\mathrm{ref}}-\ln K_{\mathrm{i},\mathrm{j}}^{\mathrm{pot},\mathrm{co}})$$ (5)

Therefore, the equilibrium constant describing the exchange of the two ions i and j between the two fluorous phases is given by:

$$K^o=\mathrm{Exp}[-(\Delta {\mu }_{\mathrm{j},\mathrm{co}∕\mathrm{ref}}^{\mathrm{o}}-\Delta {\mu }_{\mathrm{i},\mathrm{co}∕\mathrm{ref}}^{\mathrm{o}})∕\mathrm{R}T]=\frac{{\gamma }_{\mathrm{j},\mathrm{co}}{\gamma }_{\mathrm{i},\mathrm{ref}}{K}_{\mathrm{i},\mathrm{j}}^{\mathrm{pot},\mathrm{co}}}{{\gamma }_{\mathrm{j},\mathrm{ref}}{\gamma }_{\mathrm{i},\mathrm{co}}{K}_{\mathrm{i},\mathrm{j}}^{\mathrm{pot},\mathrm{ref}}}$$ (6)

Inclusion of the activity coefficients in the constant term gives the logarithm of the formal ion exchange constant, K, as:

$$\log K=\log K_{\mathrm{i},\mathrm{j}}^{\mathrm{pot},\mathrm{co}}-\log K_{\mathrm{i},\mathrm{j}}^{\mathrm{pot},\mathrm{ref}}$$ (7)

For an ion i that does not interact specifically with either of the two fluorous solvents, $\Delta {\mu }_{\mathrm{i},\mathrm{co}∕\mathrm{ref}}^{\mathrm{o}}\approx 0$ and γ_i,co ≈ γ_i,ref. Under these circumstances, K^o as defined by equation 6 is identical with the so-called single ion distribution coefficient, $k_{\mathrm{j}}^{\mathrm{o}}$, of ion j, and K is identical with the corresponding formal single ion distribution coefficient, k_j. Because of its large size and bulky structure, the tetrabutylammonium ion is assumed in the following to be such an ion that does not interact specifically with the solvent. Table 2 shows the resulting log k_j values for all ions measured in this work. Note that the log k_j values for N(Bu)₄⁺ are 0.00 as a consequence of our assumption that this ion does not interact specifically with the solvent. In this respect, the approach used here resembles the determination of ionophore complexation constants from the potentiometric responses of ion-selective electrodes to target ions and ions that may be assumed to undergo no specific interaction with the ionophore.⁴⁴

Table 2.

Potentiometrically Determined Logarithmic Single Ion Distribution Coefficients, log k_j, Characterizing Distribution Between Perfluoroperhydrophenanthrene Membranes and Three Other Fluorous Solvents

membrane composition			log kj
solvent	[1] / mM	[6] / mM	N(Bu)4+	N(Pr)4+	NH4+	H+	Cs+	K+	Na+	Li+
4a	1.0	10	0.00c	0.10	0.13	0.00	0.00	0.14	0.38	0.23
3b	0.91	-	0.00c	0.20	0.26	0.24	-0.30	0.36	0.79	0.63
5b	1.1	-	0.00c	0.50	0.17	-0.05	0.20	-0.03	0.24	0.17

^aReference membrane contains same concentration of 6.

^bReference membrane contains no electrolyte.

^cAssumption.

Consideration of the electrolyte-free perfluoroperhydrophenanthrene phase as the reference phase and the perfluorodecalin phase as the potentially specifically coordinating phase gives only very small values for log k_j. The average log k_j for all considered ions is 0.17, and the standard deviation is 0.18, which corresponds in non-logarithmic terms to single ion distribution coefficients between 1.0 and 2.3. Since perfluorodecalin is—like perfluoroperhydrophenanthrene—a perfluorocarbon without any heteroatoms, this lack of evidence for specific ion-solvent interaction is reassuring. The data suggest that the combined experimental and systematic error pertaining to these selectivity coefficients is no more than 0.4.

Interestingly, there is equally little evidence for specific interactions between cations and perfluorotripentylamine. Values for k_j obtained from the selectivity data for the perfluorotripentylamine and perfluoroperhydrophenanthrene phases (both with electrolyte salt) are just as small as those for the perfluorodecalin phase. The mean of 0.12 and standard deviation of 0.13 is well within the experimental error.

In contrast, there is evidence for specific interactions in the case of the highly fluorinated tetraether, 3. While Table 2 shows that the larger ions Cs⁺, K⁺, and NH₄⁺ as well as H⁺ do not interact significantly with the solvent, the smaller ions Na⁺ and Li⁺ interact weakly with the tetraether ( k_Na=6.2 ± 1.4 and k_Li = 4.3 ± 1.0).

The above discussion has the advantage that it does not rely on any assumptions regarding the type of the interaction between the fluorous solvent and the cations, but it does not provide for an understanding of the ion-solvent interaction at the molecular level. For this purpose, it will be assumed in the following that the ion-solvent interaction occurs with a 1:1 complex stoichiometry:

$${\mathrm{j}}^{+}+\mathrm{L}\iff {\mathrm{jL}}^{+}$$

where L represents the solvent, j the cation, and jL⁺ their complex. Indeed, in view of the extremely weak interactions described above, 1:2 complexes with a significant stability seem unlikely. The association constant for the 1:1 complex can be formulated as follows:

$$K_{\mathrm{jL}}=\frac{a_{\mathrm{jL}}}{a_{\mathrm{j}}\left[\mathrm{L}\right]}$$ (8)

This equation can be rewritten using the activity coefficients of the ion and complex, and considering that the complex and free ion concentration add up to the total concentration of j:

$$K_{\mathrm{jL}}=\frac{{\gamma }_{\mathrm{jL}}(c_{\mathrm{jtot}}-c_{\mathrm{j}})}{{\gamma }_{\mathrm{j}}{c}_{\mathrm{j}}\left[\mathrm{L}\right]}=\frac{{\gamma }_{\mathrm{jL}}(c_{\mathrm{jtot}}∕c_{\mathrm{j}}-1)}{{\gamma }_{\mathrm{j}}\left[\mathrm{L}\right]}$$ (9)

Since the concentration of the solvent is more than three orders of magnitude larger than the concentration of the cation, j, it can be considered to be constant. The concentration terms can again be obtained from the potentiometric selectivities. As discussed elsewhere,^34,42 and in analogy with equation 2, a potentiometric sensor with a fluorous membrane will respond to an aqueous solution of ion j as follows:

$$\Delta E=E^o+\frac{\mathrm{R}T}{z_{\mathrm{j}}\mathrm{F}}\ln \frac{a_{\mathrm{j},\mathrm{aq}}}{c_{\mathrm{j},\mathrm{mem}}}$$ (10)

where a_j,aq is the activity of ion j in the aqueous sample, c_j,mem is the concentration of the free ion j in the membrane, and E^o is a constant characteristic for the ion j and the electrochemical cell. It follows that the difference between the potentials measured with a specifically interacting fluorous membrane and a reference membrane is directly proportional to ln(c_j,ref/c_j,co). It can be shown that:

$$c_{\mathrm{j},\mathrm{ref}}∕c_{\mathrm{j},\mathrm{co}}=K_{i,j}^{pot,co}∕K_{i,j}^{pot,ref}$$ (11)

The proof for equation 11 resembles the deduction of equation 5 given above (see Supplementary Information). Since c_jtot equals c_j,ref, the right hand side of this equation may be inserted into equation 9, which gives—after inclusion of the activity coefficients into the constant term—a formal complexation constant:

$$K_{\mathrm{jL}}^{\prime }=\frac{K_{i,j}^{pot,co}∕K_{i,j}^{pot,ref}-1}{\left[\mathrm{L}\right]}$$ (12)

Applying equation 12 to the sodium ion and the tetraether membrane gives a formal complexation constant of 2.3±0.8 M^-1. Solving equation 9 for the concentrations shows that 83% of all sodium ions in a tetraether membrane are interacting with a solvent molecule, while 17% show no specific interaction with the solvent. Analogously, a binding constant of 1.5±0.6 M^-1 and a percentage of 77% specifically interacting ions are obtained for lithium. While these formal complexation constants are small, t tests show for both ions that the interactions are significant even at the 99.5% confidence level.

In view of the more than thousand-fold excess of solvent molecules over cations, the high percentages of cations that do not interact specifically with the fluorous solvent molecules are quite impressive and demonstrate that the tetraether molecules have a finite but only very low tendency to interact with cations. This can be explained by the strong electron withdrawing nature of the many fluorine atoms. While the literature does not contain values for cation binding by a nonfluorinated analogue of tetraether 4 under matching conditions, the binding constant of 2.74 × 10⁴ M^-1 for Li⁺ binding to triethylene glycol dimethyl ether in 199:1 toluene-tetrahydrofuran illustrates the much stronger affinity of nonfluorinated polyethers for alkali metal ions.⁴⁵ In the absence of further experimental data, it is unclear whether the one single hydrogen atom of tetraether 4 has any appreciable effect on the stability of its cation complexes. We will further investigate how different numbers of fluorine atoms affect the shape and population of molecular orbitals and cation binding of perfluorinated ethers using experimental and computational means.

A value for the formal pK_a of perfluorotripentylamine using equation 12 cannot be determined since, within experimental error, an experimental difference between the selectivity coefficients for perfluoroperhydrophenanthrene and perfluorotripentylamine is not observed. However, assuming that the maximum combined systematic and experimental error of the selectivity coefficients (see above) may be as high as 0.4, it can be concluded from equation 12 that the formal pK_a of perfluorotripentylamine is lower than -0.5. To the best of our knowledge, this is the most quantitative assessment of the basicity of any perfluorinated trialkylamine to date.

The extremely low basicity of perfluorotripentylamine determined in these potentiometric experiments is also reflected by the geometries of three perfluorinated trialkylamines, as calculated quantum mechanically using the B3LYP density functional and the 6-311+g(d,p) basis set. While the sp³ hybridization with its nonbonding electron pair results in a tetrahedral geometry at the nitrogen atom of typical trialkylamines, the geometry of perfluorinated trialkylamines at the nitrogen center is nearly perfectly flat. Even though nonafluorotrimethylamine has among all perfluorinated trialkylamines the least electron withdrawing substitutents on the nitrogen center, the three calculated CNC bond angles of 119.7° in this compound are extremely close to the theoretical value of 120° for a fully planar geometry. The nitrogen atom lies a mere 0.08 Å above the plane formed by its three neighboring carbon atoms (see Fig. 4). In contrast, calculated and experimental values for the CNC bond angles in trimethylamine are 111±1°,⁴⁶ which is very close to the perfect tetrahedral angle of 109.5°.

Figure 4.

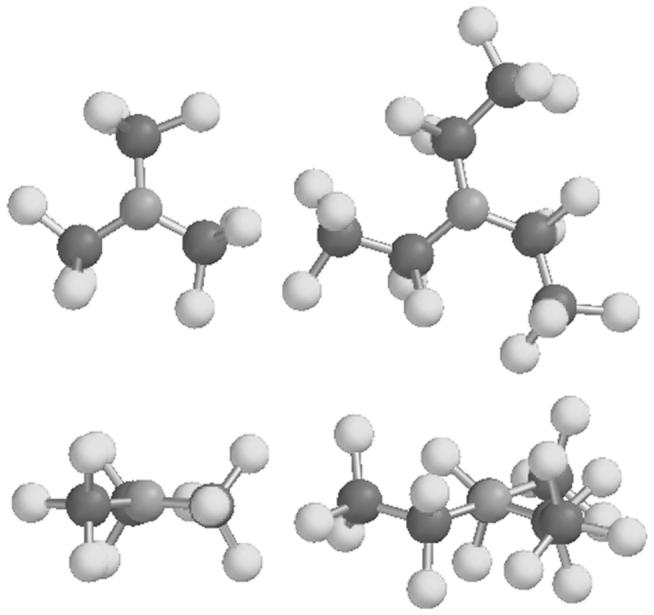
Calculated structures of nonafluorotrimethylamine (left hand side) and perfluorotriethylamine (right hand side), each molecule with a top and side view (top and bottom, respectively).

With three calculated CNC bond angles of 116.6° and the nitrogen 0.28 Å above the plane formed by its neighboring carbons, the perfluorotriethylamine geometry is also very close to planarity, but not quite as flat as for nonafluorotrimethylamine (see Fig. 4). Similarly, the optimized structure of perfluorotripentylamine, 4, exhibits average CNC bond angles of 118.7° and a nitrogen 0.17 Å above the plane formed by its neighboring carbons (structure not shown). It appears likely that the deviation from planarity is in both cases the consequence of steric repulsion between the pentafluoroethyl groups.

These results agree rather well with the interpretation of vibrational spectra,⁴⁷ which indicated a CNC bond angle for nonafluorotrimethylamine of 117.9°, and the gas electron diffraction spectra of perfluorotripropylamine, which are consistent with a CNC bond angle of 120.0°.⁴⁸ Also, the nearly perfectly planar geometry of perfluorinated trialkylamines is consistent with their low dielectric constants (e.g., perfluorotripentylamine, ε = 1.98), while a tetrahedral geometry would be expected to result in significant molecular dipoles incompatible with a low value for ε.

Conclusions

The results of this study show that perfluorinated trialkylamines have a basicity that is negligible under all but very special circumstances. Since the nearly perfectly planar geometry of these compounds at the nitrogen center also suggests a vanishing dipole moment, perfluorinated trialkylamines seem to be quite ideal inert fluorous solvents. In contrast, the coordinative properties of the highly fluorinated tetraether, though small, are significant enough to be recognized in potentiometric measurements with fluorous cation-exchanger membranes. This clearly disproves the earlier proposition that the Lewis base character of highly fluorinated ethers is non-existent. However, the interactions are weak enough that they will hardly affect chemical sensors doped with strongly binding ionophores.

This paper also introduces the only fluorophilic electrolyte salt currently known capable of lowering bulk resistance in fluorous phases. This and similar salts will be very useful in the preparation of potentiometric sensors based on receptor-doped fluorous membranes and may also find applications in other fields, such as in battery technology or fuel cell research. However, a more thorough understanding of the dependence of the molar conductivity of this salt on its concentration will be required.

Experimental Section

Reagents

Reagents of the highest commercially available grade were used. Deionized and charcoal-treated water (18.2 MΩ-cm specific resistance) obtained with a Milli-Q PLUS reagent-grade water system (Millipore, Bedford, MA, USA) was used for all sample solutions. The fluorous solvents 2 (density, 2.030 g/L), 3 (1.723 g/L), 4 (1.94 g/L), and 5 (1.941 g/L) were purchased from Alfa Aesar (Ward Hill, MA) and were used as received. All fluorous solvents but 4 are mixtures of multiple isomers and show complicated ¹⁹F NMR spectra. However, ¹H NMR spectra confirmed that none of these fluorous solvents contained significant concentrations of hydrogenated impurities. Sodium tetrakis[3,5-bis(perfluorohexyl)phenyl]borate³⁵ and [CF₃(CF₂)₇(CH₂)₃]₃N were prepared according to a previously described procedure.^21,35 The solubility of 1 in fluorous solvents was determined by ¹H NMR spectrometry. The salt {[CF₃(CF₂)₇(CH₂)₃]₃CH₃N⁺} CH₃OSO₃^- was prepared according to a literature procedure⁴⁹ from [CF₃(CF₂)₇(CH₂)₃]₃N and dimethyl sulfate.

Synthesis of 6

The fluorophilic electrolyte salt 6 was prepared by metathesis from {[CF₃(CF₂)₇(CH₂)₃]₃CH₃N⁺}CH₃OSO₃^- and sodium tetrakis[3,5-bis(perfluorohexyl)phenyl]borate, 1, in a water/benzotrifluoride system with a slight stoichiometric excess of {[CF₃(CF₂)₇(CH₂)₃]₃CH₃N⁺}CH₃OSO₃^-. After collection of the benzotrifluoride layer, filtration, and drying in the vacuum for one week at rt, 6 was obtained as a viscous, sticky oil with a faint yellow tint. π* value of solvent dipolarity/polarizability, as determined with 4-nitroanisole as solvatochromic dye:^3,22,50 1.46 ± 0.03. ¹H NMR (300 MHz, acetone-d₆, ™): 7.72 (s, 8H, Ar_o H), 7.60 (s, 4H, Ar_p H), 3.97 (m, 6H, NCH₂), 3.58 (s, 3H, NCH3), 2.4-2.7 (m, 12H, NCH₂CH₂CH₂). ¹⁹F NMR (300 MHz, acetone-d₆, ™ relative to CFCl₃): -82.3 (t, J = 10.4 Hz, N(CH₂)₃(CF₂)₇ CF₃, 9F), -82.6 (t, J = 10.6 Hz, Ar_m (CF₂)₅CF₃, 24F), -112.2 (t, J = 15.2 Hz, Ar_m CF₂, 16F), -115.0 (m, 6F, N(CH₂)₃CF₂), -122.7 to -123.3 (m, 34F, Ar_m CF₂CF₂CF₂, N(CH₂)₃CF₂CF₂CF₂CF₂CF₂), -123.9 (m, 22F, Ar_m (CF₂)₃CF₂, N(CH₂)₃(CF₂)₅CF₂), -124.2 (m, 16F, Ar_m CF₂CF₂), -124.6 (m, 6F, N(CH₂)₃CF₂CF₂), -127.3 (m, 6F, N(CH₂)₃(CF₂)₆CF₂), -127.7 (m, 16F, Ar_m (CF₂)₄CF₂). Anal. cald. for C₁₀₆H₃₃BF₁₅₅N: C, 29.77; H, 0.78; N, 0.33. Found: C, 29.90; H, 0.74; N, 0.46.

Membranes

Mitex™ membrane filters (made of pure Teflon®, 13 mm diameter, 10 μm pore size, 125 μm thick, 68% porosity) and Fluoropore™ membrane filters (pure Teflon®, 47 mm diameter, 0.45 μm pore size, 50 μm thick, 85% porosity) were obtained from Millipore. A hole punch was used to cut 13 mm diameter discs out of the larger Fluoropore™ membrane filters. Supported liquid phases were prepared by impregnating the porous membrane filters with the desired solutions. In the case of the membranes with the Fluoropore™ support, two membrane filters were layered on top of each other for all selectivity measurements except when measuring selectivity for N(Bu)₄⁺ and N(Pr)₄⁺, for which 4 membranes were layered on top of each other. Fluorous solution was added to the surface of the membrane filter until it looked glossy, which usually required 12-18 μL per membrane filter.

Electrodes

The fluorous membranes prepared in this way were mounted into custom-machined electrode bodies made from poly(chlorotrifluoroethylene) and were mechanically sealed around the perimeter, leaving an exposed region 8.3 mm in diameter. The electrode bodies were equipped with an inner Ag/AgCl reference and internally filled with a 1 mM solution of the primary ion chloride. An electrochemical cell was obtained by immersion of the thus fabricated electrode and an external reference electrode of the double junction type (DX200, Mettler Toledo, Switzerland; saturated KCl as inner solution and saturated KCl as bridge electrolyte) into the sample solution. All electrodes were conditioned in a 100 mM solution of the primary ion chloride for 2-3 hours prior to measurement.

Potentiometric Measurements

EMF Suite 1.02 (Fluorous Innovations, Arden Hills, MN) was used to control an EMF 16 potentiometer (Lawson Labs, Malvern, PA) for all potentiometric measurements. The input impedance of the potentiometer exceeded 10 TΩ. Selectivity coefficients were determined by the fixed interference method⁵¹ for Li⁺, Na⁺, K⁺, NH₄⁺, and H⁺, while the separate solution method⁵¹ was employed for (C₃H₇)₄N⁺, and (C₄H₉)₄N⁺. Nernstian responses were confirmed for all ions in the concentration range where selectivities were tested, and the average standard deviation in the logarithm of the selectivity coefficients was 0.13. Activity coefficients were calculated according to a two-parameter Debye-Hückel approximation.⁵²

Conductimetry/Resistance Measurements

The same experimental setup as for potentiometry was also used for conductimetry, allowing the Teflon® support and electrode body to define the conductivity cell dimensions. All DC conductivities were determined in a Faraday cage with an EMF 16 potentiometer using the method of potential reduction by a known shunt,⁵³ using the same type of 1.0 GΩ resistors (±0.01 GΩ, 2.5 W, Digi-Key, Thief River Falls, MN) as in our previous work.³⁶

Impedance Spectroscopy

All impedance measurements were performed with a Solartron SI 1287 Electrochemical Interface (Solartron Analytical, Farnborough, Hampshire, UK) configured for two-electrode measurements. Due to the high resistance of the membranes in the cells, the amplitude of the AC signal was set to 1.0 V. Smaller applied AC potentials showed no significant difference except when membrane resistances became sufficiently high to cause erratic readings from the instrument. A four-electrode setup was also tested with similar cells but yielded no significant difference. All measurements were performed with the same electrode setup as for the potentiometric measurements, except that the reference electrode was an Ag/AgCl reference with a surface area of 13 cm² immersed directly into the sample solution. KCl solutions (10 mM) were used as the internal filling and sample solutions for all measurements.

The dielectric constant of perfluoroperhydrophenanthrene was measured with an AH 2500A 1 kHz Ultra-Precision Capacitance Bridge (Andeen-Hagerling, Cleveland OH) with a 350G Closed Electrode Cell (Dielectric Products, Watertown MA).

Differential Scanning Calorimetry

The T_g of 3 was determined using a Q1000 Thermal Analyzer (TA Instruments, New Castle, Delaware). The sample was allowed to thermally equilibrate at 25 °C for 5 min, warmed to 40 °C at a rate of 10 °C/min, allowed to equilibrate for 5 min, cooled to -100 °C at a rate of 20 °C/min, allowed to equilibrate for 5 min, and then warmed to 25 °C at a rate of 10 °C/min. The T_g was calculated from the observed heat flow profile during the final temperature ramp.

Computational Details

Quantum-mechanical geometry optimizations were performed on all three molecules using the Gaussian03 software package (Gaussian, Wallingford, CT) on a 364-processor IBM SP system at the Minnesota Supercomputing Institute and an Alienware MJ-12 dual-CPU workstation running under the SuSE Linux Professional 9.3 operating system. Each optimization was done using the B3LYP density functional⁵⁴ and the 6-311+g(d,p) basis set, specifying an energy change convergence criterion of 1×10^-6 kcal/mol per iteration. Centroids were calculated using SYBYL 7.0 for Linux (Tripos, St. Louis, MO) and the compounds were visualized in SPARTAN ’02 Linux/Unix (Wavefunction, Irvine, CA).