Surface Assisted Transient Displacement Charge Technique. I. Photoinduced Charge Transfer in Self-assembled Monolayers

Abstract

Surface assisted photoinduced transient displacement charge (SPTDC) technique was developed in order to study light induced charge transfer in surface bound molecules and applied to investigation of self-assembled monolayers of 7-diethylaminocoumarin and 2,4-dinitrophenylamine. The dipole moment change measured by SPTDC correlates reasonably well with that measured in solution by standard PTDC technique and with semiempirical calculations. Shortening of the excited state lifetime of surface immobilized coumarin due to stimulated emission was observed in both fluorescence and dipole measurements. The dipole signal decline in low polarity solvents indicates the importance of dipole-dipole interaction that causes reorientation of molecules upon photoexcitation.

INTRODUCTION

The photoinduced transient displacement current (PTDC) technique is a direct method of measuring photoinduced excited state dipole moments.^1-8 Unambiguous data interpretation makes PTDC very useful in analyses of the extent of charge separation in excited molecules. The time resolution of the technique (ca. 0.5 ns) does not allow rates of charge separation greater than 2×10⁹ s^-1 to be measured directly. However, it is sufficient for detecting many charge transfer species and their charge recombination rates. There are no intrinsic limitations on use of polar solvents, but solvent conductance is a restrictive factor. Since the latter is usually higher in polar solvents, the technique is most efficient in nonpolar solvents.

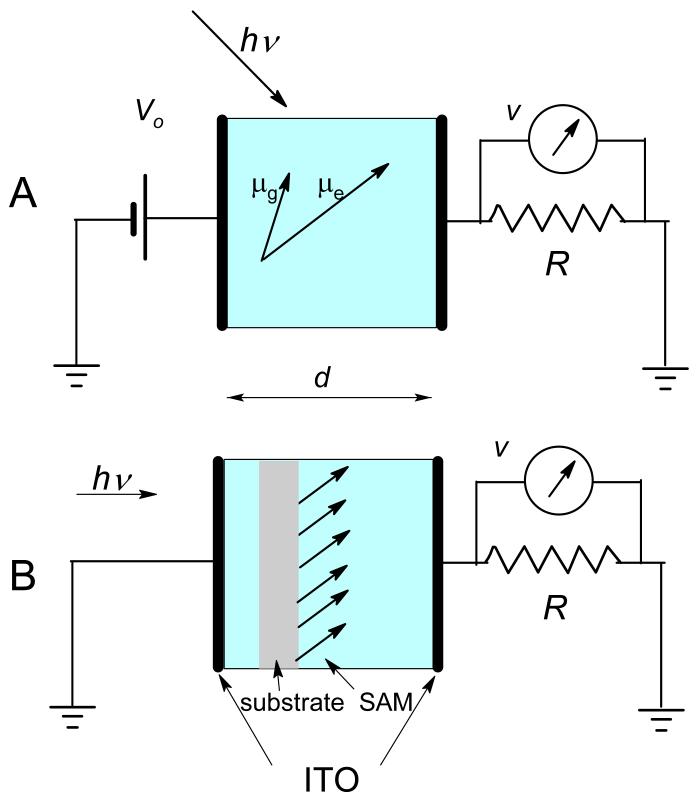
A simplified sketch of the method, shown in Figure 1A, illustrates the parallel electrode cell filled with solution in series with the load resistor, R, under applied voltage. Depending on R, two modes can be distinguished: the displacement current and the charge displacement modes. The former is identified by a 50 Ω load resistor, in which case the circuit RC time is short and the signal is primarily proportional to the time derivative of dipole concentrations. In the charge displacement mode, with a large load resistor (we use either 1 MΩ or 20 kΩ) and, consequently, a large circuit RC time, the signal is proportional to the dipole concentrations. In this oversimplified description, the rotation time is presumed fast but in the real treatment, it is included in signal convolution. PTDC signal appears due to dipole rotation directed by the external electric field and would be zero without the orientation it provides.

Figure 1.

A. A schematic representation of the photoinduced transient displacement current (PTDC) setup. The ground state, μ_g, and the excited state, μ_exc, dipole moments illustrate a greater alignment of μ_exc with the applied electric field. The displacement current is measured in the circuit across the resistor, R. B. Illustration of the surface assisted photoinduced transient displacement charge (SPTDC) setup. Here the ground and the excited state dipole moments are oriented by the surface.

When studying charge transfer in large molecules or complexes, such as DNA and proteins, one often encounters that rotation of species is slower than charge recombination. In standard geometry of PTDC, such a condition prevents full development of the signal because its decline is faster than its rise. To overcome this shortcoming and eliminate the use of the external electric field, we proposed an alternative means of dipole orientation: by immobilizing molecules on flat surfaces.¹

We have previously reported that molecules immobilized on flat surfaces and oriented by it do indeed allow observation of their photoinduced dipole signal.¹ A better control for orientation of molecules can be achieved by means of covalent attachment^9-11 or using Langmuir-Blodgett films.^12,13 The purpose of this article is to evaluate whether a quantitative analysis of the dipole moment change upon photoexcitation in such a technique is feasible and investigate the underlying advantages and disadvantages.

THEORY

Phenomenon of photoinduced voltage in a monolayer is very similar to the so-called ‘surface potential’ of a floating monolayer. The latter is often described using the Helmholtz equation,^1,14,15 which treats the dipoles at the surface as two layers of opposite charges with surface density, σ, separated by the distance l. The potential difference across such a layer is given by:

$$v=l\sigma ∕{\epsilon }_0,$$ (1)

where ε_o is permittivity of free space. One can reformulate Equation (1) for the photovoltage signal, v, caused by the intramolecular dipole moment change:

$$\Delta {\mu }_{\perp }=e\Delta l_{\perp }$$ (2)

due to the electron (with charge e) movement over the distance Δl_⊥ perpendicular to the surface upon photoexcitation. Hence Equation (1) becomes:

$$v=\frac{<\Delta {\mu }_{\perp }>N_{\Omega }}{{\epsilon }_{0}S},$$ (3)

where the number of excited dipoles, N_Ω, and the electrode area, S, are introduced. The average perpendicular projection of the dipole moment difference, <Δμ_⊥>, is calculated from the averaged perpendicular projections of the excited, μ_exc<cosθ>_exc, and the depleted ground state, μ_g<cosθ>_g, dipole moments:

$$<\Delta {\mu }_{\perp }>={\mu }_{\mathit{exc}}{<\cos \theta >}_{\mathit{exc}}-{\mu }_g{<\cos \theta >}_g={\mu }_{\mathit{exc}}\int f_{\mathit{exc}}\left(\theta \right)\cos \theta d\Omega -{\mu }_g\int f_g\left(\theta \right)\cos \theta d\Omega$$ (4)

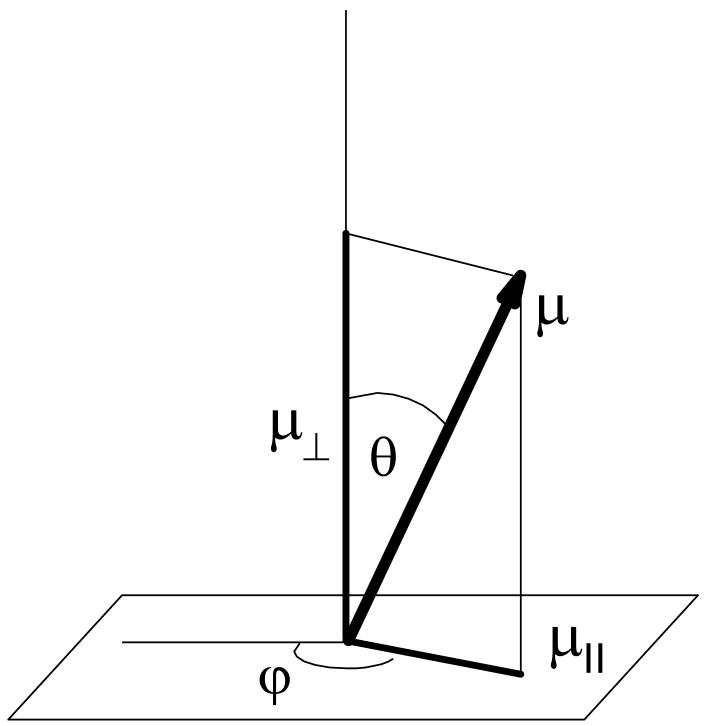
where θ is the angle between the direction of the dipole moment and the axis normal to the surface (see Figure 2). We wrote Equation (4) this way to emphasize that the angular distributions, f_g(θ) and f_exc(θ), of dipoles in the ground and excited states may differ. The latter can also depend on time due to rotation of excited molecules.

Figure 2.

Illustration of the Eulerian angles, θ and φ, for a dipole, μ, on the surface.

Orientation of dipoles in the ground and excited states can be different because the transition moment and the dipole moments of both states are not necessarily aligned. One also has to take into account variation of excitation probabilities for dipoles with different orientations on the surface. If we presume no rotation and random distribution of the ground state dipoles throughout a hemisphere, we can evaluate Equation (4) as:

$$<\Delta {\mu }_{\perp }>=\left({\mu }_{\mathit{exc}-{\mu }_g}\right)\int f\left(\theta \right)P\left(\theta \right)d\cos \theta =\left({\mu }_{\mathit{exc}-{\mu }_g}\right)\frac{{\int }_0^1\cos \theta {\sin }^2\theta d\cos \theta }{{\int }_0^1{\sin }^2\theta d\cos \theta }=\frac{3}{8}\left({\mu }_{\mathit{exc}-{\mu }_g}\right)=\frac{3}{8}\Delta \mu ,$$ (5)

where we assumed that the dipole moments of both states are collinear (same f(θ)), and that laser excitation normal to the surface produces excitation distribution, P(θ), along the transition moment that is parallel to both dipole moments. We labeled the dipole moment change upon excitation as:

$$\Delta \mu ={\mu }_{\mathit{exc}}-{\mu }_g$$ (6)

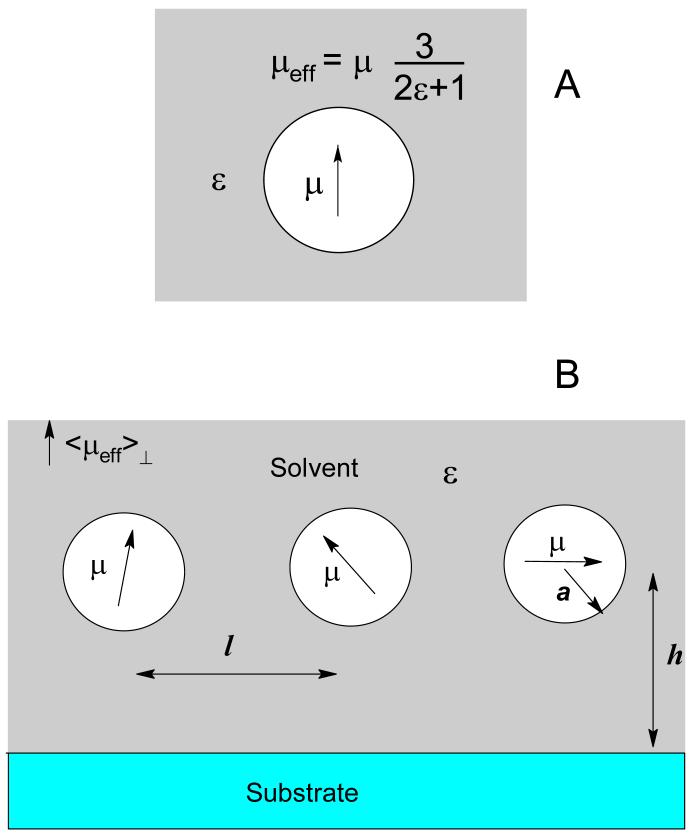
Equation (3) offers the solution for Helmholtz potential, v, in vacuum, whereas in reality the cell is often filled with medium, usually liquid solvent, with a dielectric constant ε. In Onsager’s semicontinuum model,^1,16,17 a molecule with a nonzero ground state dipole moment can be represented as a point dipole, placed in the center of a cavity and surrounded by continuous medium with dielectric constant ε. Following this model, one can realize that a point dipole moment, μ, in a cavity creates an electric field outside the cavity (Figure 3A) identical to that created by a point dipole μ_eff:

$${\mu }_{\mathit{eff}}=\frac{\mu }{(1-\gamma )\epsilon +\gamma }$$ (7)

Figure 3.

A. A point dipole moment, μ, placed in the center of a spherical cavity of radius a, creates an electric field outside the cavity identical to that of an effective point dipole, μ_eff = 3μ/(2ε + 1). B. Point dipoles, μ, placed in the centers of identical spherical cavities of radius a, interact with the substrate, distant by h, and each other, with l being the separation distance between dipoles.

This effective dipole moment is smaller than μ because of cancellation from the solvent and depends on the shape of molecule via the anisotropy factor γ, which equals 1/3 for a spherical cavity and goes to zero for a very prolate molecule. The value of μ itself increases with increasing solvent polarity but to a lesser extent. Solvent polarized by the dipole, provides the reaction field collinear with the dipole moment and causes its increase if the solute polarizability volume, α, is nonzero. The dipole moment, μ:

$$\mu =\frac{{\mu }_0}{1-\frac{\alpha }{a^3}\frac{2(\epsilon -1)}{2\epsilon +1}}$$ (8)

can become significantly larger than its gas phase value, μ_o,^1,17 especially for highly polarizable small molecules. Since the reaction field is much greater than any accessible external field, even for a very small dipole moment, μ from Equation (8), not μ_o, represents the meaningful description of the dipole moment in solution.¹ The situation might differ if the dipole is surrounded by other solute dipoles in close proximity. The effect of proximal substrate also contributes to the departure from the described picture of independent dipoles.

The problem with applying Equation (7), as a means to substitute dipole moment μ_eff for μ, is in the lack of unambiguous transformation of a group of spherical cavities, with point dipoles inside, into the Helmholtz layer of charges. Instead of forcing dipoles into a Helmholtz layer, let us retain the approximation of independent dipoles in spherical cavities, i.e. that l ≫ a and h ≫ a (Figure 3B), for which the restriction of them being on a plane will be also lifted. Then, following Onsager’s semiempirical approximation, the total electric polarization of the solution, P, can be calculated as a sum of polarizations from solvent and solute molecues:^1,16,17

$$\overrightarrow{P}={\overrightarrow{P}}_{\text{solvent}}+{\overrightarrow{P}}_{\text{solute}}=\sum _j{\left(n_j{\overrightarrow{\mu }}_j\right)}_{\text{solvent}}+\sum _i{\left(n_i{\overrightarrow{\mu }}_i\right)}_{\text{solute}}$$ (9)

The first term can be estimated from the solvent’s macroscopic dielectric constant, ε, and the definition, ε_oE + P = εε_oE:

$${\overrightarrow{P}}_{\text{solvent}}\approx {\epsilon }_0\overrightarrow{E}\cdot (\epsilon -1)$$ (10)

where E is the average electric field in the cell and the overall volume of solvent molecules is presumed insignificantly small compared to the volume of solvent. The second term in Equation (9) can be calculated if the angular distribution of solute dipole moments, f_i(θ), and their values, μ_i, are known. Realization that the integral of the field from a point dipole, E_μ, over the region outside its spherical cavity, V> V_e, is exactly zero:^17,18

$${\int }_{V>V_e}{\overrightarrow{E}}_{\mu }dV=0$$ (11)

allows convenient simplification in calculating P_solute as a product of solute dipole concentration, n_i, and the average projection of their dipole moments onto the axis perpendicular to the electrodes, <μ_⊥>_i:

$$P_{\text{solute}}=\sum _i{n}_i{<{\mu }_{\perp }>}_i$$ (12)

Note that Equation (12) presumes zero net interaction with other dipoles, i.e. it would not be correct for a nonspherical cavity or when interaction between solute dipoles is not negligible due to their high concentration.

Upon photoexcitation, some dipole moments change. Assuming that there is only one sort of excited dipoles, μ_exc, the solute electric polarization change, ΔP_solute, depends on time through the concentration of excited states, n_exc(t), and the average projections of the ground and excited state dipole moments, which may also depend on time:

$$\Delta P_{\text{solute}}\left(t\right)=n_{\mathit{exc}}\left(t\right){\langle \Delta \mu \rangle }_{\perp }=n_{\mathit{exc}}\left(t\right)({\langle {\mu }_{\mathit{exc}}\rangle }_{\perp }-{\langle {\mu }_g\rangle }_{\perp })$$ (13)

In the standard PTDC technique the dipole orientation is induced by the external electric field. When it happens quickly, the angular distributions of each type of dipoles are at equilibrium and their average projections along the field (perpendicular to the electrodes) depend on the external electric field, E:

$${<{\mu }_i>}_{\perp }=\phi \frac{{\mu }_i^{2}E}{3k_{B}T}$$ (14)

making the electric polarization change after photoexcitation equal to:

$$\Delta P_{\text{solute}}\left(t\right)=n_{\mathit{exc}}\left(t\right)({\mu }_{\mathit{exc}}^2-{\mu }_g^2)\phi \frac{E}{3k_{B}T}=n_{\mathit{exc}}\left(t\right)\phi \frac{\Delta \left({\mu }^2\right)}{3k_{B}T}E$$ (15)

The factor φ combines corrections due to the difference of the electric field on a dipole because of surrounding solvent and surrounding solvent polarization. For a spherically shaped molecular cavity it equals:^1,3

$$\phi ={\left(\frac{3\epsilon }{2\epsilon +1}\right)}^2\frac{{(2\epsilon +n_D^2)}^2}{3(2{\epsilon }^2+n_D^4)}$$ (16)

where n_D is the solvent’s refractive index. From Equation (15) the dipole signal in PTDC under conditions of fast molecular rotation is proportional to the change of dipole moment squared:

$$\Delta {\mu }^2={{\mu }_{\mathit{exc}}}^2-{\mu }_g^2,$$ (17)

For calculating the dipole signal, i.e. the voltage drop across the load resistor, one needs to calculate the charge at the electrodes, Q, which is given by the product of displacement, D, and the electrode area, S, normalized by 4π:

$$Q=DS=\{\epsilon {\epsilon }_{0}E+P_{\text{solute}}\}S$$ (18)

If presumed uniform, the electric field inside the cell, E, is given by the voltage drop across the cell, v_cell, divided by the cell gap, d:

$$E=v_{\text{cell}}∕d$$ (19)

Then the voltage, v, measured across the load resistor, R, arises from the displacement current:^1,17

$$v=R\frac{dQ}{dt}=\epsilon {\epsilon }_{0}RS\frac{dE}{dt}+RS\frac{d{P}_{\text{solute}}}{dt}$$ (20)

After substituting E from Equation (19) and using v = - v_cell (in standard PTDC v = V₀ - v_cell, with V₀ being is applied voltage), one obtains the time variation of the dipole signal, v:

$$v+{\tau }_{RC}\frac{dv}{dt}=RS\frac{d{P}_{\text{solute}}}{dt}$$ (21)

Here the RC time of the circuit is introduced:

$${\tau }_{RC}=R\epsilon C_0=R\frac{{\epsilon }_0\epsilon S}{d},$$ (22)

It is obvious from the derivation that Equation (21) is identical for both, the standard PTDC and the surface assisted PTDC techniques. The difference is in how the solute polarization, P_solute, is calculated: compare Equation (13) and. Equation (15).

First, let us compare this solution with the Helmholtz layer potential. In the charge displacement mode (i.e. with large τ_RC), the first term in Equation (21) can be neglected and it simplifies to:

$$\frac{dv}{dt}=\frac{RS}{{\tau }_{RC}}\frac{d}{dt}\left(n<\Delta {\mu }_{\perp }>\right),$$ (23)

After integrating and substituting τ_RC from (22) and N_Ω/Sd for n, we obtain the expression for v:

$$v\left(t\right)=\frac{<\Delta {\mu }_{\perp }>}{\epsilon {\epsilon }_0}\frac{N_{\Omega }}{S}$$ (24)

This result almost coincides with previous derivations^14,15 of the Helmholtz layer potential, also given as a product of μ/ε and the density of molecules, but with a different meaning of ε. The dielectric constant, ε, in Equation (23) is that for a bulk solution, where dipoles are randomly distributed, while Demchak and Fort,¹⁵ and then Taylor and Bayes¹⁴ arrived at a similar formula with ε being the dielectric constant of the Helmholtz layer only.

Another important aspect of using Equation (22) involves handling stray capacitance, which could be comparable with that of the cell itself. Stray capacitance affects the amplitude of the dipole signal, especially in solvents of low polarity, because the signal drops across both, the stray capacitance, C_s, and the cell capacitance, εC_o. The correction automatically gets included if the RC time of the circuit that combines both capacitances:¹

$${\tau }_{RC}=R(\epsilon C_0+C_s),$$ (25)

Equation (21) is the basis for evaluating PTDC and SPTDC dipole signals. In standard PTDC (, which is used for solutions under an applied electric field,) the assumption that each dipole interacts only with the solvent and external field is justifiable and allows straightforward calculation of average dipole moment projection using Equation (14). The result:¹

$$v+{\tau }_{RC}\frac{dv}{dt}=\phi \frac{V_{0}R}{d^2}\frac{\Delta \left({\mu }^2\right)}{3k_{B}T}\frac{dN}{dt}$$ (26)

presumes instantaneous rotation of dipoles but is free from other assumptions, which makes PTDC powerful for unambiguous recovery of dipole moment changes from v(t). The treatment is extendable towards incorporating rotation by using a single rotational diffusion time; appropriate equations can be found elsewhere.^1-3

In SPTDC, at least in the realized form, additional information about dipole distributions and their dynamics is required and data interpretation becomes more sensitive to the model. A good starting point for discussing the dipole signal in SPTDC is the approximation mentioned above of uniform angular dipole distribution on hemisphere and no significant rotation before relaxation of excited molecules to the ground state. This approximation should work well for large molecules and other rigidly oriented dipoles. Combined with the angular dependence of excitation probability from Equation (5), it simplifies Equation (23):

$$v=\frac{3}{8}\frac{R{N}_{\Omega }}{d{\tau }_{RC}}\Delta \mu$$ (27)

where the number of excited dipoles on the surface, N_Ω, can be measured during the experiment from the amount of absorbed energy. Equation (27) should allow determination of Δμ from the dipole signal magnitude, v.

As will be shown in this paper, the approximation of independent nonrotating dipoles should be applied with great care to small molecules like coumarin covalently linked to silica. A reasonable agreement is observed only in polar solvents, where intermolecular dipole-dipole interaction is suppressed but in less polar solvents molecular rotation becomes significant and is necessary for explaining the signal decline.

EXPERIMENTAL

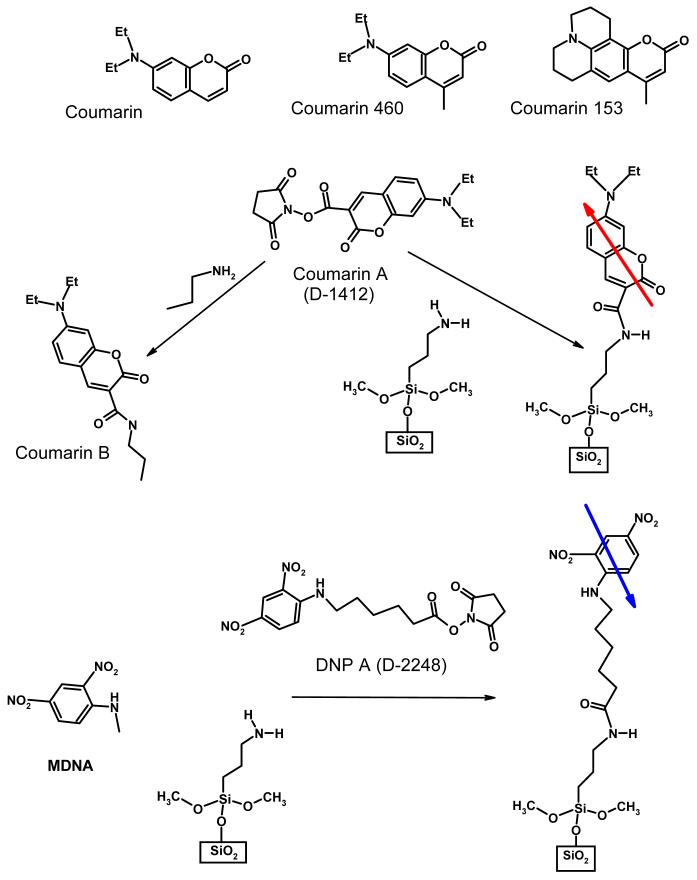
7-diethylaminocoumarin-3-carboxilic acid succinimidyl ester (commercial name D-1412) and from here on termed coumarin A), 6-(2, 4-dinitrophenyl)aminohexanoic acid succinimidyl ester (commercial name D-2248) and from here on termed DNP A, both from Molecular Probes, coumarin 153 and coumarin 460, both from Exciton, Inc., were used without purification. Aminated form of coumarin A (from here on termed coumarin B) was prepared by reacting coumarin A with 1-propylamine (see Figure 4).

Figure 4.

Chemical structures of the molecules discussed in this study. Immobilized on the surface coumarin and DNP have their dipole moments shown by arrows.

Substrates: mica, and polished quartz slides (12 × 25 × 0.3 mm) from Quartz International, were modified by trimethoxy aminosilanes (3-amino-propyltrimethoxysilane, from Aldrich), and then stained by a dye on one side to form a self assembled monolayer (SAM) using previously described procedure.^9,10 Quartz slides were first cleaned for 30 min in 0.1N NaOH, then in 1/1 MeOH/HCl for another 30 min and rinsed in copious amount of deionized (DI) water. This was followed by 2 hours of heating in concentrated H₂SO₄ and rinsing with DI water. The final step of cleaning was done immediately prior to silanization - the slides were boiled in DI water, rinsed in acetone and dried at 100°C. In case of mica, the upper layer was peeled off prior to use, followed by boiling in DI water and drying. Cleaned slides were silanized from 2% v/v acetone solution of trimethoxyaminosilane, washed with acetone and baked at 110°C in oven for 5 minutes.

Staining the silanized slides by dye molecules (either coumarin A or DNP A) was performed only on one side of the substrate. For that, a drop of 0.6 mM DMSO solution of a dye was placed between the slide and the surface of a glass Petri dish. The stained slides were washed in acetone and dried in an oven at 100°C. No noticeable deterioration of the dye molecule surface concentration was observed within a month after staining when stored under dark dry conditions or in dry organic solvents.

Excited state dipole moments in solutions were measured using a standard time-resolved photoinduced transient displacement current (PTDC) setup. Third harmonic of Nd:YAG pulses shifted on either H₂, CH₄ or CF₄ (to make 416 nm, 396 nm or 366 nm, respectively) were used for excitation. The pulses were 20 picosecond long and delivered by “Orion SB-R” Nd:YAG laser from MPB. The signal was measured across the 50 Ω input resistor of a digital oscilloscope, TDS 684A (1 GHz bandwidth), from Tektronix. Solution of a dye with a typical concentration of 10^-4 M was circulated through the dipole cell with two parallel flat stainless steel electrodes in between quartz windows for laser excitation. The experiments were conducted at room temperature with an external voltage 600V applied across a 0.65 mm gap between the electrodes with area 1.3 cm².

Since the rotation time of coumarin is fast (τ_r < 0.2 ns in nonviscous solvents), the dipole signal was well described by Equation (26). This simplification left three parameters for describing the signal - the dipole moment change, (Δμ²)^1/2, the excited state life time, τ_F, and the RC time, τ_RC. The dipole moment change described the signal magnitude, and τ_F and τ_RC determined the shape of the signal. All three parameters were varied in order to fit the signal. Optimized fittings provided the values for (Δμ²)^1/2, τ_F and τ_RC. Inclusion of the estimated rotation time, τ_r ∼ 0.2 ns, had insignificant effect on the fittings and the dipole moment values.

In the modified surface assisted PTDC (SPTDC) version, a dipole signal was measured across the input 20 kΩ resistance of a P6249 high impedance probe (4 GHz),¹⁹ from Tektronix. The cell was designed to suit the modifications necessary to the SPTDC technique for studying photoinduced charge transfer in surface immobilized molecules. Two identical ITO (indium-tin-oxide) semitransparent electrodes (10 Ω/square surface resistance) were held 3 mm apart (by a dielectric spacer) facing each other so that the overlapping area was 2.5×2.5 cm². Ideally, the dipole signal in SPTDC is independent of the gap distance between the electrodes (see Equation (24)) if the width of the electrodes is much greater than the distance between them. However, in reality the cell capacitance (and its ratio to stray capacitance) varies with the gap distance. For the sake of simplicity, the gap was maintained constant at, 3mm for all the experiments, which allowed for easy evaluation of the cell and stray capacitance. The latter was measured to be ca. 4.3 pF, which was comparable with that of the empty cell itself. Stray capacitance affects the amplitude of the dipole signal, especially in solvents of low polarity because the signal drops across both the stray capacitance, C_s, and the cell capacitance. The correction is automatically included in the RC time of the circuit that combines both capacitances, as shown by Equation (25). There is a significant limitation for dipole measurements on interfaces when using the SPTDC technique: the amount of molecules that can be placed in SAM is very small, even when using a few slides stacked on top of each other in the cell. Therefore, in order to reduce the noise and enhance the capability of measuring small signals, the cell was shielded by aluminum foil.

Fluorescence kinetics were measured in the same setup using an InGaAs photodiode (model 1437, 25 GHz) from New Focus. Fluorescence spectra were detected using a fiber optic spectrometer, SD2000, from Ocean Optics, the CCD of which was triggered by the laser. Two slides in contact with each other at their stained sides were placed vertically at 45° with respect to the incoming laser beam in a 1 cm quartz cuvette. To minimize scattering, the gap between the slides was filled with toluene. The liquid served not only as a refractive index matching fluid but also minimized potential photooxidation of coumarin. Luminescence was collected by a fiber via a short focal length lens. A glass filter with the short wavelength cutoff at 435 nm was placed between the fiber and the detector to shield undesired laser scattering. The luminescence was measured at different incoming laser light polarizations and at two different positions of the fiber with respect to the slides. Parallel orientation was achieved by placing the fiber under the sample; for perpendicular orientation the fiber was placed behind the vertically standing slides at 90° with respect to the laser beam. Neutral density filters were used to vary the laser intensity.

RESULTS

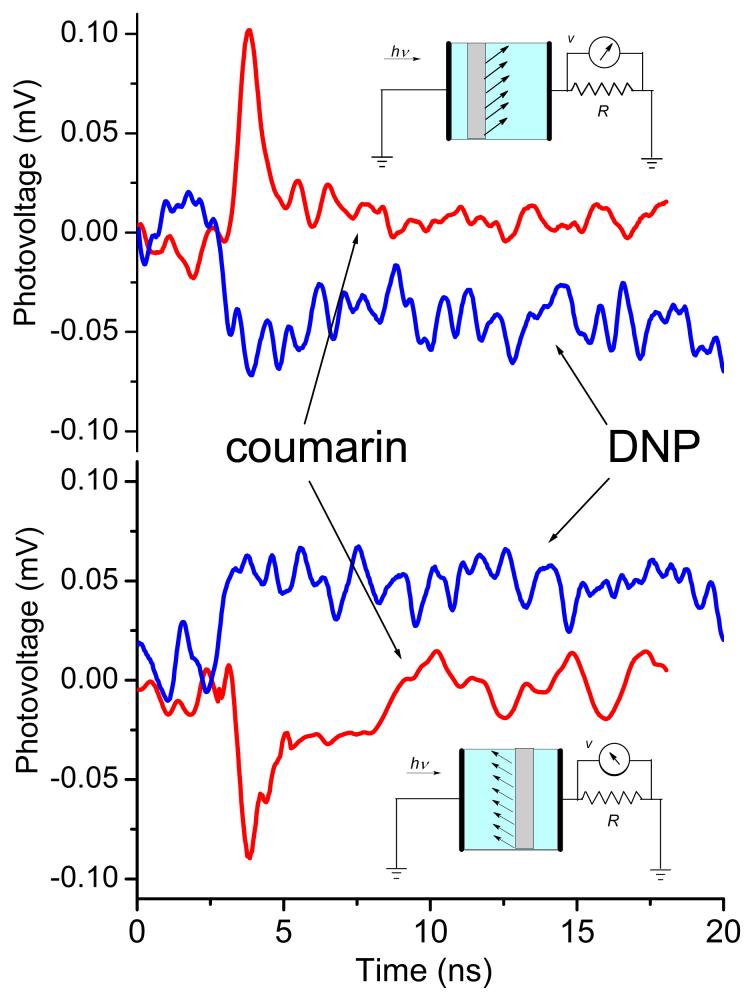
As Figure 4 illustrates, immobilized coumarin and DNP have their dipole moments oriented oppositely with respect to the surface. Moreover, their excited state dipole moments increase upon excitation almost perfectly (within 10°) along the ground state dipole directions. Thus, these two molecules represent opposite directions for photoinduced transient charge displacement. Figure 5A shows SPTDC photovoltage signals from SAM of coumarin and DNP immobilized on silica and immersed in ethanol. When oriented the same way with respect to the electrodes, the dipole signals for coumarin and DNP showed different signs, in agreement with opposite dipole moment change in them as a result of photoexcitation. Flipping the substrates inside the cell changed the direction of the charge displacement. This resulted in the opposite sign of the dipole signals but no change in the amplitude, as seen in Figure 5B.

Figure 5.

SPTDC dipole signals for coumarin and DNP self assembled monolayers immobilized on one side of quartz slides immersed in ethanol. Two orientations of the stained side with respect to the electrodes are given, as illustrated by the cartoons. The dipole signal signs are opposite to each other, in agreement with the directions of photoinduced charge displacement; they are opposite for coumarin and DNP.

There are two additional differences between coumarin and DNP that were clearly visible in their dipole signals. First, the excited state of coumarin relaxes to the ground state primarily from its short-lived singlet state via fluorescence. DNP, on the other hand, does not fluoresce at all because most of its excited states convert to the long lasting triplet state, thus the dipole signal for DNP had a longer lifetime. Second, the signal amplitude for DNP was smaller than that for coumarin (<Δμ_⊥> is almost 7 times less), even though their anticipated dipole moment changes are comparable. The disparity is easy to rationalize as being due to a longer flexible chain that links DNP to the surface and diminishes anisotropy of dipole distribution at the surface. Because of these complications, we focused mainly on coumarin.

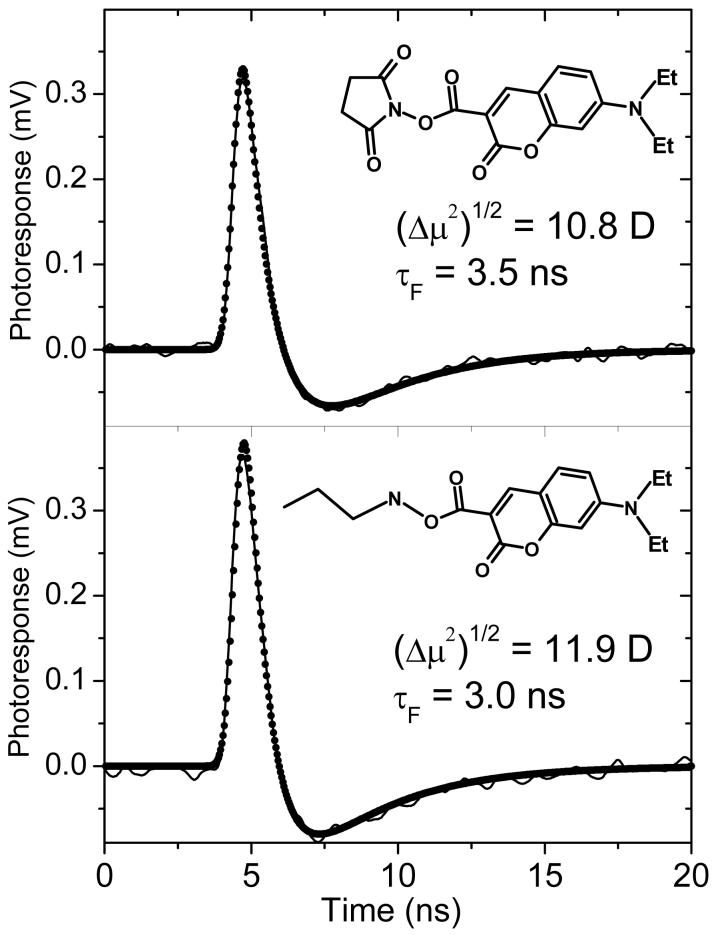
For the purpose of calibration, the dipole signal of coumarin was studied by standard PTDC technique in solution. Both, coumarin-A and coumarin-B, that mimics its surface bound version in SAM, showed nice dipole signals in solution (see Figure 6). The best-fit curves were practically insensitive to variation of the rotational time from zero to the estimated from hydrodynamic volume, τ_r ∼ 0.2 ns. The obtained excited state dipole moment values, equivalent to (Δμ²)^1/2 of Equation (17) were found to be quite close, 10.8 D and 11.9 D for coumarin-A and coumarin-B, respectively, as were the respective excited state lifetimes, τ_F = 3.5 ns and 3.0 ns in toluene. Intersystem crossing time to the triplet state was no shorter than 40 ns making the triplet yield below 10%. The dipole moments were the same for three solvents of different polarities: toluene, dichloromethane, and hexane.

Figure 6.

Photoinduced transient displacement current signals for the two forms of coumarin in toluene solution measured by the standard PTDC technique. Top: coumarin-A; bottom: carboxamide analogue, coumarin-B. The signals (solid lines) were measured with 22 μJ of absorbed laser energy at 416 nm in a cell with 600 V applied across the 0.65 mm gap between the electrodes. The best-fit signals (points) were calculated with the rotation time of 0.2 ns and the ground state dipole moments presumed zero. The excited state dipole moment values (equivalent to (Δμ²)^1/2 of Equation (17)) were 10.8 D and 11.9 D, respectively.

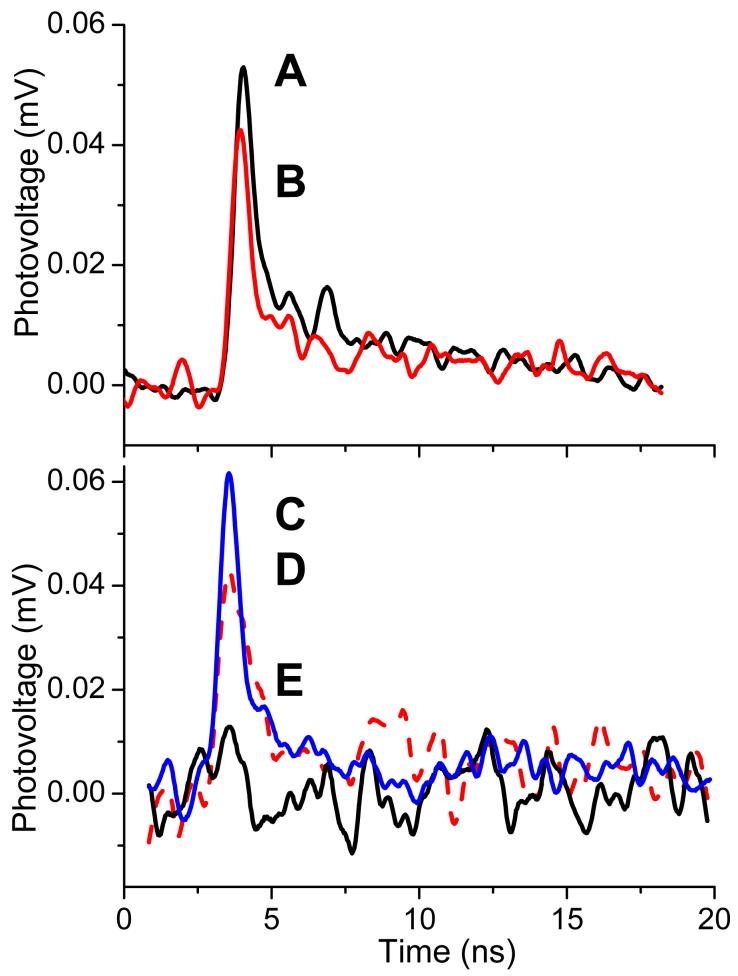
Figure 7 shows SPTDC dipole signals from coumarin SAM on different substrates and in three representative solvents. Both substrates shown in Figure 7A, mica and quartz, have surface hydroxyl groups that were utilized for coumarin SAM construction. The signals were normalized by the number of substrates and to the same incident energy used in the experiments. Thus, the amplitude of each signal corresponds to the signal obtained from one substrate. The difference of the dipole signal amplitudes is not dramatic and probably reflects the difference in the number of excited molecules as well as in the average angle of their orientation with respect to the surface. The necessary information can be obtained from absorption spectra, but only quartz substrates possess suitable transparency in the region of interest to use for this evaluation.^9,10

Figure 7.

SPTDC dipole signals for coumarin immobilized on one side of different substrates and in different solvents. A: quartz slides in ethanol, B: mica slides in ethanol, C: quartz slides in ethanol, D: quartz slides in toluene, E: quartz slides in hexane. A and B are normalized for the same incident laser energy and the number of slides. Signals C through E are normalized by the absorbed energy, 7 μJ at 396 nm.

In our previous optical studies,^{Error! Reference source not found.9,10} we have found that the absorption spectra of coumarin SAM were different from those in solution by being broader and less dependent on the solvent. From linear dichroism measurements, it was concluded that the molecules’ angular distribution was fairly close to a random on hemisphere with some preference of parallel to the surface orientation in nonpolar solvents. The average projection of the angle between the transition dipole moment and the surface normal, <cos²θ>, can be calculated from the absorption intensities of parallel, A_∥, and perpendicular, A_⊥, orientation to the surface:^9,10

$$<{\cos }^2\theta >=\frac{A_{\perp }}{2A_{\parallel }+A_{\perp }}$$ (28)

As Table 1 illustrates, <cos²θ> was close to 1/3 in ethanol, the expected value for random dipole orientation on hemisphere, and declined for nonpolar toluene and hexane. Accordingly, the dipole signal amplitude, and the corresponding <Δμ_⊥>, was the largest in high polarity ethanol, see Figure 7B and Table 1. The decline of <Δμ_⊥> in nonpolar toluene and hexane was much greater than the change of <cos²θ>, which suggests that the static approximation of Equation (6) is insufficient to describe the dipole signal, at least in low polarity solvents There should be a contribution from changing angular distributions, i.e. reorientation. The effect of reorientation was even more dramatic without solvent and will be discussed in the paper that follows.

Table 1.

Experimental values for SPTDC dipole signal fitting parameters

	Coumarin SAM			DNP SAM
	Hexane	Toluene	Ethanol	Ethanol
<Δμ⊥>, D	∼0.07	0.3	1.1	-0.16c
τF, nsa		0.5	0.75	c
τisc, nsb		10	17	< 1 nsc
<cos2θ>d	0.23	0.30	0.32	0.33

^aapparent lifetime of the singlet state

^bintersystem crossing time

^cfor the triplet state with presumed 100% intersystem crossing yield and time constant less than 1 ns

^dcalculated using Equation (28) from absorption spectra.

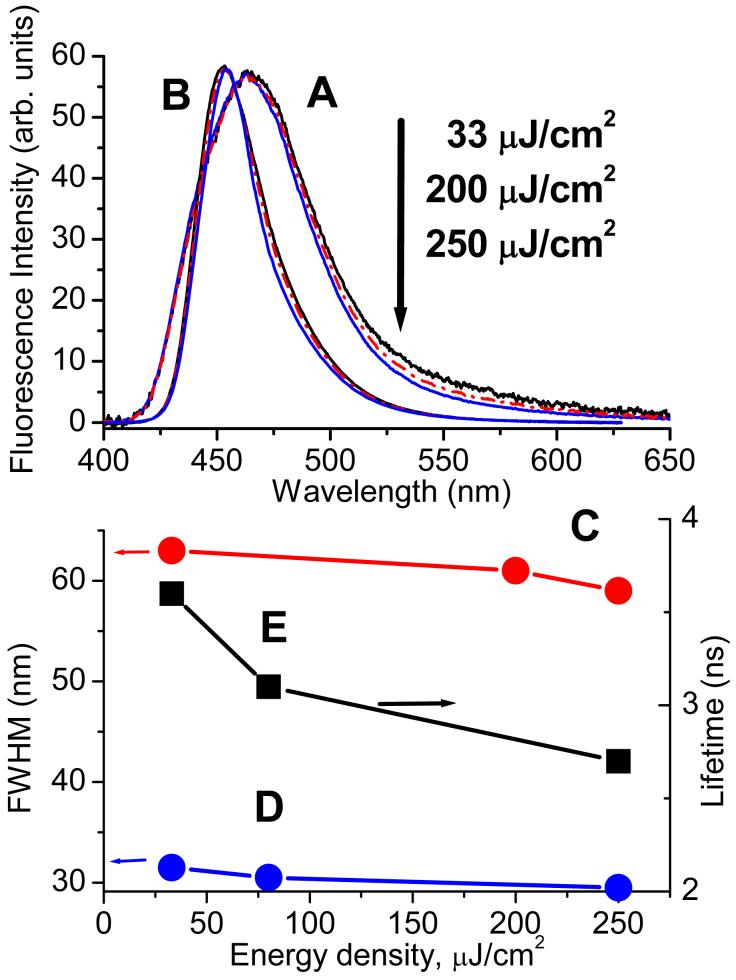
The initially surprising result of the experiments with coumarin SAM was that the dipole signal had a much shorter lifetime than that measured in standard PTDC and in fluorescence kinetics in solution. The fluorescence measurements for coumarin SAM led us to conclusion that the observed effect of the lifetime shortening should be attributed to stimulated emission of coumarin in SAM. Figure 8 shows normalized fluorescence spectra of coumarin SAM upon excitation at 396 nm measured parallel to the surface substrate at different laser energy densities: 33, 200, and 250 μJ/cm². A low pass (435 nm cut) glass filter was used to screen off the laser scattering. Although it slightly distorted the high-energy wings of the spectra, it allowed for clear observation of the spectral energy redistribution on the red wing upon varying the laser energy, as seen in Figure 8A. The observed emission intensity was a close to linear function of the incident laser energy for the given range but the spectra did demonstrate significant narrowing that was manifested by the decrease of the full width at half maximum (FWHM) shown in Figure 8B. The effect of spectral narrowing was similar for both light polarizations.

Figure 8.

Top: Fluorescence spectra of coumarin-B in toluene solution (B) and coumarin SAM in toluene (A) at different laser energy densities; spectra are normalized by laser energy. Bottom: Corresponding FWHM of the spectra above: D - coumarin-B and C - for coumarin SAM and the excited state lifetime for coumarin-B in solution (E). Concentration of coumarin-B in solutions was 2×10^-5 M (OD_{396 nm} = 0.9).

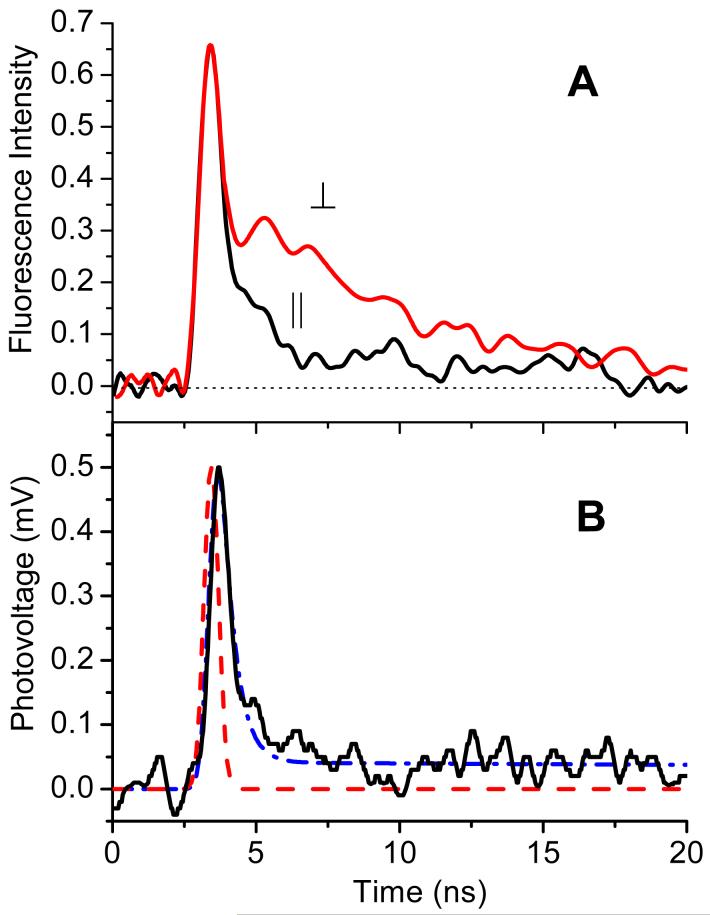
The assignment of the effect to stimulated emission was supported by pronounced changes in fluorescence kinetics. Figure 9A illustrates that fluorescence decay from coumarin SAM had two components - fast and slow. Fluorescence measured parallel to the film’s surface, ∥, had mostly fast decay. For the same incident energy (250 μJ/cm²), fluorescence kinetics ‘perpendicular’ to the surface, ⊥, had an additional slower component that resembled fluorescence of spontaneous emission. Measurements at much lower intensities could have provided additional proof of the stimulated emission interpretation (only slow fluorescence component would be expected) but, unfortunately, they were not possible due to the sensitivity limitations.

Figure 9.

Comparison of the fluorescence kinetics (A) and SPTDC dipole signal (B) for SAM of coumarin in toluene. Fluorescence was detected parallel (∥) and perpendicular (⊥) to the surface (see text for details). The dipole signal (solid line in B) is shown with the laser time profile (dashed line) and the best fit (dash-dot), corresponding to the dipole moment change, <Δμ_⊥> = 0.3 D, singlet excited state lifetime, τ_F = 0.5 ns, and the intersystem crossing time, τ_isc = 10ns. The latter causes formation of the long lasting triplet state component.

The stimulated emission hypothesis was also corroborated by observation of a similar effect for the same molecule in liquid solutions. Figure 8A illustrates that, in a toluene solution of coumarin-B, spectrum narrowing was observed at similar excitation intensities as in the case of SAM. The same low pass 435 nm glass filter was used for blocking laser scattering. Since the fluorescence spectrum of coumarin-B was narrower in solution as compared to SAM, one could see the suppression of both low-energy and high-energy wings. The fluorescence kinetics in solution also indicated enhancement of the deactivation rate due to stimulated emission - the lifetime shortened (Figure 8B) in agreement with the spectrum narrowing at increasing laser energies. Similar lifetime shortening was observed for the dipole signal in standard PTDC in solution. Data in Fig.6 are given for low laser energy, where lifetime shortening was insignificant.

High molecular concentration of coumarin in SAM causes alteration of its optical properties, including absorption spectrum broadening, enhanced excitonic interaction between molecules and greater rates of energy transfer. Notably, high density of SAM allowed observation of stimulated emission from the films upon laser excitation even without a resonator cavity. Fluorescence kinetics from SAM and SPTDC dipole signal, decayed similarly faster than those in solution. Figure 9B illustrates that the SPTDC dipole signal from coumarin SAM in toluene looked almost identical to the fluorescence kinetics parallel to the surface in Figure 9A with corresponding excited state lifetime, τ_F = 0.5 ns. The best fit for the dipole signal in toluene was achieved with <Δμ_⊥> = 0.3 D. To account for a small long-lived component in the dipole signal, the intersystem crossing route leading to the triplet state formation was also introduced into the fitting scheme. Presuming the same <Δμ_⊥> for the triplet excited state, the estimated yield was approximately 4%, which reasonably agrees with the reported triplet yields for aminocoumarins.^20,22,25,26

DISCUSSION

Both, coumarin and DNP possess significant dipole moments in the ground and excited states. Due to this fact, the results of PTDC and SPTDC techniques that measure Δμ² and <Δμ_⊥>, respectively, cannot be compared directly. In order to calculate the dipole moment change upon photoexcitation, it is necessary to know the ground state dipole moment, μ_g. Semiempirical calculations, such as AM1, have been reported to offer reasonable accuracy for such estimates.²² We employed semiempirical methods (using Hyperchem 6.0 package²³) for calculating the dipole moments in the ground and excited states, as well as transition dipole moments for both molecules. Three additional coumarins were also included for comparison. The results are summarized in Table 2.

Table 2.

Calculated characteristics of the ground and the first excited states

		AM1a					ZINDOb					PM3c
		μgd	μexce	Δμf	$\sqrt{\Delta {\mu }^2}$g	ΔEh	μgd	μexce	Δμf	$\sqrt{\Delta {\mu }^2}$g	ΔEh	μgd	μexce	Δμf	$\sqrt{\Delta {\mu }^2}$g	ΔEh
Coumarin	i	6.0	8.0	2.0	5.3	-0.13	7.8	9.2	1.4	4.9	5.5	5.7	8.2	2.5	5.9	-1.2
	j	6.2	8.4	2.2	5.7		7.9	11.3	3.4	8.1		5.9	8.8	2.9	6.5
Coumarin 153	i	6.2	11.0	4.8	9.1	0.05	7.3	11.3	4.0	8.6	2.8	6.1	11.4	5.3	9.6	-0.7
	j	6.4	11.2	4.8	9.2		7.5	11.6	4.1	8.8		6.4	11.7	5.3	9.8
Coumarin 460	i	6.2	8.0	1.8	5.1	-0.15	8.3	11.1	2.8	7.4	5.5	5.9	8.2	2.3	5.7	-1.2
	j	6.3	8.4	2.1	5.6		8.4	11.5	3.1	7.9		6.1	8.8	2.7	6.3
Coumarin A	i	6.8	9.5	2.7	6.6	0.01	9.2	12.1	2.9	7.9	4.3	7.0	10.3	3.3	7.6	-1.0
	j	7.0	9.9	2.9	7.0		9.3	12.3	3.0	8.0		7.3	10.9	3.2	8.1
Coumarin B	i	6.2	9.0	2.8	6.5	-0.03	7.3	9.6	2.3	6.2	5.0	5.9	9.3	3.4	7.2	-1.1
	j	6.4	9.5	3.1	7.0		7.5	10.3	2.8	7.1		6.2	9.9	3.7	7.7
DNP A		8.9	10.1	1.2	4.8	k	9.3	12.6	3.3	8.5	k	8.8	10.2	1.4	5.2	k
DNP B		10.1	11.3	1.2	5.1	k	11.3	14.5	3.2	9.1	k	10.4	11.7	1.3	5.4	k
MDNA		7.8	8.9	1.1	4.3	k	7.8	11.3	3.5	8.2	k	8.0	9.4	1.4	4.9	k

^aAM1 method was used for the ground state geometry optimization and CI calculations using 16 orbitals (8 LUMO and 8 HOMO)

^bZINDO/S was used for CI(16 orbitals), orbital overlapping: σ-σ =1.267 and π-π = 0.585

^cPM3 was used for CI(16 orbitals)

^dground state dipole moment in Debye

^eexcited state dipole moment in Debye

^fdipole moment change, according to Equation (6), in Debye

^geffective dipole moment change according to Equation (17), in Debye

^henergy difference between syn and anti conformations, in kcal/mol

ⁱsyn conformation of diethylamine

^janti conformation of diethylamine

^konly the lowest energy conformation was analyzed

The ground state geometries were optimized using AM1 method and two energetically close conformers of aminocoumarins, with syn- and anti- orientations of alkyl groups on amines were analyzed. For comparison, PM3 and ZINDO/S were also used for calculating the dipole moments and spectra. In ZINDO/S, the standard overlap weighting factors (σ-σ =1.267 and π-π = 0.585) were used.²⁴

The results of semiempirical calculations for all coumarins can be summarized as follows: 1) the syn- and anti- conformers have very close energies and their optical and charge distribution properties in both ground and excited states are similar; 2) the ground state dipole moments of coumarin-A and B are not very different from those of other 7-aminocoumarins whether experimentally measured or obtained from semiempirical calculations;^20-22,26 ab-initio and DFT calculations also show similar results;^27,28 3) excited state dipole moments are always greater than the ground state dipole moments and point in the same direction; 4) transition moments are almost parallel to both the ground and excited state dipole moments; 5) the dipole moment change is smaller than experimentally measured.

The discrepancy between the experimental and theoretical dipole moments should not be surprising since the experimentally measured (Δμ²)^1/2 were obtained in solution, which should be different from the gas phase values given in Table 2. One can mimic the experimental conditions by scaling the gas phase values of μ using Equation (8) and a calculated molecular polarizability. The latter was calculated using ZINDO/S with the external electric field similar to the anticipated reaction field, E_R:

$$E_R=\frac{\epsilon -1}{2\epsilon +1}\frac{2\mu }{a^3}$$ (29)

For μ ∼ 10 D and the molecular radius, a = 5.4 Å, the reaction field can be quite large, E_R varies from 0.0011 a.u. in hexane to 0.0016 a.u. in ethanol. This field is much greater than the experimentally accessible electric fields, making the polarizability-enhanced dipole moment almost independent of the external electric field. The excited state polarizability along the main axis for such a field was calculated to be α = 73 ų and 75 ų for coumarin-B and coumarin-A, respectively. Combination of these with Equation (8) suggests that the dipole moment of coumarin in toluene can increase by almost 30% from its gas phase value, and even more in solvents of greater polarity. Additional correction for nonsphericity of the coumarin’s slightly prolate shape was not significant in this case. Dependence of the dipole moment (in both states) on solvent polarity should exist but for coumarin it was experimentally found to be insignificant (between hexane, toluene and methylene chloride). Because of the solvent induced dipole moment enhancement, molecular polarizability is also different from that in the gas phase, usually smaller, so that the polarizability correction appears as nonlinear, with saturation, and the solvent dependence of μ to becomes weak. Experimental polarizability values for coumarins in different solvents are smaller than 10 ų.^27,29

Thus the theoretical (gas phase) value of coumarin’s dipole moment, (Δμ²)^1/2(gas) = 7 ± 1 D from Table 2 can be scaled using the polarizability correction (a factor of 1.5) to achieve a reasonable agreement with the experimentally observed value, (Δμ²)^1/2(solvent) = 11 ± 1 D. A similar scaling factor, ca. 1.5, was required for coumarin 153 in order to match the theoretical gas phase value, (Δμ²)^1/2 = 9.1 D, with the experimentally measured, (Δμ²)^1/2(solvent) = 14 D.¹ One should anticipate a similar conversion factor for calculating Δμ(solvent) from the theoretical Δμ(gas), which leads to the estimate of Δμ (solvent) ∼ 1.5Δμ (gas) ∼ 4.5 D.

Using the above estimated Δμ (solvent) = 4.5 D, the anticipated value of <Δμ_⊥> measured in SPTDC can be calculated from Equation (5) as <Δμ_⊥> = 3/8Δμ = 1.7 D. This value is close to what was measured in ethanol, <Δμ_⊥> = 1.1 D, but discrepancy with those in toluene and hexane is much more dramatic (see Table 1). The discrepancy cannot be attributed to the solvent dependence of the dipole moments themselves, since PTDC measurements in solution confirmed the lack of such.

AM1 calculations for DNP suggest a slightly smaller <Δμ_⊥> (gas) ∼ 1.2 D but ZINDO/S method gave almost the same value <Δμ_⊥>(gas) ∼ 3 D, as for coumarin. Both ground and excited state dipole moments are almost parallel to the transition moment but orientation of all dipoles is opposite with respect to the linker when compared with coumarin (see Figure 4). The dipole moment is primarily ‘localized’ on dinitroaniline itself as it is clear from comparison of DNP A and DNP B with N-methyl-2,4-dinitroaniline (MDNA) in Table 2. The long linker chain makes the orientation distribution with respect to the surface spread over a broad range of angles exceeding 90°, which substantially cancels the net polarization. The excited state of DNP does not fluoresce and the signal observed was due to the long-lived triplet excited states. If the experimental signal was fitted with presumption of 100% yield to the triplet state, the dipole moment change in ethanol was small, <Δμ_⊥> ∼ -0.16 D, much smaller than that for coumarin (see Table 1).

The correlation of <Δμ_⊥> in different solvents with the degree of perpendicular to the surface orientation, given as <cos²θ> in Table 1, is only qualitative. In part, this is due to different moments of angular distribution evaluated in the two methods. The second moment of distribution obtained in optical measurements (A ∞ <cos²θ>), is different from the first moment of distribution provided in SPTDC (see Equation (5)). Nevertheless, the discrepancy cannot be fully assigned as due to this effect because of a much more severe decline of <Δμ_⊥> in SPTDC. Dipole reorientation after excitation is the only reasonable explanation to the effect that contributes significantly. One should anticipate a stronger dipole-dipole interaction in low polarity solvents, as also seen in anisotropy of optical absorption. Dipole moments increased as a result of excitation have stronger repulsion from surrounding dipoles, which causes them to tilt towards the surface even greater and thus a stronger decline of dipole signal in nonpolar solvents. Even more dramatic realization of this effect should be expected without solvent present. Indeed, the dipole signal in SPTDC becomes even opposite to that in solution and it is discussed in the accompanied paper.³⁰

The effect of dipole reorientation should be insignificant if large molecules are used, for which this method is designed. So far we found no suitable intermediate case, where both, PTDC and SPTDC, could be applied equally well.

CONCLUSIONS

Surface assisted photoinduced transient displacement charge technique (SPTDC) was developed experimentally and theoretically and employed to study charge transfer in coumarin and DNP self assembled monolayers covalently attached to solid oxide surfaces. The signal arises due to the change in dipole moment resulted from photoinduced intramolecular charge transfer in surface bound molecules and their reorientation. For small molecules at high density the dipole signal strongly depended on solvent polarity and decayed more dramatically in low polarity solvents. The effect arises because of a strong intermolecular dipole-dipole interaction that was visible in the ground state absorption but emerged even stronger as fast dipole reorientation after their excitation. Accordingly, SPTDC dipole signal was smaller in low polarity solvents and for molecules on long flexible chain such as DNP.

High surface concentration of coumarin molecules covalently immobilized on the surface in SAM was sufficient for observing stimulated emission upon optical excitation. It appeared in the lifetime shortening and the fluorescence spectrum narrowing even without resonant cavity.