Cyclization cascade of allenyl azides: A dual mechanism

Abstract

A density functional theory based computational approach to describing the mechanistic course of the allene azide cycloaddition cascade sequence has been developed. The results of these calculations permit characterization of key reactive intermediates (diradicals and/or indolidenes), and explain the different behaviour observed in the experimental studies between conjugated and non-conjugated species. Furthermore, computational analysis of certain intermediates offer insight into issues of regioselectivity and stereoselectivity in cases where different reaction channels are in competition, suggesting suitable substitutions to achieve a single regioisomer in the indole synthesis via azide-allene cyclization.

1 Introduction

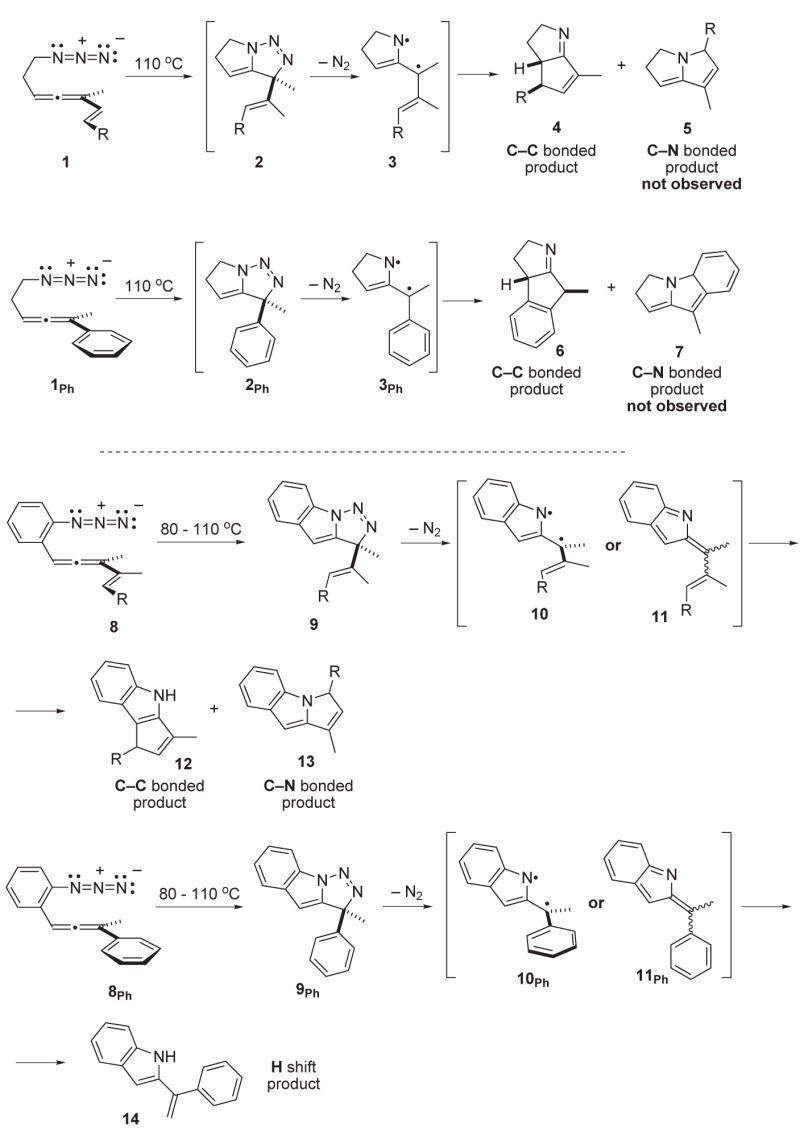
The construction of core C—C bonds in sterically hindered environments remains an enduring challenge in complex molecule synthesis. Towards this end, cyclization reactions that proceed through diradical closures offer the promise of facile bond formation in congested locations as a consequence of the typically minimal activation barriers for diyl union compared with heteropolar and/or closed-shell alternatives. However, the development of diradical cyclization chemistry has been hampered by the rather limited collection of synthesis methods that can generate diyl intermediates. One recent advance in this area emerged upon exploration of the thermochemistry of 5-azidoallenes, exemplified by 1 and 8 and their aryl analogues 1_Ph and 8_Ph (Figure 1).^{1, 2} Mild heating (110 °C) of these substrates initiated a cascade sequence postulated to proceed through (i) initial allene/azide [3+2] cycloaddition, (ii) N₂ loss from the intermediate triazoline to afford a diyl, and (iii) diyl cyclization through the appended unsaturation (alkene or arene) to furnish the closed shell products 4/6 and 12/13/14, respectively.

Figure 1.

Preliminary results and mechanistic speculation for the azide-allene cyclization cascade sequence.

The putative intermediate (singlet) diyls 3, 3_Ph and 10, 10_Ph have the options of closure to form either C—C bonds (→4/6 or 12, respectively) or C—N bonds (→5/7 or 13, respectively) from both the unconjugated 1, 1_Ph and conjugated 8, 8_Ph substrates. In addition, the conjugated substrates 8 and 8_Ph present a distinct and alternative option to diyl chemistry; reaction through the closed shell 2-indolidene intermediate 11 and 11_Ph. This putative intermediate might arise by either bond rotation/electronic reorganization of a first-formed (singlet) diyl 10, 10_Ph or by direct N₂ extrusion from the triazoline 9 and 9_Ph, respectively. The preliminary reports of this chemistry did not provide any evidence that permits a distinction to be made between these mechanistic options.

A thorough computational study of these systems is described in this report. By dissecting these cascade processes into their component steps and comparing the relative activation barriers of these steps, insight into the following questions can be garnered:

• Why does the unconjugated substrate 1 yield only the C—C bonded product 4 upon thermolysis, whereas the conjugated analogue 8 provides both C–C 12 and C–N 13 bonded products in roughly equal amounts?

• Which intermediate, the diyl 10 or the closed shell alternative 11, is formed first from 9, and which of these species is the direct precursor to the tetracyclic products 12/13?

• What is the basis for the strictly cis stereochemical outcome upon cyclization of diyl 3 to form 4?

• Why do the alkenyl-bearing substrates 8 yield tetracycle through participation of the alkene, whereas the aryl-bearing analogue 8_Ph does not engage the aryl ring in C–C bond formation, but rather forms a simple 2-styrylindole product 14?

This study will disclose the key steps of the cascade process responsible for the observed stereocontrol and regiocontrol. Moreover, the detailed description of the reaction profiles for the formation of the two regioisomers 12 and 13 from 8 may form the basis for developing strategies to steer the reaction towards one product or the other.

2 Computational methods

The density functional theory³ in its Kohn–Sham⁴ formulation was employed throughout this work. All of the stationary points were computed with B3LYP,⁵ a three parameter hybrid⁶ functional combining the 1988 exchange functional by Becke⁷ with the correlation functional by Lee, Yang, and Parr⁸ as implemented in Gaussian03.⁹ A dual level scheme was used to ensure high quality in the computed values. Geometry optimization, and frequencies were computed with the 6–31G(d,p) basis set, and further energy refinement and properties were computed with the split-valence, triple-ζ, 6–311+G(d,p) basis set. This scheme usually is noted as B3LYP/6–311+G(d,p)//B3LYP/6–31G(d,p). Diffuse functions were included in this methodological scheme, as some structures exhibited large localized negative partial charges in preliminary results. The choice of DFT and the Pople basis sets is backed by earlier studies in which this method offered reasonable results at a moderate cost despite the presence of diradical species in the reaction profile.^10–12

Due to the potential diradical character of some of the structures considered in this work, the internal and external stability of the wavefunctions was computed via the Hermitian stability matrices A and B in all cases.¹³ For all the structures exhibiting unstable restricted wavefunctions, the spin-symmetry constraint of the wavefunction was released (i.e. expanding the SCF calculation to an unrestricted space, UB3LYP). leading to stable unrestricted wavefunctions.

As a test of the method, the activation energies for several known complementary diyl formation reactions were computed; very good agreement with experiment was observed in all cases (see Supporting Information).

Nucleus independent chemical shifts (NICS)¹⁴ and the anisotropy of the current induced density (ACID)¹⁵ were evaluated using the gauge-independent atomic orbitals (GIAO)¹⁶ and the continuous set of gauge transformations (CSGT),¹⁷ respectively, to help describe whether the transition states exhibit aromatic character. Solvation effects on relative energies have been taken into account with the polarizable continuum model (PCM) in cases where comparisons to experiment required it.^18–20

Complete active space SCF (CASSCF) calculations were performed with the 6–31G(d) basis set to accurately describe the diradical character of several key intermediates. These calculations were performed with GAMESS package.²¹ The active space in the CASSCF calculations presented in this work include the entire π system of the diyl intermediate, resulting in a six electrons in six orbitals active space, usually noted CASSCF(6,6).

3 Results and discussion

3.1 Non conjugated allenyl azides

3.1.1 Mechanism of the reaction cascade

The cascade reaction sequence occurring under thermal activation yields a single product (4 or 6, depending on the starting material) when the azide and allene moieties are not connected through conjugation (cf. reactants 1 and 1_Ph in Figure 1). Moreover, the reaction proceeds with complete stereocontrol to furnish a single diastereomer of bicyclic product 4. This degree of control is surprising in light of the typically modest levels of diastereoselectivity reported to attend diradical collapse in other systems.²²

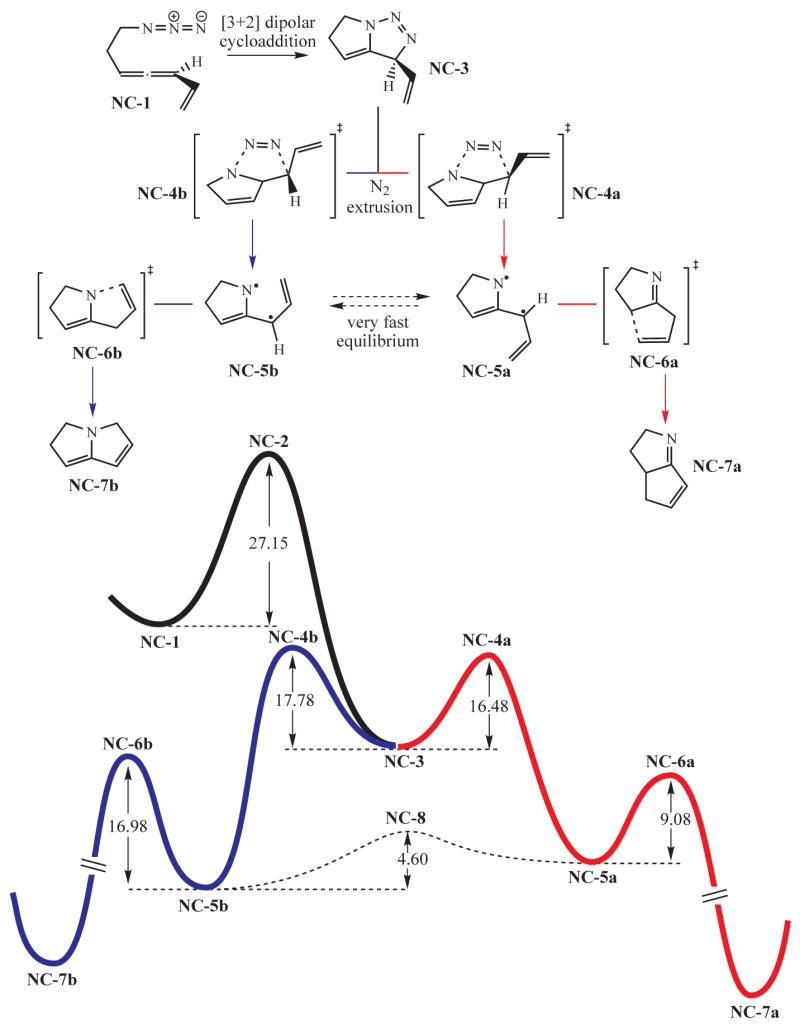
Calculations on the model system NC-1 (Figure 2) provide support for the preliminary mechanistic picture proposed in earlier work.¹ The first step is rate limiting and involves a [3+2] dipolar cycloaddition of the azide moiety to the distal allene alkene (see Figure 2), a process whose activation energy is computed to be 27.2 kcal/mol. All the remaining steps towards the imine NC-7a are much more affordable in terms of activation energies. The triazoline NC-3 releases nitrogen very easily (16–17 kcal/mol), yielding two isomeric diyls NC-5a and NC-5b that potentially could undergo cyclization to form two products, NC-7a and NC-7b, respectively. However, two mechanistic features favour convergence from both isomeric diyls. First, a very fast equilibrium which interconverts diyls NC-5a and NC-5b is available (4.6 kcal/mol). Second, the cyclization of NC-5a via transition state NC-6a to furnish the C—C bonded product NC-7a is much faster than the cyclization of its isomeric diyl to yield the C—N bonded product NC-7b. As a consequence, it is arguable that diyl NC-5b formed by nitrogen extrusion from the triazoline NC-3 undergoes isomerization to NC-5a and then cyclization to NC-7a via transition state NC-6a.

Figure 2.

Mechanistic profile for the reaction cascade of non conjugated allenyl azides.

3.1.2 Regio- and stereochemistry

Closure of the diyl diyl intermediates appears to strongly favor the transition state NC-6a to form a C—C single bond. That this transition state is substantially lower in energy than the alternative NC-6b can be traced to two features; (1) the greater stability of the C—C bond formed from NC-6a is felt to some extent in NC-6a, lowering its energy relative to NC-6b and (2) the spin density is considerably larger on carbon compared to nitrogen in NC-6a and its predecessor NC-5a (see Figure 3). Note that the latter point is also compatible with the results of a frontier orbital analysis,²³ taking into account that carbon exhibits a larger orbital coefficient than nitrogen.

Figure 3.

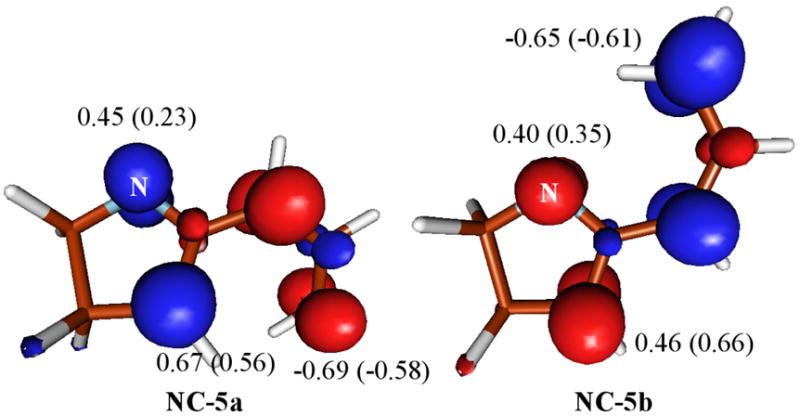
Isosurface of the spin density (0.02 e) at the diyl intermediates NC-5a and NC-5b. Values are the Mulliken spin density at the intermediate geometry and at the corresponding transition state geometry (in parentheses) in atomic units.

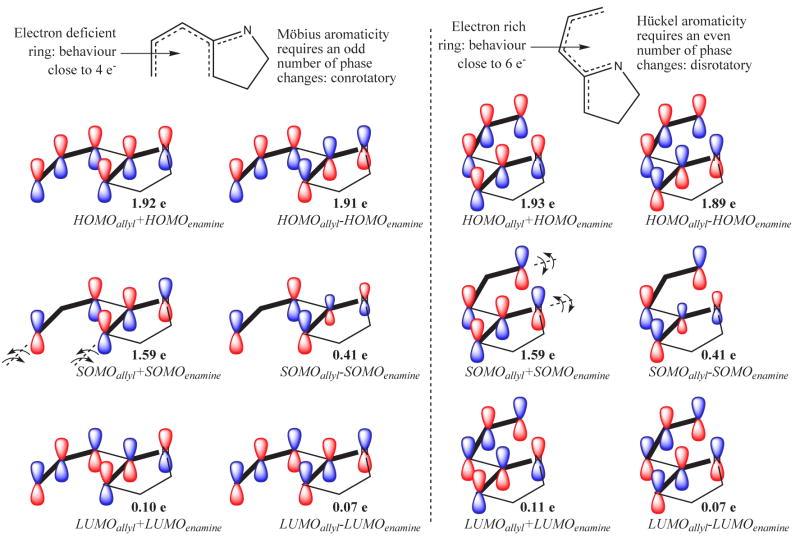
An explanation for the high stereoselectivity observed upon C–C bond formation from NC-5a can be found in a surprising place - the Woodward-Hoffmann (W-H) rules for ring closure. Even though this system is neither a [4n] nor a [4n + 2] π-electron system, the calculations detailed below provide a rationale for the closure of this formal 5-electron array that shares theoretical underpinnings with the venerable W–H dogma. A hint that electronic (orbital) control of stereochemistry might be paramount can be found in earlier calculations on the isoelectronic vinyl oxyallyl diyl system, which showed that this diyl system could be visualized as two disconnected radical species; an allyl fragment and an enol radical.¹² Complete active space SCF (CASSCF) calculations were performed for the ring closure transition state NC-6a. In addition, similar calculations with the alternative transition state NC-6b were quite revealing as well, even though it is unlikely that this species plays a role in product formation (vide supra). This methodology allows for a reliable orbital analysis of the diradical electronic structure in order to identify the source of stereoselectivity. The natural orbitals computed at the CASSCF level are illustrated in Figure 4. Strikingly, transition state NC-6a is found to conrotate towards the product NC-7a whereas its C—N bond forming counterpart NC-6b undergoes disrotatory motion towards NC-7b. This divergence of motion suggests that a W–H-like frontier orbital interaction might be governing the transition state character in both cases. Apparently, the polarization of the electron density caused by the electronegative nitrogen atom leads to C—C bond-forming ring closure via an electron deficient five electron system. Similarly, any C—N ring closure would have had to proceed through an electron enriched cyclic structure. Therefore, the observed C—C bond formation to give NC-7a should resemble a four electron cyclization whereas the hypothetical C—N bond formation (NC-7b) is more similar to a six electron cyclization in the classical W–H nomenclature. All the CASSCF natural orbitals in the active space are fully consistent with this view and present the appropriate number of phase changes for a four electron conrotatory and a six electron disrotatory ring closure, respectively (see Figure 4).

Figure 4.

CASSCF natural orbitals of the active space of transition states for the C—C bond forming cyclization NC-6a (left) and C—N bond forming cyclization NC-6b (right). Bold lines indicate the disconnected ally and enamine radicals and the proposed allyl and enamine orbital combinations leading to each natural molecular orbital. Natural orbital populations are also provided to help quantify the diradical character inherent to these species (41% for both NC-6a and NC-6b, DR = [2 - n(HOMO)]· 100).²⁴

3.2 Conjugated allenyl azides

3.2.1 Mechanism of the reaction cascade

Bridging the allene and azide moieties by an aryl group (cf. 8, Figure 1) dramatically changes the nature of the intermediates and as a consequence the outcome of the reaction cascade, which now yields two regioisomers (12 and 13 in Figure 1). The first steps are very similar to those postulated for the disconnected reactant 1. Using model system C-1 for computational efficiency, the initial [3+2] dipolar cycloaddition now appears to proceed with concomitant six electron hetero-electrocyclic closure to form the bicyclic core of C-3 (see Figure 5). In marked contrast to the earlier non-conjugated series, the subsequent nitrogen extrusion does not yield a diyl. The extrusion reaction now leads to a pair of closed shell heterocyclic products C-5a and C-5b. These calculations indicate that the barrier to interconversion between these geometrical isomers (via orthogonal diyl C-8) cannot be surmounted under the experimental conditions, and so they are formed and exist as discrete and independent species. Both regioisomers C-5a and C-5b then undergo electrocyclic ring closures (E.R.C.) independently to yield C-7a and C-7b, respectively. In this last and strongly exergonic step, rearomatization of the arene group provides a substantial driving force for reaction. This summary evokes several questions: What is the basis for favoring concerted N₂ extrusion rather than stepwise loss of N₂ via diyl inter-mediates? What is the basis for the population distribution of C-5a and C-5b? The lack of equilibration between these two species guarantees that the regiochemistry of product formation will depend only on this ratio. These issues are addressed below.

Figure 5.

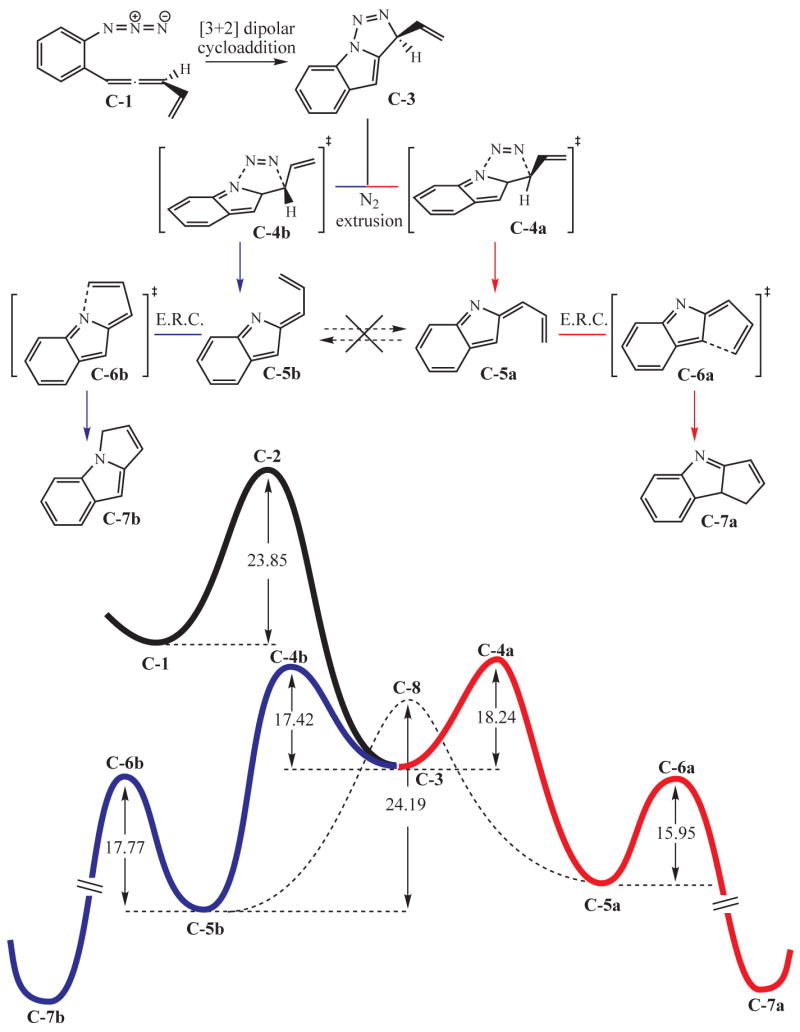
Mechanistic profile for the reaction cascade of conjugated allenyl azides.

3.2.2 N₂ loss

One of the more interesting and unanticipated results from these computational studies emerges from considering the possible pathways for formation of the indole products 19 and 20 from the putative intermediate triazoline 15 (see Figure 6). A priori, three distinct mechanistic manifolds can be envisioned:

Figure 6.

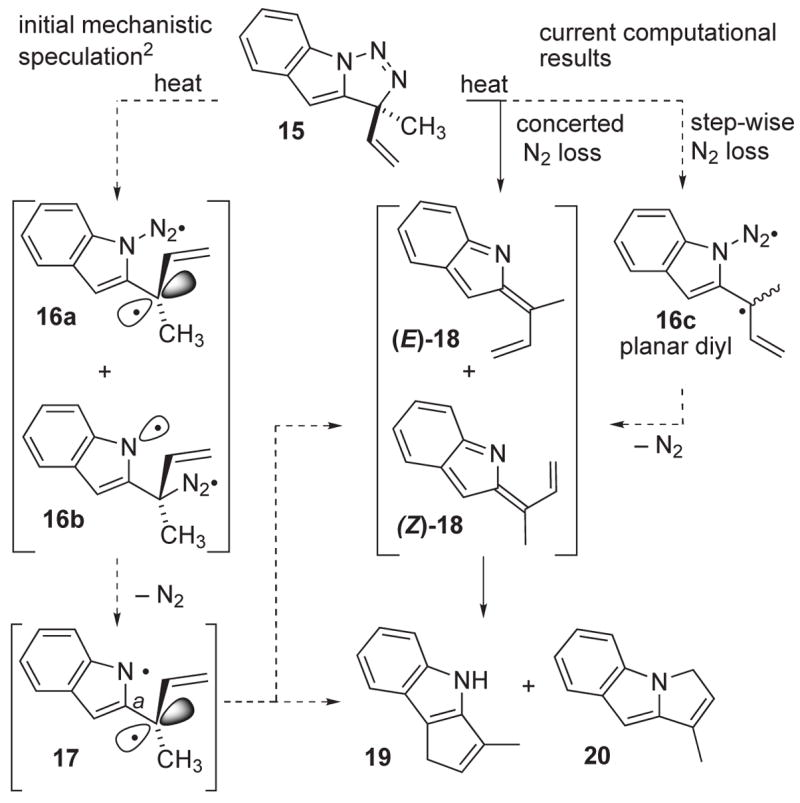
Mechanistic alternatives for the N₂ loss process.

• Single C–N or N–N bond scission to furnish intermediate diazo radicals 16a and 16b, respectively, followed by loss of nitrogen to deliver the orthogonal singlet diyl 17. This diyl could cyclize directly via either clockwise or counterclockwise rotation about bond a to furnish either the C–C bonded product 19 (counterclockwise) or the C–N bonded product 20 (clockwise).

• Bond a rotation within 17 but without bond formation could temporarily park the diyl as the closed shell indolidenes (E)-18 and (Z)-18, species which themselves then would cyclize to the observed products 19 and 20, respectively.

• Concerted elimination of nitrogen (N₂) from 15 to afford the indolidenes (E)-18 and (Z)-18 directly en route to products 19 and 20.

Transition states for C–N bond cleavage from 15, and concerted loss of N₂ from this same substrate were located. Attempts to identify a transition state corresponding to N–N cleavage within 15 led instead to the same concerted transition state found above. These computational results indicate a strong bias toward concerted loss of N₂ from 15: ΔG^‡=17.4 kcal/mol for direct 15→18 conversion, and ΔG^‡=25.0 kcal/mol for 15→16a.

The lower activation barrier for concerted loss of N₂ from 15 was unexpected, given that this transformation corresponds to a formally disallowed [10π+ 2π] thermal, suprafacial pericyclic retrocycloaddition in the W-H designation. How can this apparent repudiation of the venerable W-H rules be reconciled with the long history of adherence to same for (retro)cycloaddition processes? The key to understanding this potential disconnect lies in appreciating the orthogonal disposition of the scissile C–N and N–N bonds with the remaining π system. Two additional techniques were applied to illuminate this issue: ACID (anisotropy of the current induced density), which helps visualize delocalization of electron density as might be expected in a concerted (aromatic) bond cleavage/formation process, and NICS (nucleus independent chemical shift), which computes the chemical shift at points in space where there are no nuclei. The ACID representation of the concerted elimination of N₂ from 15 (see Figure 7) indicates that there is essentially no electron density “flowing” between the N=N fragment and the remainder of the (orthogonal) π system at the transition state. Moreover, a quick visual comparison with model Diels–Alder reactions shows evident differences in electron density delocalization at the cleavage points between a Diels–Alder nitrogen cycloreversion and the N₂ extrusion under study here. In addition, the NICS data provide support for this interpretation by illustrating that there is essentially no shielding effect in the spatial region inside the cleaving ring. For comparison, an analogue calculation on model Diels–Alder and hetero-Diels–Alder reactions (butadiene and ethylene, and butadiene and nitrogen, respectively) reveals a NICS value of ca. 17 ppm. Thus, these calculations suggest that there is no electronic communication between the two halves (N₂ and indole fragment) as the C–C and C–N bonds cleave in a concerted manner, and it is only as the transition state is surmounted that the rotation of bond a, which is required to bring the two electronic halves into conjugation, can occur. This “non-least-motion” type of mechanistic pathway, familiar in the chemistry of carbene and ketene cycloadditions, inter alia, then can deliver the closed shell species (E)-18 and (Z)-18, and then the observed products 19 and 20, respectively. However, the lack of electronic communication between the two unsaturated fragments at the transition state for bond cleavage places this case outside of the W-H umbrella.

Figure 7.

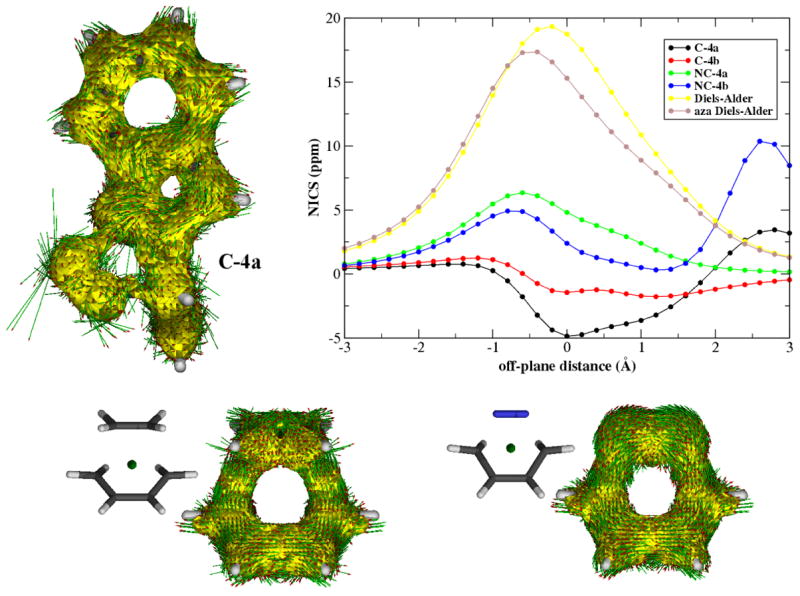
0.05 au ACID isosurface for the transition state involved in the concerted loss of N₂ C-4a and for model Diels–Alder reactions. Plot of the Nucleus Independent Chemical Shift (NICS) for relevant transition states related with the N₂ extrusion.

3.2.3 Regioselectivity

The reaction cascade presented in previous work would become a more valuable synthesis methodology if regiocontrol could be achieved. As discussed above, product regiochemistry is determined at the transition state corresponding to N₂ loss, 21→22→23, Figure 8. The electronic structure and geometry of transition state 22 was subjected to analysis, leading to the identification of key steric interactions that have the potential to influence the rotational preference of bond a (cf. 22a) and hence the regioisomer distribution of the product. As bond a rotates in a counterclockwise direction (illustrated in 22a, see projection at the top of Figure 8 to distinguish the clockwise and counterclockwise rotations), the steric interaction between R₁ and R₂ diminishes in severity while at the same time the steric interaction between R₁ and the vinyl appendage increases. In contrast, clock-wise rotation about bond a (cf. 22b) engenders the opposite steric profile. Therefore, the energetic trade-off between the burgeoning R₁/vinyl steric interaction in 22a and the similarly increasing R₁/R₂ steric interaction in 22b should determine the ultimate regioisomer distribution. The experimental data and related computational results presented in Fig. 8 bear out this premise. When R₁ = H and R₂ = CH₃, there is little difference between the two competing steric interactions, and therefore there is little observed preference between the C—C bonded product 24a and its C—N bonded alternative 24b. However, increasing the size of R₂ (R₁ = H) leads to a corresponding increase in formation of the C—C bonded product regioisomer 24a, a result consistent with an increasingly severe R₁//R₂ steric penalty in the clockwise rotation of 22b. The computational results support these observations as well. In the one case (R₁ = H, R₂ = t-Bu) where both theory and experiment coincide, the calculated result (24a/24b = 2.8:1 at 110 °C) matches remarkably well with the observed value (24a/24b = 2.7:1). This encouraging correspondence between calculation and experiment augurs well for the predictive value of this computational methodology. In that vein, if both R₁ and R₂ were non-hydrogen (R₁ = CH₃, R₂ = t-Bu), selectivities for the C—C bonded regioisomer 24a greater than 99:1 (ΔΔG^‡ = 4.4 kcal/mol) would be expected.

Figure 8.

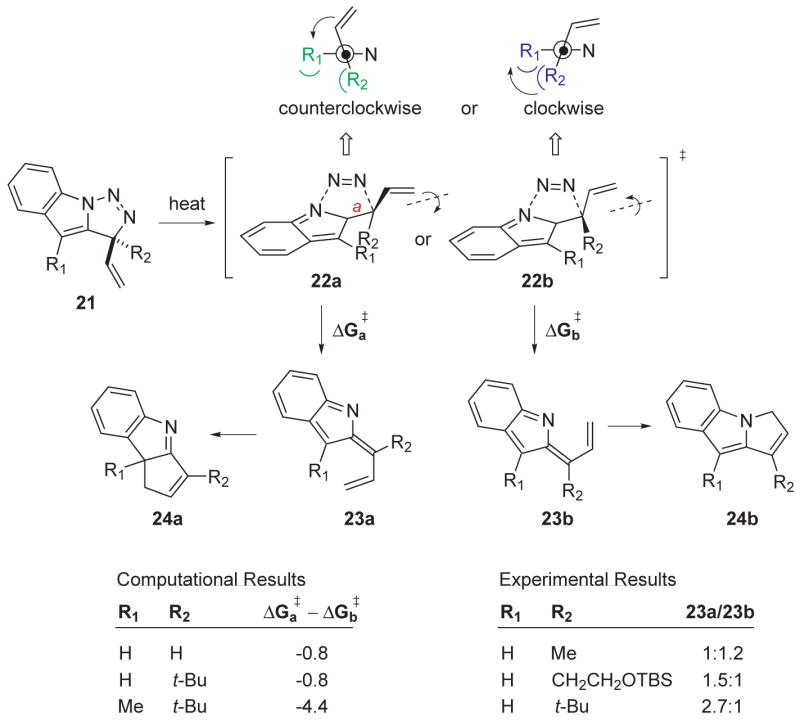
Computational and previous experimental work on the effect of substitution with bulky groups on regioisomer production. Newman projections of the allene group are included with the transition states and strong(weak) steric interactions are indicated in blue(green).

3.2.4 Aryl analogues

The replacement of the terminal vinyl units in 1 and 8 with aryl rings led to a divergence of behaviour between the non-conjugated and conjugated systems, Figure 1. The simple non-conjugated aryl derivative 1 behaves similarly to its vinyl counterpart with the exception that it recovers the arene ring’s aromaticity through tautomerization following C—C bond formation (compare products 4 and 6 in Figure 1). The aryl substituted conjugated substrate 8_Ph, however, does not undergo C—C bond forming ring closure upon thermolysis, as does its vinyl analogue. Rather a hydrogen shift intervenes and diverts a putative indolidene intermediate 18 to a 2-styryl indole product 14 (Figure 9). The difference in behavior between the conjugated and non-conjugated substrates can be attributed to a competition between the relative aromatic resonance energies of the two aryl components within 18_Ph, a competition that is absent in the non-conjugated series. In 18 the recovery of aromaticity in the indole fragment via electrocyclization provides a strong driving force to provide C–C and C–N bonded products 21 and 22, respectively (Figure 9). However, in 18_Ph this same electrocyclization is accompanied by loss of significant aromatic resonance energy as a new C–C or C–N bond is formed to the arene. The trade-off between the gain in indolic aromatic resonance energy upon C–C (or C–N) bond formation and the loss of same at the arene fragment must influence the product distribution. This competition can be resolved by the intervention of a second, independent pathway by which the indole can recapture its aromaticity, but at no expense to the arene unit; formal [1,7] hydrogen shift from the methyl group to either the indolidene’s C(3) position (from (E)-18_Ph or to it’s nitrogen (from (Z)-18_Ph) to furnish 14_Ph or it’s tautomer, tau-14_Ph, respectively. Tau-14_Ph, if formed, then could proceed to the observed product 14 by simple proton shift.

Figure 9.

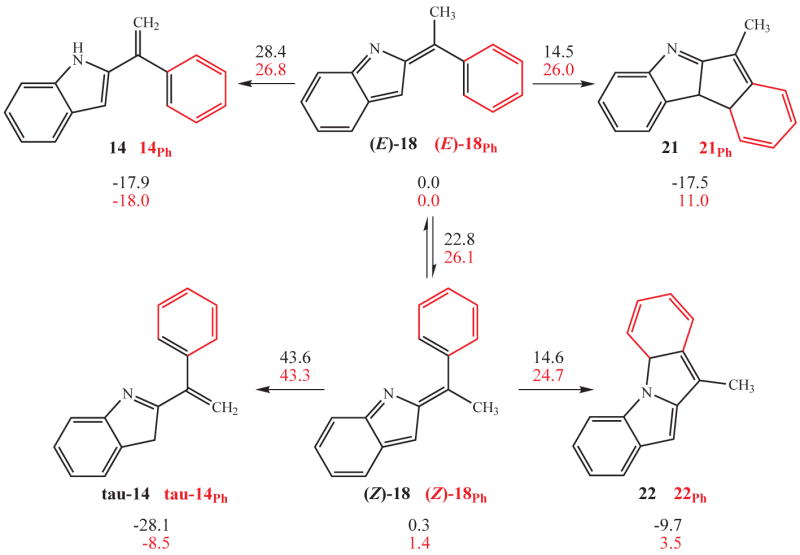
Cyclization pathways for aryl-substituted conjugation disconnected and conjugation connected allene azides.

The calculations support this mechanistic interpretation. The energy barrier for the final C—C bond forming cyclization of ((E)-18_Ph into 21_Ph suffers a severe penalty when compared to its vinyl counterpart (from 14–15 kcal/mol (vinyl) to 25–26 kcal/mol (phenyl)). The increase in the electrocyclic ring closure barrier heights for the phenyl-substituted series allows the alternative [1,7]-H shifts to be expressed. The calculated barrier height for the C–H bond forming shift of (E)-18_Ph into 14_Ph at 26.8 kcal/mol is only slightly higher than the calculated (E)-18_Ph→21_Ph electrocyclization barrier, but the related [1,7] C—H-to-N–H shift extending from (Z)-18_Ph, at over 40 kcal/mol, is unlikely to be expressed experimentally. However, the calculated barrier to interconversion of (Z)-18_Ph into (E)-18_Ph (26.1 kcal/mol) is likely to render this isomerization process facile under the experimental conditions.

Thermodynamics also works against C–C bond formation in the phenyl-substituted series. The final product of the ring closure, 21_Ph, is thermodynamically unstable with respect to the indolidene intermediate (E)-18_Ph by 11.0 kcal/mol. As a point of comparison, the vinyl-substituted series, with no loss of aromatic resonance energy, exhibits very favorable thermodynamics upon participation in the cyclization (-17.5 kcal/mol for (E)-18 to 21). Similar numerical values attend the cyclization options of the phenyl- and vinyl-substituted (Z)-indolidenes 18 and 18_Ph as well (see Figure 9). Therefore, the mechanistic landscape is open to the interpretation that whereas (Z)-18 and (Z)-18_Ph are probably dead ends, their isomerization to (E)-18 and (E)-18, respectively open the possibility that all of the indolidene intermediate is funnelled to 21 via electrocyclic ring closure or to 14_Ph via the [1,7] H shift described above. Both a kinetically accessible pathway to 14_Ph, and a large thermodynamic disincentive to form 21_Ph and 22_Ph, guide the chemistry of the intermediate indolidene 18_Ph.

4 Conclusion

Several questions regarding the mechanistic intricacies of the allenyl azide cyclization cascade were posed in the Introduction. The computational results reported herein address and clarify all of these issues. The primary question of C—C vs. C—N bond formation appears to hinge on the distinct nature of the key intermediates. The non-conjugated system appears to proceed through an intermediate diyl that favors C—C bond forming cyclization at the more electron rich carbon radical site,, whereas the conjugated system progresses through closed-shell indolidene alkene isomers whose ultimate fate (C—C or C—N bond formation) is determined by the (E)/(Z) alkene isomer ratio. In the conjugated substrate series, a diyl intermediate was not found along the reaction coordinate, emphasizing the mechanistic dissimilarity between the reactions of the conjugated and non-conjugated allenyl azides. The diyls that are formed from the non-conjugated substrates cyclize with complete stereochemical control through a 5-electron conrotatory process resembling the familiar 4n-type W-H electrocyclizations. Finally, the competition between electrocyclization and [1,7]-hydrogen shift within the conjugated system-derived indolidene depends on the nature of the terminal unsaturation; if an alkene is present, electrocyclization is preferred energetically and tricyclic product is formed, whereas if the terminal unsaturation is an arene ring, disrupting its aromaticity is too penalizing, and the [1,7] H-shift predominates. Overall, these results point to the value of computational approaches in disentangling complex reaction sequences that may feature bis allylic diradicals. The DFT-based approach appears robust and has the potential to guide future experimental research by offering testable predictions on issues of selectivity.

Supplementary Material

1si20070322_07. Supporting Information Available.

Cartesian coordinates and SCF energies of all the computed molecules, further calculations to check the methodology employed and the full cite for reference ⁹. This material is available free of charge via the Internet at http://pubs.acs.org.