Trajectory Clustering: a Non-Parametric Method for Grouping Gene Expression Time Courses, with Applications to Mammary Development

Abstract

Trajectory clustering is a novel and statistically well-founded method for clustering time series data from gene expression arrays. Trajectory clustering uses non-parametric statistics and is hence not sensitive to the particular distributions underlying gene expression data. Each cluster is clearly defined in terms of direction of change of expression for successive time points (its ‘trajectory’), and therefore has easily appreciated biological meaning. Applying the method to a dataset from mouse mammary gland development, we demonstrate that it produces different clusters than Hierarchical, K-means, and Jackknife clustering methods, even when those methods are applied to differences between successive time points. Compared to all of the other methods, trajectory clustering was better able to match a manual clustering by a domain expert, and was better able to cluster groups of genes with known related functions.

1 Introduction

Clustering is one of the most widely used approaches for analysis of genome-wide expression data. All clustering methods make assumptions about the nature of the items clustered and the definition of “similarity” among those items. For example, the popular K-means clustering method assumes that items to be clustered can be described by values drawn from K univariate Normal distributions. When the assumptions underlying a clustering method are violated, that method is unlikely to produce clusterings that reflect the true underlying groupings of the data. In addition to their distributional assumptions, K-means and other widely used clustering methods are not specifically able to take into account the relationship among adjacent points in a time series.

In this paper, we introduce “trajectory clustering,” a non-parametric method of clustering gene expression data from time course experiments. No assumptions about the distributional nature of gene expression levels are required, nor are uniformly spaced time points or any assumptions about the behavior of expression between time points. Furthermore, the method itself involves no free parameters (such as the K in K-means) which must be estimated separately. The trajectories used in our clustering method are defined by the direction of change between adjacent time points in a series. The direction of change can take on one of three possible values: increasing, decreasing or flat. For a time series containing N time points, there are N-1 changes, and 3^N-1 possible trajectories.

We apply trajectory clustering to a dataset from mouse mammary gland development, and show that the trajectory clusters correspond better to a manually derived expert clustering, and group genes with known biological function more accurately than two other popular clustering methods, Hierarchical and K-means. Data was acquired by Affymetrix oligonucleotide-based microarray data showing secretory activation in the mouse mammary gland. Secretory activation is a unidirectional process that takes place with high temporal coherence during the physiological transition from pregnancy to lactation (Neville et al, 2002). Many of the biochemical events in this process have been studied extensively for more than three decades (Wilde et al. 1986; Mellenberger and Bauman, 1974; Kuhn, 1968), and it is clear that many of the changes are transcriptionally regulated (Rosen et al. 1999). However, the molecular mechanisms that regulate and coordinate these changes in vivo are not well understood. Because the process is complex, the most efficient way to approach the problem is to begin with a global analysis of gene expression prior to, during and subsequent to secretory activation.

2 Methods

2.1 Acquisition of time course data from mice

Five time points were collected between day 12 of pregnancy and day 9 of lactation, with 4 replicates at each data point. Four FVB mice were sacrificed for each of the time points investigated (P12, P17, Lac1, Lac2, and Lac9). Both fourth mammary glands were removed from each animal and the imbedded lymph nodes excised. The mammary tissue was stored in RNAlater stabilization buffer (Qiagen, Valencia, CA) at -20 °C according to protocol. Total RNA was isolated and purified from each sample following the Qiagen RNA extraction/clean-up protocol. Using a spectrophotometer and the RNA 6000 Nano Assay (Agilent Technologies, Palo Alto, CA), purity, concentration and integrity of the total RNA was verified. If the samples qualified, the RNA was amplified, labeled, and fragmented following the 2002 protocol for eukaryotic target preparation (Affymetrix, Santa Clara, CA). The labeled and fragmented cRNA products of the Affymetrix protocol were again verified for sample integrity and concentration using RNA 6000 Nano Assay. Accepted samples were hybridized to Affymetrix Mu74Av2 microarray chips. Raw data were gathered from scanned array chips using Affymetrix Microarray Suite version 5.0. All animal procedures were approved by the Institutional Animal Care and Use Committee of the University of Colorado Health Sciences Center.

2.2 Computational analysis

We describe our computational approach in three phases. First, we describe how we selected portions of the raw data for further analysis. Then, we describe the details of the trajectory clustering algorithm itself. Finally, we describe the processes by which we evaluated the method and compared it to other approaches. All original algorithms were implemented in Matlab v6.1.R12 (MathWorks Inc); others were either implemented in Matlab or were from the GeneSpring (Silicon Genetics, Inc.) expression array analysis toolkit.

2.2.1 Identifying genes with significant changes during the time course

Many mammary genes are not related to secretory activation, and therefore most genes' expression will not change significantly over the course of this experiment. Before analyzing the genes putatively related to secretory activation, we applied three computational methods to filter out genes which did not vary significantly during the course of the experiment.

The first filter (Hogg & Craig, 1978, p175) identifies genes with at least moderate variance over the entire experiment; genes which do not vary at all are not likely to be related to secretory activation. Since we can assume that most genes are not related to activation, then the gene with the median variance is a reasonable model of null variation, that is, the variation due to factors other than secretory activation. We calculate the variance s² for each gene. The null hypothesis is that these variances represent random and Normally distributed noise. We can then compute the statistic W=(N-1)s²/median(s²) where N is the number of observations of the gene, which is approximately chi-square distributed with N-1 degree of freedom. We calculate a p value for rejecting the null hypothesis that the gene did not vary, and perform the False Discovery Rate (FDR) multiple testing correction, (Benjamini et al, 1995) setting the false discovery rate to be 10%. This results in a list of genes with significantly greater variation than the median variation gene, with at most 10% of that list including genes having true variation less than or equal to median variation.

Our second filter uses Affymetrix's mRNA detection call to exclude all genes with an Absolute Call of “Absent” in all experiments. The third filter is used to test the consistency of the gene across replicates of a particular time point. Genes whose within-replicate coefficient of variation was greater than 0.03 were removed. These preprocessing steps screen out genes with low variance, low mRNA levels, and inconsistent expression measurements.

The final preclustering step is to apply the non-parametric Kruskal-Wallis statistic to select genes whose expression levels are significantly different between at least two time points. Kruskal-Wallis is the non-parametric equivalent of an ANOVA test. We then again perform the False Discovery Rate test for multiple comparison correction for these genes, setting FDR to 0.015. The initial filtering steps greatly reduce the number of genes tested, and hence reduce the penalty in statistical power incurred by this correction.

2.2.2 The Trajectory Clustering algorithm

Trajectories are defined to be a sequence of length T-1, where T is the number of time points, and each element of the sequence is either I (increase), D (decrease), or F (flat). For example, all the genes whose expression decreased at each point in a four measurement series would be assigned to cluster DDD. Given a list of genes which varied significantly across at least two time points, the goal of the clustering algorithm is to assign each of these genes to a particular trajectory. Because the Kruskal-Wallis test requires at least one significant difference, no gene should ever be assigned to the sequence of all flat (FFFF).

When the Kruskal-Wallis test identifies a significant difference between an adjacent pair of points, the assignment of the gene to the I or D trajectory is trivially based on the sign of the difference. However, it is possible that a significant difference is found between expression levels that are not adjacent, yet none of the adjacent pairs themselves are found to be significantly different. For example, the expression of a gene at time point 3 may be significantly greater than at time point 1, yet there may not be a significant difference between the expression levels at time points 1 and 2, nor between the expression levels at time points 2 and 3. The challenge in this situation is to determine whether to assign this gene to the II trajectory, the FI trajectory or the IF trajectory.

We will first present a solution to this problem in the three point case, and then generalize it to N points. Let T_ij represent the interval between time points i and j. The nontrivial case arises when T₁₃ is significant, but not T₁₂ or T₂₃. It is possible that T₁₂ and T₂₃ contribute equally to the difference in T₁₃, or the difference might be heavily weighted toward T₁₂ or T₂₃. We discriminate between these possibilities as follows. For each of these genes, we sort the expression levels and assign a rank to each measurement, then calculate the mean rank difference C_i,j,k,l = |R_i-R_j| - |R_k-R_l| for the transitions from i to j and k to l, where the Rs are the average rank of the expression level at a particular time point (over all replicates). By assumption, the difference between points i and l is statistically significant, but the differences between i and j and between k and l are not. The C value is a non-parametric measure of the relative contribution of the two transitions to the difference between the first and last point. A large positive C value means the first transition made more of a contribution to the total difference than the second transition, and therefore that we should assign that gene to the (I or D)F trajectory depending on the sign of the overall difference. A large negative value implies an F(I or D) trajectory, and a value near zero means that the relative contributions are similar and the trajectory should be either II or DD. In the three time point example above, we are interested in C_1,2,2,3.

All that remains is to determine where the cutoff should be for being “near” zero. Since there are many orderings in which both mean ranks are the same, many C_i,j,k,ls will be exactly zero. However, we might also reasonably treat small differences in average rank by assuming that the relative contributions are similar. We used an ad hoc, percentile-based cutoff C*, calling the top C* percentile of the negative differences, and the bottom C* percentile of the positive differences to be near zero. In this dataset, the clustering is not very sensitive to the particular choice of C*. We chose C* to allow average rank differences of <= 1 to count as near zero. Any C* between 26 and 31 achieved this for most of the clusters, so we selected C*=30 for the analysis below. If the distribution of C scores were known, a statistically sound cutoff could be specified, but that is currently an open problem.

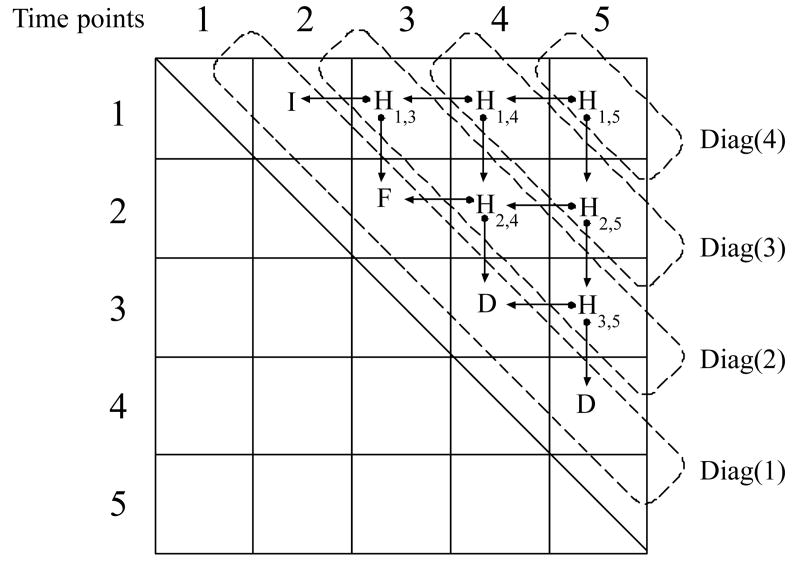
The above approach can be generalized to more than three time points. We initialize an upper diagonal matrix H with bits set to one based on the significance tests, i.e. H_ij = 1 if the null hypothesis was rejected for T_ij, and 0 otherwise. We work three points at a time, starting with the final time point and executing along successive diagonals. Additional bits are set to 1 based on the following process. At the end of the process, the last diagonal of the H matrix can be straightforwardly translated to a particular trajectory, substituting F for 0s and either I or D for 1s, depending on the sign of the difference. Figures 1 (pseudocode) and 2 describe the process in detail.

Figure 1.

Pseudocode for iterative clustering of more than 3 time points. diag(i) is the ith diagonal of the matrix counting from the main diagonal; it is equivalent to Matlab's diag function.

Figure 2.

Recursive expansion of the three point case, starting with the final time point (see pseudocode in Figure 1) and executing along successive diagonals. Diag(x) represents the values in x's diagonal, shown by the dashed-boxes. The last diagonal is translated to the a trajectory by sign.

2.3 Manual clustering

One of the authors [Neville] has long experience in secretory activation, and performed an ad hoc, semi-manual clutering of the genes, using tools available in GeneSpring (Silicon Genetics, www.sigenetics.com) and her extensive knowledge of the biology of secretory activation. The ad hoc method required direct user interaction and took many hours to complete, and relied on a variety of unsupported assumptions. The procedure was as follows. Beginning with the same list of genes that varied significantly over at least one pair of time points, each pair of adjacent time points was tested for differences using the Mann-Whitney U test (which is equivalent to the Kruskal-Wallis test when there are only two conditions) with a critical level of P< 0.05. These were assigned to the I or D trajectory using the fold change filter with the fold difference set at 1.1. All genes that did not fit this criterion were initially assigned to the F trajectory. These cutoffs were set to coincide with intuition for a subset of the important genes which we examined manually. The one interval sets were combined into 81 preliminary classes reflecting the patterns of expression over the four intervals in the dataset.

Classes containing two or more flat sets in a row (e.g. DDFF, IFFD, IFFF, FFFF) were further examined to determine whether there was a statistically significant change over two or more consecutive intervals. For each FF class an initial sort was made into genes that changed or remained flat over two intervals using the Mann-Whitney test as describe above. For FFF or FFFF classes the genes were initially examined in sets of FF classes. Those that showed no significant change were examined by eye over 4 or 5 time points. A significant change was seen in about 200 genes in classes containing the FF, FFF and FFFF patterns, about half the genes in FF and FFF trajectories and all the genes in the FFFF trajectories as predicted.

As with the automated method, the hardest problem is to apportion the changes in these genes over the two, three, or four intervals over which a significant change was noted. To do this each of the intervening adjacent pairs was tested using a Welsh t-test with a critical value of 0.20. Again, this particular value was selected because it agreed with the expert's intuitions about the assignments; also note that the Normality assumptions underlying this test are not valid for this data. Adjacent pairs which were different under this test we assigned to either I or D, all others were left as F.

2.4 Other clustering techniques

For comparison to more established techniques, hierarchical and K-mean clustering were used to cluster our time series data. In hierarchical clustering (Eisen MB et al. 1998), two types of similarity metric were calculated; Euclidean distance and jackknife correlation (Heyer LJ, et al. 1999). A complete-linkage hierarchical clustering was used for the purpose of computing a dendrogram that represent all elements into a single tree. We used Matlab's “cluster” function to draw a horizontal line on the dendrogram tree, and produced the user defined number of clusters. We divided the hierarchical tree into 20 and 9 clusters, to obtain results comparable to the trajectory method (see results). In addition, K means clustering (Tavazole, S. et al, 1999) is designed to partition the data into K groups by minimizing the within-group sum-of-squares. We used the K means algorithm in GeneSpring with Pearson correlation to partition the genes into 20 and 9 clusters.

3 Results

3.1 Significantly varying genes and their trajectory clusters

The preprocessing and Kruskal-Wallis test resulted in 1358 genes with at least one significant difference (with FDR=0.015, so approximately 20 of these are likely false positives). There are 4 intervals between the points and therefore the potential to generate 3⁴=81 trajectories (actually 80, since FFFF cannot be occupied with this method). Figure 3 shows the 72 populated clusters, identifying the trajectory and the number of genes in the cluster; 20 of these were occupied by 20 or more genes. These 20 large clusters contained 975 (or 72%) of the total genes. We therefore used 20 as the target for K means and hierarchical clustering.

Figure 3.

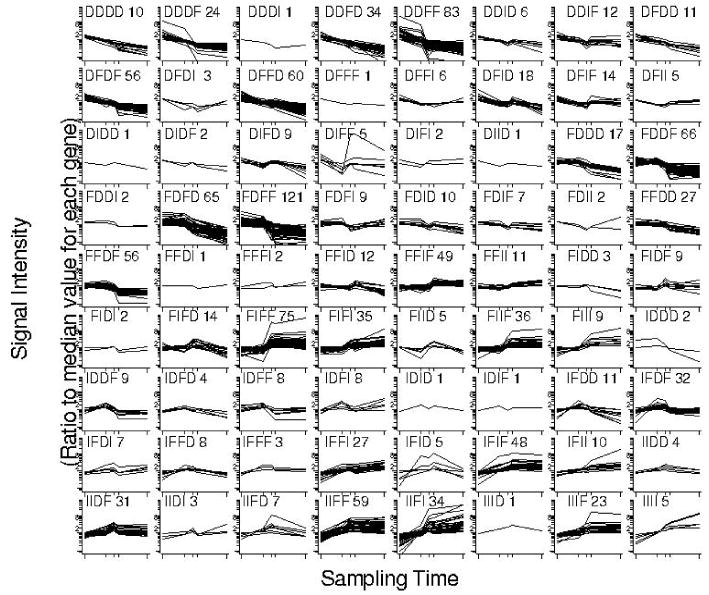
Clusters produced by automatic trajectory clustering for secretory activation in the mammary gland. Four replicates at each of five time points, Pregnancy days 12 and 17 and lactation days 1, 2 and 9, are represenedt in each plot. Intensities were normalized to the median for each gene and plotted on a log scale.

3.2 Comparison with manual trajectory clustering

Manual clustering resulted in 73 clusters which in general overlapped the results of the automated algorithm, particularly in the twenty large clusters. Table 1 shows the degree of overlap between each of the clustering methods and the manual method. In mouse mammary gland secretory activation studies, the two middle intervals (P17-Lac1-Lac2) showed the greatest number of significant changes, we therefore also combined clusters that had the same trajectories for these two central transitions, creating 9 clusters. In this latter analysis 77.4% of the genes mapped to the same cluster in the automatic and manual methods (Table 1). Furthermore, inspection suggested that genes that differed between the automatic and manual methods diverged only slightly in assigned trajectories, and then only when the difference between two time points was small relative to the variance of the time points.

Table 1. Clustering quality measures (see text). TC is trajectory clustering, KM is K-means and JK is hierarchical jackknife.

Number of interval	Number of manual Cluster	Other cluster	Number of other Cluster	Percent of other Cluster to manual Cluster	Discrimination index
4	73	TC	72	55.1	0.80
4	20	TC	20	61.0	0.75
2	9	TC	9	77.4	0.56
4	20	KM	20	41.0	0.78
2	9	KM	9	28.6	0.59
4	20	JK	20	39.4	0.59
2	9	JK	9	30.0	0.34
Using mean difference values
4	20	KM	20	34.6	0.47
2	9	KM	9	32.9	0.42
4	20	JK	20	26.9	0.57
2	9	JK	9	43.9	0.48

3.3 Comparison with other clustering methods

The same mapping approach was used to compare 20 and 9 clusters from K-Means and hierarchical jackknife methods to the manual clusterings. We matched each K-means and hierarchical cluster to the manual cluster that had the most genes in common, without allowing multiple matches. As seen in Table 1, 41% and 28.6% of the genes in the 20 and 9 K-Means clusters mapped on to the most closely corresponding manual cluster. Similarly, 39.4% and 30% of the 20 and 9 hierarchical Jackknife clusters were mapped on to the manual clusters. To ensure a fair comparison, we performed another set of K-Means and hierarchical Jackknife clusters using differences between adjacent time points rather than the raw values. The results show that 34.6% and 32.9% of 20 and 9 K-Means clusters, and 26.9% and 43.9% of hierarchical Jackknife clusters mapped on to the closest manual cluster.

3.4 Separation of functional groups by trajectory clustering

Although trajectory clustering produces a statistically well-founded grouping that is much more similar to the ad hoc expert grouping than traditional methods, it is unclear how well the manual clustering represents biological reality. To determine whether trajectory clustering could separate and/or identify biologically relevant genes we examined the genes associated with six functional classes known to be important in secretory activation (milk proteins, energy metabolism, fatty acid synthesis, cholesterol synthesis, adipocyte-specific and fatty acid degradation), and measured the purity of each cluster with respect to these classes. A discrimination index was calculated as follows. For each cluster, consider each pair of functional groups A and B. If the cluster contains only genes of one or the other functional group, the cluster gets a discrimination score of 1. If the cluster contains both groups, it gets a score of 1 - {(G_A + G_B) / (Tot_A + Tot_B)}, where G_A and G_B are the number of genes of each functional type in the cluster and Tot_A and Tot_B are the total number of genes in that functional group. The discrimination score for the cluster is the mean score over all pairs of functions. Table 1 shows the discrimination scores. Both automatic and manual trajectory clustering gave a discrimination index of 0.80 using the full number of clusters derived here. All other methods gave lower discrimination scores, although the K-means method for 20 clusters gave an index of 0.78 which is quite close.

We also examined each of the genes with known function specifically in the trajectory clustering. With one exception milk genes clustered into related groups all beginning with I, indicating that they all increase significantly at the end of pregnancy. All continued to increase in subsequent intervals falling into 4 related groups with slightly different patterns of expression. The one gene that does not increase during pregnancy (clustered to FFIF 75) is PTHrP, a gene encoding a protein hormone involved in calcium regulation (Neville et al, 2002), which could be deleterious in the pregnant animal and may, therefore be differentially regulated. The genes of energy metabolism, with two exceptions, fell into downward going clusters, suggesting a relative fall in ATP generation in this tissue, which must devote most of its energy to synthetic reactions and transport. Of greatest interest of the genes for fatty acid and cholesterol synthesis; both groups cluster predominantly to FIFF 75 and are, therefore, turned off during pregnancy, turning on immediately after birth of the pups, a point at which our histological studies show that secretion is activated (McManaman, J. and Neville, M.C., unpublished). These genes are likely, therefore, to be coordinately regulated and indeed many in both classes are up-regulated by the transcription factor SREBP-1 (Horton, et al. 2002). Interestingly SREBP-1 itself falls into the cluster FFIF 75. Genes that mediate fatty acid degradation, in general by the β-oxidation pathway were distributed among four clusters showing different butrelated patterns of decrease. The mammary gland contains several different tissue compartments whose proportion changes with secretory development. We know that the milk protein genes reflect the epithelial compartment and assume that the changes in the metabolic pathways illustrated also represent this compartment. In order to evaluate changes in another tissue compartment, the adipose compartment which is quite prominent in the mammary gland, we examined the expression pattern of 5 adipose specific genes. These genes cluster into 5 distinct clusters, which have in common a D in first interval, the interval that reflects late pregnancy. We know from other studies (McManaman and Neville, unpublished) that a the relative proportion of adipose tissue declines steeply during pregnancy, with much small changes during lactation as reflected in the variation in the last three time intervals. We also examined two categories of genes known to decrease during secretory activation, adipocyte specific genes and genes that are involved in fatty acid degradation. Both segregated into predominantly down-going clusters.

4 Discussion

Trajectory clustering is a non-parametric clustering method using only the direction of change between subsequent time points to group genes in time course study. Clustering using various ad hoc schemes to conform as closely as possible to expert intuition gave quite similar results to trajectory clustering, and rather different than the other methods. More importantly, trajectory clustering also showed the ability to discriminate among genes in relevant functional categories better than the alternative methods.

Trajectory clustering has a natural interpretation, unlike the other methods studied. In this case, where each interval studied represents a well-characterized and different process, linking gene change directions to each of these intervals facilitates interpretation. For example, two important synthetic processes, milk protein synthesis, and lipid and sterol synthesis show distinct temporal activation. Thus the synthesis of all but one of the proteins we have classified as milk proteins are turned on in late pregnancy; many of these (see group IFIF 48) do not change between late pregnancy and the first day after birth, increasing sharply on the second day of lactation. Many of these molecules including β-casein, and whey acidic protein are known to be regulated by stat5, a mediator of prolactin signaling, whose mRNA and phosphorylation change little over the period of parturition (Rosen, et al. 1999). On the other hand the genes that regulate lipid synthesis are known to be regulated by the transcription factor, SREBP-1. A large proportion of these genes does not increase during pregnancy but are activated on the first day of lactation. SREBP-1 shows a similar pattern of activation, suggesting that its activation and up-regulation are needed to turn on lipid and cholesterol synthesis. A number of other transcription factors are found in these two clusters, JunD1, Pou 11 and TCFL4 (MCX) are located in IFIF whereas NFAT and Sox13 are found in FIFF. These genes are candidates for further investigation.

The spread of some classes of functionally related genes across similar clusters (e.g. FIFF and FIIF) suggests that collapsing some distinctions may be of biological value. Certainly as the number of time points increases, the number of trajectories increases exponentially, and therefore some cluster combining is probably warranted. Since each trajectory has a well defined relationship to all the others, we expect in future work to be able to identify a well-founded method for combining trajectory clusters as defined here.