The dual-basin landscape in GFP folding

Abstract

Recent experimental studies suggest that the mature GFP has an unconventional landscape composed of an early folding event with a typical funneled landscape, followed by a very slow search and rearrangement step into the locked, active chromophore-containing structure. As we have shown previously, the substantial difference in time scales is what generates the observed hysteresis in thermodynamic folding. The interconversion between locked and the soft folding structures at intermediate denaturant concentrations is so slow that it is not observed under the typical experimental observation time. Simulations of a coarse-grained model were used to describe the fast folding event as well as identify native-like intermediates on energy landscapes enroute to the fluorescent native fold. Interestingly, these simulations reveal structural features of the slow dynamic transition to chromophore activation. Experimental evidence presented here shows that the trapped, native-like intermediate has structural heterogeneity in residues previously linked to chromophore formation. We propose that the final step of GFP folding is a “locking” mechanism leading to chromophore formation and high stability. The combination of previous experimental work and current simulation work is explained in the context of a dual-basin folding mechanism described above.

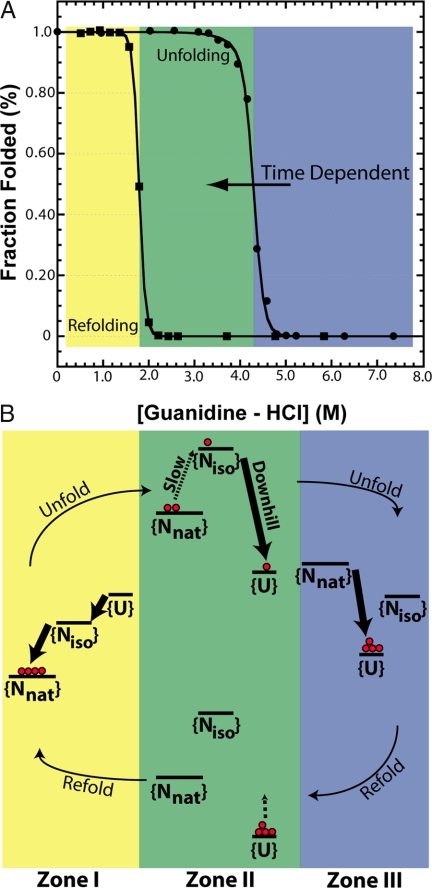
GFP has become a common reagent in biochemistry laboratories because of its ability to fold and form a visually fluorescent chromophore through autocatalytic cyclization and dehydration/oxidation reactions (1). Recent studies on the folding of GFP have shown multiple kinetic phases (2, 3) and high barriers to folding that lead to a slow “drift” of the unfolding equilibrium transition curve (4). In fact, a “superfolder” variant of GFP (sfGFP) (5) has an apparent hysteresis in equilibrium folding that is observed in the experiment (6, 7) shown in Fig. 1A. Considering the apparent nonthermodynamic behavior observed in experiment, can we use simulation to probe the free-energy landscape and explain these results?

Fig. 1.

The observed experimental hysteresis and proposed mechanism for GFP is shown. (A) Experimental equilibrium unfolding and refolding transitions of sfGFP induced by Gdn-HCl in 12.5 mM Tris·HCl (pH 6.8) at 25°C after 96 h. The folded state was measured by chromophore fluorescence excited at 450 nm and observed at 508 nm (slit-width 3 nm). Filled circles show the unfolding transition, and filled squares show the refolding transition. Lines are fits to a two-state model for refolding and a three-state model for unfolding. The unfolding and refolding transitions do not coincide and show hysteresis. The unfolding curve also exhibits time dependence and collapses toward the refolding transition over months (data not shown). Different zones of transition curves are colored yellow (I), green (II), and blue (III). (B) Representative transition rates and stabilities of the unfolded {U}, collapsed {N_iso} and native {N_nat} ensembles of GFP in our model are depicted as a qualitative schematic. In Zone I, refolding occurs via the {U} → {N_iso} → {N_nat} route. In Zone III, the protein unfolds downhill from {N_nat} → {U}. During unfolding in Zone II, the slow {N_nat} ⇔ {N_iso} exchange becomes rate limiting, and the exact stability of {N_nat} with respect to {U} does not govern the transition. Rare fluctuations crack the GFP barrel on time scales much longer than the typical experimental equilibration time, allowing the protein to reach the {N_iso} state and then proceed to the unfolded state via downhill unfolding. The unfolding transition slowly moves toward lower denaturant concentrations as the experimental observation time gets longer because of this mechanism. Thus, the unfolding transition approaches the refolding transition observed over time with the rate limited by rare fluctuations. During refolding, the {N_iso} ⇔ {U} transition is equilibrated, and because {U} is more stable than {N_iso}, proteins that start in the unfolded state stay unfolded.

Proteins whose folding has been optimized by evolution have a sufficiently smooth, funneled energy landscape, with an ensemble of folding routes directed toward the native structural basin (8–10). Coarse-grained models with potentials designed to bias the protein toward the native basin, structure-based (Gō) models (11), have been able to capture the main structural features of the folding mechanism observed in experiments. Because these models are energetically unfrustrated, the agreement to experiments demonstrate that typical well folding proteins have such small amounts of residual energetic frustration that the observed structural heterogeneity observed in folding is mostly determined by geometrical properties of the native structure.

Although it is a good folder, GFP has a folding landscape that differs from most proteins because of a structural rearrangement needed to produce an active chromophore. GFP with an active chromophore exhibits an apparent hysteresis, where folding and unfolding occur on the order of minutes to hours, whereas the hysteresis zone collapses on the order of months (6). If the active chromophore is mutated out, the protein exhibits typical fully reversible thermodynamics. Here, we propose that folding and unfolding of GFP occur in a typical folding funnel, with a proposed additional basin. Interconversion between basins via a local high barrier transition associated with the chromophore occurs, leading to the hysteresis observed in experimental folding.

The current work uses a combination of experimental and simulation techniques to probe the free-energy landscape of GFP. The simulation utilizes a topology-based model, using a recent method to improve sampling on a large, high contact-order protein (12). Simulation results focus on the U-to-N transition and are consistent with previous experimental work on the folding of GFP, picking up the frustration, intermediates, and high barriers previously observed (2–4, 13–16). Previous experimental results are presented with the simulations to explain some consequences of a dual basin in folding, and how it can lead to the nonthermodynamic behavior observed in experiment. The dual basins in the funnel lead to a barrier controlled, fast-folding step and a subsequent prefactor-controlled slow search step to lock the barrel for subsequent chromophore isomerization.

Results

Structure of GFP.

The structure of the GFP family of proteins exists as an 11-stranded β-barrel, with an unusual kinked α-helix running through the center, which contains a unique backbone rearrangement to make the fluorescent chromophore. The helix makes contacts with all of the strands of the barrel and makes contacts over the entire sequence, causing extremely high contact order. The helix contacts are highlighted to guide the eye on a contact map in supporting information (SI) Fig. S1 Bottom Right. Protein folding has been linked to the formation of the chromophore, because the protein is in its folded form (17) before kinking of the helix and chromophore formation (18). Our coarse-grained model captures some structural aspects of the chromophore that are important in describing folding through a noncanonical kink in the central α-helix. Recent work on GFP-family chromophore isomerization using crystallography and molecular dynamics has revealed chromophore isomerization in fluorescent proteins (19–21) and major differences in the interior hydrogen-bond networks between chromophore isomerizations (22–24).

Kinetic Simulations and Intermediates.

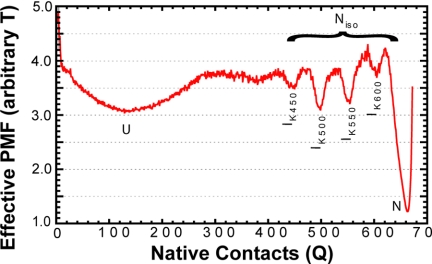
Kinetic analyses (see Materials and Methods) showed two-state folding observed in 70%, on-pathway intermediates in 26%, and several misfolded (off-pathway) species (4%) in our analysis of 250 folding trajectories. A graph of the probability mass function (PMF) of observing the protein at a given number of native contacts (Q) during all trajectories versus Q is shown in Fig. 2. Local minima at particular Q values indicate unfolded, native, and intermediate species. The unfolded state corresponds to low values of Q, whereas the folded state corresponds to a value Q≈672 (total native contacts) as indicated. We consider an intermediate to be populated if the protein samples a specific Q for 50 time steps. For simplicity of presentation, we focus on trajectories that sample two-state or intermediate states during folding. Trajectories that misfold are discussed in the next section.

Fig. 2.

The probability mass function (PMF) of populating native contacts Q during all 250 kinetic-type trajectories is shown as a red line. Standard deviation (n = 5) is within the red line. Native and unfolded states are denoted as N and U, respectively. Kinetic intermediate states are denoted as I_Kx, where x corresponds to the number of contacts as discussed in Results. Transitions between kinetic intermediates occur between N_iso state and the N_nat state together with isomerization are responsible for the final and slow step of chromophore activation.

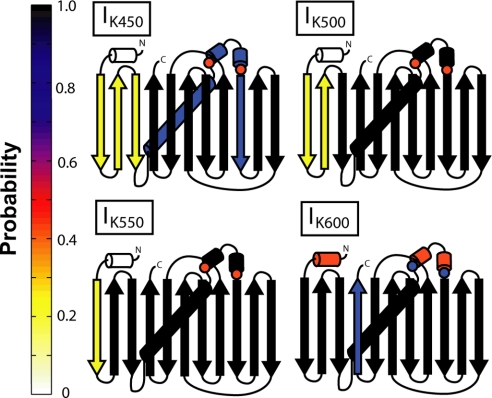
We observe two multiple routes in folding. Folding always progresses toward the native state in the routes containing intermediates. Structural information on the intermediates observed during each route is given in Fig. 3. In the first route, there are two major intermediates, I_K500 and I_K550, which are seen in 15.0% and 13.2% of trajectories, respectively, as well as a minor intermediate, I_K450 in 5.2% of trajectories. I_K450, I_K500, and I_K550 are unfolded at their N termini, missing three, two, and one β-strand, respectively, similar to results observed in single-molecule pulling experiments (13, 14) and simulation (16). In addition, I_K450 is also destabilized in the contacts between the helix and the entire barrel. Intermediate I_K600 is observed on the minor route and is missing a C-terminal strand from the barrel, similar to observations in self-organized polymer simulations (25).

Fig. 3.

Splay diagrams of kinetic intermediates. The probability of a given secondary structure being made is shown as a color on the color map on the left. Kinetic intermediates I_K450, I_K500, and I_K550 all are missing N-terminal β-strands. Kinetic intermediate I_K600 is destabilized in the central α-helix and C-terminal β-strand. Contacts related to prolines discussed are marked with circles colored with the probability of formation. Contact maps used to create this figure are presented in Fig. S1.

Experimental kinetic folding results have multiple intermediates and routes (2, 3, 6). Our simulation work supports previous experimental work as well as single-molecule pulling simulation with evidence of bifurcations in the free-energy landscape (16). Furthermore, these pathways are identified by unfolding from the C versus the N terminus, with unfolding from the C terminus the minor route, occurring in 28% of pulling simulation. Structural analysis of these intermediates shows structured areas of the protein surrounding islands of unformed contacts, denoted in figures by red circles (Fig. 3). These contacts map onto the structure near the cis-prolyl bond M88-P89 (see Discussion).

Misfolding Is Observed in Gō-Model Kinetic Simulation.

As opposed to the common perception, native structure-based models can also capture misfolding events. In this study, misfolded structures are observed 4% of the time in kinetic simulations and can be grouped into two categories (Fig. S2.). The first category (MF₇₁ in Fig. S2.) has the central α-helix unable to pack into the formed barrel, and the second category (MF₁₉₉ in Fig. S2.) is missing the first two β-strands, similar to I_K450, except the N terminus is “knotted” between strands, creating entropic traps. Thus, energetically smooth Gō models can capture topological frustration that may lead to off-pathway misfolding, as observed in this study.

Thermodynamic Simulations and Intermediates.

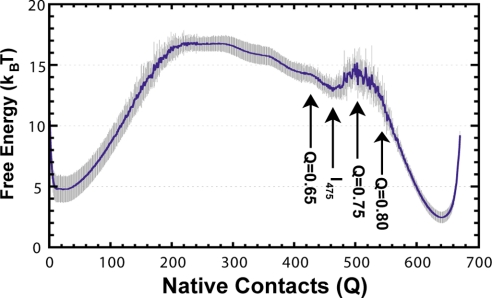
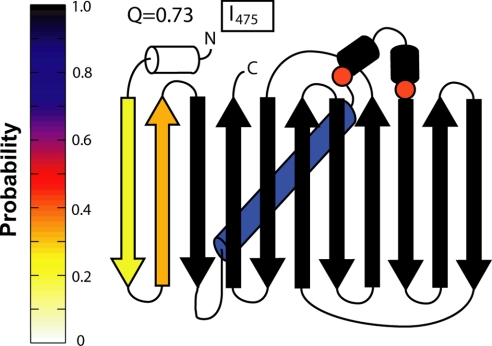
To improve thermodynamic sampling and probe equilibrium intermediates for a large, high contact-order protein, we use a method that weights the potential energy to lower the free-energy barrier during simulation as described (12). After simulation, the results are reweighted, and multiple trajectories are analyzed independently to obtain the standard deviation of calculated parameters (n = 10). The free energy as a function of Q, as determined by the weighted-histogram analysis method (WHAM) is presented in Fig. 4C. Consistent with experimental studies, our results predict a large and broad thermodynamic barrier. One clear thermodynamic intermediate (I₄₇₅) is observed.

Fig. 4.

The reweighted free energy versus the number of native contacts (Q) from thermodynamic simulations is shown as a blue line at T/T_f = 0.99. Light gray represents standard deviation when split into 10 batches of results (n = 10). The single intermediate sampled in equilibrium simulations is marked I₄₇₅, as discussed in Results. Areas of the free energy landscape probed for structural details are shown with arrows.

Intermediate I₄₇₅ has missing β-strands on the N-terminal end (Fig. 5), and is similar to the kinetic intermediate I_K500. Intermediate I₄₇₅, like I_K500, also shows contacts around residue 89 with a low probability of being made (Fig. 5, circles). The simulation intermediate is missing contacts in strands 1–3, and contacts near the prolines are unformed, whereas the residues not making contacts sample an extended strand conformation. Even in the final transition state (Q = 0.75), one strand is missing, and the proline residues have not made all contacts. In the native basin (Q = 0.80), the last strand has folded, and the proline residues indicated are making contacts (Fig. S3). These simulation results support the presence of an intermediate in equilibrium folding, with unfolded areas in the structure that correspond to areas implicated in hysteresis. Furthermore, the ability to observe an intermediate with frustration in the prolines (see below) is remarkable, even with a C_α model that does not explicitly model the chromophore and proline isomerization.

Fig. 5.

Splay diagram of the thermodynamic intermediate I₄₇₅. The probability of a given secondary structure being made is shown as a color on the color map on the left. Thermodynamic intermediate I₄₇₅ is missing two N-terminal β-strands and is similar to I_K500. Proline contacts discussed (circles), do not form until after the transition state (Fig. S3). Contact maps used to create this figure are presented in Fig. S4.

Nonthermodynamic Behavior in Experiment.

The hysteresis observed in the folding of GFP (Fig. 1A) is evidence of a kinetic process controlling unfolding during a “thermodynamic” experiment. Although the zones of reversible folding and unfolding ([Gdn-HCl] < 1.5 M),([Gdn-HCl] > 5.0 M) fold and unfold on the order of minutes to hours, the hysteretic unfolding process unfolds on the order of months (5). A chevron analysis shows transition rates in the hysteresis zone are magnitudes slower than those predicted by the folding and unfolding arms. In other words, hysteretic processes are no longer dominated by folding but by local fluctuations involving the chromophore (6). Unfolding kinetics in Zone III (Fig. 1) as a function of isomerization time show a hidden phase, consistent with isomerization (6). The dependence of hysteresis on the presence of the chromophore is confirmed with mutagenesis, either by mutating a catalytic residue for chromophore formation (R96A) or removing structural requirements for chromophore formation (Y74M/M88Y). Removal of the chromophore shows thermodynamic results similar to the refolding transition in sfGFP (6).

A slow conversion between two states with differing stabilities would lead to this result. From a folding funnel perspective, this is evidence of two native-like basins with differing stability. In the hysteresis zone, unfolding is dominated by local fluctuations controlling a transition between native {N_nat} and native-like {N_iso} states over months. Refolding is dominated by the {N_iso} to unfolded {U} transition and entails a global, concerted process. We propose that the nonthermodynamic behavior observed in the thermodynamic folding of GFP can be explained with a dual-basin folding funnel, with native basin {N_nat}, and native-like basin {N_iso} (see Discussion).

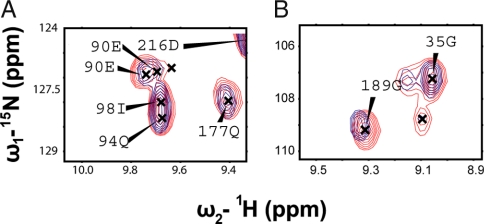
Previous work linked two prolines to the chromophore as a structural requirement for proper chromophore formation because mutation abolished both chromophore formation and hysteresis (6). Because we can trap the {N_iso} form, we perform experiments on a hysteretically trapped species of GFP using a residue-level probe, NMR spectroscopy. Fig. 6A shows a ¹H-¹⁵N HSQC for sfGFP (red) overlaid with the trapped species of sfGFP (blue) discussed previously (6). The chemical shift dispersion observed in the two spectra is nearly identical, evidence of a native-like structure (Fig. S5); however, three peaks show subtle differences, as shown in Fig. 6 B and C. The third peak, which is not assigned, lies at chemical shift ¹H 7.99 ppm and ¹⁵N 125.5 ppm. The assigned, shifted residues lie near the prolines, which are linked to the chromophore. Once again, although proline isomerization is not included in a simple Gō model, our simulations seem to pick structural frustration in these areas (circles in Figs. 3 and 5). This area may be prone to geometrical frustration because of the complex topology of GFP, which leads to these two prolines folding in disfavored conformation (26).

Fig. 6.

¹H-¹⁵N HSQC spectra of native sfGFP (red) overlaid with trapped sfGFP (blue). The overall dispersion is nearly identical, except for three peaks: 90E, 189G, and an unassigned one at 7.99, 124.5 (Fig. S5). (A) A close-up of 90E shows nearby peaks with similar shifts, except for 90E, which shifts. (B) A close-up of 189G, similar to 90E. This shows that the trapped species is nearly structurally identical to native sfGFP, except in the area near these peaks, which are near previously discussed proline residues.

Discussion

A Dual-Basin Landscape Explains Hysteresis.

Unlike usual proteins, GFP with an active chromophore folds in a dual-basin energy landscape. Folding occurs by a “typical” first step in a funnel-like landscape (10), followed by a slow search through isomerization states and structural fluctuations toward the locked active basin {N_nat}. The first transition toward the soft basin {N_iso} is investigated by using a coarse-grained model, which is sufficient to extract the full ensemble of states involved in this process (11). This initial folding structure is flexible and fluctuates easily among several local minima. The flexibility of {N_iso} is apparent from the different native-like intermediates observed during simulations. These intermediate-like states proceed through the slow transition into the locked, native basin of GFP {N_nat}.

GFP must form a β-barrel then close and lock the barrel around the central chromophore containing α-helix to achieve the proper native fold. Although the chromophore is able to isomerize unhindered in solution without the structural restraints of the surrounding barrel, isomerization is limited in the folded state unless there is a hula twist (22, 23, 27). This conformational transition is responsible for the slow search toward the second basin {N_iso}. Interestingly, destabilization in nearby barrel strands is observed in backbone dynamics studies (4, 20) and may be related to chromophore isomerization, consistent with our simulation results and recent experimental results (28). Finally, although both cis and trans forms appear to be compatible within the folded barrel, the hydrogen-bonded network is altered between these states (24), leading to two folded forms of GFP with different stabilities.

Under strong refolding conditions (Fig. 1, Zone I), the bias toward the native state is sufficient to drive the full folding event. Under these highly native conditions, there is enough stabilizing energy to lock the protein into the native, fluorescent state, similar to results incorporating the C terminus during ClpXP degradation (29). Similarly, in strongly unfolding conditions (Fig. 1, Zone III), the high stability of the locked, native form is overcome, and the direct {N_nat} → {U} route is observed.

The hysteresis zone (Fig. 1, Zone II), must take into account both the stability of the different basins and the difference in time scales of the rates in the first and second steps. Hysteresis is a result of the first transition ({N_nat} ⇔ {N_iso}) being much slower than the second one ({N_iso} ⇔ {U}) during unfolding and folding. Under denaturing conditions in Zone II (Fig. 1), {N_nat} and {N_iso} are less stable than {U}, but {N_nat} is kinetically stable (Fig. 1C, Zone II). If the protein is in the {N_nat} state, it will stay in that state until unlikely, random fluctuations crack the surface and move it toward {N_iso}. Once this unlikely event occurs, unfolding is downhill toward {U}. These random fluctuations happen rarely because the structure of GFP limits conformational changes, leading to the slow drift of the unfolding transition as long as experimental observation times are shorter than the rare transitions.

The hysteresis observed at “equilibrium” is a consequence of the disparate time scales. Rare fluctuations occur between {N_nat} and {N_iso} on an extremely slow time scale (slower than experiments and folding), but once {N_iso} is populated, the transition to {U} is on a much faster time scale. However, during refolding, {U} will never populate {N_iso} because of the change in stability. The reason hysteresis is observed in experiment, is because the 96-hour “equilibration” time lies between the folding time scale of minutes and the rare fluctuation time scale of months. This leads to the result that the refolding transition is in true equilibrium, but the unfolding transition is limited by a very slow kinetic process (See Fig. 1).

Experiment and Theory Support the Dual-Basin Energy Landscape.

Simulation results show that the {N_iso} basin is flexible and composed of multiple conformations, many of which have a partially folded β-barrel around the central α-helix. Kinetic simulations show native-like intermediates, many of which have difficulty getting the last strand into the barrel (Fig. 3). Also, residues in the lid of the barrel (circles on Figs. 3 and 5) fail to form their native contacts until GFP is almost fully folded. Similarly, in thermodynamic simulations, the last step is the inclusion of the N-terminal β-strand into the fold to complete the β-barrel. In fact, the final transition state is still missing a strand; only in the final step does the barrel fully form, consistent with other simulations using a self-organized polymer model (25). These native-like intermediates observed in the simulation of GFP folding suggest that they are possible states involved en route to the active form. Jumps between these native-like intermediates combined with isomerization are responsible for the slow search in the approach to the final locking and activating transition.

During refolding, the barrel needs to cross a threshold of stability needed to fold, lock, and hold the isomerization of the chromophore and prolines in their native {N_nat} states. Refolding thus occurs in a concerted fashion under highly stabilizing conditions (Fig. 1., Zone I). Presumably, this locking during refolding entails simultaneously incorporating the final strand (simulation data) and capturing and holding the proper chromophore and proline isomerizations under highly refolding conditions (experimental data). Interestingly, the final strand appears to be able to form and hold an “improperly” isomerized chromophore under transition conditions, trapping the {N_iso} form, as observed in 1D ¹H NMR (6).

We observed subtle structural differences between {N_iso} and {N_nat} in previous NMR experiments (6). In the present study, we expand upon these results with 2D ¹H-¹⁵N HSQC analysis to pinpoint areas of structural heterogeneity between {N_nat} and {N_iso} (Fig. 6). The changes we see in the ¹H-¹⁵N HSQC spectrum map to residues adjacent to the prolines previously linked to chromophore formation (6). Although our model does not include proline isomerization, on a structural level, simulation and experiment may be compared (11, 30–33). The results from our simulations show late folding at the residues that correspond to these prolines and their neighbors (circles, Figs. 3 and 5 and Fig. S3).

Conclusions

We explore the hysteresis of GFP with the aid of a coarse-grained structure-based model. Our simulations suggest a mechanism that explains the hysteresis in the context of a dual-basin landscape consisting of an active, native form {N_nat} and a form with improper isomerizations {N_iso}. GFP exhibits a fast folding step in a usual funnel landscape, followed by a slow search step toward the active chromophore basin. It is throughout this slow search where structural locking (isomerization) and chromophore activation takes place. During this second step, folding is no longer limited by a conventional folding mechanism but the required slow search. Because hysteresis is abolished in the absence of the formed chromophore (6), we propose that chromophore isomerization is key to the process that limits the unfolding kinetics in the {N_nat} → {N_iso} transition and that hysteresis is a consequence of the barrel needing to form and lock down and properly position the chromophore.

Materials and Methods

The Model.

GFP was modeled by using only the C_α atoms as determined from the crystal structure 1EMA (34). The chromophore residue was broken into three C_α residues and was not modeled in a cyclized state for simulation, because the focus of this study was global folding and not chromophore formation. The energy function, a Gō-type model, is based only on the native structure and is considered energetically unfrustrated (35). The energy potential has been described in detail (31, 36).

Simulations.

Molecular dynamics (MD) simulations are used to obtain folding-unfolding transitions. For this study, all simulations were run using an unmodified sander_classic in the AMBER6 package (37), except during thermodynamic sampling runs.

Kinetic Runs.

Kinetics were initiated by unfolding the native structure with random initial velocities at 2.4 T_F for 0.5–1.5 ns, and then cooling at 1.2 T_F for 1 ns. Folding was initiated by running simulations for 100 ns at 0.83 T_F with the final velocities from the 1.2-T_F step. Statistics were attained by simulating 250 trajectories and analyzing them in five parts. Folding temperature T_F was 418 K and determined by using enhanced sampling.

Thermodynamic Sampling.

Thermodynamic simulations used a modified potential to increase sampling by reweighting the force using the density of states, as described in detail by Gosavi et al. (12). The parameters determined for the well are E_depth = 13.8, E_mid = 195, and σ = 92. Trajectories were simulated for 1.4 μs at temperatures between 0.998 T_F and 1.005 T_F. The density of states was reweighted from the modified potential, and the WHAM algorithm (38) was used to determine folding temperature and free energy from all simulations. Ten trajectories were analyzed by using WHAM to determine statistics of calculated parameters.

Experimental Equilibrium Folding Transition.

Equilibrium transitions were prepared as described (6). Chromophore fluorescence spectra were obtained by using the Fluoromax-2 spectrofluorimeter (Spex Edison) with an excitation wavelength of 450 nm and the emission measured at 508 nm unless otherwise noted. Equilibrium unfolding experiments were run with protein samples (0.1 mg/ml in 12.5 mM Tris·HCl at pH 6.8 and varying Gdn-HCl concentrations ranging from 0 to 7.5 M, at a temperature of 22°C. Experiments were equilibrated for 96 h. Refolding curves were run by equilibrating sfGFP in 7.6 M Gdn-HCl and subsequently refolded by dilution to varying final Gdn-HCl concentrations and equilibrated for 96 h. The fraction folded by chromophore fluorescence was monitored at 508 nm, after excitation at 450 nm (3-nm slit width).

NMR of Trapped Species.

The trapped sfGFP species was prepared as described (6). All NMR experiments were performed at 315 K on a Bruker Avance800 equipped with a triple-resonance triple-axis gradient probe. Final conditions for each sample were 30 mM phosphate buffer (pH 6.8), and 100 mM NaCl, 95% H₂O/5% ²H₂O. Data were processed by using NMRPipe (39). Two-dimensional ¹H-¹⁵N HSQC spectra were acquired for sfGFP and trapped sfGFP. Spectra were acquired with a 17-ppm spectral width using a 2D HSQC pulse program (40). Assignments for sfGFP were determined by using previous assignments for GFPuv (41) and several 3D experiments including HNCA (42), HNCACB (43), TROSY HNCA (44, 45), TROSY HNCACB (44, 45), and CBCACONH (43).

Note Added in Proof.

Recent work by Orte et al. identifies parallel routes of unfolding for a GFP variant consistent with our work.