Ignoring Dependency between Linking Variables and Its Impact on the Outcome of Probabilistic Record Linkage Studies

Abstract

Objectives

This study sought to examine the differences between ignoring (naïve) and incorporating dependency (nonnaïve) among linkage variables on the outcome of a probabilistic record linkage study.

Design and Measurements

We used the outcomes of a previously developed probabilistic linkage procedure for different registries in perinatal care assuming independence among linkage variables. We estimated the impact of ignoring dependency by re-estimating the linkage weights after constructing a variable that combines the outcomes of the comparison of 2 correlated linking variables. The results of the original naïve and the new nonnaïve strategy were systematically compared for 3 scenarios: the empirical dataset using 9 variables, the empirical dataset using 5 variables, and a simulated dataset using 5 variables.

Results

The linking weight for agreement on 2 correlated variables among nonmatches was estimated considerably higher in the naïve strategy than in the nonnaïve strategy (16.87 vs. 13.55). Therefore, ignoring dependency overestimates the amount of identifying information if both correlated variables agree. The impact on the number of pairs that was classified differently with both approaches was modest in the situation in which there were many different linking variables but grew substantially with fewer variables. The simulation study confirmed the results of the empirical study and suggests that the number of misclassifications can increase substantially by ignoring dependency under less favorable linking conditions.

Conclusion

Dependency often exists between linking variables and has the potential to bias the outcome of a linkage study. The nonnaïve approach is a straightforward method for creating linking weights that accommodate dependency. The impact on the number of misclassifications depends on the quality and number of linking variables relative to the number of correlated linking variables.

Introduction

Medical record linkage techniques are frequently applied when data from different sources must be combined to answer a clinical or public health question. ^1-7 The aim of record linkage is to combine records belonging to the same entity (same patient, same intervention, mother–child) stored in separate databases. Routine health care databases either lack a unique, identifying key or it cannot be used by researchers because of privacy concerns. Medical record linkage (MRL) uses a set of partially identifying variables to detect records belonging to the same individual (called matches). ⁸ The choice of linkage variables is often limited because linking variables must be present in both registries and ideally have a high discriminating power and are error-free. ^8-10 Frequently used variables include date of birth, zip code, gender, and (if present) first and family name. In deterministic MRL, records are considered to belong to the same individual if a predefined number of linking variables fully agrees within a pair of records. By contrast, in probabilistic MRL, 2 linkage weights are determined for each linkage variable, taking into account that the amount of evidence arising from agreement or disagreement on a linking variable is not the same for all variables. ^8,11,12 For example, agreement on date of birth provides more information that the record pair might belong together than agreement on gender, as the probability of agreeing on gender is 50% by chance alone. A positive weight (reward) is given when the values of a linking variable agree within a pair of records, and a negative weight (penalty) when the values disagree.

Linkage weights are estimated using the Fellegi-Sunter model ¹¹ based on the estimated probabilities of agreement of the variables in matching (belonging to same individual) and nonmatching record pairs (belonging to different individuals) in which the true status of each pair is unknown (latent class model). The linkage weights of each linking variable are then summed to obtain a total linkage weight for each record pair. The model also provides an estimate of the prevalence of matches among all possible record pairs. Based on the estimated prevalence of matches, a threshold value is determined. If the total weight of a record pair exceeds this threshold value, the pair is accepted as a link, otherwise the pair is classified as a nonlink. ^3,11,13

A critical assumption of the Fellegi-Sunter model for estimating linking weights is that errors in different linking variables among matches are statistically independent, and that among nonmatches, chance agreements of different linking variables are statistically independent. ¹¹ Dependency in errors between different linking variables is difficult to examine because their frequency is low and the underlying mechanisms behind errors are usually poorly understood. Because of the limited choice in linking variables, all available variables are often included although some likely violate the independency assumption, for example postal code and city of residence. ¹⁴

In this article, we examine the impact of dependency among values of different linking variables by comparing two methods for calculating linking weights: the standard naïve approach (ignoring dependency) and the new nonnaïve approach (incorporating dependency). Theory predicts that ignoring dependency inflates both reward and punishment in case of agreement and disagreement respectively, because similar information is used twice. The exact magnitude of these changes is not easy to predict, and it is even more difficult to predict the impact in terms of the number of pairs that are classified differently because of ignoring dependency. This study formally investigates the impact of ignoring dependency in the context of three different scenarios. In the first scenario we reanalyzed the real-life data from two national Dutch registries on perinatal care involving 9 linking variables, thereby comparing the naïve and nonnaïve approaches. Because the number of other available linking variables may influence the difference in the final classification of pairs between the naïve and nonnaïve approach, we linked the same datasets after reducing the number of linking variables to 5. In these two empirical scenarios we did not have a gold standard, which hampers the interpretation of differences between the naïve and nonnaïve approach (no truth). Therefore, we also simulated data, in which by design the truth is known; this approach enabled us to examine the differences between ignoring and incorporating dependency in record linkage in a more formal way.

Materials and Methods

We compared the performance of the naive (ignoring dependency) and nonnaïve approach (incorporating dependency) in three different scenarios. Scenario 1 is a real-life example of two perinatal registries in which we have used 9 linking variables; in scenario 2 we use the same two datasets but the number of linking variables was reduced to 5; and in scenario 3 we simulated two datasets also using 5 linking variables.

Scenario 1: Description of Empirical Datasets and Linking Variables

Probabilistic record linkage techniques have been used to link and combine the information from the Dutch perinatal registries from the year 2001 onward. ^15,16 These medical registries do not share a unique identifier that would easily allow for integration of all available data about a mother and her child(-ren). For this article, we used the records of singleton pregnancies in year 2003 from the midwife and obstetrician registries. For the year 2003, the midwife register contained 170,601 records of singleton pregnancies, whereas the obstetrician register contained 117,468 records. Between 40% and 60% of the women were treated by both a midwife and an obstetrician during pregnancy or delivery, and information about these women is recorded in both registries. A standard procedure for linking singleton pregnancies in the midwife and obstetrician registries (assuming full independence) has been recently validated in a specific study. From this validation study, we estimated that the overall error rate was <1%. ¹⁵

The 9 linkage variables used in this study were: mother's date of birth, mother's zip code (4 digits), gravidity (the number of previous deliveries), child's expected date of birth, child's actual date of birth, birth weight, gender, birth time schedule–hour, and birth time schedule–minute. Because child's expected date of birth and child's actual date of birth measure a similar quantity, dependency exist between these 2 variables.

Scenario 2: Description of Empirical Datasets and Linking Variables

We hypothesized that in a (more common) situation with fewer linking variables, the influence of dependency among linking variables might be greater. To examine this, we reduced the number of variables in our empirical dataset to 5 variables: date of birth of mother, postal code, date of birth of child, gender, and expected date of birth of child.

Scenario 3: Description of Simulated Datasets and Linking Variables

Because we do not have the true match status for the empirical set, we extended and validated our analysis on a set of simulated data. Values for 4 commonly used linking variables were simulated based on the distribution observed in the perinatal file: date of birth of mother, postal code, date of birth of child, and gender of child. Values of the fifth variable, child's expected date of birth, were created based on the observed distribution of the difference between expected date of birth of child and actual date of birth of child in the perinatal file. Using this approach a similar amount of dependency was created as in the empirical datasets.

Two files of size 40,000 records were simulated with these 5 variables. The prevalence of matches was set at 7,000 pairs, and a match indicator variable was introduced and set accordingly. Errors in linking variables were randomly introduced among matches based on the estimated error probabilities in the empirical data; 1.3% for date of birth of mother, 3.9% for postal code, 2.8% for date of birth of child, 10.0% for expected date of birth of child, and 0.8% for gender of child. The creation of files and performing of the linking procedure was repeated 50 times, and the mean values of these 50 runs are presented.

Medical Record Linkage: General Principles

The standard linkage approach used the Fellegi-Sunter model to calculate the linkage weights for all variables, assuming statistical independence among variables in the following way. ^13,15 First the probability of agreement among matches (m _i-probability) and among nonmatches (u _i-probability) for each variable was estimated, where ‘i’ refers to the i^th linkage variable. The m-probabilities (likelihood of agreement among true matches) are inversely related to the occurrence of errors. The m-probabilities are close to 1 if errors are rare. Errors in this context can include situations where linking variables can legitimately change in value among matches. The u-probability (agreement by chance among nonmatches) is largely determined by the number of possible values, but also by their distribution. A uniform distribution of values has the lowest likelihood of chance agreement among nonmatches. Estimation of the m _i and u _i values is difficult because the true state of each pair is unknown. Therefore, these values were estimated by analyzing the observed patterns of agreements and disagreements among all pairs. ^13,15,16 If the outcomes of the comparisons are independent between variables, the total log likelihood can be written as:

(1)

where π is the proportion of true matches among all possible record combinations, n _p the number of record pairs with pattern (y _1p , y _2p , … ,y _kp), y _ip is the outcome of the comparison of variable i in the pattern p (1 = agree, 0 = disagree), for i = 1, … ,k and p = 1, … ,2^k. The number of parameters to be estimated equals 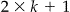, namely k m-parameters and k u-parameters and 1 prevalence parameter (π). For a dataset with k variables per record, there are 2^k unique agree/disagree comparison vectors. The expectation maximization (EM) algorithm has been used to estimate the parameters of Equation 1.

Using these m- and u-probabilities, the linkage weight of the variables are calculated in case of agreement 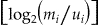and in case of disagreement: 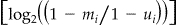. 3,8,11,13 A weight of 0 was assigned to pairs in which one or both records had a missing value on a corresponding variable. For every record pair, the linkage weights of all variables were summed. The number of estimated matches was based on the number of record pairs and the estimated prevalence of matches by the EM algorithm. This number of estimated matches was counted backward from all record pairs sorted by descending total linkage weight to obtain the threshold value (linkage weight above which record pairs were accepted as a link).

Assumption of Independence

In case of independence, conditional on whether a pair is a match or not, the probability of observing a combined outcome (agreement/disagreement) on 2 linking variables is the product of the 2 individual probabilities. Therefore, if the probability of agreement among matches for variable 1 is m ₁ and the probability of agreement among matches for another variable is m ₂, then the probability that both variables would agree among matches is given by m ₁×m ₂. In other words, the presence of a disagreement (error) on 1 linking variable among matches does not increase or decrease the likelihood that a disagreement on another variable is present. The same applies if the u-probabilities are statistically independent: the probability of observing a combined outcome on the linking variables can be written as the product of the individual probabilities (▶). In other words, when a variable agrees by chance among unrelated pairs (nonmatches), it does not affect the probability that another linking variable will agree. This is, however, not true when 2 linking variables relate to some common underlying trait, such as place of residence when using residential zip code and the hospital of admission. Therefore, only in the case of complete independence conditional on the match status can all possible patterns of agreement and disagreement be written as the product of the individual probabilities.

Table 1.

Table 1 Calculation of the Probabilities of the Occurrence of the Possible Patterns of Agreement and Disagreement Among Matches (M) and Nonmatches (U) in the Naive Strategy Assuming Independence Among 2 Linking Variables

Pattern		Probability Among Matches (M)	Probability Among Nonmatches (U)
var1	var2
+	+	m1× m2	u1× u2
+	−	m1× (1 − m2)	u1× (1 − u2)
−	+	(1 − m1) × m2	(1 − u1) × u2
−	−	(1 − m1) × (1 − m2)	(1 − u1) × (1 − u2)

+ = Linking variable agrees within a pair; − = linking variable disagrees within a pair.

m _1, m ₂, u _1, and u ₂ are estimated assuming independence.

Naïve and Nonnaïve Approach for Calculating Linkage Weights

We compared the naïve strategy, which assumes independence with the nonnaïve strategy, incorporating dependency. The naïve approach applies the calculations shown in ▶ to obtain the probabilities associated with combined outcomes on linking variables. The combined probabilities in the nonnaïve strategy were directly estimated from the observed data, thereby taking any dependency that is present into account. To estimate the combined probabilities, we replaced the individual outcomes (agreement/disagreement) of the 2 dependent linking variables by a single new variable containing the combined outcomes of the individual linking variables. For instance, we combined information on the child's expected date of birth and his or her actual date of birth by defining a new variable with 4 possible values: 0 = values within a pair disagree on both variables; 1 = values on both variables agree; 2 = only the date of birth agrees; and 3 = only the expected date of birth agrees. In the nonnaïve strategy, weights are only calculated for the outcomes of the new combined variable instead of for both variables separately. Equation 1 can be extended to incorporate dependency, for instance between variables y_k−1 and y_k, and the log likelihood of such a model is:

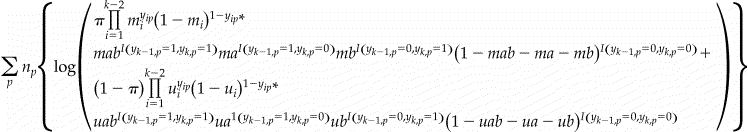(2)

where I is the indicator function, i.e., I(ϕ) = 0 if ϕ is false and I(ϕ) = 1 if ϕ is true, mab is the probability of agreement on both dependent variables (y _k−1 and y _k) among matches, ma is the probability of agreement among matches on y _k−1 only, and mb is the probability of agreement among matches on y _k only. uab is the probability of agreement only among nonmatches on both dependent variables, ua is the probability of agreement among nonmatches on y _k−1 only, and ub is the probability of agreement among nonmatches on y _k only.

Performance Parameters

In all scenarios we compared the estimated linking weights associated with agreement and disagreement according to the naïve and nonnaïve strategies. We also compared the estimated prevalence of matches and determined the number of pairs that would be classified differently by the 2 strategies, e.g., classified as link with 1 strategy and nonlink with the other strategy or vice versa. In the simulation study we directly counted the number of misclassifications for both the naïve and the nonnaïve strategies because the true status was known.

Results

Scenario 1: Empirical Dataset With 9 Linking Variables

▶ shows the linkage weights and the linkage outcome for the empirical dataset with 9 linkage variables (Scenario 1) using the naïve and nonnaïve strategy. The linkage weights were comparable between the 2 strategies except for the agreement weight associated with the pattern that both correlated variables would agree, which was considerably higher with the naïve strategy. The independence assumption in the naïve strategy is unrealistic for the variables child's expected and actual date of birth because they measure a similar quantity. This is apparent when examining the correlation between values of these variables within a single file, namely the registry of obstetricians. The Spearman correlation coefficient for expected date of birth and actual date of birth was 0.982. Despite the difference in linkage weight for the correlated variables, the estimated number of matches was comparable between the 2 strategies and only 58 record pairs were classified differently (65,787 record pairs classified as link with both strategies).

Table 2.

Table 2 Linking Weights AND Linkage Outcome for the Naïve and Nonnaïve Strategy in Empirical Datasets With 9 Linking Variables

	Pattern		Weight
	var1	var2	Naïve	Nonnaïve
Set of dependent variables
Date of birth of child (var1)	+	+	16.87	13.55
Expected date of birth of child (var2)	+	−	5.12	5.16
	−	+	3.17	3.22
	−	−	−8.58	−8.70
Other linking variables
Date of birth of mother	+		12.54	12.54
	−		−6.44	−6.53
Zip code of mother	+		10.76	10.76
	−		−4.67	−4.70
Birth weight of child	+		8.05	8.05
	−		−4.04	−4.05
Time of birth, minute	+		5.77	5.77
	−		−5.23	−5.25
Time of birth, hour	+		4.43	4.43
	−		−3.67	−3.68
Gravidity	+		1.67	1.67
	−		−3.80	−3.80
Gender of child	+		0.99	0.99
	−		−6.12	−6.12
Linkage outcome
Number of estimated matches			65,845	65,787
Agreement in classification			65,787 (99.9%)
Difference in classification			+58	0

+ = Linking variable agrees within a pair; − = linking variable disagrees within a pair.

Weight agree = log2 (m _i/u _i); weight disagree = log2 ((1 − m _i)/(1 − u _i)).

Scenarios 2 and 3: Empirical and Simulated Datasets With 5 Linking Variables

We repeated our analysis but reduced the number of linking variables to 5 because we expected the impact of ignoring dependency to be higher in a situation with fewer linking variables. The analyses were performed in empirical data, as well as in simulated data for which the true linking status was known. ▶ shows the linkage weights for the scenario with 5 linking variables using the naïve and nonnaïve strategy in the empirical and simulated datasets. The overestimation of the weight associated with the pattern that both correlated variables would agree by the naïve strategy was apparent in both the empirical and simulated data. The agreement and disagreement weights for the other variables show large differences between the naïve and nonnaïve strategy in both the empirical and simulated data. The results from simulated datasets (scenario 3) show that the nonnaïve weights closely resemble the true weights.

Table 3A.

Table 3A Linkage Weights for Naïve and Nonnaïve Strategy for Scenario 2 (Empirical Datasets) and 3 (Simulated Datasets, Mean of 50 Runs) Both Using 5 Variables

Linking Variables	Pattern		Scenario 2: Empirical Datasets			Scenario 3: Simulated Datasets
			Weight Naïve	Weight Nonnaïve	True Weight	Weight Naïve	Weight Nonnaïve	True Weight
	var1	var2
Set of dependent variables
Date of birth of child (var1)	+	+	16.88	13.55	NA	16.86	13.77	13.77
Expected date of birth of child (var2)	+	−	5.34	5.15		5.39	5.14	5.15
	−	+	4.10	3.24		4.22	3.31	3.30
	−	−	−7.44	−7.73		−7.25	−8.54	−8.46
Other linking variables
Date of birth of mother	+		8.43	12.54	NA	8.67	12.56	12.56
	−		−0.08	−6.53		−0.10	−6.29	−6.27
Zip code of mother	+		6.71	10.76	NA	6.54	10.34	10.34
	−		−0.09	−4.73		−0.10	−4.68	−4.68
Gender of child	+		0.09	0.99	NA	0.11	0.99	0.99
	−		−0.10	−6.12		−0.12	−5.97	−5.97

+ = Linking variable agrees within a pair; − = linking variable disagrees within a pair; NA = not applicable.

▶ provides further insight by showing the underlying u- and m-probabilities that are used to calculate the linkage weights. The product of the 2 individual probabilities for agreement among nonmatches in the naïve strategy was considerably lower than the estimated probability that the child's actual and expected date of birth would both agree among nonmatches by the nonnaïve strategy (▶: 0.000007 vs. 0.000073, ratio 0.10 in the empirical data and 0.000007 vs. 0.000062, ratio 0.11 in the simulated data). The estimated probabilities for agreement among nonmatches for the other linking variables were very comparable between the naïve and nonnaïve strategy in both the empirical and simulated data. However, the estimated probabilities for agreement among matches for the noncorrelated variables were underestimated with the naïve strategy, explaining the low (dis-)agreements weights for the naïve strategy in ▶. The results of analyzing the simulated data show that the estimated probabilities by the nonnaïve strategy are in close agreement with the true probabilities for both the dependent and independent linking variables.

Table 3B.

Table 3B Estimated Probabilities Among Matches and Among Nonmatches For Naïve and Nonnaïve Strategy For Scenario 2 (Empirical Datasets) and Scenario 3 (Simulated Datasets − Mean of 50 Runs) Both Using Five Linking Variables

Linking Variables	Pattern		Probability Among Matches (M)			Ratio Naïve/ Nonn ∗	Ratio Nonn/ Truth	Probability Among Nonmatches (U)			Ratio Naïve/ Nonn	Ratio Nonn/ Truth
	var1	var2	Naïve	Nonnaïve	Truth			Naïve	Nonnaïve	Truth
Scenario 2: empirical data
Set of dependent variables
Date of birth of child (var1)	+	+	0.8411	0.8753	NA	0.96	NA	0.000007	0.000073	NA	0.10	NA
Expected date of birth of child (var2)	+	−	0.1090	0.0958		1.14		0.002693	0.002700		1.00
	−	+	0.0442	0.0242		1.83		0.002573	0.002570		1.00
	−	−	0.0057	0.0047		1.22		0.994727	0.994657		1.00
Other variables in model
Date of birth of mother	+		0.0568	0.9892		0.06		0.0002	0.0002		0.99
Zip code of mother	+		0.0580	0.9623		0.06		0.0006	0.0006		1.00
Gender of child	+		0.5327	0.9928		0.54		0.5007	0.5007		1.00
Scenario 3: simulated data
Set of dependent variables
Date of birth of child (var1)	+	+	0.8312	0.8753	0.8751	0.95	1.00	0.000007	0.000062	0.000062	0.11	1.00
Expected date of birth of child (var2)	+	−	0.1149	0.0969	0.0969	1.19	1.00	0.002732	0.002739	0.002739	1.00	1.00
	−	+	0.0474	0.0252	0.0251	1.88	1.00	0.002539	0.002541	0.002541	1.00	1.00
	−	−	0.0066	0.0027	0.0028	2.46	0.94	0.994722	0.994657	0.994657	1.00	1.00
Other variables in model
Date of birth of mother	+		0.0667	0.9872	0.9870	0.07	1.00	0.0002	0.0002	0.0002	1.00	1.00
Zip code of mother	+		0.0689	0.9610	0.9610	0.07	1.00	0.0007	0.0007	0.0007	1.00	1.00
Gender of child	+		0.5395	0.9920	0.9920	0.54	1.00	0.4989	0.4989	0.4989	1.00	1.00

^∗ nonn = nonnaïve.

NA = not applicable.

We also considered the impact of these differences in probabilities and weights on the final classification of record pairs in Scenario 2 and 3. In Scenario 2 (the empirical dataset) with the correlated variables date of birth and expected date of birth, the estimated prevalence of matches changed considerably when changing form the naïve to the nonnaïve strategy (▶). The number of matches was estimated by the naïve strategy at 1,251,752, compared with 65,951 matches by the nonnaïve strategy. The number of 1,251,752 is clearly an overestimation because it is larger than the number of records in the first file, suggesting that every woman was transferred from a midwife to an obstetrician (expected proportion around 40% to 60%). The overestimation of the prevalence of matches by the naïve strategy went together with an underestimation of the m-probabilities of the noncorrelated variables because of the high frequency of patterns with agreement on both correlated variables. Disagreements of the noncorrelated variables in a pattern with agreement on both correlated variables were regarded as errors, lowering the m-probability of the noncorrelated variables.

Table 4.

Table 4 Impact on the Classification of Record Pairs Between the Naïve and Nonnaïve Strategy in Scenario 2 (Empirical Datasets) and Scenario 3 (Simulated Datasets) Both Using 5 Linking Variables

	Scenario 2: Empirical Datasets		Scenario 3: Simulated Datasets
	Naïve	Nonnaïve	Naïve	Nonnaïve	Truth
Dataset 1	129,576		40,000
Dataset 2	116,390		40,000
Number of pairs	15,081,350,640		1,600,000,000
Estimated prevalence	8.30E-05	4.37E-06	7.07E-05	4.37E-06	4.38E-06
Number of estimated matches	1,251,752	65,951	113,069	6,998	7,000
Number of links	1,226,322	65,639	112,988	6,983	7,000
Number of false-positive links	NA	NA	106,009	51	0
Number of false-negative links	NA	NA	20	68	0

NA = not applicable.

The number of (true) matches among the simulated files (scenario 3) by design was 7,000 among a total of 40,000×40,000 record pairs (prevalence of 0.00000438). The naïve approach overestimated the number of matches in scenario 3 more than 16-fold at 113,069, whereas the nonnaïve approach correctly estimated the number of matches at 6,998 matches (▶). Based on the estimated probabilities by the naïve strategy, 106,009 false-positive links and 20 false-negative links were created. The nonnaïve strategy produced only 51 false-positive and 68 false-negative links. False-positive links with the naïve strategy were mainly record pairs with agreement on both dependent variables and disagreement on all other variables (50,018 false-positive links) and record pairs with agreement on both dependent variables and gender (49,821 false-positive links).

Discussion

We examined the impact of dependency between linking variables on the results of a record linkage study by comparing an MRL strategy that ignores dependency (the standard naïve approach) with a strategy that takes any existing dependency into account (the proposed nonnaïve approach). The standard naïve approach, as expected, overestimates the evidence in favor of a match if both correlated variables agree.

Despite the overestimation of evidence in correlated variables, the impact on the final classification of pairs was moderate in the empirical study with 9 variables, predominantly because the estimated prevalence of matches was not much affected. In other words, the naïve strategy produced on average higher weights, but the threshold to consider a record pair as link increased accordingly. The number of pairs that is classified differently therefore depends on the changes in ranking of pairs around the region of these thresholds. In our empirical study, this region of uncertainty contained only a relatively low number of pairs because of the favorable linking conditions in our example: a considerable number of linking variables, all of reasonable quality. When the number of linking variables was reduced in the empirical study, the naïve strategy clearly overestimated the number of matches. The results of the simulation study confirmed that dependency can seriously bias the estimated number of matches (prevalence) in less favorable situations with fewer linking variables. In our simulation study the estimated prevalence of matches by the naïve strategy was 16 times higher than the true prevalence, while the nonnaïve strategy did provide the correct estimate of the prevalence of matches.

In light of our results, we will discuss the advantages and disadvantages of 4 possible approaches for handling potential dependency among linking variables. Based on these discussions researchers can choose the most pragmatic approach for their linking situation.

The first approach is to ignore any possible dependency between linking variables and to estimate the u- and m-probabilities for the linking in the standard way (the naïve strategy). This approach is the simplest one, but leads to biased estimates of u- and m-probabilities, and therefore to biased weights. Although the impact on the final classification of record pairs was small in our empirical study with 9 linking variables, this might be different in situations with less discriminating or fewer linkage variables, as confirmed by our simulations and the rerun of the empirical study with 5 variables. For obvious reasons this method cannot be recommended in situations in which linking variables are strongly correlated.

The second approach is to leave out one of the dependent variables in the linkage algorithm. Although this method is correct in the sense that the dependency will disappear, there is also a loss of information by dropping one of the variables unless there is perfect correlation. The impact on the final linkage outcome of this approach will depend on whether the discriminating power of the remaining linking variables is sufficiently high. In the empirical data with 9 linking variables, 1,259 extra links were included if 1 of the 2 dependent variables was left out (pairs with agreement on the variable left in and disagreement on the variable left out).

A third approach would be to deal with dependency among linking variables by taking dependency directly into account in the estimation algorithm. This means explicitly modeling the dependency between linking variables in the likelihood equations that estimate the u- and m-probabilities. This method is statistically sound and also flexible because the researcher can see whether the fit of the model indeed improves when taking different dependencies into account. A drawback of this method is that it is technically much more demanding because it requires estimation of more parameters and programming of more complex likelihood functions.

The fourth approach is to incorporate the dependency by introducing a new variable that combines the outcomes of the individual variables (our nonnaïve strategy). This method is transparent, scientifically sound, and easy to apply in most linkage studies. However, if more than 2 correlated variables are present, the number of possible outcomes and therefore the number of weights that must be estimated grows exponentially. This makes the method less suitable for a series of linking variables that might be correlated, or if the number of outcome combinations is increased by introducing value-specific weights (the weight of agreement for a variable will differ based on the actual value) or close agreement (introducing an additional outcome of close between perfect agreement and disagreement).

Conclusion

Dependency among all available linking variables is often present and has the potential to bias the results of record linkage studies. Our proposed strategy of combining correlated linking variables is a straightforward method to deal with dependencies. It has the major advantage that existing software programs for record linkage, although based on independence, can still be used. In addition, our method uses all available information within the set of potential linking variables. Further research is needed to determine the performance and stability of our method in less favorable situations in which the number of possible outcomes increases rapidly because of many correlated variables.