Abstract
The division of thermodynamic solvation free energies of electrolytes into ionic constituents is conventionally accomplished by using the single-ion solvation free energy of one reference ion, conventionally the proton, to set the single-ion scales. Thus the determination of the free energy of solvation of the proton in various solvents is a fundamental issue of central importance in solution chemistry. In the present article, relative solvation free energies of ions and ion-solvent clusters in methanol, acetonitrile, and dimethyl sulfoxide (DMSO) have been determined using a combination of experimental and theoretical gas-phase free energies of formation, solution-phase reduction potentials and acid dissociation constants, and gas-phase clustering free energies. Applying the cluster pair approximation to differences between these relative solvation free energies leads to values of −263.5, −260.2, and −273.3 kcal/mol for the absolute solvation free energy of the proton in methanol, acetonitrile, and DMSO, respectively. The final absolute proton solvation free energies are used to assign absolute values for the normal hydrogen electrode potential and the solvation free energies of other single ions in the above solvents.
1. Introduction
For neutral species, experimental solvation free energies have been tabulated for a large number of solutes in both aqueous1-8 and nonaqueous3,9,10 solvents. Typically, these solvation free energies are determined directly from experimental partition coefficients,11 and thus their uncertainty is relatively low (∼0.2 kcal/mol).12 Determining accurate values for the solvation free energies of ionic solutes is much less straightforward than for neutral solutes. It is generally agreed that the chemical potential of an ion has no “operational meaning”13 in classical thermodynamics because the difference in electric potential between two media cannot be measured and therefore has no physical significance.14-16 Nevertheless, single-ion solvation free energies are well defined in statistical mechanics, and determining their values is an important step in understanding the structure of solutions. The potential of a medium relative to vacuum is called the potential of the phase. The single-ion solvation free energy in the potential of the phase is called the absolute solvation free energy, and it differs from the real (unmeasurable) solvation free energy by the potential of the phase. The present article is concerned with absolute solvation free energies. The single-ion solvation free energy of the proton is conventionally used to set the scale for all other single-ion solvation free energies. Understanding the partitioning of single ions between different liquid phases is also of great importance in many areas of biology. For example, the electrical signals sent by nerve cells are activated by changes in the resting cell potential that are caused by the movement of various ions across the neuronal membrane.17
Sums of solvation free energies of neutral pairs of cations and anions are well-defined and can be determined directly through the use of thermochemical cycles involving calorimetric or electrochemical measurements.7,18-22 A number of different extrathermodynamic approximations have been used16,23-30 to partition the sums of cation and anion solvation free energies into single-ion contributions. A popular method for doing this is based on the model of a structureless, spherical ion in a homogenous continuum dielectric, in which case the solvation free energy depends only on bulk electrostatic interactions with the solvent, which are independent of the sign of the ion's charge.31,32 Thus, one assumes that in a given solvent, the solvation free energy of a reference salt composed of a quasispherical cation and a quasispherical anion of about the same size can be divided equally. Once the absolute solvation free energies of these reference ions are known, the absolute solvation free energies of other single ions can then be determined using the appropriate thermochemical cycles. The justification for approximations like this is best if the ions are large so that their surface-to-volume ratio is minimized. Commonly, this approximation is invoked using tetraphenylarsonium tetraphenylborate (AsPh4BPh4, or TATB)33 as the reference salt, although other reference salts have also been used34-40 for dividing free energy, enthalpy, and entropy. A number of experimental and theoretical studies have focused their attention on the spectroscopic and thermodynamic properties of the AsPh4+ and BPh4− ions in various solvents.28,41-52 The current general consensus seems to be that charge-specific interactions do occur between these two ions and neighboring solvent molecules (thus bringing into question the validity of the TATB approximation), although some experimental28,43 and theoretical45,52 work suggests just the opposite.
Another approximation that has been used to estimate the solvation free energies of single ions is the cluster pair approximation of Coe, Tuttle, and coworkers.30,53,54 In this approximation, the absolute solvation free energy of a reference ion (usually the proton) is determined through comparisons between the stepwise clustering free energies of cation-anion pairs containing different numbers of clustering solvent molecules and their bulk solvation free energies. This approximation has been used in several places to estimate single-ion solvation free energies in water.53-56 Recently, we applied the cluster pair approximation to a database containing relative solvation free energies of ions, which are well defined even in classical thermodynamics, and accurate gas-phase clustering free energies for ion-water clusters containing up to 6 clustering water molecules.56 Using this database, we obtained a value of −266.1 kcal/mol for the absolute aqueous solvation free energy of the proton, which is in good agreement with the recommended57 value of −265.9 kcal/mol.
Compared to water, estimates of the absolute solvation free energies of single ions in other solvents16 have been very limited. Kalidas et al. reviewed a large number of transfer free energies of single ions between water and 17 different nonaqueous solvents.58 The majority of the transfer free energies listed in this compilation were determined using the TATB approximation; none of them were determined using the cluster pair approximation. Tuttle and coworkers have used the cluster pair approximation to determine the absolute solvation free energy of the proton in ammonia.54 However, based on the limited amount of solution-phase and gas-phase data available to these workers, they could only make a tentative estimate. Besides various extrathermodynamic approximations, theoretical calculations have also been used to estimate the solvation free energies of single ions in the liquid phase.59-112 However, like the majority of previous experimental work, most of these studies too have focused solely on water.
In this article, the cluster pair approximation will be used to determine the absolute solvation free energy of the proton in methanol, acetonitrile, and DMSO. For this purpose, relative solvation free energies obtained using experimental gas-phase free energies of formation and solution-phase reduction potentials and acid dissociation constants will be combined with experimental and calculated gas-phase clustering free energies.
In the first part of this article, the standard-state conventions used for gas-phase and solution-phase free energies will be outlined, followed by a description of the thermochemical cycles and experimental and theoretical data used to determine relative solvation free energies. Then, the cluster pair approximation will be briefly described, followed by the results obtained through the application of this approximation to the relative solvation free energies determined in the previous section. The accuracy of the absolute solvation free energies obtained here will then be discussed, followed by a comparison between these solvation free energies and those obtained using other extrathermodynamic assumptions and theoretical calculations.
2. Standard States
In this article, experimental and calculated gas-phase free energies use a standard-state gas-phase pressure of 1 atm. A superscript open circle denotes free energies that use this standard-state pressure. Experimental solution-phase free energies use a standard-state solution-phase concentration of 1 mol/L. A superscript asterisk denotes free energies that use this standard-state concentration. Absolute and conventional solvation free energies use for a standard state an ideal gas at a gas-phase concentration of 1 mol/L dissolving as an ideal solution at a liquid-phase concentration of 1 mol/L. A superscript asterisk denotes solvation free energies that use this standard-state concentration in the gas and solution phases. These standard state conventions, including procedures for converting various experimental quantities tabulated using other standard-state pressures and concentrations to the standard-state pressure and concentration used here, are described in full detail in the Supporting Information.
3. Relative and Conventional Solvation Free Energies of Unclustered Ions
Experimentally, only the sum of the solvation free energies of neutral combinations of cations and anions can be obtained. Consequently, solvation free energies of single ions are often tabulated as relative free energies by arbitrarily setting the free energy of solvation of some reference ion equal to zero.113 The choice of reference ion in a particular solvent is arbitrary, although by convention the proton is usually chosen. For monovalent ions, this results in a set of conventional free energies of solvation that for cations are shifted from their absolute values by the unknown value for the absolute solvation free energy of the proton
| (1) |
and conventional free energies of solvation for anions that are shifted by an equal amount in the opposite direction
| (2) |
(Above, M+ refers generically to any monovalent cation, and X− to any monovalent anion. Later in this article, BH+ will be used to refer to a monovalent cation that behaves as a Brønsted−Lowry acid, and A− will be used to refer to a monovalent anion that behaves as a Brønsted−Lowry base.) Following the above convention results in the following relationship
| (3) |
Thus, sums of conventional solvation free energies for neutral cation-anion pairs, which can be determined directly through the use of various thermodynamic cycles, are well- defined. The thermochemical cycles that are used in this article to determine conventional solvation free energies are described below.
3.1. Conventional Solvation Free Energies from Reduction Potentials
When the convention described above for the absolute solvation free energy of the proton is followed, the solution-phase free energy change associated with the following half-cell reaction
| (4) |
is equal to zero. (In the above reaction, “g” denotes the gas phase and “S” denotes the liquid solution phase.) Reduction potentials that are tabulated following this convention for the hydrogen electrode are referred to as standard reduction potentials. The half-cell reaction for the reduction of a monovalent metal cation is
| (5) |
where the symbol “cr” denotes the crystalline phase. Combining the half-cell reactions shown in eqs 4 and 5 leads to the following redox reaction
| (6) |
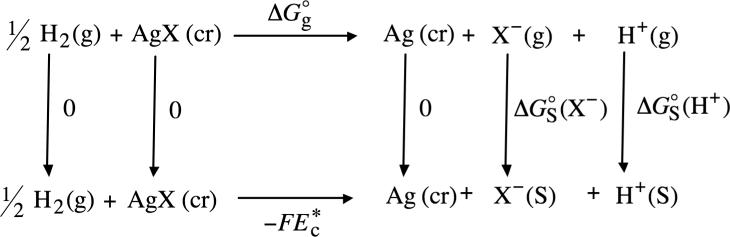
Through the use of thermochemical cycle 1 (illustrated in Scheme 1) and eq 1, the ! conventional solvation free energy of M+ can be written as
| (7) |
where and are the gas-phase free energies of formation of H+ and M+, respectively, at 298 K, F is Faraday's constant, which is equal to 23.061 kcal mol−1 V−1, and Ec* is the standard reduction potential (in volts) of M+ in the solution phase. (The free energies of formation of H2 in the gas phase and of the neutral metal atom in the crystalline phase do not appear in eq 7 because these species correspond to the standard states for the elements from which they are composed. Consequently, their gas-phase free energies of formation are defined to equal zero at all gas-phase pressures.) The superscript open circles in and denote the use of a standard-state gas-phase pressure of 1 atm. The superscript asterisk and the subscript c in Ec* denote the use of a standard-state solution-phase concentration of 1 mol/L (molarity scale). Often, standard reduction potentials taken from the literature use a standard-state solution-phase concentration of 1 mol solute per kg solvent (molality scale). The procedure that was used to convert standard reduction potentials tabulated on the molality scale to the molarity scale is described in the Supporting Information.
SCHEME 1.
Thermochemical Cycle 1
Gas-phase free energies of formation of monatomic ions can be calculated using tabulated values for the enthalpy of formation and entropies computed using the Sackur-Tetrode equation.114 In this work, enthalpies of formation of ions are tabulated following the electron convention115 for the integrated heat capacity and entropy of the electron. When this convention is followed, the electron is treated as a standard chemical element, whereby its integrated heat capacity and entropy can be computed using standard formulae from statistical mechanics. Often, Boltzmann statistics are used to compute the integrated heat capacity and entropy of the electron, although Bartmess116 and several earlier workers117-120 have pointed out that a more correct treatment of the electron uses Fermi-Dirac, not Boltzmann statistics. (Like the electron, the proton is a fermion, although for 298 K, its integrated heat capacity and entropy obtained using Boltzmann statistics differs very little from the values obtained using Fermi-Dirac statistics; see Table 3 of reference 116.) It is important to point out that conventional solvation free energies are independent of the values used for the integrated heat capacity and entropy of the electron, as long as the same values are used consistently. However, for reactions where the electron appears as a reactant or product (e.g., chemical reactions for the free energies of formation of ionic species) the gas-phase free energy of reaction does depend on the values used for the electron integrated heat capacity and entropy. For example, using the integrated electron heat capacity and entropy obtained from Fermi-Dirac statistics116 leads to a value of 361.7 kcal/mol for the free energy of formation of the gas-phase proton at 298 K and 1 atm. If instead the electron integrated heat capacity and entropy obtained from Boltzmann statistics are used, the free energy of formation of the gas-phase proton is equal to 362.6 kcal/mol at 298 K and 1 atm. In this work, all free energies of formation of gas-phase ions are tabulated using the electron integrated heat capacity and entropy obtained using Fermi-Dirac statistics. Further details regarding the different conventions that are commonly used for treating the thermochemistry of the electron, the equations and literature references that were used to determine the enthalpies, entropies, and free energies of formation of ions used in this article, and the procedure used to convert entropies computed using a standard-state gas-phase pressure of 1 bar to a standard-state gas-phase pressure of 1 atm, are given in the Supporting Information.
TABLE 3.
Solubility Products and Conventional Solvation Free Energies (kcal/mol) of Metal Halides in Different Solvents
| pKspa |
ΔGS*(M+) + ΔGS*(X−) |
ΔGS*,con(M+)b,c |
ΔGS*,con(X−)c |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MX | ΔGlato[MX(cr)]d | CH3OH | CH3CN | DMSO | CH3OH | CH3CN | DMSO | CH3OH | CH3CN | DMSO | CH3OH | CH3CN | DMSO |
| KCl | −155.5 | 3.1 | 8.0 | 3.1 | −155.0 | −148.5 | −155.1 | 180.2 | 174.7 | 180.9e | −335.3 | −323.2 | |
| NaCl | −171.8 | 8.3 | 2.9 | −164.3 | −171.6 | 159.1 | 164.4f | −323.4 | |||||
| AgCl | −202.8 | 13.3 | 13.2 | 10.8 | −188.5 | −188.7 | −191.9 | 146.4 | 132.4 | 144.3 | −334.8 | −321.1 | −336.2 |
| TlCl | −163.4 | 5.6 | 13.2 | 6.9 | −159.5 | −157.8 | 177.3 | 178.0 | −336.9 | −335.8 | |||
| KBr | −148.9 | 2.5 | 5.7 | 0.6g | −149.3 | −145.0 | −151.9 | 180.2 | 174.7 | 181.2h | −329.6 | −319.7 | |
| RbBr | −143.6 | 2.7 | 5.5 | −143.7 | −140.0 | 186.0 | 178.4 | −329.7 | −318.4 | ||||
| AgBr | −199.9 | 15.5 | 13.6 | 11.0 | −182.7 | −185.3 | −188.8 | 146.4 | 132.4 | 144.3 | −329.0 | −317.7 | −333.1 |
| CsBr | −138.4 | 5.8 | −134.3 | 187.8 | −322.1 | ||||||||
| TlBr | −159.4 | 8.2 | 13.0 | −152.1 | 177.3 | −329.4 | |||||||
| AgI | −196.7 | 18.5 | 14.5 | 12.1 | −175.4 | −180.8 | −184.1 | 146.4 | 132.4 | 144.3 | −321.7 | −313.2 | −328.4 |
Average value from reference 122, unless indicated otherwise.
From Table 1, unless indicated otherwise.
Based on the convention that ΔGS*,con(H+) = 0.
Gas-phase lattice free energy, calculated using eq 14.
Calculated from pKsp (KCl) and average ΔGS*,con(Cl−) value from this table.
Calculated from pKsp(NaCl) and average ΔGS*,con(Cl−) value from this table.
Average value, see text.
Calculated from pKsp(KBr) and ΔGS*,con(Br−) value from this table.
Using the gas-phase free energies of formation of ions tabulated as part of this work (see Supporting Information) and experimental121,122 values for the standard reduction potentials of different metal cations in methanol, acetonitrile, and DMSO, conventional solvation free energies have been determined in these solvents by eq 7. These conventional solvation free energies and the auxiliary data used in eq 7 are listed in Table 1. To verify the accuracy of eq 7, we also determined the aqueous conventional solvation free energy of Ag+ using an experimental value123 of 0.7996 V for the standard reduction potential of Ag+ in water and the tabulated values for the gas-phase free energy of formation of H+ and Ag+. Substituting these values into eq 7 gives a value of 147.2 kcal/mol for the aqueous conventional solvation free energy of Ag+, which is in perfect agreement with the aqueous conventional solvation free energy listed in the recent compilation by Fawcett.124
TABLE 1.
Gas-Phase Free Energies of Formation (kcal/mol),a Standard Reduction Potentials (Volts) and Conventional Solvation Free Energies (kcal/mol) of Metal Ions in Different Solvents
|
Ec*b |
ΔGS*,con(M+)c |
||||||
|---|---|---|---|---|---|---|---|
| M+ | ΔfG298o[M+ (g)]d | CH3OHe | CH3CN | DMSOe | CH3OH | CH3CN | DMSO |
| Na+ | 136.4 | −2.728 | −2.87e | 162.4 | 159.1 | ||
| K+ | 114.1 | −2.921 | −3.16e | 180.2 | 174.7 | ||
| Rb+ | 108.5 | −2.912 | −3.17,e −3.316f | 186.0 | 178.4 | ||
| Cs+ | 101.1 | −3.16e | 187.8 | ||||
| Tl+ | 175.6 | −0.379 | −0.682f | −0.352 | 177.3 | 170.4 | 178.0 |
| Ag+ | 232.9 | +0.764 | +0.23,e +0.096f | +0.680, +0.668 | 146.4 | 132.4 | 144.3 |
1 kcal = 4.184 kJ.
Standard reduction potential for a standard-state solution-phase concentration of 1 mol/L. If more than a single experimental Ec* value is listed, the average value was used to determine the conventional solvation free energy.
Based on the convention that ΔGS*,con(H+) = 0.
Free energy of formation obtained following the electron convention and Fermi-Dirac statistics for the electron integrated heat capacity and entropy,116 for a standard-state gas-phase pressure of 1 atm.
Reference 121.
Reference 122.
Conventional solvation free energies in methanol were also determined using experimental values for the reduction potentials at various silver halide electrodes. The half-cell reaction for the silver halide electrode is
| (8) |
Combining the half-cell reactions shown in eqs 4 and 8 gives the following redox reaction
| (9) |
Through the use of thermochemical cycle 2 (illustrated in Scheme 2) and eq 2, the conventional solvation free energy of the halide anion X− can be written as
| (10) |
where
| (11) |
The term ΔGo→* appearing in eq 10 is the free energy change associated with moving a ! solute from a standard-state gas-phase concentration of 1 atm to a standard-state solution-!phase concentration of 1 mol/L. (This free energy change has also been referred to as the “compression” work of the gas110 or the liberation free energy125) At 298 K, ΔGo→* is equal to 1.9 kcal/mol. Full details of this free energy change are given in the Supporting Information. (Note that the term ΔGo→* does not appear in eq 7 because in this equation the number of moles of reactants that move from the gas phase to solution cancels out the number of moles of products that move from the gas phase to solution.)
SCHEME 2.
Thermochemical Cycle 2
Using tabulated values for the gas-phase free energies of formation of AgCl,126 AgBr,126 and AgI126 (adjusted to a standard-state gas-phase pressure of 1 atm), as well as the gas-phase free energies of formation of H+, Cl−, Br−, and I− tabulated in this work and experimental values127 for the standard reduction potentials at the AgCl, AgBr, and AgI electrodes, conventional solvation free energies of Cl−, Br−, and I− in methanol were determined using eqs 10 and 11. These conventional solvation free energies and the auxiliary data used in eqs 10 and 11 are listed in Table 2. To verify the accuracy of eqs 10 and 11, we determined the conventional aqueous solvation free energy of Cl− using tabulated values for the gas-phase free energy of formation of AgCl, H+, and Cl−, and an experimental value123 of 0.22233 V for the standard reduction potential at the AgCl electrode in water. Substituting these values into eqs 10 and 11 gives a value of −340.1 kcal/mol for the conventional aqueous solvation free energy of Cl−. Adjusting the value for the conventional solvation free energy of Cl− listed in the compilation by Fawcett,124 which uses a standard-state gas-phase concentration of 1 bar, to a standard-state gas-phase concentration of 1 mol/L (see the Supporting Information for details regarding this standard-state conversion) gives a value of −340.4 kcal/mol, which is in good agreement with the value obtained in this work.
TABLE 2.
Gas-Phase Free Energies of Formation (kcal/mol), Standard Reduction Potentials (Volts), and Conventional Solvation Free Energies (kcal/mol) of Halide Ions in Methanol
| X− | ΔfG298o[X−(g)]a | ΔfG298o[AgX(cr)]b | Ec*c | ΔGS*,con(X−)d |
|---|---|---|---|---|
| Cl− | −56.4 | −26.2 | −0.0221 | −334.8 |
| Br− | −56.2 | −23.2 | −0.1507 | −329.0 |
| I− | −52.1 | −15.8 | −0.32987 | −321.6 |
Free energy of formation obtained following the electron convention and Fermi-Dirac statistics for the electron integrated heat capacity and entropy,116 for a standard-state gas-phase pressure of 1 atm.
Experimental values were taken from ref 126, and adjusted to a standard-state gas-phase pressure 1 atm using the procedure described in the Supporting Information.
Standard reduction potential for a solution-phase concentration of 1 mol/L. Values were taken from reference 127.
Based on the convention that ΔGS*,con(H+) = 0.
3.2. Conventional Solvation Free Energies from Solubility Products
Experimental values for the equilibrium constant associated with the following chemical reaction
| (12) |
have been measured for a number of salts in both water and in nonaqueous solvents (this equilibrium constant is usually referred to as the solubility product, or Ksp). Through the use of thermochemical cycle 3 (illustrated in Scheme 3), the sum of the solvation free energies for the neutral cation−anion pair M+X− can be written as
| (13) |
where pKsp and are the negative common logarithm of the solubility product and the lattice free energy of the crystalline salt, respectively. The lattice free energy is given by
| (14) |
SCHEME 3.
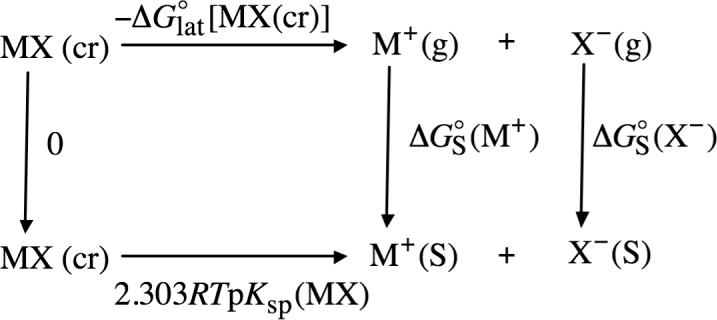
Thermochemical Cycle 3
Using tabulated values for the free energies of formation of various salts126 (adjusted to a standard-state gas-phase pressure of 1 atm), the gas-phase free energies of formation of ions tabulated in this work, and experimental122,128 values for the solubility products of different salts, sums of solvation free energies for different cation−anion pairs in methanol, acetonitrile, and DMSO were determined using eqs 13 and 14. For the majority of the salts considered in this work, experimental values for their solubility products were taken from ref122, in which the authors have compiled experimental values taken from their own work and from a number of other experimental and review papers. In cases where more than a single experimental value for a given salt in a given solvent was listed by these authors, we took the average of all the listed values, except in cases where an experimental value was designated “uncertain” by these authors, in which case it was not used to calculate the average. More recently, Labban and Marcus129 measured the solubilities of KCl and KBr in several nonaqueous solvents, including acetonitrile and DMSO. The solubility products of KCl and KBr computed using Labban and Marcus' data are both within 0.1 pKsp units of the average pKsp values computed using the data from ref122. (Reference122 does not contain data for KCl or KBr in DMSO.) For KBr in DMSO, the pKsp value used in this work (0.6) is the average of three different experimental values: 0.5,130 0.5,131 and 0.7.129 (The pKsp value taken from ref131 was extrapolated to 298 K using pKsp values measured at five other temperatures by these workers.) The sums of solvation free energies obtained using eqs 13 and 14 and the auxiliary data used in these equations are listed in Table 3.
To verify the accuracy of eqs 13 and 14, we determined the aqueous solvation free energy of the Ag+Cl− cation−anion pair using tabulated values for the free energy of formation of AgCl, Ag+, and Cl−, and an experimental value123 of 9.75 for the pKsp of AgCl in water. Substituting these values into eqs 13 and 14 gives a value of −193.4 kcal/mol for the aqueous conventional solvation free energy of the Ag+Cl− cation−anion pair. Taking the sum of the conventional solvation free energies of Ag+ and Cl− in water from the compilation by Fawcett124 gives a value of −193.2 kcal/mol, which is in good agreement with the value obtained in this work.
Using the sums of solvation free energies in Table 3, conventional solvation free energies of Cl−, Br−, and I− in methanol, acetonitrile, and DMSO were determined by subtracting from the solvation free energies of different cation−anion pairs the conventional solvation free energies of the corresponding cations from Table 1. (For example, the conventional solvation free energy of I− in acetonitrile was determined by subtracting from the solvation free energy of the Ag+I− cation−anion pair the conventional solvation free energy of Ag+ from Table 1.) Thus, all of the conventional solvation free energies of anions that are listed in Table 3 are anchored to the data in Table 1. In DMSO, conventional solvation free energies for Na+ and K+ are not listed in Table 1. Instead, these conventional solvation free energies were determined using the data in Tables 1 and 3, as described below. The conventional solvation free energy of Na+ in DMSO was determined by subtracting from the solvation free energy of the Na+Cl− cation-anion pair the average value of the conventional solvation free energy for Cl− obtained using the Ag+Cl− cation-anion pair and the Tl+Cl− cation-anion pair (these two conventional solvation free energies are listed in the final column of Table 3 and are within 0.4 kcal/mol of one another). Two values for the conventional solvation free energy of K+ in DMSO were determined in a similar fashion using the K+Cl− and K+Br− cation-anion pairs and the conventional solvation free energies of Cl− and Br−. Thus, the conventional solvation free energy of Na+ in DMSO is anchored to the data in Table 3 as well as to the conventional solvation free energies of Ag+ and Tl+ from Table 1. Similarly, the conventional solvation free energy of K+ in DMSO is anchored to the Table 3 as well as to the conventional solvation free energy of Ag+ from Table 1.
3.3. Conventional Solvation Free Energies from Acid Dissociation Constants
Shown in thermochemical cycle 4 (illustrated in Scheme 4)132 are the chemical reactions for the dissociation of a cationic Brønsted−Lowry acid (BH+) in the gas phase and in the solution phase. Through the use of thermochemical cycle 4 and eq 1, the conventional solvation free energy of BH+ can be written as
| (15) |
where is the gas-phase acidity of BH+, which is equal to Go(B) + Go (H+) − Go(BH+), is the solvation free energy of the neutral species B, and pKa(BH+) is the negative common logarithm of the solution-phase acid dissociation constant of BH+. Shown in thermochemical cycle 5 (illustrated in Scheme 5)132 are the chemical reactions for the dissociation of a neutral Brønsted−Lowry acid (AH) in the gas phase and in the solution phase. Through the use of thermochemical cycle 5 and eq 2, the conventional solvation free energy of A− can be written as
| (16) |
where is the gas-phase acidity of AH, which is equal to Go (A− + Go (H+) − Go(AH), is the solvation free energy of the neutral species AH, and pKa(AH) is the negative common logarithm of the solution-phase acid dissociation constant of AH.
SCHEME 4.
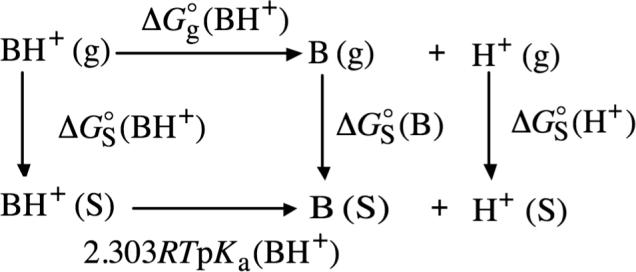
Thermochemical Cycle 4
SCHEME 5.
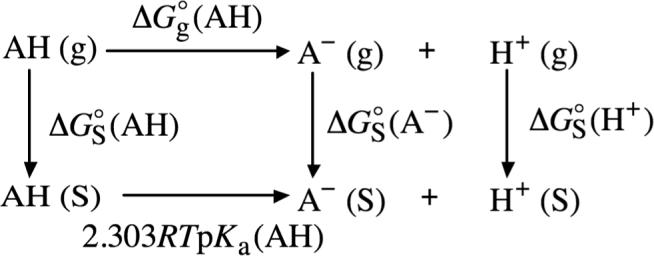
Thermochemical Cycle 5
Listed in Table 4 are experimental pKa values of neutral and cationic acids in methanol, acetonitrile, and DMSO.133-156 An experimental value for the solvation free energy is available10 for ethanol in DMSO; for all remaining neutral species, the solvation free energies in methanol, acetonitrile, and DMSO were calculated at the SM5.43R12,157/mPW1PW158/6−31+G(d,p)159 level of electronic structure theory, using gas-phase geometries optimized at the mPW1PW/MIDI!160-162 level of electronic structure theory (note that the mPW1PW functional is also called mPW0, mPW1PW91, and MPW25). All SM5.43R calculations were performed using a locally modified version163 of the Gaussian 03164 electronic structure package. Using the experimental pKa data in Table 4, experimental values for the gas-phase acidity,165 and experimental and calculated values for the solvation free energies of neutral species, conventional solvation free energies were determined using eqs 15 and 16 for all of the acids in Table 4. These conventional solvation free energies and the auxiliary data used in eqs 15 and 16 are listed in Table 5.
TABLE 4.
Acid Dissociation Constants in Different Solvents
| pKaa |
||||
|---|---|---|---|---|
| ion | neutral | CH3OH | CH3CN | DMSO |
| NO2− | nitrous acid | 7.5 | ||
| NO3− | nitric acid | 8.9136 | ||
| CH3CO2− | acetic acid | 9.5,140 9.6,135 9.6,148 9.6,156 9.7,154 9.8139 | 22.3,147 22.3,151 22.3153 | 12.3 |
| CH3CH2CO2− | propionic acid | 9.7,140 9.7156 | ||
| NCCH2CO2− | cyanoacetic acid | 18.0152 | ||
| CF3CO2− | trifluoroacetic acid | 12.7153 | ||
| C6H5CO2− | benzoic acid | 9.3,140 9.3,156 9.4,134 9.4,137 9.4,149 9.5139 | 20.7,142 20.7141 | 11.0 |
| p−FC6H4CO2− | 4-fluorobenzoic acid | 9.2156 | ||
| C6H5O− | phenol | 14.3,156 14.4,142 14.5148 | 26.7,138 27.2143 | 18.0 |
| p-NO2C6H4O− | 4-nitrophenol | 11.1,140 11.3,156 11.5148 | ||
| CH3O− | methanol | 29.0 | ||
| C2H5O− | ethanol | 29.8 | ||
| NH4+ | ammonia | 10.8156 | 16.5138 | 10.5 |
| CH3NH3+ | methylamine | 11.0156 | 18.4138 | 11.0 |
| (CH3)3NH+ | trimethylamine | 9.8156 | ||
| C5H10NH2+ | piperidine | 11.1156 | ||
| pyridineH+ | pyridine | 5.4,142 5.4156 | 12.3,138 12.3146 | 3.5 |
| C6H5NH3+ | aniline | 6.1156 | 10.6,138 10.7,144 10.7146 | 3.6 |
For anions, pKa of the neutral species. For cations, pKa of the ionic species. For methanol and acetonitril the literature reference for each experimental value is listed to the right of the value in superscript. For DMSO, a experimental values were taken from reference 155.
TABLE 5.
Absolute (Neutral Species) and Conventional (Ionic Species) Solvation Free Energies of Brønsted-Lowry Acids and Bases (kcal/mol)
| pKaa |
ΔGS* (neutral)b |
ΔGS*,con (ion)c |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ion | neutral | ΔGgod | CH3OH | CH3CN | DMSO | CH3OH | CH3CN | DMSO | CH3OH | CH3CN | DMSO |
| NO2− | nitrous acid | 333.7 | 7.5 | −4.2 | −329.6 | ||||||
| NO3− | nitric acid | 317.8 | 8.9 | −5.7 | −313.3 | ||||||
| CH3CO2− | acetic acid | 341.4 | 9.7 | 22.3 | 12.3 | −7.2 | −6.5 | −7.4 | −337.3 | −319.5 | −333.9 |
| CH3CH2CO2− | propionic acid | 340.4 | 9.7 | −7.1 | −336.2 | ||||||
| NCCH2CO2− | cyanoacetic acid | 323.7 | 18.0 | −8.5 | −309.6 | ||||||
| CF3CO2− | trifluoroacetic acid | 316.7 | 12.7 | −7.4 | −308.7 | ||||||
| C6H5CO2− | benzoic acid | 333.0 | 9.4 | 20.7 | 11.0 | −9.7 | −9.4 | −10.3 | −331.8 | −316.1 | −330.2 |
| p-FC6H4CO2− | 4-fluorobenzoic acid | 330.0 | 9.2 | −8.6 | −328.0 | ||||||
| C6H5O− | phenol | 342.9 | 14.4 | 27.0 | 18.0 | −8.2 | −7.5 | −8.1 | −333.5 | −315.6 | −328.4 |
| p-NO2C6H4O− | 4-nitrophenol | 320.9 | 11.3 | −11.0 | −318.5 | ||||||
| CH3O− | methanol | 375.0 | 29.0 | −4.8 | −342.2 | ||||||
| C2H5O− | ethanol | 371.3 | 29.8 | −5.3f | −337.9 | ||||||
| NH4+ | ammonia | 195.7 | 10.8 | 16.5 | 10.5 | −5.0 | −4.5 | −4.3 | 177.9 | 170.7 | 179.0 |
| CH3NH3+ | methylamine | 206.6 | 11.0 | 18.4 | 11.0 | −4.6 | −3.7 | −3.6 | 188.9 | 179.8 | 189.9 |
| (CH3)3NH+ | trimethylamine | 219.4 | 9.8 | −5.0 | 203.0 | ||||||
| C5H10NH2+ | piperidine | 220.0 | 11.1 | −6.5 | 200.3 | ||||||
| pyridineH+ | pyridine | 214.7 | 5.4 | 12.3 | 3.5 | −6.4 | −6.1 | −5.6 | 202.9 | 193.8 | 206.3 |
| C6H5NH3+ | aniline | 203.3 | 6.1 | 10.7 | 3.6 | −7.4 | −7.3 | −7.1 | 189.5 | 183.4 | 193.2 |
Average value from Table 4.
Calculated (SM5.43R/mPW1PW/6−31+G(d,p)//mPW1PW/MIDI!) value, unless indicated otherwise.
Based on the convention that ΔGS*,con (H+) = 0.
For anions, gas-phase acidity of the neutral species. For cations, gas-phase acidity of the ionic species. Experimental data are from reference 169.
eThis conventional solvation free energy was not used.
Reference 10.
3.4. Comparison Between Conventional Solvation Free Energies Obtained Using Different Methods
With the exception of eqs 15 and 16, which have appeared in several of our previous papers,7,56,111 the accuracy of all of the equations that were used in this article to determine conventional solvation free energies in this article were verified by comparing conventional aqueous solvation free energies determined using these equations to those listed in the compilation by Fawcett.124 In all cases, the conventional aqueous solvation free energies determined here are in good agreement with those reported by Fawcett. This is encouraging, because it demonstrates not only the correctness of the equations used here but also, more importantly, the accuracy of the experimental gas-phase and aqueous-phase data that were used to test the equations. For all of the polyatomic ions considered in this article, the conventional solvation free energies were determined using only one of the equations described above (either eq 15 or 16), so that a comparison between these conventional solvation free energies, which might provide some insight into the relative accuracy of the experimental pKa data that were used in this article, is not possible. Equations 10 and 13 have both been used to determine the conventional solvation free energies of Cl− and Br−, and I− in at least one of the nonaqueous solvents considered in this work. Thus, the conventional solvation free energies of these anions can be used to examine the relative accuracy of the remaining solution-phase experimental data used in this article. An additional check on the relative accuracy of the data in Table 3 (and thus Table 1) can be made because in all three solvents, two or more values for the conventional solvation free energies of Cl− and Br− have been determined in each solvent using experimental solubility products of different salts. For example, for Br− in methanol, eq 13 has been used to make four independent determinations of its conventional solvation free energy based on experimental values for the solubility products of KBr, RbBr, AgBr, and TlBr and the conventional solvation free energies of corresponding cations. The largest difference between any of the four values listed in Table 3 for the conventional solvation free energy of Br− in methanol is 0.7 kcal/mol. The largest discrepancy between any of the conventional solvation free energies listed in Table 3 for a given anion in a given solvent is 4.4 kcal/mol, which is the difference between the conventional solvation free energy of Br− in acetonitrile determined using the solubility product of AgBr and the conventional solvation free energy of Ag+, and the value obtained using the solubility product of CsBr and the conventional solvation free energy of Cs+. Besides this difference, all of the remaining conventional solvation free energies listed in Table 3 for a given anion in a given solvent are within 2.3 kcal/mol of one another.
Next, we can compare the relative accuracy of the solution-phase data used in eq 10 to that used in eq 13. Using eq 10 leads to values of −334.8, −329.0, and −321.6 kcal/mol for the conventional solvation free energies of Cl−, Br−, and I−, respectively, in methanol. From Table 3, the average values for the conventional solvation free energies of Cl−, Br−, and I− are −335.7, −329.4, and −321.7 kcal/mol, respectively. The differences between these two sets of conventional solvation free energies are 0.9, 0.4, and 0.1 kcal/mol for Cl−, Br−, and I−, respectively.
4. Conventional Solvation Free Energies of Clustered Ions
Conventional solvation free energies of clustered ions can be defined in the same way as unclustered ions, that is
| (17) |
| (18) |
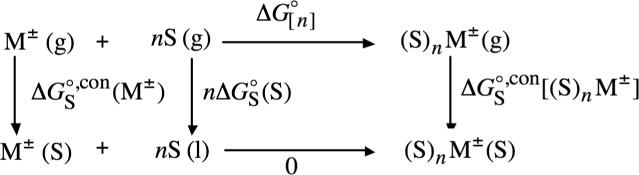
where n is the number of clustering solvent (S) molecules. Through the use of thermochemical cycle 6 (illustrated in Scheme 6)132 the conventional solvation free energy of clustered cations and anions can be written in terms of the conventional solvation free energy of their analogous unclustered ions according to
| (19) |
where M± is the same as M+, X−, BH+ and A−, is the free energy associated with moving the solute from the gas phase into its own pure liquid phase (often, we refer to this free energy as a “self solvation free energy”166) and is the sum of the stepwise clustering free energies of M± with n solvent (S) molecules in the gas-phase
| (20) |
where
| (21) |
Note that the concentration of the pure liquid does not appear in eq 19 because we use as a standard state an ideal dilute solution, for which the activity of the pure liquid is very nearly equal to unity.167 In this standard-state, the free energy associated with the following reaction
| (22) |
which we have also used in previous work7,56,111 and is shown in the bottom leg of thermochemical! cycle 6, is equal to zero for any value of n.168
SCHEME 6.
Thermochemical Cycle 6
Free energies of self solvation can be determined using the following equation166
| (23) |
where Mo is equal to 1 mol/L, Po is the pressure (24.45 atm) of an ideal gas at 1 molar concentration and 298 K, and Mliq is the molarity of the solute in its pure liquid form, which can be calculated from the density of the solute in its pure liquid state and its molecular weight
| (24) |
Using eqs 23 and 24, we determined the free energies of self solvation of methanol, acetonitrile, and DMSO. These solvation free energies and the auxiliary data used in eqs 23 and 24 are listed in Table 6.
TABLE 6.
Solvation Free Energies of Different Solutes in Their Pure Liquids
Experimental values are available for the gas-phase free energies associated with attaching one or more methanol, acetonitrile, or DMSO molecules to many of the monatomic ions in Tables 1-3, as well as to some of the polyatomic ions listed in Table 5.169 These experimental gas-phase free energies are listed in Table 7, for up to n = 3 in some cases. For some of the polyatomic ions in Table 5, we used eq 21 to calculate the gas-phase free energy associated with attaching a single solvent molecule to the ion. These calculated gas-phase clustering free energies, which are also listed in Table 7, are described below.
TABLE 7.
Gas-Phase Clustering Free Energiesa (kcal/mol) of Ions with Various Solvents
| CH3OH |
CH3CN |
DMSO |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| (0,1) | (1,2) | (2,3) | (0,1) | (1,2) | (2,3) | (0,1) | (1,2) | (2,3) | |
| Cl− | −10.0 | −7.0 | −4.7 | −9.5 | −7.1 | −5.0 | −12.5 | −8.9 | −6.0 |
| Br− | −8.4 | −6.3 | −4.2 | −8.7 | −6.2 | −3.9 | −10.9 | −7.8 | −5.4 |
| I− | −5.9 | −4.4 | −3.1 | −6.6 | −4.6 | −3.0 | −9.2 | −6.2 | −4.1 |
| NO2− | −8.7 | ||||||||
| NO3− | [−7.3] | ||||||||
| CH3CO2− | −10.5 | −9.4 | [−10.2] | ||||||
| CH3CH2CO2− | [−8.0] | ||||||||
| NCCH2CO2− | [−7.0] | ||||||||
| CF3CO2− | [−9.0] | ||||||||
| C6H5CO2− | [−7.3] | [−7.6] | [−7.7] | ||||||
| p-FC6H4CO2− | [−6.9] | ||||||||
| C6H5O− | [−8.1] | [−7.0] | [−7.9] | ||||||
| p-NO2C6H4O− | −5.0 | ||||||||
| CH3O− | [−17.4] | ||||||||
| C2H5O− | [−14.0] | ||||||||
| Na+ | −16.7 | −14.2 | −9.9 | −23.6 | −18.5 | −12.7 | −31.0 | ||
| K+ | −12.5 | −7.6 | −6.2 | −18.0 | −13.4 | −9.8 | −25.8 | −18.9 | −11.7 |
| Rb+ | −15.3 | −11.5 | −8.3 | ||||||
| Cs+ | −13.7 | −10.3 | −7.2 | ||||||
| NH4+ | [−16.1] | −20.4 | −13.6 | −8.4 | [−29.1] | ||||
| CH3NH3+ | −11.8 | [−17.6] | [−23.1] | ||||||
| (CH3)3NH+ | −8.8 | −4.6 | −2.5 | ||||||
| C5H10NH2+ | [−7.6] | ||||||||
| pyridineH+ | [−8.8] | [−13.9] | [−18.3] | ||||||
| C6H5NH3+ | [−9.6] | [−14.4]b | [−18.9] | ||||||
Gas-phase free energy change for the reaction (S)i—1M±+S→(S)iM±, for a standard-state gas-phase pressure of 1 atm. Experimental free energies are from reference 169. Calculated (B97−1/MG3S) free energies are listed in brackets.
An experimental value of −12.0 kcal/mol is reported for this free energy, but was not used in this work (see text).
Theoretical gas-phase clustering free energies were calculated at the B97−1170/MG3S171 level of theory using Gaussian 03.164 (Because the MG3S basis set is not available in the distributed version of Gaussian 03, the “gen” keyword, which allows Gaussian 03 to read an external, user-defined basis set, was used for all B97−1/MG3S calculations. The MG3S basis set can be downloaded via the internet at http://comp.chem.umn.edu/basissets/.) All gas-phase clustering free energies were calculated using a single gas-phase geometry for each solvent molecule, each unclustered ion, and each clustered ion (full geometry optimizations were carried out for all of the clustered ions considered in this work); that is, we did not average over multiple conformations. Gas-phase free energies were calculated following the harmonic-oscillator rigid-rotor approximation.172 When the rigid-rotor approximation is followed for computing the entropy, a contribution equal to RTlnσ, where σ is the symmetry number of the molecule, is added to the calculated gas-phase free energy. (For example, the symmetry number for the ammonium cation, which belongs to the Td point group, is equal to 12, so 1.47 kcal/mol is added to the gas-phase free energy; when symmetry is enforced in the Gaussian 03 program, this is done automatically.) Because for many of the molecules considered in this article the above contribution to the gas-phase free energy is not negligible, we were careful to ensure that symmetry was enforced during all gas-phase calculations (when doing so led to a lowest-free-energy structure). The optimized gas-phase geometries for methanol and DMSO belong to the Cs point group; the optimized gas-phase geometry for acetonitrile belongs to the C3v point group. For the majority of the clustered ions, conformational analyses were required in order to identify the global minimum. For this, we used the same level of theory as above. With the exception of the global minimum for the ammonium-acetonitrile cluster, which belongs to the C3v point group, the geometries corresponding to the global minima for the remaining clustered ions belong to the C1 or Cs point groups. The symmetry point groups and Cartesian coordinates for all of the clustered ions for which B97−1/MG3S geometries were calculated are listed in the Supporting Information.
Using eqs 19 and 20, the free energies of self solvation listed in Table 6, the experimental and calculated gas-phase clustering free energies in Table 7, and the conventional solvation free energies of unclustered ions from Tables 1, 2, 3, and 5, we determined conventional solvation free energies for clustered ions containing up to, in some cases, three methanol, acetonitrile, or DMSO molecules. For the halide anions, in cases where more than one value for the conventional solvation free energy of the unclustered ion is available, we used the average value from Tables 2 and 3. Tables containing all of the conventional solvation free energies of unclustered ions that were used in eq 19, as well as the resulting conventional solvation free energies for all of the clustered ions, are included in the Supporting Information.
5. Cluster Pair Approximation for Determining Absolute Solvation Free Energies of Single Ions
The cluster pair approximation described by Coe, Tuttle, and coworkers.30,53,54 is based on the approximation that the difference between the absolute solvation free energy of a positive and negative cluster ion goes to zero as the cluster size becomes infinite, that is173
| (24) |
Using eqs 17-19, the above equation can be written as174
| (25) |
The left-hand-side (lhs) of the above equation is an approximation to the proton's solvation free energy, based on conventional solvation free energies of unclustered ions and the gas-phase free energy associated with attaching n solvent molecules to the cation and to the anion. On the right-hand-side (rhs) of the above equation are the absolute solvation free energy of the proton and the gas-phase free energy associated with attaching an infinite number of solvent molecules to an anion and to a cation already containing n solvent molecules. All three of the quantities on the rhs of eq 25 are unknown. Thus, the goal of eq 25, which is also referred to as the cluster pair approximation, is to identify a cation−anion pair for which the term in brackets on the rhs of eq 25 equals zero, in which case the lhs of eq 25 is equal to the proton's true aqueous solvation free energy (note that this ideal cation−anion pair need not actually exist). It has been shown30,53,54 that an effective way to do this is by plotting the lhs of eq 25 against half the difference between the conventional solvation free energy of X− and M+ for different values of n, giving n straight lines that share a common intersection point at the true value for the solvation free energy of the proton. This is the approach that will be used in this article.
6. Absolute Solvation Free Energy of the Proton and Normal Hydrogen Electrode Potential in Different Solvents
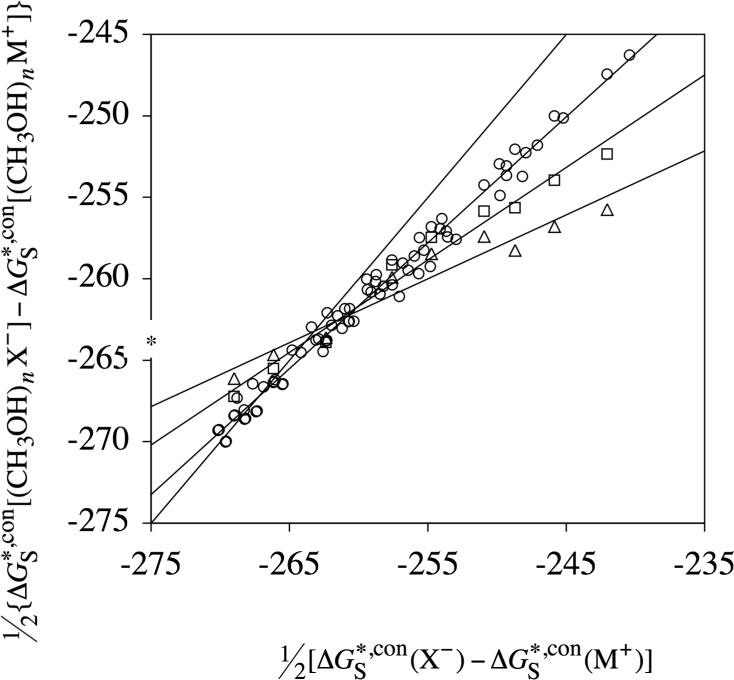
6.1. Methanol
Shown in Figure 1 is a plot of half the difference between conventional solvation free energies of anions and of cations for cluster ions containing up to three methanol molecules against half the difference between conventional solvation free energies of anions and of cations containing no methanol molecules, for different numbers of clustering methanol molecules. The differential conventional solvation free energies in this plot were computed using the conventional solvation free energies in Tables 1, 2, 3, and 5 and the gas-phase clustering free energies in Table 6. All of the conventional solvation free energies that were used to determine the differential solvation free energies shown in Figure 1 are listed in Table S2 in the Supporting Information. (Tables S3 and S4 list the conventional solvation free energies that were used to determine the differential solvation free energies plotted in Figures 2 and 3.) The straight lines in Figure 1 are best-fit lines for different numbers of clustering methanol molecules. The line for n = 0 (no clustering methanol molecules) is the ideal line (y = x). The ordinate of the intersection point between each line gives an approximate value for the absolute solvation free energy of the proton, so in all, 6 individual determinations can be made from the data shown in Figure 1 (The 4 straight lines give 6 unique intersection points between different values of n.) To determine the best value of the absolute solvation free energy of the proton, we used the same method of statistical analysis as in our earlier work.56 For this, the average intersection ordinate of the ith straight line with all others (Yi) is given by
| (27) |
where
| (28) |
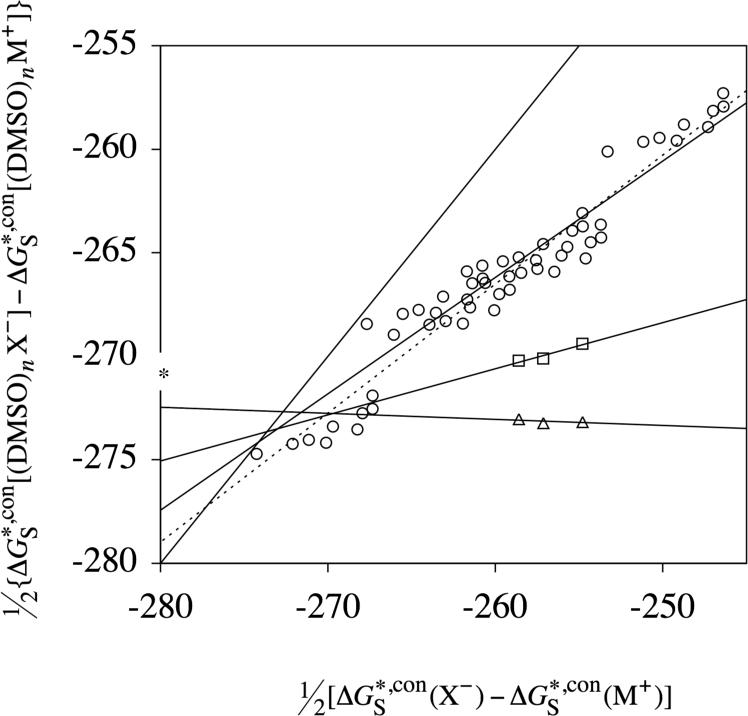
In the above equation, yij is the ordinate of the intersection point between the ith and jth straight line, and mii and bi are the slope and intercept, respectively, of the ith straight line. We take the best value for the absolute solvation free energy of the proton to equal the unweighted average of the four Yi values determined using eqs 27 and 28. For the data in Figure 1, this average equals −263.5 kcal/mol. The standard deviation of the 6 values of yij from the average value of yij is 2.0 kcal/mol. The individual slopes, intercepts, Yi and yij values obtained from the data shown in Figure 1, as well as from the data shown in Figures 2 and 3 (described below), are included as Supporting Information. Note that we could have also used weighted values of yij according to the probable errors of each of the straight lines i and j. Indeed, the standard deviations of the 3 straight lines in Figure 1 do increase with n (number of clustering methanol molecules). However, this type of analysis would not take into account that the ordinate of the intersections between the lines with larger slopes (low n) are more prone to error because small changes in their slopes will cause the correspondingly largest variations in the value of the ordinate.
Figure 1.
Half the difference between conventional solvation free energies of anions and of cations in methanol for cluster ions containing up to three methanol molecules plotted vs half the difference between conventional solvation free energies of anions and of cations in methanol containing no methanol molecules. Differences between cluster ions containing one methanol molecule are plotted as circles, two as squares, and three as triangles. The ordinate of the average intersection point between each of the straight lines is an estimate of the value for the absolute solvation free energy of the proton. The asterisk on the ordinate is the absolute solvation free energy that results from using the TATB approximation.
Figure 2.
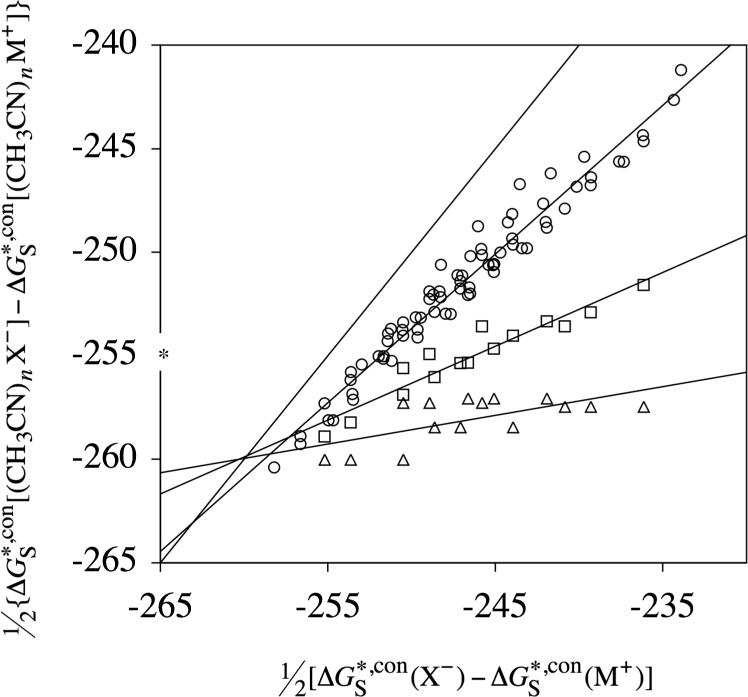
Same as Figure 1, except for acetonitrile.
Figure 3.
Same as Figures 1 and 2, except for DMSO. The dashed line is the best-fit line computed using differential solvation free energies between all anions and all cations, containing up to a single DMSO molecule (open circles). The corresponding solid line is the best-fit line computed after excluding differential solvation free energies between anions and pyridinium (lower leftmost open circles). The slope and intercept obtained after excluding pyridinium (solid line) was used to obtain the final value of the absolute solvation free energy of the proton in DMSO.
Through the use of thermochemical cycle 7 (illustrated in Scheme 7), the absolute solvation free energy can be used to set the normal hydrogen electrode potential according to
| (26) |
where is the gas-phase free energy of formation of the proton. (The free energy of formation of H2(g) and of the electron do not appear in eq 26 because they are equal to zero.) As was pointed out above, the value for the free energy of formation of the proton depends on whether Boltzmann or Fermi-Dirac statistics are used to compute the integrated heat capacity and entropy of the electron. In this article, we have used the electron integrated heat capacity and entropy reported by Bartmess,116 which were obtained using Fermi-Dirac statistics. When these values for the electron integrated heat capacity and entropy are used, the free energy of formation of the gas-phase proton equals 361.7 kcal/mol at 298 K and 1 atm, which when substituted into eq 26 gives a value of −4.34 V for the normal hydrogen electrode potential in methanol. (Using the electron integrated heat capacity and entropy obtained from Boltzmann statistics leads to a value for the normal hydrogen electrode potential 0.04 V more negative than the value above).
SCHEME 7.
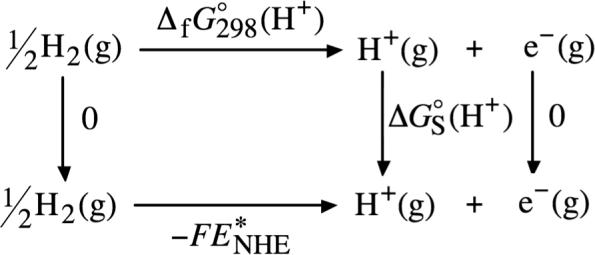
Thermochemical Cycle 7
6.2. Acetonitrile
Applying eqs 27 and 28 to the data in Figure 2 gives an average value of −260.2 kcal/mol for the absolute solvation free energy of the proton in acetonitrile. The standard deviation of the 6 values of yij from the average value of yij is 1.4 kcal/mol. In our initial fit, we discovered that for n = 1, the differences between the conventional solvation free energies of anions and of anilinium (9 data points) were systematically more positive than the differences between the conventional solvation free energies of anions and of the remaining cations by ∼3 kcal/mol. The experimental value for the gas-phase free energy associated with attaching a single acetonitrile molecule to anilinium is −12.0 kcal/mol.169,175 We also calculated this free energy at the B97−1/MG3S level of theory, which leads to a value of −14.4 kcal/mol. When the calculated instead of the experimental value for the gas-phase clustering free energy is used to determine the conventional solvation free energy of the anilinium-acetonitrile cluster, the differences between the conventional solvation free energies of clustered anions and of the anilinium-acetonitrile cluster fall into line with the remaining data points. Because of this, we used the calculated instead of the experimental value for this clustering free energy in our final fit, which is the one shown in Figure 2.
Substituting the value obtained above for the absolute solvation free energy of the proton in acetonitrile (−260.2 kcal/mol) and the value for the free energy of formation of the gas-phase proton obtained using Fermi-Dirac statistics for the integrated heat capacity and entropy of the electron into eq 26 gives a value of −4.48 V for the normal hydrogen electrode potential in acetonitrile.
6.3. DMSO
Applying eqs 27 and 28 to all of the data in Figure 3 gives an average value of −273.7 kcal/mol for the absolute solvation free energy of the proton in DMSO. The standard deviation of the 6 values of yij from the average value of yij is 1.8 kcal/mol. For n = 1, the differences between the conventional solvation free energies of anions and of pyridinium, which are shown in the lower left-hand corner of Figure 3, tend to fall on a different line than the differences between the conventional solvation free energies of anions and of the remaining cations. Because of this, we removed all of the differences between the conventional solvation free energies of anions and of pyridinium, and then repeated the n = 1 fit using the remaining data. The resulting best-fit line is shown as a solid line in Figure 3.
Experimental gas-phase clustering free energies for ion-DMSO clusters containing more than a single DMSO molecule are scarcer than for the other solvents considered in this work. Experimental clustering free energies for n > 1 are only available for 4 of the ions in Table 6 (Br−, Cl−, I−, and K+). The best-fit lines for n = 2 and n = 3, albeit based on the minimum amount of data points required to determine a statistically meaningful best-fit line, suggest that the best-fit line for n = 1 obtained after removing pyridinium (solid n = 1 line) is more accurate than the best-fit line obtained using all of the data (dashed n = 1 line). Applying eqs 27 and 28 to the slopes and intercepts of the solid n = 1 line and the n = 2 and n = 3 lines in Figure 3 gives an average value of −273.3 kcal/mol for the absolute solvation free energy of the proton in DMSO. The standard deviation of the 6 values of yij from the average value of yij is 0.6 kcal/mol.
Substituting the final value obtained above for the absolute solvation free energy of the proton in DMSO (−273.3 kcal/mol) and the value for the free energy of formation of the gas-phase proton obtained using Fermi-Dirac statistics for the integrated heat capacity and entropy of the electron into eq 26 gives a value of −3.92 V for the normal hydrogen electrode potential in DMSO.
7. Accuracy of the Absolute Solvation Free Energies Obtained in This Work
In our previous work where we applied the cluster pair approximation to aqueous solution,56 we estimated that the uncertainty associated with the absolute aqueous solvation free energy of the proton is no less than 2 kcal/mol. Based on the uncertainties associated with the experimental and calculated data used in this work, we estimate that uncertainties associated with the absolute solvation free energy of the proton in methanol and acetonitrile are 2−3 kcal/mol. For DMSO, where only a limited amount of gas-phase clustering data for n > 1 is available, the estimated uncertainty for the absolute solvation free energy of the proton is 3−4 kcal/mol.
Because many of the gas-phase clustering free energies for singly clustered polyatomic ions that were used in this work were obtained theoretically (all gas-phase clustering free energies for clusters containing more than a single solvent molecule are experimental), an important issue is what effect the inclusion of these theoretical data has on the overall accuracy of the results obtained here. In previous work where we determined the absolute aqueous solvation free energy of the proton using the cluster pair approximation,56 we showed that augmenting experimental gas-phase clustering data with theoretical data had little effect on the accuracy of the predictions made there. The same level of theory that was used in that work, B97−1/MG3S, was also used here because it has been shown in several places176-179 to perform well for nonbonded interactions in the gas phase. To further demonstrate the accuracy of this level of theory, we calculated gas-phase clustering free energies for all of the polyatomic ions in Table 7 for which experimental n = 1 clustering free energies are available (total of 8 ion-solvent clusters). Excluding the difference between the experimental and calculated value for the anilinium-acetonitrile cluster (the experimental value for this free energy may be in error, see above), the mean unsigned error between the calculated and experimental clustering free energies for the remaining 7 ion-solvent clusters is only 0.26 kcal/mol. The maximum difference is 1.82 kcal/mol, which is the difference between the calculated and experimental gas-phase clustering free energy of the acetate−methanol cluster.
Besides gas-phase clustering free energies for singly clustered ions, calculated values for the solvation free energies of neutral species were used in eqs 15 and 16 to determine conventional solvation free energies. In this work, we used the SM5.43R continuum solvation model to calculate solvation free energies of neutral species. The accuracy of this model has been previously demonstrated in several places,12,157 where it has been shown that for typical neutral organic compounds, the solvation free energies calculated using this model are accurate to within ∼0.5 kcal/mol. Thus, the accuracy of the results obtained here has most likely not been compromised by the inclusion of calculated solvation free energies of neutral species. On the contrary the consistency of the theoretical and experimental data gives us further confidence in the soundness of our approach.
Most of the experimental pKsp values used in this work are sufficiently large so as to safely assume that the solvation free energies of the corresponding salts are fairly representative of the ion pairs in infinitely dilute solution. A notable exception is the experimental pKsp of KBr in DMSO (equal to 0.6), which we used to determine the conventional solvation free energy of K+ in DMSO. In this case, the ionic strength of the saturated solution is equal to 1 mol/L, whereas the concentration of pure DMSO is 14 mol/L. Thus, for this electrolytic solution the above assumption of a dilute solution does not apply. However, we also determined the conventional solvation free energy of K+ in DMSO using an experimental value (3.1) for the pKsp of KCl. The conventional solvation free energies of K+ from these two pKsp values are within 0.3 kcal/mol of one another, suggesting the above concern is not a serious issue.
Finally, it should be noted that in this work, we assume all experimental pKa values correspond to the equilibrium constant between the neutral and ionic species in their completely dissociated states. Ion pairing is generally negligible in solvents with dielectric constants above 40, whereas its importance depends on the structure of the solvent and the electrolyte for solvents with dielectric constants of 15−20.180 The solvents considered in this paper have dielectric constants of 32.66 (methanol), 35.94 (acetonitrile), and 46.45 (DMSO), and we will assume that ion pairing is negligible.
8. Previous Estimates of the Absolute Solvation Free Energy of the Proton in Methanol, Acetonitrile, and DMSO
Kalidas and coworkers58 have reported values for the transfer free energies of single ions between water and 17 different organic solvent systems, including pure methanol, acetonitrile, and DMSO. Based on a careful evaluation of the available literature data, these authors were able to list recommended values for the transfer free energies of the proton between water and the above solvents. All of these recommended transfer free energies were obtained using the TATB approximation. The values recommended by these workers for the transfer free energy of the proton between water and methanol, acetonitrile, and DMSO are 2.1, 10.7, and −4.6 kcal/mol, respectively. These transfer free energies, as well as the transfer free energies discussed below, are listed in Table 8. (It is worth noting that the value above for the transfer free energy of the proton between water and DMSO has been used by Pliego and Riveros to determine the absolute solvation free energies of 30 other monovalent ions in DMSO.181)
TABLE 8.
Solvation Free Energy of the Proton (kcal/mol) and Normal Hydrogen Electrode Potential (Volts) in Different Solvents
|
a |
||||
|---|---|---|---|---|
| solvent | b | c | this work | literature |
| H2O | −265.9d | −4.24 | − | − |
| CH3OH | −263.5 | −4.34 | 2.4 | 2.1e |
| CH3CN | −260.2 | −4.48 | 5.7 | 10.7e |
| DMSO | −273.3 | −3.92 | −7.4 | −4.6,e −7.3f |
Transfer free energy of the proton from water to the solvent in this row.
Absolute solvation free energy of the proton obtained using the cluster pair approximation.
Normal hydrogen electrode potential. These values were obtained using the values for the electron integrated heat capacity and entropy reported by Bartmess,116 who used Fermi-Dirac statistics. Using Boltzmann statistics for the integrated heat capacity and entropy of the electron gives values of −4.28, −4.38, −4.52, and −3.96 V for the normal hydrogen electrode potential in water, methanol, acetonitrile, and DMSO, respectively.
Reference 53.
Reference 58.
Reference 107.
Combining Tissandier et al.'s value for the absolute aqueous solvation free energy of the proton (−265.9 kcal/mol), with the values for the absolute solvation free energy of the proton obtained here lead to transfer free energies of 2.4, 5.7, and −7.4 kcal/mol for methanol, acetonitrile, and DMSO, respectively. For methanol, the transfer free energy obtained here using the cluster pair approximation is within 0.3 kcal/mol of the value recommended by Kalidas et al. Considering the uncertainties associated with the absolute solvation free energies obtained here, the agreement between the transfer free energy of the proton in DMSO obtained here and that reported by Kalidas et al. is satisfactory. On the other hand, for acetonitrile the agreement between the value obtained here and that reported by Kalidas et al. is not very good (5.0 kcal/mol difference). One reason for this difference is that errors might be present in the experimental data used by Kalidas et al. to derive this transfer free energy. Indeed, unlike most of the transfer free energies recommended by these workers, which are average values taken from several places, the experimental data used to determine the transfer free energy of the proton between water and acetonitrile was taken from a single source.182 Furthermore, Kalidas et al. list this value as tentative and state that it “must be considered doubtful at this stage.”
It is important to point out that, like the transfer solvation free energies reported in this work, many of the transfer free energies reported by Kalidas et al. are also based on differences between experimental standard reduction potentials and solubility products in water and in nonaqueous solvents (see ref 183). The uncertainties in the relative solvation free energies determined using these data are relatively small, whereas for single ions we assign uncertainties that are much larger (2−4 kcal/mol) based on our estimate of the uncertainty associated with the extrathermodynamic assumption used in this article (i.e. the cluster pair approximation) for splitting well-defined sums of solvation free energies into single-ion values. It is not exactly clear what value for the uncertainty should be assigned to the single-ion transfer free energies reported by Kalidas et al., although these authors state that their values are accurate “within the constraints of the TATB assumption” to ±0.7 kcal/mol. However, the above differences, as well as previous experimental41,42,44,46-48 and theoretical work,49-51 suggest that the uncertainty associated with single ion solvation free energies obtained using the TATB assumption is larger than 0.7 kcal/mol (and perhaps larger than any of the uncertainties reported here).
Recently, Westphal and Pliego performed high-level gas-phase calculations on Li+ and Na+ clusters containing up to four and five explicit DMSO molecules, respectively.107 Using these clustered ions and a dielectric continuum model, these workers calculated the absolute solvation free energies of Li+ and Na+ using an equation similar to eq 19 shown here. Based on the difference between the calculated absolute solvation free energies of these ions, these workers determined the absolute solvation free energy of the proton in DMSO to be −273.2 kcal/mol. Combining this value with Tissandier's value for the absolute aqueous solvation free energy of the proton leads to a transfer free energy of −7.3 kcal/mol, which is in nearly perfect agreement with the value obtained in this work.
Besides the two extrathermodynamic assumptions discussed above (cluster pair and TATB) single-ion solvation free energies have also been estimated based on measurements of the Volta (outer) potential between two different phases brought into contact with one another.18,184-193 Unlike the solvation free energies obtained using the cluster pair or TATB approximations, the solvation free energies obtained from these types of experiments contain, in addition to the free energy required to couple the solute to the bulk solvent, a free energy term that depends on the surface potentials of the two phases that are brought into contact with one another. (As discussed in the first paragraph of the present article, the solvation free energies resulting from these types of experiments are usually referred to as real solvation free energies to distinguish them from absolute, or Gibbs, solvation free energies, which do not contain the contribution due to the potential of the phase.) Because it is generally agreed that the surface potential of a bulk liquid cannot be directly measured experimentally, one must resort to extrathermodynamic assumptions or theoretical calculations in order to make direct comparisons between real and absolute solvation free energies of single ions. (The distinction between real and absolute solvation free energies does not need to be made when one considers the transfer for pairs of ions with no net charge because the contribution to the solvation free energy due to the potential of the phase cancels out.) For example, Coetzee192 assigned tentative values to the surface potential of several nonaqueous solvents by combining transfer free energies obtained from measurements of Volta potential differences and those estimated using the TATB approximation.194
In this article and in our previous work,111,195,196 we have assigned values to the normal hydrogen electrode potential using the absolute solvation free energy of the proton, which does not contain the contribution to the free energy due to the potential of the phase. However, in other work (cf. ref191), real solvation free energies, which do contain this contribution, have been used to assign a value to the normal hydrogen electrode potential. In principle, it is correct to use either real or absolute solvation free energies for assigning a value to the normal hydrogen electrode potential, because, as pointed out by Trasatti,197 there are several different, but equally valid ways to define the normal hydrogen electrode potential. However, reported values for the normal hydrogen electrode potential are often used in conjunction with thermochemical cycle 7 in order to “back out” the absolute value for the solvation free energy of the proton. Thus, from a practical standpoint, one must be aware of whether this value represents a real or an absolute solvation free energy, since these two quantities can differ significantly. (A recent theoretical estimate of the surface potential of bulk water puts this value at −12.7 kcal mol−1 e−1.198) The distinction between these two quantities can become especially important when absolute solvation free energies obtained from continuum solvation calculations, which do not include the contribution due to the potential of the phase, are unknowingly combined with solvation free energies that do contain this contribution. Because of this, for applications that involve the use of solvation free energies obtained from continuum solvation calculations (e.g., calculating absolute acid dissociation constants via thermochemical cycles 4 and 5), we recommend using the absolute solvation free energies reported in this article.
9. Conclusions
Using a combination of experimental gas-phase free energies of formation and solution-phase reduction potentials and acid dissociation constants, conventional solvation free energies of unclustered ions in methanol, acetonitrile, and DMSO were determined. These conventional solvation free energies were then combined with experimental and calculated gas-phase clustering free energies to determine conventional solvation free energies of ion-solvent clusters containing up to three solvent molecules. The cluster pair approximation was applied to the above data in order to determine the absolute solvation free energy of the proton in methanol, acetonitrile, and DMSO. For methanol, the value obtained here agrees fairly well with an earlier value based on the TATB approximation, whereas the agreement is satisfactory for DMSO and not very good for acetonitrile. The values for the absolute solvation free energy of the proton obtained in this work should be useful as standards against which the absolute solvation free energies of other single ions can be derived. For example, Table 9 shows the absolute single-ion solvation free energies of the ions considered in this work.
TABLE 9.
Absolute Single-Ion Solvation Free Energies ΔGS* (in kcal/mol) in Four Solventsa
| ion | H2Ob | CH3OHc | CH3CNc | DMSOc |
|---|---|---|---|---|
| H+ | −265.9 | −263.5 | −260.2 | −273.3 |
| Na+ | −103.2 | −101.1 | −101.1 | −108.9 |
| K+ | −86.0 | −83.3 | −85.5 | −92.2 |
| Rb+ | −80.6 | −81.8 | ||
| Cs+ | −75.1 | −72.4 | ||
| Tl+ | −87.6 | −86.2 | −89.8 | −95.3 |
| Ag+ | −118.7 | −117.1 | −127.8 | −129.0 |
| NH4+ | −85.2 | −85.6 | −89.5 | −94.3 |
| CH3NH3+ | −76.4 | −74.6 | −80.4 | −83.4 |
| (CH3)3NH+ | −61.1 | −60.5 | ||
| C5H10NH2+ | −64.2 | −63.2 | ||
| pyridineH+ | −61.1 | −60.6 | −66.4 | −67.0 |
| C6H5NH3+ | −72.4 | −74.0 | −76.8 | −80.1 |
| Cl− | −74.5 | −71.5 | −62.4 | −62.7 |
| Br− | −68.3 | −65.8 | −59.3 | −59.8 |
| I− | −59.9 | −58.2 | −53.0 | |
| NO2− | −56.3 | |||
| NO3− | −53.1 | |||
| CH3CO2− | −77.6 | −73.8 | −59.3 | −60.6 |
| CH3CH2CO2− | −76.2 | −72.7 | ||
| NCCH2CO2− | −49.4 | |||
| CF3CO2− | −59.3 | −48.5 | ||
| C6H5CO2− | −71.2 | −68.3 | −55.9 | −56.9 |
| p-FC6H4CO2− | −64.5 | |||
| C6H5O− | −71.9 | −70.0 | −55.4 | −55.1 |
| p-NO2C6H4O− | −57.8 | −55.0 | ||
| CH3O− | −95.0 | −68.9 | ||
| C2H5O− | −90.7 | −64.6 | ||
| CH2NO2− | −76.5 | −61.3 | ||
| CH3SOCH2− | −67.7 | −55.4 |
Supplementary Material
Acknowledgments
This work was supported by the National Institutes of Health training grant for Neuro-physical-computational Sciences, by the U. S. Army Research Office under the Multidisciplinary Research Program of the University Research Initiative through Grant No. DAAD19-02-1-0176, by the National Science Foundation (Grant Nos. CHE06-10183 and CHE03-49122), and by the Office of Naval Research under Grant No. N 00014-05-01-0538.
Footnotes
Supporting Information Available: A description of the standard state conventions used in this article, thermochemical conventions for the enthalpy and heat capacity of the electron, enthalpies, entropies, and free energies of formation of monatomic ions, conventional solvation free energies of unclustered and clustered ions, slopes and intercepts for the cluster pair fits, and B97−1/MG3S optimized geometries. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Cabani S, Gianni P, Mollica V, Lepori L. J. Solution Chem. 1981;10:563. [Google Scholar]
- 2.Abraham MH, Whiting GS, Fuchs R, Chambers EJ. J. Chem. Soc., Perkin Trans. 2. 1990:291. [Google Scholar]
- 3.Leo AJ. Masterfile from MedChem Software. BioByte Corp.; Claremont, CA: 1994. [Google Scholar]
- 4.Physical/Chemical Property Database (PHYSPROP) SRC Environmental Science Center; Syracuse, NY: 1994. [Google Scholar]
- 5.Yaffe D, Cohen Y, Espinosa G, Arenas A, Giralt F. J. Chem. Inf. Comput. Sci. 2003;43:85. doi: 10.1021/ci025561j. [DOI] [PubMed] [Google Scholar]
- 6.Sander R. Henry's Law Constants. In: Linstrom PJ, Mallard WG, editors. NIST Chemistry WebBook, NIST Standard Reference Database Number 69. National Institute of Standards and Technology; Gaithersburg, MD: Jun, 2005. [Google Scholar]
- 7.Kelly CP, Cramer CJ, Truhlar DG. J. Chem. Theory Comput. 2005;1:1133. doi: 10.1021/ct050164b. [DOI] [PubMed] [Google Scholar]
- 8.Rizzo RC, Aynechi T, Case DA, Kuntz ID. J. Chem. Theory Comput. 2006;2:128. doi: 10.1021/ct050097l. [DOI] [PubMed] [Google Scholar]
- 9.Li J, Zhu T, Hawkins GD, Winget P, Liotard DA, Cramer CJ, Truhlar DG. Theor. Chem. Acc. 1999;103:9. [Google Scholar]
- 10.Kelly CP, Thompson JD, Hawkins GD, Chambers CC, Giesen DG, Winget P, Cramer CJ, Truhlar DG. Minnesota Solvation Database version 2.0.1. University of Minnesota; Minneapolis, MN: 2006. pp. 55455–0431. [Google Scholar]
- 11.Cramer CJ, Truhlar DG. In: Free Energy Calculations in Rational Drug Design. Reddy MR, Erion MD, editors. Kluwer/Plenum; New York: 2001. p. 63. [Google Scholar]
- 12.Thompson JD, Cramer CJ, Truhlar DG. J. Phys. Chem. A. 2004;108:6532. [Google Scholar]
- 13.Klotz IM, Rosenberg RM. Chemical Thermodynamics. 5th ed. Wiley; New York: 1994. p. 459. [Google Scholar]
- 14.Guggenheim EA. J. Phys. Chem. 1929;33:842. [Google Scholar]
- 15.Guggenheim EA. J. Phys. Chem. 1930;34:1540. [Google Scholar]
- 16.Cox BG. Annu. Repts. Prog. Chem. 1973;A70:249. [Google Scholar]
- 17.Hodgkin AL. Biol. Rev. 1951;26:339. [Google Scholar]
- 18.Izmailov NA. Russ. J. Phys. Chem. 1960;34:1142. [Google Scholar]
- 19.Rosseinsky DR. Chem. Rev. 1965;65:467. [Google Scholar]
- 20.Pliego JR, Jr., Riveros JM. Chem. Phys. Lett. 2000;332:597. [Google Scholar]
- 21.Llano J, Eriksson LE. J. Chem. Phys. 2002;117:10193. [Google Scholar]
- 22.Bhattacharyya R, Lahiri SC. Z. Phys. Chem. 2004;218:515. [Google Scholar]
- 23.Conway BE. Annu. Rev. Phys. Chem. 1966;17:481. [Google Scholar]
- 24.Parker AJ. Chem. Rev. 1969;69:1. [Google Scholar]
- 25.Popovych O. Crit. Rev. Anal. Chem. 1970;7:73. [Google Scholar]
- 26.Kolthoff IM. Pure Appl. Chem. 1971;25:305. [Google Scholar]
- 27.Conway BE. J. Solution Chem. 1978;7:721. [Google Scholar]
- 28.Marcus Y. Pure Appl. Chem. 1986;58:1721. [Google Scholar]
- 29.Krestov GA. Thermodynamics of Solution. Ellis Horwood; New York: 1991. [Google Scholar]
- 30.Coe JV. Int. Rev. Phys. Chem. 2001;20:33. [Google Scholar]
- 31.Born M. Z. Physik. 1920;1:45. [Google Scholar]
- 32.Cramer CJ, Truhlar DG. In: Rev. Comp. Chem. Boyd DB, Lipkowitz KB, editors. Vol. 6. VCH Publishers; New York: 1995. p. 1. [Google Scholar]
- 33.Alexander R, Parker AJ. J. Am. Chem. Soc. 1967;89:5539. [Google Scholar]
- 34.Bernal J, Fowler R. J. Chem. Phys. 1933;1:515. [Google Scholar]
- 35.Fajans K, Johnson O. J. Am. Chem. Soc. 1942;64:688. [Google Scholar]
- 36.Vewrey TE. Rec. Trav. Chim. 1942;61:127. [Google Scholar]
- 37.Mishchenko KP. Russ. J. Phys. Chem. 1952;26:1736. [Google Scholar]
- 38.Grunwald E, Baughman G, Kohnstam C. J. Am. Chem. Soc. 1960;82:5801. [Google Scholar]
- 39.Breck WG, Lin J. Trans. Faraday Soc. 1965;69:222. [Google Scholar]
- 40.Popovych O, Dill AJ. Anal. Chem. 1966;38:588. [Google Scholar]
- 41.Coetzee JF, Sharpe WR. J. Phys. Chem. 1971;75:3141. [Google Scholar]
- 42.Jolicoeur C, Dinh The N, Cabana A. Can. J. Chem. 1971;49:2008. [Google Scholar]
- 43.Alexander R, Parker AJ, Sharpe JH, Waghorne WE. J. Am. Chem. Soc. 1972;94:1148. [Google Scholar]
- 44.Jolicoeur C, Friedman HL. J. Solution Chem. 1974;3:15. [Google Scholar]
- 45.Kim JI. J. Phys. Chem. 1978;82:191. [Google Scholar]
- 46.Farmer RM, Sasaki Y, Popov AI. Aust. J. Chem. 1983;36:1785. [Google Scholar]
- 47.Shao Y, Stewart AA, Girault HH. J. Chem. Soc. Faraday Trans. 1991;87:2593. [Google Scholar]
- 48.Stangret J, Kamienska-Piotrowicz E. J. Chem. Soc. Faraday Trans. 1997;93:3463. [Google Scholar]
- 49.Schurhammer R, Wipff G. J. Mol. Struct. (THEOCHEM) 2000;500:139. [Google Scholar]
- 50.Schurhammer R, Wipff G. J. Phys. Chem. A. 2000;104:11159. [Google Scholar]
- 51.Schurhammer R, Engler E, Wipff G. J. Phys. Chem. B. 2001;105:10700. [Google Scholar]
- 52.Wachter W, Buchner R, Hefter G. J. Phys. Chem. B. 2006;110:5147. doi: 10.1021/jp057189r. [DOI] [PubMed] [Google Scholar]
- 53.Tissandier MD, Cowen KA, Feng WY, Gundlach E, Cohen MJ, Earhart AD, Coe JV. J. Phys. Chem. A. 1998;102:7787. [Google Scholar]
- 54.Tuttle TR, Jr., Malaxos S, Coe JV. J. Phys. Chem. A. 2002;106:925. [Google Scholar]
- 55.Bartels DM, Takahashi K, Cline JA, Marin TW, Jonah CD. J. Phys. Chem. A. 2005;109:1299. doi: 10.1021/jp0457141. [DOI] [PubMed] [Google Scholar]
- 56.Kelly CP, Cramer CJ, Truhlar DG. J. Phys. Chem. B. 2006;110:16066. doi: 10.1021/jp063552y. [DOI] [PubMed] [Google Scholar]
- 57.Camaioni DM, Scherdtfeger CA. J. Phys. Chem. A. 2005;109:10795. doi: 10.1021/jp054088k. [DOI] [PubMed] [Google Scholar]
- 58.Kalidas C, Hefter G, Marcus Y. Chem. Rev. 2000;100:819. doi: 10.1021/cr980144k. [DOI] [PubMed] [Google Scholar]
- 59.Tunon I, Rinaldi D, Ruiz-Lopez MF, Rivail JL. J. Phys. Chem. 1995;99:3798. [Google Scholar]
- 60.Florián J, Warshel A. J. Phys. Chem. B. 1997;101:5583. [Google Scholar]
- 61.Schüürman G, Cossi M, Barone V, Tomasi J. J. Phys. Chem. A. 1998;102:6706. [Google Scholar]
- 62.da Silva CO, da Silva EC, Nascimento MAC. J. Phys. Chem. A. 1999;103:11194. [Google Scholar]
- 63.Vogel HJ, Juffer AH. Theor. Chem. Acct. 1999;101:159. [Google Scholar]
- 64.Chen I-J, MacKerrel AD., Jr. Theor. Chem. Acct. 2000;103:483. [Google Scholar]
- 65.Meijías JA, Lago S. J. Chem. Phys. 2000;113:7306. [Google Scholar]
- 66.Pliego JR, Jr., Riveros JM. J. Phys. Chem. B. 2000;104:5155. [Google Scholar]
- 67.Silva CO, da Silva EC, Nascimento MAC. J. Phys. Chem. A. 2000;104:2402. [Google Scholar]
- 68.Topol IA, Tawa GJ, Caldwell RA, Eissenstat MA. J. Phys. Chem. A. 2000;104:9619. [Google Scholar]
- 69.Jang YH, Sowers LC, Çagin T, Goddard WA., III J. Phys. Chem. A. 2001;105:274. [Google Scholar]
- 70.Liptak MD, Shields GC. Int. J. Quantum Chem. 2001;85:727. [Google Scholar]
- 71.Liptak MD, Shields GC. J. Am. Chem. Soc. 2001;123:7314. doi: 10.1021/ja010534f. [DOI] [PubMed] [Google Scholar]
- 72.Ohno K, Kamiya N, Asakawa N, Inoue Y, Sakurai M. Chem. Phys. Lett. 2001;341:387. doi: 10.1021/ja015589w. [DOI] [PubMed] [Google Scholar]
- 73.Toth AM, Liptak MD, Phillips DL, Shields GC. J. Chem. Phys. 2001;114:4595. [Google Scholar]
- 74.Zhan C-G, Dixon DA. J. Phys. Chem. A. 2001;105:11534. [Google Scholar]
- 75.Adam K. J. Phys. Chem. A. 2002;106:11963. [Google Scholar]
- 76.Chipman DM. J. Phys. Chem. A. 2002;106:7413. [Google Scholar]
- 77.Davies JE, Doltsinis NL, Kirby AJ, Roussev CD, Sprik M. J. Am. Chem. Soc. 2002;124:6594. doi: 10.1021/ja025779m. [DOI] [PubMed] [Google Scholar]
- 78.Feierberg I, Åqvist J. Theor. Chem. Acct. 2002;108:71. [Google Scholar]
- 79.Klicic JJ, Friesner RA, Liu S-Y, Guida WC. J. Phys. Chem. A. 2002;106:1327. [Google Scholar]
- 80.Li H, Hains AW, Everts JE, Robertson AD, Jensen JH. J. Phys. Chem. B. 2002;106:1327. [Google Scholar]
- 81.Liptak MD, Gross KC, Seybold PG, Feldgus S, Shields GC. J. Am. Chem. Soc. 2002;124:6421. doi: 10.1021/ja012474j. [DOI] [PubMed] [Google Scholar]
- 82.Lopez X, Schaefer M, Dejaegere A, Karplus M. J. Am. Chem. Soc. 2002;124:5010. doi: 10.1021/ja011373i. [DOI] [PubMed] [Google Scholar]
- 83.Satchell JF, Smith BJ. Phys. Chem. Chem. Phys. 2002;4:4314. [Google Scholar]
- 84.Zhan C-G, Dixon DA. J. Phys. Chem. A. 2002;106:9737. [Google Scholar]
- 85.Asthagiri D, Pratt LR, Ashbaugh HS. J. Chem. Phys. 2003;119:2702. doi: 10.1063/1.2202350. [DOI] [PubMed] [Google Scholar]
- 86.Camaioni DM, Dupuis M, Bentley J. J. Phys. Chem. A. 2003;107:5778. [Google Scholar]
- 87.Grossfield A, Ren P, Ponder JW. J. Am. Chem. Soc. 2003;125:15671. doi: 10.1021/ja037005r. [DOI] [PubMed] [Google Scholar]
- 88.Jang YH, Goddard WA, III, Noyes KT, Sowers LC, Hwang S, Chung DS. J. Phys. Chem. B. 2003;107:344. [Google Scholar]
- 89.Klamt A, Eckert F, Diedenhofen M, Beck ME. J. Phys. Chem. A. 2003;107:9380. doi: 10.1021/jp034688o. [DOI] [PubMed] [Google Scholar]
- 90.Li G, Cui Q. J. Phys. Chem. B. 2003;107:14521. [Google Scholar]
- 91.Mujika JI, Mercero JM, Lopez X. J. Phys. Chem. A. 2003;107:6099. [Google Scholar]
- 92.Almerindo GI, Tondo DW, Pliego JR., Jr. J. Phys. Chem. A. 2004;108:166. [Google Scholar]
- 93.Barone V, Improta R, Rega N. Theor. Chem. Acct. 2004;111:237. [Google Scholar]
- 94.da Silva CO, Barbosa AGH, da Silva ET, da Silva ELL, Nascimento MAC. Theor. Chem. Acct. 2004;111:231. [Google Scholar]
- 95.Fu Y, Liu L, Li R-Q, Guo Q-X. J. Am. Chem. Soc. 2004;126:814. doi: 10.1021/ja0378097. [DOI] [PubMed] [Google Scholar]
- 96.Namazian M, Halvani S, Noorbala MR. J. Mol. Struct. (THEOCHEM) 2004;711:13. [Google Scholar]
- 97.Quenneville J, Popovic DM, Stucherbrukhov AA. J. Phys. Chem. B. 2004;108:18383. [Google Scholar]
- 98.Rempe S, Asthagiri D, Pratt LR. Phys. Chem. Chem. Phys. 2004;6:1966. [Google Scholar]
- 99.Schmidt am Busch M, Knapp EW. ChemPhysChem. 2004;5:1513. doi: 10.1002/cphc.200400171. [DOI] [PubMed] [Google Scholar]
- 100.Simonson T, Carlsson J, Case DA. J. Am. Chem. Soc. 2004;126:4167. doi: 10.1021/ja039788m. [DOI] [PubMed] [Google Scholar]
- 101.Gao D, Svoronos P, Wong PK, Maddalena D, Hwang J, Walker H. J. Phys. Chem. A. 2005;109:10776. doi: 10.1021/jp053996e. [DOI] [PubMed] [Google Scholar]
- 102.Han J, Deming RL, Tao F-M. J. Phys. Chem. A. 2005;109:1159. doi: 10.1021/jp045936z. [DOI] [PubMed] [Google Scholar]
- 103.Jensen JH, Li H, Robertson AD, Molina PA. J. Phys. Chem. A. 2005;109:6634. doi: 10.1021/jp051922x. [DOI] [PubMed] [Google Scholar]
- 104.Kaminski GA. J. Phys. Chem. B. 2005;109:5884. doi: 10.1021/jp050156r. [DOI] [PubMed] [Google Scholar]
- 105.Popovic DM, Quenneville J, Stucherbrukhov AA. J. Phys. Chem. B. 2005;109:3616. doi: 10.1021/jp046535m. [DOI] [PubMed] [Google Scholar]
- 106.Takano Y, Houk KN. J. Chem. Theory Comput. 2005;1:70. doi: 10.1021/ct049977a. [DOI] [PubMed] [Google Scholar]
- 107.Westpahl E, Pliego JR., Jr. J. Chem. Phys. 2005;123:074508. doi: 10.1063/1.2001632. [DOI] [PubMed] [Google Scholar]
- 108.Eckert F, Klamt A. J. Comput. Chem. 2006;27:11. doi: 10.1002/jcc.20309. [DOI] [PubMed] [Google Scholar]
- 109.Gutowski KE, Dixon DA. J. Phys. Chem. A. 2006;110:8840. doi: 10.1021/jp061851h. [DOI] [PubMed] [Google Scholar]
- 110.Kastenholz MA, Hünenberger H. J. Chem. Phys. 2006;124:224501. doi: 10.1063/1.2201698. [DOI] [PubMed] [Google Scholar]
- 111.Kelly CP, Cramer CJ, Truhlar DG. J. Phys. Chem. A. 2006;110:2493. doi: 10.1021/jp055336f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Lamoureux G, Roux B. J. Phys. Chem. B. 2006;110:3308. doi: 10.1021/jp056043p. [DOI] [PubMed] [Google Scholar]
- 113.Lewis GN, Randall M, Pitzer KS, Brewer L. Thermodynamics. 2nd ed. McGraw-Hill; New York: 1961. p. 399. [Google Scholar]
- 114.McQuarrie DA. Statistical Mechanics. University Science Books; Sausalito, California: 2000. [Google Scholar]
- 115.Lias SG, Bartness JE, Liebman JF, Holmes JL, Levin RD, Mallard WG. J. Phys. Chem. Ref. Data. 1988;16(Suppl 1) [Google Scholar]
- 116.Bartmess JE. J. Phys. Chem. 1994;98:6420. [Google Scholar]
- 117.Toman RC. J. Am. Chem. Soc. 1921;43:1592. [Google Scholar]
- 118.Lewis GN, Latimer WM. J. Am. Chem. Soc. 1922;44:1008. [Google Scholar]
- 119.Fermi E. Z. Phys. 1926;36:902. [Google Scholar]
- 120.Sommerfeld A. Z. Phys. 1928;47:1. [Google Scholar]
- 121.Strehlow H. Electrode Potentials in Non-Aqueous Solvents. In: Lagowski JJ, editor. The Chemistry of Nonaqueous Solvents. Academic Press; New York: 1966. p. 134. [Google Scholar]
- 122.Kolthoff IM, Chantooni MKJ. J. Phys. Chem. 1972;76:2024. [Google Scholar]
- 123.Lide DR, editor. CRC Handbook of Chemistry and Physics. 87th ed. CRC Press; Boca Raton, FL: 2006. [Google Scholar]
- 124.Fawcett WR. J. Phys. Chem. B. 1999;103:11181. [Google Scholar]
- 125.Ben-Naim A. Solvation Thermodynamics. Plenum; New York: 1987. [Google Scholar]
- 126.Wagman DD, Evans WH, Parker VB, Schumm RH, Halow I, Bailey SM, Churney KL, Nutall RL. J. Phys. Chem. Ref. Data. 1982;11(Suppl 2) [Google Scholar]
- 127.Salomon M. In: Physical Chemistry of Organic Solvent Systems. Covington AK, Dickinson T, editors. Plenum Press; New York: 1973. p. 190. [Google Scholar]
- 128.Janz GJ, Tomkins RPT. Nonaqueous Electrolytes Handbook. II. Academic Press; New York: 1973. p. 115. [Google Scholar]
- 129.Labban AKS, Marcus Y. J. Solution Chem. 1991;20:221. [Google Scholar]
- 130.Kenttämma J. Suomen Kemistilehti. 1960;B33:179. [Google Scholar]
- 131.Gopal R, Jha JS. Ind. J. Chem. 1974;12:618. [Google Scholar]
- 132.In several earlier papers where we used this thermochemical cycle,7,56,111 the solvation free energies appearing in the vertical legs were denoted by a superscript asterisk, meaning transfer from a standard-state gas-phase concentration of 1 mol/L to a standard-state liquid-phase concentration of 1 mol/L, and the symbol for the free energy change associated with moving from a standard-state gas-phase pressure of 1 atm to a liquid-phase concentration of 1 mol/L was left out of the diagrams (but not the equations) for simplicity. In this paper, we use an equivalent, and perhaps simpler convention in which the solvation free energies appearing in the vertical legs are denoted by a superscript open circle. The equations resulting from the thermochemical cycles that appear in this article are indentical to those equations appearing in our earlier papers.
- 133.Ogston AG. Trans. Faraday Soc. 1936;32:1679. [Google Scholar]
- 134.Kolthoff IM, Lingane JJ, Larson W. J. Am. Chem. Soc. 1938;60:2512. [Google Scholar]
- 135.Shedlovsky T, Kay RL. J. Phys. Chem. 1956;60:151. [Google Scholar]
- 136.Kolthoff IM, Bruckenstein S, Chantooni MKJ. J. Am. Chem. Soc. 1961;83:3927. [Google Scholar]
- 137.Julliard J, Dondon M-L. Bull. Soc. Chim. Fr. 1963:2535. [Google Scholar]
- 138.Coetzee JF, Padmanabhan GR. J. Phys. Chem. 1965;69:3193. [Google Scholar]
- 139.Konovalov OM. Zh. Fiz. Khim. 1965;39:693. [Google Scholar]
- 140.Julliard J. Bull. Soc. Chim. Fr. 1966:1727. [Google Scholar]
- 141.Kolthoff IM, Chantooni MKJ. J. Phys. Chem. 1966;70:856. [Google Scholar]
- 142.Rochester CH. Trans. Faraday Soc. 1966;62:355. [Google Scholar]
- 143.Kolthoff IM, Chantooni MKJ, Bhowmik S. Anal. Chem. 1967;39:315. [Google Scholar]
- 144.Kolthoff IM, Chantooni MKJ, Bhowmik S. Anal. Chem. 1967;39:1627. [Google Scholar]
- 145.Rochester CH. J. Chem. Soc. B. 1967:33. [Google Scholar]
- 146.Chantooni MKJ, Kolthoff IM. J. Am. Chem. Soc. 1968;90:3005. [Google Scholar]
- 147.Kolthoff IM, Chantooni MKJ, Bhowmik S. J. Am. Chem. Soc. 1968;90:23. [Google Scholar]
- 148.Bolton PD, Rochester CH, Rossall B. Trans. Faraday Soc. 1970;66:1348. [Google Scholar]
- 149.Leung CS, Grunwald E. J. Am. Chem. Soc. 1970;74:696. [Google Scholar]
- 150.Chantooni MKJ, Kolthoff IM. J. Phys. Chem. 1975;79:1176. [Google Scholar]
- 151.Kolthoff IM, Chantooni MKJ. J. Am. Chem. Soc. 1975;97:1376. [Google Scholar]
- 152.Kolthoff IM, Chantooni MKJ. J. Am. Chem. Soc. 1976;98:5063. [Google Scholar]
- 153.Jasinski T, El-Harakany AA, Halaka FG, Sadek H. Croat. Chem. Acta. 1978;51:1. [Google Scholar]
- 154.Chantooni MKJ, Kolthoff IM. Anal. Chem. 1979;51:133. [Google Scholar]
- 155.Bordwell FG. Acc. Chem. Res. 1988;21:456. [Google Scholar]
- 156.Rived F, Roses M, Bosch E. Anal. Chim. Acta. 1998;374:309. [Google Scholar]
- 157.Thompson DJ, Cramer CJ, Truhlar DG. Theor. Chem. Acc. 2005;113:107. [Google Scholar]
- 158.Adamo C, Barone V. J. Chem. Phys. 1998;108:664. [Google Scholar]
- 159.Hehre WJ, Radom L, Schleyer P. v. R., Pople JA. Ab Initio Molecular Orbital Theory. Wiley; New York: 1986. [Google Scholar]
- 160.Easton RE, Giesen DJ, Welch A, Cramer CJ, Truhlar DG. Theor. Chim. Acta. 1996;93:281. [Google Scholar]
- 161.Li J, Cramer CJ, Truhlar DG. Theor. Chim. Acta. 1998;99:192. [Google Scholar]
- 162.Thompson JD, Winget P, Truhlar DG. PhysChemComm. 2001;4:72. [Google Scholar]
- 163.Chamberlin AC, Kelly CP, Thompson JD, Xidos JD, Li J, Hawkins GD, Winget P, Zhu T, Rinaldi D, Liotard DA, Cramer CJ, Truhlar DG, Frisch MJ. MN-GSM, version 6.0. University of Minnesota; Minneapolis, MN: 2006. pp. 55455–0431. [Google Scholar]
- 164.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JA, Jr., Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalamani G, Rega N, Petersson GA, Nagatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. Gaussian 03, revision D.01. Gaussian, Inc.; Wallingford, CT: 2003. [Google Scholar]
- 165.Lias SG, Bartness JE, Liebman JF, Holmes JL, Levin RD, Mallard WG. Ion Energetics Data. In: Linstrom PJ, Mallard WG, editors. NIST Chemistry WebBook; NIST Standard Reference Database Number 69. National Institute of Standards and Technology; Gaithersburg MD: Mar, 2003. [Google Scholar]
- 166.Winget P, Hawkins GD, Cramer CJ, Truhlar DG. J. Phys. Chem. B. 2000;104:4726. [Google Scholar]
- 167.Keeports D. J. Chem. Educ. 2005;82:999. [Google Scholar]
- 168.Lewis GN, Randall M, Pitzer KS, Brewer L. Thermodynamics. 2nd ed. McGraw-Hill; New York: 1961. p. 272. [Google Scholar]
- 169.Meot-Ner MM, Lias SG. Binding Energies Between Ions and Molecules, and the Thermochemistry of Cluster Ions. In: Linstrom PJ, Mallard WG, editors. NIST Chemistry WebBook, NIST Standard Reference Database Number 69. National Institute of Standards and Technology; Gaithersburg, MD: Mar, 2003. [Google Scholar]
- 170.Hamprecht FA, Cohen AJ, Tozer DJ, Handy NC. J. Chem. Phys. 1998;109:6264. [Google Scholar]
- 171.Fast PL, Sanchez ML, Truhlar DG. Chem. Phys. Lett. 1999;306:407. [Google Scholar]
- 172.Cramer CJ. Essentials of Computational Chemistry: Theories and Models. Wiley & Sons; Chichester, U.K.: 2002. p. 321. [Google Scholar]
- 173.Klots CE. J. Phys. Chem. 1981;85:3585. [Google Scholar]
- 174.A full description of the steps required in going from eq 23 to eq 24 is given in reference 55.
- 175.Meot-Ner (Mautner) M, El-Shall S. J. Am. Chem. Soc. 1986;108:4386. [Google Scholar]
- 176.Zhao Y, Truhlar DG. J. Chem. Theory. Comput. 2005;1:415. doi: 10.1021/ct049851d. [DOI] [PubMed] [Google Scholar]
- 177.Dahlke EE, Truhlar DG. J. Phys. Chem. B. 2005;109:15677. doi: 10.1021/jp052436c. [DOI] [PubMed] [Google Scholar]
- 178.Zhao Y, Schultz NE, Truhlar DG. J. Chem. Theory Comput. 2006;2:364. doi: 10.1021/ct0502763. [DOI] [PubMed] [Google Scholar]
- 179.Johnson ER, DiLabio GA. Chem. Phys. Lett. 2006;419:333. [Google Scholar]
- 180.Reichardt C. Solvents and Solvent Effects in Organic Chemistry. 3rd ed. Wiley-VCH; Weinheim: 2003. p. 48. [Google Scholar]
- 181.Pliego JR, Jr., Riveros JM. Phys. Chem. Chem. Phys. 2002;4:1622. [Google Scholar]
- 182.The reference given by Kalidas et al. for the experimental transfer free energy of the proton between water and acetonitrile is: Das K, Das AK, Kundu K. Electrochim. Acta. 1981;26:471. This value was also reported in: Cox BG, Hedwig GR, Parker AJ, Watts DW. Aust. J. Chem. 1974;27:477.
- 183.Popovych O. J. Phys. Chem. 1984;88:4167. [Google Scholar]
- 184.Hush NS. Aust. J. Sci. Res., Ser. A. 1948;1:480. [Google Scholar]
- 185.Randles JEB. Trans. Faraday Soc. 1956;52:1573. [Google Scholar]
- 186.Case B, Hush NS, Parsons R, Peover ME. J. Electroanal. Chem. 1965;10:360. [Google Scholar]
- 187.Case B, Parsons R. Trans. Faraday Soc. 1967;63:1224. [Google Scholar]
- 188.Zagórska I, Koczorowski Z. Rocz. Chem. 1970;44:1559. [Google Scholar]
- 189.Parsons R, Rubin BT. J. Chem. Soc. Faraday Trans. 1974;70:1636. [Google Scholar]
- 190.Gomer R, Tryson G. J. Chem. Phys. 1977;66:4413. [Google Scholar]
- 191.Trasatti S. Pure Appl. Chem. 1986;58:955. [Google Scholar]
- 192.Coetzee JF, Dollard WJ, Istone WK. J. Solution Chem. 1991;20:957. [Google Scholar]
- 193.Parfenyuk VI, Chankina TI. Russ. J. Phys. Chem. 2001;38:326. [Google Scholar]
- 194.Marcus Y. Pure Appl. Chem. 1983;55:977. [Google Scholar]
- 195.Lewis A, Bumpus JA, Truhlar DG, Cramer CJ. J. Chem. Educ. 2004;81:596. [Google Scholar]
- 196.Winget P, Cramer CJ, Truhlar DG. Theor. Chem. Acc. 2004;112:217. [Google Scholar]
- 197.Trasatti S. Electrochmica Acta. 1990;35:269. [Google Scholar]
- 198.Sokhan VP, Tildesley DJ. Mol. Phys. 1997;92:625. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.