Adding Explicit Solvent Molecules to Continuum Solvent Calculations for the Calculation of Aqueous Acid Dissociation Constants

Abstract

Aqueous acid dissociation free energies for a diverse set of 57 monoprotic acids have been calculated using a combination of experimental and calculated gas and liquid-phase free energies. For ionic species, aqueous solvation free energies were calculated using the recently developed SM6 continuum solvation model. This model combines a dielectric continuum with atomic surface tensions to account for bulk solvent effects. For some of the acids studied, a combined approach that involves surrounding the conjugate base (anion) by a single explicit water molecule that is bound to the anion, and then surrounding the resulting anion-water cluster by a dielectric continuum, significantly improves the agreement between the calculated pK_a value and experiment. This suggests that for some anions, particularly those concentrating charge on a single exposed heteroatom, augmenting implicit solvent calculations with a single explicit water molecule is required, and adequate, to account for strong short-range hydrogen bonding interactions between the anion and the solvent. Using the polyprotic acid H₂CO₃, we also demonstrate the effect of adding several explicit waters by calculating the pK_a of bicarbonate (HCO₃⁻) using as the conjugate base carbonate (CO₃²⁻) bound by up to three explicit water molecules. With each addition of an explicit water molecule, the accuracy of the calculated pK_a value increases—adding three explicit waters gives a calculated pK_a that is in excellent agreement with experiment.

1. Introduction

Since Bjerrum's and Hammett's early work on substituent effects and solvent effects on acidity,¹ there has been continuing and substantial interest in predicting pK_a constants. Many of the methods that have been developed take advantage of empirical relationships between various molecular properties (either experimental or calculated) and pK_a, although recent work has focused on making pK_a predictions by directly calculating the free energy change associated with the acid dissociation process.^2-41 This growing interest in direct pK_a calculation has occurred because empirical correlations between pK_a and various molecular properties have often been restricted to one or a few classes of compounds, such as substituted benzoic acids. Furthermore, in cases where correlations have been developed based on larger and more diverse sets of compounds, it remains unclear whether these correlations can be readily applied to molecules outside the data sets within which they were originally developed, for example, their applicability to transition states, weak acids, and other compounds for which limited experimental pK_a data exist is open to question.

The most challenging aspect of directly calculating pK_a values is accurately accounting for the effect of solvent in a physical way. Solvation modeling is particularly challenging for ionic species due to strong electrostatic effects arising from unbalanced localized charges. For neutral species, implicit solvent models^42,43 have been successful in predicting various liquid-phase properties. In these types of models, the electrostatic response of a bulk solvent is usually approximated as a homogenous, dielectric continuum, making them an attractive alternative to computationally more demanding explicit solvent simulations. Explicit simulations require special treatment of finite-size effects⁴⁴ whereas implicit solvent models directly incorporate the bulk continuum limit. Implicit solvation models, though, require a decision as to which subsystem is to be treated as an explicit solute, with the remainder implicit. In a purely electrostatic implicit model, the implicit subsystem must be well-described by the bulk dielectric constant, but it is well known that such a bulk model breaks down in the first solvation shell. Including implicit first-solvation-shell effects that depend on the atomic number⁴⁵ and geometry⁴⁶ of specific local solvent-exposed regions of the solute allows one to include these specific solvation effects. Nevertheless questions remain about the minimum size of the system that must be treated explicitly to calculate quantitatively accurate free energies of solvation and pK_a constants. For example, for reactions involving RO⁻, should one consider RO⁻, RO⁻(H₂O), or RO⁻(H₂O)_n with n > 1 as the solute?

We recently developed an implicit solvation model for aqueous solvent, called Solvation Model 6 (SM6).⁴⁷ This model uses a dielectric continuum to treat electrostatic effects combined with atomic surface tensions to account for first-shell solvation effects, and it has been shown to give aqueous solvation free energies accurate to within ∼0.5 kcal/mol for typical neutral solutes. During the development of this model, we found that some solutes containing concentrated regions of charge density (the majority of these being anions) required a significantly different parametrization than most of the other solutes in our training set. By replacing these solutes by their analogous monohydrated clusters (i.e., using a larger explicit region) we were able to obtain a single set of parameters that simultaneously fit (with reasonable accuracy) all of the neutral and ionic data in our training set. We concluded from this that strong local solute-solvent interactions play an important role in the aqueous solvation of some solutes, and in these cases, an implicit solvent model based on the minimal definition of the solute is not able to account for these interactions. Implicit solvation models that include one or more solvent molecules in the explicit subsystem have been called a combined dielectric-continuum model^48-50 or a cluster-continuum model.^51,52 We will also call it a combined implicit-explicit model.

Such a combined implicit-explicit solvent approach has seen recent use in direct pK_a calculations (some earlier applications focused on calculating solvatochromic shifts^53,54). Pliego and Riveros⁵² calculated pK_a values for 17 species using an implicit-explicit solvent approach for the charged species (for the neutral species, these workers did not include explicit water molecules), and were able to greatly improve the accuracy of calculated pK_a constants as compared to pure continuum models^55,56 without making any further empirical adjustments besides the addition of explicit water molecules. Although Pliego and Riveros considered only a small number of compounds, their work suggests that for some ions, including explicit water molecules in the calculation is important for calculating pK_a. Adam carried out similar calculations¹³ for carboxylic acids and phenols and found that the slope of the plot of experimental pK_a versus calculated acid dissociation free energy could be brought into much better agreement with experiment with the addition of explicit water molecules (again, explicit water molecules were added only to the ionic species). This work also suggests that accounting for explicit solvent effects may be necessary in order to make accurate predictions of pK_a.

An important challenge associated with adding explicit solvent molecules to implicit solvent calculations is that it is difficult to determine how many solvent molecules are required in order to reach convergence. The work of Pliego and Riveros⁵² and Adam¹³ illustrates this problem. In both studies different numbers of explicit solvent molecules (up to three in some cases) were used for different solutes (e.g., in the work of Adam, phenols required a single explicit water molecule in order bring the calculated and experimental pK_a values into close agreement with one another, but carboxylic acids required two explicit water molecules). Thus, it is unclear how many explicit solvent molecules are required (if any) for compounds not included in their work.

The present article will examine what effect adding a single explicit solvent molecule to continuum solvation calculations has on the accuracy of pK_a predictions. We will also examine to what extent the addition of several explicit water molecules has on the accuracy of the prediction in cases where more than a single site exists on the conjugate base for strong hydrogen bonding interactions. For this, we will calculate the pK_a of bicarbonate using carbonate bound by up to three explicit water molecules.

2. Computing Acid Dissociation Free Energies from Solvation Free Energies

The standard-state free energy change associated with the following reaction, $\Delta G_{\mathrm{aq}}^{\ast }$,

$$\mathrm{AH}\left(\mathrm{aq}\right)\to {\mathrm{A}}^{-}\left(\mathrm{aq}\right)+{\mathrm{H}}^{+}\left(\mathrm{aq}\right)$$ (1)

is related to the aqueous pK_a according to⁵⁷

$$\mathrm{p}{K}_{\mathrm{a}}=\frac{\Delta G_{\mathrm{aq}}^{\ast }}{RT\ln \left(10\right)}$$ (2)

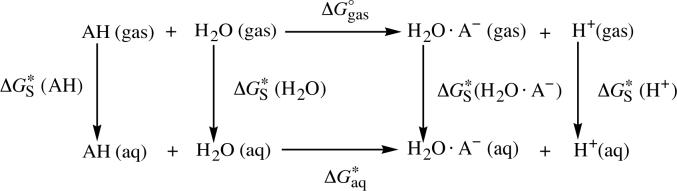
where R is the universal gas constant and T is the temperature. Using the thermodynamic cycle shown in Scheme 1, $\Delta G_{\mathrm{aq}}^{\ast }$ may be expressed in terms of the aqueous solvation free energies of the acid AH and its conjugate base A⁻

$$\Delta G_{\mathrm{aq}}^{\ast }\left(\mathrm{AH}\right)=\Delta G_{\mathrm{gas}}^{\mathrm{o}}\left(\mathrm{AH}\right)+\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{A}}^{-}\right)-\Delta G_{\mathrm{S}}^{\ast }\left(\mathrm{AH}\right)+\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{H}}^{+}\right)+\Delta G^{\mathrm{o}\to \ast }$$ (3)

where $\Delta G_{\mathrm{S}}^{\ast }\left(\mathrm{AH}\right)$ and $\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{A}}^{-}\right)$ are the standard-state aqueous solvation free energies of AH and A⁻, respectively, $\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{H}}^{+}\right)$ is the aqueous solvation free energy of H⁺, $\Delta G_{\mathrm{gas}}^{\mathrm{o}}\left(\mathrm{AH}\right)$ is the gas-phase acidity of AH, defined by

$$\Delta G_{\mathrm{gas}}^{\mathrm{o}}\left(\mathrm{AH}\right)=G_{\mathrm{gas}}^{\mathrm{o}}\left({\mathrm{A}}^{-}\right)+G_{\mathrm{gas}}^{\mathrm{o}}\left({\mathrm{H}}^{+}\right)-G_{\mathrm{gas}}^{\mathrm{o}}\left(\mathrm{AH}\right)$$ (4)

and ΔG^○→* is the free energy change associated with moving from a standard state that uses a concentration of 1 atm in the gas phase and 1 mol/L in the aqueous phase (denoted by the superscript “^○”), to a standard state that uses a concentration of 1 mol/L in both the gas and aqueous phase (denoted by the superscript “*”). The ideal-gas law yields

$$\Delta G^{\mathrm{o}\to \ast }=RT\ln \left(24.46\right)$$ (5)

At 298 K, ΔG^○→* is 1.89 kcal/mol.

Scheme 1.

The acid dissociation free energy of AH in the aqueous phase may also be expressed in terms of the aqueous solvation free energy of the acid AH and its monohydrated conjugate base, H₂O·A⁻, using the thermodynamic cycle shown in Scheme 2

$$\Delta G_{\mathrm{aq}}^{\ast }\left(\mathrm{AH}\right)=\Delta G_{\mathrm{gas}}^{\mathrm{o}}({\mathrm{H}}_2\mathrm{O}\cdot {\mathrm{A}}^{-})+\Delta G_{\mathrm{S}}^{\ast }({\mathrm{H}}_2\mathrm{O}\cdot {\mathrm{A}}^{-})\text{-}\Delta G_{\mathrm{S}}^{\ast }\left(\mathrm{AH}\right)\text{-}\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{H}}_2\mathrm{O}\right)+\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{H}}^{+}\right)$$ (6)

The gas-phase free energy $\Delta G_{\mathrm{gas}}^{\mathrm{o}}({\mathrm{H}}_2\mathrm{O}\cdot {\mathrm{A}}^{-})$ in the above equation is equal to the sum of the gas-phase acidity of AH, $\Delta G_{\mathrm{gas}}^{\mathrm{o}}\left(\mathrm{AH}\right)$, and the gas-phase binding free energy of H₂O·A⁻, where this latter free energy is equal to $G_{\mathrm{gas}}^{\mathrm{o}}({\mathrm{H}}_2\mathrm{O}\cdot {\mathrm{A}}^{-})-G_{\mathrm{gas}}^{\mathrm{o}}\left({\mathrm{H}}_2\mathrm{O}\right)-G_{\mathrm{gas}}^{\mathrm{o}}\left({\mathrm{A}}^{-}\right)$. Note that the standard-state correction to the free energy, ΔG^○→*, does not appear in eq 6 because in Scheme 2, the number of moles on the products and reactants side is equal.

Scheme 2.

One can also replace H⁺ by H₃O⁺ in the above equations, and in fact we have recommended doing this for many purposes. However, for calculating pK_a values we recommend using the experimental value for $\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{H}}^{+}\right)$, as discussed in Section 4. We also note that that $\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{H}}^{+}\right)$ drops out for the important problem of calculating substituent effects on pK_a values (i.e., differences in pK_a values).

3. Experimental Data

All experimental and calculated data are for a temperature of 298 K. When available, we used experimental data to calculate $\Delta G_{\mathrm{aq}}^{\ast }\left({\mathrm{H}}^{+}\right)$ in eqs 3 and 6. For all of the acids studied here, experimental values for the gas-phase acidity, $\Delta G_{\mathrm{gas}}^{\mathrm{o}}\left(\mathrm{AH}\right)$, and the aqueous solvation free energy (for neutral species) are available,^47,58-60 and these were used in eqs 3 and 6. For the majority of the solute-water clusters studied here (monohydrated anions), experimental values are available⁶¹ for the gas-phase binding free energy, and these were used in eq 6. For the aqueous solvation free energy of the proton, $\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{H}}^{+}\right)$, we used Zhan and Dixon's value of −264 kcal/mol.⁶² Experimental pK_a data were taken from the compilation of Stewart;⁶³ pK_a data not available in this compilation were taken from these additional sources.^64-66

4. Computational Methods

In cases where experimental values for the gas-phase binding free energies are not available, we calculated them at the at the B97−1⁶⁷/MG3S⁶⁸ level of theory, using the Gaussian 03 program.⁶⁹ (For atoms of atomic number 14 or lower, the MG3S basis set is identical to the older 6−311+G(2df,2p) basis^70,71). Aqueous solvation free energies of unclustered anions were calculated at the SM6/MPW25/6−31+G(d,p) level, using MPW25/MIDI! optimized gas-phase geometries (in Pople-style notation, this calculation is denoted SM6/MPW25/6−31+G(d,p)//MPW25/MIDI!). Note that MPW25 is a shorter name for the mPW1PW91 functional of Adamo and Barone, which is also called mPW0.⁷² The aqueous solvation free energies of clustered anions were calculated at the SM6/MPW25/6−31+G(d,p)//B97−1/MG3S level of theory. The SM6 method is implemented in the smxgauss,⁷³ hondoplus,⁷⁴ and gamessplus⁷⁵ programs.

5. Results and Discussion

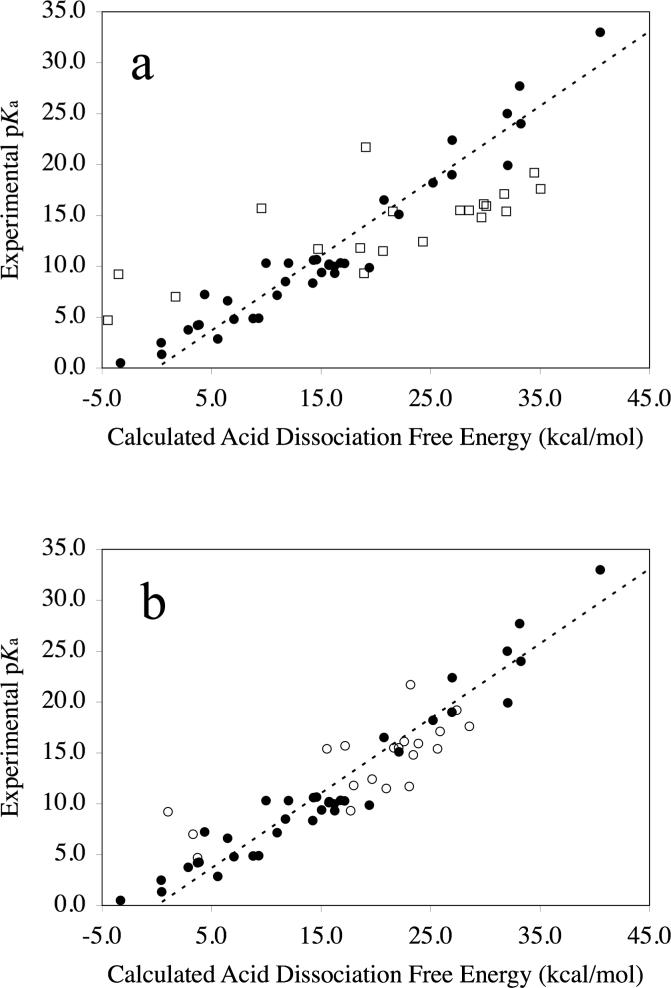
Shown in Table 1 are the acid dissociation free energies calculated using eq 3, as well as the experimental pK_a values, for all 57 acids studied in this work (the additional column in this table is discussed below). For those acid dissociation free energies calculated using eq 3, we used experimental values for $\Delta G_{\mathrm{gas}}^{\mathrm{o}}\left(\mathrm{AH}\right)$, $\Delta G_{\mathrm{S}}^{\ast }\left(\mathrm{AH}\right)$, and $\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{H}}^{+}\right)$, and calculated values for $\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{A}}^{-}\right)$. A plot of the experimental pK_a against the acid dissociation free energies obtained using eq 3 for all 57 acids yields a regression equation with a slope of 0.71/RTln(10) (r² = 0.76). This plot is shown in Figure 1a. To see what effect the addition of a single explicit water molecule would have on calculated acid dissociation free energies, we added a single water molecule around some of the conjugate bases (anions), and then used the calculated aqueous solvation free energies of the resulting solute-water clusters, $\Delta G_{\mathrm{S}}^{\ast }({\mathrm{H}}_2\mathrm{O}\cdot {\mathrm{A}}^{-})$, along with experimental values for $\Delta G_{\mathrm{gas}}^{\mathrm{o}}({\mathrm{H}}_2\mathrm{O}\cdot {\mathrm{A}}^{-})$ (when available), $\Delta G_{\mathrm{S}}^{\ast }\left(\mathrm{AH}\right)$, $\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{H}}_2\mathrm{O}\right)$, and $\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{H}}^{+}\right)$, to calculate $\Delta G_{\mathrm{aq}}^{\ast }$ according to eq 6. The criteria we used to decide to which of the anions to add an explicit water molecule are the same criteria that we used during the development of our SM6 model.⁴⁷ In particular, we added a single explicit water molecule to any anion containing three or fewer atoms and to any anion with one or more oxygen atoms bearing a more negative partial atomic charge than bare water solute. Of the 57 acids in Table 1, 20 of them satisfy one or both of these criteria. The acid dissociation free energies calculated using eq 6 for these 20 acids are listed in Table 1. Plotting the experimental pK_a values of all 57 acids against the acid dissociation free energies obtained using eq 6 (20 of the acids in Table 1) combined with the remaining acid dissociation free energies using eq 3 (37 of the 57 acids in Table 1), yields a regression equation with a slope of 0.87/RTln(10) (r² = 0.86), which is a substantial improvement compared to when eq 3 was used to calculate acid dissociation free energies for all 57 acids. This plot is shown in Figure 1b.

TABLE 1.

Calculated Dissociation Free Energies (SM6) Used to Develop the Correlation pK_a = m/RTln(10) + b.

AH	ΔGaq* (eq 3)a Implicit Solvent	ΔGaq* (eq 6)b Implicit + Explicit Solvent	Expt. pKa
trifluoroacetic acid	1.4		0.5
dichloroacetic acid	5.2		1.4
pyruvic acid	5.1		2.5
chloroacetic acid	10.3		2.9
formic acid	7.6		3.8
benzoic acid	8.4		4.2
acrylic acid	8.6		4.3
hydroperoxyl radical	0.2	8.4	4.7
acetic acid	11.8		4.8
propanoic acid	13.5		4.9
hexanoic acid	14.0		4.9
thiophenol	11.2		6.6
hydrogen sulfide	6.4	8.0	7.0
4-nitrophenol	15.7		7.1
2-nitrophenol	9.1		7.2
3-nitrophenol	19.0		8.4
2-chlorophenol	16.5		8.5
hydrogen cyanide	1.2	5.7	9.2
1,1,1,3,3,3-hexafluoropropan-2-ol	23.6	22.4	9.3
3-hydroxyphenol	21.0		9.3
4-chlorophenol	19.8		9.4
4-hydroxyphenol	24.1		9.9
phenol	20.9		10.0
3-methylphenol	20.4		10.1
nitromethane	20.4		10.2
4-methylphenol	21.9		10.3
cyanamide	14.7		10.3
methanethiol	16.7		10.3
2-methylphenol	21.5		10.3
ethanethiol	19.0		10.6
1-propanethiol	19.3		10.7
methyl hydroperoxide	25.4	25.7	11.5
hydrogen peroxide	19.4	27.8	11.7
ethyl hydroperoxide	23.3	22.7	11.8
2,2,2-trifluoroethanol	29.0	24.4	12.4
2-methoxyethanol	34.4	28.1	14.8
acetamide	26.8		15.1
benzyl alcohol	36.6	30.4	15.4
1,2-ethanediol	26.3	20.3	15.4
methanol	32.4	26.4	15.5
allyl alcohol	33.2	26.8	15.5
water	14.3	21.9	15.7
ethanol	34.8	28.6	15.9
1-propanol	34.6	27.3	16.1
acetaldehyde	25.5		16.5
isopropanol	36.4	30.6	17.1
2-butanol	39.8	33.3	17.6
4-nitroaniline	29.9		18.2
acetone	31.7		19.0
t-butanol	39.2	32.1	19.2
3-pentanone	36.8		19.9
acetylene	23.8	27.9	21.7
diphenylamine	31.7		22.4
chloroform	38.0		24.0
acetonitrile	36.7		25.0
aniline	37.9		27.7
dimethyl sulfoxide	45.2		33.0
X/Yc	57/0	37/20
m	0.71	0.87
b	3.15	1.45
r2	0.76	0.86

^aAqueous dissociation free energy, calculated using experimental values for ΔG_gas^o (A⁻), ΔG_S* (AH), and ΔG_S* (H⁺), and calculated values for ΔG_S* (A⁻), in eq 3.

^bAqueous dissociation free energy, calculated using experimental values for ΔG_gas^o (H₂O · A⁻), ΔG_S* (AH), ΔG_S* (H₂O), and ΔG_S* (H⁺), and calculated values for ΔG_S* (H₂O · A⁻), in eq 6.

^cX is the number of ΔG_aq* values calculated using eq 3 that were used to develop the correlation between experimental pK_a and ΔG_aq*; Y is the number of ΔG_aq* values calculated using eq 6 that were used to develop the correlation between experimental pK_a and ΔG_aq*.

Figure 1.

Experimental pK_a plotted against the calculated acid dissociation free energy. The dashed line is the expected result obtained using eq 2 (slope = 1/RTln(10); intercept = 0). Solid circles indicate acid dissociation free energies calculated using eq 3 (no explicit water). (a) Open squares indicate acids whose dissociation free energies will be calculated using eq 6 (single explicit water molecule; see Figure 1b). (b) Open circles indicate acid dissociation energies calculated using eq 6 (single explicit water molecule added to the conjugate base).

The results obtained here can be compared to several other recent results. Klamt et al.²³ used an implicit solvent model^76,77 to calculate aqueous acid dissociation free energies for 64 different acids, without the addition of explicit water molecules. These workers found a highly significant correlation (r² = 0.98) between the experimental pK_a and calculated acid dissociation free energy. However, the resulting slope was only 0.58/RT ln(10), which is significantly lower than the expected slope of 1/RT ln(10). Based on their results, as well as the results from two other studies,^14,17 Klamt et al. drew the startling conclusion that the experimental pK_a scale must depend differently on the free energy of dissociation than is generally assumed. Klicić et al.¹⁷ used eq 3, along with an implicit solvent model, to calculate dissociation free energies for a diverse data set containing 121 acids. With the exception of the 18 sulfonamides included in Klicić et al.'s data set (which required a different regression equation than the remaining acids), there is a strong correlation between experimental pK_a and the calculated dissociation free energy for the remaining 103 acids (r² = 0.97). However, the slope is only 0.53/RTln(10), which is very close to the value obtained by Klamt et al. Chipman¹⁴ calculated acid dissociation free energies in water for 6 different acids (water, methanol, ethanol, phenol, formic acid, acetic acid, and benzoic acid) using an implicit solvent model. Plotting experimental pK_a versus the calculated dissociation free energies reported by Chipman yields a slope of 0.51/RTln(10) (r² = 0.99). Interestingly, Chipman also calculated dissociation free energies for the six acids above in the aprotic solvent DMSO using the same implicit model that he used for water, and a plot of the experimental pK_a versus the calculated dissociation free energies for five of the six acids (an experimental pK_a value in DMSO is not available for formic acid), yields a regression equation with a slope equal to 0.84/RTln(10) (r² = 0.99). Based on these results, Chipman concluded, very reasonably, that for water, implicit solvent models alone are unable to account for strong anion-water interactions in the first solvation shell, and suggested that in such cases where these interactions are expected to be important, better results might be obtained by augmenting continuum solvent calculations with other complementary methods that are especially designed to account for specific short-range interactions.

Adam calculated aqueous dissociation free energies using two approaches.¹³ In the first approach, an implicit solvent model was applied to 40 carboxylic acids and 20 phenols. A plot of the experimental pK_a values against the calculated dissociation free energies for each of these two classes of compounds results in two regression equations with slopes of 0.44/RTln(10) (r² = 0.86) and 0.50/RTln(10) (r² = 0.97), for the carboxylic acids and phenols, respectively. In the second approach, Adam repeated the implicit solvent calculations, each time successively adding a single explicit water molecule to the conjugate bases (the neutrals were modeled without explicit water molecules added throughout) until good agreement was obtained between the calculated and experimental slope of the resulting regression equation. For the phenols, adding a single water molecule to each of the anions results in a regression equation with a slope of 0.88/RTln(10) (r² = 0.93). For the carboxylic acids, a slope of 0.93/RTln(10) (r² = 0.81) was obtained, but only after two explicit water molecules were added.

Based on the results presented here, as well as the results obtained by several other workers, we can make several conclusions regarding the calculation of acid dissociation constants. First, although several other studies^14,17,23 have shown that some implicit solvent models, without being augmented with explicit water molecules, can lead to very good predictions of the ordering of pK_a constants because there is a strong correlation between the calculated dissociation free energy and the experimental pK_a, the unusually low slopes of the resulting regression equations suggest that significant systematic errors are present in the underlying methods used to develop them.

Second, for some anions, an implicit model alone is unable to account for strong solute-solvent interactions in the first solvation shell, and for these types of solutes, treating one water molecule explicitly significantly increases the absolute accuracy of the calculated acid dissociation free energy. It is encouraging that a simple approach in which only a single water molecule is added to the calculation increases the accuracy because it avoids the problems⁴² introduced by the introduction of larger numbers of explicit solvent molecules (e.g., conformational sampling problems, computational cost). Furthermore, the above results are encouraging because, as pointed out in an earlier paper,⁴⁷ adding a small number of explicit water molecules to continuum solvation calculations is much more straightforward than making large adjustments to the boundary between the solute and the continuum solvent (i.e. making large adjustments in the values used for the empirical atomic radii), using atom-typed radii,^34,78-82 or using charge-dependent molecular cavities.^83-89 Finally, applying this strategy yields a regression equation between the experimental pK_a and calculated acid dissociation free energy that obeys, reasonably well, the firmly founded thermodynamic relationship⁵⁷ between the dissociation free energy and pK_a.

Ideally we would give a definite prescription for cases in which a specific water molecule should be added to implicit solvent model calculations. However, it is not possible to do this in a way that covers the great diversity of possible cases that occur in applications. One prescription would be to add an explicit water whenever one wants to improve the accuracy, since adding an explicit water should almost always improve the accuracy when the effect is large, but it is relatively safe because it cannot make the accuracy much worse when the effect is small. The reason that adding explicit water might not always make the calculation more accurate is that the free energies of cavitation and dispersion and changes in the solute's translational, vibrational, and rotational free energy all change, and the parametrized surface tensions and the explicit solute-water and (possibly) water-water interactions are not necessarily accurate enough to account for small changes quantitatively. As an example of how large errors are reduced, we note that the pK_a value calculated here for phenol, whose conjugate base does not fall under one of the criteria explained above for adding explicit water, is 15.4. Adding a single explicit water molecule to phenoxide and using eq 6 leads to a calculated pK_a of 12.3, which is in better agreement with the experimental value of 10.0. We should also point out that although we obtain better results in cases where we do add explicit water, for many of the acids studied here, we obtain reasonably good results without the explicit water. As an example of a case where excellent results are obtained without explicit water, so that the results cannot improve when water is added, we consider the calculated pK_a for formic acid, whose conjugate base also does not fall under either of the criteria that we used above for adding explicit water; this pK_a is in perfect agreement with the experimental pK_a without addition of explicit water. Naturally, the agreement between the calculated and experimental pK_a does diminish when an explicit water molecule is added to the calculation, but only by a moderate amount (2 pK_a units). Despite cases like this, the results above show that when one considers a statistically meaningful set of cases, addition of a single explicit water molecule improves the accuracy of calculated pK_a.

The next obvious question is: what effect does adding more than a single explicit water have on the accuracy of SM6? This question becomes especially important when one considers divalent ions, for which several sites may be available for strong solute-solvent hydrogen bonding interactions. To examine this more closely, we calculated the pK_a of the bicarbonate anion (HCO₃⁻) using CO₃²⁻ bound by up to three water molecules. For comparative purposes, we also calculated the pK_a of HCO₃⁻ using the thermodynamic cycle shown in Scheme 1 (i.e., no bound waters):

$$\mathrm{p}{K}_{\mathrm{a}}\left({{\mathrm{HCO}}_3}^{-}\right)=(\Delta G_{\mathrm{gas}}^{\mathrm{o}}\left({{\mathrm{HCO}}_3}^{-}\right)+\Delta G_{\mathrm{S}}^{\ast }\left({{\mathrm{CO}}_3}^{2-}\right)-\Delta G_{\mathrm{S}}^{\ast }\left({{\mathrm{HCO}}_3}^{-}\right)+\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{H}}^{+}\right)+\Delta G^{\mathrm{o}\to \ast })∕2.303\log RT$$ (7)

where $\Delta G_{\mathrm{gas}}^{\mathrm{o}}\left({{\mathrm{HCO}}_3}^{-}\right)$ is the gas-phase acidity of HCO₃⁻, and $\Delta G_{\mathrm{S}}^{\ast }\left({{\mathrm{CO}}_3}^{2-}\right)$ and $\Delta G_{\mathrm{S}}^{\ast }\left({{\mathrm{HCO}}_3}^{-}\right)$ are the aqueous solvation free energies of CO₃⁻ and HCO₃⁻, respectively. The value that we used for $\Delta G_{\mathrm{S}}^{\ast }\left({{\mathrm{HCO}}_3}^{-}\right)$ in eq 7 was obtained using the thermodynamic cycle shown in Scheme 1. For this, we used a theoretical⁹⁰ value of 332.2 kcal/mol for the gas-phase acidity of carbonic acid, (H₂CO₃), an experimental⁹¹ value of 6.4 for the pK_a of H₂CO₃, the experimental⁶² value for the solvation free energy of the proton, and a calculated (SM6/MPW25/6−31+G(d,p)//MPW25/MIDI!) value for the aqueous solvation free energy of H₂CO₃ to arrive at a $\Delta G_{\mathrm{S}}^{\ast }\left({{\mathrm{HCO}}_3}^{-}\right)$ value of −71 kcal/mol. The remaining free energy that is needed to calculate the pK_a of HCO₃⁻ with eq 7 is the aqueous solvation free energy of CO₃²⁻, for which the SM6/MPW25/6−31+G(d,p)//B97−1/MG3S level of theory gives a value of −292 kcal/mol. Substituting the above values into eq 7 leads to a calculated pK_a of −3, which is in poor agreement with the experimental⁹² value of 10.3. This poor agreement is expected for unclustered calculations involving systems with such a large charge to volume ratio.

For pK_a calculations based on carbonate-water clusters we applied the thermodynamic cycle shown in Scheme 2

$$\begin{array}{cc}\hfill \mathrm{p}{K}_{\mathrm{a}}\left({{\mathrm{HCO}}_3}^{-}\right)=& (\Delta G_{\mathrm{gas}}^{\mathrm{o}}\left({{\mathrm{HCO}}_3}^{-}\right)+\Delta G_{\mathrm{B}.\mathrm{E}.}^{\mathrm{o}}\left[{\left({\mathrm{H}}_2\mathrm{O}\right)}_n{{\mathrm{CO}}_3}^{2-}\right]+\Delta G_{\mathrm{S}}^{\ast }\left[{\left({\mathrm{H}}_2\mathrm{O}\right)}_n{{\mathrm{CO}}_3}^{2-}\right]\hfill \\ \hfill -& \Delta G_{\mathrm{S}}^{\ast }\left({{\mathrm{HCO}}_3}^{-}\right)-n\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{H}}_2\mathrm{O}\right)+\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{H}}^{+}\right)\text{-}\left(n\text{-}1\right)\Delta G^{\mathrm{o}\to \ast })∕2.303\log RT\hfill \end{array}$$ (8)

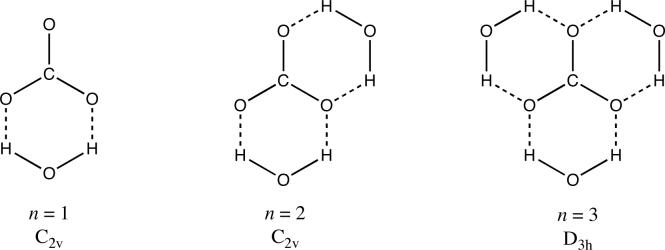
where $\Delta G_{\mathrm{gas}}^{\mathrm{o}}\left({{\mathrm{HCO}}_3}^{-}\right)$ is the gas-phase acidity of HCO₃⁻, $\Delta G_{\mathrm{B}.\mathrm{E}.}^{\mathrm{o}}\left[{\left({\mathrm{H}}_2\mathrm{O}\right)}_n{{\mathrm{CO}}_3}^{2-}\right]$ is the free energy associated with binding n water molecules to CO₃²⁻ in the gas phase, which is equal to $G_{\mathrm{gas}}^{\mathrm{o}}\left[{\left({\mathrm{H}}_2\mathrm{O}\right)}_n{{\mathrm{CO}}_3}^{2-}\right]-G_{\mathrm{gas}}^{\mathrm{o}}\left({{\mathrm{CO}}_3}^{2-}\right)-n{G}_{\mathrm{gas}}^{\mathrm{o}}\left({\mathrm{H}}_2\mathrm{O}\right),\text{and}\Delta G_{\mathrm{S}}^{\ast }\left[{\left({\mathrm{H}}_2\mathrm{O}\right)}_n{{\mathrm{CO}}_3}^{2-}\right]$ is the aqueous solvation free energy of the resulting carbonate-water cluster. For $\Delta G_{\mathrm{gas}}^{\mathrm{o}}\left({{\mathrm{HCO}}_3}^{-}\right)$, we used a calculated value of 479 kcal/mol obtained at the G3⁹³ level of theory. This value is in perfect agreement with the value recently reported by Gao and coworkers⁴¹ for the same level of theory. Gas-phase binding energies of the three clusters were calculated at the B97−1/MG3S level of theory. Combining these values with the $\Delta G_{\mathrm{S}}^{\ast }\left({{\mathrm{HCO}}_3}^{-}\right)$ value from above, experimental values for $\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{H}}_2\mathrm{O}\right)$ and $\Delta G_{\mathrm{S}}^{\ast }\left({\mathrm{H}}^{+}\right)$, and calculated (SM6/MPW25/6−31+G(d,p)//B97−1/MG3S) values for $\Delta G_{\mathrm{S}}^{\ast }\left[{\left({\mathrm{H}}_2\mathrm{O}\right)}_n{{\mathrm{CO}}_3}^{2-}\right]$, leads to calculated pK_a values of 3, 6, and 10 for n = 1, 2, and 3, respectively. These results are summarized in Table 2, along with the results obtained using the bare carbonate dianion. The structures of the three (H₂O)_nCO₃²⁻ clusters that were considered here are shown in Figure 2.

TABLE 2.

Gas-phase binding free energies of (H₂O)_nCO₃²⁻ (kcal/mol) and calculated pK_a values^a of HCO₃⁻ obtained without (n = 0) and with (n > 0) the addition of explicit water molecules to CO₃²⁻, using different continuum solvation models for calculating the aqueous solvation free energy of (H₂O)_nCO₃²⁻. The experimental pK_a of HCO₃⁻ is 10.3.

n	ΔGB.E.o[(H2O)nCO32−]b	SM6c	SM5.43Rd	DPCM/98e
0	0	−3 (13)	9 (1)	18 (8)
1	−28	3 (7)	14 (4)	23 (13)
2	−49	6 (4)	19 (9)	25 (15)
3	−67	10 (0)	23 (13)	38 (28)

^aAbsolute deviations relative to experiment are given in parentheses.

^bCalculated (B97−1/MGS3) values.

^cSM6/MPW25/6−31+G(d,p)//B97−1/MG3S

^dSM5.43R/MPW25/6−31+G(d,p)//B97−1/MG3S

^eDPCM/98/HF/6−31G(d)//B97−1/MG3S; UAHF atomic radii used.

Figure 2.

Carbonate-water clusters considered in this study. Dashed lines represent hydrogen bonds.

The excellent agreement between the experimental pK_a of HCO₃⁻ and the pK_a obtained using the (H₂O)₃CO₃²⁻ cluster in eq 8 suggests that hydrogen-bonding interactions between water and the divalent CO₃²⁻ anion are accurately accounted for with three explicit waters. This is consistent with the statement above that adding explicit waters should almost always improve the results when the effect is large. Table 2 also shows that the accuracy of the pK_a prediction increases in a stepwise fashion as explicit waters are added. Finally, for some of the acids in Table 1, the above results suggest that the accuracy of the pK_a prediction can further be improved by the addition of more than one explicit water molecule to the conjugate base.

Finally, it is worth comparing the above results to those obtained using two other continuum solvation models: SM5.43R^94,95 and the dielectric version^55,96,97 of PCM (DPCM) with the UAHF method for assigning atomic radii⁷⁹ as implemented in Gaussian 98⁹⁸ (we will refer to this second model as DPCM/98). For this, we calculated the pK_a of HCO₃⁻ using $\Delta G_{\mathrm{S}}^{\ast }\left[{\left({\mathrm{H}}_2\mathrm{O}\right)}_n{{\mathrm{CO}}_3}^{2-}\right]$ values (where n = 0, 1, 2, or 3) calculated with SM5.43R and DPCM/98. The results of these calculations are summarized in Table 2. We chose the SM5.43R model for comparison against because it is the most recent previous version of our series of continuum solvation models. The older Gaussian 98 implementation of DPCM was chosen because it was recently shown⁴⁷ to perform better than several other implementations of PCM for calculating aqueous solvation free energies of ionic solutes. The data in Table 2 show for both SM5.43R and DPCM/98, the closest agreement between the calculated and experimental pK_a of HCO₃⁻ is for n = 0, and the accuracy of the calculated pK_a decreases significantly as explicit water molecules are added to the calculation. (This counterintuitive result has also been pointed out in a previous paper⁴⁷). Thus, unlike SM6, adding explicit water molecules to these continuum solvent calculations is not an effective strategy for improving the quality of the calculation.

6. Conclusions

The present article and our previous work⁴⁷ show that in many cases when an accurate implicit solvent model is used, the addition of explicit solvent molecules in not necessarily required for obtaining reasonable estimates of the pK_a. However, when strong specific solute-solvent hydrogen bonding interactions are expected to play an important role in the aqueous phase, adding a single explicit water molecule to the calculation significantly improves the accuracy of the pK_a prediction. This brings the slope of the pK_a scale into reasonable agreement with the experimental slope, and, despite the recent claims made by Klamt et al.²³, should eliminate any doubts as to the correctness of the standard thermodynamic treatment⁵⁷ of pK_a.

To see what effect adding multiple explicit waters has on the accuracy of calculated pK_a values in cases where several sites are available for strong solute-solvent hydrogen-bonding interactions, we calculated the pK_a of HCO₃⁻ using carbonate-water clusters bound by up to three explicit water molecules. It was shown that the accuracy of the prediction significantly improved with each addition of an explicit molecule—the calculated and experimental pK_a of HCO₃⁻ are in excellent agreement when three explicit water molecules are added to the conjugate base (CO₃²⁻). When two other continuum models, SM5.43R and PCM, are used instead of SM6, the accuracy of the calculated pK_a for HCO₃⁻ significantly worsens upon each addition of an explicit water molecule. Based on this result, as well as previous work,⁴⁷ we do not suggest applying these other continuum solvent models to solute-solvent clusters, and we feel that the results obtained from such calculations should be interpreted with some degree caution.