Abstract
The impact of the A-type γ-aminobutyric acid (GABA-A) receptor in gonadotropin releasing hormone (GnRH) neurons is controversial. In adult GnRH neurons, the GABA-A receptor conductance has been reported to either hyperpolarize or depolarize GnRH neurons. Regardless of whether GABA is inhibitory or excitatory in GnRH neurons, GABAergic input would be integrated with post-synaptic potentials generated by other synaptic inputs. We used dynamic current clamping and compartmental computer modeling to examine the integration of alpha-amino-3-hydroxy-5-methyl-4-isoxazole propionic acid (AMPA)-type glutamatergic input and GABA-mediated input in both the hyperpolarizing (inhibitory) and depolarizing (excitatory) modes. In both living and model neurons, action potentials were most likely a few ms after a maximum in AMPA conductance coincided with a minimum in inhibitory GABA. Excitatory GABA interacted differently with AMPA, with spikes most likely, in both dynamic clamping of living neurons and in model neurons, when a maximum in AMPA coincided with the decay from peak of a maximum in GABA. Distributing synapses along the dendrite maximized the temporal relationship between AMPA and GABA conductances and therefore, the potential for spiking. Thus, these two dominant neurotransmitters could interact in multiple frames to generate action potentials in GnRH neurons.
Keywords: GnRH, synaptic integration, compartmental model, glutamate, GABA, hypothalamus
Hypothalamic GnRH neurons form the final pathway for integration of signals regulating reproduction. The control of GnRH neurons has been proposed to reflect both their intrinsic electrical properties and the input they receive from presynaptic neurons (Kusano et al., 1995; reviewed by Lopez et al., 1998). Despite the relatively precise requirements in the timing of GnRH pulses for proper reproductive function (Pohl et al., 1983), GnRH neurons have heterogeneous electrophysiological properties (Sim et al., 2001; Spergel et al., 1999). Moreover, emerging evidence suggests that GnRH neurons may differ in their responses to at least one key hypothalamic neurotransmitter, γ-aminobutyric acid (GABA). Application of ligands for the GABA-A receptor indicate that GABA-A receptor-mediated events in adult GnRH neurons are hyperpolarizing in some studies (Han et al., 2002 and 2004), whereas others indicate they are depolarizing (DeFazio et al., 2002). Likewise, electrophysiological recordings aimed at determining the impact of endogenous GABA have revealed differences in responses. Using perforated patch recording, blocking of endogenous GABAergic transmission caused membrane depolarization in most GnRH neurons (80%), indicating that endogenous GABA inhibits GnRH neurons (Han et al., 2004). A second study reported a suppression of firing rates in most active GnRH neurons following application of GABA receptor antagonists (Moenter and DeFazio, 2005) suggesting endogenous GABA is excitatory in GnRH neurons.
Discrepancies in the reported actions of GABA within a population of neurons are not unique to the GnRH system (Carter and Regehr 2002; Chavas and Marty 2003). Differences in the action of GABA are generally attributed to issues surrounding the regulation of chloride homeostasis. The reversal potential for chloride depends on the ratio of the external to internal concentration of the ion through the Nernst Equation: . Since the ideal gas constant, R, the temperature, T, the number of excess electrons on the chloride ion, n, and the Faraday Constant, F are all positive, and since the natural logarithm of a number greater than one is always positive, then if the concentration of chloride outside the cell is greater than that inside the cell, then the ratio in the Nernst equation will be positive, and the reversal potential will be negative. Since chloride is the main ion carried by the GABA-A receptor channel, the relative values of the chloride reversal potential and the resting membrane potential of the cell will determine whether a GABA-A mediated input will be depolarizing or hyperpolarizing. It is now clear that the reversal potential for chloride and therefore, the actions of GABA can be modulated (see Cupello 2003 for review). Several physiological conditions have been reported to lead to differences in the response to GABA. For example, the reversal potential for chloride shifts in cortical neurons due to changes in intracellular chloride concentrations during times of high GABA input (Gulledge and Stuart 2003). In active GnRH neurons, GABA may also be excitatory through this mechanism (Moenter and DeFazio, 2005). Differences in chloride transporter expression between GnRH neurons have been reported (DeFazio et al., 2002; Leupen et al., 2003). Up-regulation of NKCC2 expression by testosterone and dihydrotestosterone has been reported in males and females in neurons of the substantia nigra (Galanopoulou and Moshe 2003). The NKCC2 transporter acts to remove chloride ions from the cell. Thus, GABA may be excitatory or inhibitory in individual neurons based on NKCC2 expression, or potentially excitatory and inhibitory in the same neuron based on changes in activity and accumulation of intracellular chloride.
Independent of whether GABA is excitatory or inhibitory, GABAergic input would be integrated with that of other presynaptic neurons providing input to GnRH neurons. For example, glutamate is a second dominant neurotransmitter in the mammalian hypothalamus (Decavel and van den Pol, 1990; van den Pol et al., 1990). There is general agreement that glutamate excites GnRH neurons (Kuehl-Kovarik et al., 2002 and 2005; Suter, 2004). However, it is unclear how synaptic integration of glutamatergic input in GnRH neurons would be affected when GABA is excitatory, as would be the case with a suppression of the NKCC2 transporter or chloride increase due to high GABA activity, or when GABA is inhibitory as would be the case in a situation with reduced intracellular chloride. In the present study, we used the techniques of dynamic current clamping and compartmental modeling, where we were able to set the reversal potential for simulated GABA inputs, to examine integration of glutamatergic input with both inhibitory and excitatory GABA.
Materials and Methods
Tissue preparation
Hypothalamic slices (200 μm) were prepared using a vibrating microtome (Slicer HR-2; Sigmann Elektronik, Hueffenhardt, Germany) from male GnRH-GFP mice in which GnRH neurons express green fluorescent protein (GFP; Spergel et al., 1999). The average age of mice used for whole-cell voltage clamp recordings of spontaneous post-synaptic currents (PSCs) was 92 ± 2.6 days (n = 19), and the average weight was 26.7 ± 0.67 grams. The average age of mice used for dynamic current clamp recordings was 63.3 ± 5.2 days (n = 13), and the average weight was 22.3 ± 1.4 grams. The Institutional Animal Care and Use Committee of Emory University and the University of Texas at San Antonio approved all procedures. Mice were anesthetized with halothane and decapitated. Brains were quickly removed and placed in cold (1-2°C), artificial cerebrospinal fluid (ACSF) solution containing (in mM): NaCl (125), NaHCO3 (24), KCl (2.5), CaCl2 (1), MgCl2 (1), and glucose (10), equilibrated with 95% O2/5% CO2, pH 7.3-7.4. Slices were incubated in ACSF for 1-2 hours at 32°C, transferred to a recording chamber mounted on the stage of an upright microscope (Axioskop, Carl Zeiss Microimaging Inc., Thornwood, NY), and then continuously perfused with ACSF (32°C). GnRH neurons were identified through their GFP expression using epifluorescent excitation at 470 nm with a 60X water immersion objective. To prevent excessive exposure of the slices to the epifluorescent excitation, a shutter (Uniblitz, Vincent Associates, Rochester, NY) was used between the light source (AttoArc, Carl Zeiss) and the objective. Slices were illuminated 100 ms every 1.5 s during identification.
Electrophysiology
Recordings were made with an Axoclamp 2B amplifier (Axon Instruments; Union City, CA). Pipettes (9-12 MΩ) were fabricated from borosilicate glass (AM Systems, Carlsborg, WA) using a pipette puller (PP-83; Narishige, Tokyo, Japan) and coated with Sylgard 184 (Dow Corning, Midland, MI) to minimize pipette capacitance. Electrodes were positioned using piezoelectric micromanipulators (Luigs and Neumann, Ratingen, Germany). Data were digitized at 10 kHz using custom software. When studying activity of GnRH neurons in response to simulated GABAergic inputs, picrotoxin (40 μM; Tocris, Ellisville, MO), a GABA-A receptor antagonist, was added to the bath solution to block endogenous GABA receptor activation. Likewise, when studying both AMPA and GABA effects, the AMPA/kainate receptor antagonist 6-Cyano-7-nitroquinoxaline-2,3-dione (CNQX, 10 μM; Tocris) and the NMDA receptor antagonist D(-)-2-Amino-5-phosphonopentanoic acid (AP-5, 100 μM; Tocris) in addition to picrotoxin (40 μM) were included in the bath solution to block non-NMDA and NMDA glutamatergic receptors, and GABA-A receptors respectively.
Dynamic Current Clamp Recording
Three basic parameters that characterize the electrical activity of neurons are voltage or electrical potential, current, or flow of charge, and conductance, or its inverse, resistance. In a living synapse, the conductance is proportional to the number of ion channels that are open at any given time. Thus, the value of conductance is never negative. The relation between voltage, current and conductance is described mathematically by Ohm's Law: Ii = gi(Vm − Ei). In this formula, Ii is an ionic current, gi is the conductance for this current, Vm is the membrane potential, and Ei is the reversal potential for the ionic species that carries the current. The reversal potential for a given ion will depend on the relative concentration of that type of ion in the exterior and interior of the cell. As indicated in Ohm's law above, if the conductance gi increases, then there will be a proportional increase in the magnitude of the current Ii, as long as there is a non-zero driving force (Vm − Ei). Similarly, if the conductance is unchanged, but the reversal potential Ei changes, then a larger or smaller current will flow depending on whether the change in Ei causes an increase or a decrease in the magnitude of the driving force. The sign of the current that flows is determined by the sign of the driving force.
Dynamic current clamping is used to apply the electrical equivalents of synaptic currents to neurons. In this technique, the injected current mimics biophysical currents. The currents that flow in living cells, such as the GABA-A synaptic current, are characterized by a time-varying conductance and a reversal potential. Thus, one can construct simulated synapses in which one defines both the magnitude and time course of the conductance and the reversal potential. For dynamic clamping experiments, one simulates a pre-defined pattern of synaptic input by storing a conductance waveform that is the sum of many individual post-synaptic conductance events. This waveform can then be applied multiple times to the same cell, or to different cells. Since the membrane potential changes in a living neuron, the dynamic current clamp uses feedback from a neuron to a computer, where Vm is updated online (in our experimental configuration at 10 kHz). The computer program adjusts the injected current to reflect changes in driving force that occur with alterations in Vm (Sharp et al., 1993). Thus, the magnitude of inputs applied using the dynamic current clamp depends on the activity of the recorded neuron.
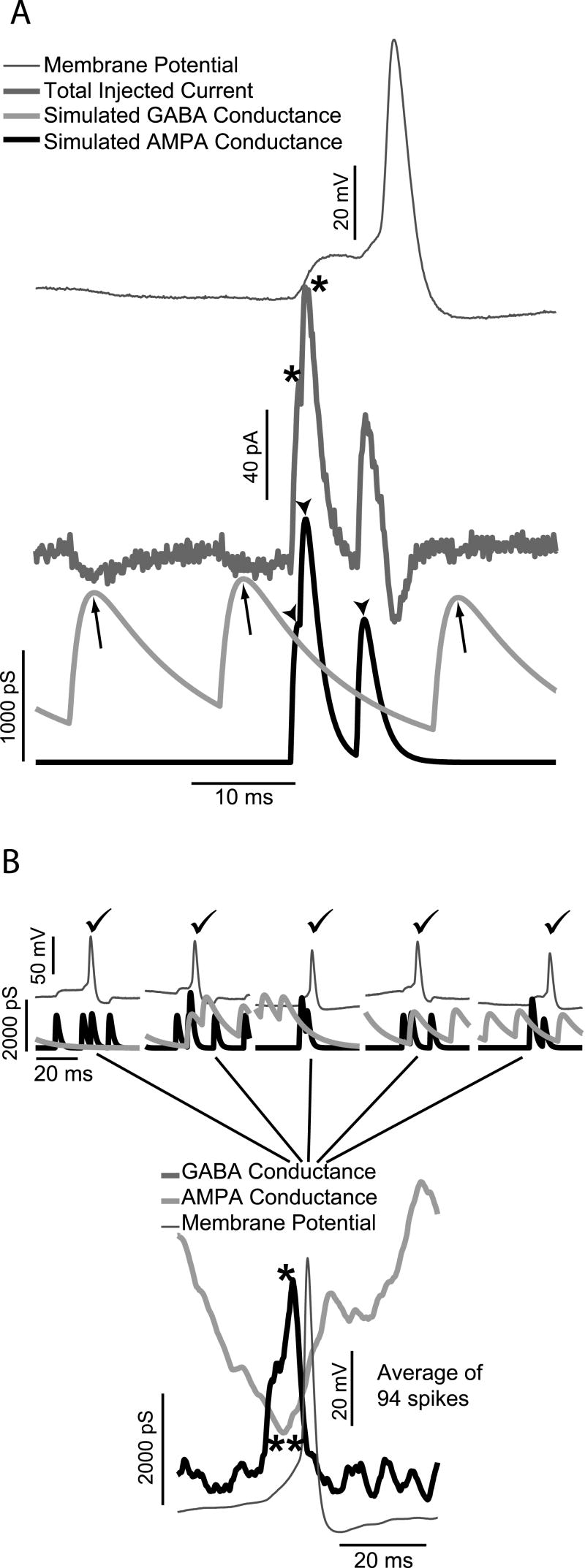
Fig. 1A shows application of simulated AMPA and inhibitory (reversal potential -70 mV, simulating reduced intracellular chloride) GABA inputs to a living GnRH neuron via dynamic clamping. The bottom traces are the simulated AMPA and GABA conductances. In this case, there were three simulated GABAergic synaptic events (at arrows), and three closely spaced AMPA-type synaptic events (at arrowheads). Two of the AMPA events (at asterisks) are spaced closely enough together in time that they sum to a double peak. The middle trace shows the current that was injected into the cell by the dynamic clamp. During a recording, the instantaneous values of the membrane potential (Vm) from the neuron, the conductance (gi) from the conductance waveform and the reversal potential (Ei) as set in the simulation are used to calculate the current to be injected (Ii) using Ohm's Law (Ii = gi(Vm − Ei)). The top trace shows the voltage response of the cell. The membrane potential first decreases due to the hyperpolarizing current from the simulated GABA inputs, then rapidly rises due to the much larger depolarizing current from the simulated AMPA inputs. In this case, the total input was sufficient to drive the cell past threshold, and it fired an action potential. Note that the peak of the action potential coincides with a non-zero GABA conductance. This leads to a much larger hyperpolarizing current. This is because the membrane is highly depolarized leading to an increase in the driving force. Careful examination of the current trace shows that the current deflection for the third GABA input is somewhat smaller than those for the first two, reflecting the fact that the driving force for the GABA current is smaller at this time because the membrane potential is closer to the inhibitory GABA reversal potential (-70 mV in these experiments).
Fig. 1.
Diagrams of Dynamic Current Clamping and Spike-Triggered Averaging. A: A short section of dynamic clamp recording, applying simulated AMPA and inhibitory GABA conductances to the soma of a living GnRH neuron. The top trace is the recorded membrane potential. The current injected by the dynamic clamp is shown as the second trace from the top. The two bottom traces are the GABA (gray) and AMPA (black) conductance profiles used in the experiment where arrows indicate increases in the GABA conductance and arrowheads indicate increases in the AMPA conductance. After two closely-spaced AMPA inputs (at asterisks), the membrane depolarizes past threshold, and the cell fires an action potential. B: Examples of 5 sections of voltage and conductance traces from the same dynamic clamping experiment as above, where there was an action potential in each case (indicated by check marks). In the spike-triggered average, the conductance and voltage traces are aligned at the time of the peak of the action potential, and the average of all traces for all detected action potentials is recorded. The lower part of the figure shows the result of such an averaging procedure for a total of 98 action potentials recorded from one cell.
Analysis: Spike-triggered Averaging
The analysis of the results of the dynamic clamping experiments to understand how GnRH neurons integrate synaptic inputs involves the technique of spike-triggered averaging. To understand the nature of inputs that lead to spikes, one looks at the inputs in a small temporal window before and after each spike. The process is illustrated in Fig. 1B. At the top of the figure are five sections of the voltage and conductance traces where the simulated synaptic inputs caused action potentials (indicated by check marks). In the spike-triggered averaging procedure, these sections are chosen to cover a symmetrical time interval centered on the peak of the action potential. One set of three traces, for the voltage and the two conductance waveforms, is stored for each detected spike. The lower panel in the figure shows the result when 94 such sets of traces are averaged. Since this set of data came from experiments with excitatory AMPA and inhibitory GABA, the spike-triggered average shows that spikes require a maximum in the AMPA conductance (at single asterisk) which coincides with a minimum in the GABA conductance (at double asterisks).
Constructing Inputs for Dynamic Current Clamping: Electrophysiology
Simulated AMPA-type glutamatergic synaptic inputs were constructed with a reversal potential of 0 mV, based on previous measurements of PSCs in GnRH neurons (Spergel et al., 1999; Suter, 2004). Inhibitory GABAergic synapses were constructed with a reversal potential of -70 mV, a typical value for inhibitory GABA in other systems (De Jeu and Pennartz, 2002). In order to accurately simulate excitatory GABAergic input with the reported EGABA= -36.5 mV (DeFazio et al., 2002), we first performed whole cell voltage-clamp recordings where we adjusted the pipette and ACSF chloride concentrations to set the reversal potential for chloride to -36.5 mV. This allowed us to determine the characteristics of endogenous GABAergic inputs at EGABA = -36.5 mV. After measuring spontaneous GABAergic PSCs (in the presence of CNQX and AP-5 to block endogenous glutamate), picrotoxin (40 μM; Tocris) was added to the bath solution to block endogenous GABA receptor activation and thus verify that those PSCs detected were in fact mediated by GABA-A receptors.
Constructing Inputs for Dynamic Current Clamping: Analysis
The time courses of the conductance of the simulated synapses used for our dynamic current clamping experiments were defined using a double-exponential function (Equation 1): In Equation 1, the variables τ1 and τ2 are the rise and fall time constants, t is the time, and ḡsyn is the conductance amplitude.
Simulated patterns of input, with stochastic 2nd order Gamma distributions of activation times at various mean frequencies, were computed using the General Neural Simulation System (GENESIS; http://www.genesis-sim.org/GENESIS/). GABA-type synapses were constructed using Equation 1 with a τ1 and τ2 of 0.764 and 12 ms respectively. AMPA-type excitatory synapses were constructed using Equation 1, with a τ1 and τ2 of 0.5 and 1.2 ms respectively (Suter, 2004). In the dynamic clamping experiments, the reversal potential for GABA inputs was set to either -70 mV (inhibitory, simulating decreased intracellular chloride), or -36.5 mV (excitatory, simulating elevated intracellular chloride). The reversal potential for AMPA was set to 0 mV (Suter, 2004). We used peak synaptic conductance levels for AMPA and GABA inputs of 250, 500, and 1250 pS in separate simulations to study the impact of a range of plausible sizes of synaptic inputs.
We validated this conductance formula (Equation 1) by analyzing data from endogenous GABAergic PSCs. In voltage clamp measurements, the membrane potential is held constant, so the driving force (Vm − Esyn) in Ohm's Law remains constant as well. Therefore, the measured PSC should be a constant times the time-varying conductance. This means that the formula for a detected PSC should be same as that for a synapse (Equation 1), except that the conductance amplitude ḡsyn should be replaced by a current amplitude: Īsyn = ḡsyn(Vm − Esyn). This modified version of Equation 1 (Equation 2): was used to extract time constants and current amplitudes from measured PSCs, either endogenous or generated with the dynamic current clamp.
Identification and characterization of PSCs from voltage clamp and dynamic current clamp recordings were performed by custom software. The PSC analysis programs first collected all events with current amplitudes greater than baseline noise (∼ 5 pA). The three parameters in Equation 2; Īsyn, τ1 and τ2 were calculated with a curve-fitting procedure, generating a best fit of Equation 2 to each event. The resulting set of rise and fall times were then examined and events with rise or fall times significantly differing from the average values were rejected. The same analysis was applied to the voltage clamp data of spontaneous PSCs and to the dynamic clamp data of injected current, to verify that the two types of input were similar.
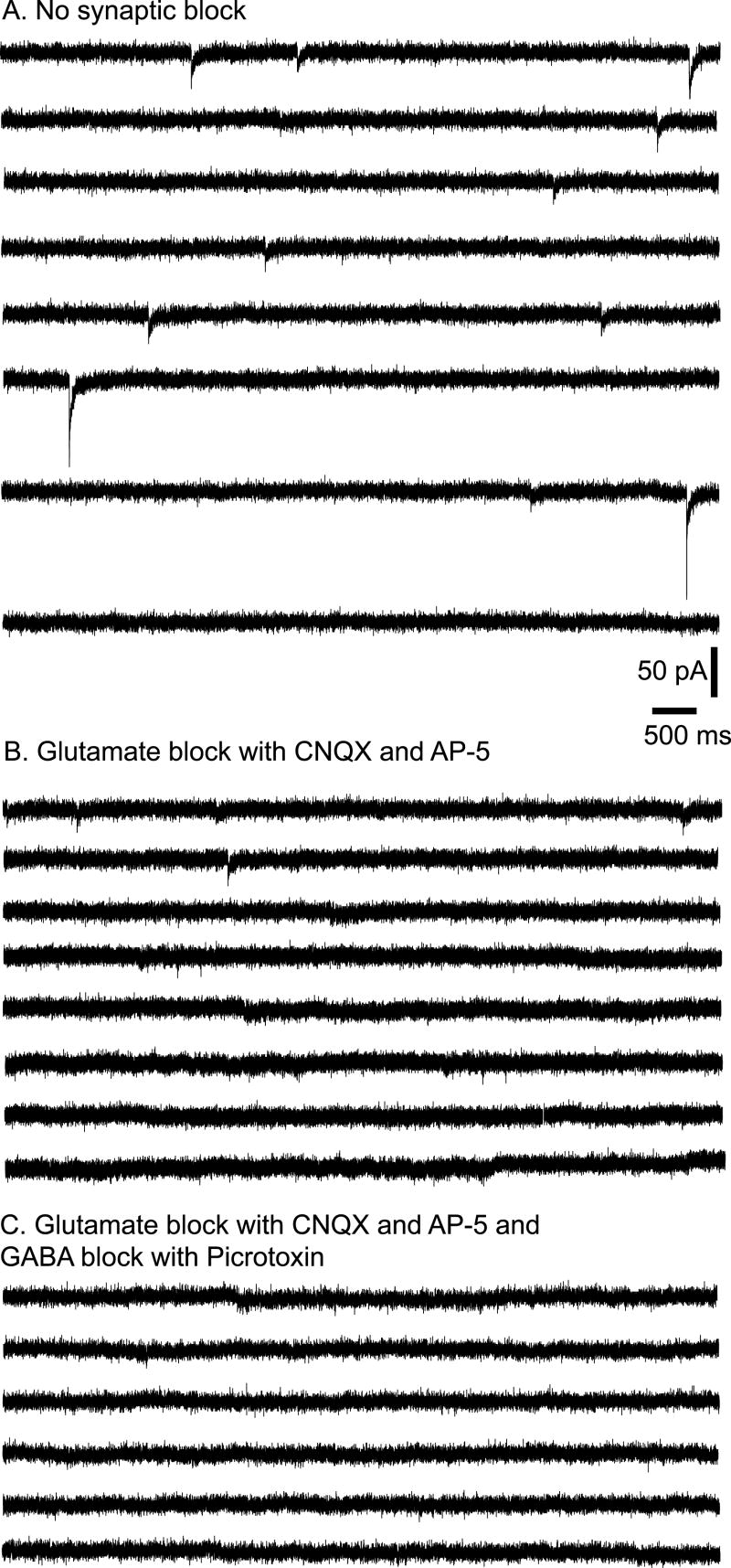
Fig. 2 shows spontaneous PSCs in an adult GnRH neuron with EGABA set to -36.5 mV. Recordings were performed at a holding potential of -60 mV before (Fig. 2A) and after (Fig. 2B) addition of the glutamate receptor antagonists CNQX and AP-5. Only a few, relatively small PSCs remained after addition of CNQX and AP-5, and these could be blocked by the GABA-A receptor antagonist picrotoxin (Fig. 2C).
Fig. 2.
Spontaneous PSCs when EGABA = -36.5 mV. Representative traces from a GnRH neuron at a holding potential of -60 mV. A: Mostly glutamatergic PSCs in the absence of added antagonists. B: Tiny GABAergic PSCs in the presence of the glutamate receptor antagonists CNQX and AP-5. C: Lack of any PSCs in the presence of CNQX, AP-5, and the GABA-A receptor antagonist Picrotoxin.
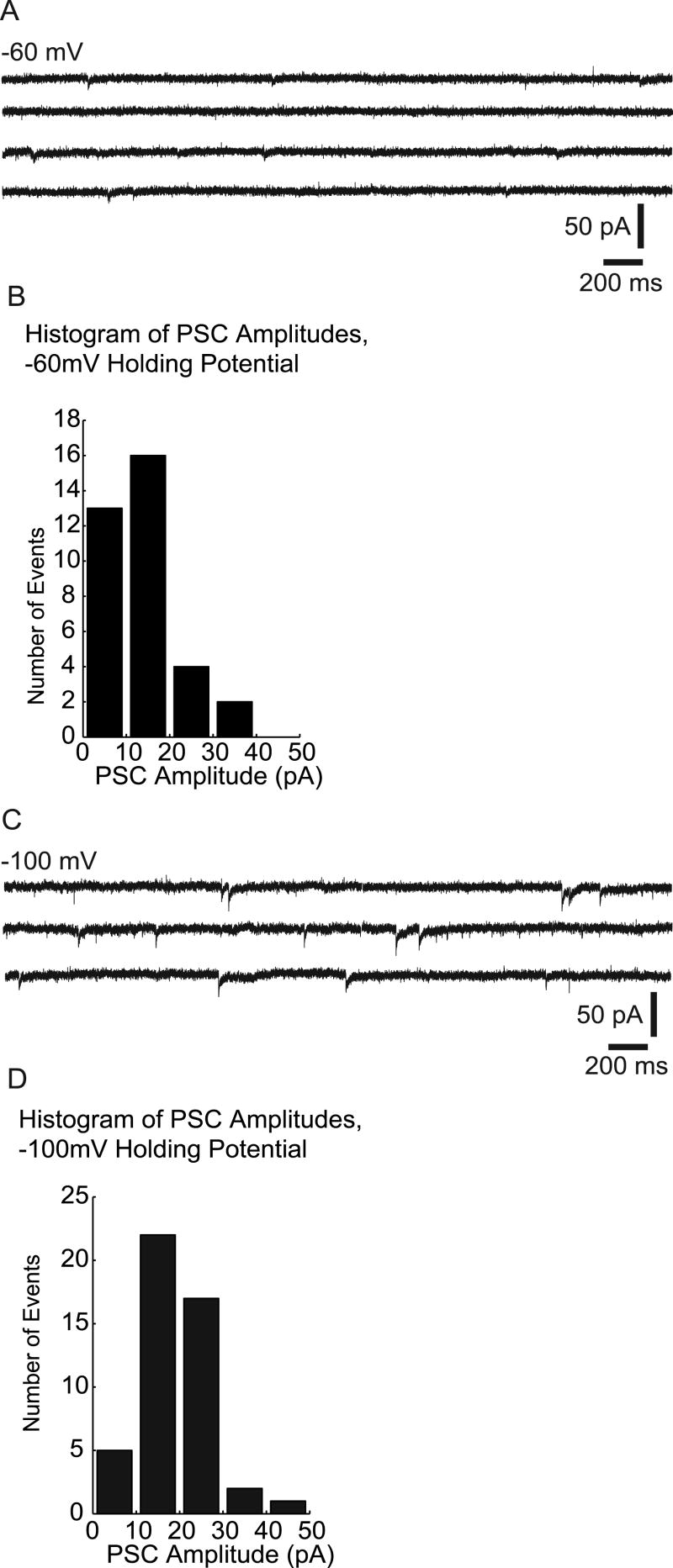
To isolate GABAergic PSCs for characterization, we bath applied CNQX and AP-5 (Fig. 3A and B). With EGABA = -36.5 mV, endogenous GABA-mediated events (Fig. 3A) had average current amplitudes (mean ± standard error) of 14 ± 1.2 pA (Fig. 3B) when we used a holding potential of -60 mV, thus imposing a driving force on the chloride ion of ∼ 20 mV. We then examined GABAergic PSC amplitudes after changing the holding potential from -60 to -100 mV, thereby imposing a driving force of ∼ 60 mV (Fig. 3C and D) which increased the amplitude of GABAergic inputs by ∼34% (to 18.7 ± 1.2 pA). In a second group of neurons, we examined GABAergic PSC amplitudes using symmetrical chloride concentrations between the pipette and bath solutions (130 mM) and a holding potential of -60 mV, imposing a 60 mV driving force on the chloride ion. The average amplitude of PSCs in this recording configuration was 20.2 (± 2.1) pA. This is comparable to the amplitude of spontaneous endogenous GABAergic events in a male mouse from this line using a 60 mV driving force for a GABA mediated event (Spergel et al., 2001).
Fig. 3.
Voltage clamp recordings of endogenous GABAergic Post-Synaptic Currents (PSCs) for excitatory GABA at two holding potentials. A: Voltage clamp data of recorded PSCs at a holding potential of -60 mV in CNQX and AP-5 to block endogenous glutamatergic synaptic input. B: Histogram of detected PSC amplitudes for endogenous GABAergic events at a holding potential of -60 mV. The mean current amplitude was 14 ± -7 pA. C: Voltage clamp data of recorded PSCs at a holding potential of -100 mV, other conditions unchanged from A. D: Histogram of detected PSC amplitudes for detected endogenous GABAergic events at a holding potential of − 100 mV. Increasing the driving force on the chloride ion by lowering the holding potential increases the amplitude of GABA-mediated PSCs.
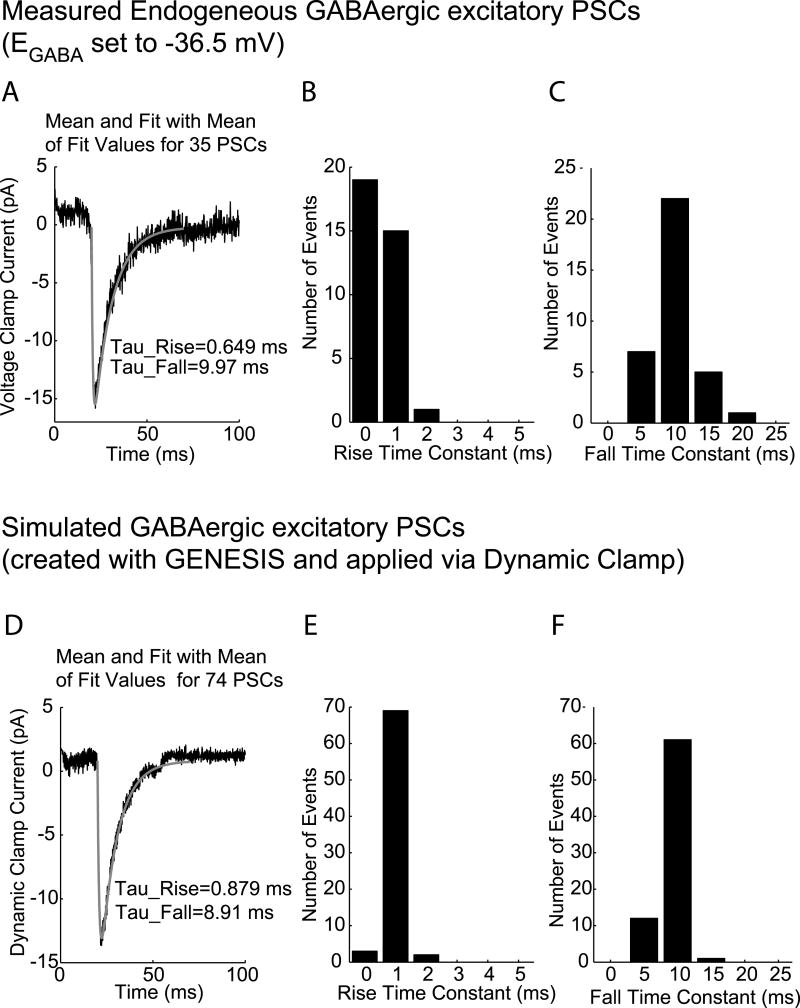
To validate our simulated inputs, we compared endogenous and simulated GABAergic currents (Fig. 4). We analyzed recordings of 35 endogenous PSCs and compared their amplitude and time course with 74 recorded currents generated in GnRH neurons during application of our simulated GABAergic conductances. When applied with dynamic clamping, the range of amplitudes of GABAergic currents induced by our simulated GABAergic conductance was 9.5-15.7 pA (average 11.5 ± 0.12 pA). Thus, the average amplitudes of spontaneous and simulated PSCs was similar (14.0 vs ∼ 12 pA). However, PSCs derived from simulated conductances were more homogenous than endogenous PSCs. The average of all analyzed currents for endogenous and simulated inputs is shown as the black lines panels A and D, respectively. For each set of current events (endogenous or generated to simulate synaptic inputs), averages of the best-fit amplitude and time constants were calculated. Using these average fit parameters, a theoretical curve for the average response in each of the two situations was calculated using Equation 2. These theoretical curves are plotted in gray on top of the average traces in panels A and D.
Fig. 4.
Comparison of endogenous and simulated GABAergic PSCs with a GABA reversal potential of -36.5 mV. A: Mean trace with average fit, and histograms of rise (panel B) and fall (panel C) times from fits to endogenous data. D-F: Mean trace with average fit (D), and histograms of rise and fall times (E and F) from fits to dynamic current clamp data.
The distributions of the rise and fall time constants of individual events are shown in panels B and C, for endogenous currents and panels E and F for simulated GABAergic inputs. Based on these analyses, Equation 2 accurately describes the amplitude and time course of endogenous GABAergic currents and thus our simulated synapses faithfully replicate endogenous synaptic events.
Compartmental modeling
One of the limitations of dynamic current clamping is that the current injecting electrode is located in the soma. This is an accurate way of simulating somatic synaptic inputs, but does not allow one to examine spatial integration of synaptic inputs. However, with the compartmental models, synaptic input can be applied at the soma, or in any distribution among the soma and dendrite compartments. Thus, using compartmental models, the effects of spatial distribution of synaptic inputs and local integration in the dendrite can be systematically examined.
The starting point for our models was the model of GT1-7 cells by LeBeau et al., (2000). The GT1-7 cell line is an immortalized hypothalamic GnRH cell line, originally produced by genetically targeted tumorigenesis (Mellon et al., 1990). This cell line has been shown to release GnRH, and is a well-studied model of the GnRH neuron system. The equations for the currents in the models of LeBeau et al. were based on voltage-clamp measurements in GT1-7 cells. These models were highly accurate and well-represented the activity of the GT1-7 cell line, but these cultured cells do not express the extended dendrites of living GnRH neurons. To increase the computational simplicity of our models, which have hundreds of computational compartments representing the dendrites, we wanted to have the smallest set of currents that would allow the models to accurate duplicate the activity of living cells. We also wanted to include only currents that had been explicitly identified previously in GnRH neurons. For these reasons, we did not include the T-type calcium, muscarinic potassium, or pacemaker Ca2+-carrying inward leak currents from the models of LeBeau et al., (2000). Somata contained Fast Na+, Delayed Rectifier K+ (Kusano et al., 1995) and Inward Rectifier K+ (Kusano et al., 1995; Wagner et al., 1998), and L-type Ca2+ conductances (Kusano et al., 1995; Spergel 2007). Fast Na+ and Delayed Rectifier K+ conductances were incorporated in dendrites and axons.
The first, passive dendrite versions of our models have been published elsewhere (Roberts et al., 2006). The model in this study used the branching GnRH neuron morphology from the previous model, and was tuned to the same passive and active measured electrophysiology. The model was constructed in the General Neural Simulation System (GENESIS) based on anatomical reconstruction of a biocytin-filled GnRH neuron, from which active and passive electrical activity was measured in whole-cell recordings. After the passive cell parameters (membrane leak resistance, membrane capacitance and axial resistance) were determined by a fit to passive data, Hodgkin-Huxley type voltage gated conductances were added to selected compartments in the model to duplicate measured active electrophysiological activity.
The densities of active and passive electrical properties in the various parts of the models were determined by Genetic Algorithm tuning. First, the passive response to short current injection pulses was matched, and then the active properties were adjusted to accurately match resting membrane potential, the shape and frequency of measured somatic action potentials generated by somatic current injection, and to propagate action potentials from the distal tip of the dendrite to the distal tip of the axon. The set of parameters with the best fit to the measured electrophysiology was chosen.
Results
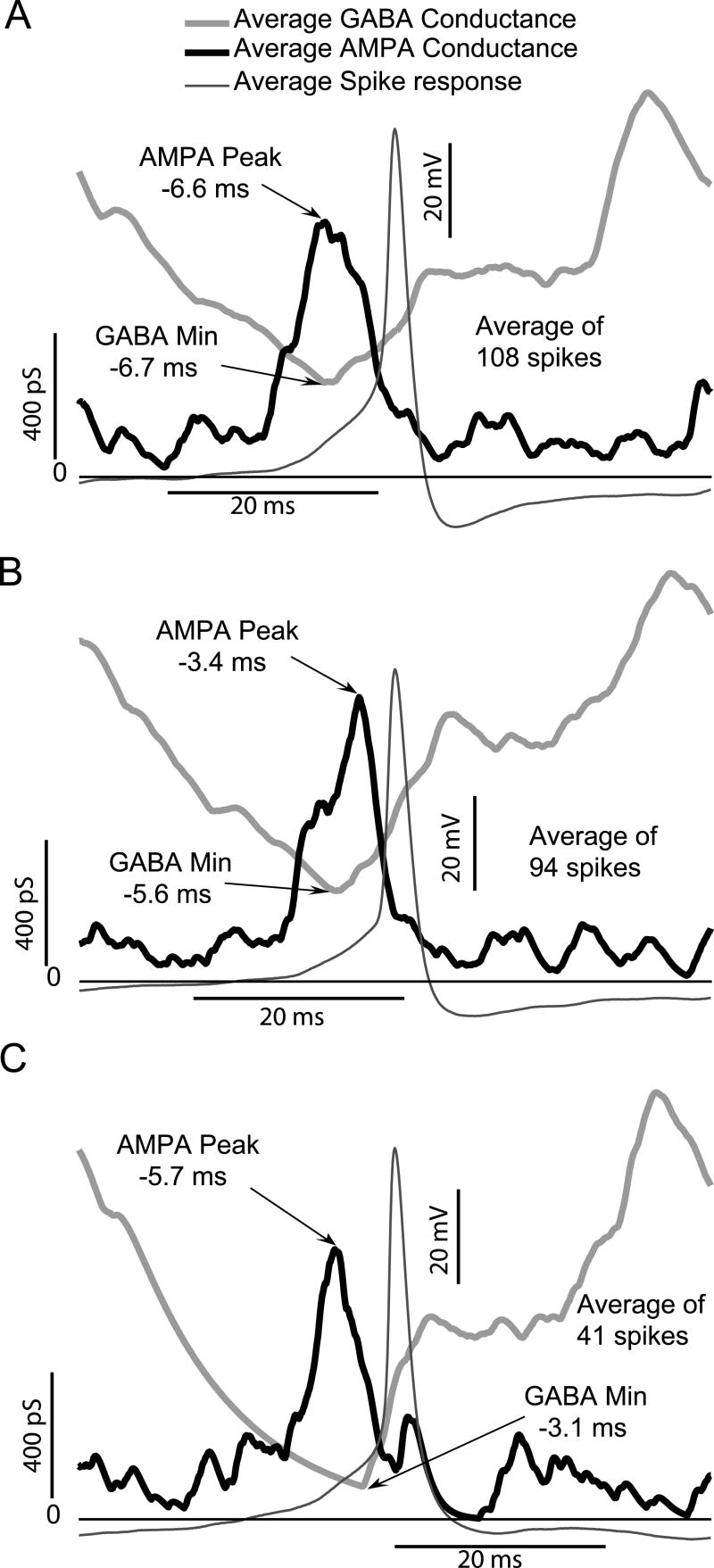
Fig. 5 shows spike triggered averaging in 3 representative neurons (panels A-C) to define the temporal relationship between AMPA-type excitation and inhibitory GABA (with a reversal potential of -70 mV, simulating reduced intracellular chloride) for action potential generation when simulated inputs were applied to living GnRH somata via dynamic clamping. Action potentials in GnRH somata were a consequence of an increase in AMPA-type excitation, as indicated by the peak in the AMPA conductance. Spikes occurred within 5.23 (±1.65) ms of the peak in the AMPA conductance, a finding which is consistent with our earlier dynamic clamping results using only AMPA-type conductances (Suter, 2004). However, when the AMPA-type conductance was applied to GnRH neurons in combination with GABAergic inhibition, action potentials required a decrease in GABA-mediated inhibition. Spikes occurred within 5.13 (±1.84) ms of a minimum in GABAergic inhibitory conductance. Thus, the peak of the AMPA-conductance and the minimum in the GABA conductance were roughly coincident.
Fig. 5.
Spike-Triggered Averages of AMPA and inhibitory GABA conductances applied to three different living GnRH neurons via dynamic clamping. In all three cells, action potentials were associated with a maximum in AMPA conductance coincident with a minimum in inhibitory GABA conductance.
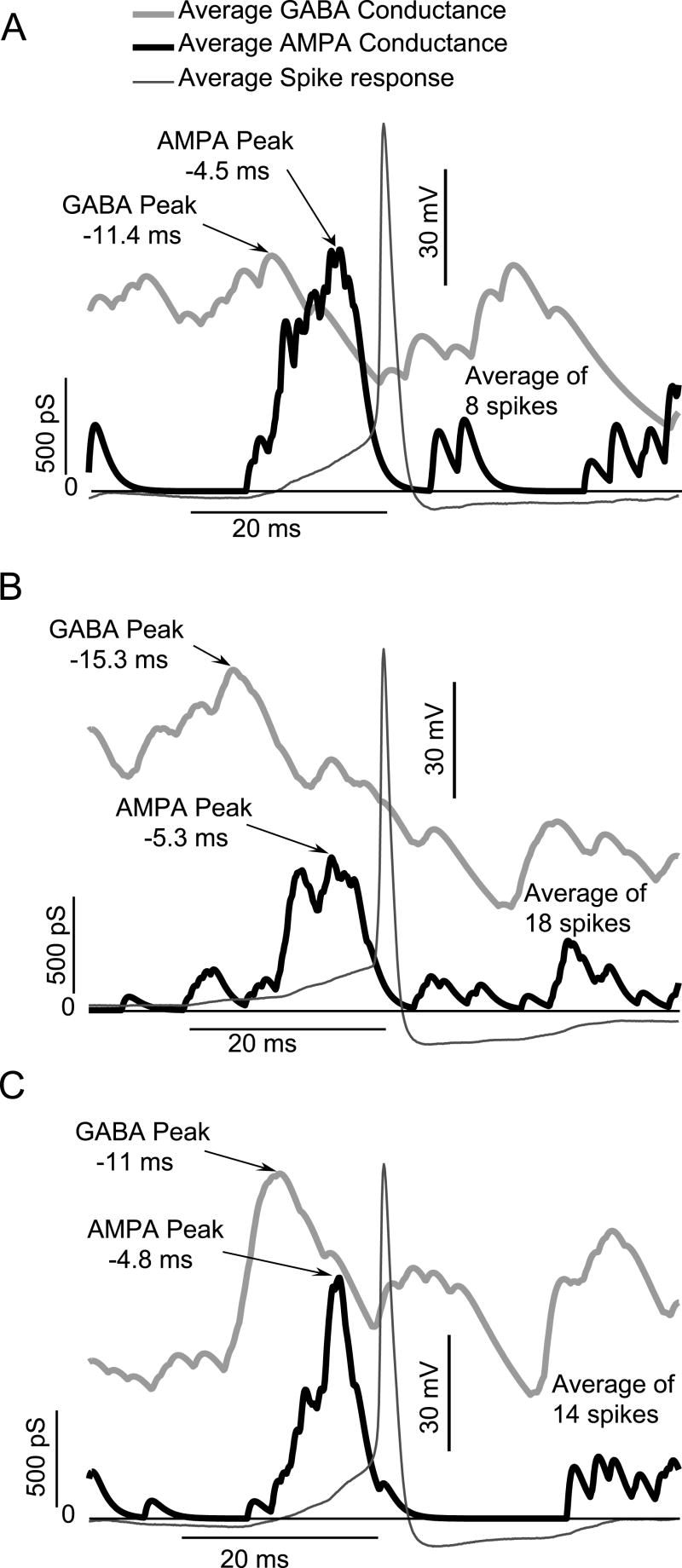
Fig. 6 shows spike triggered averaging in 3 representative neurons (panels A-C) to define the temporal relationship between AMPA-type excitation and GABA-type excitation (with a reversal potential of -36.5 mV, simulating increased intracellular chloride) for action potential generation when simulated inputs are applied to living GnRH somata via dynamic clamping. Action potentials in GnRH somata occurred immediately following an increase in AMPA-type excitation, as indicated by the peak in the AMPA conductance 4.9 (±0.4) ms prior to spiking. However, there was a temporal shift in the relationship between AMPA and GABA inputs when GABAergic inputs were excitatory, as opposed to inhibitory. Specifically, action potentials occurred when the maximum of AMPA-type excitation now occurred during the descending phase of a peak in GABAergic excitation. The maximum of the average GABA conductance occurred 12.6 (± 2.4) ms before action potentials, resulting in a delay between the two conductances of approximately 7.7 ms. This is in contrast to the timing of inputs for GABAergic inhibition where spiking was observed when maxima of AMPA and minima of GABA inputs were coincident (see Fig. 5).
Fig. 6.
Spike-Triggered Averages of AMPA and excitatory GABA conductances applied to three different living GnRH neurons via dynamic clamping. In all three cells, action potentials were associated with a maximum in AMPA conductance occurring on the downward slope after a maximum in the excitatory GABA conductance.
Spatial interactions
Dynamic clamping is a powerful tool for applying inputs to somata. However, applying inputs only to somata may not adequately reflect interactions when inputs are spatially separated along the dendrite. For example, activation of one type of excitatory synapses can attenuate the amplitude of other near-by inputs by reducing the ionic driving force on these inputs (by depolarizing the membrane potential). This leads to a less than linear summation of potentials generated from nearby inputs during dendritic integration of post-synaptic potentials (PSPs). Furthermore, activation of inputs and integration of signals along the dendrite will lead to distortion of synaptic signals due propagation delays between signal integration in the dendrite and arrival of the integrated signal at the soma (see Gulledge et al., 2005 for review). Dynamic clamping (which requires the whole cell recording configuration) of GnRH dendrites is not tractable due to the small dendrite diameters. Thus, we used our compartmental models of GnRH neurons, which allow us to distribute inputs along the dendrite, to study spatial interactions between GABA and AMPA. We focused on the first 260 μm of dendrite because it appears that synapses located beyond this length generate dendritic as opposed to somatic action potentials (Roberts et al., in press, Endocrinology). Therefore, we focused on somatically generated action potentials so that we could directly compare integration based on the same mode of spike generation.
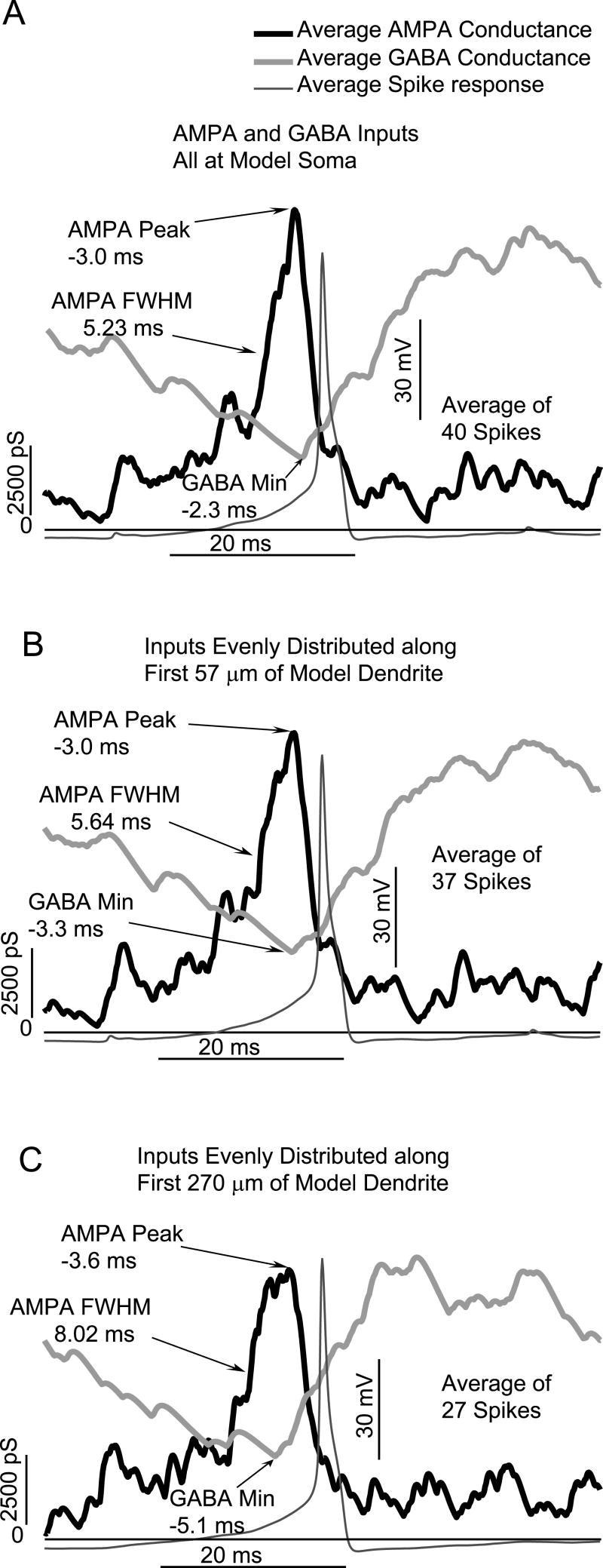
Fig. 7 shows the impact of distributing excitation mediated by AMPA and inhibitory GABA (with a reversal potential set to -70 mV, simulating reduced intracellular chloride) along the dendrite in model GnRH neurons. As seen with dynamic clamping in living GnRH neurons, spikes were associated with a maximum in AMPA and a minimum in GABA. Distributing inputs along the dendrite contributes a variable delay in propagation of the PSP to the soma for spike generation. This widens the window for the dendritic GABA-AMPA interactions that lead to action potential generation. This wider temporal window is evident in the width of the AMPA peak, as measured by the Full Width at Half Maximum (FWHM). For AMPA and inhibitory GABA both at the soma, the FWHM of the AMPA peak is 3.0 ms. When inputs were distributed along the first 57 μm of the dendrite, the AMPA FWHM increased to 5.64 ms. Distributing inputs along the first 260 μm of the dendrite further increased the width of the AMPA peak to 8.02 ms. Thus, distributing inputs along the dendrite creates a wider window for optimal integration with GABA inputs. However, the passive attention of distally integrated PSPs led to an over-all decrease in spike number as inputs were spatially distributed from the soma (40 spikes) to 260 μm of dendrite (27 spikes).
Fig.7.
Effects of spatial distribution of AMPA and inhibitory GABA conductances on the activity of a model GnRH neuron. In all cases, spikes are associated with a maximum in AMPA coincident with a minimum in GABA. A: For all inputs at the model soma, the AMPA Full Width at Half Maximum (FWHM) is 5.22 ms. B: For inputs distributed along first 57 μm of model dendrite, the FWHM increases to 5.64 ms. C:. For inputs distributed along the first 260 μm, the FWHM increases to 8.02 ms.
Fig. 8 illustrates impact of distributing excitatory AMPA and excitatory GABA inputs (with a reversal potential set to -36.5 mV, simulating increased intracellular chloride) along the GnRH dendrite in model neurons. Action potentials occurred when the peak of the AMPA conductance was co-incident with the decay phase of the excitatory GABA conductance, similar to results with dynamic clamping. Distributing inputs along the dendrite broadened the AMPA conductance peak from a FWHM of 2.27 ms for inputs at the soma to 4.82 ms for inputs distributed along 260 μm. Due to the slower time course of GABAergic inputs, they were less impacted by distribution along the dendrite (19.8 ms FWHM for soma vs. 21.4 ms FWHM for inputs along 260 μm of dendrite). The passive attenuation of PSPs integrated in the distal dendrite led to an over-all decrease in spike number as inputs were spatially distributed from the soma (35 spikes) to 260 μm of dendrite (23 spikes).
Fig. 8.
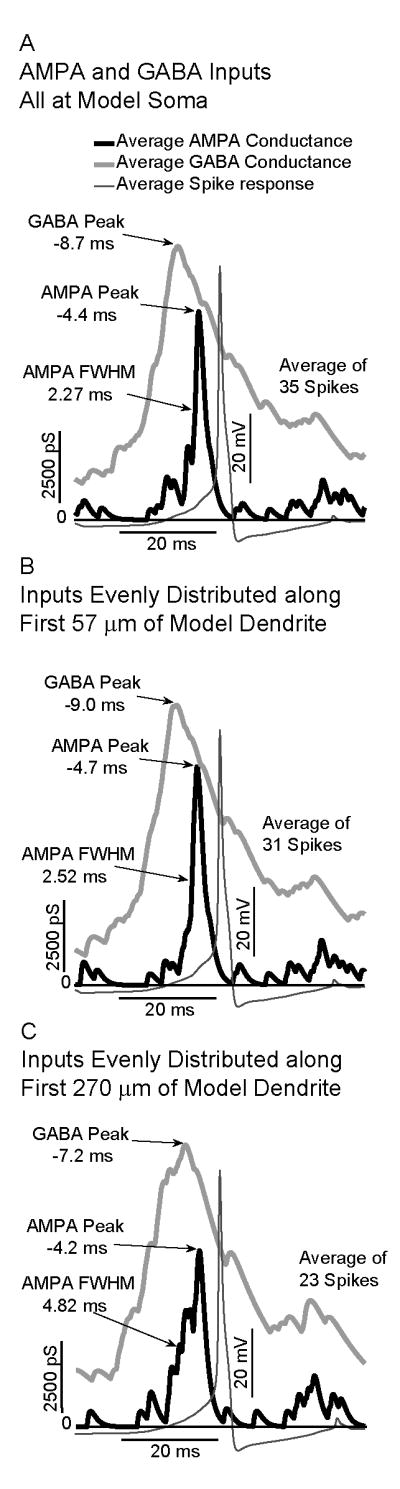
Effects of spatial distribution of AMPA and excitatory GABA conductances on the activity of a model GnRH neuron. In all cases, spikes are associated with a maximum in AMPA occurring on the downward slope after a maximum in the excitatory GABA conductance. A: For all inputs at the model soma, the AMPA Full Width at Half Maximum (FWHM) is 2.27 ms. B: For inputs distributed along first 57 μm of model dendrite, the FWHM increases to 2.52 ms. C:. For inputs distributed along the first 260 μm, the FWHM increases to 4.82 ms.
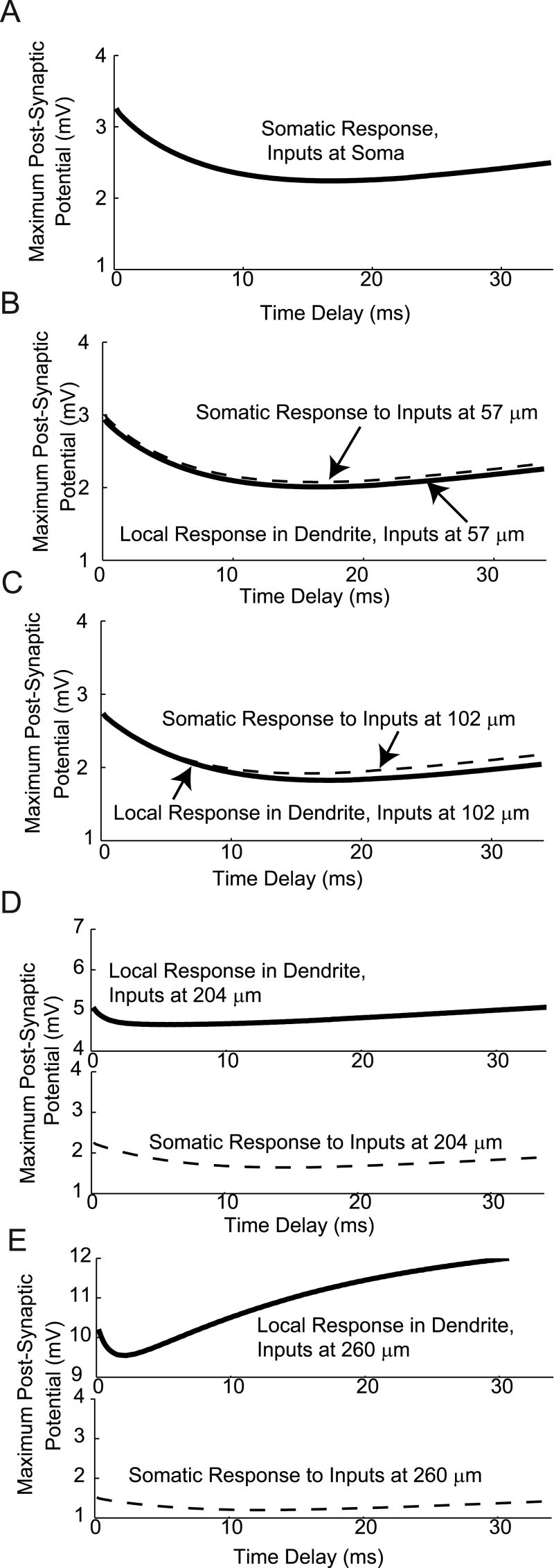
Three main effects of distributing inputs along the dendrite are attenuation of PSPs due to resistive losses, delays introduced by finite propagation times along the dendrite and an increase in the magnitude of PSPs due to the lower capacitance of the thinner diameter dendrite. To assess the effects of these temporal delays in isolation from the dendritic attenuation and propagation delays, we examined the effect of varying temporal delays between single GABA and AMPA inputs at the soma, where there is no propagation delay. Pairs of synaptic inputs, insufficient to drive spiking at the soma at any time delay, were applied to the soma. As the delay between the time of activation of GABA and the time of activation of AMPA was varied, the maximum amplitude of the soma voltage after the inputs was assessed. The maximum of the somatic PSP was plotted as a function of the GABA-AMPA activation delay for both modes of GABA input (excitatory and inhibitory). The results of these delay-time simulations are presented in Fig. 9. This was done with excitatory AMPA (with a reversal potential of 0 mV), and both inhibitory (panel A; with a reversal potential of -70 mV) and excitatory GABA (panel B, with a reversal potential of -36.5 mV).
Fig. 9.
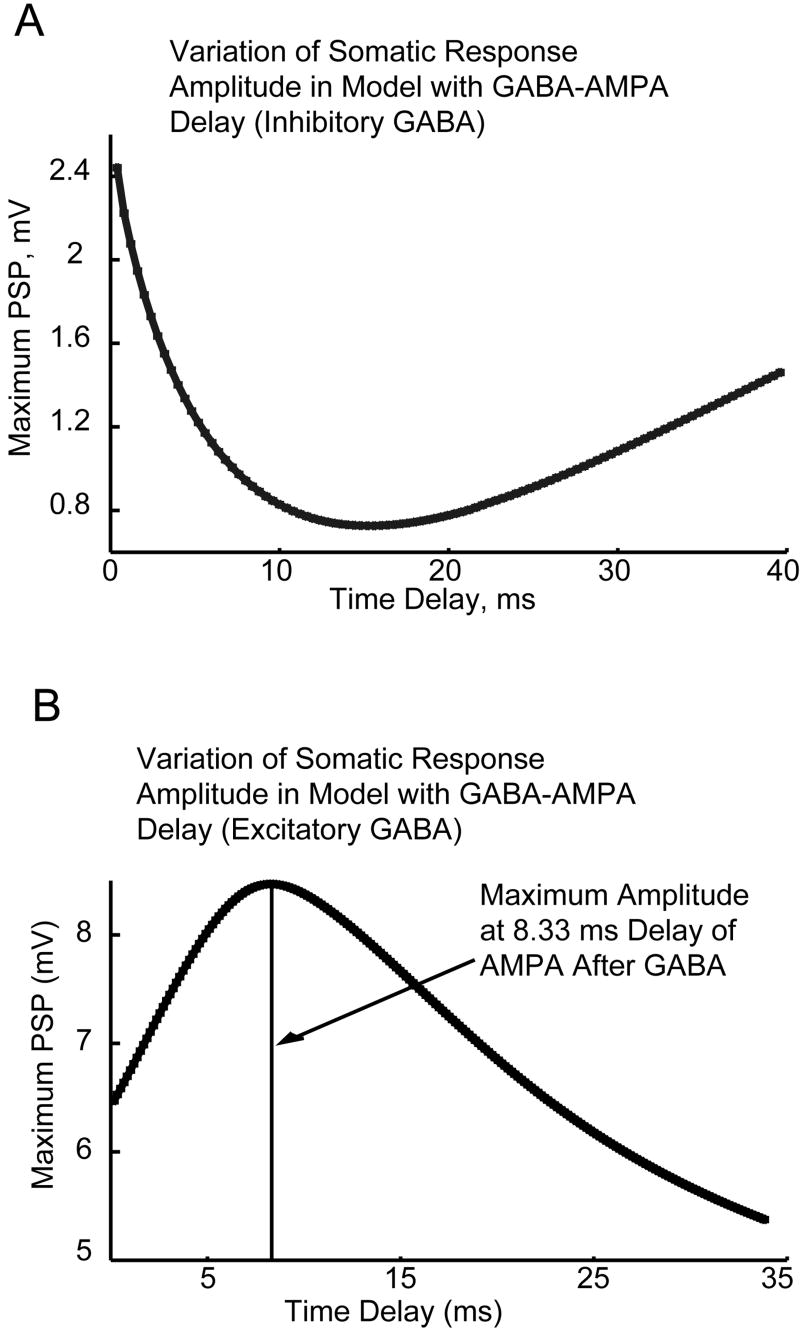
Modeling of the effects of temporal delays on integration of AMPA and GABA. The time delay between a single GABA synaptic event and a single AMPA synaptic event was varied, and the maximum resulting Post-Synaptic Potential (PSP) recorded. A: For inhibitory GABA, the maximum PSP occurs with coincident inputs (delay of 0 ms), with a maximum in inhibition (minimum in PSP) occurring with a delay of 15 ms. B: For Inhibitory GABA, the maximum PSP occurs with a delay of 8.33 ms.
The maximum PSP (which would be associated with the maximum probability of generating a spike for larger amplitude inputs), occurred when the unitary AMPA and inhibitory GABA inputs were activated at the same time (a delay of 0 ms). As the delay increased, the GABA conductance became more effective at inhibiting the AMPA conductance. A maximum in inhibition (as indicated by a minimum in the PSP) occurred for an AMPA synapse activated approximately 15 ms after the GABA input. As detailed in figures 5 and 7, for GABAergic inhibition and AMPA excitation in living cells with dynamic clamping, and in model GnRH neurons, respectively, these unitary delay results explain the observation that spikes are most associated with an AMPA input occurring just before a rise in GABA input.
For the case of excitatory GABA (panel B), with a depolarizing reversal potential of -36.5 mV, the results of the unitary temporal delay simulations were qualitatively different. In these simulations, the maximum PSP increased with the delay of the AMPA input after the activation of the GABA input, with a maximum in facilitation at a delay of 8.33 ms. Again, this explains the shapes of the curves in figures 6 and 8, for integration of AMPA and excitatory GABA in living cells with dynamic clamping, and in model neurons, respectively. In these results, the maximum probability of spiking was found when the AMPA inputs occurred on the declining phase of a GABA input, with a delay of several ms.
Dendritic integration of PSPs
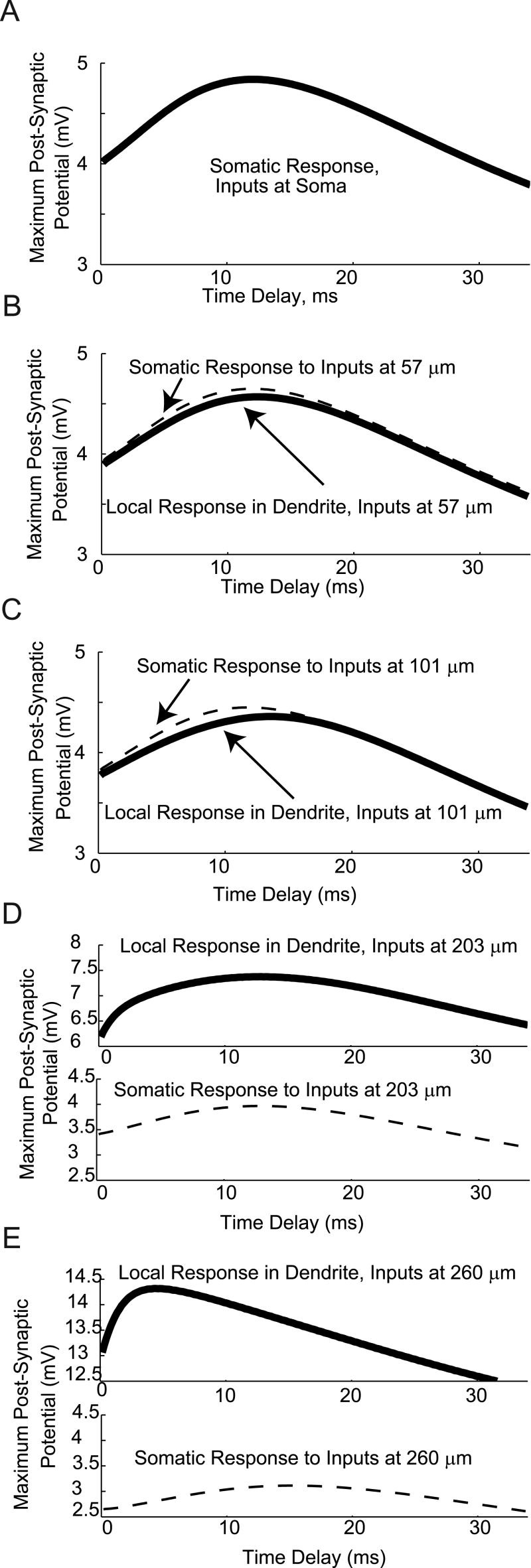
The interplay between active conductances and passive parameters and morphology serve to break a dendrite into functional micro-domains whose efficiency in generating action potentials in response to synaptic inputs varies with location. These effects, of initially decreasing, then increasing synaptic efficiency, explain the differences in integration of AMPA and GABA inputs as a function of distance, as shown for continuing activity in the spike triggered average graphs of Figure 7 and 8, and in the delay plots of figure 9.
Figures 10 and 11 show local dendritic integration of simulated GABA and simulated AMPA inputs (solid lines) in different compartments of the model GnRH neuron. The subsequent somatic responses to the dendritically integrated signal are shown for reference (in dashed lines). Figure 10 shows GABA and AMPA integration when the GABA inputs are inhibitory (reversal potential = -70mV). Figure 11 examines integration of excitatory GABA (reversal potential = -36.5 mV) and AMPA.
Fig. 10.
Comparison of dendritic and somatic integration of AMPA and inhibitory GABA. The effects of time delay between a single inhibitory GABA synaptic event and single AMPA synaptic event was evaluated in the soma (Panel A) and four dendrite compartments (Panels B-E). For each delay time, the maximum Post-Synaptic Potential (PSP) was recorded, and plotted as a function of delay time. For all four panels, the local response is shown as a solid line. For the four dendrite compartments, the maximum PSP recorded in the soma is shown as a dashed line.
Fig. 11.
Comparison of dendritic and somatic Integration of AMPA and excitatory GABA. The effects of time delay between a single excitatory GABA synaptic event and single AMPA synaptic event was evaluated in the soma (Panel A) and four dendrite compartments (Panels B-E). For each delay time, the maximum Post-Synaptic Potential (PSP) was recorded, and plotted as a function of delay time. For all four panels, the local response is shown as a solid line. For the four dendrite compartments, the maximum PSP recorded in the soma is shown as a dashed line.
For Inhibitory GABA (Fig. 10), the AMPA and GABA inputs act to oppose each other. Thus, for all the PSP amplitude versus distance curves in Figure 10, there is a local maximum in the PSP at zero delay, where the slower GABA input has not had time to turn on and oppose the faster, depolarizing AMPA input. In the case of integration of inhibitory GABA with AMPA, there is a minimum in the PSP amplitude versus distance curves. These minima indicate delays at which the GABA input is maximally efficient at inhibiting the AMPA input.
For inhibitory GABA (with a -70 mV reversal potential, simulating reduced intracellular chloride), the temporal window of integration for AMPA and GABA inputs widens with distance from the soma to the inputs, until the start of the local spike generation region, at which it again shifts to shorter times and becomes narrower. Nonetheless, the decreased local capacitance in the distal dendrite compartments causes the AMPA inputs to be much more effective, so that even in the face of GABAergic inhibition, the minimum PSP for inputs at 260 microns is almost 10 mV, nearly 5 times the minimum at the soma.
When GABA is excitatory (with a reversal potential of -36.5 mV, simulating increased intracellular chloride), the soma exhibits a relatively sharp temporal tuning curve for inputs (Fig. 11 panel A). This limits the time for synaptic integration, due to the decay of the voltage change generated by a synaptic input. The width of the PSP versus delay curve initially increases as the inputs are moved further from the soma along the dendrite. This leads to a broadening of the temporal window for optimal integration of AMPA and GABA inputs when inputs are located on dendrites (panels B-E). In more distal dendritic compartments, where spike initiation has been shown to be local (Roberts et al., Endocrinology, in press), the window for optimal temporal integration narrows again. In both cases (e.g., inhibitory and excitatory GABA), the amplitude of the local post-synaptic potential (measured in the compartment with the synapses) is greatest for the most distal compartment (at 260 μm from the soma; panel E), due to the smaller diameter, and therefore smaller capacitance, of the dendrite.
Discussion
Hypothalamic GnRH neurons form the final output pathway for the central control of reproduction through their intermittent release of the GnRH peptide. As such, they integrate the internal and external signals regulating pulsatile GnRH secretion (Herbison, 2006). Multiple neuronal phenotypes provide synaptic input to GnRH neurons (Todman et al., 2005). It is unknown how these synaptic inputs are integrated at the level of the single GnRH neuron. In the present study, we focused on integration of two key neurotransmitters in the neuroendocrine hypothalamus; glutamate, which is generally agreed to be excitatory in GnRH neurons and GABA. Since GABA may be either inhibitory or excitatory, we examined synaptic integration of both GABA excitation and GABA inhibition with AMPA-type inputs.
Dynamic current clamping is a particularly useful approach for studying synaptic integration. Voltage clamping allows one to identify individual synaptic currents of a particular phenotype or potentially discriminate synaptic currents of several phenotypes (see Fig. 2). However, because membrane potential is maintained at a holding potential, one can not determine whether detected synaptic currents generate action potentials. Alternatively, standard current clamping approaches allow one to detect PSPs, but one can not discriminate the phenotypes of synaptic inputs which have lead to these post synaptic potentials. This is particularly problematic when one wishes to determine the integration of PSPs whose timing overlaps in generation of action potentials. With dynamic clamping, simulated synaptic events, with time courses similar to endogenous currents, can be used to study action potential generation in a living cell.
On the other hand, in absence of in vivo recordings, it is very difficult to construct simulations that accurately reflect physiological input patterns to neurons. This is a particular problem for the GnRH system where in vivo recordings from single GnRH neurons have yet to be obtained. Recordings of post-synaptic events from GnRH neurons in slices may not accurately reflect in vivo inputs. As elegantly shown by Wintermantel et al., (2006), presynaptic neurons providing input to GnRH neurons are found throughout the hypothalamus. Fibers from more distal hypothalamic structures would be severed in the preparation of hypothalamic slices. Thus, depending on the location of afferent somata (and slice orientation), relative frequencies (and patterns) of input in slices may differ from those in vivo. If the frequency of inputs is high, then the interactions between inputs will be more frequent. By using stochastic patterns of GABA and AMPA inputs to GnRH neurons at moderate frequencies in our dynamic clamping and modeling studies, we were able to examine a wide variety of patterns of individual inputs, and thus extract the optimal interactions between inputs that would be most likely to drive firing.
The effect of GABAergic inputs will depend on the physiological state of the post-synaptic GnRH neuron. Since chloride is the main ion that flows through the GABA-A receptor channel, whether a GABAergic input to a given GnRH neuron will be excitatory or inhibitory will depend on the internal chloride concentration. The intracellular chloride concentration in GnRH neurons may vary for several physiological reasons. The level of NKCC2 in different GnRH neurons may differ because they are part of a functionally distinct sub-population of GnRH neurons. Cells with a higher level of NKCC2 will have a decreased level of intracellular chloride, and thus a more negative chloride reversal potential. However, a majority of GnRH neurons have undetectable NKCC2 expression by in-situ hybridization (DeFazio et al., 2002), rendering GABA excitatory. The internal concentration of chloride can also be affected by presynaptic GABAergic activity itself. The main ion carried by the GABA-A receptor channel is chloride, so as the level of GABA input increases, so will the flow of chloride into the cell (Gullege and Stewart 2003). It appears GABA is more likely to be excitatory in active GnRH neurons by virtue of the observation that GABA-A receptor antagonists decrease activity in active GnRH neurons (Moenter and DeFazio, 2005). Thus, the high levels of GABAergic synaptic input in GnRH neurons (Sim et al., 2000) may increase intracellular chloride levels and, consequently, raise the reversal potential for chloride.
For this study, we concentrated on two possible situations; where the GABA reversal was either -36.5 mV (excitatory GABA, simulating increased intracellular chloride), or where the GABA reversal potential was -70 mV (inhibitory GABA, simulating decreased intracellular chloride). The results of the current study indicate that not only will the response of GnRH neurons to GABAergic input change based on physiological shifts in the reversal potential for chloride but that integration of GABA and glutamate will be qualitatively different in these two physiologic states.
Integration of glutamate with GABAergic inhibition
The present results from both dynamic current clamping in living GnRH neurons and models of GnRH neurons show that the interaction between excitatory AMPA and inhibitory GABA involves the GABA conductance directly decreasing the impact of any AMPA conductance following it. The present data indicate that this occurs on a PSP by PSP basis with the maximum shunting with due to activation of GABA with a time delay of 15 ms relative to activation of the AMPA input. Thus, from a functional standpoint this finding indicates that inhibitory GABAergic inputs provide effective inhibition of incoming excitation through so-called shunting inhibition as opposed to a chronic hyperpolarization of the GnRH neuronal membrane.
From a physiological standpoint, decreases in GABAergic inhibition have been proposed to mediate in part the pubertal increase of GnRH secretion in non-human primates (Keen et al., 1999) and rodents (Goroll et al., 1993). In both animal models, increases in release of endogenous glutamate or ligands for glutamate receptors were also reported. The precise phase relationships of changes in levels of GABA and glutamate are difficult to discern due to limitations of push pull perfusion and/or microdialysis. This consideration notwithstanding, our findings in single GnRH neurons suggest that effective prepubertal inhibition by GABA would require either relatively precise coordination of GABAergic input with other forms of excitation, or high frequencies of independent GABAergic input to increase the probability of shunting by chance (Sim et al., 2000).
Integration of glutamate with GABAergic excitation
In immature hypothalamic neurons, GABA is depolarizing (Gao and van den Pol, 2001) and shunts depolarization mediated by glutamate during the peak of the GABA conductance. However, during the decay phase of the GABA depolarization, GABA facilitates glutamate's excitatory actions (Gao et al., 1998). It is important to note that these effects are observed in conditions were glutamate alone could not stimulate action potentials. Thus, the situation is different in mature GnRH neurons where only glutamatergic conductances derived from either application of glutamate agonists (Kuehl-Kovarik et al., 2002 and 2005) or simulated AMPA-type synapses (Suter, 2004) both result in action potentials.
The temporal relationship between AMPA and GABA excitation in both dynamic current clamping and model somata is similar to that reported in immature hypothalamic neurons where glutamatergic inputs did not independently cause firing (Gao et al., 1998). Specifically, action potentials occurred when the maximum of the AMPA conductance was co-incident with the descending phase of a peak in the excitatory GABA conductance. Our results extend these findings and indicate that mature GnRH neurons (when GABA is excitatory) may integrate AMPA- and GABA-type inputs in a fashion that is similar to immature hypothalamic neurons. The most likely mechanism is that the GABA input raises the membrane potential of the cell by charging up the cell capacitance, pre-conditioning the cell to make the AMPA inputs more effective.
Increases in GABAergic excitation have been reported between a variety of physiological conditions (Sullivan and Moentor, 2003; Sullivan et al., 2003; Sullivan and Moenter, 2004a; Sullivan and Moenter, 2004b; Sullivan and Moenter, 2005). Our findings indicate that increases in GABAergic input can modulate firing in GnRH neurons by interacting with other conductances. Thus, reported increases in frequency of GABAergic events in whole cell recordings, coupled with the longer time course of the GABAergic conductance, support the hypothesis that changes in frequency of GABAergic inputs, even in the face of relatively constant AMPA input, could control action potential discharges. In this regard, an earlier study in cortical neurons suggested that GABAergic inputs with a depolarized reversal potential could function as a “sophisticated device” for modulating firing patterns (Morita et al., 2005). Accordingly, GABAergic input in the excitatory mode may be an important component in the control of spiking and thus, a target conductance for physiological modulation of GnRH neuronal firing.
Spatial interactions between GABA and AMPA due to dendritic synapses
Based on the results from our compartmental models, it appears that there is a relatively wide temporal domain in which GABAergic inputs and AMPA-type inputs would interact to cause spiking, particularly when the AMPA inputs are distributed along the dendrite. These AMPA-type inputs have relatively short time courses (Suter, 2004; Kuehl-Kovarik et al., 2005). However, GnRH neurons express post-synaptic receptors for multiple neurotransmitters (Todman et al., 2005). These other excitatory conductances which have longer time courses than AMPA-inputs would create even wider temporal windows for interaction.
A recent study indicated that dendritic spines, the location of excitatory inputs, increase on GnRH somata and proximal dendrites in mice during postnatal development (Cottrell et al., 2006). This increase in dendritic spines encompassed the time interval of sexual maturation (i.e., between postnatal days 10 and 60) which is the time over which the message for the GnRH peptide increases in mice (Gore et al., 1999). Our findings suggest that the increase in GnRH secretion at the time of puberty in mice may reflect not only an increase in total excitation to the GnRH neurons but also a shift in the coordination between pre-synaptic neurons of different phenotypes. If the GABA-A receptor has a hyperpolarized reversal potential in GnRH neurons, simultaneous activation of pre-synaptic GABAergic and glutamatergic neurons would increase GnRH output. Alternatively, if GABA-A receptor has a depolarized reversal potential then maximal spiking would be observed when activation of a GABA input precedes activation of the AMPA input by about 10 ms.
Taken together, our results indicate that intracellular chloride levels (which set the reversal potential for chloride) in the GnRH neuron will determine how GABAergic inputs must interact with glutamatergic inputs in order to maximize action potentials and thus GnRH secretion. Additionally, modulation of GnRH secretion by GABA reflects both the timing and location of presynaptic inputs on GnRH neurons.
Acknowledgments
This work was supported by HD-45436 to KJS. Analysis and modeling facilities provided by the Computational Biology Initiative (http://www.cbi.utsa.edu) at the University of Texas San Antonio and the University of Texas Health Sciences Center at San Antonio which is funded by a partnership between National Institutes of Health (RR013646) and the Vice Chancellor for Medical Affairs of the University of Texas. Preliminary reports of this work were presented at 2005 Society for Neuroscience Meeting (abstracts 126.8 and 126.9).
List of Abbreviations
- GABA
γ-aminobutyric acid
- GnRH
gonadotropin releasing hormone
- AMPA
alpha-amino-3-hydroxy-5-methyl-4-isoxazole propionic acid
- CNQX
6-Cyano-7-nitroquinoxaline-2,3-dione
- NMDA
N-methyl-D-aspartic acid
- AP-5
D(-)-2-Amino-5-phosphonopentanoic acid
- PSC
post-synaptic current
- PSP
post-synaptic potential
- FWHM
Full Width at Half Maximum
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Carson B. Roberts, Department of Biology, University of Texas at San Antonio, 1 UTSA Circle, San Antonio TX, 78249 Department of Electrical and Computer Engineering, Boston University 8 Saint Mary's Street. Boston, MA 02215.
Peter Hemond, Department of Biology, University of Texas at San Antonio, 1 UTSA Circle, San Antonio TX, 78249.
Kelly J. Suter, Department of Biology, University of Texas at San Antonio, 1 UTSA Circle, San Antonio TX, 78249
References
- Carter AG, Regehr WG. Quantal events shape cerebellar interneuron firing. Nat Neurosci. 2002;5:1309–1318. doi: 10.1038/nn970. [DOI] [PubMed] [Google Scholar]
- Chavas J, Marty A. Coexistence of excitatory and inhibitory GABA synapses in the cerebellar interneuron network. J Neurosci. 2003;23:2019–31. doi: 10.1523/JNEUROSCI.23-06-02019.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cottrell EC, Campbell RE, Han SK, Herbison AE. Postnatal remodeling of dendritic structure and spine density in gonadotropin-releasing hormone neurons. Endocrinology. 2006;147:3652–3661. doi: 10.1210/en.2006-0296. [DOI] [PubMed] [Google Scholar]
- Cupello A. Neuronal transmembrane chloride electrochemical gradient: a key player in GABA A receptor activation physiological effect. Amino Acids. 2003;24:335–46. doi: 10.1007/s00726-002-0350-4. [DOI] [PubMed] [Google Scholar]
- Decavel C, van den Pol AN. GABA: a dominant neurotransmitter in the hypothalamus. J Comp Neurol. 1990;302:1019–1037. doi: 10.1002/cne.903020423. [DOI] [PubMed] [Google Scholar]
- DeFazio RA, Heger S, Ojeda SR, Moenter SM. Activation of A-type gamma-aminobutyric acid receptors excites gonadotropin-releasing hormone neurons. Mol Endocrinology. 2002;16:2872–2891. doi: 10.1210/me.2002-0163. [DOI] [PubMed] [Google Scholar]
- DeFazio RA, Moenter SM. Endogenous gamma-aminobutyric acid can excite gonadotropin-releasing hormone neurons. Endocrinology. 2005;146:5374–5379. doi: 10.1210/en.2005-0788. [DOI] [PubMed] [Google Scholar]
- De Jeu M, Pennartz C. Circadian modulation of GABA function in the rat suprachiasmatic nucleus: excitatory effects during the night phase. J Neurophysiol. 2002;87:834–844. doi: 10.1152/jn.00241.2001. [DOI] [PubMed] [Google Scholar]
- Galanopoulou AS, Moshé SL. Role of sex hormones in the sexually dimorphic expression of KCC2 in rat substantia nigra. Exp Neurol. 2003;184:1003–1009. doi: 10.1016/S0014-4886(03)00387-X. [DOI] [PubMed] [Google Scholar]
- Gao XB, Chen G, van den Pol AN. GABA-dependent firing of glutamate-evoked action potentials at AMPA/kainite receptors in developing hypothalamic neurons. J Neurophysiol. 1998;79:716–726. doi: 10.1152/jn.1998.79.2.716. [DOI] [PubMed] [Google Scholar]
- Gao XB, van den Pol AN. GABA, not glutamate, is a primary transmitter driving action potentials in developing hypothalamic neurons. J Neurophysiol. 2001;85:425–434. doi: 10.1152/jn.2001.85.1.425. [DOI] [PubMed] [Google Scholar]
- Gore AC, Roberts JL, Gibson MJ. Mechanisms for the regulation of gonadotropin-releasing hormone gene expression in the developing mouse. 1999;140:2280–2287. doi: 10.1210/endo.140.5.6711. [DOI] [PubMed] [Google Scholar]
- Goroll D, Arias P, Wuttke W. Preoptic release of amino acid neurotransmitters evaluated in peripubertal and young adult female rats by push-pull perfusion. Neuroendocrinology. 1993;58:11–15. doi: 10.1159/000126506. [DOI] [PubMed] [Google Scholar]
- Gulledge AT, Stuart GJ. Excitatory actions of GABA in the cortex. Neuron. 2003;37:299–309. doi: 10.1016/s0896-6273(02)01146-7. [DOI] [PubMed] [Google Scholar]
- Gulledge AT, Kampa BM, Stuart GJ. Synaptic integration in dendritic trees. J Neurobiol. 2005;64:75–90. doi: 10.1002/neu.20144. Review. Erratum in: J Neurobiol. 65:205-206. [DOI] [PubMed] [Google Scholar]
- Han SK, Abraham IM, Herbison AE. Effect of GABA on GnRH neurons switches from depolarization to hyperpolarization at puberty in the female mouse. Endocrinology. 2002;143:1459–1466. doi: 10.1210/endo.143.4.8724. [DOI] [PubMed] [Google Scholar]
- Han SK, Todman MG, Herbison AE. Endogenous GABA inhibits the firing of adult GnRH neurons. Endocrinology. 2004;145:495–499. doi: 10.1210/en.2003-1333. [DOI] [PubMed] [Google Scholar]
- Herbison AE. Physiology of the GnRH neuronal network. In: Neill JD, editor. Knobil and Neill's Physiology of Reproduction. San Diego, CA: Academic Press; 2006. pp. 1415–1482. [Google Scholar]
- Keen KL, Burich AJ, Mitsushima D, Kasuya E, Terasawa E. Effects of pulsatile infusion of the GABA(A) receptor blocker bicuculline on the onset of puberty in female rhesus monkeys. Endocrinology. 1999;140:5257–5266. doi: 10.1210/endo.140.11.7139. [DOI] [PubMed] [Google Scholar]
- Kuehl-Kovarik MC, Pouliot WA, Halterman GL, Handa RJ, Dudek FE, Partin KM. Episodic bursting activity and response to excitatory amino acids in acutely dissociated gonadotropin-releasing hormone neurons genetically targeted with green fluorescent protein. J Neurosci. 2002;22:2313–2322. doi: 10.1523/JNEUROSCI.22-06-02313.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuehl-Kovarik MC, Partin KM, Handa RJ, Dudek FE. Spike-dependent depolarizing afterpotentials contribute to endogenous bursting in gonadotropin releasing hormone neurons. Neuroscience. 2005;134:295–300. doi: 10.1016/j.neuroscience.2005.03.047. [DOI] [PubMed] [Google Scholar]
- Kusano K, Fueshko S, Gainer H, Wray S. Electrical and synaptic properties of embryonic luteinizing hormone-releasing hormone neurons in explant cultures. Proc Natl Acad Sci USA. 1995;92:3918–3922. doi: 10.1073/pnas.92.9.3918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeBeau AP, Van Goor F, Stojilkovic SS, Sherman A. Modeling of membrane excitability in gonadotropin-releasing hormone-secreting hypothalamic neurons regulated by Ca2+-mobilizing and adenylyl cyclase-coupled receptors. J Neurosci. 2000;20:9290–9297. doi: 10.1523/JNEUROSCI.20-24-09290.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez FJ, Merchenthaler IJ, Moretto M, Negro-Vilar A. Modulating mechanisms of neuroendocrine cell activity--the LHRH pulse generator. Cell Mol Neurobiol. 1998;18:125–146. doi: 10.1023/A:1022531411717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leupen SM, Tobet SA, Crowley WF, Jr, Kaila K. Heterogeneous expression of the potassium-chloride cotransporter KCC2 in gonadotropin-releasing hormone neurons of the adult mouse. Endocrinology. 2003;144:3031–3036. doi: 10.1210/en.2002-220995. [DOI] [PubMed] [Google Scholar]
- Luther JA, Daftary SS, Boudaba C, Gould GC, Halmos KC, Tasker JG. Neurosecretory and non-neurosecretory parvocellular neurones of the hypothalamic paraventricular nucleus express distinct electrophysiological properties. J Neuroendocrinol. 2002;14:929–932. doi: 10.1046/j.1365-2826.2002.00867.x. [DOI] [PubMed] [Google Scholar]
- Mellon PL, Windle JJ, Goldsmith PC, Padula CA, Roberts JL, Weiner RL. Immortalization of hypothalamic GnRH neurons by genetically targeted tumorigenesis. Neuron. 1990;5:1–10. doi: 10.1016/0896-6273(90)90028-e. [DOI] [PubMed] [Google Scholar]
- Moenter SM, DeFazio RA. Endogenous gamma-aminobutyric acid can excite gonadotropin-releasing hormone neurons. Endocrinology. 2005;146:5374–5379. doi: 10.1210/en.2005-0788. [DOI] [PubMed] [Google Scholar]
- Morita K, Tsumoto K, Aihara K. Possible effects of depolarizing GABA-A conductance on the neuronal input-output relationship: a modeling study. J Neurophysiol. 2005;93:3504–3523. doi: 10.1152/jn.00988.2004. [DOI] [PubMed] [Google Scholar]
- Pohl CR, Richardson DW, Hutchison JS, Germak JA, Knobil E. Hypophysiotropic signal frequency and the functioning of the pituitary-ovarian system in the rhesus monkey. Endocrinology. 1983;112:2076–2080. doi: 10.1210/endo-112-6-2076. [DOI] [PubMed] [Google Scholar]
- Roberts CB, Best JA, Suter KJ. Dendritic processing of excitatory synaptic input in hypothalamic gonadotropin releasing-hormone (GnRH) neurons. Endocrinology. 2006;147:1545–1555. doi: 10.1210/en.2005-1350. [DOI] [PubMed] [Google Scholar]
- Sharp AA, O'Neil MB, Abbott LF, Marder E. Dynamic clamp: computer-generated conductances in real neurons. J Neurophysiol. 1993;69:992–995. doi: 10.1152/jn.1993.69.3.992. [DOI] [PubMed] [Google Scholar]
- Sim JA, Skynner MJ, Herbison AE. Heterogeneity in the basic membrane properties of postnatal gonadotropin-releasing hormone neurons in the mouse. J Neurosci. 2001;21:1067–1075. doi: 10.1523/JNEUROSCI.21-03-01067.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sim JA, Skynner MJ, Pape JR, Herbison AE. Late postnatal reorganization of GABA(A) receptor signalling in native GnRH neurons. Eur J Neurosci. 2000;12:3497–3504. doi: 10.1046/j.1460-9568.2000.00261.x. [DOI] [PubMed] [Google Scholar]
- Spergel DJ, Krueth U, Hanley DF, Sprengel R, Seeburg PH. GABA- and glutamate-activated channels in green fluorescent protein-tagged gonadotropin-releasing hormone neurons in transgenic mice. J Neurosci. 1999;19:2037–2050. doi: 10.1523/JNEUROSCI.19-06-02037.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spergel DJ, Kruth U, Shimshek DR, Sprengel R, Seeburg PH. Using reporter genes to label selected neuronal populations in transgenic mice for gene promoter, anatomical, and physiological studies. Prog Neurobiol. 2001;63:673–86. doi: 10.1016/s0301-0082(00)00038-1. [DOI] [PubMed] [Google Scholar]
- Spergel DJ. Calcium and small-conductance calcium-activated potassium channels in gonadotropin-releasing hormone neurons before, during, and after puberty. Endocrinology. 2007;148:2383–2390. doi: 10.1210/en.2006-1693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan SD, DeFazio RA, Moenter SM. Metabolic regulation of fertility through presynaptic and postsynaptic signaling to gonadotropin-releasing hormone neurons. J Neurosci. 2003;23:8578–8585. doi: 10.1523/JNEUROSCI.23-24-08578.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan SD, Moenter SM. Neurosteroids alter ã-aminobutyric acid postsynaptic currents in GnRH neurons: a possible mechanism for direct steroidal control. Endocrinology. 2003;144:4366–4375. doi: 10.1210/en.2003-0634. [DOI] [PubMed] [Google Scholar]
- Sullivan SD, Moenter SM. GABAergic neurons integrate and rapidly transmit permissive and inhibitory metabolic cues to GnRH neurons. Endocrinology. 2004a;145:1194–1202. doi: 10.1210/en.2003-1374. [DOI] [PubMed] [Google Scholar]
- Sullivan SD, Moenter SM. Prenatal androgenization reprograms GABAergic drive to gonadotropin-releasing hormone neurons and has a negative impact on reproduction. Proc Natl Acad Sci USA. 2004b;101:7129–7134. doi: 10.1073/pnas.0308058101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan SD, Moenter SM. GABAergic Integration of Progesterone and Androgen Feedback to Gonadotropin-Releasing Hormone Neurons. Biol Reprod. 2005;72:33–41. doi: 10.1095/biolreprod.104.033126. [DOI] [PubMed] [Google Scholar]
- Suter KJ. Control of firing by small (S)-alpha-amino-3-hydroxy-5-methyl-isoxazolepropionic acid-like inputs in hypothalamic gonadotropin releasing-hormone (GnRH) neurons. Neuroscience. 2004;128:443–450. doi: 10.1016/j.neuroscience.2004.06.044. [DOI] [PubMed] [Google Scholar]
- Todman MG, Han SK, Herbison AE. Profiling neurotransmitter receptor expression in mouse gonadotropin-releasing hormone neurons using green fluorescent protein-promoter transgenics and microarrays. Neuroscience. 2005;132:703–712. doi: 10.1016/j.neuroscience.2005.01.035. [DOI] [PubMed] [Google Scholar]
- van den Pol AN, Wuarin JP, Dudek FE. Glutamate, the dominant excitatory transmitter in neuroendocrine regulation. Science. 1990;30(250):1276–1278. doi: 10.1126/science.1978759. [DOI] [PubMed] [Google Scholar]
- Wagner EJ, Rønnekleiv OK, Grandy DK, Kelly MJ. The Peptide Orphanin FQ Inhibits β-Endorphin Neurons and Neurosecretory Cells in the Hypothalamic Arcuate Nucleus by Activating an Inwardly-Rectifying K+ Conductance. Neuroendocrinology. 1998;67:73–82. doi: 10.1159/000054301. [DOI] [PubMed] [Google Scholar]
- Wintermantel TM, Campell RE, Porteous R, Bock D, Grone HJ, Todman MG, Korach K, Greiner E, Perez CA, Schutz G, Herbison AE. Definition of estrogen receptor pathway critical for estrogen positive feedback to gonadotropin releasing hormone neurons and fertility. Neuron. 2006;52:271–280. doi: 10.1016/j.neuron.2006.07.023. [DOI] [PMC free article] [PubMed] [Google Scholar]