Evaluation of Face Datasets as Tools for Assessing the Performance of Face Recognition Methods

Abstract

Face datasets are considered a primary tool for evaluating the efficacy of face recognition methods. Here we show that in many of the commonly used face datasets, face images can be recognized accurately at a rate significantly higher than random even when no face, hair or clothes features appear in the image. The experiments were done by cutting a small background area from each face image, so that each face dataset provided a new image dataset which included only seemingly blank images. Then, an image classification method was used in order to check the classification accuracy. Experimental results show that the classification accuracy ranged between 13.5% (color FERET) to 99% (YaleB). These results indicate that the performance of face recognition methods measured using face image datasets may be biased. Compilable source code used for this experiment is freely available for download via the internet.

1 Introduction

In the past two decades face recognition has been attracting considerable attention, and has become one of the most prominent areas in computer vision, leading to the development of numerous face recognition algorithms (Zao et al., 2003; Gross et al., 2004; Kong et al., 2005).

The primary method of assessing the efficacy of face recognition algorithms and comparing the performance of the different methods is by using pre-defined and publicly available face datasets such as FERET (Phillips et al., 1998, 2000), ORL (Samaria & Harter, 1994), JAFFE (Lynos et al., 1998), the Indian Face Dataset (Jain & Mukherjee, 2002), Yale B (Georghiades, Belhumeur, & Kriegman, 2001), and Essex face dataset (Hond & Spacek, 1997).

While the human recognition is based on what the human eye can sense, the numeric nature of the way images are handled by machines make them much more sensitive to features that are sometimes invisible to the unaided eye, such as small changes in illumination conditions, size, position, focus, etc. This can be evident by the observation of Pinto, Cox & DiCarlo (2008), who studied the widely used Caltech 101 image dataset (Fei-Fei, Fergus & Perona, 2006), and showed that an oversimplified method that is not based on object descriptive content can outperform state-of-the-art object recognition algorithms. Their study demonstrates that the design of Caltech 101 is flawed, and do not provide an accurate reflection of the problem of real-life object recognition.

Chen et al. (2001) proposed a statistics-based proof to quantiatively show that the measured performance of face recognition methods can be significantly biased if non-facial areas of the images (e.g., hair, background, etc) are used. Here we suggest that the different classes in many of the common face datasets can be discriminated based on image features that are not related to facial content, and are actually artifacts of the image acquisition process. Therefore, even if only face areas of the image are used as proposed by Chen et al. (2001), the performance figures do not always accurately reflect the actual effectiveness of the algorithm.

2 Classification Method

In order to find discriminative image features, we apply a first step of computing a large number of different image features, from which the most informative features are then selected. For image feature extraction we use the following algorithms, described more throughly in (Orlov el al., 2007):

1. Radon transform features (Lim, 1990), computed for angles 0, 45, 90, 135 degrees, and each of the resulting series is then convolved into a 3-bin histogram, providing a toal of 12 image features.

2. Chebyshev Statistics (Gradshtein & Ryzhik, 1994) - A 32-bin histogram of a 1×400 vector produced by Chebyshev transform of the image with order of N=20.

3. Gabor Filters (Gabor, 1946), where the kernel is in the form of a convolution with a Gaussian harmonic function (Gregorescu, Petkov & Kruizinga, 2002), and 7 different frequencies are used (1,2…,7), providing 7 image descriptor values.

4. Multi-scale Histograms computed using various number of bins (3, 5, 7, and 9), as proposed by Hadjidementriou, Grossberg & Nayar (2001), providing 3+5+7+9=24 image descriptors.

5. First 4 Moments, of mean, standard deviation, skewness, and kurtosis computed on image ”stripes” in four different directions (0, 45, 90, 135 degrees). Each set of stripes is then sampled into a 3-bin histogram, providing 4×4×3=48 image descriptors.

6. Tamura texture features (Tamura, Mori & Yamavaki, 1978) of contrast, directionality and coarseness, such that the coarseness descriptors are its sum and its 3-bin histogram, providing 1+1+1+3=6 image descriptors.

7. Edge Statistics features computed on the Prewitt gradient (Prewitt, 1970), and include the mean, median, variance, and 8-bin histogram of both the magnitude and the direction components. Other edge features are the total number of edge pixels (normalized to the size of the image), the direction homogeneity (Murphy et al., 2001), and the difference amongst direction histogram bins at a certain angle α and α + π, sampled into a four-bin histogram.

8. Object Statistics computed on all 8-connected objects found in the Otsu binary mask of the image (Otsu, 1979). Computed statistics include the Euler Number (Gray, 1971), and the minimum, maximum, mean, median, variance, and a 10-bin histogram of both the objects areas and distances from the objects to the image centroid.

9. Zernike features (Teague, 1979) are the absolute values of the coefficients of the Zernike polynomial approximation of the image, as described in (Murphy et al., 2001), providing 72 image descriptors.

10. Haralick features (Haralick, Shanmugam & Dinstein, 1973) computed on the image's co-occurrence matrix as described in (Murphy et al., 2001), and contribute 28 image descriptor values.

11. Chebyshev-Fourier features (Orlov el al., 2007) - 32-bin histogram of the polynomial coefficients of a Chebyshev–Fourier transform with highest polynomial order of N=23.

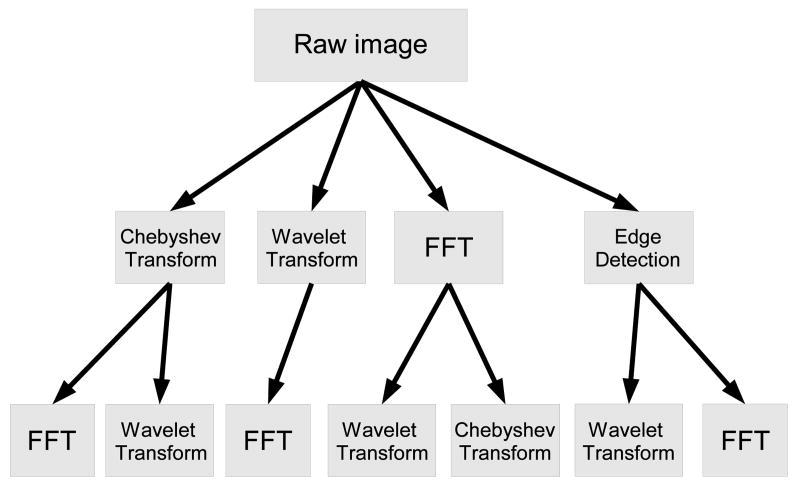
Since image features extracted from transforms of the raw pixels are also informative (Rodenacker & Bengtsson, 2003; Gurevich & Koryabkina, 2006; Orlov et al., 2008), image content descriptors in this experiment are extracted not only from the raw pixels, but also from several transforms of the image and transforms of transforms. The image transforms are FFT, Wavelet (Symlet 5, level 1) two-dimensional decomposition of the image, and Chebyshev transform. Another transform that was used is Edge Transform, which is simply the magnitude component of the image's Prewitt gradient, binarized by Otsu global threshold (Otsu, 1979).

In the described image classification method, different image features are extracted from different image transforms or compound transforms. The image features that are extracted from all transforms are the statistics and texture features, which include the first 4 moments, Haralick textures, multiscale histograms, Tamura textures, and Radon features. Polynomial decomposition features, which include Zernike features, Chebyshev statistics, and Chebyshev-Fourier polynomial coefficients, are also extracted from all transforms, except from the Fourier and Wavelet transforms of the Chebyshev transform, and the Wavelet and Chebyshev transforms of the Fourier transform. In addition, high contrast features (edge statistics, object statistics, and Gabor filters) are extracted from the raw pixels. The entire set of image features extracted from all image transforms is described in Figure 1, and consists of a total of 2633 numeric image content descriptors.

Figure 1.

Image transforms and paths of the compound image transforms.

While this set of image features provides a numeric description of the image content, not all image features are assumed to be equally informative, and some of these features are expected to represent noise. In order to select the most informative features while rejecting noisy features, each image feature is assigned with a simple Fisher score (Bishop, 2006). The feature vectors can then be classified by a weighted nearest neighbor rule, such that the feature weights are the Fisher scores.

Full source code is available for free download as part of OME software suite (Swedlow et al., 2003; Goldberg et al., 2005) at www.openmicroscopy.org, or as a “tarball” at http://www.phy.mtu.edu/∼lshamir/downloads/ImageClassifier.

3 Experimental Results

The non-facial discriminativeness between the subjects in each dataset was tested by cutting a small area from each image, such that the new sub-image did not contain face or hair. Then, the classification method briefly described in Section 2 was applied, and the classification accuracy of each dataset was recorded. The face datasets that were tested are FERET (Phillips et al., 1998, 2000), ORL (Samaria & Harter, 1994), JAFFE (Lynos et al., 1998), the Indian Face Dataset (Jain & Mukherjee, 2002), Yale B (Georghiades, Belhumeur, & Kriegman, 2001), and Essex face dataset (Hond & Spacek, 1997; Spacek, 2002). The sizes and locations of the non-facial areas that were cut from the original images is described in Table 1, and the accuracy of automatic classification of these images are also specified in the table.

Table 1.

Classification accuracy of the face datasets using a small non-facial area

Dataset	Subjects	Images per subject	Original image size	Non-facial area	Random accuracy	Non-facial accuracy
ORL	40	10	92×112	20×20 (bottom right)	0.025	0.788
JAFFE	10	22	256×256	25×200 (top left)	0.1	0.94
Indian Face	22	11	160×120	42×80 (top left)	0.045	0.73
Dataset (Females)
Indian Face	39	11	160×120	42×80 (top left)	0.0256	0.58
Dataset (Males)
Essex	100	20	196×196	42×100 (top left)	0.01	0.97
Yale B	10	576	640×480	100×300 (top left)	0.1	0.99
Color FERET	994	5	512×768	100×100 (top left)	∼0.001	0.135

For all datasets, 80% of the images of each subject were used for training while the remaining 20% were used for testing, and in all experiments the number of subjects in the training set was equal to the number of subjects in the test set. The classification accuracy results reported in the table are the average accuracies of 50 runs, such that each run used a random split of the data to training and test sets.

As can be learned from the table, face images in the ORL dataset can be classified in accuracy of ∼79% by using just the 20×20 pixels at the bottom right corner of each image. While this area in all images of the ORL dataset did not contain any part of the face, in most cases it contained small part of the clothes, which may be informative enough to discriminate between the 40 classes with considerable accuracy.

JAFFE dataset was classified in a fairly high accuracy of 94%. While in the ORL dataset the sub-images used for classification contained some clothes, in the case of JAFFE only blank background was included in the areas that were cut from the original images. These results show that the images in the JAFFE dataset can be discriminated based on features that are not easily noticeable to the human eye, and are not linked in any way to the face that appears in the image. Therefore, when the performance of a proposed face recognition method is evaluated using the JAFFE dataset, it is not always clear whether accurate recognition of the faces can be attributed to features that are based on actual face content, or to artifacts that can discriminate between seemingly blank areas.

This observation also applies to both the female and male Indian Face Datasets, where the sub-images that were used for classification are visually blank rectangles, but can practically be discriminated with accuracy substantially higher than random.

Essex face dataset includes a relatively large number of 100 individuals, but introduces a high classification accuracy of 97% when using the non-facial areas of the 42×100 top left pixels of each image. However, in the case of Essex the high classification accuracy is not surprising, since it was designed for the purpose of normalizing the faces and discriminating them from the image background (Hond & Spacek, 1997), and therefore the image backgrounds are intentionally different for each subject. This intentional background variance makes it possible to discriminate between the subjects using non-facial areas of the images. In that sense, Essex is different from other datasets such as JAFFE and the Indian face dataset, in which the background is visually consistent among images.

In the case of Yale B dataset the background is also not blank, and many recognizable objects can be seen behind the face featured in the image. However, it seems that all images were taken with the same background, so that the background is consistent among the different subjects. Despite this consistency, the 10 subjects in the dataset can be recognized in a nearly perfect accuracy of 99%, using a 100×300 pixels at the top left corner of each image.

Experiments using the widely used color FERET dataset were based on the fa, fb, hr, hl, pr, pl images. Since not all poses are present for all subjects, only five images were used for each subject such that one image was randomly selected for testing and four images of each subject were used for training. From each face image in the dataset, a 100×100 area at the top left corner was cut from the image so that the training data set of each subject was four 100×100 images, and the test set was one 100×100 image. The non-facial areas of the first 10 individuals of the color FERET dataset is shown by Figure 2.

Figure 2.

Top left 100×100 pixels of the first 10 individuals in the color FERET dataset. The IDs of the subjects are listed right to the images

As can be seen in the figure, the differences between the 100×100 non-facial areas of subjects 0002 and 0003 are fairly noticable, while other subjects such as 0001, 0002, 0004, 0005, and 0006 look very similar to the unaided eye. Using the image classification method briefly described in Section 2, 50 random splits of this 10-class subset of FERET to training and test datasets provided average classification accuracy of ∼61%, which is significantly higher than the expected random accuracy of 10%.

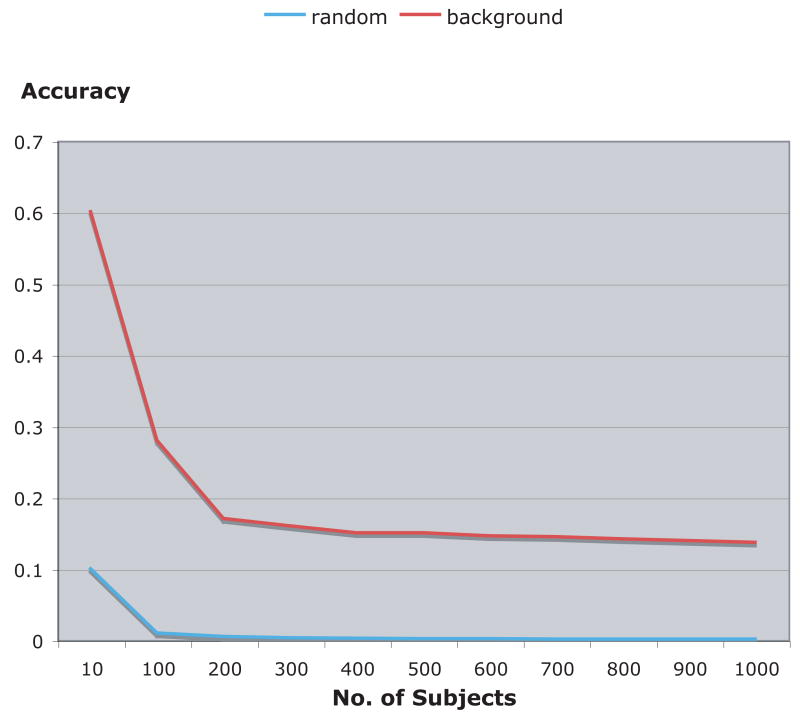
The recognition accuracy usually decreases as the number of classes gets larger. Figure 3 shows how the classification accuracy changes when more subjects are added to the face dataset, such that the number of subjects in the test set is always equal to the number of subjects in the training set, and each subject has one probe image and four gallery images.

Figure 3.

Classification accuracy of color FERET using non-facial background areas of the images (100×100 top left pixels) comparing to the expected random recognition.

As the graph shows, the recognition of the subjects using 100×100 non-facial pixels at the top left corner of each image is significantly more accurate than random recognition. While the recognition decreases as the number of subjects in the dataset gets larger, it is consistently well above random accuracy.

4 Discussion

Datasets of face images are widely common tools of assessing the performance of face recognition methods. However, when testing machine vision algorithms that are based on actual visible content, non-contentual differences between the images may be considered undesirable. Here we studied the discriminativeness between the classes in some of these datasets, and showed that the different subjects can be recognized in accuracy significantly higher than random based on small parts of the images that do not contain face or hair. In some of the described cases, the images were classified based on seemingly blank background areas.

Since the images can be discriminated based on their seemingly blank parts, it is not always clear whether highly accurate recognition figures provided by new and existing face recognition methods can be attributed to the recognition of actual face content, or to artifacts that can discriminate between seemingly blank areas.

This problem in performance evaluation can be addressed by introducing new publicly available face datasets that aim to minimize the discriminativeness of the non-facial features. This can be potentially improved, for instance, by using face datasets in which each of the face images was acquired on a different day.

In order to verify that only face features are used, face images can have a blank background area of approximately the same size of the area of the image covered by the face. Newly proposed methods can then attempt to discriminate between the subjects based on the blank areas of the images, and compare the resulting classification accuracy to the recognition accuracy of the face areas. If the classification accuracy based on the blank parts of the images is relatively close to the recognition accuracy of the face areas, it can imply that some of the face images are possibly classified based on non-facial features. In this case, the actual accuracy of the face recognition method can be deduced by the equation

$$P=C-(B-\frac{1}{N}),$$ (1)

where that P is the actual accuracy of the proposed method, C is the recognition accuracy of the face areas of the images, B is the classification accuracy when using the non-facial background of the images, and N is the number of subjects in the dataset. This approach subtracts higher-than-random non-facial recognition of the images from the face recognition accuracy, so that only face images that cannot be recognized by non-facial areas are considered accurate classification.

Full source code used for the experiments described in this paper is available for free download as part of OME software suite at www.openmicroscopy.org (recommended), or as a “tarball” at http://www.phy.mtu.edu/∼lshamir/downloads/ImageClassifier.